Novel NIR modeling design and assignment in process quality control of Honeysuckle flower by QbD

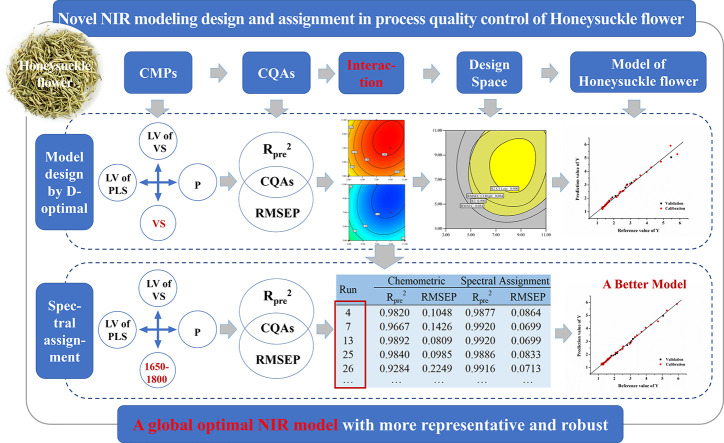
Abstract

Honeysuckle flower is a common edible-medicinal food with significant anti-inflammatory efficacy. Process quality control of its ethanol precipitation is a topical issue in the pharmaceutical field. Near infrared (NIR) spectroscopy is commonly used for process quality analysis. However, establishing a robust and reliable quantitative model of complex process remains a challenge in industrial applications of NIR. In this paper, modeling design based on quality by design concept (QbD) was implemented for the ethanol precipitation process quality control of Honeysuckle flower. According to the 56 models' performances and 25 contour plots, quadratic model was the best with R_adj² increasing from 0.1395 to 0.9085, indicating the strong interaction among spectral pre-processing methods, variable selection methods, and latent factors. SG9 and CARS was an appropriate combination for modeling. Furthermore, spectral assignment method was creatively introduced for variable selection. Another 56 models' performances and 25 contour plots were established. Compared with the chemometric variable selection method, spectral assignment combined with QbD concept made a higher R_pre² and a lower RMSEP. When the latent factors of PLS was small, R_pre² of the model by spectral assignment increased from 0.9605 to 0.9916 and RMSEP decreased from 0.1555 mg/mL to 0.07134 mg/mL. This result suggests that the variable selected by spectral assignment is more representative and precise. This provided a novel modeling guideline for process quality control in PAT.

Graphical abstract

Highlights

• •Quality by Design concept was conducted for NIR model design.
• •Strong synergic interactions among model parameters were discovered by QbD.
• •Spectral assignment was used to select variable instead of chemometric method.
• •A more robust model was established by spectral assignment combined with D-optimal.

1. Introduction

Honeysuckle flower is a common edible-medicinal food with significant anti-inflammatory efficacy [1]. It not only has a specific efficacy of detoxification, but also could be used as a heat-clearing drink. It has even been developed into products, such as Chinese famous tea drink Wang Laoji, Jiaduobao, as well as the distilled liquid of Honeysuckle flower. The annual sales of Honeysuckle flower productions are among the best in China. For example, Jiaduobao's operating income in 2016 was 24 billion yuan, ranking first in the Chinese herbal tea industry with a market share of 52.6%. In Japan, the Kobayashi's Qingfei Soup is an edible-medicinal prescription containing Honeysuckle flower.

Ethanol precipitation is a characteristic and significant process of Honeysuckle flower production, which calls for a precise quality control method. Off-line quality control methods have hysteresis leading to an insecure and unpredictable production quality [2]. To solve this issue, process analytical technology (PAT) based on chemometrics is proposed to quality control, which is especially applicable in case of complex processes [3]. Currently, NIR spectroscopy is the most commonly used PAT process analyser in pharmaceutical technology because of non-destructive measurements and real-time monitoring in process [4,5]. It is especially suitable for a complex production, which needs process quality control [6,7].

Wu et al. used NIR spectroscopy to monitor the concentration distribution of amino acids in the hydrolysis of Cornu Bubali [2]. Xu et al. proposed a multi-phase and multivariate statistical process control strategy for alcohol precipitation of Honeysuckle flower. [8]. Laub-Ekgreen et al. applied NIR spectroscopy to rapid and non-destructive salt concentration monitoring in the pickling process of squid [9]. Oxidative damage of pork myofibrils during frozen storage has been monitored by the NIR hyperspectral imaging [10].

In the application of NIR to process quality control, there is an essential factor, quantitative model. To establish an accurate NIR model, the most important part is the optimization of the critical modeling parameters (CMPs). One CMP in NIR modeling is the spectral preprocessing because of some interfering information [11]. Pizarro et al. and Christensen et al. both demonstrated the performance of quantitative NIR models established by different pre-processing methods were diverse [12,13]. Variable selection [14] is another CMP to extract useful information for modeling. Bi et al. proved that, compared with the full spectra, the NIR model established by optimal spectra achieved better performance [15]. Yuan et al. indicated that the discriminant models were improved and simplified significantly by variable selection [16]. In addition, a suitable latent factor is also a CMP to avoid over-fitting and under-fitting for modeling [17].

In classical modeling, the CMPs were optimized step-by-step. Genetic algorithm is a commonly used method to optimize the spectral pre-processing method or variable selection method [18]. Rosas et al. compared three spectral pre-processing methods for NIR process optimization of a multicomponent formulation [19]. Wu et al. used a novel method to optimize the model performance of Partial least square (PLS), interval PLS (iPLS), backward interval PLS (BiPLS) and moving window PLS (MWPLS), and point out that with different evaluation indicator, the optimal method is diverse [20]. Pan et al. found that BiPLS was the appropriate variable selection method for establishing the particle size model rather than synergy iPLS (SiPLS) [21].

Nevertheless, the established models optimized step-by-step ignored the interaction among modeling parameters and were not the best in overall situation. An integrated approach was introduced to optimize several modeling parameters simultaneously based on genetic algorithm [22,23]. Similarly, a systematic modeling method was put up by using a processing trajectory to select modeling parameters [[24], [25], [26]]. Although more valid than before, this method still needs to establish a lot of models laboriously and could not demonstrate the interaction among the parameters. Hence, modeling design is necessarily applied here to simplify the process and establish an overall optimal model.

To implement modeling design, Quality by Design (QbD) concept is a good choice [27], which was introduced in chemical manufacturing control in 2004. In the ICH Q8 guideline, QbD is defined as a systematic approach to development that begins with predefined objectives and emphasizes product and process understanding, as well as process control, based on sound science and quality risk management [28]. It was often used to optimize process parameters in pharmaceutical industry [29]. Liu et al. used it to the quality control of Angong Niuhuang Wan by Laser-Induced Breakdown Spectroscopy [30]. Dai et al. applied it to the development of a novel RP-HPLC analytical method for Huanglian [31]. Similarly, it could also be applied to optimize NIR CMPs by a design of modeling evaluation procedures.

However, the chemometrics variable selection could not discern special components in samples directly. Lee et al. argued that the different variable selection methods performed wide variability in their capabilities to identify the consistent subset of variables [32]. Du et al. also demonstrated that different chemometrics selection methods led to distinct characteristic wavelengths and bands [33]. NIR spectral assignment based on the interrelation between spectra and structure is efficacious to improve model performance and interpretation [34,35]. Chlorogenic acid is the main medicinal component of honeysuckle [36,37]. It is also used as the quality control component of honeysuckle in Chinese Pharmacopeia. Many researches proved that it played an important role in the treatment of SARS virus in 2003 and novel coronavirus pneumonia in 2019.

Therefore, a design of NIR modeling evaluation procedures was implemented by D-optimal design method according to QbD concept. Furthermore, getting the characteristic band of chlorogenic acid [38], the special component of Honeysuckle flower, by spectral assignment, this paper creatively combined this characteristic band with modeling CMPs designed by D-optimal to establish a more precise and reliable model. These also provided a reference method for modeling design and the establishment of global optimal models in PAT of edible-medicinal food.

2. Materials and methods

2.1. On-line NIR spectra acquisition and HPLC analysis in ethanol precipitation process of Honeysuckle flower

Honeysuckle flower was purchased from Ben Cao Fang Yuan Medicine Co. LTD. (Beijing, China). Its authenticity was determined by Professor Chunsheng Liu of Beijing University of Chinese Medicine. Chlorogenic acid reference standard (lot number: 110777-201005) was supplied by the National Institutes for Food and Drug Control (Beijing, China). HPLC grade acetonitrile was purchased from Tedia (USA). Deionized water was purified by Milli-Q water system (Millipore Corp., Bedford, MA, USA).

The ethanol precipitation process of Honeysuckle flower was implemented according to a specific production process parameters of a certain enterprise, which was performed in a 3 L glass reactor using an agitator at constant speed of 500 rpm. Ethanol was pumped into the reactor from the ethanol tank with a flow rate of 75 mL/min. Samples were collected during the alcohol precipitation process at 5 min intervals. 60 samples were collected in this research. Sample of 1.5 mL was drawn by a pipette gun each time. The NIR spectrum was recorded immediately after the sample collection had been completed, which was to ensure that the collected spectrum was consistent with the obtained sample. The on-line NIR spectra of this alcohol precipitation were collected by the transmission way for 16 times of each sample, setting resolving power as 2500 μm and scanning range as 1.0 μm - 2.5 μm.

Quantitative determination by high performance liquid chromatography (HPLC) of chlorogenic acid in Honeysuckle flower was implemented immediately after online NIR sensor measurement. A Waters 2695 HPLC system was used with an auto-sampler, a column temperature controller, and a diode-array detector (DAD) (SHIMADZU Corporation, Japan). Samples were separated on a Diamonsil C18 column (250 mm × 4.6 mm; 5 μm particles; Dikma) using acetonitrile and water containing 0.4% phosphoric acid (13: 87, v/v) as the mobile phase. The separation parameters have been set, column temperature as 30 °C; detection wavelength as 327 nm; flow rate as 1.0 mL/min; sample size as 10 μL.

2.2. The parameters of D-optimal design for modeling design

The spectral pre-processing methods, variable selection methods, latent factors of variable selection, and latent factors of PLS model were determined as the CMPs of for D-optimal design. Spectral pre-processing method was taken as a categorical variable, including raw, standard normal variate (SNV), Savitzky-Golay smoothing with 9 points (SG9), SG9 combined with first derivative spectra (SG9 + 1D), and SG9 combined with second derivative spectra (SG9 + 2D). Similarly, variable selection method contains of variable importance in projection (VIP), uninformative variable elimination (UVE), selection ratio (SR), moving window partial least square (MWPLS), and competitive adaptive reweighted sampling (CARS). Moreover, In order to avoid over-fitting effect and under-fitting effect, latent factors of variable selection and latent factors of PLS were both set as the numerical discrete variable including five levels from 3 to 11.

For the optimization of NIR model, the CQAs were determined as coefficient of determination of prediction set (R_pre ²) and root mean square error of prediction (RMSEP). In practical applications, the lower the RMSEP value, the more robust and accurate the models will be, while R_pre ² is opposite of RMSEP.

$${{\mathrm{R}}_{\mathrm{pre}}}^2=1-\frac{{\sum }_{i=1}^N{\left(\widehat{y_i}-y_i\right)}^2}{{\sum }_{i=1}^N{\left(\overline{y_i}-y_i\right)}^2}$$ (1)

$$\text{RMSEP}=\sqrt{\frac{{\sum }_{i=1}^N{\left(\widehat{y_i}-y_i\right)}^2}{N}}$$ (2)

where, N is the number of validation set, y_i represents the reference value of the sample i, $\widehat{y_i}$ represents the prediction value of the sample i, and $\overline{y_i}$ is the mean of the reference value of the validation set.

2.3. The implement of D-optimal design for modeling design

Kennard-stone (K-S) (PCA-Score) method was used to divide the sample set into a calibration set and validation set with a ratio as 4:1. D-optimal design was implemented by Design Expert 8.0. In this paper, D-optimal design in this research contains four factors, two nominal factors and two discrete factors. Each factor contains five levels. These parameters were shown in Table S.1 and supplemented in in Supplementary Materials. Setting blocks as 1, 56 total runs have been established and composed of 46 required model points, 5 lack-of-fit points, and 5 replicate points.

In this research, D-optimal design in this research contains four factors, two nominal factors and two discrete factors. Each factor contains five levels.

Two discrete variables were taken as examples to explain the D-optimal algorithm.

• A.Latent factors of variable selection, 3 to 11.
• B.Latent factors of PLS model, 3 to 11.

Multifactor constraints like that pictured above must be entered as an equation taking the form of:

$${\beta }_L\le {\beta }_{\mathit{1}}A+{\beta }_{\mathit{1}}B\dots \le {\beta }_U$$ (3)

where β_L and β_U are lower and upper limits, respectively.

Anderson and Whitcomb provide guidelines for developing constraint equations in Appendix 7A of their book RSM Simplified. If, as in this case for both A and B, you want factors to exceed their constraint points (CP), this equation describes the boundary for the experimental region:

$$1\le \frac{A-{\mathit{LL}}_A}{{\mathit{CP}}_A-{\mathit{LL}}_A}+\frac{B-{\mathit{LL}}_B}{{\mathit{CP}}_B-{\mathit{LL}}_B}$$ (4)

where LL is the lower level.

This last equation can be entered directly, or it can be derived by Design-Expert from the constraint points while setting up a RSM design.

2.4. NIR modeling based on characteristic bands of chlorogenic acid

In the previous study, using DMSO as the solvent and concentration as the disturbance term, the spectra of the DMSO and chlorogenic acid DMSO solutions with different concentrations were scanned. According to the second derivative spectra, it was found that the difference in the spectra was obvious in the range of 1650–1800 nm [38]. Furthermore, the NIR band of chlorogenic acid extrated by spectral assignment, 1650–1800 nm, were introduced as the characteristic variables of Honeysuckle flower. Associate with CMPs combination designed by D-optimal, this band was used to establish models instead of chemometrics variable selection methods. PLS models were developed successively by the parameter combination in Electronic Supplementary Material Table S.2.

2.5. Software for modeling design

D-optimal design and the development of design spaces have been implemented by Design-Expert (Stat-Ease, USA). The NIR models were established by ChemDataSolution (Dalian ChemDataSolution Information Technology Co. Ltd., China). All the figures were drawn by SigmaPlot 12.5 (Systat Software, USA).

3. Results and discussion

3.1. The features of Near-infrared raw spectra and quantitative analysis by HPLC method

The on-line NIR raw spectra of Honeysuckle flower were shown in Electronic Supplementary Material Fig. S.1. As seen, the wide absorption peaks of raw spectra overlapped severely and the characteristic band was difficult to identify. Therefore, it is vital to erase the influence of noise and extract suitable bands for PLS model.

Chlorogenic acid content was measured by HPLC method, of which the methodology referred to the Chinese Pharmacopeia. The separation degree, prediction degree, repetition, and stability of HPLC all matched the demands of analysis. The fitting curve revealed good linearity within the content range from 0.0792 μg to 0.7920 μg. The slope of the linear model was (1.15(+/−)0.04) × 10^6 uAU/g and the intercept (−7(+/−)1) × 10^3. The linear correlation coefficient R² of this model is 0.9999. As a result, the concentrations of chlorogenic acid as the reference are in the range of 1.1892–5.9163 mg/mL.

3.2. Modeling design in ethanol precipitation process of Honeysuckle flower according to DoE

D-optimal design was used to optimize the NIR modeling CMPs. 56 PLS models have been developed. The R_pre ² and RMSEP of these models were shown in Electronic Supplementary Material Table S.2. Three regression models had been investigated to design an optimal model. Since spectral pre-process method and variable selection method were two kinds of classified variables, their analysis was carried out through dummy variables, regarding raw and UVE as reference, respectively.

The results of variance analysis were shown in Table 1 . It can be seen that as the complexity of the model increases, from linear model to quadratic model, the R_adj ² of R_pre ² increases remarkably from 0.1395 to 0.9085 and one of RMSEP increases from 0.2183 mg/mL to 0.9465 mg/mL. It indicated that there was a strong interaction among these modeling CMPs.

Table 1.

The ANOVA results of modeling design.

CQAs	Rpre2			RMSEP (mg/mL)
Source	F value
	Linear	2FI	Quadratic	Linear	2FI	Quadratic
Model	1.8915	9.27⁎⁎⁎	13.1393⁎⁎⁎	2.5354⁎	14.5006⁎⁎⁎	22.6199⁎⁎⁎
A	3.3506	8.26⁎	13.2131⁎⁎	3.8117	10.476⁎⁎	19.0088⁎⁎
B	1.5226	1.63	0.6095	4.9911⁎	18.1239⁎⁎	19.1375⁎⁎
C	1.3597	7.02⁎⁎	13.816⁎⁎⁎	1.7039	12.3366⁎⁎⁎	26.1679⁎⁎⁎
D	1.4018	12.3⁎⁎⁎	8.6467⁎⁎	1.3596	16.9293⁎⁎⁎	11.9931⁎⁎⁎
AB	–	4.71	4.0897	–	3.6734	2.8724
AC	–	4.8⁎	5.4169⁎	–	6.2963⁎⁎	6.3197⁎⁎
AD	–	2.83	2.495	–	3.0845	2.0682
BC	–	18.01⁎⁎⁎	17.1204⁎⁎⁎	–	22.7732⁎⁎⁎	22.465⁎⁎⁎
BD	–	5.84⁎⁎	7.1531⁎⁎	–	7.7059⁎⁎	9.3885⁎⁎
CD	–	5.64⁎⁎	7.7202⁎⁎	–	7.5474⁎⁎⁎	10.9737⁎⁎⁎
A2	–	–	0.8682	–	–	0.0462
B2	–	–	7.3065⁎	–	–	8.9445⁎

Linear refers to linear regression, 2FI refers to 2 factors international regression, Quadratic refers to Quadratic regression. Model refers to the relationship between R_pre² or RMSEP and modeling parameters. A refers to latent factors of variable selection, B refers to latent factors of PLS model, C refers to spectral pre-processing method, and D refers to variable selection methods.

^⁎p < 0.05.

^⁎⁎p < 0.01.

^⁎⁎⁎p < 0.001.

Notably, this interaction was neglected when modeling parameters were optimized step-by-step. The ANOVA results of modeling design shown in Table 1 indicated the influence of four CMPs on modeling were all significant. All these demonstrated that D-optimal was an appropriate method for NIR modeling design. And quadratic model was suitable for the evaluation of models by these two CQAs.

3.3. The effects of different CMPs on the performance of the PLS model by modeling design

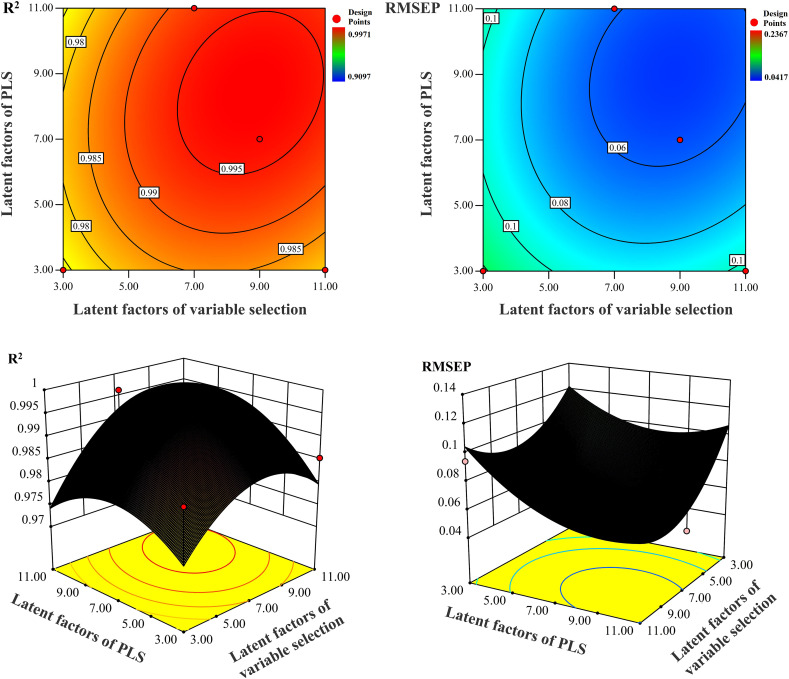
In previous research of optimizing step-by-step, the latent factors of PLS was determined by the model performance and often selected as 10, which ignores the interaction among the modeling parameters. To investigate the influence of latent factors of variable selection and latent factors of PLS on model, the contour plots and response surface plots were shown in Fig. 1 . The contours of these two plots were both concentric circles, indicating that latent factors of variable selection and latent factors of PLS had a synergistic influence on spectral pre-processing method and variable selection method. This suggested that there was an extreme value under the appropriate combination of latent factors. Therefore, it was necessary to find the relationship between latent factors of variable selection and latent factors of PLS by modeling design, rather than optimizing step-by-step.

Fig. 1.

The contour plots and response surface plots between latent factors of variable selection and latent factors of PLS.

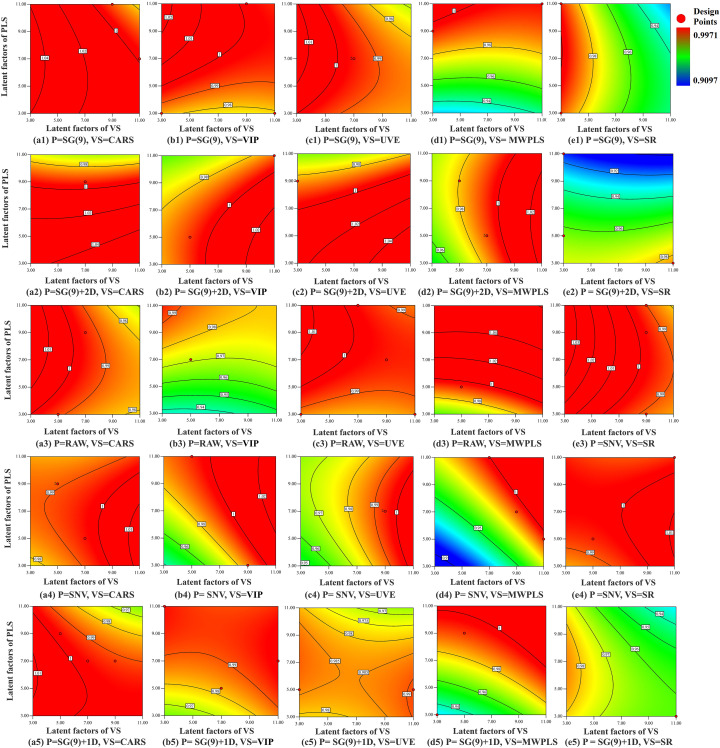
Furthermore, 25 contour plots developed by the combinations of five preprocessing methods and five variable selection methods were exhibited in Fig. 2 . The darker the color in the figure, the closer it is to the set maximum value. The lighter the color, the closer it is to the set minimum value. As seen, the model performance in the upper-left corner (Fig. 2(a1)) was the best while one in the bottom-right corner (Fig. 2(e5)) was the worst. As shown in Fig. 2, the model performance was becoming better with the increase of the complexity of the variable selection method, from SR to CARS. Oddly the trend was reversed for the raw spectra. This was because raw spectra contain a lot of noise which was often used as residuals for modeling by complex variable selection method. So the model performance was worse from CARS to SR.

Fig. 2.

Twenty-five contour plots of R_pre² developed by spectral pre-processing method (SG(9), SG(9) + 2D, raw, SNV, SG(9) + 1D), and variable selection method (CARS, VIP, UVE, MWPLS, SR).

*P refers to the spectral pre-processing method, VS refers to the variable selection method.

According to the 25 contour plots, it can be seen that spectral pre-processing method and variable selection method both had significant synergistic influence on model performance. For example, the contour in Fig. 2(a3) demonstrated that spectral pre-processing method was an important factor for modeling while variable selection method was insignificant. However, the result shown in Fig. 2(e3) was just the opposite. Moreover, when using CARS as the variable selection method, no matter which preprocessing method was chosen, a better model could be obtained under a smaller latent factor, especially for SG9. These mean SG9 and CARS was an appropriate combination for modeling.

3.4. Modeling design demonstrated by design spaces of PLS models

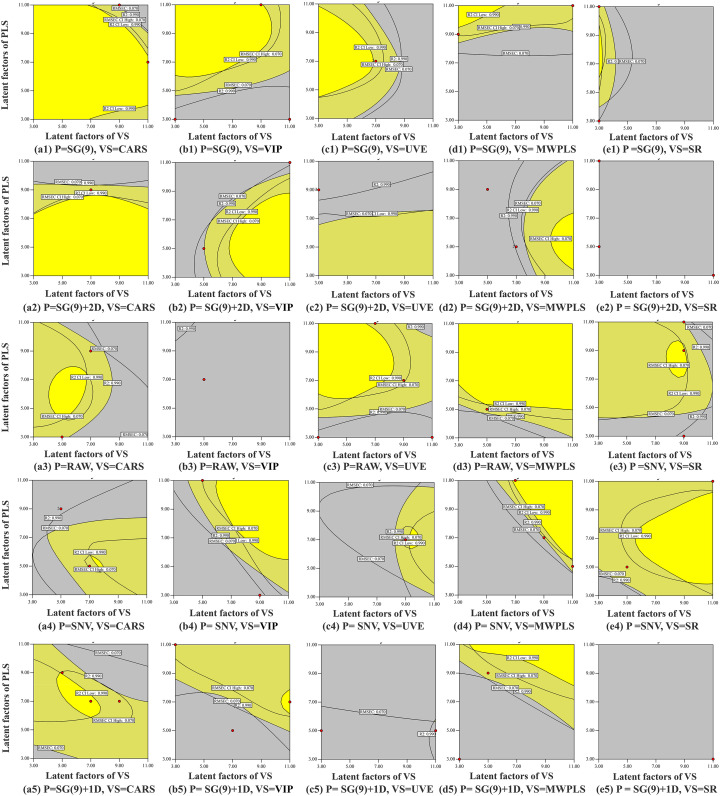
The premise of developing design space is suitable target range of the CQAs. According to the established models, the ranges were set as R_pre ² > 0.990 and RMSEP <0.070 mg/mL. Within these ranges, 25 design spaces were developed based on all spatial subsets with a confidence interval of α = 0.05 to ensure the robustness. The results were shown in Fig. 3 , of which, the x-coordinate represented the latent factors of variable selection, the y-coordinate represented the latent factors of PLS. The dark yellow was risk region, and the bright yellow region was the design space, which indicated that there were many parameter combinations can all get a perfect model performance, instead of the only one modeling path.

Fig. 3.

Twenty-five design spaces developed by P (raw, SNV, SG(9), 1D + SG(9), 2D + SG(9)) and variable selection method (VIP, UVE, SR, MWPLS, CARS).

*P refers to the spectral pre-processing method, VS refers to the variable selection method.

Furthermore, two validation points, Z1 and Z2, in design space (bright yellow region) and outside design space (dark yellow or gray region) were selected to establish quantitative models respectively. The modeling parameter combinations of two points and the comparison of two modeling results were shown in Electronic Supplementary Material Fig. S.2 and Table S.3. All CQAs of the points inside the space were better than those outside the space, which indicated the established spaces were reliable. This proves again that there was interaction among modeling parameters, and the modeling path was multiple rather than unique.

3.5. Modeling design in ethanol precipitation process of Honeysuckle flower based on spectral assignment

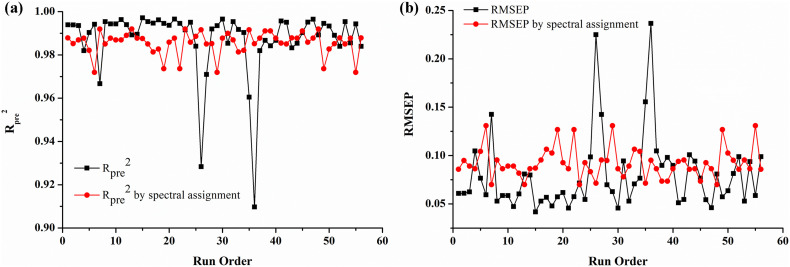
In order to establish a pertinent PLS model, spectral assignment was introduced to select variables for PLS modeling, instead of chemometric variable selection method. Chlorogenic acid is the main active ingredients of Honeysuckle flower. In our previous research, the characteristic band of chlorogenic acid was 1650–1800 nm [36]. This band was selected to establish PLS models combined with the spectral pre-process methods and latent factors of PLS designed in Electronic Supplementary Material Table S.1. 56 models were developed and their performances were shown in Electronic Supplementary Material Table S.4. Notably, compared with the chemometric variable selection method (shown in Electronic Supplementary Material Table S.2), spectral assignment method can make a higher R_pre ² and a lower RMSEP of the model when the latent factors of PLS was small (Fig. 4 ). As we all known, the smaller the latent factors of PLS, the better the applicability of the model was. Therefore, the variables selected by spectral assignment were more precise and representative, so that the model established by spectral assignment combined with QbD concept was more applicable and robust.

Fig. 4.

The model performance by two methods. (a) Chemometric; (b) spectral assignment.

3.6. An excellent NIR model established by design and spectral assignment

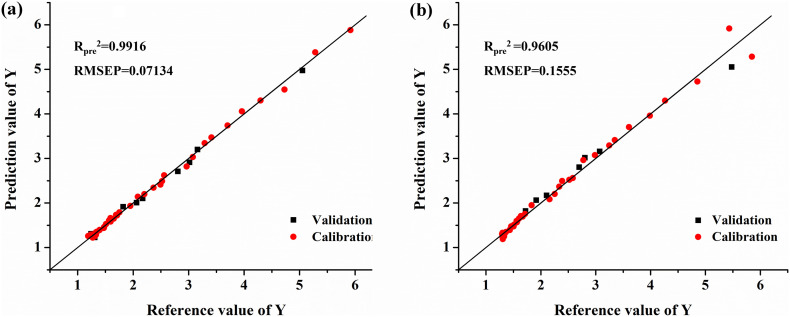
According to the model performance established by spectral assignment method combined with QbD concept, the optimal combination of parameters was using SG(9) + 2D as preprocessing method and selecting 3 as latent factors of PLS. Then PLS model was established and exhibited in Fig. 5 (a). The R_pre ² of this model was 0.9916 and the RMSEP was 0.07134 mg/mL. While the performance of model based on chemometric variable selection method was worse than spectral assignment method when the modeling parameter combination was same (Fig. 5(b)). Specifically, the R_pre ² decreased from 0.9916 to 0.9605 and the RMSEP increased from 0.07134 mg/mL to 0.1555 mg/mL. These proved once again that spectral assignment was reasonable for characteristic band selection.

Fig. 5.

(a) The optimal fitting results of PLS model by spectral assignment method. (b) The optimal fitting results of PLS model by chemometric variable selection method.

D-optimal could obtain the interaction between key modeling parameters and the best combination of CMPs. The extracted bands by spectral assignment are more representative than one selected by chemometric variable selection method. Combined with spectral assignment, D-optimal could design an appropriate parameter combination to develop a better model.

4. Conclusion

According to the results of 56 models, 25 contour plots and 25 design spaces, ANOVA illuminated that there was strong interaction among CMPs, of which appropriate combination can achieve excellent model performance. Compared with other parameter combination, SG (9) combined with CARS can make the model more robust and reliable. Moreover, spectral assignment was reasonable for characteristic band selection to establish a more pertinent and robust model when the latent factors of PLS was small. A novel modeling design idea, using spectral assignment method combined with D-optimal design, provided a perfect reference method to establish a global optimal model for process quality control in PAT.

Author contributions statement

Conceptualization and Funding acquisition were implemented by Zhisheng Wu; Data curation, Investigation, and Writing - original draft were completed by Lijuan Ma; Methodology and Software were accomplished by Lijuan Ma and Chenzhao Du; Validation is jointly completed by all authors.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Supplementary data

Supplementary material