Abstract
The mitral valve is a complex anatomical structure whose physiological functioning relies on the biomechanical properties and structural integrity of its components. Their compromise can lead to mitral valve dysfunction, associated with morbidity and mortality. Therefore, a review on the morphometry of the mitral valve is crucial, more specifically on the importance of valve dimensions and shape for its function. This review initially provides a brief background on the anatomy and physiology of the mitral valve, followed by an analysis of the morphological information available. A characterisation of mathematical descriptions of several parts of the valve is performed and the impact of different dimensions and shape changes in disease is then outlined. Finally, a section regarding future directions and recommendations for the use of morphometric information in clinical analysis of the mitral valve is presented.
Keywords: biomechanics, computational anatomy, mitral valve, mitral valve disease, morphology analysis
A complete review collating the currently available data on mitral valve morphometry, which specifies correlations between dimensions, mathematical models used to represent the valve, and how these can define changes in shape occurring with disease.
![]()
1. INTRODUCTION
The mitral valve (MV) is one of the heart’s four valves, lying between the left atrium and the left ventricle. It prevents blood from flowing backwards as it moves through the heart and it has a complex geometry, comprising the mitral annulus, the anterior and posterior leaflets, and the subvalvular apparatus (Figure 1). The latter is formed by the chordae tendineae and the papillary muscles (PM), which are inserted into the left ventricular wall (McCarthy et al., 2010; Dal‐Bianco and Levine, 2013). These structures work in synchrony towards its effective mechanics to enable closing and opening through the cardiac cycle (McCarthy et al., 2010).
FIGURE 1.
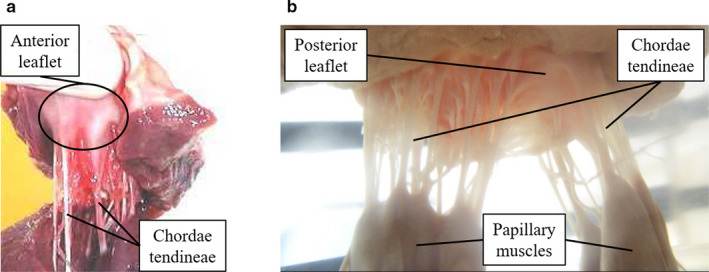
Porcine mitral valve apparatus: (a) displays the anterior leaflet and chordae tendineae and (b) focuses on the subvalvular apparatus, where chordae arise from both PMs and insert into the rough region of the posterior leaflet
The shape of the valve is key to many aspects of its function and disease, as identified by clinical studies (Lee et al., 2013; Jassar et al., 2014) as well as silico studies, based on porcine (Kunzelman et al., 2007), ovine (Eckert et al., 2009) and human (Stevanella et al., 2011) models, and in vitro studies, based on porcine (Espino et al., 2007) and ovine (Bloodworth et al., 2017) models. Assessing its morphology can reveal various normal and abnormal features, which can be associated with deteriorating clinical outcomes (Sonne et al., 2009; Lee et al., 2013; Mihaila et al., 2013; Jolley et al., 2017). Moreover, the physiological functioning of the components of the MV, as well as their ability to adapt to altered stress state imposed by the passage of blood flow, relies on their biomechanical properties and structural integrity (Espino et al., 2007; Al‐Atabi et al., 2012). The success of surgical interventions (such as edge‐to‐edge repair or chordal replacement; Al‐Atabi et al., 2012) greatly depends on the restoration of normal fluid dynamics, which typically requires valve mechanics to be corrected (Al‐Atabi et al., 2012). Thus, optimising a surgical procedure, or surgical timing for MV repair, is arduous (Gao et al., 2017b). The design of medical devices for the MV is also determined by its morphometry, with a previous in vitro study based on porcine MVs supporting the use of saddle‐shaped annuloplasty ring designs to better mimic annular shape (Jimenez et al., 2007).
The first study reviewing the anatomic structure of the MV to identify key dimensions appeared at the beginning of the 1990s and was based on excised human and porcine MV apparatus (Kunzelman et al., 1994). This yielded basic human and porcine MV ex vivo measurements concerning annular and leaflet length and height, and chordal distribution. With the evolution of medical imaging modalities, in vivo procedures, such as three‐dimensional (3D) transoesophageal echocardiography, have been used quantitatively to evaluate human MV morphology in healthy and diseased cases (Sonne et al., 2009; Delgado et al., 2009; Lee et al., 2013; Mihaila et al., 2013; Jolley et al., 2017), proving crucial for 3D printing purposes or transcatheter MV implantation, for example. On the other hand, computational studies have mathematically represented the MV (Salgo et al., 2002; Stevanella et al., 2009; Park et al., 2019), including the annulus (Salgo et al., 2002; Stevanella et al., 2009), leaflet shape (Stevanella et al., 2009; Shen et al., 2017; Park et al., 2019) and chordae architecture (Kaiser et al., 2019) from both human and porcine dimensions and characteristics. Although many sources of MV anatomy quantification exist, a single study bringing together the current best knowledge around its morphometry, including related mathematical definitions, is lacking.
This review article aims to examine the morphometry of the MV and determine the current state of mathematical definitions of its geometrical shape. The focus is on compiling ex vivo/in vivo descriptions which are currently available in the literature to define the 3D geometry of the MV. The anatomy and physiology of the MV are briefly described, followed by mathematical definitions and morphometric information available (including associations between valve dimensions). Subsequently, a description of the impact of changes in MV morphometry in valve disease is performed and future recommendations for the use of morphometric information in MV clinical analysis are given.
2. ANATOMY AND PHYSIOLOGY OF THE MITRAL VALVE
2.1. Mitral annulus and leaflets
The annulus is a ring of fibrous tissue that circumscribes the perimeter of the valvular orifice and the base of the valve, anchoring it within the left heart (Dal‐Bianco and Levine, 2013). It is adjacent to the aortic valve, sharing a fibrous continuity with the left coronary and half of the non‐coronary cusps of the aortic annulus (Ranganathan et al., 1970; Veronesi et al., 2009). This adjacent section defines the anterior portion of the mitral annulus, limited by the left and right fibrous trigones. The posterior part of the annulus is distal to the trigones and includes the lower points of its saddle shape (Dal‐Bianco and Levine, 2013). Its shape and diameter vary during the cardiac cycle (Jiang et al., 2014), making it a dynamic structure: in diastole, the annulus has a more circular shape, whereas in systole it changes into a non‐planar saddle shape in synchrony with valve closure/leaflet coaptation (Al‐Atabi et al., 2012; Dal‐Bianco and Levine, 2013; Garbi and Monaghan, 2015).
The leaflets of the MV are a continuous band of tissue extending from the annulus. According to their geometrical form and anatomical connection to the annulus, the leaflets are divided into anterior, posterior and commissural parts (McCarthy et al., 2010; Dal‐Bianco and Levine, 2013). According to previous studies focusing on the human MV, the posterior leaflet has a semilunar shape and a relatively short radial length in comparison with the anterior leaflet, being composed of three minor semi‐oval scallops: a central one opposite to the anterior leaflet, and two others, to each side (Ranganathan et al., 1970; Carpentier et al., 1995; Dal‐Bianco and Levine, 2013). The anterior leaflet, on the other hand, is dome‐shaped, longer and thicker (Ranganathan et al., 1970; Dal‐Bianco and Levine, 2013). In systole, the free edge of both leaflets coapt, closing the valve (Ranganathan et al., 1970), whereas in diastole, the free edges separate and the valve opens (McCarthy et al., 2010). Tissue characteristics of both leaflets also change according to region, as stated by previous human mitral valve studies and as displayed in Figure 2: while the central portion is thinner and smoother (clear zone), towards the free edges (coaptation region) the tissue becomes thicker and rougher (rough zone) (McCarthy et al., 2010; Al‐Atabi et al., 2012; Dal‐Bianco and Levine, 2013); this is the main area of chordae tendineae attachment (Lam et al., 1970; Dal‐Bianco and Levine, 2013). The posterior leaflet also possesses a chordae attachment area near the annulus, named the basal zone (Lam et al., 1970). Both leaflets consist of four histological layers. The uppermost one adjacent to the left atrium is the atrialis, composed of mainly aligned elastic/collagen fibres. Beneath the atrialis is the spongiosa, which consists of an extracellular matrix of proteoglycans and glycosaminglycans, along with elastic fibres, comprising the majority of the free edge. Beneath the spongiosa is the fibrosa, a major load‐bearing layer forming the central structural collagenous core of each leaflet, with aligned collagen fibres. Finally, the ventricularis layer is covered by a continuous sheet of endothelial cells folded with elastic and collagen fibres (McCarthy et al., 2010).
FIGURE 2.
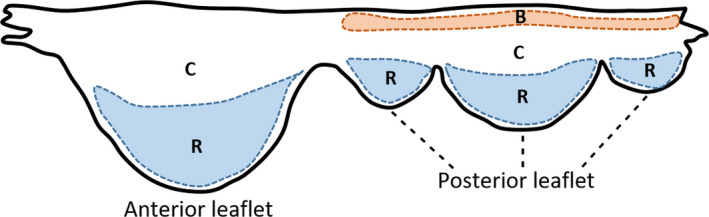
Human MV leaflet tissue areas. C, clear zone; R, rough zone; B, basal zone
2.2. Subvalvular apparatus
The chordae are chord‐like structures that arise from the tip of either of the two PMs and insert into the leaflets (Lam et al., 1970; Al‐Atabi et al., 2012). The two PMs are known as anterolateral and posteromedial, relative to the anterior and lateral body orientations and indicating the anatomical parts of the left ventricular wall into which they insert. Similarly to the mitral annulus, they are dynamic structures that move through the cardiac cycle. However, their role is unclear in the literature: previous studies focusing on dog mitral valves state that PM contraction/shortening assists in opening the MV, whereas their elongation aids in coaptation (Marzilli et al., 1980), or that MV closing relies on PM contraction instead (Hirakawa et al., 1977). The chordae themselves are characterised according to their point of attachment and size; in a human MV, the marginal chordae are thinnest and attach to the free edge of the leaflets; basal chordae are thicker and more extensible, inserting between the free edges and the leaflet’s attachment to the annulus (rough zone).
There are two thick basal chords (strut chordae) that arise from the tip of each PM and insert into the anterior leaflet: these are the largest and thickest of all chordae, having also the highest tension (Lam et al., 1970; Lomholt et al., 2002; Al‐Atabi et al., 2012; Dal‐Bianco and Levine, 2013; Wilcox et al., 2014). Their insertion region into the anterior leaflet experiences varying stretch during the cardiac cycle, which demonstrates a transfer of forces from the leaflets to the chordae and vice versa, and aids in valve function (Padala et al., 2010). There are also tertiary chordae, which originate at the left ventricular wall and connect to the basal region of the posterior leaflet (McCarthy et al., 2010; Al‐Atabi et al., 2012). According to porcine and ovine studies, different types of chordae have different functions: whereas marginal chordae maintain the leaflets closed during systole, averting regurgitation, basal chordae support and transfer loads to the leaflets, carrying also higher loads to protect marginal chordae from failure (Timek et al., 2001; Sedransk et al., 2002; Nielsen et al., 2003; Espino et al., 2005; Wilcox et al., 2014).
3. INSIGHTS INTO MITRAL VALVE MORPHOMETRY
3.1. Mitral valve key landmarks and morphometric data
Mathematical algorithms that automatically generate parametric 3D human MV models have been developed from in vivo echocardiographic data (Grbic et al., 2017), four‐dimensional computed tomography images (Ionasec et al., 2010) and 3D transoesophageal echocardiography (Mansi et al., 2012; Zhang et al., 2017). Despite the creation of patient‐specific geometries, these frameworks rely on common anatomic MV landmarks (Figure 3), from which parametric surfaces corresponding to the mitral leaflets can be generated. These include the left and right trigones, situated at the fibrous border between the mitral and aortic valves (Veronesi et al., 2009); the anterolateral and posteromedial commissures, located at the free edges, which are the interconnection points of the leaflets (McCarthy et al., 2010); the leaflet tips, corresponding to the line of each leaflet free edge (Ionasec et al., 2010; Mansi et al., 2012); the posterior annular midpoint; and the PM tips (Ionasec et al., 2010; Mansi et al., 2012).
FIGURE 3.
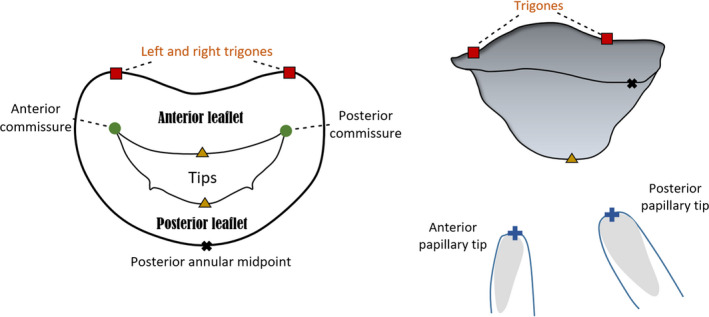
Atrial and lateral views of a mitral valve (MV) schematic model based upon nine landmarks. The annulus, anterior and posterior leaflets and papillary muscle tips can be observed
Both ex vivo and in vivo studies defined parameters that describe the human MV geometrical shape and are vital to its function. These are discretised in Table 1, and ranges of values for healthy and diseased valves are provided.
TABLE 1.
Geometric variables of the MV and healthy and diseased (significant regurgitation) literature ranges (Ranganathan et al., 1970; Kunzelman et al., 1994; Yamaura et al., 2008; Delgado et al., 2009; Sonne et al., 2009; Suri et al., 2009; Lee et al., 2013; Mihaila et al., 2013; Topilsky et al., 2013; Dudzinski and Hung, 2014; Jassar et al., 2014; Jiang et al., 2014; Kim et al., 2014; Pouch et al., 2014; Calleja et al., 2015; Machino‐Ohtsuka et al., 2016; Obase et al., 2016; Owais et al., 2016; Deorsola and Bellone, 2018)
| MV component | Geometric variables | Meaning | Ranges | |
|---|---|---|---|---|
| Healthy | Diseased | |||
| Annulus | AP diameter (mm) | Distance between anterior and posterior annular midpoints | 30 ± 6b | 38.8 ± 6.4c |
| CW (mm) | Annular diameter at the commissures | 33.3 ± 3.7c | 42.2 ± 5.9c | |
| AL–PM diameter (mm) | Diameter between anterolateral and posteromedial landmarks | 31 ± 5b | 39 ± 7b | |
| Annular circumference (mm) | Total perimeter of the annular edge | 106 ± 10c | 136 ± 19c | |
| Anterior/posterior circumferences (mm) | Perimeter of the anterior/posterior annular edges |
Anterior: 43.3 ± 8.2b Posterior: 63.01 ± 9.06b |
Anterior: 61.3 ± 8b Posterior: 75 ± 11b |
|
| Annular height (mm) | Vertical distance between highest and lowest annular points | 7.9 ± 1.9c | 5.6 ± 1.6c | |
| Annular area (mm2) | Area enclosed by the 2D projection of the annulus | 780 ± 270b | 1,343 ± 392c | |
| NPA (°) | Angle between anterior and posterior annular midpoints at the commissure | 144 ± 11b | 157 ± 12b | |
| IT distance (mm) | Distance between left and right trigones | 30 ± 3d | 31 ± 3d | |
| Leaflets | Anterior/posterior lengths (mm) | Length from anterior/posterior annular midpoints to coaptation |
Anterior: 21.2 ± 3.0c Posterior: 9.8 ± 2.0c |
Anterior: 26.3 ± 6.1c Posterior: 16 ± 5c |
| Anterior/posterior areas (mm2) | Surface area of anterior/posterior leaflets |
Anterior: 530 ± 210b Posterior: 380 ± 130b |
Anterior: 760 ± 190b Posterior: 610 ± 230b |
|
| Posterior scallop lengths (mm) | Length from each scallop free margin to annulus | P1: 5‐17; P2: 7‐20; P3: 7‐20e | P1: 16 ± 5; P2: 19 ± 6; P3: 16 ± 4b | |
| Commissural heights (mm) | Height from each commissural free margin to annulus | AL: 5‐13; PM: 4‐12e | ‐‐‐‐‐‐‐‐‐‐ | |
| Leaflet angles (°) | Angle created by the anterior/posterior leaflets with the annulus line |
Anterior: 24.6 ± 7b Posterior: 34.7 ± 9.6b |
Anterior: 33.2 ± 8.6b Posterior: 44.4 ± 11.9b |
|
| Tenting height (mm) | Distance from the annulus to coaptation | 7.4 ± 1.3a | 9.7 ± 3.2b | |
| Tenting area (mm2) | Silhouette delineated by leaflets from annulus to coaptation | 118.2 ± 32.6a | 350 ± 50a | |
| Subvalvular apparatus | PM length (mm) | Length from each PM to anterior annular midpoint |
ALPM: 28.1 ± 4.1c PMPM: 28.5 ± 4.8c |
ALPM: 40.5 ± 6c PMPM: 41.8 ± 5.9c |
| Inter‐papillary distance (mm) | Distance between PMs |
Inner: 14.4 ± 4.8b Outer: 31.1 ± 5.4b |
Inner: 26.7 ± 8.4b Outer: 43.1 ± 9.7b |
|
| Inter‐papillary angle (°) | Angle between anterior annular midpoint to both PMs | 26.2 ± 6.5d | 28.9 ± 6.3d | |
Dimensions obtained at: a, early systole; b, mid‐systole; c, end‐systole; d, averaged over cardiac cycle; e, ex vivo.
AL, anterolateral; ALPM, anterolateral papillary muscle; AL–PM, anterolateral‐posteromedial; AP, antero‐posterior; CW, commissural width; IT, inter‐trigonal; NPA, non‐planarity angle; P1, posteromedial commissural scallop; P2, posterior middle scallop; P3, anterolateral commissural posterior scallop; PM, papillary muscle; PMPM, posteromedial papillary muscle.
3.2. Annular proportions and saddle shape: geometrical relationships
The geometrical components of the annulus including annular anterior and posterior areas, the antero‐posterior (AP), the anterolateral‐posteromedial (AL–PM) and the inter‐trigonal distances, represented in Figure 4a, vary over the cardiac cycle (Jiang et al., 2014). Both anterior and posterior annular portions contribute to changes in mitral annular area: although standard literature refers to annular contraction as occurring during systole, as stated in a previous ovine study (Rausch et al., 2011), there are studies based on human MVs showing annular expansion from mid‐systole to early‐diastole and contraction between mid‐diastole and early systole (Levack et al., 2012; Jiang et al., 2014). In addition, an in vivo study based on ovine MVs showed the presence of dynamic annular strain, with the largest strains belonging to the posterior region and the commissural regions showing the least amount of variation (Eckert et al., 2009).
FIGURE 4.
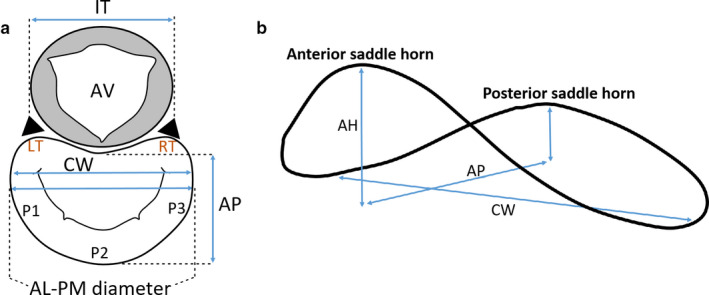
Atrial (a) and lateral (b) views of important mitral annular dimensions. AV, aortic valve; LT, left trigone; RT, right trigone; P1, P2, P3, posterior leaflet scallops; AL–PM diameter, anterolateral‐posteromedial diameter; AP, antero‐posterior distance; CW, commissural width; IT, inter‐trigonal distance
Despite this dynamic variability, the proportion concerning anterior and posterior annular circumferences in the human MV remains practically unchanged. This proportion is contradictory in the literature: whereas some studies mention that the anterior and posterior parts correspond to about 1/3 and 2/3 of the total annular perimeter (Garbi and Monaghan, 2015), others yield a proportionality of about 2/5 and 3/5, respectively (Pouch et al., 2014; Jassar et al., 2014). However, this proportion depends on the assumed division between leaflets, which is usually considered at the commissural level. Nonetheless, other studies divide the leaflets at the lowest annular height. The correct proportion is reflected in the literature values (obtained at mid‐systole) present in Table 1 (Pouch et al., 2014; Jassar et al., 2014) and is described quantitatively by Equations (1) and (2),
| (1) |
| (2) |
where A C is the total annular circumference and P AC and A AC are the posterior and anterior annular circumferences, respectively. Moreover, these proportions are confirmed by correlations found in the literature, based upon dimensional data retrieved during intra‐cardiac operations and dissection of fresh human hearts (Duplessis and Marchand, 1964). These yielded Equation (3) (R 2 = .72, p‐value < .01) and 4 (R 2 = .93, p‐value < .01),
| (3) |
where the A C and A AC are in mm,
| (4) |
where the A C and P AC are in mm. The correlation from Equation (4) was further validated through a 2D echocardiographic study concerning imaging data from 15 healthy subjects and performed by the authors. Valvar dimensions were obtained at end‐systole and generated a moderate correlation between the A C and P AC (R 2 = .674, p‐value < .01). The methodology employed for equation prediction generation, as well as further characteristics of the correlations found on our study, are present in Appendix S1.
An ex vivo human study, performed within 6 hours of MV removal, examined MV geometry by assuming the mitral annulus as a circle and the A AC and P AC as arc lengths. This work also underlined positive linear relationships between these dimensions and the mitral annular diameter (or AL–PM distance), as given by Equation (5) (R 2 = .66, p‐value < .01) and 6 (R 2 = .91, p‐value < .01) (Okamoto et al., 2007):
| (5) |
where γ represents the AL–PM distance and both variables are in cm,
| (6) |
where both variables are in cm. For Equations (5) and (6), γ is expressed as a dimensionless Z‐value in agreement with Okamoto et al. (2007). Further, the authors of this study have mathematically defined the A AC, P AC and IT distance, assuming the annulus as divided into anterior and posterior portions by the left and right trigones or commissures, as represented in Figure 5.
FIGURE 5.
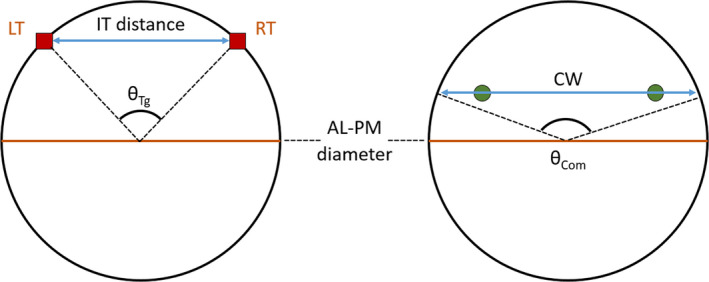
Circle representing the annulus, according to Okamoto et al. (2007), with relevant dimensions highlighted. LT, left trigone; RT, right trigone; AL–PM diameter, anterolateral‐posteromedial diameter; CW, commissural width; IT distance, inter‐trigonal distance; θTg, trigonal angle; θCom, commissural angle
Equations (7), (8), (9) represent the mathematical definitions employed by Okamoto et al. (2007),
| (7) |
| (8) |
| (9) |
where IT is the inter‐trigonal distance, γ is the AL–PM distance, is the angle between left and right trigones and θ Com is the angle between commissures at the annular plane (Okamoto et al., 2007). However, these definitions simplify the shape of the anterior leaflet to great extent and do not accurately represent its real configuration.
An association between the annular circumference and the total leaflet free edge length has also been found based on the ex vivo human MV data from Duplessis and Marchand (1964). Greater total and posterior annular circumferences were moderately correlated with increased free edge lengths, as provided in the equations below,
| (10) |
where δ represents the free edge length, and both variables are in mm (R 2 = .76, p‐value < .01),
| (11) |
where both variables are in mm (R 2 = .74, p‐value < .01),
Annular shape is distinctive due to its similarity with a saddle, being characterised by an annular height (AH) (Figure 4b). This is characteristic of a healthy valve, as it reduces leaflet stress and decreases anterior systolic strain, potentially increasing repair durability (Salgo et al., 2002; Jimenez et al., 2007). In practice, a deeper saddle relates to more apical positions of the medial and lateral aspects of the annulus, while the anterior and posterior aspects remain basal (Salgo et al., 2002). This is mathematically described by the annular height to commissural width ratio (AHCWR), which provides a quantitative measure of annular non‐planarity (Lee et al., 2013; Jassar et al., 2014; Pouch et al., 2014). According to this, we can also define the AHCWR as:
| (12) |
where ε represents the AHCWR, AH is the annular height, AP is the antero‐posterior distance and CI is the circularity index. The latter is defined as the ratio between the AP diameter and the commissural width (CW) and accounts for the greater or smaller ellipsoidal shape of the annulus (Lee et al., 2013; Pouch et al., 2014).
The human MV AHCWR profile depends on the rotational position of the annulus and has led to the generation of new annuloplasty ring designs (Jassar et al., 2014; Pouch et al., 2014). In fact, saddle shape variability impacts on leaflet stress variation (Salgo et al., 2002): a deeper saddle shape, associated with a higher AHCWR percentage (Lee et al., 2013), leads to leaflet peak stress reduction, as predicted by computational studies (Salgo et al., 2002). Further, geometrical correlations concerning the AL–PM distance and other mitral annular dimensions have been found both in the literature and in our 2D echocardiographic study. For example, a clinical 3D transoesophageal echocardiography study focusing on the end‐systolic frame yielded lower non‐planarity angles (NPA) that were associated with increased AH to the AL–PM distance ratios, as given by Equation (13) (R 2 = .70, p‐value < .01) (Warraich et al., 2012):
| (13) |
where σ represents the AH to the AL–PM distance ratio (dimensionless) and the NPA is in degrees. A moderate association between the ratio of the AH to the AL–PM distance and the ratio of the AH to the AP distance was also found (R 2 = .78, p‐value < .01) (Warraich et al., 2012):
| (14) |
where τ represents the AH to the AP distance ratio. Nonetheless, given mitral annular dynamic shape changes through the cardiac cycle (the AH suffers a total percentage change of 13.5 ± 7.8 in the cardiac cycle, for example; Tang et al., 2019), we cannot assume that the aforementioned relationships are maintained both in systole and in diastole.
Our 2D echocardiographic study revealed a moderate association between the AL–PM distance and the inter‐trigonal distance at end‐systole, displayed in Equation (15) (R 2 = .65, p‐value < .01):
| (15) |
where IT represents the inter‐trigonal distance and both variables are in mm.
The AP distance is also geometrically associated with other annular parameters in the human MV. Equations (16) and (17) present moderate correlations between the ratio of the AH to the AP distance and the NPA (R 2 = .64, p‐value < .01) and between the 2D annular area and the AP distance (R 2 = .65, p‐value < .01), respectively, generated with data obtained at end‐systole:
| (16) |
where τ is dimensionless and the NPA is in º,
| (17) |
where A na is the annular area in mm2 and AP is in mm.
The annular saddle shape has been mathematically defined through paraboloid equations, which are quadric surfaces with one axis of symmetry and no centre of symmetry (Salgo et al., 2002; Stevanella et al., 2009; Park et al., 2019). In Salgo et al. (2002), for example, hyperbolic paraboloids were employed (Salgo et al., 2002), whereas Park et al. used hyperbolic paraboloids for the saddle shape definition. In addition, they designed a ring‐shaped structure, mathematically described as a curved toroid and with empirical relationships derived below (Park et al., 2019):
| (18) |
where α L and β L are transformation parameters in lateral directions in the xy plane that define the saddle point, α V is a transformation parameter in the vertical direction in the xz plane, and β V is the transformation parameter in the vertical direction in the yz plane. These parameters vary between 0 and 1, and a and b are determined by annular dimensions:
| (19) |
| (20) |
Equation (18) allows the manipulation of lateral and vertical curve transformations representative for example of changes in saddle depth and commissural height (see Figure 6).
FIGURE 6.
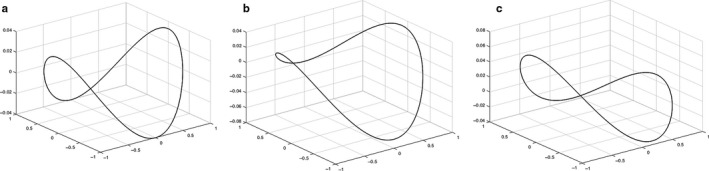
Hyperboloids representing the mitral valve (MV) saddle shape and defined by Equation 11 (Park et al., 2019) are displayed, created from literature values for CW (33.3 mm), AP diameter (28 mm), AL–PM diameter (31 mm) and AHCWR (0.237). Different commissural heights (b) and posterior annular depth (c) in comparison with a pure hyperboloid (a) can be observed, shown by changes in transformation parameters
The NPA is not the only factor influencing annular saddling; the leaflet angles (α A, and α P, represented in Figure 7) and the overall coaptation triangle (2D triangle formed by the AP diameter, anterior and posterior leaflets when the leaflets coapt), including tenting height and tenting area, also play an important role in the evaluation of human MV geometry and function (Delgado et al., 2009; Ciarka et al., 2010; Silbiger, 2011; Deorsola and Bellone, 2018). A schematic of this coaptation triangle is represented in Figure 7, as well as related linear and angular dimensions. A previous study hypothesised that the coaptation triangle of healthy valves could be based on the Golden Proportion, a ratio observed in Nature which derives from sectioning a certain segment in two different parts (Deorsola and Bellone, 2018). Such ratios yield an irrational number (rounded to .618 or 1.618) known as the Golden Proportion. This study states that the value of .618 can be obtained through the ratio between the anterior cord and the AP diameter, between the posterior and the anterior cords, and between the tenting height and the posterior cord.
FIGURE 7.
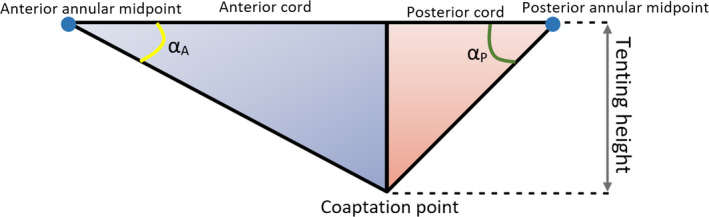
Coaptation triangle. The tenting height divides the base of the triangle (AP diameter) into two segments—the anterior and the posterior cords. α A, anterior leaflet angle; α P, posterior leaflet angle
Indeed, Deorsola et al. found strong correlations between the original coaptation triangle and the Golden (or mathematical) one at early systole (time point of measurements), showing good positive linear relationships between the AP diameter and the anterior cord (Equation 21, R 2 = .97, p‐value < .01) and between anterior and posterior cords (Equation 22, R 2 = .82, p‐value < .01):
| (21) |
where the AP diameter and A cord (anterior cord) are in mm,
| (22) |
where the A cord and P cord (posterior cord) are in mm. Unfortunately, Deorsola et al. mention that, due to technical imaging limitations, they were unable to assess the coaptation triangle and repeat measurements for each frame of the cardiac cycle in order to determine whether the Golden Proportion or the correlations found would be maintained both in systole and diastole (Deorsola and Bellone, 2018). Nonetheless, the anterior and posterior leaflet angles are an important element for the evaluation of leaflet tethering, with a posterior leaflet angle of ≥45º being an index of severe leaflet tethering in ischaemic mitral regurgitation. In fact, a previous study found that a P3 tethering angle below 28.8º would predict the improvement of this type of regurgitation after surgery (Bouma and Gorman, 2019; Sun et al., 2019). From a diagnostic and surgical point of view, this means that leaflet angles could represent important parameters to identify early anatomical alterations or to improve surgical strategy and postoperative evaluation, especially when correlated with other MV dimensions of the coaptation triangle (Deorsola and Bellone, 2018).
3.3. Leaflet dimensions and shape
Figure 8 shows anterior and posterior leaflet heights and lengths, as well as commissural length and leaflet area for a generic human MV.
FIGURE 8.
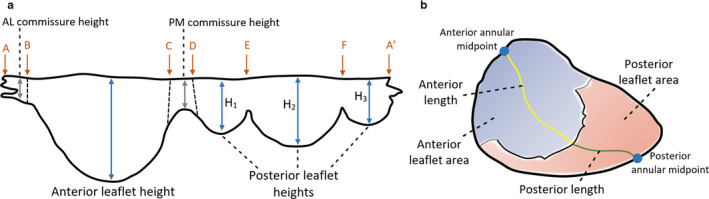
Parameters of human MV leaflet geometry, with an extended (a) and closed (b) leaflet representation. A‐B, anterolateral commissure; B‐C, anterior leaflet; C‐D, posteromedial commissure; D‐A′, posterior leaflet; D‐E, posteromedial commissural scallop (P1); E‐F, middle scallop (P2); F‐A′, anterolateral commissural scallop (P3)
Geometrical associations concerning the anterior leaflet have been determined from ex vivo human data from Duplessis and Marchand (1964). Dependencies between anterior leaflet surface area and other dimensions of the valve were discovered: correlations are present between this area and the A C (Equation 23, R 2 = .70, p‐value < .01) and A AC (Equation 24, R 2 = .81, p‐value < .01), with a moderate correlation between this area and the free edge lengths (Equation 25, R 2 = .62, p‐value < .01),
| (23) |
where A LA is the anterior leaflet surface area (in mm2) and the A C is in mm,
| (24) |
where the A AC is in mm and the A LA is in mm2,
| (25) |
where the A LA is in mm2 and δ is in mm (Duplessis and Marchand, 1964).
Similarly, further human ex vivo correlations between the posterior leaflet surface area and other dimensions of the valve were obtained from Duplessis and Marchand (1964): good associations with the A C (Equation 26, R 2 = .85, p‐value < .01) and P AC (Equation 27, R 2 = .82, p‐value < .01) and a moderate association with the free edge length (Equation 28, R 2 = .75, p‐value < .01):
| (26) |
where P LA is the posterior leaflet surface area (in mm2) and the A C is in mm,
| (27) |
where the P AC is in mm and the P LA is in mm2,
| (28) |
where the P LA is in mm2 and δ is in mm (Duplessis and Marchand, 1964).
In addition, a moderate correlation between anterior and posterior leaflet surface areas was also discovered from the data of Duplessis and Marchand (1964) (Equation 29, R 2 = .71, p‐value < .01):
| (29) |
where the A LA and P LA are in mm2 (Duplessis and Marchand, 1964).
The posterior leaflet has been mathematically characterised as a continuous shape around the annulus, with (Stevanella et al., 2009; 2011; Choi et al., 2016) or without (Kunzelman et al., 1993; Cochran and Kunzelman, 1998; Kunzelman et al., 2007; Domenichini and Pedrizzetti, 2015) scallop indentations. The main focus has been given to the mathematical definition of the complete leaflets’ free margin. This has been generated through mathematical harmonic functions (Stevanella et al., 2009), spline functions (Stevanella et al., 2011) and parametric equations (Domenichini and Pedrizzetti, 2015). However, these frameworks simplify leaflet shape to great extent, resulting in overly idealised geometries.
Better leaflet geometrical descriptions have recently been developed. Khalighi et al. (2018) built high‐quality 3D parametric models of MV leaflet surfaces using ex vivo high‐resolution images from ovine MV, obtained through micro‐computed tomography. They then employed quadric surfaces representing toroidal topology to create parametric large‐scale models of the MV and information on the deviation between parameterised models and the original geometries to derive local thickness of leaflets (Khalighi et al., 2018). Another study focused on the development of ex vivo methods to inform on the sensitivity of model performance to the accuracy of the input geometry and to acquire comprehensive datasets against which to validate computational simulations (Bloodworth et al., 2017). These works could potentially be employed on high‐fidelity MV models concerning healthy, diseased and repair states; however, as they rely on images obtained through an ex vivo imaging modality, translation to the generation of in vivo human MV models remains challenging.
3.4. Papillary muscle position and chordae insertion
The human PMs exhibit great morphological variability (Stevanella et al., 2009; 2011). Although two in number (Al‐Atabi et al., 2012), there are usually groups of muscles adjoining, reaching a total number as high as five and attaching to the left ventricular wall at its middle, upper or lower sections (Saha and Roy, 2018). Moreover, their shape is diversified, resembling either a cone (conical shape) or a elliptic paraboloid, having a truncated shape, or being bifurcated or trifurcated (Saha and Roy, 2018). Further, the number of chordae tendineae that attach to the PM, as well as their insertion distribution, is a source of variability. These features contribute to PM morphological heterogeneity, either in shape or attachment site. Therefore, current mathematical representations of the PM as unique points are restrictive and not accurately representative.
The PMs spatial position in humans has been mathematically defined, especially taking into account measurements such as their distance to the mitral annulus or to mitral coaptation (Sakai et al., 1999; Yamaura et al., 2008). Other measures of interest, such as the distance between PM or the inter‐PM angle, have also been employed to describe PM morphology (Figure 9). Some studies have provided measurements of the PM to five key annular sites named o’clock points (Figure 10) (Sakai et al., 1999; Yamaura et al., 2008). Here, each PM is associated with three distances to the annulus, allowing the description of the 3D spatial position of their tips if assumed to be a unique 3D point. More recently, another study has employed knowledge on similar measurements to build a high‐resolution 3D magnetic resonance imaging apparatus, giving rise to high‐quality 3D models of the whole human MV structure (Stephens et al., 2017).
FIGURE 9.
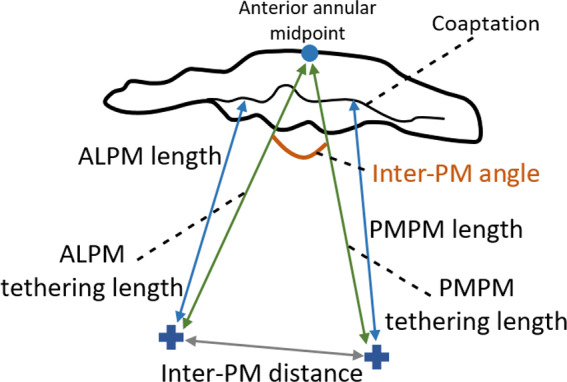
Measurements describing PM morphology. ALPM, anterolateral PM; PMPM, posteromedial PM
FIGURE 10.
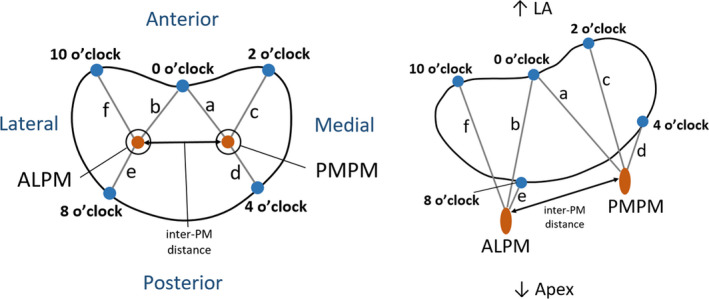
Distances between PM tips and o’clock points of mitral annulus, in axial (left) and isometric (right) views (adapted from Sakai et al., 1999; Yamaura et al., 2008). ALPM, anterolateral PM; PMPM, posteromedial PM; 0 o’clock, midpoint of the anterior annular circumference; 2 o’clock, right trigone; 10 o’clock, left trigone; 4 o’clock, separation of posterior and middle scallops of posterior leaflet; 8 o’clock, separation of anterior and middle scallops of posterior leaflet
The mathematical description of human chordae tendineae remains challenging, due to the fact that their geometry is of difficult detection through common in vivo imaging modalities (Dal‐Bianco and Levine, 2013; Khalighi et al., 2017) and meaning that human ex vivo studies are the primary sources of knowledge regarding chordal anatomy. Chordae tendineae are distinguished by their morphological diversity in number, insertion points into the leaflets, thickness and branching patterns, as given by previous human ex vivo studies (Lam et al., 1970; Gunnal et al., 2015). Regarding human MVs, it is difficult to characterise the exact insertion points of chordae into the leaflets with the imaging techniques currently available (Yamaura et al., 2008), and even the mathematical description of the location of insertion points into the PMs and into the mitral leaflets is based upon assumptions and the expertise of clinicians (Stevanella et al., 2011).
In reality, for a human MV model representation, it is common mathematically to simplify the shape of the PMs, as well as chordae insertion patterns: some studies represent the PM tips as unique 3D points where all chordae insert, as previously mentioned (Cochran and Kunzelman, 1998; Stevanella et al., 2009; Prot et al., 2010; Rim et al., 2013); others assume a parabola representing a 2D cut‐section of the PM shape, but where all chordae still insert on the tip (Park et al., 2019); and others still, assume them to have a spherical (Stevanella et al., 2011; Wang and Sun, 2013) or C‐shape (Choi et al., 2016) (schematised in Figure 11) and create different insertion points for the chordae according to their classification.
FIGURE 11.
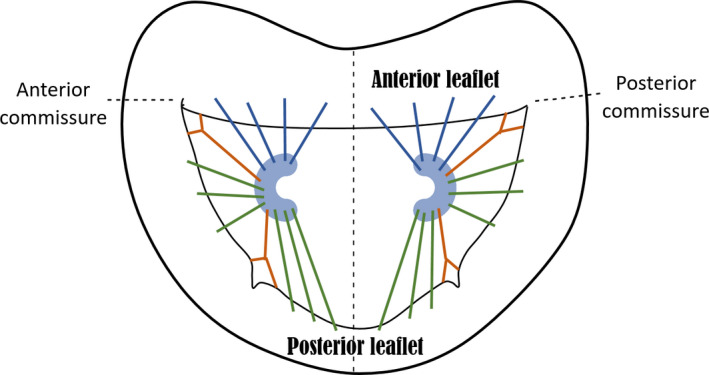
Axial view of C‐shape representation for the PMs, as present in the literature and suggested by expert surgeons, as well as a simplified depiction of chordae tendineae insertion patterns. Blue, green and orange chordae are those inserting into the anterior leaflet, posterior leaflet and paracommissural zones, respectively
Recent studies based on ovine MV have looked into further characterising chordae tendineae geometry and topology (Khalighi et al., 2017), as well as evaluating how native chordal anatomic characteristics affect valvular performance (Khalighi et al., 2019). Khalighi et al. (2017) based their investigation on high‐resolution micro‐CT derived 3D models, obtaining mathematical descriptions of the chordae such as curve‐skeleton characterisations, B‐spline parameterisations and Reeb graph representations (see Figure 12). They used the curve‐skeleton models to derive bifurcation and non‐planarity angles and also analysed the spatial distribution of chordae insertion sites into the leaflets (Khalighi et al., 2017). Their work yielded valuable information about chordal geometrical characterisation, including the presence of a non‐homogeneous cross‐sectional area along each segment (with chordal structure becoming thinner as it moves further away from the PM tip); the 2D nature of chordae, which collectively form a 3D load‐bearing support structure of the MV leaflets; and the development of analytical statistical models that describe chordae geometry, as well as binary trees, which aid in the prediction of possible shapes for chordal structure (Khalighi et al., 2017). Khalighi et al. (2019), on the other hand, found that varying cross‐sectional area, branching patterns and PM insertion points at the same origin did not greatly impact on ovine MV performance and they described an optimal chordae number range for appropriate function which eliminated over 75% of the native population of chordal insertions. Both studies then shed light on chordae tendineae geometrical characterisations which might possibly be applied to develop human MV models with simplified sub‐apparatus structures as a mean to overcome the current issues with in vivo imaging modalities.
FIGURE 12.
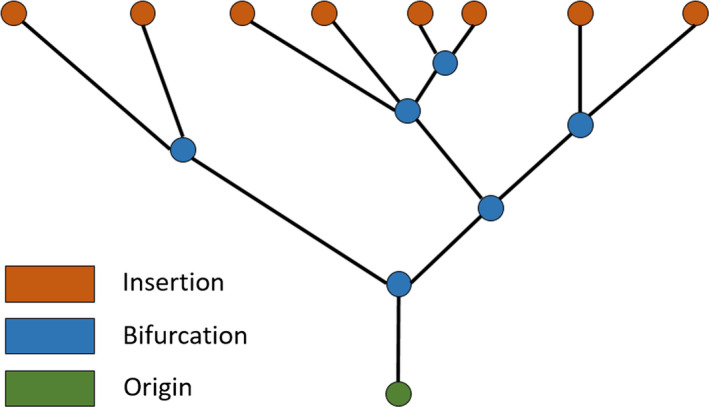
Example of Reeb graph employed to characterise chordae tendineae topology in Khalighi et al. (2017), illustrating the connectivity between branches. Green, blue and orange vertices correspond to chordal origin (at the PM level), bifurcation points and insertion points into the leaflets, respectively
4. CHANGES IN MITRAL VALVE MORPHOMETRY: DISEASE
4.1. Carpentier’s functional classification of MV disease
One of the most commonly used classifications of MV disease was designed by Carpentier (1983), sometimes referred to as the ‘pathophysiologic triad’ (Carpentier et al., 1980). It divides MV dysfunctions into three categories, all of which yield lesions that lead to clinical mitral regurgitation. These categories are based on the position of leaflet margins with respect to the mitral annulus plane: type I refers to normal leaflet motion and is associated with annular dilation and leaflet perforation; type II characterises excessive leaflet motion, usually derived from elongation or rupture of the chordae tendineae and/or the PM; and type III relates to restricted leaflet motion due to retraction of the subvalvular apparatus (IIIa) or PM displacement and left ventricular dilation, causing apical displacement (tethering) of the PM (IIIb). Further information on this classification and the associated lesions can be found elsewhere (Carpentier, 1983; Castillo et al., 2011; Stone et al., 2015). Mathematical interpretations of this classification were attempted in previous studies, for example representing annular dilation by increasing its diameter or PM displacement by increasing inter‐PM distance (Park et al., 2019). Taking this and the current literature available into account, examples of clinical lesions related to MV dysfunctional categories, and their influence in MV geometrical changes, are included in the following sections.
4.2. Geometrical changes in the mitral annulus are linked to type I dysfunction
In type I dysfunction, the human mitral annulus undergoes structural changes, becoming larger and flatter and losing its saddle shape (Mihaila et al., 2013; Lee et al., 2017). A mathematical representation of this is shown in Figure 13, where the annulus was obtained using dimensions characteristic of annular dilation, including a lower AHCWR, displayed against a healthy configuration.
FIGURE 13.
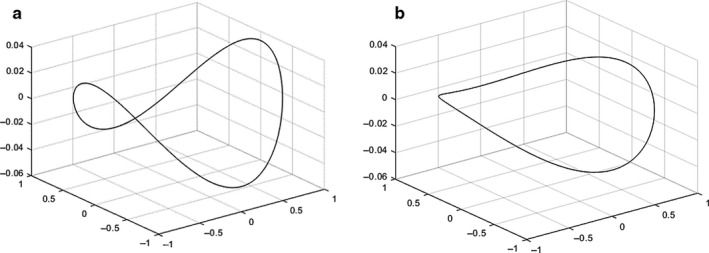
Hyperboloids representing: (a) a mitral annular normal saddle configuration; (b) a configuration associated with type I dysfunction, defined as in Park et al. (2019). The first configuration was created with the dimensions shown on Figure 6 and the diseased configuration on literature values for CW (42.2 mm), AP diameter (38.8 mm), AL–PM diameter (39 mm) and AHCWR (.132)
The increase in annular size associated with this type of mitral dysfunction compromises leaflet coaptation length and therefore prevents proper valve closing (Silbiger, 2011). For example, a previous in vitro study based on porcine MV showed that increasing annular area values (annular dilation) were associated with a decrease in the pressures needed to cause MV failure (Espino et al., 2007). The association between the effective regurgitant orifice area (EROA) and MV geometry serves as a validation of the role played by abnormalities in shape in dysfunctional cases. Concerning the human MV, increases in this index, linked to greater severity of regurgitation, have been associated with increasing annular circumference and area at end‐systole, although such associations were poorly correlated (R 2 = .38, R 2 = .48, respectively, with p‐value < .01) (Cong et al., 2018). Lee et al. (2013) have also found an inverse correlation between EROA and AHCWR in the same time frame, showing loss of MV saddle shape with increasing regurgitation (R 2 = .44, p‐value < .01) (Lee et al., 2013).
Other clinical studies have also correlated an increase in EROA with greater non‐coaptation distance between leaflets (maximal distance between both leaflet edges) at end‐systole, as given by Equation (30) (R 2 = .68, p‐value < .01) (Senechal et al., 2012):
| (30) |
where μ represents the non‐coaptation distance (in mm) and λ represents the EROA (in cm2).
In vivo human studies show that the flattening in MV shape present in disease is associated with loss of non‐planarity (Silbiger, 2011; Lee et al., 2013), quantified by increased NPAs (Mihaila et al., 2013) and greater billowing, shown as a correlation between lower AHCWR and higher values of billow volume (R 2 = .66, p‐value < .01) obtained at end‐systole:
| (31) |
where BV represented the billow volume (ml) and ε represents the AHCWR (as a percentage) (Lee et al., 2013).
In vivo studies have also shown a change in individual measurements describing annular shape in diseased cases: the AP diameter has been shown to increase in regurgitant valves (Lee et al., 2013; Mihaila et al., 2013), as well as the AL–PM diameter (Mihaila et al., 2013) and the commissural width (Lee et al., 2013). In addition, greater values of the circularity index are present in cases of regurgitation (Lee et al., 2013), associated with loss of contractility for the MV and a more dominant circular configuration through the cardiac cycle. All these associations show that abnormal human mitral geometry is intrinsically linked to mitral regurgitation (Sonne et al., 2009; Dal‐Bianco and Levine, 2013; Lee et al., 2013; Mihaila et al., 2013).
The process of annular dilation differs for anterior and posterior circumferences in the human MV, with the anterior fibrous portion being less prone to dilation (McCarthy et al., 2010). Mathematically, this means that the inter‐trigonal distance is not expected to change with mitral annular dilation (Suri et al., 2009; Calleja et al., 2015). The remaining 2/3 of the annulus (posterior annulus) is mainly muscular, dilating more easily (McCarthy et al., 2010). The anterior and posterior leaflet surface areas also increase with mitral regurgitation (Senechal et al., 2012; Dal‐Bianco and Levine, 2013; Lee et al., 2013; Mihaila et al., 2013); however, no apparent trend in dilation concerning anterior vs posterior is present in the literature.
4.3. Geometrical changes in the subvalvular apparatus are related to type III dysfunction
Configurational changes of the subvalvular apparatus have a profound impact on MV function. A previous in vitro study using porcine specimens assessed the effect of different annulo‐papillary lengths in MV coaptation, with different lengths leading to different MV states: not only are increased values associated with damage to the valve, but a shortening in annulo‐papillary lengths also induces diseased states (leaflet prolapse) (Espino et al., 2007). An optimum annulo‐papillary length is therefore needed for proper MV coaptation. In fact, type III dysfunctions of the MV have been associated with geometrical alterations of the subvalvular apparatus. Clinical studies have shown that the PMs suffer displacement in an attempt to attenuate the regurgitation effects (Silbiger, 2011; Lee et al., 2013): this is translated into increased inter‐PM distance (Kim et al., 2014; Obase et al., 2016), which has been well correlated with increased regurgitant volume in patients with severe functional ischaemic mitral regurgitation, as mathematically described by the equation below for end‐systolic data (R 2 = .84, p‐value < .01):
| (32) |
where RV represents the regurgitant volume (in ml) and υ represents the inter‐PM distance (in mm) (Jensen et al., 2010).
Type III dysfunction is also associated with increased left ventricular dimensions, which cause apical displacement of the PM. This leads to increased annulo‐papillary lengths and chordae tendineae elongation (Obase et al., 2016). Previous clinical studies have connected PM displacement with the severity of mitral regurgitation: increased apical displacement of the posteromedial PM (PMPM) was associated with greater regurgitant volume (Jensen et al., 2010) and augmented tethering distance, characteristic of PM displacement, was correlated with an increasing mitral regurgitation fraction at mid‐systole (Equation 33, R 2 stated as .64, p‐value < .01) (Uemura et al., 2005):
| (33) |
where TD represents the PMPM tethering distance (in mm/m2) and M RF represents the mitral regurgitation fraction (as a percentage).
Another clinical study found independent associations between apical displacement of the PMPM and posterior displacement of the AL–PM with increasing tenting area, related to loss of systolic annular function and regurgitation (Yiu et al., 2000). However, the obtained data were too disperse to yield strong correlations among these parameters.
5. FUTURE DIRECTIONS AND RECOMMENDATIONS FOR THE USE OF MORPHOMETRIC INFORMATION IN MITRAL VALVE CLINICAL ANALYSIS
This review paper focuses on grouping and briefly outlining the current best knowledge regarding MV morphometry by obtaining data from a range of different sources, including in vitro, in vivo and in silico studies. The quantitative data available have been analysed to derive further empirical mathematical relationships between dimensions. These can prove valuable to describe a healthy status of the MV, or to show the association between an abnormal valve shape and cases of dysfunction. It remains challenging to combine the morphometric information available in the literature to produce a coherent morphometric model of the human MV, based on mathematical correlations. Empirical relationships derived from direct correlations between dimensions and any relationships predicted analytically (or mathematically derived shapes) present with inherent differences. In addition, such correlations are derived from a specific imaging time frame, making it difficult to generalise these findings to the entire cardiac cycle.
Moreover, the use of different imaging modalities to obtain quantitative measurements, or the employment of different reference points, coordinate systems and anatomical landmarks, may lead to differing ranges for the same dimensions across studies. On the other hand, several imaging modalities present with a lack of spatial resolution, therefore making it difficult accurately to measure valve dimensions. It also remains challenging to represent the subvalvular apparatus rigorously, as current in vivo imaging modalities are unable to capture the chordae and PM properly. This is the motivation behind the use of ex vivo data in computational models, as well as complete ex vivo animal geometries, which, in combination with micro‐CT imaging, allow for high‐resolution detail of all MV components (Bloodworth et al., 2017; Khalighi et al., 2017; 2018).
Computational modelling has been directed towards the study of MV function: while some studies have focused on normal physiological valve functioning (Votta et al., 2008; Wang and Sun, 2013; Domenichini and Pedrizzetti, 2015; Gao et al., 2017a), others have focused on diseased cases (Wenk et al., 2010; Rim et al., 2013; Choi et al., 2016) and surgical procedures (Ge et al., 2014; Rim et al., 2015; Rausch et al., 2017). The first geometrical models were based on idealised shapes of the MV, derived from literature data (Kunzelman et al., 1993; Salgo et al., 2002). However, as the accuracy of MV models is highly sensitive to valve geometry, patient‐specific approaches have been preferred, with the MV apparatus being derived from medical images (Rim et al., 2013; Ge et al., 2014). Moreover, studies have been focused on less invasive methodologies for the determination of mitral tissue properties in vivo, including leaflet strains (Rego et al., 2018). Faster and more efficient methods to study MV function are becoming a reality; for example, a recent study employed a complete human heart model (Baillargeon et al., 2014) to study ventricular dilation, its impact on the MV structure and its repair through annuloplasty (Rausch et al., 2017). This demonstrates the great potential of computational simulations to optimise medical intervention, develop tailored device designs and aid in treatment management. The use of a more complete set of morphometric information on the MV, such as the one described in this paper, may aid in this endeavour, which can then be useful for studying the biomechanics associated with specific valve shapes in healthy and diseased ranges.
CONFLICT OF INTEREST
None.
AUTHOR CONTRIBUTIONS
All authors were involved in the design of the study and have critically revised the manuscript. Individual contributions are as follows: Miss Diana Oliveira: Initial draft of the manuscript; gathering of morphometric mitral valve information from the current literature, for healthy and diseased cases; statistical analysis with published data; acquisition of mitral valve anatomic data and respective data analysis. Dr Janaki Srinivasan: Acquisition of mitral valve anatomic data. Dr Dana Dawson: Clinical guidance; recommendation of the clinical database to employ and decision on which sample to use. Dr Keith Buchan: Surgical guidance; determination of relevant morphometric aspects of the mitral valve, including anatomic arrangements from the surgical point of view; advice on image sketches for the manuscript. Dr Daniel Espino: Guidance on organisation and presentation of information and data. Prof Duncan Shepherd: Guidance on organisation and presentation of information and data.
ETHICAL APPROVAL
The data obtained by the authors are for healthy volunteers recruited under the ethically approved research study ‘Exercise Capacity in Adults’ with REC reference 13/NS/0034 and IRAS ID 127501.
Supporting information
Appendix S1
Oliveira D, Srinivasan J, Espino D, Buchan K, Dawson D, Shepherd D. Geometric description for the anatomy of the mitral valve: A review. J. Anat. 2020;237:209–224. 10.1111/joa.13196
Funding information
The creation of the database employed in our study was sponsored by the University of Aberdeen, under the research study ‘Exercise Capacity in Adults’.
REFERENCES
- Al‐Atabi, M. , Espino, D.M. , Hukins, D.W. and Buchan, K.G. (2012) Biomechanical assessment of surgical repair of the mitral valve. Proceedings of the Institution of Mechanical Engineers. Part H. Journal of Engineering in Medicine, 226, 275–287. [DOI] [PubMed] [Google Scholar]
- Baillargeon, B. , Rebelo, N. , Fox, D.D. , Taylor, R.L. and Kuhl, E. (2014) The Living Heart Project: a robust and integrative simulator for human heart function. European Journal of Mechanics – A/Solids, 48, 38–47. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bloodworth, C.H.T. , Pierce, E.L. , Easley, T.F. , Drach, A. , Khalighi, A.H. , Toma, M. , et al. (2017) Ex vivo methods for informing computational models of the mitral valve. Annals of Biomedical Engineering, 45, 496–507. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bouma, W. and Gorman, R.C. (2019) Commentary: Three‐dimensional P3 tethering angle at the heart of future surgical decision making in ischemic mitral regurgitation. Journal of Thoracic and Cardiovascular Surgery, 157, 1806–1807. [DOI] [PubMed] [Google Scholar]
- Calleja, A. , Poulin, F. , Woo, A. , Meineri, M. , Jedrzkiewicz, S. , Vannan, M.A. , et al. (2015) Quantitative modeling of the mitral valve by three‐dimensional transesophageal echocardiography in patients undergoing mitral valve repair: correlation with intraoperative surgical technique. Journal of the American Society of Echocardiography, 28, 1083–1092. [DOI] [PubMed] [Google Scholar]
- Carpentier, A. (1983) Cardiac valve surgery—the ‘French correction’. Journal of Thoracic and Cardiovascular Surgery, 86, 323–337. [PubMed] [Google Scholar]
- Carpentier, A. , Chauvaud, S. , Fabiani, J.N. , Deloche, A. , Relland, J. , Lessana, A. , et al. (1980) Reconstructive surgery of mitral valve incompetence: ten‐year appraisal. Journal of Thoracic and Cardiovascular Surgery, 79, 338–348. [PubMed] [Google Scholar]
- Carpentier, A.F. , Lessana, A. , Relland, J.Y. , Belli, E. , Mihaileanu, S. , Berrebi, A.J. , et al. (1995) The ‘physio‐ring’: an advanced concept in mitral valve annuloplasty. Annals of Thoracic Surgery, 60, 1177–1185; discussion 1185–1186. [DOI] [PubMed] [Google Scholar]
- Castillo, J.G. , Solis, J. , Gonzalez‐Pinto, A. and Adams, D.H. (2011) Surgical echocardiography of the mitral valve. Revista Espanola de Cardiologia, 64, 1169–1181. [DOI] [PubMed] [Google Scholar]
- Choi, A. , McPherson, D.D. and Kim, H. (2016) Biomechanical evaluation of the pathophysiologic developmental mechanisms of mitral valve prolapse: effect of valvular morphologic alteration. Medical & Biological Engineering & Computing, 54, 799–809. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ciarka, A. , Braun, J. , Delgado, V. , Versteegh, M. , Boersma, E. , Klautz, R. , et al. (2010) Predictors of mitral regurgitation recurrence in patients with heart failure undergoing mitral valve annuloplasty. American Journal of Cardiology, 106, 395–401. [DOI] [PubMed] [Google Scholar]
- Cochran, R.P. and Kunzelman, K.S. (1998) Effect of papillary muscle position on mitral valve function: relationship to homografts. Annals of Thoracic Surgery, 66, S155–S161. [DOI] [PubMed] [Google Scholar]
- Cong, T. , Gu, J. , Lee, A.P. , Shang, Z. , Sun, Y. , Sun, Q. , et al. (2018) Quantitative analysis of mitral valve morphology in atrial functional mitral regurgitation using real‐time 3‐dimensional echocardiography atrial functional mitral regurgitation. Cardiovascular Ultrasound, 16, 13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dal‐Bianco, J.P. and Levine, R.A. (2013) Anatomy of the mitral valve apparatus: role of 2D and 3D echocardiography. Cardiology Clinics, 31, 151–164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Delgado, V. , Tops, L.F. , Schuijf, J.D. , de Roos, A. , Brugada, J. , Schalij, M.J. , et al. (2009) Assessment of mitral valve anatomy and geometry with multislice computed tomography. JACC: Cardiovascular Imaging, 2, 556–565. [DOI] [PubMed] [Google Scholar]
- Deorsola, L. and Bellone, A. (2018) Coaptation Triangle and Golden Proportion in mitral valve anatomy. Does nature play with geometry? Echocardiography, 35, 30–38. [DOI] [PubMed] [Google Scholar]
- Domenichini, F. and Pedrizzetti, G. (2015) Asymptotic model of fluid‐tissue interaction for mitral valve dynamics. Cardiovascular Engineering and Technology, 6, 95–104. [DOI] [PubMed] [Google Scholar]
- Dudzinski, D.M. and Hung, J. (2014) Echocardiographic assessment of ischemic mitral regurgitation. Cardiovascular Ultrasound, 12, 46. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duplessis, L.A. and Marchand, P. (1964) The anatomy of the mitral valve and its associated structures. Thorax, 19, 221–227. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eckert, C.E. , Zubiate, B. , Vergnat, M. , Gorman, J.H., 3rd , Gorman, R.C. and Sacks, M.S. (2009) In vivo dynamic deformation of the mitral valve annulus. Annals of Biomedical Engineering, 37, 1757–1771. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Espino, D.M. , Shepherd, D.E. , Hukins, D.W. and Buchan, K.G. (2005) The role of Chordae tendineae in mitral valve competence. Journal of Heart Valve Disease, 14, 603–609. [PubMed] [Google Scholar]
- Espino, D.M. , Shepherd, D.E. and Buchan, K.G. (2007) Effect of mitral valve geometry on valve competence. Heart and Vessels, 22, 109–115. [DOI] [PubMed] [Google Scholar]
- Gao, H. , Feng, L. , Qi, N. , Berry, C. , Griffith, B.E. and Luo, X. (2017a) A coupled mitral valve‐left ventricle model with fluid‐structure interaction. Medical Engineering & Physics, 47, 128–136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gao, H. , Qi, N. , Feng, L. , Ma, X. , Danton, M. , Berry, C. , et al. (2017b) Modelling mitral valvular dynamics‐current trend and future directions. International Journal for Numerical Methods in Biomedical Engineering, 33, 33:e2858, 1–15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Garbi, M. and Monaghan, M.J. (2015) Quantitative mitral valve anatomy and pathology. Echo Research and Practice, 2, R63–72. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ge, L. , Morrel, W.G. , Ward, A. , Mishra, R. , Zhang, Z. , Guccione, J.M. , et al. (2014) Measurement of mitral leaflet and annular geometry and stress after repair of posterior leaflet prolapse: virtual repair using a patient‐specific finite element simulation. Annals of Thoracic Surgery, 97, 1496–1503. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grbic, S. , Easley, T.F. , Mansi, T. , Bloodworth, C.H. , Pierce, E.L. , Voigt, I. , et al. (2017) Personalized mitral valve closure computation and uncertainty analysis from 3D echocardiography. Medical Image Analysis, 35, 238–249. [DOI] [PubMed] [Google Scholar]
- Gunnal, S.A. , Wabale, R.N. and Farooqui, M.S. (2015) Morphological study of chordae tendinae in human cadaveric hearts. Heart Views, 16, 1–12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hirakawa, S. , Sasayama, S. , Tomoike, H. , Crozatier, B. , Franklin, D. , McKown, D. , et al. (1977) In situ measurement of papillary muscle dynamics in the dog left ventricle. American Journal of Physiology, 233, H384–H391. [DOI] [PubMed] [Google Scholar]
- Ionasec, R.I. , Voigt, I. , Georgescu, B. , Wang, Y. , Houle, H. , Vega‐Higuera, F. , et al. (2010) Patient‐specific modeling and quantification of the aortic and mitral valves from 4‐D cardiac CT and TEE. IEEE Transactions on Medical Imaging, 29, 1636–1651. [DOI] [PubMed] [Google Scholar]
- Jassar, A.S. , Vergnat, M. , Jackson, B.M. , McGarvey, J.R. , Cheung, A.T. , Ferrari, G. , et al. (2014) Regional annular geometry in patients with mitral regurgitation: implications for annuloplasty ring selection. Annals of Thoracic Surgery, 97, 64–70. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jensen, H. , Jensen, M.O. , Smerup, M.H. , Ringgaard, S. , Sorensen, T.S. , Andersen, N.T. , et al. (2010) Three‐dimensional assessment of papillary muscle displacement in a porcine model of ischemic mitral regurgitation. Journal of Thoracic and Cardiovascular Surgery, 140, 1312–1318. [DOI] [PubMed] [Google Scholar]
- Jiang, L. , Owais, K. , Matyal, R. , Khabbaz, K.R. , Liu, D.C. , Montealegre‐Gallegos, M. , et al. (2014) Dynamism of the mitral annulus: a spatial and temporal analysis. Journal of Cardiothoracic and Vascular Anesthesia, 28, 1191–1197. [DOI] [PubMed] [Google Scholar]
- Jimenez, J.H. , Liou, S.W. , Padala, M. , He, Z. , Sacks, M. , Gorman, R.C. , et al. (2007) A saddle‐shaped annulus reduces systolic strain on the central region of the mitral valve anterior leaflet. Journal of Thoracic and Cardiovascular Surgery, 134, 1562–1568. [DOI] [PubMed] [Google Scholar]
- Jolley, M.A. , Ghelani, S.J. , Adar, A. and Harrild, D.M. (2017) Three‐dimensional mitral valve morphology and age‐related trends in children and young adults with structurally normal hearts using transthoracic echocardiography. Journal of the American Society of Echocardiography, 30, 561–571. [DOI] [PubMed] [Google Scholar]
- Kaiser, A.D. , McQueen, D.M. and Peskin, C.S. (2019) Modeling the mitral valve. International Journal for Numerical Methods in Biomedical Engineering, 35, e3240. [DOI] [PubMed] [Google Scholar]
- Khalighi, A.H. , Drach, A. , Bloodworth, C.H.T. , Pierce, E.L. , Yoganathan, A.P. , Gorman, R.C. , et al. (2017) Mitral valve chordae tendineae: topological and geometrical characterization. Annals of Biomedical Engineering, 45, 378–393. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khalighi, A.H. , Drach, A. , Gorman, R.C. , Gorman, J.H. 3rd and Sacks, M.S. (2018) Multi‐resolution geometric modeling of the mitral heart valve leaflets. Biomechanics and Modeling in Mechanobiology, 17, 351–366. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khalighi, A.H. , Rego, B.V. , Drach, A. , Gorman, R.C. , Gorman, J.H. 3rd and Sacks, M.S. (2019) Development of a functionally equivalent model of the mitral valve chordae tendineae through topology optimization. Annals of Biomedical Engineering, 47, 60–74. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim, K. , Kaji, S. , An, Y. , Nishino, T. , Tani, T. , Kitai, T. , et al. (2014) Interpapillary muscle distance independently affects severity of functional mitral regurgitation in patients with systolic left ventricular dysfunction. Journal of Thoracic and Cardiovascular Surgery, 148, 434–440e1. [DOI] [PubMed] [Google Scholar]
- Kunzelman, K.S. , Cochran, R.P. , Chuong, C. , Ring, W.S. , Verrier, E.D. and Eberhart, R.D. (1993) Finite element analysis of the mitral valve. Journal of Heart Valve Disease, 2, 326–340. [PubMed] [Google Scholar]
- Kunzelman, K.S. , Cochran, R.P. , Verrier, E.D. and Eberhart, R.C. (1994) Anatomic basis for mitral valve modelling. Journal of Heart Valve Disease, 3, 491–496. [PubMed] [Google Scholar]
- Kunzelman, K.S. , Einstein, D.R. and Cochran, R.P. (2007) Fluid‐structure interaction models of the mitral valve: function in normal and pathological states. Philosophical Transactions of the Royal Society of London. Series B, Biological Sciences, 362, 1393–1406. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lam, J.H. , Ranganathan, N. , Wigle, E.D. and Silver, M.D. (1970) Morphology of the human mitral valve. I. Chordae tendineae: a new classification. Circulation, 41, 449–458. [DOI] [PubMed] [Google Scholar]
- Lee, A.P. , Hsiung, M.C. , Salgo, I.S. , Fang, F. , Xie, J.M. , Zhang, Y.C. , et al. (2013) Quantitative analysis of mitral valve morphology in mitral valve prolapse with real‐time 3‐dimensional echocardiography: importance of annular saddle shape in the pathogenesis of mitral regurgitation. Circulation, 127, 832–841. [DOI] [PubMed] [Google Scholar]
- Lee, A.P. , Jin, C.N. , Fan, Y. , Wong, R.H.L. , Underwood, M.J. and Wan, S. (2017) Functional implication of mitral annular disjunction in mitral valve prolapse: a quantitative dynamic 3D echocardiographic study. JACC: Cardiovascular Imaging, 10, 1424–1433. [DOI] [PubMed] [Google Scholar]
- Levack, M.M. , Jassar, A.S. , Shang, E.K. , Vergnat, M. , Woo, Y.J. , Acker, M.A. , et al. (2012) Three‐dimensional echocardiographic analysis of mitral annular dynamics: implication for annuloplasty selection. Circulation, 126, S183–S188. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lomholt, M. , Nielsen, S.L. , Hansen, S.B. , Andersen, N.T. and Hasenkam, J.M. (2002) Differential tension between secondary and primary mitral chordae in an acute in‐vivo porcine model. Journal of Heart Valve Disease, 11, 337–345. [PubMed] [Google Scholar]
- Machino‐Ohtsuka, T. , Seo, Y. , Ishizu, T. , Sato, K. , Sugano, A. , Yamamoto, M. , et al. (2016) Novel mechanistic insights into atrial functional mitral regurgitation—3‐dimensional echocardiographic study. Circulation Journal, 80, 2240–2248. [DOI] [PubMed] [Google Scholar]
- Mansi, T. , Voigt, I. , Georgescu, B. , Zheng, X. , Mengue, E.A. , Hackl, M. , et al. (2012) An integrated framework for finite‐element modeling of mitral valve biomechanics from medical images: application to MitralClip intervention planning. Medical Image Analysis, 16, 1330–1346. [DOI] [PubMed] [Google Scholar]
- Marzilli, M. , Sabbah, H.N. , Lee, T. and Stein, P.D. (1980) Role of the papillary muscle in opening and closure of the mitral valve. American Journal of Physiology, 238, H348–H354. [DOI] [PubMed] [Google Scholar]
- McCarthy, K.P. , Ring, L. and Rana, B.S. (2010) Anatomy of the mitral valve: understanding the mitral valve complex in mitral regurgitation. European Journal of Echocardiography, 11, i3–9. [DOI] [PubMed] [Google Scholar]
- Mihaila, S. , Muraru, D. , Casablana, S. , Peluso, D. , Cucchini, U. , del Bianco, L. , et al. (2013) Three‐dimensional changes in mitral valve annulus geometry in organic and functional mitral regurgitation: insights for mitral valve repair. European Heart Journal, 34, 4751. [Google Scholar]
- Nielsen, S.L. , Timek, T.A. , Green, G.R. , Dagum, P. , Daughters, G.T. , Hasenkam, J.M. , et al. (2003) Influence of anterior mitral leaflet second‐order chordae tendineae on left ventricular systolic function. Circulation, 108, 486–491. [DOI] [PubMed] [Google Scholar]
- Obase, K. , Weinert, L. , Hollatz, A. , Farooqui, F. , Roberts, J.D. , Minhaj, M.M. , et al. (2016) Elongation of chordae tendineae as an adaptive process to reduce mitral regurgitation in functional mitral regurgitation. European Heart Journal of Cardiovascular Imaging, 17, 500–509. [DOI] [PubMed] [Google Scholar]
- Okamoto, H. , Itoh, Y. and Nara, Y. (2007) Geometric analysis of the anterior mitral leaflet and mitral valve orifice in cadaveric hearts. Circulation Journal, 71, 1794–1799. [DOI] [PubMed] [Google Scholar]
- Owais, K. , Montealegre‐Gallegos, M. , Jeganathan, J. , Matyal, R. , Khabbaz, K.R. and Mahmood, F. (2016) Dynamic changes in the ischemic mitral annulus: implications for ring sizing. Annals of Cardiac Anaesthesia, 19, 15–19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Padala, M. , Sacks, M.S. , Liou, S.W. , Balachandran, K. , He, Z. and Yoganathan, A.P. (2010) Mechanics of the mitral valve strut chordae insertion region. Journal of Biomechanical Engineering, 132, 081004. [DOI] [PubMed] [Google Scholar]
- Park, J. , Geirsson, A. and Bonde, P.N. (2019) Mathematical blueprint of a mitral valve. Seminars in Thoracic and Cardiovascular Surgery, 31, 399–411. [DOI] [PubMed] [Google Scholar]
- Pouch, A.M. , Vergnat, M. , McGarvey, J.R. , Ferrari, G. , Jackson, B.M. , Sehgal, C.M. , et al. (2014) Statistical assessment of normal mitral annular geometry using automated three‐dimensional echocardiographic analysis. Annals of Thoracic Surgery, 97, 71–77. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prot, V. , Skallerud, B. , Sommer, G. and Holzapfel, G.A. (2010) On modelling and analysis of healthy and pathological human mitral valves: two case studies. Journal of the Mechanical Behavior of Biomedical Materials, 3, 167–177. [DOI] [PubMed] [Google Scholar]
- Ranganathan, N. , Lam, J.H. , Wigle, E.D. and Silver, M.D. (1970) Morphology of the human mitral valve. II. The valve leaflets. Circulation, 41, 459–467. [DOI] [PubMed] [Google Scholar]
- Rausch, M.K. , Bothe, W. , Kvitting, J.P. , Swanson, J.C. , Ingels, N.B. Jr. , Miller, D.C. , et al. (2011) Characterization of mitral valve annular dynamics in the beating heart. Annals of Biomedical Engineering, 39, 1690–1702. [DOI] [PubMed] [Google Scholar]
- Rausch, M.K. , Zollner, A.M. , Genet, M. , Baillargeon, B. , Bothe, W. and Kuhl, E. (2017) A virtual sizing tool for mitral valve annuloplasty. International Journal for Numerical Methods in Biomedical Engineering, 33, 33:e02788, 1–14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rego, B.V. , Khalighi, A.H. , Drach, A. , Lai, E.K. , Pouch, A.M. , Gorman, R.C. , et al. (2018) A noninvasive method for the determination of in vivo mitral valve leaflet strains. International Journal for Numerical Methods in Biomedical Engineering, 34, e3142. [DOI] [PubMed] [Google Scholar]
- Rim, Y. , Choi, A. , McPherson, D.D. and Kim, H. (2015) Personalized computational modeling of mitral valve prolapse: virtual leaflet resection. PLoS ONE, 10, e0130906. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rim, Y. , McPherson, D.D. , Chandran, K.B. and Kim, H. (2013) The effect of patient‐specific annular motion on dynamic simulation of mitral valve function. Journal of Biomechanics, 46, 1104–1112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saha, A. and Roy, S. (2018) Papillary muscles of left ventricle—Morphological variations and its clinical relevance. Indian Heart Journal, 70, 894–900. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sakai, T. , Okita, Y. , Ueda, Y. , Tahata, T. , Ogino, H. , Matsuyama, K. , et al. (1999) Distance between mitral anulus and papillary muscles: anatomic study in normal human hearts. Journal of Thoracic and Cardiovascular Surgery, 118, 636–641. [DOI] [PubMed] [Google Scholar]
- Salgo, I.S. , Gorman, J.H. 3rd , Gorman, R.C. , Jackson, B.M. , Bowen, F.W. , Plappert, T. , et al. (2002) Effect of annular shape on leaflet curvature in reducing mitral leaflet stress. Circulation, 106, 711–717. [DOI] [PubMed] [Google Scholar]
- Sedransk, K.L. , Grande‐Allen, K.J. and Vesely, I. (2002) Failure mechanics of mitral valve chordae tendineae. Journal of Heart Valve Disease, 11, 644–650. [PubMed] [Google Scholar]
- Senechal, M. , Michaud, N. , Machaalany, J. , Bernier, M. , Dubois, M. , Magne, J. , et al. (2012) Relation of mitral valve morphology and motion to mitral regurgitation severity in patients with mitral valve prolapse. Cardiovasc Ultrasound, 10, 3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shen, X. , Wang, T. , Cao, X. and Cai, L. (2017) The geometric model of the human mitral valve. PLoS ONE, 12, e0183362. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Silbiger, J.J. (2011) Mechanistic insights into ischemic mitral regurgitation: echocardiographic and surgical implications. Journal of the American Society of Echocardiography, 24, 707–719. [DOI] [PubMed] [Google Scholar]
- Sonne, C. , Sugeng, L. , Watanabe, N. , Weinert, L. , Saito, K. , Tsukiji, M. , et al. (2009) Age and body surface area dependency of mitral valve and papillary apparatus parameters: assessment by real‐time three‐dimensional echocardiography. European Journal of Echocardiography, 10, 287–294. [DOI] [PubMed] [Google Scholar]
- Stephens, S.E. , Liachenko, S. , Ingels, N.B. , Wenk, J.F. and Jensen, M.O. (2017) High resolution imaging of the mitral valve in the natural state with 7 Tesla MRI. PLoS ONE, 12, e0184042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stevanella, M. , Votta, E. and Redaelli, A. (2009) Mitral valve finite element modeling: implications of tissues’ nonlinear response and annular motion. Journal of Biomechanical Engineering, 131, 121010. [DOI] [PubMed] [Google Scholar]
- Stevanella, M. , Maffessanti, F. , Conti, C.A. , Votta, E. , Arnoldi, A. , Lombardi, M. , et al. (2011) Mitral valve patient‐specific finite element modeling from cardiac MRI: application to an annuloplasty procedure. Cardiovascular Engineering and Technology, 2, 66–76. [Google Scholar]
- Stone, G.W. , Vahanian, A.S. , Adams, D.H. , Abraham, W.T. , Borer, J.S. , Bax, J.J. , et al. (2015) Clinical trial design principles and endpoint definitions for transcatheter mitral valve repair and replacement: part 1: clinical trial design principles: a consensus document from the Mitral Valve Academic Research Consortium. Journal of the American College of Cardiology, 66, 278–307. [DOI] [PubMed] [Google Scholar]
- Sun, X. , Jiang, Y. , Huang, G. , Huang, J. , Shi, M. , Pang, L. , et al. (2019) Three‐dimensional mitral valve structure in predicting moderate ischemic mitral regurgitation improvement after coronary artery bypass grafting. Journal of Thoracic and Cardiovascular Surgery, 157(1795–1803), e2. [DOI] [PubMed] [Google Scholar]
- Suri, R.M. , Grewal, J. , Mankad, S. , Enriquez‐Sarano, M. , Miller, F.A. Jr. and Schaff, H.V. (2009) Is the anterior intertrigonal distance increased in patients with mitral regurgitation due to leaflet prolapse? Annals of Thoracic Surgery, 88, 1202–1208. [DOI] [PubMed] [Google Scholar]
- Tang, Z. , Fan, Y.T. , Wang, Y. , Jin, C.N. , Kwok, K.W. and Lee, A.P. (2019) Mitral annular and left ventricular dynamics in atrial functional mitral regurgitation: a three‐dimensional and speckle‐tracking echocardiographic study. Journal of the American Society of Echocardiography, 32, 503–513. [DOI] [PubMed] [Google Scholar]
- Timek, T.A. , Nielsen, S.L. , Green, G.R. , Dagum, P. , Bolger, A.F. , Daughters, G.T. , et al. (2001) Influence of anterior mitral leaflet second‐order chordae on leaflet dynamics and valve competence. Annals of Thoracic Surgery, 72, 535–540. [DOI] [PubMed] [Google Scholar]
- Topilsky, Y. , Vaturi, O. , Watanabe, N. , Bichara, V. , Nkomo, V.T. , Michelena, H. , et al. (2013) Real‐time 3‐dimensional dynamics of functional mitral regurgitation: a prospective quantitative and mechanistic study. Journal of the American Heart Association, 2, e000039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Uemura, T. , Otsuji, Y. , Nakashiki, K. , Yoshifuku, S. , Maki, Y. , Yu, B. , et al. (2005) Papillary muscle dysfunction attenuates ischemic mitral regurgitation in patients with localized basal inferior left ventricular remodeling: insights from tissue Doppler strain imaging. Journal of the American College of Cardiology, 46, 113–119. [DOI] [PubMed] [Google Scholar]
- Veronesi, F. , Corsi, C. , Sugeng, L. , Mor‐Avi, V. , Caiani, E.G. , Weinert, L. , et al. (2009) A study of functional anatomy of aortic‐mitral valve coupling using 3D matrix transesophageal echocardiography. Circulation: Cardiovascular Imaging, 2, 24–31. [DOI] [PubMed] [Google Scholar]
- Votta, E. , Caiani, E. , Veronesi, F. , Soncini, M. , Montevecchi, F.M. and Redaelli, A. (2008) Mitral valve finite‐element modelling from ultrasound data: a pilot study for a new approach to understand mitral function and clinical scenarios. Philosophical Transactions. Series A, Mathematical, Physical, and Engineering Sciences, 366, 3411–3434. [DOI] [PubMed] [Google Scholar]
- Wang, Q. and Sun, W. (2013) Finite element modeling of mitral valve dynamic deformation using patient‐specific multi‐slices computed tomography scans. Annals of Biomedical Engineering, 41, 142–153. [DOI] [PubMed] [Google Scholar]
- Warraich, H.J. , Chaudary, B. , Maslow, A. , Panzica, P.J. , Pugsley, J. and Mahmood, F. (2012) Mitral annular nonplanarity: correlation between annular height/commissural width ratio and the nonplanarity angle. Journal of Cardiothoracic and Vascular Anesthesia, 26, 186–190. [DOI] [PubMed] [Google Scholar]
- Wenk, J.F. , Zhang, Z. , Cheng, G. , Malhotra, D. , Acevedo‐Bolton, G. , Burger, M. , et al. (2010) First finite element model of the left ventricle with mitral valve: insights into ischemic mitral regurgitation. Annals of Thoracic Surgery, 89, 1546–1553. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilcox, A.G. , Buchan, K.G. and Espino, D.M. (2014) Frequency and diameter dependent viscoelastic properties of mitral valve chordae tendineae. Journal of the Mechanical Behavior of Biomedical Materials, 30, 186–195. [DOI] [PubMed] [Google Scholar]
- Yamaura, Y. , Watanabe, N. , Ogasawara, Y. , Tsukiji, M. , Okahashi, N. , Okura, H. , et al. (2008) Three‐dimensional echocardiographic measurements of distance between papillary muscles and mitral annulus: assessment with three‐dimensional quantification software system. Journal of Echocardiography, 6, 67–73. [Google Scholar]
- Yiu, S.F. , Enriquez‐Sarano, M. , Tribouilloy, C. , Seward, J.B. and Tajik, A.J. (2000) Determinants of the degree of functional mitral regurgitation in patients with systolic left ventricular dysfunction: a quantitative clinical study. Circulation, 102, 1400–1406. [DOI] [PubMed] [Google Scholar]
- Zhang, F. , Kanik, J. , Mansi, T. , Voigt, I. , Sharma, P. , Ionasec, R.I. , et al. (2017) Towards patient‐specific modeling of mitral valve repair: 3D transesophageal echocardiography‐derived parameter estimation. Medical Image Analysis, 35, 599–609. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Appendix S1


