Abstract
Tyrosinase (TYR) is a metalloenzyme classified as a type-3 copper protein, which is involved in the synthesis of melanin through a catalytic process beginning with the conversion of the amino acid l-Tyrosine (l-Tyr) to l-3,4-dihydroxyphenylalanine (l-DOPA). It plays an important role in the mechanism of melanogenesis in various organisms including mammals, plants, and fungi. Herein, we used a combination of computational molecular modeling techniques including molecular dynamic (MD) simulations and the linear interaction energy (LIE) model to evaluate the binding free energy of a set of analogs of kojic acid (KA) in complex with TYR. For the MD simulations, we used a dummy model including the description of the Jahn–Teller effect for Cu2+ ions in the active site of this enzyme. Our results show that the LIE model predicts the TYR binding affinities of the inhibitor in close agreement to experimental results. Overall, we demonstrate that the classical model provides a suitable description of the main interactions between analogs of KA and Cu2+ ions in the active site of TYR.
Keywords: tyrosinase, inhibition, kojic acid, Jahn-Teller effect, binding free energy, computational chemistry
1. Introduction
Melanin is present in many organisms where it plays several key roles including photoprotection, thermoregulation, and wound healing. In humans, the melanin pigment is also responsible for the color of skin, eyes, and hair [1,2,3]. The abnormal loss of melanin and depigmentation can be a serious facial aesthetic and dermatological problem among humans [4]. On the other hand, increasing melanin synthesis and accumulation of these pigments occur in many types of skin disorders, including neurodegeneration associated with Parkinson’s disease and skin cancer [5,6,7]. Tyrosinase (TYR) is one of the key enzymes in mammalian melanin synthesis [8] and its function in melanin biosynthesis is well documented [9]. A recent article has reviewed the importance of inhibitors of TYR, which are utilized in cosmetic and medicinal industries as depigmentation agents and also in food and agriculture industries as antibrowning compounds [10]. Therefore, inhibitors of TYR are a class of important clinical drugs.
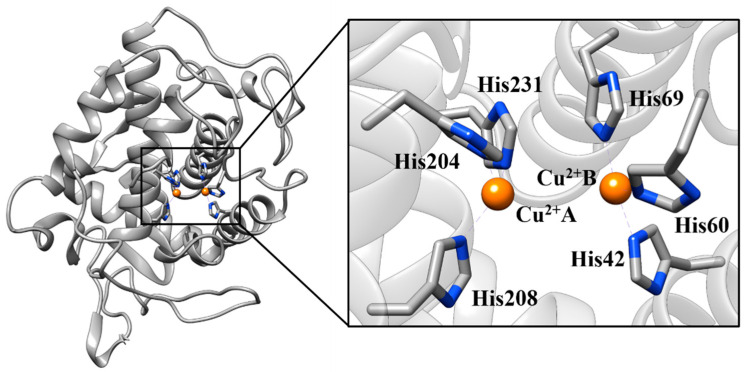
TYR is a metalloenzyme found in animal tissues, mushrooms, and plants [11,12,13]. There are two copper ions (Cu2+) in the active site of tyrosinase. Each Cu2+ coordinates with three histidine residues (Figure 1) [14,15]. In its catalytic cycle (Figure 2), the l-Tyrosine (l-Tyr) is hydroxylated to l-3,4-dihydroxyphenylalanine (l-DOPA), a phase called monophenolase, and then l-DOPA is oxidized to o-dopaquinone, a phase called diphenolase [1,16]. Melanin is then rapidly formed by the spontaneous polymerization of o-dopaquinones [15,17].
Figure 1.
The catalytic site of tyrosinase (TYR) where Cu2+ ions interact with key histidine residues (Protein Data Bank (PDB) code 5I38).
Figure 2.
Melanogenesis stages catalyzed by the tyrosinase (TYR) enzyme.
Examples of TYR inhibitors are kojic acid (KA) [18], tropolone (TRO) [19], coumarins [20], vanillic acid, vanillin, and vanillic alcohol [21]. Particularly, KA is used as a positive standard in experimental measurements [22,23]. However, it has been reported that kojic acid has side effects such as a high sensitization potential, causing irritant contact dermatitis and displaying considerable toxicity [24,25,26]. Therefore, the development of TYR inhibitors with efficient bioactivity and less toxicity is a relevant branch of scientific research. Recently, we have used molecular modeling approaches to investigate biomolecular systems with an emphasis on enzymatic reactions and inhibition [27,28,29,30,31,32,33,34,35,36,37,38,39].
Herein, we report a computational study of analogs of KA in complex with TYR from Bacillus megaterium (TYRBm). We also compared the binding of these inhibitors with l-Tyr and l-DOPA, where a dummy atom model [40] was used to represent Cu2+ ions in the active site of TYRBm. This model provides a suitable description of structural and electrostatic effects by using “dummy” atoms around a metal ion and has been applied successfully on previous studies [41,42,43]. The binding free energies for the set of ligands were calculated with the linear interaction energy (LIE) approach [44]. Overall, this work shines a light on the inhibitor–tyrosinase complex interactions, which is paramount for the development of new inhibitors of TYR.
2. Results and Discussion
2.1. Molecular Docking Simulations
To evaluate the technical procedures used for molecular docking, a re-docking simulation was carried out using the atomic coordinates of natural substrates (l-Tyr and l-DOPA) and the KA inhibitor as an experimental reference. Our molecular re-docking results are summarized in Table 1. According to the re-docking procedure, all ligands bind into the active site of TYR and maintain key interactions with Cu2+ ions. Besides, the conformations obtained from molecular docking procedures are in good agreement with experimental data, demonstrated by small root-mean-square deviation (RMSD) values (< 0.50 Å) when superimposed with the experimental structures. The binding affinity values computed by the MOLDOCK scoring function appear to follow reality since l-Tyr and l-DOPA are natural substrates of TYR (excellent binding energies) while KA is a competitive inhibitor [45] with slightly weaker binding energy. Our molecular docking results are in agreement with previous in silico studies [46,47,48,49,50,51]. The 3D structures of the molecular docking results are available in Protein Data Bank (PDB) format in the Supplementary Materials.
Table 1.
MOLDOCK scoring (in kcal/mol) and RMSD (in Å) values for re-docking procedures.
| Compound | MOLDOCK | RMSD |
|---|---|---|
| l-Tyr | −89.77 | 0.22 |
| l-DOPA | −90.25 | 0.29 |
| KA | −69.26 | 0.31 |
l-Tyr: l-Tyrosine; l-DOPA: l-3,4-dihydroxyphenylalanine; KA: kojic acid
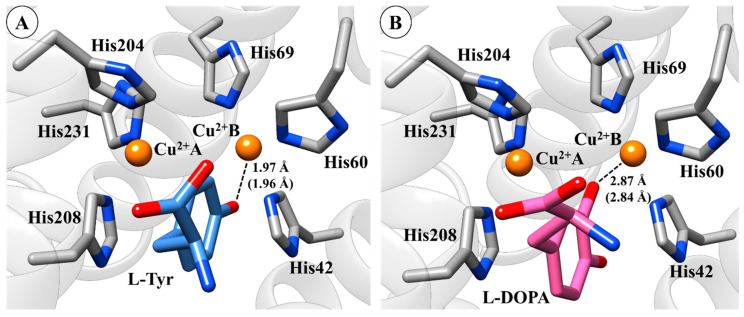
By performing a structural analysis of molecular docking results, some key interactions between groups of ligands and amino acid residues of TYR should be highlighted. It is worth mentioning that the hydroxyl group of l-Tyr ligand is positioned towards Cu2+B ion (distance 1.97 Å) and the aromatic ring of l-Tyr interacts with His208 through a π–π stacking interaction (Figure 3A). Note that these interactions are in agreement with experimental data [17,52,53], which demonstrate that the re-docking protocol used here was able to reproduce these key interactions in the active site of TYR. In the l-DOPA system, the re-docking results show that the phenol group of l-DOPA is also positioned towards a Cu2+B ion (distance 2.87 Å), which is also in agreement with previous studies (Figure 3B) [53,54,55].
Figure 3.
Binding mode of l-Tyrosine (l-Tyr) (A) and l-3,4-dihydroxyphenylalanine (l-DOPA) (B) in the active site of tyrosinase (TYR) obtained by re-docking. The 3D structures of the molecular docking results are available in Protein Data Bank (PDB) format in the Supplementary Materials (see Figure S1).
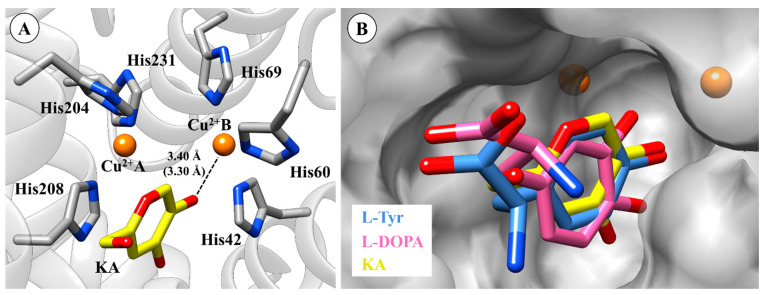
For the KA system, the inhibitor is stabilized by π–π stacking interaction in the active site of TYR (see Figure 4A), which agrees with a published crystal structure [45]. The oxygen atom of the hydroxyl group of KA is positioned towards the Cu2+B ion (distance 3.4 Å). Finally, the overlay between the l-Tyr, l-DOPA, and KA in the active site of TYR is depicted in Figure 4B.
Figure 4.
Binding mode of KA (kojic acid) (A) in the active site of tyrosinase (TYR) and (B) overlapping of l-Tyr, l-DOPA, and KA. Crystal (in parenthesis) and docking distances are reported in ångström (Å). The 3D structures of the molecular docking results are available in Protein Data Bank (PDB) format in the Supplementary Materials.
According to the re-docking results above and previous studies [46,49,56], the docking protocol used can be confidently applied to describe TYR systems. Then, by using the same re-docking procedures, analogs of KA were submitted to the docking protocols. Our results suggest that KA analogs bind to the active site of TYR, acting as competitive inhibitors, since they display similar interactions as KA with the enzyme. Among the most important interactions is the interaction with a key residue His208 through π–π stacking interaction, which has been related to the binding of TYR inhibitors into the catalytic site [57]. To improve our understanding of the binding of TYR inhibitors, TRO [58], a potent inhibitor of TYR, was submitted to molecular docking analysis. For the TRO system, the docking results agree with the binding mode of this inhibitor complexed with TYR from Agaricus bisporus [59,60].
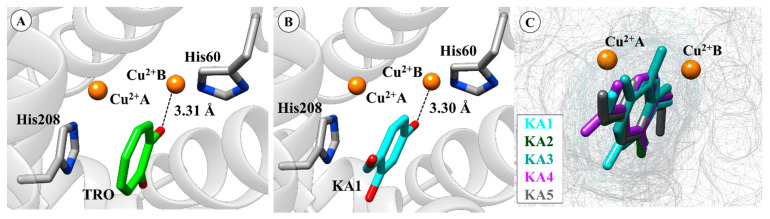
In particular, hydroxyl groups of TRO and KA1 interact with Cu2+B (Figure 5) producing distances from 3.31 Å and 3.30 Å, respectively. It can be seen that KA2 (3.30 Å), KA3 (3.67 Å), KA4 (3.33 Å) and KA5 (3.65 Å) also interact directly with Cu2+B. Among the most important interactions, we can highlight the interaction with a key residue His208 through π–π stacking interaction with all KA analogs.
Figure 5.
(A) Anchoring mode tropolone (TRO) on the active site of tyrosinase (TYR). (B) Anchoring mode KA1 on the active site of TYR. (C) Overlapping KA1, KA2, KA3, KA4 and KA5 on the active site. Docking distances are reported in ångström (Å). The 3D structures of the molecular docking results are available in Protein Data Bank (PDB) format in the Supplementary Materials (see Figure S2).
Molecular docking results of KA analogs and TRO as inhibitors of TYR are summarized in Table 2.
Table 2.
MOLDOCK scoring values (in kcal/mol) of tyrosinase (TYR) inhibitors.
| Inhibitor | MOLDOCK |
|---|---|
| TRO | −72.31 |
| KA | −69.26 |
| KA1 | −68.72 |
| KA2 | −67.26 |
| KA3 | −62.76 |
| KA4 | −65.45 |
| KA5 | −55.47 |
TRO: Tropolone; KA: Kojic acid.
2.2. Molecular Dynamics (MD) Simulation and CuDum Model
After molecular docking, 10 ns of classical MD simulations were performed for each system, where the CuDum model [40] was used for describing Cu2+ ions in the active site of TYR. Each copper ion is bridged by the imidazole rings of three His residues and three water molecules, so that a distorted octahedral geometry is observed (see Figure S3 in Supplementary Materials).
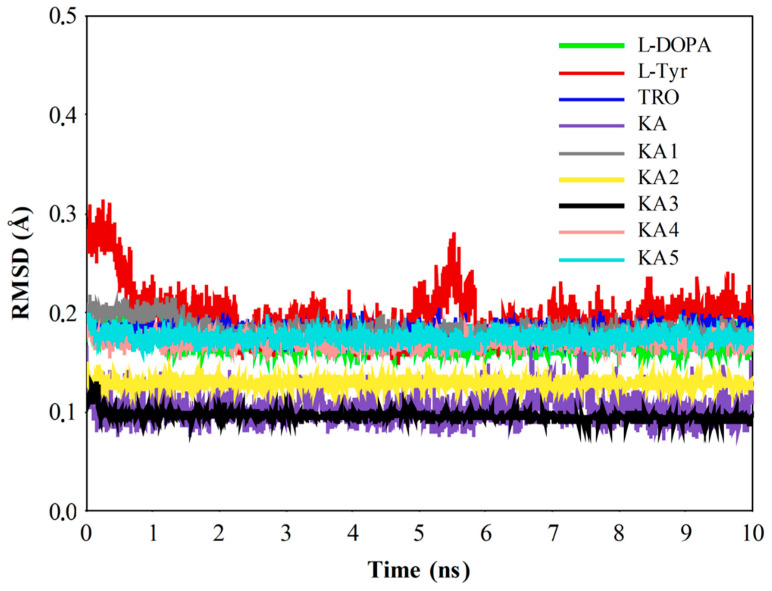
According to the MD results, natural substrates (l-Tyr and l-DOPA), TRO, and KA and its analogs are stable in the catalytic site of TYRBm (Figure 6), and interactions with copper ions and the amino acid residues constituting the active site are observed. Since the computed compounds have similar structures, they exhibit similar interactions with residues His42, His60, His204, Asn205, His208, and Val218, as presented in previous studies [47,48,50,51]. Thus, the molecular behavior of compounds interacting with the catalytic site of TYR is similar. Particularly, the l-Tyr system achieves structural stability after 6 ns of MD simulations, while other systems show stability during all 10 ns of MD.
Figure 6.
Root-mean-square deviation (RMSD) plot of tyrosinase (TYR) systems during 10 ns of molecular dynamic (MD) simulations.
As discussed previously, the CuDum model was applied to describe the Cu2+ ions in the catalytic site of TYR, where the introduction of dummy atoms surrounding the metal ion allows suitable capture of both structural and electrostatic effects (see details in Figure S3 in Supplementary Materials). Our MD results show the expected distance between the histidine residues present in the catalytic site and their respective Cu2+ ions (Table 3) in complexes with substrates (2.14 Å ± 0.03) and inhibitors (2.10 Å ± 0.03), which was also observed in previous studies [61]. According to Liao and co-workers, this classical Cu2+ model captures both the Jahn−Teller effect and maintains stable coordination geometries during MD simulations of metalloproteins without the need for artificial bonds between the metal center and the ligands. From our MD simulations, it was observed that the repulsion interaction between Cu2+A and Cu2+B ions are not excessive since the average atomic distance between these Cu2+ ions is only 0.70 Å higher than in a reported crystal structure [45]. Such a charge distribution in the dummy atom is particularly advantageous in systems with multiple metal centers, since the redistribution of charges reduces the excessive repulsion between metal sites [42].
Table 3.
Experimental and average simulated distances (in Å) between His residues (or water molecules) and copper ions (Cu2+A and Cu2+B) in the TYRBm-KA system. The experimental distances for His residues were taken from the crystal structure (Protein Data Bank (PDB) code: 5I38) [45]. For the water molecules, the experimental values are 1.96 and 2.28 Å for water molecules in the equatorial and axial positions, respectively [69].
| Residue (Atom) | Ion | Experimental Distance | Average Simulated Distances |
|---|---|---|---|
| His204 (NE2) | Cu2+A | 2.09 | 2.15 ± 0.07 |
| His208 (NE2) | 2.07 | 2.30 ± 0.07 | |
| His231 (NE2) | 2.02 | 2.02 ± 0.11 | |
| WT572 (O) | 2.28 | 2.34 ± 0.07 | |
| WT613 (O) | 1.96 | 2.11 ± 0.04 | |
| WT657 (O) | 1.96 | 2.12 ± 0.03 | |
| His42 (NE2) | Cu2+B | 2.09 | 2.00 ± 0.09 |
| His60 (NE2) | 2.07 | 2.33 ± 0.06 | |
| His69 (NE2) | 2.02 | 2.01 ± 0.10 | |
| WT610 (O) | 1.96 | 2.11 ± 0.03 | |
| WT646 (O) | 1.96 | 2.12 ± 0.03 | |
| WT653 (O) | 2.28 | 2.26 ± 0.06 |
His: Histidine; WT: Water; NE2: Nitrogen atom; O: Oxigen atom; Cu2+: Copper ion.
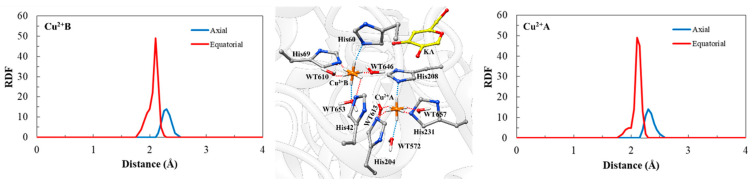
Here, the CuDum model produces stable Cu2+ ion binding sites during the MD simulations of the TYRBm systems (Figure 6). Furthermore, direct interactions between metal ions and substrates/inhibitors bound to the catalytic site of enzymes are observed. In the simulations of TYRBm with the CuDum model, His208 residue prefers to interact with the axial dummy atom of Cu2+A, while the His204 and the His231 residues interact with the equatorial dummy atoms. For Cu2+B, the His60 residue prefers to interact with the axial dummy atom, while His42 and His69 residues interact with equatorial dummy atoms, which agrees with findings from the experiment [62,63,64,65] and other quantum-mechanics-based calculations [66,67,68] (Figure 7).
Figure 7.
A representative snapshot of dummy models in TYRBm-KA system taken from molecular dynamic (MD) simulations (on center). Radial distribution function around Cu2+A (right) and Cu2+B (left) for CuDum models into the catalytic site of TYRBm-KA system. The enzyme portion is shown in the cartoon model, while the metal-binding sites are shown in the space-filling (CPK) model. Particularly, Cu2+ ion are in orange and their dummy atoms are in white. The 3D structure of this figure is available in Protein Data Bank (PDB) format in the Supplementary Materials.
Throughout the MD simulations, the coordination geometry remains a distorted octahedral for the CuDum model with the His residues, and the bond distances are quite close to those in the crystal structure (PDB ID: 5138) [45] (Table 3). The coordination of water molecules to CuDum is in good agreement with an experimental finding that the aqueous involvement [69] is necessary for the oxidation catalytic activity at the metal-binding site of the TYR enzyme [1,16]. Therefore, the applied CuDum model captures the Jahn–Teller effect occurring in the catalytic site of the TYR system and stable coordination geometries are maintained during the MD simulations with no artificial bonds being observed between the metal centers and their residue-ligands.
2.3. Linear Interaction Energy (LIE)
The thermodynamic knowledge of the binding affinity between a protein–inhibitor system is key to a better understanding of molecular recognition. Therefore, an accurate and efficient method to compute binding free energy (ΔGbind) is essential in computer-aided drug design [70]. A set of ΔGbind methods is available, from rigorous methods such as thermodynamic integration (TI) [71] and free energy perturbation (FEP) [72] as well as simple empirical scoring functions computed in molecular docking [73]. The first methods are computationally more expensive, since they demand extensive sampling of multiple intermediate nonphysical states, making them unsuitable for application in high-throughput scenarios [74]. On the other hand, the empirical scoring functions are good for predicting binding poses in protein–ligand systems, even for large chemical databases [75], but they usually fail in quantitatively predicting and ranking ΔGbind values [76]. Therefore, a suitable alternative in terms of effectiveness and efficiency to compute ΔGbind is by taking into account the configurational space for the ligand, protein–ligand, and solvent in the protein–ligand bound and unbound states only [77]. These features offer advantages for both rigorous free energy methods (in terms of efficiency) and empirical scoring functions (in terms of accuracy) [78,79]. Among the so-called end-point methods, we have applied in this study the linear interaction energy (LIE) approach [44].
As discussed above, the binding affinity of inhibitors towards enzymes is key for the development of new drug candidates [80]. Here, we applied the LIE approach [44] to describe the binding free energy values of the ligands (natural substrates and inhibitors). The method was developed as an alternative to more time-consuming free energy perturbation calculations [78,79,81,82,83]. Several research groups have reported LIE calculations on various systems using different programs, force fields, and computational procedures [49,84,85,86].
Here, the last 4 ns of MD simulations for each system were used to compute binding free energy values. The results for the binding affinity of the ligands computed through LIE are depicted in Table 4. The empirical parameters α and β, used directly in the calculation of the binding affinity, were obtained in two ways to serve as a point of comparison and thus perceive which parameters best represent the system with the metal protein TYR. In the first linear regression model, the parameters were obtained directly from the literature (α = 0.181 e β = 0.5, 0.43, 0.37 and 0.33) [87] and for the second model, the parameters (α = 0.197 and β = 0.342) were obtained from the linear fitting with experimental binding free energy, where, in both models, the Jahn–Teller effect is taking into account that the CuDum model was used in all MD systems for the bound models. Here, the ΔGLIE1 refers to binding energy values computed by α and β parameters from literature, while ΔGLIE2 values are computed by including α and β from the linear fitting procedure. The values of α and β used for each inhibitor in the ΔGLIE1 model are described in Table S1 of the Supplementary Materials.
Table 4.
Theoretical and experimental binding free energy values (in kcal/mol) calculated for each tyrosinase (TYR) system.
| Molecule | ΔVvdW | ΔVele | ΔGLIE1 | ΔGLIE2 | ΔGEXP |
|---|---|---|---|---|---|
| l-DOPA | −17.95 ± 0.53 | −22.93 ± 1.02 | −10.79 ± 0.32 | −11.20 ± 0.33 | |
| l-Tyr | −12.44 ± 0.37 | −20.91 ± 0.82 | −9.13 ± 0.24 | −9.47 ± 0.22 | −9.50 |
| TRO | −12.9 ± 0.19 | −15.16 ± 0.97 | −7.93 ± 0.53 | −7.60 ± 0.48 | −8.30 |
| KA | −5.68 ± 0.08 | −18.24 ± 0.26 | −7.04 ± 0.27 | −7.28 ± 0.28 | −7.46 |
| KA1 | −8.76 ± 0.30 | −11.32 ± 0.53 | −5.31 ± 0.24 | −5.51 ± 0.25 | −5.99 |
| KA2 | −12.91 ± 0.03 | −11.68 ± 0.12 | −6.17 ± 0.15 | −6.42 ± 0.15 | −5.85 |
| KA3 | −6.09 ± 0.44 | −14.19 ± 0.18 | −6.34 ± 0.80 | −5.98 ± 0.72 | −5.73 |
| KA4 | −16.68 ± 0.05 | −5.56 ± 0.10 | −4.83 ± 0.66 | −5.05 ± 0.68 | −5.24 |
| KA5 | −17.14 ± 0.10 | −3.75 ± 0.08 | −4.69 ± 0.03 | −4.53 ± 0.02 | −4.68 |
l-DOPA: l-3,4-dihydroxyphenylalanine; l-Tyr: l-Tyrosine; TRO: Tropolone; KA: Kojic acid; vdW: Van der Waals; ele: Electrostatic; LIE: Linear interaction energy; EXP: Experimental
The values of binding affinity, derived from molecular dynamics (MD) trajectories from the LIE method are in good agreement with the experimental data reported in previous studies [45,49,58,88,89]. To provide more reliable results and to enhance the robustness of the approach used for the prediction of the binding free energy of the compounds studied, we applied α and β parameters from the linear fitting between polar and non-polar terms and experimental binding free energy, which was satisfactory. Particularly, the absolute binding energies calculated for L-Tyr, TRO, and KA using LIE (models 1 and 2) agree with the experimental values (−9.50, −8.30, and −7.46 kcal/mol, respectively) [45,58]. Although LIE is an approximation method, these results provide good confidence regarding the efficacy of the applied procedures.
In general, the theoretical binding affinities of KA analogs from the MD trajectories through the LIE method are in excellent agreement with experimental data (Table 4). The KA5 inhibitor showed the weakest binding affinity with the TYRBm enzyme (also according to experiment, ΔGEXP = −4.68 kcal/mol), the reason for this weaker affinity was not revealed in the experimental paper [89]; however, our MD simulations suggest that absence of the hydroxyl group can be responsible for its weak binding.
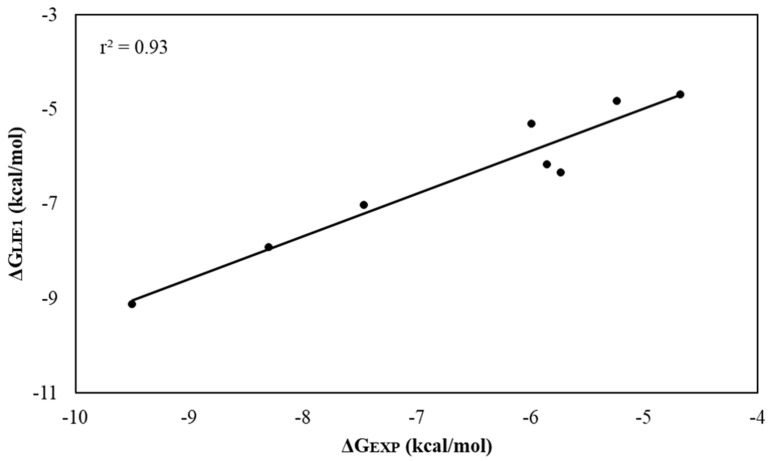
The coefficients of determination (r2) obtained for the linear regression of predicted values versus the observed contributions were equal to 0.93 and 0.94 for LIE model 1 (Figure 8) and model 2, respectively. These results suggest that the standard parameterization (model 1) and that obtained from the linear fitting procedure (model 2) (Figure S4) of LIE are both robust methods that reproduce the experimental affinities of TYR inhibitors.
Figure 8.
Linear regression graph between ΔGLIE1 and ΔGEXP. Values in kcal/mol.
2.4. Residual Decomposition Analysis
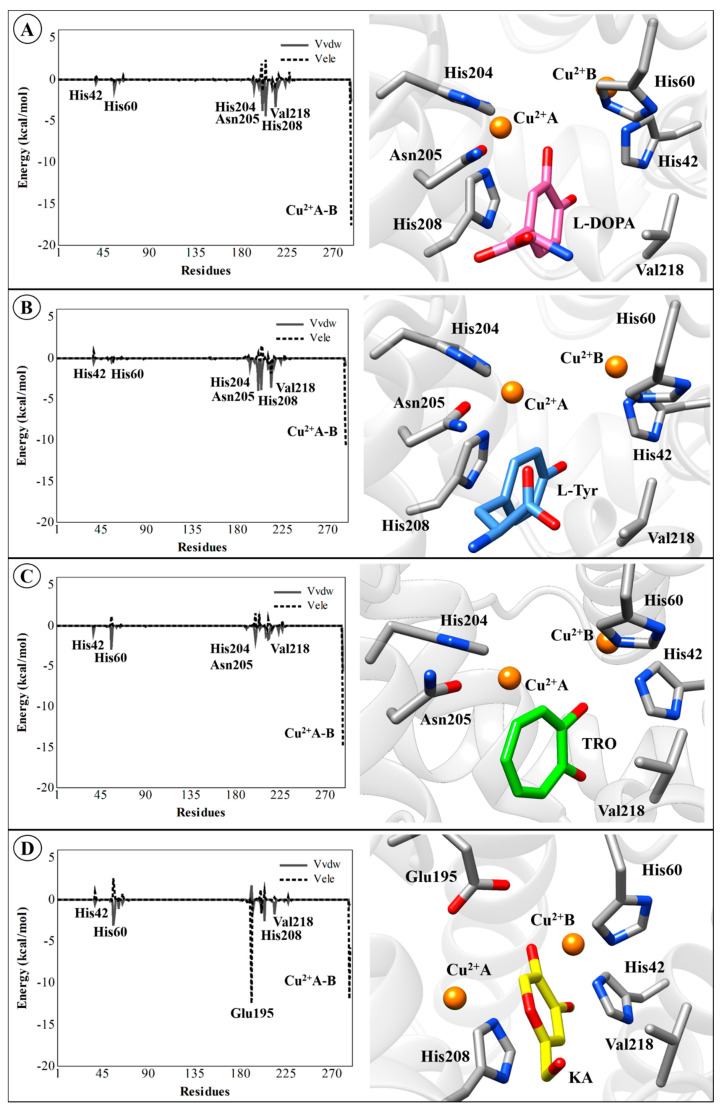
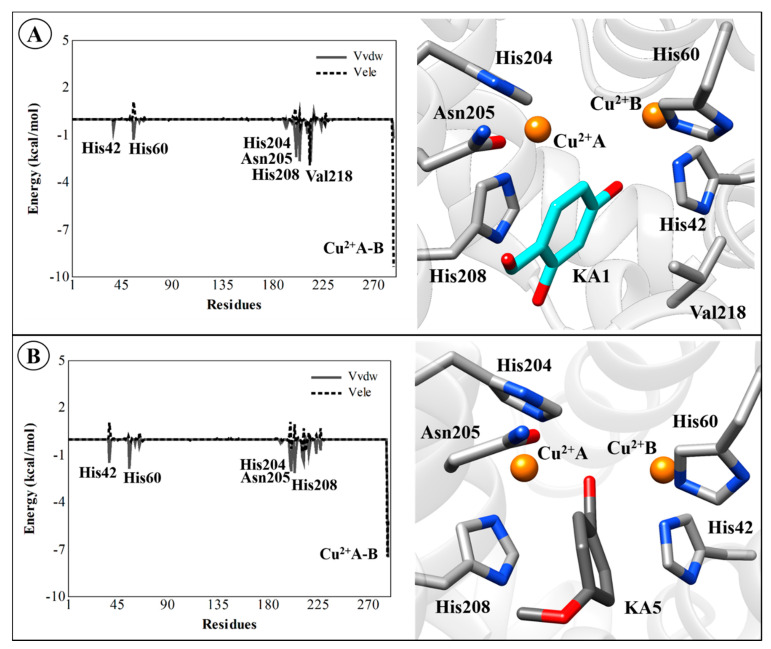
Although there is no rigorous way to decompose free energies into contributions into protein–ligand systems from the MD simulations [90,91], the electrostatic and van der Waals interaction energies of the TYR–ligand complexes can be computed to identify which residues are important for binding. Therefore, the average electrostatic and van der Waals interaction energies for all compounds were evaluated. These interactions for natural substrates (l-DOPA and l-Tyr), inhibitors (TRO and KA), the most active (KA1) and the less (KA5) active analog for the TYR residues (including Cu2+ ions) are presented in Figure 9 and Figure 10. The Cu2+A and Cu2+B ions make the largest contributions to the electrostatic component of the average ligand–residue interactions, as can be seen in Table 5. However, particularly for the TYRBm–KA complex, the Glu195 residue makes considerable electrostatic contributions (−12.45 kcal/mol) to the ligand–enzyme interaction energy through a hydrogen interaction between the carboxylic acid group of amino-acid residue and the hydroxyl group of KA.
Figure 9.
Average ligand–residue interaction energies (in kcal/mol) overall in compounds used in the linear interaction energy (LIE) calculations for the residues that contribute most to the ligand-surrounding electrostatic (dashed line) and (solid line) Van der Waals. (A) TYRBm-l-DOPA, (B) TYRBm-l-Tyr, (C) TYRBm-TRO, (D) TYRBm-KA. The 3D structures of this figure are available in Protein Data Bank (PDB) format in the Supplementary Materials Materials (see Figure S5).
Figure 10.
Average ligand–residue interaction energies (in kcal/mol) overall in compounds used in the linear interaction energy (LIE) calculations for the residues that contribute most to the ligand-surrounding electrostatic (dashed line) and (solid line) van der Waals. (A) TYRBm-KA1 and (B) TYRBm-KA5. The 3D structures of this figure are available in Protein Data Bank (PDB) format in the Supplementary Materials.
Table 5.
Electrostatic contributions (Vele, in kcal/mol) of Cu2+A and Cu2+B ions calculated by the linear interaction energy (LIE) method.
| Complex | Dummy Atom | Distance (Ligand—Cu2+) |
Vele |
|---|---|---|---|
| TYRBm—l-DOPA | Cu2+A | 2.79 | −17.63 |
| Cu2+B | 4.45 | −4.16 | |
| TYRBm—l-Tyr | Cu2+A | 3.75 | −10.81 |
| Cu2+B | 4.69 | −7.39 | |
| TYRBm—TRO | Cu2+A | 2.21 | −15.04 |
| Cu2+B | 4.73 | −1.98 | |
| TYRBm—KA | Cu2+A | 5.27 | −5.70 |
| Cu2+B | 4.82 | −11.88 | |
| TYRBm—KA1 | Cu2+A | 4.56 | −9.37 |
| Cu2+B | 5.46 | −2.26 | |
| TYRBm—KA2 | Cu2+A | 3.09 | −8.59 |
| Cu2+B | 3.76 | −1.42 | |
| TYRBm—KA3 | Cu2+A | 3.71 | −9.91 |
| Cu2+B | 3.68 | −7.77 | |
| TYRBm—KA4 | Cu2+A | 3.68 | −2.50 |
| Cu2+B | 3.46 | −1.07 | |
| TYRBm—KA5 | Cu2+A | 3.59 | −5.22 |
| Cu2+B | 3.64 | −7.47 |
Interestingly, compounds that have hydroxyl groups exhibit interaction with one of the Cu2+ ions (A or B). Particularly, KA5 interacts with the Cu2+ ions through its aldehyde group. However, this interaction is not observed for the other compounds. These results are in concordance with previous studies that recognize molecules containing hydroxyl groups as potential TYR inhibitors [49,92,93,94]. As can be observed in Table 4, ΔVele and ΔVvdW terms vary widely among these ligands. Particularly, the electrostatic contributions from Cu2+ ions implies that the ΔVele term has a strong influence on the binding affinity of ligands. Structurally, these energetic contributions can be traced back to the strength of the interaction between the Cu2+ ion and the hydroxyl group of the ligands, except for the KA5, which interacts through an aldehyde group.
The non-polar free energy contribution, calculated from the change in ligand-surrounding van der Waals energy, shows some residues present in the catalytic site of TYR, such as His204, Asn205, His208, and Val218, which are important for the non-polar interactions (van der Waals) with natural substrates l-DOPA (Figure 9A) and l-Tyr (Figure 9B), with average values of −1.54, −3.86, −4.12, and −3.45 kcal/mol, respectively. For other systems, van der Waals interactions have suitable contributions (see Figure S4 in Supplementary Materials). However, it should be noted that these interactions are not as easily interpreted as the polar term in the LIE method because they do not only take into account the van der Waals interactions but also size-dependent terms such as the hydrophobic effect [44,95]. It is worth mentioning that, in general, the non-polar contribution (van der Waals) is less expressive than the polar (electrostatic) contribution. The binding affinity is favored by polar interactions, mainly from the copper ions present in the active site. Therefore, the obtained correlation between activity and only a few interaction energies suggests that efficient LIE models may be based on only monitoring a subset of the ligand–residue interactions. All values of polar and non-polar contributions for all TYR systems are detailed in Tables S2 and S3 in Supplementary Materials.
3. Materials and Methods
3.1. Molecular Docking Simulations
The initial atomic coordinates for the simulations were extracted from the Protein Data Bank (PDB) under codes 5I38 [45], 4P6R [53], and 4P6S [53], which are TYR from Bacillus megaterium (TYRBm) with KA, l-Tyr, and l-DOPA in the active site, respectively. In this stage, copper ions were described only as van der Waals spheres at the active site of TYR. The molecular docking simulations were performed using Molegro Virtual Docker (MVD) version 5.5 [73], which has been applied successfully for TYR systems [46,49,56]. In this software, the search algorithm named as MOLDOCK is applied by computing a heuristic search algorithm, where a differential evolution and a cavity prediction algorithm are taken into account [96]. The MOLDOCK, which is an extension of the piecewise linear potential (PLP), includes new hydrogen bonding and electrostatic contributions. A re-ranking scoring function is also computed to select the most promising docking result among those found by the docking algorithm. The re-docking procedure shows that the algorithm used was able to predict the binding mode of KA, l-Tyr, and l-DOPA in the active site of TYR. The MOLDOCK scoring function (Equation (1)) [96] was used to rank the potential ligand poses.
| (1) |
The MOLDOCK scoring function was set with a grid resolution of 0.30 Å. It was set at a maximum iteration of 3000 with a simplex evolution size of 100. The best pose with a smaller RMSD value was selected for subsequent ligand–protein interaction energy analysis. The score for ligand–protein non-bonding interactions was obtained through:
| (2) |
where is the piecewise linear potential and and correspond to the charges of i and j atoms, respectively. Finally, is the interatomic distance between i and j atoms. Intramolecular interactions are obtained through:
| (3) |
where is the torsion and is the penalty attributed when the distance between two atoms is lower than 2 Å.
Finally, KA analogs were built by using MarvinSketch version 17.27 [97] and structure optimizations at PM6 level [98] were carried out in Gaussian09 [99]. All compounds studied here are depicted in Table 6. It is worth noting that during the molecular docking, Cu2+ ions in the active site of TYR were treated as Van der Waals sphere, where electrostatic interaction was neglected.
Table 6.
Experimental inhibition (Ki) and dissociation (Kd) constants for Tyrosinase (TYR) ligands.
| Molecules | Nomenclature IUPAC | Structure 2D | Ki (Kd) |
|---|---|---|---|
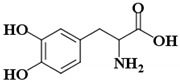
| l-DOPA | (2S)-2-amino-3-(3,4-dihydroxyphenyl)propanoic acid |
|
- |
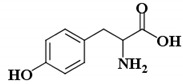
| l-Tyr | (2S)-2-amino-3-(4-hydroxyphenyl)propanoic acid |
|
* (0.1 µM) [45] |
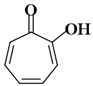
| TRO | 2-Hydroxy-2,4,6-cycloheptatrien-1-one |
|
0.8 µM [58] |
| KA | 5-Hydroxy-2-(hydroxymethyl)-4H-pyran-4-one |
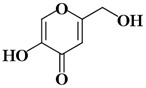
|
3.5 µM [45] |
| KA1 | 2,4-dihydroxybenzaldehyde |
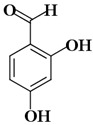
|
41.55 µM [88] |
| KA2 | 3,4-dihydroxybenzaldehyde |
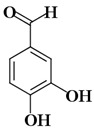
|
52.96 µM [88] |
| KA3 | 3-hydroxy-1,2-dimethyl-4(1h)-pyridone |
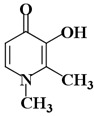
|
64 μM [49] |
| KA4 | 5-hydroxy-4-oxo-4h-pyran-2-carboxylic acid |
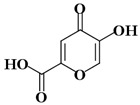
|
145 μM [49] |
| KA5 | 4-Methoxybenzaldehyde |
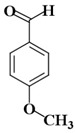
|
376 μM [89] |
l-DOPA: l-3,4-dihydroxyphenylalanine; l-Tyr: l-Tyrosine; TRO: Tropolone; KA: Kojic acid. * Kd value (dissociation constant) for the substrates.
3.2. Molecular Dynamics (MD) Simulations
The best-ranked structures obtained from molecular docking results were selected as starting structures for the MD simulations. In this stage, Cu2+ ions present in the active site of TYRBm were treated by using the Cu2+ dummy model (CuDum) proposed by Liao and coworkers [40]. The MD simulations were performed using the Q program [100]. The OPLS-AA force field [101] and TIP3P water model [102] were selected to describe the solute (enzyme and ligands) and solvent (water), respectively. Particularly, classical parameters for the ligands (natural substrates and inhibitors) were obtained through an automatic parameterization carried out by MACROMODEL [103]. Initially, pKa values of all titratable residues were computed by using the PROPKA method [104] as implemented in the PDB2PQR server [105] at neutral pH.
Then, all systems were solvated with a 20 Å radius simulation sphere of the TIP3P water model [102] centered on the center of mass of the respective ligand. The simulation sphere was subjected to polarization and radial constraints by applying the surface constrained all-atom solvent (SCAAS) model [106] at the sphere surface, to describe appropriately the properties of bulk water. Titratable residues close to the sphere boundary were modeled in their neutral form to account for dielectric screening [100].
Afterwards, each system was submitted to the following MD simulation phases: (a) heating, (b) equilibration, and (c) production, which was selected for data collection. Non-bonded interaction energies were computed by applying a 10 Å cutoff, excluding only the ligand atoms. Long-range electrostatic interactions were computed through the local reaction field (LRF) multiple expansion approach [107]. The non-bonded pair lists and the ligand-surrounding interaction energy values were saved every 25 steps. To save computational resources, all atoms outside of the 20 Å radius simulation sphere were restrained to their initial positions [100].
Initially, 5000 steps of MD simulations were applied using a very short time step (equal to 0.1 fs) and T = 1K, coupled to a strong bath (0.1 fs bath coupling), where heavy atoms were restrained by applying a force constant equal to 50 kcal/mol∙Å2. After, each system was gradually heated to 300 K over 50 ps with time step and the bath coupling equals to 1 fs and 100 fs, respectively. The restrain force constant applied on all solute-heavy atoms was gradually removed.
Finally, for each system, 10 nanoseconds (ns) of MD simulations at 300 K were performed out for the data collection. The time step was set to 2 fs, and all bonds involving hydrogen atoms were restrained applying the SHAKE [108] algorithm. Particularly, for the water (free state) simulations, ligands were kept to the center of their water simulation sphere by using a weak harmonic restraint to the center of mass of the ligands.
3.3. Linear Interaction Energy (LIE) Approach
MD results obtained in the previous section in combination with the LIE approach [44] were used to calculate the binding affinities of KA and its analogs into the TYRBm enzyme. The LIE method uses the ensembles of the free ligand in solution and the protein–ligand complex to calculate the change in free energy associated with binding to the protein [44]. Then, the difference in interaction energies between them is used to calculate the free binding energy, according to Equation (4):
| (4) |
where the α parameter is the empirically derived non-polar scaling factor and β is the scaling factor of the polar contribution dependent on the chemical nature of the ligand [87]. The term represents the average of the ligand surrounding van der Waals (water plus protein in the “bound” case and only water in the “free” term subscript). The term represents the average for electrostatic interaction energies from the simulations of bound and free ligand [44].
Particularly, the LIE parameters (α and β terms) are typically obtained from the literature (α = 0.181 and β = 0.33−0.50) [87] and obtained by linear fitting the ligand-surrounding interaction energies versus experimental binding affinities.
The experimental binding affinity values were calculated using Equation (5):
| (5) |
The experimental Ki values were obtained from literature [45,49,58,88,89].
4. Conclusions
We investigated the accuracy of molecular docking and MD simulations in combination with the LIE method on a set of TYR inhibitors. Particularly, during MD simulations, a dummy model including the description of the Jahn–Teller effect for Cu2+ ions in the active site of the TYR enzyme was included. The standard form and parameterization of the LIE method accurately reflect the binding activities of compounds in the catalytic site of TYR. The TYR–ligand interactions were analyzed in detail, and it was found that the binding free energies of the studied set of TYR inhibitors and their natural substrates can be described mainly by electrostatic contributions of Cu2+ ions present in the catalytic site of the enzyme. Binding free energy results computed with the LIE method, using standards and specific scaling parameters for the LIE equation, also agree very well with experimental binding values. Thus, a combination of computational techniques may facilitate the understanding of potential TYR inhibitors and the prediction of main features for improvement of their inhibitory activity.
Acknowledgments
The work was granted access to the computational resources of the South African Centre for High-Performance Computing (https://www.chpc.ac.za/) and the University of Florida Research Computing (http://researchcomputing.ufl.edu). L.S.M., J.R.A.S., J.L. and C.N.A. thank PROPESP/UFPA for payment of the publication fee.
Supplementary Materials
Supplementary materials can be found at https://www.mdpi.com/1422-0067/21/13/4783/s1. Figure S1: Theoretical binding mode of (A) KA2 and (B) KA3 compounds on the active site of TYR; Figure S2: Theoretical binding mode of (A) KA4 and (B) KA5 compounds on the active site of TYR; Figure S3: 3D representation of the CuDum model. The structural and energetic effects of the Cu2+ ion is computed by the point charge of the metal ion which is distributed to six “dummy” atoms with partial charge δ+ on axial and equatorial positions; Figure S4: Linear regression graph between ΔGLIE2 and ΔGEXP. Values in kcal/mol; Figure S5: Average ligand–residue interaction energies (in kcal/mol) overall in compounds used in the LIE calculations for the residues that contribute most to the ligand-surrounding electrostatic (dashed line) and (solid line) van der Waals. (a) TYRBm-KA2, (b) TYRBm-KA3, (c) TYRBm-KA4; Table S1: Empirical LIE parameters used on ΔGLIE1 model; Table S2: Individual polar and non-polar residual contributions of L-DOPA, L-Tyr, TRO, and KA systems. The values are reported in the kcal/mol; Table S3: Individual polar and non-polar residual contributions of KA analogs systems. The values are reported in the kcal/mol.
Author Contributions
Conceptualization, J.L., C.N.A. and J.R.A.S.; methodology, J.L. and J.R.A.S.; software, L.S.M. and J.R.A.S.; validation, J.L., H.G.K. and J.R.A.S.; formal analysis, J.L., H.G.K. and J.R.A.S.; investigation, L.S.M., J.L. and J.R.A.S.; writing—original draft preparation, L.S.M., J.L. and J.R.A.S.; writing—review and editing, L.S.M., H.G.K., J.L. and J.R.A.S.; visualization, J.L. and J.R.A.S.; supervision, J.L. and J.R.A.S.; project administration, J.R.A.S.; funding acquisition, J.L., C.N.A. and J.R.A.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Council for Scientific and Technological Development (CNPq grants 407096/2016-7, 424662/2016-7 and 402572/2018-1). L.S.M thank FAPESPA and CAPES financial agencies for providing scholarships during the development of this study.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- 1.Chang T.-S. An Updated Review of Tyrosinase Inhibitors. Int. J. Mol. Sci. 2009;10:2440–2475. doi: 10.3390/ijms10062440. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Kim Y.-J., Uyama H. Tyrosinase inhibitors from natural and synthetic sources: Structure, inhibition mechanism and perspective for the future. Cell. Mol. Life Sci. 2005;62:1707–1723. doi: 10.1007/s00018-005-5054-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Saghaie L., Pourfarzam M., Fassihi A., Sartippour B. Synthesis and tyrosinase inhibitory properties of some novel derivatives of kojic acid. Res. Pharm. Sci. 2013;8:233–242. [PMC free article] [PubMed] [Google Scholar]
- 4.Brenner M., Hearing V.J. The protective role of melanin against UV damage in human skin. Photochem. Photobiol. 2008;84:539–549. doi: 10.1111/j.1751-1097.2007.00226.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Cestari T.F., Dantas L.P., Boza J.C. Acquired hyperpigmentations. An. Bras. Dermatol. 2014;89:11–25. doi: 10.1590/abd1806-4841.20142353. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Nayak C.S., Nouveau S., Agrawal D., Kohli M., Bernerd F., Misra N. Skin hyperpigmentation in Indian population: Insights and best practice. Indian J. Dermatol. 2016;61:487–495. doi: 10.4103/0019-5154.190103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Dogra S., Sarangal R. Pigmentary disorders: An insight. Pigment. Int. 2014;1:5. doi: 10.4103/2349-5847.135429. [DOI] [Google Scholar]
- 8.Tief K., Hahne M., Schmidt A., Beermann F. Tyrosinase, the Key Enzyme in Melanin Synthesis, is Expressed in Murine Brain. JBIC J. Boil. Inorg. Chem. 1996;241:12–16. doi: 10.1111/j.1432-1033.1996.0012t.x. [DOI] [PubMed] [Google Scholar]
- 9.Hearing V.J., Tsukamoto K. Enzymatic control of pigmentation in mammals. FASEB J. 1991;5:2902–2909. doi: 10.1096/fasebj.5.14.1752358. [DOI] [PubMed] [Google Scholar]
- 10.Zolghadri S., Bahrami A., Khan M.T.H., Muñoz-Muñoz J.L., Garcia-Molina F., Garcia-Canovas F., Saboury A.A. A comprehensive review on tyrosinase inhibitors. J. Enzym. Inhib. Med. Chem. 2019;34:279–309. doi: 10.1080/14756366.2018.1545767. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Coates C.J., Nairn J. Diverse immune functions of hemocyanins. Dev. Comp. Immunol. 2014;45:43–55. doi: 10.1016/j.dci.2014.01.021. [DOI] [PubMed] [Google Scholar]
- 12.Khanom F., Kayahara H., Tadasa K. Tyrosinase Inhibitory Activity of Bangladeshi Indigenous Medicinal Plants. Biosci. Biotechnol. Biochem. 2000;64:1967–1969. doi: 10.1271/bbb.64.1967. [DOI] [PubMed] [Google Scholar]
- 13.Olianas A., Sanjust E., Pellegrini M., Rescigno A. Tyrosinase activity and hemocyanin in the hemolymph of the slipper lobster Scyllarides latus. J. Comp. Physiol. B. 2005;175:405–411. doi: 10.1007/s00360-005-0002-6. [DOI] [PubMed] [Google Scholar]
- 14.Decker H., Schweikardt T., Nillius D., Salzbrunn U., Jaenicke E., Tuczek F. Similar enzyme activation and catalysis in hemocyanins and tyrosinases. Gene. 2007;398:183–191. doi: 10.1016/j.gene.2007.02.051. [DOI] [PubMed] [Google Scholar]
- 15.Kanteev M., Goldfeder M., Fishman A. Structure–function correlations in tyrosinases. Protein Sci. 2015;24:1360–1369. doi: 10.1002/pro.2734. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Halaban R., Patton R.S., Cheng E., Svedine S., Trombetta E.S., Wahl M.L., Ariyan S., Hebert D.N. Abnormal Acidification of Melanoma Cells Induces Tyrosinase Retention in the Early Secretory Pathway. J. Boil. Chem. 2002;277:14821–14828. doi: 10.1074/jbc.M111497200. [DOI] [PubMed] [Google Scholar]
- 17.Claus H., Decker H. Bacterial tyrosinases. Syst. Appl. Microbiol. 2006;29:3–14. doi: 10.1016/j.syapm.2005.07.012. [DOI] [PubMed] [Google Scholar]
- 18.Kobayashi Y., Kayahara H., Tadasa K., Tanaka H. Synthesis of N-kojic-amino acid and N-kojic-amino acid-kojiate and their tyrosinase inhibitory activity. Bioorganic Med. Chem. Lett. 1996;6:1303–1308. doi: 10.1016/0960-894X(96)00221-1. [DOI] [Google Scholar]
- 19.Kahn V., Andrawis A. Inhibition of mushroom tyrosinase by tropolone. Phytochemistry. 1985;24:905–908. doi: 10.1016/S0031-9422(00)83150-7. [DOI] [Google Scholar]
- 20.Liu J., Wu F., Chen L., Zhao L., Zhao Z., Wang M., Lei S. Biological evaluation of coumarin derivatives as mushroom tyrosinase inhibitors. Food Chem. 2012;135:2872–2878. doi: 10.1016/j.foodchem.2012.07.055. [DOI] [PubMed] [Google Scholar]
- 21.Bagheri-Kalmarzi M., Sajedi R., Asadollahi E., Mahmoodi N.O., Haji-Hosseini R. Effect of vanillin and its acid and alcohol derivatives on the diphenolase activity of mushroom tyrosinase. Mol. Biol. Res. Commun. 2013;1:74–82. doi: 10.22099/mbrc.2013.630. [DOI] [Google Scholar]
- 22.Cabanes J., Chazarra S., Garcia-Carmona F. Kojic Acid, a Cosmetic Skin Whitening Agent, is a Slow-binding Inhibitor of Catecholase Activity of Tyrosinase. J. Pharm. Pharmacol. 1994;46:982–985. doi: 10.1111/j.2042-7158.1994.tb03253.x. [DOI] [PubMed] [Google Scholar]
- 23.Rodrigues A.P.D., Carvalho A.S.C., Santos A.S., Alves C.N., Nascimento J.L.M.D., da Silva E.O. Kojic acid, a secondary metabolite from Aspergillus sp., acts as an inducer of macrophage activation. Cell Boil. Int. 2011;35:335–343. doi: 10.1042/CBI20100083. [DOI] [PubMed] [Google Scholar]
- 24.García-Gavín J., González-Vilas D., Fernández-Redondo V., Toribio J. Pigmented contact dermatitis due to kojic acid. A paradoxical side effect of a skin lightener. Contact Dermat. 2010;62:63–64. doi: 10.1111/j.1600-0536.2009.01673.x. [DOI] [PubMed] [Google Scholar]
- 25.Hashemi S.M., Emami S. Kojic acid-derived tyrosinase inhibitors: Synthesis and bioactivity. Pharm. Biomed. Res. 2015;1:1–17. doi: 10.18869/acadpub.pbr.1.1.1. [DOI] [Google Scholar]
- 26.Kim H., Choi J., Cho J., Kim S.Y., Lee Y.-S. Solid-phase synthesis of kojic acid-tripeptides and their tyrosinase inhibitory activity, storage stability, and toxicity. Bioorganic Med. Chem. Lett. 2004;14:2843–2846. doi: 10.1016/j.bmcl.2004.03.046. [DOI] [PubMed] [Google Scholar]
- 27.Araújo J.D.O., dos Santos A.M., Lameira J., Alves C.N., E Lima A.H.L. Computational Investigation of Bisphosphate Inhibitors of 3-Deoxy-d-manno-octulosonate 8-phosphate Synthase. Molecules. 2019;24:2370. doi: 10.3390/molecules24132370. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.da Costa C.H.S., Bichara T.W., Gomes G.C., dos Santos A.M., da Costa K.S., E Lima A.H.L., Alves C.N., Lameira J. Unraveling the conformational dynamics of glycerol 3-phosphate dehydrogenase, a nicotinamide adenine dinucleotide-dependent enzyme of Leishmania mexicana. J. Biomol. Struct. Dyn. 2020;25:1–12. doi: 10.1080/07391102.2020.1742206. [DOI] [PubMed] [Google Scholar]
- 29.Pereira P.R.M., Araújo J.D.O., Silva J.R.A., Alves C.N., Lameira J., E Lima A.H.L. Exploring Chloride Selectivity and Halogenase Regioselectivity of the SalL Enzyme through Quantum Mechanical/Molecular Mechanical Modeling. J. Chem. Inf. Model. 2020;60:738–746. doi: 10.1021/acs.jcim.9b01079. [DOI] [PubMed] [Google Scholar]
- 30.Sanusi Z.K., Lawal M.M., Govender T., Maguire G.E.M., Honarparvar B., Kruger H.G. Theoretical Model for HIV-1 PR That Accounts for Substrate Recognition and Preferential Cleavage of Natural Substrates. J. Phys. Chem. B. 2019;123:6389–6400. doi: 10.1021/acs.jpcb.9b02207. [DOI] [PubMed] [Google Scholar]
- 31.Sanusi Z.K., Govender T., Maguire G.E.M., Maseko S.B., Johnson L., Kruger H.G., Honarparvar B. An insight to the molecular interactions of the FDA approved HIV PR drugs against L38L↑N↑L PR mutant. J. Comput. Mol. Des. 2018;32:459–471. doi: 10.1007/s10822-018-0099-9. [DOI] [PubMed] [Google Scholar]
- 32.Sanusi Z.K., Lawal M.M., Govender T., Baijnath S., Naicker T., Maguire G.E.M., Honarparvar B., Kruger H.G. Concerted hydrolysis mechanism of HIV-1 natural substrate against subtypes B and C-SA PR: Insight through molecular dynamics and hybrid QM/MM studies. Phys. Chem. Chem. Phys. 2020;22:2530–2539. doi: 10.1039/C9CP05639D. [DOI] [PubMed] [Google Scholar]
- 33.Silva J.R.A., Cianni L., Araújo D., Batista P.H.J., de Vita D., Rosini F., Leitao A., Lameira J., Montanari C.A. Assessment of the Cruzain Cysteine Protease Reversible and Irreversible Covalent Inhibition Mechanism. J. Chem. Inf. Model. 2020;60:1666–1677. doi: 10.1021/acs.jcim.9b01138. [DOI] [PubMed] [Google Scholar]
- 34.Tolufashe G.F., Halder A.K., Ibeji C.U., Lawal M.M., Ntombela T., Govender T., Maguire G.E.M., Lamichhane G., Kruger H.G., Honarparvar B. Inhibition of Mycobacterium tuberculosis l,d-Transpeptidase 5 by Carbapenems: MD and QM/MM Mechanistic Studies. Chemistry. 2018;3:13603–13612. doi: 10.1002/slct.201803184. [DOI] [Google Scholar]
- 35.Fakhar Z., Govender T., Lamichhane G., Maguire G.E.M., Kruger H.G., Honarparvar B. Computational model for the acylation step of the β-lactam ring: Potential application for l,d-transpeptidase 2 in mycobacterium tuberculosis. J. Mol. Struct. 2017;1128:94–102. doi: 10.1016/j.molstruc.2016.08.049. [DOI] [Google Scholar]
- 36.Lameira J., Bonatto V., Cianni L., Rocho F.D.R., Leitão A., Montanari C.A. Predicting the affinity of halogenated reversible covalent inhibitors through relative binding free energy. Phys. Chem. Chem. Phys. 2019;21:24723–24730. doi: 10.1039/C9CP04820K. [DOI] [PubMed] [Google Scholar]
- 37.Lawal M.M., Sanusi Z.K., Govender T., Tolufashe G.F., Maguire G.E.M., Honarparvar B., Kruger H.G. Unraveling the concerted catalytic mechanism of the human immunodeficiency virus type 1 (HIV-1) protease: A hybrid QM/MM study. Struct. Chem. 2018;30:409–417. doi: 10.1007/s11224-018-1251-9. [DOI] [Google Scholar]
- 38.Lockhat H.A., Silva J.R.A., Alves C.N., Govender T., Lameira J., Maguire G.E.M., Sayed Y., Kruger H.G., Kruger H.G. Binding Free Energy Calculations of Nine FDA-approved Protease Inhibitors Against HIV-1 Subtype C I36T↑T Containing 100 Amino Acids Per Monomer. Chem. Boil. Drug Des. 2016;87:487–498. doi: 10.1111/cbdd.12690. [DOI] [PubMed] [Google Scholar]
- 39.Ntombela T., Fakhar Z., Ibeji C.U., Govender T., Maguire G.E.M., Lamichhane G., Kruger H.G., Honarparvar B. Molecular insight on the non-covalent interactions between carbapenems and l,d-transpeptidase 2 from Mycobacterium tuberculosis: ONIOM study. J. Comput. Mol. Des. 2018;32:687–701. doi: 10.1007/s10822-018-0121-2. [DOI] [PubMed] [Google Scholar]
- 40.Liao Q., Kamerlin S.C.L., Strodel B. Development and Application of a Nonbonded Cu2+ Model That Includes the Jahn–Teller Effect. J. Phys. Chem. Lett. 2015;6:2657–2662. doi: 10.1021/acs.jpclett.5b01122. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Duarte F., Bauer P., Barrozo A., Amrein B.A., Purg M., Åqvist J., Kamerlin S.C.L. Force Field Independent Metal Parameters Using a Nonbonded Dummy Model. J. Phys. Chem. B. 2014;118:4351–4362. doi: 10.1021/jp501737x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Oelschlaeger P., Klahn M., Beard W.A., Wilson S.H., Warshel A. Magnesium-cationic Dummy Atom Molecules Enhance Representation of DNA Polymerase β in Molecular Dynamics Simulations: Improved Accuracy in Studies of Structural Features and Mutational Effects. J. Mol. Boil. 2006;366:687–701. doi: 10.1016/j.jmb.2006.10.095. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Saxena A., Sept D. Multisite Ion Models That Improve Coordination and Free Energy Calculations in Molecular Dynamics Simulations. J. Chem. Theory Comput. 2013;9:3538–3542. doi: 10.1021/ct400177g. [DOI] [PubMed] [Google Scholar]
- 44.Aqvist J., Medina C., Samuelsson J.-E. A new method for predicting binding affinity in computer-aided drug design. Protein Eng. Des. Sel. 1994;7:385–391. doi: 10.1093/protein/7.3.385. [DOI] [PubMed] [Google Scholar]
- 45.Deri B., Kanteev M., Goldfeder M., Lecina D., Guallar V., Adir N., Fishman A. The unravelling of the complex pattern of tyrosinase inhibition. Sci. Rep. 2016;6:34993. doi: 10.1038/srep34993. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Benouis S., Ferkous F., Kraim K., Allali A., Saihi Y. Molecular docking studies on arbutin analogues as inhibitors of tyrosinase enzyme. Synth. Rev. Sci. Technol. 2019;25 [Google Scholar]
- 47.Gong Y., Qin X.-Y., Zhai Y.-Y., Hao H., Lee J., Park Y.-D. Inhibitory effect of hesperetin on α-glucosidase: Molecular dynamics simulation integrating inhibition kinetics. Int. J. Boil. Macromol. 2017;101:32–39. doi: 10.1016/j.ijbiomac.2017.03.072. [DOI] [PubMed] [Google Scholar]
- 48.Gou L., Lee J., Yang J.-M., Park Y.-D., Zhou H.-M., Zhan Y., Lü Z.-R. The effect of alpha-ketoglutaric acid on tyrosinase activity and conformation: Kinetics and molecular dynamics simulation study. Int. J. Boil. Macromol. 2017;105:1654–1662. doi: 10.1016/j.ijbiomac.2016.12.015. [DOI] [PubMed] [Google Scholar]
- 49.Lima C.R., Silva J.R.A., Cardoso E.D.T.C., da Silva E.O., Lameira J., Nascimento J.D., Brasil D.D.S.B., Alves C.N. Combined Kinetic Studies and Computational Analysis on Kojic Acid Analogs as Tyrosinase Inhibitors. Molecules. 2014;19:9591–9605. doi: 10.3390/molecules19079591. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Wan J.-X., Lim G., Lee J., Sun X.-B., Gao D.-Y., Si Y.-X., Shi X.-L., Qian G.-Y., Wang Q., Park Y.-D. Inhibitory effect of phloroglucinol on α-glucosidase: Kinetics and molecular dynamics simulation integration study. Int. J. Boil. Macromol. 2019;124:771–779. doi: 10.1016/j.ijbiomac.2018.11.268. [DOI] [PubMed] [Google Scholar]
- 51.Xiong S.-L., Lim G.T., Yin S.-J., Lee J., Si Y.-X., Yang J.-M., Park Y.-D., Qian G. The inhibitory effect of pyrogallol on tyrosinase activity and structure: Integration study of inhibition kinetics with molecular dynamics simulation. Int. J. Boil. Macromol. 2019;121:463–471. doi: 10.1016/j.ijbiomac.2018.10.046. [DOI] [PubMed] [Google Scholar]
- 52.Deeth R.J., Diedrich C. Structural and mechanistic insights into the oxy form of tyrosinase from molecular dynamics simulations. JBIC J. Boil. Inorg. Chem. 2009;15:117–129. doi: 10.1007/s00775-009-0577-6. [DOI] [PubMed] [Google Scholar]
- 53.Goldfeder M., Kanteev M., Isaschar-Ovdat S., Adir N., Fishman A. Determination of tyrosinase substrate-binding modes reveals mechanistic differences between type-3 copper proteins. Nat. Commun. 2014;5:4505. doi: 10.1038/ncomms5505. [DOI] [PubMed] [Google Scholar]
- 54.Chen J., Yu X., Huang Y. Inhibitory mechanisms of glabridin on tyrosinase. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2016;168:111–117. doi: 10.1016/j.saa.2016.06.008. [DOI] [PubMed] [Google Scholar]
- 55.Ii K.L.Y., Kassouf C., Dolinska M.B., Anderson D.E., Sergeev Y.V. Human Tyrosinase: Temperature-Dependent Kinetics of Oxidase Activity. Int. J. Mol. Sci. 2020;21:895. doi: 10.3390/ijms21030895. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Huang X.-X., Yan Z.-Y., Liu S., Wang X.-B., Song S. Investigation of chemical constituents of safflower and their tyrosinase inhibitory activity. J. Asian Nat. Prod. Res. 2018;21:248–256. doi: 10.1080/10286020.2018.1430775. [DOI] [PubMed] [Google Scholar]
- 57.Nokinsee D., Shank L., Lee V.S., Nimmanpipug P. Estimation of Inhibitory Effect against Tyrosinase Activity through Homology Modeling and Molecular Docking. Enzym. Res. 2015;2015:1–12. doi: 10.1155/2015/262364. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Espín J.C., Wichers H.J. Slow-Binding Inhibition of Mushroom (Agaricusbisporus) Tyrosinase Isoforms by Tropolone. J. Agric. Food Chem. 1999;47:2638–2644. doi: 10.1021/jf981055b. [DOI] [PubMed] [Google Scholar]
- 59.Ismaya W.T., Rozeboom H.J., Weijn A., Mes J.J., Fusetti F., Wichers H.J., Dijkstra B.W. Crystal Structure ofAgaricus bisporus Mushroom Tyrosinase: Identity of the Tetramer Subunits and Interaction with Tropolone. Biochemistry. 2011;50:5477–5486. doi: 10.1021/bi200395t. [DOI] [PubMed] [Google Scholar]
- 60.da Silva A.P., Silva N.D.F., Andrade E.H.D.A., Gratieri T., Setzer W.N., Maia J.G.S., da Silva J. Tyrosinase inhibitory activity, molecular docking studies and antioxidant potential of chemotypes of Lippia origanoides (Verbenaceae) essential oils. PLoS ONE. 2017;12:e0175598. doi: 10.1371/journal.pone.0175598. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Si Y.-X., Yin S.-J., Park D., Chung H.Y., Yan L., Lü Z.-R., Zhou H.-M., Yang J.-M., Qian G.-Y., Park Y.-D. Tyrosinase inhibition by isophthalic acid: Kinetics and computational simulation. Int. J. Boil. Macromol. 2011;48:700–704. doi: 10.1016/j.ijbiomac.2011.02.015. [DOI] [PubMed] [Google Scholar]
- 62.Matoba Y., Kihara S., Bando N., Yoshitsu H., Sakaguchi M., Kayama K., Yanagisawa S., Ogura T., Sugiyama M. Catalytic mechanism of the tyrosinase reaction toward the Tyr98 residue in the caddie protein. PLoS Boil. 2018;16:e3000077. doi: 10.1371/journal.pbio.3000077. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Monzani E., Quinti L., Perotti A., Casella L., Gullotti M., Randaccio L., Geremia S., Nardin G., Faleschini P., Tabbi’ G. Tyrosinase Models. Synthesis, Structure, Catechol Oxidase Activity, and Phenol Monooxygenase Activity of a Dinuclear Copper Complex Derived from a Triamino Pentabenzimidazole Ligand. Inorg. Chem. 1998;37:553–562. doi: 10.1021/ic970996n. [DOI] [PubMed] [Google Scholar]
- 64.Persson I., Persson P., Sandström M., Ullström A.-S. Structure of Jahn–Teller distorted solvated copper(ii) ions in solution, and in solids with apparently regular octahedral coordination geometry. J. Chem. Soc. Dalton Trans. 2002:1256. doi: 10.1039/b200698g. [DOI] [Google Scholar]
- 65.Rulıisek L., Vondrášek J. Coordination geometries of selected transition metal ions (Co2+, Ni2+, Cu2+, Zn2+, Cd2+, and Hg2+) in metalloproteins. J. Inorg. Biochem. 1998;71:115–127. doi: 10.1016/S0162-0134(98)10042-9. [DOI] [PubMed] [Google Scholar]
- 66.Orio M., Bochot C., Dubois C., Gellon G., Hardré R., Jamet H., Luneau D., Philouze C., Reglier M., Serratrice G., et al. The Versatile Binding Mode of Transition-State Analogue Inhibitors of Tyrosinase towards Dicopper (II) Model Complexes: Experimental and Theoretical Investigations. Chem. A Eur. J. 2011;17:13482–13494. doi: 10.1002/chem.201100665. [DOI] [PubMed] [Google Scholar]
- 67.Bochot C., Gouron A., Bubacco L., Milet A., Philouze C., Reglier M., Serratrice G., Jamet H., Belle C. Probing kojic acid binding to tyrosinase enzyme: Insights from a model complex and QM/MM calculations. Chem. Commun. 2014;50:308–310. doi: 10.1039/C3CC47469K. [DOI] [PubMed] [Google Scholar]
- 68.Zou C., Huang W., Zhao G.K., Wan X., Hu X., Jin Y., Li J., Liu J. Determination of the Bridging Ligand in the Active Site of Tyrosinase. Molecules. 2017;22:1836. doi: 10.3390/molecules22111836. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Nomura M., Yamaguchi T. Concentration dependence of EXAFS and XANES of copper (II) perchlorate aqueous solution: Comparison of solute structure in liquid and glassy states. J. Phys. Chem. 1988;92:6157–6160. doi: 10.1021/j100332a061. [DOI] [Google Scholar]
- 70.Murcko M.A. Computational Methods to Predict Binding Free Energy in Ligand-Receptor Complexes. J. Med. Chem. 1995;38:4953–4967. doi: 10.1021/jm00026a001. [DOI] [PubMed] [Google Scholar]
- 71.Kirkwood J.G. Statistical Mechanics of Fluid Mixtures. J. Chem. Phys. 1935;3:300. doi: 10.1063/1.1749657. [DOI] [Google Scholar]
- 72.Zwanzig R.W. High? Temperature Equation of State by a Perturbation Method. I. Nonpolar Gases. J. Chem. Phys. 1954;22:1420. doi: 10.1063/1.1740409. [DOI] [Google Scholar]
- 73.Kitchen D., Decornez H., Furr J.R., Bajorath J. Docking and scoring in virtual screening for drug discovery: Methods and applications. Nat. Rev. Drug Discov. 2004;3:935–949. doi: 10.1038/nrd1549. [DOI] [PubMed] [Google Scholar]
- 74.Amaro R.E., Baron R., McCammon J.A. An improved relaxed complex scheme for receptor flexibility in computer-aided drug design. J. Comput. Mol. Des. 2008;22:693–705. doi: 10.1007/s10822-007-9159-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Shoichet B.K., McGovern S.L., Wei B., Irwin J.J. Lead discovery using molecular docking. Curr. Opin. Chem. Boil. 2002;6:439–446. doi: 10.1016/S1367-5931(02)00339-3. [DOI] [PubMed] [Google Scholar]
- 76.Genheden S., Ryde U. The MM/PBSA and MM/GBSA methods to estimate ligand-binding affinities. Expert Opin. Drug Discov. 2015;10:449–461. doi: 10.1517/17460441.2015.1032936. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.de Ruiter A., Oostenbrink C. Free energy calculations of protein–ligand interactions. Curr. Opin. Chem. Boil. 2011;15:547–552. doi: 10.1016/j.cbpa.2011.05.021. [DOI] [PubMed] [Google Scholar]
- 78.Christ C.D., Mark A.E., van Gunsteren W.F. Basic ingredients of free energy calculations: A review. J. Comput. Chem. 2009;31:1569–1582. doi: 10.1002/jcc.21450. [DOI] [PubMed] [Google Scholar]
- 79.Hansen N., van Gunsteren W.F. Practical Aspects of Free-Energy Calculations: A Review. J. Chem. Theory Comput. 2014;10:2632–2647. doi: 10.1021/ct500161f. [DOI] [PubMed] [Google Scholar]
- 80.Mobley D.L., Dill K.A. Binding of Small-Molecule Ligands to Proteins: “What You See” Is Not Always “What You Get”. Structure. 2009;17:489–498. doi: 10.1016/j.str.2009.02.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Aqvist J., Luzhkov V.B., Brandsdal B.-O. Ligand Binding Affinities from MD Simulations. Accounts Chem. Res. 2002;35:358–365. doi: 10.1021/ar010014p. [DOI] [PubMed] [Google Scholar]
- 82.Brückner S., Boresch S. Efficiency of alchemical free energy simulations. I. A practical comparison of the exponential formula, thermodynamic integration, and Bennett’s acceptance ratio method. J. Comput. Chem. 2010;32:1303–1319. doi: 10.1002/jcc.21713. [DOI] [PubMed] [Google Scholar]
- 83.Tofoleanu F., Lee J., Pickard F.C., König G., Huang J., Baek M., Seok C., Brooks B.R. Absolute binding free energies for octa-acids and guests in SAMPL5. J. Comput. Mol. Des. 2016;31:107–118. doi: 10.1007/s10822-016-9965-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.de Alencar N.A.N., Sousa P.R.M., Silva J.R.A., Lameira J., Alves C.N., Martí S., Moliner V. Computational Analysis of Human OGA Structure in Complex with PUGNAc and NAG-Thiazoline Derivatives. J. Chem. Inf. Model. 2012;52:2775–2783. doi: 10.1021/ci2006005. [DOI] [PubMed] [Google Scholar]
- 85.Chen J., Wang R., Taussig M., Houk K.N. Quantitative Calculations of Antibody−Antigen Binding: Steroid−DB3 Binding Energies by the Linear Interaction Energy Method. J. Org. Chem. 2001;66:3021–3026. doi: 10.1021/jo001619m. [DOI] [PubMed] [Google Scholar]
- 86.Ljungberg K.B., Marelius J., Musil D., Svensson P., Norden B., Aqvist J. Computational modelling of inhibitor binding to human thrombin. Eur. J. Pharm. Sci. 2001;12:441–446. doi: 10.1016/S0928-0987(00)00185-8. [DOI] [PubMed] [Google Scholar]
- 87.Hansson T., Marelius J., Aqvist J. Ligand binding affinity prediction by linear interaction energy methods. J. Comput. Mol. Des. 1998;12:27–35. doi: 10.1023/A:1007930623000. [DOI] [PubMed] [Google Scholar]
- 88.Maghsoudi S., Adibi H., Hamzeh M., Ashrafi-Kooshk M.R., Rezaei-Tavirani M., Khodarahmi R. Kinetic of mushroom tyrosinase inhibition by benzaldehyde derivatives. J. Rep. Pharm. Sci. 2013;2:156–164. [Google Scholar]
- 89.Kubo I., Chen Q.-X., Nihei K.-I., Calderón J.S., Cespedes-Acuña C.L. Tyrosinase Inhibition Kinetics of Anisic Acid. Z. Naturforschung C. 2003;58:713–718. doi: 10.1515/znc-2003-9-1021. [DOI] [PubMed] [Google Scholar]
- 90.Smith P.E., van Gunsteren W.F. When Are Free Energy Components Meaningful? J. Phys. Chem. 1994;98:13735–13740. doi: 10.1021/j100102a046. [DOI] [Google Scholar]
- 91.Mark A.E., van Gunsteren W.F. Decomposition of the Free Energy of a System in Terms of Specific Interactions. J. Mol. Boil. 1994;240:167–176. doi: 10.1006/jmbi.1994.1430. [DOI] [PubMed] [Google Scholar]
- 92.Yin S.-J., Si Y.-X., Qian G.-Y. Inhibitory Effect of Phthalic Acid on Tyrosinase: The Mixed-Type Inhibition and Docking Simulations. Enzym. Res. 2011;2011:1–7. doi: 10.4061/2011/294724. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 93.Muñoz-Muñoz J.L., Garcia-Molina F., Varón R., Garcia-Ruiz P.A., Tudela J., Garcia-Canovas F., Rodriguez-Lopez J.N. Suicide inactivation of the diphenolase and monophenolase activities of tyrosinase. IUBMB Life. 2010;62:539–547. doi: 10.1002/iub.348. [DOI] [PubMed] [Google Scholar]
- 94.Khatib S., Nerya O., Musa R., Shmuel M., Tamir S., Vaya J. Chalcones as potent tyrosinase inhibitors: The importance of a 2,4-substituted resorcinol moiety. Bioorganic Med. Chem. 2005;13:433–441. doi: 10.1016/j.bmc.2004.10.010. [DOI] [PubMed] [Google Scholar]
- 95.Carlsson J., Aqvist J. Calculations of solute and solvent entropies from molecular dynamics simulations. Phys. Chem. Chem. Phys. 2006;8:5385–5395. doi: 10.1039/B608486A. [DOI] [PubMed] [Google Scholar]
- 96.Thomsen R., Christensen M.H. MolDock: A New Technique for High-Accuracy Molecular Docking. J. Med. Chem. 2006;49:3315–3321. doi: 10.1021/jm051197e. [DOI] [PubMed] [Google Scholar]
- 97.MarvinSketch (Version 17.27, Calculation Module Developed by ChemAxon) [(accessed on 11 June 2020)]; Available online: https://chemaxon.com/products/marvin.
- 98.Stewart J.J.P. Optimization of parameters for semiempirical methods V: Modification of NDDO approximations and application to 70 elements. J. Mol. Model. 2007;13:1173–1213. doi: 10.1007/s00894-007-0233-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 99.Frisch M.J., Trucks G.W., Schlegel H.B., Scuseria G.E., Robb M.A., Cheeseman J.R., Scalmani G., Barone V., Mennucci B., Petersson G.A., et al. Gaussian 09. Gaussian, Inc.; Wallingford, CT, USA: 2009. [Google Scholar]
- 100.Marelius J., Kolmodin K., Feierberg I., Aqvist J. Q: A molecular dynamics program for free energy calculations and empirical valence bond simulations in biomolecular systems. J. Mol. Graph. Model. 1998;16:213–225. doi: 10.1016/S1093-3263(98)80006-5. [DOI] [PubMed] [Google Scholar]
- 101.Jorgensen W.L., Maxwell D.S., Tirado-Rives J. Development and Testing of the OPLS All-Atom Force Field on Conformational Energetics and Properties of Organic Liquids. J. Am. Chem. Soc. 1996;118:11225–11236. doi: 10.1021/ja9621760. [DOI] [Google Scholar]
- 102.Jorgensen W.L., Chandrasekhar J., Madura J., Impey R.W., Klein M.L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983;79:926–935. doi: 10.1063/1.445869. [DOI] [Google Scholar]
- 103.Schrödinger Schrödinger Release 2020-1: MacroModel. Schrödinger LLC; New York, NY, USA: 2020. [Google Scholar]
- 104.Li H., Robertson A.D., Jensen J.H. Very fast empirical prediction and rationalization of protein pKa values. Proteins Struct. Funct. Bioinform. 2005;61:704–721. doi: 10.1002/prot.20660. [DOI] [PubMed] [Google Scholar]
- 105.Dolinsky T.J., Nielsen J.E., McCammon J.A., Baker N.A. PDB2PQR: An automated pipeline for the setup of Poisson–Boltzmann electrostatics calculations. Nucleic Acids Res. 2004;32:665–667. doi: 10.1093/nar/gkh381. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 106.King G., Warshel A. A surface constrained all-atom solvent model for effective simulations of polar solutions. J. Chem. Phys. 1989;91:3647–3661. doi: 10.1063/1.456845. [DOI] [Google Scholar]
- 107.Díaz L., Bujons J., Delgado A., Gutiérrez-De-Terán H., Aqvist J. Computational Prediction of Structure−Activity Relationships for the Binding of Aminocyclitols to β-Glucocerebrosidase. J. Chem. Inf. Model. 2011;51:601–611. doi: 10.1021/ci100453a. [DOI] [PubMed] [Google Scholar]
- 108.Ryckaert J.-P., Ciccotti G., Berendsen H.J. Numerical integration of the cartesian equations of motion of a system with constraints: Molecular dynamics of n-alkanes. J. Comput. Phys. 1977;23:327–341. doi: 10.1016/0021-9991(77)90098-5. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.