Filament Rigidity Vies with Mesh Size in Determining Anomalous Diffusion in Cytoskeleton

Abstract

The diffusion of microscopic particles through the cell, important to processes such as viral infection, gene delivery, and vesicle transport, is largely controlled by the complex cytoskeletal network – comprised of semiflexible actin filaments and rigid microtubules – that pervades the cytoplasm. By varying the relative concentrations of actin and microtubules, the cytoskeleton can display a host of different structural and dynamic properties that in turn impact the diffusion of particles through the composite network. Here we couple single-particle tracking with differential dynamic microscopy to characterize the transport of microsphere tracers diffusing through composite in vitro networks with varying ratios of actin and microtubules. We analyze multiple complementary metrics for anomalous transport to show that particles exhibit anomalous subdiffusion in all networks, which our data suggest arises from caging by networks. Further, subdiffusive characteristics are markedly more pronounced in actin-rich networks, which exhibit similarly more prominent viscoelastic properties compared to microtubule-rich composites. While the smaller mesh size of actin-rich composites compared to microtubule rich-composites plays an important role in these results, the rigidity of the filaments comprising the network also influences the anomalous characteristics that we observe. Our results suggest that as microtubules in our composites are replaced with actin filaments, the decreasing filament rigidity competes with increasing network connectivity to drive anomalous transport.

Graphical Abstract

Introduction

The cytoskeleton is a key player in numerous cellular functions from proliferation to mobility. Because the cytoskeleton is a dense network of protein filaments, it also crowds and hinders the diffusion of particles and macromolecules, thereby contributing to a host of additional processes such as gene delivery, vesicle transport, and viral infection.^1–5 To better understand these processes and to advance biomedical technologies, we must elucidate the precise mechanisms by which cytoskeletal crowding affects particle transport.^6–11 Understanding transport through polymer composites is also critical to diverse industrial applications such as molecular sieving, wetting and nano-electronics.^12–14

While cytoskeletal crowding is critical to cellular function, in vitro studies investigating the impact of cellular crowding on diffusion have largely used small synthetic crowders or globular proteins to mimic the cellular environment.^15–20 In attempts to more closely match the cytoskeleton environment, crowding by networks of actin filaments have also been studied, though to a lesser extent.^21–25 While these studies have advanced the understanding of transport in crowded environments, they fail to capture the complex structure and inter-filament interactions that exist in the cytoskeleton,²⁶ which consists of multiple types of protein filaments including actin filaments and microtubules. Conversely, complementary in vivo studies,^27–32 which maintain the complexity of the cellular environment, are unable to accurately characterize and tune the relative concentrations of the different components, a necessity when teasing apart the roles that each filament plays in crowded transport.

One of the most intriguing consequences of crowding that these previous studies have revealed is the emergence of anomalous diffusion, in which the center-of-mass mean-squared displacement (MSD) of diffusing particles does not scale linearly with time.^{21–22, 33–35} Specifically, MSD = 2K(Δt)^α where α < 1 for subdiffusion and α > 1 for superdiffusion, and the transport coefficient K reduces to the diffusion coefficient D when α = 1 (normal diffusion). Subdiffusion has been reported for particles in in vitro systems of dextran,¹⁷ actin,²¹ and microtubules,³⁶ as well as in vivo studies of intracellular proteins.^{27, 29} Several physical mechanisms have been suggested to account for subdiffusion including excluded volume, heterogeneous transport, viscoelasticity, and caging.^{2, 15, 21, 27, 33–34, 37–39} Viscoelasticity and caging have also been shown to result in non-Gaussian particle displacements with hopping between cages manifesting as large tails in displacement distributions. These mechanisms also typically result in non-ergodic transport in which the ensemble-averaged MSD is distinct from the time-averaged MSD. However, linking anomalous transport properties to underlying mechanisms has proven difficult. While certain mechanisms lead to transient subdiffusion over a limited timescale, others result in long-lived hampered transport.^{6, 22, 39–40} These differences are often undetectable over the spatiotemporal range of most tracking or scattering techniques.² Further, the heterogeneous nature of some anomalous transport modes has made it difficult to compare single-particle tracking results to standard models and predictions.^41–42

To address these outstanding problems, we use a model cytoskeleton system comprised of co-entangled actin and microtubules to elucidate the effects of cytoskeletal crowding on micro-particle transport. We couple single-particle tracking (SPT) with differential dynamic microscopy (DDM) to map the transport properties from the level of single tracer particles to the ensemble scale over a large spatiotemporal range (Figure 1).

Figure 1: We employ two complementary techniques to quantify the transport dynamics of micro-particles in actin-microtubule composites.

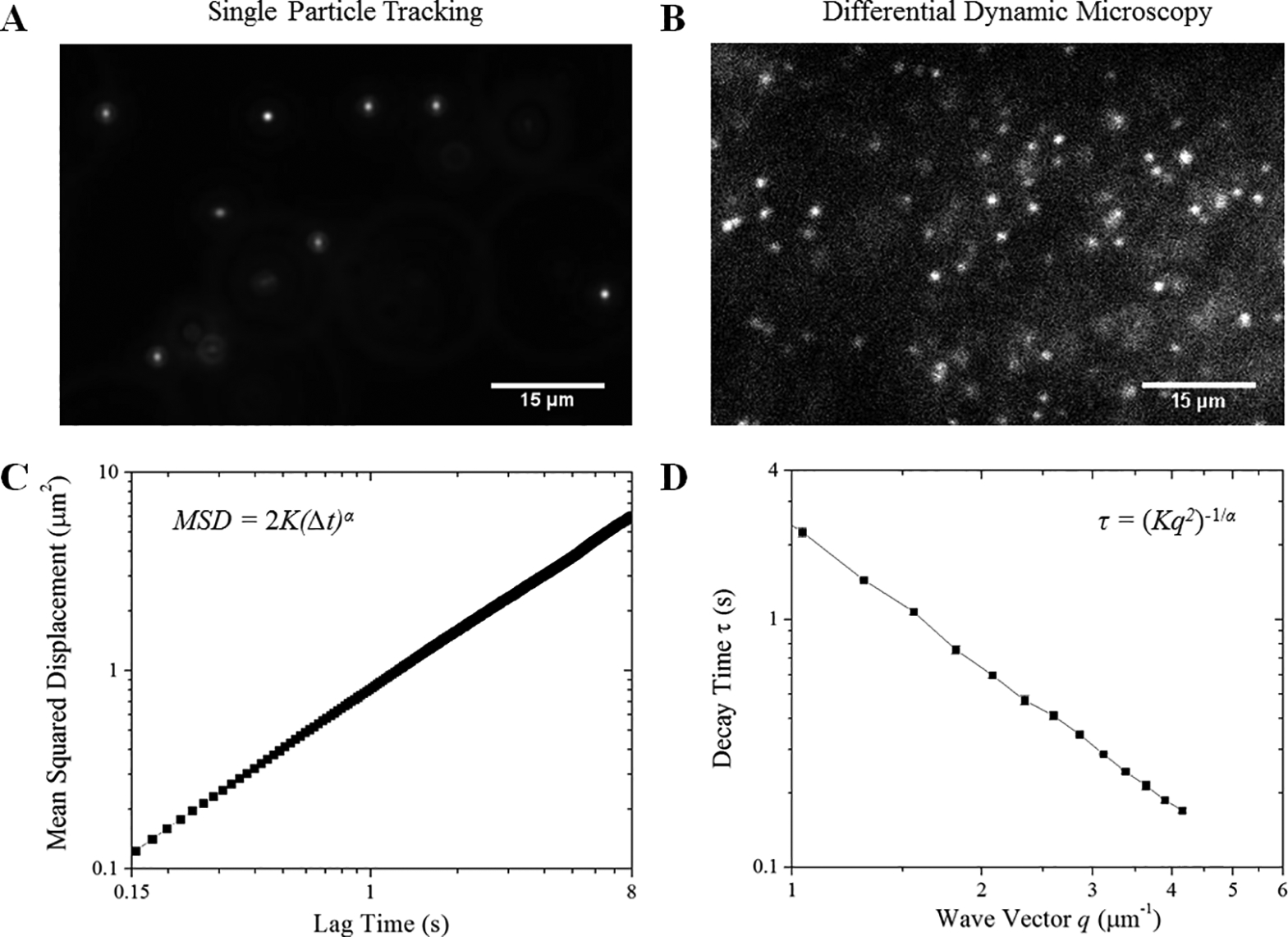
Fluorescent 1-μm-diameter microspheres diffusing in cytoskeleton composites are imaged using (A) widefield fluorescence microscopy and (B) light-sheet microscopy and analyzed using (C) single-particle tracking (SPT) and (D) differential dynamic microscopy (DDM). (A) For SPT, 400-frame videos with ~75 particles in view are acquired at 45 fps and used to determine the trajectories of individual tracers. (B) For DDM, 5000-frame videos with ~1000 particles in view are acquired at 4 to 40 fps, and used to determine ensemble transport properties. (C) For SPT, the mean-squared displacement (MSD) of diffusing particles is plotted versus lag time (Δt). We fit the MSD to the power law function MSD = 2K(Δt)^α, producing the transport coefficient (K) and scaling exponent (α). (D) The characteristic decay times (τ) of density fluctuations over spatial scales of 2μ/q are plotted versus the magnitude of the wave vector q. We fit our data to the function τ = (Kq²)^−1/α to extract the transport coefficient (K) and scaling exponent (α). Data shown in C and D are for particles diffusing in buffer.

Prior work has found that the degree of anomalous subdiffusion of tracer particles within networks strongly depends on the network mesh size relative to the particle size.²¹ Other studies have linked increasingly anomalous subdiffusion with increasingly stiff filaments comprising the network.⁴³ We directly test the applicability of these findings to the composite cytoskeleton by creating actin-microtubule networks in which we fix total protein concentration but vary the ratio of rigid microtubules to semiflexible actin filaments. As the fraction of actin in the composite increases, the mesh size decreases, while at the same time the network becomes increasingly comprised of more flexible filaments. We therefore expect that the diffusive behavior of tracer particles will be pulled in opposite directions as actin fraction increases: more anomalous due to decreasing mesh size and less anomalous due to decreasing filament stiffness. Our experimental methods yield multiple indicators of anomalous diffusion including the subdiffusive scaling exponent α and network viscoelasticity, as well as deviations from Gaussianity and ergodicity. Interestingly, most but not all indicators show that mesh size holds greater influence than polymer stiffness over the subdiffusive behavior.

Methods

Sample Preparation

Proteins:

Rabbit skeleton actin monomers and porcine brain tubulin dimers are purchased from Cytoskeleton (AKL99, T240; St. Denver, CO) and suspended in PEM-100 [100 mM piperazine-N,N’-bis(ethanesulfonic acid) (pH 6.8), 2 mM MgCl₂, 2 mM EGTA]. Resuspended actin and tubulin solutions are flash-frozen with liquid nitrogen and stored at −80 °C at concentrations of 1 mg/mL and 5 mg/mL, respectively.

Tracers:

The tracers are carboxylated fluorescent YG microspheres (diameter = 1.019 ± 0.032 μm) purchased from Polysciences Inc (15702–10; St. Warrington, PA). We further coat tracers in BSA via EDC activation of the carboxyl groups to prevent nonspecific binding to proteins.

Experimental Samples:

Composite networks of actin and microtubules are prepared using previously optimized and validated protocols.⁶ Briefly, we suspend actin monomers and tubulin dimers in an aqueous buffer composed of PEM-100, 2 mM ATP, 1 mM GTP, 5 μM Taxol, and 0.05% Tween to a final protein concentration of c = c_A + c_T = 11.4 μM where c_A and c_T are the molar concentrations of actin monomers and tubulin dimers. The prepared tracer particles are then mixed into the solution. For single-particle tracking experiments, a trace amount of particles are added whereas for DDM a ~300× higher particle concentration is used. Final solutions are pipetted into a sample chamber consisting of either a glass slide and coverslip separated by ~100 μm with double-sided tape (SPT) or capillary tubing that is index-matched to water (DDM). Chambers are sealed with epoxy and incubated at 37 °C for 60 minutes to form an entangled network of actin filaments and microtubules. We investigate composites with five different relative concentrations of actin to tubulin, which we quantify by the molar fraction of actin in the composite φ_A = c_A / (c_A + c_T). We keep the total molar concentration fixed at 11.4 μM. However, because of the different molecular weights of actin monomers (42 kDa) and tubulin dimers (110 kDa), as we vary φ_A the mass concentration varies from 0.5 mg/ml for φ_A = 0 to 1.2 mg/ml for φ_A = 1. We compute the mesh size ξ of the composites via ξ⁻³ = (0.3C_A^−1/2)⁻³ + (0.89C_T^−1/2)⁻³ where C_A and C_T are the mass concentrations of actin and tubulin in units of mg/ml.⁶ The mesh sizes for composites with φ_A = 0, 0.25, 0.5, 0.75 and 1 are 0.79, 0.70, 0.57, 0.49 and 0.42 μm, respectively. The length distributions for actin and microtubules in all composites are similar with measured values of 8.7 ± 2.8 and 17.8 ± 9.7 μm, respectively.

Imaging:

For the single-particle tracking experiments, we image the particles using an Olympus IX73 inverted fluorescence microscope with a 20× 0.4 NA objective and a Hamamatsu ORCA-Flash 2.8 CMOS camera (180 nm/pixel). For each composite, 50 videos are recorded at 45 fps for 400 frames. Each video has >40 trackable particles for a total of >2,000 particles tracked in 2 samples for each condition. We use custom-written particle-tracking scripts (MATLAB) to track the tracer trajectories and measure the x and y displacements of the tracers between each frame. Using these displacements, we compute mean-squared displacements in the x and y directions. The average of <Δx²> and <Δy²> (MSD), shown in Figure 1, is used to determine both the transport coefficient K as well as the degree of anomalous diffusion. Specifically, MSDs are fit to a power law function MSD=2K(Δt)^α where α is the subdiffusive scaling exponent (Figure S1). For a system exhibiting normal Brownian diffusion, the transport coefficient (K) is equal to the diffusion coefficient (D), and α = 1. While we acquire particle trajectories over the time interval [0.02 – 8.8 s], we only use the interval [0.15 – 8 s] (corresponding to [0.79 – 42 rad/s]) in our analysis. For shorter times the frame-to-frame bead displacements are not significantly larger than our centroid localization precision of ~90 nm (0.5 px).⁴⁴ At 0.15 s, the MSDs are all on the order of a squared pixel (180 nm)² or more (Figure 2A), so are no longer below our tracking imprecision. We also removed the last 0.8 s of data as the statistics begin to drop and the data is biased by larger particles.⁴⁵ Error analysis is performed by analyzing random subsets of 5 videos and calculating the standard error in K and α values from all ten subsets. The MSDs calculated for all subsets for each condition are shown in Figure S2.

Figure 2. The presence of actin in composites hinders transport and leads to more pronounced anomalous subdiffusion across a wide spatiotemporal range.

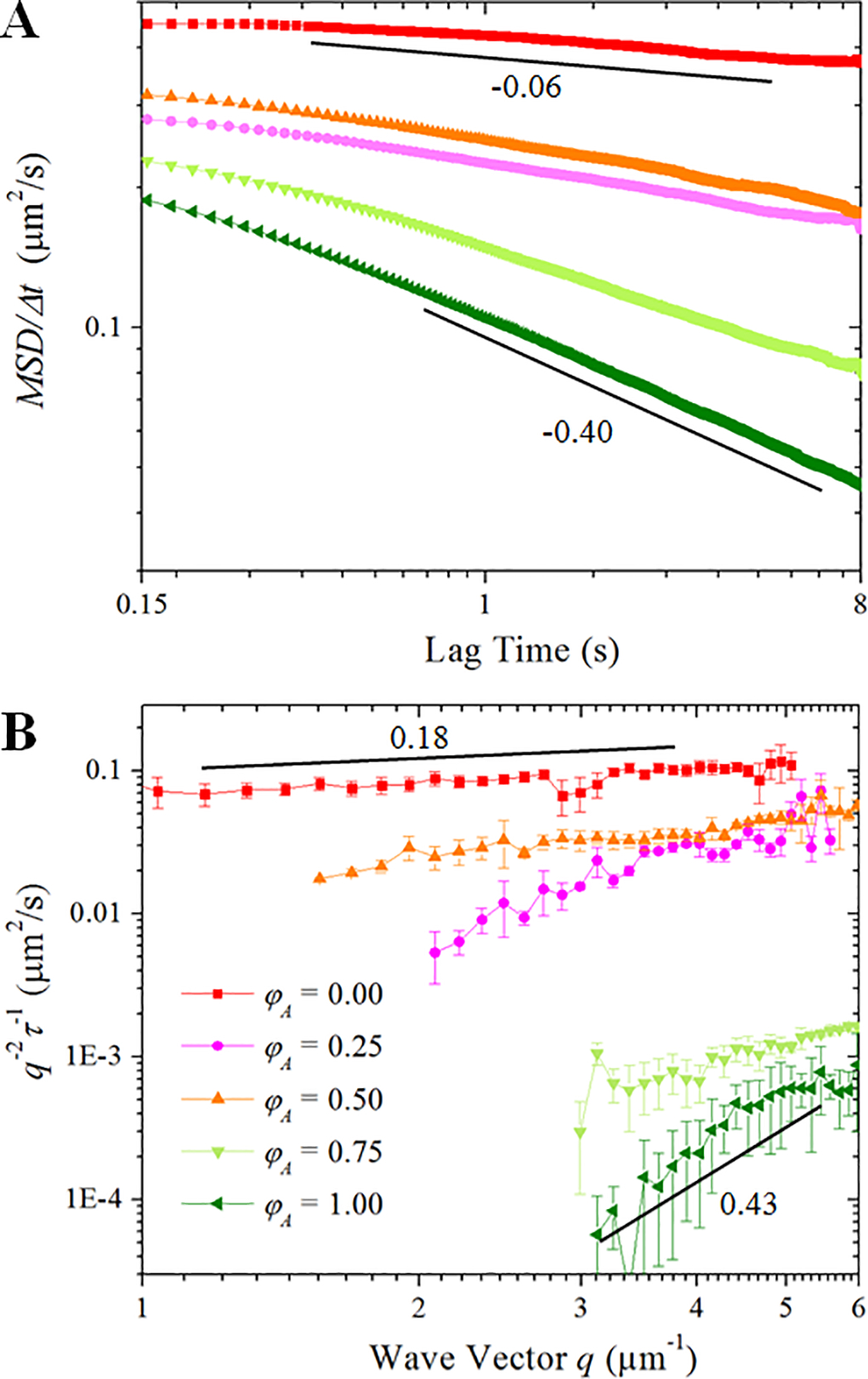
(A) Mean-squared displacements (MSD) divided by lag time Δt, as determined from particle-tracking. Slopes report scaling exponents of α - 1, such that a particle undergoing normal diffusion exhibits a slope of 0 whereas subdiffusion results in negative slopes. As shown, all composites exhibit φ_A-dependent subdiffusion (increasingly negative slopes), with the actin network causing the most pronounced subdiffusion with α = 0.6. (B) The decay time, τ, of density fluctuations with wave vector q are determined from DDM. Plots of 1/(q²τ) vs. q would yield a slope of 0 for normal diffusion. The upward slopes we observe indicate subdiffusion for all composites with the actin network exhibiting the greatest degree of subdiffusion (α = 0.57).

We also evaluate probability distributions of the measured displacements (Δx, Δy) for various lag times (Δt) and fit to single and double Gaussians to determine deviations from normal diffusion (Figures 4 and S3). Finally, we compute the non-Gaussianity parameter ${\beta }_{\text{NG}}=\frac{1}{3}\frac{\langle \overline{{\delta }^4\left(\Delta t\right)}\rangle }{{\langle \overline{{\delta }^2\left(∆t\right)}\rangle }^2}-1$ (Figures 4 and S4) and the ergodicity breaking parameter $EB=\frac{{\langle {\left(\overline{{\delta }^2(∆t)}\right)}^2\rangle -\langle \overline{{\delta }^2\left(∆t\right)}\rangle }^2}{{\langle \overline{{\delta }^2\left(∆t\right)}\rangle }^2}$ where δ²(Δt) is the time-averaged MSD.^{34, 46} For normal diffusion, both β_NG and EB are zero, whereas anomalous transport manifests as β_NG > 0 and/or EB > 0.

Figure 4. Tracers in cytoskeleton composites exhibit non-Gaussian anomalous diffusion.

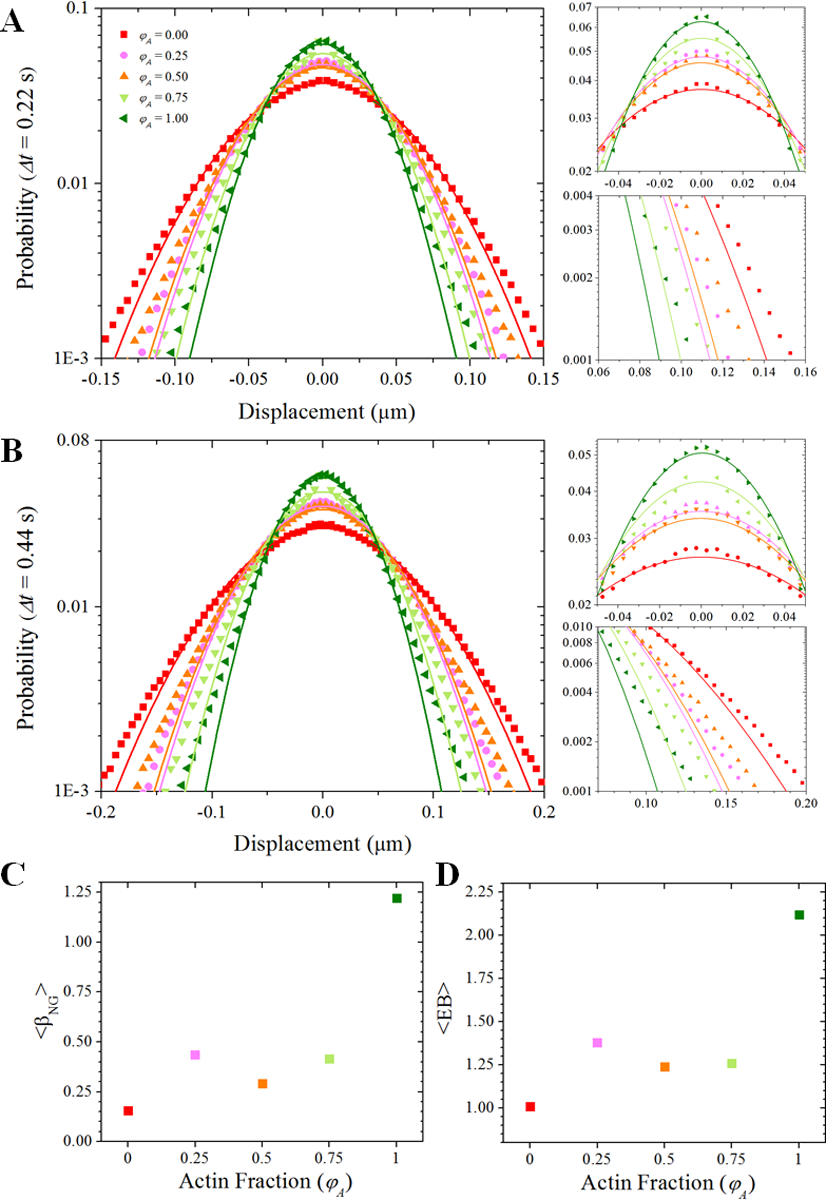
(A,B) Probability distributions of particle displacements for each φ_A (color-coded symbols) for lag times of (A) 0.22 seconds (10 frames) and (B) 0.44 seconds (20 frames). Color-coded solid lines are fits to a Gaussian function for each distribution. For the PDFs shown in (A) and (B), we zoom-in on the peaks and tails of the distributions in the plots to the right. These plots highlight the poor fitting to a normal distribution, a signature of anomalous diffusion. The higher than expected probability of near-zero displacements suggests that tracers are being trapped or caged in the networks. The long non-Gaussian tails (i.e., more large displacements than expected) are suggestive of hopping events. (C) The non-Gaussianity parameter is greatest for φ_A = 1 and least for φ_A = 0. However, between φ_A = 0.25 and φ_A = 0.75 we see relatively little change in the non-Gaussianity. (D) The same trend observed with the non-Gaussianity parameter is seen with the ergodicity breaking parameter.

To determine the viscoelastic properties of the network, we use previously described one-point microrheology methods^47–49 to extract the complex shear modulus G*(ω)=G’(ω)+iG”(ω) from the MSDs. From G* we evaluate the storage modulus G’(ω), loss modulus G”(ω) and complex viscosity η*(ω)= [G’²+iG”²]^1/2/ω. Briefly, we compute linear viscoelastic moduli (G’(ω), G”(ω)) via the generalized Stokes-Einstein relation:⁴⁷

$$G^{*}\left(\omega \right)=G^{\prime }\left(\omega \right)+i{G}^{″}\left(\omega \right)=\frac{k_{B}T}{i\omega \langle \Delta r^2\left(\omega \right)\rangle \pi a} ,$$

where k_B is Boltzmann’s constant, T is the absolute temperature, <Δr²(t)> is the MSD, <Δr²(ω)> is the Fourier transform of <Δr²(t)>, and a is the radius of the beads. The Fourier transform of <Δr²(t)> is obtained by:⁴⁹

$$-{\omega }^2\langle \Delta r^2\left(\omega \right)\rangle =\left(1-e^{-i\omega t_1}\right)\frac{\langle \Delta r^2\left(t_1\right)\rangle }{t_1}+2D{e}^{-i\omega t_N}+{\sum }_{k=2}^N\left(\frac{\langle \Delta r^2\left(t_k\right)\rangle -\langle \Delta r^2\left(t_{k-1}\right)\rangle }{t_k-t_{k-1}}\right)\left(e^{-i\omega t_{k-1}}-e^{-i\omega t_k}\right)$$

where 1 and N in the equation represent the first and last point from the oversampled MSD data. Oversampling is done using the PCHIP MATLAB function. More details about the data analysis can be found in Ref.⁴⁸.

For DDM experiments, we image samples in a capillary tube using a customized light-sheet microscope, which uses a 488 nm excitation laser, a 10× 0.25 NA excitation objective, and a 20× 1.0 NA imaging objective. Using an Andor Zyla 4.2 sCMOS camera, 4 videos of 5000 frames were recorded for each sample at rates ranging from 4 to 40 fps. The video dimensions are 256×768 pixels, and the videos are analyzed by examining regions of interest of 256×256 pixels (50 μm × 50 μm). We follow the methods, described below, used in other applications of DDM to study diffusion in cytoskeletal networks.^{2, 50}

From each 256×256 pixel region of interest, we obtain the image structure function D(q,Δt), where q is the magnitude of the wave vector and Δt is the lag time. To extract the dynamics of the tracer particles, for each wave vector we fit this image structure function to:

$$D\left(q,\Delta t\right)=A\left(q\right)\left[1-f(q,\Delta t)\right]+B\left(q\right),$$

where A depends on the optical properties of the sample and microscope, B is a measure of the camera noise, and f(q, Δt) is the intermediate scattering function (ISF) which we fit to a stretched exponential of the form f(q, Δt) = exp(−(τ(q)/Δt)^γ(q)) with τ being the characteristic decay time for fluctuations that span a spatial scale of 2π/q and γ being the stretching exponent. Examples of how our data fits to this equation are shown in Figure S5 and example ISFs are shown in Figure S6. We find that our data for composites with φ_A ≥ 0.75 are less well fit to this model as seen in Figures S5 and S6 since these ISFs are slower to decay than networks with φ_A < 0.75. Therefore, the values of K and α that we extract with DDM for composites with φ_A ≥ 0.75 should be viewed with caution. Additionally, the range of wave vectors over which reliable fits can be obtained is narrower in the networks of greater actin fraction. To determine whether or not we can reliably fit our data at a given wave vector, we employ the criterion used in Ref.⁵¹ and discussed in more detail in Figure S7.

Our use of a stretched exponential for the ISF was inspired by prior studies of transport within crowded or complex environments probed with DDM.^52–53 For normal diffusion, one would expect to find γ = 1.0 (i.e., a simple exponential for the ISF). However, our data is best fit with a stretching exponent between 0.4 and 0.7. The average stretching exponent varies with the actin fraction of the network as shown in Figures S8 and S9.

With the extracted decay times of density fluctuations across a range of spatial frequencies, we fit our results to τ = (Kq²)^−1/α. This allows us to find the transport coefficient, K, and the subdiffusive scaling exponent, α.

Results

We use previously optimized protocols⁶ to create model co-entangled actin-microtubule composites with varying relative concentrations of actin and microtubules, quantified by the molar actin fraction φ_A = c_A/(c_A + c_T). We use both SPT and DDM to characterize the transport of microspheres diffusing through the composites (Figure 1). These complementary approaches cover a wide range of spatial and temporal scales – important to elucidate anomalous diffusive characteristics – and affirm that measured transport dynamics are not biased by one chosen technique.

With SPT, we track the motion of individual particles to determine mean-squared displacements (MSD) versus lag time, Δt, while with DDM we analyze the decay time, τ, of density fluctuations of an ensemble of particles across a range of spatial frequencies. As shown in Figure 2, both techniques yield similar trends with network composition which indicates that these trends are not limited to narrow spatial or temporal scales and not artifacts of one particular technique. In Figure 2A we plot MSD/Δt vs. Δt from SPT analysis. As reference, for normal Brownian motion MSD/Δt is constant with lag time (i.e., MSD/Δt~Δt⁰) and proportional to the diffusion coefficient. Conversely, we see that all MSD/Δt curves exhibit power-law decays across the entire range of lag times, indicating subdiffusive transport. The degree to which diffusion is anomalous, shown as the steepness of the power-law decay, increases with increasing φ_A. The magnitudes of the MSDs generally decrease as well, similar to previous particle-tracking experiments that found that SPT MSDs were lower in actin networks than in microtubule networks of the same molarity.²⁴ Our DDM measurements, displayed in Figure 2B, show similar trends with φ_A. Specifically, we plot 1/(q²τ) vs. q which, for normal Brownian motion, is constant and proportional to the diffusion coefficient. The power-law rise in 1/(q²τ) with q, which we observe for each composite, indicates anomalous subdiffusion. As with the SPT data in Figure 2A, from Figure 2B one observes that with increasing φ_A, transport slows and becomes more anomalous.

This trend of increasingly slow and anomalous diffusion with greater actin fraction is clearly seen in Figure 3 where we plot the transport coefficient, K, and the anomalous scaling exponent, α, determined from both SPT and DDM, as a function of φ_A (shown on a logarithmic scale in Figure S11). The magnitudes of α for the 100% actin network (φ_A=1) are comparable to previously reported values from particle-tracking experiments on actin networks.^{21, 23} In these studies, subdiffusion was attributed to caging of the particles within the actin mesh.

Figure 3. Both single-particle and ensemble transport properties become increasingly anomalous as the fraction of actin in cytoskeleton composites increases.

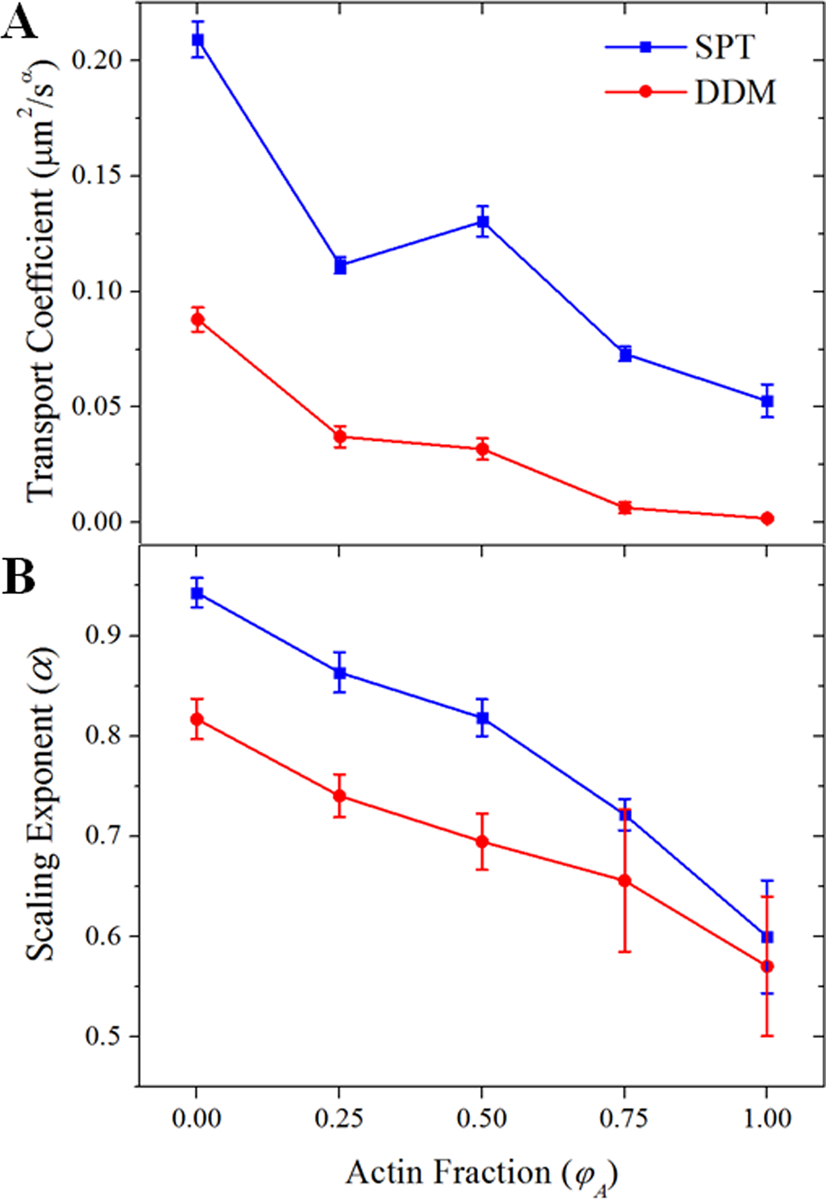
(A) We plot the transport coefficient K versus the molar actin fraction φ_A measured via SPT (blue squares) and DDM (red circles). Increasing φ_A generally slows transport. Both methods show the largest jump in K between the networks comprised of 0% and 25% actin. (B) The subdiffusive scaling exponent α decreases with φ_A. The steady increase in the degree to which transport is anomalous as the actin fraction increases is likely due to the decreasing mesh size of the composite.

We further analyze our SPT data to extract several metrics beyond just the scaling exponent α that indicate anomalous diffusion and shed light on the underlying mechanisms. Specifically, we determine the probability distribution functions (PDFs) of particle displacements, the non-Gaussianity parameter (β_NG), the ergodicity breaking parameter (EB), and the viscoelastic moduli (G’(ω), G”(ω), η*(ω)) of our networks.

We first evaluate the PDFs of particle displacements over given lag times. For normal Brownian motion, one expects such PDFs to be Gaussian with a width proportional to (Δt)^1/2. However, diffusion within crowded or viscoelastic environments is often non-Gaussian.^54–58 As shown in Figure 4, our measured probability distributions of displacements in the various networks for Δt = 0.22 s and 0.44 s are clearly non-Gaussian. The observed probability of large displacements (the tails of the distribution) are greater than a single Gaussian fit predicts, and the peak of the PDF, corresponding to small displacements, is similarly above the Gaussian fit. The PDFs are instead better fit by a sum of two Gaussians (Figure S3) each with widths that increase with lag time. The PDFs for each of our samples are not as divergent from a Gaussian as others have reported. For example, we do not observe a Laplace distribution as seen in other biomaterials⁵⁹ or in cells.⁶⁰ However, the non-Gaussian behavior can help elucidate the physical mechanism of our observed anomalous diffusion. In particular, non-Gaussianity is often attributed to the viscoelasticity of the networks or heterogeneous transport dynamics as observed in other biological and complex environments.^{54, 57–58}

To further characterize the non-Gaussianity of the particle dynamics, we calculate the non-Gaussian parameter β_NG (Δt) (Figure S4). We find that β_NG (Δt) for each network decays to a non-zero plateau, signifying that the diffusion we measure is indeed a non-Gaussian process. From this plateau we compute an average value, <β_NG>, shown in Figure 4C. We find that <β_NG> is greatest in the 100% actin network (φ_A=1) and least in the network comprised purely of microtubules (φ_A=0), consistent with our measured subdiffusive scaling exponent α. However, we do not observe the same monotonic trend with increasing actin fraction we observed in the case of α, which scaled roughly linearly with the mesh size ξ (Figure S10). Rather, <β_NG> decreases between the φ_A = 0.25 and φ_A = 0.5 composites before increasing again between the φ_A = 0.5 and φ_A = 0.75 composites. These variations are all relatively small compared to the large jump in values between networks of φ_A = 0.75 and φ_A = 1. To further probe this intriguing behavior we also compute the ergodicity breaking parameter EB. Similarly to β_NG, EB reaches a time-independent plateau from which we compute an average. As shown in Figure 4D, the trend of EB with φ_A is quite similar to that for β_NG.

The fact that both β_NG and EB display this non-monotonic dependence on φ_A (and thus on ξ), not apparent in α, suggests that these parameters may be sensitive to properties of the network beyond the mesh size, such as the filament stiffness, that may contribute to anomalous transport.

Therefore, we next examine the viscoelasticity of our composites. Subdiffusion and non-Gaussianity are known to occur in viscoelastic environments and we can use our SPT data to extract the storage modulus G’(ω), loss modulus G”(ω) and complex viscosity η*(ω). As shown in Figure 5, G’ increases with increasing actin fraction over the entire frequency range and exhibits an increasingly pronounced frequency-independent plateau – both signatures of elasticity. The low-frequency complex viscosity, from which we can estimate the zero-shear viscosity η₀, likewise increases as φ_A increases, while at the same time η*(ω) curves exhibit more viscoelastic shear-thinning. This general trend of increasing viscoelasticity with φ_A is similar to studies reported in cells which show that actin filaments are the primary contributors to the viscoelasticity that cells exhibit.^30–32 However, Figure 5 shows that these signatures of viscoelasticity do not increase smoothly with φ_A. To quantify the dependence of viscoelasticity on φ_A, we plot η₀ and the frequency-averaged storage modulus <G’> for each network (Figure 5D). As can be inferred from Figures 5A–C, while both η₀ and the <G’> generally increase with actin fraction, the φ_A = 0.5 composite breaks this trend for both quantities, similar to the non-Gaussianity and ergodicity breaking parameters.

Figure 5. Composites exhibit pronounced viscoelastic properties which vary with actin fraction.

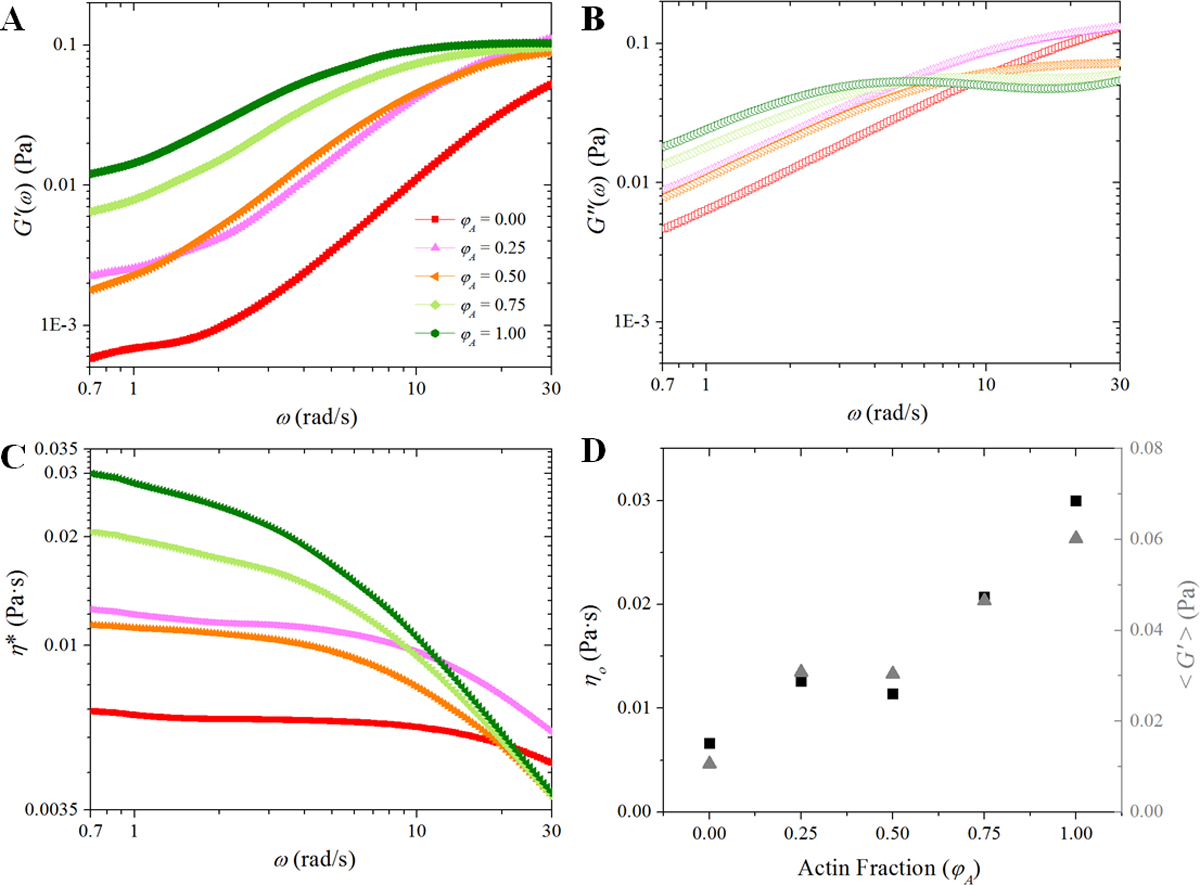
(A) Storage and (B) loss moduli, G’(ω) and G”(ω), are plotted vs. frequency (ω). (C) The complex viscosity η*(ω) vs. ω is plotted. (D) The zero-shear viscosity, η₀, (left axis) and the average storage modulus, <G’(ω)>, (right axis) are plotted vs. actin fraction. While increasing the fraction of actin within the composite generally serves to increase the viscoelasticity, there is relatively little change in η₀ and <G’(ω)> between the φ_A = 0.25 and φ_A = 0.5 composites.

Discussion

Our SPT and DDM data indicate anomalous subdiffusion in all composites with a marked dependence on the fraction of actin in the composite. Namely, particle transport generally slows and becomes more anomalous as the actin fraction increases, but the exact dependence of several metrics on φ_A are complex as shown in Figure 6 (see Table S1 for the values plotted in Figure 6). The change in particle transport as actin fraction increases is likely attributable to two competing factors: the decreasing mesh size and the decreasing network stiffness. Previous research has shown a sharp dependence of the subdiffusive exponent on the mesh size. However, while the mesh size decreases with increasing φ_A, the network also becomes floppier as actin filaments are ~100× less rigid than microtubules. Previous research has shown that stiffer obstacles hinder diffusion more than floppy, semiflexible ones.⁴³

Figure 6. Using multiple metrics to quantify anomalous subdiffusion showcases the role that both mesh size and polymer stiffness have on determining the degree of anomalous subdiffusion.

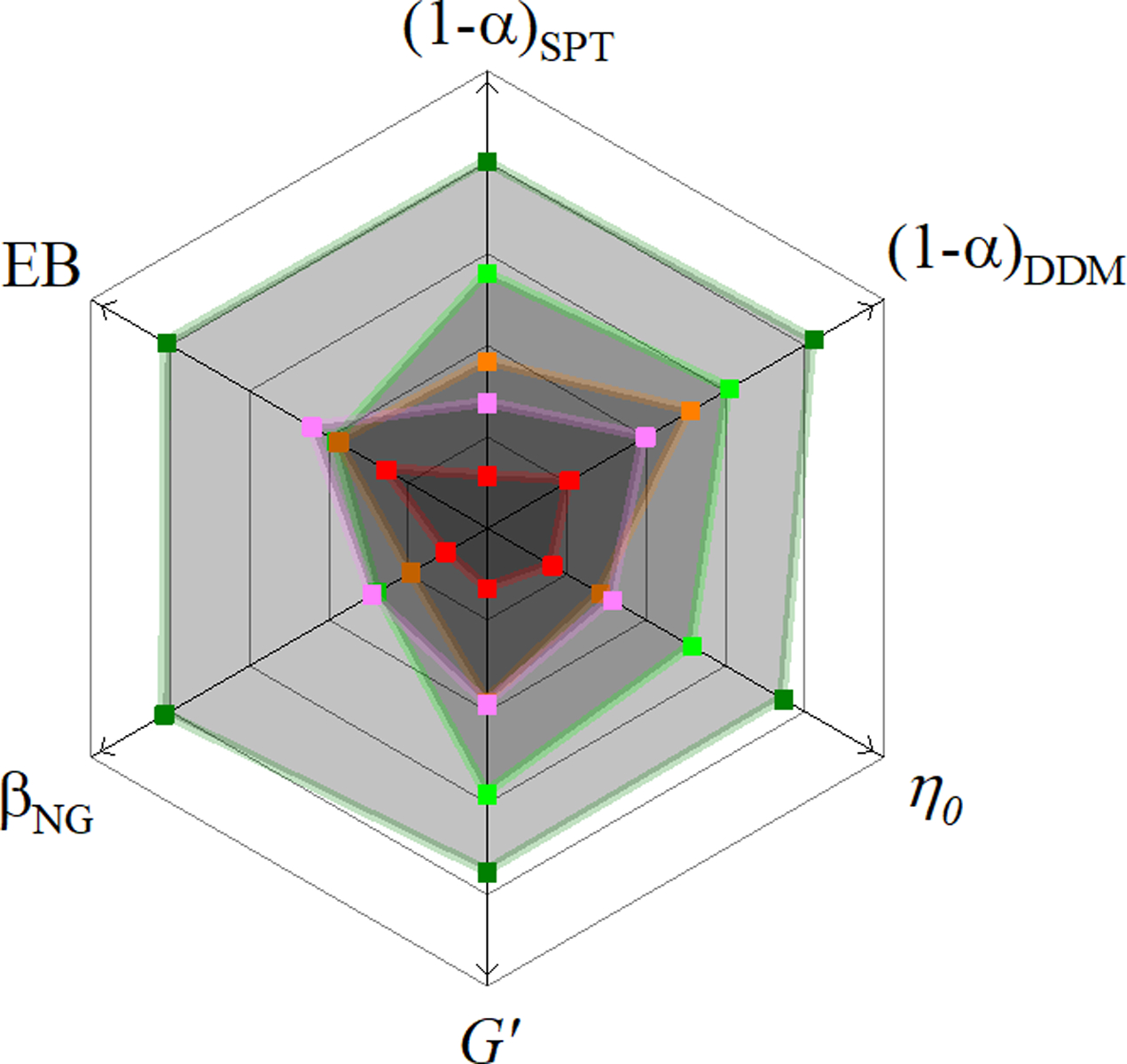
With the same color scheme used in previous figures we show how the various indicators of anomalous transport depend on the actin fraction of our composites. A greater distance from the center (in the direction of the arrows) signifies a greater degree of anomalous subdiffusion. Only for the scaling exponent α, measured either using SPT or DDM, do we observe a steady trend of increasingly anomalous transport with increasing actin fraction (and, therefore, decreasing mesh size). While all other indicators show a greater degree of subdiffusion in networks of purely actin filaments than in networks of purely microtubules, their values do not increase monotonically between φ_A = 0.25 and φ_A = 0.75 despite the fact that the mesh size ξ does. This result suggests that both the mesh size and the rigidity of the filaments comprising the network influences the transport properties.

Our finding that the subdiffusive scaling exponent α, measured either with DDM or SPT, monotonically decreases with decreasing mesh size ξ suggests that the subdiffusive transport of our tracer particles are dictated more by the mesh size than by the filament flexibility. However, the scaling of α with mesh size ξ (specifically with the ratio of the bead radius a to ξ (Figure S10)) is weaker than previously reported,²¹ suggesting that the increasing filament flexibility may also be contributing to the observed transport. In a previous report on particle diffusion within actin networks,^{21, 39} the scaling exponent α decreased linearly with (a/ξ)² whereas we observe a decrease that is approximately linear with a/ξ. The additional metrics for anomalous diffusion we evaluate add further nuance to this conclusion. All of these metrics, namely β_NG, EB, η₀, and <G’>, are non-monotonic with actin fraction for composites between φ_A = 0.25 and φ_A = 0.75 (Figure 6). Though they are all largest (indicating the most anomalous diffusion) with the 100% actin and smallest with the 0% actin networks, we observe a small local minimum for φ_A = 0.5.

These indicators of anomalous diffusion suggest that properties of the network besides the mesh size, such as the stiffness of the filaments, cannot be ignored. In our previous study on the nonlinear microrheology of similar actin-microtubule composites,⁶ we showed that 100% microtubule networks (φ_A = 0) exhibited larger resistance to large strains than 100% actin networks (φ_A = 1), due to the stiffness of the microtubules. However, this resistive force did not scale proportionally with the fraction of actin. Instead, the 50% actin composite exhibited a slightly higher force than the 30% (φ_A = 0.3) and 70% (φ_A = 0.7) actin composites. Only when the actin fraction dropped below 10% (φ_A = 0.1) was there a substantial increase in force. We rationalized this non-monotonic dependence by considering that as the fraction of actin increased, the mesh size decreased while at the same time rigid filaments (microtubules) were replaced with more flexible ones (actin). Specifically, as φ_A increased the resistive force initially sharply decreased as the composites became floppier. However, following this initial decrease, the force exhibited little dependence on φ_A, with a slight local maximum at φ_A = 0.5, as the increased floppiness of the network competed with the decreasing mesh size.

In previous microrheology experiments on actin networks, subdiffusion was attributed to particles becoming highly constrained or trapped by the network and occasionally hopping out of their cages.^{21, 23} This type of behavior, where particles can be in or out of confining cages, has also been observed in other viscoelastic environments like mucus⁵⁹ and agarose gels,⁶¹ and can often be modeled by a noisy continuous time random walk.^62–63 Continuous time random walks are predicted to be non-Gaussian and non-ergodic.³⁴ Our non-Gaussian PDFs of particle displacements, along with our non-Gaussianity and ergodicity breaking parameters, indicate that similar behavior occurs in our composites. Namely, our PDFs show that both large displacements (hopping between cages) and small displacements (fluctuations within a cage) occur more frequently than a normal distribution predicts.

As described above, in agreement with recent simulations,⁴³ our results suggest that both network mesh size and polymer stiffness appear to be influential in determining the observed anomalous subdiffusion, and the competition between these two physical properties leads to the complex dependence of several anomalous indicators on actin fraction (Figure 6). Importantly, the use of both SPT and DDM, as well as the analysis of multiple complementary anomalous transport metrics, is essential to draw these robust conclusions from our results. Further, with this approach, we can dismiss technique-dependent artifacts as the cause of correlations between the various metrics.

Conclusions

The cytoskeleton is a complex composite network of protein filaments, including actin and microtubules, that plays a key role in the transport of particles and macromolecules through the cell. However, the effect that each comprising protein, as well as the interactions between them, has on transport through the cytoskeleton remains an important unanswered question. Here, we have coupled single-particle tracking with differential dynamic microscopy to elucidate the transport properties of micro-particles through in vitro composites of actin and microtubules. This coupling allows us to map the transport properties from the level of single tracer particles to the ensemble scale over a large spatiotemporal range (Figure 1). Importantly, it also provides verification of the trends observed from each separate technique.

In single-component crowding environments (φ_A = 0 and φ_A = 1), the degree of subdiffusion correlates with the mesh size ξ no matter which indicator of subdiffusion we use. However, we observe that the scaling exponent α decreases less dramatically with a/ξ than has been reported for networks of purely actin.^{21, 39} Furthermore, we observe non-monotonic trends with φ_A for our other indicators of anomalous transport, the non-Gaussianity and ergodicity breaking parameters, which scale with the viscoelasticity of the networks. Taken together, these findings suggest that for composite networks the changing physical properties of the constituents and the resulting material properties also play important roles. Our prior research on the nonlinear microrheology of similar composite networks⁶ and recent simulation studies of transport within polymer networks⁴³ suggest that this is due to the filament rigidity vying with the mesh size of our composites.

Our data further indicate that caging underlies the anomalous transport we observe, which arises from the viscoelastic nature of the composites and results in non-ergodic, non-Gaussian transport. Our results have direct implications in viral infection, drug delivery and gene therapy, as well as industrial applications such as hydrogel design and micro-filtration. More generally, our platform can provide robust characterization of transport properties of a wide range of tracer particles and crowding networks of current interest.