Transforming choice outcome to action plan in monkey lateral prefrontal cortex: a neural circuit model

SUMMARY

In decision-making we first make a good-based choice then transform it into action to harvest the good. To elucidate neural circuit mechanism for such transformation, we investigated a neural circuit model with three modules, representing choice, integration of choice with response target and motor command, respectively. We examined three scenarios of how action could be resolved in the model and compared their implications with experimental data. Our model predicts three types of neurons with distinct functional significance, which is confirmed by a novel analysis of neural activity in lateral prefrontal cortex (LPFC) of behaving monkeys. The classification of functional neural types is much more distinct in the ventral than the dorsal region of LPFC, suggesting that action plan is initially generated based on choice outcome in ventral LPFC. Our model offers a biologically plausible neural circuit architecture that implements good-to-action transformation during economic choice.

INTRODUCTION

In our daily life, we often face choices among multiple available goods. We decide according to our subjective preference and then perform the necessary action to retrieve the choice outcome (Padoa-Schioppa and Cai, 2011; Cai and Padoa-Schioppa, 2014). Neurons in the orbitofrontal cortex (OFC, Brodmann area 13) encode both pre- (offer value) and post-decision variables (chosen value and chosen juice), suggesting together with lesion studies that OFC may be the brain locus for implementing economic choice (Padoa-Schioppa and Assad, 2006; Cai and Padoa-Schioppa, 2014). Importantly, encoding of value in this area is independent of visuospatial contingencies and motor responses (Padoa-Schioppa and Assad, 2006; Cai and Padoa-Schioppa, 2014; Grattan and Glimcher, 2014). Cai and Padoa-Schioppa (2014) demonstrated that such abstract choice outcome encoded in the OFC may be transformed into an action plan (good-to-action transformation) through the lateral prefrontal cortex (LPFC), a major output target of OFC (Saleem et al., 2014). In their study, a delay was introduced between presentation of the offers and the saccade targets and the spatial location of the offers is dissociated from the saccades necessary to obtain them. A substantial fraction of OFC neurons encoded the choice outcome but the encoding was transient and faded away during the memory period before the saccade targets were revealed to the animal. Thus, OFC neurons did not appear to maintain the memory of choice outcome. On the other hand, the choice memory trace was observed in the LPFC, where neuronal activity undergoes a transition from encoding choice outcome in goods space to representing the action plan for obtaining the chosen offer (good-to-action transformation).

In this computational work, we developed and investigated a neural circuit model for good-to-action transformation that is not only capable of realizing such transformation in a valuebased decision making task but also recapitulates the neuronal dynamics observed in LPFC, which putatively carries out the transformation. We started out with a minimal circuit model based on task demand (Figure 1), with two different scenarios to accomplish the transformation. Scenario I assumes that ultimate action selection takes place in a motor command circuit, whereas Scenario II posits that action selection is reached through consensus building in a circuit where good-based choice signal is integrated with response target input. These two different scenarios predict the presence of distinct functional neuron types. Scenario I predicted the presence of visual target encoding (TG) neurons and motor-like chosen target (CT) neurons while Scenario II predicts the existence of transition (TS) neurons which first encode target location and then transition to encode chosen target location. However, we found in the LPFC all three types of neurons, which cannot be produced by Scenario I or II alone. By enriching the circuit model with heterogeneity in network connectivity, the enhanced model Scenario III yielded all three functional neuron types under a single scenario. Moreover, the count statistics of neuron types produced by the model could match that in the LPFC. Our model provided a novel biologically plausible neural circuit that implements good-to-action transformation during economic choice. Furthermore, our computational work provided complimentary evidence that further supports the hypothesis in experimental studies that LPFC, LPFCv in particular, is a potential neural substrate for transforming choice outcome into an action plan during economic decision-making.

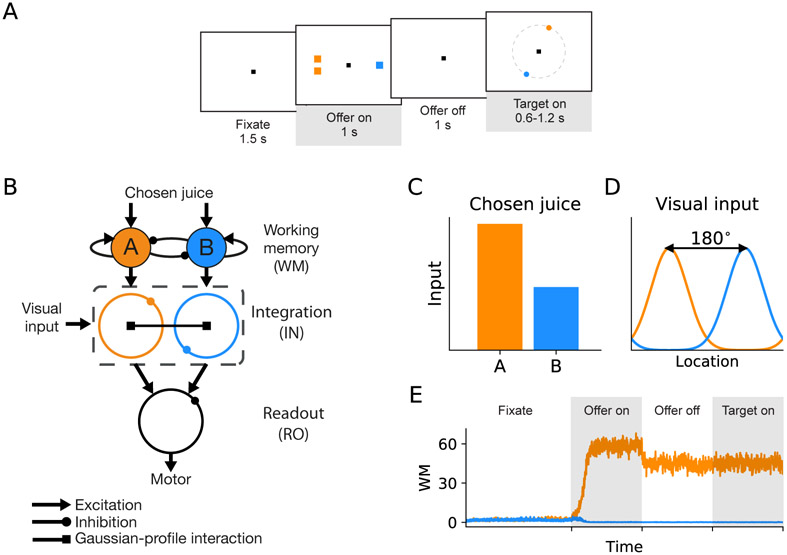
Figure 1. Task design and basic structure of neural circuit model.

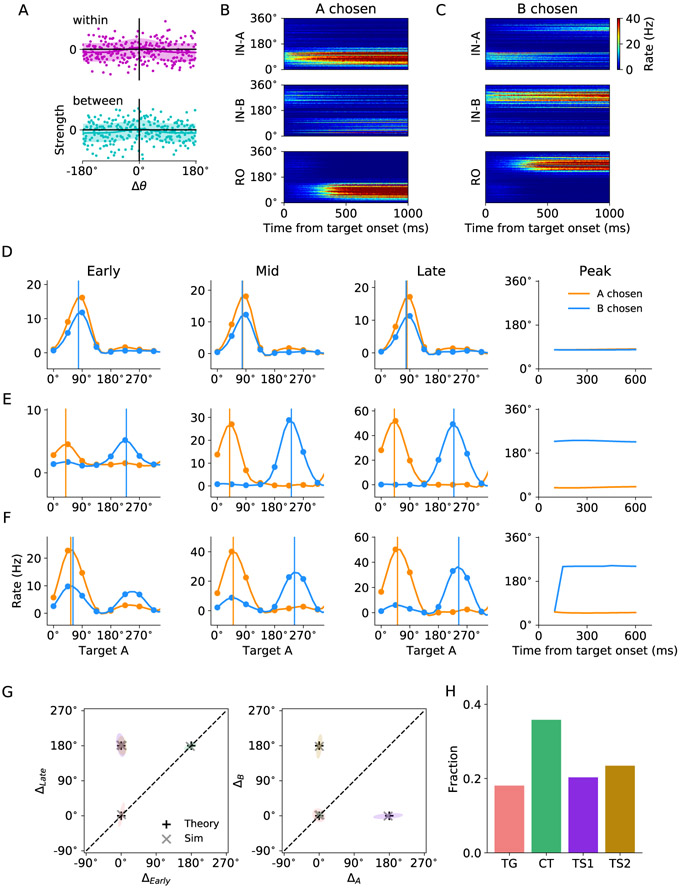
(A) The neural circuit model was constructed based on the behavioral task in Cai and Padoa-Schioppa (2014). At the beginning of the trial, the monkey fixated a center point on the monitor. After 1.5 s, two offers appeared to the left and right of the fixation point. The offers were represented by sets of color squares, with the color indicating the juice type and the number of squares indicating the juice amount. The offers remained on the monitor for 1 s, and then they disappeared. The monkey continued fixating for another 1 s, after which two saccade targets appeared. The location of the saccade targets was randomly selected on a circle centered on the fixation point out of eight possible locations, with the two saccade targets on opposite sides of the fixation point. The saccade targets were of different colors corresponding to the colors of the two juices. The monkey maintained fixation for an additional randomly variable delay (0.6-1.2 s) before the center fixation point was extinguished, which served as the “go” signal. (B) Schematic of the circuit model. The working memory (WM) neuronal population in LPFC receives chosen juice input. The integration (IN) neuronal population integrate visual input from sensory areas and chosen juice input from WM. Finally, IN population project to readout (RO) population where the chosen target output is sent to the downstream motor area(s). A filled circle and a ring represent a population of homogeneous neurons and a ring network, respectively. Different types of arrows stand for different types of synaptic interaction, as specified below the circuit schematic.(C) The chosen juice input is presented during offer on period as currents of different amplitudes.(D) The visual input is presented as a Gaussian-profiled current which peaks at the direction of the target cue. Note that the two target cues are always opposite to each other, that is, 180° apart.(E) Activity profile of the WM module when A is the chosen juice, which exhibits the typical winner-take-all attractor dynamics. The shaded time intervals correspond to offer on and target on periods shown in (A).

RESULTS

A neural circuit model of good-to-action transformation

To investigate the neural mechanism underlying good-to-action transformation, we developed a neural circuit model based on the behavioral and neurophysiological data in an economic choice task that was designed to study such transformation. Figure 1A shows the design and timeline of the original task (Cai and Padoa-Schioppa, 2014). At the beginning of the trial, the monkey fixated a center point on the monitor. After 1.5 s, two offers appeared to the left and right of the fixation point. The offers were represented by sets of colored squares, with the color indicating the juice type and the number of squares indicating juice amount. The offers remained on the monitor for 1 s, and then they disappeared. The monkey continued fixating the center point for another 1 s. At the end of this delay, two saccade targets appeared (target on). The location of the saccade targets was randomly selected on a circle centered on the fixation point (eight possible locations), with the two saccade targets on opposite side of the fixation point. The color of the saccade targets matched those of the squares representing each offer. The monkey maintained fixation for a randomly variable period of 0.6-1.2 s before the center fixation point was extinguished (“go” signal), at which point the monkey indicated its choice with a saccade. The dissociation between the presentation of the offers and their associated saccade targets provided a window for observing generation of an action plan from the choice outcome (Cai and Padoa-Schioppa, 2014).

Our model is a minimal circuit model for implementing the transformation based on the experimental discoveries. Since in the monkey experiment the final action is a saccade to the chosen target located on a circle with a fixed eccentricity, a basic model circuit has a “ring” structure where neurons are selective for a directional angle ranging from 0° to 360°. Our model has three modules. The first module is a working memory (WM) module that maintains the chosen juice signal, the second module consists of two integration (IN) rings that integrate the chosen juice input and the visual input of saccade target locations, and the third module is a readout (RO) ring for action plan (Figure 1B). The WM module is modeled by a two-pool attractor network, whereas the IN and RO rings are modeled by ring networks. As in previous works (Ben-Yishai et al., 1995; Zhang, 1996; Camperi and Wang, 1998; Compte et al., 2000; Engel and Wang, 2011), in each ring, neurons are labeled by their preferred directions. Excitatory connection between a pair of neurons depends on the difference in their preferred directions, whereas lateral inhibition is uniform. The detailed network architecture and parameters are described in EXPERIMENTAL PROCEDURES.

In model simulation, the chosen juice input is presented during offer on as currents of different amplitudes (Figure 1C) since the chosen juice neurons in OFC exhibit binary activity pattern (Padoa-Schioppa and Assad, 2006; Cai and Padoa-Schioppa, 2014). The visual input for each of the two targets is represented by a Gaussian profile current which peaks at the direction of the target cue (Figure 1D). The two peaks have the same amplitude and are 180° apart. Here inputs associated with chosen juice A (B) project to IN-A (IN-B) ring during target on lasting for 1 s, which is long enough to reveal the economic choice signal that had occurred within 0.6 s (minimum target on duration in the experiment) after target onset. An example activity profile of the WM module in response to the chosen juice input is shown in Figure 1E, which exhibits the typical winner-take-all (WTA) attractor dynamics (Wang, 2002; Wong and Wang, 2006). We first considered a homogeneous synaptic connectivity model in which the level of excitatory interaction between the IN rings gave rise to different subsets of functional neuron types. To define two contrasting scenarios, we introduced a scaling parameter a such that the ratio of within- to between-ring excitatory contribution is 1 – α/2 to α/2, which implies that the total synaptic weight within the dual-ring network is constant. We first tested two distinct scenarios: (I) no excitatory interaction between the two IN rings (α = 0); (II) equal strength for between- and within-ring excitatory interaction (α = 1). Examples of the two scenarios are displayed in Figures 2B and C, when juice A is chosen and target A is presented at 90° and B at 270°. In Scenario I, two IN rings operate independently of each other. An activity bump appears at 90° in ring A and at 270° in ring B. With the stronger juice signal in A, WTA competition takes place in the downstream RO ring which results in the emergence of chosen target signal (location of target A) which directs saccade. In Scenario II, the net interaction between two neural units with similar preferred direction in different rings is excitatory. Under such scenario, the two IN rings cooperate. In detail, the stronger activity bump in ring A excites its counterpart in ring B which, in turn, suppresses the original activity bump in B. Such process is manifested as a transition of activity bump (Figure 2C). As a result, the chosen target signal emerges in both IN rings after such transition, thus providing a parsimonious circuit for good-to-action transformation. We further tested the robustness of the model performance against noise by doubling the background noise level σ_n in the two scenarios. As shown in Figure S1, the between-ring coupling in Scenario II gives smaller absolute errors in direction decoding in the RO ring upon higher noise level and thus has the advantage of enhancing networks robustness against noise. Figure 2D shows the snapshots of activity profile of the IN-B ring under Scenario II in three different time windows: the early window before the transition if any, the mid window during transition and the late window after transition. The activity bump of the IN-B ring under Scenario II initially peaks at target B location until the bump at the opposite direction grows strong enough with the support of the excitation from ring A to suppress the initial bump, leading to a transition of the peak and the ultimate emergence of the chosen target signal.

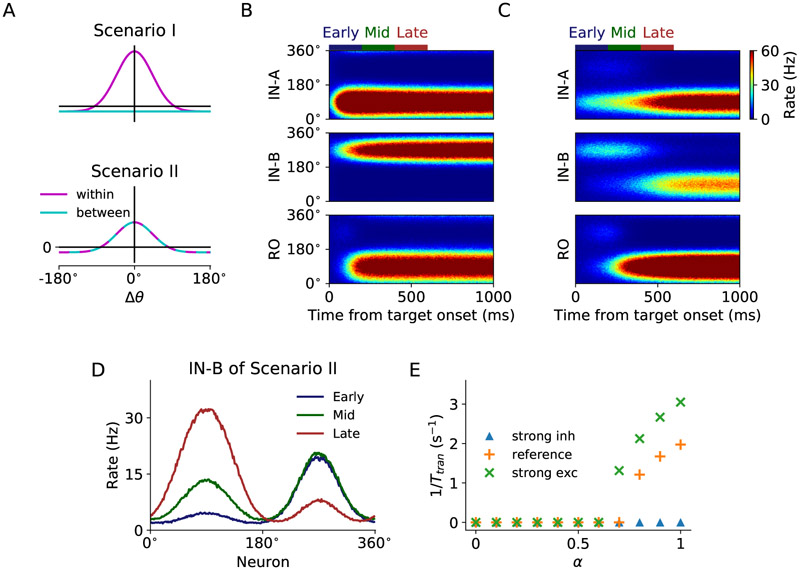
Figure 2. Model scenarios and circuit dynamics.

(A) Model scenarios and circuit dynamics for Scenario I and II. In Scenario I (α = 0)the interaction within rings follows a Gaussian spatial profile, while the interaction between rings has no spatial dependence. In Scenario II (α = 1), the interaction within and between rings follows the same Gaussian profile. The total synaptic weight within the dual-ring network is conserved in both scenarios.

(B) Scenario I: spatiotemporal activity pattern of IN and RO population of the circuit model from target onset when the chosen target is A, presented at 90°.

(C) Same as (B) but for Scenario II. Note that there is a 180° transition of the activity bump in IN-B ring during 200 – 400 ms after target onset.

(D) Activity profile of IN-B ring of Scenario II in different time windows. Early, mid and late time windows are defined at 0 – 200 ms, 200 – 400 ms and 400 — 600 ms, respectively, after target onset. The activity bump initially appears at 270°, but then another bump at chosen target location 90° grows over time and the initial bump is suppressed.

(E) Effect of between-IN ring excitatory interaction on transition time. We consider three conditions: strong inhibition (J₋ = −0.6 nA, J₊ = 1.9 nA), reference (J₋ = −0.35 nA, J₊ = 1.9 nA) and strong overall excitation (J₋ = −0.35 nA, J₊ = 2.02 nA). When inhibition is strong, no transition occurs. When excitation is sufficiently strong, transition takes place at large α. The stronger the excitation and the larger the value of α, the earlier the transition occurs, giving rise to a larger inversed transition time.

To examine how the relative strength of within- and between-ring excitatory interaction may affect transition, we varied α from zero (within-ring excitation only) to one (equal excitatory coupling). We used the inverse of transition time 1/T_tran to characterize the transition (see EXPERIMENTAL PROCEDURES). If transition does not happen during target on, 1/T_tran is set to 0. We consider three conditions: reference (J = 0.35 nA, J₊ = 1.9 nA), stronger inhibition (J = 0.6 nA, J₊ = 1.9 nA) or stronger excitation (J = 0.35 nA, J₊ = 2.02 nA) relative to reference. When inhibition is strong, no transition occurs during target on (Figure 2E, blue triangle and Figure S2, left column). When excitation is sufficiently strong, transition takes place at α ≥ 0.8 (orange “+”). As excitation grows, transition occurs with lower threshold for α (green “x”, α ≥ 0.7). In general, the stronger the excitation between the IN ring networks (that is, the larger the value of α), the earlier the transition occurs (Figure S2), giving rise to a larger 1/T_tran. Therefore, both restricted global inhibition and sufficiently strong excitation set the stage for the cooperation between the IN rings for the action signal to emerge.

Model predictions on functional neuron types

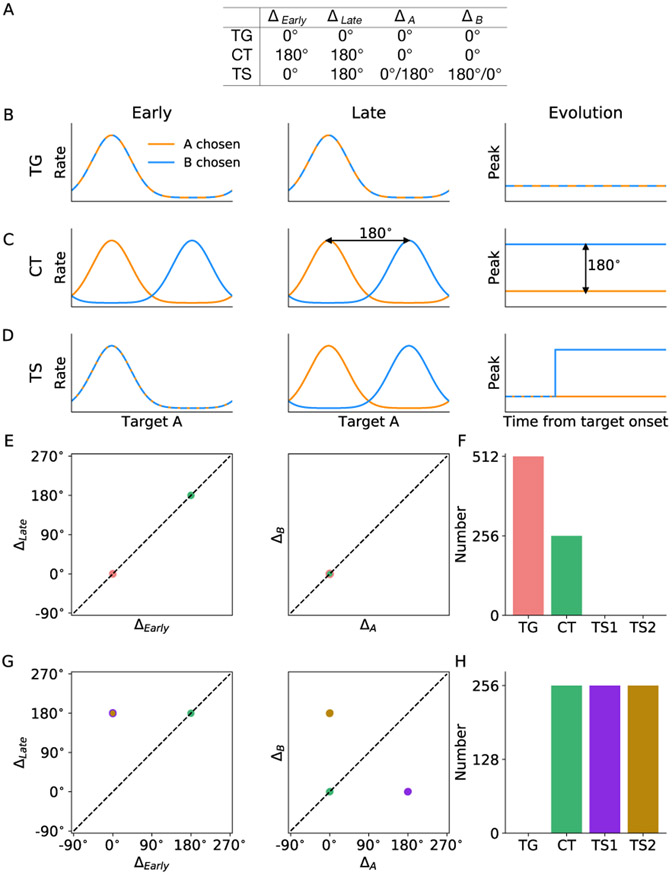
In the previous section, we demonstrated how chosen target signal emerges under a particular set of inputs (juice A is chosen and target A is located at 90°). The time evolution of network activities suggests that there are different types of neurons in our model that may serve different functions during good-to-action transformation. To characterize neurons of potential functional types, we further simulated the model with either juice A or B chosen and target A located at any of the eight possible locations. Such simulations enable us to construct tuning curves for each neuron based on the location and identity of the chosen target. As a result, Scenario I predicts the existence of visual target encoding (TG) neurons and motor-like chosen target (CT) neurons while Scenario II predicts the existence of transition (TS) neurons which first encode target location and then transition to encode chosen target location.

To characterize the property of the above three functional neuron types, we analyzed how neuron’s spatial tuning curves develop as the transformation unfolds. In accordance with Cai and Padoa-Schioppa (2014), the chosen target signal increases sharply from 200 to 400 ms after target onset and sustained for a few hundred milliseconds. In this regard, we consider two chosen juices (A and B), as well as two time windows (early and late). The early and late time windows are defined as 0 - 200 ms and 400 - 600 ms after target onset, respectively. For each neuron, we constructed four tuning curves, corresponding to the following four conditions: juice A chosen, early time window; juice B chosen, early time window; juice A chosen, late time window; and juice B chosen, late time window. The spatial tuning was constructed and is based on the location of target A, which is the abscissa of the tuning curve (see EXPERIMENTAL PROCEDURES). To further characterize neurons of different functional significance, we derived from the four tuning curves four peak values and constructed four independent peak differences for each neuron (see EXPERIMENTAL PROCEDURES). Each neuron can thus be represented in the 4-dimensional space of peak differences. According to the model, specific sets of values of the peak differences for the three functional types of neurons are listed in Figure 3A. Figures 3B-D demonstrate the spatial tuning curves as well as the temporal evolution of the peak of the tuning curves. TG neurons respond maximally to its preferred direction regardless of which juice was chosen and the time window considered. The peaks of the two tuning curves remain invariant over time and the two tuning curves completely overlap. CT neurons have different tuning curves for different chosen juice, with their peaks 180° apart, but the tuning does not change over time. The peak locations for the two tuning curves are constant and 180° apart. Finally, TS neurons behave like TG neurons in the early window, and CT neurons in the late time window. There is a 180° peak location shift for one of the two tuning curves, depending on which IN ring the neuron belongs to. The prediction of the existence of distinct classes of neurons by the two model scenarios provided us a reference to examine which scenario provides a better account for the underlying mechanism of good-to-action transformation in the LPFC.

Figure 3. Model predictions of functional neuron types.

(A) Peak differences for the three functional types of neurons according to the model. The four independent peak differences are defined to characterize the spatial tuning of every neuron during good-to-action transformation (see EXPERIMENTAL PROCEDURES). Note that the peak location of spatial tuning curves is identified with respect to target A location. TG neurons encode the location of the associated target throughout a trial, independent of whether A or B is chosen, therefore all peak differences are 0°. CT neurons carry the chosen target signal throughout, that is, Δ_A = Δ_B = 0°, whereas the peak differences between the two tuning curves at different time intervals are 180°. TS neurons behave like TG in the early stage and like CT in the late stage. If a TS neuron is in ring A, its peak location for chosen juice A is constant over time, giving rise to Δ_A = 0° (D, orange) while its peak location for chosen juice B experiences a 180° change (D, blue). Vice versa for a TS neuron in ring B. Therefore, a TS neuron will take up one of the two locations in the 4-dimensional space of peak difference.

(B-D) Left: Spatial tuning curves contingent upon the identity of chosen juice for units in the model categorized asTG, CT and TS neurons. Right: Time evolution of the peak location of the spatial tuning curves of the three neuron types.

(E) Representation of neurons in space of peak difference according to Scenario I. The 4-dimensional space was decomposed into two 2-dimensional subspaces. Note that the representations of TG and CT neurons overlap in the subspace Δ_A versus Δ_B

(F) Number of different neuron types according to Scenario I.

(G) Representation of neurons according to Scenario II as in (E). Note that the representations of TS1 and TS2 neurons overlap in the subspace Δ_Early versus Δ_Late.

(H) Number of different neuron types according to Scenario II.

At the population level, TG and CT neurons each occupy one location in the 4-dimensional space, whereas TS neurons occupy two locations depending on whether it belongs to ring IN-A or B. Figure 3E shows the locations of all 3N (N neurons in each ring) simulated neurons in the three rings of Scenario I according to the peak differences defined above. Data in the 4-dimensional space are projected onto two 2-dimensional sub-spaces for visualization. Clearly, there are two groups of neurons in the sub-space Δ_Late versus Δ_Early, and two overlapping groups in the subspace Δ_B versus Δ_A. Therefore, we can identify two distinct groups in the 4-dimensional space of peak differences and the counts are 2N for TG neurons and N for CT neurons (Figure 3F). Similar to Figure 3D, Figure 3G shows all the neurons under Scenario II. There are three distinct groups of neurons in the 4-dimensional space. One group corresponds to CT neurons, and the other two groups that overlap in the subspace Δ_Late versus Δ_Early are TS neurons. We label the group of neurons with (Δ_A, Δ_B) located at (180° , 0°) as TS1, and the other group at (0°,180°) as TS2. TS1 neurons belong to ring IN-B representing target B location and the peak of their spatial tuning curve goes through a transition when A was chosen while TS2 neurons are located in ring IN-A and the peak of their spatial tuning curve goes through a transition when B was chosen. Figure 3H illustrates N neurons for each group, mapped onto each of the three rings: CT neurons on the RO ring and TS neurons on the two IN rings.

Functional classification of neurons in LPFC

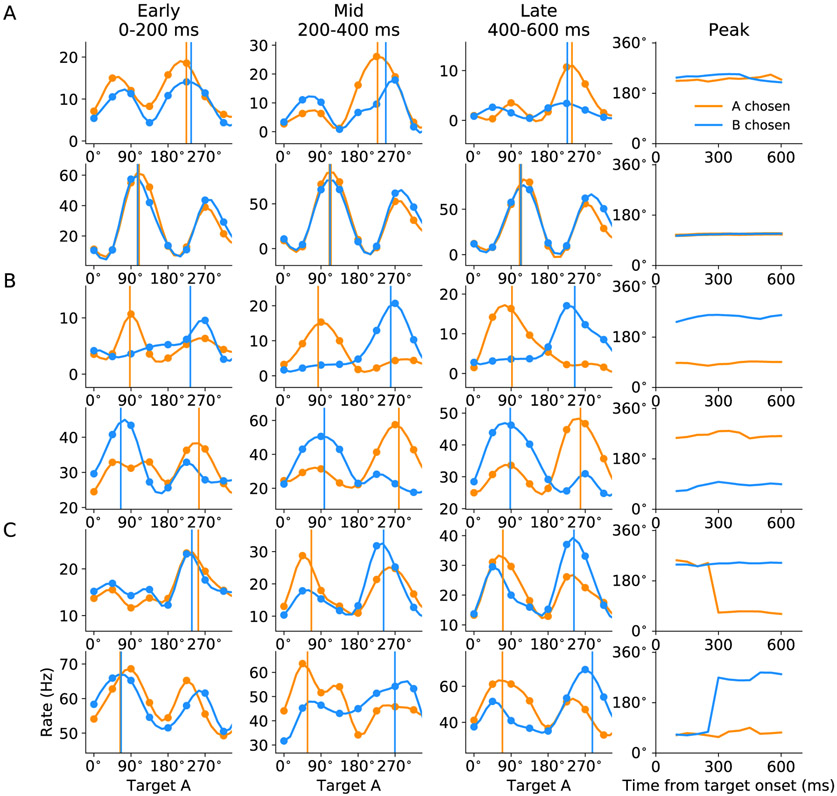
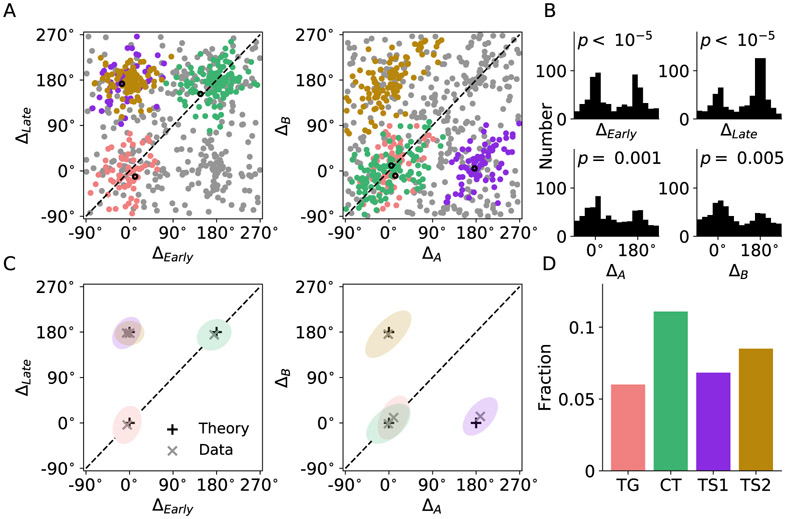
It is intriguing that our model predicts that good-to-action transformation can be implemented by the interaction among functional groups of neurons under different model scenarios. Was LPFC operating under either scenario or a mixture of both? To answer this question, we performed similar analysis focusing on the time evolution of tuning curves of 1078 neurons recorded from LPFC. We constructed the spatial tuning curves of each neuron conditioned upon the chosen juice at different time windows after target onset. Tuning curves were constructed from 0 to 700 ms after target onset using sliding time window (200 ms) in steps of 50 ms. Tuning curves of example TG, CT and TS-like neurons in early (0-200 ms), mid (200-400 ms) and late (400-600 ms) windows and the time evolution of their peaks are shown in Figure 4. The classification of all example neurons was later verified to be consistent with the outcome of population level classification. The time evolution of tuning peaks display similar characteristics as those of simulated neurons in Figure 3. Some neurons appear to have two peaks that are opposite to each other, and in most cases, one peak has substantially higher amplitude. For consistency across neurons, we identified the peak with higher amplitude as the neurons preferred spatial direction according to the approach outlined in EXPERIMENTAL PROCEDURES. Computational study and analysis on bimodally-tuned neurons are presented in the next subsection. Since spatial tuning is a characteristic feature for neurons in the ring model, we applied a 4-way ANOVA to identify spatially selective neurons in LPFC (see EXPERIMENTAL PROCEDURES). Overall, 665 neurons were found to be spatially selective, and each of them can be represented in the 4-dimensional space of peak difference. Figure 5A shows the distribution of neurons mapped onto 2-dimensional sub-spaces. We applied DBSCAN, an unsupervised density-based clustering algorithm, to search for clusters in the 4-dimensional space (see EXPERIMENTAL PROCEDURES). The analysis yielded four valid clusters, each of which is labeled by a different color (Figure 5A). The histograms of peak differences also demonstrated significant bimodal distribution for each of the four dimensions (Figure 5B). We further computed the mean and standard error for data along each dimension, represented by xs and ellipses in Figure 5C. The theoretically predicted locations of neurons are marked with +s for comparison. Strikingly, the centers of the four clusters computed from experimental data match well with the four locations predicted by the model. Importantly, all three types of neuron are well represented. Fraction for each category is displayed in Figure 5D and the number of neurons classified as TG, CT and TS are 65 (9.8%), 120 (18.0%) and 166 (25.3%), respectively. We repeated the analysis for all 1078 LPFC neurons and obtained qualitatively similar results (Figures S3A and B). As a control, the same analysis was applied to 1078 pairs of randomly generated tuning curves with firing rate values drawn from a uniform distribution. No clear pattern and no significant bimodal distribution of peak differences is observed as shown in Figures S3C and D.

Figure 4. Examples of the three neuron types from LPFC.

Spatial tuning curves and time evolution of their peak location of two putative

(A) TG neurons,

(B) CT neurons,

(C) TS neurons.

The tuning curves were constructed by cubic spline interpolation.

Figure 5. LPFC neuron type classification.

(A) Representation of spatially selective neurons in the space of peak differences. The clusters were detected with DBSCAN. Different clusters were represented by different colors with gray as unclassified. The first example neuron of each functional type in Figure 4 is marked with a black circle.

(B) Histograms for each dimension. The p-values indicate the significance of the dip test.

(C) Representation of neuron clusters in peak-difference space. Each ellipse represents one SEM of one cluster. Black pluses indicate theoretically predicted locations of peak differences for different neuron types, while gray crosses denote the center (mean) for each cluster, which are also the centers of the ellipses.

(D) Fraction of different neuron types among all the recorded LPFC neurons.

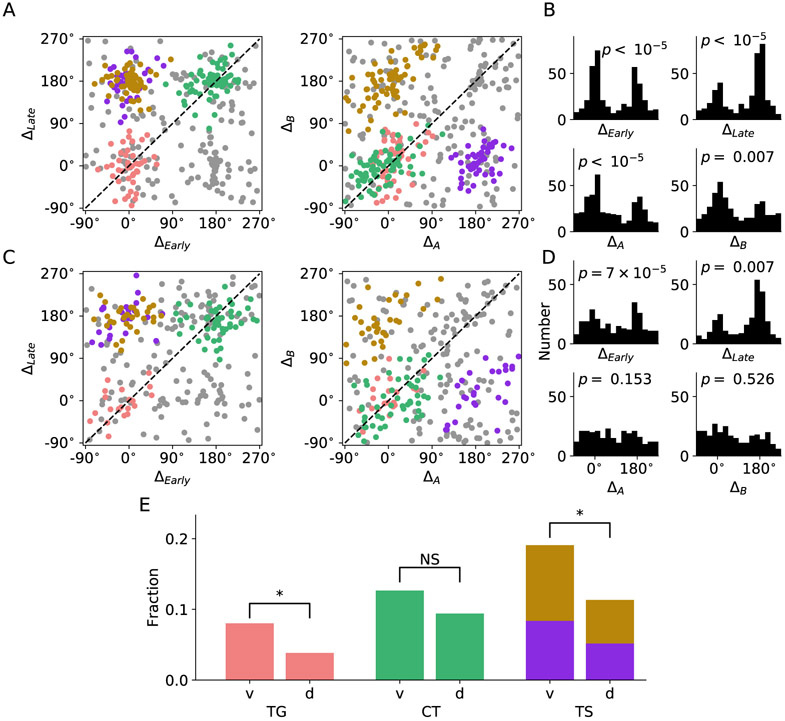
Cai and Padoa-Schioppa (2014) reported that during good-to-action transformation, spatial and action-related signal emerges earlier in LPFCv than that in LPFCd suggesting different functional roles of these two LPFC sub-regions. Therefore, we separated neurons recorded from LPFCv and LPFCd. For LPFCv, both the clustering and the bimodal distribution along each dimension are very distinct (Figures 6A and B), but such pattern was much less prominent for LPFCd (Figures 6C and D). To further characterize potential functional difference between LPFCv and LPFCd, we compared the fraction of different types of neuron identified through the clustering analysis based on 395 and 270 spatially selective neurons in LPFCv and LPFCd, respectively. Proportions of TG, TS and CT neurons are all higher in LPFCv (TG 8.0%, TS 19.1% and CT 12.7%) than that in LPFCd (TG 3.8%, TS 11.3% and CT 9.4%), with the former two showing significant difference in proportion (p <0.05, two-sample t-test) (Figure 6E). Difference in proportion of all neuron types became significant when we performed clustering analysis with stricter criteria (Figure S5, p <0.05 for all neuron types). These results corroborate with the findings by Cai and Padoa-Schioppa (2014), which suggested that LPFCv likely plays a more important role in good-to-action transformation.

Figure 6. LPFC neuron type classification.

Spatially selective neurons in Figure 5C were plotted separately for LPFCv and LPFCd.

(A) Representation of LPFCv neurons in the space of peak-difference.

(B) Histograms of LPFCv neuron count for each dimension of peak-difference.

(C) Same as (A) but for LPFCd.

(D) Same as (B) but for LPFCd.

(E) Fraction of different neuron types among all recorded neurons in LPFCv and LPFCd. Asterisks indicate significant difference in fraction (p < 0.05, two-sample t-test).

Heterogeneity in network interactions reproduces heterogeneous neuron classes

As our model simulation demonstrated, in Scenario I (Figure 2B), each of the two IN rings encodes only target location throughout the trial. In Scenario II (Figure 2C), when juice A was chosen, the IN-A ring encodes the location of target A, which is also the chosen target, throughout the trial while IN-B ring first encodes target B location but then switches to encode the chosen target location. The finding that neuron types predicted by Scenario I and II coexist in the data suggests that the LPFC circuit underlying good-to-action transformation may operate under a hybrid mode of Scenarios I and II, named Scenario III.

Based on the rationale that physiologically the connectivity between neurons is likely to be heterogeneous (Renart et al., 2003), Scenario III was set by introducing heterogeneity in both within and between ring connectivity, characterized by β (see EXPERIMENTAL PROCEDURES). Note that the Gaussian-profiled relationship still persists albeit noisier. An example connectivity profile of one neuron to all neurons in the same (top) and opposite ring (bottom) is illustrated in Figure 7A. The solid line represents the mean Gaussian-profiled connection strength and the shaded area marks one standard deviation from the mean. As a result of such heterogeneous connectivity, some neurons receive stronger within-ring excitation that supports target encoding, whereas some receive stronger between-ring excitation that facilitates transition thus eventually encode the location of chosen target. When juice A was chosen, as shown in Figure 7B, while the inputs are exactly the same as that in Scenario I, in Scenario II two activity bumps coexist in ring IN-B after transition, one encoding target B location (270°) throughout and the other encoding the chosen target location (90°). Snapshots of the activity profile of IN-B ring network at different time after target onset are presented in Figure S6. Another example simulation is displayed in Figure 7C in which juice B was chosen. In this case, two activity bumps coexist in the IN-A ring.

Figure 7. Effects of heterogeneity in network interactions on the properties of the circuit model in Scenario III.

(A) An example of interaction profiles within (top) and between (bottom) IN rings for one neuron in the ring. The mean interaction strength has a Gaussian profile and the shaded boundaries correspond to one standard deviation.

(B) Activity of model neurons when target A which appeared at 90° was chosen.

(C) Activity of model neurons when target B which appeared at 270° was chosen.

(D-F) Spatial tuning curves and time evolution of their peak location of a TG neuron (D), CT neuron and TS neuron (F). The tuning curves were constructed by cubic spline interpolation.

(G) Representation of neuron clusters in peak-difference space. Each ellipse represents one SEM of one cluster. Black pluses indicate theoretically predicted locations of peak differences for different neuron types, while gray crosses denote the mean for each cluster, or the center of the ellipse.

(H) Fraction of different neuron types.

To compare the tuning features of the recorded neurons and those in the circuit model, we performed simulation with various target input directions and different chosen juices. Some example spatial tuning curves of simulated neurons that are classified as TG, CT and TS neurons and the time evolution of their peak location in different time windows are demonstrated in Figure 7D-F. We then performed the same clustering analysis (DBSCAN) based on the activity of the simulated neurons and identified four valid clusters (Figures 7G and S7). Interestingly, the centers of the four clusters from simulation match well with the locations predicted by the theoretical accounts (marked by “+”s) of the three functional neuron types produced in Scenarios I and II. The counts of the three types of neurons are displayed in Figure 7H. All neurons in RO ring are CT neurons. As for the 512 neurons in IN rings, 139 are TG, 336 are TS, 19 are CT and 18 are unclassified. The proportion of TG, TS and CT neurons matches that identified in LPFC (Figure 5D) when the level of heterogeneity β is set at the appropriate value (2.5 nA).

Some neurons in LPFC exhibit substantial bimodal tuning (Figure 4), whereas the tuning of most model neurons is only slightly bimodal (Figure 7). Given that visual input over preferred direction of model neurons on IN rings is unimodal (Figure 4), bimodal tuning in neurons in IN rings arises from the excitatory interaction between IN rings, while neurons in RO ring simply sum input from the two IN rings. However, excitatory interaction between IN rings in the model is not sufficient to account for the bimodal tuning of LPFC neurons. LPFC neurons are known to be spatially selective and flexibly encode task-relevant information. This implies that a neuron responds whenever a target cue appears at its preferred direction, and such a response is further modulated by color after the establishment of color-juice contingencies. We test whether such a setting could account for the bimodal tuning observed in LPFC neurons. To this end, we use bimodal-tuned input as shown in Figure S8A. Figures S8B and C display the neural activity in the three ring networks when target A and B is chosen, respectively. Stronger traces of two coexisting bumps are noted compared with Figures 7B and C. At the single cell level, the bimodal tuning is also more obvious (an example TS neuron is shown in Figure S8D). Importantly, the cluster analysis yielded four clusters at approximately the same locations in the space of peak differences and similar fraction of the three neuron types (Figures S8E and F). To characterize the degree of bimodal tuning, the maximum amplitude of the tuning curve and that at the diametrical location were plotted for LPFC neurons (Figure S8G) and model neurons (Figure S8H) in the early and late time windows. Each data point represents one neuron’s bimodal tuning property contingent upon one chosen juice, therefore, each neuron contributes two points for each scatter plot. The closer to the diagonal, the more bimodal the tuning is. In both LPFC and model neurons, the degree of bimodal tuning spans a wide range, with stronger bimodality in the early than late window. These observations are possibly the consequences of heterogeneity and convergence of dynamics in the IN rings. To conclude, our attractor network model with Gaussian-profile interacting duo-rings shown in Figure 1A reproduces the major observations and neuron type statistics with both unimodal and bimodal visual input.

Effects of synaptic interactions on quantitative predictions of neuron classes

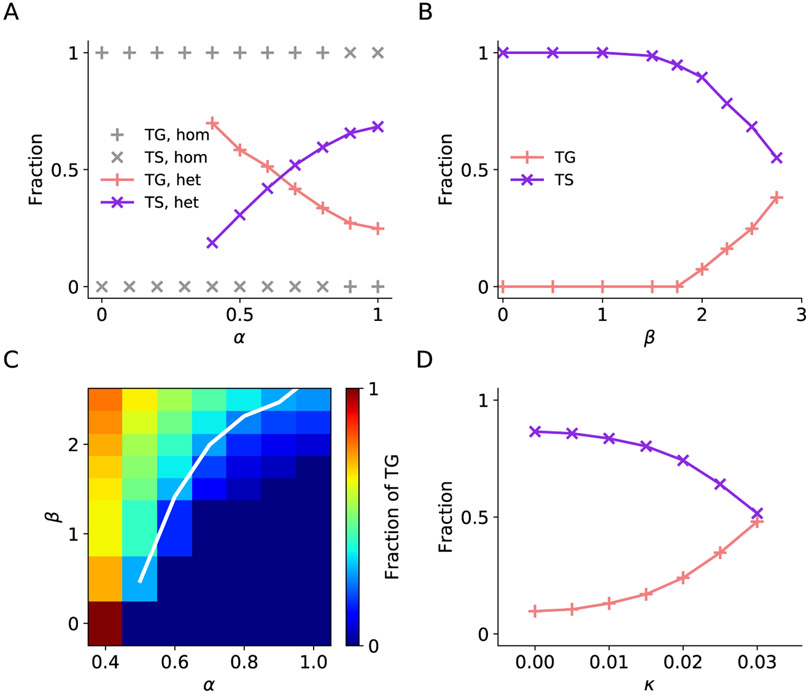
One important discovery from experimenting with the synaptic interactions of the circuit model is that synaptic interactions can give rise to different mechanisms fulfilling good-to-action transformation. In Scenario I, IN ring networks encode target location and the chosen target signal emerges in the RO ring network through WTA competition. In Scenario II, neurons in IN ring networks first encode target location then all transition to encode chosen target location due to cooperation between the rings, provided that the synaptic coupling between the IN rings are sufficiently strong. As shown in the earlier analysis (Figure 2), without heterogeneity (i.e. synaptic coupling between any neuron pairs is only dependent on their preferred direction difference and whether or not they appear in the same ring) neuronal activity in the IN rings is homogeneous, which gives rise to either TG (Scenario I) or TS (Scenario II) neurons exclusively (see gray symbols in Figure 8A). On the other hand, in Scenario III with heterogeneity in synaptic connectivity, some neurons in the IN-ring networks function as TG neurons while others function as TS neurons.

Figure 8. Effects of synaptic interactions on quantitative predictions of neuron types.

(A) Fraction of TG and TS neurons in the two IN rings as a function of between-ring excitatory interaction strength α for homogeneous network (β = 0, gray) and heterogeneous network (β = 2.5 nA, colored). Heterogeneity in network interactions gives rise to the coexistence of TG and TS neurons in the two rings. Larger α favors the existence of TS neurons.

(B) Fraction of TG and TS neurons as a function of standard deviation of excitatory interaction strength β at α = 0.9. Higher level of heterogeneity, as indicated by higher β value, favors the existence of TG neurons at large α.

(C) Fraction of TG neurons as a function of α and β. The white line indicates the fraction of TG neurons equal to 0.28, the fraction observed in experiment.

(D) Fraction of TG and TS neurons as the intrinsic neuronal heterogeneity κ varies. Here neuronal heterogeneity is implemented by drawing two Gaussian-distributed parameters for each neuron. α and β were set to be 0.9 and 2 nA, respectively. Higher level of neuronal heterogeneity, as indicated by higher κ value, favors the existence of TG neurons.

An intriguing question is under what condition(s) our model reproduces functional neuron groups that match quantitatively those discovered in the data. To approach this question, we focused on examining how strength α and heterogeneity β of synaptic coupling govern the dynamics of the circuit model, which leads to different fractions of TG and TS neurons in the two IN rings. We discovered that at a significant level of heterogeneity (β = 2.5 nA), TG and TS neurons coexist (Figure 8A). As we increase the between-ring synaptic coupling strength α, the fraction of TG neurons decreases while that of TS neurons increases. Note that to maintain network stability given the current set of other model parameters, α needs to be higher than 0.5, therefore, some data points are omitted for small α. At the same time, β must remain below 2.75 nA because strong heterogeneity gives rise to network instability. We discovered that within the working range of α and β, irrespective of the heterogeneity level, increasing α leads to higher fraction of TS neurons. On the other hand, at a fixed value of α, increasing heterogeneity β tends to increase the fraction of TG neurons (Figure 8B). For detailed quantification, we focused on investigating how the fraction of TG depends on α and β (Figure 8C). In the experimental data, the fraction of TG among the subpopulation of TG and TS neurons is 0.28. To obtain the same fraction in the model, increasing coupling strength α requires increasing heterogeneity β as indicated by the white line in Figure 8C. The behavior of the model changes gradually along the line, modulated by α and β. Furthermore, we investigated the effects of intrinsic neuronal heterogeneity κ (see EXPERIMENTAL PROCEDURES) on circuit dynamics and TG/TS ratio. As demonstrated in Figure 8D, intrinsic neuronal heterogeneity supports the emergence of TG neurons in a similar way as network connection heterogeneity. Furthermore, the network with heterogeneity in both synaptic connections and intrinsic neuronal properties recapitulate the clustering of functional neuron groups (Figure S9) as observed in the model with network heterogeneity alone.

DISCUSSION

Biophysical plausibility of the circuit model

We proposed a circuit model for good-to-action transformation in an economic choice task. The model comprises three modules: WM, IN and RO modules. The information represented in our modular circuit model presents mixed coding properties similar to that observed in the data. Before target presentation, the memorized choice outcome is maintained by the WM module, in the meantime, the choice outcome signal can also be detected in the IN module which receives direct projection from the WM module. Such observation is consistent with mixed coding of target location and chosen juice in LPFC under the same task (Cai and Padoa-Schioppa, 2014). The IN module consists of two ring networks that integrate chosen juice and target location inputs. Several other studies also suggested that LPFC, and LPFCv in particular, carries both spatial information (“where”) (Rainer et al., 1998; Kennerley and Wallis, 2009; Hoshi, 2004) and object information (”what”) (Rainer et al., 1998). In cases when transition occurs, the IN module also represents chosen target signal highlighting the fact that the IN module can carry information of multiple task-related features, especially in presence of heterogeneity in interneuronal connectivity. Such time evolution of information was also observed in the frontal eye field (FEF) (Sato and Schall, 2003), a brain region closely associated with LPFC.

Mechanistically, good-to-action transformation shares similarity with visual search. Both are visuomotor processes involving visual attention in identifying and saccading to a visual target. In visual search, attention is guided by rules and top-down attention signal is likely originated from prefrontal areas such as areas 45A, 12 and 46v (Bichot et al., 2015). Whereas in good-to-action transformation, attention is guided by choice outcome signal originated in OFC (Padoa-Schioppa and Assad, 2006; Cai and Padoa-Schioppa, 2014). Hamker (2005) proposed a model of visual search involving FEF, ventrolateral prefrontal (PF) cortex and the ventral visual pathway. In his model, during the delay period, memory for visual cues are stored in PF which is feature-selective but not spatially selective. Once the search array is on, bottom-up visual input reaches V4 and, at the same time, PF sends out top down attention signal to V4 via IT. These two streams of signals are integrated in V4, which in turn sends spatial information to FEF while collapsing the feature space. However, the property of the PF module is inconsistent with the observations of the LPFC neurons integrating both stimulus and spatial information (Rainer et al., 1998; Cai and Padoa-Schioppa, 2014; Tsutsui et al., 2016). In the meantime, in a visual search task with FEF recordings (Sato and Schall, 2003), the authors discovered that out of the 65 FEF neurons that discriminated the target from distractors in pro-saccade trials, 21 of them did not respond to the target in anti-saccade trials but responded to the endpoint of saccade, which share the same property as the CT neurons in our model. 44 responded to the target in anti-saccade trials, 38 of which also showed transition to respond to the endpoint of saccade, which resemble TS neurons. The remaining 6 did not undergo transition, which belong to the category of TG neurons. Thus, the same categories of functional neuron types exist in both FEF and LPFC, suggesting that a similar circuit mechanism may be implemented in FEF subserving visual search.

Computations with interactive ring networks

Ring network models have been widely adopted in computational work on visuospatial working memory (Compte et al., 2000; Engel and Wang, 2011), winner-take-all spatial competition (Compte and Wang, 2006; Furman and Wang, 2008) and representation of directional features (zhang, 1996; Engel and Wang, 2011; Ardid and Wang, 2013; Engel et al., 2015). In general, the interplay between local excitation and global inhibition within a ring governs the dynamics of the network. Recently, the interaction between two ring networks has been proposed to be able to account for the observations in multisensory information segregation and integration (Zhang et al., 2016a,b). In our model, the two strongly interacting IN ring network enables cooperation between neurons with the same preferred direction but receiving different sources of input (Scenario II). The coupling not only allows a more parsimonious circuit for implementation of the task but also enhances robustness of the output against noise. If the between-ring interaction is weak or non-existent, the two IN-ring network operates independently with their dynamics governed by within-ring interaction (Scenario I). In that case, the target signal is preserved without being overwritten. Whereas in Scenario III, with heterogeneity in the network connections, the resulting dynamical activity is a mixture of Scenarios I and II.

Furthermore, without heterogeneity in network connectivity, increase in between-ring connection strength α can lead to an abrupt change of operating mechanism in the IN module. As shown in Figure 2E, neurons in the IN-ring networks switch from encoding target location (Scenario I) to representing chosen target location in the end (Scenario II) when α is sufficiently large. However, such change is gradual with heterogeneity in network connectivity, rendering the coexistence of TG and TS neurons. In reality, network connections are heterogeneous and subject to modification during learning and adaptation. To account for the count statistics of neuron types in LPFC, a significant level of heterogeneity in connectivity was essential. Furthermore, neurons are biophysically diverse and such intrinsic neuronal diversity can further promote the emergence of TG neurons.

Neural substrates of good-to-action transformation

The lack of spatial selectivity in OFC neurons suggests that OFC computes value and resolves decisions in an abstract way (Padoa-Schioppa and Assad, 2006; Cai and Padoa-Schioppa, 2014). The discovery that few OFC neurons encode choice outcome (chosen juice) signal during memory period in an economic choice task further implicates that good-to-action transformation likely occurs outside of OFC. LPFCv, the ventral subregion of LPFC is a major anatomical target of the OFC (Saleem et al., 2014), therefore, LPFCv likely receives abstract choice outcome signals from the OFC (Cai and Padoa-Schioppa, 2014). LPFCv projects to LPFCd (Markov et al., 2014; Takahara et al., 2012), which is densely connected with the motor areas (Takahara et al., 2012). On the other hand, LPFCv projects strongly to 8m and 8l, both of which are regions in frontal eye field (FEF) associated with oculomotor responses (Markov et al., 2014). Although spatial and action related signals emerge earlier in LPFCv than that in LPFCd, conjunctive coding of choice outcome and action plan, which was considered a signature of transformation, was observed in both regions (Cai and Padoa-Schioppa, 2014). Thus, how these two LPFC subregions might play different roles in good-to-action transformation remain unclear. Importantly, conjunctive coding of choice outcome and action plan only indicates the presence of input and output signals related to the transformation but does not provide insights regarding the mechanisms of its implementation.

Guided by our modeling result that good-to-action transformation was carried out by the interactive double-ring network that harbors both visual target encoding (TG) and transition (TS) neurons, we further analyzed macaque LPFC data from an economic choice task. We first discovered that there are more spatially selective neurons in LPFCv. More importantly, a significantly larger fraction of TG and TS neurons are found in LPFCv than that in LPFCd. Together with the previous findings that all spatial and action-related signals appeared in LPFCv earlier than that in LPFCd (Hoshi, 2004; Kennerley and Wallis, 2009; Cai and Padoa-Schioppa, 2014), our results advanced the hypothesis that LPFCv is likely to be the first stage in the chain of good-to-action transformation (Cai and Padoa-Schioppa, 2014). Namely, an action plan is first formed in LPFCv which drives the allocation of spatial attention (Asplund et al., 2010; Donahue and Lee, 2015). Such top-down attentional signal then informs the oculomotor areas of the proper action for retrieving the chosen good.

CONTACT FOR REAGENT AND RESOURCE SHARING

Further information and requests for resources should be directed to and will be fulfilled by the Lead Contact, Xiao-Jing Wang (xjwang@nyu.edu).

EXPERIMENTAL MODEL AND SUBJECT DETAILS

All experimental data are from Cai and Padoa-Schioppa (2014), where experimental protocol and recording procedures were described in details. Two rhesus monkeys (B, male, 9.0 kg; L, female, 6.5 kg) were used in the experiments. Briefly, animals sat in an electrically insulated enclosure (Crist Instruments), their head was restrained, and the eye position was monitored with an infrared video camera (Eyelink; SR Research). Tungsten electrodes (125 mm diameter, FHC) were advanced using custom-built motorized microdrives, with a 2.5 micron resolution. Electrical signals were amplified and band-passed filtered (high pass: 300 Hz, low pass: 6 kHz; Lynx 8, Neuralynx). Action potentials were detected online (Power 1,401, Spike 2; Cambridge Electronic Design). All experimental procedures strictly conformed to the NIH Guide for the Care and Use of Laboratory Animals and with the regulations at Washington University School of Medicine. At the beginning of the trial, the monkey fixated a center point on the monitor, within a tolerance window of 2. (In a small subset of sessions, the tolerance was 3°.) After 1.5 s, two offers appeared to the left and right of the fixation point. The offers were represented by sets of colored squares, with the color indicating the juice type and the number of squares indicating juice amount. The offers remained on the monitor for 1 s, and then they disappeared. The monkey continued fixating the center point for another 1 s. (In a subset of sessions for monkey L, this additional delay lasted only 0.5 s.) At the end of this delay, two saccade targets appeared. The location of the saccade targets was randomly selected on a circle (7° radius) centered on the fixation point (eight possible locations), with the two saccade targets on opposite side of the fixation point. The color of the saccade targets matched those of the squares representing each offer. The monkey maintained fixation for a randomly variable period of 0.6-1.2 s before the center fixation point was extinguished serving as the “go” signal, at which point the monkey indicated its choice with a saccade. In total, 1082 cells were recorded: 561 cells from LPFCv (362 and 199 from monkey B and L, respectively), and 521 cells from LPFCd (267 and 254 from monkey B and L, respectively). Four of the recorded neurons were omitted from analysis due to very low firing rate. Based on the MRI and on the sequence of gray and white matter encountered during electrode penetrations, we defined the regions ventral and dorsal to the fundus of the principal sulcus as LPFCv (9/46v) and LPFCd (9/46d), respectively.

METHOD DETAILS

The values of all the parameters mentioned below are listed in the tables below.

Neural circuit model

The neural circuit model of the LPFC comprises three interconnected neuronal modules: working memory (WM), integration (IN) and readout (RO) modules, as shown in Figure 1A. All three are recurrent networks with dynamics governed by local excitation and feedback inhibition (Compte et al., 2000; Wang, 2002; Wong and Wang, 2006; Engel and Wang, 2011). In simulations, a reduced firing-rate model was used, which has been shown to reproduce neural activity of a full spiking neuronal network (Wong and Wang, 2006). The dynamics of each neuronal unit is described by a single variable s representing the fraction of activated N-methyl-D-aspartate receptor (NMDA) conductance, governed by

$$\frac{ds}{dt}=-s∕{\tau }_s+(1-s)\gamma r,$$ (1)

with γ =0.641 and τ_s =60 ms. The firing rate r is a function of the total synaptic current I (Abbott and Chance, 2005; Wong and Wang, 2006):

$$r=f(I)=\frac{aI-b}{1-\text{exp}[-d(aI-b)]},$$ (2)

with a =270 Hz nA⁻¹, b=108 Hz and d =0.154 s.

The WM module was simulated by a two-variable attractor network model (Wong and Wang, 2006). Each variable represents a neuronal population (juice A and juice B) that receives inputs ICJ from the corresponding chosen juice (CJ) module in OFC during offer on, and maintains the storage of the choice outcome during the delay period because the encoding of chosen juice was observed in LPFC but not in OFC (Padoa-Schioppa and Assad, 2006; Cai and Padoa-Schioppa, 2014) (see DISCUSSION). The total current input to unit i of the WM module is given by

$$I_i^{WM}=J_1{s}_i^{WM}+J_2{s}_j^{WM}+I_i^{CJ}+I_{n,i}^{WM},$$ (3)

where (i, j) = (A, B) or (B, A), with J₁ = 0.3725 nA and J₂ = −0.1137 nA. $I_i^{CJ}$ is set to 0.03 nA if juice i is the chosen juice, and 0.015 nA otherwise. $I_{n,i}^{WM}$ is the noisy current the WM population i receives. When simulated, activities of the two populations diverge according to the winner-take-all dynamics, which is achieved through global inhibition and structured recurrent excitation within the attractor network (Wang, 2002; Wong and Wang, 2006).

As for the ring networks, the synaptic input to a neuronal unit i in the population X originating from the population Y reads:

$$I_i^{Y\to X}=\frac{1}{N_Y}\sum _{j\in Y}{g}_{ij}^{Y\to X}{s}_j^Y,$$ (4)

where $g_{ij}^{Y\to X}$ is the synaptic coupling between the neuron j in the population Y and the neuron i in the population X. The current is normalized by the number of presynaptic neurons N_Y. The two IN and one RO ring networks were each simulated by N = 256 discrete units with equally spaced preferred directions from 0° to 360°. The synaptic couplings g_ij between neurons with preferred directions θ_i and θ_j are symmetric, and have a periodic Gaussian profile. Each IN ring network receives synaptic inputs within the ring as well as inputs from the other IN ring. For the basic circuit without heterogeneity, within each IN ring network,

$$g_{ij}^{IN-A\to IN-A}=g_{ij}^{IN-B\to IN-B}=\frac{1}{2}{J}_{-}+(1-\frac{\alpha }{2})J_{+}\text{exp}\left(-({\theta }_i-{\theta }_j{)}^2∕2{\sigma }^2\right),$$ (5)

whereas between the two IN ring networks,

$$g_{ij}^{IN-A\to IN-B}=g_{ij}^{IN-B\to IN-A}=\frac{1}{2}{J}_{-}+\frac{1}{2}\alpha J_{+}\text{exp}\left(-({\theta }_i-{\theta }_j{)}^2∕2{\sigma }^2\right).$$ (6)

The first terms of the above two equations together give the global inhibition, characterized by J₋. The second terms correspond to the excitation within the dual interacting ring networks, with its maximum strength characterized by J₊. The introduction of α conserves the total excitatory synaptic couplings and α determines the strength of between-ring excitatory contribution. Excitatory contribution in Scenario I (α=0) comes from within rings, while the excitatory contribution from within rings in Scenario II (α=1) is halved, with the rest coming from another ring. In Scenario II, the peak in another ring is located 180° away so the overall excitation is weaker relative to Scenario I (the second term in Equation (6) is small when the difference of peak direction is big). α was varied to reveal the influence of the between-ring interaction, whenever applicable. σ, which characterizes the width of the interaction profile, is set to be 43.2°.

Units in the RO ring network receive synaptic inputs within the ring as well as inputs from the two IN ring networks. Within the RO ring network,

$$g_{ij}^{RO\to RO}=J_{-}+J_{+}\text{exp}\left(-({\theta }_i-{\theta }_j{)}^2∕2{\sigma }^2\right).$$ (7)

As for the projections from the two IN rings, we consider an one-on-one interaction represented by the Kronecker delta

$$g_{ij}^{IN-A\to RO}=g_{ij}^{IN-B\to RO}=J^{IR}{\delta }_{ij},$$ (8)

where δ_ij = 1 if i = j and 0 otherwise. The RO ring network functions as the readout of the circuit. For simplicity, we use the Kronecker delta, which can be viewed as a Gaussian profile with very small σ. J^IR is set to be 0.09 nA throughout. Different values of J₋ and J₊ are used for different scenarios because, with different network connectivity structures, different levels of excitation and inhibition are necessary to maintain the network in an active dynamical state. The values of (J₋, J₊) are set to be (−0.35,2) nA for all three ring networks in scenarios I and II, and when compared with the dynamics of Scenario II, we additionally explored the effects of stronger inhibition (J₋ = −0.6 nA, J₊ = 2 nA) and stronger excitation (J₋ =−0.35 nA, J₊ =2.02 nA) in Figure 2E. The values of (J₋, J₊) are set to be (−0.8,2.32) nA when heterogeneity is introduced.

In addition, the two IN ring networks receive CJ-selective input from the WM module as well as spatial- and color-selective input from the visual pathway I^{V −A}. Therefore, the total synaptic current a neural population i in the IN-A ring receives is given by

$$I_i^{IN-A}=J^{WI}{s}_A^{WM}+I_i^{V-A}+I_i^{IN-A\to IN-A}+I_i^{IN-B\to IN-A}+I_{n,i}^{IN-A},$$ (9)

and similarly for IN-B. J^WI is set to be 0.01 nA for homogeneous networks and 0.03 nA for heterogeneous networks. The total synaptic current a neural population i in the RO ring receives reads:

$$I_i^{RO}=I_i^{RO\to RO}+I_i^{IN-A\to RO}+I_i^{IN-B\to RO}+I_{n,i}^{RO}.$$ (10)

Noisy current represents background synaptic inputs and obeys:

$${\tau }_{n}d{I}_n∕dt=-(I_n-I_0)+\sqrt{{\tau }_n}{\sigma }_n\eta (t),$$ (11)

where η(t) is a Gaussian white noise, τ_n =2 ms, σ_n =0.015 nA and $I_0^{WM}=I_0^{TG}=I_0^{RO}=I_0$. I₀ was set to be 0.3197 nA for homogeneous networks and 0.3297 nA for heteroegenous networks.

The CJ input, potentially projecting from OFC, was modeled by a two-level constant current during offer on period as shown in Figure 1B: I^CJ = 0.03 nA if the corresponding juice is chosen, and I^CJ = 0.015 nA otherwise. The input for each target cue from the visual area was presented as a Gaussian-profiled current which peaks at the direction of the target cue (θ_A for juice A and θ_B for juice B), and such input is both spatial and color-selective:

$$I_i^{V-A}=J^V\text{exp}\left(-({\theta }_i-{\theta }_A{)}^2∕2{\sigma }^2\right),$$ (12)

and similarly for I^{V −B}. J^V was set to be 0.1 nA. Note that the two target cues are always opposite to each other, thus the peaks of the input currents are 180° apart, that is, ∣θ_A – θ_B∣ = 180°.

Parameters for neural units and networks used in simulations are shown in Tables 1 and 2.

Table 1.

Parameters for Neural Units and Networks Used in All Simulations

Symbol	Value	Unit	Description
γ	0.641	-	Scaling constant of gating variable of NMDA receptors
κs	60	ms	Time constant of NMDA receptor-mediated synaptic current
a	270	Hz nA−1	Gain factor of total synaptic input in input-output function
b	108	Hz	Threshold current in input-output function
d	0.154	s	Noise factor in input-output function
J1	0.3725	nA	Effective self-coupling constant in WM module, excitatory
J2	−0.1137	nA	Effective mutual-coupling constant in WM module, inhibitory
ICJ	0.03 or 0.015	nA	CJ input current into WM module
N	256	-	Number of discrete units in ring networks
σ	43.2	◦	Width of interaction profile in ring networks
JIR	0.09	nA	Effective coupling constant from IN to RO
κn	2	ms	Time constant for background synaptic input
σn	0.015	nA	Scaling constant for standard deviation of background synaptic input
JV	0.1	nA	Peak current from visual input

Table 2.

Parameters for Neural Units and Networks Used in Different Scenarios

Symbol	Scenario I	Scenario II	Fig 7	Fig 8D	Unit	Description
J−	−0.35	−0.35	−0.8	−0.8	nA	(Mean) effective coupling for inhibition
J+	2	2	2.32	2.32	nA	(Mean) effective coupling for excitation
JWI	0.01	0.01	0.03	0.03	nA	Effective coupling constant from WM to IN
I0	0.3197	0.3197	0.3297	0.3297	nA	Mean background synaptic input
α	0	1	0.9	0.9	-	Between-ring synaptic coupling strength
β	0	0	2.5	2	nA	Standard deviation of network connectivity
κ	0	0	0	0.025	nA	Intrinsic neuronal heterogeneity

Heterogeneity in network connectivity and biophysical properties of neurons

In Scenario III, synaptic heterogeneity is introduced in the connectivity of both within and between the two IN ring networks. This was achieved by adding an extra term βR to the synaptic couplings in equations (5) and (6), where β is the standard deviation of the coupling and $R\sim \mathcal{N}(0,1)$ is a random number drawn from a normal distribution. β was set at different values for different conditions (see Table 2).

The most crucial neuronal parameters that capture the dynamics of a heterogeneous neuronal population are the baseline current I₀ and the standard deviation of the input noise σ_n (Yim et al., 2013). Therefore, neuronal intrinsic heterogeneity is implemented in the network by drawing those two parameters from Gaussian distributions for each neuron in the two IN ring networks. Here the mean of both parameters is set to be the same as that of the homogeneous neurons whereas the standard deviation of the two Gaussian distributions is varied in the same fashion, which scales linearly with κ. More explicitly, the baseline current and the standard deviation of the input noise are I₀ + κR₁ and σ_n + κR₂, respectively, where $R_1,R_2\sim \mathcal{N}(0,1)$. The standard deviation of network connectivity β is set to be 2 nA.

Bimodal visual input

The visual input is presented as a Gaussian-profiled current which has a major peak at the direction of its target cue and a smaller peak at the direction of the other target cue, located at the opposite direction (Figure S8A). Such input for juice A is given by

$${\tilde{I}}_i^{V-A}=J^V\left[\text{exp}\left(-({\theta }_i-{\theta }_A{)}^2∕2{\sigma }^2\right)+0.9\times \text{exp}\left(-({\theta }_i-{\theta }_B{)}^2∕2{\sigma }^2\right)\right].$$ (13)

To characterize the bimodal tuning in LPFC neurons, we consider the amplitude of their tuning curve at the direction opposite to the maximum versus the maximum. The closer to the diagonal, the more bimodal the tuning curve is. The parameters in Figure 7 are adopted except the followings for better performance and visual effect: J₋=−1.6 nA, J₊=2.5 nA, J_WI=0.05 nA, J^V=0.243 nA, I₀=0.31 nA, α=0.3 and β=2.0 nA.

Simulation protocol

In accordance with the economic choice task in Cai and Padoa-Schioppa (2014), each simulation trial starts with a 1.5 s fixation period (no visual and CJ inputs), followed by a 1 s presentation of the offer cues when the WM module receives the chosen juice input. Following the offer period is a 1 s delay period when offer cues were turned off. After that, two visual targets were presented for 1 s during which the two IN ring networks receive the spatially selective visual inputs. Simulations were performed using a customized code written in Python implementing Heun integration with a time step of 0.5 ms.

QUANTIFICATION AND STATISTICAL ANALYSIS

Direction decoding for circular data

In this study, both the direction encoded by a ring network of N neural units and the preferred direction of a neural unit (i.e. peak of its tuning curve) are circular. To read out such encoded or preferred direction, we defined the following complex quantity z for the direction-dependent data (Wimmer et al., 2014):

$$\mathbf{z}=z{e}^{i\phi }=\frac{{\sum }_{j=0}^{K-1}{x}_j{e}^{i{\theta }_j}}{{\sum }_{j=0}^{K-1}{x}_j},$$ (14)

where z is the modulus and φ is the encoded or preferred direction, respectively. In case of a ring network, K = N and x_j is the mean firing rate of neural unit j during the time window considered, which has a preferred direction at θ_j = j/N × 360°. Whereas in case of a neural unit, K = 8, x_j is the mean spike count during the time window considered in response to target A location θ_j = j × 45°. However, the ring networks in this task are likely to develop two activity bumps opposite to each other due to simultaneous presentation of two visual targets. We aim to identify the peak with higher amplitude as the index of each neuron’s tuning characteristics as the bigger peak would more likely be the chosen target location in the downstream circuit. Similar to neurons in the model, some of the tuning curves of the recorded LPFC neurons (Cai and Padoa-Schioppa, 2014) have double peaks opposite to each other. We accommodated such condition by introducing to equation (14) an additional parameter m

$$\mathbf{z}(m)=z(m)e^{i\phi (m)}=\frac{{\sum }_{j=0}^{K-1}{x}_j{e}^{im{\theta }_j}}{{\sum }_{j=0}^{K-1}{x}_j}\text{where}m=1,2.$$ (15)

The numerator is the m-th trigonometric moment of the circular data (Berens, 2009). The quantity is proportional to the coefficient of the discrete Fourier series of x_j. This formula with m = 2 has been used as the orientation selectivity index (Ringach et al., 2002; Scholl et al., 2013). We consider m up to two because the activity profiles in this study have either single or double peaks. To decode the direction of maximal activity, we compare z(1) and z(2), which are the “strength” of the corresponding moment. If z(1) is bigger, we take φ(1) as the decoded direction. If z(2) is bigger, we compare φ(2)/2 and $\frac{\phi (2)}{2}+{180}^{{}_{°}}$, and select the one closer to φ(1) as the decoded direction (Ringach et al., 2002).

To track the peak of a neuron’s tuning curve during good-to-action transformation, we constructed the tuning curve of each neuron based on target A location, and computed its peak for each chosen juice after target onset in a sliding time window of 200 ms with 50 ms steps.

Transition time

To determine the transition time of the activity bump in a ring network, we compute the decoded direction as described in the section above at every 1 ms time point during target on using a sliding time window of 200 ms and look for the time of sharp transition when the change of decoded direction from the previous sliding window is larger than 90°. T_tran is the center of the corresponding 200 ms sliding window.

Representation and clustering of neurons in space of peak differences

The chosen target signal, revealed in the explained variance in ANOVA analysis, rose up steadily from 150 ms to 350 ms after target onset (Cai and Padoa-Schioppa, 2014). To characterize the spatial tuning of neurons during good-to-action transformation, we defined the early and late window as 0-200 ms and 400-600 ms after target onset, respectively. At the population level, the early window captures mostly the target signal whereas the late window contains largely the chosen target information (Cai and Padoa-Schioppa, 2014). We grouped neural activity according to the time window (early or late) and chosen juice (A or B) thus derived four tuning curves and subsequently four peak values for each neuron, namely $P_{Early}^A$, $P_{Early}^B$, $P_{Late}^A$ and $P_{Late}^B$, based on target A location. The peak value can range from 0° to 360°, while according to the model prediction, the peak differences are more stereotyped and suitable for characterizing different types of neurons. Therefore, we defined four independent peak differences:

$$\{\begin{array}{cc}{\Delta }_{Early}\hfill & =P_{Early}^B-P_{Early}^A\hfill \\ {\Delta }_{Late}\hfill & =P_{Late}^B-P_{Late}^A\hfill \\ {\Delta }_A\hfill & =P_{Late}^A-P_{Early}^A\hfill \\ {\Delta }_B\hfill & =P_{Late}^B-P_{Early}^B\hfill \end{array}\phantom{\}}$$ (16)

where Δ_Early, Δ_Late, Δ_A, Δ_B ∈ [−90°, 270°]. Every neuron can be represented in the 4-dimensional space of peak differences.

We applied DBSCAN (Density-based spatial clustering of applications with noise), an unsupervised density-based data clustering algorithm to identify clusters in the 4-dimensional space. In brief, a point p is a core point if at least n_min points are within distance ϵ, the maximum radius of the neighborhood from p. These data points are said to be directly reachable from p. If p is a core point, then it forms a cluster together with all points that are reachable from it. For details, see https://en.wikipedia.org/wiki/DBSCAN and Ester et al. (1996). There are two free parameters, ϵ and n_min. We applied a self-defined criteria that a valid cluster must have at least 5% of the total neuron number. There are 1078 valid LPFC neurons, 665 spatially selective LPFC neurons and 768 simulated neurons so the minimum valid cluster size is set to be 54, 34 and 39, respectively. We selected ϵ = 65° and n_min = 20 for the spatially selective LPFC data (Figure 5). Additionally, we applied stricter clustering criteria by setting ϵ to a smaller value 55° (Figures S4 and S5), that is, the same n_min data points have to be detected in a smaller volume for a cluster to be valid. For simulation, the parameter set that best satisfied the above criteria for all simulations were found to be ϵ = 50° and n_min = 20.

Hartigan’s dip test

The null hypothesis of the test is that the distibution is unimodal (Hartigan and Hartigan, 1985). The uniform distribution is the asymptotically least favorable unimodal distribution. The corresponding significance test implemented by Nic Price (the Matlab code is available at http://www.nicprice.net/diptest/) was adopted to calculate the DIP statistic from the empirical probability density function (PDF), followed by a bootstrap sample of the dip statistic for a uniform PDF of the same size as empirical PDF. A distibution with p-value less than 0.05 is considered significantly distinct from a unimodal distribution.

Spatial selectivity

The spatial selection analysis was conducted using the same approach as in a previous study (Cai and Padoa-Schioppa, 2014). We consider the 600 ms after target onset, which is also the minimum duration before the “go” signal. To examine how spatial and action-related factors contribute to the activity of neurons in LPFCv/d, we proceeded as follows. First, we identified for each cell the preferred hemifield using a subset of trials (approximately 20%, with high chosen value). We then submitted each cell to a four-way ANOVA with factors chosen juice, chosen value, orientation, and hemifield of A, including all the interactions. For this analysis, the factor chosen value was reduced to a binary variable, high or low compared to the median. The factor orientation was a categorical variable with four levels (since there were eight possible target locations and two targets always appeared in opposite locations, there were four possible orientations). The factor hemifield of A was a binary variable depending on whether target A was in the cells preferred or antipreferred hemifield. Neurons are considered to be spatially selective if p-value is smaller than 0.01 for at least one of the following spatial factors or interactions: orientation, hemifield of A, orientation × hemifield of A, hemifield of A×chosen juice and orientation × hemifield of A×chosen juice.

DATA AND SOFTWARE AVAILABILITY

Software for modeling and data analysis is written in Python and MATLAB. Requests for source code and data should be directed to our Lead Contact.

KEY RESOURCES TABLE

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Software and Algorithms
DBSCAN clustering algorithm	Ester et al. (1996)	https://en.wikipedia.org/wiki/DBSCAN
Hartigan’s dip test	Hartigan and Hartigan (1985)	http://www.nicprice.net/diptest/