Combination of Static and Temporal Data Analysis to Predict Mortality and Readmission in the Intensive Care

Abstract

There are approximately 4 million intensive care unit (ICU) admissions each year in the United States with costs accounting for 4.1% of national health expenditures. Unforeseen adverse events contribute disproportionately to these costs. Thus, there has been substantial research in developing clinical decision support systems to predict and improve ICU outcomes such as ICU mortality, prolonged length of stay, and ICU readmission. However, the data in the ICU is collected at diverse time intervals and includes both static and temporal data. Common methods for static data mining such as Cox and logistic regression and methods for temporal data analysis such as temporal association rule mining do not model the combination of both static and temporal data. This work aims to overcome this challenge to combine static models such as logistic regression and feedforward neural networks with temporal models such as conditional random fields(CRF). We demonstrate the results using adult patient records from a publicly available database called Multi-parameter Intelligent Monitoring in Intensive Care – II (MIMIC-II). We show that the combination models outperformed individual models of logistic regression, feedforward neural networks and conditional random fields in predicting ICU mortality. The combination models also outperform the static models of logistic regression and feedforward neural networks for the prediction of 30 day ICU readmissions when tested using Matthews correlation coefficient and accuracy as the metrics.

I. INTRODUCTION

The modern intensive care unit (ICU) is a costly component of the national health care budgets accounting for 13.7% of hospital costs and 4.1% of national health expenditures [1-4]. These costs are largely explained by adverse outcomes such as prolonged length of stay in the ICU and ICU readmissions [5, 6]. For these reasons, there has been substantial research in developing clinical decision support systems to predict and prevent ICU outcomes, including ICU mortality, and ICU readmission.

Current research on the use of critical care data has focused on the use of either static data (these are generally fixed variables like gender, socioeconomic status, weight on admission) , temporal data (such as heart rate, blood pressure, lab tests) or continuous data (such as ECG, ECG).

Conventional static data analysis using methods such as Cox regression and logistic regression though very useful for finding risk factors associated with a specific disease, do not incorporate the temporal nature of the clinical data. Similarly, temporal models such as sequence analysis and association rule mining [7-9] and temporal Cox regression [10-12] generate models using the temporal nature of data. However, most of the current work suffer from challenges such as the lack of data analytics that can make sense of patient conditions using a combination of static and temporal data (sequential and continuous).

In a recent study, we performed a temporal analysis using conditional random fields (CRF) to predict ICU mortality and 30 day ICU readmissions using adult patient data from a publicly available database called MIMIC II [13]. We compared our methods using conventional analysis of logistic regression (LR) and neural networks (NN). From our analysis we found that more temporal features were selected by CRF models and included features such as arterial BP, central venous pressure, creatinine, arterial PaCO₂. In contrast, the LR and NN models picked features such as max sequential organ failure assessment (SOFA) score, metastatic cancer, minimum simplified acute physiology score (SAPS) I and presence of neurological symptoms. In addition, the data in the ICU itself is collected at higher sampling rates, though this can also vary.

In this study we extend our previous work to demonstrate a framework with which we can combine data from multiple sources, sampled at different sampling frequencies (e.g. static and temporal models (sampled at 6 hour intervals)) using ensemble techniques such as hard and soft voting. The static models include logistic regression and feed-forward neural networks, and the temporal models include conditional random fields. We combined the decisions from these individual classifiers and demonstrate our results using adult data from Multi-parameter Intelligent Monitoring in Intensive Care (MIMIC) –II.

II. METHODS

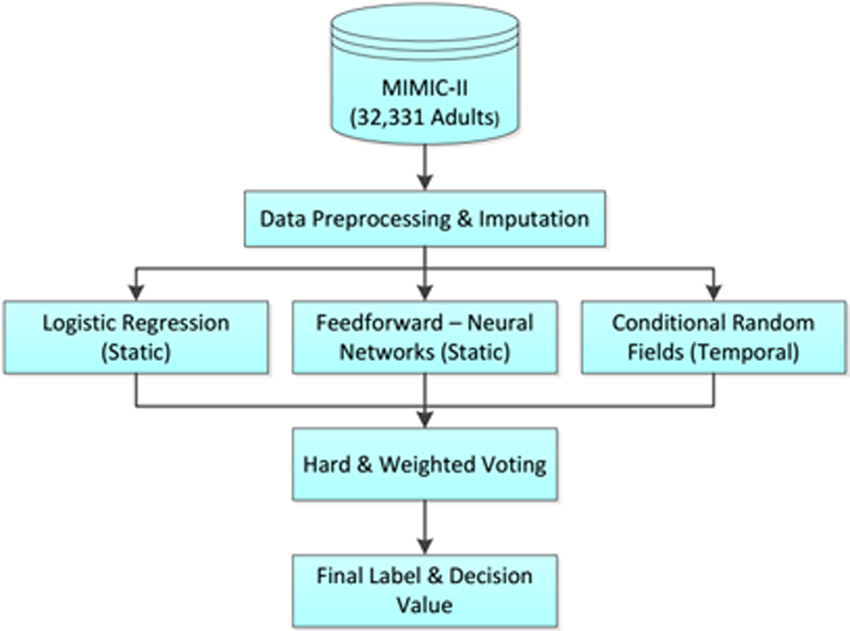
In this work, we perform a retrospective analysis of ICU data for adult patients to demonstrate the advantages of the combination of static and temporal data mining. After data preprocessing, we perform static data analysis using logistic regression and feed-forward neural networks, and temporal data analysis using conditional random fields. We then combine the decisions of these different classifiers using hard and soft voting techniques (Figure 1.)

Figure 1.

Combining static and temporal models

A. Data Source – MIMIC-II Database

This study is a retrospective data analysis using data from Multi-parameter Intelligent Monitoring in Intensive Care, second version, (MIMIC-II) database. MIMIC-II is a public ICU data repository with 32,331 adult and 8,080 neonatal records [14]. The MIMIC II data for each patient consists of static (does not change over the entire duration of the patient

ICU stay, e.g., patient demographics) and temporal (changing in time, e.g., heart rate, blood pressure) data. From a total 13,000 features in MIMIC-II database, filtered features by the number of available records to include top 2,000 features. From this 2000, we selected 87 features with the greatest clinical significance (based on clinician input). In the future, we will select features using standard feature selection techniques such as mRMR, differential expression and relieFF (as opposed to clinician input). The features included physiological measures (e.g. heart rate, blood pressure), lab results (e.g. while blood cells, red blood cells, cholesterol), administrative data (e.g. length of stay), diagnostic codes (ICD-9), and comorbidities (Table I).

TABLE I.

Feature Types in Dataset

Data Type	Examples of Measures
Demographics	Gender, Age, Height, Weight, Ethnicity, Comorbidity
Lab Data	Urea, Albumin, Bilirubin, Creatinine, Sodium
Chart Data	HR, BP, Arterial PH, Arterial PaCO2, Arterial PaO2

B. Data Preprocessing

The pre-processing of data for non-temporal analysis was performed by averaging the temporal data over the duration of stay. For temporal analysis, we binned the data into intervals of 6 hours to each chosen to reduce the effects of missing data. Then outliers whose values were physiologically impossible were removed. If the value is normally distributed, then values that deviated by ±3 standard deviations from the mean value were also removed. After preprocessing and outlier removal, the total missing data in the dataset was about 30.05 ± 30.8% (mean ± standard deviation). The missing data in the dataset was imputed using the 2 imputation techniques from our previous work [15] (‘Imp-1’ and ‘Imp-2’). Missing data imputation was important since most machine learning techniques fail or contribute to bias the presence of high missing data seen in EHR data. In this work, we had categorized the missing data into three types depending on the data properties (missing completely at random, missing at random, and missing not at random). The missing completely at random data. and missing not at random data were imputed by first clustering the data and using expectation maximization within the clusters. In this analysis, we tested two clustering techniques, kmeans (“Imp-1”) and fuzzy-c-means (“Imp-2”). For the missing not at random missing data, sampled from a copula function fit using data and the pattern of missing data. Sensitivity analysis and evaluation of the imputation techniques are found in the work by Venugopalan et. al. [15].

C. Data Mining on Static Data

For the analysis of static data, we use logistic regression and feed-forward neural networks, which are the most commonly used models in healthcare, to predict the patient outcomes of the study, ICU mortality and 30 day ICU readmission.

A logistic regression model is trained for each of the outcomes using a feature set X = {x₁, x₂ … x_n} derived from the clinical measures mentioned above. Logistic regression model calculates the probability of adverse ICU outcome given by (1)

$$h_{\theta }=\frac{e^{{\theta }_0+{\theta }_1{x}_1+{\theta }_2{x}_2+\cdots {\theta }_n{x}_n}}{1+e^{{\theta }_0+{\theta }_1{x}_1+{\theta }_2{x}_2+\cdots {\theta }_n{x}_n}}$$ (1)

The outcome group (y) is assumed to be true (1) when the probability h_θ exceeds a certain threshold. The values of parameters θ = {θ₀, θ₁, θ₂,… θ_n} are trained from the training data set by maximizing log-likelihood. In order to prevent over fitting we used L₂ regularization and minimum-redundancy maximum-relevancy (mRMR) for feature selection [16]. Hence the hyper parameters to be trained include the regularization parameter and the number of features.

Feedforward neural networks (ANN) are essentially mathematical models defining a function f ∶ X → Y or a distribution over input (X) or both input (X) and outcome (Y). The neural network consists of many interconnected nodes with each input from the input layer being fed up to each node in the hidden layer, and from there to each node on the output layer. The hyper-parameters of the model include the number of nodes and layers when optimizing the neural network. In this study, the number of input layer nodes equaled the number of features from which an optimal number was selected using mRMR and the number of hidden layers equaled 1. Hence, the hyper parameters optimized were the number of hidden layer units and the number of features selected using mRMR. The optimization of the hyper parameters for both these techniques were performed using 3×3 nested cross-validation.

D. Data Mining on Temporal Data

For the analysis of temporal patient data we used conditional random fields (CRF) [17]. CRF represents the conditional probability of the outcome,y ∈ Y given a sequence of ICU measurements x = {x₁, x₂ … x_T} i.e. p(y∣x, θ), where θ is the set of parameters. In addition we also assume certain hidden variables h = {h₁, h₂ … h_m} derived from the combination of features at each time point. The hidden states h take a value from a finite set of values given in H. The probability P(y, h∣X, θ) is given by (2).

$$P(y,h\mid X,\theta )=\frac{1}{Z}{e}^{(\theta \phi (y,h,x;\theta ))}$$ (2)

where θ is the set of parameters estimated during training, φ(y, h, x; θ) is the clique potential function, and a clique is a fully connected sub-graph [18]. Cliques in a chain CRF (used here) consists of an edge between adjacent labels (y_t-1 and y_t) as well as the edges from those two labels to the set of observations x. As a result, CRFs represent the conditional probability as (3-6)

$$P(y\mid X,\theta )={\sum }_h\frac{1}{Z}{e}^{(\theta \phi (y,h,x;\theta ))}$$ (3)

where,

$$Z={\sum }_{y,h}{e}^{(\theta \phi (y,h,x;\theta ))}$$ (4)

$$\phi (X,h,Y;\theta )={\sum }_{j=1}^T{\sum }_{l\in F}{f_l}^1(j,y,h_j,X){\theta }_l^1+{\sum }_{j,k\in E}{\sum }_{l\in F}{f_l}^2(j,k,y,h_j,h_k,X){\theta }_l^2$$ (5)

where, E, F are the number of edges and features respectively. And f_l¹, f_l²are feature transformation functions (analogous to regression here). Hence, the likelihood function is given by equation 4

$$P(Y\mid X)=\frac{1}{Z(X)}\times {\prod }_{i=1}^{n}exp\left({\sum }_h\phi (xi,h,yi;\theta )\right)$$ (6)

The log-likelihood is maximized to learn the parameters θ. The inference is done by forward-backward inference to obtain the outcome probability from the graph. Over-fitting of the CRF model is prevented by L₁ regularization of weights (the absolute values of weights are penalized). The optimization of the hyper parameters such as the number of hidden states and the L₁ regularization coefficient was performed with 3×3 nested cross-validation [19].

E. Combining Static & Temporal Models using Hard & Weighted Voting

The decision values and decisions from the 3 classifiers were combined using hard and weighted voting techniques. We tested a total of four different methods to combine the decision or decision values. In the first method (M1), combined the three classifiers by hard voting where the majority value of the decision (mode of the three decisions) was used as the label. In the second method (M2), we used the mean of the decision values from the three classifiers to get a new decision values which was used to compute the label.

The next two methods involved weighted voting, where we first weighted the decisions. The weights for each classifier was computed as follows (7)

$$Weight=log\left(\frac{C{l}_{Per}}{1-C{l}_{Per}}\right)$$ (7)

where Cl_Per is the classifier performance (Matthews Correlation Coefficient (MCC) scaled between 0 and 1). The decision values (M3) was computed as a weighted average of the decisions. This decision value was used to obtain the final label. In the last method (M4), the weights for each classifier was obtained using (7). The final decision value was the weighted average of the individual classifier decision values. The computed decision value was then used to compute the final label.

F. Evaluation of the Classification Methods

The evaluation of all the combination methods was performed using 10-fold cross validation. We repeated the process 3 times and report averaged values of Matthews correlation coefficient (MCC) and accuracy. We chose MCC as a metric because of its relative tolerance to an imbalanced population.

III. RESULTS & DISCUSSIONS

We performed a retrospective data analysis on adult data (32,331 patient records) from MIMIC –II to predict two endpoints, mortality in the ICU, and 30-day ICU readmission to demonstrate the superiority of the combination models . This dataset contains 2,334 patient records with mortality during the ICU stay and 29,997 patient records of successful discharge from the ICU. Similarly, 7,787 patient records had an ICU readmission within 30 days and 24,544 patients did not relapse into the ICU within 30 days. As mentioned above, we first performed classification using static and temporal classification methods and then combined the decision values and decisions using voting methods. The results from individual classifiers and the combined models are shown in Tables II and III. Our results indicate that the combination models outperformed the individual models when using both MCC and accuracy as the metrics for the endpoint of mortality. The methods of combining decision values and weighted voting methods have the best MCC. The best performing combination models give an improvement in MCC of 6-7% over logistic regression, 2% over neural networks and 3-8% over conditional random fields for mortality. The top features for static models (LR and NN) for mortality prediction included the SOFA scores, metastatic cancer, fluid electrolyte levels, SAPSI scores and presence of neurological symptoms, while the features of CRF models included height , SOFA scores, arterial BP, arterial PaCO₂ and creatinine. For 30 day ICU readmission, all the combination models performed better than the static models for both imputation techniques used. For Imp2, the temporal models performed better than the combination models. When MCC was used as the metric for comparison, the methods of combining decision values and weighted voting methods gave the best performance. The best performing combination models give an improvement in MCC of 33% over logistic regression, 25-26% over neural networks and 26% over conditional random fields for Imp1. The readmission models with Imp-2 performed better than combination models for ICU readmission. The top features for static models (LR and NN) for ICU readmission prediction included the hospital length of stay, presence/ absence of blood loss anemia, renal failure, red blood cell count and the presence or absence of congestive heart failure, while the features of CRF models included ICU admit age, calcium levels, presence of liver disease, creatinine levels, white blood cell count, overall payer group, arterial PaCO₂, SaO₂, renal failure, arterial PaO2 and blood loss anemia.

Table II.

Classification Results from ICU Mortality (Mathhews Correlation Coefficient) (LR = Logistic regression, NN = Neural networks, CRF = Conditional random fields, M1 = Voting, M2 = Mean of decision values, M3 = Weighted mean of decisions, M4 = Weighted mean of decision values)

	Imputation	LR	NN	CRF	M1	M2	M3	M4
Mortality	Imp1	0.47 ± 0.006	0.52 ± 0.006	0.51 ± 0.033	0.52 ± 0.003	0.54 ± 0.004	0.54 ± 0.006	0.54 ± 0.006
	Imp2	0.48 ± 0.009	0.52 ± 0.007	0.46 ± 0.098	0.52 ± 0.002	0.54 ± 0.005	0.54 ± 0.005	0.54 ± 0.006
Readmission	Imp1	0.32 ± 0.005	0.39 ± 0.004	0.39 ± 0.021	0.59 ± 0.039	0.65 ± 0.001	0.65 ± 0.001	0.65 ± 0.001
	Imp2	0.33 ± 0.007	0.39 ± 0.003	0.73 ± 0.032	0.58 ± 0.031	0.66 ± 0.003	0.66 ± 0.002	0.66 ± 0.003

Table III.

Classification Results from ICU Readmission (Accuracy) (LR = Logistic regression, NN = Neural networks, CRF = Conditional random fields, M1 = Voting, M2 = Mean of decision values, M3 = Weighted mean of decisions, M4 = Weighted mean of decision values)

	Imputation	LR	NN	CRF	M1	M2	M3	M4
Mortality	Imp1	0.94 ± 0.001	0.95 ± 0.000	0.95 ± 0.003	0.95 ± 0.000	0.95 ± 0.000	0.95 ± 0.001	0.95 ± 0.001
	Imp2	0.94 ± 0.001	0.95 ± 0.001	0.94 ± 0.004	0.95 ± 0.000	0.95 ± 0.000	0.95 ± 0.001	0.95 ± 0.001
Readmission	Imp1	0.79 ± 0.001	0.80 ± 0.000	0.80 ± 0.006	0.86 ± 0.013	0.86 ± 0.000	0.87 ± 0.000	0.86 ± 0.000
	Imp2	0.79 ± 0.001	0.80 ± 0.001	0.90 ± 0.013	0.85 ± 0.010	0.87 ± 0.001	0.87 ± 0.001	0.87 ± 0.001

IV. CONCLUSION & FUTURE WORK

Prediction models for clinically significant end-points such as ICU readmission remain challenging with limited efficacy in a wide variety of patients. In addition, ICUs also collect data at different frequency rates. In this work, we combine static models, such as logistic regression and feedforward neural networks, with temporal models such as conditional random fields(CRF), by hard and weighted voting techniques. The combined models gave a better performance as compared to individual models. The weighted models where the proportion of the decision making was based on individual performances gave the best overall performances. We can conclude that combination of multiple model types with different feature types improves the robustness of the model for complex data types and hence has the potential to enhance immediate management of a patient and the overall resource utilization.

Our work, currently combines data from only adult patients from MIMIC-II and also does not include high frequency data such as waveform data. In the future we aim to overcome these challenges and demonstrate our results on pediatric data from Children’s Healthcare of Atlanta after IRB approval. We also aim to combine intermediate features using deep-learning approaches.