Skip to main content
PMC home page
NASA Author Manuscripts logoLink to NASA Author Manuscripts
. Author manuscript; available in PMC: 2020 Jul 20.
Published in final edited form as: Geophys Res Lett. 2017 Jun 6;44(11):5739–5748. doi: 10.1002/2017GL073151

CMIP5 models’ shortwave cloud radiative response and climate sensitivity linked to the climatological Hadley cell extent

Bernard R Lipat 1, George Tselioudis 1,2, Kevin M Grise 3, Lorenzo M Polvani 1,4,5
PMCID: PMC7370987  NIHMSID: NIHMS936246  PMID: 32690980

Abstract

This study analyzes Coupled Model Intercomparison Project phase 5 (CMIP5) model output to examine the covariability of interannual Southern Hemisphere Hadley cell (HC) edge latitude shifts and shortwave cloud radiative effect (SWCRE). In control climate runs, during years when the HC edge is anomalously poleward, most models substantially reduce the shortwave radiation reflected by clouds in the lower midlatitude region (LML; ~28°S–~48°S), although no such reduction is seen in observations. These biases in HC-SWCRE covariability are linked to biases in the climatological HC extent. Notably, models with excessively equatorward climatological HC extents have weaker climatological LML subsidence and exhibit larger increases in LML subsidence with poleward HC edge expansion. This behavior, based on control climate interannual variability, has important implications for the CO2-forced model response. In 4×CO2-forced runs, models with excessively equatorward climatological HC extents produce stronger SW cloud radiative warming in the LML region and tend to have larger climate sensitivity values than models with more realistic climatological HC extents.

1. Introduction

Clouds and their radiative effects covary with large-scale atmospheric dynamics, and all are projected to coevolve with increasing CO2. There is strong evidence that increasing atmospheric greenhouse gas concentrations will contribute to poleward circulation shifts [Kushner et al., 2001; Yin, 2005; Lu et al., 2007; Hu and Fu, 2007; Barnes and Polvani, 2013], but future cloud and cloud radiative effect (CRE) changes remain unclear and account for most of the uncertainty in climate change projections [Andrews et al., 2012; Vial et al., 2013; Webb et al., 2013; Qu et al., 2014]. A dominant source of that uncertainty is tropical and subtropical low clouds and their shortwave cloud radiative effects (SWCRE) [e.g., Bony, 2005], but extratropical cloud and SW radiation biases have also been implicated [Trenberth and Fasullo, 2010; Grise et al., 2015]. Quantifying the effects of poleward circulation shifts on extratropical clouds and SWCRE may therefore help constrain the SWCRE response and ultimately climate sensitivity.

Despite emphasis on poleward eddy-driven jet shifts, for which results vary greatly by season, ocean basin, and model [Bender et al., 2011; Grise et al., 2013; Kay et al., 2014; Li et al., 2014; Grise and Polvani, 2014a; Tselioudis et al., 2016; Grise and Medeiros, 2016], observations actually show that variability in midlatitude clouds and CRE correlates more consistently and more robustly with poleward Hadley cell (HC) expansion than with jet shifts [Tselioudis et al., 2016]. The jet may shift the core of the extratropical storm clouds, but the subsiding branch of the HC limits their equatorward extent [Bender et al., 2011]. Poleward HC expansion, therefore, more effectively inhibits high clouds in the greatly insolated lower midlatitudes (~28°S–~48°S) of the present climate [Tselioudis et al., 2016] and may also relate better to future climate changes [Grise and Polvani, 2014b].

In this study we examine the relationship between Southern Hemisphere (SH) lower midlatitude SWCRE and the HC edge latitude in Coupled Model Intercomparison Project phase 5 (CMIP5) models. Since the HC edge is projected to shift poleward with increasing greenhouse gases [e.g., Lu et al., 2007], model biases in the interannual covariability of the HC edge and SWCRE may have implications for the forced model response and ultimately the equilibrium climate sensitivity (ECS) [e.g., Zhou et al., 2015]. The paper is organized as follows. Section 2 details the data and methods used. Section 3 relates the SW cloud radiative response to the intermodel spread in HC-SWCRE covariability and the climatological position of the HC edge. Section 4 concludes with a discussion of the results.

2. Data and Methods

2.1. Data

The observational radiative flux data used in this study are monthly-mean top-of-atmosphere radiative fluxes derived from the International Satellite Cloud Climatology Project (ISCCP-FD) [Zhang, 2004]. We present results using the data set corrected for satellite zenith angle and drift biases by Norris and Evan [2015], but use of the uncorrected data set did not show significant differences in the derived relationships. Data cover the period July 1983 to December 2009, but only years with the entire December-January-February (DJF) season available are analyzed. Over this period, monthly-mean meridional wind data from the European Centre for Medium-Range Weather Forecasts Interim Reanalysis (ERA-Interim) [Dee et al., 2011] are used to calculate the mass stream function.

Model radiative fluxes and dynamical variables are obtained from monthly-mean output from 22 CMIP5 models [Taylor et al., 2012], as listed in Table 1. We use two sets of model output: (1) the preindustrial (PI) control runs and (2) the abrupt 4×CO2 runs. The preindustrial control run variability is used because it is unforced, the cloud changes from varying global temperature are minimal, and the length of integration (between 300 and 1156 years) yields a robust statistical analysis; results are similar when the historical runs of the models are analyzed. To avoid biasing the results with one model, only the first ensemble member (“r1i1p1”) from each model is used. The equilibrium climate sensitivity (ECS) of each model is taken from Forster et al. [2013] (see Table 1, sixth column). The 4×CO2 SWCRE response is defined as the difference in SWCRE between the atmosphere-equilibrated (first 50 years removed) abrupt 4×CO2 run and the preindustrial control run climatology.

Table 1.

Listing and Characteristics of the CMIP5 Models Used in This Studya

Name 4×CO2 HC Edge Shift HC Edge Latitude LML HC-SWCRE LML mean ω500 LML HC-ω500 ECS
Observations - −35.83 −0.69 −3.23 −0.48 -
+HC-SWCRE Models
a bcc-csm1–1 −1.49 −33.01 1.00 5.75 2.05 2.82
b bcc-csm1–1-m −2.34 −35.01 0.39 6.91 1.06 2.87
c CanESM2 −3.44 −33.25 0.67 6.33 2.08 3.69
d CNRM-CM5v −1.02 −33.55 0.34 6.30 2.52 3.25
e FGOALS-s2 −3.17 −30.74 0.96 4.25 3.74 4.17
f GISS-E2-R −1.41 −32.98 0.16 5.58 2.11 2.11
g inmcm4 −1.14 −35.31 0.21 5.63 0.62 2.08
h IPSL-CM5A-LR −3.91 −30.41 1.66 3.60 4.87 4.13
i IPSL-CM5B-LR −1.08 −30.73 0.67 3.16 3.50 2.61
j MIROC-ESM −0.52 −31.48 1.33 4.37 3.37 4.67
k MPI-ESM-LR −1.32 −33.80 0.31 7.53 3.05 3.63
l MPI-ESM-P −1.33 −33.76 0.39 7.54 3.01 3.45
m MRI-CGCM3 −1.01 −34.18 0.15 5.53 1.90 2.60
Mean −1.78 −32.94 0.63 5.58 2.61 3.24
Neutral Model
n MIROC5 −1.40 −34.68 0.00 6.23 2.03 2.72
−HC-SWCRE Models
o CCSM4 −1.38 −36.71 −0.54 7.05 0.23 2.89
p CSIRO-Mk3–6-0 −2.36 −34.26 −0.99 - - 4.08
q GFDL-CM3 −1.55 −34.09 −0.10 7.32 3.15 3.97
r GFDL-ESM2G −1.35 −35.53 −0.54 6.64 1.51 2.39
s GFDL-ESM2M −1.28 −34.77 −0.41 6.34 2.17 2.44
t HadGEM2-ES −3.23 −33.63 −0.22 6.27 1.51 4.59
u NorESM1-M −1.42 −36.23 −0.54 6.72 0.80 2.80
v NorESM1-ME - −36.16 −0.66 6.83 0.51 -
Mean −1.80 −35.17 −0.50 6.74 1.41 3.31
Multimodel Mean −1.79 −33.79 0.20 5.98 2.19 3.26
Open in a new tab
a

Values in the first through fifth columns are calculated for DJF SH. The units of the first column are degrees latitude, where negative values correspond to poleward shifts. The units of the second column are degrees latitude, where negative values correspond to SH. The units of the third column are W m−2 deg−1, of the fourth column are hPa d−1, and of the fifth column hPa d−1. Equilibrium climate sensitivity values are reproduced from Table 1 of [Forster et al., 2013].

2.2. Methods

We compute the Hadley cell (HC) edge latitude by identifying the first two grid points from the equator where the midtropospheric (500 hPa) mass stream function changes sign and then linearly interpolating between them at 0.01° resolution to find the latitude of the first zero crossing. The shortwave cloud radiative effect (SWCRE) is defined as top-of-atmosphere upwelling clear-sky SW radiation (i.e., rsutcs) minus top-ofatmosphere upwelling all-sky SW radiation (i.e., rsut).

To remove intraseasonal variability, deseasonalized monthly-mean data are averaged over the DJF season. To examine interannual covariability, the detrended SWCRE time series are linearly regressed onto the detrended HC edge latitude time series. We refer to the SWCRE response to a 1° poleward shift of the HC edge latitude as HC-SWCRE. Positive HC-SWCRE values indicate anomalous SW warming with poleward HC edge shifts. Regionally averaged quantities are computed by first regridding to a common grid and then averaging over the point-by-point values. Statistical significance and confidence intervals are determined primarily using two-tailed Student’s t tests and validated with bootstrapping.

In this paper, we focus on results for the SH, and in particular the DJF season when solar insolation and hence the SWCRE is maximized at SH midlatitudes (Figure S1). Observations show that cloud-dynamics coupling is relatively consistent across season and region in the SH [Tselioudis et al., 2016], especially when compared to the Northern Hemisphere [Grise and Medeiros, 2016]. However, analysis for all seasons and for the annual mean was performed, and those results are also discussed.

3. Results

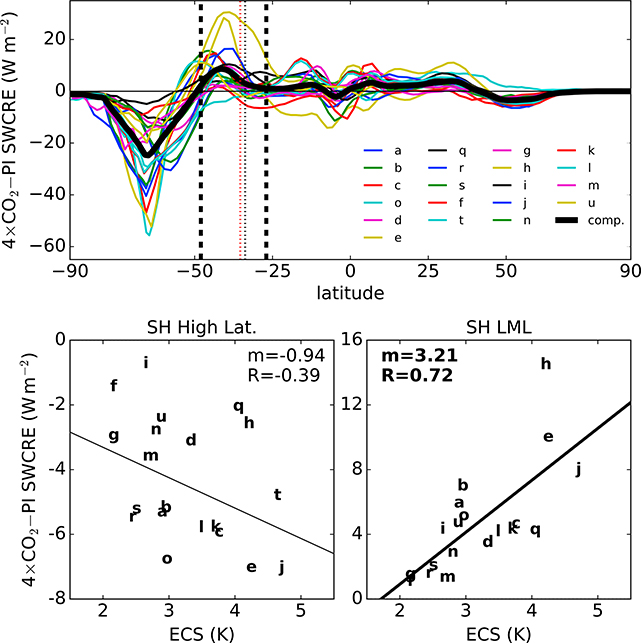
We first examine the CMIP5 model SWCRE response to increasing CO2 in order to identify regions of strong model SWCRE response. The 4×CO2-forced SWCRE response in DJF is displayed in Figure 1 (top). The major consistent response is what appears to be a dipole pattern in the SH midlatitudes: at high latitudes, defined as where the multimodel mean SWCRE response is negative (~48°S–90°S), there is an anomalous cloud-induced SW radiative cooling; at lower midlatitudes (LML, thick-dashed vertical lines in Figure 1, top), defined as where the multimodel mean SWCRE response is positive (~28°S–~48°S), there is anomalous cloud-induced SW radiative warming. Note that this dipole behavior is also present, but of smaller magnitude, in the annual-mean 4×CO2-forced SWCRE response (Figure S2 (top) in the supporting information).

Figure 1.

Figure 1.

Open in a new tab

(top) The change in zonal-mean SWCRE for each CMIP5 model from the preindustrial (PI) control climatology to the atmosphere-equilibrated 4×CO2 climatology for DJF. Positive (negative) values correspond to anomalous cloud-induced SW warming (cooling). (bottom) Least squares linear regressions of the intermodel spread in ECS on the intermodel spread in the SWCRE change averaged over the (left) higher midlatitudes and over the (right) LML (lower midlatitudes). The LML is confined between the two thick-dashed vertical lines. The multimodel mean climatological HC edge latitude is depicted for the PI runs with a black thin-dashed line and for the 4×CO2 runs with a red thin-dashed line. Each line and data point corresponds to one model (see Table 1 for model labels) Regressions statistically significant at the 95% confidence level, assessed using the Student’s t test, are denoted by thicker regression lines and bold coefficients.

The relationship of the model SWCRE response in the two regions to model climate sensitivity is explored in Figure 1 (bottom). The high-latitude response (Figure 1, bottom left) does not correlate significantly with ECS, and any relationship would not be causal as higher ECS models have larger high-latitude SW cooling. In the LML, however, the correlation is statistically significant (Figure 1, bottom right) and shows higher ECS for models with higher SW warming (see also Figure 7 of Grise et al. [2015]). A similar correlation with ECS also exists for the annual-mean SWCRE responses (Figure S2, bottom). The high-latitude response has been studied extensively and is attributed to a negative cloud-phase feedback—with increasing CO2, the melting isotherm intersecting the surface near 55°S shifts poleward and melts ice cloud into more reflective liquid cloud [e.g., Kay et al., 2014; Storelvmo et al., 2015; Ceppi et al., 2014; Ceppi and Hartmann, 2015]. We focus our analysis on the LML, where a cloud feedback mechanism has not been established. A potential mechanism is the poleward shift of the HC edge, since its subsiding branch terminates within the LML, near 34°S in the multimodel mean PI climatology (thin black line in Figure 1, top), and since the observational study of Tselioudis et al. [2016] showed that the LML clouds and SWCRE are strongly correlated with latitudinal HC edge shifts on interannual time scales. To date, no study has investigated whether the interannual variability of LML clouds and SWCRE is related to HC edge variability in models. If it is, this relationship could be predictive of the models’ SWCRE response to increased greenhouse gases and ultimately the models’ ECS [e.g., Zhou et al., 2015].

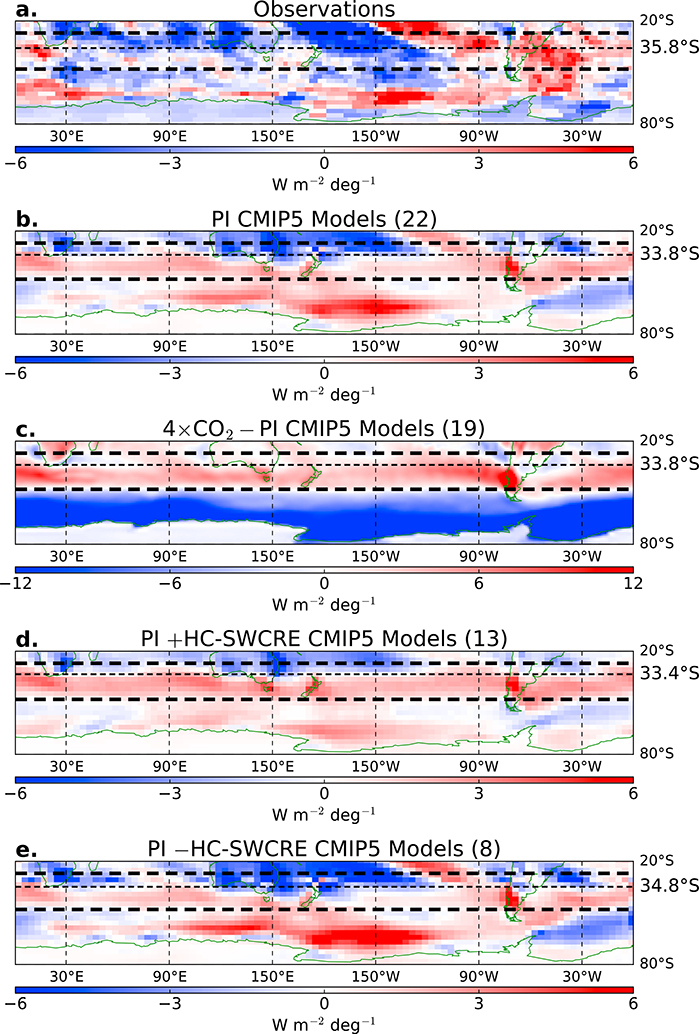
We begin by examining in Figure 2 the spatial structure of the interannual HC-SWCRE covariability for (a) the observations and (b) the multimodel mean. In observations [Tselioudis et al., 2016], the HC-SWCRE relationship in the SH LML region is mostly negative and is dominated by SW cooling, except for a region of SW warming east of South America and a tropical SW warming intrusion in the eastern South Pacific associated with a southward and westward shift of the South Pacific Convergence Zone (SPCZ). In contrast to the observations, the multimodel mean HC-SWCRE pattern, while showing a weak cooling in the central Pacific associated with a SPCZ shift, is dominated by a pronounced and zonally symmetric LML SW warming belt. We compare this with the multimodel mean spatial pattern of the 4×CO2-forced SWCRE response in Figure 2c. The colocation and statistically significant spatial correlation (R=0.53) of the multimodel mean HC-related LML SW warming region (red in Figure 2b) with the region of 4×CO2-forced LML SW warming (Figure 2c) suggests a dynamic attribution of the LML warming to poleward HC edge expansion. The question, then, is to what extent is the multimodel mean HC-SWCRE relationship representative of individual model behavior? To answer this question, we next examine the intermodel spread in the HC-SWCRE relationship about the multimodel mean.

Figure 2.

Figure 2.

Open in a new tab

DJF least squares linear regressions of the SH Hadley cell edge latitude on the SH SWCRE for (a) ISCCP-FD and ERA-Interim, (b) the CMIP5 PI multimodel mean, (d) only the +HC-SWCRE models, and (e) only the −HC-SWCRE models. Units in Figures 2a, 2b, 2d, and 2e indicate W m−2 per 1° poleward Hadley cell shift. Displayed in parentheses near the panel label is the number of models used in the composite. The LML is confined between the two thick-dashed horizontal lines, and the mean climatological HC edge latitude is depicted with thin-dashed horizontal lines, with mean value to the right. (c) The multimodel change in SWCRE for CMIP5 from the preindustrial (PI) control climatology to the atmosphere-equilibrated 4×CO2 climatology for DJF. Positive (negative) values correspond to anomalous cloud-induced SW warming (cooling). The PI Hadley cell edge latitude is depicted with gray thin-dashed horizontal lines, and the 4×CO2 Hadley cell edge is depicted with black thin-dashed lines, with mean value to the right.

The magnitude of the LML-averaged HC-SWCRE regression coefficients for all 22 CMIP5 models used is listed in Table 1, along with the values from the observational analysis. We average over the LML because of the zonal structure exhibited by both the unforced HC-SWCRE covariability (Figure 2b) and 4×CO2-forced SWCRE response (Figure 2c). Results are not sensitive to the exact choice of the LML latitude band, or whether the region is centered on the HC edge latitude. There is large intermodel spread in the PI HC-SWCRE (third column), with the majority of models showing positive HC-SWCRE values indicating mean SW warming with poleward HC edge expansion. We designate those models “+HC-SWCRE” models in contrast with models designated “−HC-SWCRE” models that produce mean SW cooling with poleward HC edge expansion; this is similar to the Type I/II classification of Grise and Polvani [2014a] in both methodology and model categorization. Even within each class of models, HC-SWCRE values vary by an order of magnitude, from about +0.15 W m−2 deg−1 to about +1.5 W m−2 deg−1 in +HC-SWCRE models, and fromabout−0.10 W m−2 deg−1 toabout−1.0 W m−2 deg−1 in −HC-SWCRE models. Beyond regression coefficients, the correlation strength also varies across models—in only one model (MIROC5) LML SWCRE seems independent of HC edge shifts using the Student’s t test, whereas in all other models the correlation is statistically significant, with some correlation coefficients as high as 0.90 (not shown). Thus, in almost all models, as in observations, robust SWCRE changes are associated with HC edge shifts; however, the sign of those LML-averaged changes is highly variable by model.

To examine the spatial distribution of the SWCRE changes in the two model classes, we plot the HC-SWCRE relationship separately for positive and negative HC-SWCRE models (Figures 2d and 2e). Unlike the observations, both model classes show a zone of consistent SW warming on the southern side of the LML region. In each of the −HC-SWCRE models (not shown) and in their multimodel mean (Figure 2d) this warming zone is narrower than in each of the +HC-SWCRE models (not shown) and their multimodel mean (Figure 2e). The −HC-SWCRE models show a more extensive SW cooling region on the equatorward side of the LML region, primarily due to a stronger SPCZ shift in the central Pacific. Note here that we have repeated the analyses performed in this study but excluding the Pacific signal, and despite its being of large amplitude, it did not change our conclusions. We also analyzed the regression of LML SWCRE onto shifts of the ITCZ and SPCZ but found our HC edge metric to correlate more strongly and more consistently. In both subsets of models, the patches of cooling on the equatorward side of the LML region extends approximately to the latitude of the climatological HC edge (thin dashed lines), with the −HC-SWCRE models having on average a more southward HC edge (34.8°S compared to 33.4°S) and therefore a larger area of SW cooling. This suggests that the HC-related SWCRE may be connected to the climatological HC edge position in each model.

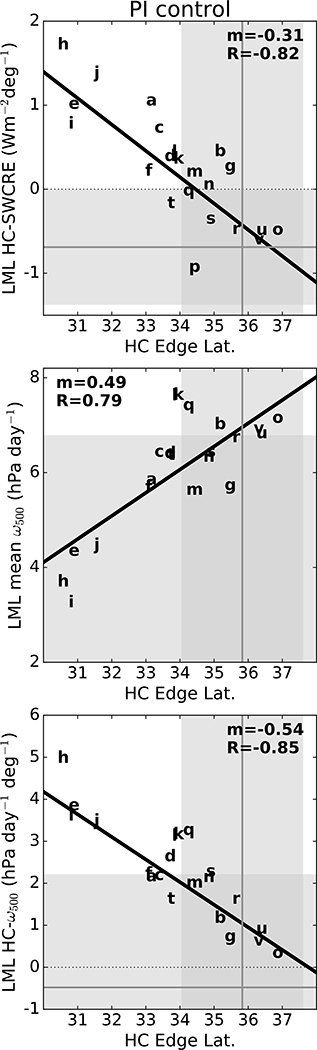
We therefore correlate the PI climatological HC edge latitude in each model with its LML HC-SWCRE in Figure 3 (top). Although grouped into two subsets in Table 1 for convenience of explanation, the model behavior is continuous—models with more equatorward (poleward) climatological HC edges have more positive (negative) HC-SWCREs. The −HC-SWCRE models agree better with both HC edge latitude and HCSWCRE observed values (gray lines and envelope); in contrast, no +HC-SWCRE model lies within the uncertainty of the observed HC-SWCRE relationship, and most do not agree with the observed HC edge latitude. This suggests that unforced model clouds’ covariability with HC edge latitude shifts may be tied to the climatological HC edge position. We therefore explore why cloud changes with poleward HC edge expansion link so robustly to the climatological HC edge position.

Figure 3.

Figure 3.

Open in a new tab

Least squares linear regressions on the intermodel spread in climatological DJF SH Hadley cell edge latitude of the intermodel spread in DJF SH (top) LML HC-SWCRE, (center) climatological mean pressure vertical velocity at 500 hPa (ω500) averaged over the LML, and (bottom) LML HC-ω500. Each data point corresponds to one model (see Table 1 for model labels). Regressions statistically significant at the 95% confidence level, assessed using a t test, are denoted by thick lines and bold coefficients (all are significant). Gray lines represent observed values (derived from ISCCP-FD and ERA-Interim), and gray shading represents the 95% confidence interval thereof.

Since midlatitude cloud optical properties and vertical structure relate to the midtropospheric vertical velocity [Tselioudis and Jakob, 2002], we examine the relationship between HC edge latitude and midtropospheric vertical velocity in the LML region. The climatological HC edge position correlates strongly with the strength of the climatological mean LML vertical velocity (Figure 3, center), and with the vertical velocity anomalies associated with HC edge shifts, as measured by the regression coefficient HC-ω500 (Figure 3, bottom). A more equatorward HC edge is associated with weaker LML mean climatological subsidence (ω at 500 hPa or ω500) and vice versa (Figure 3, center).

With poleward HC edge expansion, ω500 increases in the LML of all models (Table 1 and Figure 3, bottom). The increases in ω500 are larger in the models with weaker LML mean climatological subsidence and moreequatorward HCs (Table 1 and Figure 3). Overall, poleward HC edge expansion extends the subtropical subsidence influence into the LML region. In models with too narrow climatological HCs, this induces strong subsidence in a region which typically has weak subsidence, resulting in strong decreases in SW cloud reflection. In models with wide climatological HCs and already strong LML subsidence, the SW warming effect is small. In the observations [Tselioudis et al., 2016], there is no SW warming effect because there are more abundant and more reflective clouds, particularly at low levels, with poleward HC edge shifts. The reason for the −HC-SWCRE models’ behavior must be further explored following the analysis of Grise and Medeiros [2016], who highlight the strong control of the estimated boundary layer inversion strength on the low cloud field in the LML.

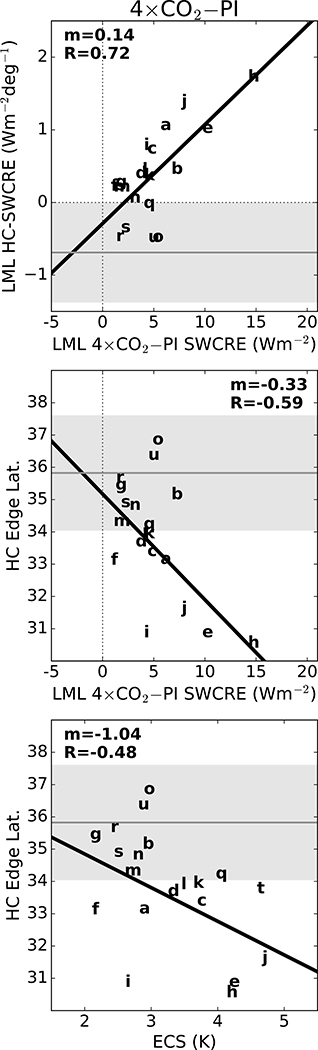
The analysis of the CMIP5 PI control runs presented so far shows that HC edge expansion is robustly associated with anomalous cloud-induced SW warming on the southward side of LML on interannual time scales (Figure 2). We now examine whether this association is also found in models’ response to 4×CO2 forcing. First we show the correlation between the strength of the model HC-SWCRE relationships and their 4×CO2 LML SWCRE warming in Figure 4 (top). The plot indicates that the extent to which models change their LML SWCRE with unforced HC edge shifts predicts to a large extent the strength of the LML SWCRE warming upon quadrupling CO2 (as noted in Grise and Polvani [2014a, Figure 11]). It was shown above (Figure 3, top) that the magnitude of HC-SWCRE relates strongly to the climatological position of the HC edge. Therefore, we correlate the 4×CO2 LML SWCRE warming with the climatological HC edge latitude across the models (Figure 4, middle). It is clear that the climatological HC edge latitude is robustly correlated with the response of LML SWCRE to 4×CO2 forcing. Therefore, this relationship represents a constraint that directly links the SW cloud radiative response to the climatological Hadley cell extent via the well-defined influence of atmospheric dynamics on cloud radiative effects.

Figure 4.

Figure 4.

Open in a new tab

Least squares linear regressions on the intermodel spread in LML averaged 4×CO2-PI SWCRE of the intermodel spread in (top) LML HC-SWCRE and (center) intermodel spread in climatological DJF SH Hadley cell edge latitude. (bottom) Least squares linear regression on the intermodel spread in equilibrium climate sensitivity of the intermodel spread in climatological DJF SH Hadley cell edge latitude. Each data point corresponds to one model (see Table 1 for model labels). Regressions statistically significant at the 95% confidence level, assessed using a t test, are denoted by thick lines and bold coefficients (all are significant). Gray lines represent observed values (derived from ISCCP-FD and ERA-Interim), and gray shading represents the 95% confidence interval thereof.

Finally, given the large correlation of the LML SW cloud radiative response with model climate sensitivity (Figure 1b), we correlate model ECS with climatological HC edge latitude (Figure 4, bottom). We find that the correlation with climatological HC edge latitude is weaker for ECS than for the SW cloud radiative response but still statistically significant. Models with more poleward climatological HCs, which more closely resemble the observations, have lower ECS than models with more equatorward HCs. This relationship between climatological HC edge and ECS is mediated by model spread in cloud-dynamics coupling in both unforced and CO2-forced runs (Figure 4). Models with more equatorward HC edges exhibit stronger increases in LML subsidence and greater cloud-induced SW warming with unforced southward HC edge shifts and thus warm more with CO2-forced southward HC edge shifts. This relationship constitutes a less robust but still statistically significant and physically motivated emergent constraint that links ECS to the climatological Hadley cell extent, although accurately assessing the statistical significance of emergent constraints is difficult [e.g., Caldwell et al., 2014].

4. Discussion

We have documented a robust interannual relationship in Southern summer between lower midlatitude SWCRE and poleward HC edge expansion. All models exhibit anomalous LML SW warming with poleward HC edge shifts. In most models (+HC-SWCRE models) the anomalous SW warming dominates the LML, while in a few models (−HC-SWCRE models) there are intrusions of tropical SW cooling. The intermodel spread in cloud-dynamics coupling seems to arise from the intermodel spread in large-scale dynamics, particularly in the climatological HC edge position. In models with more equatorward HCs, southward HC edge shifts transition the LML from a weak to a strong subsidence regime, resulting in decreased SW cloud reflection. In models with more poleward HCs, southward HC edge shifts keep the LML in a strong subsidence regime, and the SW warming effect is small (Figure 3). Note that the magnitude of the 4×CO2 SWCRE warming is not correlated with the extent of the CO2-forced HC expansion but only with the HC starting latitude. The key finding here therefore is that the LML SW cloud radiative response seems to be correlated with climatological biases in the HC extent, in line with previous studies which find a strong link between SW cloud radiative feedbacks and model climatological biases [Trenberth and Fasullo, 2010; Grise et al., 2015]. In particular, models with climatological HC edge latitudes closer to the observations show a weaker positive SW cloud radiative response and tend to have smaller ECS values.

Our analysis focuses on the cloud radiative effects of HC edge latitude shifts, and our results are consistent with Grise and Polvani [2014a] and Grise and Polvani [2014b]. Changes in the strength and structure of the HC branches can produce different cloud radiative responses that can have different effects on model climate sensitivity [e.g., Su et al., 2014]. More broadly, we note that ECS results from the competing effects of many feedback processes. Previous studies find that models with higher ECS more skillfully simulate certain cloud microphysical or thermodynamical cloud feedback processes [e.g., Fasullo and Trenberth, 2012; Sherwood et al., 2014; Tan et al., 2016]. Ouranalysisofacloud-circulationfeedbackprocesssuggeststhatmodelswithgenerally lower ECS more skillfully simulate the climatological HC extent and its interannual covariability with the LML SWCRE. The challenge then is to devise ways to synthesize the evaluation of models with diverse skills in simulating important climate feedback processes.

Our analysis of cloud-circulation interactions also brings forward two main issues: (1) how poleward circulation shifts change the subsidence and (2) how changes in large-scale subsidence imprint on clouds and their radiative effects. Regarding the latter, the same increase in subsidence may affect clouds differently depending on the model microphysics scheme [Kay et al., 2014; Storelvmo et al., 2015]. We have here examined the former with respect to the HC and have shown that biases in HC edge location affect the magnitude of subsidence increase with HC edge shifts. The model behavior is a continuous function of climatological location of the circulation. However, this may be intrinsically linked to the representation of clouds in the models, as the climatological CRE may help set the low-level baroclinicity that helps determine the location of the large-scale atmospheric circulation [Ceppi et al., 2012, 2014]. More work is needed to disentangle the relative contributions of biases in clouds and in dynamics to the biases in the coupling between them.

Our findings highlight that intermodel differences in the cloud-dynamics coupling may be due not only to model biases in thermodynamics or the representation of clouds [Grise and Medeiros, 2016] but also to intermodel differences in the climatological large-scale atmospheric circulation itself. Although the models’ representations of clouds and their radiative effects need to be improved and the biases in cloud microphysical schemes need to be addressed, advancing our understanding of cloud-dynamics coupling may come from a more realistic representation of the large-scale atmospheric dynamics itself.

Supplementary Material

Supp1

Key Points:

  • CMIP5 model SW cloud radiativeresponse and climate sensitivity is linked to the SH Hadley cell extent in each model’s control climate

  • With 4×CO2 forcing, models with narrower Hadley cells in the control climate warm more in the SH lower midlatitudes (28–48°S)

  • And a larger warming in the SH lowermidlatitudes strongly correlates with higher climate sensitivity

Acknowledgments

We thank Aiko Voigt and Peter Caldwell for helpful discussions. The lead author (B.L.) acknowledges support from the NASA Earth and Space Science Fellowship (NESSF). G.T. would like to acknowledge support by the NASA Modeling, Analysis, and Prediction (MAP) program. L.M.P. is funded by a grant from the U.S. National Science Foundation to Columbia University. The ISCCP D1 cloud data used in the analysis can be accessed at https://eosweb.larc.nasa.gov/ project/isccp/isccp_table and the ISCCP FD radiative flux data can be accessed at http://i/sccp.giss.nasa.gov/outgoing/FLUX/. The ERA-Interim reanalysis data were obtained freely from the European Centre for Medium-Range Weather Forecasts (http://apps.ecmwf.int/datasets/). All model data used in this paper are freely available through the Earth System Grid Federation (https://pcmdi9.llnl.gov/projects/esgf-llnl/), as described in Taylor et al. [2012].

We thank Haibo Liu and the Lamont-Doherty Earth Observatory for obtaining the CMIP5 data. We acknowledge the World Climate Research Program’s Working Group on Coupled Modelling, which is responsible for CMIP, and we thank the climate modeling groups for producing and making available their model output. For CMIP, the U.S. Department of Energy’s Program for Climate Model Diagnosis and Intercomparison provides coordinating support and led development of software infrastructure in partnership with the Global Organization for Earth System Science Portals.

Footnotes

Supporting Information:

Supporting Information S1

• Figure S1

• Figure S2

Citation: Lipat, B. R., G. Tselioudis, K. M. Grise, and L. M. Polvani (2017), CMIP5 models’ shortwave cloud radiative response and climate sensitivity linked to the climatological Hadley cell extent, Geophys. Res. Lett., 44, 5739–5748, doi:10.1002/2017GL073151.

References

  1. Andrews T, Gregory JM, Webb MJ, and Taylor KE (2012), Forcing, feedbacks and climate sensitivity in CMIP5 coupled atmosphere-ocean climate models, Geophys. Res. Lett, 39, L09712, doi: 10.1029/2012GL051607. [DOI] [Google Scholar]
  2. Barnes E, and Polvani L (2013), Response of the midlatitude jets, and of their variability, to increased greenhouse gases in the CMIP5 models, J. Clim, 26(18), 7117–7135, doi: 10.1175/JCLI-D-12-00536.1. [DOI] [Google Scholar]
  3. Bender F, Ramanathan V, and Tselioudis G (2011), Changes in extratropical storm track cloudiness 1983–2008: Observational support for a poleward shift, Clim. Dyn, 38(9–10), 2037–2053, doi: 10.1007/s00382-011-1065-6. [DOI] [Google Scholar]
  4. Bony S (2005), Marine boundary layer clouds at the heart of tropical cloud feedback uncertainties in climate models, Geophys. Res. Lett, 32, L20806, doi: 10.1029/2005GL023851. [DOI] [Google Scholar]
  5. Caldwell PM, Bretherton CS, Zelinka MD, Klein SA, Santer BD, and Sanderson BM (2014), Statistical significance of climate sensitivity predictors obtained by data mining, Geophys. Res. Lett, 41, 1803–1808, doi: 10.1002/2014GL059205. [DOI] [Google Scholar]
  6. Ceppi P, and Hartmann DL (2015), Connections between clouds, radiation, and midlatitude dynamics: A review, Curr. Clim. Change Rep, 1, 94–102, doi: 10.1007/s40641-015-0010-x. [DOI] [Google Scholar]
  7. Ceppi P, Hwang Y-T, Frierson DMW, and Hartmann DL (2012), Southern Hemisphere jet latitude biases in CMIP5 models linked to shortwave cloud forcing, Geophys. Res. Lett, 39, L19708, doi: 10.1029/2012GL053115. [DOI] [Google Scholar]
  8. Ceppi P, Zelinka MD, and Hartmann DL (2014), The response of the Southern Hemispheric eddy-driven jet to future changes in shortwave radiation in CMIP5, Geophys. Res. Lett, 41, 3244–3250, doi: 10.1002/2014GL060043. [DOI] [Google Scholar]
  9. Dee DP, et al. (2011), The ERA-Interim reanalysis: Configuration and performance of the data assimilation system, Q. J. R. Meteorol. Soc, 137(656), 553–597, doi: 10.1002/qj.828. [DOI] [Google Scholar]
  10. Fasullo JT, and Trenberth KE (2012), A less cloudy future: The role of subtropical subsidence in climate sensitivity, Science, 338(618), 792–794, doi: 10.1126/science.1227465. [DOI] [PubMed] [Google Scholar]
  11. Forster PM, Andrews T, Good P, Gregory JM, Jackson LS, and Zelinka M (2013), Evaluating adjusted forcing and model spread for historical and future scenarios in the CMIP5 generation of climate models, J. Geophys. Res. Atmos, 118, 1139–1150, doi: 10.1002/jgrd.50174. [DOI] [Google Scholar]
  12. Grise KM, and Medeiros B (2016), Understanding the varied influence of midlatitude jet position on clouds and cloud radiative effects in observations and global climate models, J. Clim, 29, 9005–9025, doi: 10.1175/JCLI-D-16-0295.1. [DOI] [Google Scholar]
  13. Grise KM, and Polvani LM (2014a), Southern hemisphere cloud-dynamics biases in CMIP5 models and their implications for climate projections, J. Clim, 27(15), 6074–6092, doi: 10.1175/JCLI-D-14-00113.1. [DOI] [Google Scholar]
  14. Grise KM, and Polvani LM (2014b), Is climate sensitivity linked to dynamical sensitivity? A Southern Hemisphere perspective, Geophys. Res. Lett, 41, 533–540, doi: 10.1002/2013GL058466. [DOI] [Google Scholar]
  15. Grise KM, Polvani LM, Tselioudis G, Wu Y, and Zelinka MD (2013), The ozone hole indirect effect: Cloud-radiative anomalies accompanying the poleward shift of the eddy-driven jet in the Southern Hemisphere, Geophys. Res. Lett, 40, 3688–3692, doi: 10.1002/grl.50675. [DOI] [Google Scholar]
  16. Grise KM, Polvani LM, and Fasullo JT (2015), Reexamining the relationship between climate sensitivity and the Southern Hemisphere radiation budget in CMIP models, J. Clim, 28, 9298–9312, doi: 10.1175/JCLI-D-15-0031.1. [DOI] [Google Scholar]
  17. Hu Y, and Fu Q (2007), Observed poleward expansion of the Hadley circulation since 1979, Atmos. Chem. Phys. Discuss, 7(4), 9367–9384, doi: 10.5194/acpd-7-9367-2007. [DOI] [Google Scholar]
  18. Kay JE, Medeiros B, Hwang YT, Gettelman A, Perket J, and Flanner MG (2014), Processes controlling Southern Ocean shortwave climate feedbacks in CESM, Geophys. Res. Lett, 41, 616–622, doi: 10.1002/2013GL058315. [DOI] [Google Scholar]
  19. Kushner PJ, Held IM, and Delworth TL (2001), Southern Hemisphere atmospheric circulation response to global warming, J. Clim, 14, 2238–2249. [Google Scholar]
  20. Li Y, Thompson DWJ, Huang Y, and Zhang M (2014), Observed linkages between the Northern Annular Mode/North Atlantic Oscillation, cloud incidence, and cloud radiative forcing, Geophys. Res. Lett, 41, 1681–1688, doi: 10.1002/2013GL059113. [DOI] [Google Scholar]
  21. Lu J, Vecchi G. a., and Reichler T (2007), Expansion of the Hadley cell under global warming, Geophys. Res. Lett, 34, L06805, doi: 10.1029/2006GL028443. [DOI] [Google Scholar]
  22. Norris JR, and Evan AT (2015), Empirical removal of artifacts from the ISCCP and PATMOS-x satellite cloud records, J. Atmos. Oceanic Technol, 32(4), 691–02, doi: 10.1175/JTECH-D-14-00058.1. [DOI] [Google Scholar]
  23. Qu X, Hall A, Klein SA, and Caldwell PM (2014), On the spread of changes in marine low cloud cover in climate model simulations of the 21st century, Clim. Dyn, 42(9–10), 2603–2626, doi: 10.1007/s00382-013-1945-z. [DOI] [Google Scholar]
  24. Sherwood SC, Bony S, and Dufresnse J-L (2014), Spread in model climate sensitivity traced to atmospheric convective mixing, Nature, 505, 37–42, doi: 10.1038/nature12829. [DOI] [PubMed] [Google Scholar]
  25. Storelvmo T, Tan I, and Korolev AV (2015), Cloud phase changes induced by CO2 Warming—A powerful yet poorly constrained cloud-climate feedback, Curr. Clim. Change Rep, 1(4), 288–296, doi: 10.1007/s40641-015-0026-2. [DOI] [Google Scholar]
  26. Su H, Jiang JH, Zhai C, Shen TJ, Neelin JD, Stephens GL, and Yung YL (2014), Weakening and strengthening structures in the Hadley circulation change under global warming and implications for cloud response and climate sensitivity, J. Geophys. Res. Atmos, 119, 5787–5805, doi: 10.1002/2014JD02164. [DOI] [Google Scholar]
  27. Tan I, Storelvmo T, and Zelinka MD (2016), Observational constraints on mixed-phase clouds imply higher climate sensitivity, Science, 352(6282), 224–227, doi: 10.1126/science.aad5300. [DOI] [PubMed] [Google Scholar]
  28. Taylor KE, Stouffer RJ, and Meehl GA (2012), An overview of CMIP5 and the experiment design, Bull. Am. Meteorol. Soc, 93(4), 485–498, doi: 10.1175/BAMS-D-11-00094.1. [DOI] [Google Scholar]
  29. Trenberth KE, and Fasullo JT (2010), Simulation of present-day and twenty-first-century energy budgets of the Southern Oceans, J. Clim, 23(2), 440–454, doi: 10.1175/2009JCLI3152.1. [DOI] [Google Scholar]
  30. Tselioudis G, and Jakob C (2002), Evaluation of midlatitude cloud properties in a weather and a climate model: Dependence on dynamic regime and spatial resolution, J. Geophys. Res, 107(24), 4781, doi: 10.1029/2002JD002259. [DOI] [Google Scholar]
  31. Tselioudis G, Lipat BR, Konsta D, Grise KM, and Polvani LM (2016), Midlatitude cloud shifts, their primary link to the Hadley cell, and their diverse radiative effects, Geophys. Res. Lett, 43, 4594–4601, doi: 10.1002/2016GL068242. [DOI] [Google Scholar]
  32. Vial J, Dufresne J-L, and Bony S (2013), On the interpretation of inter-model spread in CMIP5 climate sensitivity estimates, Clim. Dyn, 41(11–12), 3339–3362, doi: 10.1007/s00382-013-1725-9. [DOI] [Google Scholar]
  33. Webb MJ, Lambert FH, and Gregory JM (2013), Origins of differences in climate sensitivity, forcing and feedback in climate models, Clim. Dyn, 40(3–4), 677–707, doi: 10.1007/s00382-012-1336-x. [DOI] [Google Scholar]
  34. Yin JH (2005), A consistent poleward shift of the storm tracks in simulations of 21st century climate, Geophys. Res. Lett, 32, L18701, doi: 10.1029/2005GL023684. [DOI] [Google Scholar]
  35. Zhang Y (2004), Calculation of radiative fluxes from the surface to top of atmosphere based on ISCCP and other global data sets: Refinements of the radiative transfer model and the input data, J. Geophys. Res, 109, D19105, doi: 10.1029/2003JD004457. [DOI] [Google Scholar]
  36. Zhou C, Zelinka MD, Dessler AE, and Klein SA (2015), The relationship between inter-annual and long-term cloud feedbacks, Geophys. Res. Lett, 42, 10,463–10,469, doi: 10.1002/2015GL066698. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supp1
NIHMS936246-supplement-Supp1.pdf (147.8KB, pdf)

RESOURCES