Grain size-dependent crystal plasticity constitutive model for polycrystal materials

Abstract

Consideration of a core and mantle configuration for individual grains is a prominent method to capture the grain size-dependence in the constitutive models for polycrystal material. The mantle represents a region of the grain volume near the grain boundary where mechanical deformation is influenced by the grain boundaries, while the core represents the inner region of the grain volume. The grain size-dependence is then realized by assigning a set of values for the mechanical properties in the mantle that are different from those of the core region. However, these values for the mechanical properties of the mantle region are typically chosen arbitrarily, guided solely by the quality of the agreement between a model’s predicted stress-strain behavior with that obtained experimentally. In the present study, a physics-based method to develop the grain size-dependent crystal plasticity constitutive model on the core and mantle configuration for polycrystal materials is presented. The method is based on the assumption that any resistance to dislocation nucleation and motion in a material manifests as an increase in yield strength and a decrease in strain-hardening modulus, and the mutual relationship between yield strength and strain-hardening is an inherent material property that determines the plasticity of that specific material. Accordingly, the same single crystal plasticity constitutive model that describes the behavior of the material under loading can be used to capture the increased resistance to dislocation nucleation and motion in the grain boundary influence region. The physics-based modeling is facilitated by introducing a shear flow strain distribution in the phenomenological formulation and a pile-up of dislocation density distribution in the dislocation based formulation, such that, the resulting variations in the yield strength and the strain-hardening modulus are identical to that produced by the increased resistance in the grain boundary influence region. Thus, the increase in strength and the decrease in the strain-hardening modulus, determined as spatially varying local material properties in the mantle, are mutually related through the grain size-independent inherent plastic properties specific to the material. A simplified model that considers the grain boundary effect averaged over the grain volume is also developed under this general framework. Implementation of this simplified model is demonstrated by considering the case of a power law flow rule and a hyperbolic-secant hardening rule for the phenomenological formulation, and Taylor strength relation for the dislocation based formulation. Finally, the grain size-dependent constitutive model is validated by comparing the predicted stress-strain behavior of polycrystal copper samples under uniaxial loading with experimental results.

1. Introduction

Microstructural feature sizes such as grains and precipitates have significant effects on material deformation. The yield strength of a crystalline metallic material increases when its average grain size becomes smaller according to the Hall-Petch relationship [26,48]. Similarly, the yield strength of nickel based superalloys increases with a decrease in the average size of precipitate phase for a given volume fraction of the precipitate [10,22,32,37,43,50]. These grain size-dependent behaviors are attributed to the influence of grain boundaries on dislocation nucleation and its mobility, which in turn affects yield strength and strain-hardening in slip systems.

In classical crystal plasticity constitutive models [35], the plastic deformation of a material is captured through a set of a flow rule and a strength evolution rule that describes slipping deformation in slip systems as a function of resolved shear stress. However, these constitutive models do not have an intrinsic mechanism to capture any localized deformation arising from the geometric constraints associated with the existence of microstructural features. Therefore, classical crystal plasticity constitutive models lack the ability to predict microstructural feature size-dependent behavior observed experimentally.

The mechanism of grain size-dependent behavior has been explained as a consequence of the influence of plastic strain gradients on material response, arising primarily due to the inhomogeneous plastic deformation between neighboring grains as a result of lattice incompatibilities [16]. Accordingly, deformation gradient based grain size-dependent constitutive models that fundamentally rely on dislocation density as an internal variable to capture the evolution of dislocations were developed [15]. Dislocations are generally classified into statistically stored dislocations (SSDs) that evolve from the random trapping processes during uniform plastic strains, and geometrically necessary dislocations (GNDs) that evolve as a result of the strain gradients driven by geometrical constraints on the crystal lattice [4]. The evolution of GNDs introduces the plastic strain gradients [2]. While a number of strain gradient based models were phenomenological under the higher order mathematical formulations [12,17,18,39,53,7], others followed a more physically intuitive approach by directly introducing strain gradient effects in the evolutionary laws of internal slip system state variables [1,11,13,14,21,3,34,36,41–43,46,50,54,6,8]. However, the strain gradient based grain size-dependent constitutive models inherently lack a fundamental mechanism in their formulation to capture the yield strength variation with grain size [14,40,42,9], which results in enforcing a boundary region with pre-existing GNDs. This deficiency of the strain-gradient models is highlighted by Kubin et al. [40]. Another deficiency of the strain-gradient models is that their formulations also result in mesh sensitivity [8], which not only is a challenge in the implementation of the method, but more importantly, raises concerns regarding the physical foundation of the formulation as well.

Following an alternative approach, grain size-dependent constitutive models were developed by subdividing a grain into a core and a mantle configuration [19,20,44,51,52]. The model relies on the hypothesis that grain boundaries influence the resistance to dislocation nucleation of material points in their neighborhood, causing a change in the plastic behavior of these material points by increasing the yield strength and decreasing the strain-hardening coefficient. The mantle that surrounds the core represents the region influenced by grain boundary, and is modeled to deform differently from the core that represents the inner volume of the grain. The characteristics of the core remaining the same irrespective of the grain size an inherent length-scale naturally emerges in the constitutive model. The emerged length-scale is a measure of the relative dominance of the grain boundary influence region on the overall behavior of the material. This approach is primarily motivated by the experimental determination of increased strain-hardening near grain boundaries [25,45]. Meyers et al. [44] modeled individual grains in a polycrystalline aggregate as a composite of a work-hardened boundary layer (mantle) surrounding the grain interior (core) comprised of an annealed material. The model predicted the variation in the yield strength satisfactorily. It was also shown that the flow stress of the material can be obtained from the average of the flow stress in the dislocation-free core and the dislocation-piled-up mantle by applying a rule similar to the rule of mixture. Fu et al. [20] advanced this model by allowing for the evolution of dislocation density in the mantle. While the grain interiors were modeled using a limited form of the crystal plasticity constitutive model, the grain boundary influence regions were modeled by applying an isotropic plasticity model with a higher yield strength. The higher yield strength accounted for the increase in the resistance to dislocation nucleation and motion. The model was further advanced to the nanocrystalline regime [19] by accounting for the grain boundary rotation and slipping, thus capturing the reverse Hall-Petch effect. A lower yield strength and a higher work-hardening rate than those of the core were used in the mantle to account for the grain boundary rotation and slipping. Grain size-dependent constitutive models on the core and mantle configuration have also been developed by coupling a single-crystal plasticity constitutive model with an appropriate cohesive interface model [51,52].

Unlike the deformation gradient based models, the core and mantle based models can inherently capture the dependence of yield strength on grain size, and are relatively easy to implement. However, the core and mantle based models reported in the literature realize grain size-dependent behavior by simply applying an arbitrarily chosen set of material properties for the mantle that is different from the properties of the core, rather than by capturing the variation in the resistance to dislocation nucleation explicitly in the formulation. The arbitrarily chosen material properties are then validated by comparing the predicted material behavior for different grain sizes with those obtained experimentally.

In the present study, a physics-based grain size-dependent crystal plasticity constitutive model on a core and mantle configuration is developed by explicitly accounting for the increased resistance to dislocation nucleation and motion in grain boundary influence region. Both phenomenological and dislocation density based crystal plasticity formulations were considered for the model development. In the phenomenological formulation, the model development is facilitated by the introduction of a shear flow strain distribution in the grain boundary influence region such that the resulting variations in the yield strength and strain-hardening modulus, determined following the crystal plasticity constitutive model, are identical to that produced by the increased resistance in the grain boundary influence region. Similarly, in the dislocation density based formulation a dislocation density distribution is introduced. A major advantage of using crystal plasticity for the determination of increased resistance in the grain boundary influence is that the increase in yield strength and the decrease in the strainhardening modulus due to the grain boundary effect are not arbitrary. Instead, they are related mutually through the inherent size-independent properties specific to the material, thus making the model physics-based. As a result, the spatial distribution of the resistance to shear flow strain is the only additional information required for implementing the method to introduce size-dependence in the crystal plasticity constitutive models. The theoretical development of the method and its implementation for polycrystal material under both phenomenological and dislocation density based crystal plasticity formulations is presented in this article. Implementation of the method for capturing the precipitate-size dependence in two-phase single crystal materials using phenomenological formulation has been discussed elsewhere [22].

2. Theory

The classical crystal plasticity model is presented in Section 2.1, in a very general form suitable for the present study. The development of a general grain size-dependent constitutive model is presented in Section 2.2. The developed model is then simplified by considering the grain boundary effect averaged over the grain volume in Section 2.3. Finally, the implementation of the simplified grain size-dependent framework is demonstrated in Section 2.4 by considering a widely used specific case of flow rule and strain-hardening rule.

2.1. General crystal plasticity framework

Following the classical approach, the kinematics of elastic-plastic deformation is split into two multiplicative operations; a plastic deformation followed by an elastic deformation. The plastic deformation describes the slipping of lattices without any lattice stretching, while the elastic deformation describes the stretching and rotation of the lattices [23,24,35]. The total deformation gradient F is then given by,

$$\mathit{F}={\mathit{F}}^{*}.{\mathit{F}}^{\mathit{p}}$$ (1)

where the superscript p denotes the plastic deformation of material to an intermediate reference configuration in which lattice orientation and spacing are the same as in the original reference configuration, and the superscript * denotes the stretching and the rotation of the lattice.

The total velocity gradient L is given as,

$$\mathit{L}={\mathit{L}}^{*}+{\mathit{L}}^{\mathit{p}}=\dot{\mathit{F}}.{\mathit{F}}^{-\mathbf{1}}=\mathit{D}+\mathit{\Omega }$$ (2)

where the symmetric stretch rate D and the anti-symmetric spin tensor Ω can also be decomposed as below,

$$\mathit{D}={\mathit{D}}^{*}+{\mathit{D}}^{\mathit{p}},\mathit{\Omega }={\mathit{\Omega }}^{*}+{\mathit{\Omega }}^{\mathit{p}}$$ (3)

The velocity gradient associated with the plastic deformation, L^p, is then given in terms of Schmid’s tensor as,

$${\mathit{L}}^{\mathit{p}}={\mathit{F}}^{\mathit{p}}.{\dot{\mathit{F}}}^{{\mathit{p}}^{-1}}={\sum }_{\alpha }{\dot{\gamma }}^{(\alpha )}{\mathit{m}}^{(\mathit{\alpha })}\otimes {\mathit{n}}^{(\mathit{\alpha })}$$ (4)

where ${\dot{\gamma }}^{(\alpha )}$ is the rate of shear strain associated with the slipping in α-th slip system, m is the unit normal to the slip plane, and n is the unit vector parallel to the slip direction. Incremental formulation of plasticity theory is based on; (1) evolution of Cauchy stress on a Jaumann corotational frame of reference that rotates with the crystal lattice, J*(σ), (2) shear flow rate (slipping rate) ${\dot{\gamma }}^{(\alpha )}$, and (3) work hardening rate ${\dot{g}}^{(\alpha )}$ as given below,

$${\mathit{J}}^{*}(\mathit{\sigma })+\mathit{\sigma }\left(\mathit{I}:{\mathit{D}}^{*}\right)=\mathit{C}:{\mathit{D}}^{*},$$ (5)

where σ is the Cauchy stress, C is the tensor of elastic moduli, and I is the second order identical tensor.

The rate of slipping on a given slip system (α) is then defined as,

$${\dot{\gamma }}^{(\alpha )}={\dot{\gamma }}^{(\alpha )}\left({\tau }^{(\alpha )},g^{(\alpha )}\right)$$ (6)

where τ^(α) and g^(α) are the resolved shear stress and the shear strength, respectively.

The evolution of shear strength g^(α) due to the strain-hardening associated with the plastic behavior of a material is attributed to the nucleation and pile-up of dislocations in the grains. As the nucleation and pile-up continue under loading, the resistance to any further nucleation of dislocations also increases, exhibiting two major characteristics of strain-hardening phenomena; an increase in shear strength and a decrease in strain-hardening modulus. The increase in the shear strength and the decrease in the strain-hardening modulus represent an increase in the threshold stress to nucleate dislocation and a decrease in the material’s ability to further strain-harden, respectively. Therefore, this increase in strength and decrease in strain-hardening are not only mutually dependent through the shear flow strain or dislocation accumulated due to loading, but that mutual dependence is also a property inherent to the microstructure of a specific material. The development of a crystal plasticity constitutive model relies on this fundamental property of the material, facilitating the formulation of the evolution of shear strength and strain-hardening modulus as functions of the accumulated shear flow strain.

As the nucleation and pile-up continue under loading, the resistance to any further nucleation of dislocations also increases, exhibiting two major characteristics of strain-hardening; an increase in shear strength and a decrease in strain-hardening modulus representing an increase in the threshold stress to nucleate dislocation and a decrease in the capacity to further strain-harden, respectively. Therefore, this increase in strength and decrease in strain-hardening are not only mutually dependent through the shear flow strain or dislocation accumulated due to loading, but that mutual dependence is also a property inherent to the crystal structure of a specific material. The development of a crystal plasticity constitutive model relies on this fundamental property of the material, allowing the formulation of the evolution of shear strength and strain-hardening modulus as functions of the accumulated shear flow strain.

Following the principle of crystal plasticity constitutive modeling discussed above, the evolution of strength g^(α) can be defined either by using the accumulated shear flow or through applying the dislocation density as an independent parameter. These two different formulations are referred to as phenomenological based formulation and dislocation density based formulation, respectively. In the phenomenological based formulation, the primary concern is the average plastic shear strain, which is the overall effect of the movement of dislocations as a whole. While in the dislocation density based formulation, the constitutive behavior is described by the evolution of the dislocation density on the slip plane directly. Therefore, the dislocation density based formulation allows for a more fundamental description of the material behavior that permits the explicit description of various deformation mechanisms at the microscale level such as screw and edge dislocations, incorporation of cross-slip, and incorporation of GNDs [38,6,8]. Though the phenomenological formulation cannot capture the underlying deformation mechanisms, it only requires relatively fewer material parameters and is typically easier to implement. Since both the formulations are widely used, the development of the grain size-dependent model for both the formulations is presented.

Accordingly, in the phenomenological formulation, the evolution of strength g^(α) in a given slip system (α) due to strain-hardening can be described in terms of the cumulative shear flow strain and the rate of shear flow in each of the slip systems as given below,

$${\dot{g}}^{(\alpha )}={\sum }_{(\beta )}{h}_{\alpha \beta }(\gamma )|{\dot{\gamma }}^{(\beta )}|$$ (7)

where h_αβ, a function of the cumulative shear flow strain γ, is the strain-hardening modulus, and $\dot{\gamma }$ is the rate of shear flow. The cumulative shear flow strain γ is defined as,

$$\gamma =\sum _{(\alpha )}{\int }_0^t|{\dot{\gamma }}^{(\alpha )}|dt$$ (8)

The evolution of strength, therefore, is associated with the evolution of a material’s resistance to dislocation nucleation, which is captured through the strain-hardening coefficient as a function of the shear flow strain γ (Eq. (7)). The h_αβ corresponding to the annealed state of the material (γ = 0) is the initial strain-hardening modulus. The instantaneous shear strength of a slip system is then obtained as,

$$g^{(\alpha )}={\tau }_0+\underset{0}{\overset{t}{\int }}{\dot{g}}^{(\alpha )}dt$$ (9)

where, τ₀ is the shear strength corresponding to the annealed state of the material.

For the dislocation density based formulation, the strength is directly dependent on the local dislocation density ρ^(α) through the Taylor strength relation [13,49],

$$g^{(\alpha )}={\alpha }_d{\mu }_{d}b\sqrt{{\rho }^{(\alpha )}}$$ (10)

where α_d is a dimensionless stiffness parameter, μ_d is the shear modulus and b refers to the magnitude of the Burgers vector. The dislocation density corresponding to the annealed state of the material, ρ₀, can be determined by setting g^(α) = τ₀ in the above relationship (Eq. (10)). The evolution of the dislocation density can be expressed in a general form as,

$${\dot{\rho }}^{(\alpha )}={\dot{\rho }}^{(\alpha )}({\rho }^{(\alpha )},{\dot{\gamma }}^{(\alpha )})$$ (11)

2.2. General grain size-dependent crystal plasticity framework

In polycrystal materials, the geometric constraints on the deformation of crystal lattice in the grain boundary influence region, primarily driven by the difference in grain orientations across the grain boundaries, is expected to produce an increase in resistance to dislocation nucleation and motion. Therefore, according to the core and mantle configuration, the consideration of a grain boundary influence region (mantle) with its characteristics different from the grain interior (core) and independent of the grain size, allows for the natural emergence of a length-scale parameter leading to the grain size-dependent constitutive model.

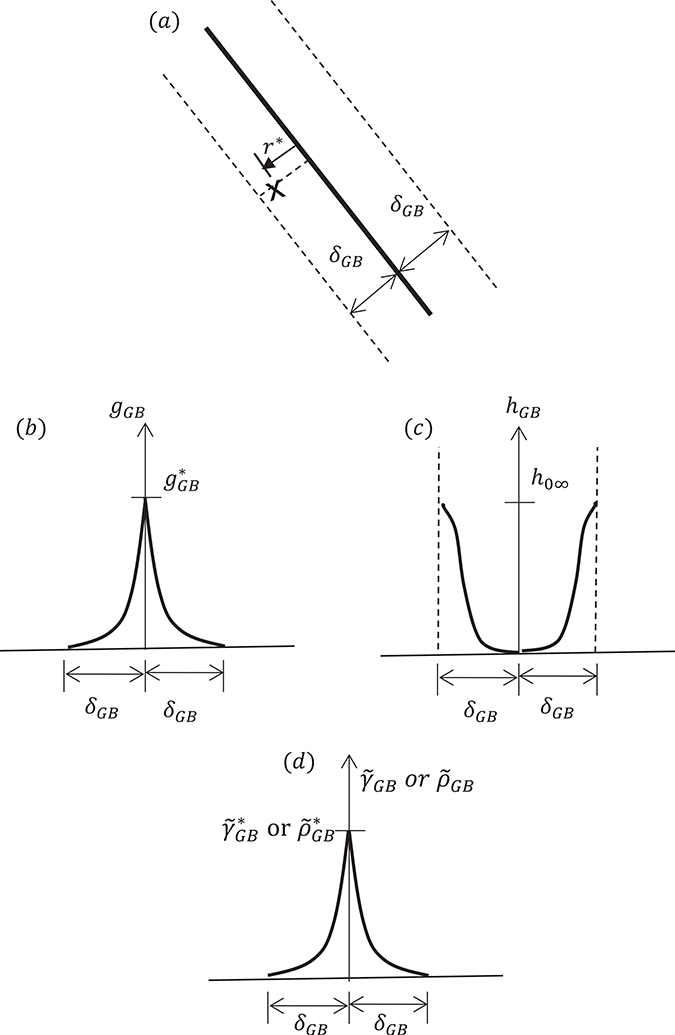
Following the treatment of the grain boundary influence region as a work-hardened region by Meyers et al. [44], we hypothesize that the increased resistance to dislocation nucleation and pile-up in the grain boundary influence region will not only produce an increase in yield strength and a decrease in strain-hardening modulus, but their mutual relationship will follow the same fundamental plastic properties specific to the material as well. That is, the consequences of an increased resistance on the plastic behavior are the same irrespective of its root cause: either the accumulation of shear flow strain under loading or the grain boundary effect. As discussed in the previous section, the mutual dependence of the strength and the strain-hardening modulus expressed through the accumulated shear flow strain in the phenomenological formulation or the pile-up of dislocation density in the dislocation based formulation is a fundamental principle of the crystal plasticity modeling framework. Hence, the increased resistance to dislocation nucleation and motion in the grain boundary influence region can also be captured using the same crystal plasticity constitutive model by introducing an appropriate distribution of cumulative shear flow strain ${\tilde{\gamma }}_{GB}$ in the phenomenological formulation or a distribution of a pile-up of dislocation density ${\tilde{\rho }}_{GB}$ in the dislocation based formulation (Fig. 1). The ${\tilde{\gamma }}_{GB}$ and ${\tilde{\rho }}_{GB}$ are termed as the grain boundary equivalent shear flow strain and grain boundary equivalent pile-up of dislocation density, respectively, since the change in the strength and the strain-hardening modulus at a material point as a result of their introduction in the constitutive model must be identical to those caused by the grain boundary effect.

Fig. 1.

(a) A schematic illustrating the grain boundary influence region (b) distribution of the strength (c) distribution of initial strain-hardening modulus (d) distribution of the equivalent shear flow strain (and equivalent pile-up of dislocation density) parameter which allows capturing the strength and strain-hardening distributions.

The method is illustrated as follows. First, the equivalent shear flow strain ${\tilde{\gamma }}_{GB}$ and an equivalent pile-up of dislocation density ${\tilde{\rho }}_{GB}$ (Eq. (12)) are considered in the grain boundary influence region of thickness (δ_GB) for the phenomenological formulation and dislocation based formulation, respectively (Fig. 1(a) and (d)),

$$\{\begin{array}{c}{\tilde{\gamma }}_{GB}\left(r^{*}\right)={\tilde{\gamma }}_{GB}\left(r^{*}\right)Phenomenological\\ or\\ {\tilde{\rho }}_{GB}\left(r^{*}\right)={\tilde{\rho }}_{GB}\left(r^{*}\right)Dislocationbased\end{array}where0\le r^{*}\le {\delta }_{GB}$$ (12)

where, r* represents the location of a material point in the grain with respect to the closest point on the grain boundary. The distribution of ${\tilde{\gamma }}_{GB}$ and ${\tilde{\rho }}_{GB}$ in the grain boundary influence region must be such that the resulting shear strength (g_GB) and strain-hardening modulus distributions (h_GB) are identical to those produced by the actual resistance due to the grain boundary effect. At the grain boundary, the values of g_GB and h_GB should correspond to a fully strain-hardened region with no further strain-hardening possible. At the intersection between core and mantle, r* = δ_GB, these values should correspond to the annealed state without any history of shear flow strain accumulation or any grain boundary effect. Therefore, g_GB decreases from its maximum value of $g_{GB}^{*}$ at the grain boundary to zero as it approaches the core (Fig. 1(b)). Conversely, the strain-hardening modulus, h_GB, increases from zero at the grain boundary to the initial strain-hardening modulus at the coremantle interface (Fig. 1(c)). Without loss of generality, a typical profile for ${\tilde{\gamma }}_{GB}$ in the phenomenological formulation or ${\tilde{\rho }}_{GB}$ in the dislocation based formulation that produces the desirable distribution of increase in strength and decrease in strain-hardening modulus with a maximum value of ${\tilde{\gamma }}_{GB}^{*}$ or ${\tilde{\rho }}_{GB}^{*}$ at the grain boundary, is shown in Fig. 1(d). In general, the ${\tilde{\gamma }}_{GB}$ or ${\tilde{\rho }}_{GB}$ distribution profile is characteristic of the grain boundary, and may vary with its location on the grain boundary depending on many factors such as relative orientation of the grains across the grain boundary at that location. Assuming that the effect of these variations is relatively small when compared to the overall grain size-dependence, the profiles for ${\tilde{\gamma }}_{GB}$ and ${\tilde{\rho }}_{GB}$ are treated as material properties that remain unchanged irrespective of the variation in the characteristics of the grain boundaries.

In the phenomenological formulation, the size-dependent constitutive model is then formulated by accounting for the effect of the resistance to dislocation nucleation in the hardening rule that describes the rate of shear strength evolution (Eq. (7)). Thus, the evolution of shear strength of a material point at an arbitrary location r* in the grain can be described as,

$${\dot{g}}^{(\alpha )}\left(r^{*}\right)={\dot{g}}^{(\alpha )}(\gamma +{\tilde{\gamma }}_{GB}\left(r^{*}\right),{\dot{\gamma }}^{(\beta )})$$ (13)

Considering the individual contributions of grain boundary effect and the strain-hardening effect due to loading explicitly, the instantaneous shear strength of a slip system (Eq. (9)) can be written as,

$$g^{(\alpha )}\left(r^{*}\right)={\tau }_{0\infty }+{g_{GB}}^{(\alpha )}\left(r^{*}\right)+\underset{0}{\overset{t}{\int }}{\dot{g}}^{(\alpha )}\left(r^{*}\right)dt$$ (14)

where, τ_0∞ is the shear strength corresponding to the annealed state of the material. The subscript ∞ indicates that the related quantity corresponds to a sample with large grains, thus not influenced by the grain boundary. The parameter g_GB^(α)(r*) is the increase in strength due to grain boundary effect.

Following the hypothesis that the mutual relationship between the increase in strength and the decrease in the strain-hardening modulus is an inherent material property, the quantity g_GB^(α)(r*) and the corresponding decrease in the strain-hardening modulus can be determined by invoking the crystal plasticity constitutive model itself. The procedure is as follows; with the goal of determining the g_GB^(α)(r*) profile, the strength evolution rate in a given slip system (α) can be considered as a linear combination of the rate of shear flow strain in all the slip systems (Eq. (7)).

$${{\dot{g}}_{GB}}^{(\alpha )}\left(r^{*}\right)={\sum }_{(\beta )}{h}_{\alpha \beta }\left(\tilde{\gamma }\left(r^{*}\right)\right){\dot{\tilde{\gamma }}}^{(\beta )}$$ (15)

The increase in strength g_GB^(α)(r*) can be determined from the rate equation as (Eq. (14)),

$${g_{GB}}^{(\alpha )}\left(r^{*}\right)=\underset{0}{\overset{{\tilde{t}}_{GB}}{\int }}{\sum }_{(\beta )}{h}_{\alpha \beta }\left(\tilde{\gamma }\left(r^{*}\right)\right){\dot{\tilde{\gamma }}}^{(\beta )}dt$$ (16)

where the upper limit of time integration, ${\tilde{t}}_{GB}$, represents the time of evolution of strength due to the formation of the ${\tilde{\gamma }}_{GB}$ in the grain boundary influence region. Since the equivalent shear flow strain ${\tilde{\gamma }}_{GB}$ is a mathematical quantity introduced in order to capture the resistance to dislocation nucleation in the grain boundary influence region, its evolution $\left({\tilde{t}}_{GB}\right)$ has no significance. Therefore, the integration in the equation to determine strength due to grain boundary effect can be transformed from the time domain to the accumulated shear flow strain domain,

$${g_{GB}}^{(\alpha )}\left(r^{*}\right)=\frac{1}{N_{ss}}\underset{0}{\overset{{\tilde{\gamma }}_{GB}\left(r^{*}\right)}{\int }}{\sum }_{(\beta )}{h}_{\alpha \beta }(\tilde{\gamma })d\tilde{\gamma }$$ (17)

where N_ss is the total number of slip systems in a grain. In this derivation, it is assumed that $\tilde{\gamma }$ is equally divided on the N_ss slip systems in the grain boundary influence region. It is important to note that the determination of g_GB^(α)(r*) for a given ${\tilde{\gamma }}_{GB}$ distribution is independent of the shear flow rule (Eq. (6)). The role of the strain-hardening modulus $h_{\alpha \beta }(\tilde{\gamma })$, a property inherent to each specific material, in modeling the grain boundary effect can be clearly observed in these relations.

Since the characteristic of the grain boundary influence region is treated as a constant, irrespective of the nature of the grain boundary or the grains across it, $g_{GB}^{(\alpha )}$ can be expressed as g_GB, an average value over all the slip-systems. Therefore, the above expression can be further simplified as,

$${g_{GB}}^{(\alpha )}\left(r^{*}\right)=g_{GB}\left(r^{*}\right)=\frac{1}{N_{ss}}\left(\underset{0}{\overset{{\tilde{\gamma }}_{GB}\left(r^{*}\right)}{\int }}{h}_s(\tilde{\gamma })d\tilde{\gamma }+\left(N_{ss}-1\right)\underset{0}{\overset{{\tilde{\gamma }}_{GB}\left(r^{*}\right)}{\int }}{h}_l(\tilde{\gamma })d\tilde{\gamma }\right)$$ (18)

where h_s and h_l are the self- and latent- hardening moduli. The strain-hardening modulus h_αβ represents the self-hardening modulus h_s when α = β, and the latent-hardening modulus h_l otherwise.

In the dislocation based formulation, the size-dependent constitutive model can be formulated by accounting for the ${\tilde{\rho }}_{GB}$ in the dislocation evolution and strength relations (Eqs. (11) and (10), respectively) as shown below.

The evolution of dislocation density can be described as,

$${\dot{\rho }}^{(\alpha )}\left(r^{*}\right)={\dot{\rho }}^{(\alpha )}({\rho }^{(\alpha )}+{\tilde{\rho }}_{GB}\left(r^{*}\right),{\dot{\gamma }}^{(\alpha )})$$ (19)

Then the strength relationship becomes,

$$g^{(\alpha )}\left(r^{*}\right)=g^{(\alpha )}\left({\rho }^{(\alpha )}+{\tilde{\rho }}_{GB}\left(r^{*}\right)\right)={\alpha }_d{\mu }_{d}b\sqrt{{\rho }^{(\alpha )}+{\tilde{\rho }}_{GB}\left(r^{*}\right)}$$ (20)

The g_GB^(α)(r*) can be obtained as,

$${g_{GB}}^{(\alpha )}\left(r^{*}\right)=g_{GB}\left(r^{*}\right)=g^{(\alpha )}\left({\rho }_0+{\tilde{\rho }}_{GB}\left(r^{*}\right)\right)-g^{(\alpha )}\left({\rho }_0\right)$$ (21)

where g^(α)(ρ₀) is equal to the strength of the grain due to the initial dislocations; i.e. the annealed state without any grain size effect.

In the phenomenological formulation, the increase in yield strength due to the grain boundary effect is captured in the constitutive model through g_GB term as per Eq. (18), while the decrease in the initial strain-hardening modulus is captured through the functional form of $h_{\alpha \beta }(\tilde{\gamma })$ specific to the material as per Eqs. (17) and (18). In the dislocation based formulation, the increase in yield strength is realized through its relationship with the existing dislocation pile-up (Eqs. (20) and (21)) explicitly, while the decrease in hardening rate is realized implicitly by reducing the evolution rate in the dislocation density (Eqs. (19) and (20)).

The g_GB (r*), in principle, can be determined experimentally. For example, the hardness profile determined on the cross-section of a sample containing large grains using a nanoindenter can potentially provide information for the determination of g_GB (r*). Hence, a nano-hardness profile obtained by taking the average of several measurements will be a good approach to derive g_GB (r*). In the absence of such detailed information, a linear profile with the value of the maximum strength at the grain boundary set to the strength of a fully work-hardened sample may be a good approximation. The challenge is to determine an appropriate ${\tilde{\gamma }}_{GB}$ in the phenomenological formulation and ${\tilde{\rho }}_{GB}$ in the dislocation based formulation that when applied to Eq. (17) and Eq. (21), respectively, agree with the experimentally measured or the assumed g_GB (r*) distribution in the grain boundary influence region. Once these material specific parameters are known, the behavior of the material for any grain size distributions can be predicted using the size-dependent crystal plasticity constitutive model.

It is important to note that the parameters ${\tilde{\gamma }}_{GB}$ and ${\tilde{\rho }}_{GB}$ should be treated as mere mathematical quantities introduced to utilize the crystal plasticity framework to conveniently capture the increased resistance to dislocation nucleation and its effect on plastic properties in the grain boundary influence region. Introduction of these terms do not contribute directly to the cumulative shear flow strain or the pile-up of dislocation density due to the mechanical loading, but influence them indirectly through higher strength and a lower strain-hardening modulus in the grain boundary influence region.

The size-dependent crystal plasticity model developed in this section can be considered as a broader framework that can capture any fundamental deformation mechanisms as long as these deformation mechanisms can be described under a core-mantle geometric grain description and they involve a modification of the material’s resistance to dislocation nucleation and motion. The resulting strengthening or softening of the material in the grain boundary influence region will cause an appropriate variation in yield strength and a corresponding variation in the strain hardening modulus in this region. Therefore, though not discussed in the present article, the developed model can be easily extended to describe the material behavior driven by such deformation mechanisms by introducing an appropriate resistance profile in the grain boundary influence region. A typical example is the reverse Hall-Petch behavior in nanocrystalline material driven by the dominance of grain boundary softening mechanisms.

2.3. Simplified model based on the grain boundary effects on an average sense over the grain volume

The general framework developed in the previous section can be simplified by considering the grain boundary effects on an average over the grain volume. In this approach, a uniform distribution of the resistance over the whole grain volume is considered such that its average effect on the grain volume is identical to the average effect produced by the actual distribution of the resistance in the grain boundary influence region. Accordingly, quantities $\overline{{\tilde{\gamma }}_{GB}}$ and $\overline{{\tilde{\rho }}_{GB}}$, which are ${\tilde{\gamma }}_{GB}$ or ${\tilde{\rho }}_{GB}$ averaged over the grain volume, respectively, are introduced.

In the phenomenological formulation,

$$\overline{{\tilde{\gamma }}_{GB}}=\frac{{\int }_V{\tilde{\gamma }}_{GB}\left(r^{*}\right)dV}{V}$$ (22)

therefore, the Eqs. (13) and (14) can be modified as,

$${\dot{g}}^{(\alpha )}={\dot{g}}^{(\alpha )}(\gamma +\overline{{\tilde{\gamma }}_{GB}},{\dot{\gamma }}^{(\beta )})$$ (23)

$$g^{(\alpha )}={\tau }_{0\infty }+\overline{g_{GB}}+\underset{0}{\overset{t}{\int }}{\dot{g}}^{(\alpha )}dt$$ (24)

where $\overline{g_{GB}}$ is the uniform shear strength equivalent to the average grain boundary effect in the grain volume. Therefore, the increase in strength due to the grain boundary effect averaged over the volume of a grain $\overline{g_{GB}}$ can be determined by modifying Eq. (18) as,

$$\overline{g_{GB}}=\frac{1}{N_{ss}}\left(\underset{0}{\overset{\overline{{\tilde{\gamma }}_{GB}}}{\int }}{h}_s(\tilde{\gamma })d\tilde{\gamma }+\left(N_{ss}-1\right)\underset{0}{\overset{\overline{{\tilde{\gamma }}_{GB}}}{\int }}{h}_l(\tilde{\gamma })d\tilde{\gamma }\right)$$ (25)

Similarly, in the dislocation based formulation, a uniform dislocation density distribution that produces the same average grain boundary effect over grain volume as the actual dislocation density distribution can be introduced as,

$$\overline{{\tilde{\rho }}_{GB}}=\frac{{\int }_V{\tilde{\rho }}_{GB}\left(r^{*}\right)dV}{V}$$ (26)

The dislocation density evolution and the strength equations (Eqs. (19)–(21)) are then modified as,

$${\dot{\rho }}^{(\alpha )}={\dot{\rho }}^{(\alpha )}({\rho }^{(\alpha )}+\overline{{\tilde{\rho }}_{GB}},{\dot{\gamma }}^{(\alpha )})$$ (27)

$$g^{(\alpha )}=g^{(\alpha )}\left({\rho }^{(\alpha )}+\overline{{\tilde{\rho }}_{GB}}\right)={\alpha }_d{\mu }_{d}b\sqrt{{\rho }^{(\alpha )}+\overline{{\tilde{\rho }}_{GB}}}$$ (28)

Therefore, $\overline{g_{GB}}$ in the dislocation density based formulation can be obtained as,

$$\overline{g_{GB}}=g^{(\alpha )}\left({\rho }_0+\overline{{\tilde{\rho }}_{GB}}\right)-g^{(\alpha )}\left({\rho }_0\right)$$ (29)

It is important to note the difference in the way the inherent length-scale parameters emerge in the material point based model and the grain volume average based model. In the material point based model, the inherent length-scale parameter does not explicitly appear in the model (Eqs. (13), (14) and (18) for the phenomenological formulation and Eqs. (19)–(21) for the dislocation based formulation), but rather emerges as a measure of the relative dominance of the grain boundary influence region with respect to grain size in the overall behavior of the grain. In the grain volume average based model, the inherent length-scale appears explicitly through the parameters $\overline{{\tilde{\gamma }}_{GB}}$ and $\overline{{\tilde{\rho }}_{GB}}$ as a function of δ_GB (Eqs. (23) and (24) in the phenomenological formulation, and Eqs. (27) and (28) in the dislocation based formulation).

2.4. Implementation for a specific case

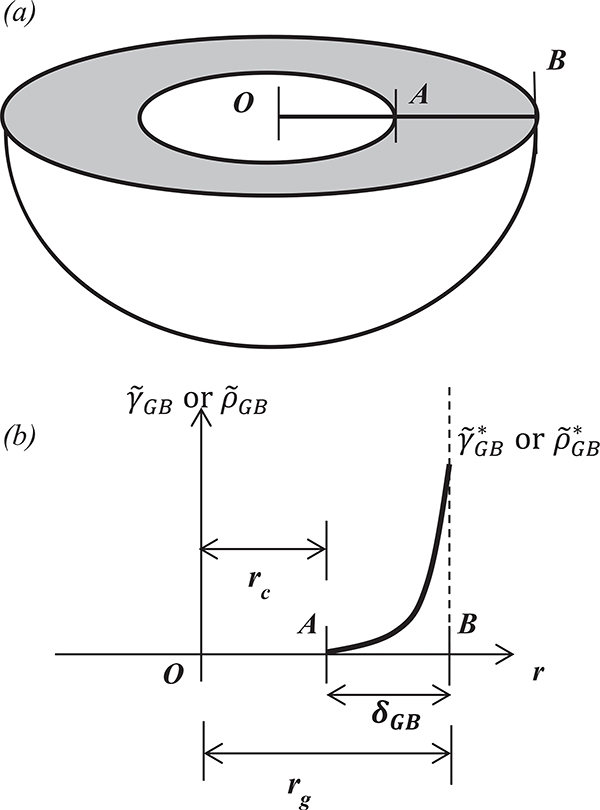
The implementation of the grain volume average based model is demonstrated for a special case of flow and strength evolution rules widely reported in the literature. For simplicity, a spherical grain with a diameter D (2r_g) representing the effective size of an actual grain with a non-spherical shape (Fig. 2) is considered.

Fig. 2.

(a) A schematic illustrating the grain boundary influence region by considering a simple spherical grain, (b) the distribution of the shear flow strain or dislocation density associated to the resistance exerted by the grain boundary.

The spherical grain shape configuration allows for consideration of a simpler coordinate system. In this case, r is the radial distance of any material point from the grain center, and the radius of the core r_c, can be described as r_c= r_g − δ_GB. Accordingly, the grain boundary influence region can be described by an r such that, r_c<r<r_g.

A typical power law flow rule for the shear flow strain can be defined as [30,31,47,5]

$${\dot{\gamma }}^{(\alpha )}=\dot{a}{\left(\frac{{\tau }^{(\alpha )}}{g^{(\alpha )}}\right)}^n$$ (30)

where τ^(α) and g^(α) are the resolved shear stress and the shear strength on the α-th slip system. The constant $\dot{a}$ refers to the slipping rate when the resolved shear stress reaches the strength, and is assumed to be the same for all slip systems. In the phenomenological formulation, a hyperbolic-secant hardening rule is considered with the coefficient h_αβ (Eq. (7)) being defined as,

$$h_{\alpha \beta }=q^{(\alpha \beta )}{h}_{0\infty }{\mathit{sech}}^2\left|\frac{h_{0\infty }\gamma }{{\tau }_s-{\tau }_{0\infty }}\right|$$ (31)

where q^(αβ) differentiates latent-hardening (α ≠ β) and self-hardening (α = β), h_0∞ is the initial strain-hardening modulus, τ_0∞ is the shear strength which is equal to the initial value of g^(α), and τ_s is the stage-I stress (break-through stress) which is taken as the maximum shear strength corresponding to fully strain-hardening condition, $g_{GB}^{*}$. Substituting the flow rule and the hardening rule (Eqs. (30) and (31)) along with the ${\tilde{\gamma }}_{GB}$ (Eq. (12)) into Eq. (18), g_GB (r) can be obtained as,

$$g_{GB}(r)=\frac{{\tilde{h}}_{0\infty }}{K}tanh\left|K{\tilde{\gamma }}_{GB}(r)\right|$$ (32)

In this formulation, the constants ${\tilde{h}}_{0\infty }$ and K are given as ${\tilde{h}}_{0\infty }=\frac{h_{0\infty }\left(\left(N_{\mathit{ss}}-1\right)q+1\right)}{N_{\mathit{ss}}}$ and $K=\frac{h_{0\infty }}{{\tau }_s-{\tau }_{0\infty }}$, respectively. The parameter q^(αβ) is the same for all the (N_ss−1) latent-hardening slip systems (referred simply as q), and it is equal to unity for the self-hardening slip system. From the grain averaged shear flow strain $\overline{{\tilde{\gamma }}_{GB}}$ (Eq. (22)), the grain averaged shear strength $\overline{g_{GB}}$ can be determined by substituting Eqs. (30) and (31) into Eq. (25),

$$\overline{g_{GB}}={\tilde{h}}_{0\infty }\underset{0}{\overset{\overline{{\tilde{\gamma }}_{GB}}}{\int }}sec{h}^2|K\tilde{\gamma }|d\tilde{\gamma }=\frac{{\tilde{h}}_{0\infty }}{K}tanh\left|K\overline{{\tilde{\gamma }}_{GB}}\right|$$ (33)

In the dislocation based formulation, the evolution of dislocation density (Eq. (11)) is considered to be driven by both the accumulation and annihilation of the dislocations described as [13,49],

$${\dot{\rho }}^{(\alpha )}=\frac{1}{b}\left(\frac{\sqrt{{\rho }^{(\alpha )}}}{K_{ac}}-2y_c{\rho }^{(\alpha )}\right)\left|{\dot{\gamma }}^{(\alpha )}\right|$$ (34)

where K_ac is a material parameter corresponding to the accumulation of the dislocation density and y_c is a critical distance between dislocations that controls the annihilation of the dislocations.

A simple linear profile for ${\tilde{\gamma }}_{GB}(r)$ or ${\tilde{\rho }}_{GB}(r)$ is considered for demonstration purpose as,

$${\tilde{\gamma }}_{GB}(r)or{\tilde{\rho }}_{GB}(r)=C\left(r-r_c\right)H\left(r-r_c\right)$$ (35)

where the constant C is given as $\frac{{\tilde{\gamma }}_{GB}^{*}}{{\delta }_{GB}}$ or $\frac{{\tilde{\rho }}_{GB}^{*}}{{\delta }_{GB}}$ for the phenomenological and dislocation based formulations, respectively. H (r−r_c) is the Heaviside step function enforcing value of 0 to the and ${\tilde{\rho }}_{GB}(r)$ profile for r≤r_c.

Substituting the grain volume averaged form (Eq. (22)) of given in the Eq. (35) into the Eq. (33), $\overline{g_{GB}}$ for the phenomenological formulation can be determined as,

$$\overline{g_{GB}}=\frac{{\tilde{h}}_{0\infty }}{K}tanh\left|K{\tilde{\gamma }}_{GB}^{*}\left(\left(\frac{3{\delta }_{GB}}{2r_g}\right)-{\left(\frac{{\delta }_{GB}}{r_g}\right)}^2+\frac{1}{4}{\left(\frac{{\delta }_{GB}}{r_g}\right)}^3\right))\right|$$ (36)

Similarly, by substituting the grain volume averaged form (Eq. (26)) of ${\tilde{\rho }}_{GB}(r)$ given in the Eq. (35) into the Eq. (28), we have,

$$\overline{g_{GB}}={\alpha }_d{\mu }_{d}b\left(\sqrt{{\rho }_0+K{\tilde{\rho }}_{GB}^{*}(\left(\frac{3{\delta }_{GB}}{2r_g}\right)-{\left(\frac{{\delta }_{GB}}{r_g}\right)}^2+\frac{1}{4}{\left(\frac{{\delta }_{GB}}{r_g}\right)}^3)}-\sqrt{{\rho }_0}\right)$$ (37)

3. Results and discussion

The grain size-dependent constitutive model was validated by: 1) verifying the Hall-Petch effect by studying the variation of $\overline{g_{GB}}$ with grain size, and 2) incorporating the grain size-dependent constitutive model on a finite element analysis (FEA) framework, and then comparing the predicted stress-strain behavior of the samples with different average grain sizes under uniaxial tensile loading to the corresponding experimental results for copper reported in literature. A linear profile was considered for and ${\tilde{\rho }}_{GB}(r)$ for the phenomenological formulation (Eq. (36)) and the dislocation based formulation (Eq. (37)), respectively.

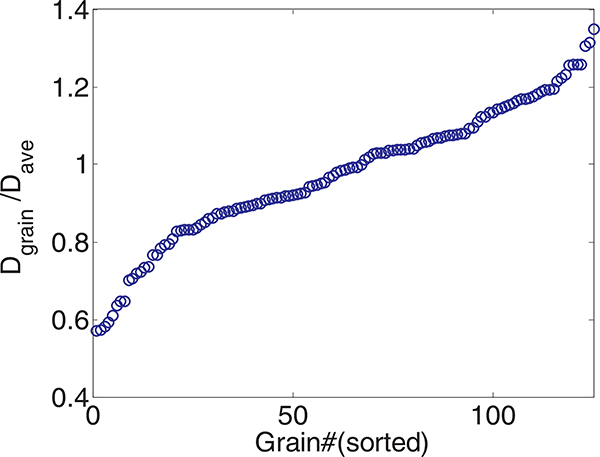
Polycrystalline samples consisting of 125 grains with random shapes and sizes generated using the Voronoi algorithm were considered as representative volume elements (RVEs) in this study (Fig. 3). Experimentally obtained stress-strain behavior for copper samples with different average grain diameters of 14 μm, 33 μm and 220 μm is available in the literature [28,29]. In addition, the stress-strain behavior for a sample with large grains (grain size-independent) was reported by Hansen et al. [29], which was obtained by extrapolating the experimental stress-strain behavior of these three different grain sizes. To validate the model proposed in this article by comparing its prediction with the above experimental results, samples with the same average grain sizes (D_ave), namely 14 μm, 33 μm and 220 μm were considered for the numerical simulation. The different average grain sizes were obtained by simply scaling the overall sample size, thus making sure that the grain shapes and orientations (Fig. 3) remained the same from sample to sample.

Fig. 3.

Polycrystal with 125 randomly oriented, shaped and sized grains.

The elastic material properties C₁₁, C₁₂, and C₄₄ for the copper cubic lattice structure and the plastic material parameters ${\dot{a}}_0$ and q were obtained from the literature [33]. Since the material properties τ_0∞, τ_s and h_0∞ required for describing plasticity were not available, an FEA simulation with a grain size-independent constitutive model and phenomenological formulation (Eqs. (6)–(9)) was performed first. These properties were then determined by matching the stress-strain behavior from the simulation with the stress-strain behavior reported for the sample with large average grains [29]. The saturated value of the ${\tilde{\gamma }}_{GB}^{*}$ corresponding to the τ_s was determined using Eq. (36) by assuming that the grain boundary influence region is thoroughly saturated. A relatively high value of 100 was considered for n in order to obtain a rate-independent flow rule. The material parameters for the dislocation based formulation were also obtained from the literature [13]. The initial and saturated dislocation densities, ρ₀ and ${\tilde{\rho }}_{GB}^{*}$ were obtained by using the Taylor strength relationship (Eq. (10)), using the same τ_0∞ and τ_s, respectively, used in the phenomenological formulation. All the material parameters used in this study are shown in Table 1. A grain boundary thickness (δ_GB) of 0.333 μm was chosen since it provided the best fit for the predicted stress-strain behavior with the experimental results for all three samples of different average grain sizes. For individual grains in the samples, the values of $\overline{{\tilde{\gamma }}_{GB}}$, $\overline{{\tilde{\rho }}_{GB}}$ and $\overline{g_{GB}}$ were determined following Eqs. (22), (26), (36) and (37).

Table 1.

Applied elastic and plastic material properties.

Material properties
τ0∞	9 MPa
τs	95 MPa
${\dot{\mathit{a}}}_{\mathit{o}}$	0.001 1/s
n	100
q	1
c11	168, 400 MPa
c12	121,400 MPa
c44	75,400 MPa
Phenomenological formulation
${\tilde{\mathit{\gamma }}}_{\mathit{GB}}^{*}$	1.07
h0∞	240 MPa
Dislocation based formulation
μd	542,000 MPa
αd	0.3
Kac	7
yc	1.6 × 10−9 m
b	2.56 × 10−9 m
ρ0	4.67 × 1012 m−2
${\tilde{\mathit{\rho }}}_{\mathit{GB}}^{*}$	5.21 × 1014 m−2

The Abaqus commercial FEA package, with the crystal plasticity constitutive model implemented through a UMAT subroutine, was used for both the grain size-independent simulation to derive material properties, and the grain size-dependent study to validate the newly developed constitutive model. The sample was subjected to a uniaxial tensile load at a loading rate of 350 MPa/s. Periodic boundary conditions were enforced on all the external faces of the RVEs [14,9]. The discretization of the sample is shown in Fig. 3. In order to ensure a good refinement, even with respect to the smallest grain size, a 20 × 20 × 20 mesh of 20-noded brick elements was considered.

3.1. Variation of $\overline{{\tilde{\gamma }}_{GB}}$, $\overline{{\tilde{\rho }}_{GB}}$, and $\overline{g_{GB}}$ with grain size

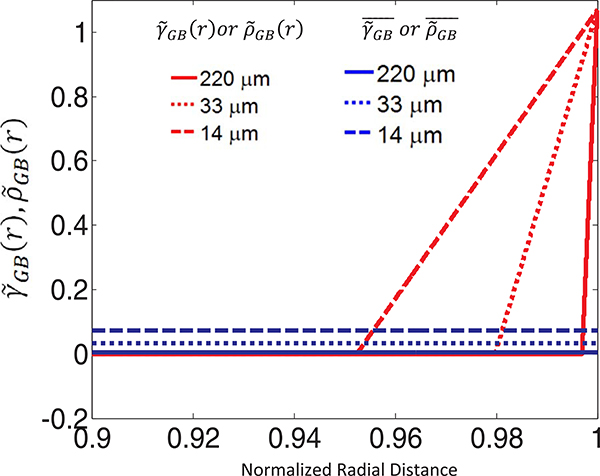
For the assumed linear profiles of ${\tilde{\gamma }}_{GB}(r)$ and ${\tilde{\rho }}_{GB}(r)$ (shown in Fig. 4), the quantities $\overline{{\tilde{\gamma }}_{GB}}$, $\overline{{\tilde{\rho }}_{GB}}$ and $\overline{g_{GB}}$, calculated for three individual grains of sizes 14 μm, 33 μm, and 220 μm (Fig. 2) are provided in Table 2. The sizes of these single grains are equal to the average grain sizes of the three polycrystal samples considered in the validation step. The horizontal axis is taken as the radial distance from the center of the grain normalized by the grain radius. As expected, $\overline{{\tilde{\gamma }}_{GB}}$, $\overline{{\tilde{\rho }}_{GB}}$ and $\overline{g_{GB}}$ increased as the grain size decreased. Also, results from both the phenomenological and the dislocation based formulations agree reasonably well.

Fig. 4.

${\tilde{\gamma }}_{GB}(r)\mathit{or}{\tilde{\rho }}_{GB}(r)$ profiles and the averaged $\overline{{\tilde{\gamma }}_{GB}}\mathit{or}\overline{{\tilde{\rho }}_{GB}}$ (horizontal lines).

Table 2.

$\overline{{\tilde{\gamma }}_{GB}}$, $\overline{{\tilde{\rho }}_{GB}}$ and $\overline{g_{GB}}$ for a single grain considering grain boundary effect.

Dgrain (μm)	Phenomenological formulation		Dislocation based formulation
	$\overline{{\tilde{\mathit{\gamma }}}_{\mathit{G}\mathit{B}}}$	$\overline{{\mathit{g}}_{\mathit{G}\mathit{B}}}$ (MPa)	$\overline{{\tilde{\mathit{\rho }}}_{\mathit{G}\mathit{B}}}$ (m−2)	$\overline{{\mathit{g}}_{\mathit{G}\mathit{B}}}$ (MPa)
14	0.0740	17.5000	3.5680e13	17.4427
33	0.0325	7.6495	1.5417e13	9.6583
220	0.0048	1.1637	2.3392e12	2.0241

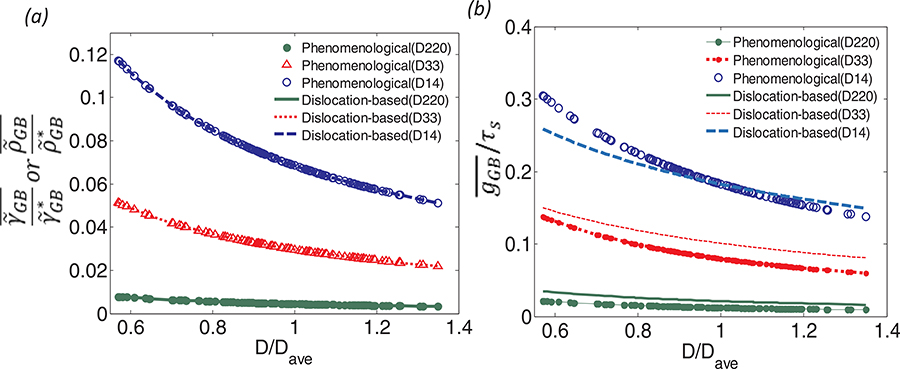
The grain size distribution in the Voronoi polycrystal sample is shown in Fig. 5, and the variations of $\overline{{\tilde{\gamma }}_{GB}}$, $\overline{{\tilde{\rho }}_{GB}}$ and $\overline{g_{GB}}$ with grain size are shown in Fig. 6. Since the diameter of the equivalent spherical representation of individual grains is different due to the difference in their grain size, the values of $\overline{{\tilde{\gamma }}_{GB}}$, $\overline{{\tilde{\rho }}_{GB}}$ and $\overline{g_{GB}}$ vary from grain to grain. As the grain size increases, the ratio of the volume of the grain boundary influence region to the volume of the grain decreases, thus decreasing the effect of the grain boundary resistance. As an example, in the sample with the smallest average grain size, 14 μm, the $\overline{g_{GB}}$ varied from 28.97 to 13.02 MPa with the increase in the size of the grains in the phenomenological formulation. It should be noted that the value of $\overline{g_{GB}}$ for a given grain represents the increase in its average shear strength over the grain volume as a result of the grain boundary effect.

Fig. 5.

The variation of the grain diameters normalized with the average grain diameter in the studied sample for 125 grains. Since the three samples with different average grain sizes are obtained by simply scaling the geometry this variation is same for all of them.

Fig. 6.

The variation of $\overline{{\mathit{g}}_{\mathit{GB}}}$ and $\overline{{\tilde{\mathit{\gamma }}}_{\mathit{GB}}}$, $\overline{{\tilde{\mathit{\rho }}}_{\mathit{GB}}}$ for the three studied samples with different average grain sizes from both the phenomenological and dislocation based formulations (a) the variation in $\overline{{\tilde{\mathit{\gamma }}}_{\mathit{GB}}}\mathit{and}\overline{{\tilde{\mathit{\rho }}}_{\mathit{GB}}}$ normalized by ${\tilde{\mathit{\gamma }}}_{\mathit{GB}}^{*}$ and ${\tilde{\mathit{\rho }}}_{\mathit{GB}}^{*}$, respectively (b) the variation in $\overline{{\mathit{g}}_{\mathit{GB}}}$ normalized by τ_s.

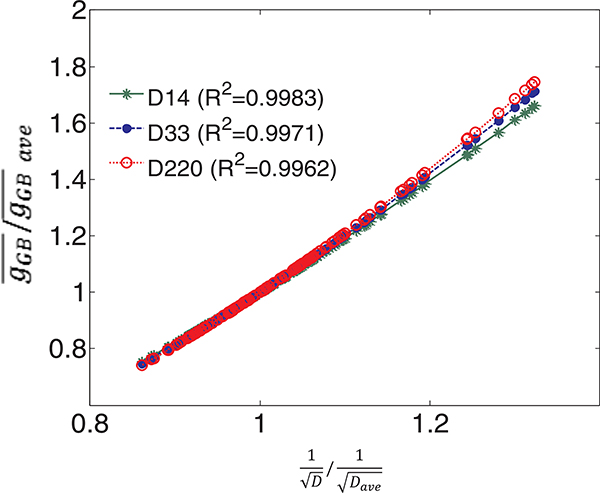
The model’s ability to capture the Hall-Petch relation was verified for the range of grain sizes in the polycrystalline sample by plotting the $\overline{g_{GB}}$ of individual grains against $\frac{1}{\sqrt{\mathit{D}}}$. The quantities $\overline{g_{GB}}$ and $\frac{1}{\sqrt{\mathit{D}}}$ were normalized by the $\overline{g_{GB}}$ of an individual grain of size equal to the average grain size (Table 2) and the corresponding $\frac{1}{\sqrt{{\mathit{D}}_{ave}}}$, respectively (Fig. 7). The R² values for the linear fit for each of the cases demonstrated reasonably good agreement. In addition, the slopes for all three cases considered agreed quite well.

Fig. 7.

Hall-Petch relationship for the three studied samples with average grain diameters of 14μm, 33μm and 220μm. R² represents the regression coefficient related to the linear fit (${\overline{g_{GB}}}_{ave}$ values are reported in Table 2).

3.2. Grain size-dependent constitutive model

In this section, validation of the grain size-dependent constitutive model to capture the size-dependent stress-strain behavior under uniaxial tensile loading is discussed. The validation was performed for both the phenomenological formulation (Eqs. (6), (8), (23), and (24)) and the dislocation based formulation (Eqs. (6), (27) and (28)). The values of $\overline{{\tilde{\gamma }}_{GB}}$, $\overline{{\tilde{\rho }}_{GB}}$ and $\overline{g_{GB}}$, obtained as functions of the grain size (discussed in the previous section), were assigned to individual elements in the finite element mesh as a material parameter in addition to the elastic and plastic material properties provided in Table 1. All the elements belonging to a given grain have the same values for $\overline{{\tilde{\gamma }}_{GB}}$, $\overline{{\tilde{\rho }}_{GB}}$ and $\overline{g_{GB}}$, calculated based on the corresponding equivalent spherical grain. The elements that overlap between two grains in the grain boundary region were associated with one of the grains based on the location of the element’s centroid.

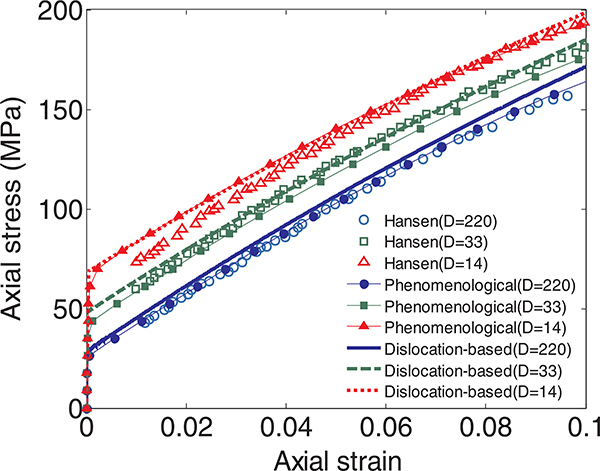
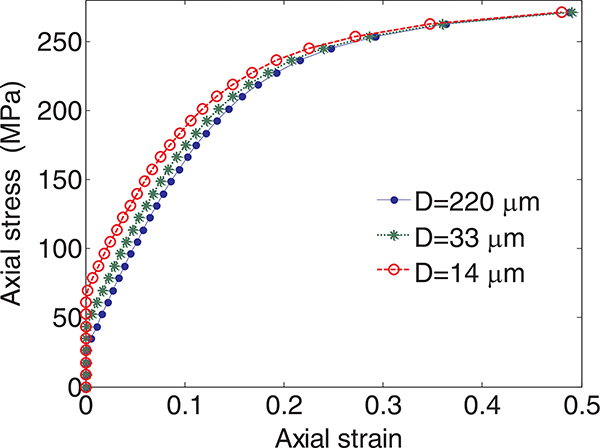
The axial stress-strain behavior under the uniaxial loading obtained for the samples with different average grain sizes are compared with the experimental results in Fig. 8. Overall, the predicted results from both the phenomenological and dislocation based formulations (Fig. 8) agree well with the experimental results. The experimental data is not sufficiently dense near the yield strength for an accurate comparison. Nevertheless, the predicted increase in yield strength with decrease in grain size shows a clear trend that matches the expected behavior. Some disagreement near the yield point observed for the case of D = 14 μm could be attributed to the inaccuracy in the measurements. The good agreement between the predicted and experimental hardening behavior (stress-strain behavior beyond yield strength) validates the ability of the proposed general constitutive framework to capture size-dependent plastic behavior, not only in terms of variation in yield strength, but in terms of the strain-hardening modulus as well. Since the experimental results were available only for three average grain sizes, the variation of the predicted yield strength of polycrystal samples was not compared against $\frac{1}{\sqrt{\mathit{D}}}$ to further validate Hall-Petch.

Fig. 8.

Axial stress-strain behavior obtained based on phenomenological and dislocation based formulations for the studied samples with grain diameters of 14 μm, 33 μm and 220 μm. (Experimental results from [28,29].

In Fig. 8, the stress-strain behavior is shown only in the strain range of 0–0.1 due to the limited availability of the experimental data. In order to validate the model for a larger strain range, the axial stress-strain response predicted by the grain size-dependent model for a strain up to 0.5 is shown in Fig. 9. Since the results from both the phenomenological and dislocation density based formulations were similar, results are only shown for phenomenological based formulation in this figure. The strain-hardening modulus varies with grain size as is quite evident in this depiction. For a given value of axial strain (or axial stress) the slope of the curve representing the hardening modulus increases with increase in grain size [27]. Results show that the increase in strength and the decrease in strain-hardening as the grain size becomes smaller lead to decrease in ductility for a given ultimate strength, which is consistent with the behavior of metals.

Fig. 9.

Predicted size-dependent axial stress-strain behavior for the studied samples for a larger strain range.

4. Conclusion

A new physics-based method to capture grain size-dependence in the crystal plasticity constitutive model on a core and mantle configuration was developed. Size-dependence was realized by accounting for the resistance to dislocation nucleation in the grain boundary influence region following the principles of crystal plasticity, rather than the current approach of arbitrary assignment of a different set of values for the mantle’s material properties. Consequently, variation in strength and the strain-hardening modulus due to the effect of grain boundaries followed the same mutual relationship that is fundamental to the plastic behavior of a specific material microstructure. In order to use the crystal plasticity constitutive modeling principles, a shear flow strain parameter in the phenomenological formulation and a pile-up of dislocation density in the dislocation based formulation, equivalent to the resistance to dislocation nucleation, were introduced. The grain size-dependent constitutive model was then derived consistent with the crystal plasticity framework. Validation of the model was performed by studying the variation of yield strength with the grain size of single grains. Results captured the increasing effect of the grain boundary in terms of an increase in yield strength and a decrease in strain-hardening with a decrease in grain size. The results demonstrate a good agreement with the Hall-Petch relationship. Subsequently, the size-dependent constitutive model was implemented on a FEA framework, and the FEA framework was used to obtain stress-strain behavior of polycrystalline samples comprised of 125 grains under uniaxial tensile loading for three different average grain diameters of 14 μm, 33 μm and 220 μm. Comparison of the predicted results with the experimental results available in literature revealed that a grain boundary influence region of 0.33 μm thickness along with a linear equivalent shear flow strain profile can describe the size-dependent stress-strain behavior of the FCC copper polycrystalline samples, both for the phenomenological and dislocation based formulations. To demonstrate the grain size effect, a polycrystal grain configuration with randomly shaped grains based on the Voronoi tessellations was considered.

In summary, the new method provides a simple physics-based alternative to the current arbitrary approach for the development of size-dependence in constitutive models on core and mantle configuration. Various manufacturing processes, such as shot-peening, cold rolling and additive manufacturing, introduce microstructural modification such as changes in texture, grain size and grain shapes, and may also produce a non-homogeneous microstructure. Physics based models that account for various characteristics of microstructural features, such as the one proposed in this work that account for grain sizes, can significantly increase the reliability of the computational models for predicting material response, and may serve as powerful tools for engineers in tailoring their designs for the specific applications of interest.

Nomenclature

F

Total deformation gradient

L

Total velocity gradient

D

Symmetric stretch rate tensor

Ω

Anti-symmetric spin tensor

γ

Shear flow strain

m

Unit normal to the slip plane

n

Unit vector parallel to the slip direction

σ

Cauchy stress

C

Tensor of elastic moduli

I

Second order identical tensor

J*

Jaumann corotational frame of reference

τ

Resolved shear stress

g

Shear strength

h_αβ

Strain-hardening modulus

t

Time

τ₀

Shear strength corresponding to the annealed state of the material

ρ

Dislocation density

α_d

Dimensionless stiffness parameter

μ_d

Shear modulus

b

Magnitude of the Burgers vector

${\tilde{\gamma }}_{GB}$

Equivalent shear flow strain in the grain boundary influence region

${\tilde{\rho }}_{GB}$

Equivalent pile-up of dislocation density in the grain boundary influence region

δ_GB

Thickness of the influence region

$g_{GB}^{*}$

Maximum strength (corresponding to fully strain-hardening condition) in the grain boundary influence region

${\tilde{\gamma }}_{GB}^{*}$

Maximum accumulated shear flow strain (corresponding to fully strain-hardening condition) in the grain boundary influence region

${\tilde{\gamma }}_{GB}$

${\tilde{\gamma }}_{GB}$ averaged over the grain volume

$\overline{{\tilde{\rho }}_{GB}}$

${\tilde{\rho }}_{GB}$ averaged over the grain volume

$\overline{g_{GB}}$

Uniform shear strength equivalent to the average grain boundary effect in the grain volume

h_s

Self-hardening moduli

h_l

Latent- hardening moduli

ρ₀

Initial dislocation density

V

Volume of the grain

D

Diameter of the grain

D_ave

Average diameter of the grains in a polycrystalline sample

r*

Location of a material point in the grain with respect to the closest point on the grain boundary

r

Radial distance of any material point from the grain center

r_g

Radius of the grain

r_c

Radius of the core

$\dot{a}$

Slip rate when the resolved shear stress reaches the strength

q^(αβ)

Parameter for differentiating latent-hardening (α ≠ β) and self-hardening (α = β)

τs

Maximum shear strength corresponding to fully strain-hardening condition

h₀

Initial strain-hardening modulus

K_ac

Material parameter corresponding to the accumulation of the dislocation density

y_c

Critical distance between dislocations for annihilation

H( )

Heaviside step function

${\tilde{h}}_{0\infty }$

A constant equal to $\frac{h_{0\infty }\left(\left(N_{\mathit{ss}}-1\right)q+1\right)}{N_{ss}}$

K

A constant equal to $\frac{h_{0\infty }}{{\tau }_s-{\tau }_{0\infty }}$

C₁₁, C₁₂, C₄₄

Cubic material elastic constants

n

Rate sensitivity exponent in the power-law flow rule