Using AMBER18 for Relative Free Energy Calculations

Abstract

With renewed interest in free energy methods in contemporary structure-based drug design there is a pressing need to validate against multiple targets and force fields to assess the overall ability of these methods to accurately predict relative binding free energies. We computed relative binding free energies using GPU accelerated Thermodynamic Integration (GPU-TI) on a dataset originally assembled by Schrödinger, Inc.. Using their GPU free energy code (FEP+) and the OPLS2.1 force field combined with the REST2 enhanced sampling approach, these authors obtained an overall MUE of 0.9 kcal/mol and an overall RMSD of 1.14 kcal/mol. In our study using GPU-TI from AMBER with the AMBER14SB/GAFF1.8 force field but without enhanced sampling, we obtained an overall MUE of 1.17 kcal/mol and an overall RMSD of 1.50 kcal/mol for the 330 perturbations contained in this data set. A more detailed analyses of our results suggested that the observed differences between the two studies arise from differences in sampling protocols along with differences in the force fields employed. Future work should address the problem of establishing benchmark quality results with robust statistical error bars obtained through multiple independent runs and enhanced sampling, which is possible with the GPU-accelerated features in AMBER.

Graphical Abstract

1. Introduction

Protein-ligand binding affinity calculation has drawn a lot of attention for many years because of its ability to significantly accelerate drug discovery by focusing experimental effort on high quality leads.^1–4 Using molecular dynamics (MD) or Monte Carlo algorithms to perform the necessary sampling, many methods have been developed to address this task^5–19: These include the linear interaction energy (LIE) approach^5–6, the Molecular Mechanics-Poisson−Boltzmann/Surface Area (MM-PBSA) and Molecular Mechanics-Generalized Born/Surface Area (MM-GBSA)^7–10 approaches, and physical pathway methods such as the Umbrella Sampling (US) method^11–12 combined with Weighted Histogram Analysis (WHAM)^20–21 or the variational free energy profile (vFEP) methods^22–23.

Another class of methods is the alchemical methods, where the thermodynamic path between two end states is defined and the free energy change is calculated based on statistical mechanical analysis of the simulations. Based on the theoretical foundation of Kirkwood, Zwanzig and Bennett among others,^{15–19, 24–25} the three most widely used alchemical methods are Thermodynamic Integration (TI),¹⁶ Free Energy Perturbation (FEP),²⁴ and (Multistate) Bennett Acceptance Ratio (MBAR).^{15, 19} FEP is based on the Zwanzig equation by considering the process of transforming A → B. The free energy change can be written as:

$$\mathrm{\Delta }\text{F}(\text{A}\to \text{B})=-\ln {⟨\exp \left(-\frac{{\text{U}}_{\text{B}}-{\text{U}}_{\text{A}}}{{\text{k}}_{\text{B}}\text{T}}\right)⟩}_{\text{A}}\text{or}\ln {⟨\exp \left(\frac{{\text{U}}_{\text{B}}-{\text{U}}_{\text{A}}}{{\text{k}}_{\text{B}}\text{T}}\right)⟩}_{\text{B}}$$ (1)

where U_B and U_A are the potential energy of A and B, k_B is the Boltzmann constant, and T is the temperature. From a practical perspective, this method is limited to small perturbations due to convergence and end state catastrophe issues, which to some extent is addressed via introducing a coupling parameter λ that varies from 0 to 1. The intermediate state λ has a potential energy U(λ), which is equal to U(A) when λ is 0, and to U(B) when λ is 1. TI computes the free energy change of this transformation by integrating the Boltzmann averaged ∂U(λ)/∂λ:

$$\mathrm{\Delta }\text{F}(\text{A}\to \text{B})={\int }_0^1{⟨\frac{\partial \text{U}(\mathrm{\lambda })}{\partial \mathrm{\lambda }}⟩}_{\mathrm{\lambda }}\text{d}\mathrm{\lambda }$$ (2)

Different functional forms of U(λ) have been constructed and tested.^26–27 MBAR calculates the free energy difference between neighboring intermediate states using:

$$\mathrm{\Delta }\text{F}(\mathrm{\lambda }\to \mathrm{\lambda }+1)=-\ln \frac{{⟨\text{w}\exp \left(-\mathrm{\beta }{\text{U}}_{\mathrm{\lambda }+1}\right)⟩}_{\mathrm{\lambda }}}{{⟨\text{w}\exp \left(-\mathrm{\beta }{\text{U}}_{\mathrm{\lambda }}\right)⟩}_{\mathrm{\lambda }+1}}$$ (3)

where w is a function of F(λ) and F(λ + 1). The equation is solved iteratively to give the free energy change of neighboring states ΔF(λ → λ + 1), which via combination yield the overall free energy change.

Another notable method is λ-dynamics,¹⁷ pioneered by Brooks and co-workers. It combines the idea of alchemical methods and US method by treating the λ variable dynamically, and generates a potential of mean force in λ-space. The initial application studies of alchemical methods were performed a few decades ago by a number of groups.^{2, 28–29} Since this time, a number of applications in both academia and industry have been reported.^30–43 However, to more reliably drive decisions in lead optimization, there are two major issues that alchemical methods should deal with, namely, adequate sampling of relevant configurations and force field accuracy.³ To address the sampling issues methods like Hamiltonian exchange and replica exchange have been developed,^44–46 while improvements in force fields, like CGenFF,⁴⁷ AMOEBA,⁴⁸ OPLS⁴⁹ and AMBER/GAFF,^50–51 have been an ongoing effort and will continue to be for the foreseeable future.

Recently, a FEP protocol was described that was able to predict the relative binding affinity over a broad range of protein-ligand complexes.¹ This approach used replica exchange with solute tempering (REST2) in combination with the OPLS2.1 force field that was carefully parameterized using an extensive training set of relevant torsional and covalent interactions.¹ The AMBER ff14SB/GAFF force fields^{50, 52} are widely used, but have not been extensively validated against such a large data set (8 systems and 330 perturbations). To fill this gap we employed the recently implemented^53–54 GPU-accelerated TI module of Amber18 to repeat the calculations for these systems in order to assess the capabilities of another force field model on this same data set. Overall, our computed results have larger average errors than the FEP+ result. The overall mean unsigned error (MUE) and root mean square deviation (RMSD) for FEP+ versus AMBER are 0.90 versus 1.17 kcal/mol, and 1.14 versus 1.50 kcal/mol, respectively. This indicates that the GPU-TI module of AMBER using the AMBER ff14SB/GAFF 1.8 force field is an alternative choice for high-throughput relative binding free energy calculations, albeit with slightly larger overall errors.

2. Methods

2.1. System preparation

All of the protein and ligand PDBs were obtained from the SI of the Wang et al. publication.¹ The atom names of the ligands were modified manually so that the common atoms of the ligands in each protein system have the same name and the unique atoms have different names. The protonation states of all the charged residues as well as Histidine residues were maintained as reported in Wang et al.. The AMBER FF14SB force field⁵⁵ was employed to describe the proteins and GAFF (version 1.8) was⁵⁰ used for the ligands. Restrained electrostatic potential (RESP) charges for the ligands were calculated at the HF/6–31G(d) level of theory using the Gaussian 09 program⁵⁶ and AMBERTools16. The parmchk utility from AMBERTools16 was used to generate the missing parameters for the ligands. The systems were solvated using the SPC/E⁵⁷ water model using cubic simulation cells. 5 Å and 10 Å were used as the minimum distance between the edge of the cell and the solute atoms of the protein and ligand systems, respectively. The resulting solvated protein/ligand systems were then charge neutralized by adding Na⁺ or Cl⁻ ions⁵⁸. The particle mesh Ewald (PME) method^59–60 was used to treat the long-range electrostatic interactions. All bonds involving hydrogen atoms were constrained using SHAKE⁶¹. The AMBER16 package⁶² was used to run the MD simulations. MD simulations for each protein-ligand system were performed to equilibrate the systems. Five steps of minimization were performed to remove close contacts. The first step minimizes the water molecules and counter ions, with the protein restrained. The second, third and fourth step restrains the heavy atoms, backbone heavy atoms, backbone carbon and oxygen atoms of the protein, while the last step minimizes the entire system. Each minimization step consisted of 20000 cycles of minimization using the steepest descent method. Afterwards the system was heated from 0 K to 300 K using the Langevin thermostat with a collision frequency of 2.5 ps⁻¹. The solute was restrained using a 5 kcal/(mol*Ų) restraining potential. Finally, the system was equilibrated at 300 K for 5 ns employing the NPT ensemble using a Langevin thermostat with a collision frequency of 1 ps⁻¹. The Berendsen barostat was used for the pressure control with a pressure relaxation time of 10 ps. The time step was 2 fs and the nonbonded cutoff was 12 Å. The last snapshot was used to generate a pdb file. Using the generated pdb file, all the protein atoms were duplicated along with the common atoms of the second ligand. The unique atoms of the second ligand were added according to the mol2 file of the second ligand, the coordinates of which were obtained from the input files from Wang, et al. The “timerge” function of the parmed.py utility of the AMBER 14 package was used to generate the dual ligand topology.

2.2. TI simulations

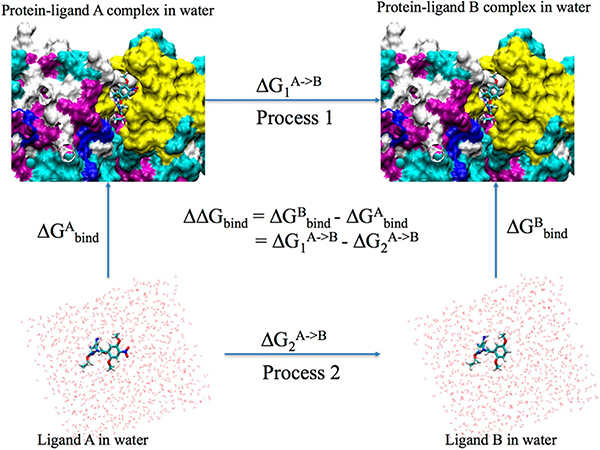
As shown in Figure 1, the relative binding free energy (ΔΔG) can be calculated as the difference between the free energies (ΔGs) of changing one ligand to the other in the protein matrix and in solution. Therefore, TI simulations for both process 1 and 2 were performed. For each process, the one-step protocol was adopted, i.e. disappearing one ligand and appearing the other ligand simultaneously. The common atoms of the two ligands were linearly transformed and the unique atoms were in the softcore region. Both the charge and vdW interactions between the disappearing (or appearing) unique atoms with the surrounding atoms were described by softcore potentials. Alternatively one can use the 3-step protocol, which consists of three steps: disappearing the charge interaction of one ligand, changing the vdW and bonded terms, and then appearing the charge of the second ligand. The one-step protocol not only takes less steps but also has the same charge for the initial and final state of the TI simulation. However, for the 3-step protocol, the charge of the system may change during the decharging/charging steps, which may affect the long-range electrostatic interactions via the use of a neutralizing background plasma in AMBER.

Figure 1.

Thermodynamic cycle used for the calculation of the relative binding free energy between protein-ligand system A and protein-ligand system B.

2.2.1. The one-step protocol

The detailed TI simulation protocol is as follows: First, using the dual ligand topology parameter file, 50000 steps of steepest descent minimization was performed. Then the system was heated from 0 to 300 K at the ps timescale, followed by 1 ns NVT equilibration at 300 K. Afterwards 1 ns pf NPT equilibration at 300 K and 1 bar was performed to equilibrate the density. These simulations were performed at λ=0.5 to equilibrate the system^63–64. No restraint was applied for these simulations and all structures were visually checked. For some perturbations, multiple runs had to be performed in order to obtain a stable starting structure. Afterwards the equilibrated structure was used as the starting structure for 12 λ windows (0.00922, 0.04794, 0.11505, 0.20634, 0.31608, 0.43738, 0.56262, 0.68392, 0.79366, 0.88495, 0.95206, 0.99078). For each λ, 1 ns of NVT equilibration was performed with the initial velocities randomly generated to give a temperature of 300 K. Afterwards 5 ns of NVT simulation was performed to collect ∂U/∂λ data. A 12-point Gaussian quadrature was used for the numerical integration of ∂U/∂λ to obtain all necessary ΔG values. The non-bonded interaction cutoff was 9.0 Å and a softcore potential^26–27 was used. The parameter α and β of softcore potential was 0.5 and 12 Ų, respectively. The time step was 1 fs for all simulations and SHAKE was not used. All TI simulations used the Berendsen thermostat with a coupling constant of 2 ps, except for the NPT equilibration step, which used the Langevin thermostat with a collision frequency of 2 ps⁻¹. We note that the Langevin thermostat is generally preferred over the Berendsen thermostat. The Berendsen barostat was used for NPT equilibration with a pressure relaxation time of 2 ps. NPT equilibration was performed using the CPU version of pmemd from the Amber14 package. The obtained results for all eight systems can be found in the Supplemental Information (SI). The input files are available at GitHub: https://github.com/linfranksong/Input_TI

3. Results and Discussion

3.1. Overall results

The ΔΔG values directly obtained from the TI calculations can be found in the SI. The mean unsigned error (MUE) and root mean square deviation (RMSD) of these values compared to experiment are summarized in SI Table 1. After obtaining the ΔΔG values, we employed the cycle closure convergence strategy described previously⁶⁵ and obtained our final ΔΔG values. Thus, the following analysis is based on the cycle-closure ΔΔG values. Table 1 summarizes the MUE and RMSD compared to experiment. The overall MUE obtained with GPU-TI of AMBER using the AMBER FF14SB/GAFF1.8 force field (AMBER for short) is 1.17 kcal/mol (0.27 kcal/mol larger than FEP+. Similarly, the RMSD is a bit higher for AMBER: 1.50 kcal/mol versus 1.14 kcal/mol for FEP+. Moreover, in our current work, we did not apply replica exchange, which could help enhance the overall sampling and improve the quality of the computed free energies. Future work will explore the role sampling (both in λ-space and phase space) plays on these systems versus the effect of force field errors.

Table 1.

Summary of the MUE and RMSD, R² and Kendall's tau coefficient (τ) of the eight systems based on cycle closure ΔΔG values.

System	# of ligands	# of perturbations	FEP+/OPLS 2.1 (kcal/mol)				AMBER GPU-TI/AMBER FF14SB + GAFF (1.8) (kcal/mol)				Difference* (kcal/mol)
			MUE	RMSD	R2	τ	MUE	RMSD	R2	τ	MUE	RMSD
Thrombin	11	16	0.76	0.93	0.17	0.21	0.46	0.62	0.50	0.54	−0.30	−0.31
Tyk2	16	24	0.75	0.93	0.48	0.54	1.07	1.27	0.24	0.26	0.32	0.34
Jnk1	21	31	0.78	1.00	0.35	0.44	1.07	1.45	0.05	0.23	0.29	0.45
CDK2	16	25	0.91	1.11	0.15	0.30	0.97	1.13	0.35	0.46	0.06	0.02
PTP1B	23	49	0.89	1.22	0.43	0.55	1.06	1.40	0.35	0.51	0.17	0.18
BACE	36	58	0.84	1.03	0.37	0.36	1.20	1.47	0.27	0.31	0.36	0.44
MCL1	42	71	1.16	1.41	0.26	0.35	1.52	1.83	0.16	0.28	0.36	0.42
P38a	34	56	0.80	1.03	0.62	0.60	1.20	1.56	0.31	0.39	0.40	0.53
Overall	199	330	0.90	1.14	0.36	0.44	1.17	1.50	0.23	0.34	0.27	0.36

^*The difference is calculated as AMBER MUE or RMSD minus Schrodinger MUE or RMSD.

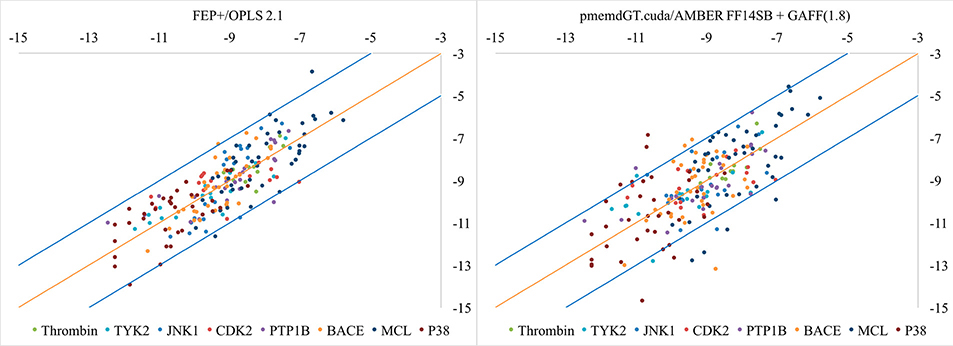
With the cycle-closure ΔΔG values, we obtained the ΔG values following the procedure of Wang, et al.. In short, in this procedure all of the ligands’ experimental values were used as a reference, and the sum of the predicted ΔG values was set to be equal to the sum of the experimental ΔG values. Though this way of calculating the offset can artificially improve the overall results, we adopted this procedure in order to better compare with Wang, et al. The predicted ΔG values were plotted against experimental ΔG values in Figure 2. We can see AMBER performs worse than FEP+. Out of the 199 ligands, 5 ligands (2.5%) for Schrödinger and 18 ligands (9.0%) for AMBER are more than 2kcal/mol off from experiment. The R² and Kendall’s tau coefficient are listed in Table 2. Figure 3 shows the individual plots of predicted versus experimental ΔG values for each of the 8 systems for both FEP+ and AMBER TI.

Figure 2.

Correlation between predicted binding free energies and experimental data for the eight systems.

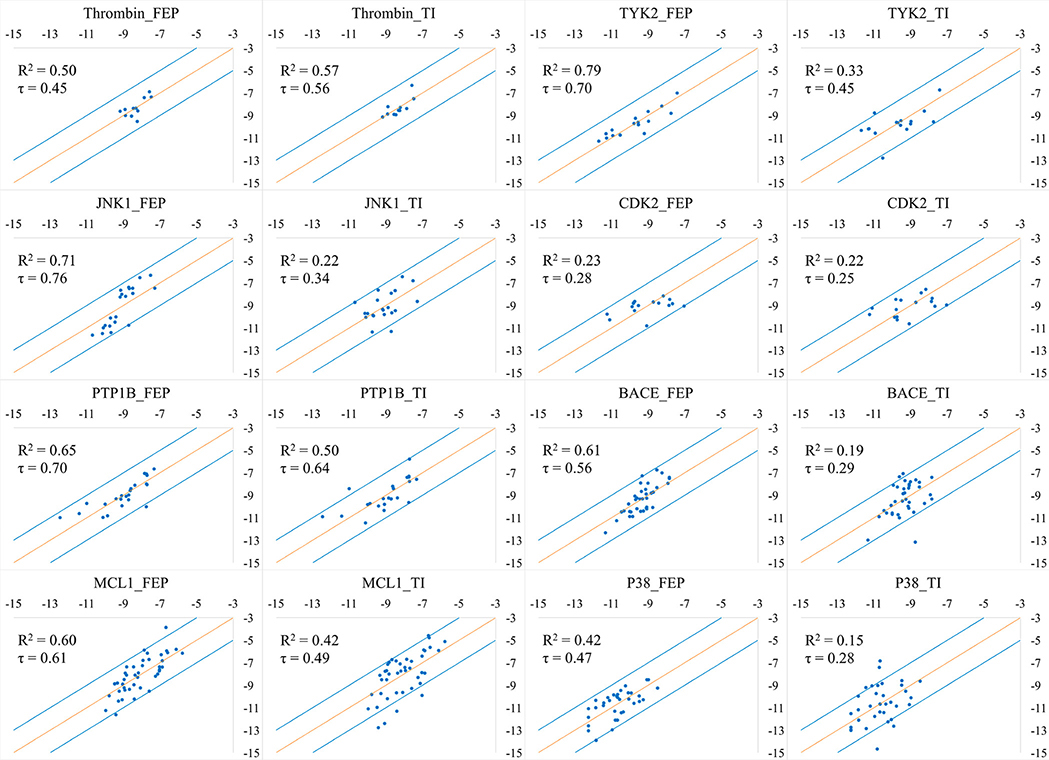
Table 2.

R2 and Kendall's tau coefficient for the correlation between predicted binding free energies and experimental data for the eight systems; τ represents the Kendall's tau coefficient.

System	# of ligands	# of perturbations	FEP+/OPLS 2.1 (kcal/mol)		AMBER GPU-TI/AMBER FF14SB + GAFF (1.8) (kcal/mol)
			R2	τ	R2	τ
Thrombin	11	16	0.50	0.45	0.57	0.56
Tyk2	16	24	0.79	0.70	0.33	0.45
Jnk1	21	31	0.71	0.76	0.22	0.34
CDK2	16	25	0.23	0.28	0.22	0.25
PTP1B	23	49	0.65	0.70	0.50	0.64
BACE	36	58	0.61	0.56	0.19	0.29
MCL1	42	71	0.60	0.61	0.42	0.49
P38a	34	56	0.42	0.47	0.15	0.28
Overall	199	330	0.66	0.62	0.44	0.48

Figure 3:

Correlation between the predicted binding free energies and experimental data for the eight systems studied herein. X axis: Experimental ΔG (kcal/mol); Y axis: Predicted ΔG (kcal/mol). τ is the Kendall’s tau coefficient.

3.2. Uncertainty estimate

To estimate the uncertainty in the calculations, we randomly selected 2 perturbations from each of the 8 systems and repeated the calculations described in section 2.2.1 twice. From Table 3, we can see most of the perturbations have standard deviations of less than 0.5 kcal/mol, except 4 of the perturbations. The overall standard deviation is 0.33 kcal/mol.

Table 3.

Estimate of the uncertainty of the calculations.

System	Ligand 1	Ligand 2	Run_1 (kcal/mol)	Run_2 (kcal/mol)	Run_3 (kcal/mol)	Average (kcal/mol)	Standard Deviation (kcal/mol)
Thrombin	1d	1c	−0.20	−0.15	−0.15	−0.17	0.03
	6e	6b	0.60	0.75	0.75	0.70	0.09
TYK2	ejm 31	ejm 46	−0.75	−0.85	−0.65	−0.75	0.10
	jmc 28	jmc 30	−2.00	−2.00	−1.90	−1.97	0.06
JNK1	18626–1	18624–1	1.50	0.95	1.05	1.17	0.29
	18659–1	18634–1	−0.95	−1.10	−0.35	−0.80	0.40
CDK2	22	lhlr	−0.55	−0.90	−0.70	−0.72	0.18
	1oiy	1h1q	1.65	1.70	2.85	2.07	0.68
PTP1B	23466	23475	−1.50	−1.60	−2.65	−1.92	0.64
	20670(2qbs)	23330(2qbq)	−1.65	−1.40	−1.85	−1.63	0.23
BACE	CAT-13a	CAT-17g	1.95	1.10	1.65	1.57	0.43
	CAT-4p	CAT-13k	−1.45	−1.20	−0.85	−1.17	0.30
MCL1	26	57	−0.85	−1.05	−1.00	−0.97	0.10
	68	45	−0.75	−0.70	−0.85	−0.77	0.08
P38	p38a_2aa	p38a_2bb	−1.35	−0.20	0.65	−0.30	1.00
	p38a_3fly	p38a 3fmh	0.00	−0.35	0.85	0.17	0.62
Overall							0.33

3.3. The “problematic cases”

As alluded to in section 2.2.1, for some perturbations, multiple runs at λ=0.5 had to be run in order to obtain a stable starting structure; for example, the ligand significantly moved in the binding pocket or the conformation of the protein changed. In order to understand the origin of this problem better, we visually checked the initial structures and the structures after minimization, and found that there were a few cases that had close contacts in the initial structure, but after minimization, the structures had improved. No clashes between the ligand and the binding site of the protein were observed after minimization. We next hypothesized that our heating protocol was too fast, which caused the observed structural issues. Hence, we repeated the “problematic cases” with a more rigorous minimization, heating and equilibration procedure. Five steps of minimization were performed to remove close contacts. The first step minimized the water molecules and the counter ions, with the protein restrained. The second, third and fourth step restrained the heavy atoms, backbone heavy atoms, backbone carbon and oxygen atoms of the protein, while the last step minimized the entire system. Each minimization step consisted of 20000 cycles of minimization using the steepest descent method. Afterwards the system was heated from 0 K to 300 K gradually over 1 ns with a coupling restraint of 5 kcal/(mol*Ų) on the solute, followed by equilibration at 300 K using the NPT ensemble for 200 ps with the same restraint. Then another 200 ps of NPT equilibration with a weaker restraint (2 kcal/(mol*Ų)) was performed. Finally the restraint was released and the system was equilibrated using NPT conditions for 600 ps. With these settings, the simulations successfully finished and the structures appeared fine after visual inspection. With the equilibrated structure, 12 λ windows were used for data collection with similar settings except: 1) the initial velocity was taken from the equilibrated structure as well as the coordinates; 2) the two end windows (0.00922 and 0.99078) used the velocity and coordinates from the equilibrated structure of the neighboring window (0. 04794 and 0. 95206). A few other differences between these new simulations and the former simulations include: 1) parmchk2 was used to generate the missing bond/angle/dihedral parameters for the ligands; 2) 22 and 12 Å was used as the minimum distance between the edge of the solvated cell and the ligand and protein/ligand systems respectively; 3) the protein/ligand system was thermalized more gradually and more steps of equilibration were used; 4) the Langevin thermostat was used with a collision frequency of 2 ps⁻¹ for all the TI simulations; 5) the CPU version of the AMBER 18 package was used instead of the AMBER 14 package for the TI simulations under NPT conditions. The overall MUE and RMSD for these perturbations are about the same: 1.61 kcal/mol and 2.09 kcal/mol for the new protocol versus 1.52 kcal/mol and 1.93 kcal/mol for the former protocol. Even so, some of the individual changes were significant, but given the differing box sizes, thermalization protocols, thermostats, etc. this wasn’t particularly surprising. Nonetheless, the average performance is relatively insensitive to the protocol employed. These data are summarized in the spreadsheet provided in the SI.

3.4. The 3-step protocol

A recent publication highlighted differences between the one-step protocol and a 3-step protocol when employing AMBER TI calculations.⁶⁶ In order to explore the impact of using one protocol over the other we performed 3-step calculations for one of the systems, i.e. the JNK1 system. As discussed above, the 3-step protocol consists of disappearing the charge, a vdW change and a charge reappearance step. For each step, the same minimization, heating and equilibration was performed at λ=0.5 as described in section 3.3. The equilibrated structure and velocities were used for the 12λ window TI calculation. The remaining settings for the TI calculations were the same as in section 2.2.1. We found that the MUE and RMSD is nearly the same as the one step protocol: 1.11 versus 1.07 kcal/mol, 1.43 versus 1.45 kcal/mol, respectively. This suggests that although there are differences between the two protocols that are worthy of in-depth exploration, the overall performance using either protocol is about the same, using the current code base and force fields. These data are summarized in SI spread sheet “FEP_vs_GTI-dG-SI”.

3.5. Discussion

In the SI (see Trend.xlsx) we summarize all of the 330 perturbations. Overall, we find that AMBER performs reasonably well for perturbations between halogens and H, CH₃ or CH₂CH₃: 44 of 49 perturbations have errors less than 2 kcal/mol, 34 of which have an error less than 1 kcal/mol. Perturbations involving large van der Waals radii changes, like Br to H or I to H, tend to have larger errors. We further analyzed the perturbations based on the “size” of the perturbation; whether there is ring appearance/disappearance or whether there is a ring type change (for example, pyridine to benzene). We classified perturbations that involved 3 heavy atoms changing or more as “big change” perturbations, and the others as “small change” perturbations. AMBER performs well for “big change” as well as “small change” perturbations: 151 of the 194 “big change” perturbations (~80%) have errors less than 2 kcal/mol, 99 of which have errors less than 1 kcal/mol; 107 of the 136 “small change” perturbations have errors less than 2 kcal/mol, 99 of which have errors less than 1 kcal/mol. Compared to “big change” perturbations, a larger percentage of “small change” perturbations have errors less than 1 kcal/mol: 69% for “small change” vs 51% for “big change” perturbations. Moreover, ring disappearance/appearance and ring type changes are also often seen in perturbation studies and they’re present in this data set as well. From our analysis, we find that AMBER performs well for both: 54 of 68 ring disappearance/appearance perturbations have errors less than 2 kcal/mol, 35 of which have an error less than 1 kcal/mol; 52 of 78 ring type change perturbations have errors less than 2 kcal/mol, 29 of which have an error less than 1 kcal/mol. While it would have been helpful to find systematic issues within certain classes of perturbations when using the AMBER class of force fields, in order to help guide force field improvement efforts, we found this wasn’t the case in the present data set.

4. Conclusions

We repeated the relative binding free energy calculations on the data set described in previous work.¹ Comparing to the Schrödinger FEP/OPLS 2.1 force field, GPU TI with AMBER FF14SB and the GAFF (1.8) force field performs reasonably well on this data set, with errors above those seen using the FEP/OPLS 2.1 force field. For the 330 perturbations, AMBER has MUE and RMSDs of 1.17 kcal/mol and 1.50 kcal/mol, which is a few tenths of kcal/mol larger than the reported values (0.90 kcal/mol and 1.14 kcal/mol).¹ For the 199 ligands, most of the binding free energy values are within 2 kcal/mol, except for 18 ligands (versus 5 reported previously¹). Interestingly, a null model, which assumes all the ΔΔG values are 0 kcal/mol, gives similar results (see SI Figure 1): 8 ligands are not within 2 kcal/mol. This is due to the small range of the experimental ΔG values: the widest range of ΔG values is 5.13 kcal/mol. To better demonstrate and test free energy approaches, data sets with larger experimental ΔG ranges should be explored. Future work will also explore the use of replica exchange and other features within AMBER to enhance the sampling (both in λ-space and orthogonal degrees of freedom). Along with technical advances we will also explore the capabilities of the next generation GAFF2 and protein force fields. Finally, test procedures for creating benchmark quality results with meaningful error estimates that can be used as a baseline for other comparisons will be explored.