An Opponent Dual-Detector Spectral Drive Model of Emmetropization

Abstract

In post-natal developing eyes a feedback mechanism uses optical cues to regulate axial growth so as to achieve good focus, a process termed emmetropization. However, the optical cues that the feedback mechanism uses have remained unclear. Here we present evidence that a primary visual cue may be the detection of different image statistics by the short-wavelength sensitive (SWS) and long-wavelength sensitive (LWS) cone photoreceptors, caused by longitudinal chromatic aberration (LCA). We use as a model system the northern tree shrew Tupaia belangeri, diurnal cone-dominated dichromatic mammals closely related to primates. We present an optical model in which the SWS and LWS photoreceptors each represent an image at different levels of defocus and different spectral lighting conditions. The model posits that an imbalance between SWS and LWS image statistics directs eye growth towards the point at which these image statistics are in balance. Under spectrally broadband (“white”) lighting, the focus of the eye is driven to a target point approximately in the middle of the visible spectrum, which is emmetropia. Calculations suggest that the SWS cone array, despite the sparse number of SWS cones, can plausibly detect the wavelength-dependent differences in defocus and guide refractive development. The model is consistent with the effects of various narrow-band illuminants on emmetropization in tree shrews. Simulations suggest that common artificial light spectra do not interfere with emmetropization. Simulations also suggest that multi-spectral multi-focal lenses, where the different optical zones of a multifocal lens have different spectral filtering properties, could be an anti-myopia intervention.

Introduction.

It is now well established that a feedback mechanism operates in growing post-natal eyes that uses optical cues to regulate the eye’s axial elongation rate so as to achieve good focus by matching the location of the retina to the focal plane, a process termed emmetropization (Norton 1999, Troilo, Smith et al. 2019). The generally accepted hypothesis is that refractive error contains the cues that guide the mechanism (Schaeffel and Howland 1991). The target of the emmetropization mechanism is minimal defocus (actually, low hyperopia easily cleared with accommodation). Hyperopic defocus (retina closer to the cornea than the focal plane) creates retinal signals (a “drive”) that increases the axial elongation rate, moving the retina to where light is in focus. Myopic defocus (retina behind the focal plane) produces a drive to slow axial elongation so that the maturing optics move the focal plane to the retina (Norton 1999, Schaeffel and Feldkaemper 2015, Troilo, Smith et al. 2019). When the refractive state reaches the target, the drive to increase or decrease axial elongation is zero.

The emmetropization mechanism evolved and normally operates in broadband (“white”) light where all wavelengths are present across the visible spectrum (400 – 700 nm). In broadband light, many cues are present in a defocused image that potentially can provide the drive that generates retinal signals used to modulate axial elongation. For instance, in a defocused eye, image contrast on the retina is reduced. The retinal image produced by a sharp light-dark edge becomes a more gradual change from higher to lower illuminance across the retina. Other cues, such as high spatial frequencies, higher order-aberrations (astigmatism, coma, etc.) and other possible cues are also altered. The specific optical cues used by the emmetropization mechanism remain unclear, but all share the basic premise that the retina doesn’t specifically detect “defocus”; rather it detects changes in the “image statistics” (such as image contrast) across the retinal surface that are produced by defocus.

Another optical cue produced by defocused images involves longitudinal chromatic aberration (LCA). Vertebrate eyes have significant LCA: long wavelengths focus farther away from the cornea than do shorter wavelengths, typically on the order of 2 to 3 Diopters (D) across the visible range (Walls 1963, Mandelman and Sivak 1983). Therefore when longer wavelengths are in better relative focus than shorter wavelengths (an indication that the eye is longer than optimal), this could provide a signal that the eye is too long and generate retinal signals that restrain axial elongation. If shorter wavelengths are in better focus than long wavelengths, this could lead to retinal signals that increase axial elongation.

In a direct assessment to determine if LCA cues are important for emmetropization, chicks were exposed to simulations of the chromatic signals expected from hyperopic and myopic defocus, and it was found that the eyes could interpret these chromatic signals appropriately (Rucker and Wallman 2009). Another way to assess if LCA provides important cues for the emmetropization mechanism is to place young animals in an environment where there is no LCA by housing them in narrow band illumination, so that it is impossible to compare image statistics at different wavelengths. If LCA cues are important, removing them should impair the ability of the emmetropization mechanism to function. While there is a high degree of variability in the results of these studies by species and the specific wavelengths used, the evidence is overwhelming that emmetropization is disrupted in narrow bandwidth light in tree shrews (Gawne, Siegwart et al. 2017, Gawne, Ward et al. 2017, Gawne, Ward et al. 2018), non-human primates (Smith, Hung et al. 2015), chicks (Rucker, Britton et al. 2015, Wang, Schaeffel et al. 2018, Rucker 2019), guinea pigs (Liu, Qian et al. 2011, Qian, Liu et al. 2013) and mice (Strickland, Landis et al. 2020). These studies suggest that the LCA cues present in broadband lighting conditions are not only important for normal operation of the emmetropization mechanism, but also are essential for it to function properly. When LCA cues are removed, the emmetropization mechanism is unable to utilize other, remaining, defocus-related cues to maintain or achieve emmetropia.

Tree shrews, like most mammals, are dichromats. Their retina contains a cone photoreceptor type sensitive to shorter wavelengths (SWS – encoded by the OPN1SW gene, peak sensitivity in tree shrews 428 nm) and another cone type sensitive to longer wavelengths (LWS – encoded by the OPN1LW gene, peak sensitivity 555 nm) (Fig. 1) (Petry and Harosi 1990, Hunt, Carvalho et al. 2009, Melin, Wells et al. 2016). In photopic lighting, rods should saturate, and combined with the low spatial acuity of the rod system, it seems unlikely that the sparse rods in tree shrews contribute significantly to emmetropization. Therefore, we assume that the only information about focus that the emmetropization mechanism can access is the spatial pattern of activation across the retina as detected by these two classes of cones. In addition, the only information about LCA that the emmetropization system can access is the difference in the activation patterns of these two classes of cones.

Fig. 1.

A, Normalized cone absorbance in our animal model, tree shrews (data from Petry and Harosi, 1990). “Net” SWS absorbance is adjusted for the optical filtering properties of the ocular tissues. The SWS cones have an absorbance peak at the blue end of the spectrum (peak, 428 nm) and are insensitive to longer wavelengths. The LWS cones have a broader absorption spectrum with a peak at 555 nm. B, Normalized intensity profiles of narrow-band red and narrow-band blue LEDs, of the type that have been commonly used in experiments on tree shrews. The red LEDs will essentially stimulate only the LWS cones, but the blue LEDs will stimulate both SWS and LWS cones because the absorbance profile of the LWS cones extends into the blue end of the spectrum.

We propose that the two arrays of cone photoreceptors independently detect “image sharpness” and have opponent effects on axial growth of the eye. If the SWS cone array detects sharper images on the retina than the LWS system, post-receptoral retinal circuitry then signals for increased axial growth (a positive drive). If the LWS cone array detects relatively sharper images on the retina, the post-receptoral circuitry then signals for slower axial growth (a negative drive). We propose a model of how the retinal image, as sensed separately by the SWS and LWS cones, varies as a function of both defocus and the spectrum of ambient light. We determine if the difference between the SWS and LWS images can plausibly distinguish between hyperopic and myopic defocus over a physiological range of values, given the known spacing of the SWS and LWS cone arrays in tree shrews and also make predictions about how changes in the shape of the spectrum of ambient light could affect emmetropization.

Methods.

The development and implementation of the model involved several steps. For a given spectrum of light, and a given position of the retina relative to the optics:

1. Calculate the size of the circular disk of light (“blur disk”) created by a single point at optical infinity, for all wavelengths in 10 nm steps.

2. At each wavelength, weight the intensities of the blur disks by the intensity of the light, the area of the blur disks, and the absorbance of both the SWS and LWS cones.

3. Combine all of the blur disks to produce a separate “point spread function” for the SWS and the LWS cones.

4. Use the point spread functions to calculate the effective spatial luminance profile on the retina, in response to a black/white edge, for the SWS and for the LWS cones.

5. Use these luminance profiles to calculate a single number, a spectral drive, which reflects the difference in image sharpness between the SWS and LWS cones and the direction of the effect on axial growth (increase or decrease).

   We then applied the model in several different lighting conditions.

6. Use the point spread functions to calculate the effective spatial luminance profiles on the retina, in response to a naturalistic grayscale image, for the SWS and LWS cones.

7. In addition, use the results of (6) to calculate the mean spatial frequency distribution of the responses of the SWS and LWS cones to an entire naturalistic grayscale image.

Because the emmetropization mechanism acts by changing the axial length of the eye (and thereby the position of the retina) and does not appear to alter the optics of the eye (Norton 1999, Wallman and Winawer 2004, Smith, Hung et al. 2014, Schaeffel and Feldkaemper 2015, Hou, Norton et al. 2018), we chose in our model to hold the optics fixed and simulate different amounts of defocus (blur conditions) by changing the location of the retina with respect to the optimal focus point of a 550 nm light. Retinal positions closer to the posterior principal plane simulated hyperopic defocus; locations farther away from the posterior principal plane simulated myopic defocus.

In our model, we ignored the effects of diffraction and higher-order monochromatic aberrations. All simulations were performed using custom routines written in Matlab version R2017b (The MathWorks, Natick, MA USA).

(1). Calculate the size of the circular disk of light (“blur disk”) created by a single point at optical infinity, for all wavelengths in 10 nm steps.

As illustrated in Fig. 2A, we assumed that the effective posterior focal length of the tree shrew eye is 5.81 mm (5,810 μm), with a pupil diameter of 3.0 mm (3,000 μm) (Norton and McBrien 1992). For simplicity, we used a single lens to represent the optics of the cornea and crystalline lens of the eye and did not include any accommodation. We assumed that all source objects are at optical infinity and that light of wavelength 550 nm at optical infinity is in perfect focus at 5,810 μm behind the posterior principal plane.

Fig.2.

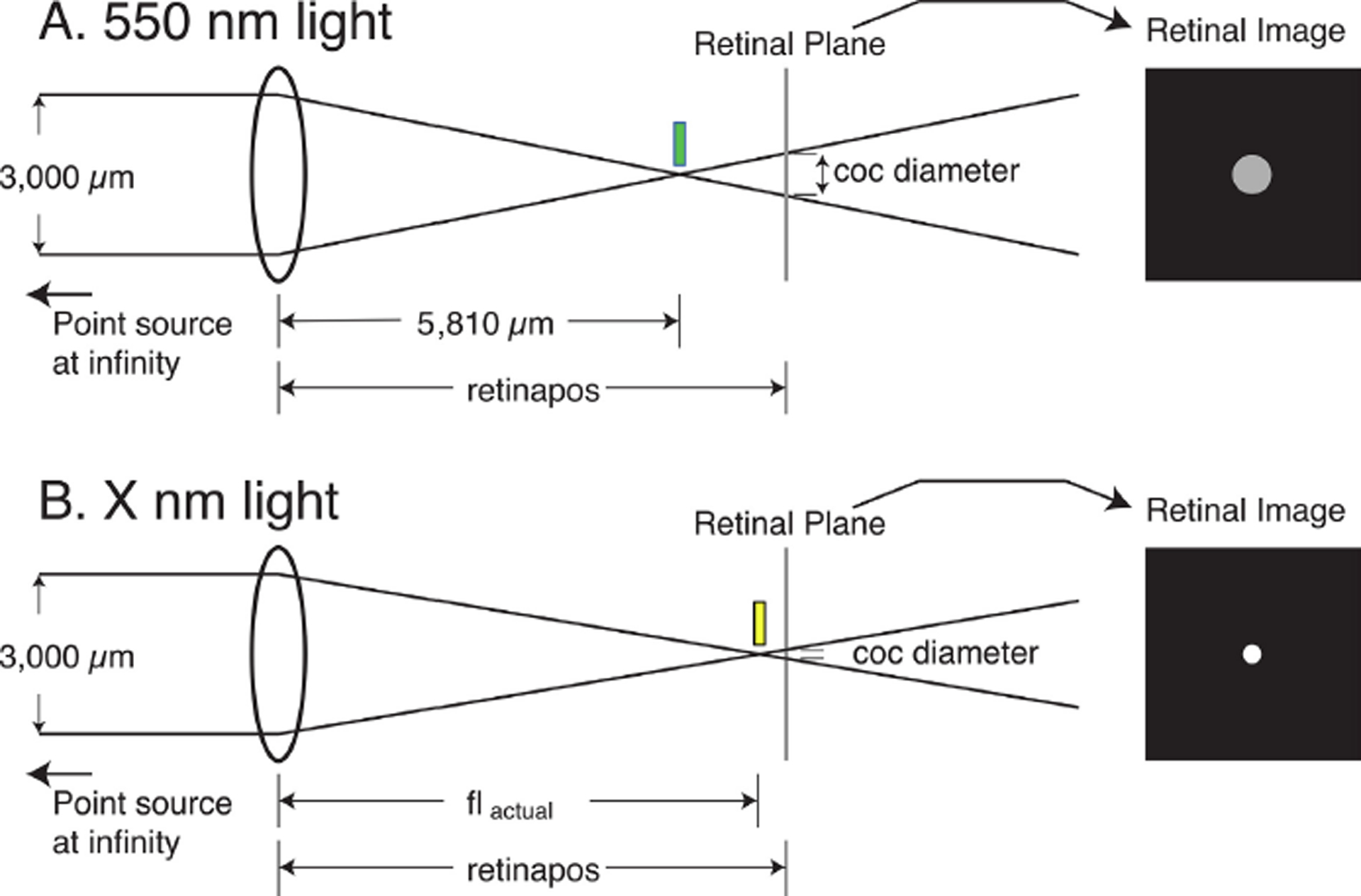
Schematic model of the calculation of the retinal circle of confusion (coc) produced by a point source at optical infinity for two different wavelengths in an eye with a fixed retinal location. The pupil diameter is assumed to be 3,000 μm. A, light of 550 nm is focused 5,810 μm behind the posterior principal plane (green bar). In this example, the retinal plane is behind the point of optimal focus (myopic defocus) so the retinal image is not a point, but an extended disk whose diameter is the circle of confusion (coc). B, the retina is located at the same position as in A, but the light is of a longer wavelength. As a result of LCA, the focal plane is farther from the posterior principal plane, resulting in a different-sized coc. In our model, this process was repeated for multiple wavelengths across the entire visible spectrum for a series of retinal positions from hyperopia to myopia.

We also assumed that tree shrew eyes have 2.77 Diopters (D) of LCA between 428 and 555 nm (Gawne, Siegwart et al. 2017) and that the point of best focus changes linearly with wavelength. Although not strictly true (Sajdak, Salmon et al. 2019), the curves of LCA versus wavelength are smoothly monotonic across the range of visible light (Mandelman and Sivak 1983), so this seems a reasonable simplifying assumption. Thus, the point of best focus shifts away from the posterior principal plane by 8.7 μm (approximately 0.26 D in a tree shrew eye) for every 10 nm increase in the wavelength of light.

$${\text{fl}}_{\text{actual}}=5810+\left(\text{lambda-550}\right)*0.87$$

Where fl_actual is the actual focal length at a wavelength of lambda nm.

To model the image of a light-dark edge on the retina, we first needed to calculate, at each retinal position, the effects on image focus of changing the wavelength across the spectrum. Fig. 2A and 2B illustrate that when the optical system images a point source on the retina, most wavelengths will not be in focus. Each defocused wavelength will produce a disk of relatively uniform intensity on the retina, that is bounded by the “circle of confusion” or “coc” (Strasburger, Bach et al. 2018). Using similar triangles, the size of the circle of confusion of the image from a point source of a given wavelength at optical infinity in an eye with a particular retinal location will be given as:

$$\text{coc}\text{=}\text{abs}\left(\left(\left({\text{fl}}_{\text{actual}}-\text{retinapos}\right)/{\text{fl}}_{\text{actual}}\right)*3000\right);$$

where coc is the diameter of the circle of confusion, and retinapos is the position of the retina in nm relative to the optics. The pupil diameter is assumed to be 3,000 μm (Norton, Wu et al. 2003).

(2). At each wavelength, weight the intensities of the blur disks by the intensity of the light, the area of the blur disks, and the absorbance of both the SWS and LWS cones.

We assumed that, at each wavelength, the coc defines a circular “blur disc” of uniform intensity (Fig. 3) (Strasburger, Bach et al. 2018). The intensity within the blur disc scales with the reciprocal of the area of the blur disc because the same amount of light is spread across a disc of larger, or smaller, area. We forced a minimal coc diameter of 2 μm to avoid infinities in the calculations.

Fig. 3.

Schematic of how the coc at each wavelength was converted to a blur-disc as detected by SWS and LWS cones. A, For a series of wavelengths in 10 nm increments from 380 to 780 nm, the diameter of the circle of confusion was calculated as illustrated in Fig. 2 (only three example wavelengths are shown here for clarity). Then the intensity of the light within each blur disc was calculated as the normalized photon count of the light spectrum at that wavelength, divided by the area of the blur disk. B, At each wavelength, the value of absorbance was determined separately for the SWS and the LWS cones, and this was used to scale the effective intensity (photon catch) of the light within the blur disks. The result was two separate series of blur disks, one for the SWS cones and one for the LWS cones.

Fig. 3A illustrates schematically how we converted the calculated intensity of the blur discs, at different wavelengths, individually for the SWS and the LWS cones. As photoreceptors are activated by photons and not the total amount of physical energy in light, we first converted the power spectrum (in μW/cm²/nm) to normalized photon counts by multiplying by the wavelength. In this regime, photon catch should be nearly linear with photoreceptor outer segment absorbance. We then calculated the diameter of the coc as illustrated schematically in Fig.2. At each of the three example wavelengths shown in the figure, we created a matrix of dimension 101 × 101 units, where each unit represented1 μm of distance across the retina. Each matrix was initialized to contain all zeros, representing no light. We then created a solid filled-in blur disc in the middle of each matrix with a diameter equal to the coc. The intensity within the blur disc was equal to the photon count at that wavelength, divided by the area of the circle. This provided the physical distribution and relative photon intensities across the retinal surface that was produced by the image of a point source at each of the three wavelengths.

The next step, illustrated in Fig. 3B was to calculate, for each blur disc, the spatial extent and effective relative intensity of light on the retina as sampled by the SWS and by the LWS cones at each of the three example wavelengths. To do this, the light intensity within each disc was weighted by the cone absorbance function at that wavelength to provide the spatial extent and effective relative intensity of light on the retina for the SWs and for the LWS cones. In our model, this was calculated in 10 nm steps for wavelengths from 380 to 780 nm.

(3). Combine all of the blur disks to produce a separate “point spread function” for the SWS and the LWS cones.

Fig. 4 illustrates how a series of blur discs (each produced at a different wavelength) were combined into a single “point spread function”. The point spread function is the effective pattern of illuminance across the surface of the retina, for a specific wavelength and retinal position, as sampled by either the SWS or LWS of cones. As any visual image can be decomposed into a large number of points, this means that these point spread functions can completely predict the pattern of activity of the SWS and LWS cone populations for any image. The point-spread functions can also be referred to as the 2D impulse responses, or the 2D kernels, of the optical system These two spatial patterns of activity - one for SWS and the other for LWS cones - are all that the neural retina has to operate on (at least as regards cone signals). They define the limits of the information that it is possible for subsequent retinal neurons to extract from an image.

Fig. 4.

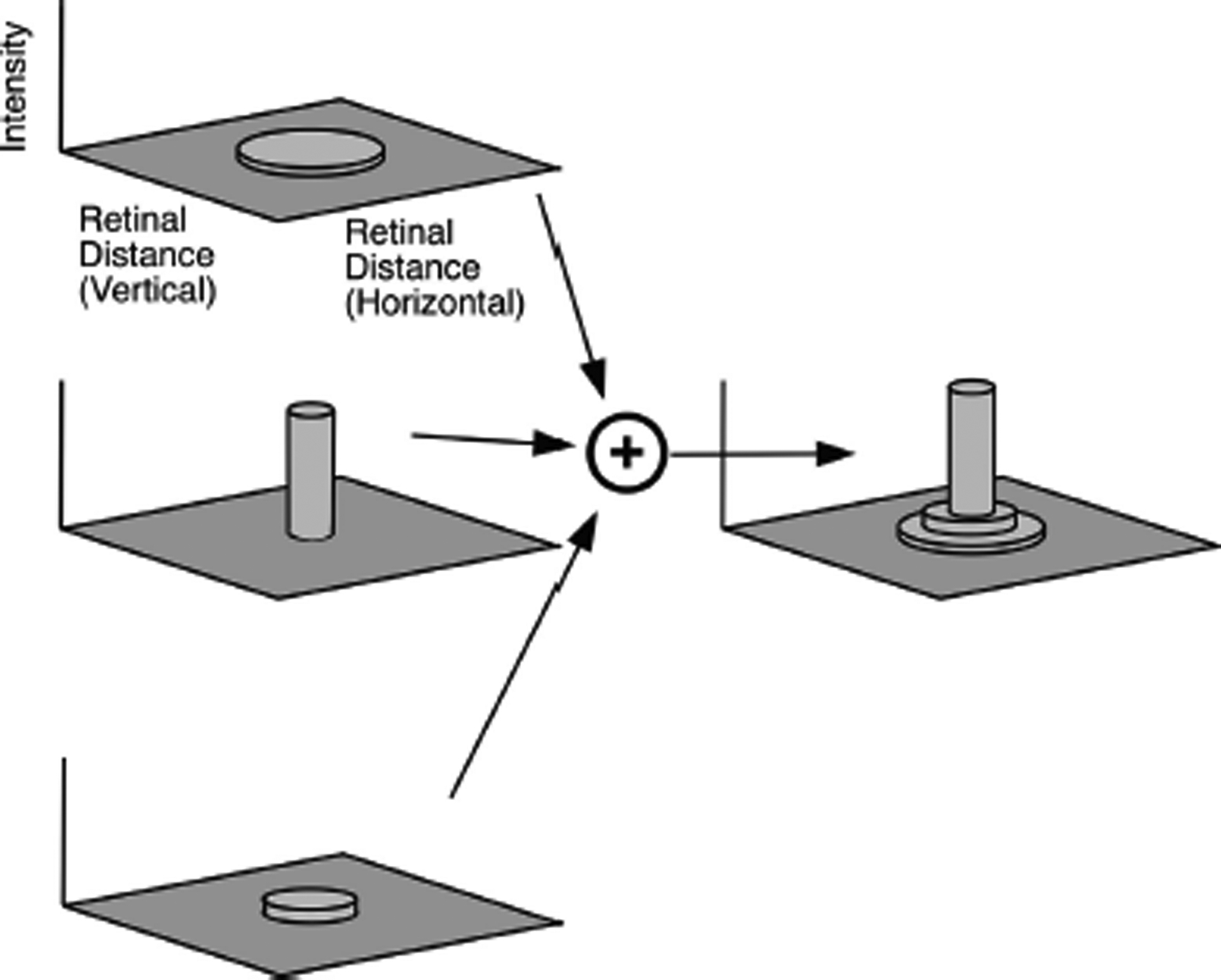
Schematic of how the blur discs for each wavelength are combined to form a single “point spread function.” The graphs to the left represent three blur discs as shown at the bottom of Fig. 3B, but in this case drawn as surface plots where the horizontal and vertical position across the retina in microns lie in the horizontal plane of the graph, and the height of the surface represents the effective intensity. These blur disks at all wavelengths are summed, and provide a composite point spread function as illustrated on the right. Because this simplified schematic uses only three wavelengths and three blur disks, the composite point spread function has a stepped appearance. Summing over all wavelengths would produce a smooth point spread function for the SWS cones and another for the LWS cones. These two point spread functions completely characterize how the SWS and LWS cones respond to any visual pattern with this spectrum of light and retinal location.

(4). Use the point spread functions to calculate the effective spatial luminance profile on the retina, in response to a black/white edge, for the SWS and for the LWS cones.

Natural images are full of extended edges, and unlike isolated points these extended edges can be robustly detected by retinal neurons even when blurred (Risner, Amthor et al. 2010). We do not claim that emmetropization is specifically driven by extended edges, but use this simplified visual stimulus to gain insight into how different levels of hyperopic and myopic blur could be translated into different activation patterns of the SWS and LWS cone arrays. The process is schematized in Fig. 5. We convolved a cone point spread function with a luminance edge to create the edge spread function. We then extracted the effective luminance profile across the retinal surface normal to the edge as detected by this cone class.

Fig. 5.

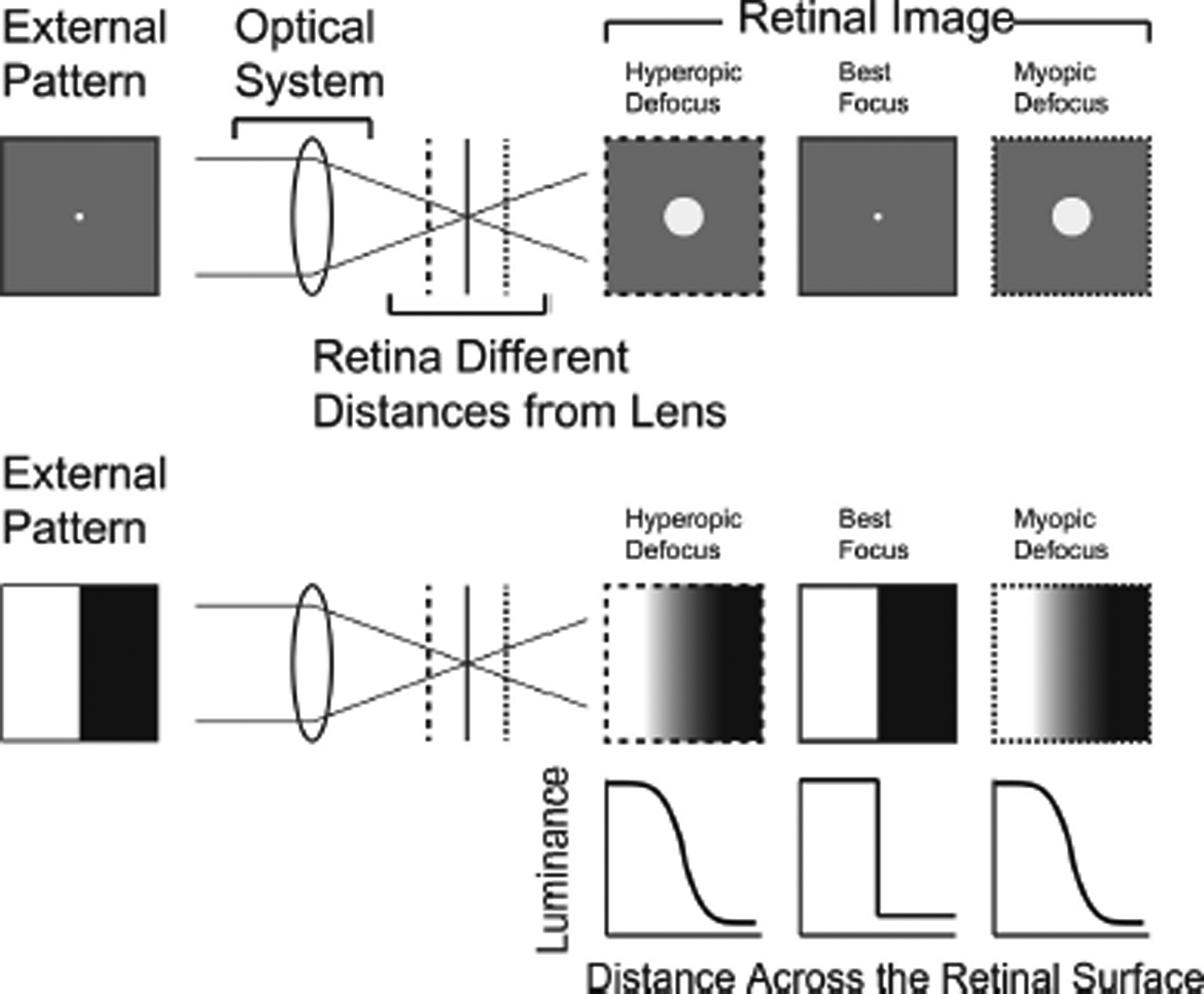
Example of going from the response of the optical system to a point source, to the response of the optical system to an extended edge. Top: The external pattern is a white dot on a gray background. The retina is located at different distances from the equivalent lens. It is the distance of the retina from the optics that is key: emmetropization works by changing the elongation of the eye, altering this distance. To the right we can see the different retinal images created by the retina being different distances from the lens. Bottom: in this example, the external pattern is a sharp edge between a dark and a light region. The retinal images created by this pattern, which are the edge spread functions, are shown on the right. These can be calculated as the convolution of the point spread function with the external image. Below the retinal images, are the profiles of illuminance across the retina as a function of blur, measured at right angles to the edge in the external pattern.

(5). Use these luminance profiles to calculate a single number, a spectral drive, which reflects the difference in image sharpness between the SWS and LWS cones and the direction of the effect length (increase or decrease).

We repeated this process separately for the SWS and LWS cones, and for a range of retinal positions from hyperopic to myopic (Fig.6). This provides a visual indication of how the SWS and LWS cones will respond to a light/dark edge when exposed to various amounts of hyperopic and myopic blur under a given illumination spectrum. We then defined a single number, the “spectral drive,” as the signed area difference between the SWS and LWS profiles to the right of the midline (Fig.6). We do not claim that the emmetropization system uses this exact metric to evaluate chromatic defocus cues. Most likely, chromatic defocus cues will be evaluated through some nonlinear combination of contrast across some range of spatial frequencies. It is also likely that emmetropization combines chromatic cues with others, such as monochromatic aberrations, temporal flicker, and absolute light levels. We only propose this metric as a crude first step to quantify the signal that the emmetropization mechanism extracts from chromatic cues to guide eye growth.

Fig.6.

Computation of the spectral drive. Top: at each position of the retina relative to the optics, we calculate the luminance profiles for a step edge (as illustrated in Fig.5) for both the SWS and LWS cones. We define the “spectral drive” as the area between these curves to the right of the midpoint as a signed quantification of the difference between the SWS and LWS responses to a step edge. When the spectral drive is positive, this is a signal that the eye is too short and needs to grow longer. When the spectral drive is negative, this is a signal that the eye is too long and should restrain its growth.

Importantly, here we normalized the blur profile for each cone type to span the range between 0 and 1. It is well established that cone photoreceptors can adapt to a wide range of light levels (Burkhardt 1994), and of course the post-receptoral retinal circuitry could also work to normalize the processing of these signals. Exactly how much the normalization of cone responses is or is not important for emmetropization is currently unknown, but using normalized responses seems a reasonable starting assumption.

We then applied this model to several different artificial ambient lighting spectra, including broad-spectrum “white” light, narrow band blue combined with narrow-band red, narrow-band red or narrow-band blue alone, limited-bandwidth green+blue, colony fluorescent light, the red+green+blue light from a computer screen, and a hypothetical multi-spectral multi-focal lens.

(6). Use the point spread functions to calculate the effective spatial luminance profiles on the retina, in response to a naturalistic grayscale image, for the SWS and LWS cones.

While natural images are dominated by lower spatial frequencies (Field 1987), it is certainly true that the real world consists of more than simple step edges. Therefore, we extended this model to natural images. We took a black and white image, and convolved it with the point spread functions for the SWS and LWS cones separately. This resulted in a model of the 2D spatial pattern of effective illuminance across the retina as sampled by the SWS and LWS cones. We normalized these images to have the same minimum and mean value across the entire image. We then took the radially averaged Fourier transform across these patterns, using the method derived from (Adams, Sincich et al. 2007), and plotted the direction-averaged power as a function of spatial frequency. We ignored the possible effect of different color objects in the environment, and assumed a purely black and white world. As most objects in the world are not brightly colored, and as the emmetropization system must average over a large number of image patches, this seems a reasonable approximation for this level of modeling.

(7). In addition, use the results of (6) to calculate the mean spatial frequency distribution of the responses of the SWS and LWS cones to an entire naturalistic grayscale image.

We note that, although the activity of the retina that is important for perception and for the visual guidance of behavior is driven by what is on the retina moment-by-moment, emmetropization averages over a considerable period of time (Zhu 2013). Primates will typically make on the order of three saccades per second, and for retinal locations not on or near the fovea (which is most of the retina), any given patch of the retina will receive on the order of 10,000 random samplings of the visual world per hour. Tree shrews do not make large saccades, but they do routinely make head movements with similar frequency as primates make saccades (unpublished observations), so the effect on retinal stimulation should be similar. Therefore, we can well approximate the effect of a complex naturalistic image on emmetropization, by averaging the image statistics across the entire image.

Results.

Broadband illuminant.

Fig. 7 illustrates the results of the model with a broadband (“white”) illuminant that had an equal number of photons per nm. Each panel in Fig.7A shows the illuminance profile of a sharp light-dark edge as a function of distance across the retina, orthogonal to the edge (see again Fig.5 and Fig.6). Blue lines are the normalized illuminance profiles as detected by the SWS cones. Red lines are the profiles for the LWS cones. Each panel shows the SWS and LWS luminance profiles (see again Fig.5) when the retina is located at a particular distance behind the posterior principal plane. The upper left panel (5670 μm) is an example when the retina is close to the posterior principle plane, a condition of hyperopic defocus. Subsequent panels from left to right and from row to row show the profiles at retinal positions farther from the posterior principle plane, first reducing the hyperopia, passing through emmetropia at 5810 μm, where 550 nm light is focused on the retina (Fig. 2) and then progressively more myopic. Each 20 μm step of retinal position between subplots represents approximately 0.6 D of optical power for a tree shrew.

Fig.7.

A. Effective illuminance profiles on the retina of a light-dark edge in broadband (white) light as detected by the SWS cone array (blue lines) and LWS cone array (red lines) when the retina is located at different distances from the posterior nodal point. The Y-axis is the (normalized) illuminance on the retina. The X-axis is the distance across the retina in micrometers. The edge has high intensity from location 0 to 50 and low intensity from location 50 to 100. A more sloped profile indicates the image is more blurred on the retina. A steeper profile indicates better focus. The circle denotes a balanced retinal location where the profile for the SWS and LWS cone arrays have nearly the same slope (and the curves largely superimpose). The subplot on the bottom row second from the right indicates the approximate retinal separation of the SWS cones across the surface of the retina (Sajdak, Salmon et al. 2019). B. Spectral drive as a function of retinal position (see Fig.6). Vertical dashed line represents the retinal position where the SWS and LWS cone arrays would experience essentially identical image statistics.

As the retinal position is moved away from the posterior principle plane, the shape of the illuminance profiles changes. At the most hyperopic retinal position (5670 μm), the SWS profile has a steeper slope than the LWS illuminance profile, indicating that the light-dark edge was in sharper focus for the SWS cones. As the retina moves away from the posterior principle plane the slope of the SWS illuminance profile becomes lower, indicating that the edge was more blurred as viewed by the SWS cone array. In contrast, at locations farther away from the posterior principle plane, the slope of the LWS illuminance profile becomes steeper. The sharpest SWS profile (at 5730 μm) is sharper than the sharpest LWS profile (at 5810μm) because the SWS cones have a relatively narrow bandwidth and the LWS cones have a much broader bandwidth (Fig. 1). The subplot on the bottom row, second from the right, has vertical bars representing the approximately 18 μm spacing of the SWS cones across the surface of the retina (Sajdak, Salmon et al. 2019). By inspection it is at least plausible that the difference in blur profiles between SWS and LWS cones could be resolved by the retina. Fig.7B illustrates the spectral drive (as schematized in Fig.6) as a function of retinal position.

Blue+ Red Illuminant.

Fig. 1B illustrates a spectrum consisting of two peaks, one at 464 nm (blue) and the other at 634 nm (red), with no intermediate wavelengths present. This spectrum spans a wide range of wavelengths, so it is not narrow band, but it is also not flat or continuous. Fig. 8 illustrates the SWS and LWS cone illuminance profiles calculated for this ambient illuminant. As in Fig. 7, the illuminance profiles change with retinal distance: at hyperopic positions (retina closer to the posterior principle plane) the SWS cones profile has a steeper slope than for the LWS cones. This gradually changes to a relatively steeper LWS profile as the retinal position in shifted to myopic defocus. In this illuminant there an extended zone where there is only a small difference between SWS and LWS profiles. At retinal positions of 5790 μm and 5810 μm, the profiles are nearly identical, so the magnitude of the signal to emmetropization should be small. However, the point at which there would be a significant signal to stop growing could be shifted by approximately 40 to 60 μm myopic compared to the result in broadband light, which would be on the order of 1.2 to 1.8 D myopic relative to the situation in broadband light. The exact target would depend on the system’s sensitivity to differences in SWS and LWS blur profiles: the overall magnitude of the spectral drive is reduced as well, so conceivably the emmetropization system might not be able to ‘home in’ on precisely the same point of zero spectral drive. The model’s prediction is qualitatively consistent with the results from a group of animals exposed to this illuminant (ARVO abstract Gawne et al., IOVS 5879, 2019) that developed −1.9 ± 0.5 (stderr) D of myopia compared with animals raised in broadband colony lighting.

Fig. 8.

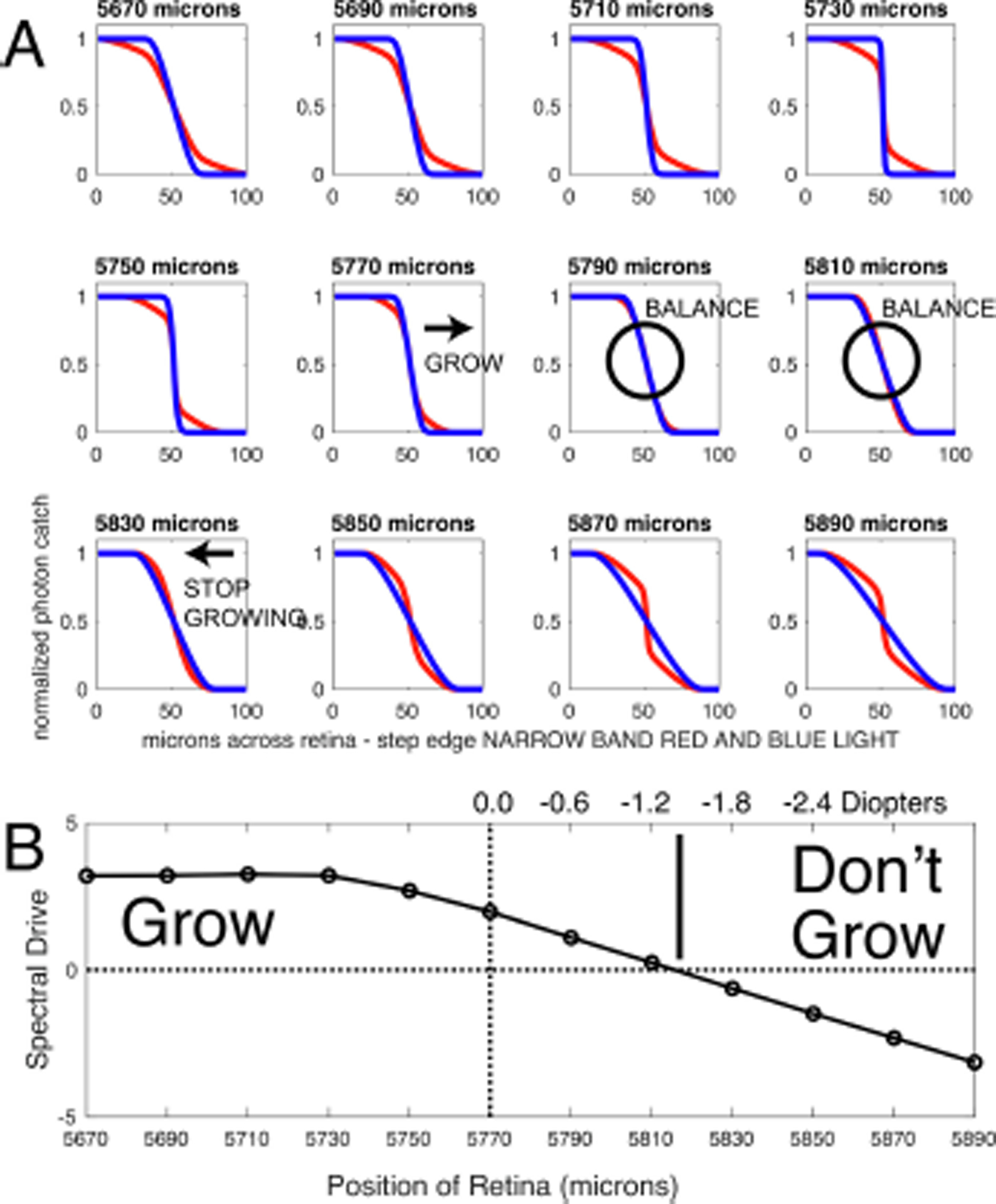
A. Results arranged as in Fig. 7, but with an illuminant consisting of narrow-band blue light and narrow-band red light. Note that, compared to the results in broad-band white light, the region of balance where the drive is near zero is enlarged and is shifted towards longer retina positions e.g. towards an elongated eye that would be myopic in white light. B. Spectral drive, arranged as in Fig.7B. The point of balance where the spectral drive is zero has been shifted to approximately −1.4 D myopic relative to the case in white light (vertical dashed line), although the drive function has also been overall reduced in magnitude as well.

Narrow band red light.

Fig.9A illustrates the spectral drive for narrow-band red light. This response to this illuminant assumes that the absence of blue light is interpreted by emmetropization as zero blue contrast. In this case the spectral drive would be strongly negative at all retinal positions, and emmetropization would be strongly biased towards hyperopia. This is consistent with the results of using narrow-band red light in tree shrews and non-human primates (Smith, Hung et al. 2015, Gawne, Ward et al. 2017).

Fig.9.

Examples of various illumination spectra and their corresponding spectral drive functions. A. Narrow band red light. B. Narrow band blue light. C. Narrow band green and narrow band blue light. D. Compact Fluorescent Light Bulb (CFL). E. Light from a RGB computer monitor set to all white. F. Multi-spectral multi-focal lens designs (see text).

Narrow band blue light.

Fig.9B illustrates the spectral drive for narrow-band blue light. Because blue light significantly excites both SWS and LWS cones, the blur profiles across the retinal surface would be identical for both cone classes, and the difference between the SWS and LWS profiles would therefore be zero at all retinal locations. This would result in the feedback error signal being forced to zero regardless of the degree of defocus, and emmetropization would drift in response to other factors, which seems to be the case in tree shrews. (Gawne, Ward et al. 2018).

Limited bandwidth light

Fig. 9C illustrates the spectral drive in response to limited bandwidth light, in this case a combination of narrow-band blue and narrow-band green light. There is a spectral drive function, it is essentially of the same form as in broad-band white light, the target is shifted slightly hyperopic but the magnitude of the drive is significantly reduced. It would be interesting to find out: what dominates in this situation, the small hyperopic shift or the reduction in overall gain? Interestingly, past a certain point, as the eye becomes too long, the magnitude of the drive function does not increase with increasing refractive error. This would suggest that, if the maximum of the drive function falls below some threshold value, emmetropization might slowly drift away from emmetropia as the integrated visual cues across a day are not quite sufficient to bring the eye to emmetropia.

Compact fluorescent light bulb.

Fig. 9D illustrates the spectral drive in response to a compact fluorescent bulb (CFL), with a spectrum similar to that used in normal colony lighting. Even though the spectrum consists of jagged peaks, the spectral drive function is smooth and virtually identical to the one in broad-spectrum light. This is consistent with many decades of experience with tree shrews under this illuminant; they emmetropize perfectly well.

Computer screen

Fig. 9E illustrates the spectral drive using as an illuminant the screen of an imac computer set to all white. The spectrum consists of three discrete peaks, but unlike the case in Fig. 9D, the spectral drive is again essentially identical to that found in broadband light.

Multi-focal multi-spectral lens

We were unable in our simulations to find any broad spectrum of light that would either significantly bias emmetropization towards hyperopia, or increase the magnitude of the drive. Fig. 9F is the result of a simulation with a multifocal lens, that has both plano and +2D zones. The plano zones are tinted so that they only pass 20% of the light below 500 nm. The +2D zones are tinted so that they only pass 20% of the light above 500 nm. The result in our model is a spectral drive significantly biased towards hyperopia, and also of substantially greater drive magnitude. In effect, this optical system has artificially increased the magnitude of LCA and biased it to target a slightly hyperopic state.

“Real-World” Illustration.

Although the visual world contains many abrupt luminance edges, it also contains complex luminance changes. Fig. 10 shows the result of calculations for how a black and white natural image (A) would be sampled by the SWS (left) and LWS cones (right) at a hyperopic retinal location (5730 μm), an intermediate (5770 μm), and a myopic (5810 μm) position. At these extreme positions, the images, as viewed by the SWS and LWS cones clearly differ. However, if the emmetropization mechanism in tree shrews is comparing the spatial image statistics as sampled by the SWS and LWS cone arrays, could it detect these differences and generate a drive to guide axial elongation to the middle position?

Fig.10.

Illustration of a natural grayscale image (top), and how, in tree shrew eyes, it would be blurred at differing retinal locations (inset numbers) as sampled the SWS (left panels) and LWS (right panels).

Can the sparse SWS cones detect defocus?

Tree shrews have with a nominal visual behavioral acuity of approximately 2 to 3 cycles/degree (Petry, Fox et al. 1984) presumably mediated by the array of LWS cones. The LWS cones have a typical inter-cone separation of approximately 6 μm across the retina, but the SWS cones are sparser, and have a relatively constant SWS to SWS cone spacing of 18 μm (Sajdak, Salmon et al. 2019). Thus, the limiting factor for resolving differential image sharpness at long vs. short wavelengths, will be the spacing of the SWS cones. This spacing would give a spatial Nyquist frequency for the SWS array of approximately 3 cycles/degree. As also seen visually in Fig.7 bottom row second panel from the right, the SWS cone array has a spatial resolution that can plausibly differentiate physiologically relevant levels of blur.

Fig. 11 shows the normalized power spectrum as a function of spatial frequency for the image in Fig. 10 for different retinal positions, and as sampled by the SWS and LWS cone arrays. In principal, myopic and hyperopic defocus could be determined by examining the relative power in the spatial frequency range of as low as one cycle per degree and higher - which is well within the visual acuity of tree shrews and even more within the range set by the SWS cones spacing. Note also that these differences are not subtle, at least not in relative terms: the relative activity in one set of cones could easily be several times higher than those in the other, in at least some frequency bands, suggesting that subsequent retinal circuitry could readily distinguish the differences.

Fig. 11.

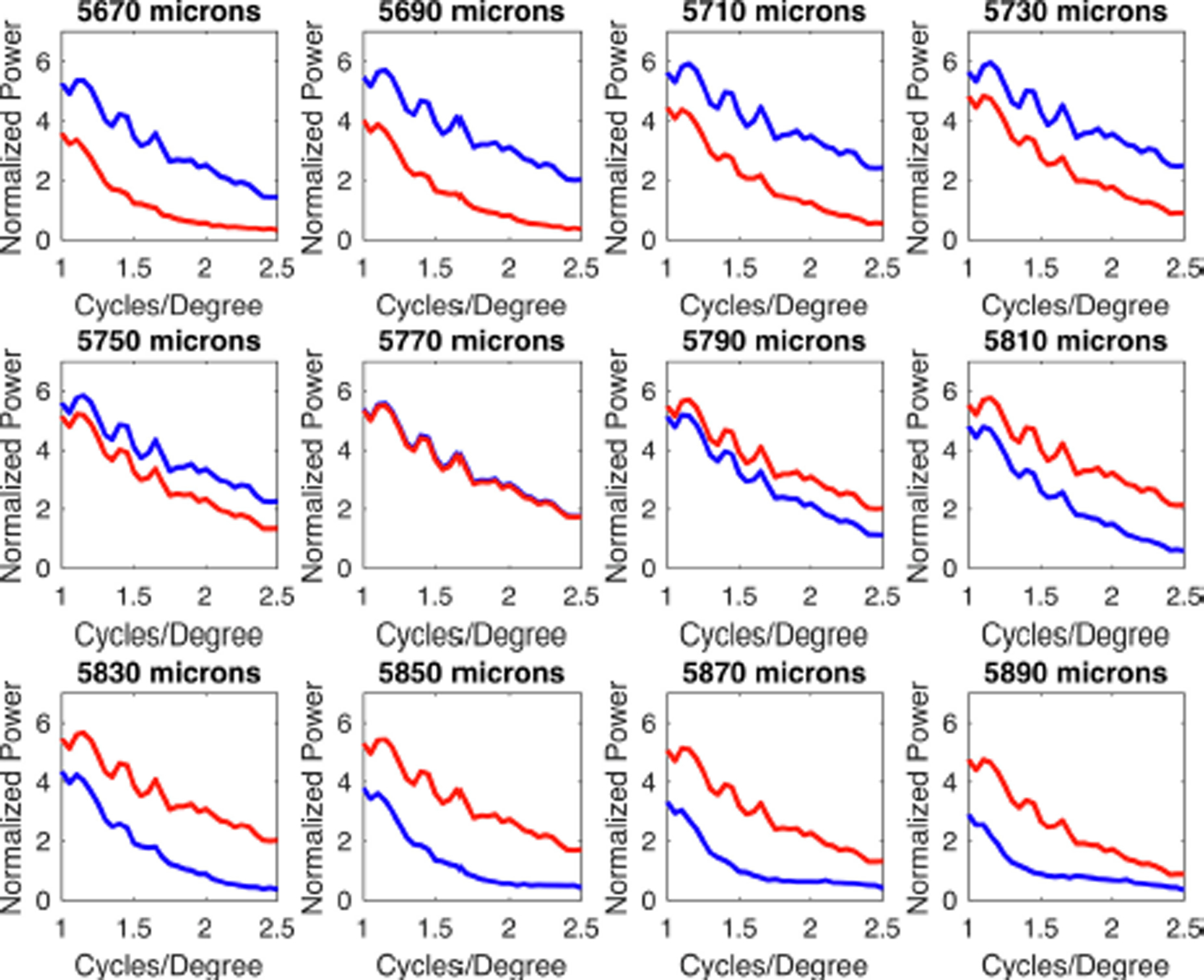
Normalized power as a function of spatial frequency as the position of the retina is varied, for the image shown in Fig. 10. Blue lines indicate the SWS cone array and red lines indicate the LWS cone array. At a retinal location of 5770 μm (middle row, second from the left) the spatial frequency distributions are identical for SWS and LWS systems. For hyperopic defocus (panels to the left and above), the SWS cones show significantly more power than the LWS cones at 1 cycle/degree and above. The opposite holds for myopic defocus.

Discussion.

That the emmetropization mechanism detects image contrast and adjusts axial growth of the eye to maximize image contrast is a familiar concept (Bartmann and Schaeffel 1994, Schaeffel and Diether 1999, Diether and Wildsoet 2005, Tran, Chiu et al. 2008). In this study we have developed a dual-detector spectral drive model using data from the dichromatic mammal, tree shrew. In our model, image sharpness is detected by two independent imaging arrays, comprised of the SWS and the LWS cones. In broadband lighting conditions, because of longitudinal chromatic aberration, the two imaging arrays cannot both simultaneously maximize image sharpness. If image sharpness (as detected by the SWS cone array contrast) is greater than that as detected by the LWS cone array, a drive is generated that increases axial growth. If image contrast is greater as detected by the LWS cone array, an opposing drive is generated that slows axial growth. The target is a retinal location where the image contrast is intermediate and approximately equal in both cone arrays.

An important point of this model is that, although the emmetropization mechanism exists to achieve and maintain good focus, it does not itself use “defocus” as the primary cue. Instead, it depends on the difference in the image statistics as sampled by the SWS and LWS cone arrays. Under a broad-band spectrum of lighting, this mechanism efficiently homes in on good focus. However, when the spectrum of light is significantly altered, shifting the target of the spectral drive, the emmetropization mechanism can become maladaptive producing a stable refractive state that is different from emmetropia, despite defocus cues.

When the response to a monochromatic light-dark edge was modeled for a physiologically relevant range of defocus, we found (Fig.11), perhaps surprisingly given the relative sparseness of the SWS cones (Muller and Peichl 1989, Sajdak, Salmon et al. 2019), that the spatial pattern on the surface of the retina could be detected by both cone arrays. Previous work has indicated that, even though the purpose of emmetropization is to maximize acuity for high spatial frequencies, emmetropization itself appears to be driven more strongly by the mid-range of spatial frequencies (Schmid and Wildsoet 1997, Tran, Chiu et al. 2008). With hindsight it is hard to see how emmetropization could depend on high spatial frequencies, as it must operate when an image is out of focus as well as when it is in focus. The results here demonstrate that it is plausible for the emmetropization system to make use of LCA cues without requiring non-physiological levels of spatial acuity, and that it can also operate robustly across a range of optical blur.

According to our model, the emmetropization mechanism should be able to accurately use differential wavelength cues in all but the most distorted light spectra, as long as the spectra span a broad band of wavelengths and have more than two peaks. Interestingly, spectra consisting of narrow band red and narrow band blue light together produce a target that is myopic, but we were unable to find a light spectrum (other than narrow band red) that could significantly either shift the target in the direction of hyperopia, or increase the magnitude of the drive signal. Simulations suggest such a result could only be achieved in broadband light by manipulating the effective magnitude of LCA, for example, by using multifocal lenses with different spectral filtering in the different optical zones (Fig.10H).

We note that this model only examines information available at the level of the photoreceptors, ignoring the considerable processing that occurs as information passes through the bipolar, horizontal, amacrine and ganglion cells. However, the retinal circuitry cannot create information that is not present in the spatial pattern of light across the photoreceptors. The information available at the photoreceptor level, as modeled here, appears to be sufficient to provide signals to subsequent retinal stages that account for the behavior of the emmetropization mechanism in both broadband and various narrow-band ambient lighting of differing peak wavelengths.

Given the evolutionary importance of in-focus images to survival, it is not surprising that defocus, as detected by the dual detector spectral drive model is not the only cue used by the emmetropization mechanism. When tree shrews and macaque monkeys housed in narrow-band red light have also worn plus-power (macaque) or minus power lenses (tree shrew), the lenses alter the refractive responses in the appropriate direction, increasing the hyperopia in macaques (Hung, Arumugam et al. 2018) and increasing the myopia in tree shrews (ARVO E-abstract Ward et al. IOVS 2745, 2017). These results emphasize that the emmetropization mechanism utilizes multiple cues related to defocus. That said, in narrow-band light the spectral cues appear to be stronger than the defocus cues and prevent achieving or maintaining emmetropia (Gawne, Ward et al. 2017, Gawne, Ward et al. 2018).

Even if our suggestion is correct that a dual detector spectral drive system guides emmetropization, it is not clear how the strength of the drive signal (Y-axis in Fig. 8) is used. In extreme cases, where drive is zero (blue illuminant) or strongly negative (red illuminant) there appears to be a strong impact on the emmetropization mechanism. However, it is unknown as yet if the lower strength of the drive signal in the blue + green illuminant (Fig. 9E) will lead to greater variability in the refractions of animals housed in this light over time. It may also be the case that, at least in humans, emmetropization does not home in on the point of exact balance between the image statistics of short and long wavelength cones, but perhaps some ratio that is biased towards the longer wavelengths. Nevertheless, for this level of modeling, the effect would be slight, and is a topic for future experiments and modeling studies.

It is important to note that the spectra used to examine the effects of wavelength on emmetropization in our tree shrews were produced either by fluorescent lamps or by light emitting diodes, not by digital monitors. One cannot model the effects of wavelength on emmetropization using standard “red-green-blue” digital images because focus varies continuously with wavelength. For example, as regards a single photoreceptor, a dim light of a wavelength at the optimal frequency cannot be distinguished from a brighter light at a less optimal wavelength that produces the same photon catch. This is the basis of color metamerism, and is why our video display technology works so well with just red, green, and blue light emitting elements. However, as regards emmetropization, these two conditions are not equivalent, because the degree of focus will be different. Thus, an analysis of this type must integrate across all wavelengths, a procedure known as hyperspectral imaging (Lu and Fei 2014).

Application to trichromatic species.

Unlike tree shrews, many primates, including most humans, are trichromats, with middle wavelength sensitive (MWS) cones added to the SWS and LWS cones presentin dichromatic species. However, we suggest that the principles of the spectral drive model would apply in trichromatic species if the MWS and the LWS cone arrays both together provide a signal to the emmetropization mechanism that opposes the signal provided by the SWS cone array (similar to the blue-yellow interaction found in chromatically-sensitive retinal ganglion cells). The peak wavelength sensitivities for the MWS and LWS cones, in humans, are very close: 530 and 560 nm. These are far removed from the 420 nm peak for the human SWS cones. Also, the LCA curve is nonlinear; focus changes more rapidly with increasing wavelength at shorter than, at longer, wavelengths (Wang, Candy et al. 2008). In humans, the difference in where light is focused between the MWS and LWS cones is approximately 0.1 D. The difference in where light is in focus between the short wavelength versus the medium and long wavelength cones is approximately 1.0 and 1.1 D, respectively. Thus, there is relatively little difference in the information about focus available to the MWS vs. the LWS cones, but a substantial difference between the SWS short and either or both of the MWS and LWS cones. We suggest that it is the difference between the image contrasts on the SWS system vs. longer (MWS & SWS) systems that is important for emmetropization. This suggestion is bolstered by the fact that emmetropization occurs in many dichromatic species (and in dichromatic humans (Qian, Chu et al. 2009)). Evidently, the (relatively) recent (Jacobs 1993, Vorobyev 2004, Jacobs 2009) evolution of trichromacy did not disrupt the emmetropization mechanism.

In humans high-acuity visual perception is mediated by the LM cone midget system in the fovea, but it has been demonstrated that emmetropization is controlled, or strongly influenced, by the peripheral visual field (Smith, Ramamirtham et al. 2007). In the peripheral retina, there is no midget system and L/M cones are much sparser then in the fovea. It may also be relevant that, as images are placed on differing retinal locations, from the central to the peripheral visual field, the ability of human subjects to discriminate long (yellow) versus short (blue) wavelengths is maintained, but the ability to discriminate green versus red is lost (Mullen and Kingdom 2002) except perhaps for very large stimuli (Kuyk 1982), making the periphery essentially dichromatic. These results suggest that the red-green contrast may be less important for emmetropization than the blue-yellow. To be sure, the way in which the emmetropization mechanism uses visual cues (which may not be conveyed to central structures) may not always match up with what is observed in centrally-mediated visual perception, but these findings still suggest that it is the long versus short wavelength comparison that is crucial for emmetropization, even in trichromatic primates. As long as the combined L+M cone mosaic is at least as spatially dense as the S cone mosaic, then according to our model, it is functionally irrelevant whether the L+M cones are or are not more densely spaced than the S cones.

In conclusion, we propose a model in which an opponent dual-detector spectral drive system utilizes longitudinal chromatic aberration to guide normal emmetropization in dichromatic tree shrews and perhaps in tri-chromatic species such as humans. To what extent a similar mechanism, or a different mechanism, operates in other species (chick, guinea pigs, mice, etc.), and if so, what are the inter-species differences, remains to be determined. The existence of a dual-detector mechanism could help to distinguish myopic from hyperopic defocus at the retinal level. It also explains why continuous exposure to some narrow-band lighting conditions could produce deviations from emmetropia in tree shrews and, perhaps in humans.

Highlights:

• A model is proposed whereby longitudinal chromatic aberration guides emmetropization

• Effects of defocus on arrays of long- and short-wavelength cones are described

• The eye is guided to a point of balance of image contrast in both cone arrays

• Sparse spacing of short-wavelength cones is not in principle a limiting factor