Effects of intergenerational exposure interventions on adolescent outcomes: An application of inverse probability weighting to longitudinal pre-birth cohort data

Abstract

Background:

There is great interest in understanding whether interventions on sugar-sweetened beverage (SSB) consumption through pregnancy and early childhood affect adolescent body mass index (BMI). Without data from randomized trials, unbiased estimation of such effects might be achieved with observational data given sufficient and appropriate adjustment for both baseline and time-varying confounders.

Objectives:

To illustrate the use of inverse probability (IP) weighting of marginal structural models (MSM) for estimating the effects of SSB consumption through pregnancy and early childhood on the mean early adolescent BMI z-score.

Methods:

Our baseline sample consisted of 1584 pregnant women from a pre-birth cohort. We defined 6 intervention intervals: early pregnancy, late pregnancy, 3, 4, 5 and 6 years. We fitted a MSM via a weighted linear regression with IP exposure and censoring weights to estimate the mean difference in BMI z-score under interventions: “maintain SSB consumption below (versus above) 0.5 servings/day in all intervals”.

Results:

The estimated difference in mean BMI z-score under interventions maintaining SSB consumption at or below (versus above) 0.5 servings/day from pregnancy to 6 years was −0.94 (95% confidence interval [CI] −1.52, −0.08). The effect estimates in pregnancy, while fixing the exposure range in childhood, was −0.05 (95% CI −0.34, 0.23) and in early childhood, while fixing the range in pregnancy was −0.89 (95% CI −1.46, −0.11). The effect estimates were largely unchanged under sensitivity analyses to different implementation choices except for the choice of time interval length.

Conclusions:

Under assumptions that include no unmeasured confounding and selection bias, and no model misspecification, results of this IP weighting application are in line with a lower mean BMI z-score in early adolescence under interventions ensuring lower, versus greater, SSB consumption in early life. This application provides a resource for researchers working with longitudinal birth cohort studies and interested in similar causal questions.

Background

Many causal questions unique to pediatric populations involve understanding effects of time-varying continuous (multi-level) pre- and postnatal exposure interventions on later offspring outcomes. For example, sugar-sweetened beverage (SSB) consumption is associated with weight gain in childhood and adulthood,^1–3 and randomized interventions that reduce SSB consumption in 4–11 year-olds and in adolescents demonstrated short-term weight loss.^4,5 Given possible developmental programming of body weight,^6,7 there is interest in understanding whether reducing SSB consumption in certain windows of early life leads to lower body mass index (BMI) in adolescence.

Because randomized trials may be costly, producing results after decisions are needed, pre-birth cohorts provide an alternative resource. Previous analyses of such cohorts, including Project Viva,⁸ have considered joint exposure effects in pre- and postnatal periods using multivariable regression.^8–11 However, multivariable regression may fail to have a causal interpretation when time-varying confounders are, themselves, affected by past exposure.^12–14 For example, newborn size may be a confounder for a childhood SSB exposure effect on adolescent adiposity but may also, itself, be affected by prenatal exposure.

By contrast, g-methods (“g” for generalized) may recover a time-varying exposure effect in this setting.^13,14 Examples of g-methods include parametric g-computation,^12,15 inverse probability (IP) weighting^16,17 and doubly-robust methods.^18–20 While many resources exist for implementing g-methods in practice,^21–25 few have focused on analysis of (pre-)birth cohorts with multi-level exposures. Here, we illustrate an application of IP weighting to estimate effects of interventions on SSB consumption through pregnancy and early childhood on early adolescent BMI z-score in Project Viva. We detail an implementation algorithm, along with background motivation, as a resource for researchers working with longitudinal (pre-)birth cohort data and interested in similar questions.

Methods

The causal question

Consider the causal effect on mean BMI z-score in early adolescence of different time-varying interventions on SSB consumption in servings/day beginning on the mothers’ consumption through pregnancy and continuing on the offspring’s consumption through childhood. Many intervention contrasts might be considered. Here, we consider representative interventions,^25–27 a class of interventions that maintain a multi-level exposure within a pre-specified range over time.

Specifically, we consider “maintain daily SSB consumption at or below x servings/day” (intervention 1) compared with “maintain above x servings/day” (intervention 2) from early pregnancy through 6 years old for a particular choice of x. Under a representative intervention,²⁵ SSB consumption for intervention 1 would be assigned as follows: On each day of the intervention period, “assign SSB consumption to an individual by randomly drawing a value from the distribution of SSB servings on that day in the observed study population amongst those who previously maintained SSB at or below x during the intervention period and have the same measured confounder and SSB history as that individual.“ Interpretation of intervention 2 under a representative intervention is equivalent but replacing “at or below x” with “above x”. We will implicitly define all interventions by one that additionally “eliminates censoring” (e.g. by loss to follow-up).^13,28

The target trial

Ideally, we would conduct a trial to estimate the effect of following intervention 1 versus 2 on later mean BMI z-score in a study population of pregnant women. We refer to this imagined trial as the target trial.¹³ This trial would recruit a large random sample of mothers at conception. Half the sample would be randomized at baseline to intervention 1 and the remainder to intervention 2. In an ideal execution of this trial, such that all participants perfectly adhered to the study protocol, and censoring of the outcome was eliminated in both study arms, an unbiased estimate of this causal effect could be obtained by simply taking the mean BMI z-score difference across the two arms. To identify sensitivity periods,²⁹ we might include two additional arms: the intervention 1 rule during pregnancy, followed by intervention 2 rule during childhood and vice versa.

Observational data: Project Viva

The above trial is unlikely to be conducted, with the multi-arm version particularly infeasible. Therefore, we must rely on observational data. Project Viva enrolled 2,670 pregnant women during their first obstetric care visit between 1999 and 2002 in Eastern Massachusetts, USA. Details are available elsewhere.³⁰ Briefly, maternal diet was assessed using a 140-item, semi-quantitative food frequency questionnaire (FFQ) once in early pregnancy and mid-late pregnancy.^31–33 Research staff collected covariate data and assessed anthropometry using standard protocols³⁴ during follow-up visits at birth, in infancy (median: 6.3 months), early childhood (median: 3.2 years), mid-childhood (median: 7.7 years), and early adolescence (median: 12.9 years). Age and sex-specific BMI z-scores were calculated using Centers for Disease Control and Prevention growth charts.³⁵ Mothers completed annual mailed questionnaires on children’s diet and lifestyle factors beginning at age one.

Motivation for g-methods

Unlike in an ideal execution of our target trial, Project Viva investigators did not assign SSB exposure at any time. Further, whether a participant is censored at a given time likely depends on both baseline and post-baseline risk factors for the outcome. Regardless of whether the data come from an observational study or an inadequately executed trial, appropriate adjustment for baseline and post-baseline confounders and selection factors for censoring is required to recover causal effects.^12,36 Under the assumptions of positivity, consistency and no unmeasured confounding and selection bias due to censoring given measured covariates (i.e. exchangeability), g-methods can be used to target contrasts in the population outcome mean had we implemented different time-varying exposure interventions specified in the target trial protocol.^13,14

Briefly, consider the causal directed acyclic graph (DAG)³⁷ in Figure 1 representing a simplified assumption on the mechanisms that produced the data in Project Viva. No unmeasured confounding given measurement of newborn size and baseline covariates holds in Figure 1 by the absence of an arrow from U, an unmeasured outcome risk factor, into SSB exposure at any time. This is a strong assumption in Project Viva. Still, even if this assumption were to hold, the coefficients on time-varying SSB exposure in a multivariable regression model will fail to have a causal interpretation even after adjustment for newborn size and baseline covariates (Supplemental materials 1).

Figure 1.

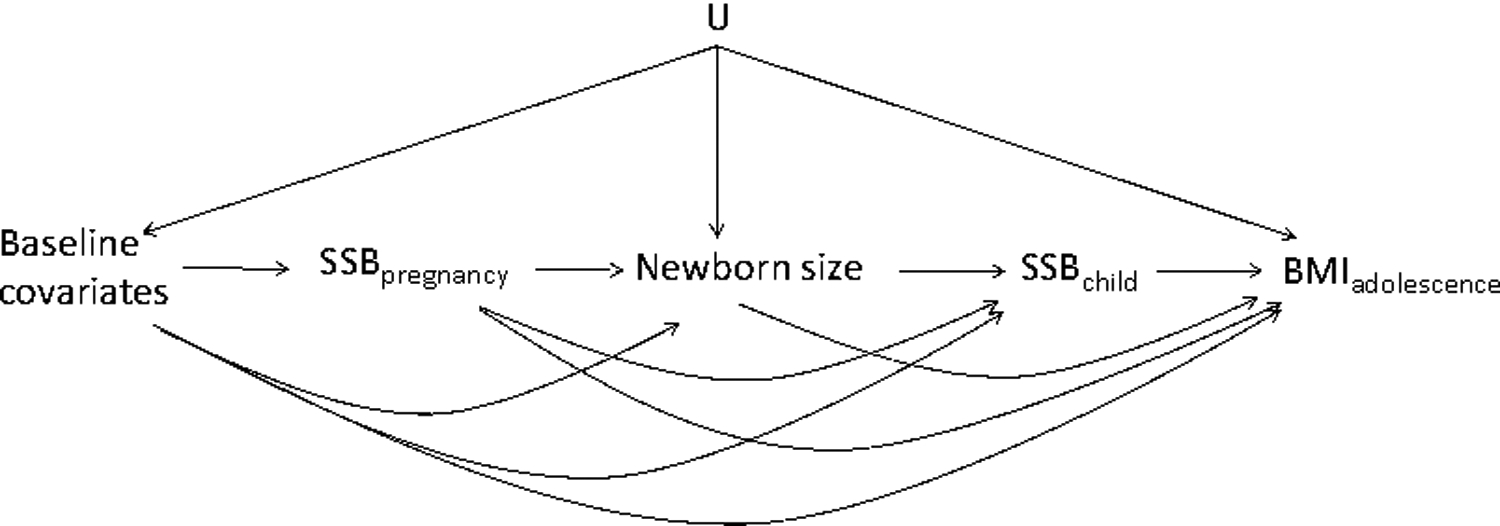
Causal directed acyclic graph representing simplified assumption mechanisms that produced Project Viva data

IP weighted estimation

IP weighted estimation, one g-method, is an approach to estimating the effect that would be observed in an ideal implementation of the target trial using observational data. Informally, in our example, weighting can create a pseudo-population in which an individual’s exposure range (at or below, versus above, x) at each time is independent of past measured covariates. Fitting an outcome regression in this pseudo-population is equivalent to fitting a weighted outcome regression in the original study population. Under the aforementioned assumptions and no model misspecification, these weighted model parameters will equal the parameters of a marginal structural model (MSM), a counterfactual outcome mean model. Below we give a step-by step description of an IP weighted algorithm for estimating effects of representative interventions on multi-level exposures on a continuous outcome. Supplementary e-materials provide annotated SAS code.

Step 1: Data set construction

Denote n as the size of the baseline sample who, as closely as possible, meet eligibility criteria for the target trial. We selected these individuals as those meeting eligibility for study enrollment at the first prenatal visit, completing the early pregnancy FFQ at or before 24 weeks and had complete baseline exposure and confounder data. This gave n=1584 (Figure S2). By restricting to those with complete baseline data the study population is changed without reliance on a missing completely at random (MCAR) assumption.³⁸ Multiple imputation can relax this assumption but requires further study in the case of g-methods (Supplemental materials 2).^39,40

Let k=0,1,2… denote a measurement interval with k=0 the baseline interval and k = K + 1 the last interval in the follow-up period (in which the outcome is measured). We defined K = 5, with k=0 the early pregnancy questionnaire, k = 1 the late pregnancy questionnaire, k = 2,3,4, and 5 the 3-, 4-,5-, and 6-year old questionnaire intervals, respectively. Because few participants reported any SSB consumption in the 1- or 2-year old questionnaires, we modified the original question and consider intervention only through pregnancy and childhood ages 3 to 6.

For k = 0, … , K, A_k denotes measured SSB exposure (servings/day), and L_k the interval k assumed confounders (Table 1), measured either in interval k or between the end of interval k - 1 and the start of interval k. Y denotes the early teen visit BMI z-score and R_k an indicator that SSB consumption is at most x servings/day in interval k (R_k = 1 if A_k ≤ x and R_k = 0 if A_k > x). For our primary analysis, we chose x = 0.5 because most children consumed less than 1 serving per day (e-Table 1). While a higher cutoff may be of interest, these result in near positivity violations (few individuals with data that support the interventions under consideration).⁴¹

Table 1.

Choices of L_k for the primary analysis.

Interval (k)	Confounders
Baseline (L0)	maternal BMI (<25, 25–29, ≥30 kg/m2), college graduate (yes, no), maternal smoking during pregnancy (yes, no), white race/ethnicity (yes, no), annual household income (>$70,000, ≤$70,000), and paternal BMI (<25, 25–29, ≥30 kg/m2).
Late pregnancy (L1)	SSB intake during early pregnancy (tertiles), caloric intake during early pregnancy (tertiles)
3 years (L2)	average SSB intake during early and late pregnancy (tertiles), average caloric intake during early and late pregnancy (tertiles) caloric intake at age 2 years (tertiles) birthweight for gestational age z-score (tertiles) BMI z-score at age 3 (tertiles) TV watching at age 3 years (<1.6 vs ≥1.6 hours/week)
4 years (L3)	Average SSB intake during early and late pregnancy (tertiles) SSB intake at 3 years (<1.5 servings/week vs. ≥1.5 servings/week) average caloric intake during early and late pregnancy (tertiles) average caloric intake at age 2 and 3 years (tertiles) birthweight for gestational age z-score (tertiles) BMI z-score at age 3 (tertiles) average hours of TV watching at age 3 and 4 years (tertiles)
5 years (L4)	average SSB intake during early and late pregnancy (tertiles), cumulative average SSB intake at 3 and 4 years (tertiles) average caloric intake during early and late pregnancy (tertiles) average caloric intake at age 2 and 3 years (tertiles) birthweight for gestational age z-score (tertiles) BMI z-score at age 3 (tertiles) average hours of TV watching at age 3 ,4 and 5 years (tertiles)
6 years (L5)	average SSB intake during early and late pregnancy (tertiles) cumulative average SSB intake at 3, 4, and 5 years (tertiles) average caloric intake during early and late pregnancy (tertiles) average caloric intake at age 2 and 3 years (tertiles) birthweight for gestational age Z score (tertiles) BMI z-score at age 3 (tertiles), average hours of TV watching at age 3, 4, 5, and 6 years (tertiles)

Define C_k+1as an indicator of censoring by interval k + 1 (C_k+1 = 1 if censored, and C_k+1 = 0 otherwise). We allowed a missing value of a confounder to be carried forward up to twice for covariates measured in more than one interval. We censored participants in the first interval of missing exposure, the outcome, or confounders (including 46 women who had no subsequent covariate measurements due to pregnancy loss). We considered other approaches to handling pregnancy loss as sensitivity analysis (Supplemental materials 2).⁴² We also censored participants in interval k if the questionnaire for that interval was returned after the corresponding age (e.g. if the 3-year old questionnaire was returned after the child turned 4). We rely on an assumed temporal order (C_k, L_k, A_k) in each k.

The data set containing these variables can be constructed in either 1) a “wide” format with one line per id or 2) a “long” format data set with one record per id and interval. The latter allows for “pooled over time” models (Step 2). In either case, additional functions of past values of exposure and confounders relative to k need to be created based on the approach to Step 2. Given covariate distributions vary between mothers and children at different ages, we used the wide format.

Step 2: Weight computation^16,25

For each participant i = 1, … , n estimate a weight W_i defined as follows. For an uncensored participant i:

$$W_i^{\overline{r}}={\prod }_{k=0}^{k=5}\left\{\frac{P\left(R_{i,k}|{\overline{C}}_k=0,{\overline{R}}_{k-1}={\overline{R}}_{i,k-1},V=V_i\right)}{P\left(R_{i,k}|{\overline{C}}_k=0,{\overline{A}}_{k-1}={\overline{A}}_{i,k-1},{\overline{L}}_k={\overline{L}}_{i,k}\right)}\right\}$$ Equation 1.

$$W_i^c={\prod }_{k=0}^{k=5}\frac{P\left(C_{k+1}=0|{\overline{C}}_k=0,{\overline{R}}_k={\overline{R}}_{i,k},V=V_i\right)}{P\left(C_{k+1}=0|{\overline{C}}_k=0,{\overline{A}}_k={\overline{A}}_{i,k},{\overline{L}}_k={\overline{L}}_{i,k}\right)}$$ Equation 2.

$$W_i=W_i^{\overline{r}}x{W}_i^c$$ Equation 3.

For a censored participant i:

$$W_i\text{=0}$$

We now explain the equations above:

Exposure weight ($W_i^{\stackrel{-}{r}}$)

Each denominator component of the product in Equation 1 is the probability of having participant i’s value of R_k (i.e., if her/his value is 1, this is the probability that R_k=1 ; otherwise, that R_k = 0) among those remaining uncensored through k (C_k=0) and with this participant’s history of SSB consumption through k-1 (${\stackrel{-}{A}}_{i,k-1}$) and confounders through k (${\stackrel{-}{L}}_{i,k}$). To estimate this probability, we can first fit a logistic regression using all participants still uncensored by k (including those censored later) with dependent variable R_k and independent variables a user-chosen function of past SSB (${\stackrel{-}{A}}_{k-1}$) and confounder history (${\stackrel{-}{L}}_k$). In practice, the flexibility of this function and the choice of confounders L_k, may be limited by sample size (Supplemental materials 3). We use the estimated coefficients from this model to “predict” participant i’s probability at k. The denominator of Equation 1 is the product of these over all intervals.

Each numerator component of Equation 1 is the same as its denominator counterpart but, instead of conditioning on the participant’s exposure and confounder history, it is conditioned on her/his exposure range history (${\stackrel{-}{R}}_{i,k-1}$) and V_i her/his values of a user-selected subset of the baseline confounders L₀ which we can choose to include no components or some/all components of L₀. Estimation proceeds as for the denominator. Unbiasedness of the algorithm requires only that the denominator model is correctly specified. The numerator serves only to stabilize the weights, which, in principle, may have smaller variability the more components of L₀ included in V but at the expense of a more complex MSM (Step 3).¹⁶ We chose V to include all L₀ components (see Table 1).

Censoring weight ($W_i^c)$

Each component of the denominator of Equation 2 is the probability of remaining uncensored through k + 1 among those who remained uncensored through k and also had participant i’s history of SSB consumption and confounders through k. Analogously, estimation can proceed by fitting a logistic regression using all participants still uncensored by k (even those who may be censored later) with dependent variable C_k+1 and independent variables a function of past SSB and confounder history. The numerator is analogously interpreted and estimated with unbiasedness only reliant on correct specification of the denominator model.

Overall weight (W_i)

An uncensored participant’s weight is the product of her/his exposure and censoring weights (Equation 3). We truncated weights greater than the 99^th percentile of the weight distribution to mitigate the influence of extreme weights.²¹ Censored participants receive a zero weight. As above, these participants contribute data through their censoring time to weight estimation for uncensored participants.

Step 3: Weighted outcome regression

$$\text{E}\left[Y^{{\overline{r}}_K}|V\right]={\beta }_0+{\beta }_1{\text{r}}_{\text{k}=0}+{\beta }_2{\text{r}}_{\text{k}=1}+{\beta }_3{\text{r}}_{\text{k}=2}+{\beta }_4{\text{r}}_{\text{k}=3}+{\beta }_5{\text{r}}_{\text{k}=4}+{\beta }_6{\text{r}}_{\text{k}=5}+{\beta }_7^{T}V$$ Equation 4

where r_k is a possible realization of R_k(either 1 or 0)

Denote $\mathrm{E}\left[Y^{{\stackrel{-}{r}}_k}\right]$ as the mean of the outcome under an intervention that sets ${\stackrel{-}{R}}_K={(R}_0,\mathrm{ }{R}_1,R_2,R_3,R_4,R_5)$ equal to some set of fixed values ${\stackrel{-}{r}}_K=(r_0,r_1,r_2,r_3,r_4,r_5)$ via a representative intervention. The average causal effect of an intervention “maintain SSB at or below 0.5 servings/day” versus “above 0.5” via representative interventions is then $E\left[Y^{{\stackrel{-}{r}}_K=(\mathrm{1,1},\mathrm{1,1},1)}\right]-E\left[Y^{{\stackrel{-}{r}}_K=\left(\mathrm{0,0},\mathrm{0,0},0\right)}\right]$. Additional comparisons can be conveniently computed and precision gained by the assumption of an MSM for $E\left[Y^{{\stackrel{-}{r}}_k}\right]$. ¹⁶Note this model must be further conditioned on levels of V selected in Step 2 (unless V is chosen empty).

Equation 4 is one possible MSM for $E\left[Y^{{\stackrel{-}{r}}_K}\right|V]$. If the model is correct, precision is gained. If incorrect, effect estimates will incur some bias. To estimate the MSM coefficients, we fit a weighted linear regression with dependent variable Y and independent variables functions of R₁ through R₅ and V, with weights from Step 2.

Step 4: Estimating the intervention mean and mean differences

Given exchangeability, positivity and consistency, correctly specified weight denominator models and the MSM and no measurement error, the estimated coefficients of the weighted regression model above can be used to estimate causal effects. Under Equation 4, the sum of the weighted estimates ${\widehat{\beta }}_1+{\widehat{\beta }}_2+{\widehat{\beta }}_3+{\widehat{\beta }}_4+{\widehat{\beta }}_5+{\widehat{\beta }}_6$ estimate the difference in mean BMI z-score had all participants maintained SSB consumption at ≤ 0.5 serving/day, versus >0.5 serving/day, in all 6 intervals under the representative intervention. By Equation 4, effects conditional on V and population-level effects (averaged over V) are equal because 1) Equation 4 includes no interaction terms between any r_k and components of V and 2) linear models are collapsible.⁴³ Generally, additional steps are needed to covert estimated MSM coefficients to time-varying causal effect estimates (Supplemental materials 3).

Using the MSM, we also estimated effects of interventions “maintain SSB consumption at or below 0.5 servings/day” versus “above 0.5 servings/day” under representative interventions in a time window t₁ holding the exposure range in remaining windows t₂ fixed under both interventions. By the absence of interactions in our MSM, this effect is assumed the same regardless of the range held fixed in t₂ (either above or below the cutoff x). We estimated two versions of this effect: 1) t₁ defined as pregnancy and t₂ defined as early childhood (${\widehat{\beta }}_1+{\widehat{\beta }}_2$) and 2) t₁ defined as early childhood and t₂ defined as pregnancy (${\widehat{\beta }}_3+{\widehat{\beta }}_4+{\widehat{\beta }}_5+{\widehat{\beta }}_6)$.

We constructed 95% confidence intervals (CIs) using a nonparametric bootstrap by sampling with replacement from the original n participants 500 times. In each of these samples we repeated steps 2 through 4 giving 500 effect estimates. We computed 95% CIs by sorting these estimates, with the 2.5% percentile the lower bound and the 97.5% percentile the upper bound. The above algorithm required several choices. Below and in Supplemental materials 2 we discuss sensitivity analysis to some of these choices.

We compared our IP weighted estimates to those obtained from two comparable unweighted linear regressions applied to our sample: (i) adjusted only for baseline confounders among those with an outcome measure and (ii) adjusted for both baseline and post-baseline confounders only among uncensored participants.

Ethnics approval

The study protocol was approved by the Institutional review boards of Harvard Pilgrim Health Care. All participants signed an informed consent.

Results

Table 2 summarizes baseline characteristics of the baseline sample. Over the follow-up, 75% of subjects were censored in the primary analysis (sensitivity analysis considered less stringent censoring rules; eFigure 2). eTable 1 shows the number of participants remaining uncensored by the start of each interval and the distributions of SSB consumption in these participants.

Table 2.

Characteristics of 1584 participants in the baseline sample

	Mean (SD) or %
Baseline SSB consumption	Total (n=1584)	≤0.5	>0.5
Maternal
Age at enrollment (years)	32.6 (4.5)	33.3 (4.2)	31.4 (4.8)
Pre-pregnancy BMI (kg/m2)
<25	64.3%	67.5%	58.9%
25–29	21.3%	21.2%	21.6%
≥30	14.4%	11.3%	19.5%
Gestational age 1st FFQ (weeks)	11.7 (2.9)	11.6 (2.9)	11.8 (3.0)
Gestational age 2nd FFQ (weeks)	29.1 (2.4)	29.1 (2.4)	29.2 (2.4)
Race/ethnicity
Black	10.4%	8.6%	13.5%
Hispanic	6.1%	4.7%	8.6%
Asian	5.6%	7.3%	2.9%
White	74.6%	76.7%	71.0%
Other	3.2%	2.7%	4.0%
College graduate
No	28.1%	21.9%	38.4%
Yes	71.9%	78.1%	61.6%
Annual household income >$70,000/year
No	35.7%	31.5%	42.8%
Yes	64.3%	68.5%	57.2%
Smoking status
Never	67.3%	68.1%	66.0%
Former	22.2%	23.7%	19.7%
Smoked during pregnancy	10.5%	8.2%	14.3%

The IP weighted estimates of the BMI z-score mean difference under interventions maintaining SSB consumption at or below (versus above) 0.5 servings/day through pregnancy and 3–6 years old was −0.94 (95% CI −1.52, −0.08) (Table 3). Estimates in pregnancy only, holding the range in childhood fixed, and in early childhood, holding pregnancy fixed were −0.05 (95% CI −0.34, 0.23) and −0.89 (95% CI −1.46, −0.11), respectively. Estimates remained largely consistent in sensitivity analyses enumerated in Table 3. However, an analysis based on wider interval lengths substantially attenuated effect estimates (Table 3; see Supplemental materials 2 for discussion of tradeoffs in information loss related to the interval length). Effect estimates were somewhat attenuated by changing the cutoff x to the 75^th percentile in each interval; in pregnancy this was slightly higher than 0.5 and in childhood slightly lower. Estimates using unweighted regression with or without conditioning on post-baseline confounders were also attenuated compared to the IP weighted estimates (Table 4).

Table 3.

IP weighted estimates of the difference in mean BMI z-score under representative interventions.

	Δ in mean BMI z-score in early adolescence
	Maintain at or below 0.5 servings/day vs above during pregnancy and early childhood (3–6 years)	At or below 0.5 servings/day through pregnancy, fixing range of early childhood consumption	At or below 0.5 servings/day through early childhood, fixing range of pregnancy consumption
Primary analysis1,	−0.94 (−1.52, −0.08)	−0.05 (−0.34, 0.23)	−0.89 (−1.46, −0.11)
Sensitivity analyses (i): missingness in baseline confounders
Exclude paternal BMI and household income from baseline confounders2	−0.83 (−1.39, −0.12)	−0.04 (−0.34, 0.26)	−0.78 (−1.25, −0.19)
Sensitivity analyses (ii): interval lengths
Wider intervals: pregnancy, 3 to 4 years, 5 to 6 years	−0.33 (−0.67, 0.01)	−0.04 (−0.21, 0.15)	−0.29 (−0.67, 0.05)
Sensitivity analyses (iii): selection of measured confounders
1+ maternal age (<30, 30 to <35, ≥ 35 years)	−0.92 (−1.53, −0.06)	−0.02 (−0.31, 0.27)	−0.90 (−1.45, −0.16)
1+ total gestational weight gain (tertile)	−1.02 (−1.56, −0.09)	−0.03 (−0.32, 0.25)	−0.99 (−1.49, −0.16)
1+ breast feeding duration (spline with 3 knots)	−0.91 (−1.47, 0.008)	−0.02 (−0.32, 0.25)	−0.89 (−1.38, −0.04)
1+ time to introduction of solid food (4 months, 4–5 months, ≥ 6 months)	−0.89 (−1.41, −0.03)	−0.08 (−0.37, 0.20)	−0.80 (−1.32, 0.06)
1+ juice intake3	−1.08 (−1.61, −0.25)	−0.21 (−0.52, 0.16)	−0.87 (−1.42, −0.08)
1+ hours of sleep4	−1.00 (−1.52, −0.08)	−0.04 (−0.34, 0.23)	−0.95 (−1.46, −0.11)
1+ newborn size z-score5	−0.98 (−1.84, −0.03)	0.06 (−0.33, 0.40)	−1.04 (−1.76, −0.18)
1+ newborn BMI z-score but exclude birth weight adjust for gestational age z-score6	−0.77 (−1.67, 0.04)	0.10 (−0.30, 0.44)	−0.87 (−1.70, −0.12)
1but exclude concurrent covariates (measured in the same questionnaire as SSB) from the models	−0.92 (−1.50, −0.08)	−0.06 (−0.34, 0.24)	−0.85 (−1.42, −0.006)
Sensitivity analyses (iv): weight model specification
Model 17	−0.91 (−1.58, −0.16)	−0.04 (−0.33, 0.25)	−0.87 (−1.48, −0.11)
Model 28	−0.91 (−1.54, −0.12)	−0.05 (−0.34, 0.25)	−0.86 (−1.38, −0.06)
Model 39	−0.93 (−1.46, −0.02)	−0.02 (−0.31, 0.27)	−0.91 (−1.42, −0.04)
Sensitivity analyses (v): definition of censoring
Censor upon first interval of any missing covariates	−0.86 (−1.50, −0.07)	−0.12 (−0.34, 0.24)	−0.74 (−1.44, −0.11)
Restrict analysis to livebirths	−0.95 (−1.50, −0.18)	−0.06 (−0.38, 0.26)	−0.89 (−1.40, −0.18)
Sensitivity analyses (vi): choice of the cutoffs
	Maintaining at or below 75th percentile vs. above during pregnancy and early childhood	Effect through pregnancy, fixing early childhood consumption	Effect through early childhood, fixing pregnancy consumption
Using 75th percentiles10 as the thresholds	−0.71 (−1.33, −0.04)	−0.04 (−0.41, 0.37)	−0.67 (−1.15, −0.09)

All 95%CIs were based on bootstrap with 500 samples.

¹Covariates in the primary analysis are listed in the Table 1. The beta coefficients were 0.09 in early pregnancy, −0.14 in late pregnancy, −0.50 in age 3, −0.03 in age 4, −0.36 in age 5, and −0.001 in age 6.

²Eligibility criteria do not require complete data on paternal BMI and household income (n=1955 at baseline)

³Include mother’s average juice intake during early and late pregnancy (tertiles) and children’s cumulative average juice intake up to time k (tertiles).

⁴Include children’s cumulative average hours of sleep up to time k (tertiles).

⁵Include newborn length z-score (tertiles).

⁶Include newborn BMI z-score (tertiles) instead of birthweight for gestational age z-score

⁷Model maternal BMI as a spline model with 4 knots (instead of categorical variables).

⁸Model birthweight for gestational age z-score and BMI z-score at age 3 as a spline model with 4 knots (instead of categorical variables).

⁹Model children’s cumulative average of TV watching as a spline model with 3 knots (instead of including categorical variables).

¹⁰75^th cutoffs were 0.83 servings/day for early pregnancy, 0.79 servings/day for late pregnancy, 0.21 servings/day for 3 and 4 years, and 0.43 servings/day for 5 and 6 years.

Table 4.

Comparisons of standard regression versus IP weighted estimates under representative interventions.

	Δ in mean BMI z-score in early adolescence
	Maintain at or below 0.5 servings/day vs. above during pregnancy and early childhood	At or below 0.5 servings/day through pregnancy, fixing range of early childhood consumption	At or below 0.5 servings/day through early childhood, fixing range of pregnancy consumption
IP weighted estimate1 (primary analysis)	−0.94 (−1.52, −0.08)	−0.05 (−0.34, 0.23)	−0.89 (−1.46, −0.11)
Standard Regression, adjusting for baseline covariates2	−0.41 (−0.86, 0.03)	0.03 (−0.19, 0.25)	−0.44 (−0.88, −0.01)
Standard Regression, adjusting for both baseline and post-baseline covariates1	−0.51(−0.92, −0.10)	−0.07 (−0.28, 0.15)	−0.44 (−0.83, −0.05)

¹Covariates in the primary analysis are listed in the Table 1.

²Adjusting for maternal BMI (<25, 25–29, ≥30 kg/m²), college graduate (yes, no), maternal smoking during pregnancy (yes, no), white race/ethnicity (yes, no), annual household income (>$70,000, ≤$70,000), and paternal BMI (<25, 25–29, ≥30 kg/m²).

Comment

Principal findings

We illustrated an application of IP weighting to estimate effects of time-varying exposure interventions that maintain SSB consumption within a pre-specified range through pregnancy and early childhood on mean BMI z-score in early adolescence. Under assumptions, estimates were in line with a protective effect of consuming at most 0.5 servings/day (versus more servings) over these periods (beta=−0.94; 95% CI −1.52, −0.08) on adolescent mean BMI z-score. Analyses assessing sensitivity periods suggest this effect is mostly explained by effects in childhood. Our results were robust to various sensitivity analyses with the largest discrepancies seen with wider measurement intervals and changing the pre-specified range.

Strengths of the study

Previous analyses of the effects of early life SSB exposure on later metabolic outcomes have relied primarily on multivariable regression without explicit definition of a target causal effect or attention to underlying causal assumptions. Here, we defined a causal effect through conceptualizing a target trial which motivated the analysis.¹³ The causal interpretation of our estimates relies on weaker assumptions than multivariable regression, allowing for the realistic assumption that post-baseline confounders are affected by exposure.

Limitations of the data

In observational analysis, causal inference rests on many untestable assumptions, including no unmeasured confounding and selection bias which reasonably fails in our case; for example, only limited measures of diet at 4–6 years were available in Project Viva. Further, SSB consumption was self-reported, thus subject to measurement error, and over year-long intervals. This design not only fails to capture time-varying changes in exposure but also potential important confounder changes within an interval.⁴⁴

Sensitivity analysis can in principle be constructed under violation of causal assumptions but generally require specific assumptions on relationships between measured and unmeasured variables.^45,46 More work is needed to develop sensitivity analysis for cohorts like Project Viva, taking into account assumptions on these particular data structures under realistically complex causal DAGs.

Further, few participants in our baseline sample consistently returned questionnaires. We censored participants to handle this missing data problem, resulting in high attrition rates. This motivated our choice to limit consideration to interventions through early childhood, rather than through adolescence.

Interpretation

Because our analysis was motivated by a target trial, the desired interpretation of our estimates is clear: given no unmeasured confounding and selection bias, consistency, positivity, correctly specified models and no measurement error, our estimates suggested maintaining SSB intake below (versus above) 0.5 serving/day in pregnancy and early childhood may lower BMI z-score in adolescents. The findings support the American Academy of Pediatrics’ dietary recommendations on limiting SSB below 4 to 6 oz per day (equivalent to 0.33–0.5 serving per day) for children 1 to 6 years.⁴⁷ Previous literature from both observational studies and randomized trials have suggested that SSB consumption in young childhood promotes weight gain in children.^1–3 However, very few studies have considered both maternal and child’s SSB intake on later BMI in children. A previous multivariable regression analysis in Project Viva came to different conclusions than the current study, reporting stronger associations in pregnancy than early childhood on later childhood BMI z-score.⁸ This analysis did not account for post-baseline confounders but also differed from the current analysis in other ways (Supplemental materials 4). In a more comparable multivariable regression analysis, we found results consistent in direction but weaker in magnitude, regardless of adjustment for post-baseline confounders (Supplemental materials 4).

Conclusions

We emulated a target trial of interventions from pregnancy through childhood on adolescent outcomes using IP weighting in a pre-birth cohort. Explicit consideration of the causal question and needed assumptions aids transparency, informing selection of less biased analytic approaches, sensitivity analysis and directions for future work when the goal is causal inference using (pre-birth) longitudinal cohort data.

Synopsis.

Study question

• Whether reducing sugar-sweetened beverage (SSB) consumption throughout early-life, or only in certain windows of early life, leads to lower body mass index (BMI) in adolescence

What’s already known

• SSB consumption is associated with childhood obesity.

What this study adds

• Under assumptions that include no unmeasured confounding and selection bias, and no model misspecification, we estimated that these children would have a lower mean BMI z-score in early adolescence had they and their mothers maintained SSB below (versus above) half serving per day through pregnancy to early childhood

• This effect is mostly explained by effects in childhood

• This application provides a resource for researchers working with longitudinal birth cohort studies and interested in similar causal questions.