Abstract
Purpose
Cardiac image segmentation is a critical process for generating personalized models of the heart and for quantifying cardiac performance parameters. Fully automatic segmentation of the left ventricle (LV), the right ventricle (RV), and the myocardium from cardiac cine MR images is challenging due to variability of the normal and abnormal anatomy, as well as the imaging protocols. This study proposes a multi-task learning (MTL)-based regularization of a convolutional neural network (CNN) to obtain accurate segmenation of the cardiac structures from cine MR images.
Methods
We train a CNN network to perform the main task of semantic segmentation, along with the simultaneous, auxiliary task of pixel-wise distance map regression. The network also predicts uncertainties associated with both tasks, such that their losses are weighted by the inverse of their corresponding uncertainties. As a result, during training, the task featuring a higher uncertainty is weighted less and vice versa. The proposed distance map regularizer is a decoder network added to the bottleneck layer of an existing CNN architecture, facilitating the network to learn robust global features. The regularizer block is removed after training, so that the original number of network parameters does not change. The trained network outputs per-pixel segmentation when a new patient cine MR image is provided as an input.
Results
We show that the proposed regularization method improves both binary and multi-class segmentation performance over the corresponding state-of-the-art CNN architectures. The evaluation was conducted on two publicly available cardiac cine MRI datasets, yielding average Dice coefficients of 0.84 ± 0.03 and 0.91 ± 0.04. We also demonstrate improved generalization performance of the distance map regularized network on cross-dataset segmentation, showing as much as 42% improvement in myocardium Dice coefficient from 0.56 ± 0.28 to 0.80 ± 0.14.
Conclusions
We have presented a method for accurate segmentation of cardiac structures from cine MR images. Our experiments verify that the proposed method exceeds the segmentation performance of three existing state-of-the-art methods. Furthermore, several cardiac indices that often serve as diagnostic biomarkers, specifically blood pool volume, myocardial mass, and ejection fraction, computed using our method are better correlated with the indices computed from the reference, ground truth segmentation. Hence, the proposed method has the potential to become a non-invasive screening and diagnostic tool for the clinical assessment of various cardiac conditions, as well as a reliable aid for generating patient specific models of the cardiac anatomy for therapy planning, simulation, and guidance.
Keywords: cardiac segmentation, convolutional neural network, magnetic resonance imaging, multi-task learning, regularization, task uncertainty weighting
1. INTRODUCTION
Magnetic resonance imaging (MRI) is the standard-of-care imaging modality for non-invasive cardiac diagnosis, due to its high contrast sensitivity to soft tissue, good image quality, and lack of exposure to ionizing radiation. Cine cardiac MRI enables the acquisition of high resolution two-dimensional (2D) anatomical images of the heart throughout the cardiac cycle, capturing the full cardiac dynamics via multiple 2D + time short-axis acquisitions spanning the whole heart.
Segmentation of the heart structures from these images enables measurement of important cardiac diagnostic indices such as myocardial mass and thickness, left/right ventricle (LV/RV) volumes and ejection fraction. Furthermore, high-quality personalized heart models can be generated for cardiac morphology assessment, treatment planning, as well as precise localization of pathologies during an image-guided intervention. Manual delineation is the standard cardiac image segmentation approach, which is not only time consuming, but also susceptible to high inter- and intraobserver variability. Hence, there is a critical need for semi-/fully automatic methods for cardiac cine MRI segmentation. However, the MR imaging artifacts such as bias fields, respiratory motion, and intensity inhomogeneity and fuzziness, render the segmentation of heart structures challenging. Figure 1 shows a reference segmentation and the results of our automatic segmentation method.
FIG. 1.
Segmentation results for LV blood-pool, LV myocardium, and RV blood-pool. First column shows the short-axis view, second and third columns show orthogonal long-axis views, and the fourth column shows generated three-dimensional models. Reference (top row) and segmentation obtained from the DMR-UNet model (bottom row). [Color figure can be viewed at wileyonlinelibrary.com]
A comprehensive review of cardiac MR segmentation techniques can be found in Ref. [1,2]. These techniques can be classified based on the amount of prior knowledge used during segmentation. First, the no-prior-based methods rely solely on the image content to segment the heart structures based on intensity thresholds, and edge- and/or region-information. Hence, these methods are often ineffective for the segmentation of ill-defined boundary regions. Second, the deformable models such as active contours and level-set methods incorporate weak-prior information regarding the smoothness of the segmented boundaries; similarly, graph theoretical models assume connectivity between the neighboring pixels providing piece-wise smooth segmentation results. Third, the Active shape and appearance models and Atlas-based methods impose very strong-prior information regarding the geometry of the heart structures and sometimes are too restricted by the training set. These weak-/strong-prior-based methods may overcome segmentation challenges in ill-defined boundary regions but, nevertheless, at a high computational cost. Lastly, Machine Learning-based methods aim to predict the probability of each pixel in the image belonging to the foreground/background class based on either patch-wise or image-wise training. These methods are able to produce fast and accurate segmentation, provided the training set captures the population variability.
In the context of deep learning, Long et al.3 proposed the first fully convolutional network (FCN) for semantic image segmentation, exploiting the capability of convolutional neural networks (CNNs)4–6 to learn task-specific hierarchical features in an end-to-end manner. However, their initial adoption in the medical domain was challenging, due to the limited availability of medical imaging data and associated costly manual annotation. These challenges were later circumvented by patch-based training, data augmentation, and transfer learning techniques.7,8
Specifically, in the context of cardiac image segmentation, Tran9 adapted a FCN architecture for segmentation of various cardiac structures from short-axis MR images. Similarly, Poudel et al.10 proposed a recurrent FCN architecture to leverage interslice spatial dependencies between the 2D cine MR slices. Avendi et al.11 reported improved accuracy and robustness of the LV segmentation by using the output of a FCN to initialize a deformable model. Furthermore, Oktay et al.12 pretrained an autoencoder network on ground-truth segmentations and imposed anatomical constraints into a CNN network by adding l2-loss between the autoencoder representation of the output and the corresponding ground-truth segmentation. Several modifications to the FCN architecture and various post-processing schemes have been proposed to improve the semantic segmentation results as summarized in Ref. [13].
To improve the generalization performance of neural networks, various regularization techniques have been proposed. These include parameter norm penalty (e.g., weight decay,14) noise injection,15 dropout,16 batch normalization,17 adversarial training,18 and multi-task learning (MTL).19 In this paper, we focus on MTL-based network regularization. When a network is trained on multiple related tasks, the inductive bias provided by the auxiliary tasks causes the model to prefer a hypothesis that explains more than one task. This helps the network ignore task-specific noise and hence focus on learning features relevant to multiple tasks, improving the generalization performance.20 Furthermore, MTL reduces the Rademacher complexity20 of the model (i.e., its ability to fit random noise), hence reducing the risk of overfitting. An overview of MTL applied to deep neural networks can be found in Ref. [21].
Multi-task learning has been widely employed in computer vision problems due to the similarity between various tasks being performed. A FCN architecture with a common encoder and task specific decoders was proposed in Ref. [22] to perform joint classification, detection, and semantic segmentation, targeting real-time applications such as autonomous driving. A similar single-encoder-multiple-decoder architecture described in Ref. [23] performs semantic segmentation, depth regression, and instance segmentation, simultaneously. The architecture was further expanded by Ref. [24] to automatically learn the weights for each task based on its uncertainty, obtaining state-of-the-art results.
In the context of medical image analysis, Moeskops et al.25 demonstrated the use of MTL for joint segmentation of six tissue types from brain MRI, the pectoral muscle from breast MRI, and the coronary arteries from cardiac computed tomography angiography (CTA) images, with performance equivalent to networks trained on individual tasks. Similarly, Valindria et al.26 employed a MTL framework to improve the performance for multi-organ segmentation from CT and MR images, exploring various encoder-decoder network architectures. Specific to the cardiac MR applications, Xue et al.27 proposed a network capable of learning multi-task relationship in a Bayesian framework to estimate various local/global LV indices for full quantification of the LV. Similarly, Dangi et al.28 performed joint segmentation and quantification of the LV myocardium using the learned task uncertainties to weigh the losses, improving upon the state-of-the-art results. Most of these MTL methods in medical image analysis aim to perform various clinically relevant tasks simultaneously. However, the focus of this work is on improving the segmentation performance of various FCN architectures using MTL as a network regularizer.
We propose to use the rich information available in the distance map of the segmentation mask as an auxiliary task for the image segmentation network. Since each pixel in the distance map represents its distance from the closest object boundary, this representation is redundant and robust compared to the per-pixel image label used for semantic segmentation. Furthermore, the distance map represents the shape and boundary information of the object to be segmented. Hence, training the segmentation network on the additional task of predicting the distance map is equivalent to enforcing shape and boundary constraints for the segmentation task.
Related work to ours include,29 which take an image and its semantic segmentation as an input and predict the distance transform of the object instances, such that, thresholding the distance map yields the instance segmentation. Similarly,30 represent the boundary of the object instances using a truncated distance map, which is used to refine the instance segmentation result. However, unlike these methods, our goal is not to perform instance segmentation, but to refine the semantic segmentation result using the distance map as an auxiliary task. The most closely related work to ours is presented in Ref. [31] for segmentation of building footprints from satellite images using a MTL framework. In their study, the truncated distance map is predicted at the end of the decoder network and is further used to refine the boundary of the predicted segmentation, resulting in increased model complexity. Unlike that work, we impose a global shape constraint at the bottleneck layer of FCN architectures, using MTL as a network regularizer without increasing the model complexity. The proposed model is customized towards cardiac MRI image segmentation, as we accommodate for slices containing no foreground pixels (in apical and basal regions). Furthermore, we demonstrate better generalization performance of the proposed network with improved cross-dataset segmentation results.
Contributions
In this work, we propose to impose shape and boundary constraints in a CNN framework to accurately segment the heart chambers from cardiac cine MR images. We impose soft-constraints by including a distance map prediction as an auxiliary task in a MTL framework. We extensively evaluate our proposed model on two publicly available cardiac cine MRI datasets. We demonstrate that the addition of a distance map regularization block improves the segmentation performance of three FCN architectures, without increasing the model complexity and inference time. We employ a task uncertainty-based weighing scheme to automatically learn the weights for the segmentation and distance map regression tasks during training, and show that this method improves segmentation performance over the fixed equal-weighting scheme. Additionally, we show that the proposed regularization technique improves the segmentation performance in the challenging apical and basal slices, as well as across several different pathological heart conditions. This improvement is also reflected on the computed clinical indices important for cardiac health diagnosis. Finally, we demonstrate better generalization ability using the proposed regularization technique with significantly improved cross-dataset segmentation performance, without tuning the network to a new data distribution.
2. MATERIALS AND METHODS
2.A. CNN for semantic image segmentation
Let be the input intensity image and be the corresponding image segmentation, with representing a set of C class labels, and representing the image domain. The task of a CNN-based segmentation model, with weights W, is to learn a discriminative function fW(·) that models the underlying conditional probability distribution p(y|x). The output of a CNN model is passed through a softmax function to produce a probability distribution over the class labels, such that, the function fW(·) can be learned by maximizing the likelihood:
| (1) |
where represents the c’th element of the vector fW(x). In practice, the negative log-likelihood –log(p(y|fW(x))) is minimized to learn the optimal CNN model weights, W. This is equivalent to minimizing the cross-entropy loss of the ground-truth segmentation, y, with respect to the softmax of the network output, fW(x).
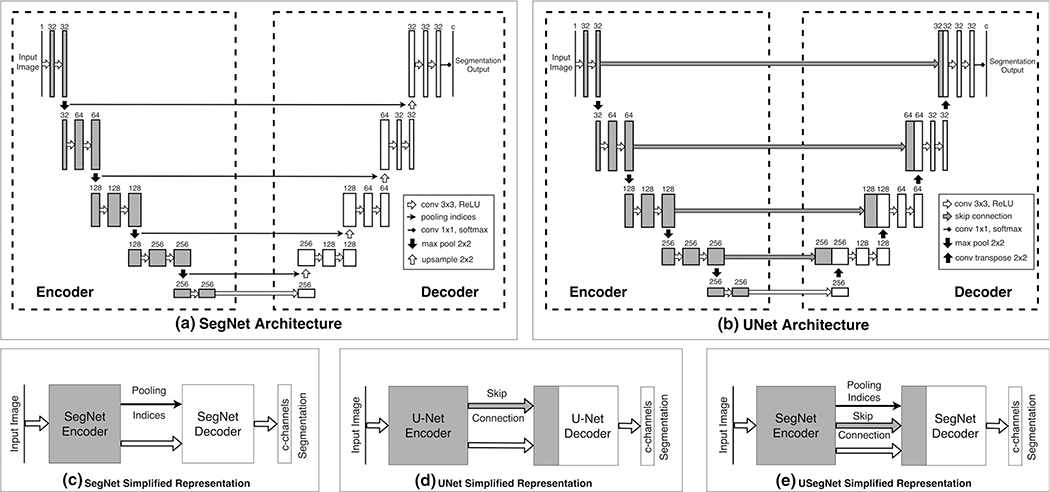
A typical FCN architecture (Fig. 2) for image segmentation consists of an encoder and a decoder network. The encoder network includes multiple pooling (max/average pooling) layers applied after several convolution and non-linear activation layers (e.g., Rectified linear unit (ReLU)32). It encodes hierarchical features important for the image segmentation task. To obtain per-pixel image segmentation, the global features obtained at the bottleneck layer need to be upsampled to the original image resolution using the decoder network. The upsampling filters can either be fixed (e.g., nearest-neighbor or bilinear upsampling), or can be learned during the training (deconvolutional layer). The final output of a decoder network is passed to a softmax classifier to obtain a per-pixel classification.
FIG. 2.
Baseline FCN architectures and their simplified block representation. The input image is passed through several convolution, rectified linear unit (ReLU) nonlinearity, and downsampling operations during encoding. This encoded representation is passed through several convolution, ReLU nonlinearity, and upsampling operations during decoding, such that, the final output has the same spatial resolution as the input. (a) SegNet Architecture: max-pooling operation is used for downsampling, such that the location of the pooled features (i.e., pooling indices) are saved; these pooling-indices are later used to map the features back in their original location during upsampling; (b) UNet Architecture: skip connections from encoder to decoder layers at different resolutions are added for better flow of information; deconvolution filters are learned for upsampling the feature maps. Simplified representations of: (c) SegNet Architecture, (d) UNet Architecture, and (e) USegNet Architecture, using both skip connections as well as the pooling indices for upsampling.
In a SegNet33 [Fig. 2(a)] architecture, the location of feature maps during downsampling (i.e., pooling indices) are saved during encoding, such that the decoder produces sparse feature maps by upsampling its inputs using these pooling indices. These sparse feature maps are then convolved with a trainable filter bank to obtain dense feature maps, and are finally passed through a softmax classifier to produce per-pixel image segmentation. Since the decoder in the SegNet architecture uses only the global features obtained at the bottleneck layer of the encoder, the high frequency details in the segmentation are lost during the upsampling process.
The U-Net architecture34 [Fig. 2(b)] introduced skip connections, by concatenating output of encoder layers at different resolutions to the input of the decoder layers at corresponding resolutions, hence preserving the high frequency details important for accurate image segmentation. Furthermore, the skip connections are known to ease the network optimization35 by introducing multiple paths for backpropagation of the gradients, hence, mitigating the vanishing/exploding gradient problem. Similarly, skip connections also allow the network to learn lower level details in the outer layers and focus on learning the residual global features in the deeper encoder layers. Hence, the U-Net architecture is able to produce excellent segmentation results using limited training data with augmentation, and has been extensively used in medical image segmentation.
We observed that learned deconvolution filters in the original U-Net architecture can be replaced by a SegNet-like decoder to form a hybrid architecture with reduced network parameters. We refer to this modified architecture as U-SegNet [Fig. 2(e)] throughout this paper, and use it as one of the baseline FCN architectures.
2.B. Distance map regularization network
The distance map of a binary segmentation mask can be obtained by computing the Euclidean distance of each pixel from the nearest boundary pixel.36 This representation provides rich, redundant, and robust information about the boundary, shape, and location of the object to be segmented. For a binary segmentation mask, where is the set of foreground pixels, ∂Ω represent the boundary pixels, and d(·,·) is the Euclidean distance between any two pixels, the truncated signed distance map, D(x), is computed as:
| (2) |
where
is the minimum distance of pixel xi ∈ x from the boundary pixels qi ∈ ∂Ω. We truncate the signed distance map at a predefined distance threshold, −T, hence assigning this maximum negative distance to the slices not containing any foreground pixels (i.e., Ω ∈ Ø), indicating all pixels in the slice are far from the foreground (typically in the apical/basal regions of cardiac cine MR images).
The distance map regularization network is a SegNet-like decoder network, upsampling the feature maps obtained at the bottleneck layer of the encoder to the size of the input image, with the number of output channels equal to the number of foreground classes (i.e., C1). For example, for a four-class segmentation problem (C = 4): background, RV blood-pool, LV myocardium, and LV blood-pool, the regularization network has three output channels, predicting the truncated signed distance maps [Eq. (2)] computed from the binary masks of the foreground classes: RV bood-pool, LV myocardium, and LV blood-pool.
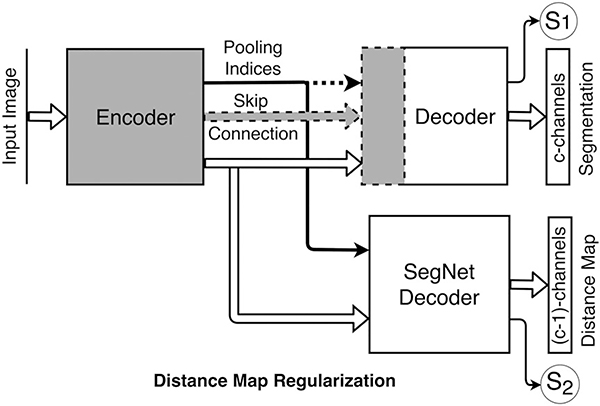
Figure 3 shows the regularization network added to the bottleneck layer of existing FCN architectures. Network training loss is the weighted sum of the cross-entropy loss for segmentation and the mean absolute difference (MAD) loss between the predicted and the reference distance maps. The network also predicts two scalars, uncertainties associated with each task, which are subsequently used to weigh the two losses as described in Section 2.C. Since our goal is to perform semantic segmentation, we do not need the distance map prediction at inference time. Therefore, we remove the regularization block after training, such that, the original FCN architecture remains unchanged. Additionally, we found that the quality (mean absolute difference) of the predicted distance maps is insufficient for improving the predicted segmentations from the standard path (see Fig. S2 in supplement).
FIG. 3.
Distance map regularizer added to the bottleneck layer. The number of distance map channels is one (1) fewer than the number of classes. Segmentation networks optionally use the pooling indices (yes/no) and skip connections (yes/no), shown by dashed lines, during decoding: (a) DMR-SegNet: pooling indices (yes), skip connections (no); (b) DMR-USegNet: pooling indices (yes), skip connections (yes); and (c) DMR-UNet: pooling indices (no), skip connections (yes). Uncertainties associated with each task —S1 corresponding to the semantic segmentation and S2 corresponding to the pixel-wise distance map regression are also predicted, then subsequently used to scale the corresponding losses during network training.
2.C. MTL using uncertainty-based loss weighting
We model the likelihood for a segmentation task as the squashed and scaled version of the model output through a softmax function: where σ is a positive scalar, equivalent to the temperature, for the defined Gibbs/Boltzmann distribution. The magnitude of σ determines how uniform the discrete distribution is, and hence relates to the uncertainty of the prediction measured in entropy. The log-likelihood for the segmentation task can be written as:
| (3) |
where is the c’th element of the vector fW(x). In the last step, a simplifying assumption , which becomes an equality when σ→1, has been made, resulting in a simple optimization objective with improved empirical results.24
Similarly, for the regression task, we define our likelihood as a Lapacian distribution with its mean and scale parameter given by the neural network output:
| (4) |
The log-likelihood for regression task can be written as:
| (5) |
where σ is the neural networks observation noise parameter — capturing the noise in the output. A constant term has been removed for simplicity, as it does not affect the optimization.
For a network with two outputs — continuous output y1 modeled with a Laplacian likelihood, and a discrete output y2 modeled with a softmax likelihood — the joint loss is:
| (6) |
where is the MAD loss of y1 and is the cross-entropy loss of y2. To arrive at Eq. (3), the two tasks are assumed independent. During the training, the joint likelihood loss is optimized with respect to W1, W2 as well as σ1, σ2.
From Eq. (6), we can observe that the losses for individual tasks are weighted by the inverse of their corresponding uncertainties (σ1, σ2) learned during the training. Hence, the task with higher uncertainty will be weighted less and vice versa. Furthermore, the uncertainties cannot grow too large due to the penalty imposed by the last two terms in [Eq. (6)]. In practice, the network is trained to predict the log variance, s:= logσ, for numerical stability and avoiding any division by zero, such that, the positive scale parameter, σ, can be computed via exponential mapping exp(s).
2.D. Clinical datasets
2.D.1. Left ventricle segmentation challenge (LVSC)
This study employed 200 de-identified cardiac MRI image datasets from patients suffering from myocardial infraction and impaired LV contraction available as a part of the STACOM 2011 Cardiac Atlas Segmentation Challenge project37,38 database.* Cine-MRI images in short-axis and long-axis views are available for each case. The images were acquired using the Steady-State Free Precession (SSFP) MR imaging protocol with the following settings: typical thickness ≤10 mm, gap ≤2 mm, TR 30–50 ms, TE 1.6 ms, flip angle 60°, FOV 360 mm, spatial resolution 0.7031 to 2.0833 mm2/pixel and 256 9 256 mm image matrix using multiple scanners from various manufacturers. Corresponding reference myocardium segmentation generated from expert analyzed three-dimensional (3D) surface finite element model are available for 100 training cases throughout the cardiac cycle. The reference segmentation for remaining 100 validation cases are retained by the organizers for an unbiased comparison of segmentation results submitted by the challenge participants.
2.D.2. Automated cardiac diagnosis challenge (ACDC)
This dataset† is composed of short-axis cardiac cine-MR images acquired for 150 patients divided into 5 evenly distributed subgroups: normal, myocardial infarction, dilated cardiomyopathy, hypertropic cardiomyopathy, and abnormal right ventricle, available as a part of the STACOM 2017 ACDC challenge.39 The acquisitions were obtained over a 6-yr period using two MRI scanners of different magnetic strengths (1.5 and 3.0 T). The images were acquired using the SSFP sequence with the following settings: thickness 5 mm (sometimes 8 mm), interslice gap 5 mm, spatial resolution 1.37–1.68 mm2/pixel, 28–40 frames per cardiac cycle. Corresponding manual segmentations for RV blood-pool, LV myocardium, and LV blood-pool, performed by a clinical expert for the end-systole (ES) and end-diastole (ED) phases are provided for 100 training cases, which we use for our cross-validation experiments. Manual segmentations for the remaining 50 test cases are kept privately by the organizers, such that an unbiased comparison of segmentation results can be performed upon submission.
2.E. Data preprocessing and augmentation
SimpleITK40 was used to resample short-axis images to a common resolution of 1.5625 mm2/pixel and crop/zeropad to a common size of 192 × 192 and 256 × 256 for LVSC and ACDC dataset, respectively. Image intensities were clipped at 99th percentile and normalized to zero mean and unit standard deviation. Each dataset was divided into 80% train, 10% validation, and 10% test set with five nonoverlapping folds for cross-validation. Train-validation-test fold was performed randomly over the whole LVSC dataset, whereas it was performed per subgroup (stratified sampling) for the ACDC dataset to maintain even distribution of subgroups over the training, validation, and testing sets. The training images were subjected to random similarity transform with: isotropic scaling of 0.8 to 1.2, rotation of 0° to 360°, and translation of −1/8th to +1/8th of the image size along both x- and y-axes. The training set for LVSC and ACDC dataset included the original images along with augmentation of two and four randomly transformed versions of each image, respectively. We heavily augment the ACDC dataset, as the labels are available only for the ES and ED phases, whereas, lightly augment the LVSC dataset, as the labels are available throughout the cardiac cycle.
2.F. Network training and testing details
Networks implemented in PyTorch‡ were initialized with the Kaiming uniform initializer41 and trained for 30 and 100 epochs for LVSC and ACDC dataset, respectively, with batch size of 15 images. RMS prop optimizer42 with a learning rate of 0.0001 and 0.0005 for single- and multi-task networks, respectively, decayed by 0.99 every epoch was used. We saved the model with best average Dice coefficient on the validation set, and evaluated on the test set.
Networks were trained on NVIDIA Titan Xp GPU. The distance map threshold was selected empirically and set to a large value of 250 pixels, that is, full distance map. The cross-entropy and the MAD loss were initialized with equal weights of 1.0, such that, the optimal weighting was learned automatically. The auxillary task of distance map regression was removed after the network training. The obtained 2D slice segmentations were rearranged into a 3D volume, and the largest connected component for each heart chamber was retained to yield the final segmentation. Model complexity and average timing requirements for training and testing the models is shown in Table I.
Table I.
Model complexity, training, and testing time. The model size for DMR networks are equivalent to corresponding baseline FCN architectures during test time.
| Train time (min/epoch) |
Test time (ms/volume) |
#Parameters (× 106) |
||||
|---|---|---|---|---|---|---|
| ACDC | LVSC | ACDC | LVSC | Train | Test | |
| SegNet | 2.49 | 14.91 | 70 | 67 | 2.96 | 2.96 |
| USegNet | 2.41 | 14.49 | 70 | 67 | 3.75 | 3.75 |
| UNet | 2.65 | 15.50 | 72 | 68 | 4.10 | 4.10 |
| DMR-SegNet | 4.44 | 20.57 | 70 (157) | 63 (94) | 3.56 | 2.96 |
| DMR-USegNet | 4.84 | 19.03 | 73 (158) | 65 (96) | 4.35 | 3.75 |
| DMR-UNet | 4.85 | 21.16 | 75 (160) | 67 (97) | 4.70 | 4.10 |
The inference time for DMR networks without removing the regularization block are shown in brackets.
2.G. Evaluation metrics
We use overlap and surface distance measures to evaluate the segmentation. Additionally, we evaluate the clinical indices associated with the segmentation.
2.G.1. Dice and Jaccard coefficients
Given two binary segmentation masks, A and B, the Dice and Jaccard coefficient are defined as:
| (7) |
where |·| gives the cardinality (i.e. the number of non-zero elements) of each set. Maximum and minimum values (1.0 and 0.0, repectively) for Dice and Jaccard coefficient occur when there is 100% and 0% overlap between the two binary segmentation masks, respectively.
2.G.2. Mean surface distance and Hausdorff distance
Let, SA and SB, be surfaces (with NA and NB points, respectively) corresponding to two binary segmentation masks, A and B, respectively. The mean surface distance (MSD) is defined as:
| (8) |
Similarly, Hausdorff distance (HD) is defined as:
| (9) |
where
is the minimum Euclidean distance of point p from the points q ∈ S. Hence, MSD computes the mean distance between the two surfaces, whereas, HD computes the largest distance between the two surfaces, and is sensitive to outliers.
2.G.3. Ejection fraction and myocardial mass
Ejection Fraction (EF) is an important cardiac parameter quantifying the cardiac output. EF is defined as:
| (10) |
where EDV is the end-diastolic volume and ESV is the end-systolic volume. Similarly, the myocardial mass can be computed from the myocardial volume as:
| (11) |
The correlation coefficients for the EF and myocardial mass computed from the ground-truth vs those computed from the automatic segmentation is reported. Correlation coefficient of +1 (−1) represents perfect positive (negative) linear relationship, whereas that of 0 represents no linear relationship between two variables.
2.G.4. Limits of agreement
To compare the clinical indices computed from the ground-truth vs those obtained from the automatic segmentation, we take the difference between each pair of the two observations. The mean of these differences is termed as bias, and the 95% confidence interval, mean ± 1.96 × standard deviation (assuming a Gaussian distribution), is termed as limits of agreement (LoA).
3. RESULTS
3.A. Segmentation and clinical indices evaluation
The proposed distance map regularized (DMR) SegNet, USegNet, and UNet models along with the baseline models were trained for the joint segmentation of RV blood-pool, LV myocardium, and LV blood-pool from the ACDC challenge dataset. The provided reference segmentation and the corresponding automatic segmentation obtained from the DMR-UNet model for a test patient is shown in Fig. 1. Automatic segmentation obtained from all networks, for ED and ES phases, are evaluated against the reference segmentation and summarized in Table II(a); also shown is the evaluation of subsequently computed clinical indices in Table II(b).
Table II.
Evaluation of the average segmentation results on ACDC dataset for RV blood-pool, LV myocardium, and LV blood-pool (mean value reported), obtained from all networks against the provided reference segmentation.
| End diastole (ED) |
End systole (ES) |
|||||||||||
| SN | DMR SN | USN | DMR USN | UNet | DMR UNet | SN | DMR SN | USN | DMR USN | UNet | DMR UNet | |
| (a) Evaluation of Average (across all heart chambers) Segmentation Results | ||||||||||||
| Dice (%) | 91.1 | 91.7** | 91.5 | 92.0** | 91.6 | 92.2** | 87.3 | 88.0* | 87.7 | 88.7** | 87.2 | 88.8* |
| Jaccard (%) | 84.0 | 85.1** | 84.7 | 85.5** | 85.0 | 85.9** | 78.1 | 79.3* | 78.7 | 80.3** | 78.3 | 80.4* |
| MSD (mm) | 0.55 | 0.53* | 0.58 | 0.52* | 0.54 | 0.53* | 0.92 | 0.85 | 0.92 | 0.84 | 1.08 | 0.83 |
| HD (mm) | 10.26 | 9.87 | 10.26 | 9.67 | 10.03 | 9.52 | 11.33 | 10.31* | 11.66 | 10.91 | 12.61 | 10.96* |
| Correlation coefficient |
Bias+LOA |
|||||||||||
| SN | DMR SN | USN | DMR USN | UNet | DMR UNet | SN | DMR SN | USN | DMR USN | UNet | DMR UNet | |
| (b) Evaluation of the Clinical Indices | ||||||||||||
| LV EF | 0.939 | 0.947 | 0.944 | 0.970 | 0.962 | 0.963 | 1.00 (13.15) | 0.31 (12.44) | 0.58 (12.57) | −0.42 (9.24) | 0.31 (10.41) | 0.40 (10.40) |
| RV EF | 0.874 | 0.871 | 0.866 | 0.895 | 0.856 | 0.870 | 1.04 (17.40) | 1.77 (17.34) | 0.85 (17.40) | 0.38 (15.42) | 0.09 (18.94) | 0.29 (18.30) |
| Myo Mass | 0.948 | 0.970 | 0.958 | 0.973 | 0.933 | 0.978 | 3.10 (32.94) | −0.43 (25.17) | 0.35 (29.65) | 0.21 (23.89) | 2.85 (37.39) | 0.80 (21.75) |
The statistical significance of the results for DM regularized model compared against the baseline model are represented by * and ** for P-values < 0.05 and 0.005, respectively. Also shown are the clinical indices evaluated for each heart chamber. The best performing model for each metric has been highlighted in bold. SN: SegNet, USN: USegNet, UNet: UNet.
Best performing model for the ED and ES phases are shown in bold case.
We observe consistent improvement in the average segmentation performance of the models after the DM-regularization. Specifically, there is statistically significant improvement§ on several segmentation metrics for all evaluated models. Same results manifest onto the clinical indices with better correlation and LoA on both EF and myocardium mass. Furthermore, the DMR-UNet model outperforms other evaluated networks in many segmentation metrics.
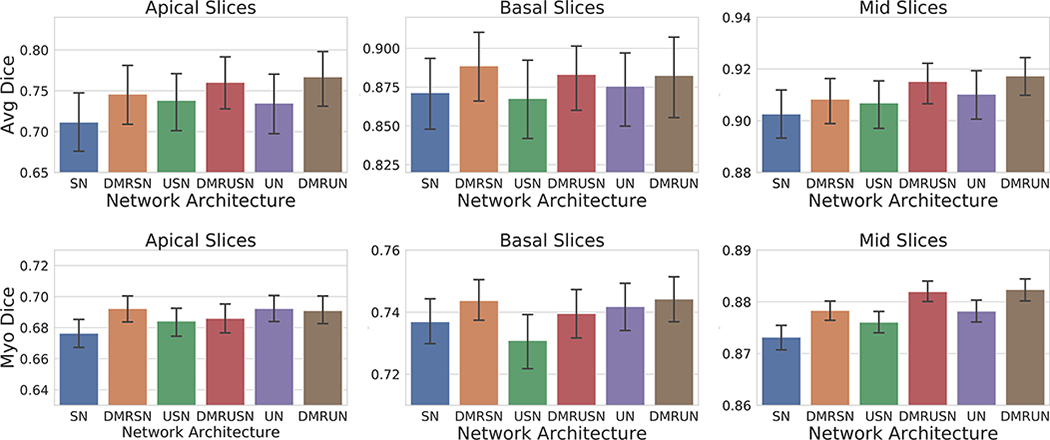
To further analyze the improvement in segmentation performance, we performed a regional analysis by subdividing the slices into apical (25% slices in the apical region and beyond), basal (25% slices in the basal region and beyond), and mid-region (remaining 50% mid slices), based on the reference segmentation. From Fig. 4(a), we can observe consistent improvement in segmentation performance at the problematic apical and basal slices39; however, due to the small size of these regions, the improvement does not have a large effect on the overall performance, though it is of significance when constructing patient specific models of the heart for simulation purposes.43 We postulate that the additional constraint imposed by a very high negative distance assigned to empty apical/basal slices prevents the network from over-segmenting these regions, hence, improving the regional dice overlap and effectively reducing the overall Hausdorff distance.
FIG. 4.
Mean and 95% bootstrap confidence interval for average Dice coefficient on apical, basal, and mid slices. Top: Average Dice coefficient for LV blood-pool, LV myocardium, and RV blood-pool segmentation on ACDC dataset (100 volumes). Bottom: Dice coefficient for myocardium segmentation on LVSC dataset (1050 volumes). SegNet: SN, DMR-SegNet: DMRSN, USegNet: USN, DMR-USegNet: DMRUSN, UNet: UN, DMR-UNet: DMRUN. [Color figure can be viewed at wileyonlinelibrary.com]
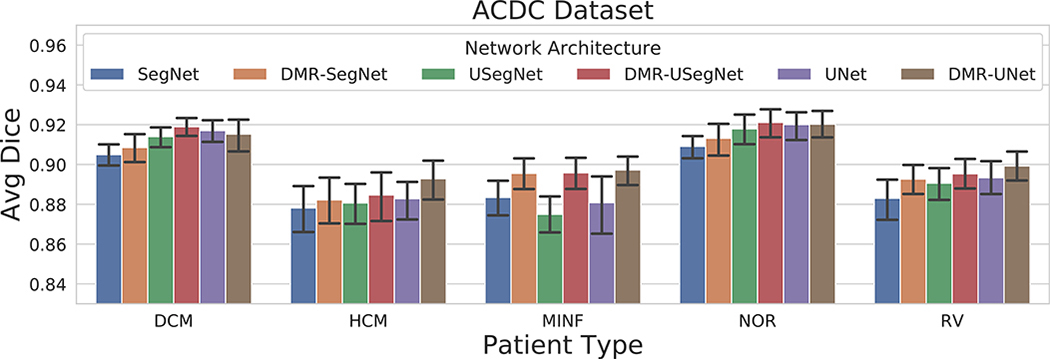
To study the effect of the distance map regularization across the five patient subgroups, we plot the average Dice coefficient for each subgroup computed for all six models in Fig. 5. As expected, we observe the segmentation performance is better for the normal patients in comparison to the pathological cases. Furthermore, we observe consistent improvement in segmentation performance after the distance map regularization for all patient subgroups.
FIG. 5.
Mean and 95% bootstrap confidence interval of average Dice coefficient for segmentation results on ACDC dataset obtained from several architectures divided according to the five subgroups: DCM — dilated cardiomyopathy, HCM — hypertrophic cardiomyopathy, MINF — previous myocardial infarction, NOR — normal subjects, and RV — abnormal right ventricle. [Color figure can be viewed at wileyonlinelibrary.com]
We segmented the heart structures from 50 patients ACDC held-out test set and submitted to the challenge organizers. Majority voting prediction of ensemble of DMR-UNet models trained for fivefold cross-validation followed by a 3D connected component analysis yielded the final segmentation. Table III shows the comparison of our segmentation results against the top three methods submitted to the challenge. Baumgartner et al.44 tested several architectures and found that 2D U-Net with a cross-entropy loss performed the best. Khened et al.45 used a 2D U-Net with dense blocks and an inception first layer to obtain the segmentation. Isensee et al. ensembled 2D and 3D U-Net architectures trained with a Dice loss to obtain the best result in the challenge. Our 2D DMR-UNet model is able to perform as good or better than the other two 2D methods; however, the combination of 2D and 3D context has marginal improvement in the Dice overlap metric. Based on this observation, we believe the ensemble of 2D and 3D DMR-UNet model should be able to perform as good or better than,46 which is not the main objective of this work. Nonetheless, we can observe the constraint imposed by the DM regularization is successful in reducing the errors in apical/basal regions, manifested in the improved Hausdorff distance.
Table III.
Comparison of the segmentation results obtained from the DMR-UNet model against the top three ACDC challenge participants, evaluated on the held-out 50 patient challenge test set.
| End diastole (ED) |
End systole (ES) |
EF |
||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| LV |
RV |
Myo |
LV |
RV |
Myo |
LV Corr | RV Corr | |||||||||
| Dice | HD | Dice | HD | Dice | HD | Corr | Dice | HD | Dice | HD | Dice | HD | Corr | |||
| Baumgartner44 | 0.96 | 6.53 | 0.93 | 12.67 | 0.89 | 8.70 | 0.982 | 0.91 | 9.17 | 0.88 | 14.69 | 0.90 | 10.64 | 0.983 | 0.988 | 0.851 |
| Khened46 | 0.96 | 8.13 | 0.94 | 13.99 | 0.89 | 9.84 | 0.990 | 0.92 | 8.97 | 0.88 | 13.93 | 0.90 | 12.58 | 0.979 | 0.989 | 0.858 |
| Isensee46 | 0.97 | 7.38 | 0.95 | 10.12 | 0.90 | 8.72 | 0.989 | 0.93 | 6.91 | 0.90 | 12.14 | 0.92 | 8.67 | 0.985 | 0.991 | 0.901 |
| DMR-UNet | 0.96 | 6.05 | 0.94 | 9.52 | 0.89 | 7.92 | 0.989 | 0.92 | 8.16 | 0.88 | 13.05 | 0.91 | 8.39 | 0.987 | 0.989 | 0.851 |
The Dice metric, Hausdorff Distance (HD), and correlation of clinical indices for all three heart chambers is shown.
Best performing model for the ED and ES phases are shown in bold case.
Table IV shows the segmentation performance evaluated on the LVSC dataset, demonstrating superior performance of the DM regularized models over their baseline. Specifically, there is statistically significant improvement on the Dice and Jaccard metric for the ED phase. Furthermore, the correlation and LoA for the myocardial mass improves after network regularization. The improvement in performance is consistent across different heart regions as shown in Fig. 4(b).
Table IV.
Evaluation of the segmentation results on LVSC dataset for LV myocardium (mean values reported), obtained from all networks against the provided reference segmentation.
| End diastole (ED) |
End systole (ES) |
|||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SN | DMR SN | USN | DMR USN | UNet | DMR UNet | SN | DMR SN | USN | DMR USN | UNet | DMR UNet | |
| Dice (%) | 82.2 | 83.0* | 82.5 | 83.2** | 83.1 | 83.6 | 83.5 | 84.2 | 83.8 | 84.3* | 84.3 | 84.6 |
| Jaccard (%) | 70.0 | 71.1* | 70.4 | 71.5** | 71.3 | 72.0 | 71.9 | 72.9 | 72.4 | 73.0* | 73.0 | 73.5 |
| MSD (mm) | 0.78 | 0.74 | 0.79 | 0.72* | 0.74 | 0.70 | 0.81 | 0.77 | 0.77 | 0.78 | 0.74 | 0.75 |
| HD (mm) | 13.20 | 13.14 | 13.67 | 13.12 | 12.98 | 12.80 | 12.96 | 12.96 | 12.71* | 13.71 | 13.08 | 12.51 |
| Mass (Corr) | 0.908 | 0.937 | 0.923 | 0.938 | 0.917 | 0.936 | 0.921 | 0.935 | 0.929 | 0.926 | 0.939 | 0.922 |
| Mass (gram) (Bias+LOA) | 2.56 (35.25) | −0.92 (29.52) | 3.91 (32.48) | 3.34 (29.08) | 2.88 (33.75) | 0.06 (29.92) | 5.48 (32.49) | 1.96 (29.58) | 5.04 (30.92) | 5.49 (31.49) | 5.18 (28.79) | 2.56 (32.18) |
The statistical significance of the results for DM regularized model compared against the baseline model are represented by * and ** for P-values < 0.05 and 0.005, respectively. The best performing model for each metric has been highlighted. SN: SegNet, USN: USegNet, UNet: UNet.
Best performing model for the ED and ES phases are shown in bold case.
We segmented the myocardium from the LVSC held-out validation set of 100 patients. Majority voting prediction from ensemble of DMR-UNet models trained for five-fold cross-validation followed by a 3D connected-component analysis yielded the final segmentation. Table V shows our segmentation results (computed per slice) compared against several other semi-/fully automatic algorithms. Reported segmentation results are computed against the consensus segmentation (CS*) built from multiple challenge submissions.38 Segmentation results for the four challenge participants — AU,47 AO,48 SCR,49 and INR,50 and the details on segmentation evaluation metrics can be found in the challenge summary report.38 The AU method47 used the interactive guide-point modeling technique to fit a finite element cardiac model to the CMR data and required expert approval of all slices and all frames. This segmentation was provided as the reference segmentation to the challenge participants. The CNN regression CNR method51 regressed the endo- and epicardium contours in polar coordinates, while manually eliminating the problematic slices beyond the apex and base of the heart, hence, obtaining a good segmentation result. The mean (std dev) of Jaccard coefficients computed for our DMR-UNet model in apical, mid, and basal slices are 0.66 (0.18), 0.77 (0.12), and 0.74 (0.17), respectively. Our DMR-UNet model has similar performance to competing fully automatic segmentation algorithms based on the fully convolutional network FCN9 and the densely connected FCN (DFCN)45 architectures. The DFCN method involves a computationally expensive region of interest (ROI) identification based on a Fourier transform applied across the cardiac cycle, followed by the circular Hough transform; whereas our method requires minimal pre-processing.
Table V.
Comparison of the LV myocardium segmentation results on the LVSC validation set against the consensus segmentation (CS*) as described in.38
| Method | SA/FA | Jaccard | Sensitivity | Specificity | PPV | NPV |
|---|---|---|---|---|---|---|
| AU47 | SA | 0.84 (0.17) | 0.89 (0.13) | 0.96 (0.06) | 0.91 (0.13) | 0.95 (0.06) |
| CNR51 | SA | 0.77 (0.11) | 0.88 (0.09) | 0.95 (0.04) | 0.86 (0.11) | 0.96 (0.02) |
| FCN9 | FA | 0.74 (0.13) | 0.83 (0.12) | 0.96 (0.03) | 0.86 (0.10) | 0.95 (0.03) |
| DFCN45 | FA | 0.74 (0.15) | 0.84 (0.16) | 0.96 (0.03) | 0.87 (0.10) | 0.95 (0.03) |
| DMR-UNet | FA | 0.74 (0.16) | 0.85 (0.16) | 0.95 (0.03) | 0.86 (0.10) | 0.95 (0.03) |
| AO48 | SA | 0.74 (0.16) | 0.88 (0.15) | 0.91 (0.06) | 0.82 (0.12) | 0.94 (0.06) |
| SCR49 | FA | 0.69 (0.23) | 0.74 (0.23) | 0.96 (0.05) | 0.87 (0.16) | 0.89 (0.09) |
| INR50 | FA | 0.43 (0.10) | 0.89 (0.17) | 0.56 (0.15) | 0.50 (0.10) | 0.93 (0.09) |
Lastly, the segmentation performance on the LVSC dataset (Table V) is significantly lower than ACDC dataset (Table III) due to large variability and noise exhibited by the LVSC data as compared to the ACDC dataset.
3.B. Cross-dataset evaluation (transfer learning)
To analyze the generalization ability of our proposed distance map regularized networks, we performed a cross-dataset segmentation evaluation. The networks trained on ACDC dataset for fivefold cross-validation were tested on the LVSC dataset, and vice versa; such that, the majority voting scheme produced the final per-pixel segmentation. We observe a significant boost in Dice coefficient of 5% to 12% for distance map regularized networks over their baseline models when trained on ACDC and tested on LVSC dataset (194 ED and ES volumes), as shown in Table VI(a). Similarly, the distance map regularized models significantly outperform the baseline models by 23–42% improvement in Dice coefficient, when trained on LVSC and tested on ACDC dataset (200 ED and ES volumes), as shown in Table VI(b). The improvement in generalization performance for the regularization networks trained on LVSC dataset is higher, likely due to the availability of large number of heterogeneous training examples. Similar improvement can be observed in the MSD and HD metric. We want to emphasize that our networks are trained separately on each dataset and are completely unaware of the new data distribution, unlike a typical domain adaptation52 setting. Nonetheless, the distance map regularized networks are able to generalize better to a new dataset compared to the baseline models.
Table VI.
Cross-dataset segmentation evaluation for LV myocardium segmentation (mean values reported).
| End diastole (ED) |
End systole (ES) |
|||||||||||
| SN | DMR SN | USN | DMR USN | UNet | DMR UNet | SN | DMR SN | USN | DMR USN | UNet | DMR UNet | |
| (a) Trained on ACDC and tested on LVSC (194 volumes) | ||||||||||||
| Dice(%) | 70.4 | 73.3** | 68.3 | 76.6** | 72.3 | 76.7** | 68.0 | 71.9** | 65.5 | 74.9** | 69.7 | 76.4** |
| Jaccard(%) | 55.6 | 58.9** | 53.6 | 62.9** | 58.0 | 63.1** | 53.3 | 58.1** | 50.8 | 61.5** | 55.5 | 63.1** |
| MSD(mm) | 2.68 | 2.07** | 3.33 | 1.80** | 2.46 | 1.80** | 3.56 | 2.93** | 4.19 | 2.58** | 3.49 | 2.35** |
| HD(mm) | 25.01 | 22.44** | 26.93 | 20.33** | 24.61 | 20.16** | 25.96 | 22.62** | 27.37 | 21.67** | 25.68 | 20.98** |
| End diastole (ED) |
End systole (ES) |
|||||||||||
| SN | DMR SN | USN | DMR USN | UNet | DMR UNet | SN | DMR SN | USN | DMR USN | UNet | DMR UNet | |
| (b) Trained on LVSC and tested on ACDC (200 volumes) | ||||||||||||
| Dice(%) | 69.5 | 78.4** | 62.5 | 80.1** | 62.1 | 80.2** | 57.7 | 77.6** | 51.9 | 79.3** | 50.3 | 79.1** |
| Jaccard(%) | 56.5 | 66.3** | 49.3 | 68.2** | 49.3 | 68.5** | 45.4 | 65.3** | 40.1 | 67.3** | 38.8 | 67.1** |
| MSD(mm) | 4.92 | 1.77** | 6.75 | 1.30** | 6.29 | 1.59** | 9.59 | 2.53** | 13.27 | 2.35** | 10.97 | 2.52** |
| HD(mm) | 26.04 | 17.06** | 29.08 | 13.93** | 29.50 | 14.16** | 35.13 | 19.25** | 39.60 | 18.77** | 37.44 | 19.58** |
The statistical significance of the results for DM regularized model compared against the baseline model are represented by * and ** for P-values < 0.01 and 0.001, respectively. SN: SegNet, USN: USegNet, UNet: UNet.
Best performing model for the ED and ES phases are shown in bold case.
We further analyzed the feature maps across different layers of the baseline and distance map regularized networks (supplementary material Fig. S3). We can observe the baseline models preserve the intensity information and propagate it throughout the network; hence, they are more sensitive to the dataset-specific intensity distribution. In contrast, the multi-task regularized networks focus more on the edges and other discriminative features, producing sparse feature maps, while ignoring dataset-specific intensity distribution. Moreover, from the feature maps at the decoding layers, we observe a clear delineation of several cardiac structures in the regularized network, while those for the baseline models are less discriminative, and contain information about all structures present in the image. Hence, we verify that MTL-based distance map regularization helps the network learn generalizable features important for the segmentation task, demonstrated by their excellent transfer learning capabilities [see Supplementary Materials for details on feature visualization (Fig. S3) and network learning curves showing the robustness of distance map regularized models against overfitting (Fig. S4)].
3.C. Comparison with models trained on different loss functions
Several modifications to the categorical cross-entropy loss have been proposed to improve segmentation results. A popular variant is weighted categorical cross-entropy, where the loss contribution of each class is multiplied by a weight proportional to the inverse frequency of that class in the training set. We compute the weights as , where c = {0,1,…,C–1} for C classes and Nc is the number of pixels of class c in the training set. The weights wc are then normalized by their median value during weighted categorical cross-entropy loss computation.
Similarly, Ronneberger et al.34 proposed a spatial weighting scheme, where the pixels closer to segmentation boundaries were assigned higher weights, to incentify the network to produce better segmentation results by avoiding misclassification of boundary pixels. The spatial weight map is computed as:
| (12) |
where wc is the weight map to balance the class frequencies, and d1 and d2 are the distances to the border of nearest and second nearest object classes. In our experiments, we set w0 = 1:0 and σ = 5.0.
Table VII summarizes the segmentation results obtained on ACDC dataset for UNet models trained on cross-entropy loss with several weighting schemes against the proposed DMR-UNet model. Although class frequency weighted training has been found to improve the performance of a model on limited availability of examples for some classes, in our segmentation problem, we have a large number of examples (pixels) for each class. Furthermore, since the number of background pixels is very high compared to other classes, the weight assigned to background pixels is extremely low, hence discouraging the model to segment ambiguous pixels as a background class, resulting in degraded segmentation performance, as shown in Table VII. Moreover, while the spatial weighting scheme only provides a slight improvement over the unweighted cross-entropy loss, there is good improvement in the distance metric due to the emphasis on the boundary pixels. Nevertheless, Table VII clearly shows that our proposed DMR-UNet model significantly outperforms all other weighting schemes, yielding highest overlap and lowest distance metrics.
Table VII.
Evaluation of the segmentation results on ACDC dataset for RV blood-pool, LV myocardium, and LV blood-pool (mean values reported), obtained from different weighting schemes of the categorical cross-entropy loss function.
| End diastole (ED) |
End systole (ES) |
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| None | Class | Spatial | Spatial w/Class | DMR UNet | None | Class | Spatial | Spatial w/Class | DMR UNet | |
| Dice (%) | 91.6 | 89.2 | 91.7 | 91.8 | 92.2 | 87.2 | 84.7 | 88.1 | 87.8 | 88.8 |
| Jaccard (%) | 85.0 | 81.2 | 85.1 | 85.2 | 85.9 | 78.3 | 74.6 | 79.3 | 79.0 | 80.4 |
| MSD (mm) | 0.54 | 0.71 | 0.53 | 0.51 | 0.53 | 1.08 | 1.25 | 0.89 | 0.95 | 0.83 |
| HD (mm) | 10.03 | 10.48 | 10.06 | 9.99 | 9.52 | 12.61 | 12.60 | 11.31 | 12.16 | 10.96 |
UNet model trained with cross-entropy loss: without any weighting, class frequency weighting, spatial weighting (with uniform class weight), and spatial with class frequency weighting, compared against the proposed DMR-UNet model.
Best performing model for the ED and ES phases are shown in bold case.
4. DISCUSSION
We performed an extensive study on the effects of hyperparameters on the performance of the proposed regularization framework. Here we summarize the effects of the learned vs fixed task weighting, and various choices of the distance map threshold. Furthermore, we analyzed the distribution of network weights before and after regularization.
Task Weighting
At first, we initialized the weights for the cross-entropy and MAD loss equally to 1.0. However, the learned weights for the cross-entropy and MAD loss were around 0.01 and 17, and 0.02 and 13 for ACDC and LVSC dataset, respectively, for the best performing models on the validation set.
To determine the effect of learned task weighting scheme presented in Section 2.C, we analyzed the average Dice coefficient of the test set segmentation results for both ACDC (100 volumes) and LVSC (1050 volumes across the full cardiac cycle) datasets with fixed vs learned weighting. From Fig. 6, we can observe a significant improvement in average Dice coefficient (based on the 95% bootstrap confidence intervals) with learned weights compared to fixed (equal) weighting. Since the scales of the two losses are different, the equal weighting scheme emphasizes the distance map regression task more than it should, hence deteriorating the segmentation performance. In contrast, the learned task weighting scheme is able to automatically weigh the two losses, bringing them to a similar scale, such that the two tasks are given equal importance, ultimately improving the segmentation performance.
FIG. 6.
Mean and 95% bootstrap confidence interval of average Dice coefficient for learned vs fixed equal weighting. Learned task weighting statistically significantly improves the segmentation performance. [Color figure can be viewed at wileyonlinelibrary.com]
Effect of Distance Map Threshold
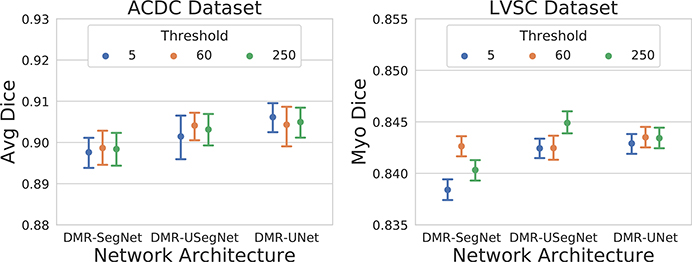
We selected three extreme values for the distance map threshold: 5, 60, and 250 pixels. The network weights for cross-entropy and MAD loss were equally initialized to (1,1) and trained with automatically learned task weighting for a fixed number of epochs. The average Dice coefficient on the test-set obtained from the best performing models on the validation-set across five-fold cross-validation is summarized in Fig. 7. We observe similar performance for different threshold values, demonstrating the low sensitivity of the proposed method to the distance map threshold. Hence, we decided to use a very high threshold of 250 pixels, which is almost equivalent to regressing the full distance map and neglecting this hyper-parameter.
FIG. 7.
Mean and 95% bootstrap confidence interval of average Dice coefficient for a range of distance map thresholds. [Color figure can be viewed at wileyonlinelibrary.com]
Network Weight Distribution
We also analyzed the weight distribution of the network before and after distance map regularization, as shown in the Supplementary Materials (Fig. S5). We observe the number of non-zero weights increase after the distance map regularization, hence, better utilizing the network capacity. A similar flattening of network weight histogram has been reported for the dropout regularization and Bayesian neural networks,53 both reducing the overfitting and hence improving generalization. Specifically, the network weights are randomly dropped during dropout, forcing the network to use the remaining weights to identify the patterns in data (spreading the weight histogram), hence creating an ensemble effect with reduced overfitting and improved generalization. We observe a similar pattern in the weight distribution after the distance map regularization.
5. CONCLUSIONS
In this work, we proposed and implemented a MTL-based regularization method for fully convolutional networks for semantic image segmentation and demonstrated its benefits in the context of cardiac MR image segmentation. To implement the proposed method, we appended a decoder network at the bottleneck layer of existing FCN architectures to perform an auxiliary task of distance map prediction, which is removed after training.
We automatically learned the weighting of the tasks based on their uncertainty. As the distance map contains robust information regarding the shape, location, and boundary of the object to be segmented, it facilitates the FCN encoder to learn robust global features important for the segmentation task.
Our experiments verify that introducing the distance map regularization improves the segmentation performance of three FCN architectures for both binary and multi-class segmentation across two publicly available cardiac cine MRI datasets featuring significant patient anatomy and image variability. Specifically, we observed consistent improvement in segmentation performance in the challenging apical and basal slices in response to the soft-constraints imposed by the distance map regularization. We also showed consistent segmentation improvement on all five patient pathology in the ACDC dataset. Furthermore, these improvements were also reflected on the computed clinical indices important for the diagnosis of various heart conditions. Lastly, we demonstrated the proposed regularization significantly improved the generalization ability of the networks on cross-dataset segmentation (transfer learning), without being aware of the new data distribution, with 5% to 42% improvement in average Dice coefficient over the baseline FCN architectures.
Supplementary Material
Figure S1: Ground-truth and automatic segmentation obtained from all trained models for a test patient. In each subfigure, the segmentation obtained from the baseline and regularized model are overlaid onto the volume and shown in first and third rows, respectively; corresponding disagreement (in black) between the obtained segmentations and the ground-truth is shown in second and fourth rows, respectively.
Figure S2: Visualization of (a) the segmentation obtained by thresholding the predicted distance map and (b) absolute error between the ground-truth and predicted distance maps for all chambers. Shown is only a cropped region around the heart, the error in predicted distance map is higher for the regions farther from the heart.
Figure S3: Feature maps visualized for the UNet (left column) and DMR-UNet (right column) model. We can observe the UNet model preserves the intensity information and propagates it throughout the network, hence, is more sensitive to the dataset-specific intensity distribution. In contrast, the DMR-UNet model focuses more on the edges and other discriminative features, producing sparse feature maps, while ignoring dataset-specific intensity distribution. However, the results obtained for intra-dataset segmentation (shown here for ACDC dataset) is similar for both models, whereas, there is a significant improvement in cross-dataset segmentation after distance map regularization.
Figure S4: Mean and 95% bootstrap confidence interval for training and validation losses (a and b), and the learned weights for cross-entropy and mean absolute difference losses (c), on ACDC and LVSC dataset across five-fold cross-validation. Since the cross-entropy loss is harder to interpret, we plot the corresponding dice loss computed during training and validation. We can observe lower difference between the training and validation dice loss for the distance map regularized models, demonstrating their ability to prevent overfitting.
Figure S5: Weights distribution before and after distance map regularization for models trained across fivefold cross-validation. We can observe the number of non-zero weights increases after the distance map regularization, hence, better utilizing the network capacity.
ACKNOWLEDGMENT
Research reported in this publication was supported by the National Institute of General Medical Sciences of the National Institutes of Health under Award No. R35GM128877 and by the Office of Advanced Cyber infrastructure of the National Science Foundation under Award No. 1808530. Ziv Yaniv’s work was supported by the Intramural Research Program of the U.S. National Institutes of Health, National Library of Medicine.
Footnotes
CONFLICT OF INTEREST
The authors have no conflict to disclose.
SUPPORTING INFORMATION
Additional supporting information may be found online in the Supporting Information section at the end of the article.
Wilcoxon signed-rank test performed for statistical significance test
Contributor Information
Shusil Dangi, Center for Imaging Science, Rochester Institute of Technology, Rochester, NY 14623, USA.
Cristian A. Linte, Center for Imaging Science, Rochester Institute of Technology, Rochester, NY 14623, USA Biomedical Engineering, Rochester Institute of Technology, Rochester, NY 14623, USA.
Ziv Yaniv, MSC LLC., Rockville, MD 20852, USA; National Institute of Allergy and Infectious Diseases, NIH, Bethesda, MD 20814, USA.
REFERENCES
- 1.Peng P, Lekadir K, Gooya A, Shao L, Petersen SE, Frangi AF. A review of heart chamber segmentation for structural and functional analysis using cardiac magnetic resonance imaging. Magn Reson Mater Phys Biol Med. 2016;29:155–195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Petitjean C, Dacher J-N. A review of segmentation methods in short axis cardiac MR images. Med Image Anal. 2011;15:169–184. [DOI] [PubMed] [Google Scholar]
- 3.Long J, Shelhamer E, Darrell T. Fully Convolutional Networks for Semantic Segmentation. in IEEE CVPR; 2015. [DOI] [PubMed] [Google Scholar]
- 4.Lecun Y, Bottou L, Bengio Y, Haffner P. Gradient-based learning applied to document recognition. Proceedings of the IEEE 1998;86:2278–2324. [Google Scholar]
- 5.Goodfellow I, Bengio Y, Courville A. Deep Learning. Cambridge: MIT Press; 2016. [Google Scholar]
- 6.LeCun Y, Bengio Y, Hinton G. Deep learning. Nature. 2015;521:436–444. [DOI] [PubMed] [Google Scholar]
- 7.Shen D, Wu G, Suk H-I. Deep learning in medical image analysis. Annu Rev Biomed Eng 2017;19:221–248. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Litjens G, Kooi T, Bejnordi BE, et al. A survey on deep learning in medical image analysis. Med Image Anal. 2017;42:60–88. [DOI] [PubMed] [Google Scholar]
- 9.Tran PV. A Fully Convolutional Neural Network for Cardiac Segmentation in Short-Axis MRI. CoRR abs/1604.00494. 2016. [Google Scholar]
- 10.Poudel RPK, Lamata P, Montana G. Recurrent fully convolutional neural networks for multi-slice MRI cardiac segmentation Reconstruction, Segmentation, and Analysis of Medical Images. Cham: Springer International Publishing; 2017:83–94. [Google Scholar]
- 11.Avendi M, Kheradvar A, Jafarkhani H. A combined deep-learning and deformable-model approach to fully automatic segmentation of the left ventricle in cardiac MRI. Med Image Anal. 2016;30:108–119. [DOI] [PubMed] [Google Scholar]
- 12.Oktay O, Ferrante E, Kamnitsas K, et al. Anatomically constrained neural networks (ACNNs): application to cardiac image enhancement and segmentation. IEEE Trans Med Imaging. 2018;37:384–395. [DOI] [PubMed] [Google Scholar]
- 13.Garcia-Garcia A, Orts-Escolano S, Oprea S, Villena-Martinez V, Rodríguez JG. A Review on Deep Learning Techniques Applied to Semantic Segmentation. CoRR abs/1704.06857; 2017. [Google Scholar]
- 14.Krogh A, Hertz JA. A Simple Weight Decay Can Improve Generalization, NIPS’91 pages 950–957, San Francisco, CA, USA; 1991. [Google Scholar]
- 15.Vincent P, Larochelle H, Bengio Y, Manzagol P-A. Extracting and Composing Robust Features with Denoising Autoencoders, ICML ‘08, pages 1096–1103, New York, NY, USA: ACM; 2008. [Google Scholar]
- 16.Srivastava N, Hinton G, Krizhevsky A, Sutskever I, Salakhutdinov R. Dropout: a simple way to prevent neural networks from overfitting. J Mach Learn Res. 2014;15:1929–1958. [Google Scholar]
- 17.Ioffe S, Szegedy C. Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift. pages 448–456, ICML’15, JMLR.org; 2015. [Google Scholar]
- 18.Goodfellow I, Shlens J, Szegedy C. Explaining and Harnessing Adversarial Examples, ICLR’15; 2015. [Google Scholar]
- 19.Caruana R Multitask learning. Mach Learn. 1997;28:41–75. [Google Scholar]
- 20.Bartlett PL, Mendelson S. Rademacher and gaussian complexities: risk bounds and structural results. J Mach Learn Res. 2003;3:463–482. [Google Scholar]
- 21.Ruder S, An overview of multi-task learning in deep neural networks, arXiv preprint. arXiv:1706.05098. 2017. [Google Scholar]
- 22.Teichmann M, Weber M, Zllner M, Cipolla R, Urtasun R. MultiNet: Real-time Joint Semantic Reasoning for Autonomous Driving, in 2018. IEEE Intelligent Vehicles Symposium (IV), pages 1013–1020, 2018. [Google Scholar]
- 23.Uhrig J, Cordts M, Franke U, Brox T. Pixel-level Encoding and Depth Layering for Instance-level Semantic Labeling. in GCPR; 2016. [Google Scholar]
- 24.Kendall A, Gal Y, Cipolla R. Multi-Task Learning Using Uncertainty to Weigh Losses for Scene Geometry and Semantics, CoRR abs/1705.07115. 2017. [Google Scholar]
- 25.Moeskops P, Wolterink JM, van der Velden BH, et al. Deep Learning for Multi-Task Medical Image Segmentation in Multiple Modalities. in MICCAI; 2016. [Google Scholar]
- 26.Valindria VV, Pawlowski N, Rajchl M, et al. , Multi-modal Learning from Unpaired Images: Application to Multi-organ Segmentation in CT and MRI. in IEEE WACV, pages 547–556; 2018. [Google Scholar]
- 27.Xue W, Brahm G, Pandey S, Leung S, Li S. Full left ventricle quantification via deep multitask relationships learning. Med Image Anal. 2018;43:54–65. [DOI] [PubMed] [Google Scholar]
- 28.Dangi S, Yaniv Z, Linte CA, Left Ventricle Segmentation and Quantification from Cardiac Cine MR Images via Multi-task Learning. in STACOM, pages 21–31; 2019. [PMC free article] [PubMed] [Google Scholar]
- 29.Bai M, Urtasun R. Deep Watershed Transform for Instance Segmentation. in IEEE CVPR pages 2858–2866, 2017. [Google Scholar]
- 30.Hayder Z, He X, Salzmann M. Boundary-Aware Instance Segmentation.in IEEE CVPR; 2017. [Google Scholar]
- 31.Bischke B, Helber P, Folz J, Borth D, Dengel A. Multi-Task Learning for Segmentation of Building Footprints with Deep Neural Networks. CoRR abs/1709.05932; 2017. [Google Scholar]
- 32.Krizhevsky A, Sutskever I, Hinton GE, ImageNet Classification with Deep Convolutional Neural Networks In: Pereira F, Burges CJC, Bottou L, Weinberger KQ, eds. Advances in Neural Information Processing Systems 25; Red Hook, NY: Curran Associates Inc.; 2012:1097–1105. [Google Scholar]
- 33.Badrinarayanan V, Kendall A, Cipolla R. SegNet: A Deep Convolutional Encoder-Decoder Architecture for Image Segmentation, CoRR abs/ 1511.00561; 2015. [DOI] [PubMed] [Google Scholar]
- 34.Ronneberger O, Fischer P, Brox T. U-Net: Convolutional Networks for Biomedical Image Segmentation. CoRR abs/1505.04597; 2015. [Google Scholar]
- 35.He K, Zhang X, Ren S, Sun J. Deep Residual Learning for Image Recognition, in IEEE CVPR; 2016. [Google Scholar]
- 36.Borgefors G Distance transformations in digital images. Comput Vis Graph Image Process. 1986;34:344–371. [Google Scholar]
- 37.Fonseca G, Backhaus M, Bluemke DA, et al. The Cardiac Atlas Project - an imaging database for computational modeling and statistical atlases of the heart. Bioinformatics. 2011;27:2288–2295. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Suinesiaputra A, Cowan BR, Al-Agamy AO, et al. A collaborative resource to build consensus for automated left ventricular segmentation of cardiac MR images. Med Image Anal. 2014;18:50–62. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Bernard O, Lalande A, Zotti C, et al. Deep learning techniques for automatic MRI cardiac multi-structures segmentation and diagnosis: is the problem solved?. IEEE Trans Med Imaging. 2018;37:2514–2525. [DOI] [PubMed] [Google Scholar]
- 40.Yaniv Z, Lowekamp BC, Johnson HJ, Beare R. SimpleITK image-analysis notebooks: a collaborative environment for education and reproducible research. J Digit Imaging. 2018;31:290–303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.He K, Zhang X, Ren S, Sun J. Delving deep into rectifiers: surpassing human-level performance on ImageNet classification in IEEE ICCV, pages 1026–1034; 2015. [Google Scholar]
- 42.Hinton G, Srivastava N, Swersky K. Neural networks for machine learning lecture 6a overview of mini-batch gradient descent. [Google Scholar]
- 43.Peters T, Linte C, Yaniv Z, Williams J. Mixed and Augmented Reality in Medicine, Chapter 16 Augmented and Virtual Visualization for Image-Guided Cardiac Therapeutics. pages 231–250, CRC Press; 2018. [Google Scholar]
- 44.Baumgartner CF, Koch LM, Pollefeys M, et al. An Exploration of 2D and 3D Deep Learning Techniques for Cardiac MR Image Segmentation. In STACOM, pages 111–119,;2018. [Google Scholar]
- 45.Khened M, Alex V, Krishnamurthi G, Densely Connected Fully Convolutional Network for Short-Axis Cardiac Cine MR Image Segmentation and Heart Diagnosis Using Random Forest, in STACOM, pages 140–151, 2018. [Google Scholar]
- 46.Isensee F, Jaeger PF, Full PM, et al. Automatic Cardiac Disease Assessment on cine-MRI via Time-Series Segmentation and Domain Specific Features, in STACOM, pages 120–129, 2018. [Google Scholar]
- 47.Li B, Liu Y, Occleshaw CJ, et al. Inline automated tracking for ventricular function with magnetic resonance imaging. JACC Cardiovasc Imaging. 2010;3:860–866. [DOI] [PubMed] [Google Scholar]
- 48.Fahmy AS, Al-Agamy AO, Khalifa A. Myocardial Segmentation Using Contour-Constrained Optical Flow Tracking, in STACOM, pages 120–128, 2012. [Google Scholar]
- 49.Jolly M-P, Guetter C, Lu X, et al. Automatic Segmentation of the Myocardium in Cine MR Images Using Deformable Registration, in STACOM, pages 98–108, 2012. [Google Scholar]
- 50.Margeta J, Geremia E, Criminisi A, et al. Layered Spatio-temporal Forests for Left Ventricle Segmentation from 4D Cardiac MRI Data, in STACOM, pages 109–119, 2012. [Google Scholar]
- 51.Tan LK, Liew YM, Lim E, et al. Convolutional neural network regression for short-axis left ventricle segmentation in cardiac cine MR sequences. Med Image Anal. 2017;39:78–86. [DOI] [PubMed] [Google Scholar]
- 52.Wang M, Deng W. Deep visual domain adaptation. Survey Neurocomput. 2018;312:135–153. [Google Scholar]
- 53.Blundell C, Cornebise J, Kavukcuoglu K, Wierstra D, Weight Uncertainty. Neural Networks. ICML’15, pages 1613–1622, JMLR.org; 2015. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Figure S1: Ground-truth and automatic segmentation obtained from all trained models for a test patient. In each subfigure, the segmentation obtained from the baseline and regularized model are overlaid onto the volume and shown in first and third rows, respectively; corresponding disagreement (in black) between the obtained segmentations and the ground-truth is shown in second and fourth rows, respectively.
Figure S2: Visualization of (a) the segmentation obtained by thresholding the predicted distance map and (b) absolute error between the ground-truth and predicted distance maps for all chambers. Shown is only a cropped region around the heart, the error in predicted distance map is higher for the regions farther from the heart.
Figure S3: Feature maps visualized for the UNet (left column) and DMR-UNet (right column) model. We can observe the UNet model preserves the intensity information and propagates it throughout the network, hence, is more sensitive to the dataset-specific intensity distribution. In contrast, the DMR-UNet model focuses more on the edges and other discriminative features, producing sparse feature maps, while ignoring dataset-specific intensity distribution. However, the results obtained for intra-dataset segmentation (shown here for ACDC dataset) is similar for both models, whereas, there is a significant improvement in cross-dataset segmentation after distance map regularization.
Figure S4: Mean and 95% bootstrap confidence interval for training and validation losses (a and b), and the learned weights for cross-entropy and mean absolute difference losses (c), on ACDC and LVSC dataset across five-fold cross-validation. Since the cross-entropy loss is harder to interpret, we plot the corresponding dice loss computed during training and validation. We can observe lower difference between the training and validation dice loss for the distance map regularized models, demonstrating their ability to prevent overfitting.
Figure S5: Weights distribution before and after distance map regularization for models trained across fivefold cross-validation. We can observe the number of non-zero weights increases after the distance map regularization, hence, better utilizing the network capacity.