Skip to main content
PMC home page
Briefings in Bioinformatics logoLink to Briefings in Bioinformatics
. 2019 Jul 5;21(4):1285–1292. doi: 10.1093/bib/bbz071

A critical review of five machine learning-based algorithms for predicting protein stability changes upon mutation

Jianwen Fang 1,✉
PMCID: PMC7373184  PMID: 31273374

Abstract

A number of machine learning (ML)-based algorithms have been proposed for predicting mutation-induced stability changes in proteins. In this critical review, we used hypothetical reverse mutations to evaluate the performance of five representative algorithms and found all of them suffer from the problem of overfitting. This approach is based on the fact that if a wild-type protein is more stable than a mutant protein, then the same mutant is less stable than the wild-type protein. We analyzed the underlying issues and suggest that the main causes of the overfitting problem include that the numbers of training cases were too small, and the features used in the models were not sufficiently informative for the task. We make recommendations on how to avoid overfitting in this important research area and improve the reliability and robustness of ML-based algorithms in general.

Keywords: protein stability, computational prediction, mutation, reverse mutation, reliability, robustness

Introduction

The ability to predict protein stability changes upon mutation is of great scientific interest and is also of broad practical importance [1–8]. For example, it can be used to estimate the effects of nonsynonymous single-nucleotide polymorphisms, which can be useful for precision diagnostics and medicine. This is especially important for genomic diseases such as cancers [9–11]. For example, it was discovered that the level of DNA methyltransferase 1 (DNMT1) was elevated in breast cancer because of an increase in protein half-life [10]. A book devoted to the modulation of protein stability in cancer therapy was published in 2009 [11].

Recognizing the great potential of predicting protein stability changes upon mutation, many different methods have been tested [12–24]. Earlier approaches included comparative analysis of relative stability between wild-type proteins (WT) and their mutants (MU) to establish principles that govern protein stability [12]. These principles were then used to design point mutants that may increase protein stability. Successful cases included decreasing the entropy of unfolding [25], engineering surface salt bridges [26], introducing disulfide bridges [27] and so on. This type of approach was made possible largely due to the structure and stability measurements of hundreds of mutant lysozymes of phage T4, made available by Dr Brian Matthews and coworkers [12]. Only a limited number of successful cases have been reported, mostly in the case of the T4 lysozyme [12].

Force field-based algorithms were also introduced decades ago and are still being actively researched [13–15]. Some of these methods have shown better-than-random performance in prospective validations but generally are not considered gold standards for improving protein stability [28]. Further, these approaches require high-resolution 3D structures and are often highly computer-intensive. Therefore, they are best suited for low-throughput analysis and prediction of proteins with known 3D structures.

In recent years, algorithms based on machine learning (ML) technologies for predicting protein stability changes upon mutation have attracted increasing attention because they often are less computer resource demanding than force field approaches, and some do not require 3D structures [16–24]. Many ML algorithms, such as support vector machines (SVM) [16–19], neural networks [20] and multiple regression and classification techniques [21, 22], have been used for the purpose. The ML methods hold great promises because they may not only provide valuable predictions to guide experiment design but also afford insights into the complex relationship between protein sequence, structure and stability. However, the performance of these algorithms has been challenged as several performance reviews failed to reproduce the high accuracies found by the authors [29, 30]. Recently, in a blind prospective validation, none of 63 mutants predicted to be stabilizing were experimentally observed to be stabilizing [31].

We proposed a simple method, based on physical principles, to evaluate methods for predicting protein stability changes upon mutation by using hypothetical reverse mutation (HRM) [32–34]. This approach is based on the fact that if a wild-type protein is more stable than a mutant protein, then the same mutant is less stable than the wild-type protein. Since then, a few more algorithms using HRM have been published, which assert better performance than older methods [35–37].

In this review, we use the HRM method to test three newly developed algorithms, along with two widely cited methods published earlier, to evaluate if there has been significant improvement in the past several years since HRM was proposed as an evaluation tool. Unfortunately, as we show in the following sections, these newer algorithms still suffer from the problem of overfitting and show no improvement over the older methods. In this critical review, we focus on identifying the sources of the problem and provide suggestions for how to move this rather important research forward.

Methods

Hypothetical reverse mutation

Protein stability changes upon mutation are often measured through changes in the alterations of folding free energies (∆∆G) between wild-type proteins and their mutants. Because free energy is a thermodynamic state function [38], the ∆∆GW→M of a mutation (W → M) equals the -∆∆GM→W of a hypothetical mutation from the mutant to the wild-type protein (M → W) (Figure 1). Mutation is a relative term: if a protein in human and mouse differs by one amino acid, the mouse protein is a mutant to the human one, and the human protein can also be considered as a mutant to the mouse wild-type protein. Thus, the reverse mutation is termed hypothetical only because the wild-type protein is already defined, not because it does not exist. In fact, it is real because both wild-type and mutant proteins do exist, confirmed by their structures. Because free energy is a state function, ∆∆G does not depend on the path between wild-type and mutant proteins, and is determined because these two endpoints are defined [39].

Figure 1.

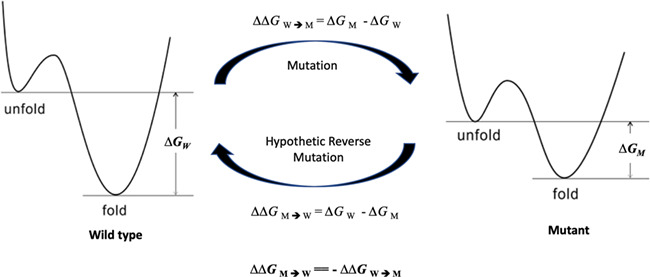
Figure 1

Open in a new tab

A schematic representation of free energy difference between wild-type and mutant proteins.

Since HRMs were not used in training the analyzed algorithms and their ∆∆GM→W can be easily obtained, they provide a simple and convenient method to test whether a predictor is robust.

Mutation datasets

We identified 125 mutations of 9 wild-type proteins in the ProTherm database [40] for which both wild-type and mutant protein structures were available. In these mutations, the ∆∆Gs of both forward and reverse mutations can be predicted based on their experimentally determined structures, and the predicted ∆∆Gs can be compared to experimental data.

The structures of these wild-type proteins and their relevant mutants were downloaded from the protein data bank (http://www.pdb.org). The median and average of RMSD of the WT and corresponding MU structure pairs are 0.263 and 0.318 Å, respectively, indicating a vast majority of the mutants did not induce significant structure change, and the qualities of the MU and WT structures are similarly good. For each mutation in the dataset, a corresponding HRM was created by swapping the wild-type protein and its mutant in a mutation (i.e., the actual mutant protein is now considered as the hypothetical wild-type protein and the actual wild-type protein is now treated as the mutant protein). The ∆∆G during an HRM was assigned with the same value but with an opposite sign to its experimental forward mutation (Figure 1).

Reviewed algorithms

We analyzed five representative algorithms: MUpro [17], I-Mutant2.0 [16], STRUM [35], mCSM [36] and DEUT [37]. The base algorithms and features used to develop models are summarized in Table 1. Three of these algorithms—namely, MUpro, I-Mutant2.0 and DUET—were developed based on the SVM algorithm [41], one of the most widely used ML algorithms (Table 1). STRUM utilized gradient-boosted regression tree and mCSM employed Gaussian process regression for regression and random forest for classification purpose.

Table 1.

Summary of reviewed algorithms

Base algorithm No. of features Structure required? Year published Type of features
mCSM [36] GP for regression, RF for classification ? Yes 2013 Graph-based atom distance patterns, pharmacophore changes, experimental conditions
DUET [37] SVM ? Yes 2014 Predictions from Site Directed Mutator (SDM) and mCSM
STRUM [35] GBRT 120 Yesξ 2016 Sequence-based, threading template-based, i-TASSER model-based
muPro [17] SVM 140 (sequence only), 40 (structure only), 160 (sequence + structure) Optional 2005 20 for the type of mutation (−1 for the deleted residue, 1 for newly introduced residue, 0 for all others); 120 (6 * 20) for next three residues for each side, 20 for the frequency of each type of residues within a sphere of 9 A
iMutant [16] SVM 42 Optional 2005 Temperature, pH, 20 mutation types, 20 spatial environment (0.9 nm) or nearby residues (9 on each side)
Open in a new tab

GBRT indicates gradient boosted regression tree; RF, random forest; GP, Gaussian process, SDM: Site Directed Mutator; ξ, may use low-resolution structure modeling; ?, no exact number was given.

Evaluation metrics

To evaluate the prediction performance of evaluated algorithms, we used several statistical metrics. The first was the percent of inconsistence, defined as the percent of mutation (W → M) and their hypothetic reverse mutation (M → W) pairs predicted with the same sign. As illustrated in Figure 1, a mutation and its HRM in reality always share the same ∆∆G values but the opposite sign. When a mutation and its HRM share the same sign, the results are two mutually exclusive situations that cannot coexist: a wild-type protein is more stable than its mutant but, at the same time, the same mutant is more stable than the wild-type protein. A high level of inconsistence strongly suggests that the predictor is overfitted by forward mutations.

We also calculated the percent of correctly predicted signs for forward mutations and reverse hypothetical mutations to demonstrate the performance gap between these two groups. At minimum, a robust predictor should be able to accurately predict whether a mutation is stabilizing or destabilizing. The Pearson and Fechner correlation coefficients of the experimental and predicted ∆∆G values were calculated for forward mutations and HRMs. In addition, we used different ∆∆G values as thresholds to convert the predictions into binary classes (i.e., stabilizing and destabilizing) and generated the area under receiver operating characteristic (ROC) curve to visualize the performance gap between W → M and M → W predictions.

Results and Discussions

The performance problem

Table 2 provides a summary of performance of all five algorithms under review. The percent of inconsistent predictions is above 70% in all five algorithms, and mCSM resulted in the worst performance: almost in 9 out of 10 cases it predicted that both forward and reverse mutations share the same sign. A close look at the percentages of correctly predicted signs of ∆∆G shows the performance of all algorithms is vastly different for forward and reverse mutations: while all algorithms predicted the signs of forward mutations at accuracies above 80%, including 97% for MUpro, the percentages dropped to ~30% for the HRMs. The Pearson and Fechner correlation coefficients of forward and reverse mutations show the same trend: all algorithms performed very well for forward mutations, but their results for HRMs essentially reveal no correlation with actual experimental data. Scatter plots of predicted versus experimental data are presented in Figure 2 and Supplementary Materials. The ROC curves and their associated AUC values suggest the same conclusion (Figure 3): the predictors were overfitted for the further mutations, and thus did not perform well for the HRMs, which were not used in the training.

Table 2.

Performance of ∆∆G prediction algorithms for mutations and hypothetical reversed mutations

Inconsistence (%) Sign correctly predicted (%) R F
W→M M→W WT→MT MT→WT WT→MT MT→WT
mCSM [36] 88.8 81.6 29.6 0.649 −0.040 0.44 0.024
DUET [37] 73.6 84 36 0.649 −0.017 0.392 −0.008
STRUM [35] 75.2 86.4 31.2 0.837 −0.055 0.648 0.056
muPro [17] 73.6 96.8 31.2 0.971 −0.018 0.888 0.008
iMutant [16] 77.6 88.8 28.8 0.937 0.048 0.824 −0.136
Open in a new tab

W indicates wild-type protein; M, mutant; R, Pearson correlation coefficient, 1 is perfect and 0 is random; F, Fechner correlation coefficient, 1 is perfect and 0 is random.

Percent of inconsistence: the percent of wild-type to mutant and mutant to wild-type pairs predicted with the same sign.

Figure 2.

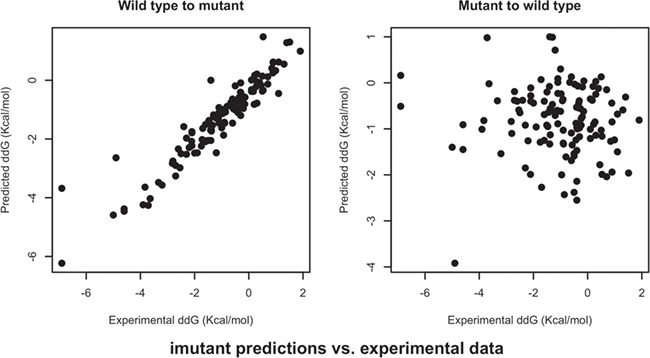
Figure 2

Open in a new tab

Scatter plots of I-Mutant2.0 predictions versus experimental data.

Figure 3.

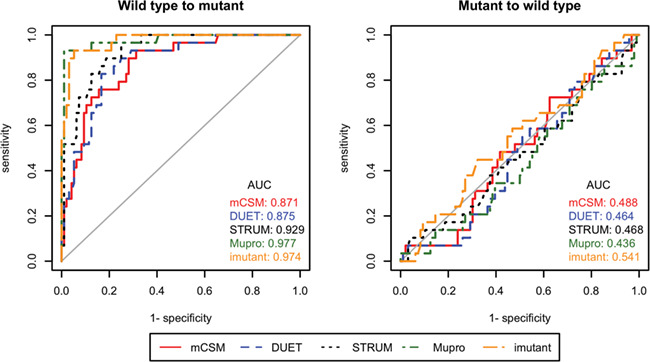
Figure 3

Open in a new tab

ROC curves and their AUCs of ∆∆G prediction algorithms for wild-type to mutant and mutant to wild-type mutations. Different ∆∆G values were used as thresholds to convert the predictions into binary stabilizing and destabilizing classes.

Taken together, all performance metrics used in the study consistently shows that the tested five algorithms were prone to overfitting. Therefore, they have little practical value. In addition, an important finding is that the newer algorithms did not show any improvement over the two older ones.

What went wrong?

The performance analyses using HRMs in this study show that the five tested ML models all suffer from the problem of overfitting. It is noteworthy that all these models were evaluated by the authors using n-fold cross validation, a common practice widely considered as an acceptable validation approach. Our results raise the question, what went wrong? To determine the causes of the problem, it is necessary to analyze the procedures of how these models were constructed in detail.

For all models derived using ML methods to have acceptable predictive power, three essential elements are required: a robust base algorithm, a sufficiently large set of training data and a set of informative features relevant to the target of prediction. Since all evaluated algorithms were based on general purpose algorithms that have been successfully utilized in many applications, the base algorithm is unlikely to be the sole source of the overfitting problem. Thus, we rationalize that the causes were more likely with the training data and features used to build models. Here we analyze the training data and the features frequently used in the models.

Training data

All algorithms reviewed in this project were developed based on the experimental data from ProTherm, a publicly available database devoted to experimentally determined protein stability changes by mutation [40]. Because ProTherm has multiple entries for some mutations from different literature, merging and filtering steps are required to eliminate redundancy. In addition, many algorithms require 3D structures to make predictions. Depending on the filtering criteria, the number of final sets of mutations passing the filtering steps was usually a few thousands. For example, mCSM was based on a set of 2648 single-point mutations in 131 different global proteins as the main dataset to build models for predicting ∆∆G [36]. STRUM instead relied on a set of 3421 single-point mutation involving 150 proteins [35]. The situation is further complicated by a report published in 2018 indicating that ProTherm contained numerous errors in sequence, structure or stability data [42]. The authors of that report concluded that 1197 (29%) of the 4148 entries in the ProTherm database with values of ∆∆G were deemed to be useful. This number of cases is small if one considers there are thousands of distinct protein domains [43] and 380 different types of single-residue mutations [42]. Protein domains are distinct functional units [44], and therefore the same type of mutation at the residue level may induce different level of stability changes to different domains. Thus, only a small percent of domains were actually represented in the training data. There are 20 different amino acid residues, each of which can mutate to one of the other 19 different residues. For each type of single-residue mutations, there are less than 10 samples on average from which to learn patterns. Similarities between amino acids vary significantly and so do the mutations. A mutation between two very different residues likely causes more changes than one between two similar residues. Therefore, although it is possible to learn patterns across different types of mutations, it is only possible if the similarities among mutations are considered in training. Unfortunately, we have not seen such information used in any current models. Thus, the task of predicting stability changes upon mutation is prone to overfitting because of the limited number of cases in the available experimental data for training and testing purposes.

Features relevant to protein stability

Even with sufficient good data, it is still necessary to find features relevant to the target property under investigation before it is possible to develop robust ML models. To determine which features are relevant to protein stability changes upon mutation, it is necessary to examine what happens when a mutation occurs.

When a residue in a protein is replaced by another residue (i.e., a mutation), chemical bonds between the outgoing residue and its neighbor residues are replaced with a new set of bonds involving the incoming residue. The difference between peptide bonds (amide bonds) linking two amino acids is usually minimal; therefore, it is often ignored for simplicity. However, a mutation brings in a different type of residue with a new set of covalent bonds, volume, ionic strength and hydrophobicity. If these properties significantly differ from those of the outgoing residue, they may cause significant changes to the conformation and the non-covalent bond network among the mutation site and surrounding residues in order to reach a new energy minimum. The degree and extent of conformation change depends on the types of the outgoing and incoming residues and also the surrounding environment. For example, a mutation of a positively charged residue replaced by another positively charged residue usually causes fewer changes than a negatively charged residue [45]. In addition, a mutation of a polar surface residue with its side chain sticking outward would require less conformation adaptation than a nonpolar residue in a well-packed hydrophobic core [46, 47]. The difference of hydrophobic effect change results in different changes in the specific heat (∆Cp), and therefore protein stability [48].

The total destabilizing and the total stabilizing energies of proteins are both about two magnitudes larger than the difference between them [49]. Most folded globular proteins are only stable by 20–60 KJ/mol, relative to their unfolded forms [49]. The energy needed to stabilize/destabilize a protein is quite small because it only takes ~5.7 KJ/mol to cause a 10-fold change in the equilibrium constant between folded and unfolded protein molecules [49]. While non-covalent bonds are usually weaker than covalent bonds, their changes may cause significant impact to the protein stability [49]. Considering the energy contribution of one typical protein hydrogen bond is in the range of 20–25 KJ/mol [50], a net gain or loss of a hydrogen bond of a mutant over its wild type counterpart can significantly (de)stabilize the mutant. There are usually hundreds of hydrogen bonds formed in a typical protein because the number of hydrogen bonds in a folded protein can be at least two per amino acid residue [51]. Further, the strength of hydrogen bonds highly depends on the distances and angles between the three involved atoms. Moreover, non-covalent bonds can also be temporary, and a surface residue may form a hydrogen bond with different residues or water molecules.

Overall, it is very challenging to generate informative features for predicting protein stability changes upon mutation. The margin of error of predicting mutation-induced stability is so small that it is unlikely it can be accurately predicted based on mainly macro properties such as the composition of the amino acid residues surrounding the mutation sites because the values of these features do not change with mutation.

Types of features relevant to protein stability changes

Based on the above analysis, it is logical to group features that may be relevant to the protein stability changes into four types: (1) the type of mutation (i.e., outgoing and incoming residues); (2) changes in the space surrounding the mutation site; (3) the environment surrounding the mutation site; (4) the conditions at which the stability change is measured (e.g., pH, temperature, etc.). Although remote residues not close to the mutation site may affect the stability changes upon mutation, its effect usually is relatively small and therefore can be ignored in most cases for simplicity. The features in group 1 are certainly different between wild type and mutant and important to protein stability; however, they alone are not very informative because the same mutation can have a stabilizing or de-stabilizing effect in different proteins or even just under different conditions in some cases. Group 2 features encode the changes to the surrounding environment induced by the mutation. They are more difficult to obtain than other groups because structures of both wild-type and mutant proteins are required. In addition, it is also challenging to find meaningful ways to measure the differences. It is important to note that the features in groups 3 and 4 remain the same for all mutations, including HRMs in the same position. Therefore, these types of features are only useful through the types 1 and 2 features. Overall, the features from the 1st two groups should be more important than the other two groups. Most of the features used in existing algorithms are from the 1st, 3rd and 4th groups because of the difficulty to obtain the important group 2 features. To give an example, we analyzed the features used in I-Mutant2.0 algorithm in detail, presented in the Supplementary Material.

Conclusion and Future Prospects

We have reviewed five representative algorithms for predicting mutation-induced stability change in proteins and found they have not yet reached a level for practical use, likely due to the limited amount of training data and unsatisfactory features upon which the current algorithms were built. For other algorithms not tested in the study, we provide the PDB codes of proteins and their mutants used in the study as supplementary materials so others can perform a quick test before they use any of these algorithms. Caution should be taken though when HRM is used to evaluate predictors. It is necessary but not sufficient to vindicate the robustness of a predictor even when it delivers similar performance for forward and reverse mutations. For example, this approach should not be used to judge methods trained on combined forward and HRMs because HRMs were already used in the training [32, 33, 52]. Therefore, these models could be overfitted in a more subtle way that requires a different approach to detect the potential overfitting problem. Besides, these models were trained on uncorrected data, consequently the predictions are not reliable anyway [42]. Thus, we do not evaluate these predictors in the present study.

Based on the analyses presented here, we believe that the keys to the success of developing ML-based methods include the availability of a significant amount of reliable experimental data and informative features for such a difficult task. While the former relies on bench scientists to perform more experiments and therefore accumulate more usable data, the latter requires intelligent collaboration between experimentalists and informaticists. Useful features need to be based on chemical/physical properties of amino acid residues around the mutation site. It is especially important to discover more informative type-2 features because they are essential but largely not used in the current models. A possible solution is to take advantage of both ML- and traditional force field-based molecular simulations by first deriving features from molecular modeling studies to generate features that model atom level interaction changes after mutation and then applying ML to find the most informative features. Although force field-based simulations are computer power demanding, recent advances in computer and software technologies such as efficient algorithms and large-scale parallel computing allow the studies to be performed within a reasonable time frame [53, 54]. A key to success is that features and models are evaluated extensively to determine whether they are informative and robust. Otherwise, any patterns detected from learning could be spurious, as an artifact of overfitting.

We hope that publication of this critical review brings a discussion about the status of the research to the community. As some of these reviewed algorithms have already been widely cited, the community needs to be made aware of the reality that these algorithms are unlikely to help them in predicting stability changes upon mutation and guiding them to design more stable proteins. Understanding the limitations of current methods is an important step that can promote more research in this important field and can improve research reproducibility and reliability in general.

A few final words: we should always have realistic expectations of the performance of predictive models. For a problem as complex as predicting stability changes upon mutation, one should never have expected good performance based on rudimentary features such as residue composition, etc. In addition, there is always a performance ceiling no matter what ML algorithm and features are used, as there are always exceptions to any possible rules and patterns discovered by ML for such a complex problem. A red flag should be immediately raised when ‘excellent’ performance is apparently achieved. More often than not, it is due to overfitting rather than genuine and robust performance. Sometimes the problem can be identified by analyzing data and features and confirmed with physical principles such as HRMs used in the present study.

Key Points

  • The ability to predict protein stability changes upon mutation is of great scientific interest and practical importance;

  • The five ML-based algorithms for predicting protein stability changes upon mutation reviewed in this study were prone to overfitting and therefore have little practical value;

  • Future development of robust algorithms for predicting protein stability changes upon mutation may rely on the availability of a very substantial increase in the volume of experimental data and informative features.

Disclaimer

The views expressed in this article are the personal opinions of the author and do not necessarily reflect policy of the US National Cancer Institute.

Supplementary Material

supplementary_material_bbz071
Click here for additional data file. (15.1KB, docx)
supplementary_figures_bbz071
Click here for additional data file. (57.2MB, docx)
125_pairs_with_know_structures_and_results_bbz071
Click here for additional data file. (23.9KB, xlsx)

Acknowledgements

I wish to thank Drs Lisa McShane, Yingdong Zhao and Yuqi Li for their valuable suggestions and support. I also thank Diane Cooper, MSLS, National Institutes of Health (NIH) Library, for her diligent editorial assistance. This work utilized the computational resources of the NIH HPC Biowulf cluster (http://hpc.nih.gov).

Jianwen Fang, PhD, is a computational biologist at the Biometric Research Program, Division of Cancer Treatment and Diagnosis, National Institutes of Health/National Cancer Institute. His research interests include integrated data analysis, structural bioinformatics, software and database development and computational drug discovery.

Funding

No external sources.

References

  • 1. Dahiyat BI. In silico design for protein stabilization. Curr Opin Biotechnol 1999;10:387–90. [DOI] [PubMed] [Google Scholar]
  • 2. Korkegian A, Black ME, Baker D, et al. . Computational thermostabilization of an enzyme. Science 2005;308:857–60. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 3. Lazar GA, Marshall SA, Plecs JJ, et al. . Designing proteins for therapeutic applications. Curr Opin Struct Biol 2003;13:513–8. [DOI] [PubMed] [Google Scholar]
  • 4. Schweiker KL, Makhatadze GI. Protein stabilization by the rational design of surface charge-charge interactions In: Shriver JW. (ed). Protein Structure, Stability, and Interactions. New York: Humana Press, 2009, 261–83. [DOI] [PubMed] [Google Scholar]
  • 5. Sterner R, Liebl W. Thermophilic adaptation of proteins. Crit Rev Biochem Mol Biol 2001;36:39–106. [DOI] [PubMed] [Google Scholar]
  • 6. Chennamsetty N, Voynov V, Kayser V, et al. . Design of therapeutic proteins with enhanced stability. Proc Natl Acad Sci USA 2009;106:11937–42. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 7. Unsworth LD, van der J, Koutsopoulos S. Hyperthermophilic enzymes—stability, activity and implementation strategies for high temperature applications. FEBS J 2007;274:4044–56. [DOI] [PubMed] [Google Scholar]
  • 8. Schoemaker HE, Mink D, Wubbolts MG. Dispelling the myths—biocatalysis in industrial synthesis. Science 2003;299:1694–7. [DOI] [PubMed] [Google Scholar]
  • 9. Li M, Kales SC, Ma K, et al. . Balancing protein stability and activity in cancer: a new approach for identifying driver mutations affecting CBL ubiquitin ligase activation. Cancer Res 2016;76:561–71. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 10. Agoston AT, Argani P, Yegnasubramanian S, et al. . Increased protein stability causes DNA methyltransferase 1 dysregulation in breast cancer. J Biol Chem 2005;280:18302–10. [DOI] [PubMed] [Google Scholar]
  • 11. Sakamoto K, Rubin E. Modulation of Protein Stability in Cancer Therapy. New York: Springer, 2009. [Google Scholar]
  • 12. Baase WA, Liu LJ, Tronrud DE, et al. . Lessons from the lysozyme of phage T4. Protein Sci 2010;19:631–41. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 13. Schymkowitz J, Borg J, Stricher F, et al. . The FoldX web server: an online force field. Nucleic Acids Res 2005;33:W382–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 14. Sheffler W, Baker D. RosettaHoles: rapid assessment of protein core packing for structure prediction, refinement, design, and validation. Protein Sci 2009;18:229–39. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 15. Zhou H, Zhou Y. Distance-scaled, finite ideal-gas reference state improves structure-derived potentials of mean force for structure selection and stability prediction. Protein Sci 2002;11:2714–26. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 16. Capriotti E, Fariselli P, Casadio R. I-Mutant2.0: predicting stability changes upon mutation from the protein sequence or structure. Nucleic Acids Res 2005;33:W306–10. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 17. Cheng J, Randall A, Baldi P. Prediction of protein stability changes for single-site mutations using support vector machines. Proteins 2006;62:1125–32. [DOI] [PubMed] [Google Scholar]
  • 18. Masso M, Vaisman II. Accurate prediction of stability changes in protein mutants by combining machine learning with structure based computational mutagenesis. Bioinformatics 2008;24:2002–9. [DOI] [PubMed] [Google Scholar]
  • 19. Montanucci L, Fariselli P, Martelli PL, et al. . Predicting protein thermostability changes from sequence upon multiple mutations. Bioinformatics 2008;24:I190–5. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 20. Wu LC, Lee JX, Huang HD, et al. . An expert system to predict protein thermostability using decision tree. Expert Systems with Applications 2009;36:9007–14. [Google Scholar]
  • 21. Gromiha MM, Oobatake M, Sarai A. Important amino acid properties for enhanced thermostability from mesophilic to thermophilic proteins. Biophys Chem 1999;82:51–67. [DOI] [PubMed] [Google Scholar]
  • 22. Huang LT, Gromiha MM. Reliable prediction of protein thermostability change upon double mutation from amino acid sequence. Bioinformatics 2009;25:2181–7. [DOI] [PubMed] [Google Scholar]
  • 23. Glyakina AV, Garbuzynskiy SO, Lobanov MY, et al. . Different packing of external residues can explain differences in the thermostability of proteins from thermophilic and mesophilic organisms. Bioinformatics 2007;23:2231–8. [DOI] [PubMed] [Google Scholar]
  • 24. Capriotti E, Fariselli P, Rossi I, et al. . A three-state prediction of single point mutations on protein stability changes. BMC Bioinformatics 2008;9(Suppl 2):S6. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 25. Matthews BW, Nicholson H, Becktel WJ. Enhanced protein thermostability from site-directed mutations that decrease the entropy of unfolding. Proc Natl Acad Sci USA 1987;84:6663–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 26. Makhatadze GI, Loladze VV, Ermolenko DN, et al. . Contribution of surface salt bridges to protein stability: guidelines for protein engineering. J Mol Biol 2003;327:1135–48. [DOI] [PubMed] [Google Scholar]
  • 27. Matsumura M, Becktel WJ, Levitt M, et al. . Stabilization of phage-T4 lysozyme by engineered disulfide bonds. Proc Natl Acad Sci USA 1989;86:6562–6. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 28. Buss O, Rudat J, Ochsenreither K. FoldX as protein engineering tool: better than random based approaches? Comput Struct Biotechnol J 2018;16:25–33. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 29. Thiltgen G, Goldstein RA. Assessing predictors of changes in protein stability upon mutation using self-consistency. PLoS One 2012;7:e46084. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 30. Khan S, Vihinen M. Performance of protein stability predictors. Hum Mutat 2010;31:675–84. [DOI] [PubMed] [Google Scholar]
  • 31. McGuinness KN, Pan W, Sheridan RP, et al. . Role of simple descriptors and applicability domain in predicting change in protein thermostability. PLoS One 2018;13:e0203819. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 32. Li Y, Zhang J, Tai D, et al. . Prots: a fragment based protein thermo-stability potential. Proteins 2012;80:81–92. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 33. Li Y, Fang J. PROTS-RF: a robust model for predicting mutation-induced protein stability changes. PLoS One 2012;7: e47247. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 34. Fang J. Reliability of machine learning based algorithms for designing protein drugs with enhanced stability. Drug Designing: Open Access 2015;4:e130. [Google Scholar]
  • 35. Quan L, Lv Q, Zhang Y. STRUM: structure-based prediction of protein stability changes upon single-point mutation. Bioinformatics 2016;32:2936–46. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 36. Pires DEV, Ascher DB, Blundell TL. mCSM: predicting the effects of mutations in proteins using graph-based signatures. Bioinformatics 2014;30:335–42. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 37. Pires DEV, Ascher DB, Blundell TL. DUET: a server for predicting effects of mutations on protein stability using an integrated computational approach. Nucleic Acids Res 2014;42:W314–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 38. Becktel WJ, Schellman JA. Protein stability curves. Biopolymers 1987;26:1859–77. [DOI] [PubMed] [Google Scholar]
  • 39. Wikipedia State Function https://en.wikipedia.org/wiki/State_function 10 May 2019, date last accessed.
  • 40. Kumar MD, Bava KA, Gromiha MM, et al. . ProTherm and ProNIT: thermodynamic databases for proteins and protein-nucleic acid interactions. Nucleic Acids Res 2006;34:D204–6. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 41. Vapnik VN. Statistical Learning Theory. New York: Wiley Interscience, 1998. [Google Scholar]
  • 42. Yang Y, Urolagin S, Niroula A, et al. . PON-tstab: protein variant stability predictor. importance of training data quality. Int J Mol Sci 2018;19:1009–1025. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 43. Mitchell AL, Attwood TK, Babbitt PC, et al. . InterPro in 2019: improving coverage, classification and access to protein sequence annotations. Nucleic Acids Res 2019;47:D351–60. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 44. Bagowski CP, Bruins W, te AJW. The nature of protein domain evolution: shaping the interaction network. Curr Genomics 2010;11:368–76. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 45. Gribenko AV, Patel MM, Liu J, et al. . Rational stabilization of enzymes by computational redesign of surface charge-charge interactions. Proc Natl Acad Sci USA 2009;106:2601–6. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 46. Strickler SS, Gribenko AV, Gribenko AV, et al. . Protein stability and surface electrostatics: a charged relationship. Biochemistry 2006;45:2761–6. [DOI] [PubMed] [Google Scholar]
  • 47. Bruno da Silva F, Contessoto VG, de Oliveira VM, et al. . Non-native cooperative interactions modulate protein folding rates. J Phys Chem B 2018;122(48):10817–24. [DOI] [PubMed] [Google Scholar]
  • 48. Spolar RS, Ha JH, Record MT. Hydrophobic effect in protein folding and other noncovalent processes involving proteins. Proc Natl Acad Sci USA 1989;86:8382–5. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 49. Day A. The Source of Stability in Proteins http://www.cryst.bbk.ac.uk/PPS2/projects/day/TDayDiss/index.html. 10 May 2019, date last accessed.
  • 50. Fleming PJ, Rose GD. Do all backbone polar groups in proteins form hydrogen bonds? Protein Sci 2005;14:1911–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 51. Gong H, Porter LL, Rose GD. Counting peptide-water hydrogen bonds in unfolded proteins. Protein Sci 2011;20:417–27. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 52. Rodrigues CHM, Pires DEV, Ascher DB. DynaMut: predicting the impact of mutations on protein conformation, flexibility and stability. Nucleic Acids Res 2018;46:W350–5. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 53. Phillips JC, Braun R, Wang W, et al. . Scalable molecular dynamics with NAMD. J Comput Chem 2005;26:1781–802. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 54. Pronk S, Pall S, Schulz R, et al. . GROMACS 4.5: a high-throughput and highly parallel open source molecular simulation toolkit. Bioinformatics 2013;29:845–54. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

supplementary_material_bbz071
Click here for additional data file. (15.1KB, docx)
supplementary_figures_bbz071
Click here for additional data file. (57.2MB, docx)
125_pairs_with_know_structures_and_results_bbz071
Click here for additional data file. (23.9KB, xlsx)

Articles from Briefings in Bioinformatics are provided here courtesy of Oxford University Press

RESOURCES