Graph- and rule-based learning algorithms: a comprehensive review of their applications for cancer type classification and prognosis using genomic data

Abstract

Cancer is well recognized as a complex disease with dysregulated molecular networks or modules. Graph- and rule-based analytics have been applied extensively for cancer classification as well as prognosis using large genomic and other data over the past decade. This article provides a comprehensive review of various graph- and rule-based machine learning algorithms that have been applied to numerous genomics data to determine the cancer-specific gene modules, identify gene signature-based classifiers and carry out other related objectives of potential therapeutic value. This review focuses mainly on the methodological design and features of these algorithms to facilitate the application of these graph- and rule-based analytical approaches for cancer classification and prognosis. Based on the type of data integration, we divided all the algorithms into three categories: model-based integration, pre-processing integration and post-processing integration. Each category is further divided into four sub-categories (supervised, unsupervised, semi-supervised and survival-driven learning analyses) based on learning style. Therefore, a total of 11 categories of methods are summarized with their inputs, objectives and description, advantages and potential limitations. Next, we briefly demonstrate well-known and most recently developed algorithms for each sub-category along with salient information, such as data profiles, statistical or feature selection methods and outputs. Finally, we summarize the appropriate use and efficiency of all categories of graph- and rule mining-based learning methods when input data and specific objective are given. This review aims to help readers to select and use the appropriate algorithms for cancer classification and prognosis study.

Introduction

Cancer is a prevalent human disease, and its underlying biology is highly complex. Currently, various large-scale genomic, epigenomic and transcriptomic data (such as gene expression, DNA methylation, copy number variation, somatic mutation, etc.) have been generated, which have greatly enhanced our understanding of the cancer biology in each type of cancers. Data availability is still not consistent; sometimes only a single-omic data (SOD) set is available for a single tissue, whereas in other cases multi-omics data (MOD) are accessible from different data repositories. Thus, there is no specific standard to analyze any data due to the availability of dependent (related) profiles as well as the heterogeneous internal relationship among the profiles. The internal design of the algorithms for each project is prepared depending on the desired objectives of the investigators such as identification of single-gene markers, combinatorial gene markers, gene modules, feed forward loops, gene signature, classifier, regression, survival validation, pathway-based markers, gene module, drug–target–disease relation, dense subgraphs, frequent closed association rules, rule-based classifier, feature mining or feature score determination, etc. or a combination of some of these. Thus, the design of such techniques always differs from each other depending upon the inputs and objective (or expectation) of the users.

Accordingly, the analysis of various cancer omics data becomes challenging. Some review articles have been published to present recent related studies [1–10]. These review articles mainly focus briefly on a few related studies. In contrast, the entire corpus in terms of all techniques such as integration/analysis type, learning type, etc. has not been considered together. The advantages and limitations of each category have not been discussed in terms of various aspects mentioned above (integration/analysis type and learning type together). In addition, previous review articles have not addressed which method might be most appropriate for a specific combination of input data type and user’s objective (or expectation).

To reduce the aforementioned limitations, we here provide a comprehensive survey of graph theory and association rule mining (ARM)-based learning algorithms used for the purpose of SOD/MOD integration or analysis. The entire set of the algorithms is first divided into three major categories, depending upon the type of data integration (or analysis). These categories are model-based integration or analysis, preprocessing integration or analysis and post-processing integration or analysis. Next each category is further divided into several sub-categories depending upon the learning style used, supervised, unsupervised, semi-supervised or survival-driven learning. A brief summary of the most well-known recently developed algorithms for each sub-category along with the other important information (such as data profiles used, statistical method and feature selection method used, outputs of the algorithms, etc.) is presented. Therefore, a total of 11 categories of methods [model-based conjoint or analysis with supervised learning (MSL), unsupervised learning (MUL), semi-supervised learning (MSSL), survival-driven approach (MSD), preprocessing conjoint with supervised learning (PRSL), unsupervised learning (PRUL), semi-supervised learning (PRSSL), survival driven learning (PRSD), post-processing conjoint with supervised learning (POSL), unsupervised learning (POUL) and semi-supervised learning (POSSL)] will be described in detail. Since the number of possible variation of the entire set of algorithms is high, it is impossible to provide a comparative study for all methods together. Finally, we provide a summary table of the appropriate use and efficiency of all the categories of graph and rule mining-based learning methods when input and specific objective are given. This review will improve understanding of the appropriate uses of different kinds of algorithms in the domains of cancer classification and prognosis.

Fundamental theory and advances in graph- and rule-based learning algorithms

A graph is a collection of vertices connected by edges. A graph is either undirected or directed. Density is a fundamental measure of a graph. Let 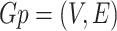be an undirected, unweighted graph and 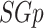be a sub-graph of it (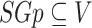). The density of 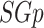(symbolized as 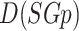) can be defined as follows:

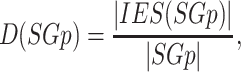(1)

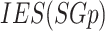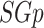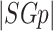where refers to an induced edge set of and denotes the cardinality of 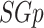. For any weighted graph, a real-valued weight function (or conical combination/weighted sum), 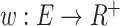can be defined as 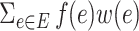. The adjacency matrix denoted as 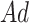of the graph 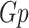of the order n can be described as a 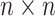matrix as follows:

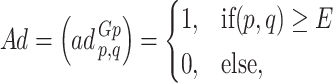where 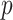and 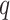are two nodes of the graph and 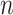is the number of nodes (vertices) in the graph.

Of note, a graph is called as a connected graph whenever all pairs of vertices are connected by paths. On the other hand, a graph is called as a disconnected graph if it contains some vertices which are not connected to each other. A cycle is a simple path which starts and terminates at a same node (vertex). The graph having no cycle is stated as a acyclic (or forest). A tree is formed whenever there exists a connected forest.

A spanning tree of the graph denotes a connected acyclic sub-graph which contains all the nodes (vertices) of the graph along with the minimal number of edges. Of note, a spanning tree must consist of 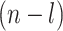edges. A minimum (weight) spanning tree is basically a subset of the edges belonging to a connected, undirected and weighted graph containing all its nodes to be connected together having no cycle, but contains minimum total interaction (edge) weight. In other words a spanning tree must contain the minimum summation value of its edge (interaction) weights. A graph can be stated as bipartite graph (bigraph) if its corresponding vertex set can be divided into two disjoint subsets by which all edges belong to these two sets as well as no two nodes (vertices) of the graph within the same subset will be adjacent. A graph is called as a complete graph if each pair of the distinct nodes (vertices) is adjacent. A clique of the graph is a complete sub-graph of that graph in which each node will be adjacent to each other. However, two graphs 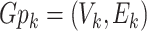and 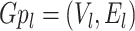can be called as isomorphic graphs whenever a bijective mapping (i.e. 1-to-1 mapping), i.e. 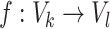(i.e. an isomorphism) occurs by which 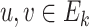exists, iff .

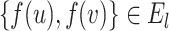Several graph pattern mining approaches such as frequent graph patterns, optimal graph patterns, graph patterns with constraints and pattern summarization have been extensively used in different areas including biomedical as well as bioinformatics domain. For graph classification, the researchers basically use decision tree-based approach and pattern-based approach. In addition, various graph compression methods such as intrusion network analysis, identifying functional (gene) module, extracting biochemical structures, building blocks for the graph clustering (classification or correlation study), mining biological conserved motifs or subnetworks are useful.

ARM [66, 68] is another widely used technique to find interesting relationships among various items (i.e. genes). Let 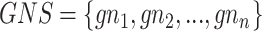be an item set (gene set) and 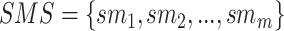be a transaction set (sample set). Thus, an association rule can be formulated as 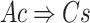, where 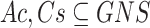and 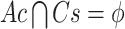. Of note, here 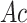and 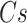refer to antecedent (or left-hand side) and consequent (or right-hand side), respectively. For example, in a biological transaction, let 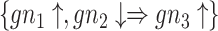be such a rule that denotes that if gene 1 is up-regulated (marked by ) and gene 2 is down-methylated (denoted as ) simultaneously, it is likely that gene 3 becomes up-regulated. It is expected that the relationship between these three genes will likely lead to disease progression. Additionally, the support (frequency) of an item set (gene set) is stated as the number of transactions (samples) in which all the participating items (genes) belonging to the item set occur together. A gene set is said to be frequent if the support is greater than a user-provided threshold value (i.e. minimum support cutoff); whereas the confidence (strength) of the rule can be stated as the ratio of the support of the entire item set to the support of its antecedent alone.

Currently, graph theory as well as ARM approaches are used extensively in various biomedical fields including cancer classification and co-expressed gene module detection. Cancer-related information has been detected from the hotspots (disease modules) in the corresponding dysregulated bio-molecular networks. Dam et al. [11] provided a survey of the existing methods of co-expression-based analysis for the RNA-seq or similar kind of profiles along with mentioning the gene markers/hubs that might have significant role in disease detection, progression and therapeutic value of the disease. They also demonstrated the integrated network analysis that might include genome-wide transcription factor binding sites, genome-wide association study, expression quantitative trait loci and many more layers of data. Differential co-expression study could explore the genes which might contained various co-expression partners between the disease condition and normal condition and which might revealed the important information regarding the regulators across the disease as well as other remaining phenotypes. Application of generalized singular value decomposition (svd) approaches, as well as various biclustering techniques to determine the modules for the corresponding cancer subtypes that might be interesting information for disease prognosis as well as precision study, was also described. Interestingly, a new gene module identification framework was developed by Jiang et al. [12] that used the double-label propagation clustering technique to enhance the biological significance of the gene modules as well as discarding the loosely connected interactions of gene pairs from the modules.

Selection of the most appropriate analysis method is complicated by both data availability and user need. While for some types of cancers only a SOD set is available from a single tissue source, multiple data sets from multiple repositories are available for others. User needs also differ between studies. At present, researchers are left to decide upon the appropriate analysis methods without sufficient information. Therefore, this comprehensive review of various graph theoretic as well as ARM algorithms used for the purpose of SOD or MOD integration is needed. Table 1 summarizes a list of graph and rule mining-based algorithms with brief information such as type of data integration (conjoint), type of learning, data type to be used, objective and the underlying statistical method or feature selection.

Table 1.

List of the graph and rule mining methods

Method	Category	Data type	Output	Statistics and feature selection
Network-constrained regularization and variable selection [48]	MSL	EXP and KEGG pathways	Network-constrained regularization for linear regression finding various subnetworks	L1-norm (Laplacian) of coefficients
Penalized logistic regression model [51]	MSL	MET	Methylation CpG loci and associated genes	Penalized logistic regression (l1 and squared l2 penalty)
SDP/SVM [116]	MSL	Protein sequence, hydropathy profile, EXP and protein interactions	Linear classifier based on the combinations of multiple kernels	SDP/SVM kernel-based statistical learning
FSMKL [117]	MSL	CNV, EXP, ER status and clinical features	Linear classifier based on the combinations of multiple kernels	Multiple kernel-based statistical learning, SimpleMKL (i.e. gradient descent method)
iBAG [118]	MSL	Multi-data	Gene subset	Multi-step study, Bayesian lasso and median probability model
MCD [119]	MSL	LoH, CNV and MET	Gene subset	Multi-step study
Anduril [120]	MSL	MET, EXP, SNP, miREXP, aCGH and exon	Comprehensive report (genetic loci along with the genes containing highly significant survival effect)	Multi-step study
Machine-learning approach to integrate big data for precision medicine [70]	MSL	EXP, drug response data and driver feature data	Molecular marker discovery	Probabilistic graphical model
Spectral graph theory [69]	MSL	Multi-data	Discriminative dense sub-networks	Graph Laplacian spectrum of graph
sglasso [40, 38]	MSL	EXP and SNP	sglasso estimator	Weighted l1-penalized RCON(V,E) model, CCM and CCD algorithm
fglasso [37, 39]	MSL	EXP and SNP	l1-penalized fglasso estimator	Weight l1-penalized factorial dynamic Gaussian Graphical Model, CCM and CCD algorithm
intNMF [79]	MUL	MET, CNV, EXP, miREXP and PEXP	Clusters subtype discovery	Nonnegative matrix factorization
iNMF [69]	MUL	Multi-data	Clusters	Nonnegative matrix factorization
Joint NMF [91, 92]	MUL	Multi-data	Gene modules	Nonnegative matrix factorization
iCluster [94]	MUL	Copy number variation and expression	Clusters	Matrix factorization l1 penalty
iCluster+ [95]	MUL	Multi-data	Clusters	Matrix factorization l1 penalty
JIVE [79]	MUL	Multi-data	Unique factors and shared factors	Matrix factorization l1 penalty
Joint Bayes Factor [98]	MUL	MET, EXP and CNV	Unique factors and shared factors	Matrix factorization student-t sparseness promoting prior
ssCCA [99]	MUL	Sequence data	Operational taxonomic unit clusters	CCA l1 penalty
CCA sparse group [100]	MUL	Two categories of data	Cluster of features containing weights	CCA l1 penalty
sMBPLS [101]	MUL	Multi-data	Feature modules	Partial least squares l1 penalty
SNPLS [102]	MUL	EXP, gene network information and drug response	Co-modules of gene-drug	Partial least squares network-dependent penalty
rMKL-LPP [111]	MUL	Multi-data	Clusters	Multiple kernel learning dimension reduction metric locality preserving projections
Normalized ImQCM [34, 35]	MUL	OD	Densely connected gene modules (i.e. quasi-cliques)	Graph mining and weight normalization inspired by spectral clustering
GEM-TREND [61]	MUL	EXP	Network discovery	Nonparametric as well as rank-based pattern matching method inspired by the method of [62]
RiboFSM [60]	MUL	SOD	Frequent subgraph	Frequent subgraph mining
ConGEMs [43]	MUL	SOD	Condensed gene co-expression modules	Weighted rank-based Jaccard and weighted rank-based Cosine measures
Bimax biclustering [53, 54]	MSSL	SOD (logical matrix)	Sub-matrices (clusters)	Finding only all one sub-matrix
CC biclustering [55]	MSSL	SOD	Sub-matrices (clusters)	Find sub-matrices containing lower score than cut-off value in a standardized data
XMotifs biclustering [58]	MSSL	SOD (logical matrix)	Sub-matrices (clusters)	Finding sub-matrix for which each row has similar motif through all the columns
Spectral biclustering [59]	MSSL	SOD	Sub-matrices (clusters)	svd in the eigenvectors for both genes and samples simultaneously
iSubgraph [63]	MSSL	EXP and miREXP	Finding closed frequent subgraphs (co-modules) having frequent up- or down-regulated molecules cancer group classification	Graph mining mixture models
Net-Cox [50]	MSD	Multi EXP	Signature genes	Cox regression model with l1/l2-norm
netSVM [52]	MSD	EXP protein EXP	Prognostic signatures building classification models	SVM
Pathway-based classification [71]	PRSL	EXP, MsigDB v1.0	Pathway markers	Z-score logistic regression
MDI [103]	PRUL	Multi-data	Clusters	Bayesian correlated clustering and DMA mixture model
Prob_BM [104]	PRUL	CNV, SNP, EXP and miREXP	Clusters	Bayesian
CNAmet [23]	PRUL	MET, EXP and CNV	Scores and corresponding P-values of genes	Multi-step study
iPAC [112]	PRUL	CNV and EXP	Gene subset	Multi-step analysis various filtering including matched aberrant genes, in-cis correlation as well as in-trans functionality
Dysfunctional module detection [74]	PRUL	EXP	Disease module features (sub-networks)	Shortest distance algorithm
Network topology-based gene marker discovery [76]	PRUL	EXP and PPI	Subnetwork identification	Randomized Steiner tree algorithm Network topology
GeneticInterPred [121]	PRSSL	PPI, EXP and protein complex data	Genetic interaction labels	Graph conjoint
Graph-based learning [122]	PRSSL	MET, miREXP, EXP and CNV	Patient scores for the purpose of classification	Graph conjoint
Combinatorial gene marker discovery [79]	PRSSL	EXP MET	Combinatorial gene markers	CoMEx statistical score and BiMax biclustering weighted support measure
TrapRM [80]	PRSSL	EXP, MET and PPI	Multi-omics association rules	Statistical test and weighted shortest distance association rule mining
NBS [75]	PRSD	EXP and PPI	Network-smoothed features/modules and cancer classification survival analysis	Network-based stratification NMF
CoxPath [123]	PRSD	MET, miREXP, EXP and CNV	Prognosis index for the individual patient	Multi-step study l1 penalty
MKGI [124]	PRSD	MET, miREXP, EXP and CNV	Final model along with patient index	GENN
ATHENA [113]	POSL	CNV, EXP, miREXP and MET	Final model along with index of patient	GENN neural networks
jActiveModules [114]	POSL	PPI, EXP and interactions between proteins and DNA	Subnetwork (i.e. hotspots of the network)	Network-simulated annealing
Network propagation [115]	POSL	PPI, mutation and gene expression	Propagated network corresponding to differential gene expression	Network
Diffusion kernel creation [83]	POSL	Gene expression data	Natural families of kernels	Heat equation spectral graph theory
PSDF [105]	POUL	CNV and EXP	Clusters	Bayesian and binary indicator feature's likelihood
BCC [106]	POUL	MET, proteomics, EXP and miREXP	Clusters	Bayesian
CONEXIC [107]	POUL	CNV and EXP	Clusters of genes related to modulators	Bayesian
PARADIGM [108]	POUL	Multi-data	Gene score gene significance in individual pathway	Pathway networks
SNF [109]	POUL	miREXP, MET and EXP	Clusters	Similarity network fusion
Lemon-Tree [110]	POUL	EXP and MET/CNV/miRNA (only one category)	Association network graphics	Module network
Causal genes and dysregulated pathways finding [81]	POUL	EXP, CNV and SNP	Causal genes and dysregulated pathways	Set-covering approach
Significantly mutated pathway detection [82]	POUL	Somatic mutation and PPI	Significantly mutated pathway	Naive approach-enhanced influence graph
Multi-view gene modules using hypo-graph mining [44]	POUL	MOD set	Multi-view modules	Dense hypo-graph mining normalized mutual information
MVDA [27]	POSSL	MOD set	Multi-view clusters	Hyper-graph based learning, normalized mutual information, optimization, etc.
MEMo [87]	POSSL	Somatic mutation, GISTIC CNV, EXP and PPI	Mutual exclusivity modules	Jaccard coefficient statistical test (switching permutation method)
Epigenetic gene marker discovery through feature selection [41]	POSSL	EXP and MET	Epigenetic gene markers	Statistical test and relevance and redundancy normalized mutual information
StatBicRM [68]	POSSL	EXP and MET	Rule-based classifier gene markers	Statistical test and biclustering association rule mining
Tumor prediction using integrated analysis of expression and methylation [93]	POSSL	EXP and MET	Rule-based classifier gene markers	Statistical test association rule mining

aCGH, comparative genomic hybridization array; ER, estrogen receptor; EXP, gene expression profile; fglasso, factorial graphical lasso; GISTIC CNV, gistic copy number variation profile; LoH, loss of heterozygosity; MET, DNA methylation profile; miREXP, miRNA expression profile; PEXP, protein expression profile; PPI, protein–protein interaction profile; sglasso, structured graphical lasso; SNP, single-neucleotide polymorphism.

Types of different graph and rule mining-based algorithms with objectives, advantages and limitations

The various graph and rule mining algorithms were grouped in a total of 11 categories in terms of combinations of several conjoint (or analysis) and learning methods (Figures 1 and 2). The brief details of input, objective (output) and description, advantages and limitations with various research works for each category are demonstrated in the following.

Figure 1.

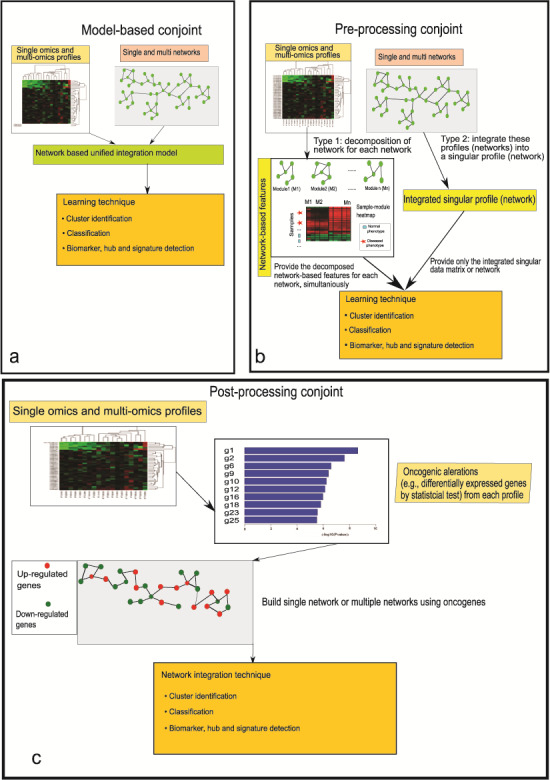
The flowchart of three categories of integration where sub-figure (a) illustrates the flowchart of model-based integration, sub-figure (b) depicts the flowchart of pre-processing-based integration and sub-figure (c) denotes the flowchart of post-processing integration.

Figure 2.

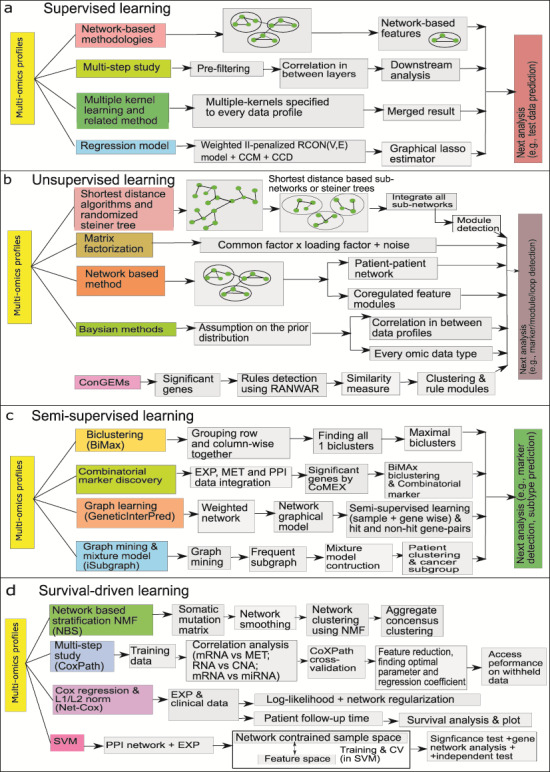
The work-flows of four categories of learning where sub-figure (a) represents the work-flow of supervised learning, sub-figure (b) illustrates the work-flow of unsupervised learning, sub-figure (c) signifies semi-supervised learning and sub-figure (d) represents the flowchart of survival-based learning.

Model-based conjoint (or analysis) with supervised learning

The 1st sub-category belonging to the model-based conjoint is MSL. It utilizes a single unified machine learning approach for integrating (or analyzing) all the genomic profiles with a single network. The majority of the mathematical model-based approaches belong to this sub-category. Notably, one unified learning framework as well as a global optimization technique has been used here. Supervised learning is useful whenever the entire data are labeled.

• MSL:

• Inputs: In general, the inputs of MSL are (i) genomic (epigenomic or similar) profiles, (ii) corresponding molecular networks and (iii) sample (phenotype) class labels.

• Objectives: The objectives of this type of algorithms are (i) cancer sample (phenotype) prediction and (ii) gene-signature (marker-gene, hub-gene or driver-gene) identification.

• Advantages: (i) This category provides best prediction of class labels for the results whenever the three kinds of inputs are available, since it uses global optimization along with only one unified framework together. (ii) Handles the problems of sparsity and heterogeneous connectivity well. (iii) Minimizes the score of the statistical loss function if kernel-based methods are used.

• Limitations: (i) Although an optimization technique is used here, the optimization strategy is very complex and difficult to understand. (ii) Scalability is very low. (iii) It is costly to use as it requires all labeled data (property of the supervised learning).

Various techniques fall into this category. The most frequently utilized network-based regularization technique is graph Laplacian regularizer. Different popular regression models are incorporated into the graph Laplacian constraint to analyze the genomic data. A network-constrained linear regression technique, which integrates a graph Laplacian constraint and the L1-norm sparse linear regression for identifying the associations among the regression coefficients [49], was developed by Li et al. (2008) [48]. Interestingly, this network-related linear regression is basically analogous to the utilization of a well-known LASSO optimization problem [48]. The graph Laplacian constraint in the linear classification models (e.g. logistic regression by Sun et al. (2012) [51]) was also utilized in many studies.

Lanckriet et al. (2004) [116] developed a computational and statistical pipeline (denoted as ‘SDP/SVM’) to conjoint the heterogeneous descriptions of the same gene set. Here, semidefinite programming (SDP), support vector machine (SVM) and simple multiple kernel-based statistical learning (abbreviated as 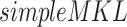, e.g. gradient descent method) were utilized. The output provided one or more linear classifiers, depending upon the combinations of kernels. A pathway-based data integration (feature selection in the context of multiple kernel learning or FSMKL) [117] was proposed, in which the integration was carried out through the utilization of multiple kernel learning. Here, the user had to provide copy number variation (CNV) data, gene expression (EXP) data, ER-status and clinical features.

Bayesian method is a well-known strategy to work on any kind of genomic profile. In 2013, the generalized version of the integrative Bayesian analysis of genomics data (generalized iBAG) [118] was proposed which conjoined profiles from various genomic platforms through a hierarchical model, including the biological relationships among them. The outcome included a subset of genes. Another method defined the multiple concerted disruption (MCD) analysis [119] of genes which allowed for the deduction of abnormal pathways as well as genes. The three kinds of data sets [viz., DNA methylation, DNA copy number and loss of heterozygosity (LOH) data sets] were provided as inputs. As outcome, a small gene set, which revealed the disruption via several mechanisms and represented the corresponding consequential alteration in gene expression, was identified. Anduril et al. [120] developed a similar kind of framework that was used to convert the fragmented large-scale profile into testable predictions. The main aim of this technique was to determine the genetic loci as well as the genes which have significant effect on the survival of the patients. It used MET, EXP, single nucleotide polymorphism (SNP), miRNA, array comparative genomic hybridization) as well as exon profiles as inputs. Lee et al. [70] introduced a new method to determine reliable gene expression markers for the purpose of determining drug sensitivity by adding the valid multi-omic prior information for every gene’s potential to drive the cancer. As inputs, EXP, drug response data and driver feature data were used. A probabilistic graphical model was applied here. Chuang et al. [69] developed a protein-network-based method to determine the sets of markers denoted as discriminative dense subnetworks obtained from protein interaction databases. Graph Laplacian and Spectrum of graph were utilized.

Furthermore, structured graphical lasso denoted by sglasso [37, 38, 40] and L1-penalized factorial graphical lasso symbolized as fglasso [37, 39, 40] were also widely used for conjoining multi-omics profiles. For the sglasso, weighted L1-penalized RCON(V, E) model, cyclic coordinate minimization (CCM) and cyclic coordinate descent (CCD) algorithms were used for modeling, whereas for fglasso, weight L1-penalized factorial dynamic Gaussian Graphical Model, CCM and CCD algorithms were used. For both the methods, EXP and SNP were used as inputs.

Model-based conjoint (or analysis) with unsupervised learning

The coefficients learned from the corresponding feature variables identify several dense subnetwork modules (clusters). Some characteristics of this category (such as use of singular unified learning framework and global optimization technique) are common with MSL, since both follow model-based integration. However, the distinctive characteristic of this type of algorithms is that these algorithms are highly useful for determining the inherent feature (structure, e.g. module) from the input data set due to their unsupervised learning style. This kind of techniques is used whenever the entire data are unlabeled (property of unsupervised learning).

• MUL:

• Inputs: The inputs of MUL are (i) genomic (epigenomic or similar) profiles and (ii) corresponding molecular networks.

• Objectives: The major objectives of this kind of algorithms are (i) subnetwork (module) detection and (ii) gene-signature (marker-gene, hub-gene or driver-gene) detection.

• Advantages: (i) This category is useful to model the underlying distribution or structure of the data for the purpose of learning more regarding the data. (ii) As MSL, the MUL also works well for handing the problems of sparsity and heterogeneous connectivity.

• Limitations: Some limitations of this category (such as optimization technique used being more difficult to understand, as well as low scalability) are common with some characteristics of MSL due to both using model-based integration. However, the performance in this category of algorithms is worse than the performance of MSL since it follows unsupervised learning whereas MSL follows supervised learning.

Selection of predictive classification strategies from high-dimensional, small-sample-sized sparse data is a major challenge whose importance has been increasing day by day in different kind of applications such as RNA-seq/microarray data analysis, functional magnetic resonance imaging study, image-based object detection and many more. In general, for those applications, the number of features/genes (dimensionality) of the profile is vastly higher than the number of samples of the profile. In addition, in many times, the data matrix might have zeros in most of the elements (called as sparse matrix/data). These two shortcomings create new challenges in case of the classification learning strategies [2, 9, 137–142].

There are various model-based conjoint algorithms which include the unsupervised learning approach. One of the straightforward approaches for unsupervised data conjoint belongs to the matrix factorization approach that basically focuses on the projection of variability among the underlying data profiles into the space of dimension reduction. Zhang et al. [91, 92] introduced a joint nonnegative matrix factorization pipeline for the MOD conjoint. It depended upon dividing a nonnegative matrix into the two objects, nonnegative loadings and nonnegative factors:

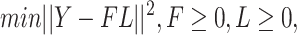(2)

where 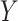denotes the matrix of methylome, mRNA transcriptome or any other omics profile having 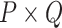dimensions; 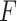symbolizes the common factor for the 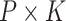dimension matrix; and 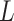refers to the 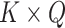dimension coefficient matrix. Instead of the fundamental correlation, the objective was to project each profile into the common fundamental space by which one can determine the coherent patterns among the profiles through examining the elements that have significant 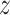scores. NMF took longer to compute and bulk memory space was needed. In case of NMF, it needed the nonnegative input matrices as well as correct normalization for these input profiles, since these contained different distributions as well as variabilities. Chalise et al. [72] proposed intNMF (an integrative approach for disease subtype classification based on NMF) to cluster multi-dimensional profiles using NMF technique. Multi-omics (viz., MET, CNV, EXP, MiREXP (miRNA expression), PEXP (protein expression), etc.) data were used. Outcomes were the resultant clusters as well as the cancer-subtype detection. A similar algorithm (integrative NMF or iNMF) was also developed by Yang and Michailidis [96]; it also utilized NMF for multi-modal omics data.

Shen et al. (2009) [94] proposed a new NMF-based technique called ‘iCluster’ that considered a regularized joint latent variable akin to 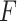in the NMF but having no non-negative constraints. The equation for decomposition in iCluster is denoted as follows:

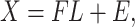(3)

where 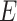is noise (or, error) term. Here, the loading coefficient 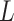is the sparsity that was induced with various categories of penalty functions in the case of different data types. In 2013, Mo et al. [95] extended the concept of iCluster (denoted as ‘iCluster+’) through the assumption of various modeling methods for the inter-relationships between 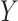and 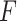across various data platforms. ‘iCluster+’ allows for different kinds of data types such as continuous, binary, sequential and categorical data with various modeling assumptions including multilogit, normal linear, logistic and Poisson distributions. The common latent variable vector F denoted the corresponding driving factors which were applied to the disease subtype assignment. Tibshirani et al. (1996) [49] introduced the least absolute shrinkage and selection operator (LASSO) penalty method to solve the issue of sparsity in 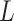. Of note, nonnegative input data matrix is not necessary for either iCluster or iCluster+, unlike for the NMF method.

Lock et al. (2013) [97] proposed a new variant of NMF method entitled ‘Joint and Individual Variation Explained’ (JIVE). Through JIVE, the original data profile of each layer was decomposed into three partitions, i.e. an approximation of the joint variation toward the data types, residual noise and an approximation of the specified structured variation for each individual data type. In detail, JIVE factors the initial data profile input matrix into the two lower-ranked representative parts, i.e. shared factor (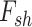) and data-specific factor (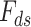) that are completely dependent upon 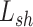and 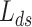, respectively. Here this is denoted as follows:

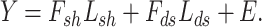(4)

Notably, the ranks of the two loading factors might not be same. Depending upon the principal component analysis for the factorization, JIVE performance suffers mainly from the outliers. Hence, the robustness of JIVE might be affected due to outliers.

In the next year of developing JIVE, Ray et al. (2014) [98] proposed another method in which Joint Bayes Factor was inverted in a way such that a common factor loadings 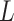was assumed for both the factors (i.e. shared factor 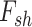as well as data-specified factor 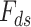). The initial data profile input (e.g. gene expression data matrix) is decomposed into shared common factors across data types, data-type specific factors and residual noise just as in JIVE. But unlike JIVE, which introduced the sparsity through L1 penalties, Joint Bayes Factor model assumes a beta-Bernoulli procedure for both factors ( 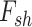and 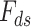). For the factor loadings (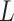), that model utilizes the student-t sparseness-promoting prior for taking into account the sparsity [125]. The decomposition equation is as follows:

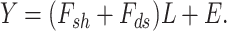(5)

The drawback of the method was that the Joint Bayes Factor falls into the linear relationship between the observational and latent spaces, and a very close relationship for various levels of data was assumed.

Another method is canonical correlation analysis (CCA) that is used to determine the relationship between the two sets of variables. CCA is extensively used in integrating two data sets. Let us assume that, in the CCA, the two profiles will be decomposed as follows:

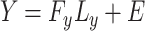(6)

and

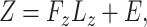(7)

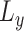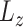where and denote the loading factor for 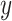-th and 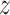-th profiles. In general, the objective of CCA is to identify the loading factors ( 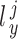and 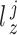depicting the 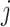-th column for loading factors) that will maximize the following correlation:

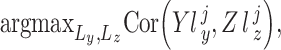(8)

where 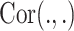stands for the correlation score between two vectors. Of note, typical CCA could not be used for the purpose of dimension reduction for estimating the inverse of a covariance matrix. For the case of MOD integration, penalization and regularization terms are included to produce more stable as well as sparse solutions of those loading factors. L1-penalized sparse CCA (sCCA) conjoint with elastic net CCA has been developed for filtering the number of variables to create more biologically relevant results [126, 127]. The latest research on CCA considered the grouped effects of the features as the structures fixed into the data sets [e.g. structure constrained CCA (ssCCA) [99], CCA-sparse group [100]].

Partial least squares (PLS) is a method that was used to maximize the covariance, and it can help to avoid the problem of sensitivity to the outliers. This can be denoted as follows:

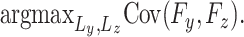(9)

The sparse solutions of the PLS (symbolized as sPLS) have been applied to work in parallel with CCA-elastic net [128]. Of note, other variants of PLS are (i) ‘sparse multi-block partial least squares’ (sMBPLS) used to solve the limit of the two data block computation by redefining the objective function as a weighted sum of the latent variables in various layers [101], (ii) sparse network regularized partial least square (SNPLS) was used to determine the co-modules estimated based on the relationship between gene expression and drug response [102].

Another technique is Regularized Multiple Kernel Learning Locality Preserving Projections (rMKL-LPPs) used to conjoin the multi-omics profiles [111]. The LPPs have been utilized for conserving the sum of distances for the k-nearest neighbors of every sample. As compared to SNF, rMKL-LPP provided more flexibility since it generated various choices of the dimension reduction techniques as well as kernels for each data type.

Some gene module identification methods using various correlation measures such as Pearson correlation coefficient, traditional TOM by [30], weighted TOM by [31, 32] and generalized TOM [33] also fall into this category. Zhang et al. (2014) [34] proposed a new method for weighted networks to produce the densely connected modules referred to as quasi-cliques. The major benefit of this approach is that the local maximum edges were applied to initiate the search for avoiding the extortionate (unreasonable) overlaps among the recognized modules. Hence, the run time of the method was significantly reduced. This methodology is highly useful for detecting a higher number of genetic modules which are enriched in both the biological functions and the chromosomal bands in the cancer profile suggesting a major contributions of copy number variations connected with the development of the cancer. Huang et al. (2018) [35] developed the corresponding R package, ‘ImQCM’. Feng et al. (2009) [61] developed a novel web-based software, ‘Gene Expression data Mining Toward Relevant Network Discovery’ (GEM-TREND) to mine the gene expression data network through finding the similar gene expression profiles and generating corresponding co-expression networks from any publicly available database. Of note, for statistical significance, a nonparametric as well as rank-based pattern matching method inspired by the method of [62] was utilized. Frequent subgraph mining is the latest topic of interest. Gawronski et al. (2014) [60] introduced a novel algorithm named as ‘Frequent subgraph mining for the discovery of RNA structures and interactions’ (RiboFSM) for identifying the meaningful patterns from either a single large graph or a set of smaller sized graphs. The graph represented all RNA structures along with the interactions. The most significant frequent patterns had been determined from the graph.

ARM is a useful tool for extracting the interesting gene sets (item sets) for any kind of data. It can generate the cause–effect relationships between the biomolecules such as genes. Mallik and Zhao [43] introduced two novel rule-based similarity measures (i.e. weighted rank-based Jaccard and weighted rank-based Cosine measures) and then prepared a novel computational framework to identify the condensed gene co-expression modules (‘ConGEMs’) through the utilization of the association rule-based learning strategy and the weighted similarity scores. The algorithm is good for retrieving the bio-marker modules from the genomic (or epigenomic) profile.

Model-based conjoint (or analysis) with semi-supervised learning

The characteristic of MSSL shared with MSL and MUL is that it also uses a unified learning framework as well as a global optimization strategy as it follows model-based conjoint like MSL and MUL. However, in the MSSL, the unsupervised learning methods have been applied to produce as well as to learn the structure from the integrated data. The supervised learning methods can also be utilized to validate best guess predictions in case of unlabeled data. This feeds the data back into the method of supervised learning as the training data set and then applies the model for making predictions on the unseen new data (test data). Interestingly, a lot of real-life machine-learning problems have fallen into this domain (semi-supervised learning) since collecting completely labeled data is time-consuming as well as highly expensive. On the other hand, unlabeled data are very cheap and very easy to accumulate and store.

MSSL:

• Inputs: The inputs of MSSL are same as mentioned for MSL [i.e. (i) genomic, epigenomic or similar kind of data profiles; (ii) corresponding molecular networks; and (iii) available sample (phenotype) class labels].

• Objectives: Since this kind of algorithms is the combination of MSL and MUL approaches, the objectives of the MSSL are also divided into two different kinds, first kind of objective includes all the objectives of MSL such as subnetwork module detection and gene-signature (marker-gene, hub-gene or driver-gene) detection, whereas the second type of objective includes all the objectives of MUL such as the prediction of the unknown class labels of the outcome has been performed using the available class label of the samples.

• Advantages: (i) It also produces good prediction of the class labels because it applies a combination of unsupervised and supervised learning approaches (property of semi-supervised learning). (ii) It is useful whenever only a few of the class labels of the entire samples are available, but majority of data remain unlabeled (property of semi-supervised learning). (iii) This is used frequently for both prediction along with data exploration. (iv) The cost is moderate (due to use of semi-supervised learning); hence, it is useful to solve most of the real life problems since it needs some data to be labeled, not all.

• Limitations: Some limitations belonging to this category (i.e. the optimization technique used being more difficult and complex to understand, as well as producing low scalability) are matched with some characteristics of MSL and MUL because all the three categories follow model-based integration. The other distinct limitations are class-label prediction result is not always consistent.

Biclustering techniques are useful for the detection of genetic modules. Binary inclusion-maximal biclustering (Bimax) algorithm [53, 54] is a popular biclustering algorithm which traverses each cell of the matrix to determine the sub-matrices having only ones in a logical (Boolean) matrix and then determines such sub-matrices, if any exist. The advantage of this method is that it is able to identify the genetic modules having a set of genes along with respective samples (class labels). Another biclustering method is Cheng and Church (CC) biclustering [55] for which the sub-matrices containing scores lower than a specified threshold value in a standardized data matrix were searched for and identified, if found. Turner et al. (2003) [57] improved the centralized idea proposed by [56]. Here data matrices were modeled to a sum of views (layers). The model was used to fit to the profile through the minimization of the error. Another reputable biclustering tool is XMotifs biclustering developed by Murali et al. (2003) [58]. This algorithm searches the sub-matrix for which each row consists of a similar motif by all the columns. The method requires a logical (Boolean) data matrix as input. Kluger et al. (2003) [59] proposed spectral biclustering which assumed that the normalized microarray data matrices contained a checkerboard structure obtained by the use of svd in the eigenvectors applied to samples and genes simultaneously.

The high heterogeneity between tumors makes generating the major tumorigenic pathways as the therapeutic targets a most challenging task. The merging of the multi-omics profiles is an interesting task to build the driving regulatory networks underlying the subgroups of the patients (samples). Ozdemir et al. (2013) [63] introduced a novel framework entitled ‘iSubgraph’ (Integrative Genomics for Subgroup Discovery in Hepatocellular Carcinoma Using Graph Mining and Mixture Models) to determine the patterns belonging to the miRNA–gene networks in which frequently up/down-regulated biomolecules in a group of patients (samples) had been observed and it would be utilized for the stratification of the patient for the hepatocellular carcinoma. The gene expression profile and miRNA expression profile had been analyzed simultaneously in terms of the structure of a graph. Here the microarray profile was firstly transformed into a graphical form that encodes the gene expression levels as well as miRNA expression levels with their internal interactions. Of note, iSubgraph technique can determine the co-operative regulation of genes as well as miRNAs although the regulation found only in a few patients (samples). The miRNA–mRNA modules were utilized in an unsupervised class prediction model for recognizing the hepatocellular carcinoma subgroups through the patient (sample) clustering through the mixture models.

Model-based conjoint (or analysis) with survival-driven approach

Survival-driven (cancer prognosis) prediction is a topic of interest for cancer patients as well as health care providers. Meanwhile, only a few strategies are available to conjoin any MOD optimized for the prognosis-related prediction. Notably, both the one unified learning framework and global optimization technique have been used here. It predicts the class labels for the results through prognosis well as it also checks the overall survival and follow-up times for the patients.

MSD:

• Inputs: The inputs of MSD are same as mentioned for MSL and MSSL [i.e. (i) genomic, epigenomic or similar data profiles; (ii) corresponding molecular networks; and (iii) available sample (phenotype) class labels.

• Objectives: The objectives of this type of algorithms are (i) cancer sample (phenotype) prediction and (ii) gene-signature (marker-gene or hub-gene) detection having prognosis study of underlying samples from the clinical data.

• Advantages: (i) Cancer prognosis (survival)-related information helps to make a decision about the management as well as therapeutic treatments of the patients. (ii) Prognostic-related markers are highly useful to more effective selection of the subgroups of patients along with various therapeutic methods.

• Limitations: Several disadvantages of this category overlap with some characteristics of the MSL, MUL and MSSL due to all four using the same type of integration (model-based integration). These are as follows: (i) the optimization technique seems to be more difficult and complex to understand. (ii) Low scalability has been produced. (iii) The result of the class-label prediction is not always consistent. There is another distinct disadvantage of this category that we need the labeled clinical data for using this category. So it is costly.

A network-based Cox proportional hazard model (abbreviated as ‘Net-Cox’) was introduced by Zhang et al. (2013) [50] for the survival study. The objective of the Cox regression is to understand the baseline hazard function (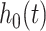) as well as the regression coefficients (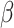) for which the associated instantaneous risk of any event during the time 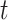for a patient 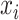could be estimated by the following equation:

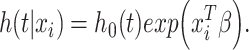(10)

In addition, the graph Laplacian constraint on the regression coefficients (i.e. 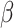) is utilized. Of note, a local optimum solution is produced through the alternation between the maximization with respect to 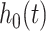and .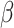

In addition, the graph Laplacian constraint in the linear classification models [e.g. support vector machines (SVMs) by Chen et al. (2011) [52]] is utilized in many works. Let us assume that 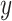is a binary response vector, i.e. 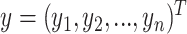, where 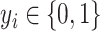. In this case, a Bernoulli likelihood function minus both the L1-norm and the graph Laplacian constraints became maximized in order to learn the linear coefficients. The probability of occurring the 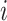-th sample in class 1 is referred to as follows:

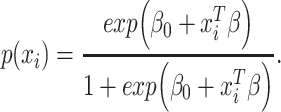(11)

The elastic net technique is utilized here in order to maximize the regularized cost function. Chen et al. (2011) [52] developed network-based SVMs (netSVMs). Suppose, the 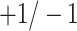binary response vector be denoted by 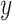. The network-constrained SVM was formulated by the addition of the graph Laplacian constraint and the hinge loss in which the subscript ‘+’ symbolized the positive part, i.e.

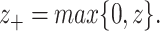(12)

Preprocessing conjoint with supervised learning

In this type of algorithms, the genomic (epigenomic or similar) profiles and the corresponding networks are analyzed individually to explore final network-based features for each profile, and then the learning models are utilized on the network-based features employed, for the purpose of predictions. Alternatively, all genomic (epigenomic or similar) profiles are integrated first, and then further analysis or learning technique conducted on the integrated data. After that, the class labels of the samples for the results are classified and gene signature (marker gene or hub gene) identified, if required. PRSL is used when the entire data are labeled (characteristics of the supervised learning).

PRSL:

• Inputs: The inputs of PRSL are same as mentioned for MSL.

• Objectives: The objectives of this type of algorithms are same as MSL [i.e. (i) classifying the samples and (ii) extracting gene-signature (marker-gene or hub-gene) for the disease], but the design of this kind of algorithms is different from MSL (mentioned in the beginning of PRSL).

• Advantages: (i) It is flexible enough to recognize the customizable subnetwork features (e.g. the recognized features) that affect the hypothesized network-related phenomena (characteristics). (ii) The density as well as size of the subnetworks can be properly specified. (iii) It is the better approach for the output/prediction for the MOD in terms of integration/analysis category.

• Limitations: (i) Network-dependent features obtained from this kind of algorithm are not found to be optimal. (ii) It is costly to use as it needs all labeled data. (iii) Some information loss might be possible during data integration since that depends upon how the profiles are integrated and based upon which criteria are used.

Lee et al. (2008) [71] introduced a novel classification methodology taking into account the features belonging to the discriminative pathways. In this case, gene expression data of the patient samples collected from each disease subtype (e.g. good prognosis or poor prognosis) were converted into a ‘pathway activity matrix’. In other words, pathway information and gene expression matrix were integrated together preliminarily. For each pathway, the activity was basically an integrated 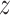-score-estimated gene-wise from the gene expression data. After covering the gene expression vector of every gene on its respective protein belonging to the pathway, the genes that produced the most discriminative functionalities (activities) were identified through a greedy search depending upon their individual power. Next the pathway activity matrix was utilized for training a classifier.

Pre-processing conjoint (or analysis) with unsupervised learning

In this type of algorithms, the integration technique is same as PRUL, but learning technique is different from PRSL. In this case, unsupervised learning technique is used. As for PRSL, the genomic or similar kind of data profiles along with the respective networks are analyzed separately to extract the final network-based features for each profile, and then the learning models are applied on the employed network-depended features. Alternatively, all genomic or similar data profiles are conjoint preliminarily, and then learning or next analysis conducted on the merged data. Thereafter, the final gene modules and genetic signature are identified. Of note, this type of algorithms (in terms of unsupervised learning) is utilized to learn the inherent structure from the input data portion. PRUL is used when the entire data are unlabeled (nature of the unsupervised learning).

PRUL:

• Inputs: The inputs of PRUL are same as mentioned for MUL.

• Objectives: (i) Finding the final gene modules or/and genetic signature. (ii) PRUL is applied for determining the inherent structure from the input data profile through unsupervised learning.

• Advantages: (i) It is flexible enough to recognize the customizable subnetwork features (e.g. the recognized features) that surely affect the hypothesized network-related phenomena (characteristics). (ii) The density as well as size of the subnetworks can be properly specified. (iii) It is the better approach for the output (prediction) for the MOD in terms of integration or analysis category. (iv) The aim of using unsupervised learning is to model the underlying distribution or structure of the data for the purpose of learning more about the data. (v) Performs well in solving the problems of sparsity and heterogeneous connectivity akin to MSL and MUL. PRUL:

• Limitations: (i) Subnetwork features found from PRUL are not optimal like PRSL. (ii) Like PRSL, information loss is possible during conjoining the data profiles. (iii) Performance of PRUL is worser than the performance of all categories that use supervised learning (such as MSL, PRSL, etc.).

Kirk et al. (2012) [103] developed a Bayesian technique for conjoining multiple profiles through unsupervised model that is called multiple data set integration (MDI). MDI can conjoin information from a wide range of various data sets as well as data types simultaneously, including the capability for modeling the time series profile explicitly through the use of the Gaussian processes. Each profile had been modeled through a Dirichlet-multinomial allocation (DMA) mixture model with the dependencies between these models accumulated by the parameters which demonstrated the agreement among the profiles. Cho and Przytycka (2013) proposed a novel computational probabilistic pipeline to model the cancer cases separately as the subtype mixtures for dealing with the cancer heterogeneity. That was as a meta-model, which summarized the outcomes of a large number of alternative models. The proposed method was applied to glioblastoma multiforme (GBM). The outcome model (symbolized as ‘Prob_GBM’) not only correctly determined known relationships but also recognized new characteristics underlining the phenotypic similarities. That pipeline could be utilized for modeling the relations between the similarity of gene expression and the potential genetic reasons relating a broad spectrum of different cancers.

Louhimo and Hautaniemi (2011) [23] introduced a novel method entitled ‘CNAmet’ to integrate the gene expression, methylation and copy number data to produce an integrated score and then estimate the 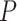-value computation using permutation statistical test. At first, the genes for which up-regulation was caused by the hypo-methylation and the higher copy number patterns or vice versa were identified, where ‘1’ and ‘0’ denote hypo-methylation and hyper-methylation, respectively, for the methylation data and amplification and lack of amplification, respectively, for the copy number data. Then the weighted score for 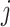-th gene for methylation profile was computed as follows:

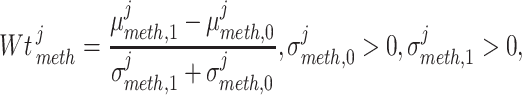(13)

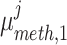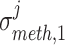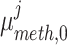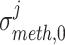where and signify the mean and standard deviation, respectively, of the methylation values of the underlying samples that have ‘1’ score, whereas and denote the mean and standard deviation, respectively, of the methylation values of the respective samples having ‘0’ score. Similarly, the weighted score for 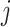-th gene for the copy number data (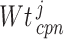) was computed. The CNAmet score for 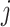-th gene (denoted as 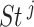) was then computed as

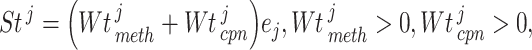(14)

where the correction term 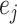is as follows:

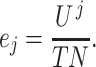(15)

Here 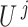is the number of samples belonging to the intersection of the samples having ‘1’ in copy number profile and methylation profile of 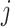-th gene, and 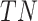stands for the total number of underlying samples. Next the statistical significance of , 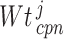and 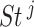was evaluated by random permutation of the corresponding labeled vectors and then recomputing 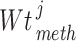, 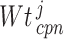and 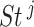. The false discovery rate technique proposed by Benjamini and Hochberg (1995) was applied to compute the 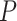-values of 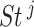. Of note, 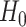states that ‘the higher score was caused because of the random event’.

However, Aure et al. (2013) [112] introduced a new framework which analyzed in-trans process-associated and cis-correlated (iPAC) genes in order to find the evidence of in-trans relation to the biological processes without the bias toward the processes of a specified function or category. The objective of this approach is to determine the cis-regulated genes for which the correlation in the expression to other genes generates further evidence of their role in the network perturbation in cancer. The aforementioned unsupervised methodology involved several statistical tests consecutively to identify the list of relevant (nonredundant) genes depending upon the integrative analysis of the gene expression and copy number profiles. A new adjustment approach handled the effects of the co-occurrence of the copy number aberrations, in terms of reducing the number of false positives.

He et al. [74] introduced a new technique for identifying the dysfunctional modules which would be validated by various categories of measurements along with different independent data sets. In that case, the disease-specified sub-networks were considered as features in which a set of known disease-related genes were mapped into the protein–protein interaction (PPI) network, and thereafter the sub-networks of the disease-associated genes had been determined as the disease-module features. Jahid et al. [76] proposed a new approach to recognize a smaller-sized sub-network for linking all the differentially expressed genes in a PPI network. Next the genes belonging to the subnetwork were utilized as the corresponding features for conducting classification of the underlying samples. Of note, the Steiner tree problem belonging to the graph theory was addressed in that work. For obtaining an optimum solution with the higher probability, a heuristic method, which was coupled with the randomization, was modeled for integrating the underlying multiple sub-optimal Steiner trees.

Preprocessing conjoint (or analysis) with semi-supervised learning

In this category of algorithms, the conjoint strategy is the same as PRSL as well as PRUL, but the learning technique is different. Here semi-supervised learning technique (mixture of unsupervised and supervised techniques) is used. In brief, unsupervised learning methods are applied to produce as well as to learn the structure from the integrated data. The supervised learning methods can also be utilized to validate best guess predictions in case of the unlabeled data. This feeds the data back into the method of supervised learning as the training data set and then applies the model for making predictions on the unseen new data. Semi-supervised learning is useful when a few of the entire data are labeled, but the majority of data remain unlabeled.

PRSSL:

• Inputs: The inputs of PRSSL are same as mentioned for MSSL.

• Objectives: Like MSSL, the objectives of the PRSSL are also divided into two individual categories of which 1st category belongs to the objectives related to unsupervised learning [i.e. (i) sub-network or gene module detection and (ii) gene-signature finding, and the 2nd objective category includes (iii) the prediction of the unknown (new) class labels of the result through learning (training) on the available class label of the underlying samples].

• Advantages: Like PRUL, (i) one of the objective of PRSSL is to identify the customized as well as flexible features which will certainly affect the network-based characteristics. (ii) Like PRUL, the density along with the size of the subnetworks could be mentioned as much as appropriate. (iv) It is a useful and better strategy for the output (prediction) for the MOD in terms of integration (or analysis) category. Besides those, other objectives of PRSSL are as follows. (v) This is used for both the prediction as well as data exploration (characteristics of semi-supervised learning). (vi) The expense is moderate because of utilizing the semi-supervised learning. Therefore, PRSSL is useful to solve most of the real-life problems since it needs some data to be labeled, not all.

• Limitations: Akin to PRSL and PRUL, (i) the network features identified from PRSSL are not optimal. (ii) As for PRSL and PRUL, information loss might be there at the time of integrating the data profiles. (iii) Some information loss might be possible during data integration.

You et al. (2010) [121] proposed a new computational method, ‘GeneticInterPred’ to predict the pairwise synthetic genetic interactions (SGI) accurately. Initially, a high-precision and high-coverage functional gene regulatory network (FGN) was built through integrating the gene expression data, protein complex and PPI. Thereafter, a graph-based semi-supervised learning (SSL) classifier was applied to determine SGI in which the topological measures of the protein pairs in the weighted FGN was utilized as the input features of the SSL classifier. Kim et al. (2012) [122] introduced an integrated pipeline which applied the multi-level genomic profile to predict the clinical outcomes in ovarian and brain cancer. From the empirical comparative results on individual genomic data, some fundamental insights regarding the level of data, which was highly informative in the clinical-type classification problem, were described and these findings with the associated biological implications for each cancer-subtype were justified. The prediction of the clinical results in the cancer was further improved whenever the prediction depended on the conjoint of the MOD (multi-layered data). That analysis enhanced the comprehensiveness of the bio-molecular pathogenesis as well as internal biological understanding of both categories of cancer.

Bandyopadhyay and Mallik (2016) [79] developed a new algorithm of combinatorial gene marker identification from the gene expression and methylation profiles. To do so, initially the gene expression and methylation profiles were integrated using the concept regarding the inverse relationship between the gene expression and methylation status, and then the statistical as well as association rule-based learning methods were applied on the integrated data. Moreover, interesting weighted association rules (classification rules having gene sets in antecedent and class in consequent) had been extracted from the algorithm. The top rules were considered as combinatorial biomarkers. Mallik and Zhao (2017) developed a new algorithm TrapRM [Transcriptomic and proteomic rule mining using weighted shortest distance-based multiple minimum supports (WSDMS) for MOD set] [80] in which the gene expression, DNA methylation and PPI profiles are first integrated, and association rules are then extracted by using three variable cutoff measures: WSDMS, weighted shortest distance-based multiple minimum confidences (WSDMC) and weighted shortest distance-based multiple minimum lifts (WSDML). Finally, gene enrichment analysis is performed to assess the biological significance of the resultant rules.

Pre-processing conjoint (or analysis) with survival driven learning

PRSD follows the same learning technique (survival) as MSD, but the data integration technique is different from MSD.

PRSD:

• Inputs: The inputs of PRSD are the same as mentioned for MSSL and PRSSL.

• Objectives: The objectives of PRSD are the same as MSD, but the design (data integration technique) is different from MSD (i.e. preprocessing conjoint instead of model-based integration).

• Advantages: As for all the algorithms that use preprocessing integration such PRSL, PRUL and PRSSL, there are some common advantages as follows: (i) It is useful to identify the flexible sub-network features that can alter the network properties. (ii) The size of the underlying subnetworks as well as the other factors (density of the network) are highlighted accurately. (iii) Also PRSD is better for the output prediction with the MOD set in terms of integration (or analysis) category. There are two more objectives that are same as the objectives of MSD.

• Limitations: (i) Subnetwork-related features obtained from PRSD are not optimal like PRSL, PRUL and PRSSL. (ii) Some information loss might be possible during data integration since that depends upon how the profiles are integrated and based upon which criteria are used. (iii) Since labeled clinical data are required, it is costly.

Hofree et al. (2013) [75] proposed a method entitled network-based stratification (NBS) for conjoining the somatic tumor genomes and gene networks. This approach allowed for stratification of cancer into the respective subtypes through clustering simultaneously the patients with the mutations in the same network regions. That method generated the network-smoothed features that were applied for the classification of samples through the label propagation on the mutation data of each individual sample on a PPI network. Mankoo et al. (2011) [123] introduced a multivariate Cox Lasso model and median time-to-event prediction method (CoxPath). It can integrate multiple genomic data types. First the features were chosen using cross-validation, and then a prognostic index for the risk stratification of the patient was determined. Next the continuous clinical outcome measures such as the recurrence time and survival time were predicted. Kaplan–Meier 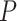-values, hazard ratios and concordance probability estimates were utilized for assessing the performance on prediction, comparing individual as well as integrated profiles. Data conjoint resulted in the best progression-free survival (denoted as ‘PFS’) signature.

Kim et al. (2016) [124] introduced a novel computational pipeline entitled meta-dimensional knowledge-driven genomic interactions. According to the outcome, each knowledge-driven genomic interaction model depending upon various genomic profiles consisted of various sets of pathway features that signified that each genomic profile category might provide outcomes in the specified cancer through a different pathway. From the MKGI models, various interactions between the pathways related to the outcomes were determined. Those included the gonadotropin-releasing hormone signaling pathway as well as the mitogen-activated protein kinase signaling pathway that were well known for having significant roles in the cancer pathogenesis. Interestingly, the reason for inclusion of the biological knowledge into the model depending on the multi-omics profiles was the capability to enhance the diagnosis as well as the prognosis and to provide better interpretability. Hence, measuring the variability in the molecular signatures depending upon these interactions between these pathways might enhance diagnosis or treatment in precision medicine.

Post-processing conjoint with supervised learning

In POSL, the genomic or similar data profiles and the respective networks are preliminarily analyzed individually to determine the list of oncogenic alternations for each profile. The recognized changes are then analyzed within the network. Then the learning models are utilized on the oncogenes. Alternatively, the network information is integrated (conjuncted) after detecting the oncogenic changes through standard statistical approaches. Here gene signature is identified, and the class labels of the samples for the outcome are predicted. In addition, the reason for using the post-processing integration (or analysis) is to evaluate how cancer-driving changes damage the normal cellular system through examining the normal influences on the corresponding network components. For multi-omics profiles, post-processing conjoint signifies that at first each profile has been analyzed separately, and then resulting outcomes from each profile integrated to retrieve final outcomes.

This category of algorithms extracts oncogene-related findings and other related information including the cancer mechanisms from the underlying network. The aim of the post-processing integration technique is to deal with either the mutations or other DNA aberrations along with the differential expression or several other molecular phenotypes of the network employed. Thus, this category of methods is interesting in general and contains a full set of information about the cancer mechanisms between the networks. But since the internal relation of the patterns between different profiles is not considered prior to the learning process, the final resulting outcome might not be optimal whenever integrating or analyzing the multi-omics data. POSL is used when the entire data are labeled (like the supervised learning).

Kim et al. (2013) [113] proposed a neural network method entitled ‘Analysis Tool for Heritable and Environmental Network Association’ (ATHENA) to conjoin several omics profiles in a supervised fashion that might further lead to a prognosis study. Here grammatical evolution neural networks (GENN) algorithm was applied for training the individual models from various data platforms. Depending upon the neural networks, the grammatical evolution approach was conducted for training the model using the chosen features which were less noisy as well as significantly related to the clinical results. Thereafter, individual models were integrated to obtain the final integrative model that might be used for multiple reasons including diagnosis as well as prognosis. ATHENA provided a flexible way to visualize the correlation of the genomics data with the clinical data [e.g. survival results (prognosis results)]. The most notable shortcoming of ATHENA is lacking interactive terms between various layers since the features were chosen from each data type separately first, and then conjoined into each respective integrated model. Ideker et al. (2002) [114] developed a network-based Cytoscape plug-in that attempted to obtain the network hotspots through the integration of gene expression profile, PPI profile and protein–DNA interaction profile. This technique depended upon the hypothesis that the molecular interactions connecting the genes were more likely to be correlated among the expression data rather than randomly picked genes belonging to the network. jActiveModules estimated the highest-scoring sub-network circuits with the help of the random sampling method as well as the iterative computation in a complete network of the molecular interactions that created further biologically interesting knowledge retrieval (discoveries) [denoted by Cline et al. (2007) [129]]. jActiveModules, which can be related to the molecular interaction network, can include the genes without dramatic gene expression fold changes.

POSL:

• Inputs: The inputs of POSL are the same as for MSL.

• Objectives and description: The major objectives of POSL are same as the objective mentioned for MSL. The data set integration approach used in POSL is post-processing, which is different from MSL and PRSL. POSL is helpful for providing a full set of information about the cancer mechanisms between the networks.

• Advantages: (i) POSL provides oncogene-related findings and other related information including the cancer mechanisms from the regulatory network. (ii) The chance of losing the information in the analysis is less since the integration has been performed after completion of individual analysis. (iii) This type of algorithms is helpful to evaluate how cancer-driving changes damage the normal cellular system through examining the actual influences on the corresponding network components.

• Limitations: (i) The final result may not be following optimal result while integrating or analyzing any MOD. The reason behind this is that the interrelation of the patterns between different profiles is not considered prior to learning process. (ii) It is costly to use (the supervised learning) as it needs all labeled data. (iii) It is less efficient in outcome prediction. (iv) There is no guarantee that optimal features are obtained.

Ruffalo et al. (2015) [115] introduced a network propagation-based integration approach that claimed to determine the key proteins across the sample level through the propagated protein networks depending upon the integrated mutation as well as the differential gene expression (DGE) data sets. Propagated mutation and DGE profiles were determined for each individual gene through the prior knowledge in the PPI pipeline. Next, feature selection was conducted on these propagated data profiles in a supervised manner, in which the top features were the most relevant features as resulting outcomes. A final set of proteins was chosen depending upon the network proximity toward the underlying samples. In the final step, logistic regression was conducted with the specified genes. That approach effectively identified the hidden set of proteins (or genes) at the pathway level having a significant role in the tumor progression or clinical outcome that might not be observed by either the differential expression analysis or the individual mutational analysis. In addition, Kondor et al. (2002) [83] developed a diffusion kernel that can be used for constructing an influence graph having the edges weighted by the influence between each gene pair.

Post-processing conjoint (or analysis) with unsupervised learning

As in POSL, in the POUL, the genomic data sets along with their corresponding networks are preliminarily analyzed separately to identify the list of oncogenic modifications for every profile. Thereafter, the recognized changes are incorporated into the network and further analyzed. The learning models are thereafter used on the resultant oncogenes. Otherwise, after identifying the oncogenic changes, the information regarding the network is merged through several statistical strategies.

In addition, the reason for using the post-processing integration (or analysis) is to evaluate how cancer-driving changes damage the normal cellular system through examining the normal influences on the corresponding network components. For multi-omics profiles, post-processing conjoint signifies that at first each profile has been analyzed separately, and then resulting outcomes from each profile are integrated to retrieve final outcomes. Notably, POUL is applied when the entire data are unlabeled (property of the unsupervised learning).

POUL:

• Inputs: The inputs of POUL are the same as mentioned for MUL.

• Objectives: Some objectives of POUL are the same as those for MUL and PRUL. Those objectives are identifying (i) the gene modules and/or (ii) the gene signature. In addition, POUL is useful for recognizing the significant inherent features from the underlying input data sets.

• Advantages: (i) As POSL, POUL approaches are interesting and full of information about the oncogenes as well as cancer mechanisms between the networks. (ii) As for POSL, the probability of information loss during the analysis is low as the data integration is conducted after the completion of individual data analysis. (iii) As for POSL, POUL algorithm is useful to evaluate how cancer-driving modifications destroy the normal cellular system via verifying the normal influences on the respective network components. (iv) The aim of using unsupervised learning is to model the underlying distribution or structure of the data for the purpose of learning more regarding the data. (v) Performs well for solving the issue of heterogeneous connectivity.

• Limitations: (i) The internal relation of the patterns between different data profiles is not considered prior to the learning process. Hence, although oncogene-related information obtained from the data are interesting, they are not a global optimal solution. (ii) Performance of POUL is worse than that of POSL due to use of unsupervised learning technique while POSL uses supervised learning. (iii) The resultant features might not be global optimal.

Akavia et al. (2010) [107] introduced a Bayesian network-based approach denoted as ‘Copy Number and Expression In Cancer’ (CONEXIC) to integrate the gene expression and CNV data. A score-guided search was then utilized to obtain the combination of genes (modulators). A list of ranks for the high-scoring modulators (i.e. ‘candidate driver genes’) was produced. The high-scoring modulators signified the genes which were correlated with the differential expression modules in the tumor samples as well as present in the either significantly amplified regions or significantly deleted regions. The main feature of CONEXIC went beyond determining the mutation drivers, since CONEXIC produced insights into the impact of the candidate drivers as well as the related genes. Bonnet et al. (2015) [110] developed an unsupervised method denoted as Lemon-Tree that was mainly focused on rebuilding the gene module networks. After obtaining the co-expressed clusters from the gene expression profile, Lemon-Tree was applied to determine the consensus modules as well as the upstream regulatory programs using some ensemble approaches. Preliminarily, any expression matrix was considered to obtain the clusters of co-expressed genes using a Gibbs sampler. Consensus modules of these co-expressed genes were integrated by the utilization of the spectral edge clustering algorithm along with a set of the gene cluster outcomes. On the other hand, several additional candidate regulator categories of data (e.g. CNV, miRNA expression and methylation profiles) were integrated with the consensus module for inferring a regulatory score computed using a decision tree structure. The benefit of using Lemon-Tree is that it can infer more closely associated short-path networks containing more significant gene ontology based categories, as compared to the method CONEXIC.

Yuan et al. (2011) [105] proposed a Bayesian nonparametric model called ‘Patient-Specific Data Fusion’ (PSDF) that was developed based on the two-level hierarchy of the Dirichlet process model, which is highly useful for clustering. It verified the concordance between the gene expression and the CNV for each individual patient. Interestingly, it also chose the top informative features (genes) and then evaluated the number of subtypes of the corresponding disease from the underlying data. Wang et al. (2014) [109] introduced a new approach denoted ‘Similarity Network Fusion’ (SNF) whose goal was to identify the patient subgroup clusters. SNF merged various data types through building a network of samples (instead of genomic features) for each individual data type, and thereafter fusing these networks into one single network. SNF is relatively flexible without the constraints for the format of the input profile. SNF worked only on the matched samples under various omics profiles (layers). Through obtaining the integrated similarities as the output among the patients under various layers, SNF provided deeper biological understanding. Lock and Dunson (2013) [106] developed Bayesian consensus clustering (BCC), a flexible and efficient clustering method that was able to model the heterogeneity as well as the dependence of different data sources. In BCC, individual clustering of the objects from each individual data source was conducted, and then the post-hoc conjoint of individual clusters carried out. Thereafter, consensus clustering was applied in order to model the source-specified structures and to identify the overall clustering. Vaske et al. (2010) [108] developed a probabilistic graphical model entitled ‘Pathway Representation and Analysis by Direct Reference on Graphical Models’ (PARADIGM) to deduce the patient-specified genetic variations, along with the inclusion of the selected pathway interactions among the genes. PARADIGM transformed each pathway belonging to the National Cancer Institute Pathway Interaction Database into an individual probabilistic model that was depicted as a factor graph having both the observed states as well as hidden states. Of note, variables belonging to the graph were utilized to illustrate the protein-coding genes, gene molecules and complexes. Kim et al. (2011) [81] proposed a new approach for identifying the causal genes and dysregulated pathways together. Firstly, differentially expressed genes were generated. Next, the genomic aberrations obtained by the mutations and copy number variations associated with the DGE were estimated. The causal paths obtained from the altered (i.e. causal) genes toward the differentially expressed target genes belonging to a PPI network were computed. The causal genes were finally determined through utilizing a set-covering methodology on all the differentially expressed target genes. Vandin et al. (2011) [82] developed a novel approach of de novo identification of the sub-networks from a genome-scale gene interaction network which were mutated in a statistically significant number of samples. Bhadra et al. (2017) [44] developed a new method using an integrated method of statistical test and normalized mutual information-based hypograph mining for generating the multi-view co-similarity gene modules from the multi-view profiles.

Post-processing conjoint with semi-supervised learning

As seen in the case of POSL and POUL, the objectives of POSSL are that first the epigenomic or genomic data profiles along with the corresponding networks are independently analyzed for extracting the list of oncogenic changes for each data profile. The resulting alterations are thereafter analyzed into the network. Then the learning models are applied to the oncogenes. Else, the network-related information is merged after identifying the oncogenic updates using statistical techniques. In common with the other post-processing integration techniques (e.g. POSL and POUL), POSSL is also used to evaluate the effect of cancer-driving changes on the normal cellular system. For multi-omics profiles, post-processing conjoint states that preliminarily analyses are conducted individually on each data profile, and thereafter the outcomes obtained from each profile is conjoined to retrieve the final outcomes. Additionally, in terms of the usability of learning method, POSSL follows the same strategies as MSSL and PRSSL.

POSSL:

• Inputs: The inputs of POSSL are the same as mentioned for MSSL and PRSSL.

• Objectives: The objectives of the POSSL are the same as MSSL and PRSSL, but the design is different from them.

• Advantages: As POSL and POUL, (i) POSSL generates interesting oncogene-associated outcome along with other related information such as the cancer mechanism obtained from the regulatory network; (ii) the overall probability of losing the underlying information during the analysis of POSSL is less because the data profile integration is conducted after completing the individual analysis; and (iii) POSSL can recognize how cancer-driving changes affect the entire normal cellular system. In addition, there are many other advantages that match those of MSSL and PRSSL. For example, (iv) POSSL is used in both the cases data exploration as well as prediction since semi-supervised learning is used here; (v) POSL is useful when a few of the entire data are labeled, but the majority of data remain unlabeled (phenomena of the semi-supervised learning). (vi) The expenses of using POSSL are moderate since semi-supervised learning is utilized here. Hence, a lot of real life machine learning problems fall into POSSL.

• Limitations: Like POSL and POUL, (i) in POSSL, the internal relation of the patterns among different data profiles are not taken into account before the learning process. As a result, despite of producing interesting oncogene-related information, findings might not be global optimal. (ii) The overall cost is moderate due to use of semi-supervised learning; hence it is useful to solve most of the real-life problems since it needs only some data to be labeled. (iii) The efficiency in outcome prediction is low. (iv) Performance of POSSL is worse than POSL, but better than POUL (property of semi-supervised learning). (v) Features may not be optimal globally.

Ciriello et al. (2012) [87] developed the mutual exclusivity module (MEMo) discovery method in which a matrix format of the underlying genes that were significantly altered by either mutations or CNV were built. The selected (altered) genes were then associated with their proximal in the Human Protein Reference Database PPI network. At the final stage, the subgraph containing all the associated gene pairs (‘cliques’) was detected for analyzing the mutual exclusiveness in the underlying data.

Mallik et al. (2013) [93] provided an integrated analysis (post-processing integration or analysis) to find the genes having the inverse relationship between their methylation and expression patterns. Maulik et al. (2015) [68] developed a new ARM method namely statistical biclustering-based rule mining (StatBicRM) to determine classification rules as well as possible potential gene markers through the integrated methodology of the statistical method and BiMax algorithm from multi-omics profiles. First of all, a new statistical approach was applied to discard the insignificant redundant genes (features) through which the significance pattern must satisfy the distribution of the underlying data (i.e. either normal or non-normal distribution). The data were then discretized as well as post-discretized Then the biclustering algorithm was utilized to determine the maximal frequent closed homogeneous gene sets. Classification rules were then generated from the employed gene sets. To recognize the potential gene markers, frequency analysis of the genes appearing in the data was then conducted. In addition, classification performance of the employed rules was conducted. Moreover, the inversely associated genes between their methylation and expression patterns were also identified. Mallik et al. (2017) [41] introduced a novel pipeline for discovering the statistically significant epigenetic gene markers through the utilization of minimal redundancy and maximal relevance condition based gene (feature) selection method for multi-omics profiles. First of all, the genes that contained both the methylation and expression values, and which follow the normal distribution, were identified. On the other hand, the genes that contained both the methylation and expression values, but did not follow the normal distribution, were also determined. In each case, a gene-selection method which generated maximal-relevant, but variable-weighted minimum-redundant genes to be the top genes, was applied. Next, student’s t-test (parametric test) was conducted on both the methylation and expression profiles containing only the normally distributed top-ranked genes to identify the genes that were both differentially methylated and differentially expressed. In a similar fashion, Limma R tool using nonparametric empirical Bayes test was performed on both the methylation and expression profiles having only the non-normally distributed top-ranked genes to determine the genes that were both differentially methylated and expressed. Moreover, the top-ranked statistically significant gene markers having inverse relationship among their methylation and expression patterns were reported along with biological validation and well as classification performance.

Critical discussion and summary of results

In this section, we first describe briefly the issues of sparsity and heterogeneous connectivity along with possible solutions. There are several methods that can handle the problem of sparseness and heterogeneous connectivity. In fact, several matrix factorization technique-based algorithms (such as iNMF and JIVE) suffer from the problem of sparseness in the dimension coefficient matrix (denoted by 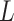). To solve the associated problem, LASSO penalty has been developed and it has been integrated into different methods. In our study, sglasso and fglasso are used for same purpose. CCA (correlation-based analysis) methods also have this sparsity issue. To solve this, different regularized and penalized factors have been incorporated into the existing CCA methods. For example, L1-penalized sCCA tied with elastic net CCA [126, 127] is useful to select the reduced highly important feature set to reduce the sparsity and make the outcome biologically interesting. In addition, sparse solutions of PLS (denoted as 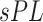) [128] is equally efficient to reduce sparsity as CCA-elastic net. Another two important methods (i.e. variants of PLS) are sMBPLS [101] and SNPLS [102]. The sMBPLS solves the limit of the two data block computation through redefining the objective function as a weighted summation of the latent variables in different layers. On the other hand, SNPLS is useful to identify the combined co-modular patterns from various pharmacogenomics profiles such as gene expression and drug-response data based on their inter-relationship. It is well known that the actual relation between different genomic layers (factors/profiles) and the response to the various distinct cancer drugs is still under debate. Under these circumstances, different large-scale pharmacogenomic profiles give the potential opportunities to enhance the state-of-the-art therapeutic methods or to provide proper guidance in the initial phase of clinical trial of compounds under the development. In SNPLS, the corresponding modular analysis has been conducted that provides the novel insights into the bio-molecular techniques regarding the procedure of functioning the drugs along with providing novel drug targets for the therapeutic value of various kinds of cancers. Furthermore, several multi-step analysis methods are useful to address the sparsity of the underlying data. Normal-gamma prior has been utilized here for enhancing the computation of the effect size as well as to handle the sparsity. In order to address the heterogeneity problem, different Bayesian approaches work better. For example, BCC [97] is an efficient clustering technique that can handle the heterogeneity along with the dependency between different data sources. In BCC, individual clustering of the objects from each individual data source was conducted, and then the post-hoc conjoint of individual clusters was carried out. Next, consensus clustering was used in order to model the source-specified structures and to identify the overall clusters. In addition, several tree or graph-based algorithms such as randomized Steiner tree and network topology based algorithm by Jahid et al. [76], dysfunctional module detection using shortest distance technique by He et al. [74] are also useful to handle the issue. TrapRM [80] is another attempt to selectively reduce the heterogeneous connectivity problem through integrating the gene expression, methylation and PPI data using the three novel dynamic threshold measures that use a weighted shortest distance based strategy. These are WSDMS, WSDMC and WSDML. Then using these three threshold measure, the corresponding ARM technique was applied to reduce the number of rules generated and to identify only the top biologically significant association rules. Serra et al. [27] developed a Multi-View Data Integration (MVDA) strategy that works well to address the issue, whereas another dense hypo-graph mining model Bhadra et al. [44] is also an efficient technique for this.

In addition, based on the literature evidences as well as our own experiments, we have reached the following significant observations:

• (i) In the model-based integration or analysis, a single unified machine-learning technique is directly utilized for integrating all the genomic profiles with a single network. On the other hand, for preprocessing integration, first the genomic data and the corresponding network are analyzed together to determine the final network-based features. After network-based feature extraction, the learning models are then utilized on the employed network-based features for the predictions; whereas for post-processing analysis, the network information has been integrated after detecting the oncogenic changes through standard statistical approaches.

• (ii) MSLs are complex to design and costly as different mathematical formulations (e.g. regression, graph Laplacian regularization, etc.) have been used and they need all labeled data, but preprocessing and post-processing approaches are simpler, less flexible, easier to understand as well as less costly.

• (iii) Model-based integration methods produce the best performance over the other remaining methods in all situations (including handling sparsity problem, heterogeneity problem, etc.) since different lasso-based methods, regularized and penalized methods, Bayesian methods, shortest distance-based or random walk-based techniques as well as other related methods belong to the model-based integration strategy. Specifically, MSL (model-based integration with supervised methods) works best for prediction.

• (iv) Post-processing analysis with unsupervised learning is best for data exploration, i.e. providing an interesting and large amount of information regarding the cancer mechanisms from the network.

• (v) PRSSL is most useful and flexible for determining highly customizable subnetwork features (e.g. dynamic modules) from network as well as it is less costly since it does not require all data to be labeled. Although its prediction performance is not better than supervised methods, the overall prediction quality is still fine with the supervised one.

• (vi) In model-based integration algorithms, the chance of obtaining optimal features (modules) is highest among all other two (preprocessing integration algorithms and post-processing integration algorithms).

• (vii) For therapeutic treatment, any kind of survival (prognosis)-driven analysis (preprocessing integrative methods with survival driven learning) is very useful, but it is costly due to the need for clinical data. Of note, the properties, examples, advantages and limitations of each integration method and learning method are individually shown in Tables 2 and 3. Table 4 represents the summary of the overall usefulness and effectiveness of the different categories of methods whenever the input and objective are given.

• (viii) For example, when the input data is either SOD or MOD containing class labels of all samples, and the objective is to identify the gene signature or gene-signature-based classifier, MSSL methods are highly useful and efficient. Also MSL, MSD, PRSL, PRSSL, PRSD, POSL and POSSL methods are useful, whereas MUL, PRUL and POUL strategies are used rarely and their performance is not so good. Some of the suggested methods are ‘Machine learning approach to integrate big data for precision medicine’ [70], Bimax biclustering, CC biclustering, Spectral Biclustering, etc.

• (ix) On the other hand, when the input data are either SOD or MOD containing class labels of all samples, but the objective is to identify the module/subnetwork detection, MUL, MSSL, PRUL and POUL methods are highly useful and efficient, whereas MSL, PRSSL, PRSD, POSL and POSSL methods are also useful. But, MSD and PRSL strategies will not be useful. Some of the suggested methods are iBAG, MCD, intNMF, iNMF, JointNMF, iCluster, iCluster+, JIVE, ssCCA, Bimax biclustering, CC biclustering, Spectral Biclustering, MDI, BCC, SNF, etc.

• (x) When the input data is SOD/MOD (big data) containing some sample class labels but not all, or SOD/MOD with all sample class labels but need for clustering toward both samples and genes together, and the objective is gene classification signature detection as well as module (subnetwork) detection, MSSL, PRSSL and POSSL are highly useful and efficient, whereas MUL, MSD, PRUL, PRSD and POUL are also useful. However, MSL, PRSL and POSL are not applicable. Some of the suggested methods are Bimax biclustering, CC biclustering, XMotifs Biclustering, spectral Biclustering, combinatorial gene marker discovery [79], etc.

• (xi) Interestingly, when the input data are either SOD or MOD containing class labels of all samples, and the objective is to identify singular gene marker (hub-gene or driver-gene), all categories of methods can be used more or less successfully. In this case, POUL and POSSL are highly useful and efficient, whereas all the other categories of methods are also useful. Some of the suggested methods are StatBicRM, epigenetic gene marker discovery through feature selection [41], ‘Machine learning approach to integrate big data for precision medicine’ [70], etc.

• (xii) In the case, when the input data are SOD/MOD containing some sample class labels, or SOD/MOD with all sample class labels but need for clustering toward both samples and genes together, and the objective is to identify a singular gene marker (hub-gene or driver-gene), POSSL is highly useful and efficient, whereas MSD, PRSD and POUL are also useful. MUL, MSSL, PRUL and PRSSL can be usable, but their performance is average in this case. All the remaining categories such as MSL, PRSL and POSL are not applicable. A suggested method is StatBicRM.

• (xiii) Whenever the input data are MOD with all sample class labels, and the objective is to identify the co-module of gene drug, MUL is then highly useful and efficient, whereas MSD and PRSD are also useful. But, the remaining categories are not applicable here. One of the suggested method is SNPLS.

• (xiv) If the input data are MOD consisting of all sample class labels, and the objective is to determine the prognosis gene signature, MSD and PRSD are highly useful and efficient. POSL is also useful. But, the remaining categories are not. Some suggested methods in this case are Net-Cox, netSVM, CoxPath, MKGI and ATHENA.

• (xv) If the input data are MOD consisting of all sample class labels, and the objective is to develop the Kernel-based classifier (or regression) model, MSL and MSD are highly useful and efficient. MUL, MSSL and PRSD are also useful. However, the reset of the categories cannot be applied. Some suggested methods in this case are SDP/SVM, FSMKL, ‘Penalized logistic regression model’ [51], sglasso, fglasso, rMKL-LPP, etc.

• (xvi) If the input data are MOD consisting of all sample class labels, and the objective is to identify pathway marker, PRSL and POUL are the categories that are highly useful and efficient for this. However, the rest of the categories are not applicable here. Some suggested methods in this case are pathway-based classification [71] and mutated pathway detection [82].

• (xvii) When the input data are MOD consisting of all sample class labels, and the objective is to identify important feature/feature-Score, PRUL, PRSSL and POUL categories are highly useful and efficient here. MSL, MUL and PRSD are also useful, whereas MSSL, MSD, PRSL, POSL and POSSL cannot be applied here. Some suggested methods in this case are Anduril, CNAmet, graph-based learning [122] and NBS.

• (xviii) If the input data are MOD containing all sample class labels, and the objective is to identify closed frequent association rules or dense subgraphs or rule-based classifier, MSSL, MSD, PRSSL and POSSL are the highly useful and efficient categories, whereas MSL, MUL, POSL and POUL are useful categories. The remaining categories cannot be applied. Some suggested methods in this case are iSubgraph, TrapRM, Lemon-Tree, ConGEMs, RiboFSM, Normalized ImQCM, etc.

• (xix) Whenever the input data are MOD consisting of all sample class labels, and the objective is to find combinatorial gene marker, PRSSL is a highly useful and efficient category. All the remaining categories cannot be used. One of the methods here is combinatorial gene marker discovery by Bandyopadhyay and Mallik [79].

• (xx) Finally, if the input data are MOD consisting of all sample class labels, and the objective is to identify gene exclusive module, POSSL is the most useful and efficient category. All the remaining categories are not applicable here. One of the methods here is MEMo.

Table 2.

Brief description of conjoint (integration) techniques

	Model-based conjoint	Pre-processing conjoint	Post-processing conjoint
Properties	● It utilizes a single unified machine-learning approach for integrating all the genomic profiles with a single network.	● The genomic data and the corresponding network are analyzed simultaneously to explore final network-based features.	● The genomic data are analyzed first to identify the list of oncogenic changes.
	● All the network-based regularization-based machine learning models fall into this category.	● The learning models are then utilized on the employed network-based features for the purpose of prediction.	● The recognized changes are then analyzed into the network.
	● The main aim is to determine subnetwork genetic modules as well as predict the cancer type.	● The integration of the genomic data and the corresponding network are conducted prior to utilizing any learning model.	● In the post-processing conjoint, the network information is integrated after detecting the oncogenic changes through the standard statistical approaches.
	● The coefficients learned from the corresponding feature variables lead to dense subnetwork modules.		● The purpose of these approaches is to evaluate how cancer-driving changes damage the normal cellular system through examining the proper influences on the corresponding network components.
	● The most frequently utilized network-based regularization technique is graph Laplacian regularizer.
Advantages	● The subnetworks are combinedly detected to make contrast the case/control groups in the study depending upon the global optimization approach. Hence, these methods generally conduct better in the prediction of the outcome.	● More flexible in detecting customizable subnetwork features by which the recognized features can make impact significantly on the hypothesized network-based properties.	● It uses either the mutations or other DNA aberrations along with the differential expression or several other molecular phenotypes of the employed network. The resultant networks are generally informative of the cancer mechanisms.
	● The underlying models might be tuned through the utilization of several parameters that are clearly defined. This increases the possibility to train the corresponding models through the cross-validation.
Disadvantages	● Requirement for better sophisticated optimization methods that is less scalable in general.	● Less efficient in outcome prediction.	● Less efficient in outcome prediction.
		● No guarantee that the recognized subnetwork features will be optimal in the prediction through the standard learning model.	● No guarantee to obtain optimal features.

Table 3.

Brief description of sub-categories of learning and prediction methods

	Supervised	Unsupervised	Semi-supervised	Survival driven
Characteristics	● Entire data are a labeled data.	● Entire data are an unlabeled data.	● A few of the entire data are labeled, but the majority of data remain unlabeled. Hence, a combination of unsupervised and supervised learning approaches might be applied.	● A topic of interest for the doctors, cancer patients as well as healthcare providers.
	● Predict the output from the input data.	● Utilized to learn for determining the inherent structure from the input data portion.	● Only a few of the entire data have been labeled although the size of the input data is big.	● Only a few number of strategies are available to conjoin any MOD optimized for the prognosis related prediction.
	● Perform prediction on the test data using the learning on the training data set.	● The aim is to model the underlying distribution or structure of the data for the purpose of learning more regarding the data.	● Example: a photo archive in which a few of the entire images has been labeled (such as person, cat, dog and tree), whereas most of the data remain unlabeled.	● Might be existed under either model-based or preprocessing conjoint.
	● Include classification problems and regression problems.	● Depend upon their own plan to identify and represent the interesting structure from the underlying data.	● A lot of real-life machine-learning problems have been fallen into this domain since it is time-consuming and highly expensive for labeling the data.
	● May be under one of the three data integration categories (model-based, preprocessing or post-processing conjoint/analysis).	● Include association and clustering problems.	● Applied to produce and learn the structure from the given input variables.
		● May be under one of the three data integration categories (i.e. model-based, pre-processing or post-processing conjoint).	● Prediction feed the data back into the method of supervised learning as the training data set and then apply the model for making predictions on the unseen new data.
			● Include expectation–maximization with generative mixture models, transductive support vector machines, co-training and multi-view learning, graph-based methods, etc.
			● Might be fallen under any of the three data integration categories (i.e. model-based, preprocessing or post-processing conjoint/analysis).
Examples	● Random Forest, linear regression, SDP/SVM [116], ATHENA [113], iBAG [118], FSMKL [117], NBS [75], etc.	● K-means, a priori algorithm, Joint NMF [91], [92], iCluster [94], iCluster+ [95], sMBPLS [101], SNPLS [102], CNAmet [23], etc.	● Deep belief networks, GeneticInterPred [121], graph-based learning [122], MEMo [87], MVDA [27], TrapRM [80], StatBicRM [68], etc.	● CoxPath [123] and MKGI [124].
Advantages	● Provide best performance as well as efficiency.	● It is used for data exploration.	● Performance is better than the unsupervised methods, but worse than the supervised methods.	● Help to make any decision about the patient management and therapeutic treatments.
	● It is used for prediction.		● Used for both the prediction as well as data exploration.	● Highly useful for effectively selecting the patient-subgroups.
Disadvantages	● Costly, as it needs all labeled data.	● Less costly.	● Moderate cost; hence, useful to solve most of the real-life problems since it needs some data to be labeled, not all.	● Need labeled clinical data, so costly.
		● Provide worse performance than the others as there is no class label of the samples.

Table 4.

Summary of the appropriate usability and efficiency of all the methods by category when input and objectives are specified

Input and objectives	Method category											Suitable algorithms
	MSL	MUL	MSSL	MSD	PRSL	PRUL	PRSSL	PRSD	POSL	POUL	POSSL
Input: SOD/MOD having class labels of all samples. Objective: gene signature or marker/gene-signature-based classifier.	+	−	++	+	+	−	+	+	+	−	+	Machine-learning approach to integrate big data for precision medicine [70], Bimax biclustering [53], [54], CC biclustering [55] and spectral biclustering [59]
Input: SOD/MOD having all sample class labels. Objective: module/subnetwork detection.	+	++	++	×	×	++	+	+	+	++	+	iBAG [118], MCD [119], intNMF [72], iNMF [96], Joint NMF [91], [92], iCluster [94], iCluster+ [95], JIVE [137], ssCCA [99], Bimax biclustering [53], [54], CC biclustering [55], spectral biclustering [59], MDI [103], BCC [106] and SNF [109]
Input: SOD/MOD (big data) having some sample class labels but not all, or, SOD/MOD with all sample class labels but need for clustering toward both samples and genes together. Objective: gene classification signature module/subnetwork detection.	×	+	++	+	×	+	++	+	×	+	++	Bimax biclustering [53], [54], CC biclustering [55], XMotifs biclustering [58], spectral biclustering [59] and combinatorial gene marker discovery [79]
Input: SOD/MOD having all sample class labels. Objective: singular gene marker/hub gene/driver gene.	+	+	+	+	+	+	+	+	+	++	++	StatBicRM [68], epigenetic gene marker discovery through feature selection [41] and machine-learning approach to integrate big data for precision medicine [70]
Input: SOD/MOD with some sample class labels or SOD/MOD with all sample class labels but need for clustering toward both samples and genes together. Objective: singular gene marker/hub gene/driver gene.	×	+−	+−	+	×	+−	+−	+	×	+	++	StatBicRM [68]
Input: MOD with all sample class labels. Objective: Co-module of gene–drug.	×	++	×	+	×	×	×	+	×	×	×	SNPLS [102]
Input: MOD with all sample class labels. Objective: prognosis gene signature.	×	×	×	++	×	×	×	++	+	×	×	Net-Cox [50], netSVM [52], CoxPath [123], MKGI [124] and ATHENA [113]
Input: MOD with all sample class labels. Objective: Kernel-based classifier/regression model.	++	+	+	++	×	×	×	+	×	×	×	SDP/SVM [116,] FSMKL [117], penalized logistic regression model [51], sglasso [38], [40], fglasso [37], [39] and rMKL-LPP [111]
Input: MOD with all sample class labels. Objective: Pathway marker.	×	×	×	×	++	×	×	×	×	++	×	Pathway-based classification [71] and Significantly mutated pathway detection [82]
Input: SOD/MOD with all sample class labels. Objective: Feature/feature score.	+	+	+−	+−	+−	++	++	+	+−	++	+−	Anduril [120], CNAmet [23], Graph-based learning [122] and NBS [75].
Input: SOD/MOD with all sample class labels. Objective: closed frequent association rules or dense subgraphs or rule-based classifier.	+	+	++	++	×	×	++	×	+	+	++	iSubgraph [63], TrapRM [80], Lemon-Tree [110], ConGEMs [43], RiboFSM [60], StatBicRM [68] and normalized ImQCM [34], [35]
Input: MOD with all sample class labels. Objective: combinatorial gene marker.	×	×	×	×	×	×	++	×	×	×	×	Combinatorial gene marker discovery [79]
Input: MOD with all sample class labels. Objective: gene exclusive module.	×	×	×	×	×	×	×	×	×	×	++	MEMo [87]

‘++’, Best or highly useful; ‘+’, good or useful; ‘+−’, average, neutral or can be used; ‘−’, rarely used or poor; ‘×’, NA or cannot be used.

Perspectives

To date, graph- and rule-based algorithms have been extensively utilized for cancer classification and prognosis using large scale genomic and other type of omics data. The internal design of the analysis algorithms is made depending on the desired objectives of the users such as identification of singular gene markers, combinatorial gene markers, gene modules, feed forward loops, gene signature, classifier, regression, survival validation, pathways marker, gene exclusive module, drug target–disease relation, dense subgraphs, frequent closed association rules, rule-based classifier, feature mining or feature score determination, etc. or a combination of some of these. Therefore, the design of these kinds of algorithms is always different among different studies depending upon the inputs and objectives of the users. Our survey covers various existing graph- and rule-based machine learning algorithms used for the purpose of SOD or MOD integration or analysis. Due to this broad topic, this review focuses mainly on the methodological design of these algorithms to facilitate the applications of these graph (orrule-based) analysis methods used for the purpose of SOD or MOD integration (or analysis) along with various purpose such as cancer classification, singular gene marker (hub-gene or driver-gene) identification, etc. as mentioned above. Moreover, we divided all these algorithms into a total of 11 categories (MSL, MUL, MSSL, MSD, PRSL, PRUL, PRSSL, PRSD, POSL, POUL and POSSL) depending upon the combinations of the type of data integration (or analysis) and learning style. After that, various well-known and most recently developed algorithms for each category were described briefly along with the other important information (such as used data profiles, used statistical method and feature selection method, outputs of the algorithms, etc.). This will help the readers to know the hierarchy of those algorithms along with the actual reason for developing those algorithms. Moreover, the summary of results for each category of methods is described briefly with appropriate examples. In addition, we suggested the methods that likely work better for certain condition. Specially, we also described some special issues such as sparsity and heterogeneity along with possible solutions for them.

Hence, through this review, the reader can easily understand which type of algorithms can be used under particular circumstances.

Key Points

• Graph- and rule-based analytics has been extensively applied for cancer classification as well as prognosis using large genomic and other similar kind of data over the past years.

• This article provides a comprehensive review of many graph- and rule-based machine learning algorithms using genomics data for cancer-specific gene modules and gene signature discovery.

• These algorithms are divided into 11 major categories based on type of data integration or analysis (model based, pre-processing and post-processing integration or analysis) and type of learning method (supervised, unsupervised, semi-supervised and survival-driven learning or analysis).

• The review provides detailed description of these categories of graph and rule mining algorithms, such as used data profiles, used statistical

  method and feature selection method, output of the algorithms and other related information.

• A summary table of the appropriate use and efficiency of all the categories of graph and rule mining-based learning methods is provided when input and specific objective are given.

• The probable solution or reduction of some critical issues such as data sparsity and heterogeneity has been described briefly.

• This study helps the reader find the appropriate algorithms for cancer classification and prognosis study.

Saurav Mallik, is a post-doctoral fellow in the Center for Precision Health, School of Biomedical Informatics, The University of Texas Health Science Center at Houston. He obtained his PhD in the Department of Computer Science & Engineering from Jadavpur University, India. His research interest includes machine learning, statistical learning and bioinformatics.

Zhongming Zhao, is the chair and professor for Precision Health and director of Center for Precision Health, School of Biomedical Informatics, The University of Texas Health Science Center at Houston. He directs the Bioinformatics and Systems Medicine Laboratory and UTHealth Cancer Genomics Core. He is the founding president of The International Association for Intelligent Biology and Medicine (IAIBM).

Funding

Research reported in this publication was partially supported by the National Library Of Medicine of the National Institutes of Health (R01LM012806) and Cancer Prevention and Research Institute of Texas (CPRIT RP180734). The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health or CPRIT.