Temporal Phenotyping for Transitional Disease Progress: an Application to Epilepsy and Alzheimer’s Disease

Abstract

Complicated multifactorial diseases deteriorate from one disease to other diseases. For example, existing studies consider Alzheimer’s disease (AD) a co-morbidity of epilepsy, but also recognize epilepsy to occur more frequently in patients with AD than those without. It is important to understand the progress of disease that deteriorates to severe diseases. To this end, we develop a transitional phenotyping method based on both longitudinal and cross-sectional relationships between diseases and/or medications. For a cross-sectional approach, we utilized a skip-gram model to represent co-occurred disease or medication. For a longitudinal approach, we represented each patient as a transition probability between medical events and used supervised tensor factorization to decompose into groups of medical events that develop together. Then we harmonized both information to derive high-risk transitional patterns. We applied our method to disease progress from epilepsy to AD. An epilepsy-AD cohort of 600,000 patients were extracted from Cerner Health Facts data. Our experimental results suggested a causal relationship between epilepsy and later onset of AD, and also identified five epilepsy subgroups with distinct phenotypic patterns leading to AD. While such findings are preliminary, the proposed method combining representation learning with tensor factorization seems to be an effective approach for risk factor analysis.

Graphical Abstract

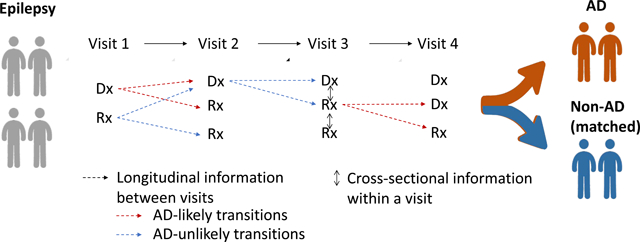
1. Introduction

Computational phenotyping is to transform medical data such as electronic health records (EHRs) into clinically meaningful combinations of diseases, symptoms, and developments [1]. These models identify latent groups of similar features (i.e., diagnosis, medication, and labs) that lie in a similar context, with the aim of grouping patients with similar conditions and providing fine-grained stratification into patient cohorts (subgroups). Such techniques provide an alternative evidence-based perspective to look at retrospective data, especially in understanding complex cohorts. A thread of early publications were named after different gems: Marble [2], Rubik [3], Granite [4]. Using entity co-occurrence information (e.g., co-morbidity and co-prescribed medications in the same encounter) as the observation, these methods leverage tensor factorization to decompose high dimensional observational tensors into smaller, lower-ranked ones that are more suitable for interpretation. Each of these methods focuses on a slightly different aspect to consider prior/expert knowledge, data sparsity, and phenotypic diversity in order to identify interesting phenotype groups that are clinically meaningful. Essentially, these are all unsupervised soft clustering models that try to stratify the data in low dimensional manifolds. Because of the lack of common discriminative objectives in these clustering approaches, the final outcome, while statistically meaningful, may not always provide clinical insights. A recent study [1] improved this mechanism by introducing a supervision term and a contextual similarity regularization term, enabling tensor factorization to be performed discriminatively in order to minimize a classification loss function towards outcome of interest (e.g., disease onset, mortality, read-mission). However, this method considers co-occurrence as a single source of information to be modeled, neglecting the temporal nature of such information as observations change over time.

On the other hand, graph decomposition based methods for computational phenotyping has been developed [5] to model the disease progression of individual patients as separate graphs. Each node in the graph represents a medical event (diagnosis, prescription, etc.) and each edge indicates a (longitudinal) transition relationship (e.g., delirium is diagnosed in the next visit after the diagnosis of Alzheimer’s disease). Instead of modeling co-occurrences, graph decomposition approaches seek to identify the most representative subgraphs to explain the disease progression. A set of core subgraphs are extracted so that their linear combination can approximate the graph of individual patients. But unfortunately, this method does not allow the integration of co-occurrence information because the edge of the graph can only represent one kind of relationship (either transition or co-occurrence). In general, there is no one-size-fits-all model as either encoding mechanism might lead to cross-sectional or longitudinal information loss.

The latest work by Yin et. al. [6] utilized deep learning to model the dynamic temporal states as hidden factors with recursive neural networks (RNN) while keeping co-occurrence patterns encoded in the tensor for joint optimization. This is the first work to harmonize information of both sources and demonstrates improved performance. One limitation of this model is that it assumes that phenotypes are static combinations of different medical events instead of evolving patterns (i.e., using the phenotype membership change over time to represent the patient’s state dynamics). For chronic disease like Alzheimer’s disease (AD), such an assumption may not be sound as temporally evolving patterns are most important to characterize a patient’s disease progression [7]. Therefore, it is an urgent task to derive transitional patterns that effectively reflect longitudinal and cross-sectional relationships between diseases. In this study, we propose to develop a disease progression phenotyping model to represent the transitional relationships while still considering the co-occurrence information. We utilize representation learning (based on co-occurrences) and tensor factorization (based on transition) in an orthogonal manner to complement each other for explicit temporal phenotyping study.

Epilepsy and AD.

Epilepsy and AD are among two of the most prevalent serious neurological disorders [8, 9]. While incidents of epilepsy are most common in the elderly, it is increasingly recognized that seizures are further over-represented in the population with AD [10, 11], occurring in up to 64% of closely monitored patients [12]. Seizures may predate AD diagnosis; epileptiform activity can precede amyloid β plaque deposition in transgenic mouse models of AD. Subtle seizure types such as brief focal unaware seizures may go undiagnosed in patients [13], lowering quality of life and predisposing to morbidity and mortality. There is also concern that seizures may hasten cognitive decline, exaggerate the effects of AD [14] and reduce life expectancy [15]. Neuropathological studies have demonstrated the presence of age related amyloid B plaque in respected temporal lobe tissue of epilepsy patients without dementia, compared to control autopsies without epilepsy [16]. Chronic epilepsy is associated with increased tau neurofibrillary tangles at mid-Break stages in patients aged 40–65 years [17], suggesting common pathophysiological pathways. The relationship between epilepsy and AD requires further elucidation. Health claims data offer a unique perspective to study such complicated relationships. The key is to make good use of the appropriate information to identify critical discriminative patterns from the big health claims data while overcoming bias, confounder, and imprecise onset time point for diseases. Using the transitional phenotype, we can understand the relationship between epilepsy and AD.

2. Methods

2.1. Dataset

We extracted the Epilepsy-AD cohort as a subset of Cerner Health Facts data (between 2000 and 2014) subscribed by UTHealth [18], which has around 50M patients from 600 Cerner client hospitals. The data elements include demographics, encounters, diagnoses, procedures, medication orders, medication administration. The epilepsy patients are identified by ICD-9 code 345.x and the AD patients are identified by 331.0. The experiment section has a detailed breakdown of our cohort. We exclude patients who are younger than 45 years; whose observation window is less than 0.5 years.

2.2. Verify Causal Relationship

Our first step is to verify the causal relationship from source disease (i.e., Epilepsy) to target disease (i.e., AD). It is also a step to confirm that our data are sufficient to support the downstream phenotyping study. For this purpose, we first selected epilepsy patients with and without developing AD, followed by using propensity score matching (PSM) algorithm [19] to find a comparable cohort of patients without epilepsy (matched on demographics and three major epilepsy risk factors: brain injury, brain tumor, and stroke). In the matching process, we select as many candidates as possible while meeting the boundary condition that each matching variable should not deviate more than 5% after matching. Finally, we conduct a χ² test to check the significance of the outcome.

2.3. Temporal Phenotyping

We propose a novel framework to capture two important aspects of patient information trajectory (1) (cross-sectional) co-occurrence pattern, (2) (longitudinal) transition pattern. As illustrated in Figure 1, EHR can be represented as a sequence of set of entities (e.g., medications, diagnoses, lab tests, conditions): visit₁ : {m₁, m₂, d₁, d₂} → visit₂ : {m₂, m₃, d₃} →, … for each patient, where m_k and d_l correspond to the medication and diagnosis in this list. Within each visit (encounter), a patient will receive a set of medication m and diagnosis d, which order does not matter. This is followed by another visit and we might observe changes in medication and diagnosis, which forms the so-called transition pattern, providing clues to the progression of the disease or other changes to the patient’s health condition. We will model the co-occurrence (within the same encounter) of entities using a skip-gram and model the transition (between encounters) of entities using tensor factorization. A joint optimization framework that considers both the trajectory similarity (in transition) and entity-level similarity (in co-occurrence) is developed to mine critical temporal phenotypes that might explain the difference between epilepsy patients who are more likely to develop AD (AD likely) vs. those who are less likely to develop AD (AD unlikely).

Figure 1:

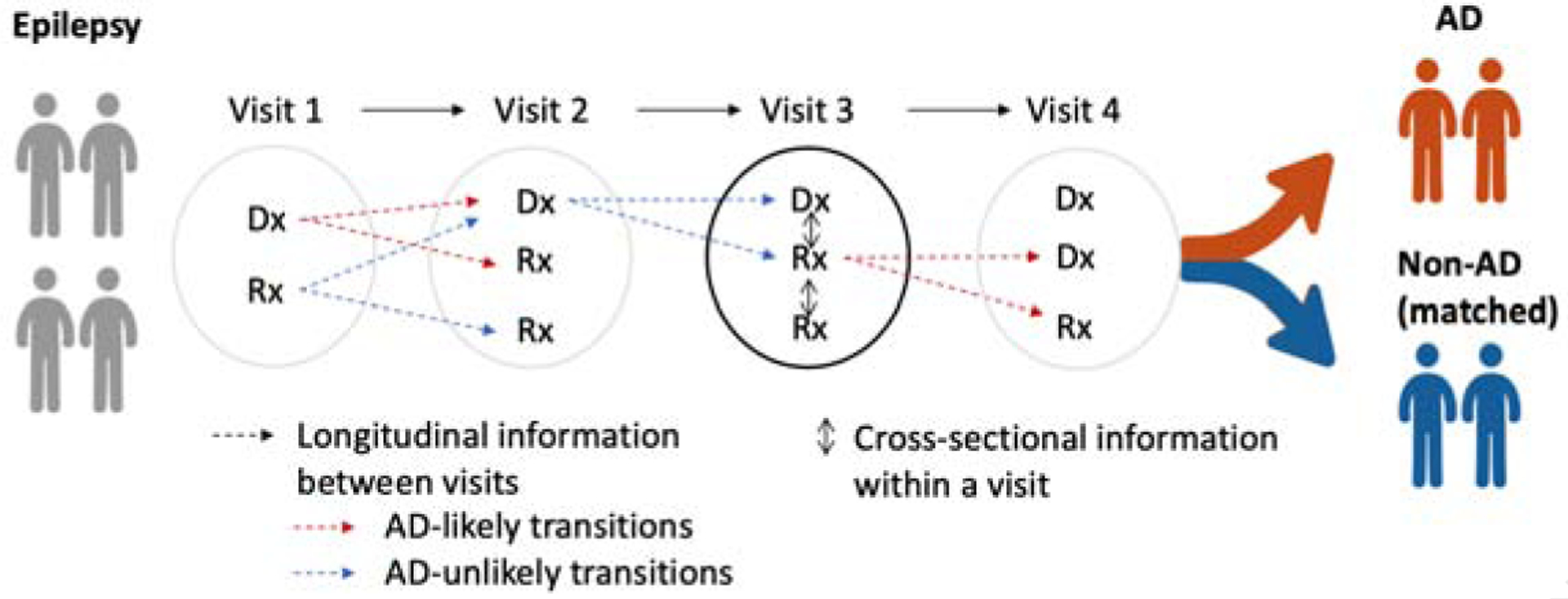
A spatial-temporal view of a patient’s progression pathway. Entities in the bag of each visit include a set of medications and diagnoses, which are subject to change from time to time. Dotted edges between visits indicate a transition in longitudinal view. Bidirectional edges within a visit indicate a co-occurrence in cross-sectional view.

2.3.1. Cross-sectional information: Co-occurrence of entities

We represent each entity as a vector representation using skip-gram [20] to reflect co-occurrence of entities within a visit. EHR data are sparse as different patients have different visit frequencies and encounters in their clinical pathway. There are a massive number of entities, which present difficulties for a simple count-based approach. A mitigation approach is to view entities in their context and represent them as dense vectors (e.g., absorbing co-occurrence information of the neighbors) to feed downstream models for analysis. Here we adopt a distributed embedding approach to assemble the information from the neighborhood of individual entities. We choose the skip-gram approach for efficiency. Likelihood of the skip-gram model for each medication m_i within a visit is:

$$\begin{array}{l}\frac{1}{K+L}\sum p\left(m_1,\cdots ,m_{i-1},m_i,\cdots ,m_K,d_1,\cdots ,d_L\right)\hfill \\ =\frac{1}{K+L}\sum _{m_k,d_l\in N\left(m_i\right)}\text{log}p\left(m_k\mid m_i\right)+\text{log}p\left(d_l\mid m_i\right).\hfill \end{array}$$ (1)

for predicting everything else m_k and d_l ∈ N(m_i) within this visit based on m_i. In order to model such probability, we use a feed-forward neural network to learn the latent embedding v, for which the dimensionality d is pre-determined and each entity m_i is represented by a dense vector $v_{m_i}$. The probability of neighbor m_k conditioned on m_i

$$p\left(m_k\mid m_i\right)=\frac{\text{exp}\left(v_{m_k}{}^T{v}_{m_i}\right)}{{\sum }_{m\ne i}\text{exp}\left(v_m{}^T{v}_{m_i}\right)}$$ (2)

is to use all the medications to infer the likelihood of m_i in a softmax fashion. Similarly, we can do it for the p(d_l|m_i) by considering all the diagnoses. The challenge to optimize the above likelihood directly is the big domain of medication and diagnosis (i.e., thousands of entities), making the computation intractable. A practical approach is to use an approximation technique called noise contrastive sampling (NCE) [21], which respects the original distribution of the data. In NCE, we basically get negative samples for each positive sample. In the case of our Eq. (2), we replace the denominator with ${\sum }_l\text{exp}\left(v_l{}^T{v}_{m_i}\right)$ where v_l is sampled from entities that are not observed in the same encounter of m_i while still satisfying the general distribution of medication. Solving this large optimization problem with L+1 samples for each entity, we will obtain the final embedding vectors.

2.3.2. Longitudinal information: Transition of entities

In addition to the co-occurrence within an encounter, transition from one entity to another entity in consecutive encounters is the key to model the progression of disease. We first derive each individual patient’s transition from previous visit to next visit. One patient, P1 follows a trajectory of entities, for example, visit₁ : {d₁, m₁} → visit₂ : {d₂, m₁} → visit₃ : {d₂, m₂}. We represent this trajectory as transitions between pairs of entities in consecutive visits: d₁ → d₂, d₁ → m₁, m₁ → d₂, m₁ → m₂, and so on. This pairwise transition can be represented as a matrix where each value refers to counts or normalized counts (i.e., transition probability) of the transitional pair across all encounters. Here, we transform the transition probability with logarithm and add o set value to make the transition probability follow the Gaussian distributions. However, this individual patient’s transition matrix contains only each individual’s different progression of diseases. To aggregate the different transitions into a population-level view, we stack the transition matrices into a 3-order matrix, i.e., tensor (Figure 2).

Figure 2:

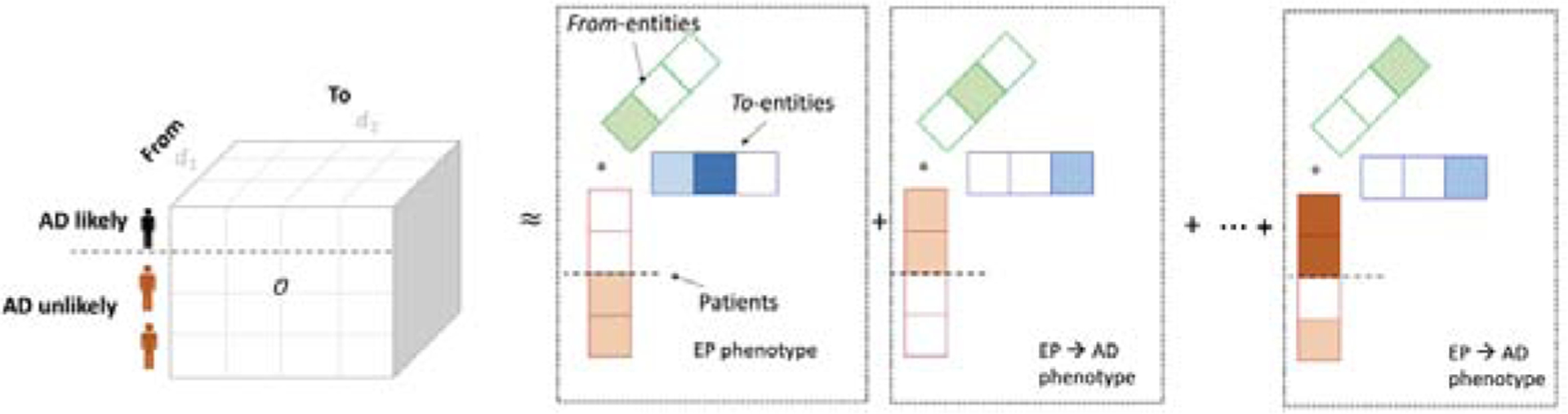
Tensor representing transition of entities across all patients. EP=epilepsy unlikely to develop AD, EP → AD = epilepsy likely to develop AD.

This 3-order tensor O has a shape of I × J × J, where I = number of patients, J = number of entities. Then, we decompose the tensor into latent dimensions to derive phenotypes, which is defined as underlying transitions from a group (cluster) of relevant entities to another group of relevant entities. The transition between groups is useful to understand generalized progression of diseases (in our case, progression of epilepsy to AD), where the transition from one entity to another does not provide a context in which the transitions happen. The most widely used tensor decomposition is CP method [22, 1]. A 3-order tensor O with a shape of I × J × J is rank-one tensor if it is an outer product of three vectors a, b, c, i.e., O = a ∘ b ∘ c where ∘ means the vector outer product. O_ijk, the element at (i, j, k) in the tensor O, is computed as a product of elements in the vector, i.e., O_ijk = a_ib_jc_k. Tensor factorization (TF) is a dimensionality reduction approach that represents the original tensor as latent dimensions. The CP model approximates the original observed tensor O as a linear combination of rank-one tensors [22]; that is, the 3-order tensor O is decomposed as minimizing difference between observed tensor and approximated tensor as

$$L=\parallel O-\sum _{r=1}^R{a}_r\circ b_r\circ c_r{\parallel }^2$$ (3)

where a positive integer R is the rank (i.e., number of phenotypes), a_r, b_r, c_rare r-th column vectors in matrix A, B, C with shape of I × R, J × R, J × R, respectively. Here, A, B, C are called as factor matrices, and A, B, C corresponds to patient, entity (where the transition comes from), entity (where the transition goes to). The R latent dimensions in the R columns of factor matrices defines phenotypes. That is, a phenotype consists of the from-entities in the column of B and the to-entities in the column of C. Individual entities are involved to the phenotype with different degree of membership, and the amount of membership is stored in the columns of B and C. Likewise, individual patients have characteristics of the R phenotypes with different extent of membership, and the amount of membership is stored in the row of A. On top of the basic TF, we can add several constraints and regularizers to enhance interpretability and discriminative power of phenotypes. Because the tensor O contains nonnegative data (counts or transition probability), we set non-negative constraints A, B, C ≥ 0 for interpretability of latent dimensions. A l₁norm regularizer to the factor matrix enhances interpretability via compact patterns as shrinking the less important coefficients to zero: L + λ · (∥A∥₁ + (∥B∥₁+ (∥C∥₁ where λ is a weight parameter to balance the tensor error and the l₁ norm loss. A supervised regularizer to the factor matrix A (which defines how much each patient is involved in the phenotypes) boosts discriminative power by separating patients into either epilepsy+AD or epilepsy [1]. The supervised TF adds logistic regression regularizer as

$$L-\mu \cdot \text{log}P(A,y\mid \theta )=L-\mu \cdot \frac{1}{1+\text{exp}(-y\cdot \theta A)}$$ (4)

where μ is a weight parameter to balance the tensor error and the loss on regularizer, θ is a parameter for discriminative logistic regression objective, and y is a label (y = 1 if epilepsy+AD; −1 epilepsy only). Therefore, our final objective function is integrating both regularizers:

$$L-\mu \cdot \text{log}P(A,y\mid \theta )+\lambda \cdot \left(\Vert A{\Vert }_1+\Vert B{\Vert }_1+\Vert C{\Vert }_1\right).$$ (5)

2.3.3. Integrating cross-sectional and longitudinal information

We incorporate the co-occurrence representation to the transition pattern to derive temporal phenotype that considers both aspects within- and between-visits. We aim to make phenotypes respect the co-occurrence similarity while reflecting the temporal dynamics of the transition pattern. We first derive pairwise similarity between entities using the co-occurrence representation: cosine(v1, v2) where v1, v2 is an arbitrary embedding vector. Then, we build a similarity matrix S with a shape of J × J. When there are multiple sources of information, coupled matrix-tensor factorization can jointly learn the factor matrices that reflect both sides of information [1]. Because the transition tensor O and the similarity matrix S share the same entity information (B and C), the loss function becomes

$$\begin{array}{l}L=\parallel O-\sum _{r=1}^R{a}_r\circ b_r\circ c_r{\parallel }^2\\ +\gamma \cdot \left(\parallel S-B{B}^T{\parallel }^2+\parallel S-C{C}^T{\parallel }^2\right)\\ -\mu \cdot \text{log}P(A,y\mid \theta )+\lambda \cdot \left(\Vert A{\Vert }_1+\Vert B{\Vert }_1+\Vert C{\Vert }_1\right).\end{array}$$ (6)

where γ is a weighting constant. We then minimize this loss to derive optimal A, B and C.

3. Results and Discussion

3.1. Matching and Causal relation

We use PSM algorithm to avoid data selection bias when building the cohort. We performed PSM in two steps: 1) matching epilepsy and non-epilepsy patients; ii) matching AD and non-AD patients among the epilepsy patients. The first step is to verify the causality between epilepsy and AD. We matched epilepsy and non-epilepsy patients using age at first observation and the observation window (As AD normally starts developing the symptoms from age of 65, we only select cases with first epilepsy onset after 55 years old). We also include the demographic (gender, race, and ethnicity) and co-morbidity (brain injury, brain tumor, and stroke) into consideration. These confounding factors achieved 61% accuracy when predicting epilepsy using the logistic regression model, which means they have a high confounding effect. Table 1 lists the discrepancy of various properties, showing that the differences are well-controlled under 5% after our matching process while keeping a large number of samples from the epilepsy group. After the matching, we use the χ² test to evaluate significance as to whether epilepsy patients have a higher chance of subsequently developing AD. Our result indicates that such a causal relation is significant with a p-value =1.92e-51 (Table 2).

Table 1:

Standardized variance before and after the propensity score matching with respect to epilepsy and non-epilepsy. We removed any epileptic patients with AD onset before epilepsy.

Features	Before matching	After matching
Age at first observation	41.26%	2.18%
Observation window	15.72%	0.51%
Gender	3.74%	0.16%
Race	4.78%	1.29%
Ethnicity	1.91%	1.77%
Brain injury	8.46%	4.65%
Brain tumor	11.30%	2.97%
Stroke	22.38%	0.58%

Table 2:

Causality between Epilepsy and AD. χ² value was 227.67 with p-value < 0.0001

	No epilepsy	Epilepsy
No Alzheimer	57,123	54,481
Alzheimer	662	1289

The second step is to build an unbiased cohort for the next phenotyping model, which investigates epilepsy patients who developed AD and those who did not develop AD in a similar observation window. We started the second step matching from the matched epilepsy patients in the first step. Among all 1,289 patients who developed AD after epilepsy, we excluded some patients (with very low drug/diagnosis counts) and kept 1,241 as cases (Epilepsy+AD). We randomly selected another 5,276 non-AD patients (controls) out of 54,481 (Epilepsy only). We extracted 97 ICD-9 diagnosis codes and 106 drugs, which are associated with at least 5% of these patients (Table 3). In all, the observed tensor had a size of (1241 + 5276) × (97 + 106) × (97 + 106) = 6517 × 203 × 203.

Table 3:

Cohort summary after matching epilepsy+AD (case) and epilepsy only (control)

Features	Cases	Controls
Number of patients	1,241	5,276
Age at first observation	74.87±8.92	68.09±10.79
Observation window	3.88±227	3.73±2.29
Gender - Female	41.70%	52.60%
Race - Caucasian	71.40%	69.90%
Race - African American	25.10%	21.80%
Ethnicity - Hispanic	0.30%	1.20%
Brain injury	2.30%	1.70%
Brain tumor	0.10%	0.60%
Stroke	15.90%	14.10%

3.2. Evaluation on Phenotyping methods

We evaluated the phenotyping methods in terms of discrimination, interpretability, and reconstruction with different levels of regularizers. As discussed in the method section 2.3.2, there were multiple regularization in computational phenotyping to encourage discrimination and interpretability while minimizing reconstruction error. First of all, we would like to have a high accuracy to discriminate groups of interest (AD vs non AD). The discriminating power was measured as area under the precision-recall curve (AUPRC) [23], which is for binary decision problems performance with highly skewed dataset. Then, we would like to have phenotypes that are easier to interpret, which is defined as less events within phenotypes (sparse) and less overlapped events between phenotypes. The sparsity of phenotype was computed as an averaged Gini index of involvement values in each phenotype (i.e., the row of B and C)[24]. The overlap between phenotypes measures the degree of overlap between all phenotype pairs [1]. Lastly, we would also like to see that inferred phenotypes have a small reconstruction error to the original data using mean squared error (MSE). These objectives are controlled by different parameters in our tensor factorization model introduced in the method section, namely μ λ γ, which corresponds to the weight for discrimination, sparsity, and adherence to co-occurrence similarity. We implemented the regularized coupled TF (Eq. 6) using Pytorch 11.4 using adaptive momentum estimation (ADAM) for optimization. We set the maximum number of iterations as 1,000. The running time was less than 15 secs with 3 parallel GPUs on DGX-2. We added dropout to logistic regression coefficients for robustness.

After extensive experiments, we found that R=30 (number of phenotypes), μ = 1, λ = 0.1, γ = 1 performs best in terms of discrimination and interpretability (Table 4, Fig. 3), by which we achieved 0.30 AUPRC; 0.25 sparsity; 0.87 overlap; and 0.69 MSE. The AUPRC was somewhat low for all settings, compared to the baseline value 1241/(1241 + 5276) ≈ 0.19. A possible explanation is that in general, AD is difficult to predict within short observation periods of older epilepsy patients. This short observation might not contain rich information and make AD prediction difficult inevitably.

Table 4:

Parameters for different experiments and our criteria of selection. Mean (standard deviation) after 10 trials. μ for logistic regression; λ for l₁-norm; γ for similarity structure.

μ	λ	γ	AUPRC	Sparsity	Overlap	MSE
0	0	0	0.2215 (0.0100)	0.2119 (0.0023)	0.8536 (0.0034)	0.5148 (0.002)
0	0	1	0.2990 (0.0196)	0.2442 (0.0038)	0.8647 (0.0085)	0.6774 (0.0078)
0	0.1	0	0.2272 (0.0097)	0.2473 (0.0048)	0.814 (0.0073)	0.5215 (0.0027)
1	0	0	0.2241 (0.0082)	0.2121 (0.004)	0.8519 (0.0069)	0.5144 (0.002)
1	0.1	1	0.2959 (0.0162)	0.2498 (0.0065)	0.8651 (0.01)	0.6893 (0.0083)

Figure 3:

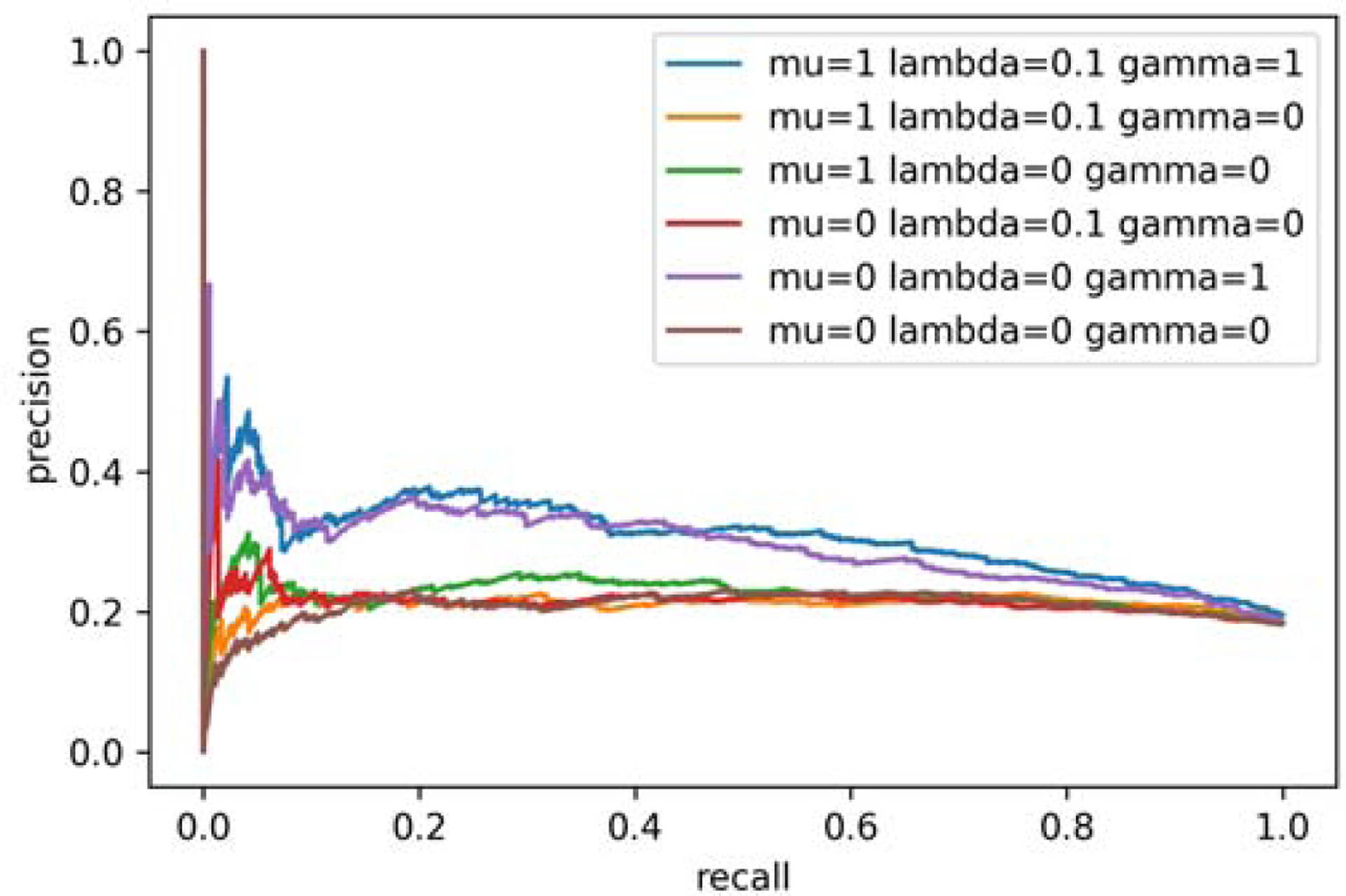
Area under the precision-recall curve on different hyperparameter settings.

We also found that the cross-sectional information significantly increases AUPRC (0.22 if γ =0 vs 0.30 if γ=1 in Table 4), implying that the cross-sectional information contains rich information on epilepsy developing AD.

After optimizing the phenotyping methods, we examined the logistic regression coefficients to evaluate each phenotype’s discriminative power. As the 30 phenotypes were predictors in the logistic regression, we selected phenotypes that separate epilepsy patients developing AD vs. epilepsy without developing AD with statistical significance. There are 21 phenotypes showing p-value < 0.05, with 15 phenotypes for epilepsy only (EP) and 6 phenotypes for epilepsy developing AD (EP+AD). To verify the relationship between the phenotypes and epilepsy progression to AD, we also report the number of patients in the two groups (either EP or EP+AD) according to the extent of involvement to each phenotype (Figure 4). Due to limited space, we only report three representative phenotypes from each group. We found that in AD likely phenotypes (P7, P9, P27) the ratio of AD patients (EP+AD) to EP only patients (EP) increases as the membership values increase. In contrast, in AD unlikely phenotypes (P1, P12, P20) the ratio of EP+AD patients to EP only patients decrease as the membership values increase. These findings are consistent with the logistic regression results in which EP+AD patients are more likely to have larger values on AD likely phenotypes and to have smaller values on AD unlikely phenotypes. Note that our cohort is imbalanced with 6,500 EP only patients and 1,289 EP+AD patients, thus the number of EP only patients is always larger than the number of EP+AD across all membership values.

Figure 4:

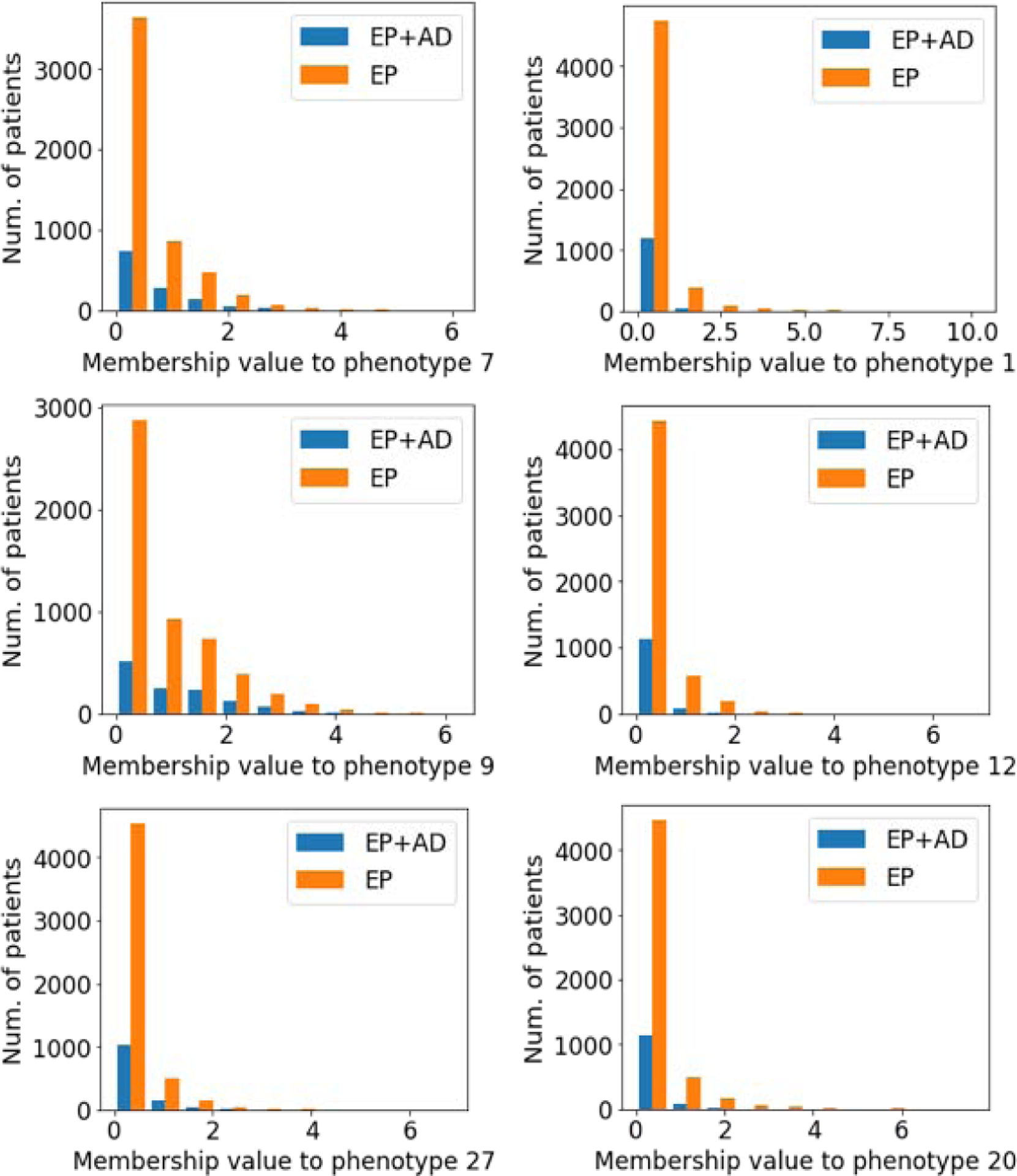
Patient’s membership distributions. Left: AD likely phenotypes, Right: AD unlikely phenotypes. EP+AD= Epilepsy patients who develop AD, EP= Epilepsy patients without developing AD.

3.3. Discovered phenotypes

We presented the discovered transitional phenotypes (Figure 5). Each phenotype is represented as a graph that consists of from-entities nodes where the transition comes from and to-entities nodes where the transition goes to. To present the most highly meaningful edges between the from- and to- nodes, we sort all the edges between the from-entities and to-entities based on edge scores and randomly selected top edges with high scores. The edge scores are computed from membership values of entities and transition probability between them, that is, the edge score for m₁ → m₂ is computed as B[m₁, r] × C[m₂, r]×[log₂(tran(m₁ → m₂))+ϵ], where m₁ ∈ from-entities, m₂ ∈to-entities of r-th phenotype, and trans(m₁ → m₂)is transition probability averaged on all patients; ϵis a positive constant added to the log2-transformed transition probability to make it nonnegative. The edge score will be high if entities are highly involved in the phenotype and transition between the two entities is prevalent. Some of the patterns are very interesting: (1) Potassium chloride is the hub in phenotype 7, which indicates these patients were suffering from, or had a setting for hypokalemia. Hypokalemia may conceivably play a role in epileptic seizures [25, 26] and new evidence indicates rubidium and potassium level alterations in AD [27]. Potassium deficiency can lead to significant decrease in lipid metabolism [28], which strengthens linkage to AD [29]. A similar connection from potassium, hypertension to AD seems to exist - an interesting longitudinal study found the use of potassium-sparing diuretics significantly reduced the risk of AD [30]. (2) Phenotype 9 is related to patients who are on Warfarin and joint disorder, followed by diagnosis of back and other cerebral degeneration disorders. Many edges in phenotype 9 are similar to those in phenotype 27, but the latter has a deeper structure and patients have disorders of back and additional symptoms involving head and neck. This seems to indicate the severity of the epilepsy (conditions are likely to be linked with incidental falling), which might be an indicator to the risk of developing AD. (3) Phenotype 23 seems to represent a slightly different group of patients who got diagnosed with epilepsy and recurrent seizures and have immediate problems with urethra and urinary tract, pneumonia, vitamin D deficiency, and mental disorders. We know pneumonia and mental disorders are often diagnosed with late stage AD patients, which may indicate something special about this phenotype group, i.e., patients may have already developed AD (or mild cognitive impairment) but the diagnosis was made later. (4) Phenotype 24 is associated with the medication of piperacillin sodium, which is mainly used to treat pneumonia and skin conditions, followed by diagnosis including other disorders of bones and cartilage, other disorders of soft tissue, etc. We know piperacillin sodium belongs to penicillin antibiotics, and often causes seizures and myoclonus [31]. This may indicate piperacillin aggravation of seizures and increased risk of AD.

Figure 5:

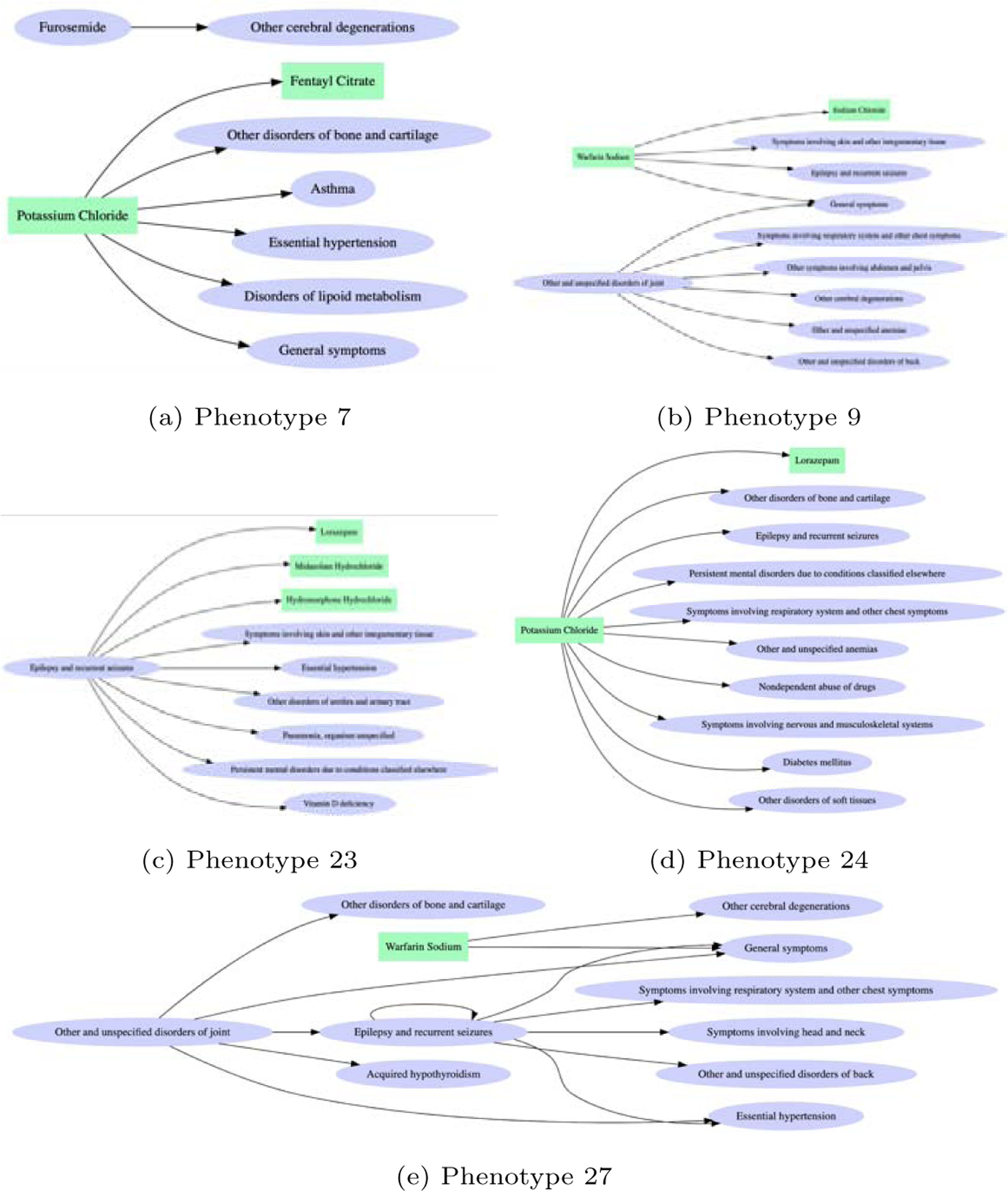
Five phenotypes for those who develop AD. Each directed edge means a transition pattern from A to B is observed between two neighboring visits with a high probability within a phenotype. For example, a large proportion of the patients in Phenotype 7 has “furosemide” in a visit at time t followed by a diagnosis of “other cerebral degeneration” at time t+1, which is illustrated by an edge. Box: medication; Oval: diagnosis.

4. Limitation and Conclusions

Despite the interesting findings and novel contribution of methodology, we admit there are some limitations of this work. We only considered the pairwise transition patterns between consecutive visits. Certain long-term effects can play an important role in the pathway from epilepsy to Alzheimer’s disease, but it might be neglected in the 3d tensor factorization. It is possible to integrate high-order transitions in tensor factorization but it is not efficient to consider every high-order combination because most high-order transitions contain duplicated transitions. This will be a future extension of our study. In summary, we confirmed the strong causal relationship between epilepsy and Alzheimer’s disease using big data, and conducted integrative computational phenotyping analysis (AUPRC^~0.30) to discriminate AD likely and unlikely phenotypes among epilepsy patients, providing signature transition patterns that might inspire clinical research. A detailed analysis of the exact phenotypic interactions with epilepsy and subsequent AD is necessary. In this study, we only analyzed epilepsy subgroups leading to AD but not AD subgroups leading to epilepsy, which can be another direction to explore in the future.

Highlights:

• Epilepsy and Alzheimer’s disease has significant causal relationship

• We developed temporal phenotyping methods to represent a disease deteriorates to other disease

• We derived five representative transitional phenotypes of epilepsy patients who develop AD