Skip to main content
NCBI home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2021 Oct 1.
Published in final edited form as: J Orthop Res. 2020 Jan 24;38(10):2272–2279. doi: 10.1002/jor.24589

Thinking Outside the Glenohumeral Box: Hierarchical Shape Variation of the Periarticular Anatomy of the Scapula Using Statistical Shape Modeling

Matthijs Jacxsens 1,2,3, Shireen Y Elhabian 4, Sarah E Brady 5, Peter N Chalmers 1, Andreas M Mueller 2, Robert Z Tashjian 1, Heath B Henninger 1,4,5
PMCID: PMC7375008  NIHMSID: NIHMS1069392  PMID: 31965594

Abstract

Variation in the shape of the glenoid and periarticular anatomy of the scapula has been associated with shoulder pathology. The goal of this study was to identify the modes of shape variation of periarticular scapular anatomy in relation to the glenoid in non-pathologic shoulders. Computed tomography scans of 31 cadaveric scapulae, verified to be free of pathology, were three-dimensionally reconstructed. Statistical shape modeling and principal component analysis identified the modes of shape variation across the population. Corresponding linear and angular measurements quantified the morphometric variance identified by the modes. Linear measures were normalized to the radius of the inferior glenoid to account for differences in scaling of the bones. Five modes captured 89.7% of total shape variation of the glenoid and periarticular anatomy. Apart from size differences (Mode 1: 33.0%), acromial anatomy accounted for the largest variation (Mode 2: 32.0%). Further modes described variation in glenoid inclination (Mode 3: 11.8%), coracoid orientation and size (Mode 4: 9.0%), and variation in coracoacromial (CA) morphology (Mode 5: 3.1%). The average scapula had a mean acromial tilt of 49±7°, scapular spine angle of 61±6°, glenoid inclination of 84±4°, coracoid deviation angle of 26±4°, coracoid length of 3.7±0.3 glenoid radii, and a CA base length of 5.6±0.5 radii. In this study, the identified shape modes explain almost all of the variance in scapular anatomy. The acromion exhibited the highest variance of all periarticular anatomic structures of the scapula in relation to the glenoid, which may play a role in many shoulder pathologies.

Keywords: scapular anatomy, glenoid, bone morphology, shoulder, statistical shape modeling

Introduction

Variation in the shape of the glenoid and the periarticular anatomy of the scapula, including the acromion and coracoid process, are associated with several pathologic conditions of the shoulder, including degenerative, overuse and posttraumatic pathologies. Both glenoid inclination as well as lateral extension of the acromion, measured as the acromial index (AI), have been related to degenerative rotator cuff tears.1–6 The critical shoulder angle (CSA) is an angular measurement combining lateral acromial extension and glenoid inclination.7 CSA above the normal threshold (>35°) has been associated with rotator cuff tears and cuff tear arthropathy, whereas CSA under the normal threshold (<30°) has been associated with primary glenohumeral osteoarthritis.7; 8 It is thought that the orientation of the moment arm of the deltoid changes according to the shape variation of the acromion and glenoid, increasing the strain on the supraspinatus tendon to keep the humeral head centered and depressed during arm elevation.9; 10 To the contrary, an in-vivo study quantifying glenohumeral joint motion found a more inferior orientation of the humeral head during abduction in normal shoulders with a higher CSA.11

Although it has been subject to debate and through biomechanical evidence is still missing, morphologic differences of the coracoacromial (CA) arch have been associated with overuse pathologies such as shoulder impingement syndrome. Anatomic factors that might contribute to this syndrome include shape variation of the acromion, variation in acromial slope, prominent bony spurs on the inferior aspect of the CA-joint or CA-ligament.12–16 and morphologic differences of the coracoid process.17–19 Moreover, a larger coracohumeral distance has been identified as an independent risk factor for traumatic anterior shoulder instability.20 This suggests that coracoid morphology and its attached soft tissues influence shoulder stability.

These prior studies emphasize the importance of the articular and periarticular bony anatomy of the scapula and its attached soft tissues, and its relation to developing degenerative, overuse or posttraumatic pathology of the glenohumeral joint. However, the relative degree of acromial variation with respect to coracoid and glenoid variation remains unknown and thus the relative importance of these factors to one another remains unknown. Ranking the anatomic variance gives us the anatomic areas upon which to focus when considering pathomechanics of a shoulder disorder.

Statistical shape modeling (SSM) is a computational method used to study geometric properties of shapes, independent of size differences.21; 22 Around the glenohumeral joint, SSM has mainly been used to approximate native anatomy for anatomic structures with bony defects.23–25 However, SSM is an ideal tool to objectively quantify shape variability within a given set of samples, without idealizing the underlying anatomy.21 Therefore, the goal of this study was to use SSM to identify the hierarchy of anatomic variance of the articular and periarticular anatomy of the scapula, and to quantify shape variation of the periarticular anatomy of the scapula in relation to the glenoid in non-pathologic shoulders.

Methods

Study Population

Ethical approval for this study was exempt via the University of Utah Institutional Review Board (IRB #11755). Unpaired cadaveric specimens with a computed tomography (CT) scan and verified to be free of any shoulder pathology by an orthopaedic surgeon at the time of dissection were included. Available demographic data included age, gender, side, height and weight.

Imaging Protocol

All specimens underwent a CT scan using a Siemens Sensation (Siemens Medical, Malvern, PA, USA) CT scanner with the following protocol: 130 kV, 512 × 512 matrix, 1.0-mm slice thickness, 0.75 pitch, 170 mAS current. Imaging data were exported to DICOM (Digital Imaging and Communications in Medicine) files for analysis.

Computational Algorithm

DICOM files were imported into Mimics (Materialise, Leuven, Belgium) and segmented using semi-automatic techniques to create 3D surfaces of the cortex.25; 26 Left scapulae were mirrored to right scapulae for consistency in SSM model generation and measurement. All 3D surfaces were aligned to a glenoid-based coordinate system26 (3-Matic, Materialise, Leuven, Belgium), in which the origin was defined as the center of the best-fit circle of the inferior glenoid; the xy-plane (plane of the glenoid) was defined by the best-fit circle of the inferior glenoid with the y-axis directed superiorly and the x-axis directed anteriorly; the z-axis was normal to the xy-plane, directed laterally; and the yz-plane (glenoid center plane) was the plane normal to the xy-plane through the supraglenoid tubercle.

To focus the analysis on the periarticular anatomy, a cutting plane was created through the scapular notch, parallel to the glenoid plane, maintaining only 3D surfaces lateral to the cropping plane. Cropped scapulae, aligned to the above described landmark-driven coordinate system, were imported into ShapeWorks to conduct the SSM using the correspondence method of Cates et al.27; 28. This method computes a statistically optimal representation of the study group variability by employing an automatic particle optimization of 2048 correspondence points that minimizes the overall information content of the model while maintaining a good sampling of surface geometry. In the current study, scaling was not factored out during the preprocessing of the 3D models, as it was considered as an important shape variation with potential clinical importance.

Similar to a prior validation study43, a validation framework was set up for the studied scapulae by comparing the quantitative metrics of the shape model generated by ShapeWorks with two other widely-used SSM tools, being Deformetrica and SPHARM-PDM. Following quantitative metrics were assessed to evaluate shape models: (1) Compactness, i.e. the ability to describe shape variability with a minimal degrees of freedom, was calculated as described by Munsell et al44; (2) Generalization, i.e. the ability of the constructed shape model to represent unseen shapes of the same class, was computed using a leave-one-out cross-validation44; (3) Specificity, i.e. the ability to construct realistic new shape instances randomly created by the shape model, was quantified by randomly generating a large number of samples from the shape space using the first eigenvectors that explain the variability and calculating the distance to the nearest training sample. The constructed shape models demonstrated an overall high quality. ShapeWorks outperformed Deformetrica and SPHARM-PDM for compactness, and SPHARM-PDM for generalization and specificity while being similar to Deformetrica for generalization and specificity.

Morphometric Measurements

Modes of variation derived from the SSM process do not directly yield linear and angular measures that may be applied on clinical radiographs, CT slices, or 3D reconstructions of DICOM data. Therefore, standard scapular measurements corresponding with the anatomic sections observed to vary in the modes of variation were used to further quantify the morphology.

The orientation of the spina scapulae (scapular spine angle) and coracoid pillar (coracoid pillar angle) were obtained by creating the best-fit plane through the middle of the spina scapulae and coracoid pillar, respectively (Supplementary Data). The best-fit plane of the acromion undersurface defined acromion tilting (Supplementary Data). These angles were measured in relation to the glenoid center plane, which bisects the glenoid longitudinally, in the plane of the glenoid (Fig. 1). The anterior, superior and lateral offset of the coracoid apex at the lateral end of the coracoid process and the base of the coracoid process, formed by the junction of the lateral border of the suprascapular notch with the medial border of the conoid and trapezoid tubercles, were obtained with respect to the origin. Coracoid length and coracoid deviation angle were obtained by the apex and base of the coracoid process as described by Chahla et al.29 The line segment from the coracoid apex to the anterolateral corner and posterolateral corner of the acromion determined the CA arch and the CA base length and angle, respectively. These distances were normalized to the radius of the best-fit circle of the inferior glenoid to compensate for size differences between scapulae.

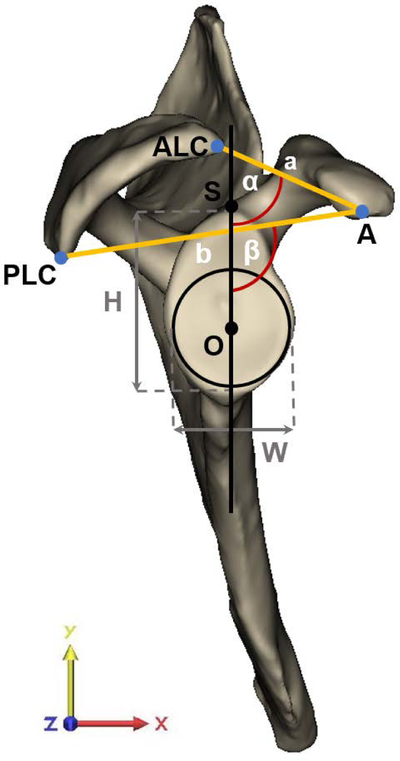
Figure 1:

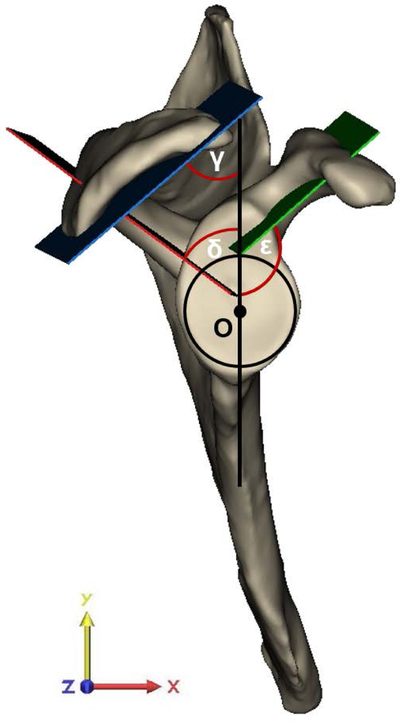
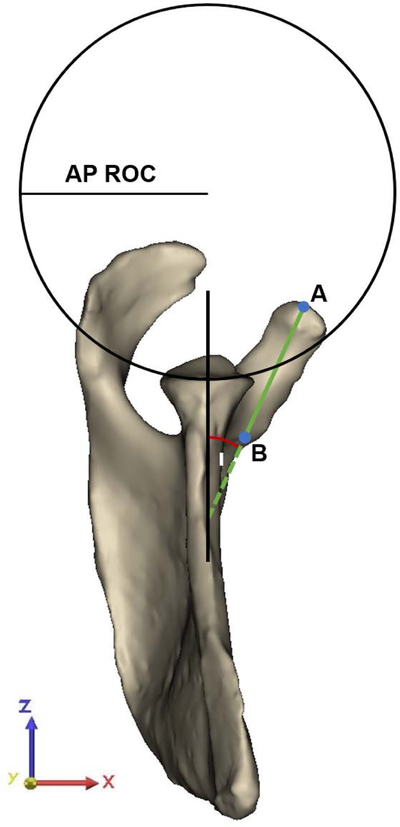
Figure 1:

Figure 1:

Figure 1:

Figure 1:

Open in a new tab

(A) Offset measures of the apex of the coracoid process (A) were determined with respect to the center of the best-fit circle (O). Angle measures were assessed in the plane of the glenoid in relation to the glenoid center plane (black line), which is defined as the perpendicular plane to the best-fit circle of the glenoid containing O and the supraglenoid tubercle (S). The anterolateral corner (ALC) and posterolateral corner (PLC) of the acromion with respect to A defined the coracoacromial (CA) arch angle (α) and the CA base angle (β), with corresponding CA arch (a) and CA base length (b). The height-width-index of the glenoid was assessed as the ratio between the height (H) and width (W) of the glenoid, as determined by the diameter of the best-fit glenoid circle. (B) Best-fit planes of the coracoid pillar (green plane), acromion undersurface (blue plane), and scapular spine (red plane) in relation to the glenoid center plane (black line) defined acromial tilting (γ), scapular spine angle (δ) and coracoid pillar angle (ε), respectively. (C) Measurements as determined in the coronal plane required the superior and inferior glenoid pole to define the superior-inferior tangent to the glenoid (blue line). The angle measured in the inferolateral quadrant of the intersection between the tangent of the glenoid and the scapular axis, defined by the trigonum scapulae (TS) and O, determined glenoid inclination (ζ). The angle between the tangent to the glenoid and the line segment connecting the most lateral point of the acromion with the inferior pole of the glenoid (green line) defined the critical shoulder angle (CSA) (θ). The latter line segment in relation to the line originating from the inferior glenoid pole perpendicular to the scapular axis (grey dashed line) determined the acromial overhang angle (η). The best-fit circle to the glenoid at the level of the glenoid center plane defined the superior-inferior (SI) radius of curvature (ROC). (D) The anterior-posterior (AP) ROC was determined similarly in the AP direction of the glenoid in the sagittal plane of the glenoid. The apex (A) and base (B) of the coracoid process defined coracoid length and the angle to the glenoid center plane, labeled as the coracoid deviation angle (ι).

Glenoid inclination was measured as the angle between the line connecting the superior and inferior pole of the glenoid and the line defined by the trigonum scapulae and the origin (scapular axis), measured in the coronal plane (yz-plane).30 The angle between the most lateral edge of the acromion and the tangent between the two glenoid poles defined CSA, similar to the 3D measurement defined by Karns et al.31 Note that the measurement in the present study differed from the standard CSA measure in that we refer to the glenoid center plane whereas in general the plane of the scapula is used as a reference. The acromial overhang angle measured the lateral extension of the acromion independent from glenoid orientation by measuring the angle between the tangent connecting the most lateral edge of the acromion with the inferior glenoid pole and the line perpendicular to the scapular axis through the inferior glenoid pole. This CSA measurement was further adapted to an angle neutral for inclination (neutral CSA). Glenoid morphology was further assessed by glenoid height-width index and the radius of curvature (ROC) in the anterior-posterior (AP) and superior-inferior (SI) directions.32

Statistical Analysis

Principal component analysis was used to reduce the correspondence data to a smaller set of linearly uncorrelated components, determining the number of modes containing significant shape variation. Descriptive statistics including mean, standard deviation, and 95% confidence intervals summarized the corresponding anatomic measurements. Shapiro-Wilk tests were used to address normal distribution for all measures. To associate the clinical measures with the modes of variation, each scapula shape was expressed with a PCA mode of variation (i.e., loading vector). For each clinical measure, we trained lasso regression models on 1000 random subsets for the data with 80/20% train/testing splits. Each regression model resulted in a weight vector with all non-zero element correspond to shape parameters (loadings) that were relevant to predicting the measurement. The regularization hyperparameter that controls model sparsity was determined using cross validation. We then computed the probability of each PCA loading to be predictive of the measurement by counting the number of times it was identified to be relevant in the 1000 subsets. To determine the inter-rater reliability, two investigators (MJ, SEB) assessed each measurement independently on 15 randomly chosen scapulae. To assess the intra-rater reliability, one investigator (MJ) repeated all measurements on the same 15 scapulae two weeks later. Reliability was evaluated using intra-class correlation coefficient (ICC) and typical error of measurement (TEM). The interpretation of ICCs was as follows: <0.400, poor; 0.401 to 0.600, fair; 0.601 to 0.750, good; 0.751 to 1.000, excellent.33 Analyses were performed with SPSS Statistics, version 24.0 (SPSS Inc., Armonk, NY, USA). The level of significance was set at p ≤ 0.05.

Results

A total of 31 shoulders (16 right, 15 left) in 31 cadavers (16 male, 15 female) with an average age of 60 (range, 40 – 78), an average height of 170 cm (range, 147 – 191 cm), an average weight of 72 kg (range, 41 – 141 kg), and an average Body Mass Index of 24.6 kg/m2 (range, 16.0 – 41.7 kg/m2) were identified without pathology and were included in the study group. The first 5 modes demonstrated a significant difference in shape variation, capturing 89.7% of total variation within the population. These modes of variation, according to rank order, represented 33.0%, 32.0%, 11.8%, 9.0%, and 3.1% of the overall shape variation, respectively.

Mode 1 (33.0% of shape variation) covered size differences among the study population (Fig. 2). Variation in Mode 2 (32.0% of shape variation) was the most substantial around the acromion, representing a variation in orientation of the acromion and spina scapulae, acromion size and lateral extension of the acromion. Mode 3 (11.8% of shape variation) primarily captured variation in prominence of the superior glenoid and glenoid fossa influencing glenoid inclination and concavity of the articular surface. Mode 4 (9.0% of shape variation) represented size and orientation of the coracoid process in the plane of the glenoid and thickness of the bone, including the bony morphology influencing the pear shape of the glenoid. The differences in coracoid deviation in the sagittal plane and the CA relationship was captured in Mode 5 (3.1% of shape variation). The anatomic measures quantifying the modes of variation illustrate the values expected from comparable analysis of radiographic or 3D data sets (Table I). Normal distribution was demonstrated for all measures except for HWI and corrected coracoid length (Table I). With the exception of HWI and the corrected measures, all non-corrected clinical measures were relevant to predict at least one of five reported modes of variation (Table II, eSupplement). Reliability of all measures was interpreted as excellent with ICCs ≥ 0.765.

Figure 2:

Figure 2:

Figure 2:

Open in a new tab

The first 5 modes of variation, (A) illustrated in the plane of the glenoid and (B) in the coronal plane, represented a significant difference in shape, capturing 89.7% of variation. Shapes are presented at ±2 SD with respect to the mean. Arrows on the mean shape highlight the areas of greatest variation captured by each mode. Mode 1 (33.0% of variation) represented scaling differences. Mode 2 (32.0% of variation) demonstrated large differences around the acromion. In Mode 3 (11.8% of variation) variation in glenoid inclination and concavity of the glenoid surface was the most substantial. Mode 4 (9.0% of variation) captured primarily differences in orientation of the coracoid pillar, coracoid process size and bony prominence. Variation in deviation of the coracoid process and the resulting coracoacromial relationship were captured in Mode 5 (3.1% of variation).

Table I:

Descriptive statistics and rater reliability of the measures

Mean ± SD 95% CI Inter-rater Intra-rater TEM Distribution
Scapular Spine Angle, ° 61 ± 6 58 – 62 0.921 0.969 1.04 Parametric
Acromial Tilting, ° 49 ± 7 46 – 52 0.904 0.991 1.02 Parametric
Glenoid Inclination, ° 84 ± 4 83 – 86 0.944 0.980 0.45 Parametric
CSA, ° 34 ± 4 33 – 36 0.934 0.779 0.53 Parametric
Acromial Overhang Angle, ° 29 ± 5 27 – 31 0.944 0.980 0.45 Parametric
AP ROC, mm 58 ± 45 42 – 74 0.866 0.924 4.20 Nonparametric
SI ROC, mm 35 ± 4 34 – 37 0.874 0.919 0.66 Parametric
HWI 1.40 ± 0.096 1.36 – 1.43 0.817 0.775 0.017 Nonparametric
Coracoid Pillar Angle, ° 135 ± 7 132 – 138 0.778 0.878 1.38 Parametric
Coracoid Apex:
 Anterior (absolute), mm 27 ± 3 26 – 28 0.809 0.810 0.62 Parametric
 Anterior (corrected), radii 2.2 ± 0.3 2.1 – 2.3 0.765 0.779 0.048 Parametric
 Superior (absolute), mm 23 ± 5 21 – 25 0.949 0.984 0.45 Parametric
 Superior (corrected), radii 1.9 ± 0.4 1.7 – 2.0 0.910 0.956 0.045 Parametric
 Lateral (absolute), radii 19 ± 3 18 – 20 0.949 0.994 0.43 Parametric
 Lateral (corrected), mm 1.6 ± 0.3 1.5 – 1.7 0.943 0.992 0.036 Parametric
Coracoid Length (absolute), mm 45 ± 4 44 – 57 0.977 0.985 0.25 Parametric
Coracoid Length (corrected), radii 3.7 ± 0.3 3.5 – 3.8 0.879 0.927 0.039 Nonparametric
Coracoid Deviation Angle, ° 26 ± 4 25 – 28 0.826 0.966 0.99 Parametric
CA Arch Length (absolute), mm 40 ± 5 38 – 42 0.932 0.955 0.68 Parametric
CA Arch Length (corrected), radii 3.3 ± 0.4 3.1 – 3.4 0.895 0.926 0.053 Parametric
CA Base Length (absolute), mm 69 ± 6 67 – 71 0.941 0.947 0.64 Parametric
CA Base Length (corrected), radii 5.6 ± 0.5 5.4 – 5.8 0.891 0.912 0.071 Parametric
CA Arch Angle, ° 78 ± 7 76 – 81 0.938 0.984 0.87 Parametric
CA Base Angle, ° 101 ± 6 99 – 104 0.953 0.997 0.61 Parametric
Open in a new tab

AP: anterior-posterior, CA: coracoacromial, CSA: critical shoulder angle, HWI: Height-Width-Index, ROC: radius of curvature, SI: superior-inferior, TEM: typical error of measurement

Discussion

Using SSM, the hierarchical order of shape variation in the periarticular region of the scapula was identified. Other than size differences, the greatest variation in shape was seen around the acromion, followed by variation in prominence of the bony articular surface of the glenoid and variation of the coracoid process. Morphologic measures of the anatomy quantified the shape variation and further supported the ranking of shape variation as seen by the modes of variation. A lasso regression analysis confirmed the relevance of the non-corrected clinical measures to assess scapular shape variation from a clinical perspective.

Lateral extension of the acromion and glenoid inclination have been determined as risk factors for rotator cuff tears and glenohumeral osteoarthritis.4; 6–8 Although both have been determined as independent factors influencing pathomechanics in biomechanical studies,9; 10; 34 most proposed measures that are associated with a risk of developing shoulder pathology integrate both anatomic structures in the measurement. CSA7 and the lateral acromion angle16 combine both structures in an angular measurement, and AI5 is measured perpendicular to the tangent to the glenoid surface, influencing the assessment of lateral acromion extension indirectly. In the present study, the acromion was the most variable anatomic structure, with a shape variation comparable to scaling differences and nearly triple the contribution of glenoid morphology that influences inclination in shape variation. This was further supported by the corresponding morphologic measures, as the standard deviation of the CSA increased when the lateral extension was measured independent for inclination by use of the acromial overhang angle. Similar findings were observed by Beeler et al., who found that differences in CSA between patients with glenohumeral arthritis and cuff tear arthropathy were predominantly attributed to the lateral acromial extension, when measured on standard AP radiographs.35 Note that in our study we refer to the glenoid center plane, as this was our main reference plane, whereas in general the plane of the scapula is used as a reference. This explains the rather high CSA values found for the non-pathologic shoulders that were included in our study.

Glenoid shape is important in normal shoulder kinematics and dynamics. Peltz et al found that glenoid morphology has substantial influence on GHJ motion, with a more superiorly oriented humeral head during abduction in flatter and less conforming glenoids.11 To recreate normal kinematics and dynamics, the current axiom in surgery skews toward reconstructing the anatomy to the premorbid state.23; 25 For instance, in shoulder instability with glenoid defects, the goal is to obtain a bone graft that reconstructs the missing bone segment accurately with a radius of curvature near to native.25; 36 Mode 3 and its corresponding measurements emphasize the substantial variance in small nuances of the articular surface that potentially influence shoulder function. These are difficult to capture with current methods like templates based on the mean shape of a normal population, or idealizing the anatomy to underlying geometry. Therefore, a SSM technique is of interest, as those nuances of glenoid shape as seen in mode 3 will be captured in such an approach.25

Coracoid shape variation has been primarily studied for its use as a bone graft in shoulder instability procedures.29; 37 Yet, the position of the coracoid process might have a more important biomechanical function than generally thought. Biomechanical studies have shown that the conjoined tendon, which attaches to the coracoid process, has a stabilizing function in native glenohumeral joints and in joints undergoing reversed total shoulder arthroplasty.45, 46 Owens et al. found that the coracohumeral distance was an independent risk factor for traumatic anterior shoulder instability, with an increased risk of instability of 20% for every 1-mm increase in coracohumeral distance.20 This was further confirmed by Jacxsens et al38, who found a more medial and superior orientation of the coracoid process in patients with anterior instability as compared to non-pathologic shoulders, suggesting that a difference in position of the coracoid process and its attaching soft tissue alter the stabilizing function of the conjoined tendon in the shoulder. On the basis of the substantial shape variation around the coracoid seen in modes 4 and 5, differences in coracohumeral distance can be explained by an underlying deviation of the coracoid process. The data provided in the present study can be used as a reference for future biomechanical studies investigating this hypothesis.

The combined shape variation of the CA arch has been previously described as the so-called “delto-fulcral triangle”.47 While this concept still needs clinical and biomechanical validation, it is hypothesized that differences in force vectors of the rotator cuff and deltoid resulting from the combined anatomic variation of coracoid process and acromial roof influences the pathomechanics of degenerative pathology such as cuff tear arthropathy and glenohumeral arthritis. It is believed to be due to an imbalance of the resulting forces. Given that only non-pathologic shoulders were included in this study, the addition of pathologic shoulders might have increased the contribution of modes capturing coraco-acromial difference in the hierarchical analysis of shape variation, including modes 2 to 5.

Variation in periarticular anatomy also has clinical importance. The scapular spine and the coracoid pillar are two periarticular regions with high bone density.39; 40 These regions are targeted when placing screws into the base plate during reverse total shoulder arthroplasty, and are especially important in revision cases, but are difficult to visualize during these procedures. Since we found significant shape variation for these regions, these measures may serve as a guideline for proper screw placement aimed at the pillar. In addition, the large detected shape variation of the acromion in relation to the glenoid is important for motion capture studies of the scapula, as the posterolateral corner of the acromion is typically used as a reference landmark.41 If this landmark is used, researchers may consider implementing a correction factor for shape variation when calculating joint angles or range of motion of the GHJ relative to the actual rotation of the humeral head on the glenoid.

The present study is limited by its small sample size of cadaveric specimens. Yet, our scapulae were representative of normal healthy specimens as reported in the literature. The 6±5° glenoid inclination in our study was similar to the inclination of 5±4° found by Ghafurian et al. and 2 ± 4° by Peltz et al. using a similar technique in non-pathologic scapulae30, 11. When using the scapula as a reference plane, our CSA measurements were all within the normal range as originally described by Moor et al.7, 31 Peltz et al. also described an SI ROC of 35±6 mm, which is similar to our SI ROC of 35±4 mm11. With a HWI of 1.40 and a 95% CI interval between 1.36–1.43, our measures were similar to the HWI of 1.43 in normal scapulae as described by Iannotti et al. and underneath the pathological cutoff of 1.58 as described by Owens et al.20, 48 Our coracoid length of 45±4 mm is similar to the coracoid length of 43 mm ± 2 mm described by Saltzmann et al. and 46 ± 4 mm by Dolan et al.49, 50. The high quality models with associated clinical measures demonstrating comparable values to other data sets justify the use of this study cohort to address the aim of our study. To focus the analysis on the periarticular anatomy with sufficient resolution, the particle optimization was limited to the anatomic structures lateral of the scapular notch. This analysis, however, omitted glenoscapular relationships and corresponding measurements including glenoid version. Measurements were assessed in relation to a glenoid-centered coordinate system, including CSA which allowed a standardized assessment of the anatomy. Nonetheless, the mean values in our study differ from those reported in the literature as CSA is typically assessed on a true AP radiograph, which is based on a different viewing angle.7; 31; 42

Conclusion

Periarticular scapular anatomy was identified as highly variable in non-pathologic shoulders, with the acromion being as variable as the mode covering size differences, representing at least three times the contribution of glenoid and coracoid anatomy to total shape variation. The identified modes of variation and the corresponding measures explain the large variance in standard scapular measures across human cohorts. Moreover, the hierarchical shape variation gives us a more nuanced insight to the contribution of shape variation of the scapular periarticular anatomy to shoulder pathology.

Supplementary Material

supp info
Supp TableS2

Acknowledgements and affiliations

This study was supported by the LS Peery Discovery Program in Musculoskeletal Research (Henninger, Jacxsens), the 10th SECEC/ESSSE Research Grant 2016 (Jacxsens, Tashjian), a grant from the Biomedical Image and Data Analysis Core (BIDAC) (Henninger, Jacxsens), the Undergraduate Research Opportunities Program (UROP) (Brady), and the National Institute of General Medical Sciences of the National Institutes of Health under grant number P41 GM103545–18.

Investigation performed at the H.K. Dunn Orthopaedic Research Laboratory, University of Utah. Ethical approval for this study was exempt via the University of Utah Institutional Review Board IRB #11755, Biomechanical Testing of Orthopaedic Devices Using Decedent Tissue Models.

Funding Statement

This work was supported by the LS Peery Discovery Program in Musculoskeletal Research, the 10th SECEC/ESSSE Research Grant 2016, a grant from the Biomedical Image and Data Analysis Core (BIDAC), the Undergraduate Research Opportunities Program (UROP), and the National Institute of General Medical Sciences of the National Institutes of Health under grant number P41 GM103545-18.

References

  • 1.Kim JR, Ryu KJ, Hong IT, et al. 2012. Can a high acromion index predict rotator cuff tears? Int Orthop 36:1019–1024. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 2.Miyazaki AN, Itoi E, Sano H, et al. 2011. Comparison between the acromion index and rotator cuff tears in the Brazilian and Japanese populations. J Shoulder Elbow Surg 20:1082–1086. [DOI] [PubMed] [Google Scholar]
  • 3.Torrens C, Lopez JM, Puente I, et al. 2007. The influence of the acromial coverage index in rotator cuff tears. J Shoulder Elbow Surg 16:347–351. [DOI] [PubMed] [Google Scholar]
  • 4.Hughes RE, Bryant CR, Hall JM, et al. 2003. Glenoid inclination is associated with full-thickness rotator cuff tears. Clin Orthop Relat Res:86–91. [DOI] [PubMed] [Google Scholar]
  • 5.Nyffeler RW, Werner CM, Sukthankar A, et al. 2006. Association of a large lateral extension of the acromion with rotator cuff tears. J Bone Joint Surg Am 88:800–805. [DOI] [PubMed] [Google Scholar]
  • 6.Daggett M, Werner B, Collin P, et al. 2015. Correlation between glenoid inclination and critical shoulder angle: a radiographic and computed tomography study. J Shoulder Elbow Surg 24:1948–1953. [DOI] [PubMed] [Google Scholar]
  • 7.Moor BK, Bouaicha S, Rothenfluh DA, Sukthankar A, Gerber C. Is there an association between the individual anatomy of the scapula and the development of rotator cuff tears or osteoarthritis of the glenohumeral joint?: a radiological study of the critical shoulder angle. Bone Joint J. 2013;95-B:935–941. [DOI] [PubMed] [Google Scholar]
  • 8.Spiegl UJ, Horan MP, Smith SW, et al. 2016. The critical shoulder angle is associated with rotator cuff tears and shoulder osteoarthritis and is better assessed with radiographs over MRI. Knee Surg Sports Traumatol Arthrosc 24:2244–2251. [DOI] [PubMed] [Google Scholar]
  • 9.Gerber C, Snedeker JG, Baumgartner D, et al. 2014. Supraspinatus tendon load during abduction is dependent on the size of the critical shoulder angle: A biomechanical analysis. J Orthop Res 32:952–957. [DOI] [PubMed] [Google Scholar]
  • 10.Viehofer AF, Gerber C, Favre P, et al. 2016. A larger critical shoulder angle requires more rotator cuff activity to preserve joint stability. J Orthop Res 34:961–968. [DOI] [PubMed] [Google Scholar]
  • 11.Peltz CD, Divine G, Drake A, et al. Associations between in vivo glenohumeral joint motion and morphology. J Biomech. 2015;48: 3252–3257. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 12.Seitz AL, McClure PW, Finucane S, et al. 2011. Mechanisms of rotator cuff tendinopathy: intrinsic, extrinsic, or both? Clin Biomech (Bristol, Avon) 26:1–12. [DOI] [PubMed] [Google Scholar]
  • 13.Michener LA, McClure PW, Karduna AR. 2003. Anatomical and biomechanical mechanisms of subacromial impingement syndrome. Clin Biomech (Bristol, Avon) 18:369–379. [DOI] [PubMed] [Google Scholar]
  • 14.Zuckerman JD, Kummer FJ, Cuomo F, et al. 1992. The influence of coracoacromial arch anatomy on rotator cuff tears. J Shoulder Elbow Surg 1:4–14. [DOI] [PubMed] [Google Scholar]
  • 15.Balke M, Schmidt C, Dedy N, et al. 2013. Correlation of acromial morphology with impingement syndrome and rotator cuff tears. Acta Orthop 84:178–183. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 16.Banas MP, Miller RJ, Totterman S. 1995. Relationship between the lateral acromion angle and rotator cuff disease. J Shoulder Elbow Surg 4:454–461. [DOI] [PubMed] [Google Scholar]
  • 17.Cetinkaya M, Ataoglu MB, Ozer M, et al. 2017. Subscapularis Tendon Slip Number and Coracoid Overlap Are More Related Parameters for Subcoracoid Impingement in Subscapularis Tears: A Magnetic Resonance Imaging Comparison Study. Arthroscopy 33:734–742. [DOI] [PubMed] [Google Scholar]
  • 18.Richards DP, Burkhart SS, Campbell SE. 2005. Relation between narrowed coracohumeral distance and subscapularis tears. Arthroscopy 21:1223–1228. [DOI] [PubMed] [Google Scholar]
  • 19.Gerber C, Terrier F, Ganz R. 1985. The role of the coracoid process in the chronic impingement syndrome. J Bone Joint Surg Br 67:703–708. [DOI] [PubMed] [Google Scholar]
  • 20.Owens BD, Campbell SE, Cameron KL. Risk factors for anterior glenohumeral instability. Am J Sports Med. 2014;42:2591–2596. [DOI] [PubMed] [Google Scholar]
  • 21.Harris MD, Datar M, Whitaker RT, et al. 2013. Statistical shape modeling of cam femoroacetabular impingement. J Orthop Res 31:1620–1626. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 22.Atkins PR, Elhabian SY, Agrawal P, et al. 2017. Quantitative comparison of cortical bone thickness using correspondence-based shape modeling in patients with cam femoroacetabular impingement. J Orthop Res 35:1743–1753. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 23.Vlachopoulos L, Luthi M, Carrillo F, et al. 2018. Restoration of the Patient-Specific Anatomy of the Proximal and Distal Parts of the Humerus: Statistical Shape Modeling Versus Contralateral Registration Method. J Bone Joint Surg Am 100:e50. [DOI] [PubMed] [Google Scholar]
  • 24.Poltaretskyi S, Chaoui J, Mayya M, et al. 2017. Prediction of the pre-morbid 3D anatomy of the proximal humerus based on statistical shape modelling. Bone Joint J 99-B:927–933. [DOI] [PubMed] [Google Scholar]
  • 25.Plessers K, Vanden Berghe P, Van Dijck C, et al. 2018. Virtual reconstruction of glenoid bone defects using a statistical shape model. J Shoulder Elbow Surg 27:160–166. [DOI] [PubMed] [Google Scholar]
  • 26.Verstraeten TR, Deschepper E, Jacxsens M, et al. 2013. Determination of a reference system for the three-dimensional study of the glenohumeral relationship. Skeletal Radiol 42:1061–1071. [DOI] [PubMed] [Google Scholar]
  • 27.Cates J, Fletcher PT, Styner M, et al. 2007. Shape modeling and analysis with entropy-based particle systems. Inf Process Med Imaging 20:333–345. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 28.Cates J, Elhabian S, Whitaker R. 2017. Chapter 10 - ShapeWorks: Particle-Based Shape Correspondence and Visualization Software. In: Zheng G, Li S, Székely G editors. Statistical Shape and Deformation Analysis: Academic Press; pp. 257–298. [Google Scholar]
  • 29.Chahla J, Marchetti DC, Moatshe G, et al. 2018. Quantitative Assessment of the Coracoacromial and the Coracoclavicular Ligaments With 3-Dimensional Mapping of the Coracoid Process Anatomy: A Cadaveric Study of Surgically Relevant Structures. Arthroscopy 34:1403–1411. [DOI] [PubMed] [Google Scholar]
  • 30.Ghafurian S, Galdi B, Bastian S, Tan V, Li K. Computerized 3D morphological analysis of glenoid orientation. J Orthop Res. 2016;34:692–698. [DOI] [PubMed] [Google Scholar]
  • 31.Karns MR, Jacxsens M, Uffmann WJ, Todd DC, Henninger HB, Burks RT. The critical acromial point: the anatomic location of the lateral acromion in the critical shoulder angle. J Shoulder Elbow Surg. 2018;27:151–159. [DOI] [PubMed] [Google Scholar]
  • 32.Peltz CD, Zauel R, Ramo N, et al. 2015. Differences in glenohumeral joint morphology between patients with anterior shoulder instability and healthy, uninjured volunteers. J Shoulder Elbow Surg 24:1014–1020. [DOI] [PubMed] [Google Scholar]
  • 33.Cicchetti DV, Sparrow SA. 1981. Developing criteria for establishing interrater reliability of specific items: applications to assessment of adaptive behavior. Am J Ment Defic 86:127–137. [PubMed] [Google Scholar]
  • 34.Moor BK, Kuster R, Osterhoff G, et al. 2016. Inclination-dependent changes of the critical shoulder angle significantly influence superior glenohumeral joint stability. Clin Biomech (Bristol, Avon) 32:268–273. [DOI] [PubMed] [Google Scholar]
  • 35.Beeler S, Hasler A, Gotschi T, et al. 2019. Critical shoulder angle: Acromial coverage is more relevant than glenoid inclination. J Orthop Res 37:205–210. [DOI] [PubMed] [Google Scholar]
  • 36.Willemot LB, Akbari-Shandiz M, Sanchez-Sotelo J, et al. 2017. Restoration of Articular Geometry Using Current Graft Options for Large Glenoid Bone Defects in Anterior Shoulder Instability. Arthroscopy 33:1661–1669. [DOI] [PubMed] [Google Scholar]
  • 37.Terra BB, Ejnisman B, de Figueiredo EA, et al. 2013. Anatomic study of the coracoid process: safety margin and practical implications. Arthroscopy 29:25–30. [DOI] [PubMed] [Google Scholar]
  • 38.Jacxsens M, Elhabian SY, Brady SE, et al. 2019. Coracoacromial morphology: a contributor to recurrent traumatic anterior glenohumeral instability? J Shoulder Elbow Surg. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 39.Karelse A, Kegels L, De Wilde L. 2007. The pillars of the scapula. Clin Anat 20:392–399. [DOI] [PubMed] [Google Scholar]
  • 40.DiStefano JG, Park AY, Nguyen TQ, et al. 2011. Optimal screw placement for base plate fixation in reverse total shoulder arthroplasty. J Shoulder Elbow Surg 20:467–476. [DOI] [PubMed] [Google Scholar]
  • 41.Wu G, van der Helm FC, Veeger HE, et al. 2005. ISB recommendation on definitions of joint coordinate systems of various joints for the reporting of human joint motion--Part II: shoulder, elbow, wrist and hand. J Biomech 38:981–992. [DOI] [PubMed] [Google Scholar]
  • 42.Suter T, Gerber Popp A, Zhang Y, et al. 2015. The influence of radiographic viewing perspective and demographics on the critical shoulder angle. J Shoulder Elbow Surg 24:e149–158. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 43.Goparaju A, Csecs I, Morris A, et al. On the evaluation and validation of off-the-shelf statistical shape modeling tools: a clinical application. shape in medical imaging: international workshop, ShapeMI 2018, held in conjunction with MICCAI 2018, Granada, Spain, September 20, 2018 Proceedings International Workshop on Shape in Medical Imaging; 2018;11167:14–27. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 44.Munsell BC, Dalal P, Wang S. Evaluating shape correspondence for statistical shape analysis: a benchmark study. IEEE Trans Pattern Analy Mach Intell. 2008;30:2023–2039. [DOI] [PubMed] [Google Scholar]
  • 45.Giles JW, Boons HW, Ferreira LM, et al. The effect of the conjoined tendon of the short head of the biceps and coracobrachialis on shoulder stability and kinematics during in-vitro simulation. J Biomech. 2011;44:1192–1195. [DOI] [PubMed] [Google Scholar]
  • 46.Pastor MF, Ferle M, Hagenah J, et al. The stabilization effect of the conjoint tendon in reverse total shoulder arthroplasty. Clin Biomech (Bristol, Avon). 2019;63:179–184. [DOI] [PubMed] [Google Scholar]
  • 47.Naidoo N, Lazarus L, Satyapal KS, et al. The morphometric anatomy of the delto-fulcral triangle: A 3D CT-based reconstruction study. J Orthop. 2017;14:62–67. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 48.Iannotti JP, Gabriel JP, Schneck SL, et al. The normal glenohumeral relationships. An anatomical study of one hundred and forty shoulders. J Bone Joint Surg Am. 1992;74:491–500. [PubMed] [Google Scholar]
  • 49.Salzmann GM, Paul J, Sandmann GH, et al. The coracoidal insertion of the coracoclavicular ligaments: an anatomic study. Am J Sports Med. 2008;36:2392–2397. [DOI] [PubMed] [Google Scholar]
  • 50.Dolan CM, Hariri S, Hart ND, et al. An anatomic study of the coracoid process as it relates to bone transfer procedures. J Shoulder Elbow Surg. 2011;20:497–501. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

supp info
NIHMS1069392-supplement-supp_info.docx (4.7MB, docx)
Supp TableS2
NIHMS1069392-supplement-Supp_TableS2.docx (17.1KB, docx)

RESOURCES