Understanding of Contemporary Regional Sea‐Level Change and the Implications for the Future

Abstract

Global sea level provides an important indicator of the state of the warming climate, but changes in regional sea level are most relevant for coastal communities around the world. With improvements to the sea‐level observing system, the knowledge of regional sea‐level change has advanced dramatically in recent years. Satellite measurements coupled with in situ observations have allowed for comprehensive study and improved understanding of the diverse set of drivers that lead to variations in sea level in space and time. Despite the advances, gaps in the understanding of contemporary sea‐level change remain and inhibit the ability to predict how the relevant processes may lead to future change. These gaps arise in part due to the complexity of the linkages between the drivers of sea‐level change. Here we review the individual processes which lead to sea‐level change and then describe how they combine and vary regionally. The intent of the paper is to provide an overview of the current state of understanding of the processes that cause regional sea‐level change and to identify and discuss limitations and uncertainty in our understanding of these processes. Areas where the lack of understanding or gaps in knowledge inhibit the ability to provide the needed information for comprehensive planning efforts are of particular focus. Finally, a goal of this paper is to highlight the role of the expanded sea‐level observation network—particularly as related to satellite observations—in the improved scientific understanding of the contributors to regional sea‐level change.

Key Points

• An overview of the current state of understanding of the processes that cause regional sea‐level change is provided

• Areas where the lack of understanding or gaps in knowledge inhibit the ability to assess future sea‐level change are discussed

• The role of the expanded sea‐level observation network in improving our understanding of sea‐level change is highlighted

1. Introduction

Global mean sea level (GMSL) is an important indicator of a warming climate (Church & White, 2011; Milne et al., 2009; Stammer et al., 2013), but changes in regional sea level are most relevant to coastal communities around the world (Kopp et al., 2015; Nicholls, 2011; Woodworth et al., 2019). The regional variability of the processes driving sea‐level change (SLC), along with their uncertainties and relative importance over different time scales, pose challenges to planning efforts. Available observations of sea level show clear spatial and temporal inhomogeneity. From satellite altimeter observations covering the time period from 1993 to present, regional rates of rise can be more than double the global average in some locations while near zero at other locations (Cazenave & Llovel, 2010). Furthermore, as a result of internal variability, the pattern of linear trends in regional sea level has shifted or reversed in many regions from the first half of the altimeter record to the second (e.g., Han et al., 2017; Peyser et al., 2016; Figure 1). Over longer time periods (i.e., hundreds of years), tide gauge records also show regional differences in the rates of SLC, owing in part to the vertical motion of the land upon which the gauges sit (e.g., Church et al., 2004; Church & White, 2006; Hay et al., 2015; Kleinherenbrink et al., 2018; Santamaría‐Gómez et al., 2014, 2017; Thompson et al., 2016). Understanding and accounting for these regional differences are critical first steps in providing information that is useful for planning efforts at the coast.

Figure 1.

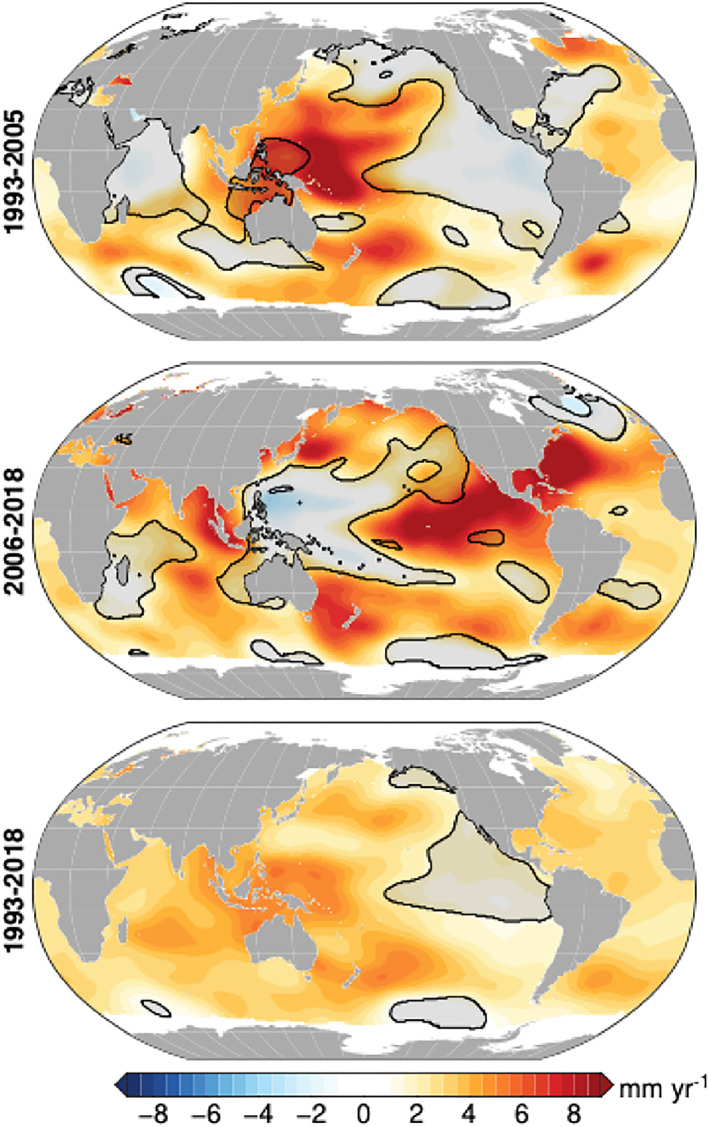
Satellite altimeter‐measured regional sea‐level trend patterns from (top) 1993–2005, (middle) 2006–2018, and (bottom) 1993–2018. Black contours and gray shading denote areas where the estimated trend is not significant at the 95% confidence level.

Due in large part to improvements in the sea‐level observing system, the processes contributing to recent SLC are now well known. The uncertainty in the budget of GMSL rise over the last decade has been reduced (Cazenave et al., 2018), allowing for an assessment of the relative contributions of different processes that are important on global scales. While more challenging on regional levels, satellite observations, along with in situ measurements, have also led to a dramatically improved understanding of the processes causing regional differences in SLC. Fundamentally, the drivers that dominantly impact GMSL have a regional signature, and no process will result in a change that is uniform across the ocean (Milne et al., 2009; Stammer et al., 2013). Similarly, no contributor to SLC is constant in time, and the time scales upon which the processes vary can differ dramatically. Separating the contributors temporally and geographically can be useful when considering a particular planning horizon, although the range of variability inherent to the individual contributors can make this difficult. Additionally, it is the combined impact of several factors operating on these different scales that is of direct importance.

The causes of global and regional SLC have been the focus of recent review papers, with regional change most comprehensively discussed and summarized in Stammer et al. (2013), Kopp et al. (2015), and Slangen et al. (2017). The understanding of these processes has progressed in recent years, and the outstanding gaps in knowledge and remaining uncertainties have shifted accordingly. The intent of the present paper is to provide an overview and update of the current state of understanding of the processes that cause regional SLC and to identify and discuss limitations and uncertainty in our understanding of these processes. Although the focus is on contemporary SLC, we do include discussion of projections of future SLC. In particular, we are concerned with areas where lack of understanding or gaps in knowledge inhibit comprehensive planning efforts at the regional level. While we do not make explicit connections to planning efforts, we expect that a detailed discussion of uncertainties could be useful to those translating science into actionable plans (e.g., Horton et al., 2018). This paper is a resource for those interested in particular aspects of regional SLC by giving a detailed presentation of the most recent estimates of their contributions and a discussion of where improvement may be made in the coming years. Finally, a goal of this paper is to highlight the potential role of the expanded sea‐level observation network–particularly as related to satellites—to understanding the contributors to regional SLC.

This paper is organized according to the individual processes of regional relative SLC, with each process covered in a section. In section 2, we provide a brief summary of how the contributors to regional sea level are separated and we present definitions for the terminology adopted in the remainder of the paper. Sections 3 through 8 discuss the individual processes contributing to regional SLC, with each section broken into two components: (1) a summary of the current state of knowledge, and (2) an overview of current limitations or areas of uncertainty and a discussion of where progress will likely be made in the coming years. In section 9, we summarize advances toward overcoming these limitations or reducing uncertainties that may be expected through recent and future additions to the sea‐level observational network, with particular emphasis on satellite‐based observations.

2. Processes Contributing to Regional SLC

As we discuss in the sections to follow, changes in sea level arise from a diverse set of physical processes. As a result, scientists from a range of disciplines are working on different questions related to sea level. The need to address the impacts of ongoing and future SLC, along with associated policy considerations, further increases the breadth of those studying or interested in SLC. This diversity and broad interest have led to inconsistency in sea‐level terminology that can hinder progress in research, communication, and policy. To address this issue, Gregory et al. (2019) have provided guidelines and clearly defined terminology for discussing SLC. In Gregory et al. (2019), SLC refers to the geocentric SLC, specifically the change in the height of sea level with respect to the terrestrial reference frame. When including the movement of the land at the coast, the phrase relative SLC is used, which is the change in the height of the mean sea surface relative to the solid surface, and thus includes the effects of vertical land motion (VLM). Given that relative SLC encompasses both geocentric SLC and VLM, and to simplify the discussion in this paper, we have chosen to use SLC to refer to changes in relative sea level for the remainder of this paper. The definition of spatial scales is separated by regional and global. The term “regional” is used to refer to processes that are considered properties of regions, with spatial of hundreds of kilometers and less. Unless specified, this includes local changes that occur at a specific geographic location. Processes are said to be of “global” scale if they contribute to variability in GMSL. The global mean refers specifically to the area‐weighted mean of SLC for the entire connected surface of the ocean.

There are several ways to separate and distinguish between the different processes contributing to regional SLC. Here, we separate the contributors into six different sections. Regional and global SLC associated with ice mass changes is divided into contributions from ice sheets (section 3) and contributions from glaciers (section 4), recognizing that the observational and measurement considerations can differ between the two. Further changes arising from variability in land water storage are presented in a separate section (section 5). Each of these three contributors are discussed first in terms of their impact on GMSL, and then in terms of their regional signature through changes in Earth Gravitation, Rotation, and Deformation (GRD), caused by redistributions of land ice and water (discussed in more detail below). The primary intent of this paper is to discuss regional SLC, but the magnitude of the regional contributions of these factors is related to the size of their GMSL contribution. These three contributors are also intentionally covered first due to the similarity of the mechanism that impacts regional SLC. Regional SLC associated with steric variability and ocean dynamics (also referred to as sterodynamic SLC) is combined into a single discussion (section 6), which includes both natural and anthropogenic contributions. This section also covers dynamic SLC that may occur as a result of freshwater input into the ocean associated with the contributors in sections 3 through 5. Given its large contribution to the SLC at the coast, a section is included on VLM, covering a range of temporal and spatial scales (section 7). Finally, as the goal here is to cover a wide range of time scales that impact regional and local SLC, a section on higher‐frequency variability is provided that includes variations in sea level associated with astronomic tides, storm surges, ocean swell, wave setup, and wave run‐up (section 8).

We use the term sea level in this paper to refer to both the lower‐frequency variations described in sections 3 through 6, and the higher‐frequency variations in section 8. Pugh and Woodworth (2014) define sea level as the sum of four main components: mean sea level, astronomical tides, a meteorological component, and waves. Using this description, sections 3 through 6 largely discuss changes in mean sea level, while section 8 covers the other higher‐frequency components. As a summary of the contributing factors covered in this paper, Table 1 provides an overview of the relevant time scales of each process in addition to the magnitude of its associated contribution on a yearly basis. One of the main takeaways from this breakdown is the wide range of time scales and subcomponents associated with each factor, and the degree to which each needs to be accounted for within any particular time frame of interest.

Table 1.

Components of Regional Sea‐Level Rise Covered in This Paper, Along With Their Relevant Time Scales and Potential Magnitude

Component	Dominant temporal scales	Potential magnitude (yearly)
Ice sheets	years to centuries	millimeters to centimeters
Glaciers (outside of ice sheets)	months to centuries	millimeters to centimeters
Steric and dynamic sea‐level change	months to decades	millimeters to meters
Land water storage	months to decades	millimeters to centimeters
High‐frequency water level variability	minutes to years	centimeters to meters
Solid earth deformation/vertical land motion	years to centuries	millimeters to meters

3. Contributions From Ice Sheets

3.1. Current State of Knowledge

Using measurements from the joint NASA (US) /DLR (Germany) Gravity Recovery and Climate Experiment (GRACE) twin satellite mission, the Greenland and Antarctic Ice Sheets lost mass and collectively contributed around 1.17 ± 0.17 mm yr⁻¹ to GMSL (Figure 2) from 2002 to 2017, about one third of the total GMSL rise (Dieng et al., 2017). This rate has been steadily increasing since the 1990s (Bamber et al., 2018). The Greenland Ice Sheet holds enough water to raise GMSL by 7.4 m, while the Antarctic Ice Sheet has the potential to increase GMSL by 58 m (Fretwell et al., 2013; Morlighem et al., 2017). Although both ice sheets are currently losing mass, they do so at different rates via different mechanisms. The Antarctic Ice Sheet mass loss has increased threefold from 2002–2007 (0.2 ± 0.1 mm yr⁻¹ sea‐level equivalent) to 2012–2017 (0.6 ± 0.1 mm yr⁻¹) (Shepherd et al., 2018) and is mostly attributed to an increase in ice sheet discharge from glacier acceleration in West Antarctica (Gardner et al., 2018; Mouginot et al., 2014; Rignot et al., 2011). This increase is driven by a combination of an intrinsic geometric instability associated with marine‐based ice sheets grounded on bedrock that deepens toward the center of the ice sheet and changes in the availability of warm, circumpolar deep water under floating ice shelves due to decadal atmospheric variability (Jenkins et al., 2016). Warm ocean water acts in tandem with atmospheric warming to thin and break up floating ice shelves (Khazendar et al., 2016 ; Liu et al., 2015 ; Paolo et al., 2015), leading to acceleration and retreat of the glaciers they buttress (Shepherd et al., 2018; Wouters et al., 2015). In contrast, the Greenland Ice Sheet mass loss is dominated by changes in surface mass balance (SMB, precipitation minus sublimation and meltwater runoff), with a smaller contribution caused by increased discharge from marine terminating outlet glaciers (Enderlin et al., 2014; Shepherd et al., 2018). Increase in runoff along the entire Greenland Ice Sheet margin is predominantly caused by atmospheric warming which promotes the intensification of ice sheet surface melt (Van den Broeke et al., 2016) and in turn rates of frontal (ocean) melting (Carroll et al., 2016).

Figure 2.

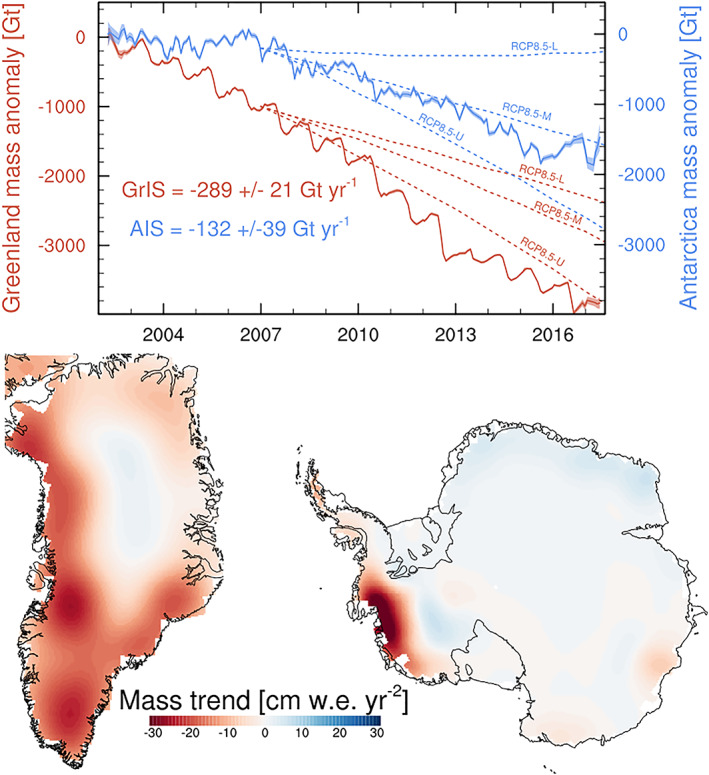
Time series and spatial patterns of ice sheet mass changes as measured by GRACE (2002–2017, Wise et al., 2018). In the upper plot, the solid lines show the GRACE mass balance from Antarctica (blue) and Greenland (red), with uncertainties contoured in the same color, and the three dotted lines show the lower, middle, and upper estimates of ice sheet mass loss in the business‐as‐usual, high‐emissions RCP8.5 future scenario (IPCC, 2013). The numbers in the upper plot give the best linear fit for each ice sheet. The lower plots show the linear trend in units of cm water equivalent per year squared over the 2002–2017 period.

Three independent observational methods are used to calculate current ice sheet mass loss rates: gravimetry, altimetry, and the input–output method (Shepherd et al., 2018). Each method has various strengths and weaknesses, with differing sensitivities to necessary corrections. Mass loss estimates from gravimetry (Velicogna & Wahr, 2006) provide the only direct measure of mass change of the ice sheets, but require a correction due to glacial isostatic adjustment (GIA) processes, which dominates the uncertainty in derived mass‐loss rates. GIA uncertainties are largest for Antarctic Ice Sheet, and while estimates vary among studies, a recent study (Caron et al., 2018) estimates Antarctic Ice Sheet GIA uncertainty to be ~40 Gt (Gigaton = 10¹² kg) per year, which is approximately 30% of the mass trend. Greenland, on the other hand, has a GIA uncertainty of ~13 Gt/yr, which is less than 5% of the Greenland Ice Sheet mass loss trend. Repeated satellite and airborne laser and radar altimetry provide detailed surface height change observations over ice sheets, but conversion from surface height to mass loss requires knowledge of spatial and temporal variability in firn density, a parameter that is poorly constrained due to sparse observations within the ice sheet interior (Pritchard et al., 2009). The input‐output method (Gardner et al., 2018; Rignot et al., 2011, 2019; Shirzaei & Bürgmann, 2012, 2018)—the only method that gives a longer time series of ice sheet mass balance (Kjeldsen et al., 2015; Rignot et al., 2019; Mouginot et al., 2019)—combines observations of ice flux across the grounding line from satellite remote sensing with modeled SMB estimates. In general, most observational time series are less than 20 years old, making the detection of mass loss acceleration in the presence of large natural variability challenging, especially in ice sheet SMB (Wouters et al., 2013). Radar altimetry from CryoSat‐2 (launched in 2010), as well as new gravimetry (GRACE Follow‐On, GRACE‐FO) and laser altimeter (ICESat‐2) missions launched in 2018, will extend the time series and provide continuous monitoring of ice sheet changes in the coming years.

We depend on a suite of numerical models to project future ice sheet changes, and these models also contribute to constraining past and present behavior. These models are traditionally used in a stand‐alone framework but are increasingly “coupled” to represent the full spectrum of ice sheet‐climate interactions. Atmospheric (surface climate and SMB) and oceanic (e.g., temperature, salinity, circulation, sea ice) forcings to the ice sheet are supplied by a variety of climate models, which are either produced for the full globe (global circulation models and climate reanalysis) or spatially limited to one particular ice sheet and surroundings (regional climate models). While circulation models historically focused on coupled ocean‐land‐atmosphere processes, modern earth system models also include the carbon cycle through dynamic atmospheric chemistry, as well as forcing of the ocean and atmosphere by the ice sheets. Regional climate models have become a preferred tool in representing ice sheet surface climate and SMB because they incorporate surface energy and snow hydrology processes and have the spatial resolutions (~5 km) necessary to accurately model the Greenland Ice Sheet and individual Antarctic Ice Sheet basins (Agosta et al., 2019; Lenaerts et al., 2017; Noël et al., 2018; Van Wessem et al., 2018), often with steep topographic slopes around ice sheet margins. However, the accuracy of any regional climate model depends on the quality of the atmospheric forcing at the model domain boundaries, and observations necessary to evaluate climate and SMB over extensive areas of northern Greenland and Antarctica are lacking.

Given geometric information, and provided appropriate atmospheric and oceanic input, ice sheet models represent the gravity‐driven flow of solid ice, from the ice divide to the floating ice shelves. Recent model development has focused on improving the representation of grounding line migration (Pattyn et al., 2012, 2013; Seroussi et al., 2014; Seroussi & Morlighem, 2018), ice front calving (Bondzio et al., 2018; Morlighem et al., 2016; Parizek et al., 2019 ; Todd et al., 2018) and the initial state of ice sheet models (Goelzer et al., 2018). In addition, models that couple ice sheet dynamics and gravitationally self‐consistent SLCs are being developed (e.g., Gomez et al., 2015) and have shown that the coupling may play an important role in ice sheet stability (Gomez et al., 2018; Larour et al., 2019). Ice properties that cannot be directly measured (e.g., basal sliding coefficient, ice shelf rheology, and damage) are now estimated using data assimilation of ice surface velocity (Arthern et al., 2015; Borstad et al., 2012; Khazendar et al., 2015; Morlighem et al., 2010). Pattyn (2017) and Goelzer et al. (2017) review the recent advances in modeling the Antarctic and Greenland ice sheets, respectively.

The relation between ice sheets and climate is defined by a two‐way connection: While ice sheets respond to atmospheric and oceanic conditions, they also influence the surrounding climate, for example, via the discharge of freshwater into oceans (Bronselaer et al., 2018 ; Schloesser et al., 2019) and changes in topographic geometries (e.g., Fyke et al., 2018). To this end, the ice sheet modeling community has increasingly focused on simulations that are fully coupled to climate models. The ongoing intercomparison of climate models (Sixth Coupled Model Intercomparison Project; CMIP6) includes several models that couple to dynamical ice sheet models for the first time (Nowicki et al., 2016). The initial development has been associated with atmosphere/ice sheet coupling over the Greenland Ice Sheet (e.g., Lipscomb et al., 2013). Major, ongoing challenges of such models include matching the temporal and spatial scales of the ice sheet model with the global models, providing accurate initial conditions for the ice sheet model, and allowing for the variable extent of the ice‐covered surface. Initial improvements have been made in the representation of SMB in earth system models guided by lessons from regional climate models (e.g., Vizcaíno et al., 2013). Advances in the coupling of ocean and ice sheet models (e.g., Goldberg et al., 2018) will continue to improve our ability to model the Antarctic Ice Sheet, particularly in West Antarctica, where oceanic forcings are likely to play a pivotal role in future ice sheet mass loss. Recent studies have demonstrated the impact of ice‐ocean coupling on such sub‐ice‐shelf melt rates and grounding line migration (Golledge et al., 2019; Jordan et al., 2017; Seroussi et al., 2017).

The ice‐sheet mass loss to the ocean strongly influences regional sea level, as associated changes in Earth's GRD responses dictate the spatial distribution of water across the global ocean (Farrell & Clark, 1976; Milne & Mitrovica, 1998; Mitrovica et al., 2001). These so‐called “sea‐level fingerprints” are crucial to determining regional SLC (Figures 3a and 3b). In general, mass loss causes a sea level fall in the near field, a reduced sea‐level rise at intermediate distances, and a greater‐than‐global‐mean sea‐level rise at larger distances. Sea‐level fingerprints can be computed for specific portions of ice sheets, enabling accurately quantified sensitivities of basin‐scale ice mass loss to local sea‐level rise at any coastal cities. The collapse of Petermann Glacier in Greenland, for example, would lead to 38% lower sea‐level rise at New York and 20% higher sea‐level rise at Tokyo relative to the global mean (Larour et al., 2017; Mitrovica et al., 2018). Estimating the current and projecting future contributions from the two ice sheets—including spatial variability in the contribution across each ice sheet—is thus critical to understanding regional SLC. Updated assessments of the regional impact on coastal cities will continue to be made as our understanding of mass loss from ice sheets advances and projections are improved.

Figure 3.

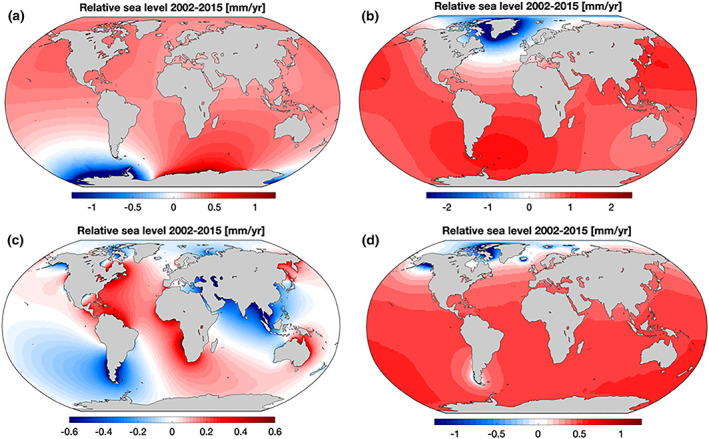
Contribution to relative sea‐level rise (mm/year) from 2002 to 2015 from (a) Antarctica Ice Sheet mass loss, (b) Greenland Ice Sheet mass loss, (c) terrestrial water storage variability, and (d) glacier mass loss. Adapted from Adhikari and Ivins (2016).

3.2. Uncertainties and Future Outlook

While significant progress has been made in recent years as described above, estimating future ice sheet contributions to sea level relies on models, which contain large uncertainties. These uncertainties exist in every stage of modeling ice sheets in future climates, from fundamental understanding of ice sheet physical processes (e.g., DeConto & Pollard, 2016), initialization (Goelzer et al., 2018), parameter, and boundary condition choices (e.g., Larour et al., 2012; Nias et al., 2016; Schlegel et al., 2015), to the quality of atmospheric and ocean forcings, which in turn rely on climate models with all their associated uncertainties (Nowicki & Seroussi, 2018; Robel et al., 2019); all of these uncertainties can limit the quality of model projections. For example, climate model‐driven projections reported in the Fifth Assessment Report of the Intergovernmental Panel on Climate Change (IPCC) underestimated mass loss from 2006 to present, especially in the case of the Greenland Ice Sheet, including in the strongest warming (business‐as‐usual) RCP8.5 scenarios (Figure 2). This example highlights the need for extensive evaluation of present‐day model performance, careful selection of model forcing, and, on the longer term, a focus on earth system model development to improve high‐latitude atmospheric (e.g., clouds, radiation, precipitation) and oceanic processes, horizontal resolution and/or statistical downscaling (Lenaerts et al., 2019). Multimodel ensembles and intercomparisons (e.g., the Ice Sheet Model Intercomparison Project, ISMIP6; Nowicki et al., 2016) will also provide critical contributions to uncertainty quantification.

Ice sheet contributions are especially important when planning for future SLC (e.g., Garner & Keller, 2018; Oppenheimer & Alley, 2016; Sriver et al., 2018; Sweet et al., 2017). The research community is increasingly employing probabilistic approaches when making projections of future sea‐level contributions from ice sheets (Edwards et al., 2019; Little et al., 2013; Ritz et al., 2015; Schlegel et al., 2018), which are necessary for holistic probabilistic projections of sea‐level rise (e.g., Kopp et al., 2014, 2017; Perrette et al., 2013, Slangen et al., 2014). Probabilistic projections, however, are subject to the same limitations as the models or structured expert judgements (e.g., Bamber & Aspinall, 2013; Bamber et al., 2019) used to construct them. There is some utility in turning to past analogs of high sea‐level contributions from ice sheets (e.g., the last interglacial or Pliocene) to calibrate ice sheet models and improve probabilistic projections (e.g., Edwards et al., 2019), but these too are impacted by prior model uncertainties, as well as by the uncertainties in paleo reconstructions. Furthermore, the efficacy of using modern ice sheet trends for constraining future contributions remains an active area of research (Kopp et al., 2017). As these deep uncertainties in ice sheet contributions are elucidated and probabilistic projections continue to improve, they will inform policy decisions that are based on projected probabilities that regional‐ and global‐scale sea levels will exceed critical levels (e.g., Bakker et al., 2017; Buchanan et al., 2016; Rasmussen et al., 2018; Sweet et al., 2017).

As ice sheet models improve in their resolution, initialization procedures, and process implementation, they become increasingly reliant on observations to both force their behavior and validate their performance. Accurate reproduction of ice sheet dynamics, especially near grounding lines, requires high‐resolution surface and bed topography (Aschwanden et al., 2016, 2019; Morlighem et al., 2014; Nias et al., 2018), estimates of basal shear stress (Parizek et al., 2013), and sub‐ice shelf bathymetry (Schodlok et al., 2012). Geometric constraints on outlet glacier dynamics have improved dramatically in recent years (e.g., Greenbaum et al., 2015; Morlighem et al., 2017; Vaughan et al., 2012), but technological advancements (e.g., radar tomography; Al‐Ibadi et al., 2018) and geophysical methods development (toward observational validation of subsurface model parameters such as basal shear stress (Brisbourne et al., 2017), temperature (MacGregor et al., 2015; Schroeder et al., 2016), and englacial velocity (Holschuh et al., 2017, 2019; Leysinger Vieli et al., 2007) could drive significant improvement in model projections. Importantly, new aerogeophysical campaigns and satellite missions will be required to collect data optimized for these new techniques, as well as to fill gaps in existing subsurface observations. Ice sheet model development should focus on including geophysical observations directly, and extending the data assimilation capabilities from the inclusion of snapshot surface observations to the inclusion of time series data (Goldberg & Heimbach, 2013; Larour et al., 2014) to take full advantage of the abundance of remote sensing observations now available.

4. Contributions From Glaciers

4.1. Current State of Knowledge

Glaciers other than the two large ice sheets store large volumes of fresh water that, when released, can seasonally augment river discharge particularly during warm and dry months (Huss et al., 2017; Huss & Hock, 2018; Immerzeel et al., 2010; Kaser et al., 2010) and contribute to changes in sea level as glaciers grow and shrink in response to changes in atmosphere and ocean forcing (Gardner et al., 2013; Kaser et al., 2006; Zemp et al., 2019). Globally, there are an estimated 200,000 glaciers covering an area of 706,000 km² (Randolph Glacier Inventory, Consortium 2017). If melted completely they would raise GMSL by 0.32 ± 0.08 m (Farinotti et al., 2019). Glaciers can be grouped into 19 distinct regions as defined by the Randolph Glacier Inventory (Pfeffer et al., 2014). Of these 19 regions, only 12 have the capacity to change sea level by ≳5 mm: six Arctic island regions, three High Mountain Asia regions, Alaska, South America, and the Antarctic islands. These 12 regions account for 99% of the total glacier volume. Relative to the much larger Antarctic and Greenland ice sheets, glaciers are typically located in more temperate environments with a large fraction of their surface area subjected to seasonal melting. This characteristic makes glaciers particularly sensitive to changes in climate. As with the ice sheet contributions discussed in the previous section, many of the estimates provided here are of the contributions of glaciers to GMSL. However, the specific geographic location of loss leads to regional variability in the resulting SLC. This spatial variability can be conveyed in sea‐level fingerprints for the glaciers, computed similarly to those for the ice sheets (e.g., Adhikari et al., 2016; Slangen et al., 2014; Figure 3).

Over the last decade, nearly all glacierized regions on Earth have been in a state of mass loss, contributing 0.71 ± 0.08 mm yr⁻¹ to GMSL over the period 2003–2009 (Gardner et al., 2013) which corresponds to 29 ± 13% of the observed GMSL rise during that period. Reager et al. (2016) extended the record of glacier mass change through November 2014 for all regions excluding High Mountain Asia and those surrounding the Greenland and Antarctic ice sheets. They found rates of loss to be ~17% higher for the 2002–2014 period than the 2003–2009 period due to accelerated rates of loss from Alaska, Canadian Arctic, and the Southern Andes. Arctic and Alaskan glaciers accounted for 75% of all glacier contributions to sea‐level rise over the 2002–2014 period (Reager et al., 2016), assuming constant 2003–2009 rates of loss for High Mountain Asia, Greenland, and Antarctic glaciers (Gardner et al., 2013). Excluding Greenland and Antarctic glaciers, Wouters et al. (2019) suggest that the rate of glacier loss over the longer 2002–2016 period (Figure 4) has returned to the 2003–2009 rate by Gardner et al. (2013). Extrapolating glaciological and geodetic data from 450 and greater than 19,000 glaciers, respectively, Zemp et al. (2019) estimated a glacier sea‐level contribution of 0.92 ± 0.39 mm yr⁻¹ over the period 2006–2016.

Figure 4.

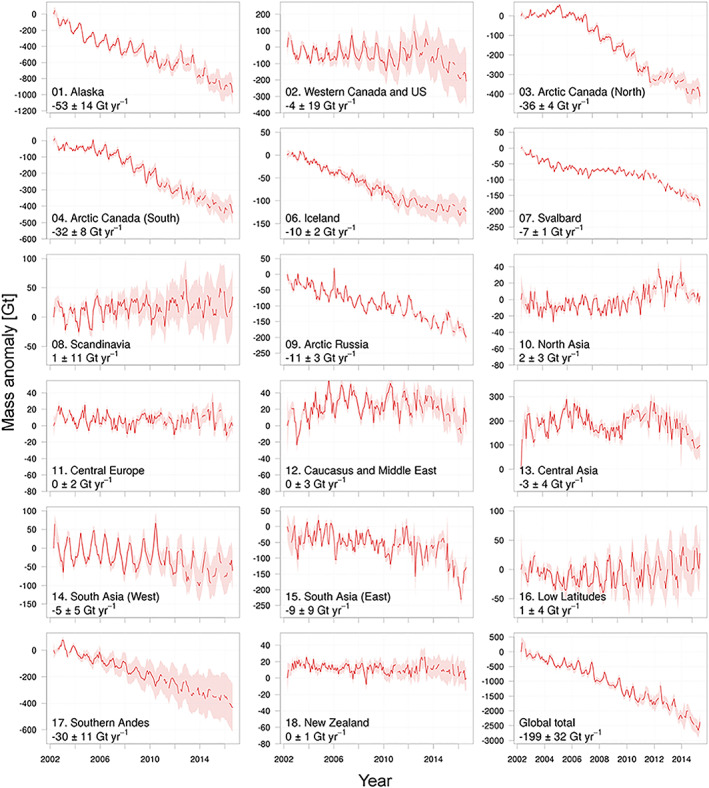
Time series of cumulative mass anomalies from GRACE for all primary glacier regions of the Randolph Glacier Inventory, except the Greenland and Antarctic periphery, covering the time period from 2002 to 2017. From Wouters et al. (2019).

These rates of loss are historically unprecedented in the observational record (Zemp et al., 2019) and can be attributed, to a large degree, to anthropogenic warming of the troposphere (Marzeion et al., 2014). A recent analysis of the glacier projections using up to six different glacier evolution models (Bliss et al., 2014; Hirabayashi et al., 2013; Huss & Hock, 2015; Marzeion et al., 2012; Radić & Hock, 2014; Slangen et al., 2017) forced with output from 8 to 15 general circulation models from the Coupled Model Intercomparison Project 5 (CMIP5) estimates that glaciers (including those in the Greenland and Antarctic periphery) will contribute 94 ± 25 mm to GMSL rise (mean of 46 model runs ± 1 standard deviation) over the period 2015 to 2100 under the low‐emission scenario RCP2.6, and 200 ± 44 mm (88 models runs) under the high‐emission RCP8.5 scenario (Hock et al., 2019).

The last two decades have seen significant advances in our ability to measure glacier change on global scales. Monitoring of ice height changes at low‐gradient slopes became possible in the early 1990s with the launch of conventional ocean radar altimeters. These altimeters were, however, limited in their ability to resolve volume changes of glaciers located in high‐relief regions. The launch of NASA's ICESat satellite laser altimeter, which operated from January of 2003 to October 2009, allowed glacier height changes to be routinely measured from space. Such measurements were complemented by gravity measurements collected by GRACE, which provided estimates of mass changes at larger glacier systems. Together, these satellites provided the first global picture of glacier mass change as seen from space (Gardner et al., 2013; Jacob et al., 2012; Wouters et al., 2019) and led to the identification of large spatial sampling biases in the ground monitoring network (Gardner et al., 2013). Such measurements are critical for improving our understanding of the response of glaciers to external forcing (e.g., Moholdt et al., 2012) and for calibrating/validating the models used to project future rates of loss (e.g., Huss & Hock, 2015; Marzeion et al., 2017; Radić et al., 2014).

The success of GRACE and ICESat motivated the launch of GRACE‐FO in May 2018 and ICESat‐2 four months later in September of 2018. Technological advances on ICESat‐2 allow it to continuously collect high‐precision and dense along‐track measurements (0.7 m) with a narrow illumination footprint (17 m) that is well suited to measuring glacier height changes in areas of complex topography. ICESat‐2 and GRACE‐FO will extend the time series of regional glacier mass change and provide increased detail and new insights to guide future modeling efforts. NASA also operated an airborne mission, Operation IceBridge that was designed to help bridge the nearly 9‐year gap in satellite laser altimetry between ICESat and ICESat‐2. Operation IceBridge began operations in 2009 and operated through the fall of 2019. While most Operation IceBridge data were collected over the ice sheets, data were also collected over the Canadian Arctic and Alaska. These data have provided details on the drivers of mass loss in these regions during the hiatus in satellite laser altimetry (Gardner et al., 2013; Larsen et al., 2015). In addition to satellite gravimetry and altimetry there has been a recent explosion in the use of large satellite optical imagery data sets to measure glacier elevations and velocities (Dehecq et al., 2015 ; Porter et al., 2018 ; Willis et al., 2012). Such efforts have advanced the understanding of how glacier flow responds to regional scale forcing (Dehecq et al., 2019) and provided improved detail on the mechanisms responsible for observed changes in glacier mass (Brun et al., 2017).

4.2. Uncertainties and Future Outlook

To make further progress in constraining future rates of glacier loss, efforts need to be dedicated to improving historical and present‐day estimates of global glacier mass balance, which will provide the context for recent changes as well as improved data for calibration of glacier mass balance models. A promising source of data to reconstruct glacier changes over the past 50 to 60 years is airborne and declassified satellite stereo imagery (Gardner et al., 2012; Pieczonka & Bolch, 2015). Working with such data is challenging, as they often need to be digitized and corrected for poorly known camera parameters and ground control. Further investment in automated techniques to extract high‐accuracy elevations from such data would help to accelerate their utilization. Reconstruction of long‐term (>60 year) historical patterns of glacier change can be improved through mapping of trimlines, moraine positions, and uplift rates (Glasser et al., 2011; Larsen et al., 2005). Additional analysis of existing field observations to incorporate improved inventories and knowledge of regional extrapolation methods will help reconcile remaining discrepancies between regional estimates of mass change derived from in situ data and remote sensing observations (Kaser et al., 2006; Pfeffer et al., 2014). In particular, potential biases in the location or sizes of sampled glaciers relative to the full population should be more thoroughly explored (Gardner et al., 2013).

Integration of field and remote sensing observations with model simulations is necessary to accurately project future trends in glacier contribution to sea level. Conventional field observations of mass balance at “benchmark” glaciers will remain a high priority to ensure continuity with long‐term records, since these provide unique opportunities for model calibration. Locations of long‐term monitoring sites, within the context of characterizing regional glacier behavior, should be revisited given the availability of previously unavailable satellite data. This is particularly important for large glacierized regions with steep gradients in environmental conditions. Field studies at these and other sites should be expanded to include detailed observations of surface and dynamic processes. Improved parameterization of surface albedo, which controls the dominant term in the surface radiation budget, can be achieved through studies of snow and ice crystal grain sizes (Painter et al., 2009) and the impacts of dust/black carbon (Flanner & Zender, 2006). Improved understanding of the impact of supraglacial debris on surface melt rates (Östrem, 1959) can be achieved by mapping debris cover extent (Scherler et al., 2018) and debris thickness (Kraaijenbrink et al., 2017; Rounce et al., 2018) globally. The conversion of volume to mass change in geodetic remote sensing assessments remains a large source of uncertainty (Huss, 2013) and can be better constrained through field measurements of near‐surface densification rates. Glaciers that terminate in lakes or the ocean have the potential for rapid changes through poorly understood calving mechanisms (Moholdt et al., 2012) and rates of subaqueous melt (Motyka et al., 2003; Sutherland et al., 2019) require expanded observations of ice thickness, grounding line locations and lake/fiord conditions. Finally, field programs should include observations of stream discharge where possible since this provides valuable information on the integrated water balance of glacierized watersheds.

The spatial coverage and temporal resolution of remote sensing data introduce challenges when attempting to integrate observations across regions. Community standards on how to leverage the strengths of each observation platform should be developed, building on past global estimates (Gardner et al., 2013). Large challenges remain with respect to projecting glacier mass changes on a global scale (see Radic and Hock (2014) for review). Current models typically use simple temperature‐index methods and most models exclude mass loss by calving and submarine melt (e.g., Hirabayashi et al., 2013; Huss & Hock, 2015; Marzeion et al., 2012; Radić & Hock, 2011; Slangen et al., 2012). Most models also use scaling methods and simple geometric models to account for glacier geometry changes as the mass changes. Methods for explicitly incorporating glacier ice flow adjustments to climate forcing into individual glacier models (e.g., Adhikari & Marshall, 2013) and regional scale models (e.g., Zekollari et al., 2019) should be more fully explored.

The highly variable terrain of alpine regions creates complex patterns in meteorological conditions that pose significant challenges to accurately quantifying precipitation, temperature, and other variables needed to force glacier evolution models. At present, between 20% and 50% of the uncertainty in projections of global glacier changes to the year 2100 is due to the spread in existing global circulation models (Huss & Hock, 2015). Significant improvement to model accuracy can be achieved through forcing the glacier models with global circulation model climate projections that have been downscaled from regional climate models run at the highest possible spatial resolution.

5. Contributions From Changes in Land Water Storage

5.1. Current State of Knowledge

Both human activities and natural climate variability have impacted the storage of water on the continents, including changes in river flow and evolving patterns of water transport between the global land masses, atmosphere, and oceans. These changes ultimately affect the state of global sea level, and also have a regional fingerprint that contributes to spatial variability in SLC (Figure 3c). For instance, the cumulative impoundment of river water in dams and reservoirs has reduced the outflow of water to the oceans and generated regional loading and gravitational responses (Fiedler & Conrad, 2010), while other activities, such as groundwater depletion, have caused regional changes to the water stored on land and a positive contribution to sea level (Chao et al., 2008; Church et al., 2013; Wada et al., 2012). Additionally, recent data from GRACE have shown that natural climate variability in the global water cycle perturbs the rate of SLC at shorter (interannual to decadal) time scales, which can influence closure of the global water budget over different observational periods (Cazenave et al., 2014 ; Dieng et al., 2015; Hamlington et al., 2019; Reager et al., 2016; Rietbroek et al., 2016). The effects of these two types of processes are distinct. On one hand, the net effects of anthropogenic processes such as reservoir construction (which causes a GMSL fall) and groundwater depletion (which causes a GMSL rise) have acted to decrease net global land water storage, reducing the secular trend in sea‐level rise over the past several decades (Church et al., 2013; Gregory et al., 2013; Wada et al., 2016). Alternatively, natural global water cycle variability can augment or offset GMSL rates by as much as ± 0.7 mm yr¹ for periods of a decade or shorter (Reager et al., 2016) and can vary substantially in magnitude from one decade to the next. While terrestrial land water storage changes are generally a secondary contributor in terms of magnitude to the long‐term global sea‐level trend budget, the proper accounting of both human activity and water cycle variability is necessary for accurate sea‐level budget closure across time and space scales.

A recent study by Wada et al. (2017) estimated that humans have so far captured a total of 10,416 km³ of water behind dams. This represents the equivalent of a 29 mm decrease in global mean sea level since 1900. When global dam‐building activity was at its historical highest during the years 1950 to 2000, average rate of SLC was offset by −0.51 mm yr⁻¹ due to reservoir impoundment. This process represents a first‐order contributor to the complete natural and anthropogenic sea‐level budget over the past 100 years, but the activity has now slowed substantially due to a decrease in global dam‐building activities in recent decades. However, current planning activity suggests a likely resurgence of reservoir construction for hydropower in the coming 20 years (Zarfil et al., 2014).

Groundwater depletion for human use represents the largest current secular trend in the global land water storage budget and also serves to drive much of the spatial variability in the pattern shown in Figure 3c. Data from GRACE has provided a means to monitor continental water storage and groundwater changes globally from a net mass change perspective (Jacob et al., 2012; Rodell et al., 2009; Shamsudduha et al., 2012; Strassberg et al., 2007; Tiwari et al., 2009; Voss et al., 2013). These observations offer a complement to studies applying large‐scale hydrological models to estimate groundwater declines and the combination of models with the GRACE data can be used to verify model accuracy. Wada et al. (2016) challenged the assumptions of many previous studies that all the depleted ground water ends up into the ocean by tracking the fate of groundwater used in irrigation. They estimate that only ~80% of depleted groundwater eventually flows to the ocean, while the other fraction ends up in different locations on land. They estimated a reduced contribution to GMSL ranging from 0.02 ± 0.004 mm yr⁻¹ in 1900 to 0.27 ± 0.04 mm yr⁻¹ in 2000. Next to the increase in ocean mass, land subsidence resulting from groundwater pumping in certain regions can have a large impact on relative sea‐level variability. This process is discussed in detail in section 7.

Natural changes in the interannual to decadal cycling of water can have a large effect on the rate of SLC over decadal and shorter periods (Lettenmaier & Milly, 2009; Llovel et al., 2011; Milly et al., 2003). For instance, El Niño–Southern Oscillation (ENSO)‐driven modulations of the global water cycle are important in decadal‐scale sea‐level budgets and can mask underlying secular trends in SLC (Cazenave et al., 2014; Hamlington et al., 2019). Because of this large interannual variability, substantial TWS trends are found in the GRACE record, but the sign and magnitude of this trend strongly depend on the time window over which the trend is estimated. For example, Reager et al. (2016) and Scanlon et al. (2018) find a net ocean mass loss due to TWS changes over 2002–2014 (Figure 5), while a more recent study suggests a positive contribution to GMSL (Kim et al., 2019). While this term can be large and is important in the interpretation of the sea‐level record, it is arguably the most challenging term in the land water budget to quantify. Water resource models and land surface models still struggle with simulating the total water storage changes (Scanlon et al., 2018), which is partially linked to their inability to model deep water storage changes, as it requires information on deep‐soil properties on a global scale. A recent parametrization approach has been introduced by Humphrey et al. (2017), in which a simple land water storage model is fed with precipitation estimates and trained using GRACE observations, and shows that the large TWS variability observed over the GRACE era is not the result of an unique event and similar variations have taken place throughout the twentieth century.

Figure 5.

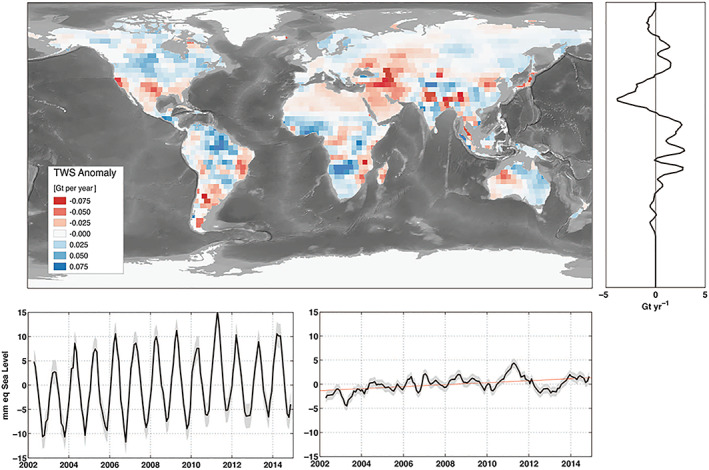
An example of trends in land water storage from GRACE observations, April 2002 to November 2014. Glaciers and ice sheets are excluded. Shown are the global map (gigatons per year), zonal trends, and full time series of land water storage (in mm yr⁻¹ SLE). Following methods details in Reager et al., (2016), GRACE shows a total gain in land water storage during the 2002–2014 period, corresponding to a sea‐level trend of −0.33 ± 0.16 mm yr⁻¹ SLE. These trends include all human‐driven and climate‐driven processes in Table 2 and can be used to close the land water budget over the study period. From Reager et al. (2016), reprinted with permission from AAAS.

5.2. Uncertainties and Future Outlook

Generally, we expect the rate of human‐driven land water storage changes to continue at current rates for several decades into the future, while the climate‐driven variability in the water cycle will respond more rapidly to transient climate conditions such as ENSO and Pacific Decadal Oscillation. However, there remain discrepancies in several of the component estimates. For many components, uncertainty due to extrapolation to a global domain and to future time periods still remains, and individual contributions likely vary substantially due to changing human and climate influences over time. Observational uncertainty in gravity‐based approaches to global and regional mass budget closure, including groundwater monitoring, are affected by uncertainties in GIA and geocenter corrections applied in these approaches (e.g., Blazquez et al., 2018).

In order to refine the accuracy of current estimates and monitor changing human and climatic influences, it is imperative to continue monitoring the terrestrial water cycle, including surface water storage and groundwater storage, from space. The GRACE‐FO mission will extend the observational record into the next decade for global mass change. Continued monitoring efforts from satellite gravimetry coupled with in situ studies will provide a longer record and allow more precise determination of uncertain terms in the global mass budget. Additionally, longer records of regional groundwater changes in response to changing water supply and demand will allow for better extrapolation of these effects into the future.

In the next decade, the availability of large ensemble simulations of Earth system models will allow for improved determination of human forcing and its influence on sea‐level contributions associated with hydrology. Continued improvements in the resolution and process representation of land surface models will also allow for better understanding of changing regional hydrology, including the inclusion of human activities and water consumption. These model developments will be supported by future observing platforms. For example, the Surface Water and Ocean Topography (SWOT) mission (Biancamaria et al., 2016) will provide the first observational estimate of global continental river discharge, thus improving our understanding of global and regional water cycles. Continued studies of terrestrial hydrology, river discharge, and the effects of river plumes on coastal ocean dynamics will deepen insight into the complex set of processes that can influence regional sea‐level variability.

6. Steric Sea‐Level and Ocean Dynamics

6.1. Current State of Knowledge

There has been a large‐scale warming of the upper 700 m of the ocean observed since the 1970s, increasing the upper ocean heat content (Abraham et al., 2013; Balmaseda et al., 2013; Boyer et al., 2016; Cheng et al., 2017; Domingues et al., 2008; Durack & Wijffels, 2010; Gleckler et al., 2016; Ishii & Kimoto, 2009; Ishii et al., 2017; Levitus et al., 2012; Lyman & Johnson, 2014; Roemmich et al., 2015; Figure 6). This warming leads to a thermosteric rise in sea level, as warm water is less dense than colder water. Changes in salinity also contribute halosteric effects to sea level (e.g., Munk, 2003) either through spatial changes in water mass properties (e.g., Llovel & Terray, 2016; Suzuki & Ishii, 2011; Volkov et al., 2017), changes in the net freshwater flux through the ocean surface (precipitation minus evaporation; Köhl et al., 2014; Llovel & Lee, 2015), inputs of glacier and ice sheet meltwater (Lorbacher et al., 2012), and river discharge (Piecuch et al., 2018). The thermosteric and halosteric effects on sea level due to a freshwater flux need to be separated for attribution purposes (Jordà & Gomis, 2013; Lowe & Gregory, 2006). From 1972 to 2008, thermosteric sea‐level rise explained roughly 50% of observed GMSL rise (Church et al., 2013; Church & White, 2011; Gregory et al., 2013) with a negligible contribution from halosteric effects. With accelerating contributions from land ice (see sections 3 and 4), that percentage has dropped to 33% since 2005, as estimated using observations from Argo profiling floats (Cazenave et al., 2018; Chambers et al., 2017).

Figure 6.

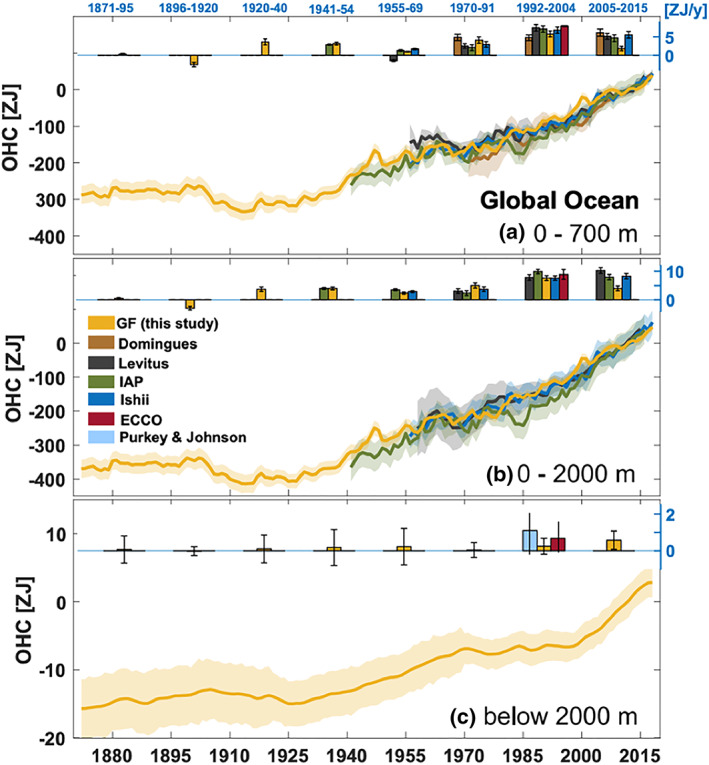
Global ocean heat content time series and trends for Green's functions and observational estimates relative to 2006–2015 for different ocean depths: (a) 0–700 m, (b) 0–2000 m, and (c) below 2000 m. From Zanna et al. (2019).

As seen in the satellite altimeter record, regional sea‐level variability can be considerably larger than the GMSL change (Figure 1). This variability is driven by the ocean's dynamic response to forcing by atmospheric variability (which itself is coupled to the ocean via heat and freshwater fluxes). For instance, on the shelf of the eastern Atlantic Ocean, low‐frequency along‐slope wind variability and dynamic SLC have been observed to be synchronous with interannual‐to‐decadal ocean circulation changes (Chafik et al., 2019). Steric SLC can result from changes in the strength and location of ocean currents, upwelling signals, and Rossby and Kelvin waves that can propagate zonally and along coastlines. For example, it has been found that the wind stress curl associated with the Pacific Decadal Oscillation explains the significant multidecadal variability that was manifest as a sea‐level rise along the Pacific coast of North America from 1993 to 2009 that was considerably smaller than the global average (Bromirski et al., 2011), while sea level in the western Pacific rose at a level 3 times higher than the global mean (Merrifield & Maltrud, 2011). Similarly, interannual variability in the trade winds influences the rate of SLC throughout the northeast Pacific (Thompson et al., 2014). Rossby waves can impinge upon the eastern seaboard of the USA, generating coastal waves that modulate the annual cycle in coastal sea level on interannual to multidecadal time scales (Calafat et al., 2018). The extent to which open‐ocean sea‐level signals are communicated to the coast is influenced by western boundary flows, frictional shelf dynamics, the latitudinal dependence of the Coriolis parameter, and details of seafloor bathymetry (e.g., Minobe et al., 2017; Wise et al., 2018, 2020).

Because the utility of observations and free‐running models is limited due to the length and span of observational coverage and inexact agreement between models and observations, tools have been developed to synthesize observations in a physical sense to further explore the mechanisms behind SLCs. Dynamically consistent ocean state estimates such as the Estimating the Circulation and Climate of the Ocean (ECCO) framework have, therefore, been heavily utilized to understand ocean heat content and steric sea‐level variability. Zanna et al. (2019) have used the ECCO framework to reconstruct ocean heat storage and transport, revealing a gain in heat content of 43.8 ± 9.1 × 10²² J (net heating of 0.49 ± 0.1 W m⁻²) since 1871, with the recent deep ocean heat content increase accelerating more quickly than the shallow ocean heat content increase (Figure 6). Their results demonstrate an active role of ocean circulation in shaping patterns of the ocean heat storage. In particular, the accelerated warming in the Atlantic basin over the past six decades can be attributed to heat convergence from changes in ocean circulation.

These results build upon previous findings using ECCO, which have analyzed drivers of ocean heat content and steric sea‐level variability over a range of time scales, but coarse (1° horizontal resolution) spatial scales. An analysis of the causes of interannual variations in steric sea level from 1993 to 2004 revealed that advection dominates in the tropical Indian and Pacific Oceans, advection by large‐scale ocean circulation and diffusion by geostrophic eddy effects are equally important in extratropical regions, and the local surface heat flux forcing is only important in a few regions like the subtropical North Atlantic Ocean (Piecuch & Ponte, 2011). Using the same output, Fukumori and Wang (2013) argued that enhanced rates of regional sea‐level rise in the western tropical Pacific Ocean have been due, in part, to anomalous air‐sea buoyancy fluxes and heat uptake. With ECCO output over a longer time period (1992 to 2010), Buckley et al. (2015) found that air‐sea heat fluxes and Ekman heat transport convergences are responsible for most of the heat content variability on all resolved (monthly to decadal) time scales in the subtropical North Atlantic Ocean, while ocean dynamics drive heat content variability on interannual time scales in the Gulf Stream region and subpolar North Atlantic Ocean. The importance of wind and buoyancy forcings as well as intrabasin and interbasin communication involved in sea‐level variability has been demonstrated by Forget and Ponte (2015) over approximately the same time period. Piecuch et al. (2017) analyzed a more recent version of ECCO, discovering that the subpolar North Atlantic Ocean cooling over 2005 to 2015 relative to 1994 to 2004 was the result of a shift in horizontal advection by the gyre. Decadal changes in the subpolar North Atlantic Ocean's circulation have been corroborated using in situ and satellite observations (Palter et al., 2016). Note, that while we focus here on ECCO as a particular example, other state estimates and ocean reanalyses are also available and can be similarly used for many of the studies discussed above.

6.2. Uncertainties and Future Outlook

Despite dramatic improvements in the sea‐level observing system in recent years, various areas of the ocean are still undersampled and this poses challenges to identifying the steric component of SLC. Although only ~13% of the ocean heat content resides in regions that are not well‐sampled by observations (Desbruyères et al., 2016; Durack et al., 2014), there is considerable bias (Garry et al., 2019) and uncertainty (Llovel et al., 2014) in this number and warming of such regions has been increasing with time (Gleckler et al., 2016). Moreover, there are few observations below 2,000 m depth, in particular (Purkey & Johnson, 2010), but analyses in regions such as the subtropical South Pacific that have sufficient observations have revealed a decade‐long intensification in ocean heat transport convergence responsible for heat accumulation (Volkov et al., 2017). To perform more global analyses, satellite altimetry is now being used to estimate the total SLC, with the mass contribution inferred from the GRACE and GRACE‐FO satellites. The difference between these two global measurements provides a reliable estimate of the steric contribution which can be independently constrained by the deep Argo program (Johnson et al., 2015; Le Reste et al., 2016). Continuation of these satellite and in situ programs will maintain long‐term monitoring of the global sea‐level budget and will elucidate the contribution and spatial variation of deep ocean warming (Llovel et al., 2014).

In the last few years several approaches have been developed which estimate ocean heat content and steric SLC using novel methods, potentially providing supplemental information to supplement incomplete in situ measurements. For example, Zhao et al. (2016) demonstrate how satellite observations of internal tides may be used to monitor ocean heat content along internal wave ray paths. This approach exploits the predictability of the tide to measure the travel time of the waves analogous to how acoustic travel time measurements have been used to infer ocean heat content (Dushaw et al., 2009; Munk & Wunsch, 1979). Tyler et al. (2017) have proposed a method to measure depth‐integrated electrical conductivity of the ocean using satellite magnetometers, and Trossman and Tyler (2019) demonstrated that there is a strong relationship between the depth‐integrated conductivity and ocean heat content on a wide range of time scales. Fasullo and Gent (2017), motivated by the initial work of Jayne et al. (2003), established a strong relationship between sea surface heights and ocean heat content in many regions of the ocean on monthly to interannual time scales. In practice, these methods remain largely exploratory and, if they prove successful, reconstruction and future monitoring of ocean heat content at every horizontal location could eventually involve either a combination of proxy‐based methods or assimilation of the proxies that provide information independent of temperature observations (e.g., Irrgang et al., 2017).

Predictions of future sea level come from a combination of observations, theories, and models with initial conditions given by state estimates such as ECCO or observational climatologies. Multimodel ensembles have been used to demonstrate that the projected patterns of future sea level are similar to the patterns that have been detected by satellite altimetry, which are largest in regions most susceptible to tropical cyclones (Fasullo & Nerem, 2018). Observations of these patterns with satellite altimetry will continue, but further improvement of the understanding of SLC in coastal regions is needed. Theory suggests that high‐resolution knowledge of coastal bathymetry is important to understand how sea level propagates from the open ocean onto shelves (Wise et al., 2018). Furthermore, the distance over which coastal trapping and offshore decay of sea level occurs is largely determined by the baroclinic Rossby deformation radius that can be directly influenced by river discharge on small spatial scales (Piecuch et al., 2018). The resolution of the data that most satellite missions provide could therefore restrict their utility in coastal inundation applications, but ICESat‐2 and SWOT, with their improved sampling near the coast, could prove to be valuable supplements to tide gauge observations for such a purpose.

7. VLM/Solid Earth Deformation

7.1. Current State of Knowledge

VLM in coastal areas can serve to exacerbate the negative impacts of SLC (Brown & Nicholls, 2015; Mazzotti et al., 2009; Nerem & Mitchum, 2002; Santamaría‐Gómez et al., 2017; Shirzaei & Bürgmann, 2018; Wöppelmann & Marcos, 2016). As subsidence can vary strongly with location it is crucial to account for both large‐scale and small‐scale processes contributing to the VLM budget. This budget is typically divided into GIA and non‐GIA components, with the latter including tectonics, and sediment and aquifer‐system compaction (Dixon et al., 2006; Frederikse et al., 2019; Meckel et al., 2006). These components impact VLM on different temporal and spatial scales, although it is their combined impact that is relevant for understanding and projecting SLC. Here, we separate the discussion into these two components of VLM. It should be noted that while observations of coastal VLM generally do not distinguish between the two, the focus here is on the specific processes leading to regional SLC.

7.1.1. GIA‐Related Vertical Land Motion

There has been more than a century of progress in our geophysical and observational understanding of GIA processes. The term GIA encompasses the GRD response of the Earth to the glacial cycles of the last ice age (Gregory et al., 2019; Milne & Mitrovica, 2008). This adjustment is global in scale, ongoing, and spatially variable, and it produces significant changes in sea level that must be removed from tide gauge and altimetry data to estimate the secular rise in GMSL due to modern climate change (e.g., Douglas et al., 2000). In regions once covered by now vanished ice sheets, for example, Canada, northeast United States, and Fennoscandia, or by larger ice sheets (e.g., Greenland), postglacial rebound of the Earth's crust leads to a fall in relative sea level that peaks at present at ~10 mm yr⁻¹. Surrounding these areas of residual crustal depression are regions of crustal uplift, and the ongoing subsidence of these so‐called peripheral bulges (e.g., both coasts of the contiguous United States) leads to an increase in the rate of SLC. It is important to note that while SLC within the “near field” of ice sheets is dominated by VLM, GIA also perturbs the local equipotential that defines the sea surface, and thus also impacts SLC. Outside these near‐field regions, changes in the height of the sea surface equipotential dominate crustal elevation changes and the processes impacting SLC include ocean siphoning, the movement of water toward zones of peripheral subsidence, and continental levering, the tilting of the crust (i.e., VLM) at continental margins due to ocean loading (Mitrovica & Milne, 2002). The net effect of these processes is a far‐field fall in sea level of up to ~0.5 mm yr⁻¹ in relatively low‐latitude ocean basins and coastal sites.

The spatial scale of the GIA signal is dependent on the viscosity of the Earth's mantle below the ice sheet, and the above discussion presents the classic view of GIA in response to melting ice sheets in cratonic regions (e.g., Laurentia, Fennoscandia). In regions characterized by anomalously low mantle viscosity (e.g., West Antarctic, Alaska, Patagonia, Iceland), the isostatic adjustment of the Earth to the last glacial cycle (which ended at ~6 ka) would be complete by the present day, and the GIA response would reflect more recent ice mass changes in response to climate events such as the Little Ice Age (LIA). A case in point is the GIA signal in coastal Alaska (Larsen et al., 2005; Tamisiea et al., 2007). In these cases, the “near field,” that is the zone of postglacial rebound and peripheral subsidence, is far more localized to the zone of ice cover.

GIA is generally distinguished from contemporary GRD effects due to ongoing changes in the mass of water stored on land as ice sheets, glaciers, and land water storage. The sea‐level patterns associated with the latter have come to be known as “sea‐level fingerprints” (Mitrovica et al., 2001). In cratonic regions, this distinction is logical given that the sea‐level response to ice mass changes is a simple superposition of an ongoing (and dominantly) viscous signal associated with ice age loading, and an elastic signal due to present‐day ice mass flux. However, in low‐viscosity regions, the distinction becomes arbitrary given that the sea‐level response at present day is sensitive to loading over a continuum of time scales during the last millennium, with viscous relaxation occurring in response to any ice mass change of decadal time scale or longer, and thus the response to changes in ice mass over the past century is not easily distinguished in a physical sense from the response due to changes associated with the LIA. Indeed, recent studies of the Earth response to ice loss in West Antarctic and the Antarctic Peninsula indicate that VLM at some sites can be dominated by viscous effects due to ice loss over the past decades to century (Nield et al., 2014; Zhao et al., 2017; Hay et al., 2017; Barletta et al., 2018).

Sea‐level fingerprints computed using elastic Earth models have a distinct and somewhat counterintuitive geometry (Farrell & Clark, 1976; Mitrovica et al., 2001). Within regions up to ~2,000 km from zones of ice melting, sea level falls as water migrates away from these areas due to the decreasing gravitational pull of the diminished ice sheet. This also impacts SLC through unloading that leads to elastic VLM. The magnitude of the sea‐level fall can reach an order of magnitude larger than (and of opposite sign to) the GMSL change associated with the melt event. At greater distances from the ice melting, sea level will rise by progressively greater amounts, and reach a magnitude 30–40% larger than the GMSL change. In regions of low viscosity, this signal is perturbed by viscous relaxation, and the geometry of the SLC (and VLM) tends move toward the viscoelastic signal associated with classic GIA.

There have been attempts to discriminate between the contributions to SLC or VLM from recent glacier/ice sheet melting and GIA using a combination of GPS and gravimetry measurements (Purcell et al., 2011; Wahr et al., 1995), multiple space‐based data sets (e.g., Wahr et al., 2000) and the geometry of the predicted responses (Spada & Galassi, 2016). Nevertheless, it is clear that the response to the full temporal range of ice mass flux must be considered in state‐of‐the‐art analyses of sea‐level data (Frederikse et al., 2018; Hamlington et al., 2018; Hay et al., 2015; Rietbroek et al., 2016). We note that while a theory for predicting gravitationally self‐consistent predictions of SLCs in response to ice mass flux is in place (Farrell & Clark, 1976; Mitrovica & Milne, 2003), applications of the theory have, with few exceptions, been based on Earth models in which viscoelastic structure varies with depth alone. Modeling efforts over the past decade are beginning to consider more realistic models with 3‐D variations in Earth structure (e.g., Hay et al., 2017; Latychev et al., 2005; Wu & van der Wal, 2003).

Space geodetic observations are responsible for tremendous advances in SLC research, including the following: (i) the determination of trends in VLM from terrestrial Global Navigation Satellite System (GNSS) stations located on bedrock (Milne et al., 2001; Blewitt et al.,2016; Figure 7), (ii) estimates of the lowest degree terms in the time varying gravity field from orbital variations of satellites (James & Ivins, 1995; Mitrovica & Peltier, 1993; Tosi et al., 2005; Yoder et al., 1983); (iii) improvements in mapping of the Earth's topography, bathymetry, and both the static and time‐varying gravity (Farr et al., 2007; Smith & Sandwell, 1997; Tamisiea et al., 2007); and (iv) the use of Interferometric Synthetic Aperture Radar (InSAR) in constraining VLM (Auriac et al., 2013). Greatly refined models of continental‐scale GIA were derived from these three data sets (e.g., Milne et al., 2001; Wahr & Davis, 2002). Over the past 15 years, the goals and requirements of the GIA community have shifted. The 2002 launch of the GRACE satellite system allowed measurement of time variations in the gravity field at length scales as short as a few hundred km. In addition, the dramatic expansion of global GNSS sites and advances in processing strategies (Blewitt et al., 2016, 2018; King et al., 2012; Wöppelmann & Marcos, 2016) have provided observations of present‐day VLM with unprecedented precision and accuracy (Figure 7).

Figure 7.

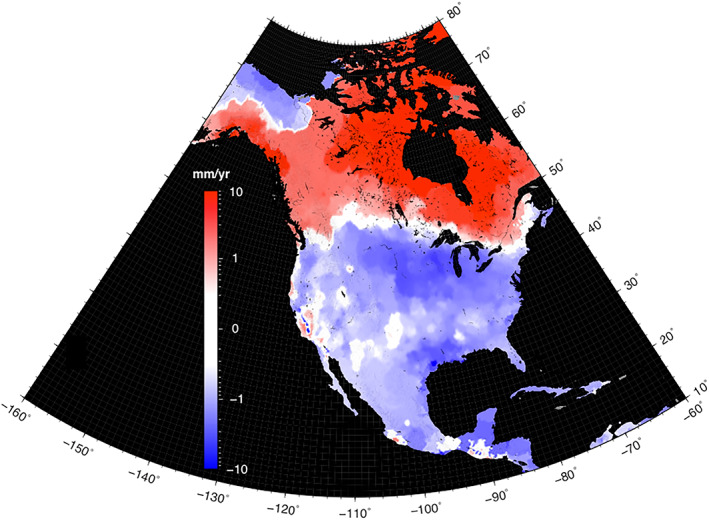
Rates of vertical land motion from GNSS observations made at over 6,000 stations across North America. VLM field is derived using MIDAS velocities in the ITRF 2014 reference frame and GPS imaging interpolation (Blewitt et al., 2018; Hammond et al., 2016). Note that logarithmic color scale is used to highlight both large and small VLM signals, with red representing upward and blue downward motion in mm/yr.

7.1.2. Non‐GIA‐Related VLM

While GIA dominates active continental‐scale VLM, the non‐GIA component of VLM results from a diverse set of processes that have widely varying geographic length scales, and these can be difficult to separate from GIA, or from each other. These processes include long‐term tectonics motions at plate boundaries (e.g., Burgette et al., 2009; Hammond et al., 2018; Mazzotti et al., 2008; Shimada & Bock, 1992), as well as coseismic and postseismic deformation (Smith‐Konter et al., 2014). Aquifer compaction produces vertical crustal deformation that is unsteady over time in response to changes in drought conditions, climate variability, and human water usage. This process has a strong anthropogenic component, as pumping of water from aquifers can cause rapid subsidence (Gatto & Carbognin, 1981; Ojha et al., 2019). In particular, aquifer depletion drives local‐scale poroelastic compaction of aquifer system resulting in a pattern of localized subsidence (Ojha et al., 2019) that is surrounded by regions of uplift due to elastic unloading of the crust (e.g., Amos et al., 2014). Some of these effects contribute to coastal VLM and thus impact SLC (Hammond et al., 2016). Contributions can also arise from sources such as volcanoes, compaction/desiccation of soils, and sediment loading in major river deltas (Brooks et al., 2007; Dixon et al., 2006; Meckel et al., 2006; Miller & Shirzaei, 2019; Nicholls & Cazenave, 2010; Stammer et al., 2013). While not only a process impacting VLM, the viscoelastic response to changes in the sediment loading could play a significant role. Sediment transport results in significant mass redistribution in many deltaic and estuarine regions, which in turn result in GRD‐induced SLCs. Several recent studies have discussed sediment transport in detail for the Dutch Wadden Sea (e.g., Bing Wang et al., 2018; Fokker et al., 2018; Van der Spek, 2018; Vermeersen et al., 2018), although the direct link between transport and the resulting GRD response has not yet been quantified for this region. Since the last glacial maximum, river routing and sediment yields vary in both space and time. The details, however, are important for present‐day VLM modeling at the coast, as the transport of sediment is important to both viscoelastic loading and unloading of the solid earth and hence, subsequent isostatic response. The modeled VLM magnitude at present‐day greatly depends on the age of the transport and the spatial contiguousness of high yield of the sediment transport during glacial transition and Holocene time (Ivins et al., 2007). Sediment isostasy produces smaller (~0.5 to 1.6 mm/yr), but more long‐lived, VLM in comparison to sediment compaction (see Karpytchev et al., 2018 and Kuchar et al., 2017 for examples from the Mississippi and Ganges‐Brahmaputra Deltas, respectively). An explicit comparison of data‐constrained model results for the Po Valley Delta suggests compaction may exceed sediment isostasy there by more than an order of magnitude (see Teatini et al., 2011 and Mey et al., 2016, for recent treatments of regional compaction and sediment isostasy in the Po Valley Delta, respectively).

Disentangling the different spatial–temporal processes that contribute to VLM is challenging. Terrestrial and spaceborne measurement capabilities have been revolutionized in recent decades and offer new and more accurate observations of VLM. GNSS networks now exist on all continents and offer precise (~2–3 mm or better) daily vertical positions and measurements of VLM rates as precise as a few tenths of a mm yr⁻¹ (Blewitt et al., 2018; Milne et al., 2001). However, GNSS networks are not homogeneously distributed, and in some coastal areas the coverage is sparse, or the data are unavailable. Complementary to GNSS, current‐day SAR missions offer global coverage at high resolution, and these images are often available free of charge (e.g., Sentinel‐1, ALOS, TerraSAR‐X, CosmoSkyMed, and the upcoming NISAR mission). Observations from InSAR are challenging in coastal regions due to the presence of vegetation and wetlands, which are responsible for a degraded interferometric signal (e.g., Zebker & Villasenor, 1992). The superposition of atmospheric propagation delays from ionospheric and tropospheric effects (e.g., Bekaert et al., 2015 Shirzaei & Bürgmann, 2012) also contribute spatially correlated errors that can be difficult to separate from localized deformation signals. In part, these problems are mitigated by the following: the consistent and frequent revisit time of ongoing SAR missions (as short as 6 days for Sentinel‐1 and 12 days for NISAR); longer wavelength systems that are less sensitive to vegetation changes; correction models informed by external data sets (e.g., Bekaert et al.,  2015 ; Doin et al., 2009); and the application of advanced time‐series InSAR processing methods (e.g., Ferretti et al., 2011; Hooper et al., 2012; Shirzaei et al., 2013; Tymofyeyeva & Fialko, 2015).

7.2. Uncertainties and Future Outlook

One of the new challenges for GIA modeling is to integrate diverse data (e.g., relative sea‐level markers, GNSS, secular gravity rates, and tide gauge records) into a properly weighted cost function for testing of global and regional models of GIA, and recent and present‐day mass changes, and subsequently providing associated uncertainty estimates. This requires dealing with data sets that range in time from as long as 150,000 years (when initializing late Quaternary ice histories) to as short as 5 years or less (when analyzing GNSS‐determined VLM). Furthermore, a main goal is to project future SLC using coupled models that fully account for viscoelastic mantle flow, gravitationally self‐consistent SLCs, and detailed ice histories during the past glacial cycle with dynamically and thermally realistic ice sheet models (Adhikari et al., 2014; Gomez et al., 2012, 2013, 2018; Konrad et al., 2015) that account for 3‐D variability in mantle structure (Gomez et al., 2018).

InSAR and GNSS are complementary in that GNSS provides long‐term stability, vector displacements, and better temporal coverage compared to InSAR, which provides high‐resolution spatial coverage. Results from one technique can be directly applicable to the other. For instance, over large scales, InSAR deformation data need to be combined with GNSS observations to precisely estimate long‐wavelength deformation signals, while GNSS observations can be used to calculate atmospheric corrections for InSAR. The InSAR measurements of surface deformation are provided in a local reference frame whereas the GNSS observations are provided in a global reference frame (i.e., with respect to the Earth's center of mass). Thus, GNSS observation can be used to transform InSAR measurements to a global reference frame suitable for studies of SLC. InSAR measurements are especially well suited to identifying localized sources of deformation such as subsidence and compaction of sediments and aquifers.

Recent studies (Yu et al., 2017, 2018) have developed correction models that combine estimates of GNSS tropospheric delay and high‐resolution weather data to correct SAR interferograms for contributions from tropospheric delay due to variations in water vapor, temperature, and pressure during the two image acquisitions. Despite their success in some cases, these models have limited spatial and temporal resolution imposed by the sparse data sets used to constrain them.

The next obvious step in such efforts is to combine the data from multi SAR sensors with GNSS observations for reliable estimation of the long‐ and short‐wavelength components of the VLM at tens of meter resolution within a global reference frame (Ojha et al., 2018; Shirzaei & Bürgmann, 2018). Further work is necessary to obtain the full covariance matrix of the VLM rate as a function of various sources of noise. Observations of the present‐day VLM rate and associated uncertainties also need to be projected forward to be compared with SLC forecasts used in flood resilience planning that are of interest to stakeholders (Shirzaei & Bürgmann, 2018). Excluding regions of low mantle viscosity (e.g., Iceland, Alaska, Patagonia, West Antarctica), the GIA contributions in VLM are quasi‐steady over several centuries, and thus a linear extrapolation might be suitable (Kopp et al., 2016). However, in those low‐viscosity regions, mass changes in the present day and over the last few decades to centuries also need to be modeled to capture viscoelastic effects that will contribute to future projections. VLM contributions due to groundwater and hydrocarbon extraction are highly nonlinear, and the residual compaction of the porous layers due to past production may last decades to centuries (Galloway & Burbey, 2011; Holzer & Galloway, 2005; Miller et al., 2017). Additionally, VLM can also occur in response to natural compaction due to sediment loading at rates between 0.1 to 1 mm yr⁻¹, which can last for 10⁵ years (Kooi & De Vries, 1998). Mechanical models accounting for the underlying physics of the VLM process are required to accurately project VLM into the future.

8. Contributions From High‐Frequency Water Level Variability

8.1. Current State of Knowledge

High‐frequency variations in sea level include those associated with astronomic tides, storm surges, and ocean waves (swell and wind waves) leading to wave setup and/or wave run‐up. Societally relevant extreme sea levels result from the combination and interaction of these phenomena with the lower‐frequency processes discussed in previous sections. High‐frequency sea‐level variability can cause impacts such as flooding, coastal erosion and sediment transport, and destruction of shoreline defenses. Because of the wide ranging economic and environmental consequences of such events, there are significant efforts to understand the superposition of the different sea‐level components, and how they are modulated by climate change and variability, individually and in combination. Table 2 lists the different phenomena discussed in this section, and Table 3 highlights some of the impacts arising from extreme sea levels. The significance of impacts is highly variable and depends on detailed site characteristics and the magnitude, duration, and frequency of the sea‐level extreme. Impacts can arise from both particularly strong storms, as well as indirect and cumulative effects of lesser‐extreme high tide flooding (Sweet et al., 2018; Wahl et al., 2018).

Table 2.

High‐Frequency Sea‐Level Phenomena

Phenomenon	Definition
Astronomical tides	fluid motion caused by the predictable orbits of the Earth and Moon
Storm surge	large‐scale motion generated by atmospheric weather systems such as hurricanes, typhoons, and extra‐tropical cyclones
Wave setup	increased coastal sea level generated by offshore breaking waves
Wind waves	waves, sometimes large, generated by wind
Ocean Swell	long‐period waves generated by remote wind or storms
Wave run‐up	wave‐driven motion at the shoreline, relevant to erosion and overtopping of coastal defenses

Table 3.

Impacts of Extreme Coastal Water Level

Impact	Main contributors
Destruction of shoreline defenses	Waves, swell, surge
Coastal erosion	Waves, swell, surge
Altered estuarine dynamics and morphodynamics	Tides
High tide flooding	Tides
Catastrophic flooding	Any and all factors combined

Knowledge of high‐frequency sea level is derived from different observing systems. Tide gauges provide the longest records of high‐frequency sea‐level variability (Woodworth et al., 2017), but they are not intended to monitor waves and wave run‐up. Wind waves and swell are monitored by the global network of—mostly coastal—wave buoys (Hemer et al., 2012), and, since 1993, satellite radar altimeters have routinely measured significant wave height (Ray & Beckley, 2012). Observations of wave run‐up are not widespread but are generally conducted for studies of coastal morphodynamics (Suanez et al., 2015) or inundation (Gallien et al., 2014).

It is useful to distinguish between statistical and dynamical descriptions of sea‐level variability, which serve complementary roles in describing, explaining, and forecasting sea‐level variability and extremes (Lowe et al., 2010). Statistical descriptions are frequently provided in the form of parametric extreme value distributions for sea‐level exceedance probabilities and return times (Buchanan et al., 2016; Wahl et al.,2017), which may be modulated by low‐frequency regional sea level (Muis et al., 2018) and other processes (Barnard et al., 2015; Wahl & Chambers, 2015). The classical statistical approach typically requires long records of high‐frequency sea‐level observations. In a recent study, Calafat and Marcos (2020) combined these observations with a Bayesian hierarchical model to compute the characteristics of sea‐level extremes for unobserved coastlines. Dynamical descriptions, through hydrodynamic models, are increasingly being used to model high‐frequency sea‐level events resulting from atmospheric forcing (Muis et al., 2016), and they may be combined with climate change scenarios to predict future sea‐level extremes (Vousdoukas et al., 2018).

One general challenge in the study of high‐frequency variability is the lack of global data sets with sufficient duration to validate either dynamic or statistical models of different high‐frequency sea‐level components (Dangendorf et al., 2016; Lowe et al., 2010). Recent work highlights the significance of the shape of extreme value distributions and the representation of uncertainty in statistical storm surge models when assessing sea‐level impacts and adaptation (Wahl et al., 2017); the need to establish consistent elevation thresholds for impact evaluation (Sweet et al., 2018); and the importance of reevaluating risk assessments as new data and analysis methods become available (Hunter et al., 2017). Site‐specific and regional studies are necessary since high‐frequency processes depend on both small‐scale geographical features and regional meteorology (Lowe et al., 2010).

Analyses of historical data have found that trends and interdecadal variability of extreme sea level are generally driven by the trend in mean sea level and large‐scale climate processes such as ENSO, rather than by trends in high‐frequency variability (Mawdsley et al., 2015; Mawdsley & Haigh, 2016; Menéndez & Woodworth, 2010; Merrifield et al., 2013; Muis et al., 2018; Wahl & Chambers, 2015). There are, however, some sites where regional changes in storm surge frequency or intensity (Reed et al., 2015; Talke et al., 2014), swell‐driven wave setup (Melet et al., 2018), and coastal morphology (de Vet et al., 2017) have impacted trends in extreme sea level. Widespread increases in the frequency of minor flooding have occurred, relative to the recent historical average (Figure 8).

Figure 8.

Change in current average annual minor tidal flood frequency relative to 1960–1980 average.

Projections of extreme sea levels have been conducted which include the combined effects of mean sea level, tides, wind waves, and storm surges. Tropical regions, with rather narrow (short‐tailed) extreme sea‐level distributions today, will experience the largest increases in flooding frequency (Vitousek et al., 2017). Beach erosion and morphodynamics are controlled by wave direction and energy, which are attributes of high‐frequency sea‐level variability. If extreme El Niño and La Niña events become more frequent in the next century, as has been predicted, then populated regions around the Pacific will be increasingly exposed to both extreme coastal erosion and flooding, independent of sea‐level rise (Barnard et al., 2015). Detailed regional projections point to the growth of lesser‐extreme events, so‐called “high tide flooding,” becoming more common in the next century along the shoreline of the United States and its territories (Dahl et al., 2017; Ray & Foster, 2016; Sweet et al., 2018; Sweet & Park, 2014), throughout the tropical Pacific (Stephens & Ramsay, 2014), in the South China Sea (Devlin et al., 2017) and, probably, worldwide (Moftakhari et al., 2018). Forecasts of tide‐related flooding are sensitive to the underlying mean SLC scenarios, and accurate prediction requires accounting for changes in the tides themselves (Mawdsley et al., 2015; Woodworth, 2010) and VLM (Karegar et al., 2017). Changes in tides have been discussed in detail in Haigh et al. (2019).

The above discussion has focused on the contribution of high‐frequency sea‐level variability to extreme coastal sea level, but nonlinear coupling of high‐frequency sea level to other processes is important, as well. Recent work has pointed out that the prediction of future cryospheric contributions to SLC must incorporate dynamical feedbacks between high‐frequency tidal variability and ice sheet behavior (Padman et al., 2018). Moreover, changes in mean sea level will eventually lead to potentially‐significant changes in the tides (Pickering & Alford, 2012; Schindelegger et al., 2018; Wilmes et al., 2017). Nonlinear feedback between waves and water depth (Arns et al., 2017), tides and morphology (de Vet et al., 2017), and fluvial and ocean processes (Moftakhari et al., 2017) are important at some sites.

8.2. Uncertainties and Future Outlook

Key uncertainties concerning high‐frequency sea‐level extremes arise from the lack of measurements of historical water level at the locations and scales needed to define the sea‐level distribution, in particular, in the tails, a fundamental quantity for assessing change and validating models of present conditions. Present studies make the case that trends in sea‐level extremes will be driven by the long‐term (but difficult to measure locally) trends in mean sea level, but improvements in the representation of geodetically referenced sea level in climate models, and their representation of factors such as projected storm tracks and intensity, will lead to a better understanding of the uncertainty or plausible range of sea‐level extremes at any particular location (Garner et al., 2017). The potential for coupling between a multitude of processes, outlined above, at small scales can lead to considerable uncertainty. Finally, changing coastal infrastructure and VLM may be associated with uncertain changes in inundation extent for a given extreme event, with profound consequences for the associated societal impacts. The latter are also affected by socio‐economic factors.

Future work relevant to high‐frequency sea level should continue to accumulate geodetically‐referenced sea‐level data to identify and attribute sea‐level extremes. Fundamental research concerning the connection between sea level at the coast and sea level offshore (past the continental shelf) should be a priority (Lobeto et al., 2018; Wise et al., 2018). Improvements in the representation of high‐frequency processes in ocean and cryosphere models will contribute to forecasting future climate (Padman et al., 2018).

Satellite altimeter missions have provided foundational data for the description of sea‐level variability since 1992. These data have enabled the development of very accurate hydrodynamic models for the ocean tide (Stammer et al., 2014), and, by inference, improvements to hydrodynamic storm surge models, since both tides and surge are distinguished primarily by the nature of the forcing rather than their dynamics, per se (Carrère & Lyard, 2003). Recent developments in delay‐Doppler techniques (Wingham et al., 2006) and Ka‐band altimetry (Bonnefond et al., 2018) are enabling water level measurements at smaller scales than conventional nadir altimetry. Studies that use altimetry to assess extreme sea levels (Lobeto et al., 2018) make extensive use of coastal tide gauge records to correlate observations at the scale of the radar footprint with sea‐level extremes at the coastline. Longer time series and higher spatial resolution will lead to the increasing use of altimetry to study sea‐level extremes in the future.

Two future satellite missions will contribute to our knowledge of the coastal impacts of high‐frequency sea‐level fluctuations. The SWOT mission will provide high‐resolution snapshots of the coastal ocean and inland waterways (Fu et al., 2009) and is scheduled for launch in 2021. The repeat period of the orbit, 21 days, is too long to temporally resolve the phenomena discussed here, but the unprecedented spatial resolution (200 m) and accuracy of the observations will undoubtedly stimulate progress in coupled modeling of tides, surges, and lower‐frequency phenomena (Turki et al., 2015). NISAR is a joint NASA and Indian Space Research Organization synthetic aperture radar mission scheduled to launch in 2022. NISAR will provide all‐weather, day/night imaging the Earth repeated 4–6 times per month, resolving coastal inundation with a horizontal resolution of 3 to 10 m (Amelung et al., 2018). It will provide crucial data for validating inundation models, and its data, when linked to extreme sea‐level information from tide gauges and satellite, should prove useful for improving digital elevation models and hydrodynamic flood models.

9. Near‐Term Outlook of Regional Relative Sea‐Level Understanding

Despite gaps in our understanding, efforts have been made to project future SLC on regional spatial scales. Recent reviews have summarized these approaches in detail (e.g., Garner et al., 2018; Horton et al., 2018) and the interested reader is referred to these articles. The extent to which the various contributions to sea level and their statistical dependencies can be combined to provide a complete and accurate assessment of future regional SLC, however, is dependent on the current uncertainties associated with each of these signals. Projections of future regional SLCs have mostly focused on physical processes related to ice‐mass loss and ocean dynamics. When combined with estimates of GIA, projections of future regional SLC are then created. Next to the uncertainties in these large‐scale changes, two assumptions are made that affect the usefulness of this approach. First, the role of ocean dynamics on local coastal sea level is not well resolved in the coarse‐resolution Earth system models that are used to project the regional changes. Decoupling between the coastal zone and open ocean acts on a wide range of time scales up to multidecadal fluctuations (Woodworth et al., 2019). Improvements in understanding the linkage between coastal sea level and ocean dynamics, and increased model resolutions, are important in establishing this link and are a key requirement for understanding future changes in coastal sea level and its variability on a wide range of time scales. Second, local VLM that is not related to GIA or contemporary GRD effects is often not incorporated into these projections. Some studies (e.g., Kopp et al., 2014) use and extrapolate contemporary rates of local VLM to project the role of VLM in future sea level. Since for many coastal locations, including many megacities, VLM is currently the dominant driver of local SLC, a thorough understanding and accompanied forecasting of local VLM is crucial in projecting future changes. Both issues depend on the local situation, and are therefore challenging to assess in global studies. Nevertheless, combining knowledge of global processes and local effects is necessary to improve local sea‐level projections.

One of the primary goals of this paper has been to identify the areas of uncertainty in each of the processes contributing to regional SLC. While we have discussed each of these uncertainties in the material above, it is important to review how some of these uncertainties may be reduced in the near future. In particular, we highlight where recent and future observation systems – particularly satellite based—can and will be used to reduce limitations and uncertainties, and subsequently improve the quality of future assessments of SLC.

1. ICESat‐2

Following on from ICESat and Operation IceBridge, ICESat‐2 will not only extend the record of regional glacier mass change, it will also provide increased spatial resolution of glaciers. Technological advances on ICESat‐2 allow it to continuously collect high‐precision and dense, along‐track measurements with a narrow illumination footprint (Neumann et al., 2019) that is well suited to measure glacier height changes in areas of complex topography (Smith et al., 2019). These fine‐scale measurements provide the opportunity to resolve several gaps in our understanding of future ice sheet and glacier mass change that will impact regional sea level. Furthermore, ICESat‐2's narrow footprint and ability to measure near‐shore bathymetry could prove to be valuable for terrestrial water investigations and coastal inundation applications when these data are analyzed in tandem with tide gauge records in allowing for near‐coast measurements of sea level.

• 2 GRACE‐FO

With the launch of GRACE‐FO, the record of mass change across the globe that began with GRACE will be extended (albeit with a 1‐year data gap between the two missions). Extending the time series of ice sheet mass change, glacier mass change, and terrestrial water storage is critical for separating the natural variability from the long‐term anthropogenic trend, and also for evaluating projections of future sea level.

• 3 Jason‐CS/Sentinel‐6

Recent studies have sought to understand the extent to which the anthropogenic pattern of regional SLC is emerging from the natural climate variability using the 25‐year altimetry record (Fasullo & Nerem, 2018; Royston et al., 2018; Hamlington et al., 2019). Such studies underscore the importance of the continuity of the observational records, as many of the sources of uncertainty discussed above can be reduced through ongoing monitoring and lengthening of the data records that are currently available. The Jason Continuity of Service (Jason‐CS) mission on the Sentinel‐6 spacecraft will launch in 2020, and will extend the continuous record of altimeter‐measured SLC into its fourth decade. With this long record, improved constraints the emergence of the forced or anthropogenic trends in sea level can be obtained, providing an opportunity to evaluate sea‐level projections and improve model‐based estimates, while allowing the monitoring of ongoing changes in sea level across a range of time and space scales.

• 4 NISAR

When launched in 2022, NISAR will provide all‐weather, day/night imaging the Earth repeated 4–6 times per month, resolving coastal inundation with a horizontal resolution of 3 to 10 m. NISAR will be immensely valuable for monitoring changes in Antarctic and Greenland ice sheet flow. As the only left‐looking SAR mission NISAR will be particularly valuable for observing changes in the southernmost regions where little information on flow variability is available. These observations will provide crucial data for validating inundation models. Furthermore, NISAR data, when linked to extreme sea‐level information from tide gauges and satellite, should prove useful for improving digital elevation models and hydrodynamic flood models. NISAR will also allow for new estimates of coastal VLM at high resolutions.

• 5 SWOT

Continued improvements in the resolution and process representation of land‐surface models will allow for better understanding of changing regional hydrology, including the inclusion of human activities and water consumption. These model developments will be supported by SWOT, which will provide the first observational estimate of global continental river discharge, helping to deepen the present understanding of global and regional water cycles. Additionally, SWOT will provide near‐coast measurements of sea level that will fill the gap between the open‐ocean measurements of altimetry and the coastal measurements of tide gauges.

• 6 In Situ Observations

In addition to the satellite systems discussed above, in situ observations of the processes contributing to SLC continue to play an essential role, both in serving to validate measurements made remotely and also in complementing the space‐based network by observing processes difficult to measure remotely. In the coming years, the deep Argo profiling float program will continue to expand, providing more measurements at depth that are critical to our understanding of the global and regional sea‐level budgets, among other processes. Additionally, tide gauges continue to provide direct measurements of SLC at many locations around the globe. Tide gauges allow for studies of the connection between the open ocean and coastal zone, provide measurements of SLC and VLM when colocated with GNSS, and measure the higher‐frequency sea‐level variability discussed in section 8. Efforts to increase the availability of tide gauge data and provide improved data sets to users are underway. As an example, the Global Extreme Sea Level Analysis (GESLA) project is in its third iteration, providing data on extreme sea levels at an increasing number of tide gauges around the globe (Woodworth et al., 2017).

10. Summary

Changes in GMSL provide an integrative measure of the state of the climate system, encompassing both the ocean and cryosphere and may be viewed as an important indicator of what is currently happening to the climate in the present and what may happen in the future. While an increase in GMSL portends an increase in sea level of some magnitude along the world's coastlines, the response on regional levels is not uniform. Water that is added to the ocean from land will not be distributed evenly everywhere (sections 3, 5) and changes in ocean dynamics add to the regional variability in sea‐level rise (section 6). Using observations from tide gauges and satellite altimetry, the extent of the spatial variability in the rate of sea‐level rise can be understood. With the recent improved understanding of GRD effects on sea level, and the suite of VLM effects outlined here, it has become clear that the use of a single global rate to describe sea level around the globe is problematic, and improved assessment of sea‐level rise on regional levels is required from a planning perspective.

Over the past century, coastal sea levels have risen over the majority of the globe. The effect of increasing sea level relative to land is a significant reduction in the elevation gap between typical high tides and a threshold elevation at which flooding begins (Sweet et al., 2018). Coastal communities were established with this gap in mind, recognizing flooding might occur under the most extreme of conditions. Recent reports (e.g., Sweet et al., 2017, 2018) have detailed the rapidly declining gap along the coastlines of the world, and the accelerated effect this has had on flood frequencies in many coastal locations. One important implication of these analyses is that the narrowed gap between high tide and flooding conditions can now be overcome by sea‐level variability on a range of time scales. Subsequently, from a decision‐making perspective, improved projections of future regional SLC are needed over a variety of time horizons, not simply the longest.

As discussed here, sea level varies on time scales from short‐term (section 8), to seasonal‐to‐decadal (sections 5 and 6) or longer (sections 3, 5). When considered in tandem with the movement of land relative to the ocean (section 7), contributions to sea level at each of these time scales can combine constructively, increasing sea levels and high‐tide flood frequencies over both the short and long terms. The gap described above is known in many locations, and time horizons can be generated over which high‐tide flood frequency will begin to increase rapidly. When considering only the long‐term trend, this time horizon is usually found to be on the order of decades. However, when combined with the other contributors to sea‐level variability, it is highly likely that in the short term (on the order of years) the cumulative effect of high‐tide flooding will extend beyond “nuisance” levels and becomes too frequent for business as usual in coastal areas. As such, there is a strong need for improved information regarding future sea‐level rise across a range of time scales.

While understanding the long‐term contributions from melting glaciers and ice‐sheets is essential, so too is understanding, quantifying, and possibly predicting the variability that will occur on seasonal to decadal time scales. Recent studies suggest that these contributors are becoming distinguishable with the records available (e.g., Fasullo & Nerem, 2018; Nerem et al., 2018). With the observations that are available—or will become available soon—coupled with improved data analysis and modeling efforts, our understanding of future regional SLC will continue to advance in the coming years. Knowing that planning efforts are underway and that sea‐level rise is already impacting many parts of the world's coastlines, it is worth taking inventory of the current state of understanding and clearly identifying areas of uncertainty that are impacting our ability to provide complete, accurate, and actionable information at the coast. Such assessments should be undertaken frequently to update relevant information in light of new science results, and to assist those tasked with translating current scientific understanding into plans that can be put into action at the coast.

Competing Interests

The authors declare no competing interests.

Materials and Correspondence

All materials and correspondence requests can be directed to B. D. H. at benjamin.d.hamlington@jpl.nasa.gov

Hamlington, B. D. , Gardner, A. S. , Ivins, E. , Lenaerts, J. T. M. , Reager, J. T. , & Trossman, D. S. , et al. (2020). Understanding of contemporary regional sea‐level change and the implications for the future. Reviews of Geophysics, 58, e2019RG000672 10.1029/2019RG000672

Data Availability Statement

Gridded Surface Height Anomalies Version 1801. Ver. 1801 available from NASA JPL PO.DAAC, CA, USA (https://doi.org/10.5067/SLREF-CDRV1). Data are also available through Wiese et al. (2017).