Abstract
G-protein coupled receptor (GPCR) mediated calcium (Ca2+)-signaling transduction remains crucial in designing drugs for various complex diseases including neurodegeneration, chronic heart failure as well as respiratory diseases. Although there are several reviews detailing various aspects of Ca2+-signaling such as the role of IP3 receptors and Ca2+-induced-Ca2+-release, none of them provide an integrated view of the mathematical descriptions of GPCR signal transduction and investigations on dose-response curves. This article is the first study in reviewing the network structures underlying GPCR signal transduction that control downstream [Cac2+]-oscillations. The central theme of this paper is to present the biochemical pathways, as well as molecular mechanisms underlying the GPCR-mediated Ca2+-dynamics in order to facilitate a better understanding of how agonist concentration is encoded in Ca2+-signals for Gαq, Gαs, and Gαi/o signaling pathways. Moreover, we present the GPCR targeting drugs that are relevant for treating cardiac, respiratory, and neuro-diseases. The current paper presents the ODE formulation for various models along with the detailed schematics of signaling networks. To provide a systems perspective, we present the network motifs that can provide readers an insight into the complex and intriguing science of agonist-mediated Ca2+-dynamics. One of the features of this review is to pinpoint the interplay between positive and negative feedback loops that are involved in controlling intracellular [Cac2+]-oscillations. Furthermore, we review several examples of dose-response curves obtained from [Cac2+]-spiking for various GPCR pathways. This paper is expected to be useful for pharmacologists and computational biologists for designing clinical applications of GPCR targeting drugs through modulation of Ca2+-dynamics.
Keywords: GPCR, Cytosolic calcium, Calcium dynamics, Feedback loops, Dose-response, Signal transduction, Network motifs, Mathematical models
Abbreviations: [Cac2+], Cytosolic calcium concentration; [CaER2+], Endoplasmic reticulum calcium concentration; AC, Adenylyl cyclase; ATP, Adenosine triphosphate; AUC, Area under the curve; C5a, Complement component 5a; Ca2+, Calcium; cAMP, Cyclic adenosine monophosphate; CHIP, C-terminus of Hsp70-Interacting Protein; CHO, Chinese hamster ovary; CICR, Calcium-induced-calcium-release; CXCR4, C-X-C Motif Chemokine Receptor 4; DAG, Diacylglycerol; ER, Endoplasmic reticulum; ERK, Extracellular signal-regulated kinase; FRET, Fluorescence resonance energy transfer; GPCR, G-protein coupled receptor; GRK, G protein-coupled receptor kinase; HEK, Human embryonic kidney; IP3, Inositol trisphosphate; IP3R, Inositol trisphosphate-receptor; ISI, Inter-spike interval; LCC, L-type calcium-channel; mGluR, Metabotropic glutamate receptor; ODE, Ordinary differential equation; PIP2, Phosphatidylinositol 4,5-bisphosphate; PKC, Protein kinase C; PLC, Phospholipase C; PMCA, Plasma membrane calcium-ATPase; RyR, Ryanodine receptor; SERCA, Sarco/endoplasmic reticulum Ca2+-ATPase; SR, Sarcoplasmic reticulum; SRM, Selective reaction monitoring; STIM, Stromal interaction molecule; VGCC, Voltage-gated calcium channel
1. Introduction
G-protein-coupled receptors (GPCRs) are the targets of approximately 40% of all pharmaceutical drugs [1]. Activation of GPCRs is known to trigger a cascade of events that lead to the modulation of cytosolic Ca2+-dynamics [2]. Pharmacological compounds targeting GPCRs can be used to modulate of Ca2+-signaling in order to treat pro-inflammatory diseases [3,4]. Specifically, it has been reported that cancer cells can be selectively killed and/or arrested by targeting Ca2+-channels [5]. The role of GPCR mediated Ca2+-signaling in chronic interstitial lung diseases, such as idiopathic pulmonary fibrosis and scleroderma has been reviewed by Janssen et al. [6]. In the context of the recent COVID-19 pandemic, Zhou et al. [7] suggested that angiotensin receptor blockers may have the potential of inhibiting viral entry and can be considered as a prospective repurposable drug for 2019-nCoV/SARS-CoV-2. Many therapeutics used to either enhance bronchodilation or prevent bronchoconstriction for treating respiratory diseases including asthma are known to target β2-adrenergic receptors [8,9] and modulate Ca2+-signaling [10]. In this context, a more profound knowledge of the role and mechanism through which cytosolic Ca2+ is regulated by GPCRs can help in curing these diseases.
Ca2+-dysregulation is known to be associated with many diseases in muscular and nervous systems. For example, in end-stage heart failure, the reduced level of sarcoplasmic reticulum Ca2+-ATPase (SERCA) expression leads to disturbed Ca2+-homeostasis [11]. Recent evidence also indicates that neuronal Ca2+-signaling is abnormal in many neurodegenerative disorders such as Alzheimer's, Huntington disease, and Parkinson's disorder [12].
Within a wide variety of cells, Ca2+ serves as an almost universal ionic messenger, delivering signals received at the cell surface to the inside of the cell. These signals are controlled by the concentration of the modulating agonists and encoded in the complex spatiotemporal behavior of cytosolic Ca2+-concentration ([Ca c 2+]), ranging from stochastic spiking to regular oscillations, and more complex waveforms [13]. Ca2+-signals regulate the intracellular processes operating over a wide time range, from neurotransmission in microseconds to gene transcription at a scale of minutes to hours [14]. Cells can quickly raise or reduce the [Ca c 2+] through tight regulation mediated through GPCRs, Ca2+-stores, channels, pumps, and exchangers. GPCR mediated [Ca c 2+]-oscillations are known to control a wide range of cellular functions amid and including cell division to apoptosis [15,16]. While in excitable cells, these functions include muscle contraction [17] and neurotransmitter release [18] in non-excitable cells, Ca2+ regulates transcription [19] and cell cycle progression [20]. For pancreatic β-cells, Ca2+-dynamics control the changes in insulin secretion [21]. Vital cellular functions like fertilization, development, differentiation, adhesion, growth, secretion, platelet activation, gene expression, and memory are also linked to Ca2+-signaling regulated by GPCRs [22,23]. Ca2+ mediates these functions by [Ca c 2+]-sensing effectors that translate Ca2+-signals with varying spatiotemporal dynamics into specific cellular responses [24]. In this scenario, the recent scientific efforts are focusing on drug screening and testing based on the quantification of Ca2+-signatures over conventional biochemical assays [13,25].
Several review papers have been published in the last three decades on the function and structure of GPCR targeting drugs as well as biomolecular details of Ca2+-signaling [[26], [27], [28]]. Many of them focus on providing a quantitative description of Ca2+-toolbox and a thorough understanding of non-linear coupled systems [[27], [28], [29], [30]]. One of these review articles characterizes the biophysical and biochemical mechanisms of Ca2+-signaling in astrocytes [27]. However, the review does not elucidate the interplay between positive and negative feedback loops yielding oscillations and how GPCR targeting agonists may encode various levels of frequencies. Another review emphasizes the key features of modeling of Ca2+-induced-Ca2+-release (CICR) through inositol trisphosphate (IP3)-receptors (IP3R) and ryanodine receptors (RyR) and how local Ca2+-release affects global oscillations [30]. The role of Ca2+-entry through store-operated channels in controlling Ca2+-signaling is emphasized in Dupont et al. [31]. However, none of these reviews address how GPCR targeting drugs modulate the Ca2+-dynamics and their relevance in perspectives of pharmacology. Here, we propose a single bridging article encompassing the details of dose-response curves obtained from [Ca c 2+]-spiking for various GPCR pathways along with the systems of ordinary differential equations (ODEs) and network motifs. To the best of our knowledge, this is the first instance of the review that combines experimental investigations as well as theoretical studies on GPCR mediated Ca2+-dynamics.
In this review, we provide the current perspectives of GPCR targeting drugs that are relevant for treating cardiac, respiratory, and neuro-diseases along with agonist-mediated encoding of Ca2+-dynamics corresponding to Gαq, Gαs, and Gαi/o signaling. Secondly, we emphasize the systems perspectives through the mathematical representation of ODEs that describe GPCR mediated Ca2+-dynamics and the underlying feedback loops. Encoding of amplitude and frequency being the two crucial features of information processing in cells, we provide a detailed analysis of network motifs present in the GPCR mediated circuits. This article also attempts to encompass the details of how the agonist concentration is encoded by Ca2+-signals. The detailed schematics of biomolecular pathways and mathematical functions presented may serve as a starting point for the construction of computational models and simulation of the dose-response curve for linking them to experimental data. Finally, this article reviews prominent examples of GPCR targeting agonist concentration-response curves of [Ca c 2+]-spiking found from experiments.
2. Role of GPCRs in regulating [Cac2+]-response
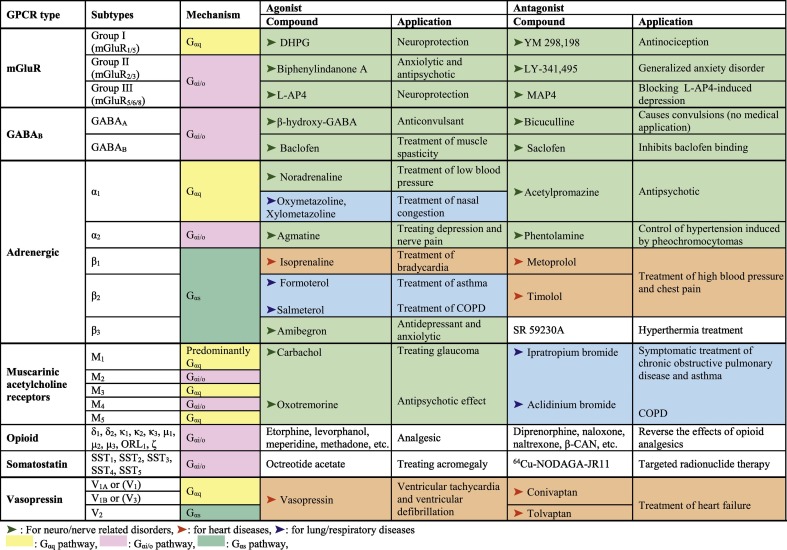
GPCRs are the heptahelical receptors on the plasma membrane that are coupled to guanine nucleotide-binding proteins (G-proteins) within the cell. The binding of the agonist to the extracellular domain of the GPCR activates the receptor and leads to a conformational change on the intracellular side of the membrane. Subsequently, the G-protein (that has three subunits, α, β, and γ) is activated in response to this conformational change. Based on the type of G-protein's α-subunit activated, the GPCRs can be classified into three major types, Gαq, Gαs, and Gαi/o coupled receptors, where each type has its own signal transduction mechanism (Fig. 1 ). Various examples of GPCRs that are known to regulate Ca2+-signaling through Gαq, Gαs, or Gαi/o pathways are presented in Table 1 . Representative FDA approved GPCR targeting drugs used to treat some of the respiratory, cardiovascular, and nervous system diseases has also been shown in Fig. 2 . Many of these GPCR targeting drugs such as irbesartan are known to modulate the [Ca c 2+]-levels and thereby assumes significance in the treatment of cardiac complications [32].
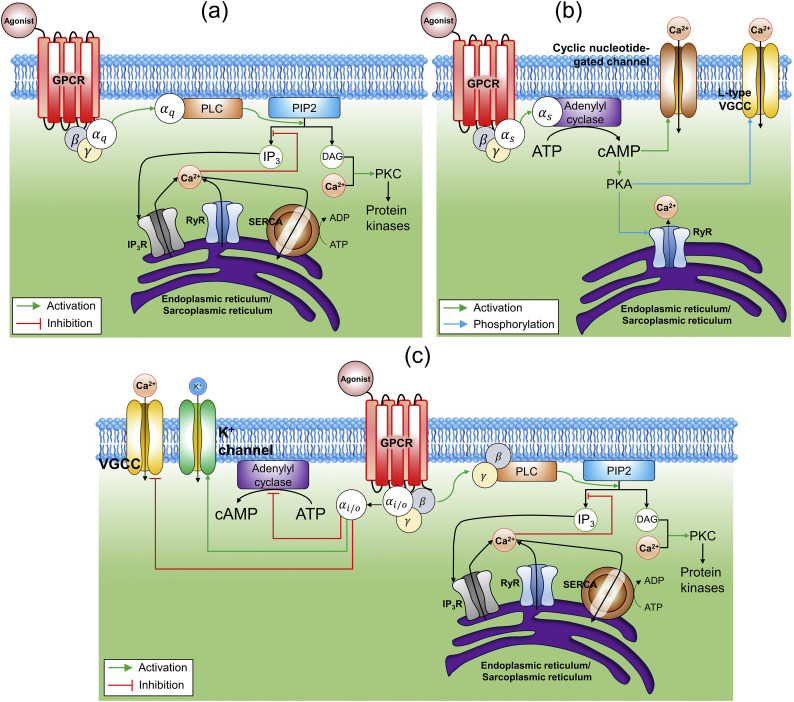
Fig. 1.
Biochemical pathway and molecular details of controlling intracellular Ca2+-dynamics through: (a) Gαq, (b) Gαs, and (c) Gαi/o coupled receptors.
Table 1.
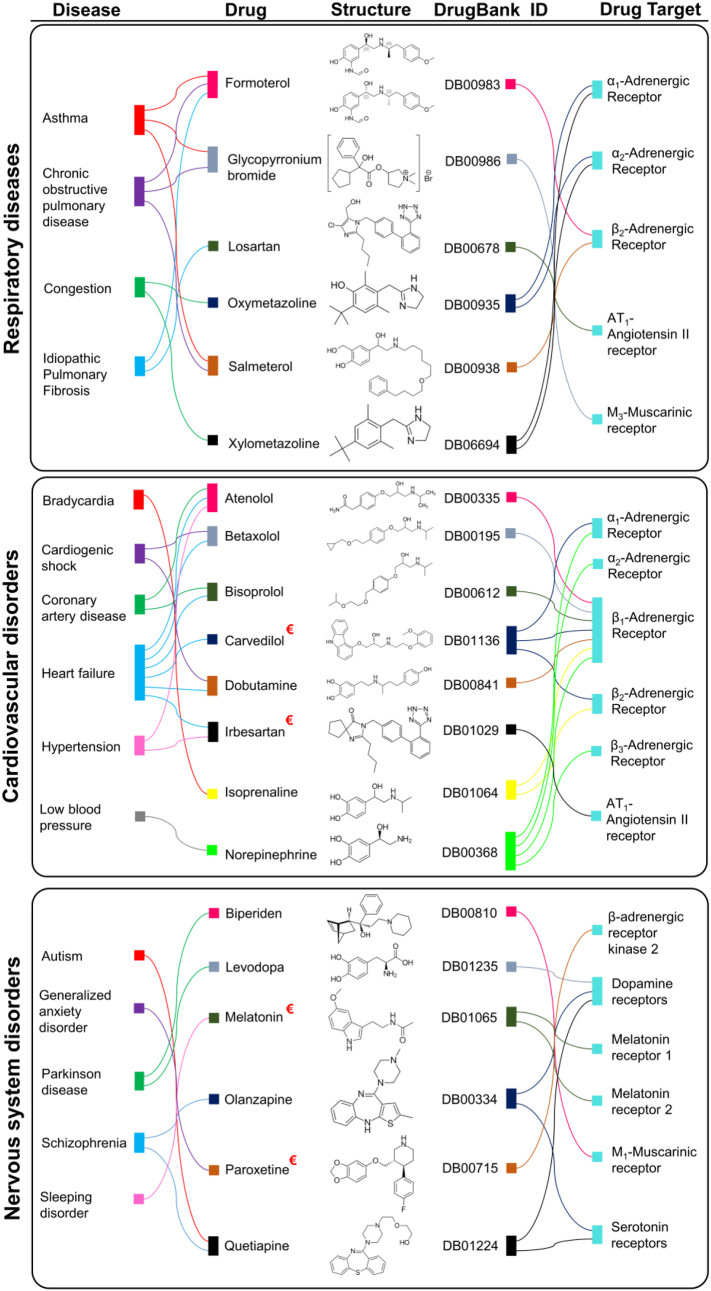
Fig. 2.
FDA approved GPCR targeting drugs corresponding to respiratory, cardiovascular, and nervous system diseases. This diagram highlights the relation between various diseases and GPCR targeting drugs.
 : GPCR targeting drugs suggested by Zhou et al. [7] for possible treatment of 2019-nCoV/SARS-CoV-2.
: GPCR targeting drugs suggested by Zhou et al. [7] for possible treatment of 2019-nCoV/SARS-CoV-2.
In the Gαq pathway, when the ligand binds to the GPCR, the α q subunit of G-protein is activated which further activates phospholipase C (PLC) which is an enzyme restricted to the plasma membrane. Once activated, PLC catalyzes the conversion of a phosphatidylinositol 4,5-bisphosphate (PIP2), a phospholipid component of the cell membrane, into IP3 and diacylglycerol (DAG). IP3 being soluble in the cytoplasm diffuses through the cell and binds to IP3-receptor (IP3R) on the surface of the endoplasmic reticulum/sarcoplasmic reticulum (ER/SR), leading to the transportation of Ca2+ from ER/SR into the cytoplasm. Additionally, Ca2+ and DAG together work to activate protein kinase C (PKC), which further phosphorylates other molecules, leading to altered cellular activity [29,42]. As per several mechanistic models, [Ca c 2+] provides positive feedback on IP3 either directly [43,44] or indirectly via stimulation of PLC [45] (Fig. 1(a)). Paroxetine (Gαq) is known to induce apoptosis through an increase in intracellular Ca2+ and the generation of reactive oxygen species (ROS) [46].
In the Gαs pathway, α s subunit of G-protein activates adenylyl cyclase (AC), which leads to the production of cyclic adenosine monophosphate (cAMP). cAMP further leads to the activation of protein kinase A (PKA) (Fig. 1(b)). PKA is known to phosphorylate several proteins that regulate excitation-contraction coupling through L-type Ca2+-channel (LCC), ryanodine receptor (RyRs), and myosin binding protein C. It has been shown that the activation of β-adrenergic stimulation may enhance SR Ca2+-release through phosphorylation of LCCs, or due to phosphorylation of LCCs and RyRs [47,48].
In the Gαi/o pathway, α i/o subunit of G-protein is known to inhibit the cAMP production as well as voltage-gated Ca2+-channels (VGCCs). In contrast to the Gαq pathway, the PLC pathway is activated here by βγ subunit (Fig. 1(c)). Melatonin (Gαi/o) is known to fine-tune intracellular Ca2+ and eliminate myocardial damage through IP3R/mitochondrial uniporter pathway [49].
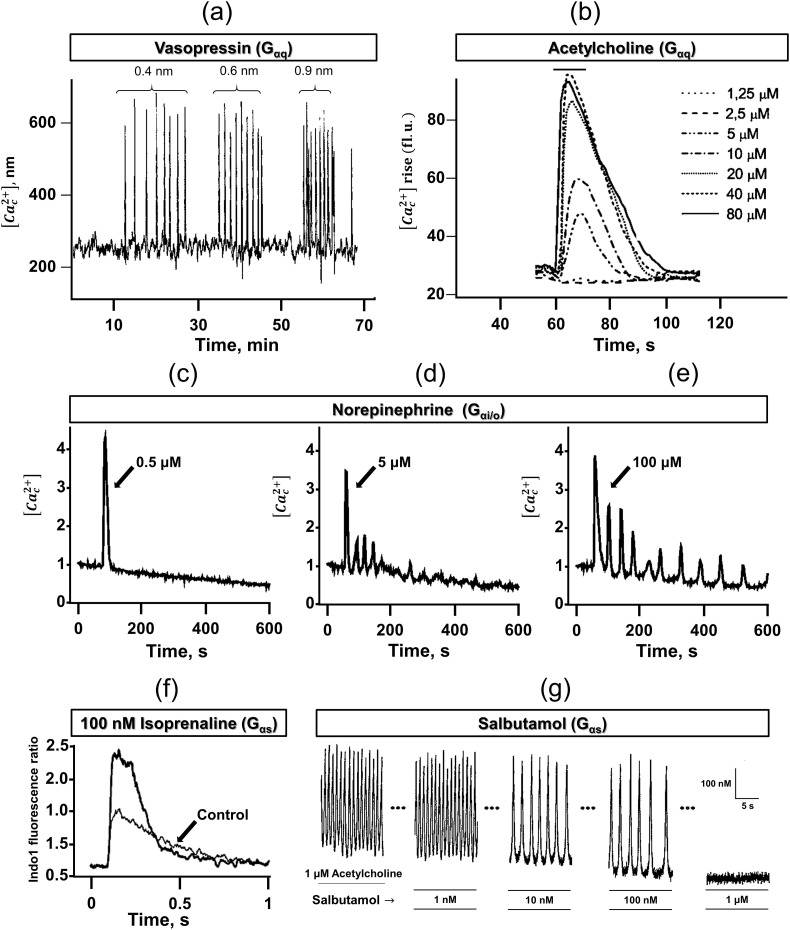
Although there have been extensive studies on Gαq mediated [Ca c 2+]-oscillation [50,51], there are few investigations for Gαi/o mediated [Ca c 2+]-oscillation. Recent studies on drug testing framework reveals Gαi/o (α2-adrenergic receptor and CXCR4) mediated modulation of Ca2+-signaling in HeLa cells [52]. Also, there are investigations where Gαs mediated signaling enhances local Ca2+-concentrations in cardiomyocytes [47]. Although it is not known exactly if there is a specific pattern present for the [Ca c 2+]-oscillations corresponding to Gαi/o, Gαq, and Gαs pathways, here we show examples of Ca2+-responses from each group. Fig. 3(a)-(b) show vasopressin and acetylcholine (Gαq) mediated [Ca c 2+]-oscillations. The pattern obtained by activation of the α2-adrenergic receptor (Gαi/o) has been shown in Fig. 3(c)-(e). Fig. 3(f) shows how activation of the β-adrenergic receptor (Gαs) modulates the Ca2+-signaling and how it is different from vasopressin mediated regulation. These curves present the agonist concentration encoding in Ca2+-signals for Gαi/o, Gαq, and Gαs signaling.
Fig. 3.
Agonist concentration encoding of Ca2+-dynamics, (a) [Cac2+]-oscillations in a single rat hepatocyte induced by the stimulation of the vasopressin receptor (Gαq pathway). An increase in drug dose shows an increase in the frequency of [Cac2+]-spikes. (b) Modulation of amplitude and area under the curve (AUC) of [Cac2+]-spikes by increasing the drug dose of acetylcholine (Gαq pathway). (c)-(e) Frequency and amplitude modulation of [Cac2+]-oscillation in a single representative HeLa cell by stimulation of α2-adrenergic receptor (Gαi/o pathway). Various dosesof norepinephrine were used. (f) Increase in Ca2+-release (amplitude modulation) by treatment of β-adrenergic receptor (Gαs pathway) using isoprenaline in rat atrial and ventricular myocytes. (g) Frequency modulation of [Cac2+]-oscillation by treatment of β2-adrenergic receptors (Gαs pathway) with increasing doses of salbutamol in porcine airway smooth muscle cells. Over a concentration range of 1 nM to 100 nM, salbutamol progressively decreased the frequency of acetylcholine-induced [Cac2+]-transients but did not alter the amplitude of the spike train. At salbutamol concentration of 1 μM, the oscillations were completely inhibited. Adapted with permission from [50,[53], [54], [55], [56]]. Copyright (2020).
3. Signal transduction: GPCR mediated regulation of [Cac2+]-oscillations
The mechanisms underlying the complex Ca2+-waveforms have lured both theoretical and experimental researchers in the past three decades. In general, deciphering these mechanisms through investigations based on experiments remains challenging due to the heterogeneity present on the oscillation patterns [57]. Thurley et al. [58] have offered a solution by relative frequency encoding instead of encoding its absolute value. It has been shown that despite the variability in the inter-spike-interval (ISI), steps in agonist concentration causes the stochastic period of the ISI to change by the same factor in all the cells. These fold changes reliably encode changes in agonist concentration, and they result in an exponential dependence of average ISI on the concentration of agonist. Hence, [Ca c 2+]-spikes enable reliable signaling in a cell population despite randomness and heterogeneity present in a population.
To date, the major modeling approach to investigate the [Ca c 2+]-oscillations in cells is based on numerical solutions of the system of differential equations (Table 2 ) [29]. Here, we describe two of these models to explain how computational modeling can be used to yield agonist-mediated [Ca c 2+]-response.
Table 2.
Description of the major model variables, Ca2+-channel/receptor details, and feedback loops present in the ODE systems corresponding to single-cell models yielding GPCR mediated [Cac2+]-oscillations.
| Model | Channels considered | Drug | Cell line/ type | ODE variables | Across plasma membrane |
Across endoplasmic reticulum |
Across mitochondria |
Feedback loops | |||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Jin | Jout | JIP3 + Jleak + JCICR | JSERCA | Jin | Jout | ||||||
| Kummer et al. (2000) [59] | IP3R, SERCA, Ca2+-ATPase, Ca2+ entry channel on plasma membrane | ATP | Hepatocyte | [Gα], [PLC], [Cac2+], [CaER2+] | k12[PLC] + k13[Gα] | --- | --- | –ve feedback of [Cac2+] on IP3R and Gα at high concentrations +ve feedback of [Cac2+] on IP3R |
|||
| Larsen et al. (2004) [60] | IP3R, SERCA, Ca2+-ATPase, Ca2+ entry channel on plasma membrane, MCU, NCLX | --- | --- | [Gα], [PLC], [Cac2+], [CaER2+], [Camit2+] | k12[PLC] + k13[Gα] | –ve feedback of [Cac2+] on IP3R and Gα at high concentrations +ve feedback of [Cac2+] on IP3R |
|||||
| De Pittà et al. (2009) [61] | IP3R, SERCA, Leak channel on ER | Glutamate | Astrocytes | [Cac2+], [CaER2+], [CaExt2+], [IP3] | --- | --- |
rcm′ ∞ 3n′ ∞ 3h3([CaER2+] − [Cac2+]) +rL([CaER2+] − [Cac2+]) |
--- | --- | +ve and –ve feedback of [Cac2+] on IP3R –ve feedback of [IP3] on IP3 production |
|
| Giri et al. (2014) [54] | IP3R, SERCA, Ca2+-ATPase | Norepinephrine | HeLa | [Gα], [PLC], [Cac2+], [CaER2+] | k12[PLCβ] | --- | --- | –ve feedback of [Cac2+] on IP3R and Gα at high concentrations +ve feedback of [Cac2+] on IP3R |
|||
[Gα]is the concentration of Gαsubunit,[PLC]is the concentration of PLC.
[Cac2+], [CaER2+]and [Camit2+]refer to Ca2+ concentration in the cytoplasm, endoplasmic reticulum, and mitochondria respectively.
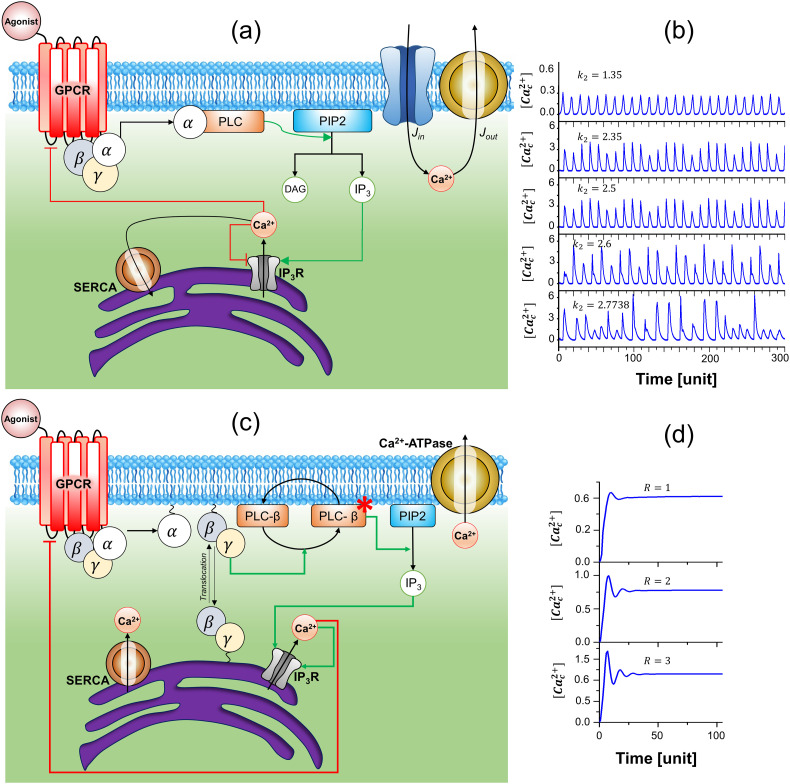
In 2000, Kummer et al. [59] developed a model to show the dynamic behavior of [Ca c 2+] with different agonist stimuli (Fig. 4(a)-(b)). They illustrated the shift from simpler [Ca c 2+]-spiking to complex and chaotic time profile with agonist stimulation which was denoted by the parameter k 2 in their ODE system. Unlike other models, they considered receptor-specific self-enhanced behavior of the activated Gα subunits and a slow negative feedback of [Ca c 2+] that inhibit the receptor (Fig. 5(a)). Further, the IP3 concentration was not considered a separate variable but was taken to be dependent on the dynamics of activated PLC.
Fig. 4.
(a) Schematic representation of GPCR mediated Ca2+-signaling pathway and network structure present in Kummer et al. [59], (b) Switching from simple to chaotic [Cac2+]-oscillations with increasing agonist stimulation have been shown with the change in the value of the parameter k2 in Kummer et al. [59] (see Eq. (1)), (c) Schematic representation of Ca2+-signaling pathway and network structure present in the model proposed by Giri et al. [54], (d) Changes in the amplitude and frequency of [Cac2+]-oscillations with increasing agonist concentration have been shown with the change in the value of parameter R in Giri et al. [54] (see Eq. (5)).
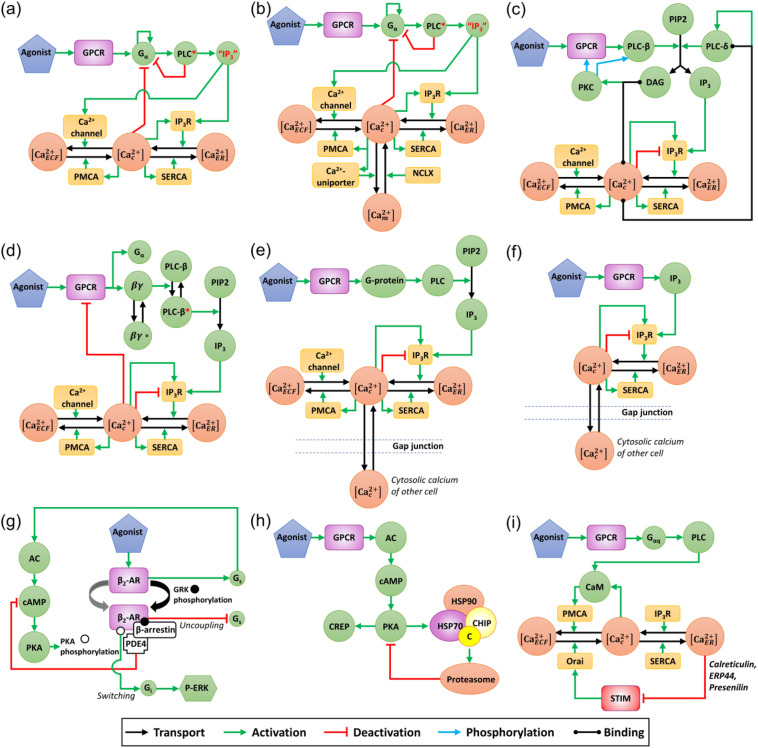
Fig. 5.
Schematic representation of primary circuits containing positive and negative feedback loops present in the GPCR signaling cascade systems reported in: (a) Kummer et al. [59] (phenylephrine (Gαq) and ATP (Gαq)-mediated Ca2+-response in hepatocyte cell line), (b) Larsen et al. [60], (c) De Pittà et al. [61] (glutamate (Gαq)-mediated Ca2+-response in astrocytes), (d) Giri et al. [54] (norepinephrine (Gαi/o)-mediated Ca2+-response in HeLa cell line), (e) Sun et al. [64] (histamine (Gαq)-mediated Ca2+-response in HUVEC cells), (f) Potter et al. [65] (ATP (Gαq) mediated Ca2+-response in NIH-3 T3/MDA-MB-231 cells), (g) Baillie et al. [66] (β-Arrestin-mediated switching of β-adrenergic receptors from Gαs to Gαi/o in HEK cells), (h) Rinaldi et al. [67] (CHIP mediated inhibition of PKA in forskolin (Gαs)-stimulated mouse embryonic fibroblast), and (i) Abell et al. [68] (Ca2+-influx mediated by STIM (Gαq) in drosophila cells). Note that various circuits exhibit different configurations of positive and negative feedback loops. The specific characteristics are motifs with inflow and outflow, fast positive feedback, negative feedback, adaptive negative feedback, and diffusible intermediates.
The mathematical structure of the model can be given as,
| (1) |
| (2) |
| (3) |
| (4) |
Their model was compared with experimental data obtained from hepatocytes stimulated with phenylephrine (Gαq) and adenosine triphosphate (ATP), but no parameter estimation was performed. Later on, in 2004, Larsen et al. [60] modified the model proposed by Kummer et al. [59] to illustrate the encoding and decoding of Ca2+-signals based on the cooperativity of Ca2+-binding to various proteins. The major objective for performing such modification is to include the role of agonist in encoding frequency, amplitude, and waveform of the [Ca c 2+]-oscillations. The network structure of this model is presented in Fig. 5(b). Larsen et al. [60] also introduced the role of the mitochondria in controlling the [Ca c 2+]-oscillations (Table 2).
Another model focusing on PKC mediated phosphorylation of GPCR and PLC-β mediated Ca2+-transport has been proposed by De Pittà et al. [61] in 2009. Their model describes glutamate-mediated [Ca c 2+]-oscillations in astrocytes. The network structure and feedback loops for this model are presented in Fig. 5(d).
In 2014, Giri et al. [54] proposed a model that included the translocation of G-protein subunits and the role of various γ subunits in controlling [Ca c 2+]-oscillation. They used the framework developed by Kummer et al. [59] and performed the modifications to include the PLC activation by Gβγ (specific to Gαi/o pathway) as well as spatial redistribution of active Gβγ between the plasma membrane and internal membrane (Fig. 4(c)-(d)). They developed a two- γ subunit models by considering different translocation rates of γ subunits present in HeLa cells. The mathematical structure of the model is presented in Eqs. (5), (6), (7), (8), (9), (10) and the network motifs are presented in Fig. 5(d).
| (5) |
| (6) |
| (7) |
| (8) |
| (9) |
| (10) |
To depict the differential translocation rates, they assumed a fast gamma subunit γ fast and slow gamma subunit as γ slow where k tf and k ts are the rate constants for translocation of fast and slow γ− subunits. Eq. (5), (6) represent the active fast and slow gamma subunits at the plasma membrane and Eq. (7), (8) represent the active fast and slow gamma subunits at the internal membrane. Eq. (10) represents the rate kinetics of [PLC β] which is analogous to Eq. (2) in the model proposed by Kummer et al. [59]. The [Ca c 2+] and [Ca ER 2+] dynamics in their model follow Eqs. (3), (4). The parameter R in Eq. (5), (6) represents the agonist concentration which modulates the [Ca c 2+]-oscillations (as shown in Fig. 5(d)). Although their model did not include the dynamics of mitochondrial Ca2+-oscillations and the details of the downstream reactions involved in the decoding process, it was validated with experimental results collected by simultaneous imaging of the protein translocation and [Ca c 2+]-oscillation.
Next, we present a detailed analysis of network motifs for a set of theoretical models describing GPCR mediated control of Ca2+-dynamics (Fig. 5a-f). The schematic representation of primary circuits containing inflow/outflow structure and feedback structures reveal how the interplay between positive and negative feedback loops gives rise to a well-defined [Ca c 2+]-oscillation. For example, studies have shown the fast positive feedback and a slow negative feedback can be defined to control the frequency and amplitude of the oscillations resulting in varied responses [54]. Such feedback structures can be useful for identifying the particular combinations of motifs that will exhibit specific types of oscillations with the GPCR targeting agonist as the stimuli. As explained in the previous section, IP3-Ca2+ cross-coupling is a key feature of the GPCR pathways. The repetitive Ca2+-release and reuptake by intracellular stores are based on positive and negative feedback of [Ca c 2+] on the IP3 or IP3R. Such biphasic feedback of Ca2+ on the IP3R is a minimum requirement to generate Ca2+-transients (Table 2). However, there can be multiple positive feedback loops (Fig. 5) present in the system that are needed for better control of frequency from the perspective of particular physiology. For example, additional positive feedback loops like autocatalytic feedback may give rise to chaotic oscillations (Fig. 5(a)) [59]. Moreover, translocation coupled with reactions may lead to damping in oscillations (Fig. 4(d),5(d) Giri et al. [54]).
The detailed investigation of the models depicting receptor-mediated Ca2+-dynamics shows that the circuits include four types of feedback including positive feedback of agonist on PLC [54,59,60], Ca2+-feedback on the IP3R (Ca2+ activation and inhibition of the IP3R) [61], positive feedback of Ca2+ on PLC [62], and negative feedback of Ca2+ on IP3 by activation of IP3-kinase [63]. Table 2 shows the distribution of these loops in literature on the modeling of Ca2+-dynamics. Similarly, the schematic representation of network structures shown in Fig. 5 reveals both similarities and dissimilarities between different models.
Although there are some computational investigations indicating the presence of feedback structures corresponding to GPCR signaling network, limited investigations focus on gathering experimental data proving these structures. Here, we discuss the recent progress in experimental investigations on various feedback inhibition on receptors present in the circuit. An experimental report showed that extracellular signal-regulated kinase (ERK)-mediated regulation of G protein-coupled receptor kinase (GRK) is involved in establishing negative feedback on GPCR (β2-AR, Gs) through receptor phosphorylation (Fig. 5(g)) [66]. Moreover, a recent report showed the GPCR mediated cAMP elevation leads to activation of PKA and release of catalytic subunit C (PKAc) [67]. Further, the recruitment of chaperone bound ligase that mediates ubiquitylation and proteolysis of PKAc, acts as a negative feedback for restricting PKA activities (Fig. 5(h)) [67]. Along with modeling studies, Giri et al. [54] show the experimental evidence of βγ translocation triggered by Gi-coupled receptor activation, that leads to damping of [Ca c 2+]-oscillation (Fig. 5(d)). Another report shows the presence of parallel adaptive feedback in Gq-coupled signaling using RNAi to knockdown SERCA, plasma membrane Ca2+-ATPase (PMCA), and stromal interaction molecule (STIM) and lowering of expression (Fig. 5(i)) [68]. The protein concentration was measured by selective reaction monitoring mass spectrometry (SRM). The results showed that levels of these proteins are regulated by multiple feedbacks so that change in cytosolic and ER Ca2+ slowly adjusts the amount of signaling components. Parallel adaptive feedback may act with other Ca2+-signaling mechanisms such as RyRs to reconfigure local Ca2+-dynamics. A novel Ca2+-sensor elucidates that in case of malignant hyperthermia, RyR mediated Ca2+-leak alters the local Ca2+-dynamics in human skeletal muscle [69]. A combination of whole-cell physiology and Ca2+-imaging shows that dysfunction of neurons during diseased conditions may be due to a deleterious positive feedback loop associated with [Ca c 2+] mediated enhanced mGluR1 (Gq) function [70]. Some of these circuits are shown to elucidate the presence of negative feedback and adaptive negative feedback present in the GPCR signaling network (Fig. 5 (g)-(i)).
4. [Cac2+]-signature: a biomarker for drug screening
Recent advancements in imaging techniques such as confocal and two-photon microscopy have led to the measurement of the spatiotemporal oscillations in [Ca c 2+] with high precision and resolution. This makes Ca2+-flux assay as a novel tool in GPCR drug screening [35]. Specifically, Ca2+-imaging offers a platform for high-content data acquisition and optimal drug-dose screening. It has been shown that confocal imaging-based assays can be used for measurement of response at a higher spatial resolution that can be further used for classification of responses using k-means clustering and ranking of drugs [52]. Since there are a significant number of potential candidate drugs for the treatment of cardiac diseases, neuro-diseases and respiratory complications (Fig. 2), Ca2+-imaging and systems pharmacology based platforms can be used for testing various drugs and drug-drug interactions. Moreover, Ca2+-imaging offers a phenotypic drug discovery paradigm [71]. Additionally, fluorescence resonance energy transfer (FRET) based Ca2+-imaging has been shown as an attractive alternative for the identification of novel Alzheimer's disease therapeutics [72].
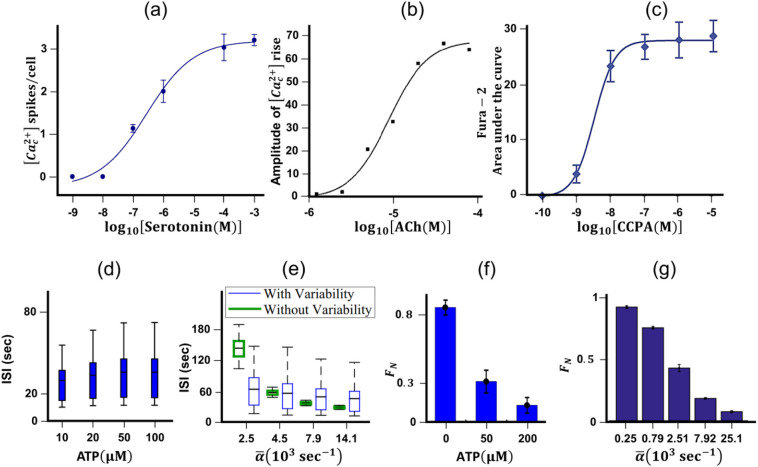
During drug screening and selection of doses, generally, [Ca c 2+]-oscillations are measured for a large range of agonist concentrations. Since we aim to present the systems perspective of the GPCR mediated Ca2+-signaling network, we present some examples of dose-response curves of [Ca c 2+]-spiking. Such response curves applying to several GPCR pathways have been investigated in [50,52,58,73]. These dose-response curves are the mathematical representation of GPCR mediated signal transduction ). There have been several studies in which dose-response of GPCR targeting agonist is presented in terms of area under the curve (AUC) and amplitude of [Ca c 2+]-response [50,73]. However, there are rather fewer investigations where the dose-response curve is constructed based on agonist-mediated frequency encoding [51]. In this scenario, we present three examples of dose-response curves for specific agonists that are used as neuromodulators (Fig.6). Saxena et al. [51] reported the dose-response curve that uses the number of [Ca c 2+]-spikes obtained through stimulation of serotonin1A receptor (Gαq coupled) in CHO cells (Fig. 6(a)). In another study [50], the dose-response curve with respect to the amplitude of acetylcholine (Gαq) mediated [Ca c 2+]-oscillation has been reported (Fig. 6(b)). An example of dose-response of 2-chloro-N6-cyclopentyladenosine targeting Adenosine-A1 receptor (Gαi/o coupled) in terms of AUC has also been shown in Fig. 6(c).
Fig. 6.
Dose-response characteristics of [Cac2+]-spiking for various GPCR targeting agonists: Experimental results and model predictions (a) Dose-response curve of [Cac2+]-spikes via. Stimulation of serotonin1A receptor (Gαq coupled) in CHO cells [51]. (b) Dose-response curve with respect to the amplitude of acetylcholine mediated [Cac2+]-oscillation in Neuro2a cells (Gαq pathway) [50], (c) Dose-response curve with respect to AUC of [Cac2+]-oscillation evoked by stimulation of Adenosine-A1 receptor (Gαi/o pathway) by 2-chloro-N6-cyclopentyladenosine in HEK293 cells [73]. Comparison of experimental and simulated dose-response with respect to ISI (d)-(e) and the fraction of non-oscillating cells (f)-(g) in ATP mediated[Cac2+]-oscillations in NIH-3 T3/MDA-MB-231 cells [65]. Copyright (2020).
The construction of such a dose-response curve and analysis of [Ca c 2+]-oscillations can provide valuable insights into drug potential, which can further aid in the faster in-vitro screening of drugs [52,74]. Although some of the experimental studies have been conducted to obtain the dose-response curves for GPCR targeting drugs, there are very few investigations on simulation of drug dose-dependent encoding of [Ca c 2+]-oscillation [54,59]. Especially, the predicted dose-response curves for GPCR targeting agonists obtained from simulations are not validated with experimental results. Mourya et al. [75] proposed a model for prediction of the dose-response for complement component 5a (C5a) in Raw 264.7 cells where parameter estimation for the dose-response curve was performed using sensitivity analysis. Simulated results for [Ca c 2+]-amplitude were in agreement with experimental values at various doses of C5a. The dose-response was found to be ultra-sensitive since multiple steps are involved in the signaling cascade starting from C5a receptor activation to Ca2+ release [75]. In 2014, Long-Fei Li et al. [76] developed another model to study the dose-response for Ca2+-flux in spermatozoa where the proposed model gives the transient Ca2+-responses to various concentrations of progesterone. Parameters were estimated by fitting the experimental data and the simulated dose-response curve was in agreement with the Ca2+-dynamics observed in experiments. However, while attempting a match between Ca2+-dynamics in a cell population, cell-to-cell variability remains the main reason for discrepancies between experiment and model results. In order to address this issue, a distribution in drug concentration was assumed for obtaining a qualitative match between simulation and experimental data on the dose-response of norepinephrine in HeLa cells [54]. In this study α2-adrenergic receptor was activated at three different doses of norepinephrine (Fig. 5(d)).
Later in 2016, another model describes histamine receptor-mediated Ca2+-dynamics that considers intercellular fluxes due to electrical and biochemical coupling between neighboring cells via gap junction. In this model, Ca2+-dynamics is regulated by the [Ca c 2+] through multiple feedback loops, which includes the dynamics of PMCA, Ca2+-channels, endoplasmic reticulum uptake, and IP3 activity (Fig. 5(e)). In their investigation, endothelial cells were treated with various doses of histamine and the proposed model could successfully predict the dependence of ISI on histamine concentration. Similarly, a stochastic model for collective Ca2+-signaling was developed that captures ATP-induced Ca2+-oscillation [65]. This model considers the IP3-mediated opening of Ca2+-channels, and the nonlinear dependence of the opening probability on the Ca2+-concentration. The corresponding model structure is shown in Fig. 5(f). In order to incorporate the cell to cell variability, all the model parameters were varied to a specific fold change and the model could predict the pattern in a change in ISI of Ca2+-oscillation in a cell population with a change in ATP concentration (Fig. 6(d)-(e)). The fraction of oscillating cells and the distribution of ISI at various doses agree well with experimental dose-response (Fig. 6(d)-(g)). In this study, a combination of modeling and experiment indicates that the frequency of Ca2+-oscillation increases with agonist dose as well as cell density due to augmented connectivity between cells. Such mathematical models validated by the experimental data can further save on the cost of performing expensive imaging experiments. This can also allow us to understand the abnormalities (diseased conditions) and the effect of drugs, as the change can be reflected through a change in parameter values in the mathematical equations [25].
Most of the existing studies that combine experimental, as well as computational investigations on dose responses, are able to capture a qualitative similarity between the predicted and experimental responses. However, cell-specific modeling of Ca2+-dynamics along with parameter estimation using an evolutionary algorithm can be crucial for the prediction of drug-dose response [25].
Another limitation of the models referred here is that they are based on the “well-stirred-reactor” assumption where all components of the signaling cascade are uniformly distributed in the cytoplasm. A state-of-art approach is to model the system as a reaction-diffusion process using partial differential equations and incorporation of stochastic parameters that are less assumptive and accounts for the inherent variability in receptor states at different time points [77,78]. However, such an approach is computationally expensive. In the future, such models have the potential to generate stochastic cellular response and cell-to-cell variability and validate the dose-response curves at tissue levels.
5. Conclusions and perspectives
It has been noticed that a large amount of information is available on GPCR targeting agonists that are central in treating cardiac, respiratory and neuro-diseases, and activate Gαq, Gαs, and Gαi/o pathways to regulate the Ca2+-dynamics (Table 1 and Fig. 2). Most experimental investigations focus on understanding the role of agonists concentration in modulating [Ca c 2+]-oscillations. Parallel to this, there have also been efforts in understanding the role of GPCR targeting drugs in regulating Ca2+-dynamics through constructing non-linear ODE models for [Ca c 2+]-oscillations (Table 2). Although some of the models describing the agonist-mediated encoding of [Ca c 2+]-oscillations are cell type-specific (Table 2) [54,59], many of the computational models describing the oscillation and the mechanisms are not specific to any cell line. Moreover, most of the computational models for Ca2+-dynamics focus on Gαq signaling and there are few investigations on Gαs and Gαi/o [54,79]. Existing models are able to decipher an interplay of positive and negative feedbacks present in the system which control uneven inter-spike-interval and frequency of [Ca c 2+]-oscillation. However, further studies are needed to be carried out to investigate the effect of specific drugs in a particular tissue type. Also, we need to have an integrated framework that investigates the dysregulation of Ca2+ in the context of various diseases.
The current paper presents a summary of G-protein coupled receptor-mediated models along with their network structures and feedback loops. Although the inclusion of all the models and mechanisms delineating GPCR mediated Ca2+-dynamics is beyond the scope of this review, it is sincere efforts of the authors to provide a clear perspective of signal transduction with two examples in detail. This review is expected to provide in-depth insight on feedback loops and understanding of crucial kinetic parameters that are involved in regulating the specific features of [Ca c 2+]-oscillations including frequency and amplitudes. This review can be used as a guideline by pharmacologists and computational biologists for comprehending the systems perspectives underlying Ca2+-signaling towards drug selection and screening of GPCR targeting drugs.
Author contribution
All authors contributed to the conception and design of the work. VD, SS and LG planned the work. VD, SG, RKG, and LG contributed to the writing of the manuscript. VD prepared the schematics and figures. KVV and LG reviewed the manuscript. All authors read and approved the final manuscript.
Declaration of Competing Interest
The authors declare that they have no competing interests.
Acknowledgements
The authors would like to thank the Director, Indian Institute of Technology Hyderabad (IIT—H), India for his support and encouragement for performing this study. The authors acknowledge the research facilities provided by IIT—H, India. The authors also thank Department of Science and Technology, India for providing financial assistance in the form of the SERB project, EMR/2016/007068. The authors thank Dr. Soumya Jana and Dr. Ajith Karunarathne for the fruitful discussions.
References
- 1.Zhang R., Xie X. Tools for GPCR drug discovery. Acta Pharmacol. Sin. 2012;33:372–384. doi: 10.1038/aps.2011.173. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Nash M.S., Young K.W., Challiss R.A., Nahorski S.R. Intracellular signalling. Receptor-specific messenger oscillations. Nature. 2001;413:381–382. doi: 10.1038/35096643. [DOI] [PubMed] [Google Scholar]
- 3.Zierler S., Hampe S., Nadolni W. TRPM channels as potential therapeutic targets against pro-inflammatory diseases. Cell Calcium. 2017;67:105–115. doi: 10.1016/j.ceca.2017.05.002. [DOI] [PubMed] [Google Scholar]
- 4.Nieto Gutierrez A., McDonald P.H. GPCRs: emerging anti-cancer drug targets. Cell. Signal. 2018;41:65–74. doi: 10.1016/j.cellsig.2017.09.005. [DOI] [PubMed] [Google Scholar]
- 5.Humeau J., Pedro J.M.B.-S., Vitale I., Nuñez L., Villalobos C., Kroemer G., Senovilla L. Calcium signaling and cell cycle: progression or death. Cell Calcium. 2018;70:3–15. doi: 10.1016/j.ceca.2017.07.006. [DOI] [PubMed] [Google Scholar]
- 6.Janssen L.J., Mukherjee S., Ask K. Calcium homeostasis and ionic mechanisms in pulmonary fibroblasts. Am. J. Respir. Cell Mol. Biol. 2015;53:135–148. doi: 10.1165/rcmb.2014-0269TR. [DOI] [PubMed] [Google Scholar]
- 7.Zhou Y., Hou Y., Shen J., Huang Y., Martin W., Cheng F. Network-based drug repurposing for novel coronavirus 2019-nCoV/SARS-CoV-2. Cell Discov. 2020;6:14. doi: 10.1038/s41421-020-0153-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Walker J.K.L., Fisher J.T. Editorial overview: respiratory: GPCR signaling and the lung. Curr. Opin. Pharmacol. 2014;16:iv–vi. doi: 10.1016/j.coph.2014.05.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Wendell S.G., Fan H., Zhang C. G protein–coupled receptors in asthma therapy: pharmacology and drug action. Pharmacol. Rev. 2020;72:1–49. doi: 10.1124/pr.118.016899. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Nair P., Milan S.J., Rowe B.H. Addition of intravenous aminophylline to inhaled beta2 -agonists in adults with acute asthma. Cochrane Database Syst. Rev. 2012 doi: 10.1002/14651858.cd002742.pub2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Hasenfuss G., Pieske B. Calcium cycling in congestive heart failure. J. Mol. Cell. Cardiol. 2002;34:951–969. doi: 10.1006/jmcc.2002.2037. [DOI] [PubMed] [Google Scholar]
- 12.Pchitskaya E., Popugaeva E., Bezprozvanny I. Calcium signaling and molecular mechanisms underlying neurodegenerative diseases. Cell Calcium. 2018;70:87–94. doi: 10.1016/j.ceca.2017.06.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Saxena A., Dhyani V., Suman G., Giri L. 2019 41st Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC) 2019. Effect of topology and time window on probability distribution underlying baclofen induced Ca2 response in hippocampal neurons*. [DOI] [PubMed] [Google Scholar]
- 14.Berridge M.J., Bootman M.D., Roderick H.L. Calcium signalling: dynamics, homeostasis and remodelling. Nat. Rev. Mol. Cell Biol. 2003;4:517–529. doi: 10.1038/nrm1155. [DOI] [PubMed] [Google Scholar]
- 15.Bhosale G., Sharpe J.A., Sundier S.Y., Duchen M.R. Calcium signaling as a mediator of cell energy demand and a trigger to cell death. Ann. N. Y. Acad. Sci. 2015;1350:107–116. doi: 10.1111/nyas.12885. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Chemaly E.R., Troncone L., Lebeche D. SERCA control of cell death and survival. Cell Calcium. 2018;69:46–61. doi: 10.1016/j.ceca.2017.07.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Kuo I.Y., Ehrlich B.E. Signaling in muscle contraction. Cold Spring Harb. Perspect. Biol. 2015;7:a006023. doi: 10.1101/cshperspect.a006023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Kaeser P.S., Regehr W.G. Molecular mechanisms for synchronous, asynchronous, and spontaneous neurotransmitter release. Annu. Rev. Physiol. 2014;76:333–363. doi: 10.1146/annurev-physiol-021113-170338. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Dolmetsch R.E., Xu K., Lewis R.S. Calcium oscillations increase the efficiency and specificity of gene expression. Nature. 1998;392:933–936. doi: 10.1038/31960. [DOI] [PubMed] [Google Scholar]
- 20.Machaca K. Ca2 signaling, genes and the cell cycle. Cell Calcium. 2010;48:243–250. doi: 10.1016/j.ceca.2010.10.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Fridlyand L.E., Jacobson D.A., Kuznetsov A., Philipson L.H. A model of action potentials and fast Ca2 dynamics in pancreatic β-cells. Biophys. J. 2009;96:3126–3139. doi: 10.1016/j.bpj.2009.01.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Carafoli E. Calcium signaling: a tale for all seasons. Proc. Natl. Acad. Sci. U. S. A. 2002;99:1115–1122. doi: 10.1073/pnas.032427999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Institute of Biochemistry Ernesto Carafoli, E, Carafoli C.B. Klee, Chief Laboratory of Biochemistry Claude B Klee . Oxford University Press; USA: 1999. Calcium as a Cellular Regulator. [Google Scholar]
- 24.Balaji R., Bielmeier C., Harz H., Bates J., Stadler C., Hildebrand A., Classen A.-K. Calcium spikes, waves and oscillations in a large, patterned epithelial tissue. Sci. Rep. 2017;7 doi: 10.1038/srep42786. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Upadhyay V., Teja R.S., Dhyani V., George K., Swain S., Mitra K., Giri L. 2019 9th International IEEE/EMBS Conference on Neural Engineering (NER) 2019. A model screening framework for the generation of Ca2 oscillations in hippocampal neurons using differential evolution. [DOI] [Google Scholar]
- 26.Clapham D.E. Calcium Signaling. Cell. 2007;131:1047–1058. doi: 10.1016/j.cell.2007.11.028. [DOI] [PubMed] [Google Scholar]
- 27.Manninen T., Havela R., Linne M.-L. Computational models for calcium-mediated astrocyte functions. Front. Comput. Neurosci. 2018;12:14. doi: 10.3389/fncom.2018.00014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Calcium Signaling Adv. Exp. Med. Biol. 2020 doi: 10.1007/978-3-030-12457-1. [DOI] [Google Scholar]
- 29.Dupont G., Falcke M., Kirk V., Sneyd J. 2016. Models of Calcium Signalling, Interdisciplinary Applied Mathematics. [DOI] [Google Scholar]
- 30.Thul R. Translating intracellular calcium signaling into models. Cold Spring Harb Protoc. 2014;2014 doi: 10.1101/pdb.top066266. [DOI] [PubMed] [Google Scholar]
- 31.Dupont G., Combettes L., Bird G.S., Putney J.W. Calcium Oscillations. Cold Spring Harb. Perspect. Biol. 2011;3:a004226. doi: 10.1101/cshperspect.a004226. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Sakai T., Naito A.T., Kuramoto Y., Ito M., Okada K., Higo T., Nakagawa A., Shibamoto M., Yamaguchi T., Sumida T., Nomura S., Umezawa A., Miyagawa S., Sawa Y., Morita H., Lee J.-K., Shiojima I., Sakata Y., Komuro I. Phenotypic screening using patient-derived induced pluripotent stem cells identified Pyr3 as a candidate compound for the treatment of infantile hypertrophic cardiomyopathy. Int. Heart J. 2018;59:1096–1105. doi: 10.1536/ihj.17-730. [DOI] [PubMed] [Google Scholar]
- 33.Wiśniewski K., Car H. (S)-3,5-DHPG: a review. CNS Drug Rev. 2002;8:101–116. doi: 10.1111/j.1527-3458.2002.tb00218.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Galici R., Jones C.K., Hemstapat K., Nong Y., Echemendia N.G., Williams L.C., de Paulis T., Conn P.J. Biphenyl-indanone a, a positive allosteric modulator of the metabotropic glutamate receptor subtype 2, has antipsychotic- and anxiolytic-like effects in mice. J. Pharmacol. Exp. Ther. 2006;318:173–185. doi: 10.1124/jpet.106.102046. [DOI] [PubMed] [Google Scholar]
- 35.Tuncel M., Ram V.C.S. Hypertensive emergencies. Etiology and management. Am. J. Cardiovasc. Drugs. 2003;3:21–31. doi: 10.2165/00129784-200303010-00003. [DOI] [PubMed] [Google Scholar]
- 36.Rang H.P., Dale M.M., Ritter J.M., Flower R.J., Henderson G. Elsevier Health Sciences; 2011. Rang & Dale’s Pharmacology. [Google Scholar]
- 37.Pasternak G.W. Opioid receptors: the early years. Opiate Receptor. 2011:59–91. doi: 10.1007/978-1-60761-993-2_4. [DOI] [Google Scholar]
- 38.Rylova S.N., Stoykow C., Del Pozzo L., Abiraj K., Tamma M.L., Kiefer Y., Fani M., Maecke H.R. The somatostatin receptor 2 antagonist 64Cu-NODAGA-JR11 outperforms 64Cu-DOTA-TATE in a mouse xenograft model. PLoS One. 2018;13 doi: 10.1371/journal.pone.0195802. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Konstam M.A., Gheorghiade M., Burnett J.C., Jr., Grinfeld L., Maggioni A.P., Swedberg K., Udelson J.E., Zannad F., Cook T., Ouyang J., Zimmer C., Orlandi C. Efficacy of vasopressin antagonism in heart failure outcome study with Tolvaptan (EVEREST) investigators, effects of oral tolvaptan in patients hospitalized for worsening heart failure: the EVEREST outcome trial. JAMA. 2007;297:1319–1331. doi: 10.1001/jama.297.12.1319. [DOI] [PubMed] [Google Scholar]
- 40.Treschan T.A., Peters J. The vasopressin system: physiology and clinical strategies. Anesthesiology. 2006;105:599–612. doi: 10.1097/00000542-200609000-00026. (quiz 639–40) [DOI] [PubMed] [Google Scholar]
- 41.Udelson J.E., Smith W.B., Hendrix G.H., Painchaud C.A., Ghazzi M., Thomas I., Ghali J.K., Selaru P., Chanoine F., Pressler M.L., Konstam M.A. Acute hemodynamic effects of conivaptan, a dual V(1A) and V(2) vasopressin receptor antagonist, in patients with advanced heart failure. Circulation. 2001;104:2417–2423. doi: 10.1161/hc4501.099313. [DOI] [PubMed] [Google Scholar]
- 42.Lodish H.F., Berk Lodish (zipursky Matsudaria, A), Berk J.E. Darnell, Zipursky S. Lawrence, Baltimore D., Matsudaira P. Scientific American Library; 2000. Molecular Cell Biology. [Google Scholar]
- 43.Bezprozvanny L., Watras J., Ehrlich B.E. Bell-shaped calcium-response curves of lns(l,4,5)P3- and calcium-gated channels from endoplasmic reticulum of cerebellum. Nature. 1991;351:751–754. doi: 10.1038/351751a0. [DOI] [PubMed] [Google Scholar]
- 44.Neher E., Augustine G.J. Calcium gradients and buffers in bovine chromaffin cells. J. Physiol. 1992;450:273–301. doi: 10.1113/jphysiol.1992.sp019127. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Lavrentovich M., Hemkin S. A mathematical model of spontaneous calcium(II) oscillations in astrocytes. J. Theor. Biol. 2008;251:553–560. doi: 10.1016/j.jtbi.2007.12.011. [DOI] [PubMed] [Google Scholar]
- 46.Cho Y.-W., Kim E.-J., Nyiramana M.M., Shin E.-J., Jin H., Ryu J.H., Kang K.R., Lee G.-W., Kim H.J., Han J., Kang D. Paroxetine induces apoptosis of human breast cancer MCF-7 cells through Ca-and p38 MAP Kinase-dependent ROS generation. Cancers. 2019;11 doi: 10.3390/cancers11010064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Shen J.-X. Isoprenaline enhances local Ca2+ release in cardiac myocytes. Acta Pharmacol. Sin. 2006;27:927–932. doi: 10.1111/j.1745-7254.2006.00383.x. [DOI] [PubMed] [Google Scholar]
- 48.Shen A., Chen D., Kaur M., Bartels P., Xu B., Shi Q., Martinez J.M., Man K.-N.M., Nieves-Cintron M., Hell J.W., Navedo M.F., Yu X.-Y., Xiang Y.K. β-blockers augment L-type Ca channel activity by targeting spatially restricted βAR signaling in neurons. Elife. 2019;8 doi: 10.7554/eLife.49464. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Wang J., Toan S., Li R., Zhou H. Melatonin fine-tunes intracellular calcium signals and eliminates myocardial damage through the IP3R/MCU pathways in cardiorenal syndrome type 3. Biochem. Pharmacol. 2020;174:113832. doi: 10.1016/j.bcp.2020.113832. [DOI] [PubMed] [Google Scholar]
- 50.Shelukhina I., Spirova E., Kudryavtsev D., Ojomoko L., Werner M., Methfessel C., Hollmann M., Tsetlin V. Calcium imaging with genetically encoded sensor Case12: facile analysis of α7/α9 nAChR mutants. PLoS One. 2017;12 doi: 10.1371/journal.pone.0181936. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Saxena R., Ganguly S., Chattopadhyay A. Comparative analysis of calcium spikes upon activation of serotonin(1A) and purinergic receptors. PLoS One. 2012;7 doi: 10.1371/journal.pone.0051857. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Gupta R.K., Swain S., Kankanamge D., Priyanka P.D., Singh R., Mitra K., Karunarathne A., Giri L. Comparison of calcium dynamics and specific features for G protein–coupled receptor–targeting drugs using live cell imaging and automated analysis. SLAS DISCOVERY Adv. Sci. Drug Discovery. 2017;22:848–858. doi: 10.1177/2472555217693378. [DOI] [PubMed] [Google Scholar]
- 53.Woods N.M., Cuthbertson K.S., Cobbold P.H. Repetitive transient rises in cytoplasmic free calcium in hormone-stimulated hepatocytes. Nature. 1986;319:600–602. doi: 10.1038/319600a0. [DOI] [PubMed] [Google Scholar]
- 54.Giri L., Patel A.K., Karunarathne W.K.A., Kalyanaraman V., Venkatesh K.V., Gautam N. A G-protein subunit translocation embedded network motif underlies GPCR regulation of calcium oscillations. Biophys. J. 2014;107:242–254. doi: 10.1016/j.bpj.2014.05.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Freestone N.S., Ribaric S., Scheuermann M., Mauser U., Paul M., Vetter R. Differential lusitropic responsiveness to beta-adrenergic stimulation in rat atrial and ventricular cardiac myocytes. Pflugers Arch. 2000;441:78–87. doi: 10.1007/s004240000397. [DOI] [PubMed] [Google Scholar]
- 56.Prakash Y.S., van der Heijden H.F., Kannan M.S., Sieck G.C. Effects of salbutamol on intracellular calcium oscillations in porcine airway smooth muscle. J. Appl. Physiol. 1997;82:1836–1843. doi: 10.1152/jappl.1997.82.6.1836. [DOI] [PubMed] [Google Scholar]
- 57.Saxena A., Dhyani V., Jana S., Giri L. 2020 National Conference on Communications (NCC) IEEE; 2020. Application of kohonen-self organizing map to cluster drug induced Ca 2 + response in hippocampal neurons at different drug dose; pp. 1–6. [Google Scholar]
- 58.Thurley K., Tovey S.C., Moenke G., Prince V.L., Meena A., Thomas A.P., Skupin A., Taylor C.W., Falcke M. Reliable encoding of stimulus intensities within random sequences of intracellular Ca2+ spikes. Sci. Signal. 2014;7 doi: 10.1126/scisignal.2005237. ra59. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Kummer U., Olsen L.F., Dixon C.J., Green A.K., Bornberg-Bauer E., Baier G. Switching from simple to complex oscillations in calcium signaling. Biophys. J. 2000;79:1188–1195. doi: 10.1016/S0006-3495(00)76373-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Larsen A.Z., Olsen L.F., Kummer U. On the encoding and decoding of calcium signals in hepatocytes. Biophys. Chem. 2004;107:83–99. doi: 10.1016/j.bpc.2003.08.010. [DOI] [PubMed] [Google Scholar]
- 61.De Pittà M., Goldberg M., Volman V., Berry H., Ben-Jacob E. Glutamate regulation of calcium and IP3 oscillating and pulsating dynamics in astrocytes. J. Biol. Phys. 2009;35:383–411. doi: 10.1007/s10867-009-9155-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Han J.M., Tanimura A., Kirk V., Sneyd J. A mathematical model of calcium dynamics in HSY cells. PLoS Comput. Biol. 2017;13 doi: 10.1371/journal.pcbi.1005275. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Gaspers L.D., Bartlett P.J., Politi A., Burnett P., Metzger W., Johnston J., Joseph S.K., Höfer T., Thomas A.P. Hormone-induced calcium oscillations depend on cross-coupling with inositol 1,4,5-trisphosphate oscillations. Cell Rep. 2014;9:1209–1218. doi: 10.1016/j.celrep.2014.10.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Sun J., Hoying J.B., Deymier P.A., Zhang D.D., Wong P.K. Cellular architecture regulates collective calcium signaling and cell contractility. PLoS Comput. Biol. 2016;12 doi: 10.1371/journal.pcbi.1004955. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Potter G.D., Byrd T.A., Mugler A., Sun B. Communication shapes sensory response in multicellular networks. Proc. Natl. Acad. Sci. U. S. A. 2016;113:10334–10339. doi: 10.1073/pnas.1605559113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Baillie G.S., Sood A., McPhee I., Gall I., Perry S.J., Lefkowitz R.J., Houslay M.D. beta-Arrestin-mediated PDE4 cAMP phosphodiesterase recruitment regulates beta-adrenoceptor switching from Gs to Gi. Proc. Natl. Acad. Sci. U. S. A. 2003;100:940–945. doi: 10.1073/pnas.262787199. [DOI] [PMC free article] [PubMed] [Google Scholar] [Retracted]
- 67.Rinaldi L., Delle Donne R., Catalanotti B., Torres-Quesada O., Enzler F., Moraca F., Nisticò R., Chiuso F., Piccinin S., Bachmann V., Lindner H.H., Garbi C., Scorziello A., Russo N.A., Synofzik M., Stelzl U., Annunziato L., Stefan E., Feliciello A. Feedback inhibition of cAMP effector signaling by a chaperone-assisted ubiquitin system. Nat. Commun. 2019;10:2572. doi: 10.1038/s41467-019-10037-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Abell E., Ahrends R., Bandara S., Park B.O., Teruel M.N. Parallel adaptive feedback enhances reliability of the Ca2+ signaling system. Proc. Natl. Acad. Sci. U. S. A. 2011;108:14485–14490. doi: 10.1073/pnas.1018266108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Cully T.R., Choi R.H., Bjorksten A.R., Stephenson D.G., Murphy R.M., Launikonis B.S. Junctional membrane Ca dynamics in human muscle fibers are altered by malignant hyperthermia causative RyR mutation. Proc. Natl. Acad. Sci. U. S. A. 2018;115:8215–8220. doi: 10.1073/pnas.1800490115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Meera P., Pulst S., Otis T. A positive feedback loop linking enhanced mGluR function and basal calcium in spinocerebellar ataxia type 2. Elife. 2017;6 doi: 10.7554/eLife.26377. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Lewis K.J., Silvester N.C., Barberini-Jammaers S., Mason S.A., Marsh S.A., Lipka M., George C.H. A new system for profiling drug-induced calcium signal perturbation in human embryonic stem cell-derived cardiomyocytes. J. Biomol. Screen. 2015;20:330–340. doi: 10.1177/1087057114557232. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Honarnejad K., Kirsch A.K., Daschner A., Szybinska A., Kuznicki J., Herms J. FRET-based calcium imaging: a tool for high-throughput/content phenotypic drug screening in Alzheimer disease. J. Biomol. Screen. 2013;18:1309–1320. doi: 10.1177/1087057113502672. [DOI] [PubMed] [Google Scholar]
- 73.Rittiner J.E., Korboukh I., Hull-Ryde E.A., Jin J., Janzen W.P., Frye S.V., Zylka M.J. AMP is an adenosine A1 receptor agonist. J. Biol. Chem. 2012;287:5301–5309. doi: 10.1074/jbc.M111.291666. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Ma Q., Ye L., Liu H., Shi Y., Zhou N. An overview of Ca mobilization assays in GPCR drug discovery. Expert Opin. Drug Discovery. 2017;12:511–523. doi: 10.1080/17460441.2017.1303473. [DOI] [PubMed] [Google Scholar]
- 75.Maurya M.R., Subramaniam S. A kinetic model for calcium dynamics in RAW 264.7 cells: 2. Knockdown response and long-term response. Biophys. J. 2007;93:729–740. doi: 10.1529/biophysj.106.097501. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Li L.-F., Xiang C., Zhu Y.-B., Qin K.-R. Modeling of progesterone-induced intracellular calcium signaling in human spermatozoa. J. Theor. Biol. 2014;351:58–66. doi: 10.1016/j.jtbi.2014.02.026. [DOI] [PubMed] [Google Scholar]
- 77.Powell J., Falcke M., Skupin A., Bellamy T.C., Kypraios T., Thul R. A statistical view on calcium oscillations. Adv. Exp. Med. Biol. 2020;1131:799–826. doi: 10.1007/978-3-030-12457-1_32. [DOI] [PubMed] [Google Scholar]
- 78.Gómez-Aguilar J.F., Abro K.A., Kolebaje O., Yildirim A. Chaos in a calcium oscillation model via Atangana-Baleanu operator with strong memory. Eur. Phys. J. Plus. 2019;134 doi: 10.1140/epjp/i2019-12550-1. [DOI] [Google Scholar]
- 79.Montefusco F., Pedersen M.G. Mathematical modelling of local calcium and regulated exocytosis during inhibition and stimulation of glucagon secretion from pancreatic alpha-cells. J. Physiol. 2015;593:4519–4530. doi: 10.1113/JP270777. [DOI] [PMC free article] [PubMed] [Google Scholar]