Abstract
HIV-1 protease (PR) is the viral protein responsible for virion maturation, and its mechanisms of action remain incompletely understood. PR is dimeric and contains two flexible, symmetry-related flaps which act as a gate to inhibit access to the binding pocket and hold the polypeptide substrate in the binding pocket once bound. Wide flap opening, a conformational change assumed to be necessary for substrate binding, is a rare event in the closed and bound form. In this study, we use molecular dynamics (MD) simulations and advanced MD techniques including temperature-acceleration and string method in collective variables to study the conformational changes associated with substrate unbinding of both wild-type and F99Y mutant PR. The F99Y mutation is shown via MD to decouple the closing of previously unrecognized distal pockets from substrate unbinding. To determine whether or not the F99Y mutation affects the energetic cost of wide flap opening, we use string method in collective variables to determine minimum free-energy mechanism for wide flap opening in concert with distal pocket closing. The results indicate that the major energetic cost in flap opening is disengagement of the two flap-tip Ile50 residues from each other and is not affected by the F99Y mutation.
Graphical Abstract
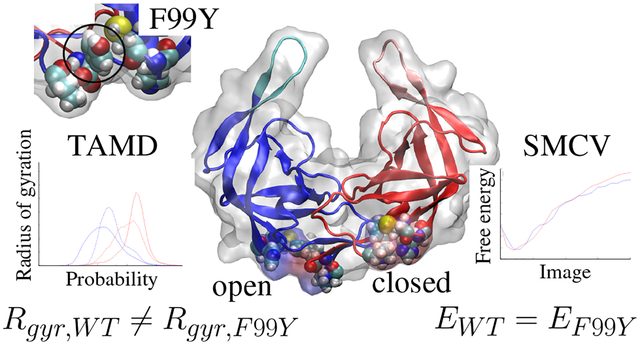
Introduction
HIV requires a maturation step involving the cleavage of Gag poly-protein (Gag-Pol) into the virus’s integral proteins by HIV protease (PR)1–3. This cleavage is a necessary and limiting step in the HIV lifecycle and understanding the mechanism by which protease works is important for overall understanding of this lifecycle. PR is a symmetric homodimer which forms a toroidal shape around the substrate binding pocket when in the closed form. The binding pocket becomes accessible through a gating mechanism of two flexible flap tips formed by β-turns at residues 46 to 56 of each monomer4,5. The flaps can visit several conformations, including the closed and tightly bound conformation when a substrate is in the binding pocket, the curled and closed apo conformation, and the wide open conformation6. Once unbound, the flaps are highly flexible, though they prefer to remain closer to the protein and do not frequently visit wide open conformations7–9. When a non-native substrate is sufficiently small, the protein may remain in the slightly open conformation to accept it,10,11 though this mechanism of binding is not available for the native substrate due to its size. For this reason, it is commonly believed that the flaps must open wide in order to function properly.
Molecular dynamics (MD) simulations allow visualization and characterization of protein movement with atomic precision and time scales not available through physical experiments. Moreover, advanced MD simulation techniques, such as temperature-accelerated MD (TAMD) and string method in collective variables (SMCV), afford us the ability to view and analyze protein movements during rare events typically outside of MD time scales12. TAMD uses temperature biasing to observe rare events in complex systems and has previously been used to study protein large-scale and loop conformational changes13,14. SMCV minimizes the free energy associated with a general conformational change and thus determines the most probable mechanism of the transition and 1-dimensional free energy profile associated with the change. SMCV has been applied to many biological processes including protein folding15, membrane fusion16,17, and small molecule diffusion18.
In this work, we use MD simulations and advanced MD techniques to study the conformational changes associated with the flap opening and binding pocket preparation of PR. By direct TAMD simulation, we first characterize conformational changes associated with substrate unbinding, with particular focus on the so-called distal pockets (DPs) on the opposite side of the PR dimer from the flaps. We examine the link between DP closing and substrate unbinding by studying both WT and F99Y mutant PR. We use SMCV to determine the minimum free energy pathway and thus most probable mechanism of flap opening in both wild-type and mutant PR, and we determine what role if any the DPs play in mediating the energetics of flap opening.
Methods
System generation and common simulation protocols
We generated an all-atom explicit water system of PR starting from the crystal structure of a protease-substrate complex in the closed and bound form (PDB ID 1F7A)19. The substrate is a 9-residue peptide representative of the full binding epitope of the capsid/p2 cleavage site of HIV-1 Gag-Pol. The structure was solvated in a water box padded with 10Å on each side. The protein, originally in an inactive form through a D25N mutation, was un-mutated to the wild-type using the VMD Mutator plugin20.
All molecular dynamics were simulated using using NAMD v. 2.1120 and visualized with VMD21. The CHARMM forcefield is used22,23 with TIP3P waters24. A Langevin piston barostat25,26 maintains a pressure of 1 bar with a period of 200 fs and a damping time of 100 fs. Temperature is held constant at 310 K using a Langevin thermostat27 with a damping coefficient of 1 ps−1. Protein orientation and position are fixed using the NAMD Colvars package28 through a force on all backbone carbons. Protein orientation is maintained with a force constant of 1,000 kcal/mol/radian2 and protein position with a force constant of 100 kcal/mol·Å2. RATTLE is used to keep bondlengths constrained and a 2 fs timestep is used. A cutoff of 10Å was used for non-bonded interactions, and a 1-Å grid spacing was used for the long-range electrostatics particle-mesh Ewald method.
Temperature-accelerated MD (TAMD)
In order to study spontaneous substrate unbinding within reasonable computational time, we used temperature-accelerated MD (TAMD) simulations. TAMD increases the accessibility of high free-energy states by tethering a collective variable (CV) to fictitious particle that moves slowly and diffusively on the physical free-energy landscape. Full details of this method have been extensively detailed before12,13,29–31 and will only be briefly reiterated here. One first invokes the definition of some vector of M CV components θ*(x) as functions of configuration x. For each component, we introduce an auxiliary variable θj and a multidimensional harmonic potential to tether the CV’s componentwise to the auxiliaries, resulting in the following extended potential energy and configurational dynamics:
| (1) |
| (2) |
| (3) |
where mi is the mass of xi, V (x) is the interatomic potential, κ is the spring constant of the restraining force, γ is the Langevin friction coefficient, and η is white noise with unit variance at temperature β−1. In TAMD, the dynamics of the auxiliary variables are intentionally slowed down relative to the fundamental variables by using a large value of the fictitious friction :
| (4) |
where is the mass of the fictitious particle. Here, the first term on the right hand side is the instantaneous force on the variable and the second term, ξj is the thermal noise at fictitious temperature, . In order to observe higher energy states, the fictitious temperature should be higher than the simulation temperature. Since the ensemble average of the restraining force provides an estimate of the negative gradient of the free energy as a function of the CV’s at point θ, the force acting on θ is an approximation of the gradient of the free energy at that local point. In this way, the auxiliary variables move at high temperature on the free-energy surface computed at β−1 as if it were a potential energy surface.
CV’s must be selected with care to accelerate the desired outcome while minimizing effects of unbiased, “hidden” variables. In the current study, the desired outcome includes opening of the flap tips and movement of the substrate out of the binding pocket. We anticipate that both of these movements will have significantly slower inherent time scales than normal protein fluctuations. We have chosen to accelerate the cartesian coordinates of the N- and C-termini of the substrate peptide to accelerate its movement relative to the pocket. Flap opening is described as the two distances between each flap tip and the center of the binding pocket.
In this work, TAMD is performed within NAMD through the CFACV package32. Relevant TAMD parameters include fictitious friction of 500 ps−1 for all CV components, a spring constant κ of 100 kcal/mol-Å2 for all components, and a fictitious temperature β−1 of 6 kcal/mol.
String method in collective variables (SMCV)
In order to evaluate the energetics of flap-opening, we used string method in collective variables (SMCV). The purpose of SMCV is to determine a one-dimensional minimum free energy pathway (MFEP) through a multi-dimensional CV space29,33–35. We present a very brief description here. Starting with a multidimensional free energy surface, F(z), any one-dimensional path embedded in CV space may be denoted parametrically z(a), where scalar a parameterizes distance along the path. By definition, the MFEP is that z(a) for which forces perpendicular to it on the free-energy landscape vanish, i.e.:
| (5) |
where M is the metric tensor. The MFEP is found by relaxation from a chosen initial string following the fictitious dynamics:
| (6) |
The first term represents a steepest descent on the free-energy surface, and the second represents maintaining the parameterization. To solve this equation, we work with a discrete path made of S images z(a) = {z0, z1, …, zS−1}. These images are prepared by assigning MD systems to appropriate values of z and running individual MD simulations to equilibrate each at its assigned initial z value. (This equilibration is made efficient by harvesting initial image systems from TAMD simulation trajectories.) From this set of initial images, each image’s assigned z is updated in two steps: first, an forward finite-difference based on M∇F, and second, reparameterization to enforce equal neighboring interimage spacing along the string. In the first step, we approximate the free-energy gradient and metric tensor via straightforward averaging over Nsamp MD time steps between updates of z defined by Eq. 6:
| (7) |
| (8) |
For both SMCV calculations performed here, we considered S = 24 images. For each image, two independent MD systems are used: one for computing ∇F and the other M; this means 48 individual MD systems are used to find a single MFEP. The string friction γ is initially set at 0.001 and the steps per string update Nsamp is 20. After ≈ 2.7 × 106 string updates, γ is updated to 0.05 and Nsamp is changed to 100. Convergence is assessed by saturation of the RMS fluctuations of z(a). Once converged, free-energy along the string is computed by fixing z’s and running 20 ns MD simulations to compute mean forces at each image location. The local tangential projection of these mean forces are then numerically integrated along parameter a to compute the free energy along the pathway.
Results and discussion
Enhanced simulations of substrate unbinding from the closed and bound state
We used a combination of MD and TAMD simulations to characterize PR conformational changes during substrate unbinding. Table 1 summarizes these simulations. MD was performed to prepare the crystallographic model (1F7A) for TAMD (both with and without substrate) and SMCV (without substrate only). In simulation WT-MDholo, the substrate-bound protein did not display any large scale conformational changes and the flaps remained tightly closed. An apo form was generated by deleting the substrate to generate MDapo, and in a standard 20-ns MD simulation this structure quickly reconfigured into the closed and curled form typically seen in the apo state6. The curled structure is similarly long-lived with no large scale conformational changes or unbinding of the flaps.
Table 1:
Single-image simulations.
| Designation | no. replicas | no. atoms | duration (ns) |
|---|---|---|---|
| WT-MDholo | 1 | 24,606 | 20 |
| WT-MDapo | 1 | 30,867 | 20 |
| WT-TAMDholo | 10 | 24,606 | 20 |
| WT-TAMDapo | 10 | 30,867 | 20 |
| F99Y-MDholo | 1 | 31,094 | 20 |
| F99Y-MDapo | 1 | 33,560 | 20 |
| F99Y-TAMDholo | 10 | 31,094 | 20 |
| F99Y-TAMDapo | 10 | 33,560 | 20 |
TAMD simulations introduced a new question into the availability and accessibility of the binding pocket to a substrate. We observed 10 independent substrate unbinding simulations using the TAMD protocol with the CV set as described in section. Substrate unbinding was observed in each TAMD simulation within the 20 ns designated.
Secondary conformational changes have been studied previously including a flattening of the protein linked to elbow engagements36,37. A similar movement is observed in the TAMD simulations of flap opening. We have quantified this using an angle defined by the quaternary structure of the dimeric complex. This angle, denoted here α, is formed from a vertex at the center of mass of residues 23 to 26 on both monomers and legs that reach to the alpha carbon of residue 40 on each monomer, as seen in Fig. 1. The normal domain of the protein angle appears to be between approximately 140° and 160°. In order to accept the substrate, a synergistic movement between the flaps and the connected elbows must occur as seen in Fig. 1A. Without engagement of the elbow region and wide protein angle, the binding pocket remains hindered by the 80s loop and not readily accessible to a substrate, as seen in Fig. 1B.
Figure 1:
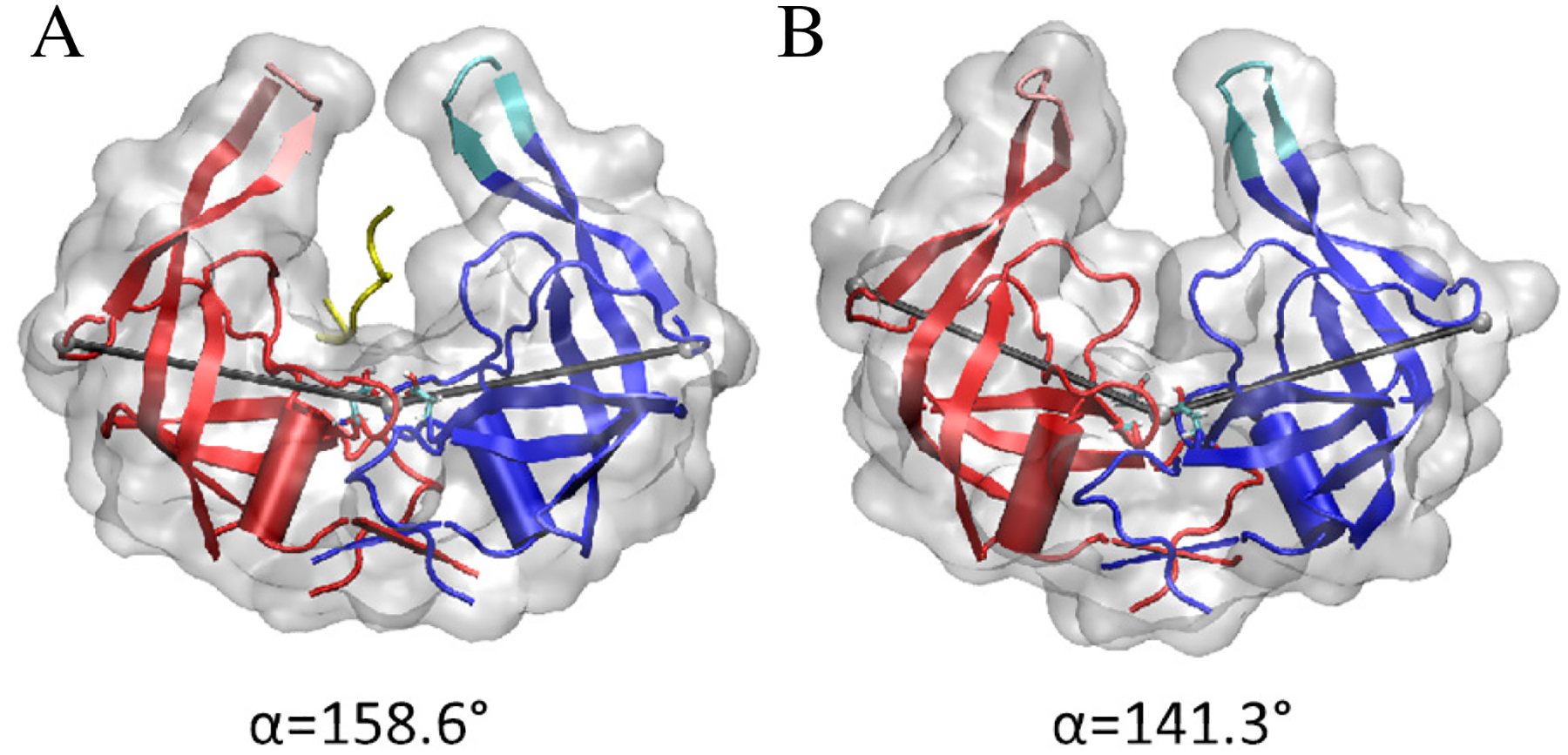
The quaternary angle α subtended at the center of residues 23 to 26 at the base of the protein and the alpha carbons on residues 40 on the turn of the beta loop which makes up the elbow region in each of the two monomers. The angle is shown in grey with the centers represented by grey spheres. Two representative values of α are shown with the flaps in a similarly open position. In A, the elbows are engaged and the binding pocket is in the fully open state (α ≈ 160°). In B, the elbows are disengaged and the binding pocket is in the closed state (α ≈ 140°).
TAMD simulations indicate that elbow engagement is a necessary and limiting step in substrate movement into or out of the binding pocket but is not directly correlated to wide flap opening. During substrate unbinding events, elbow engagement is correlated to flap opening width. Prior to the substrate’s exit from the pocket, elbow engagement is necessary and can delay substrate movement out of the pocket if not engaged. Indications of this phenomena may be seen in the Supporting Information. Throughout WT-TAMDholo simulations, elbow engagement is highly correlated to flap opening as seen in Fig. 2A. Conversely, in the absence of the substrate in WT-TAMDapo simulations, this correlation vanishes with wide flap opening occurring without significant elbow engagement as seen in Fig. 2B. The correlation between flap opening and elbow engagement only in the presence of a substrate suggests elbow engagement is more energetically favorable in the holo vs apo state.
Figure 2:

2-D probability density function of the quaternary angle α and flap distance from base in the (A) presence and (B) absence of a substrate. The areas of least density are shown in white and the areas of most density are shown in blue. Areas of moderate density are shown in green.
Hydrophobic pocket exists distal to binding pocket
There exist complementary movements in the protein structure during elbow engagement which tend to correlate with substrate unbinding. These movements include a change in the state of hydrophobic pocket which exists distal to the binding pocket. This distal pocket (DP) involves the N- and C-termini of opposing monomers in addition to several other residues including a cysteine at residue 67 and histidine at residue 69 as shown in the open and closed states in Fig. 3A. The DP exists in the open and solvated state normally in the apo protein with the phenylalanine at the C-terminus (F99) fully solvated similar to that seen in Fig. 3B. During a substrate unbinding event, DP’s close onto themselves with F99 curling into the protein structure and P1, C67, and H69 folding onto the pocket to protect the interior from the solvent as seen in Fig. 3C. This movement is highly correlated to the protein angle; the pocket is in the closed position when the elbows are fully engaged and open when the elbows are disengaged.
Figure 3:

Hydrophobic pocket distal to the binding pocket (DP) formed by P1, C67, H69, and F99 shown in the open and closed states. (A) A protein with flaps in similar positions with chain A (blue) with the elbows disengaged and DP open and chain B (shown in red) with the elbows engaged and DP closed. (B) DP in the fully open, solvated state. (C) DP in the closed state.
Similar to elbow engagement, the state of the distal pocket is not correlated to wide flap opening but it is observed as a critical protein movement towards extrication of the substrate from its bound position. Proof of the relationship between the motions as indicated by elbow engagement is included in the Supporting Information. The DP forms a bi-modal distribution of open and closed states when observed over simulations. In Fig. 4, the probability density distribution of radius of gyration of the DP’s is shown for WT-MDapo, WT-MDholo, WT-TAMDapo, and WT-TAMDholo. In the absence of a substrate, the pocket remains in the open state as indicated by a higher radius of gyration even during accelerated wide flap opening events. In the presence of a substrate, the DP’s exist more readily in the closed state with a wider distribution during WT-TAMDholo simulations which progress from the bound to unbound state.
Figure 4:
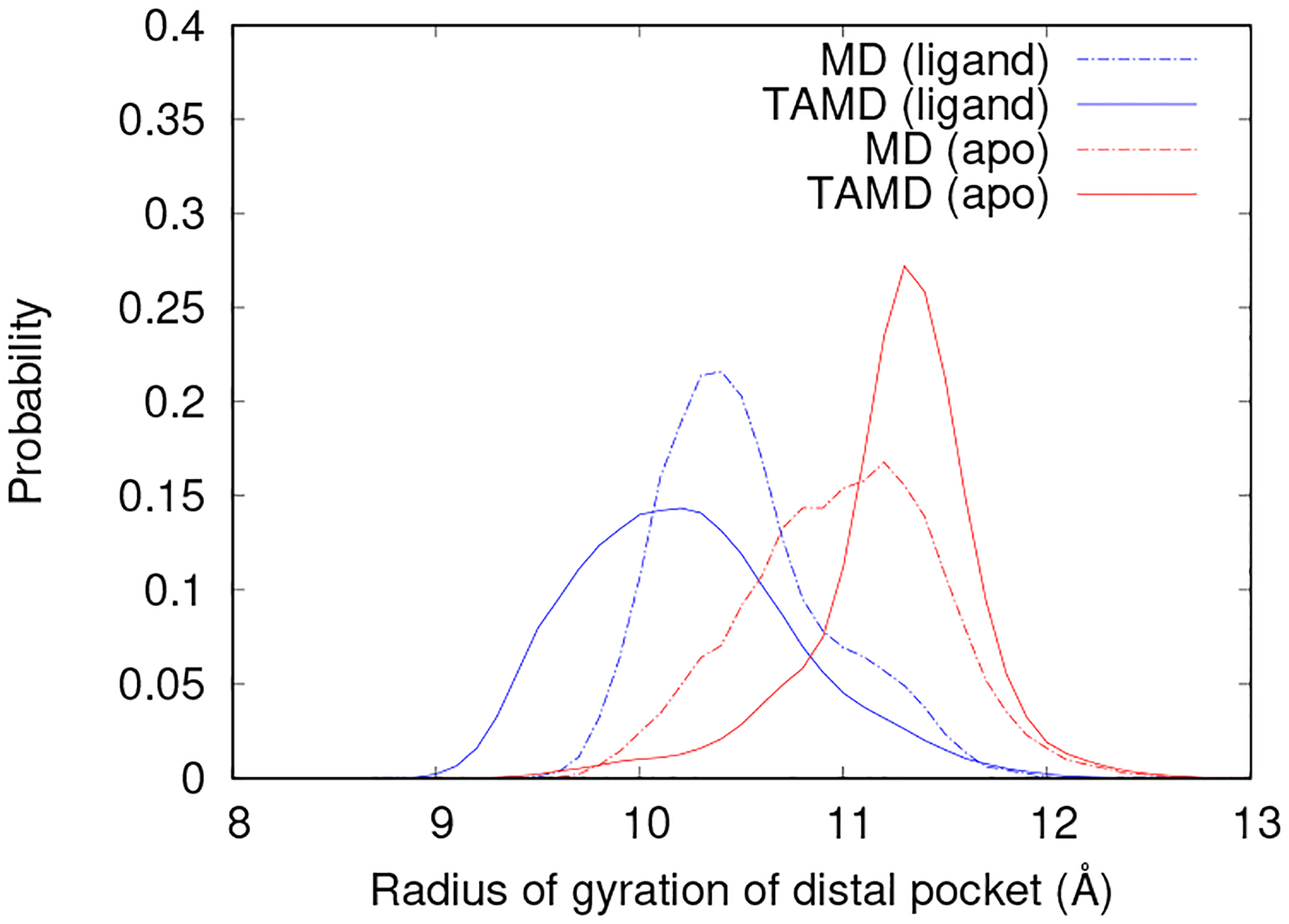
The probability density function of the radius of gyration of the DP for WT-MD (dashed lines) in the closed and bound state and WT-TAMD (solid lines) during flap opening in the apo state (shown in red) and in the presence of a substrate (shown in blue).
F99Y mutation affects conformational changes during substrate unbinding
To better understand how the distal hydrophobic pocket may contribute to stabilizing the open flaps, a main residue in the distal pocket, F99 is mutated to the structurally similar but hydrophilic tyrosine residue as seen in Fig. 5. F99Y-MD and F99Y-TAMD simulations of 20 ns were performed on the apo and substrate-bound states as outlined in Table 1. F99Y-MD simulations indicate that the closed structures in substrate-bound and apo states are metastable similar to WT proteins.
Figure 5:
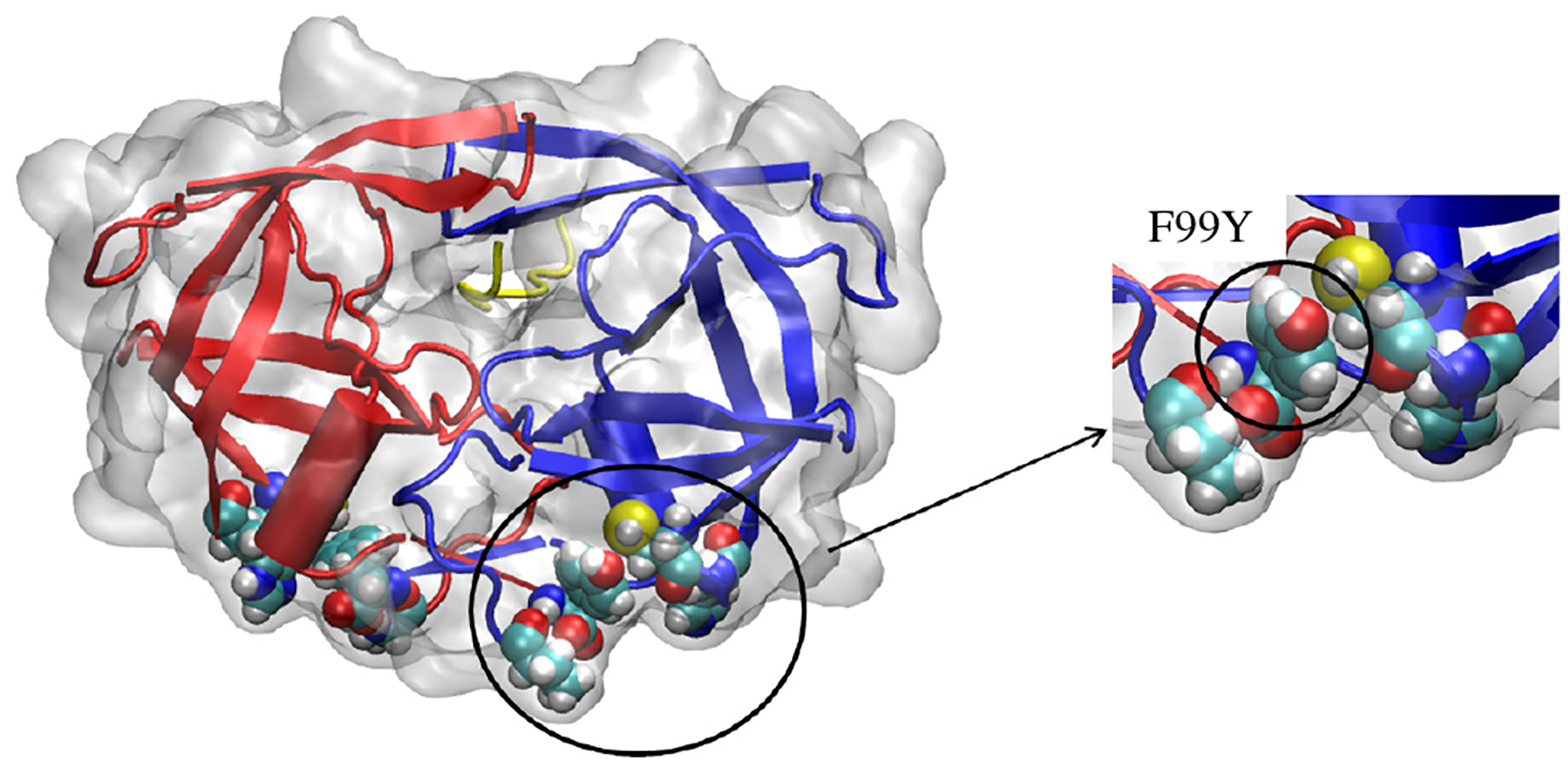
HIV-1 protease with residue 99 mutated from phenylalanine to tyrosine. The mutated distal pocket remains in the open position throughout F99Y-MD and F99Y-TAMD simulations.
F99Y-TAMD simulations are performed in 10 independent replicas using the CV described in section to observe opening of the flaps and substrate unbinding. With the mutation, the substrate unbinds and exits the binding pocket in all 10 F99Y-TAMD simulations similar to WT. Unlike the WT protein, the flaps retain Ile50 contact as the substrate exits the binding pocket in several instances. The elbows are not drawn back and engaged and the distal pocket remains effectively open with residue 99 on the hydrophobic surface similar to Fig. 5 and not tucked up into the protein as seen in WT. During substrate unbinding events, elbow engagement does not occur despite quick movement out of the binding pocket. In contrast to the unbinding events with WT PR, the protein is not flattened in its prime binding state at any point in the unbinding process. While the transition from closed and bound to open flaps was an irreversible process with WT, a reformation of the apo bound state is observed with F99Y after substrate unbinding. As the mutation hinders the ability of the DP to close, it additionally hinders regular flexibility of the flaps necessary to form and maintain the wide open conformation.
The mutant DP remains in the open state in the presence of a substrate as seen in Fig. 6. The apo protein exhibits little change in behavior of DP’s as WT exhibits open pockets. The altered behavior in TAMDholo removes a natural movement indicated for preparing the protein for substrate binding. In the mutant, change in the DPs remains highly correlated to elbow engagement. Therefore, limiting DP closure propagates through to other protein movements. Additional data regarding F99Y protein movement during TAMD simulations may be seen in the Supporting Information.
Figure 6:
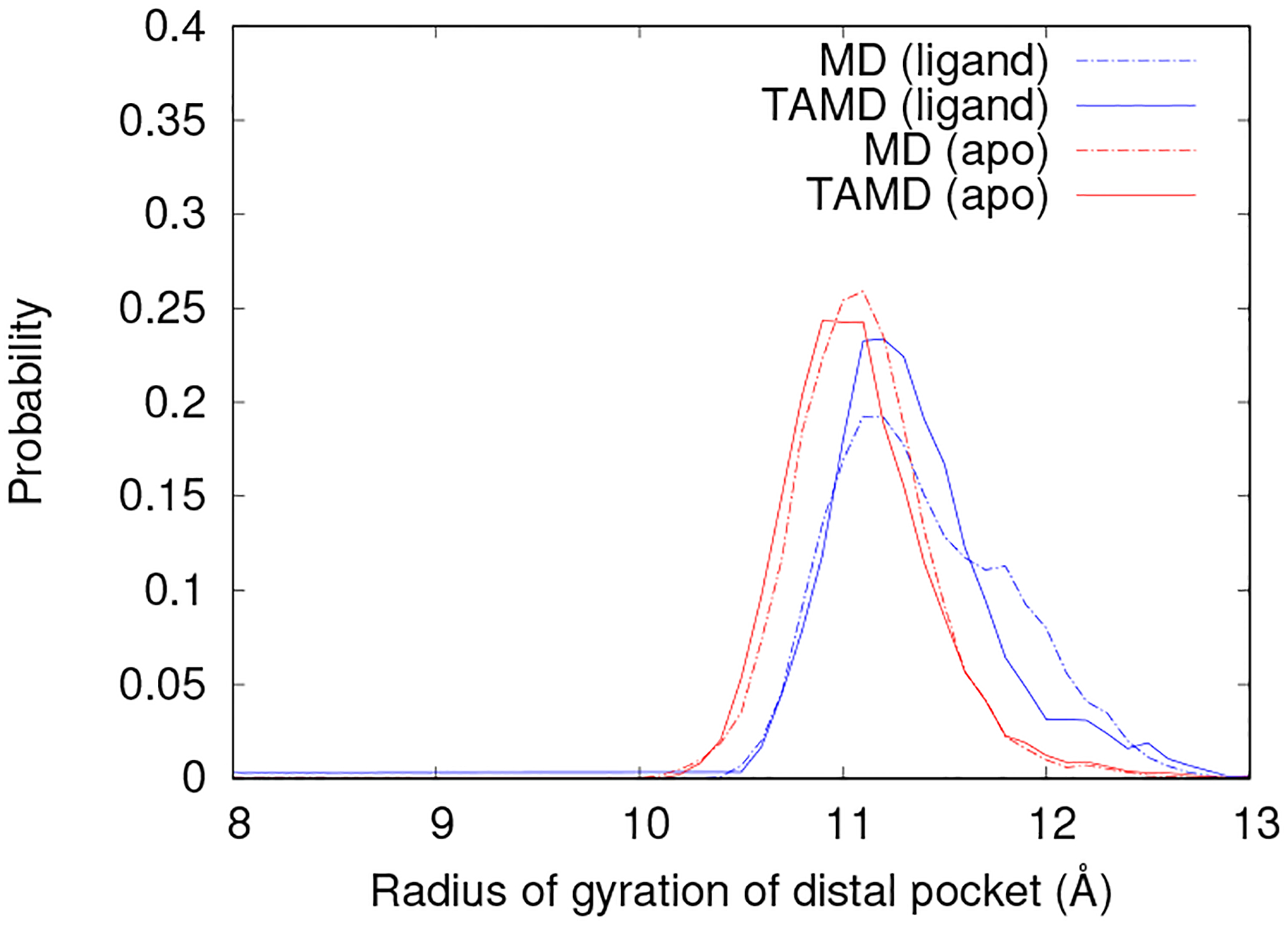
The probability density function of the radius of gyration of the DP for F99Y-MD (dashed lines) in the closed and bound state and F99Y-TAMD (solid lines) during flap opening in the apo state (shown in red) and in the presence of a substrate (blue).
Distal pocket closure stabilizes open flap configuration
We use SMCV to explore the transition pathway for preparing a protein for substrate binding. We determine the protein ready to accept the substrate may be described as one with wide open flaps and closed DP’s. SMCV minimizes the energetic cost of a transition in CV space to find the minimum free energy pathway, or most probable pathway of a conformational change. In the current study, the string consists of 24 equidistant images representing distinct conformational states along the pathway. Due to the end of the string occurring in an unstable transition state, it is not anticipated that the ends will fall in low energy wells and therefore they must be fixed to obtain the correct pathway. The reproducibility of starting and ending images are crucial to the simulation findings due to this fact. The starting image is chosen as a representative snapshot from an equilibrated MD simulation of the closed and unbound state (MDapo). The end image is a snapshot from a representative TAMD simulation at a point when the substrate is actively exiting the binding pocket. Using an image from an active unbinding event, we assume that the protein is primed to accept a substrate in this conformation.
The primed fully-open conformation is found to be dependent on both the opening of the flaps and the closing of the distal pockets through repeat TAMD simulations of substrate unbinding. CV’s are chosen to represent the two important slow moving variables as the cartesian coordinates of the center of mass of the flap tips (xA, yA, zA, xB, yB, zB) and the radius of gyration of the four residues, P1, H67, C69, and F99, which constitute the distal pocket (rgyr,A, rgyr,B). A time trace of initial CV progression is shown in Fig. 7. In the initial string, the flaps open linearly and symmetrically and the distal pockets close in a linear fashion with respect to radius of gyration.
Figure 7:
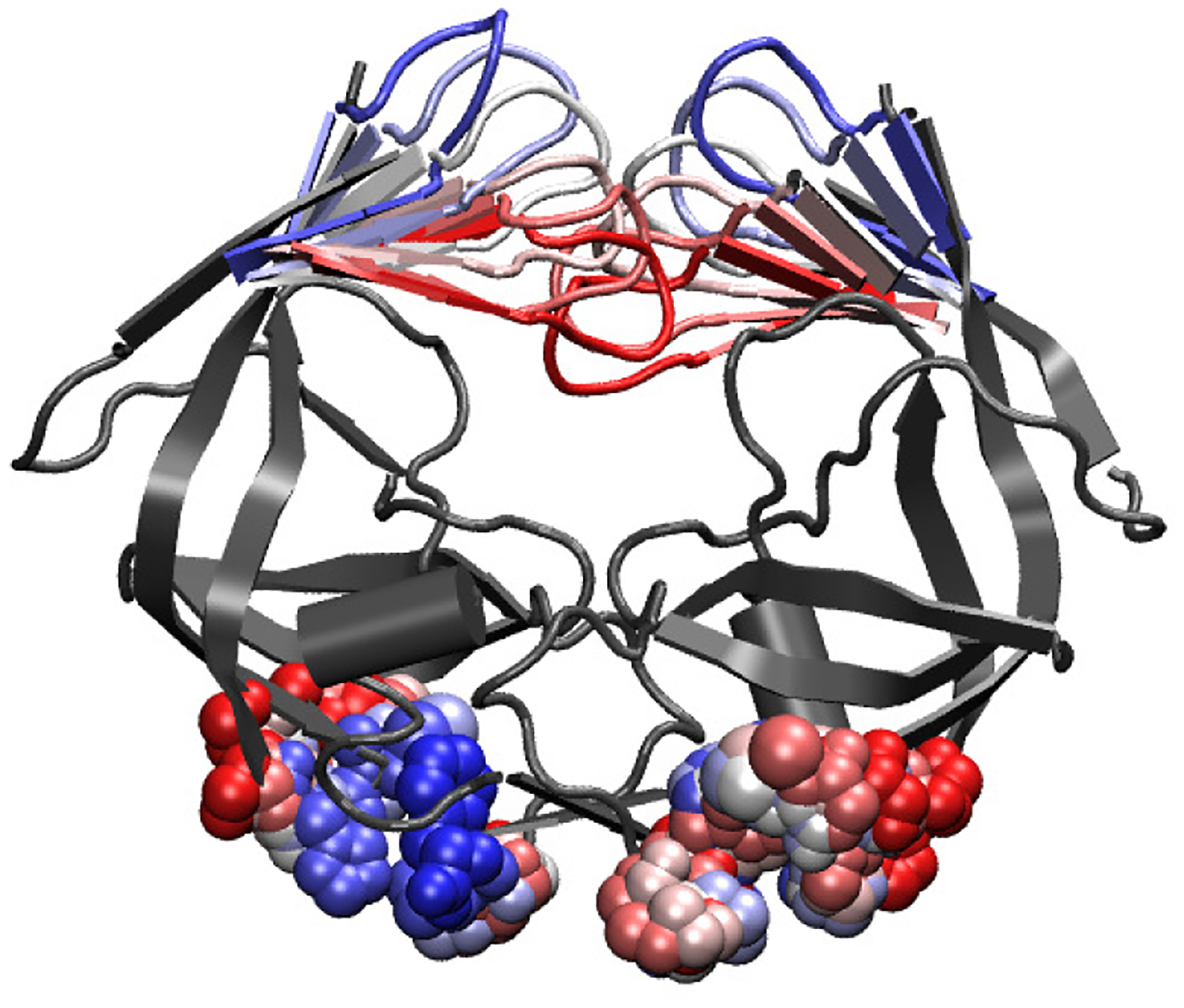
String progression of the CV’s associated with flap opening through SMCV. CV’s include the cartesian coordinates of the center of mass of the flap tips and the radius of gyration of the DP on each monomer. String progresses from red to white to blue.
The SMCV simulation was run for over 300 ns until full convergence is obtained. Convergence is assumed by long scale stabilization of RMSD of the CV’s. Parameters were adjusted after ≈ 2.7 × 106 steps to obtain quicker, more reliable convergence as described in section.
Throughout the string method simulation, CV’s moved significantly from their initial linear progression as seen in Fig. 8A and Fig. 8B. The distal pockets now fit into the anticipated dual modes of open or closed as denoted by the initial images plateauing around 11Å and the final images stabilizing below 10 Å. The DP’s commence the process of moving from the open to closed state around image 10 and complete this procedure by image 16. DP’s do not close in concert with the flaps opening. In the equilibrated string, flap opening occurs on an approximately linear fashion with respect to the distance of the flaps from the base. If we study the interactions between the flaps, the opening can be observed in a bimodal fashion defined by the presence of interactions between Ile50 residues on the turn of each flap tip as seen in Fig. 8C. Ile50 interactions are known to be a crucial component for maintaining the closed state37. In the flap opening string, Ile50 interactions release between image 16 and 17 correlating with the transition of the DP’s from open to fully closed which occurs at image 16. Loss of Ile50 interactions indicates a movement towards a wide open flap conformation.
Figure 8:

Results at the minimum free energy pathway for apo flap opening of WT and F99Y mutant PR. A: Radius of gyration of DP’s (WT) B: Distance between flaps and base (WT) C: Distance between Ile50’s at flap tip (WT) D: Radius of gyration of DP’s (F99Y) E: Distance between flaps and base (F99Y) F: Distance between Ile50’s at flap tip (F99Y)
The free energy profile of the conformational change was calculated using over 20 ns of equilibration time for each image to achieve fully converged mean forces. The resulting free energy profile is shown in Fig. 9. There are several regions of interest in this free energy profile. The first noted point of interest is that we encounter a free energy minimum a couple images in from the initial starting image. Though the starting image was taken from an observed metastable state, its movement was fixed due to restraints on the string method calculations and therefore not minimized with respect to the CV energetic landscape. We can see from this study that the true minimum free energy state lays slightly past the conformation identified from the MD equilibrated conformation. We do not anticipate this to greatly affect the findings. A substantial increase in free energy is not observed from loss of Ile50 interaction though a large increase of free energy is observed through forcing tightly closed DPs. The true closed stable state of the DPs appears to be around 10 Å.
Figure 9:
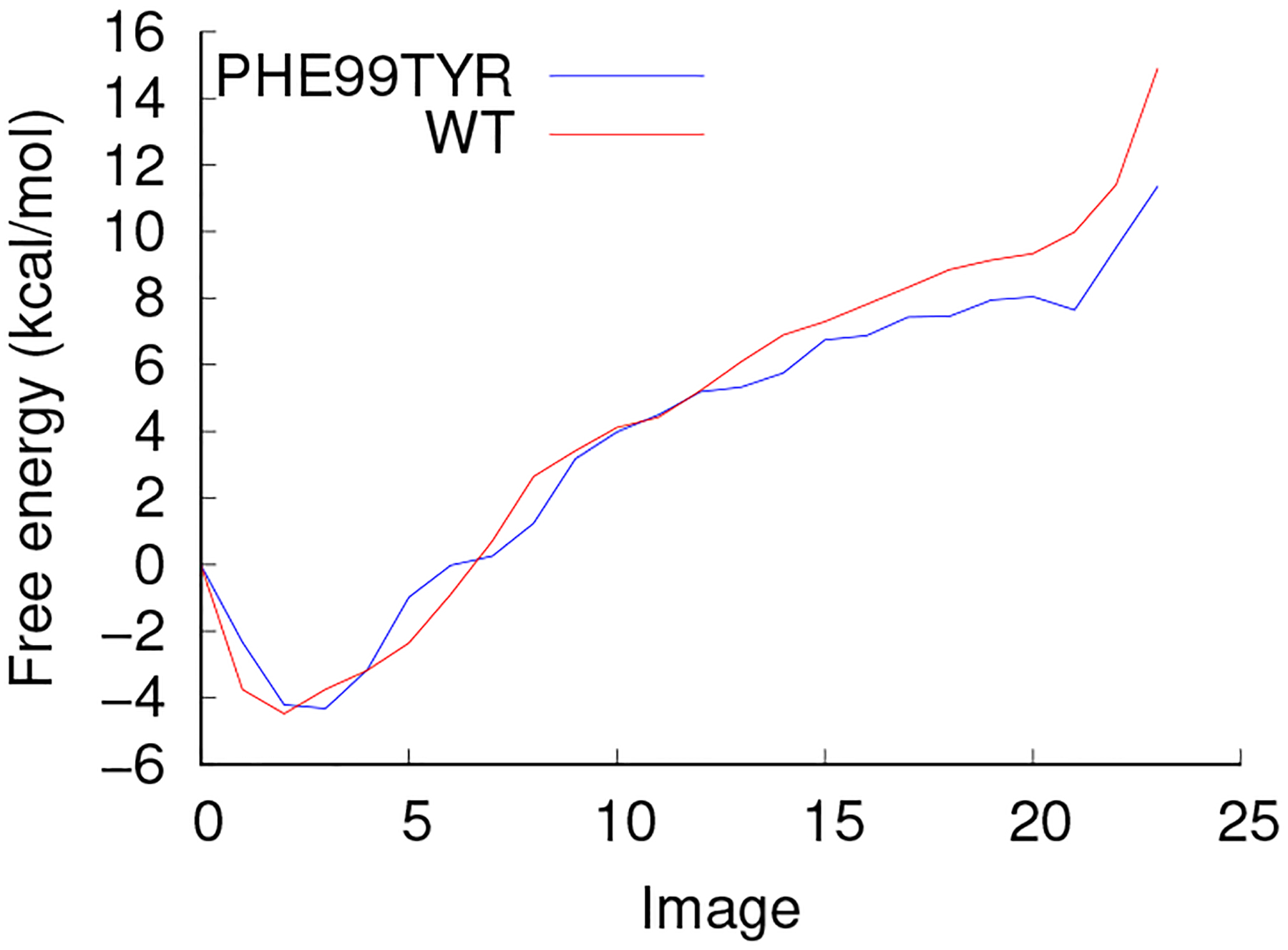
Free energy profile for apo flap opening of WT (red) and F99Y mutant (blue) PR
Mutation from hydrophobic to hydrophilic residue in DP has no effect on free energy profile of wide flap opening
SMCV was performed on the F99Y mutant in a similar manner to WT. For these simulations, string friction is maintained at 0.05 and the steps per string update is 100. The string ran for approximately 55 ns of simulation time or 5 × 105 string updates until convergence is obtained. The initial string was produced by mutating F99Y for each image in the converged WT SMCV string with 100 ps of equilibration MD with CV’s fixed. Despite this initial bias towards a known minimum pathway for WT, the transition pathway moved significantly during SMCV calculations with the mutated DP. Though initial movement occurred, the results indicate a similar, albeit less conclusive, pathway towards flap opening which involves a bimodal DP distribution and correlated loss of Ile50 interactions. The radius of gyration of DP’s, distance between flaps and base, and distance between Ile50’s may be seen in Figs. 8D, 8E, and 8F, respectively.
The differences between the F99Y mutant and WT are slight but expected. The DP’s stabilize to a more open state in the beginning of the simulation around 12 Å similar to the open state seen in F99Y – TAMDapo simulations. The DP’s begin to close around image 6 with full closure around image 14. At image 13, when the pockets are almost fully closed, Ile50’s momentarily lose contact but regain contact by image 14. At image 14, one of the distal pockets reopen while with Ile50’s maintain contact. By image 16, the Ile50 residues lose contact and the pocket on chain A recloses. The change in behavior from the WT PR is not drastic and we see similar correlations between the Ile50 bonds releasing as the pockets fully close.
Based on TAMD results that the flaps stay in a conformation similar to the slightly open or curled state even while biasing flap opening, we would anticipate that the energetic cost associated with opening the flaps would be higher than that of WT PR which freely visited the wide open conformation during similar TAMD simulations. We measured the free energy profile by thermodynamic integration with 50 ns of simulation time on each of the 24 images. The resulting free energy profile is very similar to that of WT PR as seen in Fig. 9. The hydrophilic residue in position 99 did not increase the energetic cost required to open the flaps while simultaneously closing the distal pockets.
Changes in DP behavior during F99Y-TAMD simulations indicate that an energetic barrier exists towards DP closure when a hydrophilic residue resides within the pocket. These simulations maintain open pockets throughout the length of the simulation even when the flaps are open and elbows are engaged. The apparent energetic barrier is not recovered in the energetically minimized free energy profile found from SMCV. There are several limitations to SMCV which may inhibit the energetic barrier from significantly contributing to the recovered free energy profile. The energetic cost associated with hydrophobic interactions is anticipated to be small compared to the cost of opening the flaps to the wide open state. In addition, in the SMCV simulations, CV’s are selectively chosen to observe the effect of pocket closure and flap opening on the free energy while other protein movements are not accounted for. Since the free energy is only minimized within the CV space we choose to explore, hidden variables may exist which are inhibiting pocket closure in the long time scale MD simulations but may be moving too slowly to be adequately captured in SMCV.
Previous research points to the importance of residues within the distal pocket to enzymatic activity but directly implicates the N-terminus (Pro1) in hindering efficient enzyme catalysis38,39. Enzymatic inhibition occurs when residue 1 remains connected to its precursor which renders the N-terminus immobile and by consequence removing the ability of the distal pocket to close. Conversely, when the C-terminus (Phe99) remains attached to its precursor, PR remains fully functional40,41. This research is in agreement with the F99Y mutation not increasing the free energy of flap opening and further suggests that the energetic cost associated with DP closure may be more conserved in the residues which close around the DP.
Conclusion
In this work, we have studied the unbinding mechanism of HIV-1 protease and the hidden protein changes which occur during substrate unbinding. TAMD results indicate that PR undergoes a conformational change involving elbow engagement which leads to accessibility to the binding pocket for a substrate. We observed a hydrophobic pocket that exists distal to the binding pocket that is directly linked to elbow engagement and substrate movement out of the pocket but does not affect the availability of flap opening. The free energy profile of wide opening of flap tips as well as the related motion of a hydrophobic pocket distal to the binding pocket is probed through SMCV. The distal pocket correlates to the release of interactions between the important Ile50 residues at the flap tips. The energetic cost associated with opening the flaps to the wide open position is great, almost 14 kcal/mol, which is to be expected as it is a rare event occurring on a 100 μs time scale7,8,42.
To show the relationship between flap opening and hydrophobic distal pocket closing, the C-terminal residue of each monomer at position 99 was mutated F99Y. This mutation exhibits different behavior than WT PR during MD and TAMD simulations with the distal pocket effectively open and elbows disengaged throughout the simulation even during a substrate unbinding event. Reformation of the closed stated was observed with F99Y when no instances of reformation of the closed state were seen with WT. The minimum free energy profile is calculated for flap opening of the mutant through SMCV. The free energy profile of a string with beginning and end points fixed is very similar between the mutant and WT indicating little effect to the energetic cost of opening the flaps and closing the distal pockets when residue 99 is mutated to a hydrophilic tyrosine.
Supplementary Material
Acknowledgement
Research reported in this publication was supported by the National Institutes of Health under award number R01GM100472. Work reported here was run on hardware supported by Drexel’s University Research Computing Facility and by the Extreme Science and Engineering Discovery Environment (XSEDE)43, which is supported by National Science Foundation grant number ACI-1548562.
Footnotes
Supporting Information Available
Supporting Information Available: additional data pertaining to protein movements during TAMD simulations. This material is available free of charge via the internet at http://pubs.acs.org.
References
- (1).Peng C; Ho BK; Chang TW; Chang NT Role of human immunodeficiency virus type 1-specific protease in core protein maturation and viral infectivit–y. Journal of Virology 1989, 63, 2550–2556. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (2).Konvalinka J; Kräusslich HG; Müller B Retroviral proteases and their roles in virion maturation. Virology 2015, 479–480, 403–417. [DOI] [PubMed] [Google Scholar]
- (3).Freed EO HIV-1 assembly, release and maturation. Nat. Rev. Microbiol 2015, 13, 484–496. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (4).Loeb DD; Swanstrom R; Everitt L; Manchester M; Stamper SE; Hutchison CA Complete mutagenesis of the HIV-1 protease. Nature 1989, 340, 397–400. [DOI] [PubMed] [Google Scholar]
- (5).Nicholson LK; Yamazaki T; Torchia DA; Grzesiek S; Bax A; Stahl SJ; Kaufman JD; Wingfield PT; Lam PY; Jadhav PK et al. Flexibility and function in HIV-1 protease. Nat. Struct. Biol 1995, 2, 274–280. [DOI] [PubMed] [Google Scholar]
- (6).Tóth G; Borics A Flap opening mechanism of HIV-1 protease. J. Mol. Graphics Modell 2006, 24, 465–474. [DOI] [PubMed] [Google Scholar]
- (7).Ishima R; Freedberg DI; Wang YX; Louis JM; Torchia DA Flap opening and dimer-interface flexibility in the free and inhibitor-bound HIV protease, and their implications for function. Structure 1999, 7, 1047–1055. [DOI] [PubMed] [Google Scholar]
- (8).Sadiq SK; De Fabritiis G Explicit solvent dynamics and energetics of HIV-1 protease flap opening and closing. Proteins: Struct., Funct., Bioinf 2010, 78, 2873–2885. [DOI] [PubMed] [Google Scholar]
- (9).Li D; Ji B; Hwang K; Huang Y Crucial roles of the subnanosecond local dynamics of the flap tips in the global conformational changes of HIV-1 protease. J. Phys. Chem. B 2010, 114, 3060–3069. [DOI] [PubMed] [Google Scholar]
- (10).Pietrucci F; Marinelli F; Carloni P; Laio, a. Substrate binding mechanism of HIV-1 protease from explicit-solvent atomistic simulations. J. Am. Chem. Soc 2009, 131, 11811–11818. [DOI] [PubMed] [Google Scholar]
- (11).Sadiq SK; Noe F; De Fabritiis G Kinetic characterization of the critical step in HIV-1 protease maturation. Proc. Natl. Acad. Sci. U. S. A 2012, 109, 20449–20454. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (12).Abrams C; Bussi G Enhanced sampling in molecular dynamics using metadynamics, replica-exchange, and temperature-acceleration. Entropy 2014, 16, 163–199. [Google Scholar]
- (13).Abrams CF; Vanden-Eijnden E Large-scale conformational sampling of proteins using temperature-accelerated molecular dynamics. Proc. Natl. Acad. Sci. U. S. A 2010, 107, 4961–4966. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (14).Vashisth H; Maragliano L; Abrams CF “dFG-Flip” in the insulin receptor kinase is facilitated by a helical intermediate state of the activation loop. Biophys. J 2012, 102, 1979–1987. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (15).Zheng W; Qi B; Rohrdanz MA; Caflisch A; Dinner AR; Clementi C Delineation of folding pathways of a β-sheet miniprotein. J. Phys. Chem. B 2011, 115, 13065–13074. [DOI] [PubMed] [Google Scholar]
- (16).Müller M; Smirnova YG; Marelli G; Fuhrmans M; Shi AC Transition path from two apposed membranes to a stalk obtained by a combination of particle simulations and string method. Phys. Rev. Lett 2012, 108, 1–5. [DOI] [PubMed] [Google Scholar]
- (17).Fuhrmans M; Marelli G; Smirnova YG; Müller M Mechanics of membrane fusion/pore formation. Chem. Phys. Lipids 2015, 185, 109–128. [DOI] [PubMed] [Google Scholar]
- (18).Bucci A; Abrams CF Oxygen pathways and allostery in monomeric sarcosine oxidase via single-sweep free-energy reconstruction. J. Chem. Theory Comput 2014, 10, 2668–2676. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (19).Prabu-Jeyabalan M; Nalivaika E; Schiffer CA How does a symmetric dimer recognize an asymmetric substrate? A substrate complex of HIV-1 protease. J. Mol. Biol 2000, 301, 1207–1220. [DOI] [PubMed] [Google Scholar]
- (20).Phillips JC; Braun R; Wang W; Gumbart J; Tajkhorshid E; Villa E; Chipot C; Skeel RD; Kalé L; Schulten K Scalable molecular dynamics with NAMD. J. Comput. Chem 2005, 26, 1781–1802. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (21).Humphrey W; Dalke A; Schulten K VMD: Visual molecular dynamics. J. Mol. Graphics 1996, 14, 33–38. [DOI] [PubMed] [Google Scholar]
- (22).MacKerell AD; Bashford D; Bellott M; Dunbrack RL; Evanseck JD; Field MJ; Fischer S; Gao J; Guo H; Ha S et al. All-atom empirical potential for molecular modeling and dynamics studies of proteins. J. Phys. Chem. B 1998, 102, 3586–3616. [DOI] [PubMed] [Google Scholar]
- (23).MacKerell AD; Banavali NK All-atom empirical force field for nucleic acids: II. Application to molecular dynamics simulations of DNA and RNA in solution. J. Comput. Chem 2000, 21, 105–120. [Google Scholar]
- (24).Jorgensen WL; Chandrasekhar J; Madura JD; Impey RW; Klein ML Comparison of simple potential functions for simulating liquid water. J. Chem. Phys 1983, 79, 926–935. [Google Scholar]
- (25).Martyna GJ; Tobias DJ; Klein ML Constant pressure molecular dynamics algorithms. J. Chem. Phys 1994, 101, 4177–4189. [Google Scholar]
- (26).Feller SE; Zhang Y; Pastor RW; Brooks BR Constant pressure molecular dynamics simulation: The Langevin piston method. J. Chem. Phys 1995, 103, 4613–4621. [Google Scholar]
- (27).Grest GS; Kremer K Molecular dynamics simulation for polymers in the presence of a heat bath. Phys. Rev. A 1986, 33, 3628–3631. [DOI] [PubMed] [Google Scholar]
- (28).Fiorin G; Klein ML; Hénin J Using collective variables to drive molecular dynamics simulations. Mol. Phys 2013, 111, 3345–3362. [Google Scholar]
- (29).Maragliano L; Fischer A; Vanden-Eijnden E; Ciccotti G String method in collective variables: Minimum free energy paths and isocommittor surfaces. J. Chem. Phys 2006, 125, 024106. [DOI] [PubMed] [Google Scholar]
- (30).Maragliano L; Vanden-Eijnden E Single-sweep methods for free energy calculations. J. Chem. Phys 2008, 128, 184110. [DOI] [PubMed] [Google Scholar]
- (31).Vanden-Eijnden E Some recent techniques for free energy calculations. J. Comput. Chem 2009, 30, 1737–1747. [DOI] [PubMed] [Google Scholar]
- (32).Abrams C cfacv: Friendly release with Zenodo integration. 2016; 10.5281/zenodo.47013. [DOI]
- (33).E W; Ren W; Vanden-Eijnden E String method for the study of rare events. Phys. Rev. B 2002, 66, 052301. [DOI] [PubMed] [Google Scholar]
- (34).Maragliano L; Vanden-Eijnden E A temperature accelerated method for sampling free energy and determining reaction pathways in rare events simulations. Chem. Phys. Lett 2006, 426, 168–175. [Google Scholar]
- (35).Maragliano L; Vanden-Eijnden E On-the-fly string method for minimum free energy paths calculation. Chem. Phys. Lett 2007, 446, 182–190. [Google Scholar]
- (36).Liu Z; Huang X; Hu L; Pham L; Poole KM; Tang Y; Mahon BP; Tang W; Li K; Goldfarb NE et al. Effects of hinge-region natural polymorphisms on human immunodeficiency virus-type 1 protease structure, dynamics, and drug pressure evolution. J. Biol. Chem 2016, 291, 22741–22756. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (37).Yu Y; Wang J; Chen Z; Wang G; Shao Q; Shi J; Zhu W Structural insights into HIV-1 protease flap opening processes and key intermediates. RSC Adv. 2017, 7, 45121–45128. [Google Scholar]
- (38).Louis JM; Nashed NT; Parris KD; Kimmel AR; Jerina DM Kinetics and mechanism of autoprocessing of human immunodeficiency virus type 1 protease from an analog of the Gag-Pol polyprotein. Proc. Natl. Acad. Sci. U. S. A 1994, 91, 7970–7974. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (39).Louis JM; Clore GM; Gronenborn AM Autoprocessing of HIV-1 protease is tightly coupled to protein folding. Nat. Struct. Biol 1999, 6, 868–875. [DOI] [PubMed] [Google Scholar]
- (40).Wondrak EM; Louis JM Influence of flanking sequences on the dimer stability of human immunodeficiency virus type 1 protease. Biochemistry 1996, 35, 12957–12962. [DOI] [PubMed] [Google Scholar]
- (41).Sadiq SK; Noe F; De Fabritiis G Kinetic characterization of the critical step in HIV-1 protease maturation. Proc. Natl. Acad. Sci. U. S. A 2012, 109, 20449–20454. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (42).Hornak V; Okur A; Rizzo RC; Simmerling C HIV-1 protease flaps spontaneously open and reclose in molecular dynamics simulations. Proc. Natl. Acad. Sci. U. S. A 2006, 103, 915–920. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (43).Towns J; Cockerill T; Dahan M; Foster I; Gaither K; Grimshaw A; Hazlewood V; Lathrop S; Lifka D; Peterson G et al. Accelerating scientific discovery. Comput. Sci. Eng 2014, 16, 62–74. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


