Abstract
Brady, Konkle and Alvarez (2009) argued that statistical learning boosts the number of colors that can be held online in visual working memory (WM). They showed that when specific colors are consistently paired together in a WM task, subjects can take optimal advantage of these regularities to recall more colors, an effect they labelled “memory compression”. They proposed that memory compression is a product of visual statistical learning, an automatic apprehension of statistical regularities that has been shown in prior work to be disconnected from explicit learning. If statistical learning enables an expansion of the number of individuated representations in visual WM, it would require revision of virtually all models of capacity in this online memory system. That said, this provocative claim is inconsistent with multiple studies that have found no improvement in WM performance following numerous repetitions of specific sample displays (e.g., Olson and Jiang, 2004; Logie, Brockmole and Vandenbroucke, 2009). Here, we replicate the Brady et al. findings but show that memory compression effects were restricted to subjects who had perfect explicit recall of the color pairs at the end of the study, suggesting that statistical regularities boosted performance by enabling contributions from long term memory. Thus, while memory compression effects provide an interesting example of the tight collaboration between online and offline memory representations, they do not provide evidence that statistical regularities can augment the number of individuated representations that can be concurrently stored in visual WM.
Keywords: visual working memory, memory capacity, statistical learning
Introduction
Working memory (WM) is an online memory system that enables the maintenance and manipulation of information during virtually all cognitive tasks. Capacity in this memory system is a stable individual trait (Conway, Cowan, Bunting, Therriault, & Minkoff, 2002; Xu, Adam, Fang, & Vogel, 2017) that exhibits robust correlations with broad measures of intellectual ability such as fluid intelligence and scholastic achievement. Thus, there has been sustained interest in manipulations that could enhance WM capacity. In the present work, we focus on the role of statistical regularities in WM capacity, and whether such regularities can yield robust increases in the number of items stored in WM. In an influential paper, Brady, Konkle and Alvarez (2009) demonstrated that when specific colors were likely to be paired in a WM recall procedure, memory performance was enhanced relative to a condition without those regularities. Brady et al. concluded that statistical regularities enabled subjects to concurrently represent a larger number of colors in WM via “compression” of the information in line with the observed regularities. Although it is clear that statistical regularities yielded enhanced performance in the Brady et al. study, we argue that this evidence alone does not establish whether a larger number of colors was stored in WM. Here, we provide evidence for the alternative hypothesis that subjects boosted performance by retrieving the needed information from long term memory (LTM).
Embedded process models of WM provide a useful perspective for framing this question. These models conceive of WM as one component of an ensemble of memory processes that includes both online and offline memory representations (e.g., Cowan, 1999; Ericsson & Delaney, 1999; Jonides et al., 2008; Oberauer, 2002). For example, Cowan’s conception includes a base “layer” that represents the full contents of long-term memory (LTM). Within the LTM layer, there is “activated LTM”, which refers to the subset of LTM that is still latent but readily accessible because of priming or recency. Finally, there is a small handful of representations that can be maintained “online” or in the “focus of attention”. Critically, it is the focus of attention that has typically been the subject of debates regarding WM capacity. That is, while most theorists acknowledge that LTM has a virtually unlimited capacity, and while the number of representations in LTM that can be “activated” remains unclear, there is strong consensus that the focus of attention is highly limited in the amount of information that can be concurrently maintained (Cowan, 2001; Fukuda, Awh, & Vogel, 2010). Thus, a key question is whether statistical regularities enable a larger number of items to be represented online in the focus of attention. Clear evidence for such an expansion of online memory capacity would require significant revision for most leading models of WM. Alternatively, it is plausible that subjects could encode statistical regularities into LTM, and then retrieve that information to boost performance in a WM task. While embedded process models highlight the opportunity for this kind of collaboration between WM and LTM, this explanation does not require any change to the number of individuated representations that can be actively maintained in the focus of attention.
Improvement in VWM performance has classically been explained with chunking, the integration of separate items into a unit for storage in memory (Mathy & Feldman, 2012; Miller, 1956; Thalmann, Souza, & Oberauer, 2019). Chen and Cowan (2009) provided a clear demonstration that associations in LTM can boost performance in a WM task. They trained subjects until they had perfect explicit recall of a list of word pairs and showed that subjects could subsequently hold precisely the same number of pairs in mind as they could random unpaired words. Thus, unitizing pairs of words via associative learning enabled subjects to double the number of individual words that they could accommodate in the WM task. Critically, this explanation does not require any change to the number of individuated items held in the focus of attention, because the needed associative knowledge can be retrieved from LTM at the time of test.
Moreover, we note that chunking does not allow subjects to circumvent the 3–4 item limit that is apparent with random individual items (Luck & Vogel, 1997; Zhang and Luck, 2008; Adam et al., 2017). Instead, performance is sharply limited to precisely the same number of unitized chunks. Thus, we argue that a common limited resource – sometimes conceived of as a set of “pointers” – is required for the storage of both individual items and chunks. Here, the notion that WM storage in constrained by a limited number of content-free pointers dovetails with the object-based benefits observed in past behavioural work. That is, WM performance is better when subjects remember both the color and orientation of each individuated stimulus compared to when the same information is distributed amongst a larger number of single feature objects (Luck & Vogel, 1997; Olson & Jiang, 2002; Wheeler & Treisman, 2002).
Further evidence for an LTM-based explanation of memory compression effects comes from a study that measured access time in a similar procedure (Huang & Awh, 2018). This study replicated the benefits of statistical regularities observed in the Brady et al. (2009) study but showed that they only manifested when subjects had a relatively long period of time (>1 second) following the test probe. Contrary to what might be expected if the additional information was held “online” in WM following chunk formation within immediate memory (Chekaf, Cowan, & Mathy, 2016), the longer response times provided initial evidence for a relatively slow retrieval of the color pair from LTM (Bradmetz & Mathy, 2008). A natural explanation for this finding is that subjects encoded the color pairs into LTM and retrieved the needed information when the test probes were presented. Here again, this explanation does not require any change in the number of representations that can be maintained in the focus of attention.
By contrast, Brady et al. (2009) argued that statistical learning enabled the compression of information held in WM, such that a larger number of colors were maintained online during the WM task. This interpretation was motivated by past studies of visual statistical learning (e.g. Fiser & Aslin, 2001, 2002; Turk-Browne, Jungé, & Scholl, 2005; Turk-Browne, Scholl, Chun, & Johnson, 2008) that have shown that observers can learn subtle statistical relationships automatically and without awareness of those regularities (Chun & Jiang, 1999; Turk-Browne et al., 2005, 2008). For example, observers gained knowledge of the base-pairs of shapes that made up a complex visual scene even though the base-pair structure of the scenes was irrelevant to the task (Fiser & Aslin, 2001). Statistical learning, particularly visual statistical learning, is often thought to involve unconscious statistical computations, forming the required associations between elements for the efficient chunking of information (Perruchet & Pacton, 2006). In fact, statistical learning bears so much similarity to implicit learning that some believe they are produced by the same general mechanism (Perruchet & Pacton, 2006; Turk-Browne et al., 2008). The fact that statistical learning can occur in the absence of awareness also implies that such learning may help to optimize processing in familiar contexts while minimizing the load on limited capacity systems for perception and selection. Mathy and Feldman (2012) have suggested that the redundancy of encoded information is automatically processed, such that more compressible information takes up less encoding space and is thereby more memorable. In line with this interpretation, Brady et al. (2009) reported that the small number of subjects who reported noticing the regularities did not show a larger memory compression effect than the subjects who did not report explicit awareness of the color pairs. A caveat for this conclusion, however, is that there were very few subjects who did not report awareness of the regularities in the Brady et al. study. Thus, a more sensitive test of this key question is needed.
Statistical learning provides a tempting interpretation for memory compression effects, but another challenge for this hypothesis – aside from the plausibility of contributions from LTM – is that multiple past studies have found no benefit from exact repetitions of sample displays in similar working memory tasks (Logie, Brockmole, & Vandenbroucke, 2009; Olson & Jiang, 2004). For example, Olson and Jiang (2004), using displays quite similar to those of Brady et al. (2009), found subjects did not improve in change detection for repeated relative to novel displays, even though a subsequent test of recognition memory showed that subjects had acquired accessible long-term memories of the displays. These findings challenge the hypothesis that the improved recall with the inclusion of statistical regularities in the Brady et al. (2009) study were produced by an automatic process akin to visual statistical learning. Instead, we hypothesize that the benefits of statistical regularities may be contingent on the acquisition of explicit long-term memories of the regularities, as well as task conditions that are conducive to the retrieval of that associative knowledge. This hypothesis predicts that memory compression effects, unlike past demonstrations in the implicit learning literature, will be directly connected to subjects’ explicit knowledge of the statistical regularities. In this case, subjects could improve performance by retrieving the relevant associations from LTM at the time of test, even though the number of representations held concurrently online in WM did not change. Relevant to this point, the studies by Olson and Jiang (2004) and Logie et al. (2009) observed null effects of repetition using change detection procedures, while the Brady et al. (2009) studies employed recall. One possibility is that unhurried recall responses are more conducive to LTM retrieval, either because of the distinct cognitive requirements for recall versus recognition or simply because recall tasks run at a slower pace that provides more time for LTM retrieval.
To this point, Brady et al. (2009) did examine whether subjects tended to store one item from each pair and then use mnemonic inference to retrieve the associated color when the test display was presented. Brady et al. argued against this alternative explanation with two findings. First, performance when a low probability pairing was probed was better in the patterned condition than in the uniform condition, consistent with the hypothesis that memory compression left more resources available for storing those low probability items in the patterned condition. However, this effect is also consistent with our LTM account of performance, whereby subjects stored only one item (or a content-free label; Huang & Awh, 2018) from the rest of the pairs in the display, thus providing access to LTM representations of the high probability pairs and leaving mnemonic resources available for storing the low probability pairs. Second, Brady et al. found that when subjects recalled the wrong color from a low probability pair, they did not report the associated high probability color more frequently. We agree that this finding rules out a specific version of postperceptual inference in which subjects ignore one of the colors during encoding and then infer that color during recall. But this finding does not rule out the possibility that subjects identified the high probability pairs during the encoding phase of the trial, and subsequently stored a single item only when high probability pairs were noticed. Thus, while past findings argue against a specific version of the postperceptual inference account, our explicit LTM account of these memory compression effects remains viable. In the present work, we provide further evidence for this account by directly examining the relationship between explicit LTM knowledge and the boost in performance observed with statistical regularities.
Experiment 1
We replicated the Brady et al. (2009) study but added an objective awareness test of subjects’ LTM for each color pair. Brady et al. also queried subjects about whether they had noticed the pairings and found that the benefit in the patterned condition was not reliably different between subjects who reported noticing the pairs and those who did not. An important caveat for this conclusion, however, is that there were only 10 subjects in the patterned condition of the studies in the Brady et al. paper. Thus, the null result in question – equivalent compression effects in subjects who did and did not notice – was based on a sample size of only three (Experiment 1) and two (Experiment 2) subjects who did not notice the regularities. Here, we collected data from a total of 64 subjects (32 in both Experiments 1 and 2), each of whom participated in both the patterned and the uniform conditions. This within-subjects design, combined with an objective test of subjects’ knowledge of the color pairings, provided a more sensitive test of whether memory compression effects were linked to explicit knowledge of the color pairs.
Method
Observers
32 observers (19 females) were recruited from the local University of Chicago community and received monetary compensation ($10/hour) for their time. All reported normal or corrected-to-normal visual acuity, normal color vision and gave informed consent. Procedures were approved by the University of Chicago Institutional Review Board.
Apparatus
Stimulus displays were generated in MATLAB using the Psychophysics Toolbox (Brainard, 1997; Pelli, 1997) and shown on a 24-inch BenQ XL2430T LCD monitor with spatial resolution set to 1920 × 1080 and refresh rate set to 120 Hz. Observers were seated in a dark room with a viewing distance of approximately 70 cm.
Stimuli
Observers were presented displays with eight color items in four pairs arranged around the fixation point (Figure 1). Each color item was presented as squares with side length of 1.8° of visual angle or as circles with diameter 1.8° of visual angle (see Manipulation). Each item was assigned one of eight colors without replacement: red, green, blue, magenta, cyan, yellow, black and white. The four pairs were presented in fixed, equidistant locations 1.7° of visual angle from the central fixation point. Items within a pair were separated by a center-to-center distance of 2.0°.
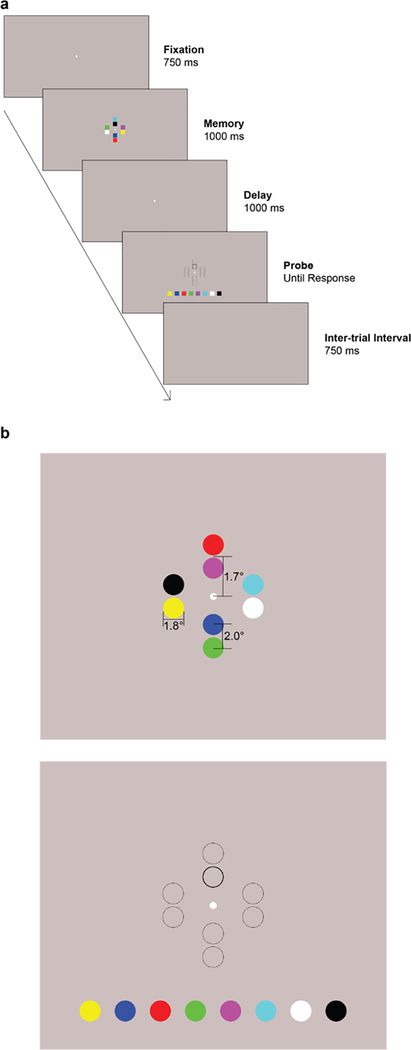
Figure 1.
(a) The trial procedure for the experiment. A fixation dot was presented for 750 ms before eight colors were presented, arranged in four pairs around the fixation point, for 1000 ms. After a 1000 ms delay, observers were instructed to click on the color of the item probed with the thicker border outline. A 750 ms inter-trial interval with a blank screen followed. (b) Examples of the stimuli display and probe display. Participants were shown one shape for the first half of the experiment and shown the other shape for the second half of the experiment. Distances shown in degrees of visual angle.
Manipulation
Observers completed a set of blocks for each condition, patterned and uniform. To reduce any carryover effects from the first set of blocks, a different shape was used in the second set of blocks. For example, if color items were presented as squares in the first set of blocks, color items were presented as circles in the second set of blocks, or vice versa. Both starting condition and stimulus shape was counter-balanced between observers.
In the uniform condition, the colors in each trial were chosen randomly, such that it was equally likely for a color to be paired with any other color. In the patterned condition, the colors were not chosen randomly. A joint probability matrix was constructed containing the probabilities of each color pair being presented. The diagonal of this matrix was set to zero to prevent the same color from appearing twice in a single display. Each observer was assigned four high-probability pairs (probability = 80/372 ≈ .2151)1 randomly with the constraint that each color was assigned to only one high-probability pair. The fifty-two remaining possible color pairs were assigned a uniform probability (probability = 1/372 ≈ .0027). On each trial, four pairs were drawn using the joint probability matrix without replacement, with the constraint that a color could not be drawn more than once.
In the final block of the patterned condition, the regularities in color pairings were removed, such that the block was identical to a block from the uniform condition. The amount of learning can then be quantified by taking the difference in performance between the average of the first nine blocks and the final block.
Procedure
Observers completed a total of 20 blocks (10 blocks of each condition) containing 60 trials in each block. Each block took approximately 6 minutes, and the overall study lasted approximately two hours. Observers were allowed to take short breaks at the end of each block. Observers completed all blocks within a condition before starting the other condition. The starting condition was counterbalanced between observers.
The general procedure for each trial is shown in Figure 1. At the beginning of each trial, a fixation point was displayed for 750 ms. Four color pairs were then presented around fixation for 1000 ms. Observers were instructed to remember the color of each item. A delay period followed for 1000 ms before observers were presented with a probe to recall the color of a randomly selected item. In the probe display, the locations of the color items in the memory array were outlined with a thin black line. The probe item to be recalled was outlined with a thicker black line. Below the probe display, an array of all possible colors was presented. The observer was instructed to click on the color below the display that was presented at the probed location.
To get a precise estimate of subjects’ explicit knowledge of the color pairings, we tested their ability to recall the paired colors at the end of the study. After completing all 20 blocks, observers were presented a color item in the middle of the screen and were asked to click on the color they thought was most likely to appear with the shown color (Figure 2).
Figure 2.
The test for awareness of statistical regularities. Observers were shown a color in the middle of the screen and asked to click on the color that was most likely to appear with the color shown.
Results
To estimate VWM performance, we measured the percentage of correct responses (PC) for each block. These were used to estimate the number of colors observers could recall (K) using the following formula from Brady et al. (2009) (see Appendix for derivation):
Performance across conditions
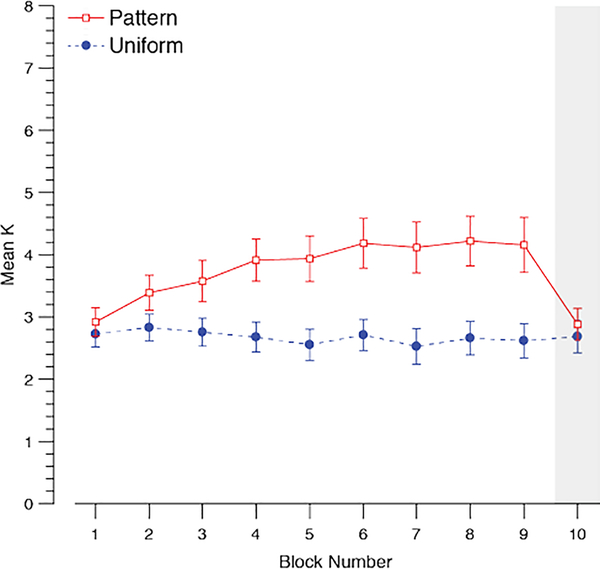
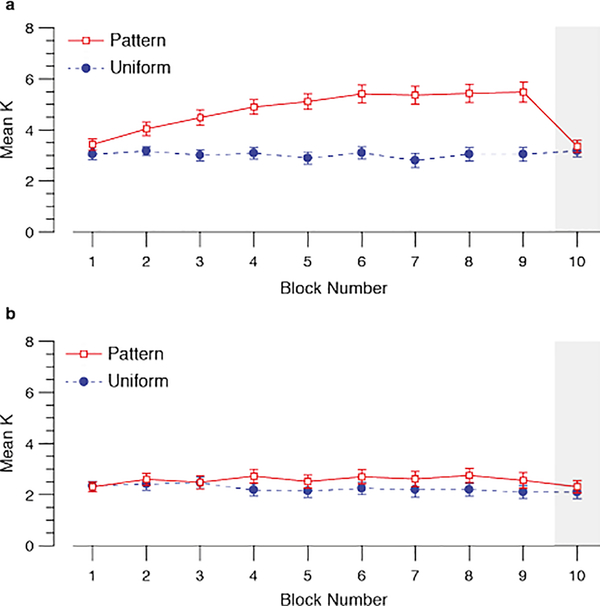
As Figure 3 illustrates, we replicated the advantage Brady et al. (2009) reported in the patterned condition. We observed a statistically significant effect of condition (patterned vs. uniform), F(1,31) = 41.30, p < .001 and a statistically significant effect of block, F(8, 248) = 8.96, p < .001. There was a significant interaction between condition and block, F(8,248) = 8.66, p < .001. Capacity for colors increased significantly across the patterned condition, F(8,248) = 13.33, p < .001, whereas performance did not change across blocks in the uniform condition, F(8,248) = 1.04, p = .40.
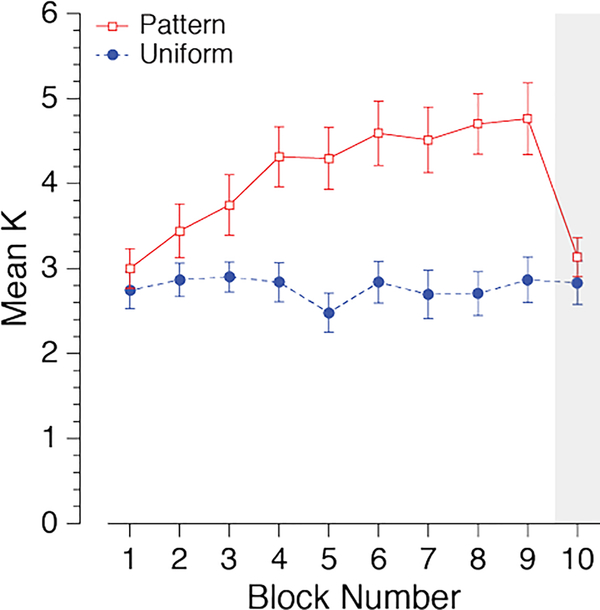
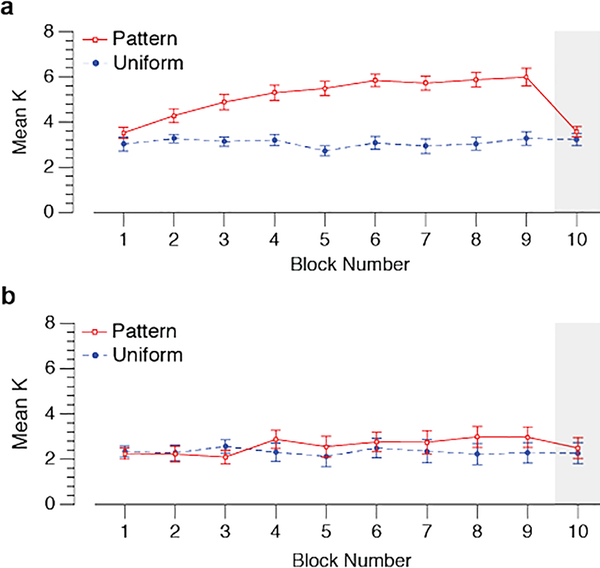
Figure 3.
The average number of items remembered (K) in each block for both conditions. The shaded bar indicates the last block in which statistical regularities were removed from the patterned condition. Error bars indicate ±1 S.E.M.
There was no difference in performance in the first block across conditions, t(31) = 1.04, p = .31, but performance in following blocks was significantly higher in the patterned condition, all t(31) > 2.39, all p < .02. In the last block where regularities were removed in the patterned condition, performance was not significantly different from performance in the uniform condition, t(31) = 1.79, p = .08. We also replicated these findings using a linear mixed effects logistic regression analysis of accuracy across trials for each condition, which avoids inflating the number of repeated tests to examine learning across time. We used the ‘lme4’ package (Bates, Mächler, Bolker, & Walker, 2015) in R (R Core Development Team, 2013) to conduct the analysis.2 The likelihood of a correct response was significantly larger for the patterned condition than the uniform condition (b = 0.63, SEb = 0.067, z = 9.42, p < .001) but not across trials (b = −1.39×10−5, SEb = 2.48×10−4, z = –0.06, p = 0.96). There was a significant interaction between condition and trial number (b = 6.50×10−4, SEb = 1.42×10−4, z = 4.57, p < .001) suggesting the change in likelihood of a correct response across trials was significantly higher for the patterned condition compared to the uniform condition.
Observers remembered 2.8 colors on average in the uniform condition. This is consistent with the mean performance in Brady et al. (2009) in which average K was 2.7 and 3.4 in Experiment 1 and 2 respectively. Observers remembered 4.8 colors on average after viewing the regularities in the stimulus displays (Block 9 of the patterned condition). This was significantly higher than the 3.1 colors remembered on average when the regularities were removed from the displays (Block 10 of the patterned condition), t(31) = 5.29, p < .001. Thus, we replicated the learning effects observed in the Brady et al. (2009) study.
Postperceptual inference
To test whether observers stored a single color from each pair, and then inferred the identity of the other color at the end of the trial, Brady et al. (2009) examined whether observers were more likely to report the high probability color associate of the adjacent item. Given such a strategy, observers would guess incorrectly on trials where a low-probability pair was probed and they would systematically guess the typical partner of the adjacent color. For example, if the observers had learned a blue-green color pairing, this kind of postperceptual inference would bias them to report green when blue was paired with a low probability partner. Brady et al. (2009) found no such effect and concluded that postperceptual inference did not play a role in the memory compression effect. We observed the same result. On average, 76 trials per observer (2427 trials across 32 observers, 14% of total trials) tested a low-probability pair. If observers were inferring the colors of the display using the high-probability pairings, their responses would more often be the high-probability color of the adjacent item. However, observers reported the high-probability color of the adjacent item only 11% of the time (where chance is 1/7 or 14%). In addition, we found that observers’ performance improved over blocks on trials where the low-probability pair was probed (Figure 4). K when low-probability pairs were probed (M = 3.8) was significantly greater in Block 9 of the patterned condition than in Block 10 of the patterned condition, when all pairs were low-probability (M = 3.1), t(31) = 2.66, p = .012. These findings suggest that high probability pairs required a smaller portion of limited mnemonic resources, thereby enhancing performance for other items in the display. Thus, we agree with Brady et al. that subjects were not encoding a single item from each pair, and then using postperceptual inference to boost performance with high probability pairs. However, we note that this analysis does not rule out the possibility that subjects selectively stored a subset of colors only when they recognized familiar pairs during encoding.
Figure 4.
The average number of items remembered (K) when a low-probability pair was probed for each block. The shaded area indicates the last block in which statistical regularities were removed from the patterned condition. Error bars indicate ±1 S.E.M.
Primacy effects
Because we employed a within-subjects design in which subjects participated in both the patterned and uniform conditions, we looked for possible carryover effects between conditions. Indeed, the order of conditions affected the size of the memory compression effect. A mixed three-way ANOVA revealed a statistically significant between-subject effect of condition order on performance, F(1, 30) = 9.88, p < .004. There were significant two-way interactions between condition order and the main effect of condition, F(1, 30) = 8.22, p = .008, and between condition order and the main effect of blocks, F(8,240) = 2.08, p = .04. There was a statistically significant three-way interaction between the condition order and the performance on condition across blocks, F(8,240) = 3.02, p < .003, suggesting that the difference in performance across blocks in the patterned and uniform conditions was significantly greater for observers that started with the patterned condition than observers that started with the uniform condition (Figure 5). Thus, the advantage in the patterned condition was reduced for subjects who experienced the uniform condition first (Jungé, Scholl, & Chun, 2007).
Figure 5.
Average number of items remembered (K) in each block indicating (a) subjects who completed the patterned condition first showed a larger improvement than (b) subjects who completed the uniform condition first. Error bars indicate ±1 S.E.M.
Are memory compression effects contingent on awareness?
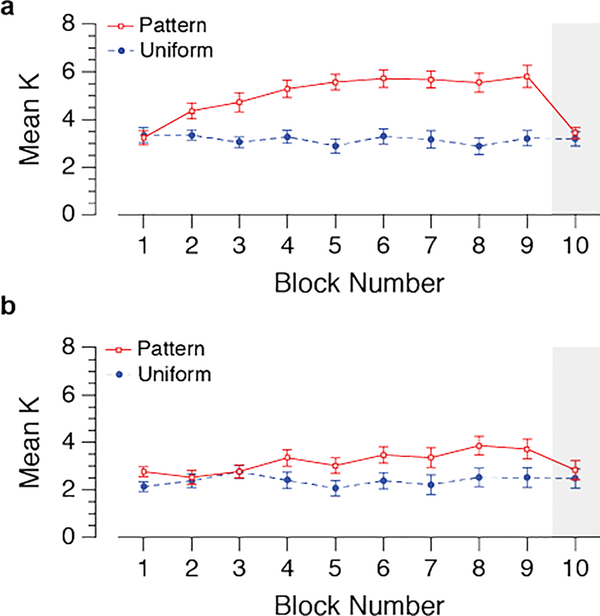
The results thus far have provided a close replication of those reported by Brady et al. (2009). The central question, however, is whether or not these memory compression effects are contingent on subjects’ explicit knowledge of the color pairings. We classified subjects as “aware” based on a strict criterion that they recall all the high probability pairs at the end of the study. While subjects with less than perfect performance may still have substantial awareness, the results show that subjects falling below this stringent criterion showed no evidence of the memory compression effect. 19 of the 32 observers were aware of the statistical regularities at the end of the experiment (5 out of the 16 observers who completed the uniform condition first and 14 out of the 16 observers who completed the patterned condition first).
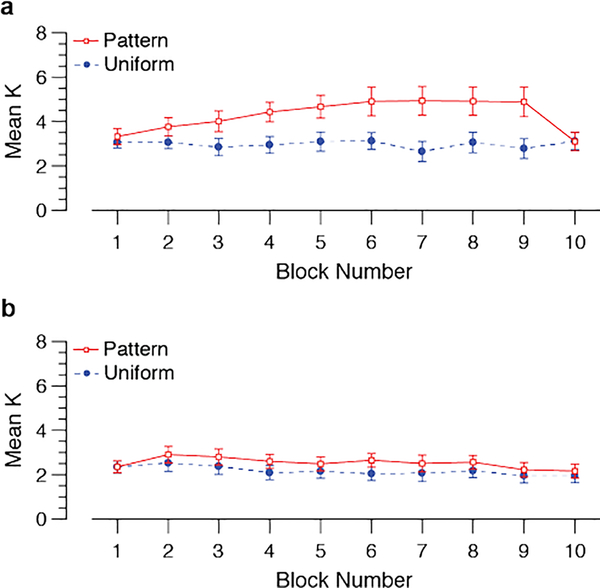
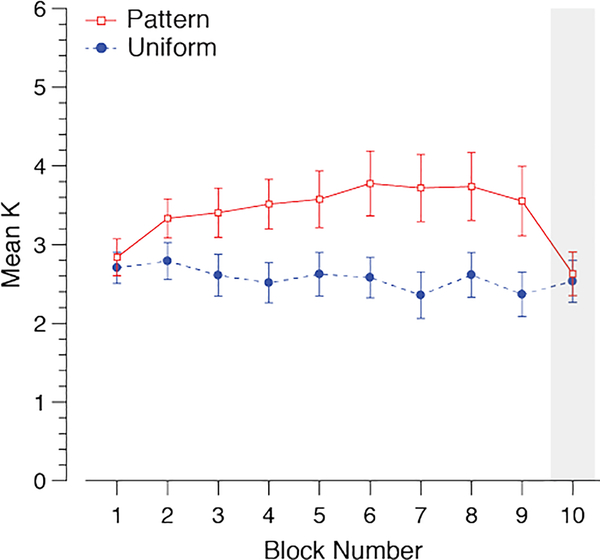
A mixed three-way ANOVA (aware versus unaware; block; condition) revealed a main effect of awareness, with higher accuracy in the aware group (M = 57%) than in the unaware group (M=40%), F(1,30) = 17.59, p < .001. There was a significant interaction between awareness and condition, F(1,30) = 41.80, p < .001, and between awareness and block, F(8,240) = 2.08, p = .039. Finally, there was a statistically significant three-way interaction between awareness, block and condition, F(8,240) = 2.25, p = .025 (Figure 6). For subjects who were aware of the color pairings, performance in patterned blocks improved with each successive block while performance in the uniform condition did not change; thus, for aware subjects there was a significant interaction between condition and block, F(8,144) = 10.83, p < .001. By contrast, for subjects who could not report all the color pairings at the end of the study, performance in the patterned and uniform conditions remained stable and equivalent throughout the study; thus, for unaware subjects there was no main effect of condition and no interaction between condition and block, F(8,96) = 1.27, p = .27. Therefore, the increase in the number of items remembered in the patterned condition was contingent on explicit awareness of the color pairings.
Figure 6.
Average number of items remembered (K) in each block for (a) “aware” subjects who correctly reported all color pairings at the end of the study and (b) “unaware” subjects who did not report all color pairings correctly. Improvement from inclusion of statistical regularities appears to occur only in the “aware” subjects. Error bars indicate ±1 S.E.M.
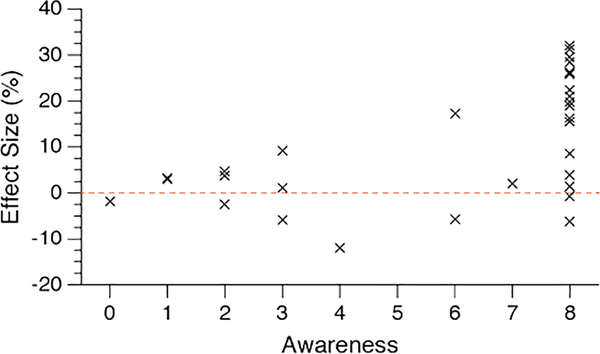
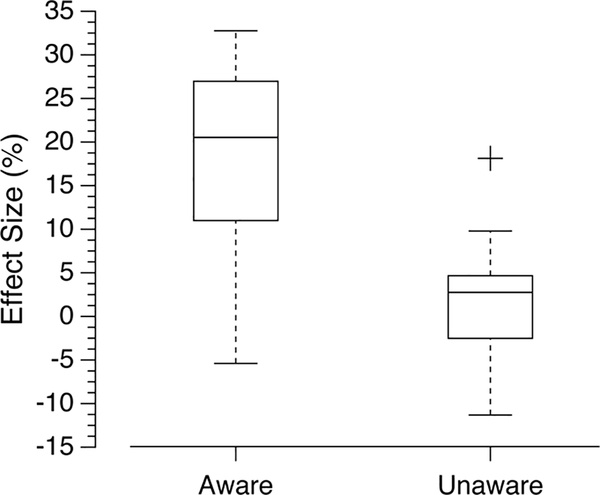
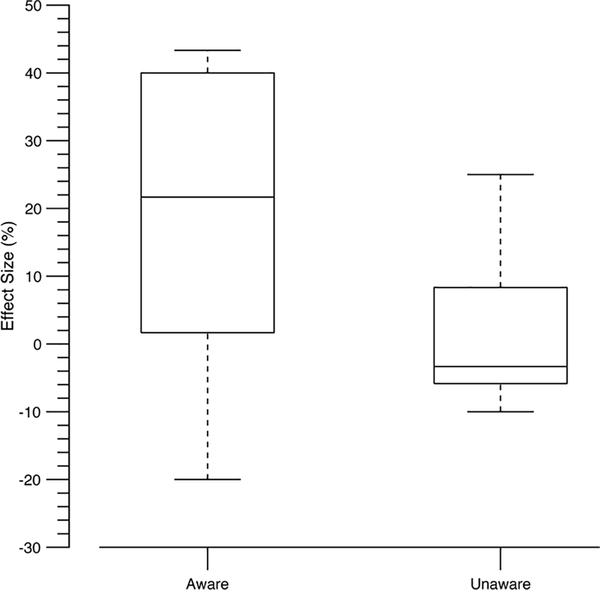
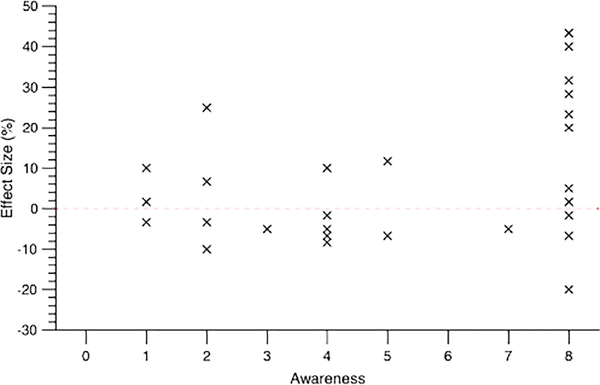
We first computed effect size by taking the difference between average performance in the first 9 blocks and the 10th block of the patterned condition to capture the amount of learning that occurred (see Figure 7). Mean effect size for aware observers was 17.9% whereas mean effect size for unaware observers was 1.3% (see Figure 8). A regression analysis showed that the number of correct responses on the awareness test was a significant predictor of effect size, b = 2.68, SEb = .68, t(31) = 3.92, p < .001. Aware observers showed a significant difference in performance between the penultimate and last block of the patterned condition, t(18) = 6.82, p < .001 whereas unaware observers showed no significant difference, t(12) = .62, p = .55. Thus, only aware observers remembered a reliably larger number of colors in the patterned condition.
Figure 7.
Effect size as a function of the number of items correct in the explicit awareness test. Effect size was calculated by taking the difference in percentage correct between the average of the first nine blocks and the ultimate block in the patterned condition.
Figure 8.
Effect size for “aware” observers, who correctly reported all color pairings in the explicit awareness test, and for “unaware “observers, who did not. Effect size was calculated by taking the difference in percentage correct between the average of the first nine blocks and the ultimate block in the patterned condition.
Experiment 2
Most observers completing the patterned condition first were explicitly aware of the statistical regularities in the display, whereas observers completing the uniform condition first were mostly unaware of associations between items. Due to numerous trials without statistical regularities, observers who completed the uniform condition first may have been primed to think that no statistical regularities are in the display in the patterned condition. In Experiment 2, we replicated Experiment 1 with a design in which each condition was presented in alternating blocks, reducing the primacy effect relative to when all trials of one condition were completed in a single block.
Method
The method was identical to Experiment 1 except for the following:
Observers
32 observers were tested in total. 16 observers (9 females) were recruited from the local University of Chicago community and completed the experiment for monetary compensation ($10/hour), and 16 observers (7 females) were recruited from the undergraduate psychology student population from the University of Sydney and completed the experiment for course credit. None of these subjects participated in the previous experiment. All reported normal or corrected-to-normal visual acuity, normal color vision and gave informed consent.
Procedure
Observers completed a total of 20 blocks containing 60 trials each. Observers alternated between blocks of the two conditions: a patterned condition block followed by a uniform condition block, or vice versa. The starting condition was counterbalanced across observers. Participants completed an awareness test after completing all trials.
Results
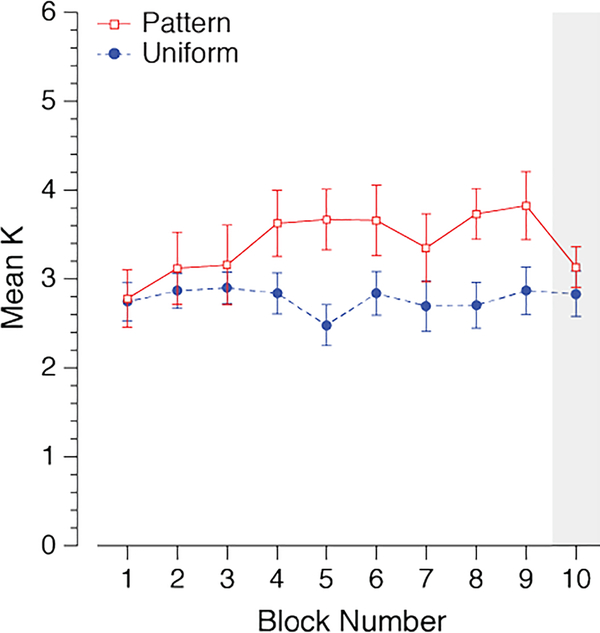
Performance across conditions
We observed a statistically significant effect of condition (patterned vs. uniform) averaged across blocks, F(1,31) = 36.72, p < .001 but no significant effect of block averaged across conditions, F(8,248) = .69, p = .70. There was a significant interaction between condition and block, F(8,248) = 4.419, p < .001. Capacity for colors significantly increased across blocks in the patterned condition, F(8,248) = 2.15, p = .32, whereas there was no change across blocks in the uniform condition, F(8,248) = .93, p = .49. There was no effect of condition in the first block, t(31) = .70, p = .49, but performance was significantly higher in the patterned condition in all subsequent blocks, all t(31) > 2.59, all p < .02. In the last block where regularities were removed from the patterned condition, performance was not significantly different between conditions, t(31) = .56, p = .58. The pattern of results from these statistical analyses was replicated using a linear mixed model fitting capacity estimates (K) across condition and blocks for each individual. This statistical analysis showed a significant effect of condition, t(31.00) = 6.06, p < .001, and a significant interaction between condition and block, t(479.00) = 4.97, p < .001, but no main effect of block, t(31.00) = 0.52, p = 0.61.3
Observers remembered 2.6 colors on average in the uniform condition, consistent with mean performance in Brady et al. (2009) and Experiment 1 of the present study. Observers remembered 3.6 colors on average after viewing the regularities in the stimulus displays (Block 9 of the patterned condition). This was significantly higher than the 2.6 colors remembered on average when the regularities were removed from the displays (Block 10 of the patterned condition), t(31) = 3.10, p = .004.
Postperceptual inference
On average, 76 trials per observer (2419 trials across 32 observers, 14% of total trials) tested a low-probability pair. Observers reported the high-probability color of the adjacent item only 11% of the time (where chance is 1/7 or 14%). Similarly to Experiment 1, observers’ performance varied significantly as a function of the number of high-probability pairs in the display (K = 2.4, 2.8, 3.1, 3.3, 3.7 for 0, 1, 2, 3, and 4 high-probability pairs respectively in the display, averaged across the entire experiment), F(4,124) = 3.5, p = .01.
Primacy effects
There was no significant interaction between condition order and the main effect of condition, F(1,30) = .55, p = .46, and there was no three-way interaction between the starting condition and the effect of condition across blocks, F(8,240) = .65, p = .73. This suggests that alternating between conditions every block eliminated the primacy effect observed in Experiment 1.
Awareness
16 out of the 32 observers correctly identified all the colors paired in the high-probability pair with each of the eight colors. A mixed three-way ANOVA revealed a statistically significant difference in performance averaged across all blocks between aware and unaware observers, F(1,30) = 7.87, p = .01. There was a significant two-way interaction between awareness and the average performance between conditions, F(1,30) = 21.46, p < .001 but not between awareness and performance across blocks, F(8,240) = 1.95, p = .054. However, there was a significant three-way interaction between awareness and the difference in performance across blocks between conditions, F(8,240) = 2.74, p = .007.
To characterize the interactions between awareness and performance, we examined aware and unaware observers separately as we did in Experiment 1. Among unaware participants, average performance was statistically higher in the patterned condition compared to the uniform condition, F(1,15) = 19.76, p < .01, but this effect was very small and did not change across blocks, F(8,120) = .82, p = .59. Moreover, there was no significant interaction between the conditions and the blocks suggesting the trajectory for performance did not differ in the uniform and patterned condition, F(8,120) = .58, p = .79. Indeed, the advantage in the patterned condition was over 30 times larger for aware (19.6%) compared to unaware (0.6%) participants, based on the difference between performance in the penultimate and final blocks in the patterned condition. In addition, the difference between the patterned and uniform conditions had a different trajectory across blocks, such that the learning effect grew with additional exposures in the aware subjects but showed no such interaction with block in the unaware subjects. Among aware participants, K was significantly higher in the patterned condition, F(1,15) = 155.10, p < .001 but not across blocks, F(8,120) = 1.77, p = .09. Importantly, there was a significant interaction on performance across blocks between conditions, F(8,120) = 3.48, p < .001, suggesting the change in performance across blocks was different between conditions (see Figure 10). That is, among aware participants, performance significantly improved in the patterned condition compared to the uniform condition, but among unaware participants, there was no improvement in either the patterned or the uniform condition.
Figure 10.
Aggregate performance across blocks for (a) “aware” observers who correctly reported all color pairings in the explicit awareness test and for (b) “unaware” observers who did not. The shaded area indicates the last block were statistical regularities were removed from the patterned condition. Error bars indicate ±1 S.E.M.
To summarize, Experiment 2 replicated the finding that the advantage in the patterned condition was largely restricted to subjects with perfect explicit knowledge of the color pairings (see Figure 12). Although there was a statistically reliable advantage in the patterned condition for unaware subjects, this effect does not appear to provide evidence for the cumulative effects of statistical learning because the effect was extremely small and did not show the monotonic increase in number of items remembered across blocks that was observed by Brady et al. (2009) and in our first experiment. The number of correct responses on the explicit awareness test was a significant predictor of the effect size, b = 1.57, SEb = .61, t(31) = 2.56, p = 0.016. Thus, Experiment 2 replicated the finding that the benefits of statistical regularities were strongly dependent on the degree to which observers acquired explicit knowledge of the color pairings. Aware observers showed a significant difference in performance between the penultimate and last block of the patterned condition, t(15) = 3.82, p = .002, whereas unaware observers showed no significant difference, t(15) = .26, p = .79.
Figure 12.
Effect size for aware observers, who correctly reported all color pairings in the explicit awareness test, and for unaware observers, who did not correctly report all color pairings, in Experiment 2.
Aggregated Results
We aggregated the data across experiments to examine whether there were significant differences in our results between experiments and to further increase sensitivity. In Experiment 1, participants completed all the blocks within one condition (patterned blocks or uniform blocks) before the other, whereas in Experiment 2, participants completed the blocks from each condition in alternating fashion. Any significant differences would likely be due to differences in block order.
Comparison between experiments
The effect of condition on memory performance was not significantly different between experiments, F(1,62) = 3.06, p = .09, nor was average performance across blocks between experiments, F(8, 496) = 1.90, p = .06. Additionally, the interaction between the condition and block was not significantly different between experiments, F(8,496) = 1.32, p = .23. To further investigate the difference in performance across blocks, we analysed the patterned blocks and uniform blocks separately. Memory performance significantly increased across blocks in the patterned condition, F(8,496) = 11.715, p < .001, and this increase was significantly different between experiments, F(8,496) = 2.067, p = .037, indicating that the learning effect was significantly larger in Experiment 1 compared to Experiment 2. There was no difference in performance across blocks in the uniform condition, F(8,496) = .96, p = .46, and performance was not significantly different between experiments, F(8,496) = 1.00, p = .44.
These results indicate that the improvement in memory performance in the patterned condition was significantly larger in Experiment 1 with the blocks containing statistical regularities grouped together compared to Experiment 2 in which patterned blocks alternated with blocks that did not contain statistical regularities.
Overall effects
Collapsing the data of both experiments, memory performance was significantly better in the patterned condition compared to the uniform condition, F(1,63) = 74.07, p < .001, and significantly changed across blocks, F(8,504) = 4.73, p < .001. The change in memory performance across blocks was significantly different between the conditions, F(8,504) = 12.49, p < .001. As reported above, memory performance significantly increased in the patterned condition, but did not change in the uniform condition.
Effect of awareness
Across this study, there were 35 aware participants (19 from Experiment 1 and 16 from Experiment 2), and 29 unaware participants (13 from Experiment 1 and 16 from Experiment 2). Averaged across blocks, the difference in memory performance between conditions was larger for aware than for unaware participants, F(1,62) = 60.65, p < .001. In addition, the trajectory of this effect across blocks was steeper for aware than for unaware participants, F(8,496) = 4.59, p < .001. Thus, the aggregate results mirrored the results of both Experiment 1 and 2.
In unaware participants, memory performance was significantly higher in the patterned condition than in the uniform condition, F(1,28) = 7.71, p = .01, but did not change across blocks, F(8,224) = .31, p = .96. Additionally, there was no interaction between the condition and performance across blocks, F(8,224) = 1.17, p = .32. By contrast, aware participants showed a significant difference in memory performance between conditions, F(1,34) = 159.98, p < .001, and a significant change across blocks, F(8,272) = 8.46, p < .001. Critically, aware participants showed a significant interaction between memory performance across blocks and the condition, F(8,272) = 16.17, p < .001, indicating that only aware participants show significant improvement in the patterned condition compared to the uniform condition. This pattern of findings was consistent with the results of both Experiment 1 and 2.
General Discussion
We replicated the results of Brady et al (2009), showing that performance was substantially higher in a patterned condition in which specific colors were consistently paired together in a WM task. This powerful effect, however, was contingent on awareness of the colour pairings, such that improved recall was completely absent (Experiment 1) or negligible (Experiment 2) in subjects who did not have perfect explicit recall of the color pairs at the end of the study. These findings are inconsistent with the hypothesis that statistical learning, an automatic process that is disconnected from explicit awareness (Perruchet & Pacton, 2006; Turk-Browne et al., 2008), was responsible for improved performance in the patterned condition. Moreover, this hypothesis fails to explain multiple studies that did not observe improved WM performance after large number of repetitions of memory displays that were quite similar to those in the Brady et al. (2009) study (Logie et al., 2009; Olson & Jiang, 2004). For example, in the Olson and Jiang (2004) study change detection performance was unaffected by 24 exact repetitions of the sample display. No memory compression effect was observed with repetition, despite clear evidence from subsequent recognition tests that subjects had acquired long-term memories of those displays. Thus, both our findings and others call into question whether statistical learning provides the right framework for understanding the advantage in the patterned condition.
The embedded process model of WM provides a natural explanation for the advantage in the patterned condition, based on the interactions between WM and LTM that are required by most complex tasks. We propose that a subset of subjects (those aware of the statistical regularities) were able to encode robust long-term memories of the color pairs, and then retrieve this information at the time of test. Thus, without any change in the number of representations held online in the focus of attention, subjects can exploit associations stored in LTM to boost behavioural recall. This is precisely what Chen and Cowan (2009) observed when they directed subjects to encode word pairs into LTM. In a subsequent WM task, participants could remember the same number of pre-learned pairs of words as they could random individual words. Moreover, our alternative explanation may also illuminate why other studies found no advantage when memory displays were repeated up to 24 times (Logie et al., 2009; Olson & Jiang, 2004). Both the present study and Brady et al. (2009) used a recall procedure to test WM performance, while the Logie et al., (2009) and Olson and Jiang (2004) studies employed a two-alternative choice response (same versus different). It is possible that this relatively rapid mode of responding was not conducive to the effortful retrieval of long-term memories for the repeated displays. This explanation fits the findings of Huang and Awh (2018), who found that the statistical regularities in the Brady et al. (2009) task were only evident after more than a full second had elapsed after the onset of the test display, in line with a sluggish retrieval of the needed information from LTM. Consistent with this possibility, Logie et al. (2009) found benefits with repeated displays when they used a probed recall procedure (similar to that in the present work), but not a change-detection procedure. Thus, the robust benefits of statistical regularities in the Brady et al. (2009) procedure can be reconciled with other null effects (Logie et al., 2009; Olson & Jiang, 2004) by the hypothesis that different methods for testing working memory are more or less conducive to the retrieval of related information from LTM.
In both of our experiments, observers who were unaware of the statistical regularities showed either negligible or no improvement in recall accuracy. In contrast to the kind of statistical learning that has been highlighted in past studies (Fiser & Aslin, 2001, 2002; Turk-Browne et al., 2005, 2008) in which subjects apprehended statistical regularities in the absence of explicit awareness of those regularities (Chun & Jiang, 1999; Turk-Browne et al., 2005, 2008), the observed improvement in memory recall is strongly contingent on explicit awareness of the regularities. However, this result does not rule out that visual statistical learning may shape performance in a VWM task or lead to obtaining explicit knowledge (Smyth & Shanks, 2008; Turk-Browne, Yi, & Chun, 2006). For instance, Umemoto et al. (2010) measured change detection performance when one quadrant – unbeknownst to subjects – was more likely to contain the changed item when the test display was presented. They found that memory encoding was biased towards the quadrant most likely to contain the changes, and subsequent measures of explicit knowledge showed no difference in effect size between subjects who could and could not identify the dominant quadrant. This result and others (Beck, Angelone, Levin, Peterson, & Varakin, 2008; Jiang, Swallow, & Rosenbaum, 2013) suggest that implicit knowledge of likely target positions can elicit useful biases in the items that are encoded into WM.
Interestingly, there is at least some evidence that location may have a special status in these implicit learning demonstrations. Beck et al. (2008) found that equally predictive cues in the shape and color dimensions were ineffective at eliciting useful encoding biases. Likewise, we have also found that subjects did not benefit when an item of a specific color was most likely to change its orientation during a change detection procedure (Umemoto and Awh, unpublished). The notion that location may have a privileged status in visual processing is a longstanding one. Some have argued that location is automatically attended and stored in WM (e.g. Foster, Bsales, Jaffe, & Awh, 2017; Rajsic & Wilson, 2014; Schneegans & Bays, 2017; Tsal & Lavie, 1988) and that spatial attention is a fundamental component of feature integration (Treisman & Gelade, 1980). That said, Beck et al. (2008) noted that the nonspatial cues in their study were not explicitly task relevant, and this alone may have precluded apprehension of the relevant probabilities. Thus, further work is needed to determine the boundary conditions under which implicit knowledge can guide performance in VWM.
In conclusion, while many studies have shown that statistical regularities can be automatically apprehended and exploited in the absence of conscious awareness of those regularities, this does not appear to be an accurate framing of the memory compression effects in the Brady et al. (2009) procedure. Instead, the benefits of statistical regularities in this procedure may be best characterized as a collaboration of WM and LTM that entails no change in the number of items stored online in WM. These findings also challenge a key assumption that underlies the memory compression hypothesis offered by Brady et al. (2009). The notion of memory compression presumes that information is the “currency” of WM, such that improvements in performance are viewed as evidence for a reduction in the total amount of information that must be stored online. By contrast, if WM capacity is limited by the number of individuated representations, then a natural prediction is that WM storage will be limited to the same number of unitized chunks as individual memoranda that do not benefit from associative learning. Hence, while memory compression effects have sometimes been presented as a challenge to models proposing discrete capacity limits in WM, the present work shows that this and other examples of chunking are fully compatible with this view once the collaboration between WM and LTM is considered. Thus, while there will surely be continued interest in any manipulation that may boost online memory capacity, this is not the best explanation for the memory compression effect examined here.
Figure 9.
The average number of items remembered (K) across blocks in Experiment 2. The shaded area indicates the last block where statistical regularities were removed from the patterned condition. Error bars indicate ±1 S.E.M.
Figure 11.
Effect size as a function of the number of items each subject correctly reported the color pairing in the explicit awareness test at the end of Experiment 2. Effect size was calculated by taking the difference in percentage correct between the penultimate and ultimate blocks in the patterned condition.
Figure 13.
Aggregate performance across blocks in both conditions combined across both experiments. The shaded area indicates the last block where statistical regularities were removed from the patterned condition. Error bars indicate ±1 S.E.M.
Figure 14.
The average number of items (K) remembered across blocks for (a) “aware” observers from both experiments who correctly reported all color pairings in the explicit recall test and for (b) “unaware” observers from both experiments who did not correctly report all color pairings. The shaded area indicates the last block where statistical regularities were removed from the patterned condition. Error bars indicate ±1 S.E.M.
Appendix
Derivation of K Formula
The task in the current study is an eight-alternative forced choice, and observers may choose the correct answer if they know it or guess it by chance. Therefore, to estimate capacity (K), we need to estimate the number of correct answers from knowing the colors and the number of correct answers from guessing. We use the same formulation derived by Brady et al. (2009).
If an observer remembers K items, observers will be correct on the K/8 trials which a remembered item is probed. On the remaining trials, the observer may get these trials correct 1/8th of the time. Therefore, percent correct (PC) in terms of K will be:
Making K the subject:
Footnotes
These probability values were replicated from Brady et al. (2009). With eight colors, there are 56 possible pairs of two different colors. The 8 colors were randomised into 4 pairs and these pairs were assigned a weight of 80 to ensure a high-probability of selection. The remaining 52 colour pairs were given a weight of 1. The sum total of the weights is 372.
We used the ‘glmer’ function to conduct the model fitting with the Adaptive Gauss-Hermite Quadrature method. Models that included random intercepts and slopes for subjects across trials for each condition failed to converge. The analysis reported here is for the model with random effects for each condition and fixed intercepts for each subject.
The complete linear mixed model did not converge. The results of the model reported included a random effect of condition and block across individuals. The t-statistics and p-values reported were generated using the ‘lmerTest’ package in R, which applies Satterthwaite’s method to adjust the degrees of freedom for each effect.
References
- Bates D, Mächler M, Bolker B, & Walker S (2015). Fitting Linear Mixed-Effects Models Using lme4. Journal of Statistical Software, 67(1), 1–48. 10.18637/jss.v067.i01 [DOI] [Google Scholar]
- Beck MR, Angelone BL, Levin DT, Peterson MS, & Varakin DA (2008). Implicit learning for probable changes in a visual change detection task. Consciousness and Cognition, 17(4), 1192–1208. 10.1016/j.concog.2008.06.011 [DOI] [PubMed] [Google Scholar]
- Bradmetz J, & Mathy F (2008). Response times seen as decompression times in Boolean concept use. Psychological Research, 72(2), 211–234. 10.1007/s00426-006-0098-7 [DOI] [PubMed] [Google Scholar]
- Brady TF, Konkle T, & Alvarez GA (2009). Compression in Visual Working Memory: Using Statistical Regularities to Form More Efficient Memory Representations. Journal of Experimental Psychology: General, 138(4), 487–502. [DOI] [PubMed] [Google Scholar]
- Brainard DH (1997). The psychophysics toolbox. Spatial Vision, 10, 433–436. [PubMed] [Google Scholar]
- Chekaf M, Cowan N, & Mathy F (2016). Chunk formation in immediate memory and how it relates to data compression. Cognition, 155, 96–107. 10.1016/j.cognition.2016.05.024 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen Z, & Cowan N (2009). Core verbal working-memory capacity: The limit in words retained without covert articulation. The Quarterly Journal of Experimental Psychology, 62(7), 1420–1429. 10.1080/17470210802453977 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chun MM, & Jiang Y (1999). Top-Down Attentional Guidance Based on Implicit Learning of Visual Covariation. Psychological Science, 10(4), 360–365. 10.1111/1467-9280.00168 [DOI] [Google Scholar]
- Conway ARA, Cowan N, Bunting MF, Therriault DJ, & Minkoff SRB (2002). A latent variable analysis of working memory capacity, short-term memory capacity, processing speed, and general fluid intelligence. Intelligence, 30(2), 163–183. 10.1016/S0160-2896(01)00096-4 [DOI] [Google Scholar]
- Cowan N (1999). An embedded-processes model of working memory. Models of Working Memory: Mechanisms of Active Maintenance and Executive Control, 20, 506. [Google Scholar]
- Cowan N (2001). Metatheory of storage capacity limits. Behavioral and Brain Sciences; New York, 24(1), 154–176. [DOI] [PubMed] [Google Scholar]
- Ericsson KA, & Delaney PF (1999). Long-term working memory as an alternative to capacity models of working memory in everyday skilled performance.
- Fiser J, & Aslin RN (2001). Unsupervised statistical learning of higher-order spatial structures from visual scenes. Psychological Science, 12(6), 499–504. [DOI] [PubMed] [Google Scholar]
- Fiser J, & Aslin RN (2002). Statistical Learning of Higher-Order Temporal Structure From Visual Shape Sequences. Learning, Memory, 28(3), 458–467. [DOI] [PubMed] [Google Scholar]
- Foster JJ, Bsales EM, Jaffe RJ, & Awh E (2017). Alpha-band activity reveals spontaneous representations of spatial position in visual working memory. Current Biology, 27(20), 3216–3223. e6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fukuda K, Awh E, & Vogel EK (2010). Discrete capacity limits in visual working memory. Current Opinion in Neurobiology, 20(2), 177–182. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang L, & Awh E (2018). Chunking in working memory via content-free labels. Scientific Reports, 8(1), 23 10.1038/s41598-017-18157-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jiang YV, Swallow KM, & Rosenbaum GM (2013). Guidance of spatial attention by incidental learning and endogenous cuing. Journal of Experimental Psychology: Human Perception and Performance, 39(1), 285–297. 10.1037/a0028022 [DOI] [PMC free article] [PubMed] [Google Scholar] [Retracted]
- Jonides J, Lewis RL, Nee DE, Lustig CA, Berman MG, & Moore KS (2008). The mind and brain of short-term memory. Annu. Rev. Psychol, 59, 193–224. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jungé JA, Scholl BJ, & Chun MM (2007). How is spatial context learning integrated over signal versus noise? A primacy effect in contextual cueing. Visual Cognition, 15(1), 1–11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Logie RH, Brockmole JR, & Vandenbroucke ARE (2009). Bound feature combinations in visual short-term memory are fragile but influence long-term learning. Visual Cognition, 17(1–2), 160–179. 10.1080/13506280802228411 [DOI] [Google Scholar]
- Luck SJ, & Vogel EK (1997). The capacity of visual working memory for features and conjunctions. Nature, 390(6657), 279–281. 10.1038/36846 [DOI] [PubMed] [Google Scholar]
- Mathy F, & Feldman J (2012). What’s magic about magic numbers? Chunking and data compression in short-term memory. Cognition, 122(3), 346–362. 10.1016/j.cognition.2011.11.003 [DOI] [PubMed] [Google Scholar]
- Miller GA (1956). The magical number seven, plus or minus two: some limits on our capacity for processing information. Psychological Review, 63(2), 81–97. 10.1037/h0043158 [DOI] [PubMed] [Google Scholar]
- Oberauer K (2002). Access to information in working memory: Exploring the focus of attention. Journal of Experimental Psychology: Learning, Memory, and Cognition, 28(3), 411. [PubMed] [Google Scholar]
- Olson IR, & Jiang Y (2002). Is visual short-term memory object based? Rejection of the “strong-object” hypothesis. Perception & Psychophysics, 64(7), 1055–1067. 10.3758/BF03194756 [DOI] [PubMed] [Google Scholar]
- Olson IR, & Jiang Y (2004). Visual short-term memory is not improved by training. Memory & Cognition, 32(8), 1326–1332. 10.3758/BF03206323 [DOI] [PubMed] [Google Scholar]
- Pelli DG (1997). The VideoToolbox software for visual psychophysics: Transforming numbers into movies. Spatial Vision, 10(4), 437–442. [PubMed] [Google Scholar]
- Perruchet P, & Pacton S (2006). Implicit learning and statistical learning: one phenomenon, two approaches. Trends in Cognitive Sciences, 10(5), 233–238. 10.1016/j.tics.2006.03.006 [DOI] [PubMed] [Google Scholar]
- R Core Development Team. (2013). R: A language and environment for statistical computing.
- Rajsic J, & Wilson DE (2014). Asymmetrical access to color and location in visual working memory. Attention, Perception, & Psychophysics, 76(7), 1902–1913. [DOI] [PubMed] [Google Scholar]
- Schneegans S, & Bays PM (2017). Neural architecture for feature binding in visual working memory. Journal of Neuroscience, 3493–16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smyth AC, & Shanks DR (2008). Awareness in contextual cuing with extended and concurrent explicit tests. Memory & Cognition, 36(2), 403–415. 10.3758/MC.36.2.403 [DOI] [PubMed] [Google Scholar]
- Thalmann M, Souza AS, & Oberauer K (2019). How does chunking help working memory? Journal of Experimental Psychology: Learning, Memory, and Cognition, 45(1), 37–55. 10.1037/xlm0000578 [DOI] [PubMed] [Google Scholar]
- Treisman AM, & Gelade G (1980). A feature-integration theory of attention. Cognitive Psychology, 12(1), 97–136. 10.1016/0010-0285(80)90005-5 [DOI] [PubMed] [Google Scholar]
- Tsal Y, & Lavie N (1988). Attending to color and shape: The special role of location in selective visual processing. Perception & Psychophysics, 44(1), 15–21. 10.3758/BF03207469 [DOI] [PubMed] [Google Scholar]
- Turk-Browne NB, Jungé JA, & Scholl BJ (2005). The Automaticity of Visual Statistical Learning. Journal of Experimental Psychology: General, 134(4), 552–564. 10.1037/0096-3445.134.4.552 [DOI] [PubMed] [Google Scholar]
- Turk-Browne NB, Scholl BJ, Chun MM, & Johnson MK (2008). Neural Evidence of Statistical Learning: Efficient Detection of Visual Regularities Without Awareness. Journal of Cognitive Neuroscience, 21(10), 1934–1945. 10.1162/jocn.2009.21131 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Turk-Browne NB, Yi D-J, & Chun MM (2006). Linking Implicit and Explicit Memory: Common Encoding Factors and Shared Representations. Neuron, 49(6), 917–927. 10.1016/j.neuron.2006.01.030 [DOI] [PubMed] [Google Scholar]
- Umemoto A, Scolari M, Vogel EK, & Awh E (2010). Statistical Learning Induces Discrete Shifts in the Allocation of Working Memory Resources. Journal of Experimental Psychology. Human Perception and Performance, 36(6), 1419–1429. 10.1037/a0019324 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wheeler ME, & Treisman AM (2002). Binding in short-term visual memory. Journal of Experimental Psychology: General, 131(1), 48–64. 10.1037/00963445.131.1.48 [DOI] [PubMed] [Google Scholar]
- Xu Z, Adam KCS, Fang X, & Vogel EK (2017). The reliability and stability of visual working memory capacity. Behavior Research Methods, 1–13. 10.3758/s13428-017-0886-6 [DOI] [PMC free article] [PubMed] [Google Scholar]