Realization of an intrinsic ferromagnetic topological state in MnBi₈Te₁₃

The discovery of an intrinsic ferromagnetic axion insulator MnB_i8Te₁₃ paves the way for quantized magnetoelectric effect.

Abstract

Novel magnetic topological materials pave the way for studying the interplay between band topology and magnetism. However, an intrinsically ferromagnetic topological material with only topological bands at the charge neutrality energy has so far remained elusive. Using rational design, we synthesized MnBi8Te13, a natural heterostructure with [MnBi₂Te₄] and [Bi₂Te₃] layers. Thermodynamic, transport, and neutron diffraction measurements show that despite the adjacent [MnBi₂Te₄] being 44.1 Å apart, MnBi₈Te₁₃ manifests long-range ferromagnetism below 10.5 K with strong coupling between magnetism and charge carriers. First-principles calculations and angle-resolved photoemission spectroscopy measurements reveal it is an axion insulator with sizable surface hybridization gaps. Our calculations further demonstrate the hybridization gap persists in the two-dimensional limit with a nontrivial Chern number. Therefore, as an intrinsic ferromagnetic axion insulator with clean low-energy band structures, MnBi₈Te₁₃ serves as an ideal system to investigate rich emergent phenomena, including the quantized anomalous Hall effect and quantized magnetoelectric effect.

INTRODUCTION

Over the past decade, topology has taken the center stage in condensed matter physics and materials science, emerging as an organizing principle of the states of matter (1). Many topological phases, such as quantum spin Hall insulators, quantum anomalous Hall (QAH) insulators, three-dimensional (3D) topological insulators (TIs), and Weyl semimetals, have been observed (2, 3). Despite tremendous progress, the dominant majority of known topological materials (apart from the QAH insulators) are nonmagnetic materials, whereas studies on magnetic topological materials have been far more limited. In contrast to their nonmagnetic counterparts, magnetic topological materials allow a distinct set of new topological states including the axion insulator, the magnetic Weyl semimetals, the Chern insulators, and the 3D QAH insulators (2, 3). Furthermore, magnetism is a natural way to induce nonnegligible electronic interactions, paving the way for studying the interplay between band topology and correlations. Therefore, topological magnetic materials have emerged as the frontier of the field. Since the realization of the QAH state in the magnetically doped TI thin films Cr_0.15(Bi_0.1Sb_0.9)_1.85Te₃ (4), recent studies have identified a range of topological magnetic materials such as Fe₃Sn₂, Co₃Sn₂S₂, Mn₃Ge, and Co₂MnGa (5–9). However, the magnetically doped TI thin films are nonstoichiometric systems where disorder and inhomogeneity are unavoidable. Fe₃Sn₂, Co₃Sn₂S₂, Mn₃Ge, and Co₂MnGa are all large carrier density metals where substantial topologically trivial bands coexist with the topological bands at the chemical potential (5–9). To avoid these drawbacks, an intrinsically ferromagnetic (FM) topological material with magnetic ions occupying their own crystallographic sites and with only the topological bands at the charge neutrality energy is strongly desired but has so far remained elusive.

Recently, MnBi₂Te₄, a van der Waals (vdW) compound composed of the septuple layers (SLs) of [MnBi₂Te₄], was identified as an intrinsic magnetic topological material with clean band structure (10–32). Unfortunately, magnetic moments in MnBi₂Te₄ are antiferromagnetically (AFM) coupled across adjacent [MnBi₂Te₄] planes (15, 31). Therefore, although the quantized anomalous Hall conductance was observed at a record-breaking temperature of 4.5 K, it requires an external magnetic field as large as 12 T to polarize the system into the FM state (21, 22). Can we reduce the interlayer AFM coupling between the adjacent Mn layers to realize intrinsic FM? One material design strategy is to increase the interlayer distance between the adjacent Mn layers. How can we achieve it? Structurally, SL blocks have great compatibility with quintuple (QL) blocks of [Bi₂Te₃], as suggested by the existence of GeBi₄Te₇, which has alternating [GeBi₂Te₄] SL and [Bi₂Te₃] QL building blocks (33). This superior compatibility provides us flexible structural control to reduce the interlayer magnetic coupling by increasing the interlayer distance between the adjacent [MnBi₂Te₄] layers. Based on our material design strategy, here, we report the discovery of an intrinsic FM TI MnBi₈Te₁₃. Despite the interlayer distance between the adjacent [MnBi₂Te₄] SLs being 44.1 Å, it is striking and surprising that our thermodynamic, transport, and neutron diffraction measurements indicate that MnBi₈Te₁₃ has long-range FM order below 10.5 K, with the easy axis along the c axis. Our first-principles calculations and angle-resolved photoemission spectroscopy (ARPES) measurements further suggest that it is an intrinsic FM axion state. Considering the natural heterostructure nature of MnBi₈Te₁₃, our finding provides a superior material realization to explore zero-field QAH effect, quantized topological magnetoelectric effect, and associated phenomena.

RESULTS

Crystal structure of MnBi₈Te₁₃

Although the existence of MnBi₈Te₁₃ was mentioned (34), its crystal structure was never reported, partially due to the difficulty in growing the MnBi₈Te₁₃ phase and separating it from the other members in the MnBi_2nTe_3n+1 family. We managed to grow high-quality MnBi₈Te₁₃ single crystals and solved the crystal structure of MnBi₈Te₁₃ by refining the room-temperature powder x-ray diffraction (XRD) pattern using various structure models. We found that MnBi₈Te₁₃ crystallizes in the R-3m space group with the lattice parameters: a = b = 4.37485(7) Å, c = 132.415(3) Å, α = β = 90°, γ = 120°. The refinement results and structural parameters are summarized in tables S1 and S2. The powder XRD pattern and the Rietveld refinement are shown in Fig. 1A. The low-angle diffraction peaks can be well indexed as the (0 0 L) with lattice parameter c as 132.415(3) Å (see the inset of Fig. 1A), which is longer than the parameter c of 101.825(8) Å in MnBi₆Te₁₀. The formation of MnBi₈Te₁₃ is also visualized by the scanning transmission electron microscopy (STEM) image, as shown in Fig. 1B. The STEM image shows vdW structures, which is composed of repeating units of one SL block made of seven atomic layers and three consecutive QL blocks made of five atomic layers. The chemical analysis via the wavelength dispersive spectroscopy measurement results in the elemental composition of the sample as Mn:Bi:Te = 0.74(3):8.2(1):13, where the Mn:Bi ratio is slightly smaller than the ideal 1:8. The smaller than ideal Mn:Bi ratio is also observed in other MnBi_2nTe_3n+1 because of the Bi substitution on Mn sites (16, 31).

Fig. 1. Crystal structure of MnBi₈Te₁₃.

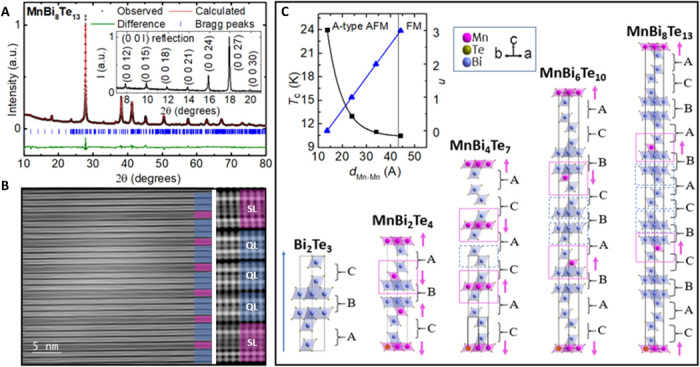
(A) Powder XRD and the refinement of MnBi₈Te₁₃. Inset: Low-angle (0 0 l) XRD peaks of the cleaved ab surface of MnBi₈Te₁₃. a.u., arbitrary units. (B) STEM images of MnBi₈Te₁₃ made on a focused-ion beam sample. The purple blocks label the [MnBi₂Te₄] SL, and the blue blocks mark the [Bi₂Te₃] QL. (C) Schematic drawing of the crystal and magnetic structure of MnBi_2nTe_3n+1 (n = 0, 1, 2, 3, and 4) with the stacking sequence listed. A, B, and C represent the bilayers of BiTe₆ octahedra whose bottom Te atoms, center Bi atoms, and top Te atoms are on the cell edges, respectively. Magenta arrow, magnetic structure in the order state; blue block, edge-sharing BiTe₆ octahedra; magenta block, edge-sharing MnTe₆ octahedra, which are connected to the blue block via edge sharing. Inset: T_c (the critical temperatures) versus d_Mn-Mn (the interlayer distance between the adjacent Mn-Mn layers) and n versus d_Mn-Mn in MnBi_2nTe_3n+1 (n = 1, 2, 3, and 4).

The crystal structure is shown in Fig. 1C. It is characterized by the alternating stacking of monolayer of MnTe₆ octahedra that are well separated by a number of monolayers of BiTe₆ octahedra running along the c axis. The distance between the nearest Mn-Mn interlayers is 44.1 Å, which is much larger than 13.6 Å for MnBi₂Te₄, 23.8 Å for MnBi₄Te₇, and 33.9 Å for MnBi₆Te₁₀, as shown in the inset of Fig. 1C. The stacking sequence of the MnBi_2nTe_3n+1 series can be rationalized (31). Using Bi₂Te₃ shown in Fig. 1C as the starting point, along the c axis, the stacking sequence of Bi₂Te₃ is -A-B-C-A-B-C-, where A, B, and C represent the bilayers of BiTe₆ octahedra whose bottom Te atoms, center Bi atoms, and top Te atoms are on the cell edges, respectively. The “Mn” layer can replace “A” or “B” or “C” bilayers of BiTe₆ octahedra to make MnBi_2nTe_3n+1. For example, as shown in Fig. 1C, for MnBi₂Te₄, the stacking sequence is -Mn(B)-C-Mn(A)-B-Mn(C)-A-; for MnBi₄Te₇, the stacking sequence is -Mn(B)-C-A-; and for MnBi₆Te₁₀, the stacking sequence is -Mn(B)-C-A-B-Mn(C)-A-B-C-Mn(A)-B-C-A-. When it comes to MnBi₈Te₁₃, the stacking sequence is Mn(B)-C-A-B-C-Mn(A)-B-C-A-B-Mn(C)-A-B-C-A-, exactly identical to the one we obtained based on our powder x-ray refinement. Therefore, with the stacking rule, we can easily assign the stacking sequence for the yet-to-be-discovered higher n members of MnBi_2nTe_3n+1 or design new magnetic TIs with the QL and SL building blocks.

Long-range ferromagnetism and its strong coupling with charge carriers in MnBi₈Te₁₃

As a comparison, the physical properties of MnBi₆Te₁₀ where two [Bi₂Te₃] QLs are sandwiched between the adjacent [MnBi₂Te₄] SLs are also presented. The inset of Fig. 2 (A and B) presents the temperature-dependent specific heat data of MnBi₈Te₁₃ and MnBi₆Te₁₀, respectively. A specific heat anomaly associated with the magnetic phase transition is observed, which determines the ordering temperature as 10.5 K for MnBi₈Te₁₃ and 11.0 K for MnBi₆Te₁₀. The magnetic properties of MnBi₈Te₁₃ are shown in Fig. 2 (A, C, and E), whereas those of MnBi₆Te₁₀ are presented in Fig. 2 (B, D, and F). The data indicate that, with the c axis as the easy axis, MnBi₈Te₁₃ is FM below 10.5 K, while MnBi₆Te₁₀ is AFM below 11.0 K. Figure 2 (A and B) presents the zero-field-cooled (ZFC) and FC magnetic susceptibility data, χ^c (H ∥ c) and χ^ab (H ∥ ab), measured at 0.1 kOe for MnBi₈Te₁₃ and MnBi₆Te₁₀, respectively. Sharp contrast can be seen. A large bifurcation of ZFC and FC data of χ^c appears below 10.5 K in MnBi₈Te₁₃, where upon cooling the ZFC data decrease but the FC data increase, suggesting the formation of FM domains. However, for MnBi₆Te₁₀, we observed a sharp cusp feature centering at 11.0 K in χ^c, similar to the ones in AFM MnBi₂Te₄ and MnBi₄Te₇ (17, 35) but with a small bifurcation of ZFC and FC data below 9 K. Furthermore, at 2 K, the magnitude of the FC χ^c in MnBi₈Te₁₃ is orders larger than that in AFM MnBi₂Te₄, MnBi₄Te₇, and MnBi₆Te₁₀ (17, 35). This strongly suggests different types of ground states in these two materials, with MnBi₈Te₁₃ being FM and MnBi₆Te₁₀ being AFM. Our conclusion is further confirmed by the hysteresis loop of isothermal magnetization curves M^c(H) (H ∥ c) shown in Fig. 2 (C and D) for MnBi₈Te₁₃ and MnBi₆Te₁₀, respectively. At 2 K, unlike the M^c(H) data where multiple-step features are observed because of the spin-flop transition in MnBi₂Te₄ (15, 17) and spin-flip transition in MnBi₄Te₇ (35) and MnBi₆Te₁₀, M^c(H) in MnBi₈Te₁₃ shows a typical hysteresis loop for FM materials with coercivity of H_c = 0.75 kOe and saturation remanence of M_r = 3.1 μ_B/Mn. Upon warming, H_c decreases as the hysteresis loop shrinks in area due to the enhanced thermal fluctuations. Figure 2E shows the M^ab(H) and M^c(H) of MnBi₈Te₁₃ up to 7 T, where a field of 10.4 kOe is required to force spins to saturate in the ab plane. This value is 11.3 kOe for MnBi₆Te₁₀ (Fig. 2F). Both sets of data indicate Ising anisotropy, with the c axis as the easy axis in these two compounds. Ising anisotropy has also been suggested in MnBi₂Te₄ by the inelastic neutron scattering measurement (28). The saturation moment measured at 7 T for MnBi₈Te₁₃ is M_s = 3.5(1) μ_B/Mn, whereas it is 3.4(1) μ_B/Mn for MnBi₆Te₁₀. In both cases, M_s is smaller than 4.6 μ_B/Mn, the obtained value from our density functional theory (DFT) calculation, but similar to 3.6 μ_B/Mn in MnBi₂Te₄ (17) and 3.5 μ_B/Mn in MnBi₄Te₇ (35). The reduced Mn saturation moment in MnBi₈Te₁₃ is likely due to the Mn site disorder as suggested in MnBi₂Te₄ and MnBi₄Te₇ (16,34). The fitted Weiss temperatures of MnBi₈Te₁₃ are ${\mathrm{\Theta }}_w^{\mathrm{ab}}$ = 12.8 K and ${\mathrm{\Theta }}_w^c$ = 12.1 K, suggesting FM exchange interactions. The fitted effective moments are ${\mathrm{\mu }}_{\text{eff}}^{\mathrm{ab}}=5.4 {\mathrm{\mu }}_B$/Mn and ${\mathrm{\mu }}_{\text{eff}}^c=5.1 {\mathrm{\mu }}_B$/Mn, indicating weak single-ion anisotropy. Although the effective moment is smaller than 5.9 μ_B/Mn for a Mn²⁺ ion, it is similar to MnBi₂Te₄, MnBi₄Te₇, and MnBi₆Te₁₀ (17, 35).

Fig. 2. Transport and thermodynamic properties of MnBi₈Te₁₃.

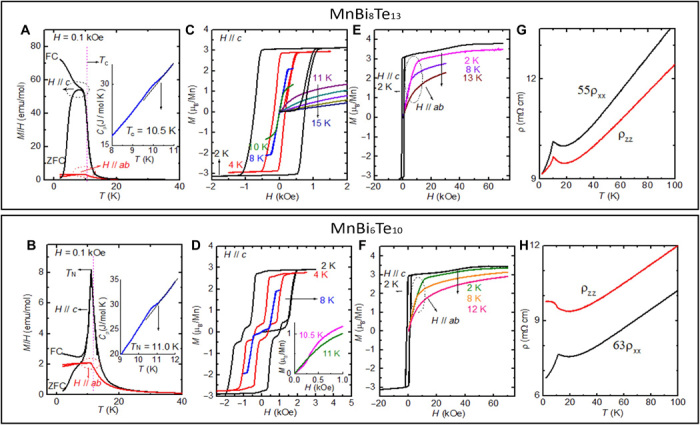
As a comparison, physical properties of MnBi₆Te₁₀ are also shown. (A and B) Temperature-dependent susceptibility taken at H = 0.1 kOe for MnBi₈Te₁₃ (A) and MnBi₆Te₁₀ (B). Inset: Temperature-dependent specific heat: (A) MnBi₈Te₁₃ and (B) MnBi₆Te₁₀. The criterion to determine T_c and T_N is shown in the inset. (C and D) Magnetic hysteresis loop of isothermal magnetization at low fields with H ⊥ c for MnBi₈Te₁₃ (C) and MnBi₆Te₁₀ (D). (E and F) Magnetic hysteresis loop of isothermal magnetization up to 7 T with H ⊥ c and H ⊥ ab: MnBi₈Te₁₃ (E) and MnBi₆Te₁₀ (F). (G and H) Anisotropic resistivity, ρ_xx and ρ_zz, for MnBi₈Te₁₃ (G) and MnBi₆Te₁₀ (H).

Figure 2G presents the temperature-dependent in-plane (ρ_xx) and out-of-plane resistivity (ρ_zz) of MnBi₈Te₁₃. Above 20 K, upon cooling, both ρ_xx and ρ_zz decrease semilinearly. Upon further cooling, when approaching T_c, because of the stronger scattering from enhanced spin fluctuations, both values increase (36, 37). Then, a sharp drop appears in both curves below 10.5 K due to the loss of spin scattering. The drop in ρ_zz below T_c is distinct from that in MnBi₂Te₄, MnBi₄Te₇, and MnBi₆Te₁₀ (see Fig. 2H) (17, 35), where the antiparallelly aligned Mn moments enhance resistivity via the spin-flip scattering. Therefore, the drop in ρ_zz again suggests FM ordering in MnBi₈Te₁₃ because the parallelly aligned Mn moments along the c axis eliminate such spin-flip scattering and thus reduce electric resistivity.

To confirm the long-range FM phase transition in MnBi₈Te₁₃, we have performed single-crystal neutron diffraction experiments at various temperatures. The quality of the instrument resolution limited magnetic Bragg peaks indicates that the stacking faults in this crystal are minimal. Figure 3A shows the Bragg reflection (1 0 1) at 4.5 and 15 K. It is evident that the peak intensity enhances substantially from 15 to 4.5 K, indicating the development of long-range magnetic ordering with the propagation vector k = 0. Starting from the nuclear space group R-3m with Mn atoms occupying the Wyckoff position (0, 0, 0) and k = 0, through symmetry analysis (38), we obtained the k-maximal magnetic subgroup as R-3m′ whose symmetry only allows the presence of an FM arrangement with the Mn spins along the c axis. Its magnetic structure is illustrated in Fig. 1C. The order parameter of MnBi₈Te₁₃ was measured from 4.5 to 15 K. As shown in Fig. 3B, a power law was used to fit the intensity of magnetic reflection (1 0 1) as a function of temperature. The fit yields the critical temperature 9.8(3) K and a critical exponent β = 0.4(1). The former is consistent with our thermodynamic measurements. The latter is considerably larger than the value of 0.125 expected for the Ising model in two dimensions, excluding this possibility (39). More data at lower temperatures could better define the critical behavior.

Fig. 3. Neutron diffraction data of MnBi₈Te_13.

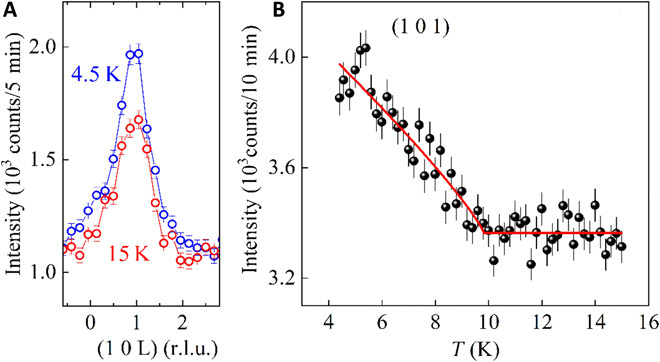
(A) Rocking curve scan for Bragg peak (1 0 1) of MnBi₈Te₁₃ at 4.5 and 15 K through neutron diffraction. r.l.u., reciprocal lattice units. (B) Temperature-dependent intensity of the magnetic reflection (1 0 1) of MnBi₈Te₁₃. The solid line stands for the power-law fit using $I=A{(1-\frac{T}{\mathrm{T}\mathrm{c}})}^{2\mathrm{\beta }}+B$, where β is the order parameter critical exponent (39).

Strong coupling between charge carriers and magnetism is observed in MnBi₈Te₁₃ through the magnetotransport measurements, as shown in Fig. 4. ρ_xx(H), ρ_zz(H), and ρ_xy(H) follow the same hysteresis as that in M(H). Using n = H/eρ_xy, our 50-K data correspond to an electron carrier density of 1.66 × 10²⁰ cm⁻³, similar to that of MnBi₂Te₄ (26). Figure 4F shows the ρ_xx(H) curves up to 9 T at various temperatures. The overall “W” shape was observed at low temperatures. The W-shaped MR(H) was previously observed in MnBi₄Te₇³⁸, where it was suggested to be a combination of nonmagnetic parabolic MR contribution and negative MR originating from FM fluctuations. Unlike MnBi₄Te₇ where the W-shaped behavior was observed far above its transition temperature 13 K, in MnBi₈Te₁₃, the MR quickly changes from the deepest W shape at T_c into a parabolic shape at just a few degrees above it. This may suggest weak FM fluctuations above T_c in MnBi₈Te₁₃.

Fig. 4. Magnetotransport properties of MnBi₈Te₁₃.

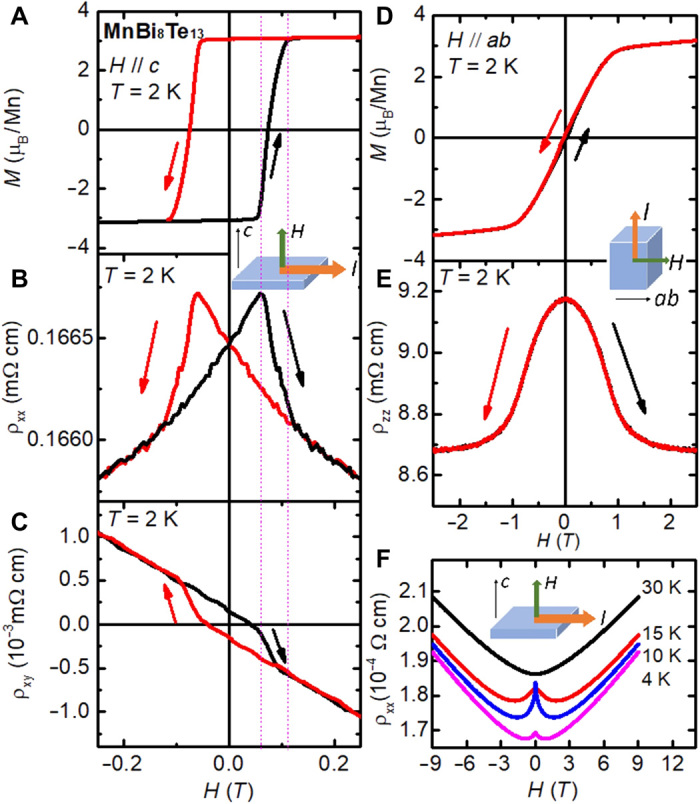
(A to C) Field-dependent magnetization M (A), transverse magnetoresistivity of ρ_xx (B), and Hall resistivity ρ_xy (C) at 2 K with I ∥ ab and H ‖ c. (D and E) Field-dependent magnetization M (D) and transverse magnetoresistivity of ρ_zz (E) at 2 K with I ∥ c and H ∥ab. (F) Transverse magnetoresistivity of ρ_xx with I ∥ ab and H ‖ c at various temperatures.

FM axion state revealed by DFT calculation

To investigate the band topology, in the FM configuration with the spin oriented along the c axis, we calculated the electronic band structure of MnBi₈Te₁₃. Using the experimentally determined lattice parameters and atomic positions, our calculation shows only a continuous bulk energy gap (note S3). In contrast, using the experimental lattice parameters with relaxed atomic positions, our calculation indicates a 170-meV global energy bandgap (Fig. 5B). By comparing our DFT calculation with the experimental ARPES data, the one with relaxed atomic positions describes the material well.

Fig. 5. DFT band structure of MnBi₈Te₁₃ calculated using the experimental lattice parameters with relaxed atomic positions.

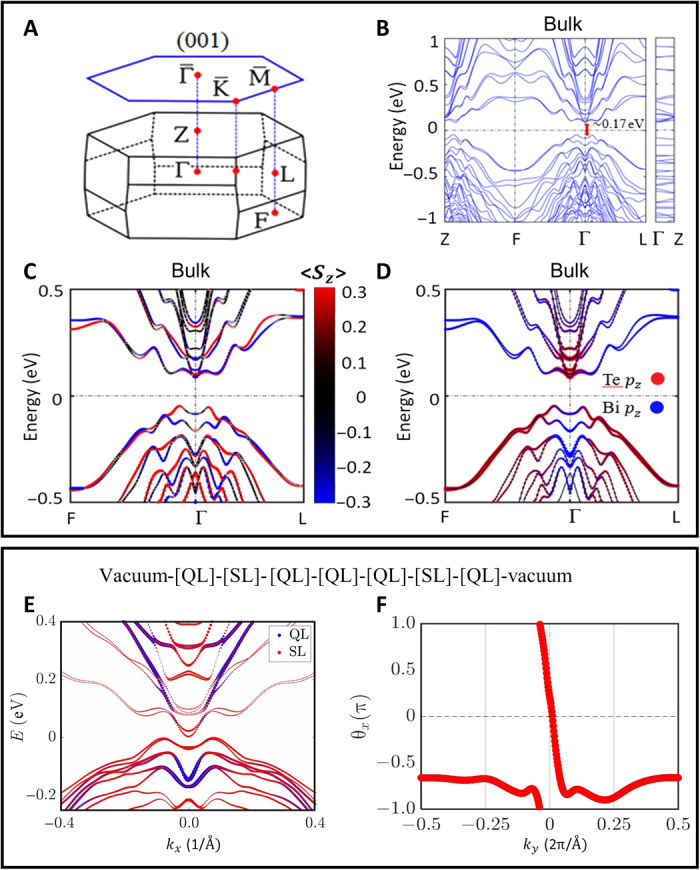
(A to D) Bulk band structure. Bulk Brillouin zone (BZ) and the (001) surface BZ of MnBi₈Te₁₃ with the high symmetry points marked (A). Bulk band structure of MnBi₈Te₁₃ in the out-of-plane FM configuration, with spin-orbit coupling and correlation parameter U included (B). Spin-resolved band structure zoom in around the Γ point (C). Orbital-resolved band structure zoom in around the Γ point (D). The red and blue dots indicate Te p_z and Bi p_z orbitals, respectively. There are clear band inversions between the Te p_z and Bi p_z states at the Γ point. (E and F) DFT calculation of a seven-layered finite-sized slab model corresponding to the QL₁ surface arrangement, i.e., with vacuum-[QL-SL-QL-QL-QL-SL-QL]-vacuum. (E) Band structure of this slab model. The sizes of the blue and red dots represent the fraction of electronic charge residing in the topmost QL and the nearest-neighboring SL, respectively. (F) Evolution of the sum of Wannier charge centers (WCCs) along k_y in the k_z = 0 plane. The trajectory of WCC is an open curve traversing the whole BZ once, indicating the Chern number C = 1 in the k_z = 0 plane.

To highlight the spin splitting in the presence of FM ordering, we present the <S_z> resolved band structure in Fig. 5C. The band structure projected on the Bi p and Te p orbitals shows that the bands near the Fermi level mostly originate from the Bi p and Te p orbitals. As shown in Fig. 5D, there are clear band inversions between the Bi p_z and Te p_z states. The Bi p_z orbitals reach deep into the valence bands, indicating multiple possible band inversions that originate from the different [Bi₂Te₃] QL and [MnBi₂Te₄] SL of MnBi₈Te₁₃.

The presence of clear band inversions around the Γ point hints toward a topological phase. To unravel the exact topology of this system, we first compute the Chern number in the k_z = 0 and k_z = π planes. In both planes, the Chern number is found to be zero. Next, we compute the parity-based higher-order Z₄ invariant, which is given by

$$Z_4={\sum }_{i=1}^8{\sum }_{n=1}^{n_{\text{occ}}}\frac{1+{\mathrm{\xi }}_n({\mathrm{\Gamma }}_i)}{2}\text{mod}4$$ (1)

Here, ξ_n (Γ_i) is the parity of the nth band at the ith time reversal invariant momentum (TRIM) point Γ_i and n_occ is the number of occupied bands. The Z₄ invariant is well defined for an inversion symmetric system, even in the absence of time reversal symmetry (40–42). The odd values of Z₄ (1, 3) indicate a Weyl semimetal phase, while Z₄ = 2 implies an insulator phase with a quantized topological magnetoelectric effect (axion coupling θ = π) (43). A detailed list of the number of occupied bands with even (n⁺_occ) and odd (n⁻_occ) parity eigenvalues at the eight TRIM points is shown in table S3. Based on this, the computed Z₄ invariant is found to be 2, which demonstrates that MnBi₈Te₁₃ is an intrinsic FM axion insulator.

It is noted that, in calculations with or without atomic relaxation, the characteristics of band inversion and the topology of whole system remain the same, i.e., an FM axion state. In addition, we have investigated the evolution of the band structures by changing lattice constants a, b (in-plane), and c (out-of-plane) simultaneously. Within the range from −3 to +3% in MnBi₈Te₁₃, we did not find any crossing point or the additional band inversion feature. Our calculation reveals that the axion phase in MnBi₈Te₁₃ is quite stable.

Surface state revealed by ARPES and DFT

To investigate whether surface states appear in MnBi₈Te₁₃, we have performed small-spot (20 μm× 50 μm) ARPES scanned across the surfaces of MnBi₈Te₁₃. According to the crystal structure of MnBi₈Te₁₃, four different terminations are expected during the cleave, as visualized in the cartoon pictures in Fig. 6. Our ARPES data and DFT calculations reveal distinguishing surface states for the four different terminations of MnBi₈Te₁₃, which are summarized in Fig. 6.

Fig. 6. The comparison of ARPES data and DFT calculation on MnBi₈Te₁₃.

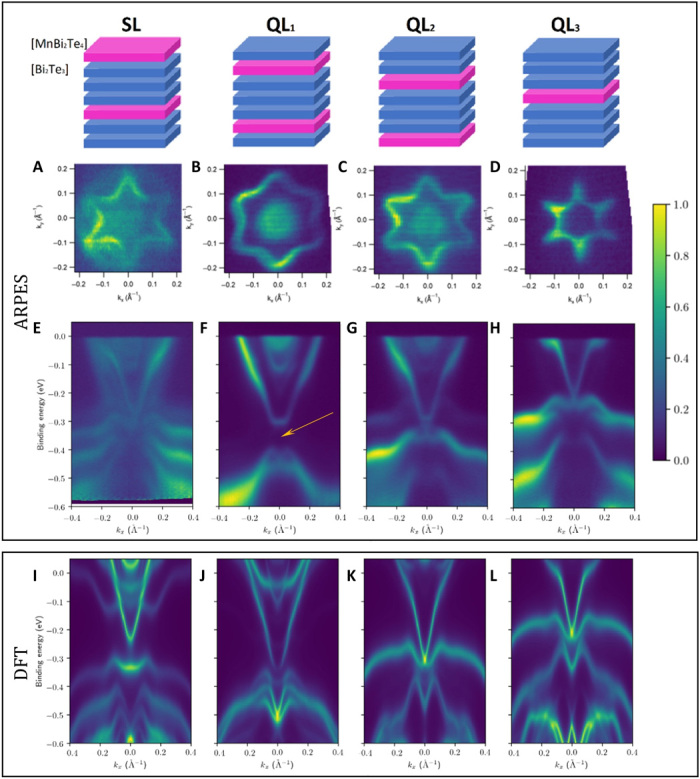
(A to D) Experimental ARPES isoenergy surfaces at the Fermi level measured with 26 eV, 20 μm×50 μm spot-sized linear horizontal light at 12 K: (A) SL, (B) QL₁, (C) QL₂, and (D) QL₃ termination. All Fermi surfaces show the expected sixfold symmetry with clear distinctions. (E to H) Experimental ARPES E-k spectrum cut along the M → Γ → M high symmetry direction for various terminations. A large and clean gap in the surface states of the QL1 termination is observed in (F), as highlighted by the arrow that points to the charge neutrality point suggested by DFT calculations. (I to L) Calculated DFT E-k spectrum cut along the M → Γ → M high symmetry direction for various terminations. We shift the Fermi level to match the experimentally observed Fermi level for each termination.

Figure 6 (A to D) shows the isoenergy surfaces at the Fermi level, which uniquely fingerprints each of the four possible terminations of MnBi₈Te₁₃. We identify a unique circular Fermi surface for the SL termination, which has been observed in other MnBi_2nTe_3n+1 (n = 1, 2, 3) (44–46). We find that the QL_n terminations show a dominant sixfold symmetric Fermi surface with decreasing cross-sectional area from QL₁ to QL₃. Our assignment of the isoenergy surfaces to the respective terminations for MnBi₈Te₁₃ is consistent with previous measurements on the simpler MnBi₂Te₄, MnBi₄Te₇, and MnBi₆Te₁₀ compounds (24, 44–46). Figure 6 (E to H) presents the experimental ARPES E-k maps along the M → Γ → M high symmetry direction. Different types of surface states are observed for each of the four terminations. For the SL termination, a gapless or nearly gapless surface state appears (Fig. 6E), consistent with the gapless surface state observed on the SL termination in previous ARPES measurements of MnBi₂Te₄, MnBi₄Te₇, and MnBi₆Te₁ (24, 44–46). The QL₃ termination, which is unique to MnBi₈Te₁₃, shows mass renormalization near the Fermi level (Fig. 6H). Furthermore, a large surface gap of ~105 meV centering around the charge neutrality point of −0.35 eV is revealed in the QL₁ termination and is highlighted by the arrow (Fig. 6F). We find that the spectra taken below and above the transition temperature are very similar in terms of the size of the gap, except for thermal broadening of the electrons (note S2). This has been observed in various magnetic TIs, including MnBi₂Te₄, MnBi₄Te₇, and MnBi₆Te₁₀, and the origin of it is under debate (24, 47). This aspect will also be discussed more in note S2.

To confirm the topological nature of MnBi₈Te₁₃, we calculated the surface spectral weight throughout the (001) surface Brillouin zone (BZ) using the semi-infinite Green’s function approach for SL, QL₁, QL₂, and QL₃ terminations correspondingly, as shown in Fig. 6 (I to L). Each state is plotted with a color corresponding to the integrated charge density of the state within the topmost QL or SL. In addition, we shift the Fermi level to match the experimentally observed Fermi level.

Excellent agreement between the experimental ARPES data and DFT calculation is achieved for the QL_n terminations as shown in Fig. 6. Our calculation suggests that the sizable surface bandgap presented in the QL₁ termination around −0.35 eV is a hybridization gap induced from the hybridization effect between the topmost QL and the nearest-neighboring SL (note S4). Although the calculated bandgap value is smaller than that from ARPES, it is a well-known problem in that generalized gradient approximation (GGA) generally underestimates the bandgap in semiconductors and insulators (48, 49). The hybridization gap seems universal in MnBi_2nTe_3n+1, which has been suggested for MnBi₆Te₁₀ (50) and MnBi₄Te₇ (51). However, until now, it is unclear if the hybridization gap exists and supports QAH in the 2D limit. To settle down this issue, we have performed DFT calculation on a seven-layered finite-sized slab model with the arrangement of vacuum-[QL-SL-QL-QL-QL-SL-QL]-vacuum, i.e., a structure that has the QL₁ termination on both surfaces. The main features of the slab results shown in Fig. 5E are consistent with our semi-infinite Green’s function approach. We then calculate the Chern number of this slab model based on the Wilson loop method (52). Our result shows a nontrivial Chern number (C = 1) in this hybridization gap (Fig. 5F), demonstrating that MnBi₈Te₁₃ is a QAH insulator in its 2D limit if the Fermi level is gated to the middle of the large hybridization gap.

As a consequence of strong exchange fields from the Mn magnetic layer in the SL termination, our calculation on the SL termination results in a parabolic large gapped surface band dispersion in the bulk energy gap (Fig. 6I). This is in sharp contrast with the gapless Dirac surface state revealed by the ARPES (Fig. 6E). For the SL termination, the deviation between ARPES and DFT calculation as well as the gapless Dirac surface state are universal in the MnBi_2nTe_3n+1 family (n = 1, 2, 3) (24, 44–46). The unexpected gapless surface state is argued to be caused by the surface spin reconstruction when the magnetic [MnBi₂Te₄] layer is at the vacuum-sample interface (24, 45, 46). Further experiments in identifying the spin reconstruction on the SL termination are urged to settle down this issue.

DISCUSSION

We have presented the realization of the intrinsic FM topological material, MnBi₈Te₁₃. Our work has several implications. First, our theoretical calculations show that MnBi₈Te₁₃ is an FM axion insulator. Such a topological axion state suggests a quantized magnetoelectric coupling and an emergent axion electrodynamics. Therefore, the optical responses of MnBi₈Te₁₃, especially in the terahertz regime, may be of great interest. Second, the intrinsic ferromagnetism paves the way for the realization of QAH state at zero magnetic field. Third, when it is exfoliated into the 2D version, the superlattice nature and the stacking of vdW MnBi₈Te₁₃ make it possible to fabricate richer combinations of natural heterostructures than those from AFM MnBi_2nTe_3n+1 (n = 1, 2, 3). Various emergent properties such as QAH state and Quantum Spin Hall state are proposed (36) for such heterostructures. Furthermore, the observation of long-range magnetic order is notable considering the extremely large separation of 44.1 Å between the adjacent [MnBi₂Te₄] SLs; further investigations will shed light on the mechanism of the long-range magnetic ordering in MnBi₈Te₁₃ and will advance our understanding on the magnetism in vdW materials. Last, our work here generally establishes natural heterostructuring as a powerful way to rationally design and control magnetism and other broken symmetry states in layered vdW materials.

METHODS

Sample growth and characterization

We grew single crystals of MnBi_2nTe_3n+1 (n = 3 and 4) using self-flux (17, 35). Around 20 g of Mn, Bi, and Te elements with the molar ratio of MnTe:Bi₂Te₃ as 15:85 was loaded into a 5-ml alumina crucible and then sealed inside a quartz tube under one-third atmosphere of Ar. The sample ampule was heated up to 900°C, stayed for 5 hours, and then quickly air-quenched to room temperature. It was then placed inside a furnace, which was preheated to 595°C. The ampule stayed at 595°C for 5 hours and then slowly cooled down to the decanting temperature in 48 hours. We then let the ampule stay at the decanting temperature for about 24 hours before we separated the single crystals from the liquid flux using a centrifuge. By varying the decanting temperature, we could obtain different phases of MnBi_2nTe_3n+1 (note S1). We found out that the growth window for MnBi₄Te₇ and MnBi₆Te₁₀ is around 2°, while the one for MnBi₈Te₁₃ is limited to be only 1° barely above the melting temperature of the flux. The method to determine the decanting temperature for each phase is described in note S1 in detail. Bi₂Te₃ is the inevitable side product. We also noticed that with increasing n numbers, the chance of the intergrowth between Bi₂Te₃ and MnBi_2nTe_3n+1 (n = 3, 4) got enhanced. Therefore, extra care was paid in screening out the right piece. XRD at low angles for both the top and bottom (0 0 l) surfaces as well as powder XRD were performed on a PANalytical Empyrean diffractometer (Cu Ka radiation). Structural determination based on powder XRD was done using FullProf Suite software (53). STEM was measured on a sample prepared by focused-ion beam, and images are made on a Cs-corrected transmission electron microscope (Titan, Thermo Fisher Scientific, FEI) at 300 kV. Images are Bragg-filtered. Electric resistivity was measured in a Quantum Design (QD) DynaCool Physical Properties Measurement System. All samples were shaped into thin rectangular bars, and the four- and six-probe configurations were used for electrical resistivity and Hall resistivity, respectively. The magnetoresistivity was symmetrized using ρ_xx(B) = (ρ_xx(B) + ρ_xx(−B))/2, and the Hall resistivity was antisymmetrized using ρ_xy(B) = (ρ_xy(B)−ρ_xy(−B))/2. The magnetization was measured using the QD Magnetic Properties Measurement System. The piece used for the magnetization measurement was later ground into fine powder, whose powder XRD pattern showed no impurity and was used for structural determination.

Single-crystal neutron diffraction

Single-crystal neutron diffraction experiments were performed at the HB-3A DEMAND single-crystal neutron diffractometer equipped with a 2D scintillation Anger camera with 0.6-mm spatial resolution at the High Flux Isotope Reactor at Oak Ridge National Laboratory in the temperature range of 4.5 to 15 K (54). Neutron wavelength of 1.551 Å was selected by using a bent perfect Si-220 monochromator. Rocking curve scans, which cover the full peak profile of the Bragg reflection (1 0 1), were carried out at 4.5 and 15 K, respectively. The peak (1 0 1) was selected for revealing the magnetic ordering parameter from 4.5 to 15 K.

First-principles calculations

The bulk band structures of MnBi₈Te₁₃ were computed using the projector augmented wave method as implemented in the VASP package (55–57) within the GGA (58) and GGA plus Hubbard U (GGA + U) (59) scheme. On-site U = 5.0 eV was used for Mn d orbitals. The spin-orbit coupling was included self-consistently in the calculations of electronic structures with a Monkhorst-Pack k-point mesh 5 × 5 × 5. The experimental lattice parameters were used. The atomic positions were relaxed until the residual forces were less than 0.01 eV/Å. We used Mn d orbitals, Bi p orbitals, and Te p orbitals to construct Wannier functions, without performing the procedure for maximizing localization (60).

The surface spectral weight throughout the (001) surface BZ was calculated using the semi-infinite Green’s function approach for four distinct surface terminations. We set up four different models to calculate the surface state to compare with the ARPES data, for example, for the SL termination, the semi-infinite Green’s function model was set as vacuum-[SL-QL-QL-QL]-[SL-QL-QL-QL]-infinite; to get that of the QL₁ termination, the model was set to be vacuum-[QL-SL-QL-QL]-[QL-SL-QL-QL]-infinite. This method was valid because the thickness of the QL or SL is about 10 Å, which roughly equals the typical escape depth of photoelectrons.

ARPES measurements

ARPES measurements on single crystals of MnBi₈Te₁₃ were carried out at the Stanford Synchrotron Research Laboratory (SSRL) beamline 5-2 with photon energies of 26 eV with linear horizontal polarization and a 20 μm× 50 μm beam spot. Single-crystal samples were top-posted on the (001) surface and cleaved in situ in an ultrahigh vacuum better than 4×10⁻¹¹ torr and a temperature of 15 K.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/6/30/eaba4275/DC1