High-resolution 3-dimensional photonic scan-derived equations improve body surface area prediction in diverse populations

Abstract

Objective:

Equations for predicting Body Surface Area (BSA) produce flawed estimates, especially for individuals with obesity. We aimed to compare BSA measured by a 3-dimensional photonic scanner (BSA_3DPS) to BSA predicted by six commonly cited prediction equations, and to develop new prediction equations if warranted.

Methods:

We validated the 3DPS against manual measurements by breadth caliper for body thicknesses measured at three anatomical sites on a mannequin. BSA was derived from 3DPS whole body scans of 67 males and 201 females, ages 18-83; BMIs 17.8-77.8 kg/m², and varied race/ethnicities.

Results:

Width and depth measurements by 3DPS and caliper were within 1%, except for hip, error 1.8%. BSA_3DPS differed from BSA predicted by each equation (p<0.05), except for males by DuBois (p=0.60), Tikuisis (p=0.27) and Yu (p=0.45), and for females by Tikuisis (p=0.70). The combined and sex-specific equations obtained by regressing ln(BSA) on ln(W) and ln(H), are (W=weight kg; H=height m, R² and SEE correspond to ln(BSA)): Combined: BSA_3DPS=0.03216 x W^0.4904 x H^0.3769, R²=0.982, SEE=0.021; Males: BSA_3DPS=0.01624 x W^0.4725 x H^0.5231; Females: BSA_3DPS=0.01522 x W^0.4921 x H^0.5231, R²=0.986, SEE=0.019.

Conclusion:

New height and weight BSA equations improve BSA estimations in BMI ≥ 40 kg/m², African Americans, Hispanic Americans and Asian Americans.

INTRODUCTION

Total body surface area refers to the combined skin, hair, and nail covered areas of the human body. Due to variations in body size across individuals, BSA has been used since 1883 (1) to normalize specific measures of biological function for multiple clinical purposes. A height-weight BSA calculation is widely used as, a comparative index for energy expenditure when caloric requirements are estimated in kcal/m² (2); to calculate glomerular filtration rate in nephrology for normalizing comparisons of renal function (3) and has been proposed to replace body water as the scaling factor for the determination of hemodialysis dose (4); to calculate fluid replacement needs for normal maintenance and from abnormal losses due to vomiting or diarrhea (5); when calculating drug dosages for chemotherapy, chronic Hepatitis B, antivirals, antimicrobials, antifungals and tumor grading agents (6-9); scaling for cardiovascular variables including cardiac output and stroke volume (10); in organ transplantation when calculating total liver volume index for liver transplantation (9); and in the evaluation and treatment of burns(9).

The complex shape and contours of the human body make it difficult to measure BSA directly, which has led to the development of several prediction equations for estimating BSA. Despite being developed over 100 years ago and based on an extremely small sample, the DuBois equation continues to be the most commonly used prediction equation in clinical practice. The DuBois equation has been shown to underestimate BSA for low BMIs (11) and both underestimate (12, 13) and overestimate (11) BSA for high BMIs. Under- or overestimation may lead to inadequate treatment (12). Given the high global prevalence of obesity and its disproportionate impact on racial and ethnic groups, along with the large array of clinical uses for estimated BSA, alternatives to the empirically derived equations currently in use may be needed. Three-dimensional body scanning offers a viable approach for estimating BSA using triangulation techniques to produce more precise measurements (14). Currently available 3DPS-based prediction equations have been developed using individuals representing a narrow range of body sizes and from limited ethnic backgrounds (12, 13).

The purpose of this study was to compare BSA measured by a validated criterion high resolution digital 3-dimensional photonic scanner (3DPS) to BSA predicted from six weight- and height-based prediction equations, in adults from four ethnic backgrounds and over a wide range of BMI. We hypothesize that BSA_3DPS will differ from BSA predicted from the six weight- and height-based equations. Should differences be found, new prediction equations will be developed.

METHODS

Study Design

Cross-sectional data from a convenience sample of individuals who had participated in one of three studies conducted at St Luke’s-Roosevelt Hospital’s Body Composition Unit (15-19) were used for the analyses. These data include race/ethnicity, height, weight and whole body 3D scans. Recruitment occurred from 2004 to 2012 through newspaper advertisements and flyers posted in the local community. Studies were approved by the St. Luke’s–Roosevelt Hospital Institutional Review Board. A flowchart of 3D scans available for inclusion in analyses is shown in Figure S1, Supplemental page 7 of 9.

A validation of the 3DPS against manual measurements conducted to facilitate the comparison of 3DPS to empirical equations based on manual measurements is described in the supplemental section. Figure S2, Supplemental page 8 of 9, shows a cross-section of the chest used for comparison. A summary of BSA validation studies are presented in Table S1, Supplemental pages 3-5 of 9.

Participants

Subjects were free of health conditions that would impact hydration status, independent, ambulatory, community-dwelling individuals. Post-bariatric surgery participants were intentionally excluded to avoid artifacts due to excess skin. Race/Ethnicity was determined by self-report.

Methods of Measurement

Body weight was measured to the nearest 0.1 kilogram (Ohaus Champ (CD11) General Purpose Bench Scale, Pine Brook, NJ) and height to the nearest 2 millimeters using a stadiometer (Holtain, Crosswell, Wales) while subjects wore tight fitting minimal underwear without shoes.

3-D photonic image scanning measurements

The 3DPS (Model # C9036-02, Hamamatsu Photonics K.K., Hamamatsu, Japan) is a non-invasive optical method (14, 15) and was previously validated for the measurements of body volume (15), body circumference and segment length (15-17). The scan system has four photonic image production units or cameras mounted on four corner poles. Each unit has an eye-safe class-1 laser-light source (664 nm) and a high speed, high-resolution digital camera. The scan field is 200 cm high, 100 cm wide and 60 cm deep. During scan acquisition, the subject wore a tight-fitting cap to minimize air-spaces between the hair and skull, and well-fitting underwear that clung to the skin surface. Arms were positioned with hands holding the handlebars and subject stood on footprints, which were equidistant from the center point. With this standardized position, subjects’ arms were abducted from the trunk and there was no contact between the legs. Subjects were asked to remain motionless during scanning that included 3 repeated scans during normal breathing. The reported body surface area (BSA, cm²) and calf circumference (CC, cm) values were calculated from the first scan, unless there was movement, in which case the second scan was used. Technical Error of the Measurement (TEM) was calculated from the 3 repeated scans which were performed without repositioning. In a random sample of 75 subjects, 32 males and 43 females, mean weight 105.0 kg, height 167.9 cm, and BMI of 37.0 kg/m² representing the 17-77 BMI range, TEM was 0.49% for BSA. The TEMs for four subgroups: BMI <30, 30.0-34.9, 35.0-39.9 and ≥ 40 are presented in Table S2. In our laboratory, 12 subjects (6 males and 6 females) with mean weight 53.2 kg, height 149.4 cm, and BMI 21.8 kg/m², were scanned 3 times on 3 consecutive days. The TEMs were 0.30% for body volume and 0.43% for BSA, respectively. BSA coefficient of variation was 1.05% with an intraclass correlation (a measure of reliability) of 0.99.

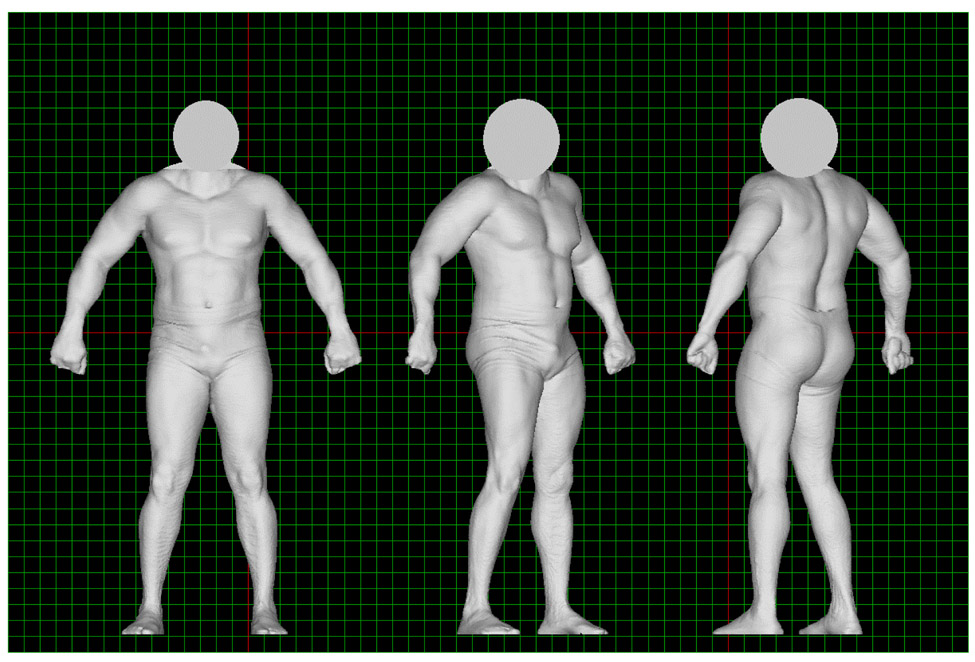
The 3DPS software, Body Line Manager, v 1.3, uses triangulation mathematics to detect the position of the light point that is projected onto the surface of an object and reflected to the cameras. During the scanning process, the four cameras move vertically and simultaneously. Laser-light points project onto the subject’s surface and reflect to the cameras, producing a maximum of 2,560 measurement points at each horizontal slice. A vertical measurement pitch can be selected as 2.5 or 5 mm. Acquired in the current study were 800 cross-sections over a 2-meter vertical scan field, in 10 seconds with a 2.5 mm pitch interval (total = 2,048,000 data points). The density of the data points from a 10-second scan of the body surface of a scanned subject is 16 data points/cm². The Body Line Manager software on a PC computer connects the points to generate a 3D whole body image, and calculate total and regional body volumes, circumferences, lengths, widths, and thicknesses as described previously (15). The software calculates surface areas digitally over the body surface regions where digital data points and their confined body surface areas are detected by the scan camera. The sum of the digital areas over the entire body surface is the total BSA (see detailed explanation in the supplemental section). This 3DPS method has high accuracy, reliability and reproducibility for the measurement of total and regional body volumes (15). Figure 1 shows the total body image generated by the 3DPS for an adult. Figure S3, Supplemental page 9 of 9, shows a total body image generated by the 3DPS for three adults of varying body shape.

Figure 1.

Total body image generated by the 3DPS of an adult male from various angles.

BSA prediction equations

Presented in Table 1 are six commonly used BSA prediction equations selected based on frequency of citation from among 50 equations identified in an extensive literature review. All six equations predict BSA from weight and height alone with the exception of one (20) that also includes calf circumference.

Table 1.

Selected BSA prediction equations for comparison with 3DPS derived BSA

Authors (reference)	Body Surface Area measurement method	Equation	Population
			N and Race	Demographics
DuBois & DuBois, 1916 (19)	Coating method	BSA=0.007184 x W0.425 x H0.725	N=9 North American	Age: 1.75-36 W: 6.27-93.0 H: 73.2-184.2 BMI: 15.3-41.50 BSA: 0.3699-1.9000
Gehan & George, 1970 (22)	N=163 coating method N=222 surface integration N=16 triangulation	BSA=0.0235 x W0.51456 x H0.42246	N=401 Cited from Boyd E., which published in Minneapolis, 1935.	<5yrs: N=229 5-20yrs: N=42 ≥20yrs: N=130
Jones, 1985 (18)	Coating method	BSA=0.327+0.0071W+0.0292CC	N=15 Caucasian female	Age: 17-39 W: 47.0-80.8 H: 154.7-174.9 BSA: 1.5500-2.0600 CC: 30.3-38.7
Nwoye & Al-Shehri, 1989 (24)	Coating method and planimetry (not including penis and scrotum as their error <1%; one side only in limbs and the head)	BSA=0.001315 x W0.2620 x H1.2139	N=20 African male (Nigerians- southern nationalities)	Age: 18-55 W: 49.0-90.5 (Mean 65.1) H: 151.7-192.7(Mean 173.7) BMI: 18.98-24.12(Mean 21.46) BSA: 1.6890-2.4160 (Mean 2.0630)
Tikuisis, 2001 (25)	3D laser scanning technology	M: BSA=0.01281 x W0.44 x H0.60 F: BSA=0.01474 x W0.47x H0.55	N=641 North American and European	Male (N=395) Age: 18-64 W: 48.9-156.8 H: 149.7-198.2 BSA: 1.4900-2.7130 Female (N=246) Age: 19-63 W: 45.0-140.7 H: 145.3-187.9 BSA: 1.3800-2.6620
Yu, 2010 (26)	Gemini 3D scanners	BSA=0.00713989 x W0.4040 x H0.7437	N=270 Taiwanese	Age: 18-64 Male (N=135) H: 167.2±6.2 BMI: 22.8±5.0 Female (N=135) H: 155.4±5.3 BMI: 22.9±5.3
Ashby-Thompson (current investigation)	Hamamatsu 3DPS	Combined: BSA3DPS=0.03216 x W0.4904 x H0.3769 M: BSA3DPS=0.01624 x W0.4725 x H0.5231 F: BSA3DPS=0.01522 x W0.4921 x H0.5231	N=113 Caucasian N=92 African American N=43 Hispanic N=9 Asian N=11 Other	Male (N=67) Age: 18-74 W: 55.9-245.1 H: 166.6-177.5 BMI: 20.1-77.8 (mean: 36.0) BSA: 1.6-3.3 (mean: 2.187) Female (N=201) Age: 18-83 W: 51.4-193.7 H: 145.1-180.9 BMI: 17.8-74.6; (mean: 38.0) BSA: 1.7-2.5 (mean: 2.106)

N=sample size; Age=years; W=weight (kg); H=height (cm); BMI=body mass index (kg/ m²); BSA=body surface area (m²); CC=upper calf circumference (cm).

-The DuBois and DuBois (21) equation is the most widely used BSA prediction equation and was developed in a small sample of 9 children and adults (race not specified) using the Coating method (22). Coating involves covering the body with a substance of a known or measurable area. The individual coatings are then fitted together on cross-sections of paper and measured by direct geometry (22) or other methods such as planimetry (23) or electronic digitization (20).

-The Gehan & George (24) equation was developed in 401 US children and adults using the coating method (n=163; (22)), surface integration (n=222; (25)), and triangulation (n=16; (25)). Surface integration represents the human body geometrically as a rectangular prism or as a series of truncated cones. Triangulation involves marking off regular geometric figures, chiefly triangles, on the body. The area of each figure is calculated from its linear dimensions.

-The Jones et al (20) equation was developed in a small (n=15) sample of Caucasian adult females using both the coating and direct digitizing methods.

-The Nwoye (26) equation was developed in a small sample (n=20) of African adult males, all of whom were lean based on BMI<22 kg/m², using the coating method and planimetry or by weighing the polythene coating material and computing the area from a standard curve (22).

-The Tikuisis (27) equation was developed in an adult male and female sample (n=641; BMI<40kg/m²) from North America and Europe using 3-dimensional laser scanning (WB4 Whole Body Colour 3D Scanner).

-The Yu (28) equation was developed in Asian adults, including 135 males (height 167.2±6.2 cm, BMI 22.8±5.0 kg/m²) and 135 females (height 155.4±5.3 cm, BMI 22.9±5.3 kg/m²). This study used two scanners for BSA measurements, a Gemini 3D whole body scanner and a high-resolution Gemini 3D hand/foot scanner (designed by Industrial Technology and Research Institute).

Statistics

Descriptive statistics were calculated for age, sex, race/ethnicity, and anthropometric measures, for BSA_3DPS, and for the estimated BSA’s using six published equations. The hypothesis that the mean values for the BSA obtained from the seven different methods, BSA_3DPS and six equations, were equal was tested using a mixed model analysis. The fixed effects in the model were method, sex, and method by sex interaction. Subject was considered a random effect. Since there was a significant method by sex interaction, contrasts were constructed to compare the mean BSA_3DPS to the mean estimated BSA of each equation for males and females separately. Regression analysis modeled the relationship between BSA_3DPS and weight, height, age, sex, and race. Dummy variables modeled the effects of sex and race. BSA_3DPS, weight, and height were transformed using the natural logarithm of each variable. Repeated measures ANOVA models were constructed to investigate differences in BSA by the Tikuisis, Dubois and the new 3DPS-based equation using weight, height, sex and race among five subgroups: African-Americans, Hispanic Americans, Asian Americans and Other, and individuals with Class III obesity (BMI ≥ 40kg/m²). Primary and secondary endpoints did not change during the course of the study or during post-hoc analyses. Analyses not pre-specified are considered exploratory. All statistical analyses were performed with SAS version 9.2 (SAS Institute Inc., Cary, NC) and STATA version 10.1 (STATA Corp, College Station, TX) statistical software packages for personal computer. The level of significance for all statistical tests of hypotheses was 0.05.

RESULTS

Comparison of 3DPS and manual measurements on mannequin

3DPS and caliper measures were within 1%, except for hip with 1.8% error (p=0.18). Mean errors and CVs are presented in Table S3, Supplemental page 7 of 9.

Demographic and Body Composition Characteristics

Adults (67 males, 201 females) ages 18–83 years, with BMI’s 17.8 to 77.8 kg/m² were included in the analysis. Of these, 42.2% were non-Hispanic Caucasian, 34.3% non-Hispanic African-American, 16% Hispanic-American, 3.4% Asian-American and 4.1% Other/Mixed race. Sex and racial/ethnic distribution and descriptive characteristics are presented in Table 2. The mixed model analysis of BSA showed significant main effects for sex (p=0.0054) and method (p<0.0001), and a significant interaction between method and sex (p<0.0001). Presented in Table 3 are descriptive statistics for the six BSAs by sex and the results of testing the null hypothesis that the mean BSA_3DPS is equal to each of the mean BSAs from the prediction equations (Table 1). For males, the mean BSA_3DPS was less than the mean predicted BSAs by Gehan (p<0001), Jones (p<0.0001, and Nwoye (p<0.0001); however, the mean estimated BSAs by DuBois & DuBois (p=0.5975), Tikuisis (p=0.2675) and Yu (p=0.4504) were not different from the mean BSA_3DPS. For females, the mean BSA_3DPS was less than the mean predicted BSA’s by Gehan (p<0.0001), Jones (p<0.0001), and Nwoye (p<0.0192), and was greater than the mean estimated BSA by DuBois & DuBois (p<0.0001) and Yu (p<0.0001). For females, there was no significant difference between the mean BSA_3DPS and the estimated BSA using Tikuisis’ (p=0.7028) equation. Also presented are the relative errors associated with each method compared to the 3DPS, and examples of BSA by specified method for two participants.

Table 2.

Ethnic distribution of study sample (n=268) and subject characteristics

	Caucasian		African-American		Hispanic		Asian		Other
	Male	Female	Male	Female	Male	Female	Male	Female	Male	Female
N	29 (10.8%)	84 (31.3%)	15 (5.6%)	77 (28.7%)	11 (4.1%)	32 (11.9%)	6 (2.2%)	3 (1.1%)	6 (2.2%)	5 (1.9%)
Age (yrs)	53.0±10.1 (32-74)	46.7±13.5 (20-74)	43.6±12.4 (18-60)	52.8±16.7 (18-83)	41.1±12.2 (22-56)	40.9±10.9 (25-64)	51.3±13.8 (38-68)	37.0±17.3 (27-57)	42.2±13.8 (25-59)	51.2±15.0 (36-76)
Weight (kg)	121.5±41.1 (59.3±196.4)	104.2±22.7 (54.6-149.6)	108.6±34.1 (68.7±165.5)	100.8±33.8 (51.4-190.6	118.3±54.0 (79.4-245.1)	98.6±27.4 (58.8-193.7)	69.0±10.1 (55.9-82.6)	73.0±14.6 (56.3-83.6)	80.3±5.1 (75.9-87.8)	94.5±33.2 (57.6-132.3)
Height (cm)	175.6±7.1 (161.6-186.4)	163.2±6.2 (145.1-178.8)	176.0±6.8 (160.3-187.9)	163.4±6.5 (152.0-180.9)	170.0±5.3(159.8-177.5)	161.9±6.7 (146.7-171.9)	171.3±7.6 (159.0-177.9)	163.3±6.7 (155.8-168.6)	167.6±8.0 (157.5-175.8)	164.2±7.8 (153.4-173.4)
BMI (kg/m2)	39.0±11.5 (20.6-58.7)	39.2±8.6 (20.9-63.2)	34.7±9.2 (21.4-51.0)	37.6±11.9 (17.8-73.0)	40.7±17.3 (27.4±77.8)	37.7±10.6 (24.0-74.6)	23.4±2.1 (20.1-26.1)	27.7±7.4 (19.8-34.5)	28.7±3.0 (24.6-31.3)	34.4±9.5 (22.6-44.0)

Values are mean ± standard deviation (range)

Table 3.

Comparison of the measured BSA to the predicted BSA using selected equations

	BSA3DPS	DuBois	Gehan	Jones	Nwoye	Tikuisis	Yu
Male
Mean BSA (±SD)	2.187±0.410	2.195±0.382	2.295±0.457*	2.330±.0480*	2.333±0.304*	2.203±0.387	2.177±0.363
Mean Relative Error (±SD) (predicted - measured)/measured		0.006±0.024	0.047±0.024	0.063±0.043	0.078±0.071	0.009±0.022	−0.001±0.028
Example 1: BSA by method for a male participant H=177.5cm W=245.14kg	3.318	3.181	3.554	3.895	2.987	3.224	3.102
Female
Mean BSA (±SD)	2.106±0.313	2.037±0.265*	2.157±0.323*	2.288±0.385*	2.125±0.208*	2.109±0.294	2.021±0.252*
Mean Relative Error (±SD) (predicted - measured)/measured		−0.030±0.028	0.024±0.024	0.085±0.051	0.017±0.068	0.003±0.023	−0.037±0.031
Example 2: BSA by method for a female participant H=160.4cm W=51.41kg	1.482	1.522	1.524	1.507	1.754	1.533	1.531

Note: Value presented are mean ± standard deviation

^*significantly different from 3DPS at p<0.05 BSA=body surface area (m²)

Since the predicted mean BSA using Tikuisis’ equation was not different from the mean BSA_3DPS for males and females, linear regression methods were used to test the null hypothesis that the relationship between BSA_3DPS and BSA predicted by Tikuisis was consistent with the line of identity. For males and females, the null hypothesis was rejected (p<0.0001). For males and females, the slopes were significantly greater than unity (p<0.0001) which suggests that the difference between the slope and the line of identity is proportional to the BSA.

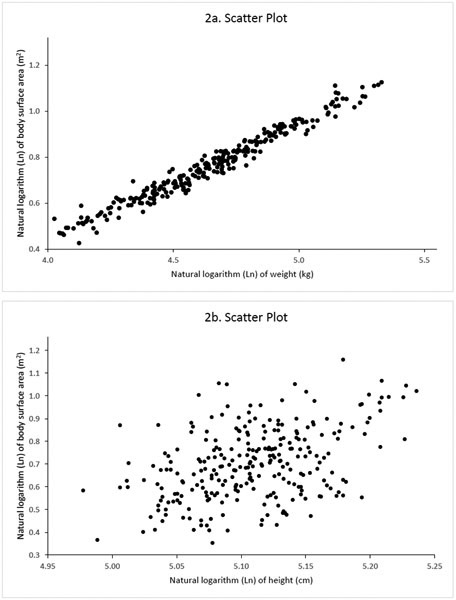
Figures 2a and 2b present the scatter plots of the natural logarithm of BSA versus the natural logarithm of weight and the natural logarithm of height, respectively. The relationship between the natural logarithm of BSA and the natural logarithm of weight or the natural logarithm of height indicate linear relationships between the variables. Table 4 provides the regression equation to predict BSA_3DPS using weight, height, sex, and race as independent variables. Age was not included in the model as its effect was not significant (p=0.63). There were significant effects of race (p<0.0001) and sex (p<0.0001), and no interaction between race and sex (p=0.879). There were interactions between weight and race (p=0.020) and weight and sex (p=0.001), and no interactions between height and race (p=0.14) and height and sex (p=0.1275). There were no differences among Asian (A), Caucasians (C), Hispanics (H), and others (p=0.4125); however, African Americans (AA) were significantly different from the others (p<0.0001). Using the equation provided in Table 4a, BSA by race and sex is:

Figure 2.

Scatter diagram of the natural logarithm (ln) of measured body surface area (BSA) (meters squared) by 3DPS versus the natural logarithm (ln) of (A ) weight and (B ) height.

Table 4.

Regression equation to predict ln(BSA) using weight, height, sex, and race.

Variable	coefficient	Standard error	P-value	R2	SEE
ln(wt)	0.476	0.006	0.001
ln(ht)	0.509	0.027	0.001
sex x ln(wt)	0.027	0.008	0.001
AA x ln(wt)	−0.017	0.007	0.020
sex	−0.103	0.035	0.003
AA	0.099	0.034	0.004
constant	−4.068	0.136	0.001
Fit				0.989	0.016
Regression equation to predict ln(BSA) using weight, height, and sex.
Variable	coefficient	Standard error	P-value	R2	SEE
ln(wt)	0.472	0.007	0.001
ln(ht)	0.523	0.032	0.001
sex x ln(wt)	0.020	0.008	0.018
sex	−0.065	0.038	0.090
constant	−4.121	0.157	0.001
Fit				0.986	0.019
Regression equation to predict ln(BSA) using weight and height.
Variable	coefficient	Standard error	P-value	R2	SEE
ln(wt)	0.490	0.005	0.001
ln(ht)	0.377	0.029	0.001
constant	−3.437	0.141	0.001
Fit				0.982	0.021

Note: ln=natural logarithm; wt=weight (kg); ht=height (cm); BSA=body surface area (m²); sex=1 for female subject, sex=0 for male subject; AA = 1 for African American subjects, AA=0 all other subjects.

• Non-AA females: BSA (m²) =0.01544 x weight^0.5028 x height^0.5091

• Non-AA males: BSA (m²) =0.01711 x weight^0.4757 x height^0.5091

• AA females: BSA (m²) =0.01705 x weight^0.4856 x height^0.5091

• AA males: BSA (m²) =0.01889 x weight^0.4586 x height^0.5091

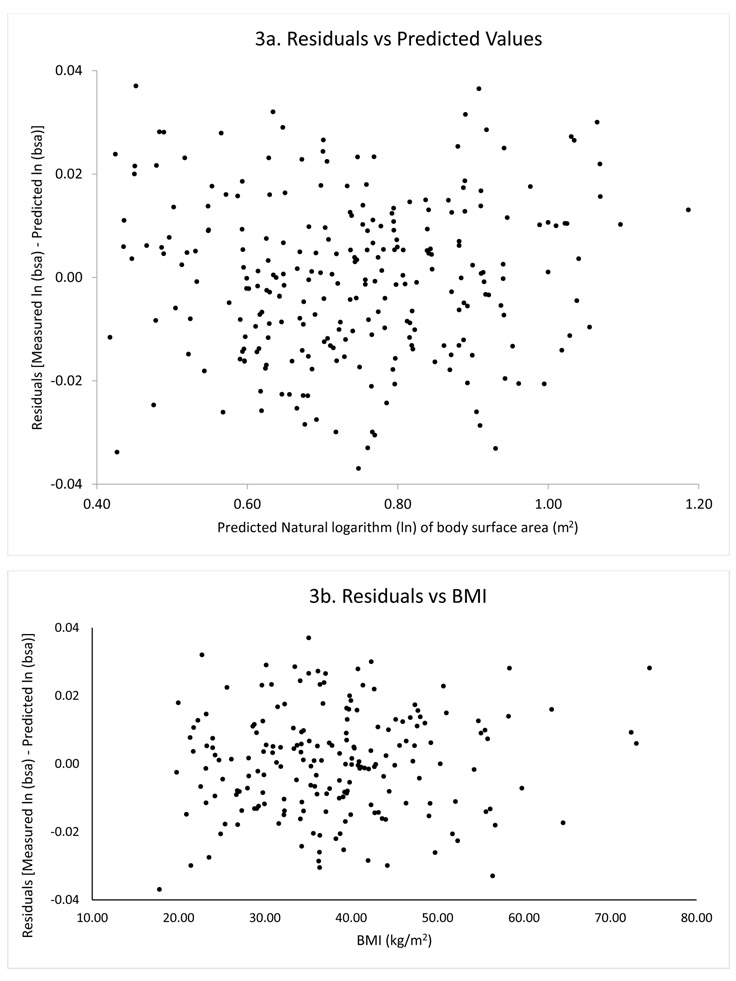
For a given weight and height, females have a significantly greater BSA than males, and African Americans have a significantly greater BSA than non-African Americans. Figures 3a and 3b present scatter plots of the residual [measured ln(bsa) – predicted ln(bsa)] versus the predicted values and residual versus BMI, respectively. The absence of patterns in these scatter plots suggests that the model describes the data uniformly across the range of predicted values and BMI. The distribution of the residuals was consistent with a normal distribution using the Shapiro-Francia normality test (p=0.9274).

Figure 3.

Scatter diagram of BSA residual (A ) versus BSA (meters squared) predicted values and (B ) versus BMI.

Although there was a statistically significant effect of race, including race in the model minimally increased the R² from 0.986 to 0.989. Therefore, a second model was derived that eliminated race, retaining weight, height, and sex. Sex specific BSA equations are in Table 4:

• Females: BSA (m²) = 0.01522 x weight^0.4921 x height^0.5231

• Males: BSA (m²) = 0.01624 x weight^0.4725 x height^0.5231

Eliminating sex from the model had a minimal effect on the R², decreasing from 0.986 to 0.982. With weight and height alone in the model, the equation (Table 4) is:

• BSA (m²) = 0.03216 x weight^0.4904 x height^0.3769

Presented in Table 5 are the results for specific subgroup (African American, Hispanic, Asian, Other, BMI >40kg/m²) comparisons of predicted BSA by 3DPS equation using weight, height, sex and race to predicted BSA using the DuBois and Tikuisis equations. Subgroup comparisons [mean difference± standard error; significance set at p<0.05] showed among individuals with BMI ≥40 kg/m², mean BSA was smaller by Dubois (0.094 ± 0.004 m²), but did not differ by Tikuisis compared to the new 3DPS-based equation. Among African Americans, mean BSA was smaller by both Dubois (0.079 ± 0.004 m²) and Tikuisis (0.020± 0.004 m²) compared to the new 3DPS-based equation. Among Hispanic Americans, mean BSA was smaller by Dubois (0.037 ± 0.006 m²), but larger by Tikuisis (0.020 ± 0.006 m²) compared to the new 3DPS-based equation. Among Asian Americans, mean BSA was larger by both Dubois (0.033 ± 0.008 m²) and Tikuisis (0.044 ± 0.008 m²) compared to the new 3DPS-based equation. Among participants identified as “Other”, mean BSA did not differ by Dubois and was larger by Tikuisis (0.031 ± 0.010 m²) compared to 3DP-based equations.

Table 5.

Comparison of predicted BSA (m²) using selected equations by subgroup

	BSA3DPS	DuBois	Tikuisis
Subgroups
African American	2.140±0.359	2.060±0.323*	2.119±0.347*
Hispanic	2.097±0.342	2.060±0.307*	2.117±0.322*
Asian	1.765±0.148	1.798±0.144*	1.808±0.146*
Other	1.938±0.279	1.938±0.247	1.970±0.269*
BMI ≥40 kg/m2	2.458±0.257	2.364±0.257*	2.450±0.244

Note: Value presented are mean ± standard deviation

^*significantly different from 3DPS at p<0.05

DISCUSSION

High resolution 3D photonic scanning is a quick and accurate method of measuring BSA in individuals able to stand upright and remain motionless for 10 seconds. No other technique exists to reliably measure BSA other than weight- and height-based prediction equations, which explains their proliferation. Differences were found between BSA_3DPS and BSA by prediction equations for three of the six equations in males and for five equations in females. The differences were sex and method dependent. New equations are presented that predict BSA using weight, height, sex, and ethnicity. The new equations predict BSA uniformly across a wide range of BMI. Overall, a minimum of ninety-eight percent of the variability in BSA can be accounted for by each of the new equations.

Of the six equations evaluated, only Tikuisis, a 3DPS-based equation (27) produced estimates that were not significantly different from BSA_3DPS in both males and females. Our population differed from that of Tikuisis with a wider age (18-83 vs 18-64 years) and BMI range (17.8-77.8 vs 21.3-39.9 kg/m²); race/ethnicity was not described. The Tikuisis equation tends to underestimate BSA for higher BMIs and overestimate BSA for lower BMIs.

Most empirically derived equations overestimated BSA, similar to previous reports (27-30). Compared to BSA_3DPS, BSA overestimation ranged from 0.4 to 6.7% (mean 3.9%) in males and from 0.1% to 8.6% (mean 3.0%) in females. Daniell et al. (29), in their evaluation of BSA_3DPS against 15 empirically derived equations, found 13 of the 15 equations overestimated BSA by less than 2%. Daniell also reported significant interaction effects between BSA_3DPS and BMI. The precision of the estimated BSA decreased with increasing BMI such that the bias (difference between equation-estimated BSA and BSA_3DPS) increased as BMI increased, suggesting the need for BMI-specific BSA equations in some instances. Kuehnapfel et al (30) evaluated BSA_3DPS against 18 empirically derived equations and found that empirical formulae overestimated BSA for subjects with obesity and underestimated BSA in lean subjects. Both the Daniell and Kuehnapfel studies (29, 30) involved homogeneous samples of Caucasian origin only, thus limiting their generalizability. Our data showed no interaction between BSA_3DPS and BMI (Figure 3b).

Within our data, two people with the same weight and height have different surface areas if they differ by ethnicity and/or sex. These two factors, ethnicity and sex, were statistically significant. If one considers the R² of the models, including race in the model, although statistically significant, provides very little practical improvement in the model: with race, R²=0.989 and without race, R²=0.986, which represents an improvement of 0.003. This may be a case of statistical significance without practical importance. All equations are presented allowing readers to make their own determination about statistical significance versus practical importance. In the Kuehnapfel study (30), from among 18 equations, including DuBois and three newly developed 3DPS-based equations, the 3DPS-based sex and BMI adjusted equation produced the smallest bias. Differences in BSA estimates by sex could be explained by differences in anatomy. Differences in BSA by race/ethnicity could be explained by differences in shape or body proportions. For the same BMI, in NHANES data, non-Hispanic blacks had greater leg mass and smaller trunk mass and waist circumference than non-Hispanic white and Mexican-American groups, which could translate to the greater BSA observed here in African-Americans (31).

The Hamamatsu technology, and other similar high-resolution scanning technologies, have limited availability due to cost. Consequently, there has been a recent surge in the development of laser based imaging technologies (32-35) and associated Apps (36) driven largely by the demand for devices that estimate body composition and body shape easily, and for personalized health assessments in weight management. The devices currently being marketed have lower resolution and sensitivity compared to the 3DPS scanner reported here. These new technologies show promise, but they cannot yet replace empirical BSA formulae. The complexity of newly developed equations is often cited as a barrier to their adoption and clinicians have opted for simplified equations at the expense of precision (37, 38). Patient safety should be of utmost concern and the precision of BSA estimates may have treatment consequences (9, 13). Using the most extreme cases shown in Table 3, if the measured BSA is 3.318 m² (Example 1), and drug X is dosed at 50mg/m², the patient should receive 165.9 mg. BSA estimates by the 6 equations under comparison range from 2.987-3.895 m² indicating patient dosing with 149.4 - 194.8 mg. Consequently, the dose calculated based on the Nwoye equation would under prescribe by 10% and over prescribe by 16% using the Jones equation. Perhaps more critically, the lowest BSA measured was 1.482 m² (Example 2, female). Dosing by all 6 equations would result in overtreatment in the magnitude of 2 to 17%. With this in mind, we propose the development of an App that would easily calculate BSA based on our formulae and which would be readily available to clinicians.

Study Strengths and Limitations

Among the strengths of the study are the large, ethnically diverse sample with a large age and BMI range. No other study has measured such a diverse group to evaluate BSA. The measurement accuracy and precision of the scanner used is also a strength.

Limitations include a partial measurement of the palm. Participants held onto handlebars to maintain a constant pose; therefore, scans were performed with closed fists. This omission represents a very small portion of total BSA. Measurement of the soles of the feet were not accounted for in the BSA estimation. Another limitation is the uneven representation of sex within the study population, with males representing just 25% of cohort. Additionally, persons under 18 were not studied. Our findings cannot be generalized to populations beyond those included in our sample including individuals with an overhanging fold of skin and tissue from below the naval encountered after rapid and massive weight losses. Finally, an independent data set would be useful to test the models presented in this manuscript.

These findings expand knowledge of the validity of using weight and height to estimate total body surface area. 3DPS offers a quick, noninvasive, and risk-free approach to obtaining several clinically significant measurements, including BSA. However, high resolution 3DPS is only available at select research institutions and not readily available to the public. Weight and height are easily measured in clinical settings. Using data obtained from a high-resolution 3DPS, new BSA prediction equations are presented for use in the absence of scanning technology. These new equations are generalizable to individuals across a wider range of ages, BMIs and ethnicities compared to the Dubois & Dubois and Tikuisis equations. Specifically, these new equations improve BSA estimations for individuals with BMI ≥ 40 kg/m², African American, Hispanic Americans and Asian Americans.

What is already known about this subject?

• Precise estimates of the body surface area (BSA) are needed for many clinical applications. BSA is most commonly calculated by prediction equations.

• The available equations may not be appropriate for all populations, including individuals with obesity.

What does your study add?

• Our study expands BSA estimation to a wider range of individuals, including higher BMI and more racial/ethnic categories

• A greater level of precision for the estimation of the BSA is conferred due to the higher resolution of the 3D photonic scanner used.