Low-Dimensional Spatio-Temporal Dynamics Underlie Cortex-Wide Neural Activity

Summary

Cognition arises from the dynamic flow of neural activity through the brain. To capture these dynamics, we used mesoscale calcium imaging to record neural activity across the dorsal cortex of awake mice. We found that the large majority of variance in cortex-wide activity (~75%) could be explained by a limited set of ~14 ‘motifs’ of neural activity. Each motif captured a unique spatio-temporal pattern of neural activity across the cortex. These motifs generalized across animals and were seen in multiple behavioral environments. Motif expression differed across behavioral states and specific motifs were engaged by sensory processing, suggesting the motifs reflect core cortical computations. Together, our results show that cortex-wide neural activity is highly dynamic, but that these dynamics are restricted to a low-dimensional set of motifs, potentially allowing for efficient control of behavior.

eToc

Behaviors arise from the flow of neural activity through the brain. MacDowell and Buschman show cortex-wide neural activity, in mice, can be explained by a set of 14 motifs, each capturing a unique spatio-temporal pattern of neural activity. Motifs generalized across animals and behaviors, suggesting they capture core patterns of cortical activity.

Introduction

The brain is a complex, interconnected network of neurons. Neural activity flows through this network, carrying and transforming information to support behavior. Previous work has associated particular computations with specific spatio-temporal patterns of neural activity across the brain [1–3]. For example, sequential activation of primary sensory and then higher-order cortical regions underlies perceptual decision making in both mice [4] and monkeys [5,6]. Similarly, specific spatio-temporal patterns of cortical regions are engaged during goal-directed behaviors [7], motor learning and planning [8,9], evidence accumulation [10], and sensory processing [11]. Previous work has begun to codify these dynamics, either in the synchronous activation of brain regions [3,12] or in the propagation of waves of neural activity within and across cortical regions [13,14]. Together, this work suggests cortical activity is highly dynamic, evolving over both time and space, and that these dynamics play a computational role in cognition [15,16].

However, despite this work, the nature of cortical dynamics is still not well understood. Previous work has been restricted to specific regions and/or specific behavioral states and so, we do not yet know how neural activity evolves across the entire cortex, whether dynamics are similar across individuals, or how dynamics relate to behavior. This is due, in part, to the difficulty of quantifying the spatio-temporal dynamics of neural activity across the brain.

To address this, we used mesoscale imaging to measure neural activity across the dorsal cortical surface of the mouse brain [17]. Then, using a convolutional factorization approach, we identified dynamic ‘motifs’ of cortex-wide neural activity. Each motif captured a unique spatiotemporal pattern of neural activity as it evolved across the cortex. Importantly, because motifs captured the dynamic flow of neural activity across regions, they explained cortex-wide neural activity better than ‘functional connectivity’ network measures.

Surprisingly, the motifs clustered into a limited set of ~14 different spatio-temporal ‘basis’ motifs that were consistent across animals. The basis motifs captured the majority of the variance in neural activity in different behavioral states and in multiple sensory and social environments. Specific motifs were selectively engaged by visual and tactile sensory processing, suggesting the motifs may reflect core cortical computations. Together, our results suggest cortex-wide neural activity is highly dynamic but that these dynamics are low-dimensional: they are constrained to a small set of possible spatio-temporal patterns.

Results

Discovery of spatio-temporal motifs of cortical activity in awake, head-fixed mice

We performed widefield ‘mesoscale’ calcium imaging of the dorsal cerebral cortex of awake, head-fixed mice expressing the fluorescent calcium indicator GCaMP6f in cortical pyramidal neurons (Figure 1A; see STAR Methods [18]). A translucent-skull prep provided optical access to dorsal cortex, allowing us to track the dynamic evolution of neural activity across multiple brain regions, including visual, somatosensory, retrosplenial, parietal, and motor cortex (Figure 1A, inset and Figure S1A, [17]). We initially characterized the dynamics of ‘spontaneous’ neural activity when mice were not performing a specific behavior (Figure 1B, N=48 sessions across 9 mice, 5-6 sessions per mouse, each session lasted 12 minutes, yielding a total of 9.6 hours of imaging). These recordings revealed rich dynamics in the spatio-temporal patterns of neural activity across the cortex (Video S1, as also seen by [19–21,11]).

Figure 1. Discovery of spatio-temporal patterns in cortical activity of awake, head-fixed mice.

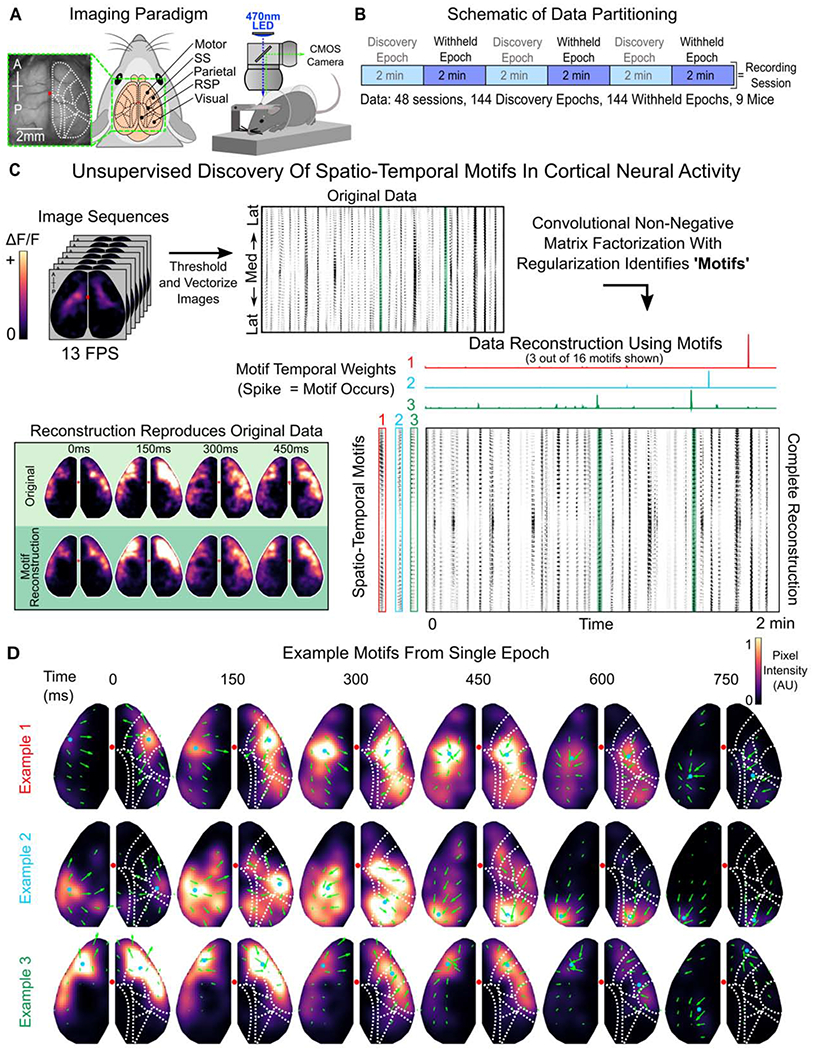
(A) Schematic of imaging paradigm. Mice expressing GCaMP6f in cortical pyramidal neurons underwent a translucent skull prep to allow mesoscale imaging of neural activity across the majority of dorsal cortex. Red dot denotes bregma. Cortical parcellation follows Allen Brain Atlas. General anatomical parcels are labeled. Motor, motor cortex; SS, somatosensory cortex; Parietal, parietal cortex; RSP, retrosplenial cortex; Visual: visual cortex (See Figure S1A for complete parcellation of 24 regions; 12 per hemisphere).

(B) Schematic of data partitioning. 9 mice were imaged for 12 minutes a day for 5-6 consecutive days. Recording sessions (N=48) were divided into 2-minute epochs (n=144). Alternating epochs were used for discovering spatio-temporal motifs in neural activity or were withheld for testing generalization of motifs.

(C) Schematic of unsupervised discovery of spatio-temporal motifs from a single epoch. Mesoscale calcium imaging captured patterns of neural activity, measured by change in fluorescence ΔF/F), across the dorsal cortex (top left). Imaged activity was thresholded to isolate activity from noise, vectorized (top-middle, black=activity), and then decomposed into dynamic, spatio-temporal motifs (bottom-right; 3 example motifs shown along left, temporal weightings along top). Convolving motifs with temporal weightings reconstructed the original data (bottom-left; snapshot of data is highlighted in green throughout, corresponding to activity in motif 3, which is shown in image format in bottom row of D). Note: only 3 out of 16 example motifs and their corresponding temporal weightings are shown; data reconstruction in bottom right used all 16 motifs.

(D) Timecourses of the 3 example motifs in panel C showing spatio-temporal patterns of neural activity across dorsal cortex. Arrows indicate direction of flow of activity across subsequent timepoints (see STAR Methods). Blue dot denotes center of mass of the most active pixels in each hemisphere (>=95% intensity). Red dot denotes bregma. Dotted white lines outline anatomical parcels as in A. Only every other timepoint is shown. For visualization, motifs were filtered with 3D gaussian (across space and time), and intensity scale is normalized for each motif. Intensity value is arbitrary as responses are convolved with independently scaled temporal weightings to reconstruct the normalized ΔF/F fluorescence trace (see STAR Methods).

See also Figures S1, S2, Tables S1, S3, and Video S1.

Our goal was to capture, quantify, and characterize the dynamic patterns of activity in an unbiased manner. To do so, we used convolutional non-negative matrix factorization (CNMF [22]) to discover repeated spatio-temporal patterns of neural activity, in an unsupervised way (Figure 1C; see STAR Methods). CNMF identified ‘motifs’ of neural activity; these are dynamic patterns of neural activity that extend over space and time (Figure 1C, bottom left, shows an example motif and the corresponding original data). Motifs involved neural activity in one or more brain regions and lasted up to 1 second in duration. Motif duration was chosen to match the dynamics of neural activity in our recordings (Figure S1B–D; see STAR Methods) as well as the duration of large-scale cortical events in previous studies [2].

Once identified, the algorithm used these motifs to reconstruct the original dataset by temporally weighting them across the entire recording session (Figure 1C; transients in temporal weightings indicate motif expression). Importantly, overlapping temporal weightings between motifs are penalized, which biases factorization towards only one motif being active at a given point in time. This allowed us to capture the spatio-temporal dynamics of neural activity as a whole, rather than decomposing activity into separate spatial and temporal parts (see STAR Methods).

Figure 1D shows three example motifs identified by CNMF from a single 2-minute recording epoch. Many of the identified motifs show dynamic neural activity that involves the sequential activation of multiple regions of cortex (top two rows in Figure 1D). For instance, example motif 1 starts in somatosensory/motor regions and, over the course of a few hundred milliseconds, propagates posteriorly before ending in the parietal and visual cortices (Figure 1D, top row). To aid in visualizing these dynamics, the arrows overlaid on Figure 1D show the direction and magnitude of activity propagation of the top 50% most active pixels between subsequent timepoints (as in [23]). Other motifs were more spatially restricted, engaging either one (or more) brain regions simultaneously (e.g. third row in Figure 1D). In total, we identified 2622 motifs across 144 different 2-minute epochs of imaging (3 independent epochs from each of 48, 12-minute recording sessions; Figure 1B, light blue ‘discovery epochs’).

Motifs captured the flow of activity across the brain during a brief time period (~1 second). By tiling different motifs across time, the entire 2-minute recording epoch could be reconstructed. On average, each 2-minute recording epoch could be reconstructed by combining ~19 motifs (Fig 2A; 95% Confidence Interval (CI): 18-20; the number of observed motifs was not due to constraints from the CNMF algorithm, see STAR Methods, SI, and Figure S1E). This captured 89.05% of the total variance of neural activity on average (Figure 2B; CI: 87.78-89.68%; N=144 discovery epochs; see STAR Methods; see Table S1 for statistics split by individual mice). To achieve this, individual motifs occurred repeatedly during a recording session. Over half of the motifs occurred at least 3 times during a 2-minute epoch, with motifs occurring 2.48 times per minute on average (Figure 2C; CI: 2.38-2.59). The broad distribution of the frequency of motifs suggests all motifs are required to explain cortex-wide neural activity. Indeed, the cumulative percent explained variance (PEV) in neural activity captured by individual motifs shows a relatively gradual incline (Figure 2D, see STAR Methods). On average, no single motif captured more than 20% of the variance of the recording epoch, and 14 motifs were needed to capture over 90% of the relative PEV. Importantly, the number of discovered motifs and their explained variance was robust to changes in the regularization hyperparameter of the CNMF algorithm and data processing, suggesting it is a true estimate of the number of motifs needed and not a consequence of our analytical approach (see STAR Methods, SI, and Figures S1F–H, S2A–E).

Figure 2. Motifs capture majority of variance in neural activity.

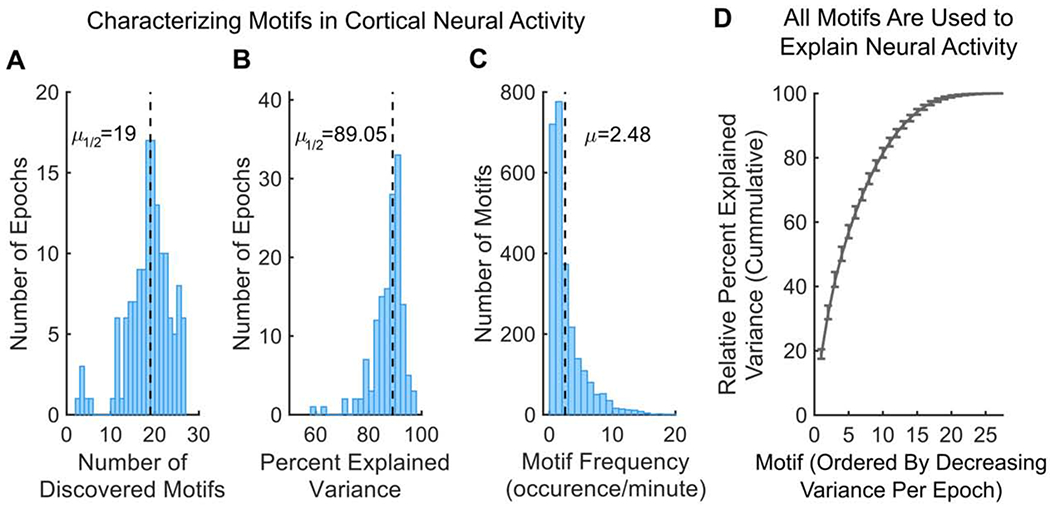
(A) Distribution of number of discovered motifs per discovery epoch (N=144). Dotted line indicates median. 2622 motifs were discovered in total.

(B) Distribution of the total percent of variance in neural activity explained by motifs per discovery epoch. Dotted line indicates median.

(C) Distribution of how often motifs occurred during discovery epochs. A motif was considered active when its temporal weighting was 1 standard deviation above its mean (e.g. transients in Figure 1C in occurrences per minute; see STAR Methods). Dotted line indicates mean.

(D) Cumulative sum of relative percent explained variance (PEV) of each motif in withheld epochs. Relative PEV was calculated as the PEV of each motif divided by the sum of all motif PEVs in an epoch. For each epoch, motifs are ordered by their relative PEV (i.e. the first motif is the most common motif, which is not necessarily the same motif for all epochs). Line and error bars indicate mean and 95% CI, respectively.

All p-values estimated with Wilcoxon Signed-Rank tests. See also Figures S1, S2, and Tables S1, S3.

Motifs capture the dynamic flow of neural activity across the cortex

Next, we tested whether motifs simply reflected the co-activation of brain regions or if they captured the dynamic flow of neural activity between regions. Previous work has found neural activity can be explained by the simultaneous activation of a coherent network of brain regions (i.e. zero-lag, first-order correlations, as seen in functional connectivity analyses; [3]). The CNMF approach used here is a generalization of such approaches; it can capture spatiotemporal dynamics in the motifs, but it is not required to do so if dynamics are not necessary to capture variance in neural activity. Therefore, to test whether neural activity is dynamic, we tested whether dynamics were a necessary component of the motifs.

First, we determined whether motifs simply reflected the static engagement of a network of regions. To this end, we measured the autocorrelation of neural activity during the timecourse of each motif. Consistent with dynamic motifs, the correlation of activity patterns within a motif quickly decayed with time (Figure 3A; mean half-life τ across all motifs was 113ms +/− 2ms, bootstrap; when fit to individual motifs, 25%-50%-75% of τ was 66ms - 117ms - 210ms; see STAR Methods). While activity patterns at adjacent motif timepoints (75ms apart) were spatially correlated (Pearson’s r=0.39 CI: 0.38-0.40, p<10⁻¹⁶, Wilcoxon Signed-Rank Test versus r=0, right-tailed; N=2622 Motifs), this similarity quickly declined when time points were farther apart (Pearson’s r=0.098 CI: 0.095-0.10 at 375ms and r=0.043, CI: 0.039-0.047 at 600ms; a decrease of 0.29 and 0.35, both p<10⁻¹⁶, Wilcoxon Signed-Rank Test). Similarly, the mean spatial pattern of activity of a given motif, averaged across the timecourse of the motif, was dissimilar from individual timepoints within the motif (Figure 3B; median dissimilarity 0.58, CI: 0.57-0.58 across motifs).

Figure 3. Motifs capture the flow of neural activity across the cortex.

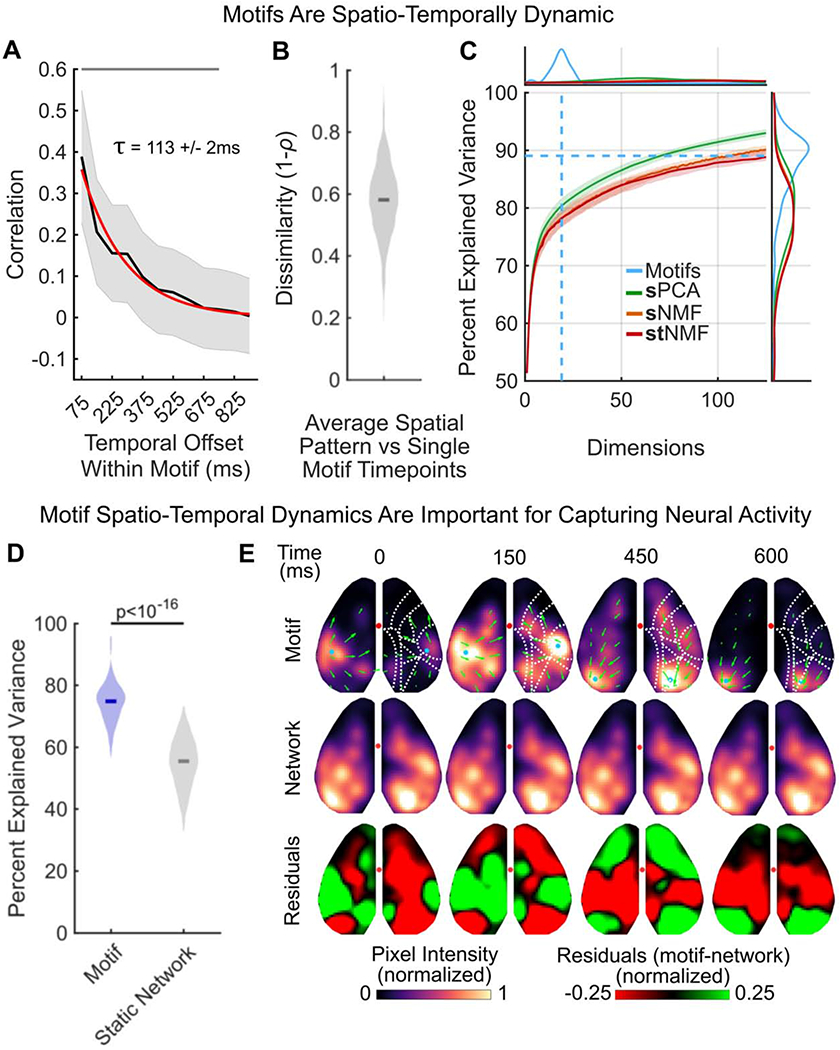
(A) Cross-temporal autocorrelation of motifs (N=2622). Average spatial correlation of activity (y-axis) was calculated for different temporal offsets (x-axis) within a motif. For example, an offset of 75ms indicates the correlation between timepoint N and timepoints N-1 and N+1 (given sampling frequency of 13.33 Hz). Black line and gray shading denote mean and standard deviation, respectively, across all motifs. Red line shows exponential fit to autocorrelation decay. Mean half-life of autocorrelation decay (τ) across all motifs was 113ms +/− 2ms SEM.

(B) Average dissimilarity between each timepoint of a dynamic motif and the mean spatial activity of that motif; averaged across frames of the motifs. Full distribution shown, depicts average dissimilarity per motif (N=2622 motifs). Dark line indicates median.

(C) Comparison of reconstruction of neural data by CNMF motifs (blue), spatial principal components analysis (sPCA, green), spatial non-negative matrix factorization (sNMF, orange) and space-by-time non-negative matrix factorization (stNMF, red). Details of factorization approaches are provided in the text and in the STAR Methods. Central plot shows percent of variance in neural activity explained (y-axis) as a function of number of dimensions included (x-axis). Lines show median variance explained, shaded regions show 95% confidence interval. Dashed light blue lines show median number of motifs discovered (vertical) and the median percent explained variance (horizontal) captured by CNMF motifs across discovery epochs (N=144). (top) Plot shows the probability density function (PDF) of number of motifs discovered per discovery epoch (blue), as well as the PDF of the minimum number of dimensions needed to capture the same amount of variance using sPCA (green), sNMF (orange), and stNMF (red). (right) PDF of percent explained variance by motif reconstructions (blue) across epochs, as well as the PDF of percent of variance explained by sPCA (green), sNMF (orange), and stNMF (red) when the number of dimensions is restricted to match the number of discovered motifs in each epoch. For visualization, x-axis is cropped to 125 dimensions.

(D) Percent of variance in neural activity explained by dynamic motifs (blue) and static networks (grey), defined as the average activity across the motif. Both static networks and motifs are fit to the data in the same manner (see STAR Methods). Full distribution shown; dark lines indicate median. Analyses performed on withheld epochs (N=144).

(E) An example motif (top row; example motif 2 from Figure 1D) and its corresponding static network (middle row). Bottom row shows normalized residuals between dynamic motif and static network. For calculation of residuals, motif and networks were scaled to the same mean pixel value per timepoint. Display follows Figure 1D.

All p-values estimated with Wilcoxon Signed-Rank tests. See also Figure S1 and Tables S1, S3.

Second, we tested whether dynamics in the motifs were necessary to fit neural activity. To do this, we compared the fit of CNMF-derived motifs to alternative decomposition approaches that do not consider temporal dynamics. We used two ‘static’ decomposition techniques that are standards in the field: spatial Principal Components Analysis (sPCA) and spatial Non-Negative Matrix Factorization (sNMF; see STAR Methods). Both approaches required >3 times more dimensions to capture the same amount of variance as the motifs (Figure 3E; on average, 64.5 and 93 dimensions for sPCA and sNMF, respectively). If restricted to 19 dimensions, sPCA and sNMF explained significantly less variance in neural activity than motifs (Figure 3E; sPCA: 79.87% CI: 78.72-81.46% a difference of 9.18%, p<10⁻¹⁶; sNMF 77.95% CI: 76.63-79.42% a difference of 11.10%, p<10⁻¹⁶, Wilcoxon Signed-Rank Test). It is important to note CNMF has more free parameters in each dimension, compared to PCA/sNMF. However, the free parameters in CNMF can only capture contiguous spatio-temporal patterns of neural activity. Therefore, the fact that dynamic motifs capture significantly more variance than temporally constrained approaches suggests brain activity has complex spatial-temporal dynamics that are not captured by traditional decomposition STAR Methods but can be captured by the motifs.

Finally, we tested whether the spatial and temporal components of neural activity were separable. CNMF-derived motifs assume the spatial and temporal components of neural dynamics cannot be separated. In other words, a motif captures a specific pattern of cortical activity across both space and time. However, an alternative hypothesis is that the spatial and temporal components of neural activity are separable [24]. In this model, space and time components can be combined to create the observed spatio-temporal dynamics (e.g. different spatial patterns of cortical activity could share the same timecourse or, vice versa, the same spatial pattern could follow multiple timecourses). To discriminate these hypotheses, we compared the fit of CNMF-derived motifs to space-by-time Non-Negative Matrix Factorization (stNMF [24,25]), which decomposes neural activity into independent spatial and temporal dimensions. Compared to CNMF, stNMF needed >5 times more dimensions to explain the same amount of variance and, when restricted to 19 dimensions, stNMF captured significantly less variance (77.60% CI: 76.30-78.93% a difference of 11.45%, p<10⁻¹⁶, CI Wilcoxon Signed-Rank Test). This suggests the spatio-temporal dynamics of cortex-wide neural activity are non-separable and are well captured by the motifs.

Motifs generalize to withheld data and across animals

If the neural dynamics captured by CNMF reflect true, repeated, motifs of neural activity, then the motifs identified in one recording session should generalize to other recording sessions. To test if motifs generalized, we refit the motifs identified during a recording ‘discovery’ epoch to withheld data (Figure 1B, purple, N=144 ‘withheld epochs’). Motifs were fit to new epochs by only optimizing the motif weightings over time (i.e. not changing the motifs themselves, see STAR Methods).

Indeed, the motifs generalized; the same motifs could explain 74.82% of the variance in neural activity in withheld data from the same recording session (Figure 3D, purple, CI: 73.92-76.05%; see Figure S1I for robustness to sparsity parameter; see STAR Methods). This was not just due to fitting activity on average: motifs captured neural activity at each timepoint during a recording epoch, explaining the majority of the variance in the spatial distribution of neural activity in any given frame (60-80%, Figure S1J).

Dynamics were important for the ability to generalize. To show this, we created ‘static networks’ by averaging neural activity across the timecourse of each motif. This maintained the overall spatial pattern of activity, ensuring the same network of brain regions was activated, but removed any temporal dynamics within a motif (Figure 3E; see STAR Methods). When the static networks were fit to withheld data, they captured significantly less variance in neural activity compared to the dynamic motifs (Figure 3D, gray; static networks captured 55.50%, CI: 53.74-57.09%; a 19.32% reduction, p<10⁻¹⁶, Wilcoxon Signed-Rank Test).

Similarly, motifs generalized across animals: motifs identified in one animal cross-generalized to capture 68.19% of the variance in neural activity in other animals (Fig; 4A, green; CI: 66.74-69.35%, a decrease of 6.63% compared to generalizing within animals, purple, p<10⁻¹⁶, Wilcoxon Signed-Rank Test; N=144 withheld epochs; see STAR Methods).

Figure 4. Motifs cluster into a low-dimensional set of basis motifs.

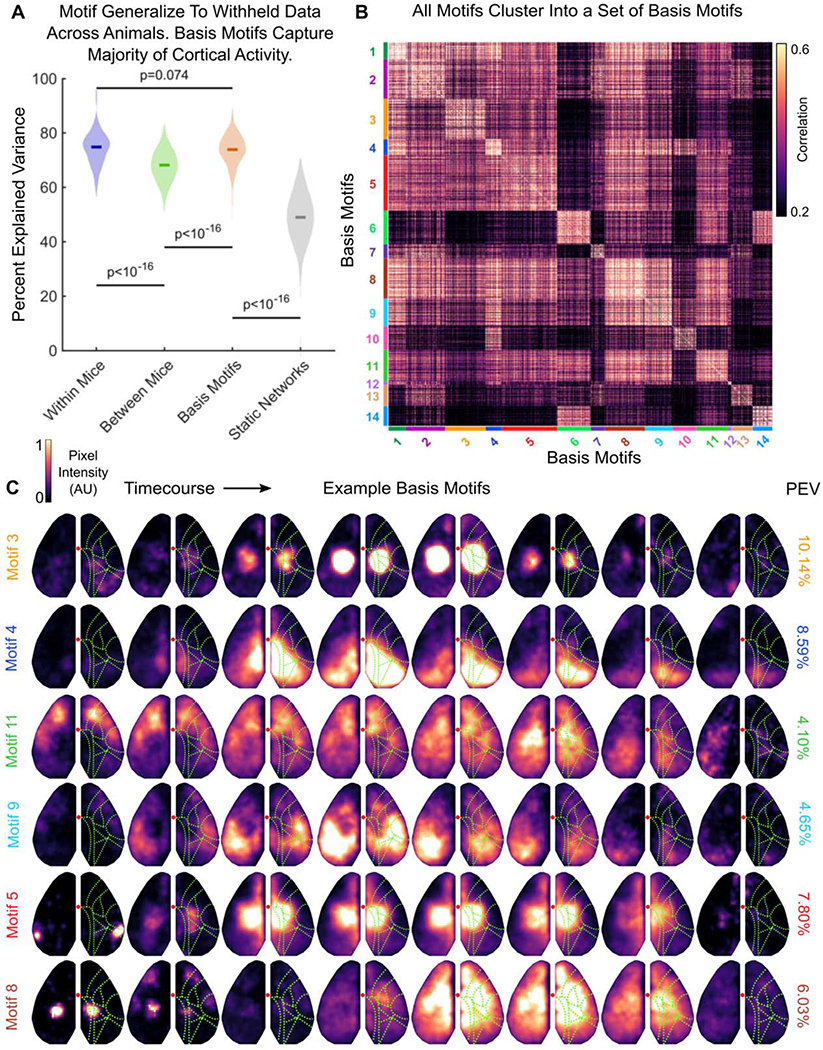
(A) Comparison of the percent of variance in neural activity explained by motifs from the same mouse (within; purple), by motifs from other mice (between; green), by basis motifs (orange), and by static network versions of basis motifs (gray). Static networks for each basis motifs were derived as in Figure 3 (see STAR Methods). All show fit to withheld data (N=144). Full distribution shown; dark lines indicate median. Horizontal lines indicate pairwise comparisons. All p-values estimated with Mann-Whitney U-test.

(B) Pairwise peak cross-correlation between all 2622 discovered motifs. Motifs are grouped by their membership in basis motif clusters. Basis motif identity is indicated with color code along axes. Group numbering (and thus the sorting of the correlation matrix) is determined by relative variance explained by each basis motif.

(C) Representative timecourses for example basis motifs. Example basis motifs were chosen to display the diversity of patterns observed in motifs. See Figure S3 for all basis motifs, Movie S2 for full motif timecourses, and Table S2 for written description of motifs. Display follows Figure 1D, except without direction of flow arrows. Right column shows the relative percent explained variance in neural activity captured by each basis motif.

See also Figures S3, S4, S5, and Tables S1, S2, S3, and Video S2.

Motifs cluster into a low-dimensional set of basis motifs

The ability of motifs to generalize across time and animals suggests there may be a set of ‘basis motifs’ that capture canonical patterns of spatio-temporal dynamics. To identify these basis motifs, we used an unsupervised clustering algorithm to cluster all 2622 motifs that were identified across 144 discovery epochs over 9 mice. Clustering was done with the Phenograph algorithm, using the peak of the temporal cross-correlation as the distance metric between motifs [26,27] (see STAR Methods). Motifs clustered into a set of 14 unique clusters (Figure 4B). For each cluster, we defined the basis motif as the mean of the motifs within the ‘core-community’ of each cluster (taken as those motifs with the top 10% most within-cluster nearest neighbors).

Similar to the motifs discovered within a single session, the basis motifs captured the dynamic engagement of one or more brain regions over the course of ~1 second (Figure 4C; all basis motifs are shown in Figure S3 and Movie S2, and described in Table S2; motifs are numbered according to their relative explained variance, detailed below). The seven examples shown in Figure 4C reflect the diversity of dynamics captured by the basis motifs: while some engaged a single brain region (e.g. motif 3), most captured the propagation of activity across cortex (e.g. motifs 4, 11, and 9). For example, motif 4 captures the posterior-lateral flow of activity from retrosplenial to visual cortex. Similarly, motif 11 captures a cortex-wide anterior-to-posterior wave of activity that has been previously studied [28–30]. As expected, these dynamics were similar to those found in individual recording sessions (e.g. basis motif 9 matches example motif 2 in Figure 1D).

At the same time, the same brain region, or network of regions, can be engaged in multiple basis motifs. For instance, parietal cortex is engaged in motifs 3, 5 and 8 (Figure 4C). In motif 3, neural activity remains local to parietal cortex for the duration of the motif. However, in motif 5 parietal activity is prefaced by a burst of activity in rostrolateral cortex. In motif 8, activity starts in parietal cortex before spreading across the entire dorsal cortex. Similarly, several motifs (6, 8, 11, and 14) involve coactivation of a network of anterolateral somatosensory and primary motor cortices; a coupling observed in previous mesoscale imaging studies [17,31,32]. Thus, basis motifs reflect the ordered engagement of multiple brain regions, likely reflecting a specific flow of information through the brain.

Basis motifs explained the large majority of the variance in neural activity across animals (73.91% CI: 73.14-75.19%, Figure 4A, orange; N=144 withheld epochs). This is similar to the variance explained by motifs defined within the same animal (Figure 4A, purple vs. orange; a 0.91% reduction, p=0.074; Wilcoxon Signed-Rank Test, N=144 withheld epochs). It is significantly more variance explained than when using motifs defined in another animal (Figure 4A, orange vs. green plots; a 5.72% increase in explained variance; p<10⁻¹⁶, Wilcoxon Signed-Rank Test). This improvement is likely because basis motifs are averaged across many instances, removing the spurious noise that exists in individual motifs and resulting in a better estimate of the underlying ‘true’ motif that is consistent across animals.

As before, dynamics were important for basis motifs; when spatial-temporal dynamics were removed, the variance explained dropped significantly (Figure 4A, gray vs orange plots; static networks captured 48.99% CI: 47.15–51.30% of variance, 24.92% less than dynamic motifs, p<10⁻¹⁶, N=144 withheld epochs, Wilcoxon Signed-Rank Test). Furthermore, all basis motifs were necessary to explain neural activity; individual basis motifs explained between 2% and 20% of the variance in neural activity (Figure 4C; for explained variance of all basis motifs see Figure S3).

The high explanatory power of the 14 basis motifs suggests they provide a low-dimensional basis for capturing the dynamics of neural activity in the cortex. This is consistent with the number of motifs (~19) identified in each recording session (the slightly lower number of basis motifs could reflect spurious noise in individual sessions). Importantly, the number of discovered basis motifs was robust to CNMF parameters (Figure S4A) and potential hemodynamic contributions to basis motifs were minimal (Figure S4B–D, see STAR Methods). In addition, the low number of basis motifs was not due to the resolution of our approach. We estimated the functional resolution of our imaging approach by correlating pixels across time. This revealed ~18 separate functional regions in dorsal cortex (Figure S4E). Individual motifs engaged multiple of these regions over time (Figure 4C), consistent with the idea that motifs were not constrained by our imaging approach. Indeed, the number of motifs observed was substantially less than the possible number of motifs; even if motifs engaged only 1-2 of these regions, there are still 18²=324 different potential motifs, much higher than the 14 we observed. Finally, low dimensionality of basis motifs was not due to compositionality of motifs across time, as this was penalized in the discovery algorithm and the temporal dependency between motifs was weak (Figure S5; see STAR Methods).

Specific motifs capture visual and tactile sensory processing

To begin to understand the computational role of specific basis motifs, we measured the response of the motifs to tactile and visual stimuli (Figure 5A, see STAR Methods). Previous work has found sensory responses are recapitulated during rest [11]. Therefore, we were interested in whether our basis motifs, which were defined during rest, can also capture neural dynamics related to sensory processing. To this end, nine mice were imaged while passively experiencing moving visual gratings and somatosensory stimuli to their whiskers (see STAR Methods).

Figure 5. Specific basis motifs reflect processing of specific stimulus modalities.

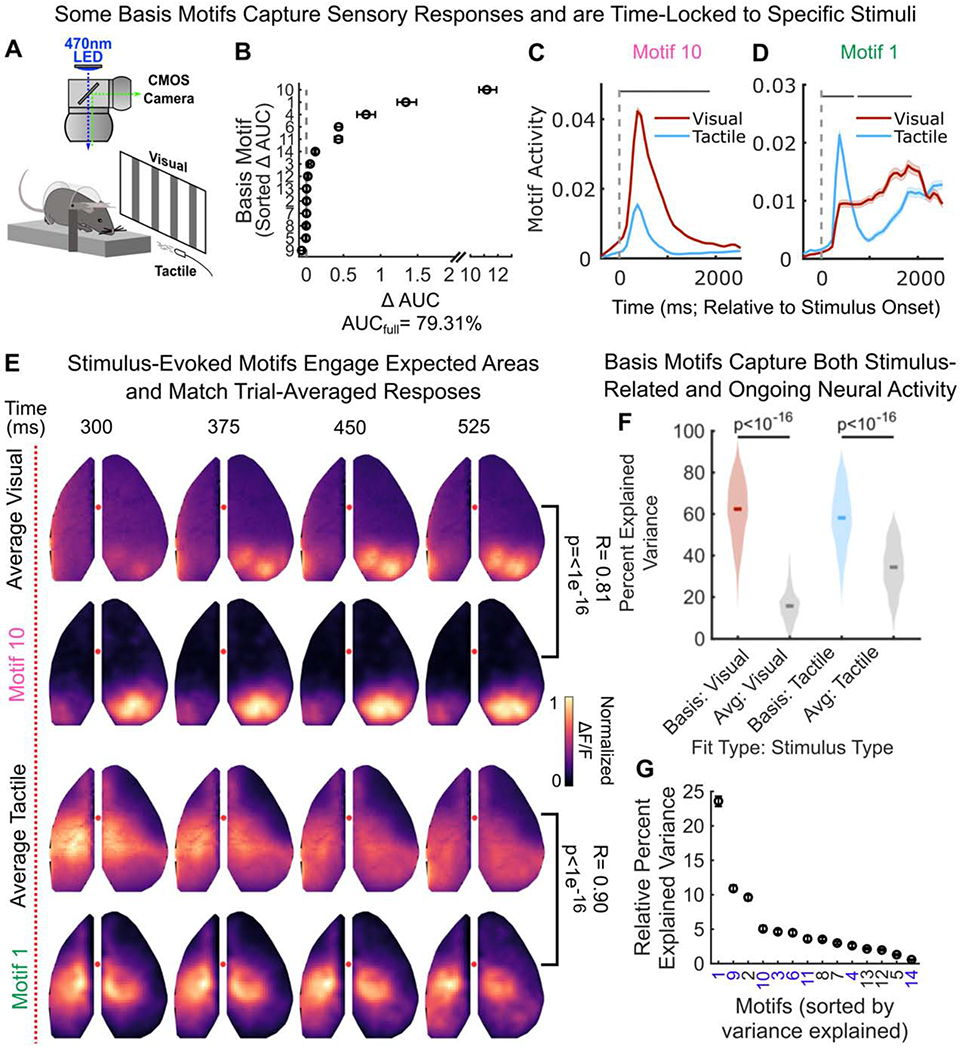
(A) Schematic of sensory stimulation paradigm. All stimuli were delivered on animals’ left side.

(B) Contribution of each motif to decoding whether a visual or tactile stimulus was delivered, assessed as the decrease in decoding accuracy when a motif is left out (see STAR Methods). Motifs ordered by decreasing contribution. Marker and error bars show median and 95% CI of 50 cross-validations. AUC_full reflects decoding accuracy when using all motifs.

(C-D) Timecourse of (C) motif 10 and (D) motif 1 activity relative to stimulus onset (vertical dotted line). Lines and shaded regions indicate mean +/− SEM motif activity in response to visual (red; N=1109) and tactile (blue; N=1110) stimulation. Motif activity calculated as the mean pixel value of a motif reconstruction over time (see STAR Methods). Horizontal grey bar indicates significant difference in motif activity between visual and tactile stimuli (p_Bonferroni < 0.05, two-sample t-test; see STAR Methods).

(E) Comparison of the trial-averaged stimulus-evoked response and the stimulus-evoked response of the selective basis motifs in C-D. First two rows show responses for visual stimuli; third and fourth rows for tactile stimuli. Correlation between average response and basis motif is indicated along right side (pixelwise correlation, Pearson’s ρ). As amplitude of response is arbitrary, pixel intensities were normalized from 0-to-1 before correlation.

(F) Basis motifs explain more of the variance in neural activity than the average stimulus response. Distributions show the percent of variance in neural activity during the 5s after stimulus onset explained by basis motifs (colors) or average responses (gray). Full distribution shown; dark lines indicate median. Significance computed with Wilcoxon Signed-Rank test.

(G) Relative percent of the variance captured by each motif across all sensory trials, during the 5s after stimulus onset. Marker and error bars show median and 95% CI. Purple labels denote motifs that contributed to stimulus decoding (panel B) and/or were stimulus-evoked (Figure S6). Black labels denote motifs that were not related to visual or tactile stimuli.

See also Figure S3, S6 and Tables S1, S3.

First, we tested whether motif activity, in general, discriminated between these two forms of sensory stimulation. To this end, we trained a classifier to discriminate between visual and tactile stimuli using the activity of basis motifs on each trial (motif activity was taken as the peak in the 2s after stimulus onset). Consistent with sensory-evoked responses, the identity of the stimulus could be decoded from the activity of motifs (AUC 79.31% CI 78.68-79.82% on withheld data, 50 cross validations). Next, to determine if a specific motif was selectively engaged by visual or tactile stimuli, we measured the relative contribution of each motif to the performance of the decoder. This was done by measuring the decrease in decoder accuracy after leaving that motif out (see STAR Methods). As seen in Figure 5B, three basis motifs (10, 1, and 4) were strongly selective for visual or tactile stimulation, and 7 out of 14 basis motifs showed some selective engagement.

In particular, motif 10 was selectively induced by visual stimulation (Figure 5C), while motif 1 was selectively induced by tactile stimulation (Figure 5D; see Figure S6 for sensory response of other motifs). The spatio-temporal pattern of activity of these two motifs matched the trial-averaged response to their associated stimulus: motif 10 captured activity in visual cortex, while motif 1 captured activity in motor, somatosensory and parietal cortices (Figure 5E). Reflecting this overlap, both motifs were significantly correlated with the trial-averaged response (Pearson’s r=0.81, p<10⁻¹⁶, for correlation between the average visual response and motif 10, and r=0.90, p<10⁻¹⁶, for correlation between the average tactile response and motif 1, all taken during the 13 timepoints post stimulation onset).

While certain basis motifs were evoked by sensory stimuli (Figure 5B), all motifs were expressed in both sensory environments (Figure S6A–B). During sensory stimulation, many of these other motifs captured trial-by-trial ‘noise’ in neural activity. For both stimuli, basis motifs, identified at rest, captured the majority of variance in neural activity (Figure 5F; variance captured by basis motifs visual: 58.13% CI: 57.11-59.18%; tactile: 62.37% CI: 61.42-63.62%, N= 1110 tactile and 1109 visual stimulus presentations; see STAR Methods; see Table S1 for results split by individual mice). This was significantly more variance than could be explained by the mean response to each sensory stimulus alone (Figure 5F; Mean response fits: visual: 17.25% CI: 16.61-17.72%; tactile: 34.42% CI: 33.34-35.40%; difference between motif and mean fits: visual: 40.88%, p<10⁻¹⁶; tactile: 27.95%, p<10⁻¹⁶; Wilcoxon Signed-Rank Test). Furthermore, even the motifs that did not selectively differentiate sensory stimuli (Figure 3B) and/or respond to stimulus onset (Figure S6) still captured a large amount of variance in neural activity (Figure 5G; motifs 2, 5, 7, 8, 12, and 13 together captured 27.90% CI: 27.29-28.75% of variance per trial).

There was even variability in which motif was evoked in response to the same sensory stimulus. For example, tactile stimulation evoked both motif 1 and motif 4 (Figure S6). However, the activity of these motifs was anti-correlated across trials (Pearson’s r= −0.13 CI: −0.20 to −0.07, p=10⁻⁴, permutation test, left-tailed vs no correlation; correlation used the peak amplitude in activity during 2s post-stimulus onset). This anti-correlation suggests the two motifs reflect two different patterns of neural activity processing the same sensory stimulus. Altogether, these results highlight the high variability in responses to a sensory stimulus across trials [33]. Typically, such variability would be discarded as ‘noise’ unrelated to sensory processing. Instead, our results suggest this variability has structure: it is due to the engagement of other motifs that are, presumably, related to other, ongoing, computations.

Finally, we sought to determine whether motifs reflect general stimulus processing or specific stimulus features. To this end, we compared motif expression in response to two visual stimuli (Figure 6; gratings moving medial to lateral or lateral to medial; see Figure S6I for similar analysis of tactile stimuli). Motifs were not engaged differently by the two visual stimuli (p>0.24 for all 14 motifs; Mann-Whitney U-Test; N=554 and 555 stimulus presentations for medial to lateral and lateral to medial grating, respectively). For example, the visually responsive motif 10 responded equally to both stimuli (Figure 6A). This was not due to limits in spatial resolution of our imaging approach or analytical smoothing. Figure 6B shows pixel-wise classification of the same data can decode stimulus identify (p=0.022, N=9 animals, one-sample t-test; see STAR Methods). However, the same classification analysis on data reconstructed from motif activity failed to distinguish between stimuli (p=0.87, N=9 animals, one-sample t-test; difference between classification on original and reconstructed data was significant, p=0.016, paired-sample t-test). Thus, the specifics of visual stimuli were encoded in the residuals after fitting the motifs. However, these details contributed minimally to the overall neural activity during the stimulus. The stimulus-specific residuals captured only 3.85% +/− 0.70% SEM of the explainable variance (Figure 6C). In contrast, motifs captured the vast majority of explainable variance (19.23% +/− 3.23% SEM for stimulus-specific motif 10; 76.92% +/− 3.86% SEM, for remaining motifs; Figure 6C). Taken together, our results show that motifs capture large-scale patterns of neural activity but are generally agnostic to the finer-grain local activity that represent specifics of stimuli. This is consistent with the idea that motifs capture the broader flow of information across cortical regions.

Figure 6. Basis motif 10 reflects general visual stimulus processing.

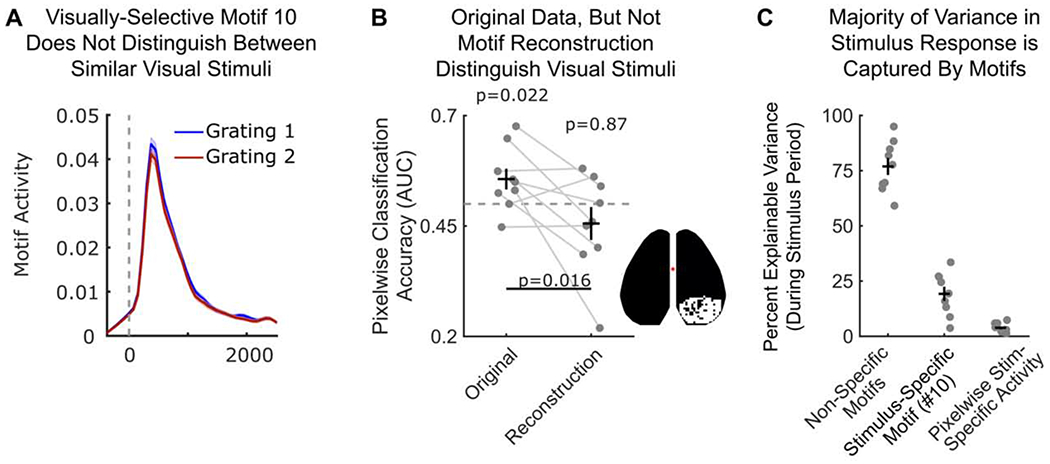
(A) Timecourse of motif 10 intensity relative to onset (vertical dotted line) of visual grating 1 (blue; N=554) or visual grating 2 (red; N=555). Display follows Figure 5C–D. No significant differences were observed between stimuli at any timepoint. p>0.11 for all timepoints; two-sample t-test.

(B) Visual stimuli can be decoded from neural response but not motif response. Classification was done using a support vector machine (SVM) classifier (see STAR Methods) and accuracy is shown for withheld validation trials. Markers indicate classifier performance (measured with AUC) for each animal (N=9). Classifiers were trained on either raw pixel values (left column) or reconstructed motif response (right column). Inset shows pixels used for classification (see STAR Methods). Dotted line denotes chance (AUC=0.5). Significance computed with one-sample t-test.

(C) Percent explainable variance in neural activity in response to visual stimuli captured by motifs and stimulus-specific residuals. Stimulus specific residuals are the trial-averaged residuals of motif reconstructions to each visual stimulus type. Data points correspond to mice (N=9). Black bars denote mean (horizontal) and SEM (vertical).

See also Figure S3, S6 and Tables S1, S3.

Basis motifs generalize across behaviors but depend on behavioral state

So far, we have described the motifs of neural activity in animals ‘at rest’ (Figures 1–4) or passively perceiving stimuli (Figures 5–6). To test whether motifs can explain neural activity in other behavioral states, we imaged dorsal cortex of two new mice, for 1 hour, while they were head-fixed on a transparent treadmill (Figure 7A; neither mouse was used to define the basis motifs). As with the original mice, basis motifs captured the majority of variance in neural activity in both animals (Mouse 1: 64.42%, Mouse 2: 66.66%). The ability of basis motifs to generalize outside the set of animals in which they were discovered provides further support for the idea that basis motifs capture core, repeated, spatio-temporal dynamics in neural activity.

Figure 7. Basis motifs generalize to new animals, across behavioral states, and to social environments.

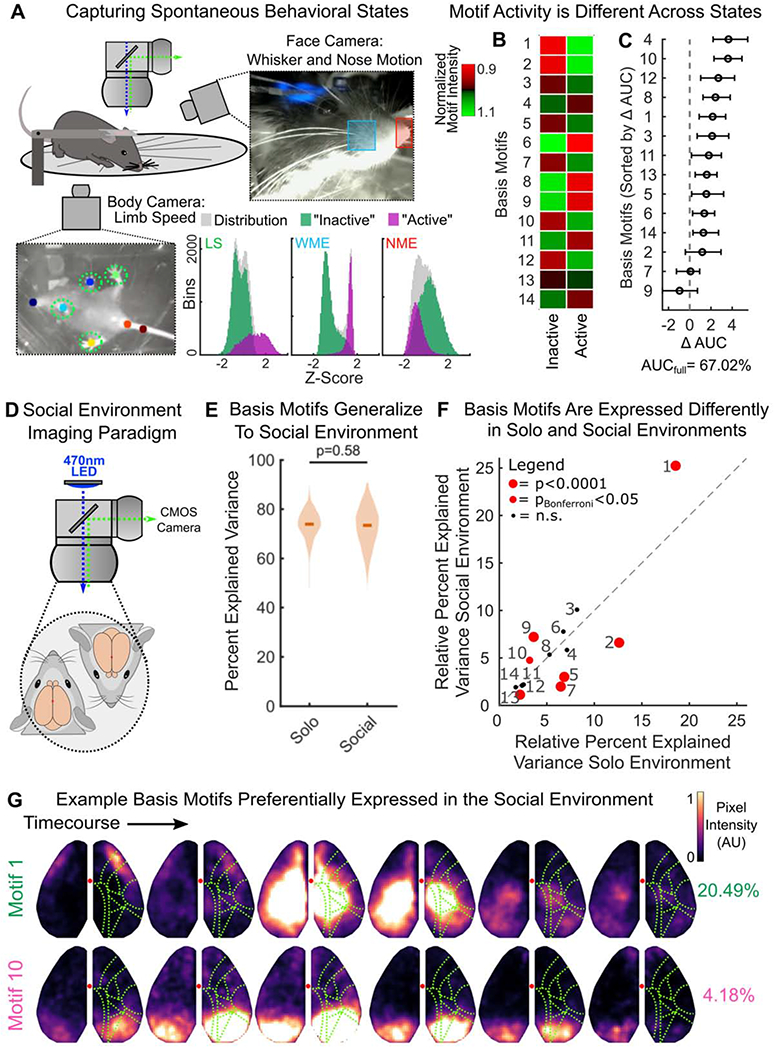
(A) Schematic of simultaneous mesoscale imaging and video capture of spontaneous behavior of head-fixed mice on a transparent treadmill. Two new mice, not from the original cohort, were used. Blue and red squares indicate area used to measure whisker pad motion energy (WME) and nose motion energy (NME), respectively. Colored dots indicate tracked position of the forelimbs, nose, and tail. These were used to estimate limb speed (LS). Distribution of behavioral variables are shown in three histograms along bottom. Gaussian mixture models fit to the distributions of LS, WME, and NME simultaneously. Two states were discovered: an “active” and “inactive” state (inset; purple and green respectively, see STAR Methods).

(B) Motif activity in active and inactive behavioral states. Heatmap shows the relative mean activity of each motif (y-axis) during each state (x-axis). Motif activity was estimated as the mean pixel value of a motif reconstruction over time during N=498 periods of activity/inactivity during 2 hours of recording (see STAR Methods). To assess relative activity in each behavioral state, motif activity was normalized by the mean activity in each state (e.g. divided by column mean), and then normalized to the mean activity in across states (e.g. divided by row mean). Data is combined across animals, who both were in the active state the majority of the time (active: 87% and 72%; inactive: 13% and 28% of time for each animal, respectively).

(C) Motif contributions to decoding active vs inactive behavioral states. Motifs ordered by decreasing contribution. Marker and error bars show mean and 95% CI of 50 cross-validations. AUC_full reflects decoding accuracy when using all motifs.

(D) Schematic of social environment imaging paradigm.

(E) Comparison of the percent of variance in neural activity that could be explained when animal was alone (at rest, ‘solo’) or when paired with another animal (‘social’). Basis motifs were estimated in the solo setting and then fit to withheld data in both settings (as in Figure 4C; N=144 and N=123 withheld epochs for solo and social settings, respectively). Full distribution shown; dark lines indicate median.

(F) Scatter plot of the relative variance captured by each basis motif in the solo environment (x-axis; N=144 epochs) versus the social environment (y-axis; N=123 epochs). Motif labels are indicated with numbers, red markers indicate significant differences in expression rate between environments. Identity line shown along diagonal.

(G) Example basis motifs preferentially expressed in the social environment. Display and motif labels follow Figure 4.

All p-values estimated with Mann-Whitney U-test. See also Figures S3, S7, and Tables S1, S3.

Given the association of specific motifs with processing of sensory stimuli (Figure 5), we tested whether specific motifs were correlated with particular behaviors. Building from recent work, we used infrared cameras to track the behavior of the animals during imaging [34,31]. However, unlike sensory processing, there was no clear association between specific motifs and common behaviors (e.g. grooming, onset of walking, stopping walking, paw repositioning, sniffing, whisking, etc.). Instead, we found that the rate of motif expression changed with the animals ‘behavioral state’.

Animals had two general behavioral states; an ‘active’ state (high whisker pad energy, low nose motion energy, high limb speed) and an ‘inactive’ state (low whisker pad energy, high nose motion energy, low limb speed; Fig 7A). These states were identified by fitting a gaussian mixture model to the distribution of limb speed, whisker pad motion energy, and nose motion energy for each animal independently (Figure 7A; see STAR Methods). Animals typically stayed in a behavioral state for several seconds before switching (median duration for active state: 2.65s and 2.46s, inactive: 7.88s and 11.54s, in mouse 1 and 2 respectively).

Motif expression differed between the two behavioral states. As expected, cortical activity was increased during the active state and so the activity of most motifs was higher (p<0.1 for 12/14 motifs). To compensate for this difference in baseline activity, we normalized the activity of each motif by the average activity of all motifs in a given state. The resulting relative motif expression showed two different patterns between the two states (Figure 7B). For example, motif 1, which is associated with sensory processing (Figure 5C), was expressed 9% more during the active state, while motif 6 was expressed 11% more during the inactive state. To assess differences in motif expression between the two behavioral states, we used a classifier to decode the behavioral state from the activity of all 14 basis motifs (mean classification AUC was 67.02% CI: 65.45-68.66% on withheld data, 50 cross-validations, see STAR Methods). Most motifs contributed to this decoding accuracy (Figure 7C, assessed by a decrease in classifier accuracy when leaving each motif out in turn, see STAR Methods). Therefore, while motifs were not specific to an individual behavior, how often a motif is expressed may differ between behavioral states.

Similar results were seen when animals were engaged in social behaviors. Using a novel paired-imaging paradigm, two mice were simultaneously imaged under the same widefield macroscope (Figure 7D; see STAR Methods). Mice were head-fixed near one another (~5mm snout-to-snout), enabling sharing of social cues (e.g. whisking, sight, vocalizations, olfaction). To add richness to the sensory environment, mice were intermittently exposed to male mouse vocalizations and synthetic tones (see STAR Methods). In this way, the social environment provided a complex, unstructured sensory environment that is fundamentally different from the solo, low-sensory environment used to define the basis motifs. Even in this vastly different environment, basis motifs defined in the original environment captured 73.41% (CI: 71.85-75.23%) of the variance in neural activity (Figure 7E, right orange plot). This was similar to the variance explained in the solo environment (Figure 7E, left orange plot; 73.91% CI: 73.14-75.19%; difference between the solo and social environments=0.50%, p=0.49, N=144 solo epochs, N=123 social epochs; Mann-Whitney U-test).

As before, the expression of many basis motifs changed with behavioral state. Half of the basis motifs significantly changed their relative explained variance in the social environment compared to baseline (Figure 7F; 7/14 were different at p_Bonferroni<0.05, Mann-Whitney U-test; significantly more than chance, p=10⁻¹⁴, binomial test). Given the nature of social interactions in mice, one would expect tactile- and visual-associated motifs to be increased. Consistent with this prediction, several motifs elevated in the social environment (motifs 1, 9, and 10) were also elevated in the sensory environments and engaged somatosensory and/or visual regions (Figure 7F–G, 4C, and S6).

Together, these results suggest basis motifs do not reflect specific behaviors (e.g. grooming, walking, or social interactions). Instead, we find motifs are expressed in a variety of behavioral states, likely because these states engage the same cognitive processes (e.g. processing visual stimuli when walking or socially interacting). Therefore, relative differences in the expression of particular motifs may reflect behavior-specific biases in cognitive processing (e.g. increased tactile processing when active vs. inactive, Figure 7B).

Discussion

Spatio-temporal dynamics of cortex-wide activity

Our results show that neural activity is highly dynamic, evolving in both time and space. Leveraging mesoscale calcium imaging in mice, we tracked the spatio-temporal dynamics of neural activity across the dorsal surface of the cortex. Using a convolutional factorization analysis, we identified ‘motifs’ in neural activity. Each motif reflected a different spatio-temporal pattern of activity, with many motifs capturing the sequential activation of multiple, functionally diverse, cortical regions (Figures 1–3). Together, these motifs explained the large majority of variance in neural activity across different animals (Figure 4) and in novel behavioral situations (Figure 5–7).

A couple of the basis motifs captured patterns of activity observed in previous work, supporting the validity of the CNMF approach. For example, previous work has studied spatio-temporal waves of activity that propagate anterior-to-posteriorly across the cortex at different temporal scales [28–30]. Motifs 1 and 11 recapitulate these waves, along with their temporal diversity (motif 1 = fast, motif 11 = slow; Figure S3 and Table S2). In addition to these previously reported motifs, we also discovered several additional, spatio-temporally distinct, anterior-to-posterior propagating waves (motifs 2, 4, and 9).

Similarly, brain regions that were often co-activated in motifs were aligned with previously reported spatial patterns of co-activation in the mouse cortex [17,31,32]. For example, motifs 6, 8, 11, and 14 include coactivation of anterolateral somatosensory and motor regions. This pattern is observed often and reflects the close functional relationship between motor activity and somatosensory processing. Here, we extend this work by showing neural activity can flow within and between these networks in different ways.

Relatedly, previous work using mesoscale imaging demonstrated that the mouse cortex exhibits repeating patterns of activity [11]. However, this work relied on identifying average patterns evoked by sensory stimuli (visual, tactile, auditory) and correlating the spatially and temporally static templates of those patterns to activity in resting animals. As we demonstrate, stimulus-evoked patterns capture considerably less variance in neural activity than the motifs, even in response to sensory stimuli themselves (~15-35% for stimulus responses versus ~60% for motifs).

Previous work has also used zero-lag correlations to show the brain transitions through different functional network states over time [3,35–37]. Here, we show that these functional network states themselves have rich dynamics, reflecting specific sequential patterns of activity across the network. By encapsulating these dynamics, motifs are able to capture significantly more of the variance in neural activity compared to static networks. Furthermore, we found the spatial and temporal dynamics were not separable (Figure 3E), suggesting the previously identified static functional networks may have specific temporal dynamics associated with their engagement.

Motifs of neural activity may reflect cognitive computations

Each motif captured a different spatio-temporal pattern of neural activity. As neural activity passes through the neural network of a brain region, it is thought to be functionally transformed in a behaviorally-relevant manner (e.g. visual processing in visual cortex or decision-making in parietal cortex). Therefore, the dynamic activation of multiple regions in a motif could reflect a specific, multi-step, ordered transformation of information. In this way, the basis motifs would reflect a set of ‘core computations’ carried out by the brain.

Consistent with this hypothesis, specific motifs were associated with specific cognitive processes, such as tactile and visual processing (Figure 5). In addition, the distribution of motifs differed across behavioral states (Figure 7) and in response to social and sensory stimuli (Figures 7 and S6). This follows previous work showing the engagement of brain networks is specific to the current behavior [39,40] and that disrupting these networks underlies numerous pathologies [41–43].

Low-dimensional dynamics may facilitate hierarchical control of cognition

Our results show that the dynamics of cortex-wide neural activity are low dimensional. Motifs identified in different animals and recording sessions clustered into a set of 14 unique ‘basis’ motifs. This limited number of basis motifs captured the large majority of variance in neural activity (~75%) across animals and across behavioral states. Such a low-dimensional repertoire of cortical activity is consistent with previous work using zero-lag correlations of neural activity to measure functional connectivity between brain regions in humans (e.g. 17 functional networks, Yeo et al., 2011). However, the low-dimensionality of cortex-wide activity contrasts with recent reports of high-dimensional representations within a cortical region. Large-scale recordings of hundreds of neurons have found high dimensional (>100) representations within a brain region, with neural activity often representing small aspects of behavior (e.g. facial twitches, limb position, etc., [2,45,46]).

The difference in dimensionality of cortex-wide and within-region neural activity may reflect a hierarchical control of information processing in the brain [47–51]. In this model, behavioral state changes slowly and reflects the animal’s broad behavioral goal [52]. Achieving these goals requires engaging a set of cognitive computations (e.g. tactile/visual processing during a social interaction). On a shorter timescale, control mechanisms engage one of these cognitive computations by directing the broad flow of neural activity across the brain [53]. In other words, the control processes activate a motif. Motifs then carry the local, high-dimensional representations between regions, allowing for representation-specific behaviors. In this way, by activating specific motifs, control processes can direct the broader flow of information across brain regions without having to direct detailed single-neuron representations.

Future directions

Our approach has several limitations that motivate future research. First, although we capture a large fraction of the cortex, we are limited to the dorsal cortex and so miss out on lateral auditory cortex, cortical regions deep along the midline, and all sub-cortical regions. Second, while we probed activity in several different environments, imaging was always restricted to head-fixed animals. Third, the number and identity of motifs, as well as the relative contributions of spatial and temporal dynamics to variance in neural activity, is likely influenced by the nature of our approach. The relatively slow timecourse of GCaMP6f [18], and biases in the neural activity underlying the calcium signal [7,9] may have decreased the spatial resolution and slowed the temporal dynamics. However, it is important to note that the spatial resolution used in our imaging approach (~136 μm²/pixel) is higher than the broad activation of brain regions observed in the motifs and was high enough to capture pixel-specific information about stimuli. Furthermore, we could functionally distinguish 18 distinct regions (Figure S4E). Motifs engaged multiple of these regions, suggesting they were broader than the functional resolution of our approach. Furthermore, even given these constraints, the number of potential spatio-temporal patterns involving 18 regions is far higher than the 14 basis motifs found.

In addition to addressing these limitations, future work is needed to understand the computations associated with each motif. Here we’ve associated a few motifs with sensory processing. However, the computation underlying many of the motifs remains unknown – by cataloging motif expression across experiments and behaviors, we can begin to understand the function of each motif and gain a more holistic understanding of how and why neural activity evolves across the brain in support of behavior.

STAR Methods

Resource Availability

Lead Contact

Further information and request for resources and reagents should be addressed to Lead Contact, Timothy J. Buschman (tbuschma@princeton.edu)

Material Availability

This study did not generate new unique reagents or materials.

Data and Code Availability

Preprocessed data is available on Dryad data repository as image stacks (saved in MATLAB file format; DOI: 10.5061/dryad.kkwh70s1v; url: https://datadryad.org/stash/share/-q39l6jEbN--voeSe2-5Y3Z1pfbeYEFLO-Kf_f-cjpE. The data has been preprocessed as described below (spatially binned, masked, filtered, and then thresholded). Due to file size constraints, the full raw data is not available on the Dryad repository but is available upon request. Example data and figure generation code are available on our GitHub repository (https://github.com/buschman-lab).

Experimental Model and Subject Details

All experiments and procedures were carried out in accordance with the standards of the Animal Care and Use Committee (IACUC) of Princeton University and the National Institutes of Health. All mice were ~6-8 weeks of age at the start of experiments. Mice (N=11) were group housed prior to surgery and single housed post-surgery on a reverse 12-hr light cycle. All experiments were performed during the dark period, typically between 12:00 and 18:00. Animals received standard rodent diets and water ad libitum. Both female (N=5) and male (N=6) mice were used. All mice were C57BL/6J-Tg(Thy1-GCaMP6f)GP5.3Dkim/J ([54], The Jackson Laboratory). This mouse line, which expresses the fluorescent indicator GCaMp6f under the Thy-1 promoter in excitatory neurons of the cortex, was chosen, in part, because it is from a family of lines (denoted by the prefix “GP”) that do not exhibit the epileptiform events observed in other GCaMP6 transgenic lines [55]. 9 mice were used for solo (rest) and sensory environment widefield imaging experiments. These mice were control animals from a larger study. In that context, these animals were the offspring of female mice that received a single intraperitoneal injection (0.6-0.66mL, depending on animal weight) of sterile saline while pregnant. A subset of these mice (N=7) were used for social imaging experiments. Separate mice (N=2) were used for spontaneous behavioral state and hemodynamic correction experiments (these mice did not receive in utero exposure to saline).

Methods Details

Surgical Procedures

Surgical procedures closely followed Guo et al. [4]. Mice were anesthetized with isoflurane (induction ~2.5%; maintenance ~1%). Buprenorphine (0.1mg/kg), Meloxicam (1mg/kg), and sterile saline (0.01mL/g) were administered at the start of surgery. Anesthesia depth was confirmed by toe pinch. Hair was removed from the dorsal scalp (Wahl, Series 8655 Hair Trimmer), the area was disinfected with 3 repeat applications of betadine and 70% isopropanol, and the skin removed. Periosteum was removed and the skull was dried. A thin, even layer of clear dental acrylic was applied to the exposed bone and let dry for ~15 minutes (C&B Metabond Quick Cement System). Acrylic was polished until even and translucent using a rotary tool (Dremel, Series 7700) with rubber acrylic polishing tip (Shofu, part #0321). A custom titanium headplate with a 11mm trapezoidal window was cemented to the skull with dental acrylic (C&B Metabond). After the cement was fixed (~15 minutes), a thin layer of clear nail polish (Electron Microscopy Sciences, part #72180) was applied to the translucent skull window and allowed to dry (~10 minutes). A custom acrylic cover screwed to the headplate protected the translucent skull after surgery and between imaging sessions. After surgery, mice were placed in a clean home cage to recover. Mice were administered Meloxicam (1mg/kg) 24 hours post-surgery and single housed for the duration of the study.

Widefield Imaging

Imaging took place in a quiet, dark, dedicated imaging room. For all experiments except spontaneous behavioral monitoring (detailed below), mice were head-fixed in a 1.5 inch diameter x 4 inch long polycarbonate tube (Figure 1A) and placed under a custom-built fluorescence macroscope consisting of back-to-back 50 mm objective lens (Leica, 0.63x and 1x magnification), separated by a 495nm dichroic mirror (Semrock Inc, FF495-Di03-50x70). Excitation light (470nm, 0.4mW/mm²) was delivered through the objective lens from an LED (Luxeon, 470nm Rebel LED, part #SP-03-B4) with a 470/22 clean-up bandpass filter (Semrock, FF01-470/22-25). Fluorescence was captured in 75ms exposures (FPS = 13.3Hz) by an Optimos CMOS Camera (Photometrics). Prior to imaging, the macroscope was focused ~500um below the dorsal cranium, below surface blood vessels. Fluorescence activity was captured at 980x540 resolution (~34um/pixel) when the animal was imaged alone.

Images were captured using Micro-Manager software (version 1.4, Edelstein et al., 2014) on a dedicated imaging computer (Microsoft, Windows 7). Image capture was triggered by an analog voltage signal from a separate timing acquisition computer. Custom MATLAB (Mathworks) code controlled stimulus delivery, recorded gross animal movement via a piezo sensor (SparkFun, part #09197) attached to the animal holding tube, and captured camera exposure timing through a DAQ card (National Instruments, PCIe-6323 X Series, part #7481045-01). Timing of all camera exposures, triggers, behavioral measures, and stimulus delivery were captured for post-hoc timing validation. No frames were dropped across any imaging experiments. A camera allowed remote animal monitoring for signs of distress.

For recordings of spontaneous cortical activity, mice were head-fixed in the imaging rig and habituated for 5 minutes. After habituation, cortical activity was recorded for 12 consecutive minutes and stored as 3, 4-minute stacks of TIFF images. Qualitative real-time assessment of behavioral videos and post-hoc analysis of activity (captured by piezo sensor) revealed minimal episodes of extensive motor activity (e.g. struggling) during imaging. As our goal is to capture all behavioral states, we did not exclude these moments from our analysis. Instead, motifs captured these events alongside other cortical events.

Widefield imaging: Structured Sensory Environments

Widefield imaging was performed as above but with animals passively experiencing visual and tactile stimuli. All stimuli were provided to the animals’ left side. Recordings were 15-minutes long, divided into 90 trials of 8000ms duration. Trials were structured with a 3000ms baseline period, 2000ms stimulus period, and 3000ms post-stimulus period. Trials were separated by an inter-trial interval randomly drawn between 1000 and 1750ms.

Air puffs (10psi) were gated by solenoids (NResearch, Solenoid valve, part #161K011) and were directed at the whisker pad in either the anterior-to-posterior or posterior-to-anterior direction. Visual stimuli were gratings of 2.1cm bar width, 100% contrast, delivered on a 10inch monitor (Eyoyo, 10-inch 1920x1200 IPS LED, delivered using Pysch-Toolbox, [56]), positioned 14cm away from animals’ left eye. Gratings drifted from medial-to-lateral or lateral-to-medial at 8 cycles per second. Visual stimuli were presented for 2000ms. During these recordings, mice also received trials of auditory stimuli (e.g. 2 tones). These data were not analyzed since auditory cortex was not imaged and so no evoked response was observed. Each recording captured 30 trials of each stimulus modality. 3329 trials were captured in total across 9 animals: resulting in 1110 tactile, 1109 visual (and 1110 auditory) trials. 1 visual trial was lost due to timing issues.

Widefield Imaging: Spontaneous Behavioral State Monitoring

Widefield imaging was performed as in the original (solo) condition with minor modifications. Mice were head-fixed on a custom transparent acrylic treadmill and illuminated with infrared light (Univivi 850nm IR Illuminator). During imaging, behavioral measures were captured using two cameras: a PS3 EYE webcam (640x480 pixel resolution) focused on the animal’s whole body and a GearHead webcam (320x240 pixel resolution) focused on the animal’s face. Custom python (v3.6.4) scripts synchronized the frame exposure of the behavioral cameras at 60Hz.

Widefield Imaging: Paired Social Environment

The macroscope objectives from the above widefield imaging paradigm were replaced with 0.63x and 1.6x magnification back-to-back objectives, permitting an ~30x20mm field of view (lens order: mouse, 0.63x, 1.6x, CMOS camera). Images were acquired at 1960 x 1080 resolution (~34um/pixel). Animals were precisely positioned to be the same distance from the objective. Mice faced one another, approximately eye-to-eye in the anterior-posterior axis. Their snouts were separated along the medial-lateral axis by a 5-7 mm gap; close enough to permit whisking and social contact but prevent adverse physical interactions. A 1mm plexiglass divider at snout level ensured no paw/limb contact. Mice were positioned in individual plexiglass tubes. Pairs were imaged together for 12 consecutive minutes, once each recording day. Some pairings included mice outside this study cohort. 76 recordings from the experimental cohort were collected. After each recording, the imaging apparatus was thoroughly cleaned with ethanol and dried before imaging of the next pair (removing olfactory cues).

Animal pairs were provided with sensory stimuli consisting of playback of pre-recorded, naturalistic ultrasonic vocalizations (USVs) between adult mice, synthetic USVs, or ‘background’ noise. Naturalistic USV stimuli were obtained from the mouseTube database [57]. In particular, we used four recordings of 3 min interactions between male and estrus female wildtype C57BL/6J mice (files S2-4-4, S2-4-105, S2-4-123, S2-4-138). Details on the methods used to record these interactions are described in the original study by Schmeisser et al. [58]. To produce more salient stimuli, we reduced these 3 min recordings into 1 min recordings by using Praat software (version 6.0.23) to shorten the silent periods between USV bouts. We bandpass filtered these recordings to the 40-100 kHz range (Hann filter with 100 Hz smoothing) to reduce extraneous background noise, and down sampled the recordings to 200 kHz.

Synthetic USV stimuli were generated using a customized MATLAB script that created artificial sine wave tones matching the spectro-temporal properties of naturalistic stimuli. Specifically, synthetic stimuli had the same rate (calls per minute), average duration, and mean frequency as naturalistic USVs (we used MUPET to characterize USV properties [59]). Tones were evenly spaced throughout the synthetic stimulus. Background noise was generated from the silent periods of the 3-minute vocalization recordings. Each recording session contained 1 epoch of naturalistic USVs, 1 epoch of synthetic USVs, and 1 epoch with background noise. All acoustic stimuli were presented at ~70dB through a MF1-S speaker (Tucker Davis Technologies) placed 10cm away from both subjects.

Quantification and Statistical Analysis

Statistical Analysis:

All analyses were performed in MATLAB (Mathworks). Number of mice used was based on previously published studies [9,7,11]. As described throughout STAR Methods and main text, analyses were performed on 11 separate animals, across multiple recording sessions, and 4 behavioral environments (e.g. biological replicates). Analyses were validated across a range of processing parameters (e.g. technical replicates). All statistical tests, significance values, and associated statistics are denoted in the main text. P-values below machine precision are reported as p<10⁻¹⁶. All 95% confidence intervals were computed using MATLAB bootci function (1000 bootstrap samples).

Widefield Imaging Preprocessing

Image stacks were cropped to a 540x540 pixel outline of the cortical window. Images were aligned within and across recordings using user-drawn fiducials denoting the sagittal sinus midline and bregma for each recording. For anatomical reference (Figures 1A and S1A), recordings were aligned to a 2D projection of the Allen Brain Atlas, version CCFv3 using bregma coordinates (Oh et al., 2014; ABA API interfacing with MATLAB adapted from https://github.com/Sainsbury WellcomeCentre/AllenBrainAPI ). The complete 2D projection is shown in Figure S1A. As they are only intended to be local references, the parcel outlines overlaid in Figures 1, 4, 5 were created by manually tracing this 2D projection (Inkscape Vector Graphics Software).

Changes in fluorescence due to hemodynamic fluctuations may confound the neural activity captured by widefield imaging [7,61,62]. However, previous work has found hemodynamic contributions to fluorescent signal using similar widefield imaging approaches are minimal [19,21,63] , and can be mitigated by removing pixels corresponding to vasculature [9]. To mitigate impact of hemodynamic contributions, we masked pixels corresponding to vasculature. To identify vasculature, the middle image of each recording was smoothed with a 2D median filter (neighborhood 125 pixels²) and subtracted from the raw image. As vasculature pixels are much darker than pixels of neural tissue, we created a vasculature mask by thresholding the reference image to pixels intensities >= 2.5 standard deviations below the mean. To remove noise, the mask was morphologically closed with a 2-pixel disk structuring element. A vasculature mask was created for each recording. Supplemental experiments, outlined below, demonstrated that vascular masks successfully mitigated the contribution of hemodynamics to our signal.

Vasculature masks were combined with a manually drawn outline of the optically accessible cortical surface and applied to each recording to conservatively mask non-neural pixels. Masks removed the sagittal sinus, mitigating vascular dilation artifacts. Additionally, masks removed peripheral lateral regions, such as dorsal auditory cortex, where fluorescence contributions across animals may be differentially influenced by individual skull curvature. After alignment and registration, recordings were spatially binned to 135x135 pixels (~68μm²/pixel). Masked pixels were ignored for spatial binning. Normalized activity was computed as change in fluorescence, e.g. ΔF/F over time according to $\frac{F-F_0}{F_0}$ Baseline fluorescence, F₀, was computed as the rolling mean of a 9750ms window (130 timepoints) across the entire recording duration. ΔF/F was computed individually per pixel and using the baseline fluorescence for each time point. To remove slow fluctuation in signal (e.g. due to change in excitation intensity), pixels traces were detrended using linear least squares fit. Recordings were then bandpass filtered at 0.1 to 4Hz (10^th order Butterworth filter).

In order to isolate neural activity, pixel traces were thresholded at 2 standard deviations above the mean. This was done to remove spurious, low-intensity noise in the calcium signal. This is akin to thresholds used to isolate spiking activity in two-photon calcium imaging and electrophysiological signals [64,65]. Threshold level did not significantly change any of our conclusions, as similar results were observed when thresholding at the mean (see Figure S2).

After filtering and thresholding, recordings were spatially binned again to a final size of 68x68 pixels (~136μm²/pixel). Pixels with zero variance during an epoch (e.g. masked pixels) were ignored for all subsequent analyses. Subsequent factorizations require non-negative pixel values so recordings where normalized to range of 0 to 1 using the maximum and minimum pixel values per recording. The 12-minute solo and social recordings were divided into six, 2-minute epochs. Alternating epochs were used for motif discovery or withheld for testing (Figure 1B) to control for any potential shift in behavioral state (and thus cortical activity) over the recording session. For solo recordings this resulted in 144 ‘discovery’ and 144 ‘withheld’ epochs.

For social recordings, cortices of individual animals were cropped to 540x540 pixels and preprocessing followed as above. Again, recordings were divided into 2-minute epochs, resulting in a total of 228 ‘discovery’ and ‘withheld’ epochs. Given the proximity of the animals, whiskers from one animal sometimes entered the imaging field of view of the paired animal, creating artifacts easily detected upon manual inspection. All epochs were manually inspected and epochs with any whisker artifacts (N=105) were removed, resulting in 123 ‘discovery’ and ‘withheld’ epochs (8.2 hours in total).

For sensory trials, which were 8 seconds in length, each trial’s ΔF/F was calculated using the mean of the first 26 timepoints (~2s) as baseline fluorescence. Burst in activity were discovered by thresholding traces at 1 standard deviation per pixel. Due to light-artifact of visual stimuli leaking through the ipsilateral cortical bone in a subset of recordings, a more conservative mask on the ipsilateral hemisphere was used for all sensory environment analyses (as shown in Figure 5E). Accordingly, this mask was used for all analyses in Figures 5–6, including quantification of motifs in the original (solo) environment. All other preprocessing steps were followed as above.

Multiwavelength Hemodynamic Correction

Additional experiments using multiwavelength hemodynamic correction were performed to confirm that vasculature masking mitigated hemodynamic contributions to motifs (Figure S4B–D). Hemodynamic correction followed [31]. In brief, widefield imaging was performed while strobing between illumination with a blue LED (470nm, 0.4mW/mm²) and violet LED (410nm, LuxDrive LED, part #A008-UV400-65 with a 405/10 clean-up bandpass filter; Edmund Optics part #65-678). Each exposure was 35.5ms and light from both LEDs were collimated and coupled to the same excitation path using a 425nm dichroic (Thorlabs part #DMLP425). Illumination wavelengths alternated each frame. Strobing was controlled using an Arduino Due with custom MOSFET circuits coupled to frame exposure of the macroscope (as in [10]). After vasculature masking and spatial-binning to 135x135 pixels, violet-exposed frames (e.g. noncalcium dependent GCaMP6f fluorescence, Lerner et al., 2015) were rescaled to match the intensity of blue-exposed frames. ΔF/F was then computed as ΔF/F_blue - ΔF/F_violet. Remaining preprocessing steps followed original (solo) experiments.

Motif Discovery

We used the seqNMF algorithm (MATLAB toolbox from [22]) to discover spatio-temporal sequences in widefield imaging data. This method employs convolutional non-negative matrix factorization (CNMF) with a penalty term to facilitate discovery of repeating sequenc es. All equations below are reproduced from the main text and Tables 1 and 2 of Mackevicius et al. [22]. For interpretability, we maintained the nomenclature of the original paper where possible.

We consider a given image as a P x 1 vector of pixel values and a recording image sequence (i.e. recording epoch) as a P x T matrix, where T is the number of timepoints in the recording. This matrix can be factorized into a set of K smaller matrices of size P x L representing short sequences of events (e.g. motifs). Collectively this set of motifs is termed W (a P x K x L tensor).

Each pattern is expressed over time according to a K x T temporal weighting matrix termed H. Thus, the original data matrix can be approximated as the sum of K convolutions between the motifs in W and their corresponding temporal weightings in H:

$$X_{pt}\approx {\tilde{X}}_{pt}=\sum _{k=1}^K\sum _{\ell =0}^{L-1}{W}_{pk\ell }{H}_{\text{k}\left(\text{t}-\ell \right)}\equiv {\left(W⊛H\right)}_{pt}$$ (equation 1)

Here, ⊛ indicates the convolution operator. The values of W and H were found iteratively using a multiplicative update algorithm. The values of L (the maximum duration of motifs) and K (the maximum number of motifs) are important free parameters to consider. If smaller than the true values, both L and K will artificially restrict the motifs; resulting in motifs that are too short (if L is too small) or forcing different motifs to combine into a single motif (if K is to small). If L and K are larger than the true values they will not artificially alter the motifs because the regularization of CNMF (detailed below) will render unused timepoints and motifs blank (e.g. zero-valued). However, larger values quickly increase the computational cost of CNMF (an important consideration given the size of the datasets and number of fits used here).

Unless otherwise noted, L was set to 13 frames (975ms). This L value was chosen because it is well above the duration of GCaMP6f event kinetics and qualitative assessment of imaging recordings suggested most spontaneous events were < 1000ms in duration; agreeing with previous findings [2]. Furthermore, post-hoc analyses revealed that activity within motifs resolved within the 975ms motif duration and that our choice of L maximized the explanatory power of the discovered motifs (Figure S1B–D).

Unless otherwise noted, K was set to 28 motifs. Changing the K values (within reasonable bounds) did not have a significant effect on the median number of discovered motifs (Figures S1E), and a K of 28 was higher than the maximum number of motifs discovered in any epoch (Figure 2A; the maximum number of motifs discovered in any epoch was 27). Furthermore, our choice of K did not restrict the number of basis motifs discovered (Figure S4A). Thus, our choice of K did not analytically restrict the number of motifs discovered or the limit the dimensionality of the basis motifs.

The seqNMF algorithm improves upon typical CNMF by including a spatio-temporal penalty term into the cost function of the multiplicative update algorithm. In brief, this reduces redundancy between motifs: 1) multiple motifs do not describe the same sequence of activity; 2) a single motif is not temporally split into separate motifs; and 3) motifs are encouraged to be non-overlapping in time. This penalty termed is implemented as follows:

$$R=\lambda {\Vert \left(W\stackrel{T}{⊛}X\right)S{H}^T\Vert }_{1,i\ne j}$$ (equation 2)

Here, temporal overlap (correlation) between motifs is captured by SH^T. S is a T x T temporal smoothing matrix where S_ij = 1 when |i – j| < L; otherwise S_ij = 0. Thus, each temporal weighting in H is smoothed by a square window of length 2L-1, increasing the product of motifs that temporally overlap within that window.

Competition between spatio-temporal structure of motifs is achieved by calculating the overlap of motifs in W with the original data as follows

$${(W\stackrel{T}{⊛}X)}_{kt}={\sum }_{\ell }{\sum }_p{W}_{pk\ell }{X}_{p\left(t+\ell \right)}$$ (equation 3)

Motifs containing similar patterns will overlap with the original data matrix at the same times. The notation || · ||_1,i≠j ignores penalizing terms along the diagonal such that spatial and temporal autocorrelation of motifs is not penalized. λ is a tunable parameter that controls the magnitude of the penalty term. The result of this penalty, when implemented as a cost function in the multiplicative update algorithm for fitting H and W, is to bias factorization such that only one motif is active at a given timepoint. For motif discovery, λ = 0.0005 which reflected the optimal tradeoff between quality of fit, motif overlap, and number of discovered motifs (Figure S1F). Importantly, a similar number of motifs were found across 6 order of magnitude of λ, suggesting our results did not depend on the exact value.

Additionally, the seqNMF algorithm contains optional orthogonality constraints to bias factorizations towards parts-based and events-based factorizations. In widefield imaging data, parts-based would preferentially detect spatially independent motifs. Events-based factorizations, used in this study, would preferentially discover temporally independent motifs that correspond to specific instantiations of sequential activity patterns. This was achieved with an additional smoothed orthogonality cost term penalizing overlap in motif temporal weightings:

$$R_{Hortho}=\frac{{\lambda }_{Hortho}}{2}{\Vert HS{H}^T\Vert }_{1,i\ne j}$$ (equation 4)

The magnitude of λ_orthoH was set to 1 based on preliminary experiments (not shown) and remained unchanged for all motif discovery experiments, including the parameter sweeps of λ and K described above. All fitting processes were run for 300 iterations; at which point the cost function leveled out (Figure S1G).

Table S3 contains a complete list of all adjustable parameter values of the seqNMF algorithm toolbox used for each experiment. Descriptions for parameters not discussed above can be found in original work. To discover motifs in paired social recordings, the same K and L values (28 and 13) were used. λ was refit following the procedure described above.

Note, one change was made to the seqNMF algorithm toolbox. For convenience, the smoothing matrix S was multiplied by 0.01. Specifically, line 98 of original seqNMF code: smoothkernel = ones(1,(2*L)-1) replaced with smoothkernel = 0.01*ones(1,(2*L)-1). This allowed λ values to be 100x larger and, therefore, easier to read.

Visualizing Motif Activity Flow

To aid in visualization of motif patterns (Figures 1 and 3), we used the Horn-Schunck optical flow method to calculate the velocity vector fields between subsequent timepoints of motifs ([67]; implemented using HS function from OFAMM MATLAB toolbox, [23]). For all plots, arrows depict the direction and velocity of flow for the top 50% intensity pixels of each timepoint. The number of arrows were downsampled by a factor of three for clarity in visualization.

Comparing Motifs to sPCA, sNMF, and stNMF

Data preprocessing for Motif, sPCA, sNMF, and stNMF discovery was identical. For sPCA, pixels were treated as variables and timepoints as observations. sNMF was performed by setting L to 1 (effectively reducing equation 1 to matrix multiplication) and removing all temporal and spatial sparsity terms.

Space-by-time stNMF followed [24,25]. Here, the P x T data matrix representing each recording was factorized into a set of independent spatial (i.e. pixels of neural activity) and temporal (i.e. temporal fluctuations in activity; termed H) according to:

$$X_{pt}\approx {\tilde{X}}_{pt}=\sum _{k=1}^K\sum _{j=1}^J{W}_{pk}{A}_{kj}{H}_{tj}$$ (equation 5)

Here, K and J are the number of spatial and temporal patterns, respectively. A is a weighting matrix that contains the relationships between each independent spatial and temporal pattern. This allows each spatial pattern to be expressed according to any of the temporal patterns (and vice versa). In this way, space and time are now independent and the number of possible different patterns in stNMF is K x J. W, A, and H were fit at the same time using an iterative multiplicative update algorithm (as in CNMF; fit for 1500 iterations, well past the plateau in the loss function). If dynamics are separable in space and time, then the stNMF algorithm would explain more variance in neural activity than motifs using fewer space and time dimensions (because these dimensions can be combined in many ways). Conversely, if dynamics are not separable in space and time, then stNMF would still describe the data, but would require many more spatial and temporal dimensions than the number of motifs [24].

Refitting Motifs to Withheld Data

To refit motifs to withheld data, we used the same seqNMF algorithm, but W was fixed to the previously discovered motifs (or basis motifs) during fitting. Thus, the only updatable features of the factorization were motif temporal weightings, H. See Table S3 for a list of all parameters used during fitting. Importantly, since only temporal weightings were refit, ( was set to zero. Thus, unlike motif discovery where motifs were highly spatially and temporally independent, refit motifs did not have this constraint and thus some combinatorial motif activation was observed. However, increasing λ_Hortho had little impact on the percent of variance explained when refitting the motifs, suggesting that any compositionality had minimal impact on results (Figure S1I). Furthermore, minimal temporal dependence between motifs was observed (Figure S5). Importantly, all motifs, static networks, and time-varying networks were refit to withheld data in the same way and therefore their percent explained variance can be directly compared.

For solo and social recordings, the part-based factorization orthogonality bias was maintained as in initial discovery (see Table S3). Given the short duration of sensory trials, the orthogonality bias was not used. The same process was followed for refitting basis motifs and social basis motifs to withheld data. For all refitting processes, motifs and withheld data were first spatially smoothed with a 2D gaussian filter (σ = [1,1]). Only pixels with non-zero variance in both motifs and withheld data were used.

Generating Basis Motifs

To identify basis motifs, we used an unsupervised clustering algorithm (Phenograph [27,26]). For clustering, motifs were renormalized to 0-to-1 and spatiotemporally smoothed with a 3D gaussian filter (σ = [1,1,0.1]). The Phenograph algorithm generates a directed graph, where each node (here, an individual motif) is connected to its k nearest neighbors. Louvain community detection is then performed on this graph to cluster nodes into groups. For finding neighbors, distances between motifs were computed as the peak in their temporal crosscorrelation. The only tunable parameter of Phenograph is the number of nearest neighbors (k). k=15 was chosen based on initial experiments. Similar number of clusters (10-20) were observed for k=10 and k=20.

Basis motifs were generated by taking the mean of the core community of motifs in each cluster. The core community was defined as the top 10% of motifs in each cluster with the most within-cluster nearest neighbors. Prior to averaging, motifs were aligned to a ‘template’ motif. The template motif shared the most zero-lag peak temporal cross-correlations with all other motifs. If there were multiple templates, one was chosen at random. All motifs were zero-padded to a length of 3L (39 timepoints) to allow for some temporal jitter and aligned to these templates by their maximal cross-correlation lag. Basis motifs were then calculated by averaging the activity of these core exemplars at each timepoint. Finally, we aligned the basis motifs to one another by shifting the center of mass of activity to the middle timepoint. Timepoints with no variance across all basis motifs were removed, resulting in basis motifs that were a maximum of 26 timepoints (~2s) in duration. A complete description of each basis motif and the approximate duration of the main activity pattern in each motif is provided in Table S2.

Percent Explained Variance Calculations

For all experiments, the percent explained variance (PEV) in neural activity was defined as

$$PEV=100*\left(1-\frac{({\sigma }_X{}^2-{\sigma }_{\tilde{X}}{}^2)}{{\sigma }_X{}^2}\right)$$ (equation 6)

Where σ_x² and ${\sigma }_{\tilde{X}}{}^2$ denote the spatio-temporal variance of the original data and reconstructed data respectively.

The PEV of individual motifs was calculated by convolving the motif with its temporal weighting and computing PEV as above (see helper.reconstruct function from seqNMF toolbox). Thus, the PEV of individual motifs reflected both the frequency of motif occurrence and the quality of fit to the data. Relative PEVs of individual motifs were calculated by dividing the PEV of each motif by the total PEV across all motifs for that epoch.

Timepoint-wise PEV (Figure S1J) used the same calculation as above but was performed separately on each timepoint of an epoch. Thus, these analyses reflect solely the spatial variance in activity captured by reconstructed data for each individual timepoint.

Cross-Temporal Autocorrelation Analysis

The cross-temporal autocorrelation of each motif was calculated by computing the spatial correlation between frames of the motif at varying temporal lags. The resulting autocorrelation was then fit with an exponential to estimate the half-life of decay in the autocorrelation (τ). Pixels with no variance across motif timepoints were ignored when calculating correlation.

Static Networks

Static networks were generated for each motif by replacing all of the active timepoints of a motif with the mean activation of that motif (see Figure 3E for example). Active timepoints were defined as any timepoints with variance across pixels greater than zero. Thus, static networks represent a constant ‘state’ of activation of the same brain regions for the duration of that motif. The temporal weightings of these static networks were refit to the withheld data the same way as dynamic motifs (i.e. the activation of these states could vary throughout an epoch; described above).

Fitting Average Traces to Sensory Trials

Average stimulus responses were calculated by taking the mean of all trials across animals for visual and tactile stimuli. Different stimuli within a modality were combined to generate the average trace (e.g. visual grating 1 and 2 were averaged together). Temporal weightings of average traces were refit to trials using the same seqNMF algorithm and parameters as when refitting basis motifs, except now the average stimulus response was used in place of the motifs. Additionally, prior to fitting, trials were zero-padded which allowed the algorithm to flexibility shift the average trace timing to best match the evoked response timing of each trial. This allowed us to directly compare the PEV of the motifs and the average stimulus response.

Comparing Stimulus Evoked Motif Responses

We sought to compare the motif responses evoked by different stimuli (Figure 5C–D). Motif activity was estimated by convolving each motif with its temporal weight on each trial (as described above; see seqNMF Toolbox helper.reconstruct function). Stimulus selectivity of a motif was estimated by comparing the evoked responses to each stimulus (two-sample t-test). This was done over time, using 300ms windows, stepped every 150ms to give a timecourse of similarity. Resulting p-values were Bonferroni corrected for multiple comparisons across time and conditions (i.e. 24 comparisons in Figure 5C–D, 12 windows x 2 modalities).

Decoding Stimuli from Motif Activity

Stimuli were decoded using support vector machine classifiers with radial basis function kernels (MATLAB; fitsvm function; Sequential Minimal Optimization solver). Classifiers used the peak activity for each motif during the 2s period after stimulus-onset. Prior to training a classifier, 20% of each trial type was held out as a validation test data set. Each classifier either incorporated all the motifs or left out a single motif. Classifier accuracy was quantified using the area under the curve (AUC) of the receiver operator characteristic function (MATLAB, perfcurve function). The decoding contribution of each motif was quantified as the change in decoding AUC (on withheld data) when that motifs was left out relative to the full model.

Pixelwise Classifier Analysis Comparing Motif Responses to Stimuli

As described above, mice were presented with two different visual stimuli: visual stimulus 1 (grating drifting from medial-to-lateral) and visual stimulus 2 (grating drifting from lateral-to-medial). Mice received 15 trials of each stimulus on 4-5 consecutive recording days (60-75 total of each type per mouse). As described in the main text, the response of the ‘visual’ motif (#10) did not differ between the two stimuli. To test whether this was due to a limitation in our imaging approach, we tested whether we could classify neural responses as belonging to the two stimuli (Figure 6B).

To classify stimulation response, we used a support vector machine classifier (as above). Classification was performed on pixels restricted to the right hemisphere (contralateral to stimulus) and in the top 95% intensity percentile of motif 10 (visually-evoked motif). This resulted in a total of 6006 possible feature pixels (231 pixels across the 26 timepoints of visual stimulus presentation). For each classifier, we performed a cross-validated ANOVA feature selection to select a subset of these pixels as classification features [68]. The p-value for a one-way ANOVA comparing responses to each stimulus type was computed for each pixel in the training data. The 50 pixels with the highest −log10(p-values) were used for classification. After determining the feature vector, the classification hyperparameters were tuned within the training data, as described above.

For each mouse, pixelwise classification was performed on two datasets (Figure 6B). First it was performed on the original data (after the preprocessing steps above). Second it was performed on the reconstructed activity of the motifs fitted to this original data. Thus, for both classification procedures, the data were the same spatial resolution. The only difference between the data sets were the residuals of the motif fitting procedure. Therefore, a total of 18 classifiers were trained (2 per animal).

Relatedly, during tactile trials, mice received either an anterior-to-posterior or posterior-to-anterior air puff, both directed at the whiskers (15 trials of each stimulus on 4-5 consecutive recording days, resulting in 60-75 total of each type per mouse). However, unlike the visual stimuli, these two tactile stimuli evoked different magnitudes motif activity, likely due to differences in the two solenoids used to control the airflow impacted flow rate and air pressure (the posterior-to-anterior airpuff elicited a stronger response of all motifs). Because of concerns about differences in the strength of the stimuli, we did not do the pixel-wise classification of the tactile stimuli as was done for visual stimuli. However, stimulus-specific activity in the residuals (after fitting motifs) still only captured a small part of the total explainable variance (Figure S6I). Thus, as we saw for visual stimuli, most cortex-wide neural activity can be explained by the expression of motifs.

Quantifying Spontaneous Behavioral States

Behavioral state was quantified using the intensity of nose motion energy, whisker pad motion energy, and total limb speed. Nose and whisker pad motion energy was quantified as the mean absolute temporal derivative of pixels within a manually selected ROIs (shown on Figure 5A). The whisking speed of the mouse was faster than the frame rate of the behavioral videos. This caused the whiskers to be blurred when the animal was intensely whisking, resulting in a low value for the whisker energy measure. Therefore, whisking motion energy was inverted for all analyses (e.g. M_whisk = max(M_{whisk original})–M_{whisk original} ) so that the axes were consistent across the three behavioral variables (i.e. higher values indicate higher energy).

Markerless tracking of paw position (DeepLabCut; [34]) was used to measure limb speed. Training and validation of DeepLabCut neural network followed [69], with the network trained to identify paw position as the center point between the 1^st and 5^th digit of each paw. To improve accuracy of limb position estimates, nose, tail base, and tail root were also tracked. 360 frames from 2 animals were used for network training. One refinement iteration was performed. The network was trained until loss plateaued (120,000 iterations). Total limb speed was calculated as the summed absolute temporal derivatives of the x and y position of all four paws.

To categorize behavioral state, a gaussian mixture model (GMM) was fit to the distributions of these three behavioral variables (MATLAB; fitgmdist function; 2 components). Timepoints were assigned to one of two behavioral states according to the 2-second running product of the posterior probability of being in each state. Any timepoints with a likelihood of being in either state that was less than 0.5 were excluded from analysis (this was less than 0.01% of all timepoints in both animals).

To decode behavioral state based on motif activity, we used a support vector machine classifier (as above). Prior to training a classifier, 20% of each trial type was held out as a validation test data set. For each classifier, two hyperparameters, “box-constraint” (a regularization parameter to prevent overfitting) and “kernel scale” were tuned using cross validation within the training set data (5 folds, balanced trial types: using the MATLAB functions fitsvm and cvpartition). Hyperparameters were optimized using Bayesian optimization (MATLAB, bayesopt function).

Estimating the Working Resolution of Widefield Imaging

One concern is that the spatial resolution of our approach may have artificially limited the dimensionality of the observed motifs. Therefore, we sought to estimate the ‘working resolution’ of our approach by grouping pixels into functional clusters, defined as contiguous groups of pixels with correlated activity (Figure S4E).

To identify functional clusters, we divided each recording epoch into 1 second time periods (17,280 total 1-second periods, each with 13 frames). A pixelwise correlation matrix was computed for each 1-second period. Next, PCA was applied to each correlation matrix, producing a (pixel x component) matrix of ‘eigenconnectivities’. These eigenconnectivities reflected the dominant correlation patterns across pixels during that 1-second period (similar to approaches by [70,71]).

The first eigenconnectivity from each 1-second time period were concatenated together, creating a (pixel x 17,280) matrix that captured the wide variety of different possible spatial patterns across the cortex. We then used Phenograph (k=15) to group pixels according to their correlation across these spatial patterns. This produced 37 ‘functional clusters’ of highly correlated pixels (Figure S4E; 18 in left and 19 in right hemisphere. Similar results (~20 clusters per hemisphere) were observed by performing PCA on each 1-second time period and then clustering as above (i.e. without first creating a correlation matrix; this creates an ‘eigenimage’ instead of an ‘eigenconnectivity’ as in [72]).

The resulting ~19 functional clusters per hemisphere is likely a lower-bound of the imaging resolution, given that our imaging approach can still capture pixel-wise activity (Figure 6B). Even using this lower bound, the dimensionality of our motifs is far less than the possible dimensionality of our approach. For example, even if motifs engaged only 1-2 functional clusters, there are still 18²=324 possible patterns, suggesting that the observed dimensionality was not artificially limited by our imaging approach.

Supplementary Material

2

Video S1. Example Widefield Imaging of in vivo Cortical Activity. Related to Figure 1. Shows an example of widefield imaging (left) alongside a video of animal’s behavior (right).

3

Video S2. All Basis Motifs. Related to Figure 4. Basis motif display follows Figure 4C. For video visualization, all motifs were convolved with a 450ms gaussian temporal weighting vector to mimic a burst in activity.

Key Resources Table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Experimental Models: Organisms/Strains
Mouse: Thy1-GCaMP6f: C57BL/6J-Tg(Thy1-GCaMP6f)GP5.3Dkim/J	The Jackson Laboratory	RRID:IMSR_JAX:028280
Software and Algorithms
MATLAB 2017a-2018b	Mathworks	N/A
seqNMF MATLAB Toolbox	[22]	N/A
MUPET MATLAB Toolbox	[54]	N/A
OFAMM MATLAB Toolbox	[23]	N/A
Psychtoolbox-3 MATLAB Toolbox	[55]	N/A
Python version 3.6.4	Python Software Foundation	N/A
DeepLabCut Python Library	[34]	N/A
Signal Processing and Analysis code for Widefield Imaging data	This manuscript	N/A

Highlights.

Cortex-wide imaging revealed rich spatio-temporal dynamics of neural activity in mice

A set of 14 motifs captured repeated spatio-temporal patterns of neural activity

The same motifs were seen in different animals and generalized across behaviors

Motifs may reflect core cortical computations, such as sensory processing