Deep learning for prediction of the air quality response to emission changes

Abstract

Efficient prediction of the air quality response to emission changes is a prerequisite for an integrated assessment system in developing effective control policies. Yet representing the nonlinear response of air quality to emissions controls with accuracy remains a major barrier in air quality-related decision-making. Here we demonstrate a novel method that combines deep-learning approaches with chemical indicators of pollutant formation to quickly estimate the coefficients of air quality response functions using ambient concentrations of 18 chemical indicators simulated with a comprehensive atmospheric chemical transport model (CTM). By requiring only two CTM simulations for model application, the new method significantly enhances the computational efficiency compared to existing methods that achieve lower accuracy despite requiring 20+ CTM simulations (the benchmark statistical model). Our results demonstrate the utility of deep-learning approaches for capturing the nonlinearity of atmospheric chemistry and physics and the prospects of the new method to inform effective policymaking in other environment systems.

Graphical Abstract

Air pollution is a global concern due to its harmful effects on human health¹, climate², agriculture and ecosystem health³, and visibility⁴. Ambient PM_2.5 (particulate matter with aerodynamic diameter less than 2.5 μm) and ozone (O₃) are among the highest risk factors for global premature mortality^1,5, with PM_2.5 pollution estimated to have contributed to 2.9 million deaths globally in 2017 and O₃ pollution to nearly a half million deaths⁶. A central challenge in effectively controlling the sources of ambient PM_2.5 and O₃ is that the dominant contributors to these pollutants are emitted precursors such as sulfur dioxide (SO₂), nitrogen oxides (NO_x), ammonia (NH₃), and volatile organic compounds (VOCs)⁷ that undergo chemical transformations in the atmosphere. The chemical reactions that lead to O₃ and PM_2.5 formation involve highly nonlinear processes across multiple phases that vary significantly with meteorological conditions and precursor levels. Despite their complexity, these chemical pathways ultimately dictate the strong nonlinear responses of PM_2.5 and O₃ to precursor emission changes^8–12 and must be accurately modeled.

Comprehensive chemical transport models (CTMs) implemented with the most recent knowledge of atmospheric science are the preferred tools for simulating the chemical and physical processes occurring in the atmosphere¹³. Numerical experiments such as simulating air quality under conditions of reduced precursor emission levels relative to a baseline case (i.e., “brute force” method) can be conducted to investigate the response of air quality to emission changes¹⁴. The sensitivity of air pollutant concentrations to emission sources can also be explored with advanced techniques such as the decoupled direct method (DDM)¹⁵, higher-order DDM¹⁶, and adjoint sensitivity analysis¹⁷. Contributions of emissions to ambient concentrations can be estimated using ozone source apportionment technology¹⁸, particulate matter source apportioning technology¹⁹, the integrated source apportionment method^20–21, and source-oriented models²². These methods are practical for quantifying the relative contributions of emission sources to air pollution and the sensitivity of air pollution to limited changes in emissions²³; however, they are computationally expensive and do not address prediction of air quality responses to emission changes for the wide range of possible scenarios of interest to policymakers.

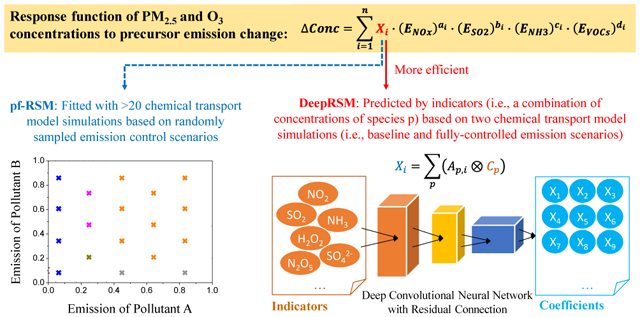
Efficient and accurate prediction of air pollutant responses to emission changes is a key component of the integrated assessment systems commonly used by policymakers to quickly achieve multiple objectives. Integrated assessment models for air pollution control quantify the influence of future policies on air pollution levels using process parameterizations and are used to analyze the benefits and costs of emission controls in designing efficient strategies to attain air quality goals^24–28. The Air Benefit and Cost and Attainment Assessment System (ABaCAS) is an integrated assessment system that connects air pollution emission control with health benefit and cost estimation²⁹. In ABaCAS, the response of pollutant concentrations to emission changes is predicted in real-time with a response surface model (RSM) developed from many CTM simulations using advanced statistical interpolation techniques^30–31. Recently, a series of innovations have improved the representation of nonlinear interactions among precursors from sources in multiple regions in extended versions of the original RSM (i.e., E-RSMs)^32–34. To ensure model accuracy, the development of RSM and E-RSM requires many control scenarios to be simulated with a CTM, with heavy computational burden that limits the adaptability and broad application of RSMs. To partially address this issue, a RSM based on polynomial functions (pf-RSM) was recently developed using prior knowledge from earlier RSM studies to reduce the number of CTM simulations required for RSM development by 60%³⁵. However, implementation of the pf-RSM still requires at least 20 CTM simulations, and such computational cost remains a significant barrier to the broad adoption of RSM technology.

In the pf-RSM, polynomial functions were fitted individually for each spatial grid cell and therefore did not consider the moderate degree of spatial correlation that is common among air pollutants. Also, the functions were fitted solely based on simulated O₃ and PM_2.5 concentrations without considering the concentrations of related chemical species. Many species are influenced by common atmospheric processes and reactions and are highly correlated in the atmosphere. Moreover, concentrations of secondary pollutants, such as O₃ and PM_2.5, may largely be determined by the ambient levels of their precursors. Previous studies suggest that certain combinations of related chemical species can be used as indicators for O₃ and PM_2.5 chemistry^36–37. Studies have also shown that the response of O₃ and PM_2.5 to changes in precursor levels can be identified from changes in concentrations of related species³⁸, as illustrated with Empirical Kinetic Modeling Approach (EKMA) diagrams of the response in O₃ and PM_2.5 concentrations to changes in NO_x and VOC concentrations^39–40. Such relationships imply that nonlinearity in the O₃ and PM_2.5 response to precursor emission changes can be quantified using combinations of ambient concentrations of certain species (hereafter indicators), and that the indicator-pollutant relationships are independent of location or time.

Despite the potential predictive value of the chemical indicators, previous RSMs have been directly fit to O₃ and PM_2.5 concentrations, because collinearity associated with the moderately-correlated indicators cannot be resolved with statistical regression models. In contrast, neural network algorithms are well suited to address collinearity issues and have been used in recent air quality prediction studies^41–42. Moreover, convolutional neural networks (CNNs) can potentially enhance predictive capability by preserving important spatial features of pollutants through the network. Although previous studies have used neural networks to forecast air quality under varying meteorological conditions and develop concentration fields for retrospective periods, deep learning methods have not been applied to comprehensively address air quality prediction under varying emission levels, which is of central importance to policymakers.

In this study, we present a novel method called the Deep-learning-based response surface model (DeepRSM) to characterize the response of O₃ and PM_2.5 concentrations to the full range of emission changes using a deep CNN with carefully designed architecture and training method. The training and test data for the DeepRSM model is based on brute-force simulations with the Community Multiscale Air Quality (CMAQ) CTM (Table S1) on domains that cover China (noted as CN27) and three polluted regions within China (i.e., Northern China Plain, NCP; Fen-Wei Plain, FWP; and Chuan-Yu region, CYR) (Figure S1). The DeepRSM based on the trained CNN can reliably estimate the responsiveness of O₃ and PM_2.5 concentrations to emission changes for any domain and time period in real-time using only ambient concentrations of related chemical species from two simulations (i.e., baseline and fully-controlled emission scenarios). To demonstrate the performance of DeepRSM, we evaluated DeepRSM predictions against CTM results in a series of experiments with different types and numbers of training datasets, as summarized in Table S2. DeepRSM predictions are also compared with those of the existing RSM method, which serves as the benchmark case in this study.

Methods

(1). CTM Configuration

The pf-RSM and DeepRSM were developed using CTM simulations with the CMAQ model (version 5.2; www.epa.gov/cmaq). Baseline concentrations and the responses of PM_2.5 and O₃ to emission controls were simulated for a matrix of 40 emission control scenarios (Table S1) as part of our previous pf-RSM development³⁵. The four modeling domains are shown in Figure S1. Simulations for the CN27 domain used 27km by 27km horizontal resolution, and simulations for the three nested domains (i.e., NCP, FWP and CYR) used finer resolution of 9 km by 9 km. Modeling was performed for January, April, July and October in 2017 to represent winter, spring, summer and fall, respectively. O₃ concentrations were analyzed based on afternoon averages (12:00pm-6:00pm local time), and PM_2.5 concentrations were based on daily or monthly averages.

The emission data were developed by Tsinghua University based on a bottom-up method with high spatial and temporal resolution. Meteorological fields were based on simulations with the Weather Research and Forecasting (WRF, version 3.7) model. The configurations of the WRF and CMAQ models matched those of our previous study^43–44. The performance of the CMAQ model for predicting O₃ and PM_2.5 concentrations was thoroughly evaluated using ambient measurements^43–44 and shown to be acceptable based on recommended benchmarks for comparisons with ground-based observations.

(2). pf-RSM Configuration

Our previous study suggested that nonlinear response of O₃ and PM_2.5 concentrations to precursor emission controls can be represented by a set of polynomial functions (i.e., pf-RSM)³⁵. The structure of the polynomial function is expressed as follows:

$$\Delta \mathit{\text{Conc}}={\sum }_{i=1}^n{X}_i\bullet {\left(E_{NOx}\right)}^{a_i}\bullet {\left(E_{SO2}\right)}^{b_i}\bullet {\left(E_{NH3}\right)}^{c_i}\bullet {\left(E_{\mathit{\text{VOCs}}}\right)}^{d_i}$$ (E1)

Where ΔConc is the response of the O₃ and PM_2.5 concentrations (i.e., change relative to the baseline concentration) calculated from a polynomial function of five variables (E_NOx, E_SO2, E_NH3, E_VOCs); E_NOx, E_SO2, E_NH3, and E_VOCs are the ratios of emission changes relative to baseline emissions for NO_x, SO₂, NH₃, and VOC, respectively; and a_i, b_i, c_i, and d_i represent the nonnegative integer powers of E_NOx, E_SO2, E_NH3, and E_VOCs, respectively. X_i (the coefficient of term i) is determined by fitting the polynomial function for each spatial grid cell in the pf-RSM using 20 to 40 CTM simulations. The 14 terms used to represent the PM_2.5 and O₃ responses to emission controls were determined previously in designing the pf-RSM and are shown in Figure 1.

Figure 1.

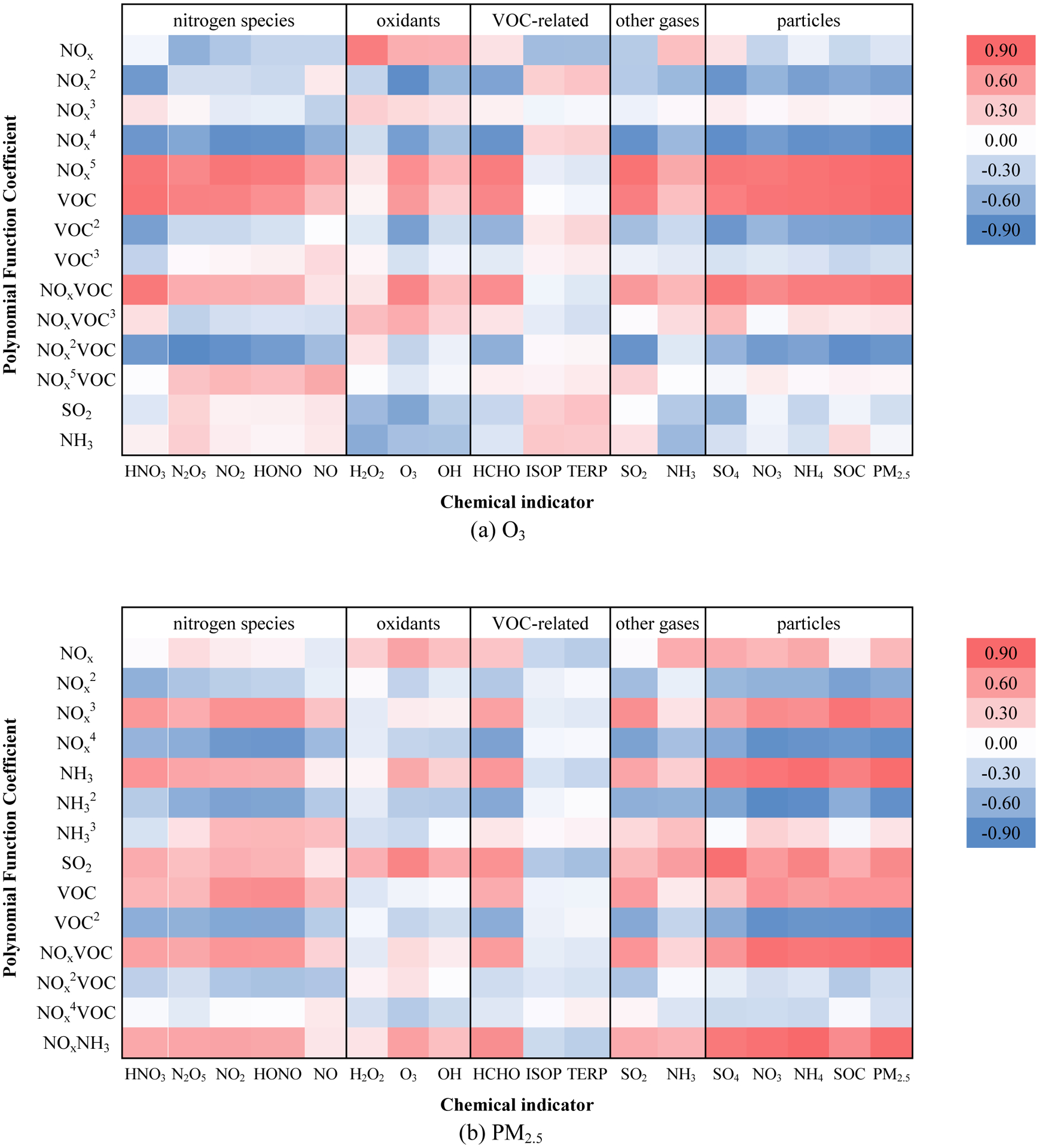
Correlation among the 14 coefficients (row) of terms in the response functions for O₃ (a) and PM_2.5 (b) and the incremental change in concentrations of the indicators (column) between the baseline and clean-condition simulations for the CN27 domain.

(3). Neural Network Training

The CNN was selected as the neural network in this study because of its advantages in analyzing image data^45–46, and the similarity of spatial distributions of ambient pollution concentrations to image data. Also, CNNs are relatively good at representing complex nonlinear behavior compared with other machine learning methods, and are therefore suitable for representing the O₃ and PM_2.5 response functions.

Dataset.

We collected pollutant concentrations from CTM modeling for 480 days (four domains × four months × 30 days per month) for 40 emission control scenarios plus the baseline- and clean-conditions simulations (42 simulations overall; see Table S1). We conducted numerical experiments to test DeepRSM performance on each of the four spatial domains. To evaluate the temporal transfer capabilities of the DeepRSM (-TT experiments), we used the first 25 days in each month as the training dataset and the last five days in each month as the test dataset. To evaluate the domain transfer capabilities of the DeepRSM (-DT experiments), we used all 360 days from the three domains that were not being tested as the training dataset and the last five days in all months (20 days in total) from the domain being evaluated as the test dataset. For -DT experiments with fine-tuning, we included in the training dataset an additional 5 or 20 days that were randomly selected from the first 25 days in each month from the domain being evaluated.

More training data could lead to an improved CNN model, while the computational cost of numerical air quality model is too heavy to create abundant training data. Data augmentation has shown its ability in improving the performance of CNN with low-level task (i.e., the output value at each location is only related to the input values spatially close to the location)^45–46 which is also the case for atmospheric concentration response to emissions we studied here. Therefore, we randomly cropped the indicator maps by size of 96 for data augmentation to improve the CNN performance.

DeepRSM training strategy.

Since the relative change in pollutant concentration is the metric often used by policymakers, we adopt an objective function that measures the relative loss between predicted and simulated concentrations:

$$\mathcal{L}\left(\widehat{y},y\right)=\frac{1}{\mathit{\text{NHWC}}}{\sum }_{n=1}^N{\sum }_{i,j,c}\frac{{\left||{\widehat{y}}_{i,j,c}^{\left(n\right)}-y_{i,j,c}^{\left(n\right)} |\right|}_1}{y_{i,j,c}^{\left(n\right)}},$$ (E2)

where $\widehat{y}$ and y denote the DeepRSM-predicted and CTM-simulated pollutant concentrations, respectively. The variable N denotes the number of samples, and H,W and C denote the height, width, and number of channels of y, with i ∈ [0,H], j ∈ [0,W],c ∈ [0,C]. All model hyper-parameters were chosen using holdout validation datasets. The objective function is optimized using Adam⁴⁷ with β₁ = 0.9, β₂ = 0.999 and a mini-batch size of 32. The learning rate starts from 0.0002 and linearly decay to zero at the end of training. To reduce the risk of over-fitting, we applied L₂ weight regularization on all trainable parameters during training and fine-tuning. For each simulated day, one group of indicators (i.e., the concatenated baseline and clean-condition indicators) corresponds to one group of coefficients in the polynomial response function. However, 40 concentration labels are available that correspond to the 40 emission control scenarios simulated with CMAQ. To achieve computationally efficiency with the deep CNN, we calculate the average of the objective function over all emission control scenarios in one day, and then backpropagate the gradients of the average loss to update our model and complete one epoch. The DeepRSM and DeepRSM+ models are trained for 5000 epochs in -TT and -DT experiments and are fine-tuned for another 1000 epochs in fine-tuning experiments.

Evaluation metric.

Validation of the model performance is critical⁴⁸. For consistency with the performance evaluation of the benchmark model^{30–31, 34}, the performance of the DeepRSM was evaluated using two statistical indices, namely the MeanNE and the 95^th MaxNE, which are also commonly used in evaluating the performance of atmospheric numerical modeling⁴⁹. They are calculated as follows:

$$\mathit{\text{MeanNE}}=\frac{1}{N}{\sum }_{i=1}^N\frac{\left|M_i-O_i\right|}{O_i}$$ (E3)

$$\mathit{\text{MaxNE}}=\text{max}\left(\frac{\left|M_i-O_i\right|}{O_i}\right)$$ (E4)

Where M_i and O_i are the DeepRSM-predicted and CMAQ-simulated value of the i^th data in the series, and ThN represents the number of records (i.e., number of datasets multiplied by the number of grid cells)

Results

(1). The principle of the DeepRSM

The basic principle of the DeepRSM is that the coefficients in the response functions for PM_2.5 and O₃ from the pf-RSM can be accurately estimated from indicator species rather than by fitting results of CTM simulations based on random samples of emission scenarios. This design eliminates the need for a large number of computationally expensive CTM simulations as in the previous pf-RSM approach. To deploy the DeepRSM, only two CTM simulations are required: one for baseline emission levels and one for “clean” emission levels, where all anthropogenic PM_2.5 and O₃ precursor emissions are fully controlled.

The key design elements of the DeepRSM are the selection of the O₃ and PM_2.5 response indicators (i.e., concentrations of relevant chemical species under baseline and clean conditions) and the architecture of the CNN. To ensure the efficiency of the DeepRSM, we selected 18 chemical indicators that are relatively important to O₃ and PM_2.5 formation from the 130+ chemical species that are simulated in the CMAQ model. The indicators are either products or reactants in chemical reactions involving O₃ or PM_2.5 and are represented in all major CTMs. The pf-RSM model predicts strong correlations between the coefficients of the 14 terms in the PM_2.5 and O₃ response functions and the changes in indicator concentrations between the baseline and clean emission simulations. These correlations are consistent with current knowledge in atmospheric chemistry. For example, the coefficient of the linear term for NO_x emissions in the O₃ response function exhibits the strongest positive correlation with H₂O₂ concentrations (r = 0.8) but negative correlation with concentrations of the nitrogen species (r = −0.3 ~ −0.6) (Figure 1a). These relationships reflect the behavior that NO_x emission control tends to reduce O₃ when H₂O₂ is high and NO_x is low (NO_x-limited regime⁵⁰) but increase O₃ when NO_x is high and H₂O₂ is low (VOC-limited regime).

The strong correlations between indicators and response function coefficients in Figure 1 imply that valuable information for predicting the response functions for PM_2.5 and O₃ is contained in the indicators. However, extracting this information is challenging because the coefficient of each term is positively or negatively correlated with multiple indicators. For example, the PM_2.5 components (SO₄, NO₃, NH₄, and SOC) are highly correlated with the majority of coefficients in both the O₃ and PM_2.5 response functions (Figure 1). Such collinearity among the chemical indicators motivates use of neural network technology, which has advantages over traditional statistical regression in resolving complex relationships.

Deep neural networks have led to a series of breakthroughs in a wide range of fields due to their powerful expressive ability to approximate complex nonlinear functions^51–52. A deep CNN with residual connection⁵³ is employed here for four reasons. First, deep neural networks can efficiently solve highly nonlinear regression problems and are therefore potentially suitable for resolving the collinearity among chemical indicators. Second, CNNs can effectively use spatial relationships among nearby chemical indicators that may contribute to local pollutant concentrations. Third, CNNs with the convolutional kernel applied over space can well represent the common atmospheric processes and reactions occurring across the domain. Finally, residual connection is indispensable for modern deep CNN models, and a deep network is needed to provide high accuracy in modeling the complex processes that influence atmospheric chemistry.

The architecture of the DeepRSM model is illustrated in Figure 2. We use spatial concentration fields of 18 chemical indicators under baseline and clean conditions to represent the predictive features of the system. We concatenate the indicator fields for both scenarios before feeding them into our DeepRSM model. The first convolutional layer of the DeepRSM model transforms the 36 input channels of indicator maps into 128 channels of feature maps. This layer is followed by eight residual blocks and one convolutional layer through which the number of channels is maintained at 128 to increase the expressiveness of the network. The last convolutional layer transforms the number of channels from 128 to 14, which represent the coefficients in the standard polynomial function based on prior knowledge from pf-RSM development. O₃ and PM_2.5 concentrations are calculated as the inner product of the coefficients in the last layer and the corresponding response function terms based on the specific emission control scenario. We use a LeakyReLU⁵⁴ as the nonlinear activation function because it preserves negative gradients and performs well in low-level regression tasks. Our results suggest that the DeepRSM (trained with the CN27 dataset as one example) can well reproduce the spatial and seasonal variations in the coefficients of the PM_2.5 and O₃ response functions, with results similar to those of the pf-RSM (Figure S2).

Figure 2.

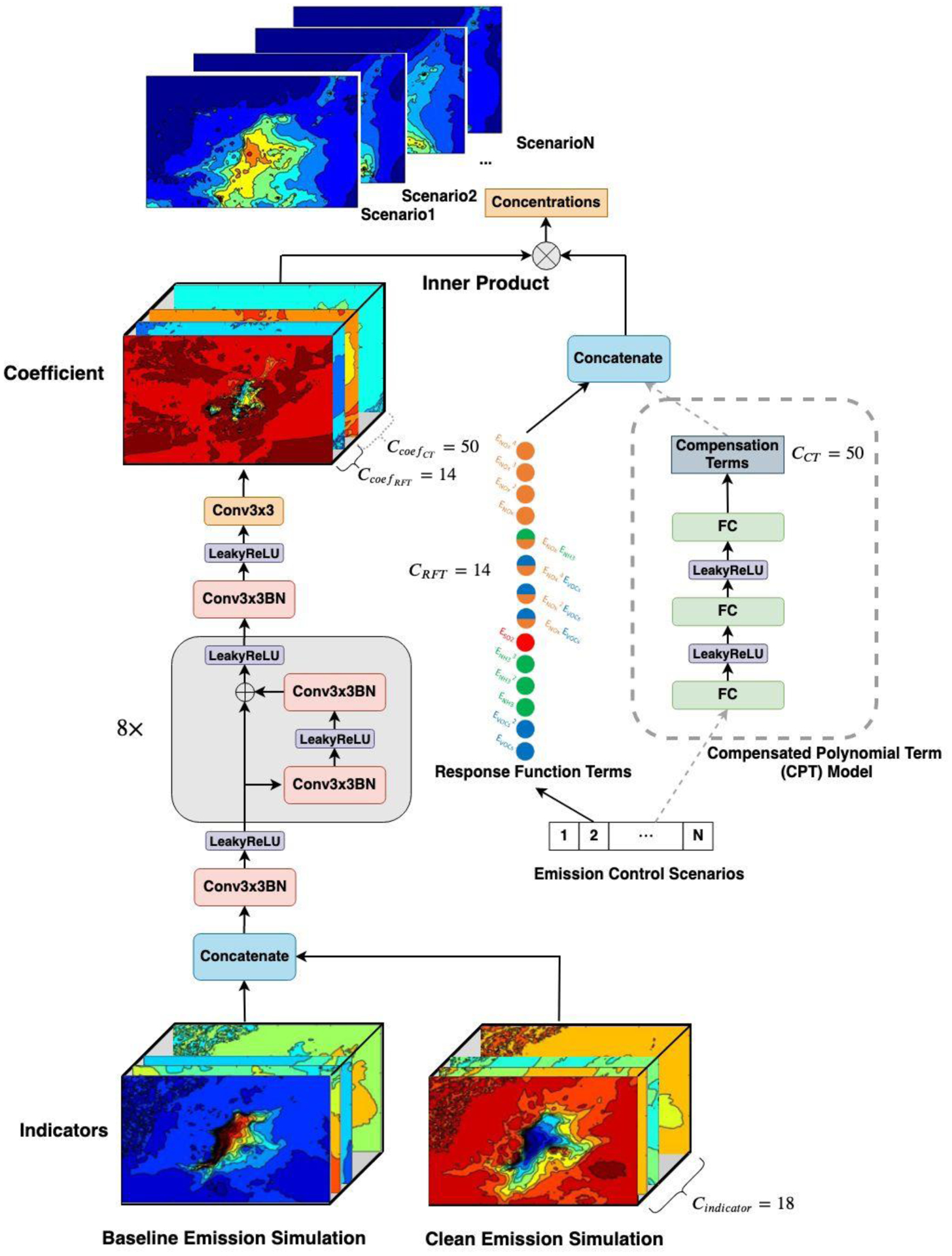
The CNN architecture of the DeepRSM with optimized polynomial structure for predicting the air quality response functions. Conv3×3BN: 3×3 convolution followed by batch normalization; LeakyReLU: leaky rectified linear unit activation function; FC: fully connected layer

Although the polynomial function in the pf-RSM was carefully designed in our previous study, uncertainty still exists in the functional form of air quality responses to precursor emission changes. Therefore, in addition to the DeepRSM based on the 14 terms of the pf-RSM response function, we developed the DeepRSM+ model that augments the polynomial function with 50 additional implicit terms to reduce the approximation error. The additional terms are automatically learned from the emission control factor vector using a compensated polynomial term model (CPT Model in Figure 2) and are not associated with an analytical functional form. The CPT Model uses three fully connected layers of width 128 to learn the nonlinear transformation from the emission control factor vector to the values of the additional 50 terms. The total number of terms in the augmented polynomial function is 64, which equals the number of coefficient maps and channels in the last convolutional layer of the DeepRSM+ model.

(2). The DeepRSM is effective across time periods and spatial domains

A key advantage of the DeepRSM is that the trained deep CNN is generally transferable across time periods (i.e., temporal transfer, TT) and spatial regions (i.e., domain transfer, DT). To examine the temporal transfer capabilities, we trained the DeepRSM model using data from the first 25 days in each of four months and applied it to predict concentration responses in the last five days of each month on the same domain (i.e., -TT experiment in Table S2 for PM_2.5 and O₃, Figure 3 for PM_2.5, and Figure S3 for O₃). Evaluation of the DeepRSM predictions against CTM results demonstrates good performance, with mean normalized error (meanNE) less than 5% and 95^th maximal NE (95^th MaxNE) less than 10%. The performance of the DeepRSM based on two CTM simulations in the –TT experiment is significantly better than that of the pf-RSM, which is based fitting with 20 CTM scenarios, and demonstrates the transferability of the DeepRSM to time periods not included in the training data.

Figure 3.

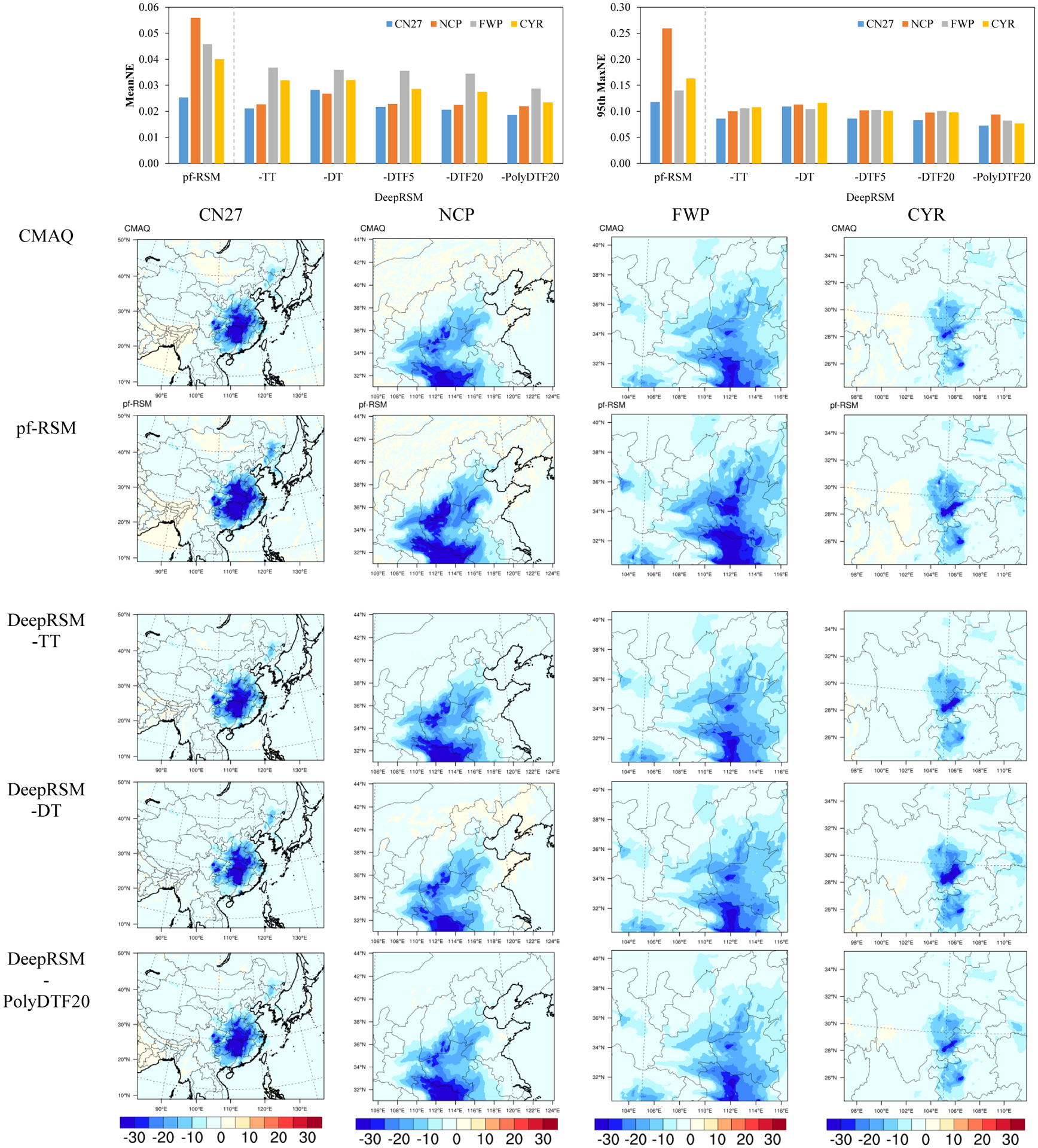
pf-RSM and DeepRSM performance in predicing PM_2.5 responses to emissions in different numerical experiments. -TT: training based on same spatial domain but different days than testing; -DT: training based on different spatial domains than testing; -DTF5, -DTF20, and -PolyDTF20: -DT experiments based on fine-tuning procedure. Results are based on Jan. 30 for control scenario #35 in Table S1 (emission change ratios of NO_x, SO₂, NH₃ and VOC are 92.0%, −84.2%, −98.0%, and −33.6%, respectively).

To examine the transferability of the DeepRSM to different spatial domains, the air quality response predicted in one domain was evaluated based on the DeepRSM model trained with data from the other three domains (i.e., -DT experiment in Table S2, Figure 3, and Figure S3). The -DT experiment is a greater test for the DeepRSM than the -TT experiment, because differences in air quality simulated for different regions and grid resolutions are much larger than for air quality simulated for different days for the same region and resolution. Despite the greater challenge, the DeepRSM performance is only slightly degraded in the -DT experiment compared to the -TT experiment. The DeepRSM exhibits similar or slightly better performance than pf-RSM in the -DT experiment in all domains except for CN27.

Predicting concentrations on the CN27 domain is relatively challenging using the DeepRSM based on training data from the three smaller domains that do not fully encompass the CN27 domain. However, the DeepRSM performance can be readily improved as necessary using a fine-tuning procedure in which the model is dynamically updated using very little additional training data. To demonstrate the performance improvement, we fine-tuned the DeepRSM models trained in the -DT experiments using an additional 5 or 20 days of data from the test domain and a relatively small number of epochs (i.e. -DTF5 and -DTF20 cases in Figure 3 and Table S2). The fine-tuning method is especially effective for reducing prediction bias for the CN27 domain.

DeepRSM predictions of the daily variation in air quality response was also evaluated for the -DT experiment in which no data for the test domain was used in training (Figure S4 for PM_2.5 and Figure S5 for O₃). The results indicate that the daily variations in air quality response predicted by the DeepRSM are similar to those simulated with CMAQ across all four months and domains. Moreover, the spatial distributions of air quality responses are also consistent with CMAQ simulations, as shown in Figure S6–S9 for PM_2.5 and Figure S10–S13 for O₃. The results of the -TT and -DT experiments demonstrate that the DeepRSM can efficiently and reliably capture variations in PM_2.5 and O₃ response across space and time.

To further examine the ability of the DeepRSM to predict the nonlinear response of air quality to emission changes, we generated PM_2.5 and O₃ isopleths for DeepRSM predictions in the -DT experiment for simultaneous changes in emissions of two precursors (Figure S14–S15): PM_2.5 response to NO_x and VOC emissions (Figure S14a), PM_2.5 response to SO₂ and NH₃ emissions (Figure S14b), O₃ response to NO_x and VOC emissions (Figure S15a), and O₃ response to SO₂ and NH₃ emissions (Figure S15b). We included 25 colored dots in the isopleths that correspond to CMAQ predictions that were not used in model training for comparison with the DeepRSM predictions. We also compared isopleths based on pf-RSM predictions with those based on the DeepRSM. These comparisons indicate that the DeepRSM generally captures the nonlinear response of O₃ and PM_2.5 to precursor emission changes across seasons. For instance, the DeepRSM predicts that O₃ chemistry is strongly VOC-limited in January and NO_x-limited in July and that the PM_2.5 response to NO_x and VOC emission changes has a similar, but weaker, dependence on oxidant abundance as O₃. The DeepRSM results also suggest that the effectiveness of NO_x and NH₃ emission controls for PM_2.5 reduction increases with increasing control (from 1 to 0 in Figure S14). The concentration responses predicted by the DeepRSM generally agree well with those simulated by CMAQ, and the DeepRSM isopleths are consistent with the pf-RSM isopleths, despite use of only two CTM simulations by the DeepRSM.

As mentioned above, the performance of the DeepRSM can be further improved by optimizing the polynomial structure using the DeepRSM+ model. The DeepRSM+ model adopts 50 additional terms that are learned from the emission control factor vector using the CPT model to reduce the approximation error of the polynomial function. In all experiments, the DeepRSM+ model with optimized polynomial structure based on fine-tuning with an additional 20 simulation days (i.e., -PolyF20 experiment in Table S2, Figure 3, and Figure S3) exhibits the best performance, with MeanNE < 5% and 95^th MaxNE < 10% across all months and domains. The value of the compensation terms is also evident in the isopleth comparison displayed in Figure 4. The compensation terms adjust the DeepRSM toward the CTM simulation results, particularly along edges of the isopleths where emission control factors are close to 0 (fully-controlled) or 2 (doubled). These conditions are relatively hard to resolve using the DeepRSM model based on the 14-term polynomial function alone.

Figure 4.

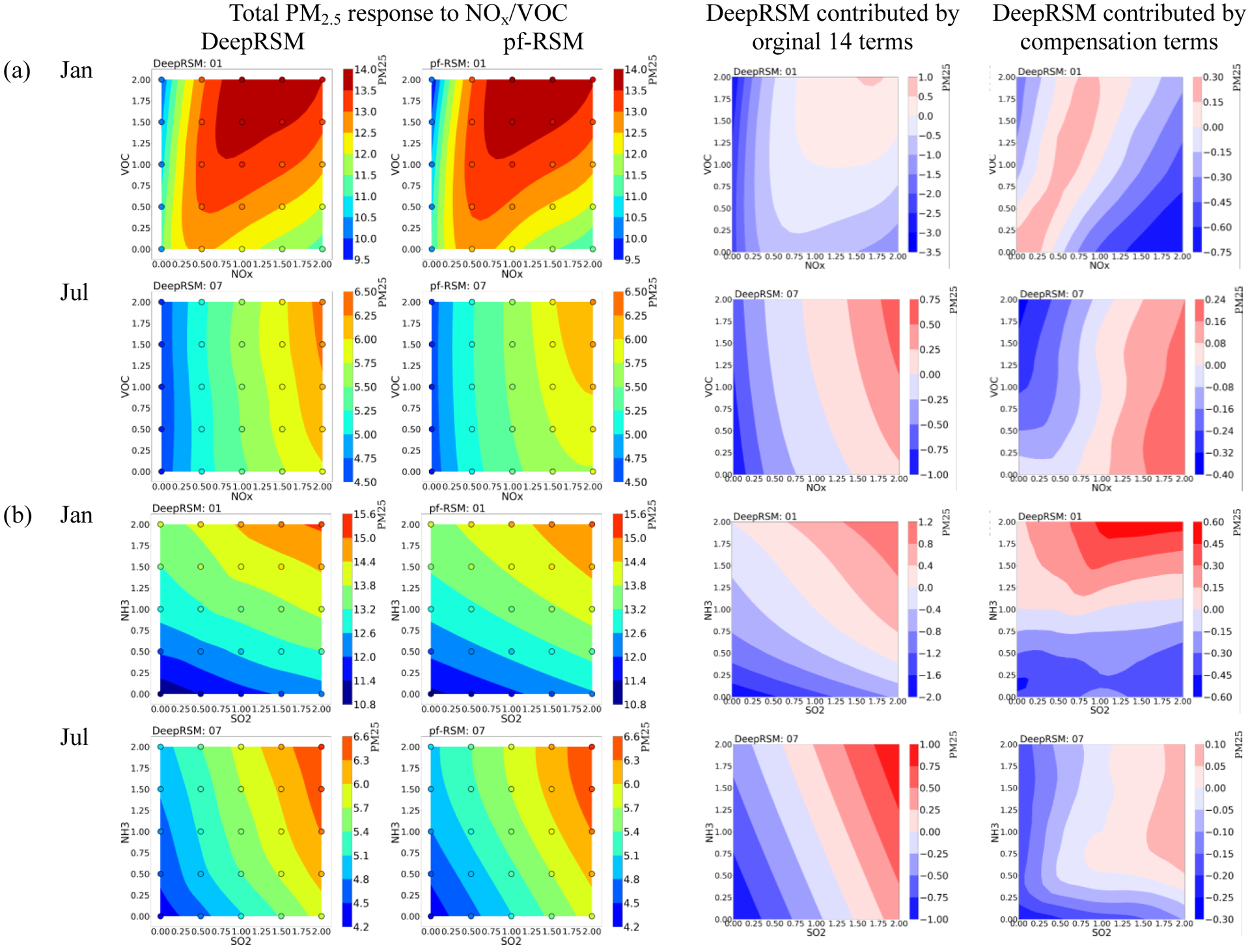
The isopleths of PM_2.5 response to NO_x/VOC (a) and SO₂/NH₃ (b) emission change (baseline = 1) predicted by pf-RSM and DeepRSM for the CN27 domain (the values are averages of all grid cells and days; the color dots represent the simulated value in CMAQ)

(3). Interpretability of the DeepRSM for prediction of air quality response

The success of the DeepRSM implies that information from only two states (i.e., baseline and fully-controlled scenarios) is needed to fit the curved concentration surface in four-dimensional space (i.e., emission changes of NO_x, SO₂, NH₃ and VOCs) using the trained deep CNN. Concentrations throughout the four-dimensional space cannot be predicted accurately using only PM_2.5 or O₃ concentrations from the two states; however, rich information for the prediction of PM_2.5 and O₃ is contained in the states in the form of the chemical indicators. Therefore, the DeepRSM predictions are not based only on PM_2.5 and O₃ concentrations at two points, but two pairs of vectors including the full suite of chemical indicators in addition to PM_2.5 and O₃ concentrations. The set of indicators contain sufficient information to represent the key atmospheric chemical and physical processes independent of spatial location or time period. The DeepRSM represents the atmospheric processes by linking the coefficients of the air quality response functions and the indicators in an efficient way, as follows.

If we consider a single grid cell in a CTM as a box model, the concentration change over time can be written as follows:

$$\frac{d\left[P\right]}{dt}=\sum _i{f}_i\left(k_i,\left[I_{1,\dots ,s}\right]\right]$$ (E5)

where [P] is the concentration of air pollutant (i.e., PM_2.5 or O₃); f_i is the numerical function of process i (e.g., transport, chemistry, deposition) that contributes to the pollutant concentration; k_i is related to geographic (e.g., land cover) and meteorological variables (e.g., temperature, solar radiation, wind) but independent of concentrations; and [I_s] is the concentration of reactant s in bi- or tri- molecular reaction. The ambient concentrations of the gaseous precursors for O₃ and PM_2.5 (i.e., [I_p], where p = NO_x, SO₂, NH₃, and VOCs) are approximately proportional to their emissions (E_p), as follows:

$$\left[I_p\right]\propto E_p$$ (E6)

Although the forms of the f_i terms differ significantly for different processes, they can all be approximated with polynomial functions. Using the precursor emissions as independent variables, E1 can be represented as a polynomial function of precursor emissions, as follows:

$$\frac{d\left[P\right]}{dt}=\sum _j{g}_j\left(k_j, \left[I_{1,\dots ,r}\right], E_p\right)$$ (E7)

where g_j is the j^th term in the polynomial function of precursor emissions.

The average concentration of P over an integration period can be estimated based on E3 according to the following:

$$\overline{\left[P\right]}=\sum _j{g}_j\left(\overline{k_j},\overline{\left[I_{1,\dots ,r}\right]},E_p\right)$$ (E8)

Equation E4 is of the same form as the polynomial function used in the pf-RSM. Therefore, the accuracy of the pf-RSM suggests that the coefficient of each term is roughly constant and unrelated to the variation of E_p, but still related to the constant k_i and concentration of reactant [I_s]. Thus, we can conclude that the coefficient of each term is only determined by the concentration of reactants and the geographic or meteorological factors. Since the coefficient of each term is constant in the response function and does not change with emissions, the concentration of reactants can be determined from a single baseline-emission simulation to develop the response functions. Considering the challenges in representing the geographic and meteorological factors, we additionally use the concentration of reactants under clean conditions (fully-controlled scenario) to further represent such influence. More importantly, the difference in concentrations from the two scenarios (baseline and fully-controlled) can be used to indicate the influence of the controllable fraction of the total emissions, since some emissions cannot be readily controlled (e.g., biogenic sources and regional emissions from outside the target area).

To promote interpretability of the machine-learning results, we examined the relative contribution of each indicator to the coefficients in the PM_2.5 response function (Figure 5). In general, the wide range of the contribution of each indicator to the coefficients demonstrates the advantage of machine learning for feature extraction from the raw 18 indicators. The coefficient for the linear NH₃ emission term (Term 2) is strongly determined by the indicators HNO₃, nitrate (NO₃), ammonium (NH₄), and PM_2.5. The coefficient for the linear SO₂ emission term (Term 5) is strongly determined by the indicators OH, sulfate (SO₄), and ammonium (NH₄). For high order NO_x emission terms (Terms 8, 12, 13, 14), the coefficients are most influenced by indicators associated with complex free radical oxidation reactions. These relationships are consistent with known mechanisms of atmospheric chemistry and indicate that the DeepRSM based on deep learning is scientifically reasonable in addition to performing with high accuracy and efficiency.

Figure 5.

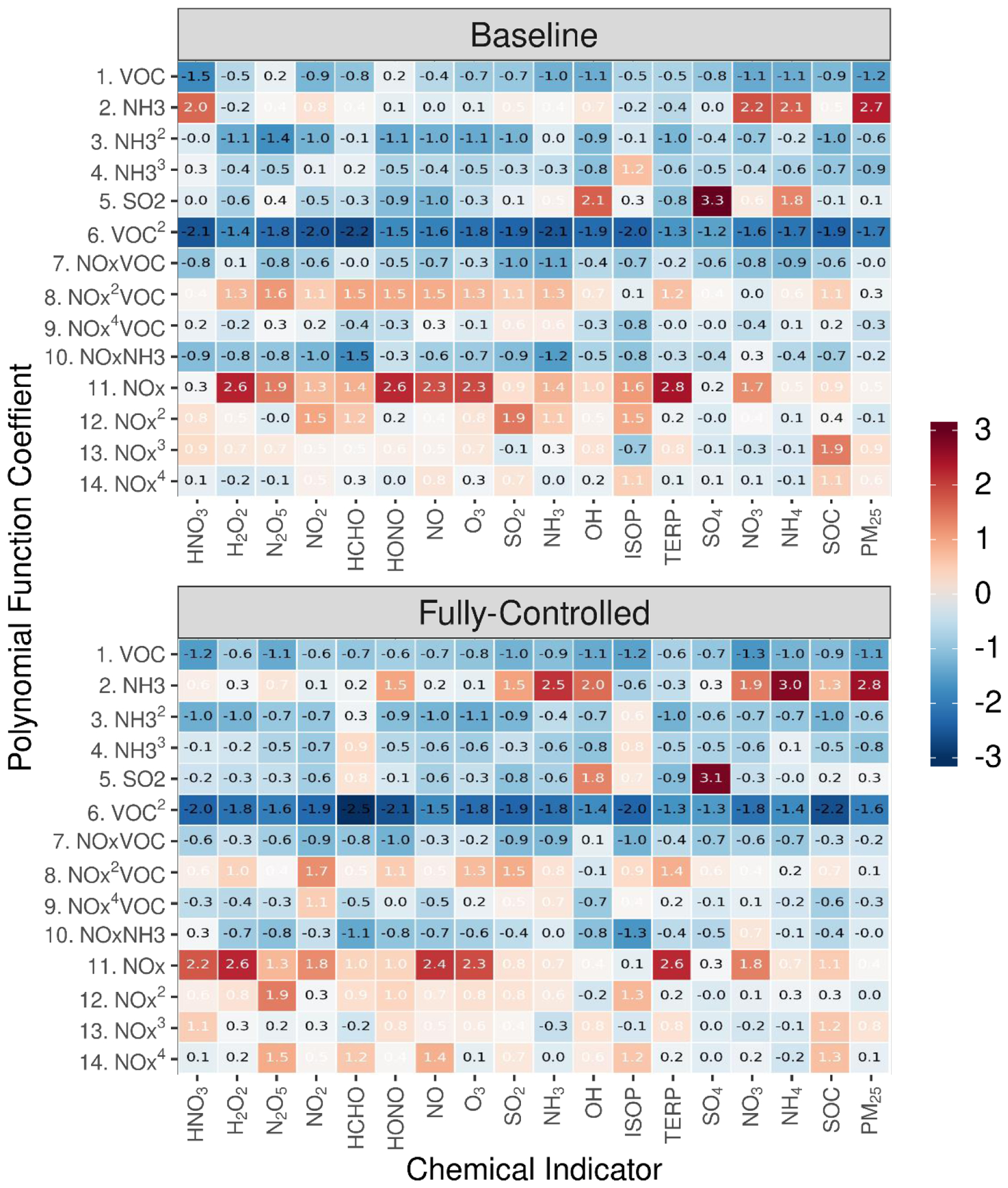
The relative contribution of each indicator to the coefficients of 14 terms in PM_2.5 response function (from the highest shown as Red, to the lowest shown as Blue)

Our study is the first to apply deep-learning technology in predicting the air quality response to emission changes by linking CNN and RSM technologies using a carefully selected set of chemical indicators and novel model design. The new DeepRSM developed in this study significantly improves the real-time prediction of air quality for the full range of policy-relevant control strategies, compared to previous methods such as the original RSM.

Since the DeepRSM links the coefficients of the PM_2.5 and O₃ response functions with chemical indicators independent of time and space, it can be applied for any study period or domain. The good performance of the CNN for days (-TT experiments) and spatial domains (-DT experiments) not represented in the training data supports this use. Compared to traditional regression methods (e.g., the pf-RSM benchmark case), the DeepRSM has higher efficiency and accuracy, and thus can be applied for real-time air quality response prediction in integrated assessment systems to inform long-term air quality management. It can also be applied for daily air quality forecasting to inform emergency actions to protect public health using a combination of short-term pollutant controls.

The scientific implications of our study are that the ambient concentrations of the chemical indicators are key factors for determining the nonlinear response of air quality to emission changes. This finding does not imply that other factors are unimportant, since factors such as meteorology and geographic characteristics are likely somehow already considered in the CNN through the change in indicator concentrations between the clean and baseline conditions. This study also reveals an important fact that, for systems that can be represented deterministically (e.g., atmospheric air pollution), we can interpret the full pathway using information from the initial and final states alone. However, training networks to adequately represent such systems is a major challenge, which requires full knowledge of the relevant factors (indicators) and ample training data.