Abstract
The Na+/Ca2+ exchanger of Drosophila melanogaster, CALX, is the main Ca2+-extrusion mechanism in olfactory sensory neurons and photoreceptor cells. Na+/Ca2+ exchangers have two Ca2+ sensor domains, CBD1 and CBD2. In contrast to the mammalian homologs, CALX is inhibited by Ca2+ binding to CALX-CBD1, whereas CALX-CBD2 does not bind Ca2+ at physiological concentrations. CALX-CBD1 consists of a β-sandwich and displays four Ca2+-binding sites at the tip of the domain. In this study, we used NMR spectroscopy and isothermal titration calorimetry (ITC) to investigate the cooperativity of Ca2+ binding to CALX-CBD1. We observed that this domain binds Ca2+ in the slow exchange regime at the NMR chemical shift timescale. Ca2+ binding restricts the dynamics in the Ca2+-binding region. Experiments of 15N chemical exchange saturation transfer and 15N R2 dispersion allowed the determination of Ca2+ dissociation rates (∼30 s−1). NMR titration curves of residues in the Ca2+-binding region were sigmoidal because of the contribution of chemical exchange to transverse magnetization relaxation rates, R2. Hence, a novel, to our knowledge, approach to analyze NMR titration curves was proposed. Ca2+-binding cooperativity was examined assuming two different stoichiometric binding models and using a Bayesian approach for data analysis. Fittings of NMR and ITC binding curves to the Hill model yielded nHill ∼2.9, near maximal cooperativity (nHill = 4). By assuming a stepwise model to interpret the ITC data, we found that the probability of binding from 2 up to 4 Ca2+ is approximately three orders of magnitude higher than that of binding a single Ca2+. Hence, four Ca2+ ions bind almost simultaneously to CALX-CBD1. Cooperative Ca2+ binding is key to enable this exchanger to efficiently respond to changes in the intracellular Ca2+ concentration in sensory neuronal cells.
Significance
CALX-CBD1 is the Ca2+-sensor domain of the Na+/Ca2+ exchanger of Drosophila melanogaster. It consists of a β-sandwich and contains four Ca2+ binding sites at the distal loops. In this study, we examined the cooperative binding of four Ca2+ ions to CALX-CBD1 using NMR spectroscopy and isothermal titration calorimetry experiments. NMR and isothermal titration calorimetry data were analyzed using the framework of the binding polynomial formalism and Bayesian statistics. A novel, to our knowledge, approach to analyze NMR titration data in the slow exchange regime was proposed. These results support the view that CALX-CBD1 binds four Ca2+ with high cooperativity. The significant ligand binding cooperativity exhibited by this domain is determinant for the efficient allosteric regulation of this exchanger by intracellular Ca2+.
Introduction
Ca2+ is a key intracellular regulator and an important second messenger (1). Hence, cells developed various mechanisms to control the intracellular Ca2+ concentration very precisely (2,3) Among those, the Na+/Ca2+ exchanger (NCX) is particularly relevant (4) After the Ca2+-ATPases, the NCX is one of the most important mechanisms for the extrusion of intracellular Ca2+, particularly in excitable cells (5). The NCX couples the translocation of one Ca2+ to the countertransport of three Na+ across the cell membrane (5,6). It consists of a large transmembrane domain, involved in ion translocation across the lipid bilayer, and a large intracellular loop that connects transmembrane helices 5 and 6 and that is responsible for the regulation of exchanger activity. Binding of Ca2+ to two calcium-binding domains (CBD1 and CBD2), located at the NCX cytoplasmic loop, activates the exchanger, enabling the in and out flux of Na+ and Ca2+. The Na+/Ca2+ exchanger of Drosophila melanogaster, so-called CALX, is unusual because Ca2+ binding to the CBDs inhibits this exchanger (7). This behavior is curious because the CALX and the NCX display ∼44 of amino acid sequence identity (8) and are believed to share the same architecture. The CALX Na+/Ca2+ exchanger is found in Drosophila photoreceptor cells and in olfatory sensory neurons, where it is the main Ca2+ extrusion mechanism (9,10). CALX plays an essential role in light-mediated signaling. Mutation of CALX in transgenic flies caused a reduction in light signal response amplification, whereas its overexpression generated significant retinal degeneration (9).
The CBDs are also called CALX-β motifs (8) or CALX-β domains (11). They appear adjacent to each other, separated by a linker of three amino acids that is highly conserved among exchangers of different organisms (12,13). The CALX-CBD2 domain does not bind Ca2+ at physiological concentrations (14). Hence, in the CALX exchanger, the regulatory Ca2+-binding sites are located only in the CBD1 domain (13). The CALX-CBD1 crystal structure shows four Ca2+ in the distal loops of the CBD1 β-sandwich, at the tip of the domain (Fig. 1 A; (15)). The four Ca2+-binding sites are located at ∼4 Å from each other. A series of negatively charged residues provides most of the anchoring points for Ca2+ coordination. Most of these residues are located in the EF loop and at the C-terminus (Fig. 1 A), near the linker with CBD2. CALX-CBD1 was also crystallized in the apo state and in an intermediate state (15). Although the apo state structure shows no electron density for the EF loop, the crystal structure of the intermediate state shows two Ca2+ at sites Ca1 and Ca2. The intermediate state structure is very similar to the fully loaded Ca2+-bound state, with a backbone root mean-square deviation of only 0.3 Å. These observations indicate that the binding of Ca2+ to sites Ca1 and Ca2 is sufficient to stabilize the structure of the Ca2+-binding region of CALX-CBD1 (15). Furthermore, they suggest that the Ca2+-binding mechanism is sequential, rather than the simultaneous binding of four Ca2+ to sites Ca1–Ca4 in all-or-none fashion (15).
Figure 1.
Binding of Ca2+ stabilizes CALX-CBD1. (A) Crystal structure of CALX-CBD1 in the holo state (Protein Data Bank, PDB: 3EAD (15)) is shown. Ca2+ ions are shown as green spheres. Residues whose 1H-15N crosspeaks appear only in the presence of Ca2+ are indicated and shown as gray spheres. The assigned residues in the unbound state are shown in blue. (B) Superposition of 1H-15N HSQC spectra of CALX-CBD1 recorded in the absence (blue) and presence (red) of 20 mM of CaCl2 is shown. (C) DSC experiment showing the thermal denaturation of CALX-CBD1 in the absence (blue), and presence of Ca2+ (red) is given. The protein melting temperatures, Tm, under these conditions are 55.3 and 69.6°C for the apo state and Ca2+-bound states, respectively. To see this figure in color, go online.
The Ca2+-binding cooperativity exihibited by the CBDs is critical to enable them to function as efficient allosteric switches of the Na+/Ca2+ exchangers. Therefore, in this work, we used NMR spectroscopy and isothermal titration calorimetry (ITC) experiments to investigate the Ca2+-binding properties of CALX-CBD1. Consistent with the crystallographic data, we observed that CALX-CBD1 displays substantial backbone flexibility near the Ca2+-binding sites. Experiments of 15N chemical exchange saturation transfer (CEST) and of 15N Carr-Purcell-Meiboom-Gill (CPMG) relaxation dispersion, recorded at the Ca2+/CALX-CBD1 stoichiometric molar ratio, allowed the determination of Ca2+ dissociation rates. Ca2+-binding cooperativity was examined by ITC and NMR titration experiments, assuming different stoichiometric binding models and using a Bayesian approach for data analysis. The NMR titration curves obtained for residues near the Ca2+-binding sites displayed an accentuated sigmoidal behavior, which could be accounted for by calculating the effective transverse magnetization relaxation rates, R2eff, at each titration point, using the exact solution of the Bloch-McConnell equation (16). In summary, this study sheds new, to our knowledge, light on the Ca2+-binding cooperativity of CALX-CBD1.
NMR titration theoretical framework
In an NMR titration experiment, in which the protein-ligand binding equilibrium follows the slow exchange regime, a titration curve may be built by computing the variable η, the intensity ratio of the protein NMR signal in the bound state at a given ligand concentration, I, and at saturating conditions, Imax:
| (1) |
Assuming a Lorentzian lineshape, the maximal intensity of a 1H-15N HSQC (Heteronuclear Single Quantum Coherence) crosspeak may be written as
| (2) |
where C is a constant that takes into account the physical dimensions of the equilibrium magnetization; and are the effective transverse relaxation rates for the 15N and 1H nuclei, respectively; pB is the population of protein molecules in the bound state; and R2INEPT is the relaxation rate during the INEPT magnetization transfer period of duration Δ. The latter is also affected by chemical exchange between the apo and bound states.
The relaxation of transverse magnetization during the INEPT period may be estimated at every titration point using the Bloch-McConnell matrix (Eq. S35) as follows:
| (3) |
where is a 180° rotation matrix, M0 = is the initial magnetization, and the final magnetization is given by Mf = . Without loss of generality, in the slow exchange regime, the initial magnetization may be written as M0 = M0([0 pA 0 pB]T), where M0 is a constant and pA is the population of the protein in the apo state.
Reff2,H and Reff2,N may be calculated using the exact solution for R2 in chemically exchanging systems derived by Leigh (16). For this analysis, we considered the lowest eigenvalue of the characteristic matrix of the Bloch-McConnell equation because in our case, the NMR signal of the bound state must be sharper than that of the apo state. Therefore, Reff2 was written as
| (4) |
where
| (5) |
ΔΩ is the chemical shift difference between the apo and bound states, koff is the complex dissociation rate constant, and kon is the pseudo-first-order association rate constant. and are the transverse relaxation rates of the apo and the bound states, respectively.
Under conditions of saturation, i.e., when all ligand binding sites are occupied, tends to , and tends to the average transverse relaxation rates of in-phase and antiphase coherences, R′2; hence, the exchange contribution to the effective transverse relaxation rates is negligible, and the crosspeak intensity is given by
| (6) |
Therefore, it is convenient to rewrite the variable η as
| (7) |
where . In this work, as an approximation, we assumed that R′2 is equal to . The population of protein molecules in the apo and in the bound states may be written in terms of the binding polynomial (Eq. S6):
| (8) |
One should note that the population pB, as defined here, contains the contribution of all protein bound states. By substituting Eq. 8 into Eq. 7, we may restate η as
| (9) |
An analogous binding curve could be derived by monitoring the intensity decrease of the protein NMR signals of the apo state.
Methods
CALX-CBD1 expression and purification
A DNA fragment corresponding to residues 434–555 from the Drosophila melanogaster CALX 1.1 was PCR amplified from the CALX1.1 cDNA and cloned in fusion with an N-terminal six-histidine tag in the vector pET-28a (Novagen, Gibbstown, NJ), using NdeI and XhoI restriction sites. Protein expression was carried out in Escherichia coli BL21-CodonPlus (DE3)-RIL (Agilent, Santa Clara, CA). Uniform labeling with 15N or with 15N and 13C was achieved by overexpression in M9 supplemented with 1.0 g/L of 15NH4Cl (Cambridge Isotopes Laboratories, Tewksbury, MA) and/or 4.0 g/L of 13C-labeled glucose (Cambridge Isotopes Laboratories). Bacterial cultures were grown at 37°C to an OD600 of 0.7, at which point the temperature was decreased to 18°C and protein overexpression was induced by the addition of 0.4 mM of isopropyl-β-D-thiogalactopyranoside (Thermo Fisher Scientific, Waltham, MA) overnight. Cells were harvested by centrifugation and the cell pellets stored at −20°C. Approximately 10 g of cells was suspended in 100 mL of lysis buffer (20 mM Tris (pH 7.0), 200 mM NaCl, 5 mM β-mercaptoetanol, 0.1 μg/mL of pepstatin and aprotinin, 1.0 mM phenylmethylsulfonyl fluoride, and 1 mg/mL lysozyme), and subsequently lysed by sonication using a VCX 500 (Sonics, Newton, CT) instrument. The cell lysate was clarified by centrifugation at 21,000 × g for 1 h, and the supernatant was applied into a 5 mL Ni2+ column (HisTrap; GE Healthcare, Chicago, IL), pre-equilibrated with buffer A (20 mM sodium phosphate (pH 7.4), 300 mM NaCl, 5 mM β-mercaptoethanol, 10 mM imidazole), washed with five column volumes of buffer A, and eluted with 0.5 M of imidazole. Fractions containing CALX-CBD1 were combined, concentrated to 2 mL using an Amicon concentrator with a 3 kDa cutoff (Millipore, Burlington, MA), and applied into a gel filtration Superdex 75 (16/600) column (GE Healthcare) pre-equilibrated with the gel filtration buffer (20 mM Tris (pH 8.0), 200 mM NaCl, 5 mM β-mercaptoethanol, 1% (V/V) glycerol). Finally, the desired fractions were combined and applied into a MonoQ 10/100 (GE Healthcare) column, pre-equilibrated with the gel filtration buffer, and eluted with a gradient of 1.0 M of NaCl. To prepare NMR samples, the eluted CALX-CBD1 was concentrated and buffer exchanged to 20 mM Tris-HCl (pH 7.4), containing 5 mM β-mercaptoethanol, 200 mM NaCl, 1% (V/V) of glycerol, and 10% of D2O. Protein concentration was determined by measuring the absorbance at 280 nm, assuming ε280 = 7575 M−1 cm−1. The molecular weight of CALX-CBD1 was confirmed as being 16.025 kDa using mass spectrometry using MALDI (Matrix Assisted Laser Desortion Ionization) in TOF/TOF (Time of Flight) mode recorded on a MALDi Ultraflextreme instrument (Bruker, Billerica, MA). Unless otherwise mentioned all chemicals were purchased from Merck KGaA, Darmstadt, Germany.
NMR spectroscopy
All NMR spectra were recorded on a Bruker AVANCE III spectrometer (Bruker) equipped with a TCI CryoProbe and operating at 800 MHz (1H frequency). CPMG-based 15N relaxation dispersion experiments were additionally recorded on a Bruker Avance III-HD spectrometer operating at 600 MHz (1H frequency) and equipped with a TCI cryoprobe. NMR experiments were carried out at 308 K unless otherwise stated. All NMR data were processed with NMRPipe (17) and analyzed using the CcpNmr Analysis software (18). Protein samples used for backbone resonance assignment consisted of ∼200 μM of 15N/13C double-labeled CALX-CBD1. The apo state sample contained 2 mM of EDTA, whereas the Ca2+-bound sample contained 20 mM of CaCl2. Backbone (1HN, 15N, 13Cα, 13CO) and side-chain (13Cβ) resonance assignments for CALX-CBD1 were obtained from the analysis of three-dimensional HNCA, HN(CO)CA, HNCO, HN(CA)CO, CBCA(CO)NH, and HNCACB experiments. The assigned chemical shifts for CALX-CBD1 in the Ca2+-bound state were deposited in the Biological Magnetic Resonance Data Bank under the accession code BMRB: 27787.
Longitudinal R1 and rotating-frame (R1ρ) relaxation rates and the [1H]-15N heteronuclear Nuclear Overhauser Effect (NOE) were measured using standard 15N relaxation methods recorded as pseudo-three-dimensional or interleaved experiments (19,20). Protein samples consisted of 380 μM of N-labeled CALX-CBD1 containing CaCl2 at a molar ratio of 16:1 (CaCl2/protein). The R1ρ experiment was recorded using spin-lock field strength γB1/2π = 1013 Hz. Rotating-frame R1ρ relaxation was sampled at 4, 8, 16, 24, 35, 44, 58, 66, 80, 92, 104, and 115 ms, whereas longitudinal R1 relaxation was sampled at 150, 300, 450, 600, 900, 1250, 1500, 1800, 2000, 2250, and 2500 ms. The heteronuclear NOE was recorded using a saturation time of 3.0 s. The recycle delay was set to 4.0 s for the R1 and R1ρ experiments, whereas a delay of 5.0 s was used for the heteronuclear NOE experiment. R1 and R1ρ relaxation rates were determined by fitting the crosspeak intensity decays to an exponential decay function consisting of two parameters, the intensity at time zero and a decay rate. The uncertainties of the peak heights were taken from the noise level in each spectrum, whereas the uncertainties of the fitted parameters were estimated using Monte Carlo (at least 1000 iterations). R1ρ relaxation rates were measured at two different 15N carrier frequencies, 123.942 and 110.942 ppm, satisfying the conditions presented by Massi et al. (20). The chosen R1ρ-values corresponded to the smallest Ω/(γB1) ratio, in which Ω is the resonance offset in hertz, indicating best alignment of the magnetization with the spin-lock field. R2-values were obtained by correcting R1ρ for off-resonance effects using the following relation: R2 = R1ρ/sin2θ − R1(cosθ/sinθ)2, where θ = arctan(γ B1/Ω).
A relaxation-compensated Bruker pulse sequence (hsqcrexetf3gpsitc3d) was used for all CPMG-based 15N relaxation dispersion experiments, using constant relaxation times of 40 or 50 ms. The experiments were recorded as a series of two-dimensional (2D) planes with CPMG field strengths of 50, 100, 150, 200, 250, 300, 350, 400, 500, 600, 700, 800, and 900 Hz, and a reference spectrum measured by omitting the CPMG period. The crosspeak intensities were converted into effective transverse relaxation rates doing R2eff = −1/Texln(I/I0), where I0 is the crosspeak intensity in the reference spectrum. Uncertainties of R2eff were calculated by error propagation, assuming the noise level as the uncertainty in the crosspeak heights in each spectrum. CPMG relaxation dispersion curves recorded at 600 and 800 MHz were simultaneously fitted to the Bloch-McConnell equation assuming a two-site chemical exchange model (Eq. S35) through the calculation of the following equation using a home-made python script:
| (10) |
where M0 is the initial transverse magnetization aligned with the y axis, n is the number of CPMG periods, and is given by
| (11) |
where is the Bloch-McConnell equation for the transverse magnetization and is a 180° rotation matrix. The python functions matrix_power from the numpy package and expm from the scipy package were used to calculate Mtot. CEST experiments were recorded using a Bruker implementation of the CEST experiment described by Vallurupalli and co-workers (21). A weak 15N radio frequency field of γB1/2π = 25 Hz and a CEST exchange period Tex of 400 ms were used. The power level for the saturation radio frequency field was calculated from the calibrated 15N hard pulse assuming linear amplifiers. The saturation field offset was varied from −1250 to 1250 Hz in intervals of 25 Hz, covering the entire 15N spectral width. A reference spectrum was recorded with Tex set to 0. CEST profiles were fitted to the Bloch-McConnell equation (Eq. S33), assuming a two-site exchange model, or to the Bloch equation, using a similar strategy as that used to compute the evolution of the magnetization during the CPMG period. The exchange rate kex, the population of the apo state pA, the offset difference between the apo and the bound states ΔΩ, and the 15N R1 and R2 rates for the apo and the bound states were treated as free parameters. Ca2+ dissociation rates were obtained by doing koff = kex × pA, where pA = 1 − pB, with A referring to the population of the apo state and B to the fully Ca2+-bound state.
The NMR titration was carried out using a sample of 180 μM of CALX-CBD1 in 10 mM Tris (pH 7.4), containing 200 mM NaCl, 1 mM phenylmethylsulfonyl fluoride as protease inhibitor, and 10% of D2O. This preparation was previously incubated with 10 mM EDTA to remove residual Ca2+. The EDTA was removed by a series of concentration and dilutions using an Amicon (Millipore) with a cutoff of 3 kDa at 4°C. A series of 1H-15N HSQC spectra were recorded at 308 K as matrices of 1024 × 128 complex points. The NMR data was processed without apodization to apply the theoretical model outlined in the previous section. The data set was zero filled up to 4096 × 2048 points before Fourier transformation. Aliquots from a 5 M CaCl2 stock solution, prepared in the same buffer, were added to the NMR sample up to final Ca2+ concentrations of 5, 15, 25, 50, 70, 90, 190, 340, 490, 740, 990, 1490, 1990, or 3990 μM. Only well-isolated 1H-15N HSQC crosspeaks belonging to residues 452–456, 458–460, 479, 481, 483, 486–491, 512, 514–516, 518–520, 523, 525, 549, 550–552, and 555 of CALX-CBD1 in the Ca2+-bound form were considered for the analysis. Crosspeak intensities were determined from interpolation of a 2D numerical function (2D spline) as detailed in Fig. S1. The factor η was calculated according to Eq. 1 for each crosspeak along the titration. Only intensities above the noise level of each spectrum were considered for the analysis. The baseline threshold was determined by calculating the absolute intensity at 1σ of the baseline distribution (68%). The intensity level at the plateau of the binding curve, Imax, was determined as the mean intensity value of the three greatest Ca2+ concentrations: 1490, 1990, and 3990 μM of CaCl2. The NMR titration curves were fitted to Eq. 9. The protein population in the apo state, pA, was calculated according to the Hill model. The dissociation constant (Kd) and the Hill coefficient (nHill) were treated as free parameters. The 1H and 15N chemical shift differences between the apo and the Ca2+-saturated states (ΔΩN and ΔΩH); the Ca2+ dissociation rates (koff); and the transverse relaxation rates of apo , and bound state , were considered as nuisance parameters. We used a Gaussian distribution as prior information for the dissociation rate, for the 15N transverse relaxation rates of the bound state, and for the dissociation constant. The distributions were centered at koff = 30 s−1, = 14 s−1, and Kd = 2.52 μM and displayed σ = 10 and 20% for the first two parameters and for the last parameter, respectively. This prior information was based on the results obtained from the CPMG relaxation dispersion experiment, the 15N transverse relaxation rates determined for CALX-CBD1 in the bound state, and ITC experiments. The protein NMR concentration used for the NMR titration experiment was set to 180 μM using a narrow Gaussian prior with a σ equal to 10% of this value.
Calorimetry
ITC experiments were carried out using a Malvern VP-ITC instrument (Malvern Panalytical, Malvern, UK) at 35°C. Samples of CALX-CBD1 of nominal concentrations 2, 5, 10, 15, 20, and 229 μM in 20 mM Tris-HCl (pH 7.4), 200 mM NaCl, 5 mM β-mercaptoethanol, and 1% (V/V) glycerol were treated with 10 mM of EDTA. The EDTA was removed by buffer exchange using an Amicon centrifugation device (Millipore), and the sample was transferred to the calorimeter cell. The injection syringe was filled with a solution of CaCl2 at 300, 500, or 7600 μM in the same buffer. The experiments consisted of a first injection of CaCl2 of 2 μL, followed by 28 injections of 10 μL of CaCl2. Peak integration was carried out using the instrument software, providing the heat energy released in each Ca2+ injection. The ITC binding curves were fitted to Eq. S28 assuming different stoichiometric binding models, as described in the Supporting Materials and Methods. The Bayesian approach used to fit the ITC data was based on Nguyen and co-workers (22). Fits to the Hill model considered the dissociation constant Kd, the Hill coefficient (nHill), and the molar binding enthalpy (ΔHbind) as free parameters, whereas fits to the stepwise model treated Kd,1, Kd,2, Kd,3, Kd,4, and ΔHbind as free parameters. As proposed by Nguyen and co-workers (22), we included a set of nuisance parameters involved in the theory, among which are the ligand concentration in the syringe [L]o, the protein concentration in the cell [P]tot, the heat offset Qo, and the Gaussian error of the ITC data σ for each ITC curve. The latter was considered the same for all data points. Therefore, in total, there were 16 nuisance parameters for each stoichiometric model. In the case of the stepwise model, the protein concentration in the calorimeter cell was taken from a Gaussian distribution centered at calibrated values. The calibration of the protein concentration values was done by a global fitting of the ITC binding curves to a model of n independent binding sites with the same affinity, in which n was constrained to 4 using a narrow Gaussian prior with . This calibration was important because of the inaccuracy in the determination of the active protein concentration, which was ∼10–15% far from the nominal value in all experiments except for that performed with the lowest protein concentration (2 μM), where it was ∼50% off (Fig. S2). The script implemented to globally fit ITC data using Bayesian statistics may be obtained upon request or in the GitHub (https://github.com/jodarie/CalBayS_v1).
Micro-differential scanning calorimetry (DSC) experiments were performed on a VP-DSC (MicroCal, Northampton, MA) instrument. The CALX-CBD1 concentration used in the DSC experiments was ∼100 μM with or without CaCl2 at a molar ratio of 10:1 (Ca2+/CBD1).
Results
CALX-CBD1 displays significant backbone flexibility in the apo state
The 1H-15N HSQC spectrum of the CALX-CBD1 domain recorded in the absence of Ca2+ displayed well-dispersed crosspeaks, which are indicative of a well-folded protein. However, ∼23 of the expected 1H-15N correlations were missing. All apo state residues that could be assigned are located at the bottom of the domain, opposite to the four Ca2+-binding sites (Fig. 1). In contrast, in the presence of 20 mM of CaCl2, all the expected 1H-15N crosspeaks were observed (Fig. 1; Fig. S3), and 111 out of 121 backbone resonances were successfully assigned through the analysis of triple-resonance NMR experiments. These observations suggest that the tip of the domain, near the Ca2+-binding sites, experiences flexibility at the NMR chemical shift timescale but becomes rigid upon Ca2+-binding. Consistent with this observation, the crystal structure of CALX-CBD1 in the apo state does not show electron density for residues 516–522 at the EF loop, indicating flexibility at the Ca2+-binding region (15). The EF loop contains six negatively charged residues. It is, therefore, not surprising that it exhibits flexibility in the apo state. Micro-DSC experiments showed that the binding of Ca2+ leads to an increase of CALX-CBD1 thermal stability by ∼15°C (Fig. 1). A similar increment in thermal stability upon Ca2+-binding was observed for classical C2 domains belonging to PKC isoenzymes (23). Measurements of 15N relaxation rates, R1 and R2, and the heteronuclear NOE, carried out in the presence of excess of Ca2+, confirmed that CALX-CBD1 behaves as a rigid protein in the Ca2+-bound state (Fig. S4). An analysis of the overall tumbling rate based on 15N R2/R1 ratios for all 1H-15N spin pairs, assuming isotropic tumbling, yielded τc = 9.5 ns under our NMR conditions. Larger 15N transverse relaxation rates were detected for residues 539–546, at β-strand G, near the β-bulge, far away from the Ca2+-binding sites (Fig. S4). These larger R2 rates could be due to a conformation exchange process on a slow (microsecond to millisecond) timescale or to transient oligomerization of the domain involving the β-bulge. Consistent with the latter hypothesis, we observed that the NMR sample tends to aggregate with time.
CALX-CBD1 Ca2+-binding affinity determined by NMR
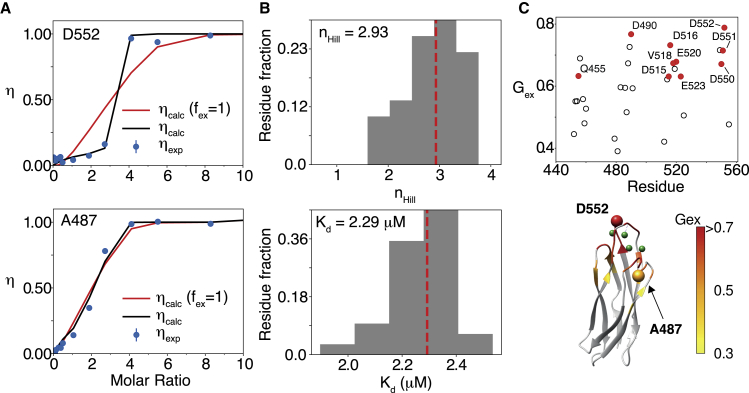
To investigate the mechanism of Ca2+-binding to CALX-CBD1, we carried out NMR titration experiments. 1H-15N HSQC spectra of CALX-CBD1 recorded in the absence and presence of increasing Ca2+ concentrations showed that Ca2+ binding occurs in slow exchange at the NMR chemical shift timescale. Furthermore, only crosspeaks for the apo and the Ca2+-saturated states were observed as reported before for the mammalian ortholog NCX-CBD1 (24). Considering that crosspeaks due to intermediate Ca2+-bound states were not detected, this scenario is consistent with the cooperative binding of four Ca2+ to CALX-CBD1. Ca2+-binding curves were calculated by monitoring the intensity increase of well-isolated NMR signals of the protein in the bound state according to Eq. 1. To avoid bias in the determination of the crosspeak intensities, a 2D cubic spline function was maximized for each crosspeak, as shown in Fig. S1. Interestingly, all residues located at the tip of the domain, near the Ca2+-binding sites, or involved in Ca2+ coordination such as D552 displayed sigmoidal Ca2+-binding curves. In contrast, crosspeaks of residues located further away from the Ca2+-binding sites, such as A487, displayed nearly hyperbolic binding curves (Fig. 2; Fig. S5). As shown in (Fig. 2 A), the accentuated sigmoidal Ca2+-binding curves did not agree with the Hill model, even when maximal cooperativity, nHill = 4, was assumed. Therefore, the accentuated sigmoidal profile of some of the Ca2+-binding curves is not due to ligand binding cooperativity. Because CALX-CBD1 experiences significant backbone flexibility in the apo state, the binding of Ca2+ must be accompanied by conformational changes at the Ca2+-binding sites. Therefore, we examined the possibility that conformational selection or induced-fit contributions to the Ca2+-binding equilibrium would lead to highly sigmoidal Ca2+-binding curves. These possibilities were discarded because simulations of the stepwise model, considering four binding events and an induced-fit or conformational selection step, did not lead to binding curves displaying sigmoidal behavior.
Figure 2.
NMR titration. (A) Typical examples of NMR titration curves are shown. Residue D552 displays an accentuated sigmoidal behavior (top left) in comparison with A487 (bottom left). Red lines are fits to the Hill model, and black lines are fits to Eq. 9 using the binding polynomial for the Hill model. Error bars were computed from the noise level in the spectra. (B) Histograms of the obtained values for the Hill coefficient (nHill) and affinity (Kd) for all analyzed residues are given. The red line indicates the median of the distribution. (C) Quantitative analysis of the magnitude of exchange contribution to the NMR titration curve is shown as a function of the residue number and mapped on the crystal structure of CALX-CBD1 (PDB: 3EAD). The Gex parameter is defined in Fig. S6. Residues indicated in red (left) are involved in Ca2+ coordination. To see this figure in color, go online.
The sigmoidal behavior of the Ca2+-binding curves can be explained by considering the existence of chemical exchange contributions to the NMR lineshapes. Simulations of binding curves computed with Eq. 9 and using the exact solution for , Eq. 4, in the case of a two-site chemical exchange model (16) showed that deviations from the usual behavior of the Hill model might be significant outside the extreme limits of the titration curve (Ca2+/CBD1 ≈ 0 or Ca2+/CBD1 ≈ 4), i.e., when (Fig. 3). In the absence of chemical exchange, i.e., when koff = 0, η is equivalent to pB, and the Ca2+-binding curve follows the Hill model (Fig. 3). In contrast, when the chemical exchange contributions to R2 increase, the binding curve may deviate from the expected behavior, as observed in our experimental data (Fig. 2). It is worth noting that the existence of undetectable intermediate Ca2+-bound states, displaying large R2 rates, could provide an alternative explanation for the observed sigmoidal Ca2+-binding curves. This hypothesis is consistent with the approach proposed here; however, the inclusion of additional binding constants and relaxation rates because of a more complex stoichiometric model would make the data analysis rather more complicated.
Figure 3.
Contributions of chemical exchange to NMR titration curves. Simulation of η (bottom) and fex (top) as a function of the ligand/protein molar ratio is shown. (A) koff = 40 s−1 was kept constant while ΔΩ was varied from 0 to 120 Hz. (B) ΔΩ = 80 Hz was left constant while koff was varied from 0 to 100 s−1. (C) koff = 40 s−1 was kept constant and R2,A = R2,B for both 15N and 1H nuclei while ΔΩ was varied from 0 to 120 Hz. η and fex were calculated according to Eq. 9 assuming the Hill model (Eq. S25) and the following relaxation rates: = 150, = 50, = 42, and = 14 s−1 for the 1H and 15N spins. The relaxation rate during the INEPT transfer periods was calculated numerically assuming Δ = 5.2 ms. The total protein concentration was 180 μM, dissociation constant Kd = 4 μm, nHill = 4, and ΔΩH = 0 Hz. To see this figure in color, go online.
Analysis of the probability distribution functions of the free parameters indicated that Kd and nHill are well defined for most residues. The representative values obtained from the median of the distributions of all analyzed residues are shown in Fig. 2 B and indicate that nHill = 2.93 and Kd = 2.29 μM. The determined Hill coefficient (nHill = 2.93) indicates that Ca2+ binds cooperatively to CALX-CBD1. Importantly, this analysis did not include prior information for the following parameters: , ΔΩN, and ΔΩH. The extent of deviation from the profile expected for each binding curve in the absence of exchange was estimated through an empirical parameter Gex. The latter was defined as the ratio of the area of the experimental binding curve relative/the area of a rectangle from molar ratios 0 to 4 (Fig. S6). This analysis does not depend on the convergence of the fitted parameters, but rather depends on the shape of the binding curve. Gex may be qualitatively associated to the degree of chemical exchange contribution to the transverse relaxation rates at a specific HN site. As shown in Fig. 2 C, all residues involved in Ca2+ coordination in the crystal structure displayed the largest deviations and hence the largest Gex-values.
Determination of Ca2+ dissociation rates (koff) by 15N relaxation experiments
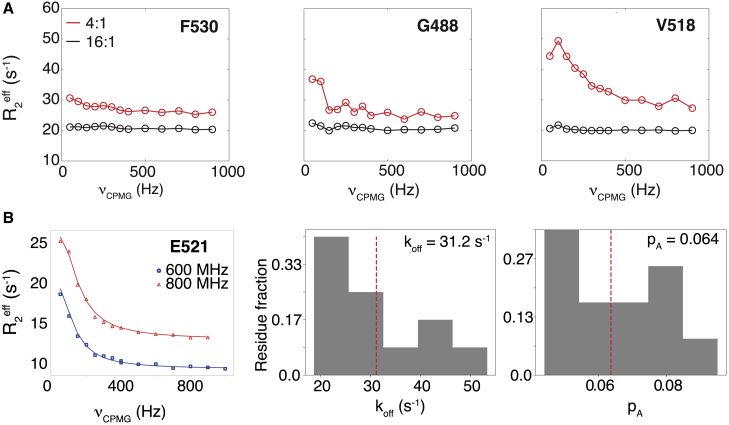
CEST experiments are informative about dynamic processes that occur in the slow exchange regime, at the millisecond timescale (21). Therefore, we investigated whether 15N CEST experiments could reveal information on the kinetics of Ca2+ binding to CALX-CBD1. The observed CEST effects were interpreted assuming a two-site exchange model, corresponding to CALX-CBD1 in equilibrium between the apo and the fully Ca2+-saturated states. To take advantage of all backbone resonance assignments available for CALX-CBD1 in the Ca2+-bound state, we recorded 15N-CEST experiments on samples prepared in the presence of CaCl2 at the stoichiometric 4:1 molar ratio (Ca2+/CALX-CBD1). Under this condition, crosspeaks due to the apo state are not detected. As shown in Fig. 4, three different CEST profiles were observed. Residues located at the bottom of the domain, i.e., far away from the Ca2+-binding sites, displayed a single and narrow CEST dip, which did not change upon the addition of an excess of Ca2+ (Fig. 4). In contrast, residues at the tip of the domain or involved in Ca2+ coordination displayed broadened CEST dips, which became significantly narrower upon the addition of an excess of Ca2+. A total of four residues located at or near the Ca2+-binding sites, N456, V518, F519, and L549, displayed a single CEST dip and a shoulder, whereas only G550, which coordinates Ca2+ at Ca3, displayed two well-separated CEST dips. Residues that displayed the greatest broadening effects are the ones closer to the Ca2+-binding sites and are expected to experience the largest chemical shift changes upon Ca2+-binding (Fig. 4). The absence of two well-separated CEST dips precluded a quantitative analysis of the 15N-CEST profiles for most CALX-CBD1 residues, with the exception of N456, V518, F519, and G550. Their 15N-CEST profiles were fitted to the Bloch-McConnell equation assuming a two-site exchange model. It was found that the population of the apo state, pA, was in the range of 5–8%, whereas kex was in the range of 310–521 s−1 (Fig. S7).
Figure 4.
Representative 15N CEST profiles. Peaks that show no evidence of chemical exchange (Narrow) at the molar ratio of 4:1 (Ca2+/CALX-CBD1) and that show nearly two CEST dips (Broad) or eventually two dips (Split) are color coded on the crystal structure of CALX-CBD1 (PDB: 3EAD (15)). The color coding was based on the ratios of 15N R2/R1 obtained at 4:1 molar ratio (Ca2+/CBD1) relative to 16:1. The relaxation rates were obtained by fitting the CEST profiles to the Bloch equation. Residues 530, 488, and 518 are shown as spheres. To see this figure in color, go online.
To obtain further kinetic information on the binding of Ca2+ to CALX-CBD1, we recorded CPMG-based 15N R2 dispersion experiments on CALX-CBD1 samples prepared in the presence of CaCl2 at the stoichiometric 4:1 molar ratio (Fig. 5). As observed in the CEST experiment, residues located near the Ca2+-binding sites displayed more dispersion than the ones located further away. The dispersion was significantly reduced or absent in the presence of an excess of Ca2+, indicating that the exchange phenomenon was due to the Ca2+-binding equilibrium (Fig. 5). Dispersion curves obtained at two spectrometer frequencies (600 and 800 MHz) were fitted simultaneously to a two-site exchange model, yielding the absolute chemical shift difference between the apo and the Ca2+-bound states, the exchange rate, and the population of the Ca2+-bound state. Prior information on kex obtained from the quantitative analysis of the CEST experiment was used to fit the CPMG dispersion curves. Hence, sampled kex-values were taken from a Gaussian distribution centered at 454 s−1 with 1σ = 104.5 s−1. The dispersion curves of a total of 12 residues could be analyzed, yielding a representative Ca2+ dissociation rate (koff) of ∼31.2 s−1 and an apo state population of ∼6% (Fig. 5). As much as 42.5% of all analyzed residues displayed koff in the range of 20–25 s−1, near the Ca2+ dissociation rate of 18.5 s−1 measured by stopped flow using a fluorescent Ca2+ chelator (13).
Figure 5.
15N relaxation dispersion experiments. (A) Representative 15N CPMG relaxation dispersion curves obtained at 4:1 (red) and 16:1 (black) Ca2+/CALX-CBD1 molar ratios are shown. The residue number is indicated in the figure, and the location on the structure is shown in Fig. 4. A constant relaxation time of 50 ms was used for these experiments. (B) Fitting of 15N CPMG relaxation dispersion curves obtained for E521, obtained at 800 and 600 MHz (1H frequency) using a constant relaxation time of 40 ms, to a two-site exchange model (left) are shown. Histograms of the Ca2+ dissociation rates and populations of the apo state determined by fitting the profiles obtained for residues 452, 453, 456, 488, 490, 491, 515, 516, 518, 521, 523, 549, and 552 are given. The red line indicates the median of the distribution, and the representative values are indicated in the figure. To see this figure in color, go online.
Thermodynamics of Ca2+-binding
The thermodynamics of Ca2+ binding to CALX-CBD1 was investigated by ITC. To have a better statistics for the fitted parameters, four ITC experiments were carried out using different protein concentrations in the calorimeter cell. Global fitting of all ITC binding curves to a stoichiometric model assuming n independent binding sites was carried out as indicated in the Methods, yielding a dissociation constant, Kd = 0.214 ± 0.005 μM, in agreement with previous ITC data reported in the literature (Fig. S2; (14)). However, because CALX-CBD1 binds Ca2+ cooperatively, we tested other stoichiometric models. Hence, we fitted the ITC binding curves to the Hill model (Fig. S8), obtaining a dissociation constant of Kd = 2.52 μM and a Hill coefficient nHill = 2.99 (Table 1), in agreement with the nHill determined independently by NMR titrations (Fig. 2). Because a characteristic of the Hill model is the strong correlation between the Hill coefficient (nHill) and the dissociation constant (Kd) (Fig. S8), we tested whether a stepwise model of four binding events was able to capture the Ca2+-binding cooperativity of CALX-CBD1. We assumed a mean molar binding enthalpy (ΔHbind; see Eq. S31) instead of individual binding enthalpies for each Ca2+-binding site. This assumption is justified because the four Ca2+-binding sites are located at ∼4 Å from each other in the CALX-CBD1 crystallographic structure (15), and each Ca2+ ion is coordinated by two or more electron donor groups from different amino acids. Here, the simultaneous fitting of the four ITC binding curves was key to alleviate the degeneracy among the stepwise dissociation constants (Fig. 6). In addition, the application of Bayesian statistics to sample the space of the parameters was critical to make reliable estimations for Kd,1–Kd,4 and to examine the degree of correlation between each of them (Fig. 6). The probability distribution functions indicated that Kd,3 and Kd,4 are well defined and equal to 0.34 and 0.85 μM, respectively (Fig. 6; Table 1). Kd,1 is well defined with a median value of 148 μM, but its distribution is rather wide. Finally, the degeneracy of Kd,2 was only partially resolved. Nevertheless, the trend for Kd,2 is in the nanomolar range (Fig. 6; Table 1). To improve the resolution of Kd,2, two additional ITC experiments were performed at protein concentrations near our instrument detection limit, 2 μM, and closer to Kd,1 at 229 μM. However, the simultaneous fitting of the six ITC curves to the stepwise model did not alleviate the degeneracy on Kd,2 (Fig. S9). The greater degeneracy observed for Kd,2 relative to the other dissociation constants could be related to the fact that the experiments were carried out using protein concentrations well above its value. To test whether the dissociation constants Kd,1–Kd,4 reported in Table 1 are consistent with the saturation being reached near the 4:1 molar ratio as observed in the ITC and NMR titrations (Figs. 2, 6, and S5), we simulated the expected behavior of the binding isotherm for the stepwise model. As shown in Fig. S10, the average number of ligands bound, ν, as defined by Eq. S20, approaches saturation at molar ratios near 4–5, in agreement with our experimental observations. The statistical significance of fitting the four ITC binding curves to the more complex model (stepwise) relative to the simpler models (independent and Hill) was evaluated using the Akaike information criterion (AIC) (25). The AIC is a function of the likelihood penalized by the number of parameters. Fig. S11 shows that the AIC is lowest for the stepwise model, indicating that this model is preferable relative to the other ones.
Table 1.
Thermodynamic Binding Constants Obtained Using ITC
| Kd | nHill | Kd,1 (β1) | Kd,2 (β2) | Kd,3 (β3) | Kd,4 (β4) | ρ2 | ρ3 | ρ4 | ΔHbind | |
|---|---|---|---|---|---|---|---|---|---|---|
| Hill | 2.52 | 2.99 | N/A | N/A | N/A | N/A | N/A | N/A | N/A | −5.39 |
| Stepwise | N/A | N/A | 148 (0.0068) | 0.00023 (29.4) | 0.34 (86.4) | 0.85 (101.7) | 1310 | 1.26 | 1.14 | −4.99 |
Kd and Kd,i are in units of micromolars and ΔHbind in kcal/mol. βi is in units of 106i M−i. ρ is a dimensionless factor. N/A, not applicable.
Figure 6.
Ca2+-binding cooperativity investigated by ITC. (A) Calorimetric titrations of CALX-CBD1 with CaCl2 using different total protein concentrations in the calorimeter cell ([P]tot,0). The thermograms were fitted to the stepwise model assuming four binding events. (B) One-dimensional marginalized parameter distributions and 2D marginalized distributions of pairs of thermodynamic parameters are shown. The 1σ confidence contour region is shown in cyan, and the 2σ confidence contour region is shown in green plus cyan. Kd,i are in units of micromolars and ΔHbind in kcal/mol. The plots are in logarithmic scale. To see this figure in color, go online.
To evaluate the Ca2+-binding cooperativity of CALX-CBD1 according to the stepwise model, we calculated the ρ factor as proposed by Wyman and Phillipson (26). The latter is defined as the ratio between the overall association constants βi (see Eq. S19) normalized by the number of combinations in each binding event (Wn,i) (24,26):
| (12) |
where i = 2, …, n and n is the total number of binding sites. When ρi > 1, the binding sites display positive cooperativity. In contrast, when ρi ⩽ 1, the binding sites are anticooperative or independent (26). As shown in Table 1, binding of two, three, or four Ca2+ ions to CALX-CBD1 is favored by approximately three orders of magnitude in comparison with the binding of a single Ca2+ ion, indicating a large positive cooperativity among the four Ca2+-binding sites.
Discussion
In this study, we investigated the Ca2+-binding properties of CALX-CBD1 using NMR spectroscopy and ITC experiments, in combination with Bayesian statistics for data analysis. The NMR data indicated that CALX-CBD1 binds four Ca2+ in an all-or-none fashion, as observed previously for the NCX-CBD1 (27,28). Furthermore, indirect measurements of Ca2+ dissociation rates, obtained from the analysis of 15N R2 dispersion and 15N CEST experiments, are in agreement with the Ca2+ off rates determined directly by stopped-flow fluorescence measurements (13). The NMR spectra showed no evidence of the existence of an intermediate state of CALX-CBD1 with Ca2+ at sites Ca1 and Ca2, as observed by crystallography (15). A possible explanation for this discrepancy is that in highly cooperative systems, the intermediate states are less populated than the apo and the fully bound states.
It is noteworthy that the nHill coefficients determined by the analysis of NMR and ITC binding curves were in very good agreement with each other (Fig. 2; Table 1). The determined nHill indicates that the binding of four Ca2+ to CALX-CBD1 is a highly cooperative process (Fig. 2). Curiously, the nHill coefficient obtained for CALX-CBD1 in this study (nHill ∼2.9) is greater than that determined for the NCX-CBD1 from the analysis of equilibrium 45Ca2+ binding assays (nHill = 2.0) (29), suggesting that the CALX-CBD1 binds Ca2+ slightly more cooperatively than its mammalian ortholog. Because the two CBDs share the same Ca2+-binding mode, the reason for this difference is not clear.
Even though the Hill model captures the binding cooperativity of the system in terms of the Hill coefficient, it represents an extremely limiting situation in which all ligands bind simultaneously. Moreover, the Hill model has the inconvenience that the nHill is strongly correlated with the Kd, as indicated by our analysis (Fig. S8). Therefore, to have additional insights on the cooperative binding of Ca2+ to CALX-CBD1, we analyzed the ITC binding curves assuming a stepwise model of four binding events. Ca2+-binding cooperativity of CALX-CBD1 was evaluated in terms of the ρ factor. According to Wyman and Phillipson (26), the ρi factor may be interpreted as the ratio of the arithmetic mean probability of binding i and i + 1 ligands, without distinguishing the binding sites. Then, cooperativity is understood as the excess probability of binding i + 1 ligands over the probability of binding i ligands. This analysis showed that the probability of binding of two, three, or four Ca2+ ions to CALX-CBD1 is approximately three orders of magnitude greater than the probability of binding of a single Ca2+ (ρ2 = 1310, whereas ρ3,4 = 1.1–1.3 (Table 1).
Interestingly, the NMR titration curves of residues located at short distances from the Ca2+-binding sites or involved in Ca2+ coordination displayed significant deviations from the expected behavior of a typical binding curve following the Hill model (Fig. 2 C). Such deviations were explained by considering chemical exchange contributions to the crosspeak intensities. This interpretation is consistent with the observation that residues whose binding curves are more sigmoidal map to the same region of the structure as the ones displaying the largest 15N chemical shift differences (ΔΩN) between the Ca2+-bound and apo states, as determined from the analysis of 15N R2 dispersion curves (Fig. 2 C; Fig. S12). It is curious, however, that the NMR titration curves obtained for the NCX-CBD1 domain in the NCX-CBD12 construct were all nearly hyperbolic (28). The explanation for this discrepancy is not clear, but the deviations from the expected behavior display a complex dependence on the exchange rates and on the differences of chemical shifts and relaxation rates between the apo and the bound states, as shown in Fig. 3.
Conclusion
Na+/Ca2+ exchangers play critical roles for the maintenance of intracellular Ca2+ homeostasis. The basal intracellular Ca2+ concentration in Drosophila photoreceptor cells is approximately 0.16 μM, but it may be elevated to 200 μM very rapidly after light stimulation (30). In this context, the exchanger activity must be tightly regulated to meet the cell’s needs. Activation of the NCX by intracellular Ca2+ is a highly cooperative process (31). The efficient Ca2+ regulation of the exchangers must be, at least in part, explained by the cooperative binding of Ca2+ to their CBD domains. Therefore, in this study, we revisited the cooperativity of Ca2+ binding to CALX-CBD1, the only domain that has binding sites for regulatory Ca2+ in the Drosophila Na+/Ca2+ exchanger. We found that four Ca2+ ions bind in a highly cooperative fashion to CALX-CBD1. According to the stepwise model, the dissociation constant of the first Ca2+ is on the order of 150 μM, whereas the dissociation constants of the second, third, and fourth Ca2+ are in the nanomolar and micromolar ranges, respectively. This observation indicates that the probability of binding of a single Ca2+ is significantly lower than that of binding from two up to four Ca2+ ions. Ca2+ dissociation must also be highly cooperative, as indicated by NMR, with off rates on the order of 30 s−1. These findings provide new, to our knowledge, insights on the Ca2+-binding cooperativity of CALX-CBD1, which is key to enable this exchanger to efficiently respond to changes in the intracellular Ca2+ concentration in sensory neuronal cells.
Author Contributions
All authors contributed to the study conception and design. P.A.M.V. and L.A.A. prepared protein samples. L.A.A. assigned backbone resonances. P.A.M.V., M.V.C.C., and M.F.S.D. did ITC experiments. Preliminary analysis codes for ITC and NMR titration curves were performed by M.F.S.D.; the final codes for data analysis on NMR and ITC experiments were designed and developed by J.D.R. and R.K.S.; M.V.C.C. and L.A.A. acquired and processed NMR relaxation and titration data. The first draft of the manuscript was written by R.K.S., M.V.C.C., P.A.M.V., and J.D.R.; all authors commented on previous versions of the manuscript. All authors read and approved the final manuscript.
Acknowledgments
This work was supported by grants from the São Paulo Research Foundation (FAPESP, 2016/07490-1) and Conselho Nacional de Desenvolvimento Científico e Tecnológico (420490/2016-7). M.V.C.C. (2016/17375-5), J.D.R. (2018/21450-8), and P.M.V. (2017/05614-8) received FAPESP postdoctorate and PhD fellowships. L.A.A. and M.F.S.D. received PhD fellowships from Coordenação de Aperfeiçoamento de Pessoal de Nível Superior (#33002010017P0 and #88882.160170/2014-01). R.K.S. receives a Conselho Nacional de Desenvolvimento Científico e Tecnológico research fellowship (#311807/2017-8). The CALX1.1 cDNA was obtained from the Drosophila Genomics Resource Center, supported by National Institutes of Health grant 2P40OD010949. The authors acknowledge Bruker BioSpin for providing the pulse sequence to record 15N CEST experiments, the Multiuser Center for Biomolecular Innovation of the São Paulo State University (Programa Equipamentos Multiusuários - EMU-FAPESP 2009/53989-4) for providing access to the 600 MHz NMR instrument, the Analytical Instrumentation Center of the University of São Paulo for providing access to the 800 MHz NMR instrument, and FAPESP for providing financial resources for the acquisition of the ITC instrument (2017/06394-1).
Editor: Michael Sattler.
Footnotes
Marcus V.C. Cardoso and Jose D. Rivera contributed equally to this work.
Marcus V.C. Cardoso’s present address is Department of Chemistry, Federal University of Ouro Preto, Ouro Preto, Brazil.
Layara A. Abiko’s present address is Focal Area Structural Biology and Biophysics, Biozentrum, University of Basel, Basel, Switzerland.
Supporting Material can be found online at https://doi.org/10.1016/j.bpj.2020.05.031.
Supporting Citations
References (32, 33, 34, 35, 36, 37) appear in the Supporting Material.
Supporting Material
References
- 1.Berridge M.J., Bootman M.D., Roderick H.L. Calcium signalling: dynamics, homeostasis and remodelling. Nat. Rev. Mol. Cell Biol. 2003;4:517–529. doi: 10.1038/nrm1155. [DOI] [PubMed] [Google Scholar]
- 2.Carafoli E. Calcium signaling: a tale for all seasons. Proc. Natl. Acad. Sci. USA. 2002;99:1115–1122. doi: 10.1073/pnas.032427999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Carafoli E., Krebs J. Why calcium? How calcium became the best communicator. J. Biol. Chem. 2016;291:20849–20857. doi: 10.1074/jbc.R116.735894. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Guerini D., Coletto L., Carafoli E. Exporting calcium from cells. Cell Calcium. 2005;38:281–289. doi: 10.1016/j.ceca.2005.06.032. [DOI] [PubMed] [Google Scholar]
- 5.Philipson K.D., Nicoll D.A. Sodium-calcium exchange: a molecular perspective. Annu. Rev. Physiol. 2000;62:111–133. doi: 10.1146/annurev.physiol.62.1.111. [DOI] [PubMed] [Google Scholar]
- 6.Khananshvili D. Sodium-calcium exchangers (NCX): molecular hallmarks underlying the tissue-specific and systemic functions. Pflugers Arch. 2014;466:43–60. doi: 10.1007/s00424-013-1405-y. [DOI] [PubMed] [Google Scholar]
- 7.Dyck C., Maxwell K., Hryshko L.V. Structure-function analysis of CALX1.1, a Na+-Ca2+ exchanger from Drosophila. Mutagenesis of ionic regulatory sites. J. Biol. Chem. 1998;273:12981–12987. doi: 10.1074/jbc.273.21.12981. [DOI] [PubMed] [Google Scholar]
- 8.Schwarz E.M., Benzer S. Calx, a Na-Ca exchanger gene of Drosophila melanogaster. Proc. Natl. Acad. Sci. USA. 1997;94:10249–10254. doi: 10.1073/pnas.94.19.10249. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Wang T., Xu H., Montell C. Light activation, adaptation, and cell survival functions of the Na+/Ca2+ exchanger CalX. Neuron. 2005;45:367–378. doi: 10.1016/j.neuron.2004.12.046. [DOI] [PubMed] [Google Scholar]
- 10.Halty-deLeon L., Hansson B.S., Wicher D. The Drosophila melanogaster Na +/Ca 2+ exchanger CALX controls the Ca 2+ level in olfactory sensory neurons at rest and after odorant receptor activation. Front. Cell. Neurosci. 2018;12:186. doi: 10.3389/fncel.2018.00186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Alonso-García N., Inglés-Prieto A., de Pereda J.M. Structure of the Calx-beta domain of the integrin beta4 subunit: insights into function and cation-independent stability. Acta Crystallogr. D Biol. Crystallogr. 2009;65:858–871. doi: 10.1107/S0907444909018745. [DOI] [PubMed] [Google Scholar]
- 12.Wu M., Tong S., Zheng L. Structural basis of the Ca2+ inhibitory mechanism of Drosophila Na+/Ca2+ exchanger CALX and its modification by alternative splicing. Structure. 2011;19:1509–1517. doi: 10.1016/j.str.2011.07.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Giladi M., Bohbot H., Khananshvili D. Dynamic features of allosteric Ca2+ sensor in tissue-specific NCX variants. Cell Calcium. 2012;51:478–485. doi: 10.1016/j.ceca.2012.04.007. [DOI] [PubMed] [Google Scholar]
- 14.Wu M., Wang M., Zheng L. Crystal structure of CBD2 from the Drosophila Na(+)/Ca(2+) exchanger: diversity of Ca(2+) regulation and its alternative splicing modification. J. Mol. Biol. 2009;387:104–112. doi: 10.1016/j.jmb.2009.01.045. [DOI] [PubMed] [Google Scholar]
- 15.Wu M., Le H.D., Zheng L. Crystal structures of progressive Ca2+ binding states of the Ca2+ sensor Ca2+ binding domain 1 (CBD1) from the CALX Na+/Ca2+ exchanger reveal incremental conformational transitions. J. Biol. Chem. 2010;285:2554–2561. doi: 10.1074/jbc.M109.059162. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Leigh J. 1971. Relaxation times in systems with chemical exchange: some exact solutions. J. Magn. Reson. 1969;4:308–311. [Google Scholar]
- 17.Delaglio F., Grzesiek S., Bax A. NMRPipe: a multidimensional spectral processing system based on UNIX pipes. J. Biomol. NMR. 1995;6:277–293. doi: 10.1007/BF00197809. [DOI] [PubMed] [Google Scholar]
- 18.Vranken W.F., Boucher W., Laue E.D. The CCPN data model for NMR spectroscopy: development of a software pipeline. Proteins. 2005;59:687–696. doi: 10.1002/prot.20449. [DOI] [PubMed] [Google Scholar]
- 19.Showalter S.A., Bruschweiler-Li L., Brüschweiler R. Quantitative lid dynamics of MDM2 reveals differential ligand binding modes of the p53-binding cleft. J. Am. Chem. Soc. 2008;130:6472–6478. doi: 10.1021/ja800201j. [DOI] [PubMed] [Google Scholar]
- 20.Massi F., Johnson E., Palmer A.G., III NMR R1 rho rotating-frame relaxation with weak radio frequency fields. J. Am. Chem. Soc. 2004;126:2247–2256. doi: 10.1021/ja038721w. [DOI] [PubMed] [Google Scholar]
- 21.Vallurupalli P., Bouvignies G., Kay L.E. Studying “invisible” excited protein states in slow exchange with a major state conformation. J. Am. Chem. Soc. 2012;134:8148–8161. doi: 10.1021/ja3001419. [DOI] [PubMed] [Google Scholar]
- 22.Nguyen T.H., Rustenburg A.S., Minh D.D.L. Bayesian analysis of isothermal titration calorimetry for binding thermodynamics. PLoS One. 2018;13:e0203224. doi: 10.1371/journal.pone.0203224. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Torrecillas A., Laynez J., Gómez-Fernández J.C. Calorimetric study of the interaction of the C2 domains of classical protein kinase C isoenzymes with Ca2+ and phospholipids. Biochemistry. 2004;43:11727–11739. doi: 10.1021/bi0489659. [DOI] [PubMed] [Google Scholar]
- 24.Vega S., Abian O., Velazquez-Campoy A. A unified framework based on the binding polynomial for characterizing biological systems by isothermal titration calorimetry. Methods. 2015;76:99–115. doi: 10.1016/j.ymeth.2014.09.010. [DOI] [PubMed] [Google Scholar]
- 25.Akaike H. A new look at the statistical model identification. IEEE Trans. Automat. Contr. 1974;19:716–723. [Google Scholar]
- 26.Wyman J., Phillipson P.E. A probabilistic approach to cooperativity of ligand binding by a polyvalent molecule. Proc. Natl. Acad. Sci. USA. 1974;71:3431–3434. doi: 10.1073/pnas.71.9.3431. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Johnson E., Bruschweiler-Li L., Brüschweiler R. Structure and dynamics of Ca2+-binding domain 1 of the Na+/Ca2+ exchanger in the presence and in the absence of Ca2+ J. Mol. Biol. 2008;377:945–955. doi: 10.1016/j.jmb.2008.01.046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Salinas R.K., Bruschweiler-Li L., Brüschweiler R. Ca2+ binding alters the interdomain flexibility between the two cytoplasmic calcium-binding domains in the Na+/Ca2+ exchanger. J. Biol. Chem. 2011;286:32123–32131. doi: 10.1074/jbc.M111.249268. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Boyman L., Mikhasenko H., Khananshvili D. Kinetic and equilibrium properties of regulatory calcium sensors of NCX1 protein. J. Biol. Chem. 2009;284:6185–6193. doi: 10.1074/jbc.M809012200. [DOI] [PubMed] [Google Scholar]
- 30.Ranganathan R., Harris G.L., Zuker C.S. A Drosophila mutant defective in extracellular calcium-dependent photoreceptor deactivation and rapid desensitization. Nature. 1991;354:230–232. doi: 10.1038/354230a0. [DOI] [PubMed] [Google Scholar]
- 31.Boyman L., Hagen B.M., Khananshvili D. Proton-sensing Ca2+ binding domains regulate the cardiac Na+/Ca2+ exchanger. J. Biol. Chem. 2011;286:28811–28820. doi: 10.1074/jbc.M110.214106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Wyman J. The binding potential, a neglected linkage concept. J. Mol. Biol. 1965;11:631–644. doi: 10.1016/s0022-2836(65)80017-1. [DOI] [PubMed] [Google Scholar]
- 33.Hess V.L., Szabo A. Ligand binding to macromolecules: allosteric and sequential models of cooperativity. J. Chem. Educ. 1979;56:289–293. [Google Scholar]
- 34.Dill K.A., Bromberg S., Stigter D. Garland Science, New York; 2003. Molecular Driving Forces: Statistical Thermodynamics in Chemistry and Biology. [Google Scholar]
- 35.Sivia D.S., Skilling J. Oxford University Press, Oxford, UK; 2006. Data Analysis: A Bayesian Tutorial. [Google Scholar]
- 36.Foreman-Mackey D., Hogg D.W., Goodman J. emcee: the MCMC hammer. PASP. 2013;125:306–312. [Google Scholar]
- 37.Freiburger L., Auclair K., Mittermaier A. Global ITC fitting methods in studies of protein allostery. Methods. 2015;76:149–161. doi: 10.1016/j.ymeth.2014.12.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.