Fluorescence Correlation Spectroscopy and Photon Counting Histograms in Finite, Bounded Domains

Abstract

Analysis of fluctuations arising as fluorescent particles pass through a focused laser beam has enabled quantitative characterization of a broad range of molecular kinetic processes. Two key mathematical frameworks that have enabled these quantifications are fluorescence correlation spectroscopy (FCS) and photon counting histogram (PCH) analysis. Although these frameworks are effective and accurate when the focused laser beam is well approximated by an infinite Gaussian beam with a waist that is small compared to the size of the region over which the fluorescent particles can diffuse, they cannot be applied to situations in which this region is bounded at the nanoscale. We therefore derived general forms of the FCS and PCH frameworks for bounded systems. The finite-domain form of FCS differs from the classical form in its boundary and initial conditions and requires development of a new Fourier space solution for fitting data. Our finite-domain FCS predicts simulated data accurately and reduces to a previous model for the special case when the system is much larger than the Gaussian beam and can be considered to be infinite. We also derived the PCH form for the bounded systems. Our approach enables estimation of the concentration of diffusing fluorophores within a finite domain for the first time, to our knowledge. The method opens the possibility of quantification of kinetics in several systems for which this has never been possible.

Significance

Methods based on fluorescence measurements of molecular concentration fluctuations, including fluorescence correlation spectroscopy and photon count histogram analysis, are widely used to determine rates of diffusion, chemical reaction, and sizes of molecular aggregates. Typically, the range over which the molecules can diffuse is large compared to the size of the focused laser beam that excites the fluorescence. This work extends these measurements to systems that are comparable in size to the excitation laser beam, including very small samples such as the interior of bacterial cells or the diffusion of molecules along individual macromolecules such as DNA.

Introduction

Fluorescence correlation spectroscopy (FCS) and associated methods such as photon counting histogram (PCH) analysis have enabled the quantification of a range of kinetic processes, especially of processes related to diffusion (1,2). The basic experiment acquires the time course of fluorescence photons emitted by fluorophores that diffuse through a small focused laser beam that illuminates a tiny fraction of a much larger sample volume or area. The light emitted by random passage of the fluorophores across the laser-illuminated region fluctuates over time and can be analyzed statistically to estimate properties of both the diffusing molecules and the surrounding medium. The classical theories of PCH and FCS for interpreting these time courses are based on laser beams with Gaussian intensity profiles that extend over a quasi-infinite domain of the total sample volume, even though most of the fluorescence is excited from a very narrow spatial range (1).

Although this is not a limitation for experiments on domains much larger than the beam waist, it precludes experiments in confined domains such as microfluidic channels, whose sizes are comparable to the laser waist (3). In addition to such cases of confinement, there are important examples in which the illumination is not well modeled by a Gaussian, such as a single-molecule experiment with a fluorescent DNA-binding protein diffusing along a DNA fragment that has a fluorescence quencher, donor or acceptor tethered to one end (4). To address this need for FCS and PCH analysis on systems with confined diffusion or non-Gaussian spatial illumination, we derived a general form of FCS and an associated PCH analysis for bounded systems under arbitrary illumination.

Background

FCS

FCS analysis begins by gathering the time course of fluctuating fluorescence intensity, I(t), and computing the temporal autocorrelation function G(τ), which is the correlation of I(t) with itself when shifted by a time interval τ: $G\left(\tau \right)=\frac{⟨\delta I\left(t\right)\delta I\left(t+\tau \right)⟩}{⟨I{\left(t\right)}^2⟩}$, in which angle brackets indicate temporal averages, t is time, and the intensity fluctuation is δI(t) = I(t) − $\langle I\left(t\right)\rangle$. The intensity fluctuation relates to the concentration of fluorophores c(r, t) at position r and time t, the brightness per fluorophore, B, and the illumination profile W(r):

$$\delta I\left(t\right)=B\int \delta c(r,t)W\left(r\right)dr,$$ (1)

where δc(r, t) = c(r, t) − C is the local fluctuation of concentration around the macroscopic concentration C. Note that the product BW(r) is actually a combination of both illumination and detection sometimes called the detectable emission intensity distribution or spatial detectivity function. B and W(r) can be measured experimentally. For classic FCS, W(r) is approximated by a Gaussian,$W\left(r\right)=\exp \left[-\left(2\left(x^2+y^2+{\left(\frac{z}{a}\right)}^2\right)/s^2\right)\right]$, where s is the laser waist and r₀ is the position of the center of the laser beam and the autocorrelation function becomes $G\left(\tau \right)=G\left(0\right){\left[\left(1+\frac{\tau }{{\tau }_d}\right){\left(1+a^{-2}\left(\frac{\tau }{{\tau }_d}\right)\right)}^{\frac{1}{2}}\right]}^{–1}$, in which a is the ratio of the of axial/lateral position of the excitation spot and the characteristic diffusion time τ_d is estimated by fitting this equation to experimental data. With a Gaussian laser beam profile and with knowledge of radius w of the Gaussian illumination profile, the diffusion coefficient D of the diffusing fluorophores can be estimated from τ_d and the prediction of the theory that τ_d = w²/4D.

The expression for the autocorrelation function can be derived via a Fourier transform approach from the diffusion equation:

$$\frac{\partial \delta c(r,t)}{\partial t}=D{\nabla }^2\delta c(r,t).$$ (2)

For an open system with no boundaries, the initial condition is that concentrations are uncorrelated spatially between any two points $r\text{'}$ and $r$, so that (1,5)

$$\langle \delta c(r,0)\delta c(r\text{'},0)\rangle =C\delta \left(r-r\text{'}\right).$$ (3)

Hence, the variance of the concentration is $\langle {\left(\delta c\left(r,0\right)\right)}^2=C\rangle$. However, for bounded, finite systems, this initial condition must be modified, and a series approach must be taken to solving the diffusion equation. We develop these approaches in the next section.

Number and brightness analysis

It is straightforward to use FCS to determine the number and brightness of fluorescent particles (molecules) in a homogeneous solution. In a typical FCS experiment, a focused laser beam with Gaussian intensity profile excites the fluorescence from the solute molecules within the volume illuminated by the beam that diffuse across the laser beam. Typically, this illuminated volume occupies a small fraction of the total volume of the solution so that the fluorescent molecules can diffuse into and out of it. The diffusion of the molecules across the laser beam produces fluctuations of the fluorescence. The diffusion coefficient is determined from the autocorrelation function of the fluctuations. The amplitude of the autocorrelation function is the inverse of the number of fluorescent molecules in the laser beam. Hence, from the amplitude of the autocorrelation of the fluorescence time course of a homogeneous solution, one can readily determine both the overall brightness of the fluorescent particles and their number and therefore, from the ratio of these two quantities, the average brightness of the particles. If the particles are aggregates of the fluorescent particles in which the brightness of an aggregate of n fluorescent particles is n times brightness of a single particle, one can therefore determine the degree of aggregation of the compound particles.

Fluorescence distribution spectroscopy, including PCH analysis and fluorescence intensity distribution analysis

Additional information can be derived from the time course of fluorescence in an FCS experiment when the region being imaged contains either fluorophores that are polymerizing or multiple species of fluorophores, each with its own unique brightness and concentration. In this case, information about the distribution of the numbers and brightnesses of fluorophores can be derived by one of two approaches: either from the higher moments of the autocorrelation function or from analysis of the temporal distribution (histogram) of the number of photon counts measured over time bins of prescribed duration. These concepts were first established by Palmer and Thompson (6,7) and by Qian and Elson (8, 9, 10), the latter calling this class of approaches “fluorescence distribution spectroscopy.” These approaches were further developed into two techniques: one, called PCH analysis, by Chen and co-workers (11), and another, called fluorescence intensity distribution analysis (FIDA), by Kask and co-workers (12,13). These two techniques are related mathematically (14), with the generating function used in FIDA representing the Fourier transform of the PCH.

However, an important difference lies in the derivation of the two methods. PCH begins with calculation of the probability associated with fluctuations for individual molecules, which arise because of spatial variations in illumination and the stochastic nature of detection. The histogram for n molecules is predicted by convolving the histogram for one molecule n times. FIDA, on the other hand, begins with consideration of the fluctuations of fluorophores and photon counts from a small volume, dV. The overall distribution of the photon counts is the convolution of the distributions for all dV-values, leading to the logarithm of the generating function of the photon counts and therefore an integration over V. PCH and FIDA are thus convolutions of molecules and convolutions of space, respectively. PCH theory assumes that the distributions for different molecules are independent of each other, whereas FIDA theory assumes that the distributions for different positions are independent of each other. Although these two procedures give the same result for open systems, we show that only PCH theory is suitable for bounded systems, whereas FIDA is not.

Previous treatments of FCS for bounded systems

Sanguigno et al. (3) studied the special case of diffusion in a bounded microchannel of width d illuminated by a Gaussian beam of waist a₀. For the case of a beam centered on the channel, they derived the generating function $g\left(\tau \right)=\frac{d}{2}\left[\frac{a_0^2}{2}+\sum _{n=1}^{\infty }{a}_n^2\text{exp}\left(-\frac{n^2{\pi }^2\tau }{2R^2{\tau }_d}\right)\right]$, where R = $\sqrt{2}d/r_k$, in which r_k is the Gaussian laser beam waist; τ_d = r_k/(4D) is the characteristic diffusion time, in which D is the diffusion coefficient with units of length/time; and $a_n=\frac{\sqrt{\pi }}{\text{R}}\text{exp}(-n^2{\pi }^2/4R^2)\cos \left(\frac{n\pi }{2}\right)\left[\text{erf}\left(\frac{in\pi }{2R}+\frac{R}{2}\right)-\text{erf}\left(\frac{in\pi }{2R}-\frac{R}{2}\right)\right]$. As described below, we used this special case to benchmark the general form derived in the next section; the general form enables different beams and autocorrelation amplitudes to be considered.

Methods

Theory

Initial conditions for bounded FCS

The initial condition for FCS in an unbounded system is 〈δc(r, 0)δc(r′, 0)〉 = Cδ(r − r′), which states that concentrations (and hence numbers of molecules in a local volume) are initially uncorrelated. This further requires that when r = r′, the variance of c at r equals its mean, as expected for a Poisson distribution. However, this initial condition does not apply in bounded systems because the limited number of molecules requires that concentration fluctuations at two different locations be negatively correlated; elevations of concentration at one location require reductions at other locations. As shown below, this leads to a binomial rather than Poisson distribution of molecules and thus a new initial condition.

The derivation begins by considering a one-dimensional (1D) bounded system with a length of d and N_total molecules, so that C = N_total/d, with an arbitrary specific point r = r′, and all other points ($r\ne r^{\text{'}}$). To obtain 〈δc(r, 0)δc(r′, 0)〉, we will derive 〈δn(r, 0)δn(r′, 0)〉 for two cases: point r = r′ and $r\ne r^{\text{'}}$ (n is the number of molecules in a small interval Δr).

First, for r = r′, the variance of concentration can be calculated as follows: for a small interval Δr, each molecule has an equal probability of p = Δr/d that it can be in Δr (and therefore a probability of 1 − p that it does not reside in Δr). Given a total number of N_total, the number of molecules n in a small interval Δr follows a binomial distribution in bounded systems, and the variance is 〈(δn)² 〉= p(1 − p)N_total, which is also the fluctuation of n at position r and time t = 0:

(4)

Second, for any other point ($r\ne r\text{'}$), needs to be derived. To do so, we considered the distribution of the sum of the number of molecules at r and r′, n(r, r′, 0) = n(r, 0) + n(r′, 0). It is worth noting that n(r, r′, 0) is not the two-dimensional joint distribution, but rather the distribution of the sum of two random variables that are supposed to be negatively correlated. Therefore, the variance of n(r, r′, 0) = n(r, 0) + n(r′, 0) is

(5)

We are seeking the last term on the right side. Because 〈δ(n(r, 0))²〉 and 〈δ(n(r′, 0))²〉 have already been derived as in Eq. 4, the only unknown term is the left side, 〈δn(r, r′, 0)²〉. To determine its expression, we consider the two small intervals at r and r′. As above, each molecule has a probability of p being at either r or r′ and a probability of 1 − p and being somewhere else. Therefore, the molecules still follow a binomial distribution. Because the interval size increases twofold (Δr becomes 2Δr), p becomes twice as big, too: p = 2Δr/d. Therefore, its variance is

(6)

Rearranging Eq. 5, substituting Eqs. 4 and 6,

(7)

At last, rewriting Eqs. 4 and 7 in terms of the local concentration, c = n/Δr, C = N_total/d:

(8)

Given a function $f\left(r-r^{\text{'}}\right)=\{\begin{array}{c}0whenr\ne r\text{'}\\ \frac{1}{\Delta r}whenr=r\text{'}\end{array}$, it can be shown that f is a δ function by proving the integral $\underset{0}{\overset{d}{\int }}f(r-r\text{'})dr$ = 1 and $\underset{0}{\overset{d}{\int }}g\left(r\right)f(r-r\text{'})dr$ = g(r′). This can be easily done because Δr and dr cancel out (these two integrals will be used in the derivation in the Appendix). Therefore, 〈δc(r, 0)δc(r′, 0)〉 can be written in a simpler form, which is a δ function subtracted by a constant:

(9)

Solution for bounded FCS

The diffusion equation (Eq. 2) over a finite domain was solved using a Fourier series approach. In this particular case, with Neumann boundary conditions, a cosine series was used: $\delta \hat{c}\left(k,t\right)=\underset{0}{\overset{d}{\int }}\delta c\left(r,t\right)\cos \frac{k\pi r}{d}dr$, in which $\delta \hat{c}$(k, t) is the Fourier transform of δc with wave number k. This leads to a solution of the diffusion equation

$$\delta \hat{c}(k,\tau )=\delta \hat{c}\left(k,0\right)\exp \left[-{\left(\frac{k\pi }{d}\right)}^{2}D\tau \right].$$ (10)

The unnormalized autocorrelation function can then be obtained (see Appendix for details):

(11)

where

$$a_k=\underset{0}{\overset{d}{\int }}W\left(r\right)\cos \frac{k\pi r}{d}dr.$$ (12)

The normalization factor can be easily obtained as $\langle I\left(t\right){\rangle }^2={\left[BC\underset{0}{\overset{d}{\int }}W\left(r\right)dr\right]}^2$. Therefore, the normalized form of the correlation function is

$$G\left(\tau \right)=\frac{2{\sum }_{k=1}^{\infty }{a}_k^2\exp \left[-{\left(\frac{k\pi }{d}\right)}^{2}D\tau \right]}{Cd{\left[{\int }_0^{d}W\left(r\right)dr\right]}^2}.$$ (13)

With the input W(r) and size d known, this equation can be used to fit an experimentally determined autocorrelation function; the diffusion coefficient D and the concentration C can then be obtained.

It should be noted that when W(r) is constant, as occurs in the case of uniform illumination, the autocorrelation g(τ) equals zero. This can be easily understood because under uniform illumination, there will be no fluctuations other than shot noise, which has no time correlation. For classic FCS in infinite systems, two sources of fluctuation other than shot noise exist: fluctuations caused by concentration fluctuations and fluctuations caused by nonuniform illumination and detection. However, for the framework developed here for FCS in bounded systems, only the nonuniform illumination and detection error contribute to noise.

Bounded PCH

As discussed earlier, PCH and FIDA were developed to measure the number and brightness in fluorophore populations within an effectively unbounded region of solution. Although these two procedures give the same result for open systems, we show here that PCH analysis is suitable for closed systems but show in the next section that FIDA is not.

For one molecule in a bounded system, the photon counting distribution is

$$P^1\left(m\right)=\frac{1}{V}\int Poiss\left(m,qW\left(\stackrel{\rightharpoonup }{r}\right)\right)dV,$$ (14)

where m is the number of photons and q is the product of the quantum yield of the fluorophores and the detection efficiency. For n particles, Pⁿ(m) is the self-convolution of P¹(m) applied n times (11). Using the following generating function, the time-consuming convolution computation can be avoided:

$$G_{closed}^1\left(\xi \right)=\sum _{m=0}{\xi }^{m}P\left(m\right)=\frac{1}{V}\int \sum _{m=0}\frac{\exp (-qW\left(\stackrel{\rightharpoonup }{r}\right)){\left[\xi qW\left(\stackrel{\rightharpoonup }{r}\right)\right]}^m}{m!}dV.$$ (15)

Finally, this yields

$$G_{closed}^1\left(\xi \right)=\frac{1}{V}\int \exp \left[(\xi -1)qW\left(\stackrel{\rightharpoonup }{r}\right)\right]dV.$$ (16)

The distribution approaches a Poisson distribution when $W\left(\stackrel{\rightharpoonup }{r}\right)$ is constant over $\stackrel{\rightharpoonup }{r}$, meaning that fluctuations are due only to the shot noise. For n molecules, $G_{closed}^n=\prod _1^n{G}_{closed}^1$. For the case of a single species of particles, $G_{closed}^n={\left[G_{closed}^1\right]}^n$. Taking ξ = e^−iω, Eq. 16 can be treated as an inverse Fourier transform that can be used to calculate the probability density function P(m).

Bounded FIDA

FIDA, however, is not as readily tailored to closed systems. The derivation of FIDA involves dividing the system into small spatial sections dV_i and can be broken into three steps. First, the distribution of photon counts P_i(n) arising from a volume dV_i can be derived. Second, the generating function for this distribution can be derived as G_i(ξ) = $\sum _{m=0}{\xi }^m{P}_i\left(m\right)$, where ξ = e^−iω. Finally, assuming, as is the case for an infinite system, that the random variables P₁(m), P₂(m), …P_n(m) are independent variables, the third step would be to calculate the generating function by taking the products of all $G\left(\xi \right)=\prod _1^n{G}_i\left(\xi \right)$. However, the functions P_i(m) are not independent variables in a bounded system because the total number of particles is constant, and all the positions compete with each other for particles. Therefore, the generating function is not simply the products. Although this problem can be solved, it does not admit a solution that is useful for analysis of experiment. Instead, the PCH analysis derived above, which involves the convolution of the distributions for single molecules, is the preferred approach.

Computational methods

The MATLAB environment (The MathWorks, Natick, MA) was used for all calculations, including data fitting. Equations 13 and 16 were solved numerically. In most cases studied, the summations were calculated over the range k or m spanning 1–10, which was sufficient for convergence. For integration of these equations, discrete forms were written, and summations were taken over increasingly fine intervals until convergence was reached, typically on the order of 100 increments. An exception was the case of d = 500 in Fig. 1 C, in which 1000 spatial increments were required to sample the Gaussian beam sufficiently because the beam was small compared to the system size. Also, for this case, the maximum of the wave number k increased from 10 to 1000.

Figure 1.

FCS in a bounded 1D system illuminated by a Gaussian beam focused at the center of the system. (A) An illustration of the system is given. In the example here, the system length is d = 2, the Gaussian beam waist is 1, the diffusion coefficient D = 0.001, and the total number of particles is 1, which leaves the concentration C = 0.5 (all parameters are dimensionless). (B) Comparison with the results of Sanguigno et al. (3) is shown. All correlation functions are normalized by G(0). For the model of (3), G(∞) must be subtracted from G(τ) to force the function to approach zero at infinite time before normalization. (C and D) Comparison of normalized (C) and non-normalized (D) autocorrelation functions for systems of different length, d, and an open system is shown. Our finite-domain FCS framework converges to the FCS framework for an open system when d is very large; using the FCS framework for smaller values of d can lead to substantial error without the corrections needed for finite domain size. Note that to enable comparison, the total number of particles in each finite-domain FCS curve varies with the system length so that the concentration is same (unity) across all cases. To see this figure in color, go online.

Monte Carlo simulations were performed to generate simulated data for fitting. Fluorophores were distributed randomly over a 1D space and moved in a randomly chosen direction for each time step with a spatial step size determined by the diffusion coefficient. Photons recorded by a detector were recorded in each time step with flux and proportional to the intensity of illumination at the fluorophores’ position. When fluorophores struck the elastic boundaries, they reflected in a way that was representative of an elastic impact.

Results and Discussion

Finite-domain FCS reduces to previous results for special cases

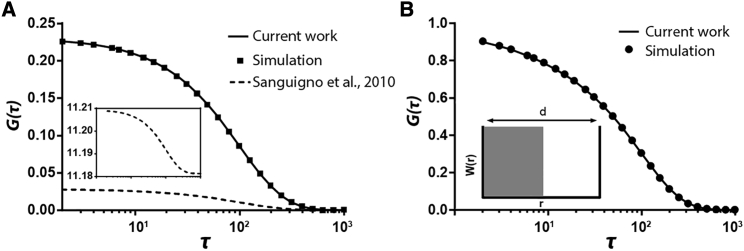
To test our theory, we calculated G(τ) for the case of molecules diffusing in a 1D system, bouncing back and forth between two walls, and compared our result with the predictions of Sanguigno et al. (3). As depicted in Fig. 1 B, the two theories match well for the special case of a Gaussian beam. In addition, when the system length is much bigger than the Gaussian beam, the correlations approach that of standard, unbounded FCS, as expected for a system that approaches conditions of being infinite (Fig. 1, C and D). The characteristic diffusion time increases with the system length until the autocorrelation function approaches the limit of an open system (Fig. 1 C).

Finite-domain FCS matches simulation data for more general cases

The calculation of (3) involves two extra steps: subtracting G(∞) from G(τ) and dividing by G(τ) − G(∞) by G(0). Note that we use the term “divide” instead of “normalize” to distinguish it from the normalization by the $\langle I\left(t\right){\rangle }^2$ that is used in standard FCS. The consequence of these extra steps is that the amplitude of the correlation is discarded in the method of (3).

For traditional FCS, this amplitude contains information about particle concentration. High concentration leads to low correlation amplitude because the fluctuations will average out. However, there is no concentration term in the derivation of (3). When comparing the raw calculation (no subtraction and division) to simulated data, our result fit the data very well, whereas the results of (3) do not fit the simulated data (Fig. 2 A, dashed line and the inset).

Figure 2.

(A) A simulation of particles diffusing through a channel under a Gaussian beam and predictions using both this work and the work of (3). The inset panel shows the raw predictions by the equations of (3), without subtracting G(∞) and without normalizing by G(0). The dashed line under the inset shows the prediction arising from subtracting G(∞) but not dividing by G(0). The solid line, which matches the simulation (symbols), shows our raw result without any extra steps. (B) The result for a square beam instead of a Gaussian beam is shown, in which the left half of the system is evenly illuminated and the right half is not at all illuminated.

In the method of (3), the calculated correlation function does not approach zero at the infinite time. That value must therefore be subtracted to force it to be zero at the infinite lag time. When deriving our equations, we had the same problem until we found that the initial condition is not a simple δ function anymore in bounded systems. Following the same derivation steps in the Appendix, it can be easily proved that with the initial condition 〈δc(r, 0)δc(r′, 0)〉 = Cδ(r − r′), the G(∞) will be $\frac{1}{Cd}$ or $\frac{1}{N_{total}}$ instead of zero, whereas N_total is the total number of particles in the system.

Compared to the method of (3), our method has two additional advantages. First, it can be used for any laser beam shape. Our theory fits simulated data very well for a square, uniform laser beam. Second, our method requires much less computational power. Using MATLAB, under the same conditions, our method improved the computation speed ∼3000-fold. This is mainly because the error function of complex numbers in the equations of (3) is expensive computationally. This method is also substantially faster than the random walk simulations used to produce the data in Fig. 2 B (Table 1).

Table 1.

Time Required to Compute G(τ) Using the Method of Sanguigno et al., the Methods in this Work, and Random Walk Simulation

	Sanguigno et al. (3)	This Work	Random Walk Simulation
Computation time	96 ± 5 s	0.026 ± 0.006 s	3.6 ± 0.1 s

For both Sanguigno’s and our method, the infinite sum was limited to only the first 100 terms (wavenumber). The simulation consisted of 10 million random walk steps with Gaussian step size.

Finite-domain FIDA and PCH

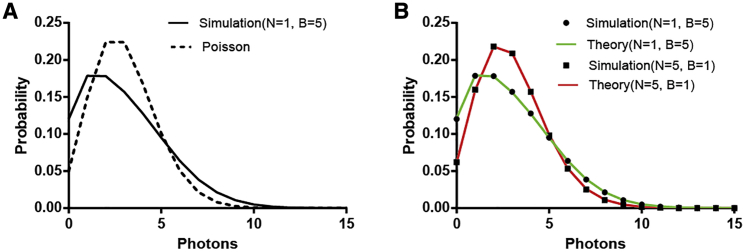
We next assessed whether the approach could be used to determine the numbers and brightnesses of multiple populations of fluorophores diffusing through a laser beam in a confined space. In Fig. 3, we calculated the PCH instead of correlation function using the same simulation described in Fig. 1. We show that our calculations fit the simulated PCH very well. At the same time, results reveal that as the number of particles increases, the distribution approaches a Poisson distribution (Fig. 3 B, N = 5, B = 1).

Figure 3.

PCH in bounded systems. (A) The histogram deviates from a Poisson distribution (with the same mean). (B) Comparison of simulated data with our finite-domain FCS theory is shown, calculated using the Fourier transform of Eq. 16. Two cases were simulated. Both give the same average intensity, which is the product of the number of particles N and their brightness B. To see this figure in color, go online.

Conclusions

The theory for reflective boundaries can be useful for single-molecule studies, as depicted in Fig. 3. Here, we suggest two potential applications. The diffusion of proteins along DNA is usually studied with relatively long DNA molecules whose lengths are much greater than the optical resolution. To obtain the diffusion rates, a fitting is required to estimate the precise position of a proteins, according to the basic principle of STORM and PALM super-resolution microscopy (15). A drawback is that the fitting step is time consuming. Here, we propose a single-molecule experiment in which short DNA can be used (Fig. 4 A).

Figure 4.

Examples of single-molecule experiments for which our finite-domain FCS theory could be useful. (A) Protein diffusion along short DNA molecules of different lengths is shown. The diffusion coefficient D = 100 nm²/s. The Förster distance is set to be 10 nm. (B) Results of fitting the 30 nm data in (A) with 1D FCS, G(τ) = $\frac{1}{\sqrt{1+\frac{\tau }{{\tau }_D}}}$, are shown. (C) Comparison of the theoretical calculation with simulated data is shown. The solid lines are the theoretical calculation, and the circles are the simulated data. Because the amplitudes for d = 5 and 10 nm are very small, we did not simulate these two cases. (D) Normalized autocorrelation functions calculated from (C) are shown. To see this figure in color, go online.

For this experiment, a DNA fragment shorter than the diffraction limit is attached to a surface. A fluorophore is conjugated to the protein, and a FRET-paired fluorophore is conjugated to the end of the DNA strand. We assume that the protein freely diffuses along the short DNA fragment and reflects back once it reaches either end. Under total internal reflection fluorescence (TIRF) microscopy, unbound proteins in solution have little effect on the measured fluorescence. The diffusion of protein thus leads to a change of the distance between the FRET pair and causes fluctuations of the detected intensity. The correlation function can be calculated and fitted with our theory for the reflective boundaries. In this case, the illumination function is W(r) = $\frac{1}{1+{(r/R_0)}^6}$, in which R₀ is the Förster distance of the FRET pair. The length of the DNA fragment can affect both the amplitude and the decay time of the correlation function (Fig. 4 A). This example highlights the importance of considering the finite domain size, because the appropriate correlation function is very different from that predicted by the 1D FCS equation G(τ) = $\frac{1}{\sqrt{1+\frac{\tau }{{\tau }_D}}}$ (Fig. 4 B).

Bacterial cells provide another popular target for single-molecule studies. A typical Escherichia coli cell spans 2 μm and has a diameter of 1 μm. The diffusion of molecules within bacterial cells is usually measured using TIRF microscopy in a plane parallel to the substratum on which the bacteria are cultured. However, if diffusion is confined in a region that is smaller than the optical resolution, it is difficult to obtain the diffusion rates. We propose that diffusion can instead be studied in the direction perpendicular to the substratum, taking advantage of the decaying excitation intensity for TIRF (16,17). As a fluorescent protein moves in the out-of-plane direction, the measured brightness will change. The intensity can be recorded, and the correlation function can be calculated and fitted to our theory, enabling estimation of the diffusion coefficient. In this case, the illumination intensity decays exponentially, so that W(r) = exp(−r/z₀).

It should be noted that our theory is based on a simple assumption that diffusion is homogenous across the media, which means there can be no absorbing boundaries, sinks, or sources of particles. However, our approach provides a starting point to derive the theory for such cases, as well as the associated initial condition.

To summarize, we derived the equations for FCS in bounded systems. These equations are applicable for any illumination function and could be potentially useful for many experiments. We also want to emphasize that the initial condition we found for solving the diffusion equations might be useful not only for FCS but also for other theoretical and experimental investigations.

Author Contributions

Y.J. conceived of and executed the study. A.M., B.X., E.L.E., and G.M.G. provided counsel and assisted with the interpretation and presentation of the work. All authors contributed to writing the final article.

Editor: Jochen Mueller.

Appendix: Derivation of the Correlation Function for Confined Fcs

The fluorescence intensity from a region illuminated by a laser is calculated as

$$I\left(t\right)=B\underset{0}{\overset{d}{\int }}c\left(r,t\right)W\left(r\right)dr,$$ (A1)

where c(r, t) is the concentration of fluorophores at position r and time t, B is the brightness per fluorophore, and W(r) is the illumination profile.

In response to a perturbation in concentration δc(r, t), the intensity fluctuates by an amount

$$\delta I\left(t\right)=B\underset{0}{\overset{d}{\int }}\delta c\left(r,t\right)W\left(r\right)dr.$$ (A2)

Therefore, the autocorrelation function can be written as

$$g\left(\tau \right)=⟨\delta I\left(0\right)\delta I\left(\tau \right)⟩=B^2\underset{0}{\overset{d}{\int }}\underset{0}{\overset{d}{\int }}drd{r}^{\text{'}}W\left(r\right)W\left(r^{\text{'}}\right)⟨\delta c\left(r,0\right)\delta c\left(r^{\text{'}},\tau \right)⟩.$$ (A3)

The autocorrelation function g(τ) can be computed from experimental observations because the intensity fluctuation can be measured. Because all terms in Eq. A3 can then be measured other than $\langle \delta c\left(r,0\right)\delta c(r^{\text{'}},\tau )\rangle$, it is possible to use Eq. A3 to calculate this. To relate these fluctuations to the diffusion coefficient, we solved the diffusion equation

$$\frac{\partial \delta c(r,t)}{\partial t}=D{\nabla }^2\delta c\left(r,t\right).$$ (A4)

Our procedure for this involved a Fourier space approach. Solution of the diffusion equation in the Fourier space is

$$\delta \hat{c}(k,\tau )=\delta \hat{c}\left(k,0\right)\exp \left[-{\left(\frac{k\pi }{d}\right)}^{2}D\tau \right].$$ (A5)

When k = 0, this becomes

$$\delta \hat{c}\left(0,\tau \right)=\delta \hat{c}\left(\mathrm{0,0}\right).$$ (A6)

For a reflective boundary, the cosine Fourier transform of δc is:

$$\delta \hat{c}\left(k,t\right)=\underset{0}{\overset{d}{\int }}\delta c\left(r,t\right)\cos \frac{k\pi r}{d}dr.$$ (A7)

Note that at time t = 0,

$$\delta \hat{c}\left(k,0\right)=\underset{0}{\overset{d}{\int }}\delta c\left(r,0\right)\cos \frac{k\pi r}{d}dr,$$ (A8)

and when k = 0,

$$\delta \hat{c}\left(\mathrm{0,0}\right)=\underset{0}{\overset{d}{\int }}\delta c\left(r,0\right)dr.$$ (A9)

Substituting Eqs. A6, A7, A8, and A9 and taking the inverse Fourier transform to transform the solution into real space and obtain δc(r′, τ), we arrive at

$$\delta c\left(r^{\text{'}},\tau \right)=\frac{\delta \hat{c}\left(0,\tau \right)}{d}+\frac{2}{d}\sum _{k=1}^{\infty }\delta \hat{c}\left(k,\tau \right)\cos \frac{k\pi r^{\text{'}}}{d}=\frac{\delta \hat{c}\left(\mathrm{0,0}\right)}{d}+\frac{2}{d}\sum _{k=1}^{\infty }\delta \hat{c}\left(k,0\right)\exp \left[-{\left(\frac{k\pi }{d}\right)}^{2}D\tau \right]\cos \frac{k\pi r^{\text{'}}}{d}=\frac{\delta \hat{c}\left(\mathrm{0,0}\right)}{d}+\frac{2}{d}\sum _{k=1}^{\infty }\delta \hat{c}\left(k,0\right)\exp \left[-{\left(\frac{k\pi }{d}\right)}^{2}D\tau \right]\cos \frac{k\pi r^{\text{'}}}{d}=\frac{1}{d}\underset{0}{\overset{d}{\int }}\delta c\left(r\text{'}\text{'},0\right)dr\text{'}\text{'}+\frac{2}{d}\sum _{k=1}^{\infty }\underset{0}{\overset{d}{\int }}\delta c\left(r\text{'}\text{'},0\right)\cos \frac{k\pi r\text{'}\text{'}}{d}dr\text{'}\text{'}\exp \left[-{\left(\frac{k\pi }{d}\right)}^{2}D\tau \right]\cos \frac{k\pi r^{\text{'}}}{d}.$$ (A10)

Hence,

(A11)

Rearranging by moving the angled brackets that represent time averages,

$$\langle \delta c\left(r,0\right)\delta c(r^{\text{'}},\tau )\rangle =\frac{1}{d}\underset{0}{\overset{d}{\int }}\langle \delta c\left(r,0\right)\delta c(r^{\text{'}}\text{'},0)\rangle d{r}^{\text{'}\text{'}}+\frac{2}{d}\sum _{k=1}^{\infty }\underset{0}{\overset{d}{\int }}\langle \delta c\left(r,0\right)\delta c(r^{\text{'}}\text{'},0)\rangle \cos \frac{k\pi r^{\text{'}\text{'}}}{d}dr\text{'}\text{'}\exp \left[-{\left(\frac{k\pi }{d}\right)}^{2}D\tau \right]\cos \frac{k\pi r^{\text{'}}}{d}$$ (A12)

The next step is to substitute the initial condition in Eq. A12. To this end, the two most important properties of the δ function are used. They are $\underset{0}{\overset{d}{\int }}\delta (r-r\text{'})dr$ = 1 and $\underset{0}{\overset{d}{\int }}g\left(r\right)\delta (r-r\text{'})dr$ = g(r′).

$$\langle \delta c\left(r,0\right)\delta c(r^{\text{'}},\tau )\rangle =\frac{1}{d}\underset{0}{\overset{d}{\int }}\left[C\delta \left(r-r^{\text{'}\text{'}}\right)-\frac{C}{d}\right]d{r}^{\text{'}\text{'}}+\frac{2}{d}\sum _{k=1}^{\infty }\underset{0}{\overset{d}{\int }}\left[C\delta \left(r-r^{\text{'}\text{'}}\right)-\frac{C}{d}\right]\cos \frac{k\pi r^{\text{'}\text{'}}}{d}d{r}^{\text{'}\text{'}}\exp \left[-{\left(\frac{k\pi }{d}\right)}^{2}D\tau \right]\cos \frac{k\pi r^{\text{'}}}{d}=\frac{C}{d}-\frac{C}{d^2}\times d+\frac{2C}{d}\sum _{k=1}^{\infty }\exp \left[-{\left(\frac{k\pi }{d}\right)}^{2}D\tau \right]\cos \frac{k\pi r^{\text{'}}}{d}\underset{0}{\overset{d}{\int }}\delta \left(r-r^{\text{'}\text{'}}\right)\cos \frac{k\pi r^{\text{'}\text{'}}}{d}d{r}^{\text{'}\text{'}}-\frac{2C}{d^2}\sum _{k=1}^{\infty }\exp \left[-{\left(\frac{k\pi }{d}\right)}^{2}D\tau \right]\cos \frac{k\pi r^{\text{'}}}{d}\underset{0}{\overset{d}{\int }}\cos \frac{k\pi r^{\text{'}\text{'}}}{d}d{r}^{\text{'}\text{'}}=\frac{2C}{d}\sum _{k=1}^{\infty }\exp \left[-{\left(\frac{k\pi }{d}\right)}^{2}D\tau \right]\cos \frac{k\pi r^{\text{'}}}{d}\cos \frac{k\pi r}{d}-\frac{2C}{d^2}\sum _{k=1}^{\infty }\exp \left[-{\left(\frac{k\pi }{d}\right)}^{2}D\tau \right]\cos \frac{k\pi r^{\text{'}}}{d}\times 0=\frac{2C}{d}\sum _{k=1}^{\infty }\exp \left[-{\left(\frac{k\pi }{d}\right)}^{2}D\tau \right]\cos \frac{k\pi r^{\text{'}}}{d}\cos \frac{k\pi r}{d}.$$ (A13)

Substituting this expression for δc(r, 0)δc(r′, τ) into the autocorrelation function of Eq. A3 yields an expression that can be fitted to estimate the diffusion coefficient D from experimental data:

(A14)