Abstract
The interplay between cell-cell and cell-substrate interactions is complex yet necessary for the formation and healthy functioning of tissues. The same mechanosensing mechanisms used by the cell to sense its extracellular matrix also play a role in intercellular interactions. We used the discrete element method to develop a computational model of a deformable cell that includes subcellular components responsible for mechanosensing. We modeled a three-dimensional cell pair on a patterned (two-dimensional) substrate, a simple laboratory setup to study intercellular interactions. We explicitly modeled focal adhesions and adherens junctions. These mechanosensing adhesions matured, becoming stabilized by force. We also modeled contractile stress fibers that bind the discrete adhesions. The mechanosensing fibers strengthened upon stalling. Traction exerted on the substrate was used to generate traction maps (along the cell-substrate interface). These simulated maps are compared to experimental maps obtained via traction force microscopy. The model recreates the dependence on substrate stiffness of the tractions’ spatial distribution, contractile moment of the cell pair, intercellular force, and number of focal adhesions. It also recreates the phenomenon of cell decoupling, in which cells exert forces separately when substrate stiffness increases. More importantly, the model provides viable molecular explanations for decoupling: mechanosensing mechanisms are responsible for competition between different fiber-adhesion configurations present in the cell pair. The point at which an increasing substrate stiffness becomes as high as that of the cell-cell interface is the tipping point at which configurations that favor cell-substrate adhesion dominate over those favoring cell-cell adhesion. This competition is responsible for decoupling.
Significance
Cells are sensitive to mechanical factors of their extracellular matrix while simultaneously in contact with other cells. This creates complex intercellular interactions that depend on substrate stiffness and play a role in processes such as development and diseases such as cardiac arrhythmia, asthma, and cancer. The simplest cell collective system in vitro is a cell pair on a patterned substrate. We developed a computational model of this system that explains the role of molecular adhesions and contractile fibers in the dynamics of cell-cell interactions on substrates with different stiffness. It is one of the first models of a deformable cell collective based on mechanical principles. It recreates cellular decoupling, a phenomenon in which cells exert forces separately, when substrate stiffness increases.
Introduction
Cells communicate with their environment and neighboring cells, transmitting forces through both. The interplay between cell-cell and cell-extracellular matrix (ECM) adhesions is complex, with junctions sharing component proteins and being connected to one another via the cytoskeleton (1). Knowledge of this interplay is relevant to understand cell-cell communication in processes such as development and pathologies, including cardiac arrhythmia (2), asthma (3,4), and cancer metastasis (5). Cell-pair studies on patterned substrates provide one of the simplest collective cell in vitro models. As previously presented in Polio et al., in a pair of airway smooth muscle cells, cell-cell coupling strength decreases with increasing ECM stiffness, whereas the total force exerted at the cell-cell interface via adhesions increases (6). Additionally, cell-cell junctions were visualized via immunostaining of β-catenin, a molecule in adherens junctions (AJs) cross-linking cadherins to the actin cytoskeleton. Visualization of β-catenin revealed that with increasing substrate stiffness, cell-cell AJs are progressively replaced by cell-ECM adhesions, such that the cell pair transitions from exerting force on the substrate as a single dipole into two separate ones (i.e., decoupling) (6). A similar increase in cell-cell forces and replacement of cell-cell with cell-ECM adhesions was presented by McCain et al. for a cell-pair setup with cardiac myocytes (7). These findings raise the question: how does raising substrate stiffness on neighboring cells lead to the cells becoming individually stronger and exerting higher force at cell-cell adhesions, themselves stabilized by force, yet cause the cells to act separately on their substrate?
This decoupling has been observed not only for cell pairs but also at a larger scale in endothelial sheets. Krishnan et al. looked at gap formation in human umbilical vein endothelial cells cultured on circular collagen islands (8). In these experiments, groups of 6–15 cells were cultured on substrates of different stiffness values in the range 1.2–90 kPa. As in cell-pair experiments, increased substrate stiffness led to higher cell-ECM and cell-cell forces. Staining of vascular endothelial cadherin (VE-cadherin) and vinculin at cell-cell boundaries showed that the increased contractile forces, exerted on stiffer substrates, did not imply higher expression of either VE-cadherin or vinculin. Enhanced formation of F-actin stress fibers via thrombin treatment, however, did cause enhanced expression of vinculin (appearing in a dotted pattern at the cell-cell boundaries) and gap formation between cells. Thrombin is an inflammatory mediator which causes increased actomyosin contractility (9).
In another study, by Kugelmann et al., actomyosin contractility was enhanced in human dermal microvascular endothelial cell confluent sheets via use of either thrombin or histamine, and α-catenin and vinculin were imaged (10). Histamine, like thrombin, is a mediator involved in inflammatory responses and acts on myosin light chain kinase, enhancing cellular contraction. α-Catenin is a protein that binds β-catenin, together cross-linking VE-cadherin and F-actin; in this study, imaging is done via an antibody that binds a particular epitope of α-catenin (i.e., α18 subunit of catenin) that is exposed during tension. Thus, an increase in α-catenin detection implies an increase in local force exertion (11). Mean changes of 201.1 ± 10.0% and 189.7 ± 9.2% in the intensity of α-catenin were measured 3 min after addition of histamine and 5 min after addition of thrombin, respectively. As in the work performed by Krishnan et al. (8), treatment with mediators resulted in vinculin becoming more visible in a dotted pattern at cell-cell boundaries. In both cases, there were gap formation and increased stress fiber formation. In Kugelmann et al. (10), cellular decoupling was identified as an increase in transendothelial electric resistance of the monolayer. Thus, both studies on endothelial sheets show that despite cell-cell adhesion reinforcement with increased actomyosin force, as evidenced by recruitment of additional molecules to the adhesion complex (i.e., vinculin or α-catenin), cells can become decoupled from one another.
To provide insight into the coexistence of cell decoupling and adhesion reinforcement, we developed a computational model of a cell pair on a rectangular pattern in which subcellular force exertion mechanisms are taken into account, specifically adhesion complex maturation (i.e., stabilization of adhesion with force carried) and stress fiber strengthening (i.e., increase in contraction force after stalling in fiber shortening). We compare simulated traction maps with those recovered in vitro through traction force microscopy (6). In the model, both cell-ECM and cell-cell bonds are stabilized by force. The model captures the drop in cell coupling with increasing substrate stiffness and simultaneous increase in cell adhesion observed experimentally. We show that this occurs only over a specific range of substrate stiffness values with the stiffness of AJs near its center. The relative sensitivity to force of focal adhesions (FAs) and AJs does regulate this phenomenon. Altogether, our results draw a clearer picture of the effects of cellular mechanics in cell decoupling.
Methods
The system studied via a computational model consists of two identical cells placed next to each other on a rigid substrate plane. The discrete element method (DEM) is a particle-based method used to represent both cells and the substrate via nodes. The DEM is different from the finite element method in that it is meshless. The bodies (i.e., two cells and substrate plane) are built, however, by setting fixed connections between the particles (i.e., nodes) and creating surfaces in three dimensions formed by two-dimensional (2D) elements (i.e., triangular mesh) (see Fig. S3). The triangles constituting the cells and substrate surfaces are used to calculate mechanical interactions between the different bodies in the system (12). This should not be confused with a mesh-based system such as the finite element method, in which the mesh is used to solve the continuum mechanical equations that govern motion.
The system is initialized such that the cells are spread on the surface and in contact with each other; thus, cell-cell and cell-ECM interfaces exist at the start of the simulations. In this way, the simulations represent the system observed experimentally, in which cell pairs are in contact with one another on patterned ligand substrates (6). A visualization of the cell and substrate displaying the meshing and substrate patterning can be found in Fig. S3. An interval of 4 h was simulated, long enough to ensure that a dynamic equilibrium was reached by the cell pair for analysis purposes. Fig. 1 consists of a schematic of the model presenting the different elements of the cells and the forces involved in the system. Formulation and implementation are presented next. Model parameters are listed along with their values and source of estimation in Table 1.
Figure 1.
Schematic of a cross section of cell pair displaying the different parts represented in the model (top). Forces involved in evolution of the mechanical system (bottom). The following relevant forces are indicated: cortical elastic spring (), cortical dissipation (), cortical bending (), local triangle and global cell area conservation (), cell volume conservation (), membrane contact (), FA (), AJ (), and stress fiber (). To see this figure in color, go online.
Table 1.
Model Parameters
| Symbol | Parameter | Value | Unit | Source |
|---|---|---|---|---|
| Rc | cell radius | 8 | μm | N/A |
| Lsubstrate | length substrate plane | 170 | μm | N/A |
| Wsubstrate | width substrate plane | 45 | μm | N/A |
| Llig | length ligand pattern | 165 | μm | N/A |
| Wlig | width ligand pattern | 40 | μm | N/A |
| kcortex | stiffness cell cortex | 2.9e−4 | N/m | (44) |
| Λd | cortex damping | 5e−1 | N ⋅ s/m | trial runs |
| kA,local | local area constraint | 5e−1 | N/m | trial runs |
| kA,global | global area constraint | 1e−8 | N/m | trial runs |
| kvolume | volume constraint | 8.5 | N/m2 | trial runs |
| kb | cortex bending constant | 8e−16 | N ⋅ m | trial runs |
| Ecortex | Young’s modulus cortex | 1e5 | Pa | (12) |
| νcortex | Poisson’s ratio cortex | 0.4 | N/A | (12) |
| Esubs | Young’s modulus substrate | 1e5 | Pa | N/A |
| νsubs | Poisson’s ratio substrate | 0.5 | N/A | (18,19) |
| Wcs | cell-substrate adhesion constant | 3.334e−4 | N/m | trial runs |
| Wcc | cell-cell adhesion constant | 1.25e−4 | Pa ⋅ s/m | trial runs |
| kgen,Δi | actin generation rate | 1.18e11 | 1/m2/s | interpolated from (13,45) |
| kdeg | actin degradation rate | 0.016 | 1/s | interpolated from (13,45) |
| Dactin | actin diffusion constant in cortex | 8e−14 | 1/s | interpolated from (45) |
| [G]Lp | actin threshold lamellipodium | 3.5e11 | 1/m2 | interpolated from (13,45) |
| [G]Lm | actin threshold lamellum | 4e10 | 1/m2 | interpolated from (13,45) |
| kFA | stiffness FA | 1e3 | N/m | (23) |
| kAJ | stiffness AJ | 1e-2 | N/m | N/A |
| kECM | stiffness substrate ligand | range (1e−4 to 1e−1) | N/m | trial runs |
| LFA,0 | resting length FA | 0.1e−9 | m | trial runs |
| LAJ,0 | resting length AJ | 2e−8 | m | trial runs |
| LECM,0 | resting length ligand | 1.4e−9 | m | trial runs |
| ron,FA | binding rate FA | 5e−3 | 1/s | trial runs |
| ron,AJ | binding rate AJ | 1e−2 | 1/s | trial runs |
| disassembly rate FA at zero force | 1e−3 | 1/s | (32) | |
| disassembly rate AJ at zero force | 1e−3 | 1/s | N/A | |
| Fc | adhesion maturation parameter | 3.5e−9 | 1/N | trial runs |
| ζFA | mechanosensing parameter FA | 4.25 | N/A | trial runs |
| ζAJ | mechanosensing parameter AJ | range (0.0 to 8.5) | N/A | N/A |
| Fam | reference actomyosin force | 0.5 | nN | (46,47) |
| Lthr | stress fiber shortening threshold | 7.5e−5 | μm | trial runs |
| λt,subs | cell-substrate tangential friction | 10 | kPa ⋅ s/m | trial runs |
| λn,subs | cell-substrate normal friction | 5e11 | kPa ⋅ s/m | trial runs |
| λt,cell | cell-cell tangential friction | 5e7 | kPa ⋅ s/m | trial runs |
| λn,cell | cell-cell normal friction | 5e7 | kPa ⋅ s/m | trial runs |
| ηl | liquid viscosity | 100 | kPa ⋅ s | trial runs |
N/A, not applicable.
Cell anatomy
Triangles forming the cellular surface are also used to demarcate distinct parts of the cellular anatomy that exist at the cell-substrate interface, specifically a lamellipodium and a lamellum. The former is the outermost area, where a protrusion force would be exerted outwards toward the cell perimeter by polymerization of actin (driving retrograde flow) and pushing off nascent adhesions in cell migration. The lamellipodium has a width that varies between 1 and 3 μm. Where the lamellipodium ends, the lamellum starts, also radially located in the cell-substrate interface. In the lamellum, actin flow slows down, allowing for formation of stress fibers binding mature FAs; the lamellum has a thickness of around ∼12 μm (13). A representation of the lamella of the cells in the cell pair can be found in Fig. S3. Beyond these two areas, the inner part of the cell-substrate interface is a part of the cell body in which no protrusion or formation of FAs can occur.
To demarcate these areas of the cell-substrate interface, the cellular perimeter is first identified. Triangles in the perimeter act as sources of actin. Actin diffuses across all other triangles with a diffusion constant (Dactin) in an act representative of actin retrograde flow. Together with diffusion, the concentration of actin at each triangle i (GΔi) (units of molecules/μm2) is determined by generation at perimeter and degradation of actin; all triangles act as sinks for actin. This effectively creates a gradient of actin concentration that is highest at the edge and decays along the bottom and top surfaces of the cell. The change in concentration of actin at each triangle is given by Eq. 1:
| (1) |
where kgen,Δi is the rate at which actin is generated per surface area unit at the edge triangles of the cell and kdeg the rate at which actin is degraded in all triangles. The third term in the right-hand side of the equation corresponds to diffusion across the cell surface (i.e., across the sides of the triangular element i in the 2D mesh) according to Fick’s second law. Diffusion is implemented as a forward Euler first-order finite volume scheme in two dimensions that guarantees conservation of mass; this simple scheme suffices because the time step is restricted by the fast mechanical relaxation time. By setting two threshold values, the lamellipodium and lamellum areas are dynamically defined in simulations, [G]Lp and [G]Lm: at every time step, the concentration of actin at each triangle i is checked; if [G]Δi > [G]Lp, then the triangle is part of the lamellipodium, and if [G]Lp > [G]Δi > [G]Lm, then the triangle is part of the lamellum. If [G]Δi < [G]Lp, the triangle is considered part of the cell body.
Deformable cell model
Each of the cells is generated by subdividing an icosahedron and projecting the nodes onto a sphere (14). Using five subdivisions, this corresponds to a total of 2562 nodes (5120 triangles) for a cell. The radius of the cell as a sphere, before spreading, is Rc = 8 μm. The surface mesh represents the actin cortex of the cell underlying the cell membrane, as the connections between nodes are made viscoelastic by connecting the nodes via Kelvin-Voigt elements (i.e., an elastic spring and viscous damper in parallel). A linear elastic spring is used, with Eq. 2 describing the magnitude of the force acting on the vertices connected by a line element:
| (2) |
where dij and are the actual distance and equilibrium distance between nodes i and j (vertices) and kcortex is the spring constant of the cellular cortex. The magnitude of the force contributed by the dashpot is described by Eq. 3:
| (3) |
where Λd is the damping constant and the projection of the velocity along the connecting axis between nodes i and j. Additional forces defining mesh geometry include a local triangle and global cell area conservation (FA), a cell volume conservation (Fvolume), and a resistance to bending based on the angle between the two planes defined by neighboring triangles (Fbend). The details on implementation of these forces describing the cortex elasticity can be found in the Supporting Materials and Methods.
A general note for parameter selection is that as a multiscale model (i.e., with cellular and subcellular scales), it is difficult to set every parameter equal to an experimental measurement: Many subcellular elements (e.g., organelles, such as nucleus) are not included, and a series of simplifications and assumptions need to be made to model an active cytoskeleton. For parameters determining cortex mechanical properties, parameter values were chosen based on a previous DEM model by the authors of a single cell spreading on a surface (12). That work analyzed spreading of a single cell of a different type over a shorter timescale. For this reason, we had to change certain parameters to include the additional subcellular elements; hence, the statement “trial runs” for multiple parameters in Table 1.
Substrate plane
The substrate is modeled as a rigid plane. It is a rectangle with dimensions of 170 × 45 μm2 (Lsubstrate × Wsubstrate); it is also triangulated with a surface mesh, using right isosceles triangles with area of 2.102 μm2. Triangulation is used to define smaller areas to which the cells can attach, representative of ligand patterning. For this study, the pattern was a smaller concentric rectangle of 165 × 40 μm2 (Llig × Wlig); see Fig. S3. This was done to avoid the cells attaching all the way to the end of the substrate plane but still limit the area to which the cells could attach. Substrate triangles are also used to discretize the area of the substrate and calculate the area of interaction between cell and substrate triangles, as well as to record local forces applied on the substrate to generate a traction map that shows the spatial distribution of tractions exerted on the substrate by the cell pair.
Cell adhesion
Two types of interactions between cells and between cells and substrate are modeled: transient and multiprotein complexes. The former represents transient binding of integrin molecules on the cell surface with ligands on the substrate (in the case of cell-substrate adhesion) and cadherin molecules on the membrane of different cells (in the case of cell-cell adhesion). The latter represents discrete mature molecular adhesions that have matured into multiprotein complexes: FAs (in the case of cell-substrate adhesion) and AJs (in the case of cell-cell adhesion).
Transient adhesion between triangles that are in contact is modeled according to Maugis-Dugdale theory (15). This theory describes interactions based on spherical overlap, so the interaction force () between a surface and its surroundings is computed as the interactions between two spheres corresponding to two triangles in contact. Maugis-Dugdale theory includes both a Hertzian elastic interaction (repulsion) for a radius of interaction a (based on sphere overlap), and an extended radius b (where b > a) in which an attraction potential is defined. To do this, the local curvature of the triangulated surface is calculated based on local node coordinates; this curvature is then used to fit a unique sphere to each triangle. Spheres have a Young’s modulus (Ecortex and Esubs for cell and substrate, respectively) and Poisson’s ratio (νcortex and νsubs for cell and substrate, respectively). The attraction constant describing the attraction potential is defined for cell-substrate (Wcs) and cell-cell (Wcc) transient interactions. An in-depth description of how Maugis-Dugdale theory has been applied in the context of contact mechanics can be found in the Supporting Materials and Methods. This force, applied at triangle-triangle contacts and accounting for both attraction and repulsion, ensures that cells spread on the substrate plane and that the cell-cell interface remains smooth.
Multiprotein complexes are modeled through discrete elements at the cell nodes of the triangular mesh. In the case of cell-substrate interaction, a node in the lamellum area can form a discrete adhesion (representative of an FA) with any point on the rectangular pattern (representative of ligand on the substrate plane) as long as it is within a (vertical) distance of 0.075 μm to the plane. In the case of cell-cell interaction, any two nodes in different cells within 0.75 μm of each other can form a discrete adhesion (representative of an AJ). This maximum interaction distance is larger for cell-cell interactions to ensure that the likelihood of forming each type of adhesion is similarly dependent on a binding rate because a node binding the substrate can bind anywhere on the plane (independent of meshing), whereas a node in proximity of another cell can only bind to another node.
Discrete adhesions, representative of multiprotein complexes, are implemented as noncompressible Hookean springs. In the case of FAs, a two-spring system (in series) is used, a representation already proposed by Schwarz et al. (16): a stiff spring represents the FA (spring constant kFA), whereas a softer spring represents the underlying ligand molecule (spring constant kECM). kFA is assumed to be constant, unlike parameter kECM. The force carried by the two-spring system describing the FA at node i () is described by Eq. 4:
| (4) |
where LFA,0 and LECM,0 are the equilibrium lengths of the FA and ECM ligand fiber and L is the length at each corresponding time step. is the unit vector in the axis that runs from point j in the substrate (not necessarily a node) to cell node i. Because kFA kECM, the FAs force response is dictated by kECM (see Table 1). The spring stiffness for the ligand can be converted to a bulk stiffness felt locally by the cell value according to Eq. 5, taken from Mitrossilis et al. (17):
| (5) |
where EECM is the Young’s modulus of the substrate, νsubs is its Poisson’s ratio, and D is the diameter corresponding to the interaction area around a single cell node with the substrate. νsubs was set to 0.5 (18,19), and D was set to 1 μm (which approximates the variable diameter observed throughout simulations). EECM will be assumed to be the substrate stiffness the simulated cell senses to compare our output with experimental results, given the limitation of using a rigid plane as the substrate; this assumes that each FA only senses the substrate with which it is directly in contact. In this way, different stiffness conditions can be modeled despite using a rigid plane as the substrate. The values of the spring constant used to define ECM stiffness were kECM = [1e−4, 3e−4, 5e−4, 1e−3, 2e−3, 3e−3, 5e−3, 1e−2, 2e−2, 3e−2, 5e−2, 1e−1] N/m. This corresponds to a bulk stiffness values of EECM = [0.025, 0.075, 0.125, 0.25, 0.5, 0.75, 1.25, 2.5, 5, 7.5, 12.5, 25] kPa.
According to Maugis-Dugdale theory, by regulating interaction of the cell and substrate, the Young’s modulus (Esubs) will affect attraction and repulsion (that is, forces in the direction perpendicular to the substrate plane). Cellular traction at each substrate triangle j () is calculated according to Eq. 6:
| (6) |
where = (Fx FA,i, Fy FA,i, Fz FA,i) is the force exerted by FA i, AΔ is the area of a substrate triangle, and nFA,Δ is the number of FAs bound to the triangle. Because only in-plane forces are considered to calculate traction, the stiffness the cells perceive when contracting is determined by the ligand stiffness (kECM).Thus, kECM is the determining factor in the system’s behavior in terms of cell contractility. The conversion to a bulk modulus (i.e., EECM) through Eq. 5 was done for the sake of comparison with experimental data from Polio et al. (6).
In the case of AJs, a single noncompressible Hookean spring is used to describe the adhesion (spring constant kAJ), assumed to be constant, like parameter kFA. The force carried by a single adhesion at node i () is described in Eq. 7:
| (7) |
where LAJ,0 is the equilibrium length of the spring representing an AJ and L is the length at each corresponding time step. is the unit vector in the axis that runs from node j on one cell to node i on another cell. At each node, if in proximity of a binding target, a discrete adhesion can be formed based on a binding rate for FAs (ron,FA) and AJs (ron,AJ) in a stochastic fashion. The approach to determine formation of an FA at a node according to a binding rate is based on the knowledge that FAs are formed from reinforcement of integrin-ligand bonds once a stress fiber binds to it and applies force (20). Because we do not model discrete actin monomers, specifically their diffusion and polymerization into stress fibers (see next subsection, Stress Fibers), there is no way of determining where in the lamellum a stress fiber would bind, apply force, and turn an integrin-ligand bond into an FA. Because diffusion is a random process, for ease of implementation, we assumed a random selection of nodes within the lamella to form FAs.
Similarly, a rate dictates how often adhesions are disassembled for FAs (roff,FA,i) and AJs (roff,AJ,i); however, this rate is made dependent on the magnitude of the force carried by the adhesion in such a way that force stabilizes the adhesion reducing the disassembly rate. This is the first way in which mechanosensing is accounted for in this model, and it is based on findings showing that multiprotein adhesion complexes are capable of mechanosensing and are stabilized by force through protein recruitment (11,21,22). Based on modeling of catch bonds (23), Eq. 8 describe the relation between disassembly rate and force carried by the adhesions:
| (8) |
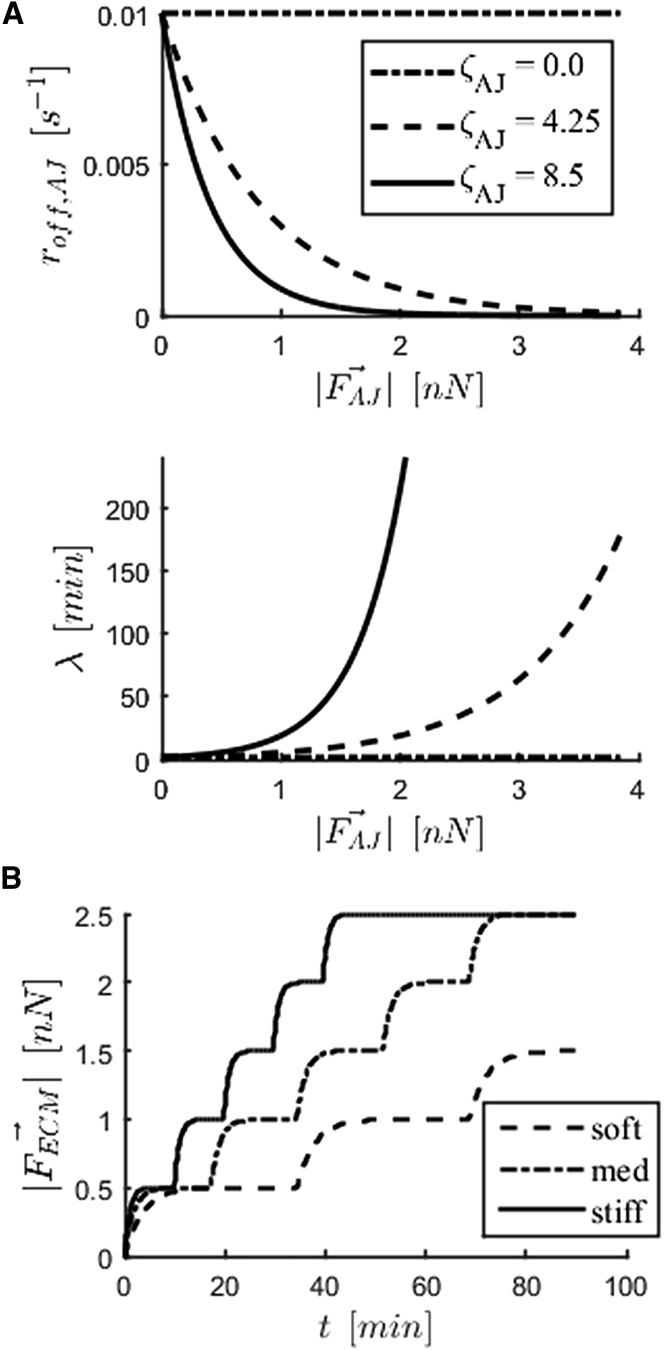
signifies the rate of disassembly when no force is carried by an adhesion; ζ and Fc are parameters that control the degree of mechanosensing. Fig. 2 A shows the effect of varying the parameter ζAJ on the disassembly rate of AJs and the corresponding expected adhesion lifetime values as a function of force. If an FA is outside of the lamellum (which can occur because of displacement of the cell nodes with force or change in shape of the lamellum), the force-dependent rate of disassembly (roff,FA,i) is increased by a factor of 10.
Figure 2.
Implementation of mechanosensing mechanisms in the cell. (A) AJ disassembly rate (roff,AJ) decreases with force carried by adhesion ()(top). Corresponding expected adhesion lifetimes (λ), where roff,AJ = 1 − e−1/2 (bottom). Parameter ζAJ dictates sensitivity to force. (B) Step increase in force carried by ECM () bound to an FA and applied by a stress fiber. Steps correspond to stalling in fiber contraction. The stiffer the substrate, the faster a fiber strengthens, taking more steps during its lifetime. Graphs shown are a result of a simulation of an isolated two-spring system (ideal case).
Because of stochasticity in the model arising from the probabilistic implementation of FA and AJ binding and disassembly, simulations are not deterministic, and a different result is expected every time a simulation is run. To be able to reliably compare results between simulations corresponding to different conditions, simulations for each condition were run in replicates (n = 5) and results averaged over these simulations.
Stress fibers
Stress fibers are simulated as a pair of equal and opposite forces acting on a pair of discrete adhesions (either two FAs or an FA and an AJ) attracting them to one another. These forces represent tension carried by stress fibers arising from the action of myosin II motors sliding along antiparallel actin bundles constituting the fiber. A fiber will form within a cell, connecting two adhesions chosen at random, if the potential fiber meets three conditions:
-
1
Adhesion is not already bound to a fiber.
-
2
The fiber has a minimum initial length of 11 μm.
-
3
The orientation angle of the fiber is equal or lesser than π/10 rad; this angle is the intersection of the projection of the fiber on the substrate plane and the long side of the rectangular ligand pattern.
Conditions 2 and 3 were set based on observations in the literature that fibers will only form along the long axis of a rectangular underlying pattern (6,7). A fiber remains bound to the nodes and exerts force as long as both nodes are engaged in a discrete adhesion; as soon as one of the two adhesions is disassembled, the fiber (and corresponding force) is deleted. A visualization of the location of FAs within the lamellum, AJs in the cell-cell interface, and stress fibers bound to these adhesions can be found in Fig. S3.
When formed, fibers have a set force magnitude (Fam, where am stands for actomyosin). The force exerted by the fiber brings the adhesions connected via the fiber closer to one another. The distance between adhesions (i.e., fiber length) is calculated at every time step and the values averaged over 10 s intervals; this is done to obtain a value of fiber length that is stable despite fluctuations due to all the different forces acting on each node. When the length ceases to change for a particular fiber f, a factor describing fiber strengthening (nstr,f) is incremented. This stalling in fiber length corresponds effectively to the moment when the difference between subsequent (i.e., 10 s apart) averaged values of the length falls below a threshold (Lthr). The force exerted by stress fiber f on node i when connecting nodes i and j is described in Eq. 9:
| (9) |
where is the unit vector in the axis that runs from node i to node j. Upon formation, fibers have a value of nstr,f = 1. With each stalling event, this factor is increased by the value of 1 up to a maximum of 5 (under the assumption that there is a limit to the force exerted by a stress fiber).
This strengthening of stress fibers is another mechanism of mechanosensing found in cells; it is based on the experimental findings by Wolfenson et al. (24) and a previous theoretical work by Parameswaran et al. (25). Wolfenson et al. (24) showed that there is a stepwise strengthening of actomyosin fibrils, concurrent with recruitment of α-actinin molecules to FAs upon stalling of underlying substrate deformation. The authors suggest that simultaneous recruitment of myosin to the fibrils is responsible for their strengthening. The interval between maturation steps depended on substrate stiffness, with strengthening occurring more often on stiffer substrates (25). These studies explain how cells exert higher tractions on stiffer substrates. An ideal dependence of fiber strengthening on substrate stiffness is shown in Fig. 2 B, which shows the evolution of the force carried by the two-spring system () representing the FA and ligand (i.e., ECM) as the force exerted by a single stress fiber increases in steps triggered by fiber stalling. The experimental findings by Wolfenson et al. (24) are recreated through the stress-fiber-strengthening mechanisms implemented in this model; fibers will stall faster in cells on stiffer substrates (rate of force increase is higher (16)) and thus undergo a strengthening step more often than fibers in cells on softer substrates. Thus, in the same time span, fibers will strengthen more and exert more force in cells on stiffer substrates.
Equation of motion
Evolution of the system is described by the equation of motion. Because cells occupy a low Reynold’s (overdamped) environment in which inertial forces are negligible (26), conservation of momentum for each node takes the form of Eq. 10:
| (10) |
The left-hand side contains the sum of all forces acting on each node at each time point. The linear force due to the springs in the Kelvin-Voigt model are summed for each node over all connections (conn.). For the Maugis-Dugdale force, because it acts on the triangles in the mesh, forces are transfixed to the nodes (12). The forces are described according to Eqs. 2, 3, 4, 7, and 9 and S3–S21.
The right-hand side of the equation shows the viscous friction, which in an overdamped environment is described by the product of friction (described by a friction tensor, Λ or Γ, defined in terms of friction coefficients, λ or η) acting on node i and its velocity (). A mathematical description of the dissipative forces in terms of friction coefficients and medium’s viscosity can be found in the Supporting Materials and Methods, in the “Dissipative forces” subsection (Eqs. S22–S27). The different sources of friction include dissipation of the actin cortex by all dampers j connected to node i according to damping constant Λd (Eq. S24); friction due to contact with substrate triangles (Γsubs), a function of tangential and normal friction coefficients (λt,subs and λn,subs, respectively) that takes into account area of triangles in contact at the cell and the substrate (Eqs. S25–S27); friction due to contact with triangles of the other cell (Γcell), a function of tangential and normal friction coefficients (λt,cell and λn,cell, respectively) calculated in the same way as friction with the substrate but for triangles of the two cells that are in contact (Eqs. S25–S27); and Stokes’ drag (Γliquid), a function of the liquid’s viscosity (ηl) (Eqs. S22 and S23).
The contributions of the friction to each node are added in a friction matrix at each time step, which, together with the summation of forces, can be used to solve for velocity and thus find the position in the next time step. Equation 10 is a first-order differential equation that couples the movements of all nodes. The system is solved iteratively for the velocities using the conjugate gradient method. Because of particular properties of the friction matrix, this system can be solved using a forward Euler scheme. This is presented in more detail in the Supporting Materials and Methods. A time step of 0.05 s was used in all simulations. All simulations are performed using the C++ particle-based software Mpacts (http://mpacts.com). Each simulation was run using an Intel Xeon Processor E5-2680 v3 on a node with 2.7 GB of memory; simulations were run in parallel utilizing the multiple nodes (20) per core. Each simulation took ∼12 h to run.
At the time of publication, Mpacts is a closed-source software. To ensure reproducibility, however, we make use of the Docker platform (https://www.docker.com). Docker allows recreation of an exact runtime computational environment. With the reproducibility package, available in GitLab (https://gitlab.mech.kuleuven.be/MAtrix/mpact-docker-reproduce-cellpair), one can create a runtime environment similar to the one that we used to run simulations presented in this work. This package allows creation of a ready-to-be-used Linux machine with Mpacts software and its dependencies installed in it. The user may change the parameter values in the simulation script, run a cell-pair simulation through Docker, and visualize the results using visualization software such as Paraview (https://www.paraview.org). Documentation for all commands, including those used in the simulation script provided, can be found in http://dev.mpacts.com/documentation/index.html. A detailed description of how to run the reproducible simulation and a description of all provided files can be found in GitLab.
Results and Discussion
Each simulation consisted of a cell pair interacting with one another on a rectangular patterned substrate for a period of 4 h. The stiffness of the substrate (EECM) as well as the parameter controlling the degree of mechanosensing of AJs (ζAJ) were varied to define the different conditions. The following values of substrate stiffness were used: EECM = [0.025, 0.075, 0.125, 0.25, 0.5, 0.75, 1.25, 2.5, 5, 7.5, 12.5, 25] kPa. To explore the effect of mechanosensing at the adhesion complexes on cell-pair coupling and its dependence on substrate stiffness, we varied ζAJ relative to ζFA. The difference in the values of ζ for each type of adhesion can represent the difference in the force-sensitive molecules responsible for stabilization with force, for example, α-catenin in AJs (11) and talin in FAs (27). Three different scenarios were considered based on the relative difference in these parameters, such that we explore what occurs when AJs are not mechanosensing, when FAs and AJs are equally mechanosensing, and when AJs are relatively more mechanosensing. These scenarios and corresponding values of parameter ζ were ζFA (4.25) > ζAJ (0.0), ζFA (4.25) = ζAJ (4.25), and ζFA (4.25) < ζAJ (8.5). Rather than choosing two arbitrary values for ζFA and ζAJ, it is more insightful to look at relative proportions of the two parameter values. FA mechanosensing was present in all simulations (i.e., a single value of ζFA was used) because mechanosensing of FAs has been more extensively studied than that of AJs; mechanosensing in AJs was only suspected, but not measured, because of structural similarities with FAs (28,29), and only recently have FRET sensors been introduced in AJs (30). Meanwhile, the role of AJ mechanosensing was questioned when analyzing cell-cell coupling, and thus, three different values were selected.
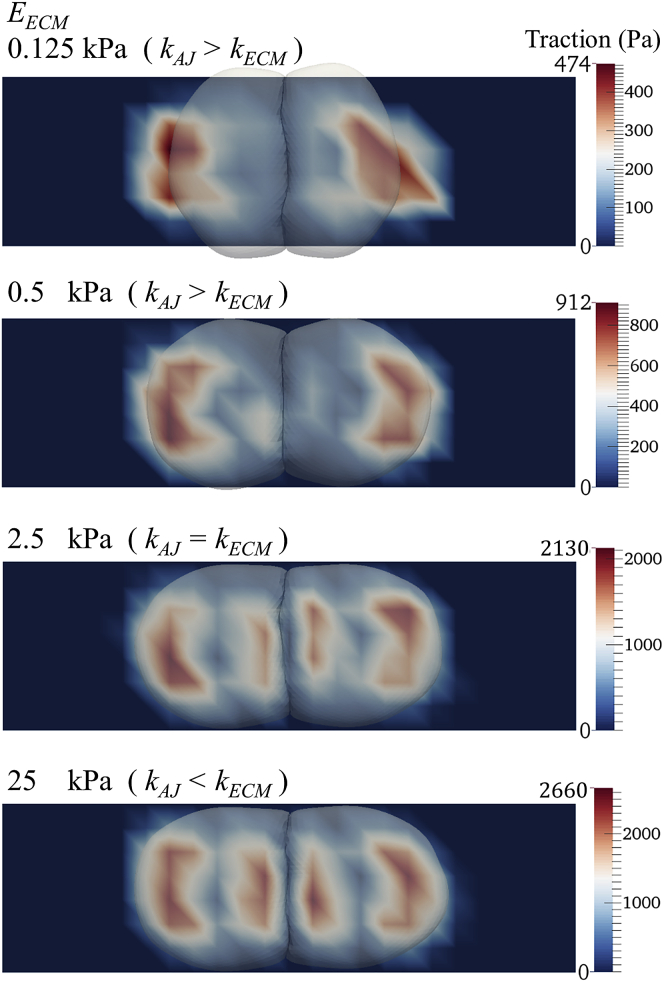
Qualitatively, decoupling with increasing ECM stiffness can be observed by the redistribution of traction forces along the cell-substrate interface. This is shown in Fig. 3, in which characteristic traction maps of cell pairs on substrates of varying stiffness along with cellular outlines are displayed: on soft substrates, the cells are coupled, and force is mostly exerted by stress fibers connecting FAs in the outer cellular lamella (i.e., farthest away from cell-cell interface) and AJs at the cell-cell interface. In the traction map, this means the highest tractions are located at the edges of the cell pair. As the substrate stiffness increases, there is a progressive decoupling, evident in the appearance of tractions also in the inner lamella (i.e., closest to the cell-cell interface). In addition to fibers connecting FAs in the outer lamella to AJs in the cell-cell interface, there are fibers connecting FAs in the outer lamella to FAs in the inner lamella. The magnitude of tractions exerted below the inner lamella become comparable to those in the outer lamella and are thus noticeable in the presented traction maps. This matches the observations made on cell pairs in vitro (6,7).
Figure 3.
Traction maps for simulation of cell pairs on substrates of varying stiffness while maintaining constant AJ stiffness. Decoupling with increasing substrate stiffness (EECM) is evidenced by the spatial redistribution of cellular tractions in the cell-substrate interface from underneath the outer region of the cell pair to underneath the cell-cell interface. These sample cases correspond to simulations with maturing FAs, but not AJs (ζFA > ζAJ). An animation of the entire simulation for each of these cases can be found as Videos S1, S2, S3, and S4. To see this figure in color, go online.
In all scenarios, there was a qualitative agreement with experiments: by simulating cells pairs on increasingly stiff substrates, the model resulted in decoupling of cells, an increase in the number of FAs, and an increase in the contractile strength of the cell pair.
To quantify this behavior, the results were analyzed using the same metrics used to characterize the behavior of cell pairs in vitro (6): intercellular force (Fj,cell), the contractile moment of the cell pair (Mxx), the number of FAs, and cell coupling (ψ). The intercellular force (Fj,cell) exerted by each cell was calculated as the unbalanced traction force exerted by the cell on the substrate through the total number of FAs (nFA,cell) of the cell, as described by Eq. 11:
| (11) |
The contractile moment of the cell pair (Mxx), as first described by Butler et al., is a scalar measure of the cell's contractile strength (31). It can be thought of as the dipole strength of a force dipole, consisting of two point forces separated by a distance. Both point forces have equal magnitude and act in opposite directions and can be calculated directly from the traction field with no additional geometrical information. This scalar metric is extremely useful in describing the contractile strength of elongated cells such as smooth muscle cells, which exert their force in a specific direction. If the cell were to change phenotype and become more like a fibroblast (as can happen in culture) and distribute its traction forces in all directions while maintaining the same strength, the contractile moment along a particular axis would be sensitive to this change and decrease even when other metrics like root mean-square traction would not be sensitive to these changes. To calculate the contractile moment, the distance along the x direction at which the traction force is exerted from the cell-cell interface (rx FA,i) is used to define the dipole along the axis. The metric was calculated according to Eq. 12:
| (12) |
where = (Fx FA,i, Fy FA,i, Fz FA,i). The distance rx FA,i is signed and calculated along the x axis (aligned with the long side of the rectangular pattern), and it is the distance from the average x position of the cell-cell interface and the FA. More details on the calculation of Mxx can be found in Fig. S4.
Because cells are known to exert higher tractions on stiffer substrates, the measure of intercellular force does not suffice to describe the coupling strength of cells. To account for this, a dimensionless ratio dubbed cell coupling (ψ) is used. This metric, defined in Eq. 13, is the average over the two cells of the ratio of the magnitude of the intercellular force exerted by each cell () to the contractile moment of the cell normalized by cell length (Nxx,cell). The normalized moment of each cell is defined in Eq. 14. A higher cell-coupling value (ψ) means relatively more force is exerted by the cells on each other; in contrast, a lower value of ψ means the cells are less coupled (relatively decoupled), with more force exerted by the cells on the substrate.
| (13) |
and
| (14) |
where Lcell is the length of the cell along the along the x axis (Fig. S4).
Values for intercellular force (Fj,cell), contractile moment of the cell pair (Mxx), number of FAs, and cell coupling (ψ) are displayed in Fig. 4, A–D. Reported values were obtained by averaging the results of the replicates (n = 5) run for each condition. For each simulation, the values at every minute over the last hour were averaged to obtain a single one; this was done to account for fluctuations in the active system. Because the values presented are means of means (average for all simulations (replicate) per condition, in which for each simulation, a value is obtained by averaging over time (t = 60 min)), the standard error of the mean is presented to show variability between replicates so comparisons between conditions can be reliably made.
Figure 4.
For a Figure360 author presentation of this figure, see https://doi.org/10.1016/j.bpj.2020.05.036.
The mechanosensing capability of adherens junctions relative to focal adhesions was varied by varying the parameter ζAJ while keeping ζFA the same. Average values for simulated cell pairs of (A) intercellular force (Fj,cell), (B) contractile moment of the cell pair (Mxx), (C) cell coupling (ψ), and (D) number of FAs bound to a stress fiber. n = 5. Error bars correspond to standard error of the mean. (E) Corresponding experimental results. Adapted from Polio et al. (6).
Force-dependent adhesion maturation regulates stress fiber dynamics
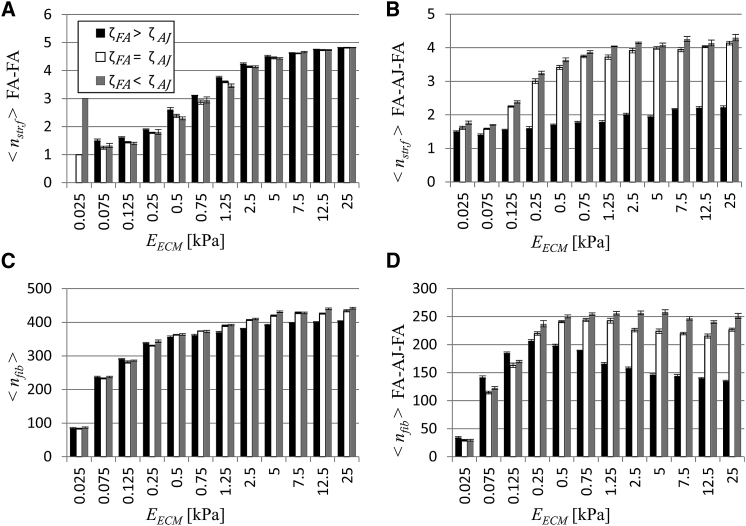
The results displayed in Fig. 4, A–C, show a drastic effect when making AJs mechanosing (ζFA ≤ ζAJ) relative to when they are not (ζFA > ζAJ). To explore what differs between these conditions, the stress fibers were more carefully analyzed. This quickly suggested that the connections between stress fibers and adhesions made a difference in terms of force response. Three different configurations in terms of connections can be defined: 1) a stress fiber connecting two FAs (FA-FA), 2) stress fibers that connect an FA to an AJ itself bound to another stress fiber (FA-AJ-FA), and 3) stress fibers that connect an FA to an AJ not bound to any other fiber (FA-AJ). A graphical representation of these configurations can be found in Fig. S5.
The factor describing fiber strengthening (nstr,f) due to stalling during shortening was recorded and analyzed. For fibers in each configuration, there was a difference in this strengthening factor. These results for the first two configurations are presented in Fig. 5, A and B. In the case of the third configuration (i.e., fibers bound to an AJ only bound to a single fiber), no fiber matured (data not shown). Also shown are the number of stress fibers in the cell pairs regardless of configuration in Fig. 5 C and the number of fibers that connect an FA to an AJ itself bound to another stress fiber (FA-AJ-FA) in Fig. 5 D.
Figure 5.
(A) Average value of factor describing stress fiber strengthening for fibers in cell pair connecting two FAs (<nstr,f> FA-FA). (B) Average value of factor describing stress fiber strengthening for fibers in cell pair connected to another via an AJ (<nstr,f> FA-AJ-FA). (C) The number of fibers in cell pair in all configurations (<nfib>). (D) The number of fibers in cell pair connected to another via an AJ(<nfib> FA-AJ-FA). n = 5. Error bars correspond to standard error of the mean.
The increase in number of stress fibers with increasing substrate stiffness (Fig. 5 C) can be attributed to the increase in fibers that connect an FA to an AJ itself bound to another stress fiber (FA-AJ-FA) on low-stiffness substrates (Fig. 5 D) and to the increase in fibers connecting two FAs (FA-FA) on high-stiffness substrates (Video S2. Animation of Top View of Simulation of Cell Pair on Substrate with Stiffness Corresponding to EECM = 0.5 kPa, Video S3. Animation of Top View of Simulation of Cell Pair on Substrate with Stiffness Corresponding to EECM = 2.5 kPa, Video S4. Animation of Top View of Simulation of Cell Pair on Substrate with Stiffness Corresponding to EECM = 25 kPa, Figure360. An Author Presentation of Fig., Document S2. Article plus Supporting Material A). Meanwhile, the fibers that connect an FA to an AJ not bound to any other fiber (FA-AJ) are few in comparison (Fig. S6 B) because less resistance to contraction prevents the adhesions from maturing.
This change in the number of fibers in different configurations at different stiffness ranges shows that there is a competition for the limited number of nodes in the lamella to which stress fibers can bind once an FA is formed. On low-stiffness substrates, stress fibers binding AJs in the cell-cell interface dominate cell-pair contraction; meanwhile, as the substrate stiffness increases (and the stiffness sensed by fibers at the cell-cell interface remains the same), stress fibers binding two FAs (FA-FA) win. At this point, forces exerted on the substrate account for most of cellular contraction. This competition between stress fibers in different configurations (demonstrated by change in ) and relative strength of each (demonstrated by change in ) explains the spatial redistribution of tractions with changing substrate stiffness shown in Fig. 3. This phenomenon is strongest when AJs are not stabilized by force (ζFA > ζAJ), such that fibers bound to the cell-cell interface have less time to strengthen. Competition among the different fiber configurations can explain how simulated results match experimental observations.
Decoupling occurs faster as substrate stiffness increases
To better understand the competition between stress fibers in different configurations, the change in number of stress fibers over time throughout the simulations was analyzed. The average number of stress fibers in both FA-FA and FA-AJ-FA configurations were quantified along with their ratio, as defined by Eq. 15:
| (15) |
This analysis is presented for the scenario in which AJs are not stabilized by force (ζFA > ζAJ) in Fig. S7. This scenario was chosen because it is the clearest, given the more drastic decoupling with increasing substrate stiffness relative to the other two scenarios (Fig. 4 C). Similar trends, however, occurred in the additional two scenarios (data not shown).
All simulations were found to have a very similar starting point with a value of φ between 0.6 and 0.8 (i.e., a few more fibers in the FA-AJ-FA configuration). During the simulation, this value increased in some conditions, symbolizing an increase in stress fibers in the FA-FA configuration and decoupling. In some cases (cases with relatively high substrate stiffness (EECM)), the value reached φ = 1, which is the substitution point of FA-AJ-FA stress fibers for FA-FA stress fibers. In other cases (cases with relatively low substrate stiffness (EECM)), φ decreased, representative of an increase in stress fibers in FA-AJ-FA configuration and associated with no decoupling.
Also revealing was the slope of the stress fiber ratio (Δφ = ). Fig. S7 shows that the slope during decoupling was different as a function of substrate stiffness (EECM). This meant that the substitution point (i.e., φ = 1) occurred earlier when substrate stiffness was higher. Thus, decoupling occurs faster as substrate stiffness increases.
Stabilization of AJs is needed for intercellular force increase
In Fig. 4 A, the intercellular force (Fj,cell) increases with substrate stiffness in the scenarios in which AJs matured with force (ζFA = ζAJ and ζFA < ζAJ), but not in the scenario in which only FAs did (ζFA > ζAJ). Without maturation of AJs, these adhesions are shorter lived, and thus, there is less time for stress fiber stalling and subsequent strengthening. Meanwhile, Fig. 5, A and B show that there is an increase in strengthening of fibers with increasing substrate stiffness in all scenarios. Albeit slight, the increase in FA-AJ-FA exists even in the scenario in which only FAs matured (ζFA > ζAJ). This revealed that even when there is no AJ maturation, by increasing the expected lifetime of AJs (the average expected lifetime of AJs is ∼17 min when ζFA > ζAJ, which corresponds to -value in Table 1), stress fibers bound to AJs can still stall and strengthen. This strengthening, however, did not result in an increase in intercellular force (Fj,cell), as shown in Fig. 4 A. This lifetime corresponds to the lifetime of adhesions observed biologically (32).
In the scenario in which AJs were not mechanosensitive (ζFA > ζAJ), despite the fact that intercellular force (Fj,cell) did not increase with substrate stiffness, there was decoupling. This is explained because cell coupling (ψ) is defined by the ratio of Fj,cell/the normalized contractile moment (Nxx cell) (Eq. 13). In this scenario, the contractile moment of the cell (Mxx,cell) increases with substrate stiffness (Fig. 5 B). The contractile moment and normalized contractile moment are related according to Eqs. 12 and 14; they have the same trend with changing substrate stiffness as shown below (despite the changes in length of cells (Lcell) because of how much the ligand molecules can be stretched by the cells) (data not shown). Competition between the different stress fiber configurations is responsible for decoupling in this case as well.
When comparing between the scenarios in which AJs matured (ζFA = ζAJ and ζFA < ζAJ), intercellular force was higher as the factor describing dynamics of mechanosensing (i.e., ζAJ) increased; this occurred particularly at higher substrate stiffness values (EECM ≥ 0.25 kPa) and can be seen in Fig. 4 A. Intercellular force is determined by force exerted by fibers bound to the cell-cell interface (the majority in configuration FA-AJ-FA), so to understand how it varies, we looked to maturation of these fibers. We did not necessarily expect ζAJ to have an effect on intercellular force because force is exerted by the stress fibers, which strengthen independently of the maturation of adhesions (i.e., nstr,f is independent of ζAJ). The increase in lifetime due to maturation does give stress fibers more time to stall and consequently strengthen.
In both scenarios (ζFA = ζAJ and ζFA < ζAJ), the factor nstr,f appears to plateau with increasing substrate stiffness (Fig. 5 B). The plateau in fibers in the configuration FA-AJ-FA is reached at a lower stiffness value relative to those in the configuration FA-FA; more specifically, in the former, the plateau is reached at around 2.5 kPa, the value of the AJ spring constant (kAJ). The stiffness of the AJs (kAJ) acts as a sort of threshold above which stiffness of the substrate (EECM) will no longer dictate intercellular force.
Experimentally, the intercellular force between cells in cell pairs increased from 0.022 to 0.15 μN (factor of ∼6.7) when cells went from 0.3 to 13 kPa (Fig. 4 E). In simulations for the scenario in which FAs and AJs are equally mechanosensitive (ζFA = ζAJ), there was an increase from 0.29 to 0.33 μN when cells went from 0.25 to 12.5 kPa; this amounts to a factor of ∼1.14. Over the entire substrate stiffness range studied, intercellular force increased by a factor closer to ∼2.2.
Increased intercellular force and increased contractile moment of the cell pair occur together
In all scenarios of maturation of AJs (relative to FAs), the contractile moment of the cell pair (Mxx) increases with substrate stiffness (Fig. 4 B). In the scenario in which only the FAs mature (ζFA > ζAJ), the contractile moment increases (unlike intercellular force) because this quantity depends on all configurations of stress fibers and adhesions and not only the configuration FA-AJ-FA (as was the case for intercellular force). Fibers bound to two FAs will increasingly strengthen with increasing substrate stiffness until they have reached the maximum factor (nstr,f = 5). Fibers in the configuration FA-FA on average near this maximum value of nstr,f = 5 at a stiffness value of EECM = 25 kPa (Fig. 5 A). In the scenarios in which AJs matured (ζFA = ζAJ and ζFA < ζAJ), the contractile moment increased more drastically with increasing substrate stiffness because of the contribution of fibers binding the interface. This is evidenced in the corresponding increase in intercellular force relative to the scenario in which only the FAs mature, already discussed (Fig. 4 A).
Experimentally, the contractile moment increased from 7.03 to 24.65 pN ⋅ m (factor of ∼3.05) when cells went from 0.3 to 13 kPa (Fig. 4 B). In simulations for the scenario in which FAs and AJs are equally mechanosensitive (ζFA = ζAJ), there was an increase from 5.29 to 12.28 pN ⋅ m when cells went from 0.25 to 12.5 kPa, which amounts to a factor of ∼2.32.
The original experimental study that motivated this model reports measurements for two different substrate stiffness values (i.e., 0.3 and 13 kPa); at 40 kPa, cells were visualized and FA and AJ markers stained, but no displacements could be measured or forces calculated because of the high stiffness (6). For these reasons, the effectiveness of the implemented mechanosensing of FAs cannot be assessed using the experimental results reported by Polio et al. (6). To do so, the total traction force applied by the cells on the substrate was quantified according to Eq. 16:
| (16) |
Ftot,cell is a scalar quantity representing the total force magnitude exerted by stress fibers on the substrate via FAs. The average total force magnitude for a single cell in the pair for all simulated conditions can be found in Fig. S8. These values can be compared to the traction force magnitudes recorded in the work by Califano and Reinhart-King (33). This study quantifies total force magnitude for individual bovine aortic endothelial cells that were in contact with other cells, in some figures even showing highly polarized cell pairs similar to our model system. Although a different cell type is used and they are cultured on collagen instead of gelatin, Fig. S8 shows that in both studies, there is an increase in cell force with increasing substrate stiffness (also evidenced by Mxx; Fig. 4 B). The simulated results match the experimental study by Califano and Reinhart-King (33) in both the range of forces of a single cell (0.2–0.8 μN) and increase over the range of substrate stiffness (1–10 kPa). This provides confidence about the implemented FA mechanosensing mechanism and results.
The stiffness of the cellular interface relative to the substrate arbitrates cell coupling
Cell coupling (ψ) is defined in terms of intercellular force (Fj,cell) and contractile moment of the cells (Nxx,cell) (a quantity related to Mxx) according to Eq. 13. On low substrate stiffness (EECM ≤ 0.125 kPa), there is a slight increase in cell coupling with increase in substrate stiffness, and maturation of AJs (ζAJ) has no effect on coupling (Fig. 4 C). A more drastic effect, however, is observed on stiffer substrates (0.125 kPa < EECM < 2.5 kPa), for which coupling decreases visibly with increasing substrate stiffness. This decrease is less drastic as the degree of mechanosensing of AJs increases (i.e., as ζAJ increases).
The change in coupling with substrate stiffness is again relatively small on the stiffest substrates, specifically at EECM ≥ 2.5 kPa, the value of the AJ spring constant (kAJ). This is expected from the definition of cell coupling in terms of intercellular force and contractile moment and their dependence on substrate stiffness: the trend in cell-coupling values is a result of the limit reached by intercellular force (Fig. 4 A) and the limit in maturation of stress fibers (Fig. 5, A and B) at this substrate stiffness. Experimentally, cell coupling also decreased: it decreased from 0.51 to 0.3 (factor of ∼0.6) when cells went from 0.3 to 13 kPa (Fig. 4 B). In simulations for the scenario in which FAs and AJs are equally mechanosensitive (ζFA = ζAJ), there was a decrease from 1.42 to 0.92 when cells went from 0.25 to 12.5 kPa; this amounts to a factor of ∼0.65. These results suggest that the substrate stiffness values probed experimentally (i.e., 0.3 and 13 kPa) lie on different sides of the perceived cell-cell interface stiffness and thus cause a difference in cell coupling.
These results suggest that AJ maturation acts counter to cell decoupling, yet it is needed for intercellular force to increase with increasing substrate stiffness. Cellular decoupling with increasing substrate stiffness could be attributed to strengthening of stress fibers. Fiber strengthening for fibers bound to the cell-cell interface, however, will be attenuated when the substrate becomes as stiff or stiffer than the perceived cell-cell interface (here dictated by AJ stiffness or kAJ) because of competition between the stress fibers in the different configurations (Fig. S5). At this point, the increase in substrate stiffness will not lead to further strengthening of fibers because the contraction dynamics of the stress fibers and adhesions configuration will be dictated by the softest link; fibers bound to AJs will not mature further, whereas those connecting two FAs will. This gives them the advantage, and over time, they will outlive and replace those exerting force on the cell-cell interface. The cells then become decoupled. This also explains why there is no strengthening of stress fibers that bind an FA to an AJ not bound to any other fiber (FA-AJ): these fibers feel only the cell-cell interface, which has a stiffness dictated by the stiffness of the cell cortex (kcortex) and a series of other parameters (e.g., kb, Wcc).
Increase in number of FAs close to cell-cell interface accompanies decline in cell coupling
Unlike cells in vitro, in which an FA only exists if reinforced, in our simulations FAs can form based on the rate of assembly (ron,FA) and continue to exist if stabilized by force, exerted mainly by stress fibers bound to the adhesion itself. For this reason, to compare the number of FAs with experimental measurements, the number of FAs in the cell pair that are bound to a fiber was tallied (Fig. 4 D).
The number of FAs was much lower at the softest substrate stiffness; here, the substrate stiffness is so low that the cell easily deforms it, and the stress fibers keep contracting and never stall, preventing the strengthening of fibers connecting two FAs. This meant no fibers in the FA-FA configuration remained at the end of the simulations at the lowest stiffness condition (EECM = 0.025 kPa) (Video S2. Animation of Top View of Simulation of Cell Pair on Substrate with Stiffness Corresponding to EECM = 0.5 kPa, Video S3. Animation of Top View of Simulation of Cell Pair on Substrate with Stiffness Corresponding to EECM = 2.5 kPa, Video S4. Animation of Top View of Simulation of Cell Pair on Substrate with Stiffness Corresponding to EECM = 25 kPa, Figure360. An Author Presentation of Fig., Document S2. Article plus Supporting Material). The cells contracted extensively, creating a larger cell-cell interface, such that they did not meet the minimum length criterion for stress fibers to form (see Methods). In substrates of all other stiffness values, a cell-substrate interface large enough for lamella to develop and fibers to form and strengthen was formed. The number of FAs increased in the interval EECM (0.075–25) kPa. Experimentally, the extent of discrete cell-substrate adhesion was measured via the area of FAs measured from fluorescence imaging; it increased from 49.03 to 80.7 μm2 (factor of ∼1.64) when cells went from 0.3 to 13 kPa (Fig. 4 E). In simulations for the scenario in which FAs and AJs are equally mechanosensitive (ζFA = ζAJ), the increase in the number of FAs when cells went from 0.25 to 12.5 kPa was from 369.91 to 589.15 adhesions; this amounts to a factor of ∼1.59.
The increase in the number of FAs can be attributed to the shift in number of the different categories of stress fibers, particularly the triumph of stress fibers binding two FAs (FA-FA) over those connecting FAs to the cell-cell interface on stiffer substrates. FAs bound to these fibers will be stabilized by the increased force with fiber strengthening. This is especially true for the inner lamella, in which only stress fibers binding two FAs can bind and exert force. This explains how in these areas close to the cell-cell interface, there is increased traction exertion with increasing substrate stiffness; the results are shown qualitatively to match experimental findings in Fig. 3.
This phenomenon, in which FAs form at a distance from where the intercellular junction and AJs form, has been observed not only with changes in substrate stiffness as a driver but brought along by substrate geometry. Tseng et al. placed mammary epithelial (MCF10A) cell pairs on square (outline), [H]-shaped, or [hourglass]-shaped (outline) micropatterns instead of a rectangular pattern (filled) and found that the cell-cell adhesions will be positioned over areas where no ligand is present (i.e., outside the pattern in which no FAs can form) (34). Although the mechanisms behind this observation remain unknown, researchers were able to show that the exertion of cell-cell forces is involved in the spatial guidance of cell-cell adhesions away from the substrate. Cells exerted lower forces at cell-cell interface (and overall) when the interface was located away from the ligand, possibly in an effort to minimize intracellular tension. In our simulations, we see intercellular tension reaches a limit despite increasing substrate stiffness (Fig. 4 A), whereas the contractile moment of the cell pair continues to increase (Fig. 4 B). The result is a decoupling of cells in which competitive binding due to differing responses to the substrate stiffness of FAs and AJs causes the FAs to replace AJs near the cell-cell interface. This suggests that in these different geometries used by Tseng et al. (34), there may be a replacement also driven by competitive binding and mediated by the differing mechanosensing attributes of FAs and AJs.
Cell decoupling will only occur in a range of substrate stiffness values
The range of substrate stiffness values was chosen after preliminary simulations showed that the cell pair stalled in its force response at both ends of the range. At the lowest value (EECM = 0.025 kPa), cells contract, creating an exceptionally large cell-cell interface and a small cell-substrate interface; very few fibers in the FA-FA configuration could form, and those binding the outer lamella to the cell-cell interface barely strengthened because of the soft substrate. This explains the sharp transition observed in the number of fibers () observed on substrates between EECM = 0.025 and 0.075 kPa (Fig. 5 C). Comparing simulations on these same stiffness values in terms of strengthening of stress fibers connected via AJs, there is no difference in terms of maturation. Together, these observations suggest that no different behavior is expected at lower stiffness values than those selected in our simulations. At the high end of the range of substrate stiffness, no further change in behavior is expected either; all quantities presented in Figs. 4, A–D and 5 plateau. This plateauing occurs because a maximum number of stress-fiber-strengthening steps were implemented (Fig. 2 B), such that there is a limit to the force that is applied by a single stress fiber. A further increase in substrate stiffness would not lead to increased intercellular force (Fj,cell) or contractile moment of the cell pair (Mxx). For this reason, we believe the model is thorough in its exploration of the effect of stiffness on cell-pair force exertion as a function of substrate stiffness.
The literature does report further changes in cell coupling on stiffer substrates, with Polio et al. showing further formation of FAs at the cell-cell interface on substrates with a stiffness of 40 kPa, demonstrated by molecular staining of vinculin and β-catenin (FAs and AJs, respectively) (6). Different behavior could be expected if cell pairs are plated on much stiffer substrates such as treated plastic (10 MPa). We must point out that additional mechanisms may be at play, such as rupture of protein complexes due to excessive force (35) and cell signaling. Modeling cells at this stiffness is not possible with the model as presented because of numerical instability resulting in a stiff system and force fluctuations that render results inaccurate (data not shown). For an accurate representation of cell pairs at higher stiffness values, these additional mechanisms would have to be implemented and a smaller time step used to address the stiff system.
Physiological implications of simulated results
Remodeling of the extracellular matrix that accompanies diseases ranging from cancer to asthma has long been thought of as a byproduct of disease progression. However, in recent years, there is increased awareness that far from being just the consequence of disease, ECM remodeling could be an important factor that drives the progression of disease (36). In our study, we examined the fundamental question of how ECM remodeling, specifically change in ECM stiffness, would affect cell-ECM versus coupling between cells. The answer is of great importance in diseases that affect microcapillaries, in which the loss of cell-cell coupling between endothelial cells leads to leaky blood vessels; in cancer; and in other diseases such as asthma, in which a loss of coupling between epithelial cells can promote faster migration and loss of integrity of the epithelial barrier, respectively. The problem is equally relevant to cells that naturally exist in a three-dimensional environment, such as smooth muscle cells in the airway and blood vessels, which need to physically connect with one another to achieve contraction of airways and blood vessels, or the coupling between cardiac myocytes needed to effect rhythmic contractions of the heart. Our model and the results presented here provide a framework to help us understand how ECM remodeling can influence cell-cell connectivity versus cell-ECM connectivity.
With the modeling of subcellular elements, the model is computationally intensive. This is a limitation if hoping to implement it at the tissue level by increasing the number of cells. To draw conclusions about the results at the tissue level and further comment on physiological implications, we would need to model some of the tissues mentioned (e.g., lung, cardiac, vascular endothelial, epithelial, cancer tumor). Future studies would first focus on larger collectives of 3–10 cells that could recreate results on cell migration (37) or shuffling during angiogenic sprouting (38). At the same time, modeling cellular migration comes with its own set of challenges, such as modeling membrane fluidity and extension. The model could be used to study gap formation in cell layers as a function of mechanical properties of subcellular elements, similar to the 2D modeling work by Escribano et al. (39); gap formation is believed to be responsible for extravasation in metastasis. The model can also be used to validate experiments using traction force microscopy of monolayers (8).
Other forces need to be accounted for if modeling specific tissues. For example, if studying vascular integrity, considerations about endothelial tissue should include not only forces carried by the ECM but also fluid shear stress. Despite these limitations, the simulated results do provide a possible explanation for behavior observed experimentally at the tissue level. Endothelial cells are known to form stronger junctions in response to flow if grown on softer matrices relative to those grown on stiffer matrices (40). This agrees with our findings. Yet the effect of shear stress is not included in our model. Another example in which our results match experimental findings occurs in liver tissue. Human liver endothelial cells cultured on stiff matrices lose their fenestrations and show increased stress fiber formation (41). Similarly, our modeled showed decoupling and an increase in stress fiber number with increasing substrate stiffness.
Conclusions
In this work, we focused on the effect of mechanosensing on cell pairs and specifically active mechanisms (i.e., adhesion maturation and stress fiber strengthening). The mechanical response of the cell, however, will be affected by additional elements, many passive. Our results show that stiffness at the cell-cell interface regulates the force response of the cell; in our simulations, this stiffness was dictated by the stiffness of AJs. Future studies with the model may ask for the effect of some of these passive mechanical factors, such as cortex stiffness (kcortex). We wonder, could varying cortex stiffness explain why different cell types show different behaviors on the same substrate stiffness? Additionally, the model can be expanded to collectives beyond cell pairs. The same way the specific configuration of stress fibers and adhesions are shown to play a role in force response to substrate stiffness, similar results can be expected of more complex configurations of these elements.
The model suggests that stalling and strengthening of stress fibers occurs faster in stress fibers that connect two FAs compared with those binding AJs. This occurs because the cell-cell interface is softer than the substrate but also because not all stress fibers bound to an AJ stall and mature; maturation requires stalling, which requires an opposing force, and this only occurs when the AJ is bound to yet a second stress fiber in the neighbor cell. As this demands binding of two instead of one stress fiber, it is less likely, thus causing stabilization of cell-cell adhesions to take longer. We also found limits in terms of substrate stiffness, relative to adhesion complex stiffness values, for which this occurs: the stiffness of the cell-cell interface, sensed as having a relatively constant stiffness, becomes a tipping point for substrate stiffness to define mechanosensing dynamics and cell strengthening. We do not expect these mechanisms to fully explain the complex interplay of cell-cell and cell-substrate adhesions; it is known that this interplay also requires chemical signaling and activation of common cellular pathways, most likely including RhoA kinase and FA kinase pathways (8,10,34,42,43). Experimental measurements at the subcellular scale can be technically difficult to obtain. This model helps quantify the role of mechanosensing in the interplay of cell-cell and cell-ECM adhesions.
Author Contributions
D.A.V., H.P., and H.V.O. designed the study. D.A.V., T.H., and B.S. conceived the model. D.A.V. implemented the model, ran simulations, and analyzed results. The group headed by H.R. developed the computational program used for coding the model and helped with trouble shooting.
Acknowledgments
Funding for this work comes from the European Research Council (FP7/2007-2013/ERC Grant Agreement no. 308223), Research Foundation - Flanders (FWO) (Grant no. G.0821.13), and FWO and European Union’s Horizon 2020 research and innovation programme (Marie Skłodowska-Curie Grant Agreement no. 665501). The computational resources and services used in this work were provided by the Flemish Supercomputer Center, funded by the FWO and the Flemish Government, department of Economy, Science, and Innovation (EWI).
Editor: Philip LeDuc.
Footnotes
Supporting Material can be found online at https://doi.org/10.1016/j.bpj.2020.05.036.
Supporting Material
4
References
- 1.Mui K.L., Chen C.S., Assoian R.K. The mechanical regulation of integrin-cadherin crosstalk organizes cells, signaling and forces. J. Cell Sci. 2016;129:1093–1100. doi: 10.1242/jcs.183699. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Matsushita T., Oyamada M., Takamatsu T. Remodeling of cell-cell and cell-extracellular matrix interactions at the border zone of rat myocardial infarcts. Circ. Res. 1999;85:1046–1055. doi: 10.1161/01.res.85.11.1046. [DOI] [PubMed] [Google Scholar]
- 3.Araujo B.B., Dolhnikoff M., Mauad T. Extracellular matrix components and regulators in the airway smooth muscle in asthma. Eur. Respir. J. 2008;32:61–69. doi: 10.1183/09031936.00147807. [DOI] [PubMed] [Google Scholar]
- 4.An S.S., Mitzner W., Liggett S.B. An inflammation-independent contraction mechanophenotype of airway smooth muscle in asthma. J. Allergy Clin. Immunol. 2016;138:294–297.e4. doi: 10.1016/j.jaci.2015.12.1315. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Tan C., Costello P., Dedhar S. Inhibition of integrin linked kinase (ILK) suppresses β-catenin-Lef/Tcf-dependent transcription and expression of the E-cadherin repressor, snail, in APC-/- human colon carcinoma cells. Oncogene. 2001;20:133–140. doi: 10.1038/sj.onc.1204052. [DOI] [PubMed] [Google Scholar]
- 6.Polio S.R., Stasiak S.E., Parameswaran H. Extracellular matrix stiffness regulates human airway smooth muscle contraction by altering the cell-cell coupling. Sci. Rep. 2019;9:9564. doi: 10.1038/s41598-019-45716-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.McCain M.L., Lee H., Parker K.K. Cooperative coupling of cell-matrix and cell-cell adhesions in cardiac muscle. Proc. Natl. Acad. Sci. USA. 2012;109:9881–9886. doi: 10.1073/pnas.1203007109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Krishnan R., Klumpers D.D., van Nieuw Amerongen G.P. Substrate stiffening promotes endothelial monolayer disruption through enhanced physical forces. Am. J. Physiol. Cell Physiol. 2011;300:C146–C154. doi: 10.1152/ajpcell.00195.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Goeckeler Z.M., Wysolmerski R.B. Myosin light chain kinase-regulated endothelial cell contraction: the relationship between isometric tension, actin polymerization, and myosin phosphorylation. J. Cell Biol. 1995;130:613–627. doi: 10.1083/jcb.130.3.613. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Kugelmann D., Rotkopf L.T., Waschke J. Histamine causes endothelial barrier disruption via Ca2+-mediated RhoA activation and tension at adherens junctions. Sci. Rep. 2018;8:13229. doi: 10.1038/s41598-018-31408-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Yonemura S., Wada Y., Shibata M. α-Catenin as a tension transducer that induces adherens junction development. Nat. Cell Biol. 2010;12:533–542. doi: 10.1038/ncb2055. [DOI] [PubMed] [Google Scholar]
- 12.Odenthal T., Smeets B., Ramon H. Analysis of initial cell spreading using mechanistic contact formulations for a deformable cell model. PLoS Comput. Biol. 2013;9:e1003267. doi: 10.1371/journal.pcbi.1003267. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Delorme V., Machacek M., Bokoch G.M. Cofilin activity downstream of Pak1 regulates cell protrusion efficiency by organizing lamellipodium and lamella actin networks. Dev. Cell. 2007;13:646–662. doi: 10.1016/j.devcel.2007.08.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Van Liedekerke P., Tijskens E., Roose D. Particle-based model to simulate the micromechanics of biological cells. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2010;81:061906. doi: 10.1103/PhysRevE.81.061906. [DOI] [PubMed] [Google Scholar]
- 15.Maugis D. Adhesion of spheres: the JKR-DMT transition using a dugdale model. J. Colloid Interface Sci. 1992;150:243–269. [Google Scholar]
- 16.Schwarz U.S., Erdmann T., Bischofs I.B. Focal adhesions as mechanosensors: the two-spring model. Biosystems. 2006;83:225–232. doi: 10.1016/j.biosystems.2005.05.019. [DOI] [PubMed] [Google Scholar]
- 17.Mitrossilis D., Fouchard J., Asnacios A. Single-cell response to stiffness exhibits muscle-like behavior. Proc. Natl. Acad. Sci. USA. 2009;106:18243–18248. doi: 10.1073/pnas.0903994106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Abidine Y., Laurent V.M., Verdier C. Physical properties of polyacrylamide gels probed by AFM and rheology. Europhys. Lett. 2015;109:38003. [Google Scholar]
- 19.Palmieri B., Scanlon C., Lee J. Substrate mediated interaction between pairs of keratocytes: multipole traction force models describe their migratory behavior. PLoS One. 2019;14:e0212162. doi: 10.1371/journal.pone.0212162. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Schwarz U.S., Gardel M.L. United we stand: integrating the actin cytoskeleton and cell-matrix adhesions in cellular mechanotransduction. J. Cell Sci. 2012;125:3051–3060. doi: 10.1242/jcs.093716. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Seddiki R., Narayana G.H.N.S., Mège R.M. Force-dependent binding of vinculin to α-catenin regulates cell-cell contact stability and collective cell behavior. Mol. Biol. Cell. 2018;29:380–388. doi: 10.1091/mbc.E17-04-0231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Elosegui-Artola A., Oria R., Roca-Cusachs P. Mechanical regulation of a molecular clutch defines force transmission and transduction in response to matrix rigidity. Nat. Cell Biol. 2016;18:540–548. doi: 10.1038/ncb3336. [DOI] [PubMed] [Google Scholar]
- 23.Bangasser B.L., Rosenfeld S.S., Odde D.J. Determinants of maximal force transmission in a motor-clutch model of cell traction in a compliant microenvironment. Biophys. J. 2013;105:581–592. doi: 10.1016/j.bpj.2013.06.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Wolfenson H., Meacci G., Sheetz M.P. Tropomyosin controls sarcomere-like contractions for rigidity sensing and suppressing growth on soft matrices. Nat. Cell Biol. 2016;18:33–42. doi: 10.1038/ncb3277. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Parameswaran H., Lutchen K.R., Suki B. A computational model of the response of adherent cells to stretch and changes in substrate stiffness. J. Appl. Physiol. 2014;116:825–834. doi: 10.1152/japplphysiol.00962.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Purcell E.M. Life at low Reynolds number. Am. J. Phys. 1977;45:3–11. [Google Scholar]
- 27.Austen K., Ringer P., Grashoff C. Extracellular rigidity sensing by talin isoform-specific mechanical linkages. Nat. Cell Biol. 2015;17:1597–1606. doi: 10.1038/ncb3268. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Lecuit T. α-catenin mechanosensing for adherens junctions. Nat. Cell Biol. 2010;12:522–524. doi: 10.1038/ncb2066. [DOI] [PubMed] [Google Scholar]
- 29.Leckband D.E., le Duc Q., de Rooij J. Mechanotransduction at cadherin-mediated adhesions. Curr. Opin. Cell Biol. 2011;23:523–530. doi: 10.1016/j.ceb.2011.08.003. [DOI] [PubMed] [Google Scholar]
- 30.Yap A.S., Duszyc K., Viasnoff V. Mechanosensing and mechanotransduction at cell-cell junctions. Cold Spring Harb. Perspect. Biol. 2018;10:a028761. doi: 10.1101/cshperspect.a028761. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Butler J.P., Tolić-Nørrelykke I.M., Fredberg J.J. Traction fields, moments, and strain energy that cells exert on their surroundings. Am. J. Physiol. Cell Physiol. 2002;282:C595–C605. doi: 10.1152/ajpcell.00270.2001. [DOI] [PubMed] [Google Scholar]
- 32.Webb D.J., Donais K., Horwitz A.F. FAK-Src signalling through paxillin, ERK and MLCK regulates adhesion disassembly. Nat. Cell Biol. 2004;6:154–161. doi: 10.1038/ncb1094. [DOI] [PubMed] [Google Scholar]
- 33.Califano J.P., Reinhart-King C.A. Substrate stiffness and cell area predict cellular traction stresses in single cells and cells in contact. Cell. Mol. Bioeng. 2010;3:68–75. doi: 10.1007/s12195-010-0102-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Tseng Q., Duchemin-Pelletier E., Théry M. Spatial organization of the extracellular matrix regulates cell-cell junction positioning. Proc. Natl. Acad. Sci. USA. 2012;109:1506–1511. doi: 10.1073/pnas.1106377109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Balaban N.Q., Schwarz U.S., Geiger B. Force and focal adhesion assembly: a close relationship studied using elastic micropatterned substrates. Nat. Cell Biol. 2001;3:466–472. doi: 10.1038/35074532. [DOI] [PubMed] [Google Scholar]
- 36.Lampi M.C., Reinhart-King C.A. Targeting extracellular matrix stiffness to attenuate disease: from molecular mechanisms to clinical trials. Sci. Transl. Med. 2018;10:eaao0475. doi: 10.1126/scitranslmed.aao0475. [DOI] [PubMed] [Google Scholar]
- 37.Jain S., Cachoux V.M.L., Ladoux B. The role of single-cell mechanical behaviour and polarity in driving collective cell migration. Nat. Phys. 2020 doi: 10.1038/s41567-020-0875-z. https://www.nature.com/articles/s41567-020-0875-z Published online May 4, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Cruys B., Wong B.W., Carmeliet P. Glycolytic regulation of cell rearrangement in angiogenesis. Nat. Commun. 2016;7:12240. doi: 10.1038/ncomms12240. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Escribano J., Chen M.B., Spill F. Balance of mechanical forces drives endothelial gap formation and may facilitate cancer and immune-cell extravasation. PLoS Comput. Biol. 2019;15:e1006395. doi: 10.1371/journal.pcbi.1006395. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Kohn J.C., Zhou D.W., Reinhart-King C.A. Cooperative effects of matrix stiffness and fluid shear stress on endothelial cell behavior. Biophys. J. 2015;108:471–478. doi: 10.1016/j.bpj.2014.12.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Ford A.J., Jain G., Rajagopalan P. Designing a fibrotic microenvironment to investigate changes in human liver sinusoidal endothelial cell function. Acta Biomater. 2015;24:220–227. doi: 10.1016/j.actbio.2015.06.028. [DOI] [PubMed] [Google Scholar]
- 42.Mikelis C.M., Simaan M., Gutkind J.S. RhoA and ROCK mediate histamine-induced vascular leakage and anaphylactic shock. Nat. Commun. 2015;6:6725. doi: 10.1038/ncomms7725. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Chen X.L., Nam J.-O., Schlaepfer D.D. VEGF-induced vascular permeability is mediated by FAK. Dev. Cell. 2012;22:146–157. doi: 10.1016/j.devcel.2011.11.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Pontes B., Monzo P., Gauthier N.C. Membrane tension: a challenging but universal physical parameter in cell biology. Semin. Cell Dev. Biol. 2017;71:30–41. doi: 10.1016/j.semcdb.2017.08.030. [DOI] [PubMed] [Google Scholar]
- 45.Fischer R.S., Gardel M., Waterman C.M. Local cortical tension by myosin II guides 3D endothelial cell branching. 2009;19:260–265. doi: 10.1016/j.cub.2008.12.045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Dembo M., Wang Y.-L. Stresses at the cell-to-substrate interface during locomotion of fibroblasts. Biophys. J. 1999;76:2307–2316. doi: 10.1016/S0006-3495(99)77386-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Moore S.W., Roca-Cusachs P., Sheetz M.P. Stretchy proteins on stretchy substrates: the important elements of integrin-mediated rigidity sensing. Dev. Cell. 2010;19:194–206. doi: 10.1016/j.devcel.2010.07.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Color bar indicates traction magnitude as represented on the substrate plane. Cell surface is shown as opaque surface with triangular mesh used to represent the cellular cortex. This sample cases correspond to simulations with maturing FAs but not AJs (ζFA > ζAJ).
Color bar indicates traction magnitude as represented on the substrate plane. Cell surface is shown as opaque surface with triangular mesh used to represent the cellular cortex. This sample cases correspond to simulations with maturing FAs but not AJs (ζFA > ζAJ).
Color bar indicates traction magnitude as represented on the substrate plane. Cell surface is shown as opaque surface with triangular mesh used to represent the cellular cortex. This sample cases correspond to simulations with maturing FAs but not AJs (ζFA > ζAJ).
Color bar indicates traction magnitude as represented on the substrate plane. Cell surface is shown as opaque surface with triangular mesh used to represent the cellular cortex. This sample cases correspond to simulations with maturing FAs but not AJs (ζFA > ζAJ).
4