Generation of Monophasic Action Potentials and Intermediate Forms

Abstract

The monophasic action potential (MAP) is a near replica of the transmembrane potential recorded when an electrode is pushed firmly against cardiac tissue. Despite its many practical uses, the mechanism of MAP signal generation and the reason it is so different from unipolar recordings are not completely known and are a matter of controversy. In this work, we describe a method to simulate realistic MAP and intermediate forms, which are multiphasic electrograms different from an ideal MAP. The key ideas of our method are the formation of compressed zones and junctional spaces—regions of the extracellular and bath or blood pool directly in contact with electrodes that exhibit a pressure-induced reduction in electrical conductivity—and the presence of a complex network of passive components that acts as a high-pass filter to distort and attenuate the signal that reaches the recording amplifier. The network is formed by the interaction between the passive tissue properties and the double-layer capacitance of electrodes. The MAP and intermediate forms reside on a continuum of signals, which can be generated by the change of the model parameters. Our model helps to decipher the mechanisms of signal generation and can lead to a better design for electrodes, recording amplifiers, and experimental setups.

Significance

Recording the monophasic action potential (MAP) is potentially very useful in both experimental and clinical cardiac electrophysiology and can provide valuable information about the repolarization phase of the action potential. However, despite its benefits, it currently has only a niche role. The main challenge is the technical difficulties of recording an ideal MAP. Our results provide a better understanding of the mechanisms of the generation of cardiac electrograms and may help to optimize experiments and improve tools to achieve the full potentials of recording the MAP signals.

Introduction

An extracellular electrode pushed firmly against cardiac tissue may record a near-perfect replica of the transmembrane action potential (TAP) (1). This extracellularly recorded intracellular potential is called the monophasic action potential (MAP). The MAP is different from the low-amplitude and multiphasic signals recorded when an electrode is placed near cardiac tissue but does not press against it. Assuming the recording electrode is the positive input to the amplifier and a distant electrode the negative input, a MAP signal is positive, has a higher amplitude, and closely tracks the contour and duration of the TAP.

The characteristics of MAPs have been known since the 1880s (2). Initially, the recordings were performed after causing injury to myocardium; however, atraumatic recording methods were found in the 1930s (3) and further developed into clinical MAP catheters by Franz et al. in the 1980s and 1990s (4).

Despite its long history, the mechanism of MAP signal generation and the reason it is so different from other forms of unipolar recordings are not completely known and are a matter of controversy (5). It is hypothesized that pressing the electrode into the tissue partially depolarizes the cells directly underneath the electrode, probably through opening nonspecific pressure-sensitive channels, and this contributes to the generation of MAP signals (2,6). Direct microelectrode measurements have confirmed the presence of the pressure-induced partial depolarization in Langendorff-perfused mouse hearts (resting potential −78 mV, up to −23 mV immediately under the electrode) (7). Multiple modeling studies have explored the possible mechanisms of the genesis of the MAP. Some early works assumed that the region under the electrode is passive and incapable of generating action potentials (8). More recent studies have incorporated a nonspecific stretch channel in the ionic model to account for the observed partial depolarization under the electrode (9). Tranquillo et al. further augmented this model by considering the extracellular resistance and found that the changes in the passive local tissue properties play a critical role in the genesis of the MAP (6).

In this work, we will show that, in addition to the pressure-induced partial depolarization, changes in the passive electrical properties of tissue and bath (for experimental studies) or blood pool (for clinical applications) are required to explain the generation of realistic MAPs. In addition, we will explore the effects of the electrode properties on forming the final signal recorded by amplifiers.

Intermediate forms

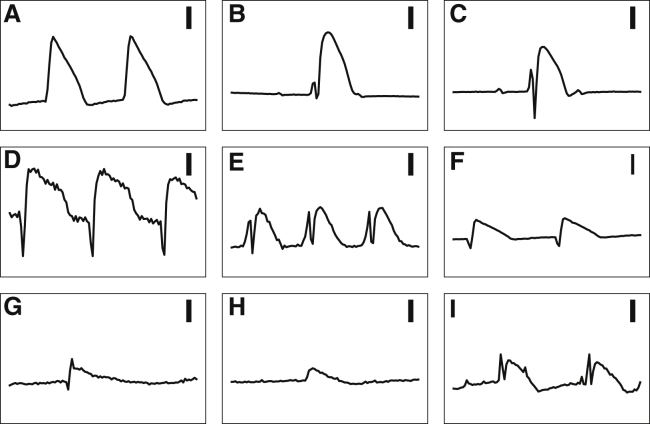
Fig. 1 shows a group of signals collected by silver (Ag) electrodes (1.6 mm in diameter), coated with a layer of silver-chloride (AgCl), from five arterially perfused rabbit ventricles (see (10) for the experimental details). The heart motion was suppressed with the injection of the myosin inhibitor blebbistatin (11). The ground was a large Ag-AgCl electrode located in the bath remote from the hearts. All experiments conform to the current Guide for Care and Use of Laboratory Animals (12) and approved by the Office of Research and Integrity Assurance at Georgia Institute of Technology.

Figure 1.

A collection of signals recorded using an Ag-AgCl electrode from five arterially perfused rabbit ventricles on a Langendorff apparatus (A-F, B-C, D-E, and G-H pairs are from the same hearts). (A) and (B) (after the initial spike) are representative MAPs; (C)–(I) are different intermediate forms. Different recordings from the same heart were obtained by moving the electrode to a different location. There are sharp and multiphasic signals in the beginning of some of the complexes. Each recording is 1 s in duration. The vertical bars are 10 mV.

Only Fig. 1, A and B depict acceptable MAPs; other panels exhibit various degrees of deformation and alteration. Usually, these intermediate forms are considered inadequate, and although useful for the timing of the upstroke of the action potential, their repolarization phase is discarded from further scrutiny. However, we believe that these forms contain useful information for deciphering the mechanisms of MAP generation. A key observation is that while pressing an electrode harder into the heart tissue, one sees a continuum of signals that gradually morph into MAPs with no apparent threshold nor qualitative distinction between MAPs and the rest of the intermediate forms. A realistic model should be able to generate both a typical MAP and various intermediate forms. In addition, the intermediate forms are the most frequently observed patterns in practice, and it would be helpful to be able to extract valid repolarization phase information from them.

Methods

In this section, we describe a step-by-step process to simulate and model how electrodes record and shape cardiac electrical activity. Action potentials are the result of active membrane properties, namely the flow of currents through ion channels. However, cardiac tissue also possesses passive properties, including membrane capacitance and intracellular and extracellular resistance (13). Additionally, recording electrodes have passive properties (see below). The combination of all these passive elements can be modeled as a complex network of capacitors and resistors that shape and alter electrograms before they reach the recording amplifier. In this work, our main goal is to develop a simple model of this passive network that nevertheless can reproduce realistic signals, whether MAPs or intermediate forms. For the sake of discussion, we split the model into two main components: biological (bidomain model) and nonbiological (recording electrode) while acknowledging that the two are, in fact, intertwined and form a single network.

Bidomain model

We use the standard bidomain methodology (14, 15, 16). The domain is a uniform isotropic three-dimensional piece of cardiac tissue (size 24 × 12.5 × 5 mm), overlaid by a conductive bath (24 × 12.5 × 2.5 mm). The governing equations of the bidomain methodology are

$$\nabla ·\left({\sigma }_i\nabla V_i\right)=\beta \left(C_m\frac{\partial V_m}{\partial t}+I_{\text{ion}}\right)$$ (1)

and

$$\nabla ·\left({\sigma }_e\nabla V_e\right)=-\beta \left(C_m\frac{\partial V_m}{\partial t}+I_{\text{ion}}\right)-I_{\text{stim}},$$ (2)

where V_i and V_e are, respectively, the intracellular and extracellular potentials; V_m = V_i − V_e is the transmembrane potential; σ_i and σ_e are the intracellular and extracellular conductivity tensors; β is the surface/volume ratio; C_m is the membrane capacitance; I_ion is the sum of membrane ionic currents; and I_stim is the extracellularly injected stimulation current. Because of the isotropy precondition, we can assume σ_i and σ_e are scalars.

We solve the equivalent parabolic-elliptic formulation of the bidomain problem (16,17),

$$\beta C_m\frac{\partial V_m}{\partial t}=\nabla ·\left({\sigma }_i\nabla \left(V_m+V_e\right)\right)-\beta I_{\text{ion}}$$ (3)

and

$$\nabla ·\left(\left({\sigma }_i+{\sigma }_e\right)\nabla V_e+{\sigma }_i\nabla V_m\right)=-I_{\text{stim}}$$ (4)

The bath is modeled as an extension of the extracellular space with a conductivity of σ_b. The side of the bath opposite to the tissue is grounded (the Dirichlet boundary condition). The other sides of the bath and tissue have a no-flow Neumann boundary condition. We use the following values for the passive tissue properties: σ_i = 1 mS/cm, σ_e = 3 mS/cm, σ_b = 10 mS/cm, β = 2000/cm, and C_m = 1 μF/cm (18,19).

For the examples in this work, we used the Mahajan rabbit ventricular ionic model (20). We chose this particular model because the recordings in Fig. 1 were from rabbit ventricles. The combined model was solved with a hybrid implicit-explicit scheme. The ionic gates were integrated with the help of the Rush-Larsen method (21); other state variables were integrated using the explicit Euler’s method with a time step Δt of 0.1 ms. The finite difference methodology was used to discretized the partial differential equations (spatial resolution Δx = 0.25 mm), and the resulting system of linear equations was solved using the iterative conjugate gradient technique.

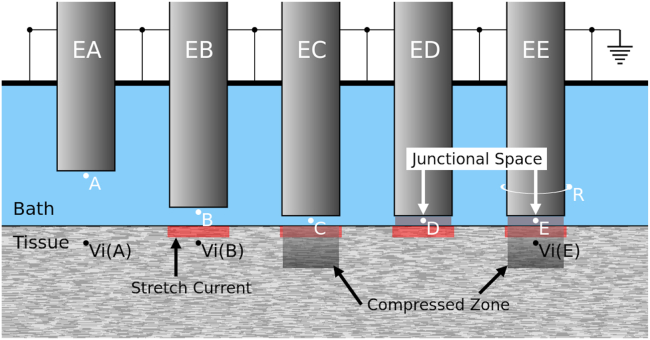
Fig. 2 shows a schematic of the model and the geometry of the recording electrodes. Each electrode has a circular cross section with a diameter D = 1 mm. EA resides in the bath near the tissue but does not press on the tissue. The other four electrodes (EB–EE) exert pressure on the tissue. We assume that, in addition to opening the stretch-sensitive channels, the application of pressure diffuses the extracellular fluid away from the region directly under the electrode while keeping the volume of the intracellular space mostly unaltered. Moreover, the conductivity of the bath in the volume occupied by the electrode is set to 0. As a result of electrode pressure, the distance between the electrode and the tissue narrows to smaller than the spatial resolution of the model (Δx). The conductivity of a volume element between the electrode and tissue is reduced compared to the bath because it is a weighted average of the conductivity of the narrow bath between the two and the zero conductivity of the electrode (volume averaging). Therefore, the effect of pressure is modeled by decreasing the extracellular conductivity in the tissue under the electrode (the compressed zone in EC and EE) and the bath region between the electrode and the tissue (the junctional space in ED and EE).

Figure 2.

The schematic of the model geometry. The three-dimensional bidomain methodology is used to model a cubic piece of cardiac tissue, overlaid with a conductive bath. The side of the bath opposite to the tissue is grounded. EA is an electrode floating in the bath that records an intermediate form signal. EB–EE are MAP electrodes that push against the tissue, partially depolarize the underlying tissue (the red bars), and variably reduce conductivity in the tissue (the compressed zone, present in C and E) and the bath between the tissue and the electrode (the junctional space, present in D and E). The signals from points A–E are shown in Fig. 3. The simulation was performed by stimulating the tissue at 2.5 Hz to initiate a planar waveform propagating perpendicular to the figure. The signal from point R, connected to a ring around EE, is shown in Fig. 4B.

Partial depolarization is modeled by adding a stretch-sensitive leak current I_press to I_ion in Eq. 3. Following (6) and based on prior experimental and modeling works, we set I_press = g_press (V_m − E_press), limited to a layer of thickness Δx immediately adjacent to the electrode (the red bars in Fig. 2), where E_press = −6 mV and g_press = 1 mS/cm (6,22). The numerical value of g_press is different from (6) to account for the different geometry and Δx.

To model the effect of pressure on the passive properties and unless otherwise specified, we have assigned ${\sigma }_e^{\text{∗}}$ = 0.25σ_e = 0.75 mS/cm in the compressed zone and ${\sigma }_b^{\text{∗}}$ = 0.25σ_b = 2.5 mS/cm in the junctional space. The compressed zone and the junctional space are cylinders of diameter D and height 4Δx and Δx, respectively. The pressure may also affect σ_i (e.g., by increasing it as a result of the change in the intracellular/extracellular ratio) and β, but these effects are secondary, and we have limited our model to the primary effects of decreased σ_e and σ_b.

Results

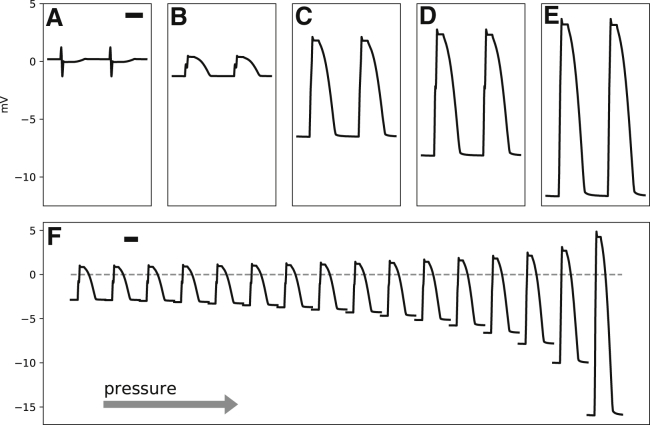
The unipolar extracellular potential (V_e) at five points A–E in Fig. 2, located in the junctional spaces of the corresponding electrodes EA to EE, are depicted in Fig. 3. The signal at A is low amplitude and multiphasic. Addition of I_press to points B to E changes the signal to monophasic. However, the amplitude of the signal at B is low, suggesting that I_press alone is not sufficient to generate MAP-like potentials with realistic amplitudes (>10 mV). Decreasing the extracellular conductivity in the compressed zone has a modest effect on the signal amplitude (Fig. 3 C). Changing the conductivity of the junctional space has a similar effect (Fig. 3 D). However, it is the combination of both the compressed zone and the junctional space that generates the most realistic signal (Fig. 3 E).

Figure 3.

(A–E) The extracellular potentials (V_e) recorded from points A–E in Fig. 2 are shown. (F) shows the signal at point E (Fig. 2) while the contact pressure gradually increases (pressure ramp) by decreasing ${\sigma }_e^{\text{∗}}/{\sigma }_e={\sigma }_b^{\text{∗}}/{\sigma }_b$ from 1 on the left to 0.1 on the right. The vertical bars represent 1 mV. The horizontal bars are 100 ms in duration.

The strength of the stretch-sensitive leak current, I_press, and the degree of the drop in the conductivity of the tissue and bath are tightly coupled. However, the exact relationship between them is not known. Therefore, to quantify the effects of varying pressure, we keep I_press constant and decrease ${\sigma }_e^{\text{∗}}$ and ${\sigma }_b^{\text{∗}}$. Fig. 3 F shows the resulting signal, recorded from the same location as point E. At low pressure, the signal is low amplitude and similar to B. As pressure increases, the signal amplitude grows. The growth is mainly in the negative direction, i.e., the resting extracellular potential becomes more negative.

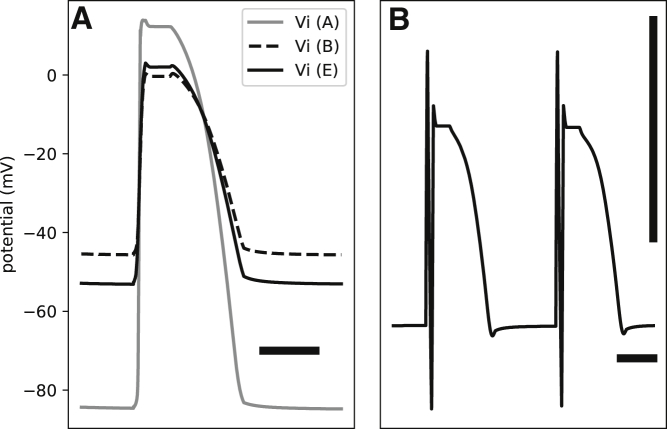
Fig. 4 A shows the intracellular potentials (V_i) at points A, B, and E. The intracellular potentials are calculated with respect to a grounding electrode in the bath. As expected, we observe partial depolarization at B and E, but V_i is lower at E than B because of a more negative resting V_e at E (see below).

Figure 4.

(A) The effect of contact pressure on the intracellular potentials (V_i) measured with respect to a remote ground in the bath is given. The gray curve shows V_i in the absence of pressure (point A in Fig. 2). Application of pressure shifts the resting V_i upward (the dashed curve, point B, Fig. 2). The presence of the compressed zone and junctional space further modifies the signal (point E, Fig. 2). (B) The signal recorded from point R in Fig. 2, which is connected to a ring around EE, is given. The signal is multiphasic and is composed of a low-amplitude MAP-like signal and a sharp spike. The horizontal bars represent 100 ms. The vertical bar is 1 mV.

The genesis of the MAP

In this section, we provide a qualitative and intuitive explanation for the genesis of the MAP. The key is the negative resting extracellular potential under the electrode, which is critical for the generation of positive and monophasic signals like the MAP (6). The stretch-sensitive leak current enters the cells under an electrode and, because of the gradient in the intracellular potential, travels laterally for a few tissue space constants before returning to the extracellular/interstitial space. The current should return to the extracellular space under the electrode to close the circuit. The return current passes either through the bath or the interstitial space; the ratio of the two is determined by the respective conductivities. We follow the bath return path. It passes through the bath and then the junctional space before closing the circuit. The bulk of the bath is grounded and is at potential 0. If the conductivity of the junctional space is low, the current is converted to a detectable potential, which is negative compared to the bath/ground (Fig. 3, E and F). This explanation is similar to the theory proposed by Schütz in 1936 to describe the genesis of the MAP, although he assumed that partial depolarization was the result of “injury potential” and not a consequence of the stretch-sensitive leak current (3).

Signal composition

If the entirety of an electrode surface is in contact with the junctional space, it will record a perfect MAP. This situation may apply to a suction catheter (23). However, electrodes have a spatial extent and usually record a mixture of the junctional and multiphasic bath (or blood pool) potentials. The resulting mixture (the composite signal) represents what is presented to the recording electrode. For example, Fig. 4 B shows the signal recorded from point R in Fig. 2, which is connected to a ring around EE. The signal is low amplitude, multiphasic, and essentially a mixture of the signals at A and E (similar to Fig. 1, E and I). If the electrode had ideal recording characteristics, then these signals also depict the input to the amplifier. However, an actual electrode tends to distort and modify the signal. This is the subject of the next section.

Recording electrode

Double-layer capacitance

Typical electrophysiology recording electrodes are either polarizing, made of an inert metal such as platinum or iridium, or nonpolarizing, usually made of AgCl-coated Ag (10). We start the discussion with polarizing electrodes.

Charge carriers in conductors are electrons and in solution are ions. Transferring electrons to and from the solution requires a chemical reaction on the surface of the electrode, which inert metallic electrodes are incapable of doing (hence the name inert). Instead, charge transfer is achieved by charging and discharging a capacitor formed at the interface between the electrode and solution. This is called the double-layer capacitance (sometimes it is called the Helmholtz capacitor). This capacitance is in series with the resistance R_s of the current path in the tissue and bath or blood pool to the return electrode (the ground).

We quantified the resulting RC circuit by using the electrochemical impedance spectroscopy (EIS) methodology (19,24). The technical details of the measurement system are described in (10). In summary, while the mechanical force was kept constant, the electrode was subjected to a set of pure tone sinusoidal currents. The resulting complex voltage response was measured, and the complex impedance, Z(ω), was calculated as the ratio of the measured voltage to the driving current. Here, ω = 2πf is the angular frequency. We used 20 test frequencies spaced evenly on a logarithmic scale between 2 and 2000 Hz, each applied for 5 s.

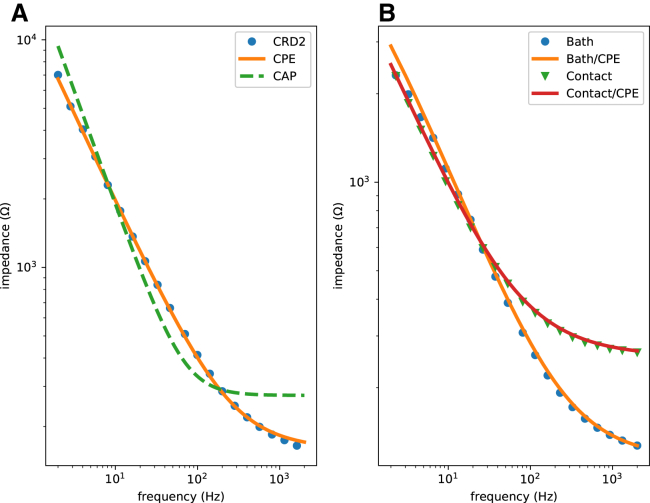
Fig. 5 A shows the impedance data for a typical clinical electrophysiology catheter (CRD-2, platinum electrode, area ∼6 mm²) (see the companion website to this work, http://svtsim.com/eis, for a collection of impedance spectrograms for commonly used cardiac electrophysiology catheters and pacemaker leads).

Figure 5.

Impedance spectrograms of an inert metallic (A, CRD-2 electrophysiology catheter) and a partially AgCl-coated Ag (B) electrode. The spectrogram in (A) fits well with a constant phase element (CPE) model (orange), but not an ideal capacitor model (dashed green). The best-fit is Q = 21 μF/s^{1 − α}, R_s = 158 Ω, and α = 0.778. The spectrogram in (B) requires a parallel faradaic current resistor to fit well. The blue dots and the orange curve are for an electrode free in the bath (Q = 48 μF/s^{1 − α}, R_s = 113 Ω, α = 0.709, and R_f = 8800 Ω). The green triangles and the red curve are for an electrode pushing into the cardiac tissue (Q = 71 μF/s^{1 − α}, R_s = 254 Ω, α = 0.675, and R_f = 16,258 Ω).

Our first attempt to fit the data to Z_C(ω) + R_s, where

$$Z_C\left(\omega \right)=\frac{1}{jC\omega },$$ (5)

is the impedance of an ideal capacitor, C is capacitance, and j = $\sqrt{-1}$, was not successful (Fig. 5 A, the green line). The reason is that the double-layer capacitor is not an ideal capacitor and exhibits frequency dependence. The double-layer capacitance is better approximated as a constant phase element (CPE) (19,24,25). For a CPE, the impedance is defined as

$$Z_{\text{CPE}}\left(\omega \right)=\frac{1}{{\left(j\omega \right)}^{\alpha }Q}=\frac{\text{cos}\left(\pi \alpha /2\right)-j\text{sin}\left(\pi \alpha /2\right)}{Q{\omega }^{\alpha }},$$ (6)

where α, for 0 ≤ α ≤ 1, is a parameter that measures the deviation of the CPE from an ideal capacitor (note that α = 1 corresponds to an ideal capacitor) and Q replaces C as a measure of the size of the capacitor. The orange curve in Fig. 5 A shows the result of fitting the experimental data to

$$Z\left(\omega \right)=R_s+Z_{\text{CPE}}\left(\omega \right)$$ (7)

For the frequency range of interest in electrophysiology, the fit is excellent.

A nonpolarizing electrode, such as an Ag-AgCl electrode, has a faradaic resistor (R_f) in parallel to the double-layer capacitor (26). This current path is a result of the

$$\text{AgCl}+e^{-}\leftrightarrow \text{Ag}\left(metallic\right)+{\text{Cl}}^{-}\left(ionic\right)$$

reaction on the surface of the electrode. Therefore, the consumption and regrowth of AgCl on the surface of the electrode allow for the exchange of electrons between the electrode and the ionic solution. In addition, R_f is in series with a redox half cell, modeled as a battery. For the Ag-AgCl electrode, the half-cell potential is 0.22 V. The effect of this battery is to shift the DC baseline, but it does not directly distort the shape of the signal. Therefore, and for simplicity, we ignore the battery in the subsequent discussion. The electrode material is not the only determinant of whether an electrode is polarizing or not; the operational voltage range also matters. A typically polarizing platinum electrode can pass faradaic current when used as a stimulating/pacing electrode with a peak voltage of >2 V (13,27). In this work, we only consider sensing electrodes.

Fig. 5 B shows the impedance data for an Ag electrode partially covered with AgCl. Now, the total impedance is

$$Z\left(\omega \right)=R_s+\left(R_f\parallel Z_{\text{CPE}}\right)$$ (8)

where || stands for

$$Z_1\parallel Z_2=\frac{Z_1{Z}_2}{Z_1+Z_2}$$ (9)

There are two sets of data in Fig. 5 B. In one, the electrode floats free in the bath (blue circles); in the other one, the electrode is pushing into the tissue (green triangles). Equation 8 fits well to both data sets.

Electrode as a high-pass filter

Armed with a reasonable model of the electrode surface, we can answer the question of signal distortion caused by an electrode. As mentioned in the previous section, a composite signal W, i.e., a weighted combination of the junctional and bath potentials, is fed into the electrode. However, this is not what is sensed by the recording amplifier. It may seem that, considering the very high input impedance of modern amplifiers, the electrode impedance should be irrelevant. However, this is not the case! The main point is that the electrode is not a geometrical point. It has a nonzero surface area such that different parts of the electrode surface are exposed to different potentials.

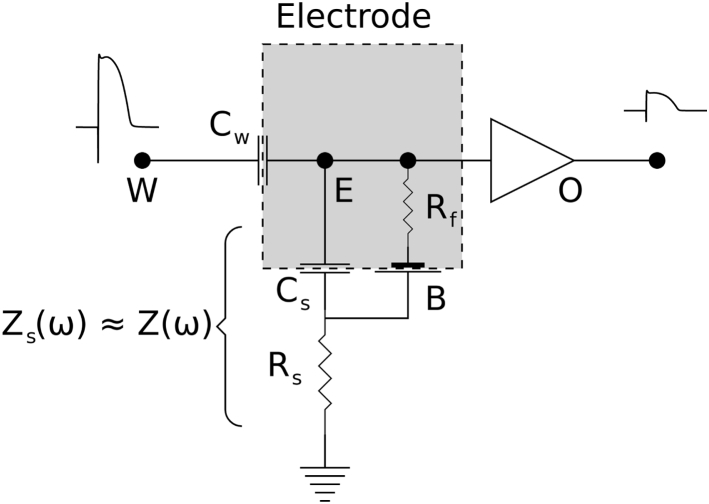
Fig. 6 depicts a lumped model of an electrode (E). This model is similar, but not identical, to models presented in (28) to describe signal distortion by metallic electrodes and glass microelectrodes and in (29) to characterize EEG electrodes. The electrode is coupled to the tissue through a coupling capacitor (C_w). The rest of the electrode is coupled to the bath or blood pool through the double-layer capacitance (C_s). In general, C_w $\ll$ C_s; therefore, the impedance of C_s is essentially the same as Z(ω), where Z(ω) is calculated from Eq. 7 or Eq. 8, depending on whether the electrode is polarizing or nonpolarizing. We parameterize the coupling capacitor using η, for 0 ≤ η ≤ 1, such that C_w = ηC_s, or equivalently,

$$Z_w\left(\omega \right)=\left(Z\left(\omega \right)-R_s\right)/\eta ,$$ (10)

where Z_w(ω) is the impedance of C_w.

Figure 6.

The lumped-element model of the electrode-tissue interface. The electrode surface is marked as a dashed rectangle. The surface impedance is split between a coupling capacitor (C_w) to the source of the composite potential (W) and a capacitor connected to the ground (C_s, assumed to be a CPE) through a resistor R_s. The faradaic resistor R_f and the half cell (B) apply to nonpolarizing electrodes (R_f = ∞ for polarizing electrodes). The output of the amplifier is an attenuated and high-pass-filtered version of W.

Point W is the entry point of the composite signal W. The circuit in Fig. 6 is a voltage divider. Therefore, the transfer function becomes

$$H\left(\omega \right)=\frac{V_o}{W}=\frac{Z\left(\omega \right)}{Z\left(\omega \right)+Z_w\left(\omega \right)},$$ (11)

where V_o is the output potential. Substituting Eq. 10, we have

$$H\left(\omega \right)=\frac{\eta Z\left(\omega \right)}{\left(\eta +1\right)Z\left(\omega \right)-R_s}$$ (12)

It should be noted that Z(ω) is complex; therefore, H(ω) is also a complex function and encodes both amplitude and phase information. At high frequencies, |Z| → R_s; hence, |H| → 1. On the other hand, as ω → 0, |Z| becomes larger and |H| → η/(1 + η) ≈ η (remember that η is generally a small number). This is the behavior of a high-pass filter. However, the filter is leaky such that even at the stopband (e.g., at DC), a portion η of the input signal still passes through the filter.

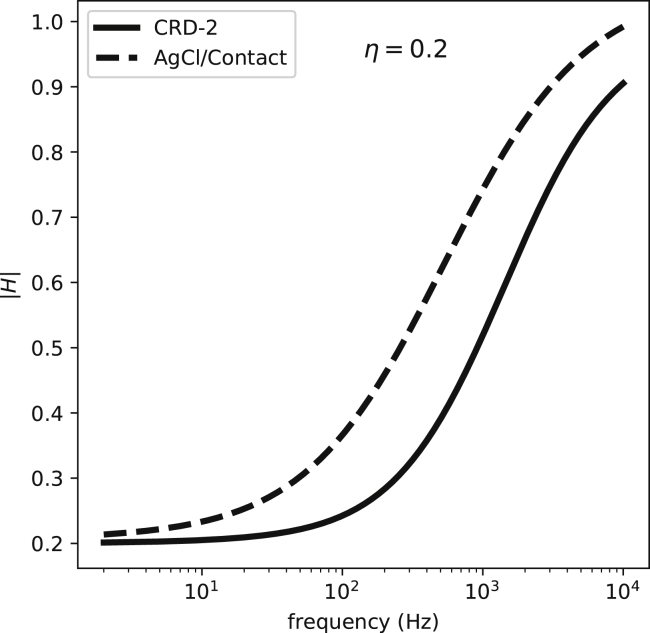
We can plug the values measured in Fig. 5 into Eq. 12 and calculate the frequency response of the corresponding electrodes (Fig. 7). In the frequency range in which the bulk of the signal power is (5–100 Hz), all these curves have a relatively flat response; hence, their primary effect is to attenuate the signal. This is one of the reasons why the amplitude of recorded signals is less than the amplitude of an action potential (∼100 mV). The transfer function approaches 1 at higher frequencies; therefore, the electrodes pass the high-frequency portion of the signal (the upstroke of the action potential) with less attenuation. Algorithm 1 summarizes the process of estimating the recorded signal by an electrode with known characteristics. Applying it to the signals from Figs. 3 and 4, we observe how the electrode preference for higher frequencies (high-pass filtering) alters the shape of the signal (Fig. 8).

Figure 7.

The transfer functions (the Bode magnitude graph) for two electrodes, a polarizing one (CRD-2) and a partially nonpolarizing one (an Ag-AgCl electrode), assuming η = 0.2, where η is the ratio of the coupling capacitance/total electrode surface capacitance. Both curves depict high-pass filters with a nonzero response in the stopband. |H| stands for the magnitude of H(ω).

Algorithm 1. The summary of the algorithm to calculate the MAP and intermediate forms.

Data

• The bidomain model parameters: the type of the ionic model and the passive properties of the tissue

• The characteristics of the recording electrodes: CPE parameters (Q, α) in parallel with R_f and in series with R_s

• The model parameter: η

Result: The input to the first stage amplifier V_o

• 1Reduce the extracellular/bath conductivity to account for the electrode contact pressure
• 2Add the pressure-sensitive leak current to the cells under the electrode
• 3Run the intracellular/extracellular/bath bidomain model to obtain V_b and V_j
• 4Calculate the composite signal W
• 5Calculate the electrode transfer function H(ω) using Eq. 12 (controlled by η and the electrode characteristics)
• 6Apply H(ω) to W to calculate V_o

Figure 8.

The effect of electrodes on shaping the signal. The figure shows the signals in Fig. 3E (A) and Fig. 4B (B) subjected to the filtering effect of a polarizing electrode (the solid curve in Fig. 7). Here, we assume W = V_j, where W is the composite signal and V_j is the junctional potential. Because the time-domain realization of a CPE is complicated, H was applied to W in the frequency domain. The horizontal bars represent 100 ms, and the vertical bars are 1 mV.

Model verification

The model presented above, especially Eqs. 11 and 12, is successful in reproducing realistic signals. However, this observation does not necessarily prove the correctness of the model. It is difficult to prove the model experimentally because W is hidden and hard to measure independently from the electrodes being modeled. One way to gain confidence in the soundness of the model is to observe that it produces the expected signal when the system is perturbed in certain ways. In this section, we present two such experiments to help with the verification of the model.

Dual electrode

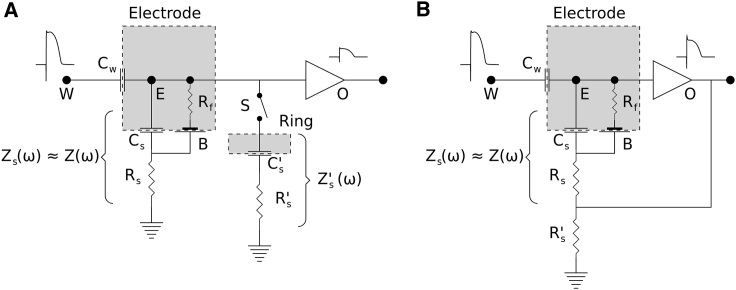
Fig. 9 A shows the schematic of the circuit used for the first experiment. We used a dual-electrode catheter. The tip electrode was very small (area 0.1 mm²) and in contact with the tissue (arterially perfused guinea pig ventricles). The ring electrode was larger (area 5 mm²) and located in the bath. Both electrodes were made of a polarizing material (MP53N, a corrosion-resistant alloy commonly used in the medical field) and could be connected together electrically (via switch S in the schematic). The choice of material and the small size of the tip were by design to exaggerate the expected signal distortion.

Figure 9.

(A) The circuit diagram of the dual-electrode setup. The catheter has two electrodes. The tip is in contact with the tissue and is similar to Fig. 6, whereas the ring is in contact with the bath and can be turned on and off using switch S. (B) The bootstrapped version of the lumped-element model of the electrode-tissue interface is shown. The output of the unity gain amplifier forms a positive feedback loop and boosts the ground connection of the voltage divider. We assume R_s′$\gg$R_s. The faradaic resistor R_f and the half cell (B) apply to nonpolarizing electrodes (R_f = ∞ for polarizing electrodes).

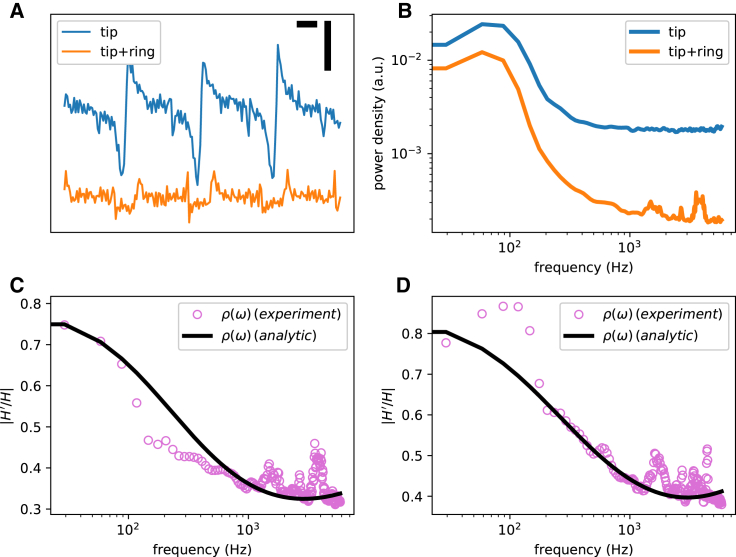
Fig. 10 A shows the signals recorded from the tip (S open) and from the combined tip and ring (S closed). Note that the signal is attenuated and distorted after the switch was closed. As we will see below, we can analytically estimate the ratio of the transfer function of the tip-only configuration to the transfer function of the combined electrodes. The same ratio can be measured experimentally as the square root of the ratio of the estimated power spectra of the signals (Fig. 10, C and D).

Figure 10.

The experimental data recorded from two guinea pig ventricles using a dual-electrode catheter. (A) Recorded signals from the tip electrode with the ring off (blue) and on (orange) are given. The horizontal bar represents 100 ms, and the vertical bar is 10 mV. Each recording was 20 s long. (B) The power spectra of the signals shown in (A) are given. (C and D) The experimental (open circles) and analytic (black line, calculated using Eq. 15) ratios of the transfer functions (the ring on/ring off ratio) for the two ventricles are shown.

Let H(ω) be the transfer function of the tip electrode (S open) and H′(ω) be the transfer function of the combined setup (S closed). Our goal is to find ρ(ω) = H′(ω)/H(ω). The starting point is Eq. 11,

$$H\left(\omega \right)=\frac{Z_s\left(\omega \right)}{Z_s\left(\omega \right)+Z_w\left(\omega \right)},$$ (13)

where Z(ω) is the complex impedance of the tip and Z_s(ω) is the impedance of the (unknown) coupling capacitor (from here on, we will use Z instead of Z(ω) to reduce clutter). Similarly, for the combined electrode,

$$H\text{'}\left(\omega \right)=\frac{Z_s\parallel Z{\text{'}}_s}{\left(Z_s\parallel Z{\text{'}}_s\right)+Z_w},$$ (14)

where Z′ is the impedance of the ring. Considering that Z_w $\gg$ Z_s > Z′_s, we have

$$\rho \left(\omega \right)=\frac{H\text{'}\left(\omega \right)}{H\left(\omega \right)}\approx \frac{Z_s\parallel Z{\text{'}}_s}{Z_s}=\frac{Z{\text{'}}_s}{Z_s+Z{\text{'}}_s}$$ (15)

Using Eq. 15, the analytic transfer function ratio (the yellow curve in Fig. 10, C and D) were calculated and were found to be a reasonable fit of the measured ratio (the purple dots).

Bootstrapping

Another modification of the system is shown in Fig. 9 B. Here, the output of the amplifier, with unity gain, is fed back as the ground electrode. In electronics, this is called “bootstrapping” and is used to convert a passive to an active filter.

With bootstrapping, the input to the electrode becomes W + V_o instead of W. Let G(ω) be the new transfer function (H(ω) is the original transfer function). The actual gain of the amplifier is β, which is assumed to be near 1. We have

$$\frac{V_o}{W+\beta V_o}=H\left(\omega \right),$$ (16)

therefore,

$$G\left(\omega \right)=\frac{V_o}{W}=\frac{H\left(\omega \right)}{1-\beta H\left(\omega \right)}\approx \frac{H\left(\omega \right)}{1-H\left(\omega \right)}$$ (17)

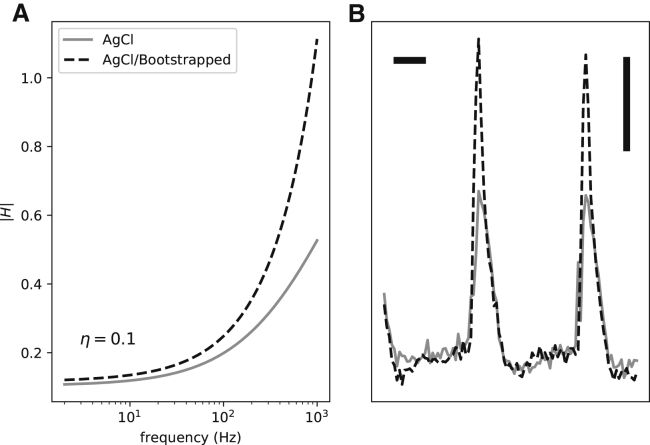
Fig. 11 A shows the transfer functions before and after bootstrapping for an AgCl electrode. The two curves mostly coincide in low frequency but diverge at high frequencies. The reason is that when H is small, 1 − H is near 1. As H becomes larger and approaches 1, the 1 − H term becomes smaller and boosts the resulting gain. Hence, G(ω) is an exaggerated high-pass filter compared to H(ω).

Figure 11.

The effects of bootstrapping on the filter transfer function (A) and a representative experimentally recorded signal from a guinea pig ventricle (B).

Fig. 11 B demonstrates the effect of bootstrapping in recordings from a guinea pig ventricle. The bootstrapped signal has a larger high-frequency component compared to the baseline recording. This can be seen as a significant difference in the upstroke region (high frequency) compared to the essentially identical repolarization phase (low frequency).

Discussion

Recording cardiac electrical activity with the help of electrodes—including MAP catheters, microelectrodes, electrophysiology catheters, pacemaker leads, and other forms—is the cornerstone of both experimental and clinical electrophysiology. However, what is recorded may not be, and usually is not, a faithful reproduction of the electrical activity at the tissue level. The complex electrical network formed by the passive elements of the cardiac tissue and the passive properties of the electrode distorts the signal. In addition, there is an interaction between the electrode and tissue such that the electrode pressure may deform the tissue and alter its passive properties.

In this work, we presented a methodical process to generate realistic signals. The core idea of our model is that the conductivity of the bath (the junctional space) and the extracellular domain (the compressed zone) decreases under a MAP electrode as a result of the electrode pressure. The observed pressure-induced partial depolarization can be modeled by the addition of a stretch-sensitive nonspecific current to ionic models. However, this leak current is not sufficient to reproduce realistic signals. Instead, we also need the reduced conductivity in the compressed zone and junctional space for the genesis of the MAP.

Another important consideration is that electrodes are not geometrical points and have finite surface areas. This fact is relevant to both the mixing of junctional and extracellular potentials and the presence of a high-pass filter at the junction of an electrode and cardiac tissue created because of the double-layer capacitance. We also showed that the MAP and intermediate forms are qualitatively similar and can be generated by the same model with a continuous change of the parameters.

We used a rabbit ventricular ionic model in this work. The main findings are not sensitive to the details of the ionic models, and any ventricular model, even a generic one such as the Beeler-Reuter model (30), should work.

Understanding the mechanisms of signal generation helps with a better design for electrodes, recording amplifier, and the experimental setup. For example, we can reduce the detrimental effects of an electrode on the amplitude and shape of the signals by making its response curve as flat as possible. Based on the transfer function equations (Eqs. 11 and 12), we can achieve this goal by making the electrode impedance (Z_w) smaller, making the series resistor (R_s) larger, or increasing the electrode contact (η). The former can be done by either decreasing the faradaic shunt resistor (R_f) by using an Ag-AgCl electrode or increasing the capacitance of the electrode, for example, by increasing its surface area as in fractal pacemaker leads (31, 32, 33). R_f can be made larger by pushing the electrode harder into the tissue, which also increases η, or by using a suction electrode. All these techniques are commonly used, and the reason they work can be understood within the unified framework presented in this work.

Most electrophysiology practitioners, whether experimental or clinical, develop an intuitive feel for how the properties of electrodes affect the signal quality. For example, it is generally appreciated that a larger electrode produces a lower frequency signal. This observation is usually attributed to a larger “antenna” effect, i.e., a larger electrode surface area records from a larger volume of tissue and averages out the signal; hence, the lower frequency. However, intuition without a solid theoretical background can be misleading. As we saw, a more accurate explanation of the effects of a larger electrode is that all electrodes act as a high-pass filter, but a larger electrode has a larger capacitance, and therefore, the cutoff frequency of the filter is shifted toward lower frequencies.

Despite its benefits, recording MAP has only a niche role in clinical and experimental electrophysiology. The main challenge is the technical difficulty of recording an ideal MAP, which requires the experiment to be optimized toward recording MAPs. The fact that MAPs and intermediate forms are just different points on the same continuum means that we can settle for a less than ideal MAP and potentially correct for distortions based on the passive properties of the electrode.

Conclusion

The MAP is one of the two extremes on the continuum of possible signals (electrograms) recorded by an electrode touching myocardium. The combination of the pressure-induced change in the tissue and bath/blood pool properties and the stretch-sensitive leak current is the keys to the generation of the MAP. The electrode passive electrical properties, especially its double-layer capacitance, distorts and attenuates the tissue-level signal before reaching the recording amplifier.

Author Contributions

S.I. designed the research and collected and analyzed the data. I.U., C.H., and F.H.F. performed the experiments. J.J.L. provided the concept. S.I. and J.J.L. wrote the manuscript with input from other authors.

Editor: Eric Sobie.