Model‐Based Analysis Reveals a Sustained and Dose‐Dependent Acceleration of Wound Healing by VEGF‐A mRNA (AZD8601)

Abstract

Intradermal delivery of AZD8601, an mRNA designed to produce vascular endothelial growth factor A (VEGF‐A), has previously been shown to accelerate cutaneous wound healing in a murine diabetic model. Here, we develop population pharmacokinetic and pharmacodynamic models aiming to quantify the effect of AZD8601 injections on the dynamics of wound healing. A dataset of 584 open wound area measurements from 131 mice was integrated from 3 independent studies encompassing different doses, dosing timepoints, and number of doses. Evaluation of several candidate models showed that wound healing acceleration is not likely driven directly by time‐dependent VEGF‐A concentration. Instead, we found that administration of AZD8601 induced a sustained acceleration of wound healing depending on the accumulated dose, with a dose producing 50% of the maximal effect of 92 µg. Simulations with this model showed that a single dose of 200 µg AZD8601 can reduce the time to reach 50% wound healing by up to 5 days.

Study Highlights.

• WHAT IS THE CURRENT KNOWLEDGE ON THE TOPIC?

☑ Mathematical models of wound healing have previously been developed to leverage experimental studies to reveal new insights about the basic biology of wound healing and to predict how interventions can impact this process.

• WHAT QUESTION DID THIS STUDY ADDRESS?

☑ We used a population modeling approach to integrate sparse experimental data from several independent mouse studies with different designs to quantify the effect of a novel pro‐angiogenic mRNA drug on wound healing dynamics.

• WHAT DOES THIS STUDY ADD TO OUR KNOWLEDGE?

☑ Our model, informed by multiple experimental datasets, suggested that a single injection of mRNA, if sufficiently large, will induce a sustained acceleration of wound healing.

• HOW MIGHT THIS CHANGE DRUG DISCOVERY, DEVELOPMENT, AND/OR THERAPEUTICS?

☑ Our model serves as a tool for addressing questions about dosing in the context of wound healing. The model quantitatively relates different preclinical studies to one another and predicts clinically meaningful scenarios. Our study suggests that VEGF‐A mRNA induces a sustained and dose‐dependent acceleration of wound healing, thereby promoting a regimen with less frequent delivery of larger doses.

Wound healing requires coordination of many biological processes that result in four overlapping phases; hemostasis, inflammation, proliferation, and remodeling. ¹ , ² , ³ This sequence must be appropriately orchestrated to adequately regenerate skin and restore its life‐preserving barrier function. ¹ , ² However, disease can alter the interplay and timing of these processes, leading to wounds that fail to heal normally. Diabetes, for example, may cause impaired wound healing, eventually resulting in chronic leg or foot ulcers. ¹ , ⁴ This remains a challenging clinical problem with a high unmet need and high costs for treatment. ⁵

Vascular endothelial growth factor A (VEGF‐A) has demonstrated an ability to accelerate impaired wound healing when administered as a recombinant protein or via naked or adenoviral vector‐mediated gene transfer. ⁶ , ⁷ , ⁸ , ⁹ Recently, we have shown that intradermal delivery of AZD8601, an mRNA designed to produce VEGF‐A, ¹⁰ accelerates cutaneous wound healing in an established murine model of diabetes. ¹¹ Although our preclinical experiments have confirmed the bioactivity of the drug and its efficacy in murine wounds, it is unclear how these findings scale to patients with diabetes, particularly in terms of optimal drug dosing and dosing regimens.

As a step toward studying AZD8601 in a clinical setting, we performed a comprehensive quantitative assessment of time series data obtained from three different mouse studies conducted in two different laboratories. In these studies, full thickness (epidermis plus dermis) circular wounds were created and epidermal wound area was quantified at specific timepoints after administration of vehicle or drug. The studies explored different doses, different dosing timepoints relative to wounding, and different number of doses. Based on the integrated dataset, we developed a pharmacodynamic (PD) model of wound area during the healing process.

Our model is inspired by the ordinary differential equation model by Bowden et al., ¹² but we focus on wound healing following pharmacological intervention. Moreover, we use a population approach to handle the longitudinally sparse data and the variability that exists between animals and studies. ¹³ The model behavior is summarized as follows. The area of a newly created wound immediately increases due to a recoil effect. ¹⁴ Healing is simultaneously initiated from a region of proliferating cells located at the perimeter of the wound. Healing rate is described by a logistic growth model that exhibits an initial exponential progression that gradually diminishes as the wound heals. To account for the observed wound healing acceleration induced by AZD8601, a stimulatory term is added to the basal healing rate. Several mathematical stimulation mechanisms are explored, including stimulation based on the transient VEGF‐A exposure, which, in turn, is modeled by a separate pharmacokinetic (PK) model. We show, however, that healing acceleration is best described by a model in which the accumulated dose drives a sustained stimulation throughout the healing process.

Using our wound healing model, we quantified nondrug parameters related to the healing of a vehicle‐treated wound, as well as drug parameters related to the wound healing acceleration. In addition, model simulations were performed to further understand how dose and timing of AZD8601 delivery impact the rate of wound healing. We also analyzed the correlation between estimated basal healing rates in individual mice and their fasting blood glucose to assess the murine diabetic model.

METHODS

Experimental model and data

Wound healing studies

Data was obtained from three independent studies conducted at the University of Virginia, United States, and at AstraZeneca, Sweden. A subset of these experimental results has previously been published elsewhere, along with detailed experimental methods. ¹¹ Procedures were conducted in accordance with ethical permits from the University of Virginia Animal Care and Use Committee or the Local Ethics Committee on Animal Experiments in Gothenburg, Sweden.

The experimental model and the study designs are illustrated in Figure 1 a,b. Circular, full thickness, cutaneous wounds of approximately 1 cm² were surgically made on the dorsum of 131 anesthetized 8‐week‐old diabetic B6.BKS(D)‐Lepr^db/J mice (Jackson Laboratory). Prior to wounding, fasted glucose measurements were taken on blood drawn from tail veins (available in Supplementary Data ). Mice received vehicle or AZD8601 (4 × 7.5 µg, 4 × 25 µg, and 4 × 50 µg) in 10 microliters of 10 mM citrate/130 mM saline injected intradermally at 4 equidistant points around the wound edge. Single injected study groups received injections on day 0 or 3, and double injected study groups received injections on days 0 and 3 ( Supplementary Data ). When dosing twice, the 4 injections at the second dosing occasion were shifted 45° to not inject in the same position twice. In anesthetized mice, wounds were serially imaged using an iPhone6 (Apple) or a Canon 600D with a Tamron SP 900 mm F/2.8 objective under bright‐field illumination. The open wound area, identified as the region in the center of the wound lacking an epithelial layer, was measured by tracing the boundary of the wound in ImageJ. ¹⁵ In study 1, wounds were imaged on days 0, 3, 6, 10, 13, and 18. In study 2, single injected groups were imaged on either day 0 and 1, or on days 0 and 3. Double injected groups were imaged on either days 0, 3, and 6 or on days 0, 3, 6, 10, and 13. In study 3, wounds were imaged on days 0, 3, 7, 10, 14, and 17. In total, 584 open wound area measurements were made ( Supplementary Data ).

Figure 1.

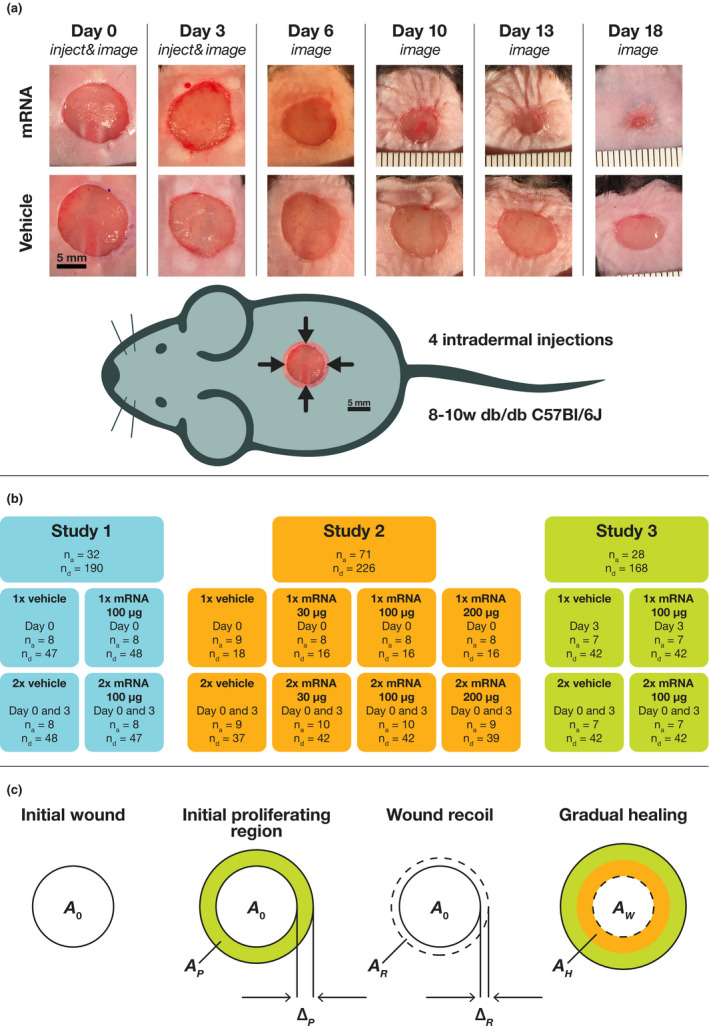
Illustration of the experimental model, the study design, and the pharmacodynamic model. (a) Wound images from study 1 are shown for double injections of 100 µg AZD8601 and vehicle. (b) Overview of the experimental study designs. Single injected groups are indicated as 1×, double injected as 2×, and the injection day(s) are stated. The numbers of animals and wound area data points in each study and group are denoted by n _a and n _d. (c) Illustration of mathematical model. After wounding, the initial wound area is $A_0$. Healing is immediately initiated from a region of proliferating cells located at the perimeter of the wound with annulus width ${\mathrm{\Delta }}_P$ and area $A_P$. Within hours, wound recoil is rapidly increasing the wound area with a region of annulus width ${\mathrm{\Delta }}_R$ and area $A_R$. As the healed area, $A_H$, gradually increases, the remaining wound area, $A_W$, decreases.

Pharmacokinetic study

In a separate study, the PK profile of VEGF‐A protein was measured after a single dose of 100 µg AZD8601. This study, including the bioanalytical methods for quantification of VEGF‐A protein in skin, have previously been described in detail. ¹¹ Briefly, intradermal injections were given in up to three separate positions in 13 mice, which were subsequently followed for up to 6 days. Animals were euthanized for measurement of VEGF‐A tissue concentration in skin at 6, 24, 48, 72, and 144 hours. A complete record of all PK data is provided in the Supplementary Data . The lower limit of quantification (LLOQ) for VEGF‐A was 0.156 pg/mg tissue. At 144 hours, 10 of 12 observations were below the LLOQ.

Mathematical modeling

Population modeling

Nonlinear mixed effects modeling was performed using Phoenix NLME version 1.3 (Certara, Princeton, NJ). For the PK models, observations below the LLOQ were handled by the M3 method. ¹⁶ PK models were estimated using the Laplacian method, and PD models with the first order conditional estimation method. Different configurations of study‐specific parameters and interindividual variability (IIV) were considered during model development. Model fits were evaluated by visual predictive check (VPC) plots, parameter precision as quantified by the relative standard error, residuals plots, and diagnosis of empirical Bayes estimates. Given satisfactory model diagnostics, final model selection was based on the Akaike information criterion with correction for small sample size (AICc). Confidence intervals for the half‐lives of mRNA and protein in the PK model were determined by bootstrapping. Model simulations were done using the parameter values of a typical animal (i.e., values of random effects set to zero).

Pharmacokinetic models

The PK of VEGF‐A mRNA and protein was modeled by:

$$\frac{\text{dmRNA}\left(t\right)}{\mathrm{d}t}=-k_1\times \text{mRNA(}t),$$

$$\frac{\text{dVEGF(}t)}{\mathrm{d}t}=k_2\times \text{mRNA(}t)-k_3\times \text{VEGF(}t),$$

$$\text{mRNA(}0)=\text{VEGF(}0)=0.$$

Here, $\text{mRNA(}t)$ is the amount of mRNA and $\text{VEGF(}t)$ the concentration of protein. The kinetic parameters $k_1$, $k_2$, and $k_3$ describe degradation of mRNA, synthesis of protein, and degradation of protein, respectively. Four versions of this model were explored, where $k_1$, $k_2$, $k_3$, or none of the parameters had a lognormal IIV. A lognormal error model was used for the observed VEGF‐A concentrations.

Swapping the values of $k_1$ and $k_3$ results in an identical model in terms of the time‐dependent VEGF‐A concentration, similarly to the well‐known phenomenon of flip‐flop kinetics. The faster and slower timescales of mRNA and protein degradation can, therefore, not be distinguished based on the VEGF‐A profiles alone. Kinetic parameters of mRNA and protein turnover in general indicate that protein degradation is the slower process. ¹⁷ However, protein hormones like VEGF‐A typically have short half‐lives, in the order of minutes, to enable rapid control. ¹⁸ Specifically, the VEGF‐A protein elimination half‐life in human plasma is maximally ~ 10 minutes ¹⁹ and ~ 3 minutes in the mouse, ²⁰ and the VEGF‐A mRNA half‐life in human lung fibroblast is ~ 1 hour. ²¹ In addition, AZD8601 is designed for extended half‐life making it very likely that the mRNA degradation is the slower of the two timescales (i.e., $k_1<k_3$).

Wound healing model for vehicle‐treated mice

The vehicle only model for vehicle‐treated wounds is illustrated in Figure 1c . The healed area, $A_H(t)$, is described by a logistic growth law,

$$\frac{\mathrm{d}{A}_H(t)}{\mathrm{d}t}=r\times (A_H(t)+A_P)\times \left(1-\frac{A_H(t)}{A_0+A_R}\right),$$

$$A_H(0)=0,$$

where r is the basal healing rate of a vehicle‐treated wound, $A_P$ the area of the region of initially proliferating cells induced by the wounding, $A_0$ the initial wound area, and $A_R$ the area of the wound recoil. The areas $A_P$ and $A_R$ are implicitly parameterized by the annulus width of the initial proliferating region and the recoil region, ${\mathrm{\Delta }}_P$ and ${\mathrm{\Delta }}_R$,

$$A_P=2{\mathrm{\Delta }}_P\sqrt{\pi A_0}+\pi {\mathrm{\Delta }}_P^2,$$

$$A_R=2{\mathrm{\Delta }}_R\sqrt{\pi A_0}+\pi {\mathrm{\Delta }}_R^2.$$

The observed wound area at time $t$, $A_W(t)$, is:

$$A_W(t)=A_0+A_R\left(1-e^{-k_R\times t}\right)-A_H(t)+\epsilon ,$$

where $k_R$ is the recoil rate constant and $\epsilon \sim N(0,{\sigma }^2)$. The transient part of wound recoil is a relatively fast process (hour‐timescale) that cannot be estimated using our experimental protocol, and $k_R$ was, therefore, fixed to 24 day⁻¹. When $A_H(t)=A_0+A_R$ (i.e., when the healed area equals the initial wound area plus the recoil area), $A_W(t)$ becomes zero and the wound is fully healed. The final model included study‐specific values of $A_0$ and $r$, study‐specific lognormal IIV for $A_0$, and a common lognormal IIV for $r$.

Wound healing models for AZD8601 stimulation

Six candidate models for wound healing in AZD8601‐treated mice were defined by the addition of a stimulatory effect, stim(t), to the healing rate:

$$\frac{\mathrm{d}{A}_H(t)}{\mathrm{d}t}=\left(r+stim(t)\right)\times \left(A_H(t)+A_P\right)\times \left(1-\frac{A_H(t)}{A_0+A_R}\right).$$

In the exposure‐driven model, $stim\left(t\right)$ is defined as:

$$\text{stim}(t)=\frac{E_{max}\times {\text{VEGF}(t)}^{\gamma }}{{\text{EC}}_{50}^{\gamma }+\text{VEGF}{(t)}^{\gamma }},$$

where $\text{VEGF(}t)$ is the concentration of VEGF‐A protein determined by the PK model, and where $E_{max}$, ${\text{EC}}_{50}$, and $\gamma$ are parameters defining the maximal stimulation, the concentration resulting in half‐maximal stimulation, and the sigmoidicity, respectively. In the five other models, stim(t) is defined as:

$$\text{stim}(t)=\frac{E_{max}\times {\text{DOSE}(t)}^{\gamma }}{{\text{ED}}_{50}^{\gamma }+{\text{DOSE}(t)}^{\gamma }}$$

where $\text{DOSE(}t)$ is a model‐specific time‐dependent function of the history of doses, and where $E_{max}$, ${\text{EC}}_{50}$, and $\gamma$ are parameters defining the maximal stimulation, the value of $\text{DOSE(}t)$ resulting in half‐maximal stimulation, and the sigmoidicity, respectively. Different choices of $\text{DOSE(}t)$ define the remaining candidate models.

In the weighted accumulated dose model, $\text{DOSE(}t)$ is defined as the accumulated dose injected up to time t, counted with a weighting for the dosing on day 3,

$$\text{DOSE(}t)=D_0\times H(t)+w\times D_3\times H(t-3).$$

here, $D_0$ and $D_3$ are the known doses given at days 0 and 3 (which may be zero), $w$ a weighting parameter, and $H\left(t\right)$ the Heaviside step function. If $w$ is fixed to 1, this model simplifies to the accumulated dose model (without weighting).

The lagging accumulated dose model is defined just like the accumulated dose model but adds a lag time parameter, $t_{\text{lag}}$, in the Heaviside step function, which delays the effect of a dose,

$$\text{DOSE}(t)=D_0\times H(t-t_{\text{lag}})+D_3\times H(t-3-t_{\text{lag}}).$$

In the weighted maximum dose model, $\text{DOSE(}t)$ is defined as the maximum dose injected up to time $t$, counted with a weighting for the dosing on day 3,

$$\text{DOSE(}t)=max\left(D_0\times H(t),w\times D_3\times H(t-3)\right).$$

Again, $D_0$ and $D_3$ are the known doses given at day 0 and 3 (which may be zero), $w$ a weighting parameter, and $H(t)$ the Heaviside step function. If $w$ is fixed to 1, this model simplifies to the maximum dose model (without weighting).

All parameters introduced in the six candidate models are estimated using the wound area measurements, except when $w$ was fixed. Final models included study‐specific values of $E_{max}$ but no IIV.

Analytical solution of the wound healing model

Under the simplification that recoil is immediate, an analytical solution for $A_H\left(t\right)$ exists for constant stimulation, $\text{stim}(t)=s$,

$$A_H(t)=\frac{A_0+A_R}{1+\frac{A_0+A_P+A_R}{\left(e^{\frac{\left(A_0+A_P+A_R\right)\times \left(r+s\right)\times t}{A_0+A_R}}-1\right)\times A_P}}.$$

Furthermore, it can be shown that the time to heal a wound to a fraction $f$ of the initial area is

$$t_f(s)=\frac{\left(A_0+A_R\right)\times \ln \left(\frac{\left(f\times A_0+A_P\right)\left(A_0+A_R\right)}{A_P\times \left(A_0-f\times A_0+A_R\right)}\right)}{\left(A_0+A_P+A_R\right)\times \left(r+s\right)},$$

giving a relative decrease in healing time,

$$\frac{t_f(0)-t_f(s)}{t_f(0)}=\frac{s}{r+s},$$

that depends on $r$ and $s$ but is independent of all other parameters, including f.

Correlation between fasting blood glucose and healing rate

Pearson’s correlation coefficient and the corresponding P value were computed for fasting blood glucose and the estimated individual healing rate.

RESULTS

Population PK model for AZD8601

A population PK model was developed to describe degradation of mRNA and the synthesis and degradation of VEGF‐A protein in the skin following administration of AZD8601. Different configurations of IIV were explored before selecting the best model in terms of AICc (Table S1 ). Estimates of the kinetic parameters are shown in Table 1 . The kinetic parameters correspond to half‐lives of 13 hours (95% confidence interval (CI) of 6–18 hours) and 3 hours (95% CI of 15 minutes to 7 hours) for degradation of mRNA and protein. VPCs and other diagnostic plots are provided in Figure S1 , demonstrating an adequate fit of the model.

Table 1.

Parameters of the pharmacokinetic model

Description	Symbol	Unit	Value (%RSE)	%IIV (%RSE)
mRNA degradation	$k_1$	hour−1	0.055 (19)	24 (25)
VEGF synthesis	$k_2$	pg mg−1 μg−1 hour−1	0.16 (25)
VEGF degradation	$k_3$	hour−1	0.23 (53)
Residual error	$\sigma$	%	35 (9)

Reporting of %IIV and residual error was done using the approximation $100\sqrt{{·}^2}$.

For the mRNA degradation, both the typical value and the IIV are estimated. Parameters were estimated with an RSE < 30%, except $k_3$ (53%).

%IIV, percent interindividual variability; %RSE, percent relative standard error.

Population PD model for vehicle‐treated wounds

A population PD model was developed to describe the wound area dynamics during healing in vehicle‐treated mice, as an intermediate step toward a model for both vehicle‐treated and AZD8601‐treated wounds. Parameter estimates are shown in Table 2 . VPCs and other diagnostic plots are provided in Figure S2 , demonstrating an adequate fit of the model.

Table 2.

Parameters of the pharmacodynamic wound healing models

Parameter description	Symbol	Unit	Study	Vehicle only model		Accumulated dose model
				Value (%RSE)	%IIV (%RSE)	Value (%RSE)	%IIV (%RSE)
Initial wound area	$A_0$	cm2	1	1.08 (4)	15 (17)	0.97 (3)	18 (13)
			2	1.00 (2)	7 (23)	1.00 (1)	8 (10)
			3	1.17 (2)	1 (37)	1.15 (1)	4 (26)
Basal healing rate	$r$	day−1	1	0.15 (23)	21 (13)	0.16 (17)	24 (10)
			2	0.095 (24)	21 (13)	0.10 (18)	24 (10)
			3	0.16 (22)	21 (13)	0.19 (15)	24 (10)
Initial proliferating region width	${\mathrm{\Delta }}_P$	cm	All	0.10 (31)		0.086 (29)
Wound recoil region width	${\mathrm{\Delta }}_R$	cm	All	0.037 (32)		0.032 (21)
Maximal stimulation of healing	$E_{max}$	day−1	1			0.054 (50)
			2			0.050 (22)
			3			0.12 (24)
Dose yielding half‐maximal stimulation	ED50	μg	All			91.8 (21)
Sigmoidicity parameter	$\gamma$	–	All			4.96 (65)
Residual error SD	$\sigma$	cm2	All	0.090 (7)		0.080 (5)

Reporting of %IIV was done using the approximation $100\sqrt{{·}^2}$.

For the initial wound area and the basal healing rate, both the typical value and the IIV are estimated. Parameters of the vehicle only model were estimated with an RSE < 30%, except for the IIV of $A_0$ in study 3 (37%), ${\mathrm{\Delta }}_P$ (41%), and ${\mathrm{\Delta }}_R$ (32%). Parameters in the accumulated dose model were estimated with an RSE < 30%, except for $E_{max}$ in study 1 (50%) and $\gamma$ (65%).

%IIV, percent inter‐individual variability; %RSE, percent relative standard error; ED₅₀, dose producing 50% of the maximal effect; E_max, maximum effect.

Wound healing acceleration is insensitive to time‐dependent VEGF‐A concentration

A population PD model for both vehicle‐treated and AZD8601‐treated wounds was defined by adding a PK‐driven stimulatory term to the healing rate. Details of the model fit are given in Table S2 . The estimate of $\gamma$ is strikingly small (0.08), which means that healing rate stimulation is relatively insensitive to the VEGF‐A concentrations. Even at very low concentrations, the stimulatory effect is still present (Figure S3 ). For instance, 11 days after a single dose, VEGF‐A concentration has decreased 6 orders of magnitude, whereas the stimulatory effect is only halved. This implies that wound healing acceleration is not directly driven by VEGF‐A concentrations, but rather modulated in a sustained way by some characteristic of the exposure history.

Healing rate stimulation is sustained and dosing day independent

Several candidate models with a sustained stimulation were considered, in addition to the exposure‐driven model. These models are purely driven by the dosing history and do not consider the mRNA and protein kinetics. Models were ranked according to their ΔAICc relative to the model with the lowest AICc (Table 3 ). Details of model fits are provided in Table S2 . The exposure‐driven model has the largest ΔAICc and is clearly worse than any of the models with sustained stimulation. Based on this, and on the results from the previous subsection, we conclude that the stimulatory effect of AZD8601 on the healing rate is sustained and not directly driven by the transient VEGF‐A exposure. Furthermore, for neither of the two sustained stimulation mechanisms (accumulated or maximum dose) did the ΔAICc motivate the inclusion of a weighting parameter. Thus, there is nothing to suggest that healing rate stimulation depends on the day of injection.

Table 3.

Model comparison by ΔAICc relative to the model with lowest AICc

Model	ΔAICc
Accumulated dose	0
Lagging accumulated dose	2.04
Weighted accumulated dose	2.11
Maximum dose	3.65
Weighted maximum dose	4.11
Exposure‐driven	17.2

AICc, Akaike information criterion with correction for small sample size.

Sustained acceleration driven by accumulated dose fits data best

The accumulated dose model was best in terms of AICc (Table 3 ). Parameter estimates for this model are shown in Table 2 and further described in the Supplementary Results . A median VPC is shown in Figure 2 and additional diagnostic plots are provided in Figure S4 , demonstrating an adequate fit of the model. Because it had the lowest AICc as well as favorable model diagnostics, the accumulated dose model was considered the preferred model for describing wound area dynamics during the healing progress, and it was used for further investigations.

Figure 2.

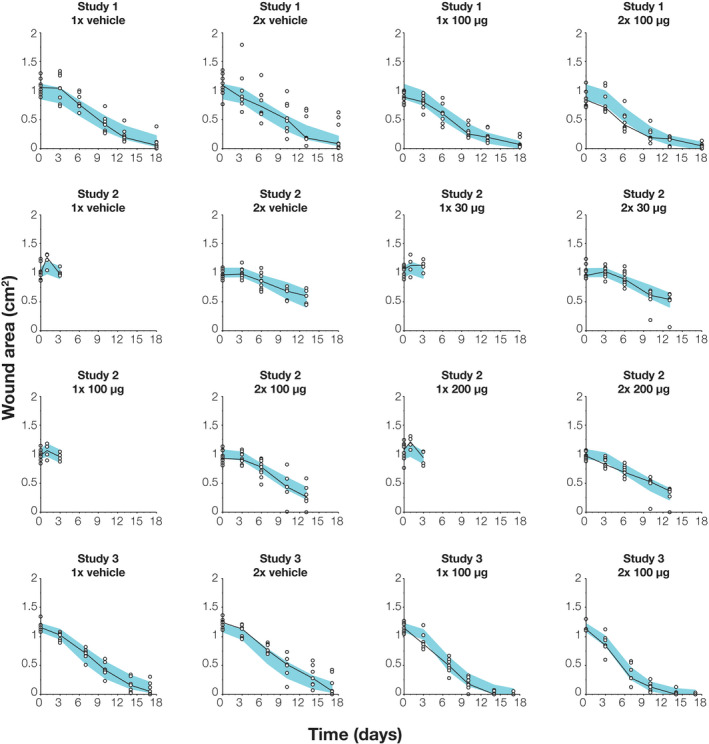
Visual predictive check for the accumulated dose model at the 50th percentile, stratified on the different groups of each study. Individual data of wound area (white disks) and their median (black dashed line) are shown together with the 90% confidence interval for the model‐predicted median (blue shaded band).

The effect of AZD8601 is immediate

Because a VEGF‐A half‐life of up to 7 hours could not be excluded, and because various steps of the wound healing process itself potentially could delay the VEGF‐A‐induced acceleration, the accumulated dose model was challenged by including a lag time between the timepoint of dosing and the onset of the stimulatory effect. An uncertain estimate of a small lag time was obtained, 0.56 days (relative standard error 78%), but comparison by AICc did not justify the inclusion of this parameter (Table 3 ). Thus, VEGF‐A‐induced acceleration of wound healing is likely relatively immediate.

Acceleration of wound healing is dose‐dependent

The accumulated dose model was used to simulate the complete wound area profiles in the three studies (Figure 3 ). In study 1, both 1 × 100 µg and 2 × 100 µg induce a clear acceleration compared with the vehicle. Initially, AZD8601‐treated wounds heal at identical rates, but the twice injected group has a slightly faster healing after the second injection on day 3. In study 2, the 2 × 30 µg group only heals marginally faster than the vehicle, whereas the 2 × 100 µg and 2 × 200 µg groups both show a clear acceleration of similar extent. In study 3, the 1 × 100 µg group displays approximately half the level of acceleration compared with the 2 × 100 µg group. The simulated profiles suggest that wound healing acceleration is dose‐dependent (i.e., larger accumulated doses produce a larger effect).

Figure 3.

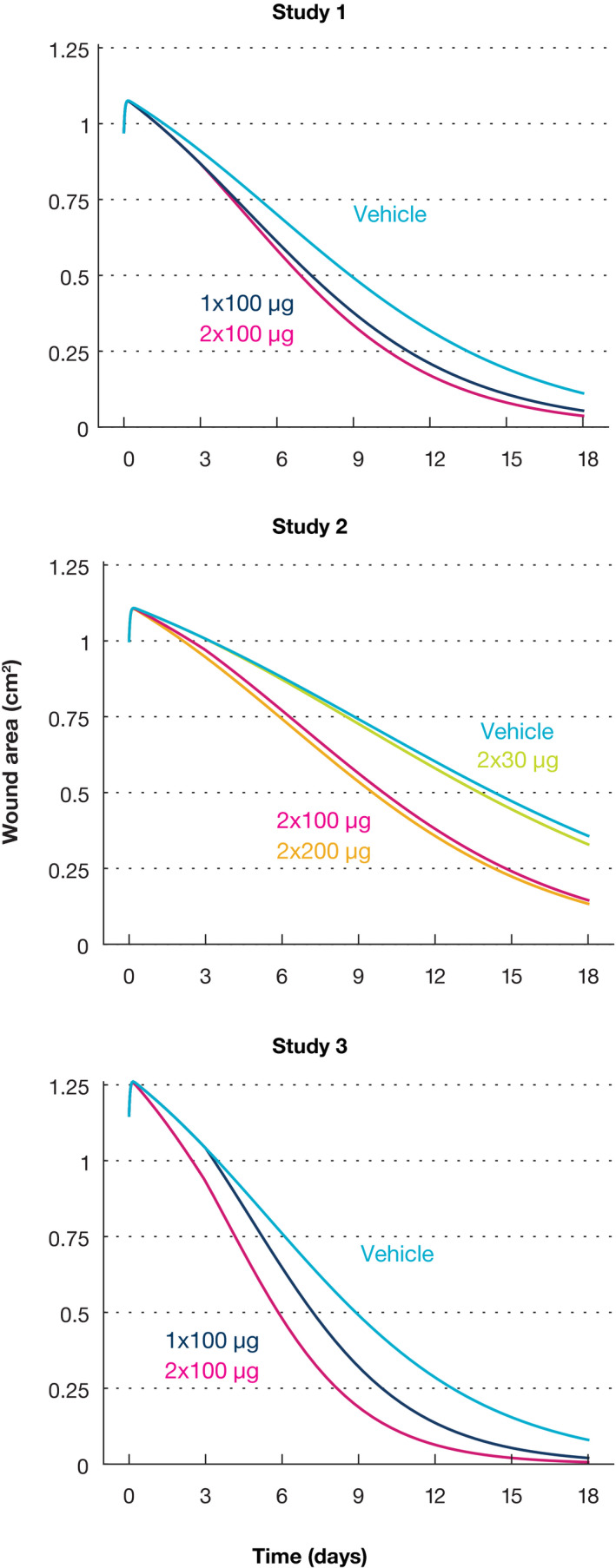
Model simulations of the complete wound healing trajectory for each group in the three studies. The model does not distinguish single or double vehicle injections, and these are shown as a single trajectory for simplicity. In addition, the single administrations in study 2 were omitted from the simulation because these groups were not followed beyond 3 days, and because the experimental protocol overlaps with the double injected groups in this time frame. In study 3, the single dose was delivered on day 3 and the trajectory coincides with the vehicle group up until this timepoint.

Healing time decrease depends on dose amount and dosing timepoint

Simulations with the accumulated dose model were performed to study the time it takes for a wound to heal to different degrees (10%, 50%, and 90%) depending on the amount of a single AZD8601 injection given on day 0 (Figure 4 ). With the parameters of study 1, a vehicle‐treated wound requires 9.1 days to heal to 50%. This is decreased by 2.3 days to 6.8 days for a 200 µg dose. In study 2, which has a similar $E_{max}$ but slower basal healing rate, and in study 3, which has a lower $E_{max}$ but similar basal healing rate, larger decreases are possible (4.7 and 3.1 days). Thus, in addition to the dose, the accelerating effect depends on a combination of both drug and nondrug parameters. Due to the sharp dose‐dependence around  the dose producing 50% of the maximal effect ( ${\text{ED}}_{50}$), 90% of the theoretical decrease in healing time is already achieved at an accumulated dose of 135 µg (study 1), 132 µg (study 2), and 129 µg (study 3). In addition, when measured in absolute days, the more complete degree of healing considered, the larger the accelerating effect becomes. However, the relative decrease in healing time is the same irrespective of the degree of healing considered (Methods). Additional simulations studying the impact of dosing timepoint relative to wounding are shown in Figure S5 and described in the Supplementary Results .

Figure 4.

Model simulations showing the impact of the amount of a single dose on day 0 on the time to 10%, 50%, or 90% wound healing in the 3 studies. The dashed intervals and the adjacent numbers show the decrease in healing time for treatment with a 200 µg injection compared with a vehicle‐treated wound.

Fasting blood glucose is not correlated to healing rate

The estimated basal healing rate in individual animals was compared with fasting blood glucose concentrations. Negligible, nonsignificant correlations were found for both vehicle‐treated animals (−0.14, P value 0.34) and for all animals (−0.13, P value 0.13). Hence, the analysis does not indicate that more diabetic animals (i.e., with higher concentrations of fasting blood glucose) have lower basal rates of wound healing.

DISCUSSION

We have developed a mathematical model that describes wound healing in diabetic mice. Specifically, the model quantifies the longitudinal wound area changes in mice treated with either vehicle or AZD8601, a VEGF‐A‐producing mRNA drug. A population modeling approach facilitated integration of multiple sparse datasets and enabled estimation of the variability in wound healing parameters between individuals and across different studies. Although our model is largely empirical, several important characteristics of the healing process were identified.

A PK model for AZD8601 was developed prior to the wound healing modeling. It was found that VEGF‐A PK in mouse skin is likely driven by degradation of mRNA, which we estimated is slower than protein degradation and, therefore, the rate‐limiting step. The mRNA half‐life was implicitly estimated from protein time series data to 13 hours, one order of magnitude greater than the reported half‐life of endogenous mRNA in human lung fibroblasts. ²¹ This is not unexpected because the base change in the mRNA of AZD8601 reduces the immunological response to single stranded mRNA, which lets more mRNA escape the endosomes, but the longer half‐life could also be due to species and cell type differences.

We then proceeded to develop a logistic growth model for vehicle‐treated wounds. This model was subsequently extended to include a stimulatory effect by VEGF‐A on the healing rate. A conventional exposure‐driven PK/PD model indicated a stimulatory effect that was insensitive to time‐dependent VEGF‐A concentrations and that lasted throughout the whole study (up to 18 days). However, after around 4 days, VEGF‐A concentrations have decreased below the endogenous concentration in vehicle‐injected mice (0.5–0.7 pg/mg tissue; unpublished data). These contradictory observations led us to dismiss a mechanism where time‐varying VEGF‐A concentration drives healing rate stimulation, and we instead decided to evaluate other models that hypothesize a sustained stimulatory effect.

Five candidate models with a sustained effect of AZD8601 on healing rate were considered. These models were different variants of two main mechanisms in which the healing rate stimulation is driven by either the accumulated dose so far or the maximum dose so far. Model selection by AICc, and diagnostic plots, showed that wound healing acceleration is best described by a sustained stimulation driven by the accumulated dose. Simulations of the accumulated dose model showed a meaningful and dose‐dependent acceleration of healing that was visible in terms of the wound area profile. Simulations are consistent with the estimates of ${\text{ED}}_{50}$ and $\gamma$, which suggest a steep dose‐dependence around 92 µg; after the 2 × 30 µg injections in study 2, stimulation is only at 11% of the potential maximum according to the E _max‐model, whereas 1 × 100 µg reaches 60% of the maximum. After 1 × 200 µg, or 2 × 100 µg, stimulation is essentially fully saturated (98% of the maximum) and little more happens for 2 × 200 µg (100% of the maximum). The dose‐dependency was further investigated by simulating the time required to reach different degrees of healing. Simulations showed that 90% of the estimated maximal decrease in healing time is achieved at an accumulated dose around 129–135 µg. Furthermore, an analytical solution of the model equations showed that the relative decrease in healing time is the same for any degree of healing.

In addition to the sustained and dose‐dependent effect on the healing rate, we identified three other characteristics of AZD8601. First, the stimulatory effect on the healing is immediate. This was concluded because the addition of a lag time parameter did not improve the model. An immediate effect is also consistent with the relatively rapid protein expression from the injected mRNA. Second, the stimulatory effect is independent of the dosing day. Again, this was concluded based on the addition of a new parameter, this time designed to identify a potential differentiation in stimulatory effect due to the dosing timepoint. Although administration on days 0 and 3 was estimated to induce a similar degree of healing rate acceleration, administration at an early timepoint is more beneficial considering the persistency of the effect. Third, the concentration of fasting blood glucose at study start does not explain the variability in basal healing rate. The absence of a correlation between glucose concentration and wound healing rate shows that the delayed wound healing in diabetic mice as compared with nondiabetic mice ⁶ , ¹² has more underlying causes than just the elevated glucose typically seen in the diabetic state.

A phase I clinical trial has previously been performed where recombinant human VEGF was topically administered to diabetic foot ulcers. ²² In that study, VEGF was dosed every second day for up to 6 weeks. This dosing schedule is interesting considering the present finding, which suggests a sustained effect for a sufficiently large dose. If AZD8601 is progressed into clinical development, study designs with frequent and smaller doses should be challenged by designs in which relatively large doses are injected with longer intervals (e.g., on a weekly or biweekly basis). Translation to human is, however, complicated by the differences between murine and human skin repair, such as the high dependence of contraction and the role of specific niches of skin stem cells in mice. ²³

This study has several limitations. To begin with, the estimated half‐lives of VEGF‐A mRNA and protein turnover were imprecise. The protein half‐life was particularly poorly estimated (95% CI of 15 minutes to 7 hours). The CI suggests that the half‐life could be very small compared to the first PK sample at 6 hours. Thus, retrospectively, we conclude that a more precise estimate would require PK sampling prior to 6 hours. However, because it turned out that VEGF‐A concentrations were not directly controlling the stimulation of healing rate, the imprecise PK estimates were not crucial for the wound healing models. Another limitation concerns the mechanism that best describes the sustained stimulation of wound healing. Although the accumulated dose model performed best in terms of AICc, the maximum dose model was also a reasonable candidate that should not be completely ruled out. Selection between the two mechanisms could be revisited in future experiments. For instance, a relatively high total dose, such as 120 µg, could be given either as a single dose or split up as 4 × 30 µg over 4 days. A failure to observe a similar degree of healing acceleration between the single and split dosing would falsify the accumulated dose model and instead favor the maximum dose model (provided that the healing rate was higher for the single dose). Yet another limitation lies in the conclusion that the stimulatory effect of AZD8601 is independent of dosing day. Because dosing only occurs on days 0 and 3, it is not known to what extent this finding generalizes to other days.

Previous wound healing models cover a broad spectrum of mathematical frameworks, model complexity, and biological detail. ²⁴ , ²⁵ Comprehensive reviews are given by Sherratt and Dallon ²⁶ and by Jorgensen and Sanders. ²⁷ On the complex end, there are partial differential equation models for epidermal wound healing, ²⁸ and dermal wound healing, including blood vessel growth. ²⁹ On the other end are completely empirical models with just a few parameters. ³⁰ , ³¹ The model we have developed is relatively simple and has limited mechanistic underpinning. In contrast to Bowden et al., ¹² we only quantified the wound area lacking an epithelial layer, and the dynamics of dermal healing was not specifically considered. Our challenge, however, was the integration of relatively sparse data (2 to 6 data points per animal) from several independent studies with different designs. A future opportunity for wound healing modeling lies in the bridging of more theoretical and mechanistic models, such as reaction‐diffusion models, with the empirical mixed effects models typically used in a pharmaceutical industry setting. ³²

In conclusion, intradermal delivery of AZD8601 induced a sustained and dose‐dependent acceleration of wound healing in diabetic mice. The long‐lasting effect of AZD8601 opens the possibility for a clinical regimen with less frequent delivery of larger doses.

Funding

M.R., A.C.B., and S.M.P. were funded with equal contributions from Research and Early Development, Cardiovascular, Renal and Metabolism (CVRM), BioPharmaceuticals R&D, AstraZeneca, Gothenburg, Sweden and Integrated Cardiometabolic Center, Karolinska Institute, Stockholm, Sweden.

Conflicts of Interest

J.A., M.W., P.G., R.F.D., K.H., and A.L. are employees of AstraZeneca and may own stock or stock options. K.R.C. is an advisor and chair of the External Science Panel for AstraZeneca and a member of the Karolinska Institutet/AstraZeneca Integrated Cardio Metabolic Center in Huddinge, and receives support for these services, as well as research support through the Karolinska Institutet Center. He is also a co‐founder and equity holder of Moderna, Inc. All other authors declared no competing interests for this work.

Author Contributions

J.A., M.R., P.G., S.M.P., K.H., and A.L. wrote the manuscript. R.F.D., K.R.C., S.M.P., and K.H. designed the research. M.W. and A.C.B. performed the research. J.A., M.R., P.G., S.M.P., K.H., and A.L. analyzed the data.

Supporting information

Figure S1

Figure S2

Figure S3

Figure S4

Figure S5

Table S1

Table S2

Supplementary Material S1

Supplementary Material S2