Skip to main content
NCBI home page
ACS Omega logoLink to ACS Omega
. 2020 Jul 7;5(28):17170–17181. doi: 10.1021/acsomega.0c01148

A Simple Method for Including Polarization Effects in Solvation Free Energy Calculations When Using Fixed-Charge Force Fields: Alchemically Polarized Charges

Braden D Kelly †,*, William R Smith †,‡,¶,*
PMCID: PMC7376688  PMID: 32715202

Abstract

graphic file with name ao0c01148_0007.jpg

The incorporation of polarizability in classical force-field molecular simulations is an ongoing area of research. We focus here on its application to hydration free energy simulations of organic molecules. In contrast to computationally complex approaches involving the development of explicitly polarizable force fields, we present herein a simple methodology for incorporating polarization into such simulations using standard fixed-charge force fields, which we call the alchemically polarized charges (APolQ) method. APolQ employs a standard classical alchemical free energy change simulation to calculate the free energy difference between a fully polarized solute particle in a condensed phase and its unpolarized state in a vacuum. APolQ can in principle be applied to any microscopically homogeneous system (e.g., pure or mixed solvents). We applied APolQ to hydration free energy data for a test set of 45 neutral solute molecules in the FreeSolv database and compared results obtained using three different water models (SPC/E, TIP3P, and OPC3) and using minimal basis iterative Stockholder (MBIS) and restrained electrostatic potential (RESP) partial charge methodologies. In comparison with AM1-BCC, we found that APolQ outperforms it for the test set. Despite our method using default GAFF parameters, the MBIS partial charges yield absolute average deviations 1.5–1.9 kJ mol–1 lower than using AM1 bond charge correction (AM1-BCC). We conjecture that this method can be further improved by fitting the Lennard-Jones and torsional parameters to partial charges derived using MBIS or RESP methodologies.

1. Introduction

Free energy calculations are important in many scientific and engineering research areas, including chemical reaction and phase equilibria,1−4 solubility,5−7 hydration free energies,8−10 and pharmaceutical drug design.11−14 Molecular mechanics (MM) models are frequently used for atomistic simulations of these phenomena using either Molecular Dynamics (MD) or Monte Carlo (MC) algorithms. MM models use force fields (FFs) to describe the interactions between molecules, which incorporate parameters for bonds, angles, and torsions that are generated using the electronic structure (ES) methodology and subsequently fitted to data with mathematically simple functions. Intermolecular interactions typically involve both Lennard-Jones (LJ) and electrostatic (Coulombic) interactions. The electrostatic interactions are traditionally modeled using fixed atom-centered partial charges. Although fixed-charge FFs give reasonable results for several properties, they are often problematic for the calculations of the free energy changes between dissimilar environments, such as hydration free energies, ΔGhyd.15,16

In this paper, we focus on the use of fixed-charge atomistic FFs for the calculation of ΔGhyd. Due to their intrinsic limitations,17 we do not consider approaches using implicit solvent methods for its direct calculation. We also do not consider explicitly polarizable atomistic FFs, which add additional parameters to the model.18−26 Despite the added computational burden of their determination27,28 such FFs currently do not always give better predictions than fixed–charge FFs,29 particularly in the case of free energy calculations.30−32

ΔGhyd calculations for fixed-charge FFs are performed by alchemically decoupling (coupling) a solute molecule from (to) its solution environment to (from) its vacuum state. This is typically performed by separately decoupling the Coulombic and LJ contributions via a sequence of λ windows. For neutral molecules, in most cases, the electrostatic contribution is the major contribution to the hydration free energy. This is even more strongly the case for ions, where the electrostatic contribution is often an order of magnitude larger than the LJ contribution. It is therefore of great importance to develop methods that can better calculate the Coulombic contribution.

One approach to incorporate polarizability when using fixed-charge FFs is to include some of its effects into the partial charges of the FF itself. For the general Amber force field (GAFF) approach,33 the default partial charges are either restrained electrostatic potential (RESP)34 at the HF/6-31G* level or the semi-empirical AM1 bond charge correction (AM1-BCC),35 which is designed to yield similar results to RESP partial charges, but are faster to calculate and less sensitive to geometry. These choices indirectly incorporate polarization effects to mimic a condensed phase environment. Another approach has been to account for polarization by way of a correction to the fixed-charge FF calculation.36−41

Whereas polarization is indirectly included in the partial charges calculated for GAFF FFs, due to its choice of ab initio theory, it is not specific to any particular solvent environment. A recent work of Zhou et al.(42) has shown, based on comparisons predicted with accurate/experimental molecular dipole moments in a vacuum, that HF/6-31G* exhibits inconsistencies (ranging from under- to overpolarization by as much as 35%). The best hydration free energy results are typically obtained by using AM1-BCC. This is likely due to the ad hoc and extensive empirical data fitting of its parameters; this also serves, however, as its greatest limitation. It is not possible to systematically improve the electrostatic interactions when using AM1-BCC without refitting the entire database of bond charge corrections. While AM1-BCC is the current “gold standard” for GAFF, which is used to compare alternative partial charge methods,36,39,40 its results are, in our opinion, of only modest quality for solvation free energies.

The fitting of the LJ parameters to experimental data can potentially compensate for an incorrect treatment of polarizability. Whereas some of the experimental data used for fitting procedures consists of hydration free energy results, the parameters are usually fitted to a broad spectrum of thermodynamic properties. In any event, the requirement for a property-specific FF is unsatisfactory in principle. Our goal is to address the deficiencies of existing polarization strategies in the context of simulations of hydration free energies, ΔGhyd, and to test our approach for a spectrum of molecule types in the FreeSolv database.10

We recently proposed a method for explicitly incorporating polarization into a fixed-charge FF free energy calculation, called the OTFP (on-the-fly-polarization) method.43 This approach decouples the electric field generated by the solvent’s MM partial charges by scaling the MM partial charges in a QM/MM snapshot proportionally to the Coulombic decoupling parameter λcoul. This allows polarity in the solute partial charges to evolve from being completely unpolarized in a vacuum to fully polarized in solution. We also showed how the cost of self-polarization of the solute could be calculated by employing double-sided perturbation techniques.

In this paper, we propose a new method that uses a polarizable continuum model (PCM)44 approach to calculate the partial charges of the solute FF. This is considerably faster than the OTFP approach and is very simple to implement. Only two solute partial charge calculations are required prior to a simulation: a vacuum charge set and a polarized charge set. The resulting relatively low computational burden makes it computationally feasible to add diffuse functions to the QM basis set used. We refer to our proposed methodology for using these charge sets in the course of the Coulomb decoupling/coupling procedure in the alchemical change calculation of the APolQ (alchemically polarized charge) polarization methodology. The overall computational cost of this method is similar to that required for a standard fixed-charge simulation, and its modularity allows different ES calculations and partial charge partitioning schemes to be easily implemented as future improvements evolve with respect to these aspects.

APolQ is applicable only to solutions with a microscopically homogeneous environment, i.e., consisting of pure solvents and homogeneous mixtures of different compositions. This is the assumed context in the subsequent sections of this paper for its description and application to the large class of systems consisting of molecules of up to moderate size. It excludes, for example, solution environments that are microscopically inhomogeneous and/or for which dielectric constants are poorly defined, an example of which is the interior of a protein molecule. Such environments can be treated either by explicitly polarizable force fields or potentially by our OTFP method.43

We test our methodology on 45 different solute molecules that range from small polar molecules to large drug-like molecules. We consider minimal basis iterative Stockholder (MBIS) and RESP partial charges. For MBIS charges, we show results using SPC/E,45 TIP3P,46 and OPC347 water FFs. For RESP, we only show results using TIP3P water because this is the default solvent for which GAFF parameters are optimized. We also compare our results with those computed using the traditional AM1-BCC fixed-charge method.

The paper is organized as follows. We first summarize our FF generation procedures, followed by a description of the MD simulation protocols used. We summarize our methodology for calculating and transitioning from vacuum to solution partial charges and accounting for the cost of self-polarization. We then describe and discuss our results followed by conclusions and recommendations.

2. Simulation Methodology

The hydration (solvation) free energy is the molar free energy change when a single solute molecule is transferred from a vacuum (ideal gas state) into pure (water) solvent, where both the gas and the solvent are at unit molarity:

2. 1

where ρsolv(P, T) is the solvent density at the specified values of T and P and μsoluteres, NVT; ∞[T, ρsolv(P, T)] is the residual chemical potential of the solute at infinite dilution in the solvent, which we refer to as the intrinsic solvation free energy. Setting the chemical potentials of both states equal to each other using the constant density form of the chemical potential43 leads to the experimentally used form of the ΔGhyd as given by

2. 2

This form assumes that solute concentrations are low enough for Henry’s law to apply in the solution and that the partial pressure of the solute, Pvap, is sufficiently low to be treated as an ideal gas.

Our proposed approach is to calculate

2.

by mutating the partial charges on the solute molecule from their vacuum-derived values to implicitly polarized partial charges in the solution as the solute is coupled to the solvent. Similarly, as in our previous work,43 which accounted for polarization explicitly and on-the-fly, we account for the cost of self-polarization in polarizing the solute by sampling the potential energy differences between states using double-sided perturbations in each Coulomb window using different charge sets in the forward and reverse perturbations.

The implicitly polarized free energy algorithm for calculating ΔGhyd of the solute involves simple modifications to standard procedures.48 In the following two sections, we first describe how we generate FF parameters and partial charges in a vacuum and in implicit solvent. We then describe the approach for calculating the effects of the solute polarization on ΔGhyd.

3. Force-Field Parameterization

We used the electronic structure software Spartan’1849 to screen all conformers of each solute in vacuum, and identify their 20 lowest energy conformers using the semi-empirical PM6. We then screened for the lowest energy conformer using the HF/6-31G* level of theory. Finally, for small molecules (less than 7 C/N/O atoms), the lowest energy conformer was further optimized at the MP2/aug-cc-pVTZ level of theory, and for larger molecules, the ωB97X-D/aug-cc-pVTZ level was used. For larger molecules, the time and memory requirements for MP2 were severe, which is why we opted to use the range-separated, dispersion-corrected hybrid-generalized gradient approximation (GGA) density functional theory (DFT) model, ωB97X-D. Intramolecular parameters were generated for GAFF(2.11) using the AmberMD tool package Antechamber,50 which was also used to generate the RESP and AM1-BCC partial charges. HORTON 2.1.151 was used for generating minimum basis iterative Stockholder (MBIS) charges using an ultrafine grid. Gaussian1644 was used for all electronic structure calculations for the solute electron densities with the exception of AM1-BCC, which used Antechamber’s program, sqm. We then converted the topology files to GROMACS files using the python program ACPYPE.52

Antechamber’s built-in use of OpenEye software53 automatically averages equivalent atom-type partial charges. We used a python script to replicate the averaging procedure used in Antechamber since this is not available in the HORTON program.

4. Alchemically Polarized Charges

In the alchemical free energy changes, the solute molecule’s interactions with its environment are decoupled over a series of λ windows {1 = λ0, λ1, ..., λN = 0}. We incorporate polarization in the fixed charge simulations by using fixed partial charges within each window with magnitudes calculated according to

4. 3

Similar to the OTFP methodology, the APolQ method uses

4. 4
4. 5

We note that this is not the same as performing a mutation, which would use different charges at each window’s endpoint in eq 4 or 5. An undesirable consequence of using different partial charges in either eq 4 or 5 is that the difference in Hamiltonian’s between two states must also account for the change in the intramolecular contribution to the Hamiltonian, rather than requiring only the difference in intermolecular contributions. Our method both avoids this extra step and simultaneously accounts for the cost of self-polarization.

As an example of the difference between a conventional alchemical free energy calculation and that of our APolQ method, we compare the equations used to calculate the free energy perturbation according to a simple forward Zwanzig perturbation expression. For a linearly scaled Coulombic free energy contribution, this is

4. 6

where A is the Helmholtz free energy and q0 is the set of solute partial charges, which are unchanged in all windows. Nk is the number of Coulomb windows, 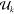Inline graphic is the potential energy, and <x>k denotes the ensemble average of the quantity x in window k.

In the APolQ method, the solute partial charges change across the Coulombic windows, and the free energy is calculated according to

4. 7

where both the scaling parameter λ and the partial charges, qk, depend on the Coulomb window. For a perturbation between any two states (windows), the same set of partial charges is used in both, and only the λ parameter changes. For example, when calculating the free energy change for two given states a and b, the forward direction perturbation will use the set of charges for state a in both state points. The perturbation in the reverse direction will necessarily use the partial charges for state b in both states. The average of these two perturbations has been shown previously43 to be equivalent to doing two perturbations characterized by both using the same partial charges, which are the average of the two sets. The relevance to the cost of self-polarization is discussed in Section 4.1.

Electron density calculations are performed in a vacuum with a high level of theory and a large basis set to avoid intrinsic overpolarization of the solute often associated with HF/6-31G* calculations. We also calculate the partial charges with the same basis set in the presence of the solvent via the use of a PCM (with default Gaussian 16 parameters) to implicitly generate the effects of a solvent on the electron density. We use MP2 for all calculations and considered the two basis sets aug-cc-pVTZ and cc-pVTZ based on their good results for polarizabilities and dipole moments, as reported by Hickey et al.(54)

For the PCM calculations, we used the respective static dielectric constants of the TIP3P, SPC/E, and OPC3 water models (ε0 = 94.0,47,55 ε0 = 70.7,56,57 and ε0 = 78.447). We note that the seemingly large differences in dielectric constants has very little effect on the partial charges produced and seems to differ only in the partial charge’s third or fourth decimal place. The relative insensitivity of solvation free energy to dielectric constants in the range of water models has been noted previously by Fennell et al.(57) We used the experimental (default) value for the dynamic dielectric constant of water available in Gaussian 16.44Figure 1 is a schematic description of our method, which also compares it to a typical GAFF free energy simulation; the latter technically requires two corrections to its endpoints, which are not required in our method.

Figure 1.

Figure 1

Open in a new tab

Hydration free energy as the difference between a solute with polarized partial charges in solution and unpolarized partial charges in a vacuum. This example uses MP2/aug-cc-pVTZ for both partial charge calculations; however, both theory and basis set can be changed.

4.1. Cost of Self-Polarization

There is a cost incurred when polarizing a solute molecule which, according to linear response theory, is equal to half the potential energy of interaction between the solvent and solute.58,59 It is possible to account for this cost of polarizing the solute molecule in solution by using half-polarized partial charges. This is done in the IPolQ-Mod method,60 which averages RESP partial charges calculated in a vacuum and implicit solvent and uses the same partial charges in all windows.

Since using half-polarized partial charges accounts for the cost of self-polarization38,59,61 (as in, e.g., IPolQ-Mod) and double-sided perturbations using APolQ are equivalent to using half-polarized partial charges for the given perturbations, this means that APolQ accounts for the cost of self-polarization in the free energy perturbations. Importantly, however, unlike actually using half-polarized charges, which is the approach of IPolQ-Mod, both endpoints of the perturbation are appropriately polarized for their particular environments. A previous work by Jia has noted that incorrect polarization intrinsic to IPolQ-Mod methods in the end states of the alchemical free energy change leads to incorrect Coulombic forces and energies between the solute and solvent.40 There are additional consequences since all 1–4 and greater intramolecular Coulombic interactions are also incorrectly polarized in all but perhaps one window when using the same set of partial charges in all windows.

Over the course of all windows, when using the APolQ method, the solute interacts first with strictly vacuum derived partial charges in the vacuum phase, retaining vacuum charges as LJ interactions are coupled to the solution environment. As the Coulomb interactions are then coupled, the partial charges increase their polarity until the solute exhibits completely polarized partial charges in the fully coupled solution phase. Double-sided perturbations account for the cost of self-polarization, and the transition from vacuum to polarized partial charges accounts implicitly for the work involved in organizing the solvent around the fully polarized solute molecule. A common double-sided perturbation method is the Bennett acceptance ratio (BAR)62 method. In the following, we used the multistate BAR method (MBAR) and have shown previously43 that MBAR equivalently accounts for self-polarization similar to BAR and the simpler Zwanzig perturbation methods.

5. Systems Studied and Simulation Details

We considered the SPC/E, TIP3P, and OPC3 water models for all simulations employing MBIS-derived partial charges. We used the TIP3P water model in the cases of RESP and AM1-BCC calculations. All calculations were performed at T = 298.15 K and P = 1 bar.

We performed calculations for 45 molecules containing C/H/N/O atoms of varying complexity from the FreeSolv database, as shown in Figure 2. Twenty-eight molecules were previously studied using our OTFP method.43 We added to this test set four linear alcohols and four alkylamines, in addition to several small cyclic molecules containing nitrogen or oxygen. For the molecules chosen, 23% of FreeSolv’s calculations using GAFF(1.7) and AM1-BCC partial charges give results within the experimental error, the same percentage shown by AM1-BCC over the entire FreeSolv database.

Figure 2.

Figure 2

Open in a new tab

Molecules studied.

All ΔGhyd calculations were performed in the NVT ensemble. We first determined the density for the OPC3 water model by following the protocol used in our previous study43 for the SPC/E and TIP3P water models. This entailed performing 10 independent NPT simulations at T = 298.15 K and P = 1 bar for 2000 water molecules. For each run, we used the GROMACS (version 2016.3) “insert-molecules” function63 to insert 2000 OPC3 water molecules into a box of length 4.3 nm. The system’s energy was then minimized using the steepest descent algorithm, terminating when a maximum force of 100 kJ mol–1 nm–1 or when 20,000 steps were reached. In all cases, the minimization converged prior to the maximum number of steps being reached. Initial velocities were then assigned from a Maxwell–Boltzmann distribution at the set simulation temperature. A short 1 ns NVT ensemble run equilibrated the system using a time step of 2 fs and a stochastic Langevin leapfrog integrator.64 Long-range electrostatic interactions were handled using the particle mesh Ewald (PME) method with a real space cutoff of 1.2 nm, tolerance of 10–6, order of 12, and Fourier spacing of 0.1 nm. A Lennard-Jones cutoff distance of 1.2 nm was employed with energy and pressure tail corrections and a neighbor list with a cutoff of 1.2 nm. The neighbor list was updated every 10 steps. We then performed an NPT ensemble equilibration for 10 ns using a Berendsen thermostat with a thermo-coupling parameter of 0.1 and a Berendsen barostat with a pressure-coupling parameter of 2.0, compressibility of 4.5 × 10–5, and reference pressure of 1 bar. We then performed an NPT ensemble production run for 15 ns using a stochastic Langevin leapfrog integrator with a thermo-couple of 1.0 and a Parrinello–Rahman barostat with a pressure couple of 5.0, compressibility of 4.5 × 10–5, and reference pressure of 1 bar. The average cubic box lengths were determined to be 3.9133 nm (TIP3P), 3.9240 nm (SPC/E), and 3.9168 nm (OPC3).

ΔGhyd calculations were initiated by assigning unique initial random number seeds for each λ window. Positions of the molecules were then randomly assigned, and energy minimization followed the same procedure as in the above procedure for the NPT simulations. A 1 ns NVT ensemble equilibration then followed, and initial velocities were uniquely assigned according to the Maxwell–Boltzmann distribution. Again, the same procedures were used as in the NVT simulation previously described. Equilibration was then followed by a 2 ns production run, which used, as its initial configuration, the final configuration of the equilibration stage. The protocol for the production stage was the same as for the equilibration stage.

Free energy calculations were evaluated using the multistate Benedict acceptance ratio (MBAR)65 as implemented in the pymbar/alchemical analysis software.66 First, the solute’s Coulombic interactions were decoupled from its solution environment followed by decoupling of the LJ interactions using λcoulomb = [0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0] and λLJ = [0.0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4 0.5 0.6 0.65 0.7 0.75 0.8 0.85 0.9 0.95 1.0]. We used a soft-core Lennard-Jones potential with GROMACS parameters sc-alpha = 0.5, sc-r-power = 6, and sc-power = 1. Potential energies of all λ windows were sampled every 100 steps for post-processing with MBAR.

6. Results and Discussion

We performed APolQ calculations for ΔGhyd using MBIS partial charges for all three water models and RESP using the TIP3P water model. We used partial charges derived from electron densities calculated using the MP2 theory in conjunction with cc-pVTZ and with aug-cc-pVTZ basis sets. We also performed “classical” ΔGhyd calculations using the AM1-BCC partial charge methods with TIP3P for comparison purposes since we used GAFF(2.11) and the results in FreeSolv are for GAFF(1.7). The results are shown as parity plots in comparison with experiments in Figures 3 and 4. Deviations from experiment and statistical measures of the agreement of the predicted and experimental results are shown in the figures and are summarized in Table 1.

Figure 3.

Figure 3

Open in a new tab

Parity plots comparing calculated and experimental results for ΔGhyd at the MP2/cc-pVTZ level of theory at T = 298.15 K and P = 1 bar for the 45 molecules of this study. Panel (a) shows results using MBIS partial charges with the TIP3P water model. Panel (b) shows results using MBIS partial charges and the SPC/E water model. Panel (c) shows results using MBIS partial charges with the OPC3 water model. Panel (d) shows results using RESP partial charges and the TIP3P water model. 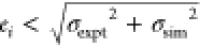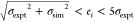Blue stars indicate results whose absolute error ei satisfies Inline graphic, where σexpt and σsim are the respective experimental and simulation uncertainties; red squares indicate outliers (ei>5σexpt); and circles indicate results satisfying Inline graphic. Experimental error bars are shown, and simulation error bars (calculated from MBAR) are within the symbol sizes.

Figure 4.

Figure 4

Open in a new tab

Parity plots comparing calculated and experimental results for ΔGhyd at the MP2/aug-cc-pVTZ level of theory at T = 298.15 K and P = 1 bar for the 45 molecules of this study. Panel (a) shows results using MBIS partial charges with the TIP3P water model. Panel (b) shows results using MBIS partial charges and the SPC/E water model. Panel (c) shows results using MBIS partial charges with the OPC3 water model. Panel (d) shows results using RESP partial charges and the TIP3P water model. Blue stars indicate results whose absolute error ei satisfies 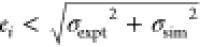Inline graphic, where σexpt and σsim are the respective experimental and simulation uncertainties; red squares indicate outliers (ei>5σexpt); and circles indicate results satisfying Inline graphic. Experimental error bars are shown, and simulation error bars (calculated from MBAR) are within the symbol sizes.

Table 1. Comparison of ΔGhyd Results (in kJ mol–1) for the 45 Species Studied in Comparison with Experimental Valuesa.

charge method basis water model RMSD AAD AD ρs
MBIS cc-pVTZ TIP3P 6.2(4.6,7.7) 4.5(3.3,5.8) 2.1(0.3,3.9) 0.78(0.56,0.92)
MBIS aug-cc-pVTZ TIP3P 6.4(4.7,8.1) 4.5(3.3,5.9) –0.8(−2.8,1.1) 0.77(0.55,0.92)
MBIS cc-pVTZ SPC/E 6.3(4.8,7.8) 4.8(3.6,6.1) 2.9(1.2,4.6) 0.81(0.62,0.94)
MBIS aug-cc-pVTZ SPC/E 6.5(4.6,8.2) 4.5(3.2,6.0) –0.5(−2.5,1.4) 0.82(0.61,0.94)
MBIS cc-pVTZ OPC3 6.2(4.7,7.6) 4.7(3.5,5.9) 2.7(1.1,4.4) 0.81(0.61,0.93)
MBIS aug-cc-pVTZ OPC3 6.3(4.5,8.0) 4.4(3.1,5.8) –0.0(−2.0,1.9) 0.81(0.62,0.93)
             
RESP cc-pVTZ TIP3P 7.5(5.1,9.6) 5.3(3.9,7.0) 4.2(2.3,6.1) 0.63(0.33,0.83)
RESP aug-cc-pVTZ TIP3P 7.4(5.5,9.2) 5.5(4.2,7.1) 2.4(0.3,4.6) 0.63(0.34,0.82)
             
OTFP
MBIS cc-pVTZ SPC/E 6.5(4.5,8.3) 4.6(3.3,6.1) –0.3(−2.3,1.7) 0.84(0.67,0.94)
             
AM1-BCC
this work   TIP3P 7.6(6.1,9.1) 6.3(5.0,7.6) 3.0(0.9,5.2) 0.81(0.63,0.91)
FreeSolv10   TIP3P 7.3(5.7,9.0) 5.9(4.6,7.2) 2.2(0.1,4.3) 0.94(0.88,0.97)
             
Riquelme36 (MBIS) BLYP/def2-TZVP SPCE 9.9(7.8,12.0) 7.7(5.9,9.6) 2.7(−0.3,5.6) 0.74(0.51,0.87)
Open in a new tab
a

All results use the MP2 theory to calculate the electron densities. On-the-fly-polarization (OTFP) is our previous method. RMSD is the root mean square deviation, AAD is the average absolute deviation (prediction – experiment), AD is the average deviation, and the Spearman rank correlation coefficient (ρs)70 is a statistical measure comparing simulation and experimental results ΔGhyd values.70 The confidence intervals (CI) are described in the text.

The quality of the agreement with experiment of a theoretical approach can be assessed by various empirical and statistical measures. All raw simulation results can be found in the Supporting Information, which enables alternative measures to be calculated. For instance, we do not include the common Pearson R2 statistic due to its well-known deficiencies67,68 in comparing predicted results with the experiment. Several measures are shown in the figures and are summarized in Table 1. The 95% CIs for RMSD, absolute average deviation (AAD), and Spearman ρs are obtained by means of empirical bootstrapping using 104 resamples with replacement (e.g., Chernick69). The confidence intervals (CI) for the AD were obtained using the Student t distribution at the 95% level.

6.1. Effect of the Basis Set

Figures 3 and 4 show parity plots against experimental data using the cc-pVTZ and aug-cc-pVTZ basis sets, respectively, for all water models. We first remark that the RMSD and AAD values for both charge methods are very similar. However, the AD values and their corresponding 95% confidence intervals (CIs) differentiate between the effects of the two basis sets. If zero is not contained within the CI, the statistical inference is that the hypothesis that predicted and experimental data are in agreement for the method is rejected at the 95% confidence level, which is evidence that the procedures underlying the FF generation yield an overall unsatisfactory prediction of the experimental values. The results in the table indicate that for all three water models and both charge methods, all methods using the cc-pVTZ basis set are unsatisfactory. However, for MBIS charges, the addition of diffuse functions in the aug-cc-pVTZ basis set yields AD CIs containing zero. This is not the case for RESP charges, whose AD CIs using both basis sets do not contain zero.

6.2. Comparison with the OTFP Method

We recently developed a method that explicitly accounts for polarization during a MD simulation which we termed on-the-fly-polarization (OTFP). The test set used to validate the OTFP methodology includes 28 of the molecules shown here. The OTFP method using MBIS partial charges partitioned from an electron density calculated at the MP2/cc-pVTZ level of theory and basis set produced the best results. We have also calculated the 17 additional molecules using this approach in the present study and are also shown in Table 1. The OTFP results are very similar to the APolQ methods, which also use MBIS.

Interestingly, despite using the cc-pVTZ basis set, the OTFP AD and its CI is similar to the MBIS APolQ methods that use diffuse functions with cc-pVTZ. The RMSD, AAD, and ρs for the MBIS OTFP and MBIS APolQ methods are nearly exactly the same. The computational advantage in using the APolQ method over the OTFP approach is that, apart from the additional requirement for calculating the solvent dielectric constant, only two partial charge calculations are required for APolQ, whereas OTFP requires multiple such calculations in each Coulomb window.

We finally note that both APolQ and OTFP can in principle be applied to pure and mixed solvents and solutions at finite solute concentrations, although only OTFP is capable of handling non-homogeneous environments.

6.3. Comparison with Post-Simulation Self-Polarization Calculations

Methods to correct fixed-charge simulation free energy calculations have been under investigation for several years.36−41 Here, we compare results with one such method that also used MBIS partial charges. In the method of Riquelme et al., the cost of self-polarization was calculated post-simulation and added onto the ΔGhyd calculated using standard alchemical free energy change with molecular dynamics. We show their results in the final row of Table 1. We note that they used partial charges derived from an electron density calculated using density functional theory with the generalized gradient approximation (GGA) exchange-correlation functional (BLYP), with a triple ζ basis set that did not include additional diffuse functions. For the 45 molecules used in this test set, our proposed method, as well as OTFP, both of which implicitly include the cost of both self-polarization and reorganization of the solvent due to changing polarity, has a lower AAD by approximately 2 kJ mol–1. The AD of Riquelme et al. was highly positive, along with all other methods that were either empirically parameterized (AM1-BCC) or calculated an electron density without using a basis set that had diffuse functions added. It is therefore possible that the Riquelme et al. results may be improved by the addition of diffuse functions. As mentioned above, accounting for the cost of polarizing a molecule is important, but not the only contribution to free energy when polarizing a molecule. The APolQ method, while accounting for the cost of self-polarization, does so as an average over many solute conformations with the solvent correspondingly adjusting around the solute. In doing so, APolQ also avoids overpolarized 1–4 and larger intramolecular interactions in windows where there should be no (or reduced) polarization in the charges. Accounting for the cost of self-polarization for a single geometry post-simulation does not account for the overpolarized intramolecular 1–4 and greater interactions in all windows and geometries of the solute during the course of the simulations. The APolQ method accounts for polarity in a way, which keeps intramolecular forces as well as intermolecular Coulombic forces and energies appropriately polarized during alchemical free energy simulations and from our results appears to improve predictions significantly.

6.4. Effect of the Water Model and Comparisons with AM1-BCC

Table 1 and Figures 3 and 4 indicate that all APolQ results yield a lower AAD and more predictions within experimental uncertainty (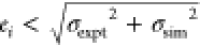Inline graphic) than those shown by AM1-BCC. All APolQ results using MBIS partial charges show lower AAD, AD values closer to 0, and higher ρs than APolQ using RESP, although their CIs overlap.

Of the MBIS results, predictions using the OPC3 water model and aug-cc-pVTZ basis set have the smallest AAD and the best AD (closest to zero) of all results.

Shown in Figure 5 are the MBIS results for all three water models using partial charges derived from electron densities calculated with diffuse functions added to the basis sets (aug-cc-pVTZ). All three water models correlate well with each other, but TIP3P and SPC/E are closer to each other than either is with OPC3. The Spearman rank coefficients ρs = 0.97 indicate strong correlation of both the OPC3 and SPC/E results with those of TIP3P. The finding that all water models give similar results is an indication of the method’s robustness because APolQ is able to perform well for different water models without requiring reoptimization of the underlying GAFF parameters.

Figure 5.

Figure 5

Open in a new tab

Parity plots comparing water models SPC/E and OPC3 with TIP3P for ΔGhyd. Dashed red line marks 2 kJ mol–1 horizontal and vertical offset from the parity line.

6.5. Influence of the Molecular Structure

Figure 6 shows a comparison of the AAD results for a selection of structural features of the solute molecules. We compare small, large, cyclic, small cyclics, rotatable (non-cyclic), nitrogen-containing, nitrogen in a cyclic ring, oxygen-containing, alkylamines, and linear alcohols. With the exception of RESP, all methods struggle with nitrogen-containing cyclic rings. MBIS partial charge methods struggle with small cyclic rings, and to a lesser degree, RESP does as well. AM1-BCC has the lowest AAD for small cyclic rings. It is not surprising that fixed atom-centered charge FFs struggle with small cyclics because either off-center partial charges or atom-centered multipoles are needed to allow the dipole to leave the plane. (It has also been shown by Swope et al.(37) that, for benzene, the quadrupole moment contributes more to polarization than does the dipole moment. This likely also occurs for other small cyclic molecules.) Since such approaches require modification of the original fixed-charge FF, they are outside of the scope of this work.

Figure 6.

Figure 6

Open in a new tab

ΔGhyd AAD comparison plot. Error bars are calculated using percentile bootstrapping at the 95% significance level.

AM1-BCC is the only partial charge method to yield the same approximate AAD for total AAD, small molecules, large molecules, and both cyclic and non-cyclic molecules. For all other methods, small and non-cyclic molecules show lower AAD values than the total AAD, as opposed to large and cyclic molecules that show larger AAD values than the total AAD. MBIS methods using TIP3P and OPC3 water models yield approximately equal or lower AAD than AM1-BCC for large and cyclic molecules. All methods show AAD values lower than those of AM1-BCC for oxygen-containing molecules. Of the MBIS methods, the TIP3P water model using the aug-cc-pVTZ basis set in the electron density calculations yields the lowest AAD for small cyclic molecules. MBIS methods also perform consistently well for linear alcohols and alkylamines.

6.6. Non-Coulombic FF Parameters

The performance of FFs in the prediction of ΔGhyd depends on the Coulombic contribution and the LJ and intramolecular contributions. In this work, for the GAFF(2.1), we have modified the Coulombic contribution by incorporating a polarization algorithm in conjunction with the partial charge calculations, while leaving the LJ and intramolecular parameters unchanged. These parameters were originally developed by empirical modifications to fit experimental data and QM calculations on the basis of the partial charges being RESP HF/6-31G* and/or AM1-BCC. When using different partial charges, these parameters are no longer optimal and should be refitted. Optimizing the LJ, and in particular the torsion parameters, will likely lead to additional improvements in our ΔGhyd predictions. This has recently been shown to be the case for RESP partial charges.71 Lennard-Jones parameter optimization is an active area of research.72,73

7. Conclusions and Recommendations

We have developed a novel approach (APolQ) for implementing polarization in the calculation of the solvation free energy, which transitions a solute molecule from having unpolarized partial charges in the decoupled (vacuum) state to polarized partial charges in the fully coupled (solution) state.

The APolQ approach for implementing polarization retains the computationally efficient fixed-charge structure of the solute and requires only two partial charge calculations (in a vacuum and implicit solvent) prior to performing a standard MM simulation. The vacuum calculation need only be performed once and is used in all solvents. The only additional calculation required for each solvent is the calculation of the implicitly polarized partial charges. This is thus a simply implemented methodology that is transferable to any solvent.

We have applied the APolQ method to the calculation of hydration free energies of 45 organic solute molecules of various complexities using MBIS and RESP partial charges. We have also applied our methodology to SPC/E, TIP3P, and OPC3 water models. All MBIS methods using diffuse functions in the basis set (aug-cc-pVTZ) contain zero within the 95% confidence interval of the average deviation (AD) from experiment, whereas AM1-BCC and APolQ RESP and MBIS using cc-pVTZ do not. In the latter cases, this indicates rejection of the hypothesis that the predictions agree with the experimental values.

We have demonstrated that APolQ in conjunction with partial charges calculated at a high level of ES theory/basis set yields superior results to the standard AM1-BCC approach, despite the fact that the latter uses fully optimized LJ and intramolecular parameters. The APolQ results can potentially be further improved by refitting these parameters.

APolQ can in principle be applied to any homogeneous system (e.g., pure or mixed solvents) and such solutions at finite solute concentrations, requiring only the solvent’s dielectric constant (from experimental data or simulation).

The APolQ algorithm is modular, allowing it to be easily improved with more sophisticated ES methods and partial charge partitioning methodologies. It is both simple and fundamentally more rigorous than the commonly used approach of keeping partial charges fixed in all alchemical windows.

Acknowledgments

The authors acknowledge the support provided by the Natural Sciences and Engineering Research Council of Canada (Strategic Program grant no. STPGP 479466-15) and the SHARCNET (Shared Hierarchical Academic Research Computing Network) HPC Consortium (www.sharcnet.ca) and Compute Canada (www.computecanada.ca). We are grateful to Professor Toon Verstraelen for several insightful email discussions.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.0c01148.

  • Raw simulation data (ZIP)

The authors declare no competing financial interest.

Notes

Basic GROMACS files used (*.top, *.gro, and *.mdp) are available at GitHub: https://github.com/BradenDKelly/APolQ/.

Supplementary Material

ao0c01148_si_001.zip (35KB, zip)

References

  1. Kofke D. A. Free energy methods in molecular simulation. Fluid Phase Equilib. 2005, 228-229, 41–48. 10.1016/j.fluid.2004.09.017. [DOI] [Google Scholar]
  2. Vega C.; Sanz E.; Abascal J. L. F.; Noya E. G. Determination of phase diagrams via computer simulation: methodology and applications to water, electrolytes and proteins. J. Phys.: Condens. Matter 2008, 153101. 10.1088/0953-8984/20/15/153101. [DOI] [Google Scholar]
  3. Kelly B.; Smith W. R. Molecular simulation of chemical reaction equilibria by Kinetic Monte Carlo. Mol. Phys. 2019, 117, 2778–2785. 10.1080/00268976.2018.1552027. [DOI] [Google Scholar]
  4. Smith W. R.; Qi W. Molecular Simulation of Chemical Reaction Equilibrium by Computationally Efficient Free Energy Minimization. ACS Cent. Sci. 2018, 4, 1185–1193. 10.1021/acscentsci.8b00361. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Sanz E.; Vega C. Solubility of KF and NaCl in water by molecular simulation. J. Chem. Phys. 2007, 014507. 10.1063/1.2397683. [DOI] [PubMed] [Google Scholar]
  6. Moučka F.; Lísal M.; Škvor J.; Jirsák J.; Nezbeda I.; Smith W. R. Molecular Simulation of Aqueous Electrolyte Solubility. 2. Osmotic Ensemble Monte Carlo Methodology for Free Energy and Solubility Calculations and Application to NaCl. J. Phys. Chem. B 2011, 115, 7849–7861. 10.1021/jp202054d. [DOI] [PubMed] [Google Scholar]
  7. Mester Z.; Panagiotopoulos A. Z. Mean ionic activity coefficients in aqueous NaCl solutions from molecular dynamics simulations. J.Chem. Phys. 2015, 142, 044507 10.1063/1.4906320. [DOI] [PubMed] [Google Scholar]
  8. Mobley D. L.; Bayly C. I.; Cooper M. D.; Shirts M. R.; Dill K. A. Small Molecule Hydration Free Energies in Explicit Solvent: An Extensive Test of Fixed-Charge Atomistic Simulations. J. Chem. Theory Comput. 2009, 5, 350–358. 10.1021/ct800409d. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Mobley D. L.; Liu S.; Cerutti D. S.; Swope W. C.; Rice J. E. Alchemical prediction of hydration free energies for SAMPL. J. Comput.-Aided Mol. Des. 2012, 26, 551–562. 10.1007/s10822-011-9528-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Matos G. D. R.; Kyu D. Y.; Loeffler H. H.; Chodera J. D.; Shirts M. R.; Mobley D. L. Approaches for Calculating Solvation Free Energies and Enthalpies Demonstrated with an Update of the FreeSolv Database. J. Chem. Eng. Data 2017, 62, 1559–1569. 10.1021/acs.jced.7b00104. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Gilson M. K.; Given J. A.; Bush B. L.; McCammon J. A. The statistical-thermodynamic basis for computation of binding affinities: a critical review. Biophys. J. 1997, 72, 1047–1069. 10.1016/S0006-3495(97)78756-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Deng Y.; Roux B. Computations of Standard Binding Free Energies with Molecular Dynamics Simulations. J. Phys. Chem. B 2009, 113, 2234–2246. 10.1021/jp807701h. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Yu W.; MacKerell A. D. Jr. Computer-Aided Drug Design Methods. J. Phys. Chem. B 2017, 1520, 85–106. 10.1007/978-1-4939-6634-9_5. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Williams-Noonan B. J.; Yuriev E.; Chalmers D. K. Free Energy Methods in Drug Design: Prospects of Alchemical Perturbation in Medicinal Chemistry. J. Med. Chem. 2018, 61, 638–649. 10.1021/acs.jmedchem.7b00681. [DOI] [PubMed] [Google Scholar]
  15. Geerke D. P.; van Gunsteren W. F. Calculation of the Free Energy of Polarization: Quantifying the Effect of Explicitly Treating Electronic Polarization on the Transferability of Force–Field Parameters. J. Phys. Chem. B 2007, 111, 6425–6436. 10.1021/jp0706477. [DOI] [PubMed] [Google Scholar]
  16. Inakollu V. S.; Geerke D. P.; Rowley C. N.; Yu H. Polarisable force fields: what do they add in biomolecular simulations?. Curr. Opin. Struct. Biol. 2020, 61, 182–190. 10.1016/j.sbi.2019.12.012. [DOI] [PubMed] [Google Scholar]
  17. Zhang J.; Zhang H.; Wu T.; Wang Q.; van der Spoel D. Comparison of Implicit and Explicit Solvent Models for the Calculation of Solvation Free Energy in Organic Solvents. J. Chem. Theory Comput. 2017, 13, 1034–1043. 10.1021/acs.jctc.7b00169. [DOI] [PubMed] [Google Scholar]
  18. Rappe A. K.; Goddard W. A. III Charge equilibration for molecular-dynamics simulations. J. Phys. Chem. 1991, 95, 3358–3363. 10.1021/j100161a070. [DOI] [Google Scholar]
  19. Rick S. W.; Stuart S. J.; Berne B. J. Dynamical fluctuating charge force fields: Application to liquid water. J. Chem. Phys. 1994, 6141. 10.1063/1.468398. [DOI] [Google Scholar]
  20. Banks J. L.; Kaminski G. A.; Zhou R.; Mainz D. T.; Berne B. J.; Friesner R. A. Parametrizing a polarizable force field from ab initio data. I. The fluctuating point charge model. J. Chem. Phys. 1999, 110, 741–754. 10.1063/1.478043. [DOI] [Google Scholar]
  21. Patel S.; Brooks C. L. III CHARMM Fluctuating Charge Force Field for Proteins: I Parameterization and Application to Bulk Organic Liquid Simulations. J. Comput. Chem. 2003, 25, 1–16. 10.1002/jcc.10355. [DOI] [PubMed] [Google Scholar]
  22. Patel S.; Mackerell A. D. Jr.; Brooks C. L. III CHARMM Fluctuating Charge Force Field for Proteins: II Protein/Solvent Properties from Molecular Dynamics Simulations Using a Nonadditive Electrostatic Model. J. Comput. Chem. 2004, 25, 1504–1514. 10.1002/jcc.20077. [DOI] [PubMed] [Google Scholar]
  23. Patel S.; Brooks C. L. III Fluctuating charge force fields: recent developments and applications from small molecules to macromolecular biological systems. Mol. Simul. 2006, 32, 231–249. 10.1080/08927020600726708. [DOI] [Google Scholar]
  24. Lamoureux G.; Roux B. Modeling induced polarization with classical Drude oscillators: Theory and molecular dynamics simulation algorithm. J. Chem. Phys. 2003, 119, 3025–3039. 10.1063/1.1589749. [DOI] [Google Scholar]
  25. Lemkul J. A.; Huang J.; Roux B.; MacKerell A. D. Jr. An Empirical Polarizable Force Field Based on the Classical Drude Oscillator Model: Development History and Recent Applications. Chem. Rev. 2016, 116, 4983–5013. 10.1021/acs.chemrev.5b00505. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Ponder J. W.; Wu C.; Ren P.; Pande V. S.; Chodera J. D.; Schnieders M. J.; Haque I.; Mobley D. L.; Lambrecht D. S.; DiStasio R. A. Jr.; Head-Gordon M.; Clark G. N. I.; Johnson M. E.; Head-Gordon T. Current Status of the AMOEBA Polarizable Force Field. J. Phys. Chem. B 2010, 114, 2549–2564. 10.1021/jp910674d. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Baker C. M. Polarizable force fields for molecular dynamics simulations of biomolecules. WIREs Comput. Mol. Sci. 2015, 5, 241–254. 10.1002/wcms.1215. [DOI] [Google Scholar]
  28. Jing Z.; Liu C.; Cheng S. Y.; Qi R.; Walker B. D.; Piquemal J.-P.; Ren P. Polarizable Force Fields for Biomolecular Simulations: Recent Advances and Applications. Annu. Rev. Biophys. 2019, 48, 371–394. 10.1146/annurev-biophys-070317-033349. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Verstraelen T.; Vandenbrande S.; Ayers P. W. Direct computation of parameters for accurate polarizable force fields. J. Chem. Phys. 2014, 141, 194114. 10.1063/1.4901513. [DOI] [PubMed] [Google Scholar]
  30. Manzoni F.; Söderhjelm P. Prediction of hydration free energies for the SAMPL4 data set with the AMOEBA polarizable force field. J. Comput.-Aided Mol. Des. 2014, 28, 235–244. 10.1007/s10822-014-9733-3. [DOI] [PubMed] [Google Scholar]
  31. Mohamed N. A.; Bradshaw R. T.; Essex J. W. Evaluation of solvation free energies for small molecules with the AMOEBA polarizable force field. J. Comput. Chem. 2016, 37, 2749–2758. 10.1002/jcc.24500. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Ding Y.; Xu Y.; Qian C.; Chen J.; Zhu J.; Huang H.; Shi Y.; Huang J. Predicting partition coefficients of drug-like molecules in the SAMPL6 challenge with Drude polarizable force fields. J. Comput.-Aided Mol. Des. 2020, 34, 421–435. 10.1007/s10822-020-00282-5. [DOI] [PubMed] [Google Scholar]
  33. Wang J.; Wolf R. M.; Caldwell J. W.; Kollman P. A.; Case D. A. Development and testing of a general AMBER force field. J. Comput. Chem. 2004, 25, 1157–1174. 10.1002/jcc.20035. [DOI] [PubMed] [Google Scholar]
  34. Cornell W. D.; Cieplak P.; Bayly C. I.; Gould I. R.; Merz K. M.; Ferguson D. M.; Spellmeyer D. C.; Fox T.; Caldwell J. W.; Kollman P. A. A Second Generation Force Field for the Simulation of Proteins, Nucleic Acids and Organic Molecules. J. Am. Chem. Soc. 1995, 5179. 10.1021/ja00124a002. [DOI] [Google Scholar]
  35. Jakalian A.; Bush B. L.; Jack D. B.; Bayly C. I. Fast, Efficient Generation of HighQuality Atomic Charges. AM1-BCC Model: I. Method. J. Comput. Chem. 2000, 21, 132–146. . [DOI] [PubMed] [Google Scholar]
  36. Riquelme M.; Lara A.; Mobley D. L.; Verstraelen T.; Matamala A. R.; Vöhringer-Martinez E. Hydration Free Energies in the FreeSolv Database Calculated with Polarized Iterative Hirshfeld Charges. J. Chem. Inf. Model. 2018, 58, 1779–1797. 10.1021/acs.jcim.8b00180. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Swope W. C.; Horn H. W.; Rice J. E. Accounting for Polarization Cost When Using Fixed Charge Force Fields. II. Method and Application for Computing Effect of Polarization Cost on Free Energy of Hydration. J. Phys. Chem. B 2010, 114, 8631–8645. 10.1021/jp911701h. [DOI] [PubMed] [Google Scholar]
  38. Swope W. C.; Horn H. W.; Rice J. E. Accounting for Polarization Cost When Using Fixed Charge Force Fields I. Method for Computing Energy. J. Phys. Chem. B 2010, 114, 8621–8630. 10.1021/jp911699p. [DOI] [PubMed] [Google Scholar]
  39. Jia X.; Li P. Solvation Free Energy Calculation Using a Fixed-Charge Model: Implicit and Explicit Treatments of the Polarization Effect. J. Phys. Chem. B 2019, 123, 1139–1148. 10.1021/acs.jpcb.8b10479. [DOI] [PubMed] [Google Scholar]
  40. Jia X. Solvation Free Energy Calculations: The Combination between the Implicitly Polarized Fixed-charge Model and the Reference Potential Strategy. J. Comput. Chem. 2019, 40, 2801–2809. 10.1002/jcc.26055. [DOI] [PubMed] [Google Scholar]
  41. Giese T. J.; York D. M. Development of a Robust Indirect Approach for MM → QM Free Energy Calculations That Combines Force-Matched Reference Potential and Bennett’s Acceptance Ratio Methods. J. Chem. Theory Comput. 2019, 15, 5543. 10.1021/acs.jctc.9b00401. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Zhou A.; Schauperl M.; Nerenberg P. S. Benchmarking Electronic Structure Methods for Accurate Fixed-Charge Electrostatic Models. J. Chem. Inf. Model. 2020, 60, 249–258. 10.1021/acs.jcim.9b00962. [DOI] [PubMed] [Google Scholar]
  43. Kelly B. D.; Smith W. R. Alchemical Hydration Free-Energy Calculations Using Molecular Dynamics with Explicit Polarization and Induced Polarity Decoupling: An On-the-Fly Polarization Approach. J. Chem. Theory Comput. 2020, 16 (2), 1146–1161. 10.1021/acs.jctc.9b01139. [DOI] [PubMed] [Google Scholar]
  44. Frisch M. J.; et al. Gaussian16; Gaussian Inc.: Wallingford CT, 2016. [Google Scholar]
  45. Berendsen H. J. C.; Grigera J. R.; Straatsma T. P. The Missing Term in Effective Pair Potentials. J. Phys. Chem. 1987, 91, 6269–6271. 10.1021/j100308a038. [DOI] [Google Scholar]
  46. Jorgensen W. L.; Chandrasekhar J.; Madura J. D.; Impey R. W.; Klein M. L. Comparison of Simple Potential Functions for Simulating Liquid Water. J. Chem. Phys. 1983, 79, 926–935. 10.1063/1.445869. [DOI] [Google Scholar]
  47. Izadi S.; Onufriev A. V. Accuracy limit of rigid 3-point water models. J. Chem. Phys. 2016, 074501 10.1063/1.4960175. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Mobley D. L.; Klimovich P. V. Perspective: Alchemical free energy calculations for drug discovery. J. Chem. Phys. 2012, 137, 230901. 10.1063/1.4769292. [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Deppmeier B.; Driessen A.; Hehre W. J.; Johnson J. A.; Ohlinger S.; Klunzinger P. E.. Spartan’18 Parallel Suite; Wavefunction, Inc.: Irvine, CA, 2019. [Google Scholar]
  50. Wang J.; Wang W.; Kollman P. A.; Case D. A. Automatic atom type and bond type perception in molecular mechanical calculations. J. Mol. Graphics Modell. 2006, 247. 10.1016/j.jmgm.2005.12.005. [DOI] [PubMed] [Google Scholar]
  51. Verstraelen T.; Tecmer P.; Heidar-Zadeh F.; Boguslawski K.; Chan M.; Zhao Y.; Kim T. D.; Vandenbrande S.; Yang D.; Gonzlez-Espinoza C. E.; Fias S.; Limacher P. A.; Berrocal D.; Malek A.; Ayers P. W.. Helpful Open-source Research TOol for N-fermion systems HORTON 2.1.1; 2015.
  52. Sousa da Silva A. W.; Vranken W. F. ACPYPE - AnteChamber PYthon Parser interfacE. BMC Res. Notes 2012, 367. 10.1186/1756-0500-5-367. [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. ROCS, OpenEye Scientific Software; Santa Fe,http://www.eyesopen.com.
  54. Hickey A. L.; Rowley C. N. Benchmarking Quantum Chemical Methods for the Calculation of Molecular Dipole Moments and Polarizabilities. J. Phys. Chem. A 2014, 3678. 10.1021/jp502475e. [DOI] [PubMed] [Google Scholar]
  55. van der Spoel D.; van Maaren P. J. The Origin of Layer Structure Artifacts in Simulations of Liquid Water. J. Chem. Theory Comput. 2006, 2, 1–11. 10.1021/ct0502256. [DOI] [PubMed] [Google Scholar]
  56. Rami Reddy M.; Berkowitz M. The dielectric constant of SPC/E water. Chem. Phys. Lett. 1989, 155, 173–176. 10.1016/0009-2614(89)85344-8. [DOI] [Google Scholar]
  57. Fennell C. J.; Li L.; Dill K. A. Simple liquid models with corrected dielectric constants. J. Phys. Chem. B 2012, 116, 6936–6944. 10.1021/jp3002383. [DOI] [PMC free article] [PubMed] [Google Scholar]
  58. Cramer C. J.Essentials of Computational Chemistry: Theories and Models; John Wiley & Sons: 2013. [Google Scholar]
  59. Karamertzanis P. G.; Raiteri P.; Galindo A. The use of anisotropic potentials in modeling water and free energies of hydration. J. Chem. Theory Comput. 2010, 6, 1590–1607. 10.1021/ct900693q. [DOI] [PubMed] [Google Scholar]
  60. Muddana H. S.; Sapra N. V.; Fenley A. T.; Gilson M. K. The SAMPL4 hydration challenge: evaluation of partial charge sets with explicit-water molecular dynamics simulations. J. Comput.-Aided Mol. Des. 2014, 28, 277–287. 10.1007/s10822-014-9714-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
  61. Cerutti D. S.; Rice J. E.; Swope W. C.; Case D. A. Derivation of Fixed Partial Charges for Amino Acids Accommodating a Specific Water Model and Implicit Polarization. J. Phys. Chem. B 2013, 117, 2328–2338. 10.1021/jp311851r. [DOI] [PMC free article] [PubMed] [Google Scholar]
  62. Bennett C. H. Efficient Estimation of Free Energy differences from Monte Carlo Data. J. Comput. Phys. 1976, 22, 245–268. 10.1016/0021-9991(76)90078-4. [DOI] [Google Scholar]
  63. Bondi A. van der Waals Volumes and Radii. J. Phys.Chem. 1964, 441. 10.1021/j100785a001. [DOI] [Google Scholar]
  64. Van Gunsteren W. F.; Berendsen H. J. C. A Leap-frog Algorithm for Stochastic Dynamics. Mol. Simul. 2007, 1, 173–185. 10.1080/08927028808080941. [DOI] [Google Scholar]
  65. Shirts M. R.; Chodera J. D. Statistically optimal analysis of samples from multiple equilibrium states. J. Chem. Phys. 2008, 129, 124105. 10.1063/1.2978177. [DOI] [PMC free article] [PubMed] [Google Scholar]
  66. Klimovich P. V.; Shirts M. R.; Mobley D. L. Guidelines for the analysis of free energy calculations. J. Comput.-Aided Mol. Des. 2015, 29, 397–411. 10.1007/s10822-015-9840-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
  67. Aggarwal R.; Ranganathan P. Common pitfalls in statistical analysis: The use of correlation techniques. Perspect. Clin. Res. 2016, 7, 187–190. 10.4103/2229-3485.192046. [DOI] [PMC free article] [PubMed] [Google Scholar]
  68. Ranganathan P.; Pramesh C. S.; Aggarwal R. Common pitfalls in statistical analysis: Measures of agreement. Perspect. Clin. Res. 2017, 8, 187–191. 10.4103/picr.PICR_123_17. [DOI] [PMC free article] [PubMed] [Google Scholar]
  69. Chernick M. R.Bootstrap Methods: A Guide for Practitioners and Researchers; John Wiley & Sons: Hoboken, NJ, 2011. [Google Scholar]
  70. Ledermann W.; Lloyd E.. Handbook of Applicable Mathematics; John Wiley & Sons Ltd.: 1984; Vol. VI. [Google Scholar]
  71. Schauperl M.; Nerenberg P. S.; Jang H.; Wang L.-P.; Bayly C. I.; Mobley D. L.; Gilson M. K. Non-bonded force field model with advanced restrained electrostatic potential charges (RESP2). Commun. Chem. 2020, 44. 10.1038/s42004-020-0291-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
  72. Mohebifar M.; Johnson E. R.; Rowley C. N. Evaluating Force-Field London Dispersion Coefficients Using the Exchange-Hole Dipole Moment Model. J. Chem. Theory Comput. 2017, 13, 6146–6157. 10.1021/acs.jctc.7b00522. [DOI] [PubMed] [Google Scholar]
  73. Visscher K. M.; Geerke D. P. Deriving a Polarizable Force Field for Biomolecular Building Blocks with Minimal Empirical Calibration. J. Phys. Chem. B 2020, 124, 1628–1636. 10.1021/acs.jpcb.9b10903. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ao0c01148_si_001.zip (35KB, zip)

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES