Kinetics of Calcite Dissolution and Ca–Mg Ion Exchange on the Surfaces of North Sea Chalk Powders

Abstract

Calcite dissolution and Ca–Mg ion exchange on carbonate rock surfaces have been proposed as potential mechanisms occurring during smart waterflooding in carbonate reservoirs. However, there is still a lack of fundamental understanding of these reactions to quantitatively evaluate their effects in the reservoir flooding process. Especially, the data on precipitation and dissolution kinetics are insufficient. In this work, the equilibration kinetics of calcite dissolution and Ca–Mg exchange was experimentally studied. The behavior of three powders was compared: pure calcium carbonate, Stevns Klint outcrop chalk, and North Sea reservoir chalk. It was found that the equilibration time for calcite dissolution was of the order of seconds for a given surface-area-to-liquid-volume ratio. The existing theory of calcite dissolution could well reproduce our observations. The Ca–Mg exchange showed two-step kinetics: the first step was fast, and it dominated the process within the first hour of reaction; the second step was slow, and it continued longer than the time of observation (2 weeks). Characteristic times for the two steps were extracted by fitting the experimental curves. A two-layer adsorption model was proposed to characterize the kinetic process and successfully matched with experimental data. The findings were further extended to flow-through scenarios. By comparing with literature data and surface complexation models, it was concluded that calcite dissolution alone was unlikely to be able to explain the additional recovery reported in the literature. The Ca–Mg exchange process could dominate the fluid–rock interactions at a high temperature in pure calcium carbonate rocks, while competitive adsorption of cations appeared to control the process at a lower temperature. Different carbonate rocks possess different properties with regard to the ion-exchange process.

1. Introduction

Smart waterflooding in carbonate reservoirs has been extensively studied in recent years. The term “smart waterflooding” denotes the approach to produce additional oil by injecting a specially prepared brine. Various chemical and physical mechanisms have been proposed to explain the observed effects. Several review works have summarized and analyzed the reported observations from different perspectives.¹⁻⁶ Among the proposed mechanisms, the dissolution of calcite mineral and the Ca–Mg ion exchange at the surface of carbonate rocks have been mentioned by several researchers.

Dissolution of carbonate minerals has been thoroughly studied in the field of geochemistry.⁷⁻¹⁰ It has also been suggested as a mechanism of smart waterflooding in carbonate rocks.^11,12 Dissolution of calcium carbonate minerals may trigger various effects that could facilitate the production of oil. Mechanisms such as improved interpore connectivity¹³ and, further, increased permeability¹⁴ were reported in association with rock dissolution. The dissolution may also affect oil production through alteration of the electric double-layer interactions.¹⁵ Hiorth et al.¹⁶ found a linear relationship between calcite dissolution and oil recovery from imbibition experiments. Nonetheless, the importance of dissolution for additional recovery was evaluated differently in different works. Whether dissolution is considered as the primary recovery mechanism¹¹ or the secondary mechanism,¹⁷ it deserves a more careful study to reveal its importance.

The exchange reaction between Mg²⁺ ions in the aqueous solution and the Ca²⁺ ions on the surface of carbonate rocks was also reported as a potential mechanism of smart waterflooding.¹⁸ The ion-exchange process may promote detachment of adsorbed polar components from oil;¹⁹ change the surface potential of the rock, expanding the electrostatic double layer; and, finally, make the surface more water-wet.²⁰⁻²²

Waterflooding of a core or a reservoir is a dynamic process. Characteristic times of the chemical or physicochemical processes that occur during waterflooding are crucial parameters to evaluate their effects. Studies of the kinetics of ion exchange in waterflooding have been carried out in numerical simulations.²³ These studies demonstrated that the ratio between the characteristic times of the convective flow and chemical equilibration (the Damköhler number) is one of the most important parameters for the efficiency of the process.

In this work, we study the kinetics of calcite dissolution and Ca–Mg ion exchange. Analysis of the experimental data makes it possible to extract characteristic equilibration times of the process. Mathematical models are proposed to describe the kinetics of the processes. The results are then coupled with the flow equations to evaluate the flow-through experiments reported in the literature.

The paper is organized as follows. Section 2 introduces the materials and experimental procedures involved in this work; Section 3 describes the experimental results and formulates the kinetic models for dissolution and exchange needed for their evaluation; Section 4 presents the modeling of the flow-through and flooding experiments found in the literature, comparing them to our experimental findings; and finally, Section 5 formulates the main conclusions of this work.

2. Materials and Methods

2.1. Materials

2.1.1. Powder Samples

Three types of calcite/chalk materials were applied in this study: pure calcite (calcium carbonate) powder purchased from VWR Chemicals, with a grain diameter less than 30 μm; outcrop chalk obtained from Stevns Klint (SK), approximately 60 km south of Copenhagen; and reservoir chalk (RS) obtained from a North Sea chalk reservoir. The powders from natural materials have a grain diameter between 53 and 160 μm.

Apart from the commercial calcium carbonate powder, Stevns Klint and reservoir chalk powders were prepared from bulk rock samples. The samples were first subjected to a cleaning procedure by methanol and toluene to remove the initially precipitated salts and organic compounds, to expose the chalk surface.

Core samples of Stevns Klint chalk (approx. 7.5 cm in length, 3.8 cm in diameter) were assembled in a classic Hassler-type core holder and flooded by methanol and toluene alternatively. The injection rate of the solvents was 0.3 mL/min, and the sleeve pressure was 20 bar. At the end of cleaning, the presence of residual salts in the methanol effluent was tested by adding 3–4 drops of 0.03 M AgNO₃ solution into the last 2–3 mL of effluent. The core was considered to be clean if no precipitation was observed.

For cleaning of the reservoir chalk samples, a Soxhlet extraction setup was applied due to highly irregular shapes of the chalk pieces. The chalk samples were first crushed by a mortar and pestle into approximately 3–5 mm diameter grains. The crushed grains were then loaded into a Soxhlet setup. Toluene and methanol were used alternatively as extraction solvents. The process was finished after a colorless toluene eluent was obtained after at least 3 days of extraction. Complete removal of salts was detected by testing the methanol eluent with AgNO₃, as described above.

The cleaned chalk samples were dried in an oven at 80 °C for 2 days. Then, the dry samples were ground by mortar and pestle into powders. The sizes of the powder particles were controlled by sieving the powder by two meshes, with mesh sizes of 63 and 150 μm. The sieved particles were collected into a glass sample bottle and sealed for later use.

Since the characteristic pore diameter of the chalk is 3 μm, the ground particles are still porous and consist of smaller elemental grains. The SEM images of the powders confirm this fact (Figure 1).

Figure 1.

SEM images of (a) calcite powder, (b) Stevns Klint powder, and (c) reservoir sample powder on different scales. It can be seen that the natural rock materials consist of much smaller grains than the selected particle grain size: 63–150 μm.

Specific surface areas (SSAs) of the powder samples were measured by the multipoint BET method with liquid nitrogen. Each powder was measured twice. The average values for calcite powder, Stevns Klint chalk powder, and reservoir chalk powder are 0.344, 2.214, and 2.661 m²/g, respectively.

It should be noted that the measured SSA of Stevns Klint chalk is slightly higher than the commonly reported 2 m²/g. This might be an indication of the appearance of new surfaces of the rock in the grinding procedure. At least, none of the measurements reported the SSA below 2 m²/g. Since we are targeting at observing the behavior of the original pore surface, it is important to have an order-of-magnitude estimation of the relative amount of the newly exposed surface. To obtain this estimate, we apply the following conceptual model of the particles: the particles are spherical and porous; the outer surface of the sphere is considered as a newly exposed area due to grinding; and the internal surface area (porosity) of a particle is the original pore surface, as in the intact rock. In this way, the new surface area of a single particle may be calculated as

1

Here, φ is the porosity of the rock and R is the radius of the particle.

The original specific surface area can be estimated with Kozeny’s equation

2

so that the internal surface area of a single particle is equal to 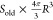. In this equation, k is the permeability of the rock and c is a dimensionless factor, as derived by Mortensen et al.²⁴

3

Applying the measured petrophysical properties of the intact core materials as input, we can obtain the estimated SSA by Kozeny’s equation, as shown in Table 1.

Table 1. Calculated SSA of the Core Samples Using Kozeny’s Equation Before They Were Ground, and the Measured SSA of the Ground Chalk Powders with the BET Method.

				SSA [m2/cm3]
core no.	k [D]	ϕ	bulk density [g/cm3]	estimate	average
SK1	0.00854	0.464	1.43	1.70	1.91
SK2	0.00544	0.464	1.43	2.13
RS1	0.00060	0.339	1.76	3.85	3.88
RS2	0.00056	0.364	1.80	4.45
RS3	0.00052	0.304	1.88	3.47
RS4	0.00089	0.377	1.66	3.75

Using the average SSA calculated from Kozeny’s equation for the two types of chalk, we can calculate the ratio between the new surface area and the original surface area for a particle diameter ranging from 63 to 160 μm (Figure 2).

Figure 2.

Ratio of a newly exposed surface area to the original surface area for Stevns Klint chalk (SK) and reservoir chalk (RS) powders. The new surface area produced in the grinding process is insignificant compared with the original surface area of the chalks.

It is clear that the newly exposed surface area is insignificant compared with the original internal pore surface. This assures that the experimental observations will be representative of the behavior of natural rock surfaces.

2.1.2. Brines

The brines were prepared by dissolving certain salts in deionized water. In this study, we examine the dissolution of calcite in pure water and the exchange process between aqueous Mg²⁺ ions and Ca²⁺ from the solid calcite. A MgCl₂ solution was used as a source of Mg²⁺. The concentration of Mg²⁺ was made to be identical to the North Sea seawater: 0.045 mol/L.

To exclude the influence of atmospheric CO₂ on the experimental process, the deionized water and MgCl₂ solution were degassed in vacuum before the experiments.

2.2. Setup

2.2.1. Reaction Setups

Two types of reaction setups were used in this work. Special attention was paid to remove the effect of the atmospheric carbon dioxide, which might dissolve in the liquid, react with the salt, and change the acidity of the solution. The first setup was constructed in a glovebox filled with nitrogen. A 1 L sample bottle was used as a reaction cell. The calcite powder and the deionized water/MgCl₂ solution were mixed in the bottle and thoroughly stirred by a magnetic stirrer to make a homogeneous mixture. The bottle was sealed by a cap to prevent evaporation.

Liquid samples from the bulk mixture were taken periodically. Upon taking samples, the cap was removed, and a syringe with a syringe filter (0.2 μm pore size) was used to extract samples and to separate the liquid from solid particles. Only 2 mL of the liquid was taken per sample so that the total amount of sampled fluid was insignificant compared with the initial volume. The liquid samples were sealed and stored in a fridge at 4 °C for later chemical analysis; no precipitation was observed upon the analysis. The pH of the bulk mixture was measured simultaneously upon extracting samples, by putting a pH probe into the mixture. Since this setup can provide a stable and reliable long-term control of the CO₂, it was used for experiments that last more than 1 day.

The second type of setup was designed for short-term experiments (less than 1 h), to facilitate the sample extraction procedure at a higher frequency. The powder and liquid were mixed in a 1 L Erlenmeyer flask with a stirring magnet. A nitrogen source was connected to the neck of the flask, with a gentle flow of nitrogen to prevent contact of the mixture with the air. The samples were extracted with the same procedure as in the first setup.

It should be mentioned that, to eliminate the concentration relaxation due to mass transfer at the particle surface, all of the samples were stirred with a speed sufficient to keep the particles suspended and to circulate the suspension. The internal diffusion in the pore space of a particle may be estimated to be fast compared to the characteristic times of the experiments. As mentioned earlier, the diameters of the particles range between 63 and 150 μm. An ion in the center of the particle needs to diffuse through the shortest distance of the particle’s radius (31.5–75 μm) to get into the bulk aqueous phase. A rough estimation can be made with a constant concentration source assumption, where the diffusion length and time can be related as²⁵

Assuming the diffusion coefficient D is 2 × 10^–9 m²/s, the diffusion time is within 5 s, which is surely negligible considering the experimental duration.

2.3. Experimental Procedure

2.3.1. Dissolution and Ion-Exchange Experiments

The prepared powders were weighed with an analytical balance and transferred into the reaction cells. Then, 1 L of the liquid was added into each cell to start the reaction. All of the experiments were performed at room temperature (20 °C). The available surface areas for dissolution and ion exchange of each type of the powder were kept identical by adjusting weights of the powders. Since the reservoir sample has the highest SSA, its mass was the smallest. The surface area of 10 g of the reservoir sample was chosen as a reference value to adjust the weights of other samples so that the calcite surface in contact with the liquid was equal to 26.6 m² in each reaction cell. The weights of the calcite and Stevns Klint powder samples were 77.36 and 12.02 g, respectively. Timing started at the moment of mixing. The elapsed time at each sampling point was recorded.

2.3.2. Analysis of the Samples

The processes studied in this work (calcite dissolution and Ca–Mg exchange) are followed by the measurement of Ca²⁺ and Mg²⁺ concentrations in the mixtures. An accurate chemical analysis of the extracted samples is essential to obtain reliable results. In this work, the Ca²⁺ and Mg²⁺ concentrations in each filtered aqueous sample are obtained by multielement analysis by inductively coupled plasma–optical emission spectrometry (ICP-OES) on an iCAP 7200 Series ICP-OES spectrometer from ThermoScientific. The metal ions are excited in an argon plasma, and the emission spectrum of each element is measured in the spectrometer and the concentration subsequently determined by reference to a standard multielement solution. The sample matrix in this case is quite simple, and samples did not require special preparation (acidation, etc.) beyond filtration.

3. Experimental Results

3.1. Calcite Dissolution in Pure Water

The dissolution of the calcite in pure water was first investigated in setup 1. The first experiment attempt lasted for approximately 4 days, and kinetics of dissolution was not captured in this experiment. The first sample was taken approximately 30 min after mixing. Calcium concentration was almost constant for each type of material throughout the experimental period, with approximately 6 mg/L for reservoir chalk and 4.5 mg/L for pure calcite and Stevns Klint chalk. pH of the solution also remained constant around 10 during the experimental period.

Since the kinetic process of dissolution was not captured in the first attempt, the experiment was replicated in the second setup with more frequent sampling in the first 15 min. The result is shown in Figure 3.

Figure 3.

Evolution of the calcium concentration for calcite dissolution in water. The concentrations did not show significant variation, apart from the first few points. The reservoir rock generally produced a slightly higher concentration than the other two materials.

Again, even though the first sample for each type of powder was taken between 22 and 34 s after mixing, the kinetic process of the dissolution was not fully captured (apart, probably, from a few initial points). This is because the solution volume is too small compared to the particle surface area, which leads to instantaneous saturation by calcite dissolution. However, the data presents two important pieces of information: first, the equilibrium was established within the time frame of the first data points; and second, the equilibrium concentration is around 5 mg/L. As will be shown in Section 4.3, a kinetic model is capable of reproducing these two characteristics with reasonable accuracy. The reservoir chalk produced a higher calcium concentration, while pure calcite and Stevns Klint outcrop gave similar and slightly lower concentrations. The equilibrium concentration of the Ca²⁺ ion ranged from 4 to 6.5 mg/L, corresponding to 10–16 mg/L calcite.

3.3. Ion Exchange

The study of the reaction between calcite/chalk powders and MgCl₂ solution (0.045 M) was performed in the first setup. The experiments lasted for a total of 2 weeks with periodical sampling from the bulk mixture. The concentrations of Ca²⁺ and Mg²⁺ in the samples together, with the doubled standard deviation of the measurements, are plotted in Figures 4 and 5.

Figure 4.

Evolution of the calcium concentration during the ion-exchange process between calcite/chalk powders and MgCl₂ solution. The process has slow kinetics over the experimental period. The most significant exchange was between pure calcite and MgCl₂ solution, while natural rocks had similar behaviors and were less active.

Figure 5.

Evolution of magnesium concentration during the ion-exchange process between calcite/chalk powders and MgCl₂ solution. Due to the high initial concentration and low extent of the exchange process, the Mg²⁺ concentration did not show considerable change.

The reaction between calcium carbonate rocks with the magnesium-containing solution is often described as an ion-exchange process, where the Mg²⁺ ions in the aqueous phase substitute the Ca²⁺ ions from the solid surface. Then, the substituted Ca²⁺ ions enter the aqueous phase.

The reaction can be monitored by either increase of calcium concentration or decrease of magnesium concentration in the bulk solution. In our experiments, the concentration of calcium shows a clear and consistent increase during the experimental period, with the most perceptible increase obtained for the pure calcite powder and a less significant increase for natural materials. Meanwhile, the magnesium concentration shows a seemingly slight decrease in the first few sampling points. However, given the high initial concentration of magnesium, low consumption in the reaction, and uncertainty of the measurement, the Mg²⁺ concentration cannot be determined with sufficient accuracy to describe the reaction.

It should be noted that, even at early times of the experiment, the calcium concentration was 4–5 times higher than that for dissolution in pure water. Afterward, the reaction rate decreased. However, it did not vanish, which indicates that the reaction did not reach equilibrium at the end of the experiment. The first samples were taken between 84 and 103 min from the beginning of the experiments, within which the fast stage of the increase of Ca²⁺ concentration should have reached equilibrium.

Similar to the dissolution experiments, due to the excessive amount of calcite, the pH of the bulk mixture was almost invariable throughout the experimental period, exhibiting a slight decrease from 9.5 to 9 (Figure 6).

Figure 6.

pH of the mixture during the ion-exchange experiments. The measured values are stable throughout the experiments.

4. Modeling of Experimental Data

4.1. Modeling of the Ion Exchange in Static Experiments

According to the experimental observations, the concentration of Ca²⁺ ions in the Ca–Mg ion-exchange experiment can be described as proceeding in two stages. The first stage proceeds rapidly when the calcite surface comes in contact with the MgCl₂ solution. In this stage, the Ca²⁺ concentration increased from 0 to approximately 22 mg/L (which is 4–5 times higher than for dissolution in pure water) and reached equilibrium within 1.5 h. The reason for this behavior was investigated using the Extended UNIQUAC model (which is implemented in ScaleCERE software). The model predicted equilibrium concentrations of Ca²⁺ in pure water and in the 0.045 M MgCl₂ solution to be 5.17 and 18.91 mg/L, respectively, which are consistent with our experimental observations. More importantly, it was found that the high Ca²⁺ concentration in the MgCl₂ solution was caused by enhanced calcite dissolution. The reason is that precipitation of Mg(OH)₂ is a strongly thermodynamically favored process, driving the solution to be slightly acidic. However, it reaches equilibrium very fast and its impact is limited. So it cannot dominate the entire duration of the experiment. The fact that the Ca²⁺ concentration kept rising after reaching approx. 22 mg/L suggests that the precipitation did not hinder further the ion-exchange process. Probably, it only covered some spots on the calcite surface, leaving most of the surface still prone to reacting with Mg²⁺ ions.

As shown in Figure 4, the second stage is slow. When the improved dissolution reaches equilibrium, it takes over control of the reaction kinetics. A characteristic equilibration time for the second process was above 2 weeks since it was observed that the process did not stop until the end of the experiment. The slow kinetics is an indication of the ion-exchange process, where the aqueous Mg²⁺ ions exchange with the surface Ca²⁺ ions in a ratio of 1:1. Although dolomite may form as a result of the ion exchange, we prefer a more general term “ion exchange” to “dolomitization”. Formation of the dolomite is a slow process, and the duration of the experiments is insufficient to provide direct evidence for it.

Given the above analysis, we propose a conceptual model to describe the observed two-stage kinetics. Assume that the Ca²⁺ ions in calcite are arranged in two layers, and each layer has a certain number of Ca²⁺ ions (capacity) that can participate in the reactions. The first layer is at the surface of calcite. The Ca²⁺ ions in this layer are in direct contact with the solution and are readily available for dissolution and ion exchange with aqueous Mg²⁺. The second layer is behind the first layer, inside the solid calcite. To exchange the Ca²⁺ ions in this layer, the Mg²⁺ ions have to get close to the surface and penetrate/diffuse through the first layer.

The two-layer statement makes it possible to define different equilibration times for the two layers. We define the characteristic equilibration times as τ₁ and τ₂ for the first and second layers, respectively. We assume also that the maximum dissolution/exchange capacity, N_max, is the same for both layers.

There are several events happening during the different times and at the different locations. The dissolution takes place at the first stage and is rapidly equilibrated. Precipitation of Mg(OH)₂ also happens in the first stage, after which the precipitated Mg(OH)₂ sits on scattered points on the surface of calcite. The ion exchange takes place throughout the experiment (in both stages) but only dominates the second stage. The exchange happens progressively from the first layer to the second.

This conceptual representation of the process results in the following mathematical formulation. Let N_i be the total molar quantities of the magnesium ions in the solution (i = 0) and in the layers (I = 1, 2, respectively). The conservation law is

4

The ions precipitate on the first layer from the solution and penetrate the first layer to the second one. The corresponding rates between the layers are v₀₁ and v₁₂. Theoretically, there may be ions going in forward and reverse directions. The rates defined here are meant to describe the net effect of the transport processes. The exchange equations are

5

6

7

Next, we define the exchange rates v₀₁ and v₁₂. We apply the simplest model of Langmuir exchange kinetics.²⁶ The rate v₀₁ is proportional to the concentration c₀ of magnesium ions in the solution and to the number N_max – N₁ of unoccupied sites in the layer

8

The value of c₀ is equal to N₀/V. In our system, the amount of magnesium ions is in excess of the available sites, N₀ ≫ N₁, N₂, so that c₀ does not vary much in the process. Then, Ac₀ may be treated as a constant equal to the inverse characteristic time of the exchange between the solution and the first layer

9

Then, eq 8 becomes

10

The definition of rate v₁₂ is more elaborate. Communication of the layers is described as a two-way process so that ions move in both directions between the layers. The net rate v₁₂ is

11

The rate v_1→2 is proportional to the number of magnesium ions in layer 1 and the fraction of unoccupied sites in layer 2. Similar to the previous derivation

12

Similarly

13

Summing up these equations results in

14

This expression may be generalized onto the case where the layers have different capacities. The result is

15

Equations 4–eq 8, with the reaction rates defined by eqs 10–Equations 4, form a system of differential equations for variables N_i (I = 1, ..., 3), with obvious initial conditions. At this point, some shortcomings of the model should be discussed. The model does not capture all of the phenomena that may occur in the system under study. One of them is the complicated aqueous speciation in the calcite equilibrated environment. Another unattained phenomenon is the calcite surface complexation/adsorption with aqueous species. The model also does not explicitly distinguish calcite dissolution and ion exchange. The dolomite formation is implicitly accounted for in the model: there are calcium, magnesium, and carbonate ions “mixed” together in the two layers of calcite. Nonetheless, the model is good at capturing experimental data within their accuracy (as shown in Figure 7). Agreement with the experimental data may indicate that the most important effects are captured by the model, and its further sophistication is unnecessary unless more experimental information become available.

Figure 7.

Comparison of the proposed two-layer model with experimentally measured Ca²⁺ concentrations. Plots (a), (b), and (c) are for pure CaCO₃, Stevns Klint, and RS powders, respectively; the plots present the results for the model where the two layers have the same capacity. Plots (d), (e), and (f) show the results with different capacities of the two layers, representing pure CaCO₃, Stevns Klint, and RS powders, respectively. The two approaches give a similar match with experimental data.

This system was solved by implementing it in Matlab and fitted with the experimentally measured calcium concentration data to obtain the essential parameters that characterize the ion-exchange process: τ₁, τ₂, and N_max (or N_max1 and N_max2). The results are shown in Figure 7. The experimental data shown in Figure 4 were transformed from the measured concentrations (mg/L) to the molar quantities N (mole).

It can be seen that both models generally capture the characteristics of experimental data. Given the average standard deviations (STDs) of the fitting, the different layer capacities result in a noticeable improvement only for the calcite powder sample. However, fitting with the equal layer capacities is also reasonable, considering the accuracy of the experimental data. For the natural samples, the two fittings behave similarly. The fitted parameters are given in Table 2; the maximum capacities are converted from mol to mol/m² surface area for a better comparison.

Table 2. Fitted parameters from the two modeling approaches that characterize the ion-exchange process. Both approaches give similar values for the parameters.

		τ1 [min]	τ2 [×104 min]	Nmax1 [×10–5 mol/m2]	Nmax2 [×10–5 mol/m2]	site density [nm–1]	STD of fitting [×10–5 mol]
pure CaCO3	2 layers eqvl.	118.4	0.95	2.88		17.3	17.4
	2 layers diff.	60.1	1.2	2.63	5.63	15.8	10.6
SK	eqvl.	30.7	6.5	2.18		13.1	3.74
	diff.	35.0	6.9	2.18	2.33	13.1	3.85
RS	eqvl.	20.3	3.0	2.37		14.3	5.02
	diff.	28.0	2.5	2.28	2.03	13.8	5.11

Generally, the two models give similar estimations of the characteristic parameters. The fitted values are consistently on the same order of magnitude. For the cases with the different capacities of the two layers, they are very similar, and the results are close to the layer capacities fitted with an assumption that they are equal. This result, that could not be guessed in advance, confirms the correctness of the two-layer model.

4.2. Modeling of the Ion Exchange in the Flooding Experiments

In this section, we discuss an impact that the kinetics of ion exchange may have on the results of smart waterflooding. The kinetic model of ion exchange is coupled with transport equations. Then, the model is compared with experimental data reported in the literature.

4.2.1. Review of Single-Phase Flow-Through Experiments

Single-phase flooding experiments with the analysis of relevant ion concentrations in the effluent may be used to examine the ion-exchange process. The flow should be fast, so that convective flow, rather than diffusion, dominates the process.

The flooding experiments reported by Zhang et al.²⁷ and Strand et al.²⁸ meet the above-mentioned requirements. They have been used to calibrate surface complexation models (SCMs).^29,30 The flooding experiments by Zhang et al.²⁷ were performed with Stevns Klint chalk samples at ambient and at elevated temperatures (130 °C). The cores were around 62 mm in length and 35.7 mm in diameter, with a high porosity at 48% and low permeability at 2–5 mDa. The cores were initially saturated with a 0.573 M NaCl solution and then flooded with a solution containing 0.504 M NaCl and equal concentrations of Ca²⁺, Mg²⁺, and SCN^– at 0.013 M. SCN^– was considered as a tracer. It is inert toward the calcite surface, and the dispersion of its concentration in the effluent reflects the dispersion of the flow. The flooding rate was 0.2 mL/min, corresponding to 9.7 PVI per day. The concentrations of Ca²⁺, Mg²⁺, and SCN^– in the produced effluent were analyzed.

It was observed that at both low and high temperatures, the production of Mg²⁺ and Ca²⁺ was delayed compared with the tracer. The interplay between the two ions was different. At low temperatures, there was no extra generation of Ca²⁺ since its concentration never exceeded the initial value. On the contrary, at high temperatures, a considerable reduction of Mg²⁺ was associated with a significant increase of the Ca²⁺ concentration, which indicates the presence of mass exchange between the aqueous Mg²⁺ and the Ca²⁺ from the rock matrix.

Single-phase flow-through experiments reported by Strand et al.²⁸ were performed with a reservoir limestone core. The core was 49.1 mm in length and 37.8 mm in diameter, with a porosity of 24.7% and a permeability of 2.7 mDa. The core was initially saturated by a 0.573 M NaCl solution and subsequently flooded by a brine containing 0.504 M NaCl and equal concentrations of Ca²⁺, Mg²⁺, and SCN^– at 0.013 M. The same flooding procedure was replicated at 20, 70, 100, and 130 °C. The injection rate was 0.1 mL/min, equivalent to 10.6 PVI per day.

Unlike the Stevns Klint chalk, the reservoir limestone core did not show an obvious indication of the mass-exchange process even at high temperatures. However, with the increase of temperature, the gap between the curves of Mg²⁺ and Ca²⁺ concentrations enlarged, which might suggest some interactions between the ions and the rock.

4.2.2. Flow-Through Model

Previously, we introduced the mathematical model for the Ca–Mg exchange process. In this section, we couple it with the 1D transport equations and match the model to the literature data. The equations are formulated for aqueous species.

The equation for the transport of a neutral tracer is

16

Here, φ is the porosity and U is the flow velocity. Similarly, the equations for the transport of Ca²⁺ or Mg²⁺ ions accounting for the exchange reactions are

17

Here, r are the reaction rates defined by the static experiments in Section 4.1. Since the volume of solutions in the static experiments is 1 L, the amount N₀ in the rate expressions may be substituted by c. Since it was demonstrated that equal capacities of the layers in the two-layer exchange fit the experimental data equally well, we apply the two-layer model with equal layer capacities. The rates are assumed to be equal (with a different sign) for calcium and magnesium ions

Another difference between flow and static experiments is that the characteristic reaction time for the exchange between the solution and the first layer (τ₁) is no longer constant. It may be recalled that, according to eq 15a, the value of τ₁ is inversely proportional to c₀. The reason for that is the frequency of the adsorption events (such events where a single ion gets adsorbed) should be proportional to the concentration of the ions. In the static experiments, the variation of the concentration was insignificant, and τ₁ could be considered as constant. However, in the transport process, concentrations of the ions may vary considerably. Then, τ₁ becomes dependent on the concentration of the reactant

The equations are transformed to the dimensionless form with the variables

18

Here, L is the length of the core and c₀ is the initial concentration of the solute. The dimensionless equations become

19

20

The rate expressions are also converted into the dimensionless form by converting the concentrations and characteristic dimensionless reaction times

Equations 18 and eqs 10 were solved numerically by an explicit finite difference method. Similar to Alexeev,²⁹ the ratio between the time step and space step was set to be 1:10, to make numerical dispersion comparable to physical dispersion. The tracer concentration in the effluent calculated by the model was compared with the measured values reported in the literature (Figure 8).

Figure 8.

Tracer concentration by the model compared to experimental data from (a) Zhang et al.²⁷ and (b) Strand et al.²⁸ The numerical dispersion is similar to the solute dispersion in porous media.

The model was adjusted to literature data by optimizing A, N_max, and τ₂, which are the key parameters that characterize the ion-exchange process. Adjustment was applied for Mg²⁺ ions, while the concentrations of Ca²⁺ ions were calculated based on the adjusted parameters (Figure 9).

Figure 9.

Modeling the experimental data by Zhang et al.,²⁷ at (a) 20 °C and (b) 130 °C, accounting for the ion-exchange reaction. The model describes better the transport properties of the ions at the high temperature.

For the experiments reported by Zhang et al.,²⁷ the model was able to reproduce the Mg²⁺ concentration in the effluent, but reproduction of the Ca²⁺ concentration was qualitatively different at low and high temperatures. At low temperatures, the model predicted a small peak of Ca²⁺ concentration, which indicates when the ion exchange was the most severe. This was not found in the experimental data. In addition, the front of Ca²⁺ concentration came before that of Mg²⁺, opposite to experimental data. At high temperatures, the model reproduced quite well the behavior of both Mg²⁺ and Ca²⁺ concentrations. This evidences that the fluid–rock interactions under high temperatures proceed according to the ion-exchange mechanism.

The observations have indicated that the interactions between the chalk surface and the Ca²⁺ and Mg²⁺ ions are fundamentally different at low and high temperatures. Other researchers^29,30 applied the surface complexation models (SCMs) for carbonate surfaces, to approximate the same experimental data. The models account for the competitive adsorption of ions on the charged carbonate surface. It was shown that the models could qualitatively reproduce the experimental observations at low temperatures, where our model failed. Apparently, at low temperatures, adsorption prevails over ion exchange, and the balance between the deposited magnesium and released calcium ions is destroyed.

At high temperatures, by tuning the equilibrium constants of ion adsorption, the SCM²⁹ qualitatively predicted the behaviors of Ca²⁺ and Mg²⁺ concentrations in the effluent. But in this case, our model of ion exchange gave a much better fit with the experimental data. The standard deviation of the fitting is 0.0676 in our approach, while it is 0.240 for the SCM.

The values of the fitted parameters are given in Table 3; the result from the static experiment of Stevns Klint chalk is also listed for comparison.

Table 3. Fitted Parameters from Flow-Through Experiments of Zhang et al.²⁷ that Characterize the Ion-Exchange Process^a.

	temp. [°C]	A [((min·mol)/L)−1]	τ2 [min]	Cmax [mmol/L]	STD of fitting [non-dimensional]
fitted with Zhang et al.27	20	37.16	15 761.3	0.78	0.0172
	130	0.14	39.2	3.08	0.0676
static experiments	20	0.73	65 000	0.58	given in Table 2

^aResults from static experiments are listed for comparison.

It may be speculated that two different processes take place when flooding chalk cores with magnesium-bearing brines: the physical adsorption of ions on the surface and the chemical exchange process between aqueous Mg²⁺ and Ca²⁺ from calcite. These two processes dominate the fluid–rock interaction at different temperatures: at low temperatures, the physical adsorption prevails, while at high temperatures, the chemical exchange is stronger and faster.

The fitted values of τ₂ (given in Table 3) support this hypothesis. At high temperatures, the second layer equilibrates within an hour. Considering that the observed differences in the flooding experiments are between 0.8 and 1.7 PVI, which corresponds to 2–4 h, equilibration of the second layer within this period means that the production of Ca²⁺ is doubled after both layers have been equilibrated. Meanwhile, at low temperatures, exchange with the second layer is just at the very early stage. In addition, at high temperatures, the value of C_max increases significantly. This indicates that more sites become accessible for exchange at high temperatures, probably, due to reduction of the energetic barrier or a possibility for ions to faster penetrate to less accessible areas of the natural tortous surface.

It should be mentioned that the static experiments were also performed at ambient temperature, but the physical adsorption was not observed. The reason is that Mg²⁺ ions were in large excess and the measured concentrations of magnesium do not change to such an extent that the changes may be detected. Instead, the Ca²⁺ concentrations were used to model the exchange process, which excluded the impact of physical adsorption.

The fitted values of parameter A show large reduction from low to high temperatures, which indicates an increase of the equilibration time of the first layer. This may be associated with the large increase of the maximum exchange capacity at the elevated temperature: more exchange sites become available, which takes a longer time to equilibrate.

Comparing the fitted parameters at 20 °C with static experiments, it can be found that both τ₂ and C_max are within the same order of magnitude. However, the value of A (related to τ₁) shows a large discrepancy. Using the highest concentration in the flooding experiments, which is 0.013 mol/L, the modeled A corresponds to τ₁ equal to 2.07 min. This value is much smaller than in the static experiments (30.7 min). This is probably associated with the sensitivity of the model, as will be further explained in Section 4.2.3. Generally, the information distilled from matching the experimental data is that the ion-exchange process is largely affected by temperature. The parameters obtained from static experiments can be very different from flooding experiments; they cannot be applied directly to simulate flow-through scenarios.

Unlike comparison with the data obtained by Zhang et al.,²⁷ modeling of the data from Strand et al.²⁸ is less successful (Figure 10). The model works well for the Mg²⁺ concentration, but the prediction for the Ca²⁺ concentration is by no means representative. As for the fitted parameters (given in Table 4, converted to dimensional values), only the maximum exchange capacity, C_max, shows a consistently increasing trend with temperature. The fitted values of A remain on the same order of magnitude at different temperatures. There was no clear correlation between τ₂ and temperature.

Figure 10.

Comparison of the model with experimental data from Strand et al.,²⁸ accounting for the ion-exchange reaction. The model matches the concentrations of the tracer and Mg²⁺ but fails to match the data for Ca². The data is obtained at various temperatures: (a) 20 °C, (b) 70 °C, (c) 100 °C, and (d) 130 °C.

Table 4. Fitted Parameters for Experimental Data of Strand et al.^28,a.

T [°C]	A [((min·mol)/L)−1]	τ2 [min]	Cmax [mmol/L]	STD of the fitting [non-dimensional]
20	0.35	5109.9	2.08	0.030
70	0.65	185.3	2.65	0.024
100	0.47	130.9	3.40	0.043
130	0.28	5109.6	4.01	0.032

^aThere is a clear increasing trend of C_max along with temperature, but other parameters do not change regularly with temperature.

A reason for the poor correlation between the predicted Ca²⁺ concentration and experimental data may be the rock mineralogy. The model for ion exchange was derived from a highly pure biogenic chalk, which is composed primarily of calcite with a negligible amount of impurities. However, the flow-through experimental data were obtained from a reservoir limestone, whose mineral composition was not clearly indicated. The limestone usually contains varying amounts of clay. The impact of clay on the transport properties of cations has been quantitatively studied.²⁹ It was pointed out that even a small amount of clay (1 wt %) can dramatically change the surface potential of the carbonate, which could further affect the adsorption of ions on the mineral surface.

4.2.3. Sensitivity Analysis

Since the model does not always behave consistently with experimental data, it is of interest to investigate its sensitivity to the parameters. We take the optimized parameters from Tables 3 and 4 as initial values, scale each parameter with a factor of 10, and find how the standard deviation (STD) varies. The result for the data from Zhang et al.²⁷ is given in Figure 11.

Figure 11.

Sensitivity analysis for the modeling of experimental data from Zhang et al.²⁷ at (a) 20 °C and (b) 130 °C. The model is more sensitive to C_max and A, but not τ₂, especially at low temperatures.

At high temperatures, all of the three parameters produced nonmonotonic behaviors of STD with a minimum point at the initial values. However, at low temperatures, the quality of fitting does not vary much upon variation of A and τ₂ in the inspected range, which suggests that these factors are probably irrelevant at low temperatures. This affirms our previous inference that different processes dominate the surface reaction at low and high temperatures.

The analysis for modeling of the data from Strand et al.²⁸ is shown in Figure 12. For all of the tested temperatures, the model is more sensitive to C_max and A than τ₂. This makes good sense because the duration of the laboratary test is too short for the second layer to engage in the reaction. It also means that core flooding experiments may not provide a full picture of the impact of ion exchange. However, at the reservoir scale, where the injection lasts for months or even years, the full potential of ion exchange may be unlocked.

Figure 12.

Sensitivity analysis for the modeling of experimental data from Strand et al.²⁸ at (a) 20 °C, (b) 70 °C, (c) 100 °C, and (d) 130 °C. Similar to previous observations, the model is more sensitive to C_max and A but not τ₂.

4.3. Modeling of the Dissolution Process in Static Experiments

The results indicate that the saturation of water by calcite was very fast (on the order of seconds). To verify the observation, we simulated the process in PhreeqC software. We adopted the rate expression of calcite dissolution derived by Plummer et al.⁷

21

where R_calcite is the dissolution rate in mmol/cm²/s, SI_calcite is the saturation index of calcite in the solution, and r_f is the forward rate constant

22

Here, [H⁺], [CO_2(aq)], and [H₂O] are the activities of the corresponding species; k₁, k₂, and k₃ are temperature-dependent constants

23

24

If T ≤ 25 °C,

25

If T > 25 °C,

26

Compared to the original expression, the contact surface area A was inserted into eq 4.

The simulation was performed for a 26.61 m² calcite surface in 1 L of water at 21 °C, and the initial pH was 7.

As shown in Figure 13, the model reasonably reproduced the two important characteristics of the experimental data (the time of reaching the equilibrium and the equilibrium value), as mentioned in Section 3.1. The equilibrium was reached around 10 s, while our experiments indicate that it is less than 20 s. The equilibrium concentration (4.77 mg/L) also reasonably matches with the experimental results, especially for pure calcite and Stevns Klint chalk. A slightly higher concentration given by reservoir chalk is probably due to the impurities of the material. The agreement between our experimental measurement and PhreeqC simulation confirms the validity and accuracy of the experimental procedure.

Figure 13.

PhreeqC-simulated calcium concentration during calcite dissolution in pure water and our experimental data. It can be seen that the model calculation matches well the experimental observations of pure calcite and Stevns Klint chalk but slightly underestimates the equilibrium concentration for reservoir chalk.

4.4. Evaluation of Calcite Dissolution in Flooding Experiments

4.4.1. Review of Experimental Data

Two-phase displacement experiments in chalk with the sequential injection of different brines are selected to evaluate the effect of calcite dissolution on oil recovery. In this study, we discuss the flooding experiments reported by Fathi et al.³¹ and Zahid et al.³² These experiments were carried out with the Stevns Klint chalk samples, similar to the materials in our static experiments.

In the work of Fathi et al.,³¹ a Stevns Klint outcrop core was flooded twice to test the EOR potential of different brines. In both tests, several brines were injected sequentially. Injection of SW at the stage increased the recovery by 7 and 5%, respectively. Additional oil was produced gradually within 2 porous volume injected (PVI) after switching the injection brine. The flooding was performed at 120 °C, and the injection rate was 1 PV/day. The compositions of the brines are given in the Appendix section.

The work of Zahid et al.³² involves 15 core flooding experiments with the Stevns Klint chalk cores. Here, we select 6 out of 13 experiments that are representative of the different experimental conditions, to avoid repetition. The experimental temperatures were 40, 90, and 110 °C. Additional recoveries ranging from 1.16 to 3.38% were observed shortly after injecting the modified seawater. The compositions of the injected brines are given in the Appendix section.

All of the tested conditions are listed in Table 5.

Table 5. Summary of the Experimental Conditions Applied to Simulate Calcite Dissolution Kinetics Using PhreeqC.

	brine	T [°C]
Fathi et al.31	FW	120
	SW
	dSW10000
	SW0NaCl
Zahid et al.32	SW	40
		90
		110
	SW0S	40
		90
		110
	SW3S	40
		110

4.4.2. Calcite Dissolution under the Reported Experimental Conditions

It was stated in Section 3 that the dissolution of calcite in pure water is a fast process. The equilibration time is on the order of seconds, and the equilibrium concentration is low (between 10 and 16 mg/L CaCO₃). The PhreeqC modeling described in Section 4.3 gave a reasonably accurate estimation of the dissolution kinetics and of the equilibrium concentration for the pure calcite and the Stevns Klint chalk.

First, we evaluate the dissolution kinetics of calcite under the experimental conditions (temperature and brine composition) involved in the reviewed works.

The Stevns Klint outcrop chalk has a specific surface area of 2 m²/g. The static dissolution process was simulated with the same experimental configurations as described in the previous section: 26.61 m² surface area in 1 L of the solution. The result is shown in Figure 14.

Figure 14.

Simulated calcite dissolution kinetics under the experimental conditions reported in (a) Fathi et al.³¹ and (b) Zahid et al.³² The temperature has a much more significant impact on the dissolution kinetics than the composition of the brine.

It can be seen that the dissolution of calcite reaches equilibrium very rapidly in both cases. For the experimental conditions in the work of Fathi et al.,³¹ the equilibrium is reached after 1 s. The different brines correspond to the different equilibrium concentrations rather than equilibration times. The brine termed dSW10000 causes precipitation of calcite instead of dissolution. Simulations based on the conditions from Zahid et al.³² show that the effect of temperature on the dissolution process is more important than the effect of the brine composition. Higher temperatures greatly enhance the dissolution of calcite. Meanwhile, the effect of sulfate concentration on dissolution is rather insignificant.

The simulated pH profiles (Figure 15) correlate with the observations. The dissolution of calcite in the brines is associated with a reduction of pH. The equilibrated solutions usually end up in slightly acidic brines, except for the experiments at 40 °C reported by Zahid et al.³²

Figure 15.

Simulated pH profiles under the experimental conditions reported in (a) Fathi et al.³¹ and (b) Zahid et al.³²

The implications of the obtained information (low dissolution times and amounts) on the flooding experiments are twofold. First, in the flooding experiments, the flow velocity of water is slow. In the reviewed works, the injection rates are 1 and 5 PV/day. On the basis of the given core data, the mobile saturation of water can be calculated using the average irreducible saturations of oil and water, and afterward, the flow velocity of the water can be calculated, which turns out to be very slow (on the order of 10^–3 mm/s). The results are given in the Appendix section.

Comparison of the equilibration time for dissolution (few seconds) and the extremely slow flow velocity shows that, apparently, the dissolution process will reach equilibrium at the very inlet of the core, while the rest of the core remains unaffected. However, in most cases, additional oil was produced immediately after switching the injection brine or increasing the temperature. Such recoveries should not be attributed to the dissolution that occurred at the inlet of the cores.

The equilibrium amount of dissolved calcite is very low. The maximum dissolved amount in the reviewed works is 350 mg/L. For the pore volume of the core, which is usually in the range of 30–40 mL for a typical Stevns Klint core, 1 L of injection brine corresponds to 25–28.5 PVIs. This injected volume is rarely achieved in the flooding experiments, so the actual amount of dissolved calcite should be even lower. Compared with the mass of the cores, which is between 55 and 130 g (calculated using the reported core data, given in the Appendix section), the dissolved mass is negligibly small, and the effect is unlikely to cause significant additional recovery.

Advanced mathematical modeling of the dynamic effect of the dissolution on the two-phase displacement is consistent with our observations.²³ Fast dissolution affects only the injection spot, almost without progressing into the rock. In addition, due to the volumetric nonadditivity (the volume contribution of the mineral decreases in solution), the dissolution front velocity decreases in the affected section.

On the other hand, Hiorth et al.¹⁶ reported a linear correlation between calcite dissolution and oil recovery in the imbibition experiments, assuming uniform dissolution inside the core. However, considering the fast dissolution kinetics, dissolution could have only happened on the surface of the core very soon after it was immersed in the imbibing fluid. When the brine penetrates further into the core, it is already saturated with CaCO₃ that was dissolved near the core surface. Additional oil production due to dissolution would thus be insignificant, even though the dissolution may have preferentially occurred at places where oil adsorbs on the calcite, as stated by Stumm, 1992 (p. 162).³³ Probably, there are other surface-chemistry mechanisms of recovery that correlate with the capability of brine to dissolve CaCO₃.

While dissolution alone is not likely to lead to a large amount of oil production, it may trigger other, probably, more important effects. Consequences such as pH alteration,¹² improved pore connectivity,¹³ modified electric double-layer interaction,¹⁵ and compaction of chalk³⁴ were reported in connection with the calcite dissolution. These mechanisms need a separate investigation.

5. Conclusions

In this work, we studied experimentally the kinetics of calcite dissolution in pure water and the Ca–Mg ion exchange on the surface of calcite. The experiments were performed with three types of powders: pure calcite, Stevns Klint outcrop chalk, and North Sea reservoir chalk. It was shown that the existing theory of calcite dissolution was able to match the observed kinetics of the tested materials. Another model was proposed to describe the kinetics of calcium–magnesium ion exchange. It was shown that the two-layer exchange model could describe the process of exchange on the two time scales. Significance of the dissolution and ion-exchange processes was evaluated for the two-phase flooding experiments and single-phase flow-through experiments reported in the literature. A numerical transport model was developed for the flow-through experiments. The main conclusions are as follows.

• The dissolution of calcite is confirmed to be a fast process, and the equilibrium concentration is low. Given the surface-area-to-liquid-volume ratio in our experiments, the equilibrium can be reached within a few seconds. Depending on the temperature and brine composition, the equilibrium concentration of calcite can range from a few milligrams to a few hundred milligrams per liter.

• It is not likely that the dissolution of calcite alone is responsible for the observed additional recovery in smart waterflooding experiments. Under the reported experimental conditions, dissolution of calcite should have occurred at the inlets of the cores, while additional oil production was observed rapidly after the injection water was changed.

• The proposed two-layer model (inner and outer) matches well with the experimental data. It is sufficient to assume that the two layers have equal capacities with regard to the adsorbed amounts of magnesium. The exchange capacity of the surface, as matched by the model, was on the order of 10^–5 mol/m²/layer.

• Due to the long equilibration time of the second layer, as described by the two-layer model, the impact of ion exchange may be more profound on the reservoir scale than in laboratory tests.

• We have compared the behavior of the ion-exchange model proposed in this work with the surface complexation models reported in the literature. Both physical adsorption and chemical exchange of Ca²⁺ and Mg²⁺ ions take place when flooding chalk cores with Mg²⁺-containing brines. The physical adsorption dominates the fluid–rock interaction at low temperatures, while in the model the chemical exchange reaction dominates at high temperatures.

• The different carbonate rocks possess different properties when it comes to the ion-exchange process. The mineralogy composition of the rock should be understood to analyze the chemical interactions.

Appendix A

Tables A1−A4.

Table A1. Brine Compositions Involved in the Flooding Experiments Reported in Fathi et al.³¹.

ion	FW [mol/L]	SW [mol/L]	dSW10000 [mol/L]	SW0NaCl [mol/L]
HCO3–	0.009	0.002	0.001	0.002
Cl–	1.07	0.525	0.158	0.126
SO42–	0	0.024	0.007	0.024
Mg2+	0.008	0.045	0.013	0.045
Ca2+	0.029	0.013	0.004	0.013
Na+	1.00	0.450	0.135	0.050
K+	0.005	0.010	0.003	0.010
ionic strength	1.112	0.657	0.197	0.257
TDS [g/L]	62.80	33.39	10.02	10.01

Table A4. Calculated Mass of the Cores Using Reported Core Information and Calcite Density of 2.71 g/cm³.

	L [cm]	D [cm]	porosity [%]	mass [g]
Fathi et al.31	7.0	3.81	45	119.0
Zahid et al.32	7.5	2.54	46.8	54.8
		3.81	43.8	130.1

Table A2. Compositions of the Brine Used in the Core Flooding Experiments Reported by Zahid et al.³².

ion	SW0S [mol/L]	SW [mol/L]	SW3S [mol/L]
Na+	0.368	0.358	0.337
K+	0.010	0.010	0.010
Mg2+	0.045	0.045	0.045
Ca2+	0.013	0.013	0.013
Cl–	0.492	0.434	0.317
HCO3–	0.002	0.002	0.002
SO42–	0	0.024	0.072
TDS [g/L]	33.39

Table A3. Calculated Flow Velocities of the Water in the Two Reviewed Works and the Parameters Used for the Calculation^a.

	L [cm]	D [cm]	PV [ml]	Swi [%]	2nd rec. [%]	Sor [%]	V [mm/s]
Fathi et al.31	7.0	3.81	35.9	8	57	39.6	0.0015
Zahid et al.32	7.5	2.54	17.8	0	61.8	38.2	0.0070
		3.81	37.5	0	69.2	30.8	0.0063

^aCompared with the very slow flow velocity, the dissolution of calcite should be considered as a fast process.

The authors declare no competing financial interest.