A SIR-Poisson Model for COVID-19: Evolution and Transmission Inference in the Maghreb Central Regions

Abstract

2019-nCoV is a virulent virus belonging to the coronavirus family that caused the new pneumonia (COVID-19) which has spread internationally very rapidly and has become pandemic. In this research paper, we set forward a statistical model called SIR-Poisson that predicts the evolution and the global spread of infectious diseases. The proposed SIR-Poisson model is able to predict the range of the infected cases in a future period. More precisely, it is used to infer the transmission of the COVID-19 in the three Maghreb Central countries (Tunisia, Algeria, and Morocco). Using the SIR-Poisson model and based on daily reported disease data, since its emergence until end April 2020, we attempted to predict the future disease period over 60 days. The estimated average number of contacts by an infected individual with others was around 2 for Tunisia and 3 for Algeria and Morocco. Relying on inferred scenarios, although the pandemic situation would tend to decline, it has not ended. From this perspective, the risk of COVID-19 spreading still exists after the deconfinement act. It is necessary, therefore, to carry on the containment until the estimated infected number achieves 0.

Introduction

Coronaviruses stand for a large family of viruses causing illnesses which range from a simple cold to more severe pathologies. Based on genetic sequence analyses, a virus was identified in December 2019 in China, as a new Coronavirus (2019-nCoV) [1–3]. This pathogen causes a disease (COVID-19) that is different from the severe acute respiratory syndrome (SARS-CoV) and the Middle East Respiratory Syndrome coronavirus (MERS-CoV) [2]. Several scientific studies have been conducted to explore the genetics of 2019-nCoV, its mode of transition, and the epidemiological characteristics of its transmission [4–6]. The infectious COVID-19 spreads via direct contact or droplets and results for the majority of cases in initial symptoms including fever, cough, dyspnea, myalgia, or fatigue. Emergency symptoms can occur. They include intestinal symptoms like diarrhea, cardiac injury, chest pain or pressure, confusion, difficulty walking, and kidney injury. The complication of the infection would lead to death [7–11]. This pandemic first spread in China was notified to the World Health Organization (WHO) in early January by the Chinese government [2, 11, 12]. One month after the beginning of the epidemy, the virus has spread in the entire world, resulting in pandemic coronavirus. As a matter of fact, WHO has declared the COVID19 as a Public Health Emergency of International Concern [12]. A few days after, the WHO raised the level of risk to a very high one in China, as well as globally. It has given instructions for the contagion prevention by avoiding close contact people, frequent hand washing, and the main important measures taken is the quarantine management [11, 13]. Since its appearance until April 29, 2020, worldwide the total number of confirmed cases is 3,137,720, the number of cures is 947,504, and the number of deaths is 218,456. The mortality rate is 6.96%, the cure rate is 30.20%, and the rate of people who are still sick is 62.84%. As for Tunisia, the total number of confirmed cases is 975, the number of cures is 279, and the number of deaths is 40. The mortality rate is 4.10%, the cure rate is 28.62%, and the rate of people who are still sick is 67.28%. For Algeria, the total number of confirmed cases is 3848, the number of cures is 1702, and the number of deaths is 444. The death rate is 11.54%, the cure rate is 44.23%, and the rate of people still sick is 44.23%. For Morocco, the total number of confirmed cases is 4321, the number of healings is 928, and the number of deaths is 168. The mortality rate is 3.89%, the cure rate is 21.48%, and the rate of people still sick is 74.64% [14, 15]. The spread of the new coronavirus pneumonia is rapid, ranging from 30 to 50 days after the first reported case, in Tunisia, Algeria, and Morocco. The pandemic state reached its peak in early April and then gradually decreased. One of the necessary tools to investigate infectious disease transmission and spread is disease mathematical modeling. In fact, various models were developed and used to understand and control infectious diseases evolution and to predict their compartmental transmission. Hoch et al., [16] developed the mathematical model Susceptible–Infectious–Removed–Susceptible (SIRS) for two divided population groups interacting with each other. Their model used five functions that provide an overview of the used mathematical forms representing different transmission processes. They simulated dynamics infection in a multi-group system and emphasized the importance of knowing the populations in contact and their related infection processes to select the most relevant between-group transmission function. Muglenga and Mubila [17] used the SIR process to model the epidemiology of malaria in a Zambian province. They analyzed the rate of infection of malaria. They predicted parameters of malaria outbreak and spread. Reduction in malaria in the studied city [17] was proposed and recommended. Götz et al. [18] modeled the dengue fever disease induced by a viral mosquito-borne infection causing illness and death in tropical and subtropical regions. They used the classical SIR model to examine the spread of dengue in Indonesia. The IR model parameters were identified and connected to meteorological data [18]. Another study elaborated a model that considers multiple single strain conditions extending the SIR model to more dimensions and allowing the modeling of a population infected by multiple viruses. They applied their model on influenza and other similar viruses [19]. Kamina et al. [20] suggested the Gillespie algorithm based on the SIR and developed a stochastic SIR model to simulate disease evolution in the population setting. They inferred the accuracy of their model, by comparing the simulated values produced by the model to those of HIV/AIDS data from 1985 to 2018 [20]. Nishiura et al. [21] utilized compartmental modeling including differential equations and maximum likelihood estimation so as to model the transmission dynamics of Zika virus infection on Yap Island 2007 and French Polynesia 2013–2014. They compared the observed and predicted weekly numbers of new cases during the early period of the Zika virus epidemic and quantified the transmission potential infection in the South Pacific demonstrating that its transmissibility is comparable to those of chikungunya and dengue viruses [21]. Another modeling framework called Bayesian Markov chain Monte Carlo was used to reconstruct the annual probability of chikungunya (CHIKV) infection and population-level immunity over a period of 60 years [22]. Their model was useful to understand the long-term epidemiology of the pathogen in the Philippines. Recently, to model Covi-D19 transmission, several studies based on the SIR model were developed such as a generalized SEIR model [23, 24], a SIR-D (dead) model [25], and a modified SEIR model [26].

In this research work, we attempt to compare the distribution of the pandemic virus at the level of the Maghreb Central countries (Tunisia, Algeria, and Morocco), since its appearance until April 29, 2020, and its link with the demographic distribution. We set formed a statistical modeling which allows predicting its transmission and the end of the containment period in these three countries. Indeed, statistical modeling was applied in epidemiology and several models have been applied to explore, predict, and control the COVID19 transmission. Moreover, we tend to predict the infected number of people in the future period for different scenarios by varying the average number R₀ of contacts by an infected individual with others.

The remaining of this paper is structured as follows: In Sect. 2, we firstly describe data. Secondly, we remind the reader of the SIR model. Finally, we proposed a reliable approach in order to predict the infected and death number in future with different scenarios. Section 3 describes the predicting results of the evolution of the pandemic and an illustrative simulation study. Section 4 wraps up the closing part and provides pertinent concluding notes.

Materials and Methods

Data Collection

In order to analyze and model the evolution of the infectious disease of COVID-19 in the Maghreb Central countries, the number of cases of people affected by the virus was collected and reported day by day [14, 15]. The study is almost over 2 months (from the disease emergence until end of April 2020. The studied variables are the evolution of the total cumulative confirmed cases, total cumulative deaths, cumulated cures, and demographic population density in infected cities [27–32].

Statistical Modeling

To accomplish our objective, a hybrid model combining a Poisson Markov process with a SIR model is introduced, called SIR-Poisson model. Through various simulations, this model manages to predict the infected and death number so as to mitigate the infection risk under various different scenarios.

The SIR Model

The simple SIR (Susceptible–Infectious–Removed) model [33] describes different states of a population. The model SIR describes three human states which are Susceptible, Infectious, and Removed. A person moves from one state to another at different rates. The model assumes that the recovered humans receive immunity against the disease. The people interact homogenously, and finally, the birth rates and natural death rates are constant. The SIR model is expressed in terms of ordinary differential equations:

$$\left\{\begin{array}{c}\frac{\text{d}S}{\text{d}t}=-\frac{\mathit{IS}}{N}\\ \frac{\text{d}I}{\text{d}t}=\frac{\mathit{IS}}{N}-I\\ \frac{\mathit{dR}}{\mathit{dt}}=I\end{array}\right)$$ 1

where S is the stock of susceptible population, I is the stock of infected, R is the stock of removed population (either by death or recovery), and N is the sum of these three parameters.

This system is nonlinear. However, it is possible to derive its analytic solution in an implicit form. Other numerical tools include such Monte Carlo methods as the Gillespie algorithm. Firstly, note that from $\frac{\text{d}S}{\text{d}t}+\frac{\text{d}I}{\text{d}t}+\frac{\text{d}R}{\text{d}t}=0$, it follows that $\text{S}\left(t\right)+I\left(t\right)+R\left(t\right)=\text{constant}=N.$

Secondly, we note that the dynamics of the infectious class depends on the following ratio:

$$R_0=\frac{\beta }{\gamma }\text{where}\beta >0\text{and}\gamma >0$$ 2

This ratio is derived as the expected number of new infections (these new infections are sometimes called secondary infections) from a single infection in a population where all subjects are susceptible. This idea can probably be more readily viewed if we state that the typical time between contacts is $T_c={\beta }^{-1}$ and the typical time until recovery $T_r={\gamma }^{-1}$. From this perspective, it follows that, on average, the number of contacts by an infected individual with others before the infected has recovered is obtained through $\frac{T_r}{T_c}=R_0$.

The Proposed SIR-Poisson Model

Let Y(t) be the infected number of people at the date t, (t = 0,1,2,…). Suppose that the conditional distribution of Y(t + 1) given Y(t) is a Poisson distribution with parameter $\left(pI\left(t\right)+\left(1-p\right)Y\left(t\right)\right).\lambda \left(t\right)$, where I(t) denotes the infected number of people given by the SIR model and $\lambda \left(t\right)$ will be estimated by the observed data (Yo(t), t = 0…T). In this case,

$$\lambda \left(t\right)=\frac{Yo\left(t+1\right)}{Yo\left(t\right)}$$ 3

Hence, we combine the SIR and Poisson Markov process in order to obtain a hybrid model. Likewise, we can estimate the death number of people at the date t. The proposed model is run in three steps:

Step 1 We use the observed data Yo(t) in the date ranging from 01-03-2020 to 30-04-2020 for each country. We estimate $\left(t\right)=\frac{Yo\left(t+1\right)}{Yo\left(t\right)}$, t = 1,…, T.

Step 2 We consider the SIR parameters $\left(\alpha ,\beta ,\gamma \right)$ model. Then, we fix $R_0=\frac{\beta }{\gamma }$ to be the average numbers of contacts by an infected individual with others before the infected has recovered. Thus, the solution I(t) of the infected number is provided by the SIR model t = 1,…, T.

Step 3 We generate the estimated observations in the future. Let $\widehat{Y}\left(t\right)$ be the estimated infected number of people at the date t, t = 1,…, S.

Let

$$\widehat{I}\left(t\right)=pI\left(t\right)+\left(1-p\right)\widehat{Y}\left(\text{t}-1\right),p\in \left[0,1\right]$$ 4

The conditional distribution of $\widehat{Y}\left(t+1\right)$ given $\widehat{Y}\left(t\right)$ is a Poisson distribution with parameter $\widehat{i}\left(t\right)\ast \lambda \left(t\right)$; t = 1,…, S. Consequently, we generate $\widehat{Y}\left(1\right),\dots ,\widehat{Y}\left(S\right)$ from the Poisson Markov process. Note that $R_0=\frac{\beta }{\gamma }$ and the proportion p are given for each scenario. If p > 0.5, in this case, we attribute more reliability for the SIR model. In this experimentation, we consider p = 0.3 and R₀ varying from 2 to 6. Note that R₀ is an indicator of the transmission risk.

This proposed approach is coded in Python 3.7. We learn how to simulate the model and how to plot and interpret the results. We use simulation to check some analytical results and to predict the infected and death number in the future.

Results and Discussions

The detected evolution and exhibited statistics suggest that the pandemic virus has spread more rapidly in Morocco and Algeria and less rapidly in Tunisia. The most affected country is Algeria, which has displayed the highest rates of deaths despite its high cure rates compared to Morocco and Tunisia.

Evolution of the Confirmed Number

The trend curve for the number of confirmed patients is increasing for the three Maghreb Central countries (Fig. 1). This pandemic transmission is very rapid for Algeria and more confirmed for Morocco, which is gaining momentum after April 14 as the number of confirmed patients practically was multiplied by 2 to April 26 (goes from 1888 to 3758). As for Tunisia, an evolution is recorded by the very slow increase from April 14. The analysis of variance (Table 1) demonstrates that there is no significant difference between Algeria and Morocco (p value = 0.596 > 0.05). However, the evolution of the confirmed cases in Tunisia is obviously different from that reported in Morocco and Algeria (p values < 0.05).

Fig. 1.

Evolution of confirmed cases in different Maghreb Central countries

Table 1.

Table of analysis of variance for confirmed cases

Groups	Source of variations	Sum of squares	DF	F	P value	Theoretical-F
Confirmed Algeria/Morocco	Inter-groups	483107,872	1	0.283	0.596	3.919
	Intra-Groups	208058698	122
Confirmed Tunisia/Algeria	Inter-groups	12631083/9	1	14.990	0.000	3.919
	Intra-groups	101957919	121
Confirmed Tunisia/Morocco	Inter-groups	17203246.3	1	16.231	0.000	3.924
	Intra-groups	121890559	115

Significance difference at probability 5% level

Evolution of the Dead Number

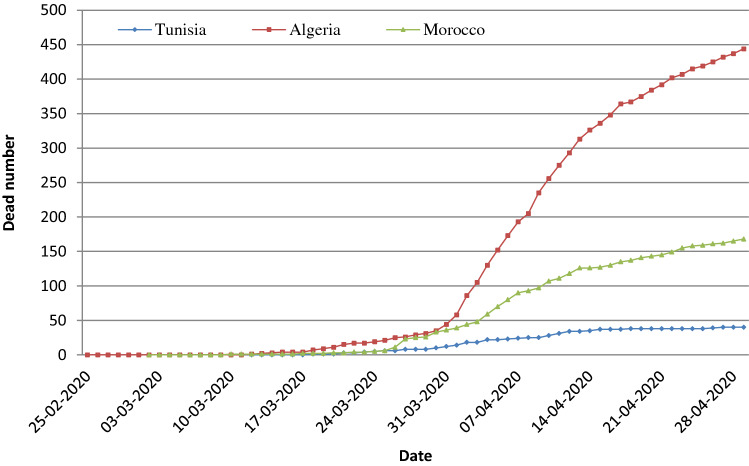
The trend in the number of deceased people is increasing for the three Maghreb Central countries (Fig. 2). This increase evolution is very important for Algeria (444 cases) and less confirmed for Morocco as it didn’t exceed 160 deaths. However, this curve is stabilized for Tunisia since April 14 at a constant number of deaths which didn’t exceed 50 deaths. These data can be assigned to the clinical situations of the 3 countries. The evolution of occurred deaths in patients varies significantly between Tunisia, Algeria, and Morocco. In fact, the analysis of variance (Table 2) indicates that there exists a significant difference between the three countries (p values < 0.05).

Fig. 2.

Evolution of the dead number in different Maghreb Central countries

Table 2.

Table of analysis of variance for dead cases

Groups	Source of variations	Sum of squares	DF	F	P value	Theoretical-F
Dead (Algeria/Morocco)	Inter-groups	187890.776	1	11.432	0.001	3.919
	Intra-groups	2005206.1	122
Dead (Tunisia/Algeria)	Inter-groups	458152.75	1	31.009	1.57E − 07	3.919
	Intra-groups	1787738.08	121
Dead (Tunisia/Morocco)	Inter-groups	57442.8719	1	26.769	9.82E − 07	3.924
	Intra-groups	246776.051	115

Demographic Distribution

The distribution of confirmed cases according to different cities of different Maghreb Central countries and the superimposition of demographic densities for inhabitants per km² are illustrated in Fig. 3. We note for these three graphs (Fig. 3a, b and c) that the capitals which comprise the most populations have the most confirmed numbers (199 for 3053 inhab/km² in Tunis or 21.58%). The two following Tunisian cities which are the most populated are Ariana and Ben Arous counting 94 confirmed for 1195 inhab/km² and 91 for 830 h/km², respectively. Greater Tunis, which is an extension of the agglomeration of the capital Tunis and which is made up of the governorates of Tunis, Ben Arous, Ariana, and Mannouba, has a 423 confirmed cases (or 45.87%) of the total confirmed number (Fig. 3a). However, we note that some cities are less dense in terms of inhabitants and yet exhibit a high number of confirmed cases, which is the case of the cities of Kebili and Medenine having 86 confirmed cases each for successive population densities of 7 and 56 inhab/km².

Fig. 3.

Confirmed and dead cases with population density in different infected cities (a: Tunisia, b: Algeria, c: Morocco)

For Algeria (Fig. 3b), we note that Alger displays the highest density of inhabitants and has a large number of confirmed (472 for 3693.63 inhab/km²), i.e., the proportion of confirmed cases is 15.09%. Meanwhile, despite being less dense, the city of Blida has the largest number of confirmed (730 for 678.58 inhab/km²) which corresponds to 23.34% of the total confirmed cases.

As for Morocco (Fig. 3c), the same remarks as Tunisia and Algeria are reported. Indeed, Casablanca exhibits the highest density of inhabitants and has a large confirmed number (982 for 352.82 inhab/km²), i.e., the proportion of confirmed cases is 26.13%. Despite being less dense, the cities of Fes-Meknes and Marrakech-Safi recorded a large confirmed number of cases (499 for 12.37 inhab/km² and 802 for 2.62 inhab/km², respectively). Certainly, the density of the population influences to a great extent the contagion. Yet, it is necessary to seek the causes of contaminations in these less populated cities. Ceremonies and weekly markets would be the main causes of contamination.

Validation of the Model Inference Framework

Testing the proposed model provides a graphical comparison between the generated data and the observed one since the start of the containment period to 29/04/2020. The obtained curves verify the ability of the model inference framework (Fig. 6a, b and c). Therefore, the system could identify a variety of parameter combinations of the average number of contacts R₀. Over this period, the estimated parameter R₀ for Tunisia is less than 2. Yet, for Algeria and Morocco it is around 3.

Fig. 6.

Real and estimated number of infected with COVI-19 for a Tunisia, b Algeria, c Morocco

Prediction of Infected and Death Number

The estimation of the prevalence and contagiousness of undocumented novel coronavirus infections is critical for understanding the overall prevalence and pandemic potential of this disease. The proposed SIR-Poisson model applies the strength of the SIR’s dynamic system combined with the Poisson Markovian model. This model was learned on the actual data set (from the disease emergency until 29 April 2020). Indeed, it is able to predict the disease spread patterns in a future period. Simulated observations were reported on Tunisia, Algeria, and Morocco (Figs. 4, 5 ). In this work, the SIR-Poisson model has predicted the infected and death number of people in the future period of 60 days (May/June 2020). By varying the transmission rate or the average number R₀ of contacts by an infected individual with others, we infer a significant difference of the infected and death numbers on a daily basis if R₀ increases from 2 to 6.

Fig. 4.

Predicted of death number with COVID-19 by varying different values of R0 for a Tunisia, b Algeria, c Morocco

Fig. 5.

Predicted number of people infected by COVID-19 during 55 days with different values of R0 for a Tunisia, b Algeria, c Morocco

Consider the three following scenarios for predict numbers of infected and dead cases:

Scenario 1 R₀= 6 (Deconfinement)

The maximal infected number is achieved around 420/day on the fiftieth day for Algeria and Morocco (Fig. 5b, c). In this case, the maximal death number is reached around 17/day (Fig. 4 b, c). In Tunisia, the situation is different, the maximal infected number is achieved around 370/day on the thirtieth day (Fig. 4a) and the maximal death number is achieved on 15/day (Fig. 5a). If R₀> 6, the situation is dangerous and the death number increases exponentially.

Scenario 2 R₀= 4 (partial confinement)

The maximal infected number is achieved around 320/day for Algeria and Morocco and 270/day for Tunisia (Fig. 4a, b and c). The maximal death number is achieved around 13/day on the fiftieth day for Algeria and Morocco and on 11/day for Tunisia (Fig. 5a, b and c). When a partial containment period is established, the situation is not much better and the infected and death numbers are important.

Scenario 3: R₀= 2 (confinement period)

In this case, the predicted infected and death numbers are very low (Figs. 4a, b, c and 5a, b, c). In fact, the maximal infected number is achieved around 170 for Morocco, 105 for Algeria, and 50 for Tunisia.

To further clarify this notion, the larger the containment period is (R₀≪ 2), the better the situation is and the smaller the infected and death numbers become. If R₀ is greater than 2 (R₀ ≫ 2), then the pandemic transmission increases rapidly and the death number increases. In this case, it is necessary to increase the containment period. Since the estimated parameter R₀ is between 2 and 3 in Maghreb Central countries in this period, the containment period will be extended (Fig. 6a, b, c). Note that these obtained results go in good agreement with the published results [34]. The three states of the Maghreb Central implemented strict measures that correspond, mainly, to locking of borders, imposing general confinement, placing suspected in quarantine, and conducting awareness campaigns as well as advice. Owing to all the taken provisions and people’s self-commitment responsibility and discipline, the results revealed that the situation in Tunisia is better and less dangerous. This fact may be explained by the big difference in the population number. In fact, the Tunisian population is about 11.9 million inhabitants; however, Algeria and Morocco’s populations are about 40 million inhabitants (43.85 and 35.9 million inhabitants, respectively). In fact, it is much easier to deal with a lower number of people. The proposed SIR-Poisson model will help the government to take an optimal deconfinement strategy (partial to total). The average number R₀ of contacts will indicate the situation during this deconfinement.

Conclusion

This study investigates the impact of COVID-19 evolution (deaths and infected numbers of cases) for the future. The simulated pandemic curves depict a significant trend during a containment period at a very early stage. Cases occurring in March 2020 may be assigned to a mode of transmission of small-scale exposure. In April 2020, they may be attributed to a mode of transmission by diffusion.

A new SIR-Poisson model is developed by combining the Poisson Markovian and the SIR models. Actually, the estimated average number of contacts R₀ is equal to 2 for Tunisia and R₀ = 3 for Algeria and Morocco. This model is able to generate the evolution of transmission which predicts the range of the infected cases in a future period with different values of R₀ (2, 4 and 6). The SIR-Poisson model was learned on the actual data set to predict the future period of the disease spread patterns over a window around 2 months.

Moreover, the downward trend in the simulated curves describing the evolution of infected cases indicates that when the parameter of the average number of contacts R₀ is low (R₀ ≪ 2). Some turning points of interest were obtained from the predicted time when the daily number of infected cases becomes smaller than the previous one.

Although the pandemic situation has tended to decline, this situation has not ended entirely. Especially after the deconfinement, when R₀≫ 2, large numbers of people will move and contact, which further increases the risk of contamination. In this case, it is necessary to increase the containment period. This prevention and control of the rebound of the epidemic will block the contamination and help the government decision for optimal deconfinement strategy.