Abstract
In this work, a researcher develops (Susceptible–Stay-at-home–Exposed-Infected–Quarantine–Recovery–Death) coronavirus pandemic, spread model. The disease-free and endemic equilibrium points are computed and analyzed. The basic reproduction number is acquired, and its sensitivity analysis conducted. COVID-19 pandemic spread dies out when and persists in the community whenever . Efficient stay-at-home rate, high coverage of precise identification and isolation of exposed and infected individuals, reduction of transmission, and stay-at-home return rate can mitigate COVID-19 pandemic. Finally, theoretical analysis and numerical results are shown to be consistent.
MSC: 34D20, 65L12, 91D30
Keywords: Coronavirus disease, Stay at home, Isolation, Theoretical analysis, Numerical simulation
1. Introduction
Coronaviruses are a large family of viruses that may cause illness in animals or humans. In humans, several coronaviruses are known to cause respiratory infections ranging from the common cold to more severe diseases such as Middle East Respiratory Syndrome (MERS) and Severe Acute Respiratory Syndrome (SARS). The most recently discovered coronavirus causes Coronavirus Disease 2019( COVID-19) [1]. Its the infectious disease caused by the most recently discovered coronavirus. This new virus and disease were unknown before the outbreak began in Wuhan, China, in December 2019. The most common symptoms of COVID-19 are fever, tiredness, and dry cough. Some patients may have aches and pains, nasal congestion, runny nose, sore throat, or diarrhea. These symptoms may appear 2–14 days after exposure, most commonly around five days [2], [3].
China was the index case of the COVID-19 pandemic. Later it rapidly spread thought the world. People infected by those initial cases spread the disease to others drastically due to human transmission [4]. Although Corona represents a major public health issue in the world, as of March 11, 2020, over 118,000 infections spanning 113 countries have been confirmed by the World Health Organization (WHO). The WHO declared this public health emergency as a pandemic [5]. As of 14 April 2020, WHO reported confirmed case and 117,021 deaths have been recorded globally [6].
The study about the spread and control of COVID-19 is essential at this time. Different scholars are study about infectious disease spread control by using modeling approach [7], [8], [9], [10], [11], [12]. Recently, researcher study about COVID-19 [13], [14], [15], [16]. The model, which is of form [17], incorporates the recommended public health interventions in the current pandemic. The recommended mitigation strategies of the pandemic are stay-at-home and isolation of exposed and infected individuals by efficient identification process. This researcher focus on the impact of control measures by varying the parameter values. The model result indicates that the containment of the pandemic requires a high level of both identification and isolation process and the contact tracing process by stay-at-home for removing infected individuals from the susceptible population.
2. Model formulation
In this work, a researcher considers that the total population is represented by , at time . The total population is dividing into seven compartments. The susceptible population , they stand for people who are capable of becoming infected. The quarantine population , they represent stay-at-home people. The exposed population , they represent people who are incubating the infection. The spreader population , they represent infectiously infected people. The quarantine population , they represent people who are isolated by clinical confirmation. The recovery population , they represent people who are recovering from the virus. The density of disease-induced death is denoted by .
The model flow chart is illustrated in Fig. 1.
Fig. 1.
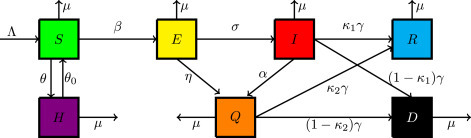
Schematic diagram of the model.
In the process of COVID-19 spreading, the spreading among these seven states is governing by the following assumptions. It is assumed that is the contact rate of susceptible individuals with spreaders, and the disease transmission follows the mass action principle. A researcher assumes that susceptible individuals home quarantine or stay-at-home at a rate of . And at a rate of , peoples lift stay-at-home order due to the ineffectiveness of home quarantine. People who completed the incubation period becomes infected at a rate of , which means is the average duration of incubation. According to clinical examination, the exposed and infectious individuals become isolated at a rate of and , respectively. The average duration of infectiousness is when is the transmission rate from infected to recovery or death. In my assumption, recovery from isolated infected is better than the infectious class due to clinical treatment. Infectious and isolated infected recover with a probability of and , and also they will die by the rate of and respectively. The parameter is the recruitment, while natural birth and death rate of each state individuals. All parameter values are non-negative.
Based on the above considerations, COVID-19 spreading leads to dynamic transitions among these states, shown in Fig. 1. The model can be described by the following system of nonlinear ordinary differential equations:
| (1) |
We have the non-negative initial conditions .
To make the mathematical analysis easier, the variables of the model (1) can be normalized as . After substitute them in (1) we can get the simplified form of the model
| (2) |
From the normalized form of the model we have to get
The first equation of the system (2) can be removed and there remains a system of six differential equations.
| (3) |
where and .
So, the feasible domain of the system (3) is
For the well-posedness of the model, we have the following lemma.
Lemma 1
The set is positively invariant to system (3) .
Proof
Denote and then system (3) can be rewritten as
where
Note that is obviously a compact set. We only need to prove that if , then for all . Note that consists of seven plane segments:
which have as their outer normal vectors, respectively. If the dot product of and normal vectors of the boundary planes are less than or equal to zero, then for all . So,
The proof is complete.
Hence, system (1) is considered mathematically and biologically well-posed in [18].
3. Theoretical analysis of the model
3.1. Equilibrium analysis
In this sub section, we show the feasibility of all equilibria by setting the rate of change with respect to time of all dynamical variables to zero. The model (2) has two feasible equilibria, which are listed as follows:
-
(i)
Disease-free equilibrium (DFE), where .
-
(ii)
Endemic equilibrium (EE) .
The existence of endemic equilibrium is computing after we have the basic reproduction number .
3.2. Basic reproduction number
Here, we will find the basic reproduction number of the model (2) using next generation matrix approach [19]. We have the matrix of new infection and the matrix of transfer . Let , the model (2) can be rewritten as:
where
The Jacobian matrices of and at the disease free equilibrium are, respectively,
where,
The inverse of is computed as
The next generation matrix is given by
Therefore, basic reproduction number is is spectral radius of matrix and basic reproduction number is obtained as follows,
3.3. Stability of the disease free equilibrium
In this subsection, we summarize the results of the linear stability of model (2) by finding the sign of eigenvalues of the Jacobian matrix around the equilibrium .
Theorem 2
If , the disease-free equilibrium of system (2) is locally asymptotically stable, and it is unstable if .
Proof
In the absence of the disease, the model has a unique disease-free equilibrium . Now the Jacobian matrix at equilibrium is given by:
(4) Here, we need to find the eigenvalue of the system from the Jacobian matrix (4). We obtain the characteristic polynomial
(5) From the characteristic polynomial in Eq. (5), it is easy to get five real negative eigenvalues of , which are and . We get the other real negative eigenvalues from the expression
(6) From the quadratic equation (6), we conclude that are negative if . Thus the equilibrium is locally asymptotically stable if . The equilibrium becomes unstable, with one positive eigenvalue, when . This completes the proof.
Physically speaking, Theorem 2 implies that disease can be eliminated if the initial sizes are in the basin of attraction of the DFE . Thus the infected population can be effectively controlled if . The effective control of the infected population is independent of the initial size, a global asymptotic stability result must establish for the DFE.
Theorem 3
If , then the disease-free equilibrium, , of system (2) is globally asymptotically stable in .
Proof
Let and consider a Lyapunov function,
Differentiating in the solutions of system (2) we get
Therefore,
whenever . Furthermore, if and only if . Thus the largest invariant set in is the singleton, . By LaSalle’s Invariance Principle the disease-free equilibrium is globally asymptotically stable in , completing the proof.
Theorem 3 completely determines the global dynamics of model (2) when . It establishes the basic reproduction number as a sharp threshold parameter. Namely, if , all solutions in the feasible region converge to the DFE , and the disease will die out from the community irrespective of the initial conditions. If , is unstable, and the system is uniformly persistent, and a disease spread will always exist.
3.4. Endemic equilibrium and its stability
3.4.1. Existence and uniqueness
The feasibility of the equilibrium is trivial. Here, we show the existence of endemic equilibrium . The values of , and are obtained by solving the following set of algebraic equations:
| (7) |
After some algebraic calculations, we get the value of as:
Therefore, there exists a unique positive solution only when . It implies that the system has a unique endemic equilibrium, .
3.4.2. Stability analysis
Theorem 4
If , then the endemic equilibrium point of system (2) is locally asymptotically stable.
Proof
The Jacobian matrix of the model at is
(8) where and .
Now, we get the characteristic polynomial of the Jacobian matrix (8) as
(9) From the characteristic polynomial (9), it is easy to get , and the other eigenvalues of the system need further finding. We obtain the others from the expression
(10) Where
(11) The polynomial (10) has negative roots (eigenvalues) if all its coefficients terms are positive, or it satisfies Routh–Hurwitz criteria of stability [20]. From (11) we can verify that and , when . Therefore, according to the Routh–Hurwitz criterion, we can get that all the roots of the above characteristic equation have negative real parts. Thus, the endemic equilibrium asymptotically stable. The proof is complete.
The local stability analysis of the endemic equilibrium tells that if the initial values of any trajectory are near the equilibrium , the solution trajectories approach to the equilibrium under the condition . Thus, the initial values of the state variables and are near to the corresponding equilibrium levels, the equilibrium number of infected individuals get stabilized if .
3.5. Sensitivity analysis of
We explore sensitivity analysis of system (2) to determine the model robustness to parameter values. This is a strategy to identify the most significance parameters of the model dynamics. The normalized sensitivity index is given by
Thus normalized sensitivity indices for parameters are obtained as
| (12) |
From the sensitivity indices calculation results, we can identify some parameters that strongly influence the dynamics of disease spread. Parameters , and have a positive influence on the basic reproduction number , that is, an increase in these parameters implies an increase in . While parameters and have a negative influence on the basic reproduction number , that is, an increase in these parameters implies a decrease in .
Here, we illustrate the graphical relationship between the basic reproduction number and the parameter values in the model (2).
A researcher can find some significant results, which have shown in Fig. 2, Fig. 3, it can be seen that large or can lead to large . That is to say, the high contact or short incubation period can increase the opportunity of disease spreading. If we reduce the transmission rate by quarantine or any appropriate control measure, then the disease outbreak will end.
Fig. 2.
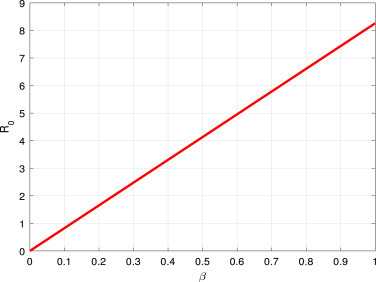
vs the parameter .
Fig. 3.
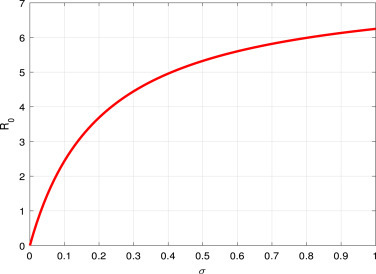
vs the parameter .
As a result of Fig. 4, and Fig. 5, decreases when increases, and increases whenever increase respectively. This finding suggested that effective stay-at-home intervention has mitigated the COVID-19 spread, while the ineffectiveness of this intervention measure can increase its spread.
Fig. 4.
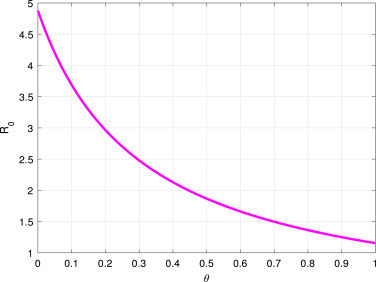
vs the parameter .
Fig. 5.
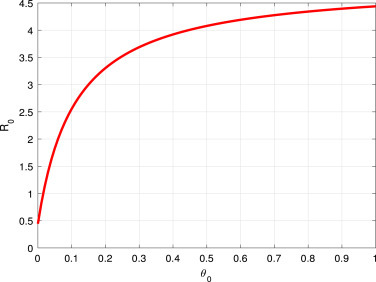
vs the parameter .
Fig. 6, and Fig. 7, shows that the increment of or can reduce . That is to say, effective quarantine of incubated and infectious individuals can reduce the opportunity of disease spreading.
Fig. 6.
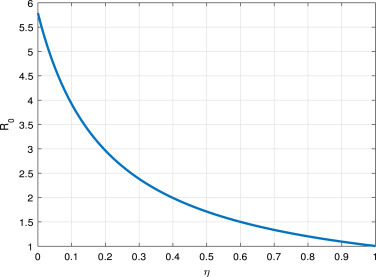
vs the parameter .
Fig. 7.
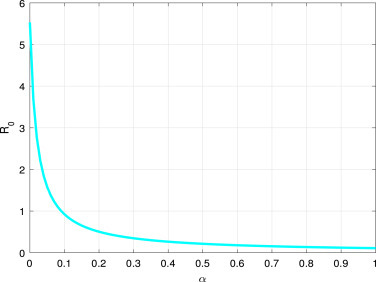
vs the parameter .
From Fig. 8, and Fig. 9, we find that, the short average time from the symptom onset to recovery or death and high value of can reduce the COVID-19 spread.
Fig. 8.
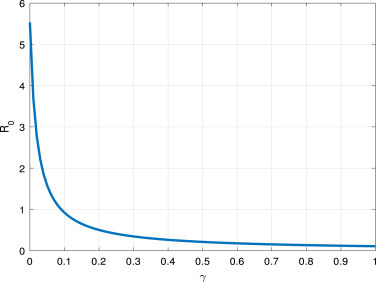
vs the parameter .
Fig. 9.
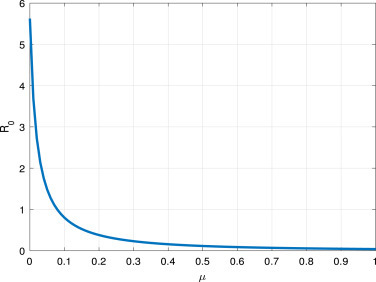
vs the parameter .
4. Numerical results and analysis
In this section, we conduct numerical simulation of the model (2) by using Matlab standard ordinary differential equations (ODEs) solver function ode45.
4.1. General dynamics
We numerically illustrate the asymptotic behavior of the model (2). We take the initial conditions .
Fig. 10 presents the trajectories of model (2) when , thus the basic reproduction number . From this figure, we can see that the disease dies out and the trajectories converge to the disease free equilibrium point . This mean that disease disappears in the community as shown in Theorem 2, and Theorem 3. Furthermore, socio-economical crisis caused by COVID-19 are removed. Finally, we have a disease free community.
Fig. 10.
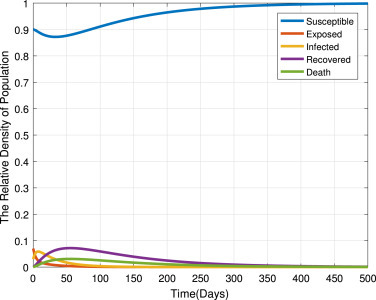
Each compartment population changes over time when .
Fig. 11 gives the trajectory plot when , the basic reproduction number is . From this figure, we can see that even for a small fraction of the infectious case at the beginning, the disease is persists in the community and stabilize in time. This means that the trajectories converge to the endemic equilibrium point. Thus, as established in Theorem 4, the disease persists in the community whenever .
Fig. 11.
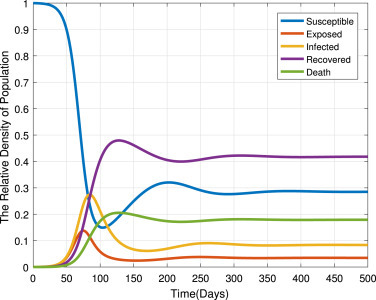
Each compartment population changes over time when .
4.2. Impact of the transmission rate
To investigate the impact of the transmission rate on the spread of COVID-19, we carry out a numerical simulation to show the contribution of transmission rate in fractional infection population density.
We set the transmission rate as , and . From Fig. 12, we can observe that infectiousness reaches a higher peak level as increases. This figure illustrates the great influence of transmission rate as shown in the sensitivity analysis. If we implemented effective contact tracing between infected and susceptible population, then the transmission rate is reduced and also the disease spread will be eliminated. The main public health measure which are implemented to reduce the transmission rate in the current pandemic are stay-at-home and quarantine or isolation of exposed and infectious infected individuals.
Fig. 12.
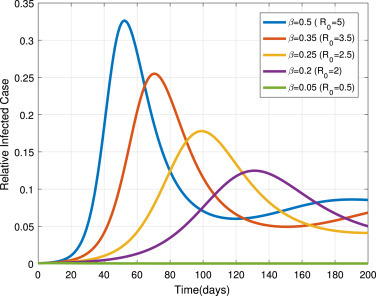
Impact of transmission rate on infected population in system (2). Colors represent different values of .
4.3. Impact of public health intervention
To study the recommended containment strategies of the pandemic, we conduct some numerical simulations whose aim is to show the contribution of public health interventions.
Here, we observe the isolation of exposed and infectious infected individuals within different rate:
Now, we set the exposed population isolation rate as , and 0.0. In Fig. 13, we can see that the infectiousness increases as decreases. It implies that effective isolation of exposed individuals by clinical identification before the symptom onset can mitigate the COVID-19 pandemic. Similarly, infectious infected isolation rate set as , and 0.0. In Fig. 14, we observe that the infectiousness density approaches the highest peak level as value decrease. It implies that the ineffective quarantine of symptomatic individuals can lead to the prevalence of the pandemic.
Fig. 13.
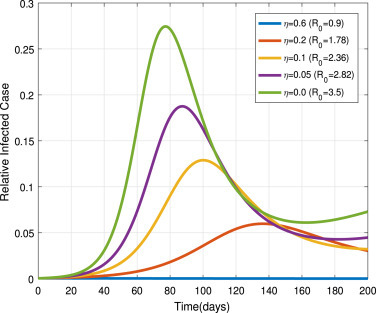
Impacts of on .
Fig. 14.
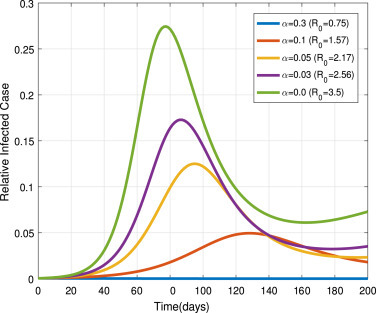
Impacts of on .
In the current critical time, public health experts and government officials announced that every individual must stay at home. Due to food security and ineffectiveness of stay-at-home people may not follow this recommendation. We observe the impact of stay-at-home efficiency and people abandoning stay-at-home in the following numerical results.
Fig. 15, shows that different stay home rates , which are chosen as , and 0.0. Its say that effective stay at home intervention measure can control the disease propagation. On the other hand, if we cannot implement this control measure, then people become susceptible at a rate of . To show its impact with , we chose different values as , and 0.0. We can be see in Fig. 16 the disease spread rises as values increases. It implies if we cannot stay-at-home for a recommended period, then pandemic prevalence occurs.
Fig. 15.
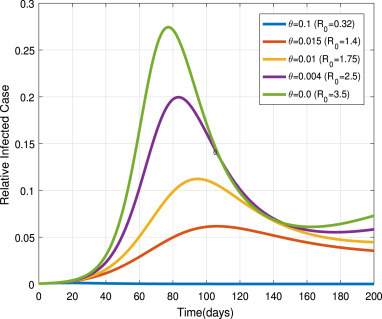
Impacts of on .
Fig. 16.
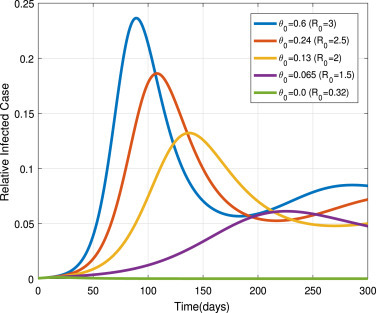
Impacts of on .
Conclusions
In this paper, a researcher investigated the dynamics of the COVID-19 spreading with a control measure. An Corona pandemic model with public health intervention was presented and analyzed theoretically as well as numerically. An essential epidemiological parameter value was computed by using the next-generation matrix approach. Furthermore, we have shown that the disease-free equilibrium globally asymptotically stable if and unstable otherwise. Given that the endemic equilibrium exists, its stability analysis gives that it is locally asymptotically stable when . The sensitivity analysis of identifies those parameters that have a positive and negative influence on the change of . Several graphs are presented to illustrate the dependence of on parameters.
Several numerical investigations were done for various scenarios to illustrate the model dynamics, showing convergence to the disease-free equilibrium when or to the endemic equilibrium when . The general dynamics of the model illustrated that the disease dies out when , while it persists in the community whenever . Moreover, the socio-economic crisis caused by this pandemic were minimized and eliminated when we implemented a relevant control measure. Numerical investigations of the effects of different parameter values of the model were also presented. Finally, robust public health intervention were shown to end the current pandemic and minimize the crisis caused by this outbreak.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- 1.van der Hoek L., Pyrc K., Jebbink M.F., Vermeulen-Oost W., Berkhout R.J., Wolthers K.C., Wertheim-van Dillen P.M., Kaandorp J., Spaargaren J., Berkhout B. Identification of a new human coronavirus. Nature Med. 2004;10(4):368–373. doi: 10.1038/nm1024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.The epidemiology and pathogenesis of coronavirus disease (COVID-19) outbreak. [DOI] [PMC free article] [PubMed]
- 3.Wu D, Wu T, Liu Q, Yang Z. The SARS-CoV-2 outbreak: what we know. [DOI] [PMC free article] [PubMed]
- 4.Organization W.H. 2020. Coronavirus disease (COVID-2019) situation reports, 73. Available on: https://www.WHO.Int/docs/default-source/coronaviruse/situationreports/20200221-sitrep-73-covid19. [Google Scholar]
- 5.HuiDS I.A.E., Madani T., Ntoumi F., Koch R., Dar O. The continuing 2019-nCoV epidemicthreatof novel coronaviruses to global health: the latest 2019 novel coronavirus outbreak in Wuhan, China. Int J Infect Dis. 2020;91:264–266. doi: 10.1016/j.ijid.2020.01.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.2020. Coronavirus disease (COVID-2019) situation reports, 85. Available on: https://www.WHO.Int/docs/default-source/coronaviruse/situationreports/20200221-sitrep-85-covid19. [Google Scholar]
- 7.Population biology of infectious diseases: Part I. Nature. 1979;280(5721):361–367. doi: 10.1038/280361a0. [DOI] [PubMed] [Google Scholar]
- 8.Brauer F., Castillo-Chavez C., Castillo-Chavez C. 2012. Mathematical Models in Population Biology and Epidemiology, vol. 2. [DOI] [Google Scholar]
- 9.Bertolaccini L., Spaggiari L. 2020. The hearth of mathematical and statistical modelling during the Coronavirus pandemic. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Diekmann O., Heesterbeek J.A.P. 2000. Mathematical Epidemiology of Infectious Diseases: Model Building, Analysis and Interpretation, vol. 5. [Google Scholar]
- 11.Hethcote H.W. The mathematics of infectious diseases. SIAM Rev. 2000;42(4):599–653. [Google Scholar]
- 12.Kermack W.O., McKendrick A.G. A contribution to the mathematical theory of epidemics. Proc R Soc Lond Ser A Math Phys Eng Sci. 1927;115(772):700–721. [Google Scholar]
- 13.Chen T.-M., Rui J., Wang Q.-P., Zhao Z.-Y., Cui J.-A., Yin L. A mathematical model for simulating the phase-based transmissibility of a novel coronavirus. Infect Dis Poverty. 2020;9(1):1–8. doi: 10.1186/s40249-020-00640-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Kucharski A.J., Russell T.W., Diamond C., Liu Y., Edmunds J., Funk S., Eggo R.M., Sun F., Jit M., Munday J.D. Early dynamics of transmission and control of COVID-19: a mathematical modelling study. Lancet Infect Dis. 2020 doi: 10.1016/S1473-3099(20)30144-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Prem K., Liu Y., Russell T.W., Kucharski A.J., Eggo R.M., Davies N., Flasche S., Clifford S., Pearson C.A., Munday J.D. The effect of control strategies to reduce social mixing on outcomes of the COVID-19 epidemic in wuhan, China: a modelling study. Lancet Infect Dis. 2020 doi: 10.1016/S2468-2667(20)30073-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Yang C., Wang J. A mathematical model for the novel coronavirus epidemic in Wuhan, China. Math Biosci Eng. 2020;17(3):2708–2724. doi: 10.3934/mbe.2020148. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Mathematical modeling and simulation study of SEIR disease and data fitting of Ebola epidemic spreading in West Africa. J Multidiscipl Eng Sci Technol. 2015;2(1):106–114. [Google Scholar]
- 18.Yorke J.A. Invariance for ordinary differential equations. Math Syst Theory. 1967;1(4):353–372. [Google Scholar]
- 19.Van den Driessche P., Watmough J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math Biosci. 2002;180(1–2):29–48. doi: 10.1016/s0025-5564(02)00108-6. [DOI] [PubMed] [Google Scholar]
- 20.DeJesus E.X., Kaufman C. Routh-Hurwitz criterion in the examination of eigenvalues of a system of nonlinear ordinary differential equations. Phys Rev A. 1987;35(12):5288. doi: 10.1103/physreva.35.5288. [DOI] [PubMed] [Google Scholar]


