Abstract
Accurate predictions of the droplet transport, evolution, and deposition in human airways are critical for the quantitative analysis of the health risks due to the exposure to the airborne pollutant or virus transmission. The droplet/particle-vapor interaction, i.e., the evaporation or condensation of the multi-component droplet/particle, is one of the key mechanisms that need to be precisely modeled. Using a validated computational model, the transport, evaporation, hygroscopic growth, and deposition of multi-component droplets were simulated in a simplified airway geometry. A mucus-tissue layer is explicitly modeled in the airway geometry to describe mucus evaporation and heat transfer. Pulmonary flow and aerosol dynamics patterns associated with different inhalation flow rates are visualized and compared. Investigated variables include temperature distributions, relative humidity (RH) distributions, deposition efficiencies, droplet/particle distributions, and droplet growth ratio distributions. Numerical results indicate that the droplet/particle-vapor interaction and the heat and mass transfer of the mucus-tissue layer must be considered in the computational lung aerosol dynamics study, since they can significantly influence the precise predictions of the aerosol transport and deposition. Furthermore, the modeling framework in this study is ready to be expanded to predict transport dynamics of cough/sneeze droplets starting from their generation and transmission in the indoor environment to the deposition in the human respiratory system.
Keywords: Droplet, Multi-component, Hygroscopicity, Deposition, Airway
Highlights
-
•
Investigated the transport and deposition of droplets in an airway.
-
•
Considered hygroscopic growth of multicomponent droplets/particles.
-
•
Modeled non-uniformed boundary temperature and mucus evaporation.
-
•
Simulations carried out for different activity strengths.
-
•
Discussed deposition efficiencies, final locations and sizes of the droplets and particles.
1. Introduction
The recent outbreak of coronavirus disease 2019 (COVID-19) raises public health concern internationally. It has been confirmed that SARS-CoV-2 can spread between humans via contacting droplets expelled from coughing or sneezing. Details on the transmission routes remain unknown, i.e., how SARS-CoV-2 can transmit within the embedded droplets/particles in the air and human respiratory systems? To answer the question, one of the key mechanisms that need to be addressed is the droplet/particle-vapor interaction.
The droplet/particle-vapor interaction, i.e., the evaporation and condensation, is critical for predicting the behavior of the droplet/particle in air. The water content of the atmospheric droplets is strongly dependent on the droplet composition and environmental relative humidity (RH) (Pilinis et al., 1989). The primary chemical components in the PM2.5 and PM10 contain sea salt, ammonium, sulfate, nitrate (Ho et al., 2003; X.; Wang et al., 2006). These components are hydrophilic and can absorb water vapor under high ambient relative humidity (RH).
For the indoor environment, such droplet/particle-vapor interaction has attracted attention when researchers attempted to model the droplets/particles transport dynamics generated from different sources. For example, Wang et al. (2019) recently simulated the evaporation of large droplets (20–80 μm) in a simplified 2D industrial building with different ambient temperature and RH conditions. Water droplets were employed to represent the industrial airborne pollutants in the form of droplets. Furthermore, Yang et al. (2019) modeled the evaporation of two types of droplets, i.e., hydrochloric and sulfuric droplets under the free-fall condition. The vapor pressure of the evaporable component on the droplet surface was modeled using a correlation generated based on experimental measurements. Similar models were also applied in the studies on the conventional cigarette smoke and electronic cigarette aerosol simulations (Y Feng et al., 2015; Longest & Xi, 2008).
The interaction between the bio-aerosol and water vapor also has been investigated. Li et al. (2018) modeled the evaporation of droplets composed of water and non-volatile solid with different cough conditions. Pure water droplets were used to investigate the effect of RH on the evaporation and dispersion of exhaled droplets (Ji et al., 2018). Using pure water droplet to represent exhaled droplets is a simplification, since experiments suggest that the composition of exhaled droplets should consist of salt, protein, and surfactant (Vejerano & Marr, 2018). Realistic composition is critical since it wills influence the evaporation dynamics of the droplets released from coughing, sneezing, and talking (Vejerano & Marr, 2018). Liu et al. (2017) considered the droplet hygroscopicity when simulating the evaporation and dispersion of the droplets emitted by coughs. Based on the Lagrangian method for the hygroscopic saline droplet (Z. Zhang, Kleinstreuer, & Kim, 2006), we developed and validated a multi-component droplet/particle-vapor interaction model (Chen et al., 2017). The difference between our predictions and the experimental results (W. Li et al., 1992) for the hygroscopic growth of NaCl particle is only ±0.2% RH (or ± 0.4 in growth ratio) (Chen et al., 2017).
To quantitatively measure the bio-aerosol transmission, accurate prediction for the deposition of inhaled droplets/particles is essential. Deposition of inhalable droplets/particles is commonly dominated by three mechanisms, i.e., inertial impaction (Kim & Fisher, 1999), sedimentation (Chen et al., 2018, Chen et al., 2018; Kleinstreuer et al., 2007), and diffusion (Zamankhan et al., 2006). Diffusion, i.e., Brownian motion, has a limited effect on micron droplets/particles (Clement Kleinstreuer, Zhang, & Li, 2008). The hygroscopic growth of the droplet/particle increases the diameter and mass of the droplet/particle. Therefore, it may further affect the droplet/particle deposition via these three deposition mechanisms.
The hygroscopic growth of the droplet/particle is determined by the water vapor concentration distribution in the airway. However, the water vapor concentration distribution is not only determined by RHs in the ambient air, but also influenced by the evaporation rate of the mucus layer that covers the airway. Wu et al. (2014) proposed a numerical method using two domains, i.e., a mucus-tissue layer and an airway lumen domain, to predict the temperature and RH distributions in the airway. We recently developed a similar method for predicting the deposition of hygroscopic droplets in a mouth-throat (MT) airway geometry with an inhalation flow rate equal to 15 L/min (Chen et al., 2018, Chen et al., 2018). The numerical predictions suggested that inhaled thermal airflow and mucus-layer interaction could significantly reduce hygroscopic growth, and thereby decrease the deposition efficiency (DE) of multi-component droplets up to 10% compared to the DE, using the constant 37 °C and 99.5% RH as the airway wall boundary conditions (Chen et al., 2017). Asgari et al. (2019) developed an experiment, which can maintain the airway surface temperature at 37 °C using 3D printed casing with a circulated water bath, for exposure studies of hygroscopic particulate matters. However, the system mentioned above still cannot represent the physiologically realistic non-uniform temperature distributions in airways (McFadden Jr et al., 1985). The inhalation flow rate affects the deposition of the hygroscopic droplet/particle. More specifically, higher inhalation flow rate increases the deposition of the hygroscopic droplets/particles due to inertial impaction. However, higher inhalation flow rate decreases the average RH-value in the airway when using a boundary condition with constant temperature and RH (Chen et al., 2017), which enhances the evaporation of the droplet. If the more realistic thermal boundary (Chen, Kleinstreuer, et al., 2018; Wu et al., 2014) and indoor air conditions (McFadden Jr et al., 1985) are considered, higher inhalation flow rate also has a stronger cooling effect on the mucus-tissue layer, which further affects the mucus evaporation. Therefore, the transport, hygroscopic growth, and deposition of multi-component droplets have not been investigated under different inhalation flow rate conditions, when employing the more realistic thermal boundary conditions.
To address the knowledge gap mentioned above, this study investigates the evaporation, hygroscopic growth, and transport of a representative multi-component hygroscopic droplet under complex airflow with the non-uniform temperature at the airway wall. The purpose of this work is to evaluate the central hypothesis, i.e., the physiologically realistic thermal boundary and inhalation flow rate conditions will significantly affect the deposition predictions of hygroscopic droplets in airways, and must be employed for all computational lung aerosol dynamics studies. The aerosol flow contains two phases, i.e., air as the continuous phase and droplets/particles as the discrete phase. Thus, the simulations are based on the Eulerian-Lagrangian method. In light of the hygroscopicity of the droplets, the droplets could evaporate in the environment with low relative humidity or absorb water vapor from the humid air. Clearly, the aerosol flow would have mass and heat transfer with the mucus layer and the airway tissue.
As the testbed to understand the fundamentals, a simplified mouth-throat (MT) airway geometry was employed in this study, and simulations were performed with validated droplet/particle transport and hygroscopic growth models at three inhalation flow rates (Q in), i.e., 15 L/min (rest condition), 30 L/min (light activity) and 60 L/min (moderate activity). Specifically, a multi-layer structure including the airway tissue and mucus layer was constructed to reproduce the heat transfer phenomenon occurred in the MT airway walls, i.e., the conduction in the airway tissue and mucus layer, latent heat loss due to mucus evaporation, and the convection of the airflow over the mucus layer. Considering the possible evaporation and hygroscopicity of the real aerosolized droplets, four components were considered, i.e., water, ethanol, sodium chloride (NaCl), and fluorescein. Water and ethanol are the most common evaporable solvents that existed in the environmental and pharmaceutical droplets/particles. NaCl stands for the sea salt and other soluble compositions. Fluorescein represents the non-evaporable and non-soluble composition, e.g., crustal matter. The validated transition shear stress transport (SST) model and discrete phase model (DPM) were employed for the prediction of the airflow and inhaled droplet/particle transport, respectively. Temperature and RH distributions in the MT airway, as well as the deposition of the hygroscopic multi-component droplets are visualized and analyzed.
2. Methodology
2.1. The simplified mouth-throat (MT) airway geometry
The simplified mouth-throat (MT) airway geometry (see Fig. 1 ) consists of two parts, i.e., an MT cavity and a mucus-tissue layer surrounding the cavity. The geometry of the MT cavity was proposed by Zhang et al. (2004). Y. Zhang, Kleinstreuer, and Kim (2006) concluded that the simplified MT models with outlet diameters of 7.5 and 8.5 mm were better in accordance to in vivo experimental data comparing to the models with other outlet diameters and the USP model. Therefore, the simplified MT cavity with a diameter of 8.5 mm was used as the fluid region in our study. Furthermore, the fluid region was covered by a 1.0 mm thick mucus-tissue layer.
Fig. 1.
Geometry and mesh of the simplified mouth-throat (MT) airway.
The mucus-tissue layer (the blue cells shown in Fig. 1) contains two sublayers, i.e., a mucus layer with a thickness of 10 μm and a tissue layer with a thickness of 990 μm. This setup ensures an accurate prediction of the temperature distribution in the mucus-tissue layer (Chen, Kleinstreuer, et al., 2018; Wu et al., 2014). The structured hexahedral mesh was generated for both the fluid region and the mucus-tissue layer. The mesh was refined in the fluid region and the mucus-tissue layer near the air-mucus interface. The mesh refinement ensured that the non-dimensional distance y + was smaller than 1.0 for the first layer of the fluid mesh cells. Mesh independence test was carried out following the same procedure that is documented in our previous study (Chen et al., 2017). The final mesh contained 2,287,197 cells for the fluid region, and 605,880 cells for the mucus-tissue region.
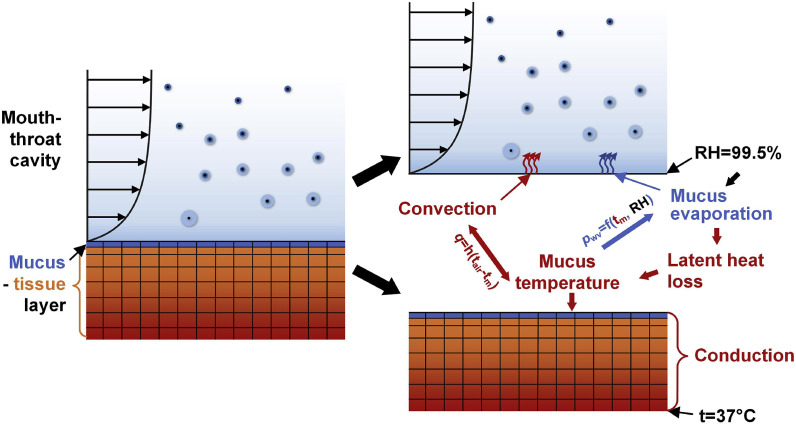
Fig. 2 visualizes the coupling mechanisms of the heat and mass transfer between air and mucus. Specifically, the airflow over the air-mucus interface affects the convective heat transfer, and the resultant water vapor flux evaporated from the mucus layer. Assuming RH = 99.5% at the air-mucus interface (Finlay, 2001), the latent heat loss due to evaporation contribute to the variations of mucus temperature.
Fig. 2.
Schematics for the coupling mechanisms of the heat and mass transfer at the air-mucus interface.
The temperature at the air-mucus interface was calculated by the iterations between the MT cavity and the mucus-tissue layer. If the temperature of a given mucus cell t m1 is known, the airflow simulation determines the heat flux due to convection and the mass flux of the water vapor, which determines the latent heat loss of the mucus layer. Note that the calculations for the airflow and the heat transfer in the mucus-tissue layer are separated. t m1 is used as the boundary surface temperature for the airflow calculation. In the mucus-tissue layer, the temperature of the same cell t m2 is obtained by solving the energy balance equation based on the conduction in the mucus-tissue layer, as well as the convection and latent heat loss due to the evaporation effect. The latter two are obtained from the calculation in the domain of the MT domain. The iteration continues until t m1 is equal to t m2.
2.2. Governing equations for the air-vapor flow
To predict the RH distribution in the airway, the transport both the dry air and water vapor were simulated. The transition SST model was employed to simulate the laminar-to-turbulent airflow (Chen et al., 2017; Chen, Kleinstreuer, et al., 2018) with flow separation in the pharynx (Heenan et al., 2003). Specifically, the governing equations are listed as follows (Menter, Langtry, Likki, et al., 2006; Menter, Langtry, & Völker, 2006):
| (1) |
| (2) |
| (3) |
| (4) |
Equations (1), (2), i.e., the k and ω equations, are modified based on the SST model (Menter, 1994) using the production term and destruction term of turbulence kinetic energy (TKE). and are determined by the intermittency (see Eq. (3)) and the transition momentum thickness in terms of the Reynolds number , (see Eq. (4)).
The scalar transport equation for both the dry air and water vapor is given by (Zhang & Kleinstreuer, 2003):
| (5) |
where and are the mass fraction and mass diffusion coefficient for species s. and are the turbulent viscosity and turbulent Schmidt number, respectively.
In order to predict the temperature of the air-vapor flow, which affects the evaporation of the droplet or hygroscopic growth of the droplet/particle, the energy equation of the air-vapor flow is given by (Yu Feng et al., 2016):
| (6) |
where H is the enthalpy of the mixture, and are the thermal conductivity and turbulent thermal conductivity, respectively.
2.3. Governing equations for the droplets and particles
A Lagrangian method was employed in this study to predict the transport, size change, and deposition of the droplets. All governing equations listed in this section were solved using in-house C codes, implemented as user-defined functions (UDFs). The droplets and particles are assumed to be spherical in our simulations. The primary deposition mechanisms are inertial impaction, sedimentation, and diffusion. The diffusion could be ignored due to the negligible Brownian motion effect on the micron-sized droplets/particles. Therefore, the main forces considered are the drag force and gravity. The Saffman's lift force is ignored due to limited droplet/particle rotation. The virtual mass force is ignored, considering the large droplet/particle-to-air density ratio. Accordingly, the droplet/particle trajectories are determined by the translation equation (Chen et al., 2012; Matida et al., 2004; Zhang et al., 2002(Kleinstreuer et al., 2008)), i.e.,
| (7) |
where is the drag coefficient determined by the droplet/particle Reynolds number, the , and are the mass, velocity, and diameter of the droplet/particle, respectively. The eddy-droplet/particle interaction, also known as the random walk model (Matida et al., 2004), the near-wall correction for the anisotropic eddy in the regions with y + <80 (Y. Wang & James, 1999), and the velocity correlation for the cells in the bottom layer are also considered.
Evaporation and hygroscopic growth of the droplet/particle are determined by the mass and energy balance equations of the evaporable/condensable vapor at the air-droplet/particle interface (Chen et al., 2017; Y; Feng et al., 2015; Longest & Kleinstreuer, 2005), which can be given by:
| (8) |
Where A is the surface areas of the droplet/particle, is the surface averaged mass flux of the evaporable/condensable component s of the droplet/particle. is determined by (Chen et al., 2017; Chen, Kleinstreuer, et al., 2018; Longest & Kleinstreuer, 2005):
| (9) |
where is the mass fraction of component s on the droplet/particle surface, is the mass fraction of component s in the ambient air, d d is the diameter of the droplet/particle, Sh is the Sherwood number, is the mass diffusivity of component s. Therefore, the mass flux of the evaporable/condensable component changes the mass and volume of the droplet/particle. Thus, the density of the droplet/particle may change during the simulation.
In addition, the energy balance of the droplet/particle is given by (Chen et al., 2017; Chen, Kleinstreuer, et al., 2018; Longest & Kleinstreuer, 2005):
| (10) |
where Nu is the Nusselt number, is the latent heat of species s, is the thermal conductivity of the fluid, is the average mass flux of species s, and are the specific heat and temperature of the droplet/particle, respectively.
2.4. Governing equations for the mucus-tissue layer
Based on the fact that the velocity of the mucus transport is lower than that of the inhaled air-droplet mixture by several orders of magnitude, the mucus movement over the tissue layer is neglected (Foster et al., 1982). The energy change of the tissue layer is mainly influenced by heat conduction. Accordingly, the energy balance equation of the mucus-tissue layer can be given by (Chen, Kleinstreuer, et al., 2018):
| (11) |
where h, and are the enthalpy, thermal conductivity and temperature of the mucus-tissue layer, respectively. is the source term representing the convective heat transfer and latent heat loss due to the evaporation, which only exists in the mucus layer. Airway tissue and mucus consist of water primarily. Thus, the heat transfer related properties of mucus-tissue layer are assumed as same as water (Chen, Kleinstreuer, et al., 2018; Wu et al., 2014).
Details for the governing equations are included in the Supporting Information.
2.5. Model validations
The numerical models affecting particle deposition have been validated in our previous study (Chen et al., 2017). The largest deposition efficiency discrepancy between our predictions and experimental results (Yu Zhang, Chia, & Finlay, 2006) in the simplified MT airway is less than 12% with Q in from 30 to 90 L/min. Furthermore, injecting 10, 000 particles could ensure that the deposition efficiency is independent of the particle number.
The droplet/particle-vapor interaction model was also validated (Chen et al., 2017). With constant RHs, the hygroscopic growths of NaCl particles were compared with benchmark experimental data (W. Li et al., 1992). The RH error for the droplet diameter at equilibrium status was approximately 0.2% (or ± 0.4 in growth ratio). In addition, the hygroscopic growths of glycerol droplets with different initial diameters were simulated with transient increasing RH conditions. Compared with most of the experimental data points of droplet diameters, the discrepancies between the numerical simulation and the experiments are less than 2% in RH. Very recently, Rajaraman et al. (2020) duplicated this model, and used the properties and conditions we proposed to validate the model. Similar model accuracy was achieved.
Heat transfer between the mucus-tissue layer and the airflow was examined in our recent study (Chen, Kleinstreuer, et al., 2018). The latent heat transfer occupied 84.7% of the total heat transfer at the air-mucus interface. This is similar to the percentage suggested by Tse et al. (Tsu et al., 1988).
2.6. Numerical setup
In light of the dilute suspension of the pollutant inhaled into the airway, the one-way coupling method was applied, which neglected the influence of droplet existence on the airflow field. Typical indoor temperature and RH were 26.7 °C and 34% (McFadden Jr et al., 1985) for the inlet of the simplified MT airway geometry. The temperature of the tissue boundary is assumed to be 37 °C. Steady simulations for the fluid phase including the boundary heat transfer in the mucus-tissue layer were performed till equilibrium thermal states were reached. Then simulations with various initial droplet diameters ranging from 2 to 20 μm were conducted to obtain the correlation between the droplet deposition efficiency and the Stokes number with three Q in, i.e., 15 L/min, 30 L/min and 60 L/min. Transient breathing brings the heat and water vapor from the deeper lung to the upper airway, and therefore, the steady simulation may underestimate the temperature and water vapor concentration in the MT airway.
Usually, the droplets released from coughing, sneezing, and talking contains water, sodium and potassium cations, chloride anion, and other organic substances (Effros et al., 2002). Therefore, the components in the droplet could be categorized into three types: 1) evaporable components, such as water and ethanol; 2) non-evaporable but soluble components, such as sodium chloride and potassium chloride; and 3) non-evaporable and insoluble components. Similar assumptions were also adopted by Liu et al. (2017) and X. Li et al. (2018). The droplets containing water, ethanol, sodium chloride, and fluorescein were modeled as an example to investigate the evaporation, hygroscopic growth, and transport behaviors of the multi-component droplets. The mass ratios of the four components were fixed as water: ethanol: NaCl: fluorescein = 400:100:100:2.5. Tang et al. (1977) indicated that the RH for the NaCl particle to deliquesce was approximately 76% at 25 °C. This suggests that the given multi-component droplet would evaporate in the T = 26.7 °C, RH = 34% environment. If the droplet evaporates completely, the diameter of the solid particle containing NaCl and fluorescein only would be 44.3% of its initial droplet. Parameter values for setting up the simulations are provided in the Supporting Information.
3. Results and discussion
The airflow velocity distributions in the simplified MT airway has been discussed in previous studies. Yu Zhang, Kleinstreuer, and Kim (2006) simulated the velocity distributions in the simplified MT airway for the flow rates of 30 L/min and 90 L/min. The velocity distributions were also provided for different flow rate conditions from 15 L/min to 90 L/min with a constant airway wall temperature at 37 °C (Chen et al., 2017). We compared the velocity distributions under different thermal boundary conditions, including 1) airway wall had a constant temperature at 37 °C, 2) ignoring the latent heat due to water vapor phase change, but including convective heat transfer, and 3) the more realistic thermal boundary condition, which is the same condition we used in this study. The simulated velocity distributions were highly similar due to the negligible effects of the temperature and RH on the fluid density (Chen et al., 2017). Therefore, the velocity field results and discussion were not provided in this study to avoid duplicated analysis.
Distributions of the temperature and RH, as well as the deposition characteristics of the multi-component hygroscopic droplets are discussed in the following sections.
3.1. Temperature distributions
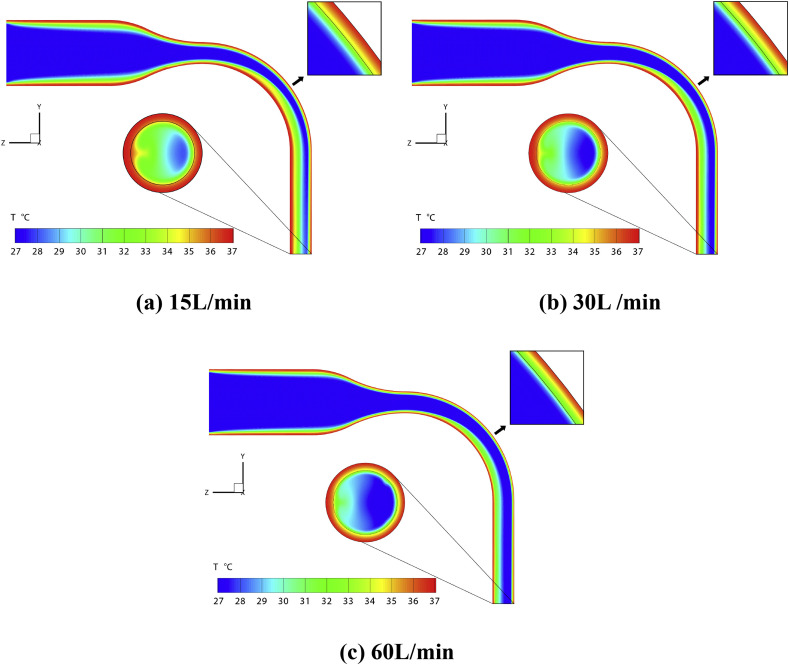
Fig. 3 illustrates the temperature distributions at the mid-plane and the trachea outlet of the simplified MT airway under the 15 L/min, 30L/min, and 60 L/min flow rate conditions. Besides, the area directly impacted by the flow near the oropharynx was enlarged to visualize the temperature gradient near the air-mucus interface (see the thin black line in the enlarged window) to the far end of the tissue layer.
Fig. 3.
Temperature distributions in the simplified MT airway with different inhalation flow rate conditions.
It can be observed that the temperature distributions at the mid-plane are similar among the cases with different Q in. The relatively cold air from the inlet travels through the MT airway; meanwhile, temperature gradient forms near the warm airway boundary. The skewed velocity profile creates two symmetric vortices in the curved pipe region (Zhang & Kleinstreuer, 2002), i.e., the oropharynx. The vortices also entrain the warm air near the boundary towards the airway center. Thus, the temperature in the throat increases faster than that in the mouth cavity.
As shown in Fig. 3 (a), more than half of the area of the fluid region at the outlet is green, indicating T > 31 °C. This area rapidly decreases to less than semicircle in Fig. 3 (b) when the flow rate increases to 30 L/min. If the flow rate continues to increase, low-temperature air (T < 28 °C) covers most areas of the outlet.
The stronger convection induced cooling effect of the higher flow rate is also noticeable in the oropharynx region. Specifically, the temperature of the air-mucus interface is approximately 34 °C for 15 L/min case. In contrast, it decreases to lower than 31 °C when Q in increases to 60 L/min.
3.2. RH distributions
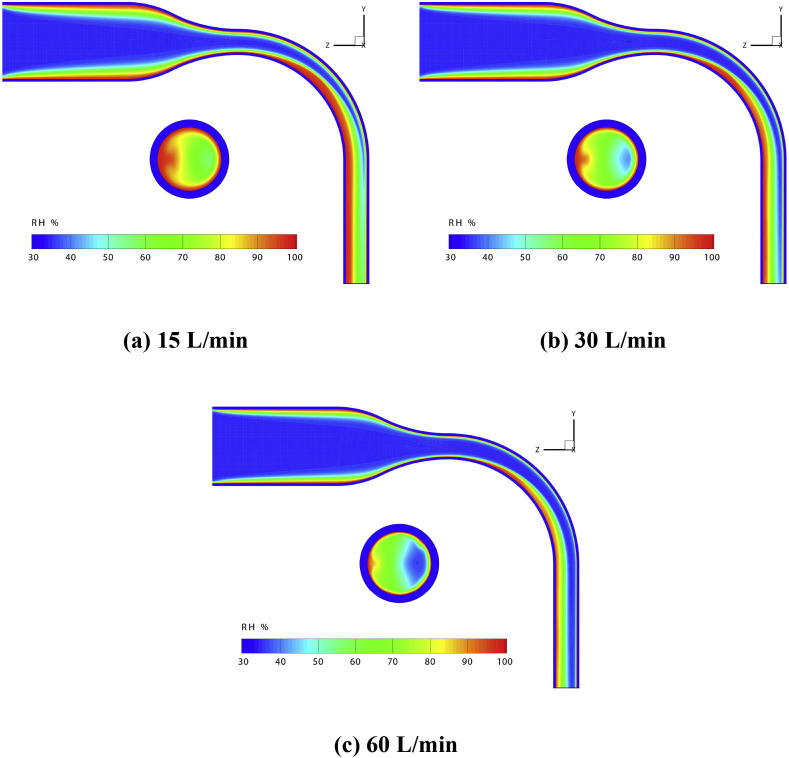
Fig. 4 shows the RH distributions in the simplified MT airway, including the contours at the mid-plane and the outlet. According to the previous studies (Cruz & Pandis, 2000; Robinson & Stokes, 1970; Tang et al., 1977), the threshold RH for NaCl particles to absorb water vapor is approximately 76%. Therefore, the area of the high RH regions in the airway determines the possibility of whether the droplet/particle could grow bigger by absorbing water vapor from the air. The region with high RH (>80%) is relatively large in Fig. 4 (a). Such a high RH region (RH > 80%) shrinks sharply in size with the increase of Q in. As shown in Fig. 4 (b), more than 1/3 area at the outlet has a localized RH higher than 80%,. However, its size reduces when the flow rate increases to 30 L/min. Furthermore, the region with RH > 80% almost disappears and shrinks into a thin layer near the air-mucus interface, when the flow rate continues to increase to 60 L/min (see Fig. 4 (c)). This suggests that hygroscopic growth of the droplet/particle can barely occur under high Q in condition.
Fig. 4.
RH distributions in the simplified MT airway for different flow rate conditions.
3.3. Deposition efficiencies (DEs)
Fig. 5 presents the relationship between the deposition efficiency (DE) of hygroscopic multi-component droplets and the Stokes number (Stk) under different Q in and thermal boundary conditions. DE is defined as the ratio of the number of droplets deposited on the airway surface to the total droplets number entered the inlet. The Stokes number, a dimensionless parameter indicating the capability of the discrete phase element to follow the surrounding flow, is defined as (Chen, Kleinstreuer, et al., 2018):
| (12) |
where is the initial droplet density, is the initial droplet diameter, is the average air velocity at the inlet and is the outlet diameter. Cheng et al. (2014) concluded that using the minimum diameter of the cross-section in the mouth-throat replica for the Stk calculation could better correlate the DE curve. Therefore, the outlet diameter of the airway was used for the characteristic length here. Solid lines with different markers shown in Fig. 5 are the predictions with the more realistic thermal boundary, while dash lines with hollowed markers are simulation results with a constant mucus temperature 37 °C, which has been widely applied for hygroscopic droplet/particle simulations (Y Feng et al., 2015; Golshahi et al., 2013; Longest & Kleinstreuer, 2005). The DEs are also correlated with the initial droplet diameter shown in Fig. S1 in the Supporting Information.
Fig. 5.
Deposition efficiencies of the hygroscopic multi-component droplets in the simplified MT airway under different flow rate and thermal boundary conditions.
In general, using the more realistic thermal boundary condition, predicted DEs are lower than those with the constant 37 °C boundary condition. However, the overestimation of DE using the constant temperature boundary condition decreases with the increase of Q in. Simulated results with the constant 37 °C boundary condition overestimate the DE more than 10% for 0.018 < Stk < 0.043 at Q in = 15 L/min. When Q in increases to 30 L/min, the difference in DEs between the two different boundary conditions remains approximately 6% for 0.018 < Stk < 0.034. When Q in further increases to 60 L/min, the difference in DEs remains 5% for 0.012 < Stk < 0.025.
It is well known that the deposition of the micron particle in the airway may occur via impaction, including secondary airflow convecting particles to the airway walls, diffusion, and/or sedimentation, i.e., gravitational effect (C Kleinstreuer, Zhang, & Li, 2008). Deposition of particles larger than 1.0 μm in the extrathoracic and upper bronchial airways through which the inhaled air passes at high speed is governed by impaction (Heyder, 2004). It is interesting to note that the DE difference between the two different boundary conditions gradually disappears when the Stk is larger than 0.04 for the 60 L/min flow rate condition. Especially, the hygroscopic growths of the droplets and particles were limited (see Fig. 7(a)) in the low RH condition (see Fig. 4 (c)). Therefore, the contribution of the hygroscopic growth to the deposition of the droplets would be limited. This observation indicates that the inertial impaction becomes more dominant on the droplet deposition when Stk increases.
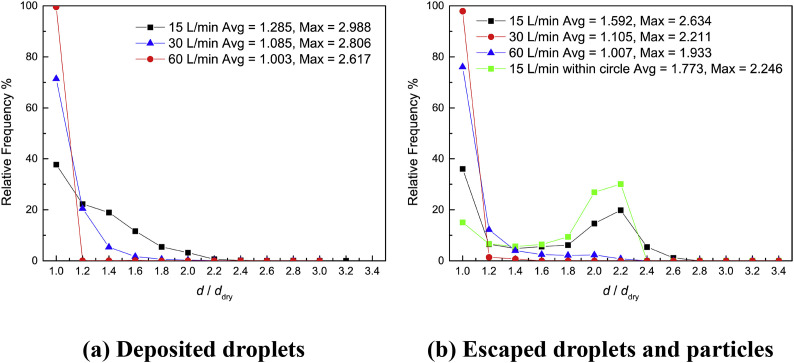
Fig. 7.
Growth ratio distributions of hygroscopic multi-component droplets and particles with the Stk = 0.036.
The intensity of indoor human activity is commonly low. The inhalation flow rate for possible medical applications, e.g., inhaler, nebulizer, is even lower. Therefore, the focus on the inhalation flow rate should be smaller than 30 L/min, representing the light activity. Neglecting the droplet hygroscopicity could underestimate the DE up to 20% for NaCl-water droplet at 37 °C (Chen et al., 2019). Besides, a more realistic airway boundary could increase the intensity of secondary flow that enhances the heat and water vapor mass transfer around the mucus-tissue layer. Therefore, it can be projected that the differences in DE predictions may also increase accordingly. Thus, in order to accurately predict the fate of the inhaled hygroscopic droplet/particle, the droplet/particle-vapor interaction and the realistic thermal boundary should be considered when estimating the health risks of the indoor airborne pollutant or the effective dose of the inhaled therapeutic aerosols.
3.4. Final droplet and particle distributions
Fig. 6 illustrates diameters and locations for the deposited droplets and escaped droplets and particles with the same initial Stk = 0.036, which means initial droplet diameters should be set as 16 μm, 11.31 μm, and 8 μm for the 15 L/min, 30 L/min, and 60 L/min conditions, respectively. The droplets would evaporate rapidly into droplet nuclei containing only NaCl and fluorescein after injecting into the airway due to low RH in the mainstream, which shrink to 44.3% of their original diameters. Sizes of the droplets and particles shown in Fig. 6 are proportionally enlarged, and a size reference is plotted on the bottom left for each figure.
Fig. 6.
Final diameters and locations of the multi-component hygroscopic droplets and particles with Stk = 0.036.
In light of the same initial Stk, the deposition patterns under three Q in conditions are similar. Besides the direct impaction on the curved pipe (oropharynx region) towards the negatie z direction, many droplets were entrained by the secondary flow and deposited on the lateral side of the tube towards the ± x directions. The secondary flow also has a substantial effect on the spatial distribution of the escaped droplets and particles. The droplets and particles escaped from the outlet surface moved circumferentially along the boundary from the –z end to the +z end, and then entrained into the tube center by the vortices. A red circle with a diameter of 2.0 mm is plotted on Fig. 6 (a). The hygroscopic growths of the droplets and particles within the circle are analyzed in Section 3.5. The majority of the droplets and particles escaped the outlet from the region close to the –z side due to the centrifugal force when traveling through the bent pipe.
The increase in the flow rate decreases the size of the regions with RH higher than the hygroscopic growth threshold for NaCl, i.e., approximately 76% (see Fig. 4). Thus, it has a significant effect on the diameters of the deposited droplets and escaped droplets and particles. The hygroscopic growth of the deposited droplets under 30 L/min condition shown in Fig. 6 (b) is weaker than that under 15 L/min condition (see Fig. 6 (a)). When the flow rate increases to 60 L/min, only a few droplets have noticeable growth in diameter. Such observations are different from our previous results when simulating the hygroscopic droplet/particle deposition with a constant 37 °C boundary condition (Chen et al., 2017). In that case (Chen et al., 2017), a large number of droplets are with noticeable hygroscopic growth with Q in = 60 L/min. The difference demonstrates the importance of using realistic thermal boundary conditions for the predictions for the hygroscopic droplet/particle deposition in the human respiratory systems.
3.5. Growth ratio distributions
Growth ratio distributions of the deposited droplets and escaped droplets and particles with the Stk = 0.036 are shown in Fig. 7. The growth ratio is defined as the ratio of the final diameter of droplet/particle to the diameter of its dry components, containing only NaCl and fluorescein. The average diameter of the deposited or escaped hygroscopic droplets/particles decreases with the increase of Q in. This is in accordance with the RH distributions discussed above. Higher Q in decreases the size of the region with RH > 80%, where hygroscopic droplet/particle can absorb water and grow larger. Notably, there is only a thin layer of air above the mucus layer, having an RH value higher than 80% at the 60 L/min condition. Thus, the droplets/particles can barely absorb water before deposition when penetrating this thin layer of high RH air. Besides, the lower flow rate also leads to a longer time for droplet/particle-vapor interaction. Therefore, the simulation has more large droplets at Q in = 15 L/min.
Also, it can be found that the average diameter of the deposited droplets is smaller than that of the escaped ones under the same condition. This observation is related to the droplet/particle trajectory in the airway. The airway mucus gradually humidifies the inhaled air, and result in a higher average RH at the outlet. Due to a similar mechanism, the maximum diameter for the deposited droplets is larger than that of escaped ones. There is an interesting increase in the number of droplets having a growth ratio approximately equal to 2.2 in Fig. 7 (b) under 15 L/min condition. This is related to the droplets and particles entrained into the tube center at the outlet (see the red circle in Fig. 6 (a) and green squares in Fig. 7 (b)). The growth ratio distribution of the droplets and particles within the circle indicates that these droplets are relatively large. 57% of these droplets and particles are within the growth ratio range from 1.9 to 2.3. Their average growth ratio value is 1.773, which is also higher than that of the droplets and particles at the whole outlet. Besides, the droplets and particles can only absorb water vapor in the high RH (>80%) region. Therefore, these large droplets are drawn into the tube center by the vortices from the airway boundary, considering their spatial distribution (see Fig. 6 (a)).
4. Summary
This study investigates the evaporation, hygroscopic growth, transport, and deposition of multi-component droplets in a simplified MT airway geometry with different inhalation flow rates (15, 30, and 60 L/min). Validated droplet/particle transport model, droplet/particle-vapor interaction model, and boundary heat transfer model were implemented in this study to accurately describe the laminar-to-turbulence pulmonary multiphase flow. The multi-component droplet contained two evaporable components, i.e., water and ethanol, one soluble component, i.e., sodium chloride, and one insoluble component, i.e., fluorescein. A mucus-tissue layer was created to simulate physiologically realistic heat transfer phenomena near the airway boundary, i.e., heat conduction in the airway tissue and mucus layer, the latent heat loss of mucus evaporation, and heat convection induced by the airflow over the mucus layer. Temperature distributions, RH distributions, droplet deposition efficiencies, deposition patterns, and droplet/particle diameter changes are visualized and discussed. Major conclusions are as follows:
-
(1)
High inhalation flow rate can substantially decrease the mucus temperature with noticeable temperature gradients in the mucus-tissue layer.
-
(2)
High inhalation flow rate can decrease the RH in the airway, which limits the hygroscopic droplet growth. No obvious hygroscopic growth of the NaCl nuclei was observed at the flow rate of 60 L/min.
-
(3)
Considering the fixed initial mass ratios of the four components (water: ethanol: NaCl: fluorescein = 400:100:100:2.5) in the droplets, ignoring the heat and water vapor mass transfer in the mucus-tissue layer can introduce approximately a 5% difference in deposition efficiency predictions for Stk < 0.04 in the simplified MT airway. More realistic airway geometry or lower inhalation flow rate would increase this difference. Therefore, it is necessary to model the mucus-tissue layer to obtain more realistic droplet deposition patterns in airways.
Numerical models employed in this study, especially the droplet/particle-vapor interaction model and the boundary heat transfer model, may help to predict better the deposition or the effective dose of inhaled aerosols, e.g., airborne pollutant, drug droplets and particles emitted from nebulizers and dry powder inhalers. These models are ready to be extended to investigate the transmission of airborne viruses. For example, it is confirmed that SARS-CoV-2 can spread via airborne droplet transmissions from human to human. With a proper model describing the change in virus concentration carried by airborne droplets/particles, quantitative virus transmission could be determined. For given number and initial size distributions of droplets generated from coughing or sneezing, evaporation, and transport of these droplets and droplet nuclei, could be easily predicted using our models for indoor environment. For the individual who is exposed to the airborne virus-laden droplets, the number of viruses transmitted to his/her pulmonary airway could also be determined by simulating the hygroscopic growth, transport and deposition of the virus-laden droplets using the same models.
5. Limitations of the study
The present numerical study is subjected to the following simplifications and assumptions:
-
(1)
A small region of the airway system, i.e., the mouth-to throat airway, is selected and simplified;
-
(2)
The mucus-tissue layer is assumed to have a uniform thickness, and heat transfer related properties are assumed to be the same as water; and
-
(3)
The initial droplet components only include water, ethanol, NaCl and fluorescein.
In light of the limitations of this study, future work will:
-
(1)
Use larger and more realistic airway geometry to model the airflow, heat transfer and water vapor mass transfer in the airway;
-
(2)
Consider actual drug particle/droplet components and their hygroscopicity to evaluate the deposition efficiency of the drug particle/droplet in lung; and
-
(3)
Perform transient simulation to include the breathing waveform, and investigate the effect of the aerosol release time on the deposition efficiencies of the hygroscopic droplets/particles.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgements
The authors gratefully acknowledge the financial support of the National Natural Science Foundation of China (grant No. 51976091 and 51606041) and the fund for the Program of Key Technology Research and Equipment Development for Green Buildings (grant No. S11330B41905).
Footnotes
Supplementary data to this article can be found online at https://doi.org/10.1016/j.jaerosci.2020.105626.
Nomenclature
- A
surface area of the droplet/particle
specific heat capacity of the fluid
specific heat capacity of the drop/particle
drag force coefficient for droplet/particle
cross-diffusion term in the transport equation of specific dissipation rate
- dd
droplet/particle diameter
initial droplet diameter
diameter of the airway outlet
mass diffusion coefficient for species s
modified term of destruction of turbulence kinetic energy
dissipation of ω
- ,
transition source and destruction source terms
gravitational acceleration, i = x, y, z
- h
enthalpy of the mucus-tissue layer
- H
enthalpy of the fluid
average mass flux of species s
- k
turbulence kinetic energy
- kc
thermal conductivity of the fluid
thermal conductivity of the mucus-tissue layer
- ktc
turbulent thermal conductivity
latent heat of evaporable component s
- md
mass of the droplet/particle
average mass flux of evaporable component s on the droplet/particle surface
mass flux of evaporable component s
- Nu
Nusselt number of the droplet/particle
production of turbulence kinetic energy
modified term of with intermittency
- ,
transition source and destruction source terms
source term for the transition momentum thickness Reynolds numbers
transport scalar for momentum thickness Reynolds number
- RH
relative humidity
source term to calculate heat transfer in the mucus layer
turbulent Schmidt number
- Sh
Sherwood number of the droplet
- Stk
Stokes number
- T
fluid temperature
droplet/particle temperature
temperature of the mucus-tissue layer
- t
time
- u
fluid velocity
velocity of the droplet/particle, i = x, y, z
instantaneous velocity of the fluid, i = x, y, z
average air velocity at the inlet
mass fraction of the component s
mass fraction of the component s on the interface of the droplet/particle
Greek
coefficient for the production term of ω
intermittency
dynamic viscosity of the fluid
turbulent viscosity
turbulent eddy viscosity
- ρ
fluid density
turbulent Prandtl number for k
turbulent Prandtl number for ω
constant for the intermittency equation
constant for the equation
- ω
specific dissipation rate
Appendix A. Supplementary data
The following is the Supplementary data to this article:
References
- Chen X., Feng Y., Zhong W., Kleinstreuer C. Numerical investigation of the interaction, transport and deposition of multicomponent droplets in a simple mouth-throat model. Journal of Aerosol Science. 2017;105:108–127. [Google Scholar]
- Chen X., Feng Y., Zhong W., Sun B., Tao F. Numerical investigation of particle deposition in a triple bifurcation airway due to gravitational sedimentation and inertial impaction. Powder Technology. 2018;323:284–293. [Google Scholar]
- Chen X., Kleinstreuer C., Zhong W., Feng Y., Zhou X. Effects of thermal airflow and mucus-layer interaction on hygroscopic droplet deposition in a simple mouth–throat model. Aerosol Science & Technology. 2018;52:900–912. [Google Scholar]
- Chen X., Ma R., Zhong W., Sun B., Zhou X. Numerical study of the effects of temperature and humidity on the transport and deposition of hygroscopic aerosols in a G3-G6 airway. International Journal of Heat and Mass Transfer. 2019;138:545–552. [Google Scholar]
- Chen X., Zhong W., Sun B., Jin B., Zhou X. Study on gas/solid flow in an obstructed pulmonary airway with transient flow based on CFD–DPM approach. Powder Technology. 2012;217:252–260. [Google Scholar]
- Cruz C.N., Pandis S.N. Deliquescence and hygroscopic growth of mixed inorganic-organic atmospheric aerosol. Environmental Science & Technology. 2000;34:4313–4319. [Google Scholar]
- Effros R.M., Hoagland K.W., Bosbous M., Castillo D., Foss B., Dunning M., Gare M., Lin W., Sun F. Dilution of respiratory solutes in exhaled condensates. American Journal of Respiratory and Critical Care Medicine. 2002;165:663–669. doi: 10.1164/ajrccm.165.5.2101018. [DOI] [PubMed] [Google Scholar]
- Feng Y., Kleinstreuer C., Castro N., Rostami A. Computational transport, phase change and deposition analysis of inhaled multicomponent droplet–vapor mixtures in an idealized human upper lung model. Journal of Aerosol Science. 2016;96:96–123. [Google Scholar]
- Feng Y., Kleinstreuer C., Rostami A. Evaporation and condensation of multicomponent electronic cigarette droplets and conventional cigarette smoke particles in an idealized G3–G6 triple bifurcating unit. Journal of Aerosol Science. 2015;80:58–74. [Google Scholar]
- Finlay W.H. Academic Press; New York, NY, USA: 2001. The mechanics of inhaled pharmaceutical aerosols: An introduction. [Google Scholar]
- Foster W., Langenback E., Bergofsky E. Lung mucociliary function in man: Interdependence of bronchial and tracheal mucus transport velocities with lung clearance in bronchial asthma and healthy subjects. Annals of Occupational Hygiene. 1982;26:227–244. [PubMed] [Google Scholar]
- Golshahi L., Tian G., Azimi M., Son Y.-J., Walenga R., Longest P.W., Hindle M. The use of condensational growth methods for efficient drug delivery to the lungs during noninvasive ventilation high flow therapy. Pharmaceutical Research. 2013;30:2917–2930. doi: 10.1007/s11095-013-1123-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heenan A., Matida E., Pollard A., Finlay W. Experimental measurements and computational modeling of the flow field in an idealized human oropharynx. Experiments in Fluids. 2003;35:70–84. [Google Scholar]
- Heyder J. Deposition of inhaled particles in the human respiratory tract and consequences for regional targeting in respiratory drug delivery. Proceedings of the American Thoracic Society. 2004;1:315–320. doi: 10.1513/pats.200409-046TA. [DOI] [PubMed] [Google Scholar]
- Ho K., Lee S., Chan C.K., Jimmy C.Y., Chow J.C., Yao X. Characterization of chemical species in PM2. 5 and PM10 aerosols in Hong Kong. Atmospheric Environment. 2003;37:31–39. [Google Scholar]
- Ji Y., Qian H., Ye J., Zheng X. The impact of ambient humidity on the evaporation and dispersion of exhaled breathing droplets: A numerical investigation. Journal of Aerosol Science. 2018;115:164–172. [Google Scholar]
- Kim C.S., Fisher D.M. Deposition characteristics of aerosol particles in sequentially bifurcating airway models. Aerosol Science & Technology. 1999;31:198–220. [Google Scholar]
- Kleinstreuer C., Zhang Z., Donohue J. Targeted drug-aerosol delivery in the human respiratory system. Annual Review of Biomedical Engineering. 2008;10:195–220. doi: 10.1146/annurev.bioeng.10.061807.160544. [DOI] [PubMed] [Google Scholar]
- Kleinstreuer C., Zhang Z., Kim C.S. Combined inertial and gravitational deposition of microparticles in small model airways of a human respiratory system. Journal of Aerosol Science. 2007;38:1047–1061. [Google Scholar]
- Kleinstreuer C., Zhang Z., Li Z. Modeling airflow and particle transport/deposition in pulmonary airways. Respiratory Physiology & Neurobiology. 2008;163:128–138. doi: 10.1016/j.resp.2008.07.002. [DOI] [PubMed] [Google Scholar]
- Li W., Montassier N., Hopke P. A system to measure the hygroscopicity of aerosol particles. Aerosol Science & Technology. 1992;17:25–35. [Google Scholar]
- Li X., Shang Y., Yan Y., Yang L., Tu J. Modelling of evaporation of cough droplets in inhomogeneous humidity fields using the multi-component Eulerian-Lagrangian approach. Building and Environment. 2018;128:68–76. doi: 10.1016/j.buildenv.2017.11.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu L., Wei J., Li Y., Ooi A. Evaporation and dispersion of respiratory droplets from coughing. Indoor Air. 2017;27:179–190. doi: 10.1111/ina.12297. [DOI] [PubMed] [Google Scholar]
- Longest P.W., Kleinstreuer C. Computational models for simulating multicomponent aerosol evaporation in the upper respiratory airways. Aerosol Science & Technology. 2005;39:124–138. [Google Scholar]
- Longest P.W., Xi J. Condensational growth may contribute to the enhanced deposition of cigarette smoke particles in the upper respiratory tract. Aerosol Science & Technology. 2008;42:579–602. [Google Scholar]
- Matida E., Finlay W., Lange C., Grgic B. Improved numerical simulation of aerosol deposition in an idealized mouth–throat. Journal of Aerosol Science. 2004;35:1–19. [Google Scholar]
- McFadden E., Jr., Pichurko B., Bowman H.F., Ingenito E., Burns S., Dowling N., Solway J. Thermal mapping of the airways in humans. Journal of Applied Physiology. 1985;58:564–570. doi: 10.1152/jappl.1985.58.2.564. [DOI] [PubMed] [Google Scholar]
- Menter F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA Journal. 1994;32:1598–1605. [Google Scholar]
- Menter F.R., Langtry R., Likki S., Suzen Y., Huang P., Völker S. A correlation-based transition model using local variables—Part I: Model formulation. Journal of Turbomachinery. 2006;128:413–422. [Google Scholar]
- Menter F.R., Langtry R., Völker S. Transition modelling for general purpose CFD codes. Flow, Turbulence and Combustion. 2006;77:277–303. [Google Scholar]
- Pilinis C., Seinfeld J.H., Grosjean D. Water content of atmospheric aerosols. Atmospheric Environment. 1989;23:1601–1606. [Google Scholar]
- Rajaraman P.K., Choi J., Hoffman E.A., O'Shaughnessy P.T., Choi S., Delvadia R., Babiskin A., Walenga R., Lin C.-L. Transport and deposition of hygroscopic particles in asthmatic subjects with and without airway narrowing. Journal of Aerosol Science. 2020:105581. doi: 10.1016/j.jaerosci.2020.105581. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robinson R.A., Stokes R.H. Butterworths; London: 1970. Electrolyte solutions. [Google Scholar]
- Tang I., Munkelwitz H., Davis J. Aerosol growth studies—II. Preparation and growth measurements of monodisperse salt aerosols. Journal of Aerosol Science. 1977;8:149–159. [Google Scholar]
- Tsu M.E., Babb A.L., Ralph D.D., Hlastala M.P. Dynamics of heat, water, and soluble gas exchange in the human airways: 1. A model study. Annals of Biomedical Engineering. 1988;16:547–571. doi: 10.1007/BF02368015. [DOI] [PubMed] [Google Scholar]
- Vejerano E.P., Marr L.C. Physico-chemical characteristics of evaporating respiratory fluid droplets. Journal of The Royal Society Interface. 2018;15:20170939. doi: 10.1098/rsif.2017.0939. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang X., Bi X., Sheng G., Fu J. Chemical composition and sources of PM10 and PM2. 5 aerosols in Guangzhou, China. Environmental Monitoring and Assessment. 2006;119:425–439. doi: 10.1007/s10661-005-9034-3. [DOI] [PubMed] [Google Scholar]
- Wang Y., James P. On the effect of anisotropy on the turbulent dispersion and deposition of small particles. International Journal of Multiphase Flow. 1999;25:551–558. [Google Scholar]
- Wang Y., Wu S., Yang Y., Yang X., Song H., Cao Z., Huang Y. Evaporation and movement of fine droplets in non-uniform temperature and humidity field. Building and Environment. 2019;150:75–87. [Google Scholar]
- Wu D., Tawhai M.H., Hoffman E.A., Lin C.-L. A numerical study of heat and water vapor transfer in mdct-based human airway models. Annals of Biomedical Engineering. 2014;42:2117–2131. doi: 10.1007/s10439-014-1074-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang Y., Song B., Wang Y., Fan J., Karkri M., Wei Y. Numerical investigation of motion of sulfuric and hydrochloric droplets with phase change in free-falling process. Building and Environment. 2019;157:16–23. [Google Scholar]
- Zamankhan P., Ahmadi G., Wang Z., Hopke P.K., Cheng Y.-S., Su W.C., Leonard D. Airflow and deposition of nano-particles in a human nasal cavity. Aerosol Science & Technology. 2006;40:463–476. [Google Scholar]
- Zhang Y., Chia T.L., Finlay W.H. Experimental measurement and numerical study of particle deposition in highly idealized mouth-throat models. Aerosol Science & Technology. 2006;40:361–372. [Google Scholar]
- Zhang Y., Finlay W., Matida E. Particle deposition measurements and numerical simulation in a highly idealized mouth–throat. Journal of Aerosol Science. 2004;35:789–803. [Google Scholar]
- Zhang Z., Kleinstreuer C. Transient airflow structures and particle transport in a sequentially branching lung airway model. Physics of Fluids. 2002;14:862–880. (1994-present) [Google Scholar]
- Zhang Z., Kleinstreuer C. Species heat and mass transfer in a human upper airway model. International Journal of Heat and Mass Transfer. 2003;46:4755–4768. [Google Scholar]
- Zhang Z., Kleinstreuer C., Kim C. Cyclic micron-size particle inhalation and deposition in a triple bifurcation lung airway model. Journal of Aerosol Science. 2002;33:257–281. [Google Scholar]
- Zhang Z., Kleinstreuer C., Kim C.S. Isotonic and hypertonic saline droplet deposition in a human upper airway model. Journal of Aerosol Medicine. 2006;19:184–198. doi: 10.1089/jam.2006.19.184. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.