A feasibility study on an automated method to generate patient‐specific dose distributions for radiotherapy using deep learning

Abstract

Purpose

To develop a method for predicting optimal dose distributions, given the planning image and segmented anatomy, by applying deep learning techniques to a database of previously optimized and approved Intensity‐modulated radiation therapy treatment plans.

Methods

Eighty cases of early‐stage nasopharyngeal cancer (NPC) were included in the study. Seventy cases were chosen randomly as the training set and the remaining as the test set. The inputs were the images with structures, with each target and organs at risk (OARs) assigned a unique label. The outputs were dose maps, including coarse dose maps and converted fine dose maps (FDM) from convolution. Two types of input images with structures were used in the model building. One type of input included the images (with associated structures) without manipulation. The second type of input involved modifying the image gray label with information from radiation beam geometry. ResNet101 was chosen as the deep learning network for both. The accuracy of predicted dose distributions was evaluated against the corresponding dose as used in the clinic. A global three‐dimensional gamma analysis was calculated for the evaluation.

Results

The proposed model trained with the two different sets of input images and structures could both predict patient‐specific dose distributions accurately. For the out‐of‐field dose distributions, the model obtained from the input with radiation geometry performed better (dose difference in %, 4.7 ± 6.1% vs 5.5 ± 7.9%, P < 0.05). The mean Gamma pass rates of dose distributions predicted with both types of input were comparable for most OARs (P > 0.05), except for the bilateral optic nerves and the optic chiasm.

Conclusions

The proposed system with radiation geometry added to the input is a promising method to generate patient‐specific dose distributions for radiotherapy. It can be applied to obtain the dose distributions slice‐by‐slice for planning quality assurance and for guiding automated planning.

1. Introduction

Intensity‐modulated radiation therapy (IMRT) has been used widely in treatment planning and can provide highly conformal dose distributions. During routine inverse treatment planning, planners usually set optimization parameters subjectively based on their experience. Studies have concluded that the quality of IMRT plans varies among institutes and planners.1, 2, 3, 4, 5, 6 Recently, mathematical algorithms have been developed for knowledge‐based planning and quality assurance (QA) with few manual interventions.7, 8, 9, 10, 11, 12, 13 The key step of these methods is to predict achievable sparing of organs at risk (OARs) with dosimetric information for an individual patient based on prior knowledge generated from a database of high‐quality treatment plans.

The machine‐learning methods based on several hand‐crafted features have been popular in the literature for predicting the dose volume histogram (DVH) or dose distributions14, 15, 16 Support vector regression with principal component analysis has been implemented to predict DVH by establishing the correlation between the features of the DVH and anatomic information.14 Artificial neural networks have been developed to predict dose distributions for pancreatic cancer,15 prostate cancer,16 and stereotactic radiosurgery.16 Voxel‐wise dose prediction cannot only generate DVH curves but also give the detailed dose distributions. A potential application is to perform voxel‐wise dose optimization and knowledge‐based isodose manipulation.16 Some studies extracted features manually and predicted dose distributions with machine‐learning methods; however, such hand‐extracted features can only capture low‐level information,17 which may be not sufficient for accurate prediction. More accurate and effective dose distributions prediction needs to be investigated using advanced algorithms.

Recent technologic improvements in hardware have allowed the evolution of deep learning methods and have brought breakthroughs in medicine.18, 19 The most famous mechanism of deep learning is convolutional neural networks (CNN). Convolutional neural networks is a powerful nonlinear method that can automatically extract hierarchical features of the data, which are often more concise and effective for prediction.20 It has shown outstanding performance in computer vision, such as image classification21, 22 object detection23 and semantic segmentation.20 Convolutional neural networks has also shown remarkable results in radiotherapy, such as automatic segmentation24, 25 deformable registration,26 response‐adaptive clinical decision‐making,27 magnetic resonance‐based synthetic computed tomography (CT) generation,28 and toxicity prediction in radiotherapy for cervical cancer.29 Therefore, it may also have potential application in three‐dimensional (3D) dose distributions prediction.

Here, we developed an intelligent system for predicting optimal patient‐specific dose distributions. It utilized the information of the planning image and segmented anatomy and modeled with a deep learning technique.

2. Materials and methods

2.A. Patient data and treatment planning

Eighty patients with early‐stage nasopharyngeal cancer (NPC) who received simultaneous integrated boost (SIB) radiotherapy between 2011 and 2016 were enrolled in this study. Approval of the study protocol was obtained from the review board of our institute.

Patients were immobilized with a thermoplastic mask in the supine position. Simulation CT images (slice thickness, 3 mm; 512 × 512 matrix) were acquired using a Somatom Definition AS 40 (Siemens Healthcare, Forchheim, Germany) or a Brilliance CT Big Bore (Philips Healthcare, Best, the Netherlands) system.

Radiation oncologists delineated the gross tumor volume of the nasopharynx (GTVnx), gross tumor volume of the metastatic lymph node (GTVnd), clinical target volume (CTV), and OARs in the planning CT. The CTV included GTVnx, GTVnd, high‐risk local regions that contain the parapharyngeal spaces, the posterior third of nasal cavities and maxillary sinuses, pterygoid processes, pterygopalatine fossa, the posterior half of the ethmoid sinus, cavernous sinus, base of skull, sphenoid sinus, the anterior half of the clivus, petrous tips, and high‐risk lymphatic drainage areas, including bilateral retropharyngeal lymph nodes and level II. A margin of 3 mm was applied around the GTVnx and CTV to create the planning GTVnx (PGTVnx) and planning target volume (PTV), respectively. The 16 OARs that we contoured are shown in Table 1. The protocol of NPC radiotherapy in our department employs a two‐phase SIB strategy.30 In the present study, only phase‐one SIB planning was used. The union of PGTVnx and GTVnd was named as Boost_all. The prescription to the Boost_all was 70 Gy in 33 fractions (2.12 Gy per fraction). The radiation dose to the PTV was 60 Gy in 33 fractions (1.82 Gy per fraction).

Table 1.

Regions of interest labeling for SImg and does constrain

Contours	Dose constrain	Label	Contours	Dose constrain	Label
Body	Dmean: ALAP	1	Optic chiasm	D1cc ≤ 54 Gy	13
L/R optic nerve	D1cc ≤ 54 Gy	2/3	Spinal cord PRV	D1cc ≤ 40 Gy	14
L/R temporal lobe	D1cc ≤ 60 Gy	4/5	Brainstem PRV	D1cc ≤ 54 Gy	15
L/R mandible	Dmean: ALAP	6/7	L/R parotid gland	D50 ≤ 30 Gy	16/17
L/R TMJ	Dmean: ALAP	8/9	PTV	D95 ≥ 60 Gy	20
L/R lens	D1cc ≤ 9 Gy	10/11	Boost_all	D95 ≥ 70 Gy	41
Larynx	Dmean: ALAP	12

L/R, left/right, ALAP, as low as reasonably possible, PRV, planning organ at risk volume; TMJ, temporomandibular joint. The PRV of the spinal cord and brainstem was defined as the spinal cord with a margin of 5 mm and brainstem with a margin of 3 mm.

The radiotherapy plans were optimized and calculated in the Pinnacle 8.0–9.10 treatment planning system (Philips Radiation Oncology Systems, Fitchburg, WI, USA). All plans were generated using equally spaced nine fixed coplanar 6 MV photon beams with step and shoot. Dosimetric objectives of target volumes and OARs for direct optimization of machine parameters are listed in Table 1. The final dose grid resolution was 0.4 × 0.4 cm in the TPS and interpolated into the same pixel size with the corresponding CT image.

The final contours and treatment plans were reviewed carefully and approved by our Head and Neck Cancer Radiotherapy Team, which comprised of 10–20 radiation oncologists with average 15 yrs’ of practice.

2.B. The prediction model using convolutional neural networks

Inspired by breakthroughs in the deep learning, we proposed an intelligent system based on CNN to predict the 3D dose distribution. Figure 1 depicts the framework of dose distributions prediction with the proposed method. The inputs were the images with structures, and the outputs were the corresponding dose distribution maps. Due to the limited number of datasets available, we used transfer learning to fine‐tune a CNN model with ResNet101.31 The model was pretrained on a large dataset (ImageNet). The net was end‐to‐end trainable and could predict the dose distributions without manual intervention.

Figure 1.

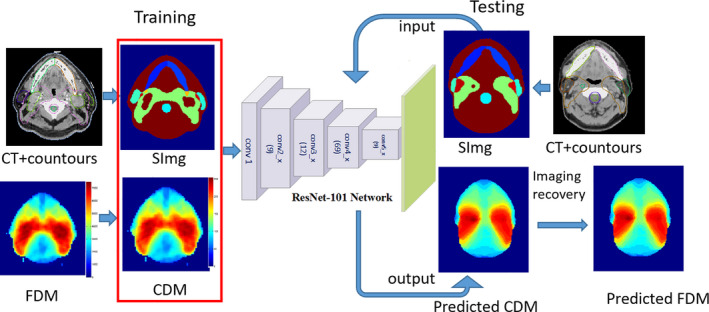
The framework of the proposed system. [Color figure can be viewed at wileyonlinelibrary.com]

2.B.1. Data preparation

In order to learn enough information for accurate dose prediction, we generated novel inputs and outputs for the deep learning network (Fig. 1). The inputs were the images with structures (named as “SImg” hereafter), with each target and OAR assigned a unique label. The outputs were the corresponding dose maps.

Inputs generation

Two types of inputs were used in the model building. The performance from each was evaluated and compared. The first type of inputs was named as “general SImg” (g_SImg) hereafter. It was the images with associated contoured structures. There were 19 regions of interest (ROIs), including 17 OARs and 2 targets contoured on the planning CT of all the cases. Each ROI was assigned a unique label as shown in Table 1. The overlap of the OAR and target was labeled with their summation, which was also unique. The second type of input involved modifying the image gray labels with information from radiation beam geometry (named as “o_SImg” hereafter). The distance to the boundary of the beam fields is an important feature for dose distributions because the dose outside of the fields drops off rapidly. Specifying the out‐of‐field voxels can achieve more accurate prediction.11 We created the o_SImg from g_SImg by adding out‐of‐field labels according to Eq. (1). To assign a unique label for each ROI of o_SImg, the labels on all the slices beyond the beam fields were added by 100 and increased additional 20 per slice from the boundary.

$$o\_S\text{Im}g=g\_S\text{Im}g+z\times 20+100$$ (1)

where z is numbers of the slice to the boundary of the beam fields in the superior–inferior direction.

Outputs generation

The outputs were the corresponding 2D dose maps. The original fine dose maps (FDM) in these cases had gray values ranged from about 0 cGy to ≈7500 cGy, so there were ≈7500 levels which were too many for pixel‐wise prediction. For efficiency and accuracy, a coarse dose map (CDM) calculated according to Eq. (2) was used in the present study.

$$CDM=min\left(\frac{\mathit{FDM}}{7500}·g(l-1),l-1\right)$$ (2)

where 7500 was about the maximum value of FDM and l was the number of levels. The l used in this study was set to 256 according to the preliminary experiments (the details of which are presented in the Section 4).

During the training phase, the CDM calculated from FDM was used to build the model. Accordingly, the proposed system predicted the CMD first during the test phase. The final predicted dose distributions were the FDM converted from CMD by convolving with a Gaussian low‐pass filter [Eq. (3)].

$$\begin{array}{cc}\hfill f(x_i,y_i)=& \frac{1}{2\pi {\delta }^2}exp\hfill \\ & \left(-\frac{{\left(x_i-\frac{h-1}{2}-1\right)}^2+{(y_i-\frac{h-1}{2}-1)}^2}{2{\delta }^2}\right)\hfill \end{array}$$ (3)

where $x_i$ and $y_i$ are coordinates of voxel i, h is the size of the filter, and $\delta$ is the standard deviation, which was set to 2.

2.B.2. Architecture of the proposed system

The proposed system was an end‐to‐end framework used to predict achievable dose distributions based on ResNet101.31 At the end of the networks, we replaced the fully connected layers with fully convolutional layers for this task. With this adaptation, the networks could predict pixel‐wise dose distributions. ResNet101 consisted of 101 weight layers with small convolution filters and two max pooling operations. There was a batch‐normalized (BN) operation following each convolution layer32, 33 BN acts as a regularizer to normalize the features, which allows us to use much higher learning rates and be less careful about initialization. Then, an element‐wise, rectified‐linear nonlinearity maximum (0, x) was applied to avoid linear equations. Networks with very deep layers are difficult to train due to vanishing gradients. To resolve this problem, ResNet101 used “shortcut connections” to add their outputs to the outputs of the stacked layers.31 It took a standard feed‐forward convolutional network and added skipped connections that bypassed a few convolutional layers at a time.

2.B.3. Experiments

Seventy of the eighty cases were chosen randomly as a training set to adjust the parameters of the dose distributions prediction model. The remaining ten cases were used as the test set to evaluate its performance. The input was the SImg with a unique label for each ROI and the output was CDM with 256 dose levels. We implemented the training and testing using Caffe.34 All computations were undertaken on a personal computer with an Intel^® Core i7 processor (3.4 GHz) and a Titan X graphics card. For these experiments, we used the parameters from the corresponding model pretrained on a large database (ImageNet) for initialization.35 Normally, the input channel of the conv1 layer should be 3 since it was pretrained on ImageNet. However, our input was the gray image of structure images, which has only one channel. We solved this problem by taking only the first channel of each filter in the “Conv1” pretrained on ImageNet when loading the model. Then, we fine‐tuned the entire network for dose distributions prediction tasks36, 37 We adopted data‐augmentation methods such as random cropping and left‐right flipping to reduce overfitting.38 We used stochastic gradient descent (SGD) with momentum to optimize the loss of function. Four main hyperparameters were set during model training.39 A batch size of 1 was used due to the limitations of GPU memory. The learning rate determines how much an updating step influences the current weights and was set initially to 0.001 in the present study. The momentum was set to 0.9. The weight decay factor governs the regularization term of the neural net for avoiding overfitting and was set to the default value of 0.0005. The loss function was computed with “SoftmaxWithLoss” built‐in Caffe. We trained our model by 50k iterations and then evaluated the model using the test set.

2.C. Quantitative evaluation

The accuracy of predicted dose distributions was evaluated against the corresponding ground truth (GT) voxel‐by‐voxel in the range of the body and normal tissue (NT) which was defined as body excluding PTV. The voxel‐based mean absolute error (MAE) was calculated using Eq. (4):

$$\begin{array}{cc}\hfill \mathit{MAE}& =\frac{1}{n}{\sum }_{j=1}^n\frac{1}{m}{\sum }_{i=1}^m|D_p(i)-D_g(i)|/\hfill \\ & prescriptionDose\times 100\%\hfill \end{array}$$ (4)

where $i$ is the index of the voxel, m is the total number of voxels for each patient, $D_p(i)$ and $D_g(i)$ are the predicted and GT dose of a voxel $i$, respectively, j is the index of the case, and n is the total number of cases in the test set.

A global 3D gamma analysis was used to evaluate the accuracy of the predicted dose distributions of each OAR. The agreement was assessed at tolerance levels of 3%/3 mm and 4%/4 mm for the γ ≤ 1 test.

To evaluate the accuracy of the predicted DVH, the MAE of DVH (MAE_DVH) of each OAR was used to calculate the difference between predicted and GT dose‐percent‐volume parameters from D99% to D1% according to Eq. (5):

$$\begin{array}{cc}& MA{E}_{\mathit{DVH}}=\frac{1}{99}{\sum }_{k=1}^{99}\hfill \\ & \left|\frac{1}{n}{\sum }_{j=1}^n\left(D_p{(j)}_{k\%}-D_g{(j)}_{k\%}\right)/PrescriptionDose\times 100\%\right|\hfill \end{array}$$ (5)

where k is the dose volume index of DVH, j is the index of the case, and n is the total number of cases in the test set. $D_p{(j)}_{k\%}$ and $D_r{(j)}_{k\%}$ are the predicted and GT dose at k% volume of the jth case.

3. Results

The result obtained from the input with radiation geometry was better for slices out‐of‐field (Fig. 2). The predicted in‐field dose distributions with both types of inputs were quite similar to the GT.

Figure 2.

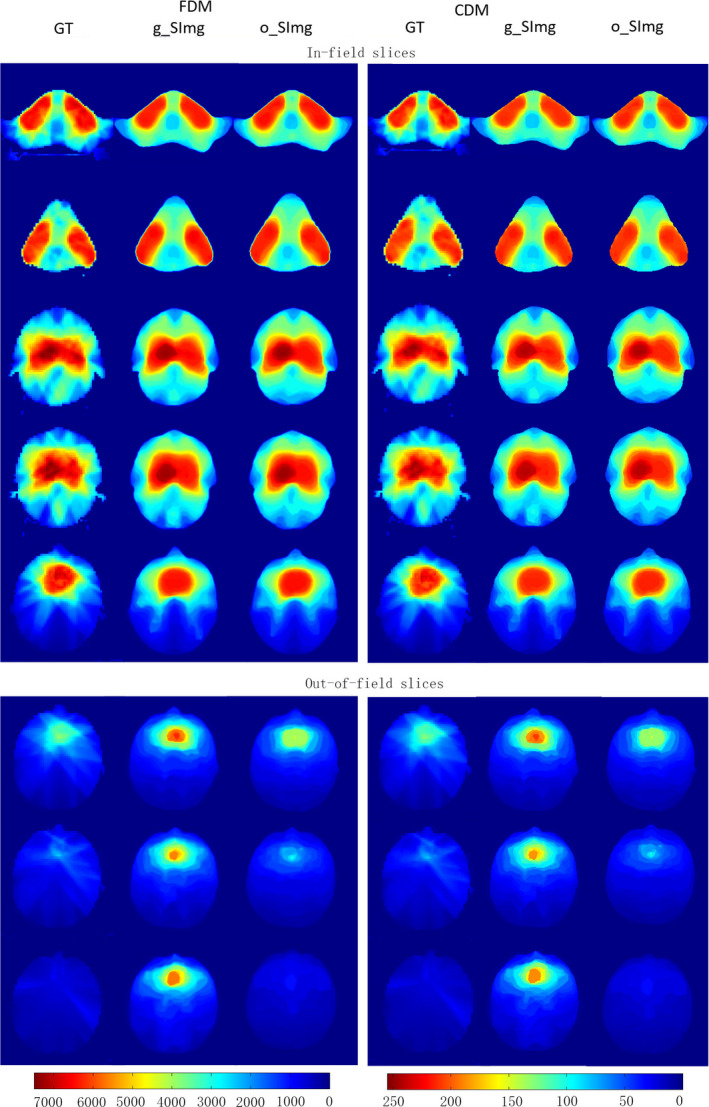
An example of coarse dose map and fine dose maps generated with two types of inputs. [Color figure can be viewed at wileyonlinelibrary.com]

The overall mean MAE_body with both types of inputs were comparable (5.5 ± 6.8% vs 5.3 ± 6.4%, P = 0.181). As for slices out‐of‐field, the result obtained from the input of o_SImg was significantly better (4.7 ± 6.1% vs 5.5 ± 7.9%, P = 0.048), while the improvement for the in‐field slices was not significant (P = 0.236).

The mean Gamma pass rates with two types of inputs were comparable for most OARs (Table 2). However, the mean pass rates for the bilateral optic nerves and the optic chiasm predicted with o_SImg were significantly higher than g_SImg (P < 0.05). For the bilateral lens, the mean pass rate also improved obviously with o_SImg, which was 10.1% with 3 mm/3% criteria, and 3.9% with 4%/4 mm criteria. However, not all the improvements were significantly different.

Table 2.

Mean pass rates of 3D gamma analysis with 3%/3 mm and 4%/4 mm criteria

	3%/3 mm (%)			4%/4 mm (%)
	o_SImg	g_SImg	P	o_SImg	g_SImg	P
L parotid	86.4 ± 7.0	87.4 ± 6.5	0.166	94.8 ± 4.6	95.8 ± 3.1	0.198
R parotid	83.2 ± 6.7	83.3 ± 6.3	0.904	94.0 ± 4.8	94.7 ± 2.9	0.546
Brainstem	79.6 ± 9.9	78.1 ± 9.0	0.444	90.5 ± 7.5	90.1 ± 6.0	0.774
Brainstem PRV	78.8 ± 9.8	77.9 ± 9.2	0.638	89.5 ± 8.1	89.6 ± 7.1	0.938
Spinal cord	83.8 ± 7.5	81.6 ± 8.4	0.029	93.9 ± 5.9	91.8 ± 7.5	0.048
Spinal cord PRV	74.7 ± 8.9	73.1 ± 7.7	0.419	86.7 ± 6.4	85.3 ± 6.5	0.357
L TMJ	92.1 ± 2.8	90.4 ± 5.2	0.165	98.6 ± 0.8	97.4 ± 2.2	0.022
R TMJ	89.9 ± 1.6	86.7 ± 2.0	0.013	97.8 ± 1.0	96.6 ± 1.4	0.088
L mandible	82.0 ± 4.3	81.4 ± 5.9	0.611	92.4 ± 4.1	92.3 ± 4.9	0.966
R mandible	78.7 ± 6.2	78.5 ± 7.0	0.793	88.5 ± 5.7	89.6 ± 5.5	0.147
L temporal lobe	83.3 ± 6.9	82.8 ± 8.9	0.873	93.1 ± 6.5	93.3 ± 4.7	0.981
R temporal lobe	83.1 ± 7.5	81.2 ± 6.8	0.234	93.4 ± 4.7	92.4 ± 4.3	0.283
Larynx	75.3 ± 11.9	75.0 ± 13.1	0.843	86.5 ± 10.2	86.7 ± 10.6	0.916
L lens	94.8 ± 11.1	79.2 ± 16.2	0.019	100.0 ± 0.1	94.7 ± 9.5	0.139
R lens	98.5 ± 4.5	93.9 ± 12.4	0.184	100.0 ± 0	97.6 ± 7.3	0.343
Optic chiasm	88.9 ± 13.7	80.8 ± 13.0	0.025	96.9 ± 6.7	90.6 ± 8.6	0.047
L optic nerve	91.0 ± 13.8	80.5 ± 12.0	0.049	97.9 ± 4.8	93.8 ± 8.2	0.049
R optic nerve	92.7 ± 10.6	82.9 ± 13.4	0.024	99.7 ± 0.6	93.5 ± 7.8	0.038
PTV	92.0 ± 3.1	91.9 ± 2.7	0.355	98.1 ± 1.2	98.1 ± 1.1	0.348
Boost_all	98.3 ± 1.2	98.3 ± 1.3	0.205	99.7 ± 0.8	99.7 ± 0.8	0.135

The mean pass rates of all ROIs with o_SImg were 86.4% with 3 mm/3% criteria and 94.6% with 4%/4 mm criteria, which were 3.3% and 1.4% higher than g_SImg, respectively. For each ROI, prediction with o_SImg had mean pass rates higher than 86% using 4%/4 mm criteria and 74.7–98.5% using 3%/3 mm criteria.

The predicted mean DVH of the bilateral optic nerves and the optic chiasm with g_SImg had some differences from GT (Fig. 3). For these ROIs, the mean MAE_DVH with g_SImg was 2.4–6.9 times greater than o_SImg (Table 3). For all the ROIs, the mean DVHs with o_SImg were quite similar to the GT (Fig. 3), and the mean MAE_DVH for each ROI were ranged from 0.5% to 2.6% (Table 3).

Figure 3.

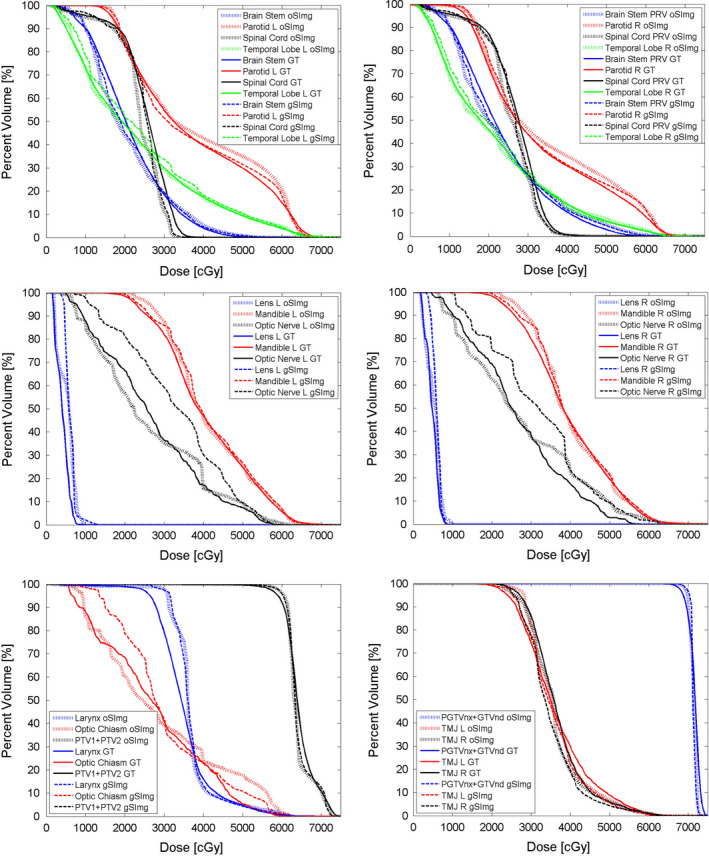
Comparison of the mean dose volume histogram of each regions of interest. [Color figure can be viewed at wileyonlinelibrary.com]

Table 3.

Comparison of MAE_DVH for each regions of interests

OARs	o_SImg (%)	g_SImg (%)	OARs	o_SImg (%)	g_SImg (%)
L parotid	2.0 ± 1.6	1.1 ± 0.6	L mandible	1.3 ± 1.4	1.2 ± 0.7
R parotid	2.1 ± 1.9	1.4 ± 0.5	L temporal lobe	0.7 ± 0.4	2.2 ± 0.8
Brainstem	1.6 ± 1.0	1.0 ± 0.7	R temporal lobe	0.7 ± 0.5	1.3 ± 0.7
Brainstem PRV	1.8 ± 1.1	1.2 ± 1.0	Larynx	2.6 ± 1.4	2.8 ± 1.9
Spinal cord	2.1 ± 0.6	1.1 ± 0.6	L lens	1.5 ± 0.2	2.8 ± 0.2
Spinal cord PRV	1.8 ± 0.6	0.9 ± 0.4	R lens	0.5 ± 0.2	1.6 ± 0.5
L TMJ	0.8 ± 0.8	1.1 ± 0.6	optic chiasm	1.8 ± 0.8	4.4 ± 3.0
R TMJ	1.5 ± 0.7	2.8 ± 0.7	L optic nerve	1.3 ± 1.1	9.0 ± 3.1
L mandible	1.2 ± 1.4	1.3 ± 0.6	R optic nerve	1.4 ± 0.9	7.2 ± 1.9
Boost_all	0.8 ± 0.6	1.0 ± 0.5	PTV	1.2 ± 0.6	1.0 ± 0.7

4. Discussion

In typical dose distributions or DVH prediction using traditional machine‐learning methods, features must be extracted for the task. The manual extraction algorithms are complicated and may only cover the shallow features for modeling. In this study, we proposed a deep learning based procedure with reasonable inputs and outputs for dose distributions prediction. We generated novel structure images with a unique label for each target and OAR as inputs and coarse dose maps as the outputs. The results show that the proposed system can generate patient‐specific dose distributions for radiotherapy using deep learning. It can be applied to obtain the dose distributions slice‐by‐slice. An early and accurate estimation of dose distributions could be applied for planning QA and for guiding automated planning.

Due to the inherent limitations of the 2D network, the network was not able to consider the radiation beam geometry. We tested two types of inputs (g_SImg and o_SImg) of which the o_SImg modified the labels on the slices out of field to deal with this problem. The proposed system with o_SImg as inputs had an overall better performance. The predicted dose distributions of all OARs had a pass rate higher than 86% with 4%/4 mm criteria. MAE_body of out‐of‐field slices using the o_SImg‐trained model was significantly lower than those using g_SImg. Because the o_SImg can help the network discriminate the slices out of the beam field, it will improve the prediction accuracy of out‐of‐field slices but not affect the accuracy of in‐field slices.

The original dose maps contained dose levels with a large range (0–7500). In order to reduce the complexity, the CDM was generated for the model. A series of preliminary experiments were carried out to determine the appropriate levels of the output. We tested CDMs with different levels (10, 30, 75, 256, 512, and 700) using two networks: VGGNet1640 and ResNet101. The results were not good enough when using high levels of 512 or 700. When the level was set low as 10 or 30, the outputs of these two networks were too coarse. For ResNet101, the setting of 256 levels performed slightly better than the setting of 75 levels. For VGGNet16, the accuracy for the setting of 75 levels was slightly better than that for the setting of 256 levels, but both were worse than ResNet101 with 256 levels. In general, using the same levels, the proposed system with ResNet101 performed relatively better than with VGGNet16. Taking accuracy and efficiency into consideration, ResNet101 with 256 dose levels was adopted for the proposed system.

For head and neck cancer, several studies have predicted achievable DVH for knowledge‐based treatment planning or the QA of planning. Junet and colleagues41 reported on the range of different median doses for the parotid. In their study, the difference between the predicted and actual plans was −17.7% to 15.3%, whereas our values were −6.8% to 7.5% for the right parotid and −8.7% to 19.6% for the left parotid. Yuan and co‐workers10 reported that the accuracy of predicted median dose for 63% of parotid could achieve within 6% error (4.2 Gy) and the values in 83% of parotid were within 10% error (7 Gy). Our results showed that the values in 80% of parotid could be predicted within 6% error and, in 90%, could be predicted within 10% error. Our study demonstrated that the proposed system with CNN was a potential tool for predicting dose distributions more accurately.

Using the proposed system to generate patient‐specific dose distributions would be complete in <10 s per patient, which is sufficient for the real‐time application. The dose distributions predicted by the proposed system could generate a DVH for each OAR, which could be converted to inverse optimization objectives and imported to commercial TPS directly as the initial values. Nwankwo et al.12 reported that dose–volume constraints extracted from the predicted dose distributions can help inexperienced planners achieve high‐quality plans to the same extent as experienced planners. As shown in Fig. 4, the prediction of dose distributions can provide detailed voxel doses with information on position coordinates. The predicted and GT DVH were quite similar in the high‐dose region (>35 Gy), but the 3D gamma analysis may not pass well in this range. Pass‐fail voxels can be marked (pink) on the 3D dose distribution maps clearly, which can guide the generation of pseudo‐structures for further constraint of inverse optimization objectives. That is, prediction of dose distributions could aid the development of a voxel‐by‐voxel cost optimization system and eliminate the need to convert the desired dose distributions to DVH values.16 The 3D global gamma analysis with 3%/3 mm and 4%/4 mm criteria was used to evaluate the accuracy of the proposed system quantitatively. Selection of suitable pass‐fail criteria should be tested in the future for planning QA or automatic planning based on predicted dose distribution maps.

Figure 4.

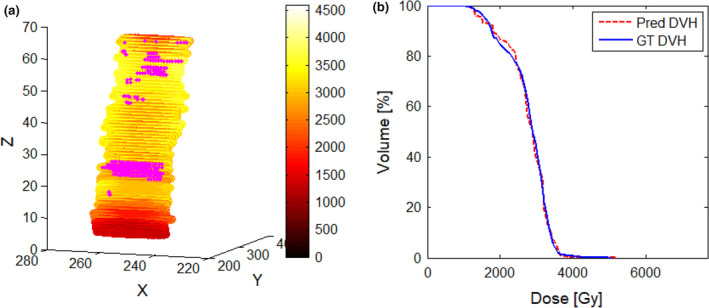
The predicted dose results trained with g_SImg for spinal cord PRV. (a) Predicted dose distributions with coordinate information; the pink maker is the pass–fail voxels using 3%/3 mm criteria. (b) Dose–volume histogram comparison between predicted and GT. [Color figure can be viewed at wileyonlinelibrary.com]

There were several limitations of the present study. First, we used the structure image as the input of the network, but the information from CT images was not considered. In fact, the dose calculation was based on the relative electron density, which is converted from Hounsfield Units (HUs) on CT. Combining the structure image with CT information may improve the dose distribution prediction. Second, the dataset comprised 80 patients, which was not very large. The CNN model could be more robust and accurate with more training data. Third, we only used IMRT data for modeling. VMAT is another widely used radiotherapy method for head‐and‐neck cases, and whether the IMRT dose distributions prediction system can be used for the VMAT model should be investigated. Fourth, we used 3D gamma analysis (criteria: 3 mm/3% and 4 mm/4%) and DVH to compare the predictions with clinical plans in the test set. The optimal acceptable criteria of model and QA for new treatment were not provided in the present study, which is better concluded from some different 3D dose distributions prediction studies with different databases. Finally, we have paid attention to the usage of CNN for a novel problem rather than the network itself. So we used the defaults setting of the networks, including the learning rate, weight decay, momentum strength, and other hyperparameters.

With the development of deep learning, more accurate and efficient networks should be tested and adopted in the proposed system. 3D CNN can capture more spatial information which may be useful for the prediction by considering upper and lower slice relationship. In addition, an open, high‐quality database and standard indices for evaluating the accuracy of the dose distributions prediction model should be established in the future to compare the performances among the different models.

5. Conclusions

This study showed the feasibility of using specific inputs and outputs to generate patient‐specific dose distributions for radiotherapy with a deep learning approach. The proposed system with radiation geometry added to the input is a promising method. It can be applied to obtain the dose distributions slice‐by‐slice for planning QA and for guiding automated planning. With further improvement of our model and application procedure in the future, this method is likely to have a considerable role in clinical work.

Conflicts of interest

The authors have no conflicts to disclose.