Early Pleistocene obliquity-scale pCO₂ variability at ~1.5 million years ago

Abstract

In the early Pleistocene, global temperature cycles predominantly varied with ~41-kyr (obliquity-scale) periodicity. Atmospheric greenhouse gas concentrations likely played a role in these climate cycles; marine sediments provide an indirect geochemical means to estimate early Pleistocene CO₂. Here we present a boron isotope-based record of continuous high-resolution surface ocean pH and inferred atmospheric CO₂ changes. Our results show that, within a window of time in the early Pleistocene (1.38–1.54 Ma), pCO₂ varied with obliquity, confirming that, analogous to late Pleistocene conditions, the carbon cycle and climate covaried at ~1.5 Ma. Pairing the reconstructed early Pleistocene pCO₂ amplitude (92 ±13 μatm) with a comparably smaller global surface temperature glacial/interglacial amplitude (3.0 ±0.5 K), yields a surface temperature change to CO₂ radiative forcing ratio of S_[CO2]~0.75 (± 0.5) °C/Wm⁻², as compared to the late Pleistocene S_[CO2] value of ~1.75 (± 0.6) °C/Wm⁻². This direct comparison of pCO₂ and temperature implicitly incorporates the large ice sheet forcing as an internal feedback and is not directly applicable to future warming. We evaluate this result with a simple climate model, and show that the presumably thinner, though extensive, northern hemisphere ice sheets would increase surface temperature sensitivity to radiative forcing. Thus, the mechanism to dampen actual temperature variability in the early Pleistocene more likely lies with Southern Ocean circulation dynamics or antiphase hemispheric forcing. We also compile this new carbon dioxide record with published Plio-Pleistocene δ¹¹B records using consistent boundary conditions and explore potential reasons for the discrepancy between Pliocene pCO₂ based on different planktic foraminifera.

1. Introduction

The Pleistocene Epoch was characterized by a sequence of glacial/interglacial climate oscillations that are recorded in geochemical records from deep-sea sediments, continental deposits, and ice cores [e.g., Imbrie et al., 1984; Lüthi et al., 2008; Joannin et al., 2010]. These records show that Earth’s surface temperature covaried with the dominant periodicities of Earth’s orbit around the Sun: orbital precession, obliquity and/or eccentricity. Nevertheless, understanding how the climate system responds to and amplifies the initial orbital insolation forcing is a long-standing problem in the field of paleoclimatology [Hays et al., 1976; Hansen et al., 1984; Imbrie et al., 1992; Hansen et al., 2005]. High-resolution records of temperature and greenhouse gas concentrations are of paramount value to elucidate the pattern and drivers of global climate change, yet continuous high-resolution ice core records of trapped ancient air are thus far restricted to the late Pleistocene (0.8 Ma to present) [e.g., Lüthi et al., 2008]. Ancient air inclusions in late Pleistocene ice-cores suggest that the partial pressure of atmospheric CO₂ (pCO₂) lagged an initial temperature perturbation [Fischer et al., 2010] such that radiative greenhouse gas forcing at most amplified the orbital pacing of Pleistocene climate, via carbon cycle feedbacks, deep-sea carbon storage and release, and radiative forcing [Anderson et al., 2009; Shakun et al., 2012]. During the early Pleistocene (2.6–1.0 Ma), obliquity set the dominant tempo of climate, and cold glacial intervals were shorter and less extreme [e.g., Lisiecki and Raymo, 2005; Huybers, 2007]. The presence of North American glacial tills indicates that early Pleistocene ice sheets at glacial maxima extended as far south as 39°N [Roy et al., 2004; Balco and Rovey, 2010].

In the early Pleistocene, both tropical [e.g., Herbert et al., 2010] and extratropical [e.g., Lawrence et al., 2009; Martínez-Garcia et al., 2010] sea-surface temperature (SST) records reveal long-term cooling in both glacial and interglacial intervals (i.e., 2 K cooler in tropics and 3–4 K cooler in high latitudes). At the same time, the glacial-interglacial amplitude of surface temperature increased from ~3 K to ~5 K from the early to late Pleistocene, as glacial temperatures cooled [Lawrence et al., 2009; Herbert et al., 2010; Martínez-Garcia et al., 2010]. The gradual cooling of the early Pleistocene glacials culminated in the mid-Pleistocene transition (MPT) when surface temperature and benthic δ¹⁸O records shifted from a dominant 41-kyr periodicity to ~100-kyr pacing, albeit without an obvious corresponding change in the periodicity of incoming solar radiation [Ruddiman et al., 1989; Clark et al., 2006]. Mechanisms put forward to explain this shift in climate response at the MPT include the exposure of crystalline bedrock and thus a more solid foundation for the Laurentide ice sheet [e.g. Clark and Pollard, 1998], changing ocean dynamics that provide increased precipitation available to build larger northern hemisphere ice sheets [Tziperman and Gildor, 2003; McClymont et al., 2008], or the consequence of long-term cooling and glacial CO₂ drawdown as a result of iron fertilization and/or reduced ocean ventilation which sequestered more carbon in the deep ocean [Köhler and Bintanja, 2008; Hönisch et al., 2009; Chalk et al., 2017]. Filling in the early Pleistocene pCO₂ data gaps with orbitally-resolved records will help to evaluate these hypotheses.

While efforts to extend the continuous ice-core pCO₂ record to the early Pleistocene are being actively pursued [Fischer et al., 2013; Higgins et al., 2015; Witze, 2015; Bibby et al., 2016], such records are not yet available. However, marine sediments provide an opportunity to estimate pCO₂ changes from earlier and warmer periods of Earth history. One leading method for estimating atmospheric pCO₂ from marine sediments is via the boron isotope ratio (δ¹¹B) recorded in the shells of planktic foraminifera. Shell δ¹¹B is primarily controlled by seawater acidity (i.e., pH). CO₂ exchanges between the atmosphere and the surface ocean depend on the partial pressure in each medium after Henry’s law. Higher atmospheric pCO₂ results in more CO₂ dissolved in seawater and thereby lowers surface ocean pH. The pH dependency of the relative abundance and isotopic signature of the two main species of boron in seawater (borate ion and boric acid) permits the δ¹¹B value of marine carbonates to reflect such changes in ocean pH (see Methods). Several studies have validated this proxy relative to ice core pCO₂ in the late Pleistocene [Hönisch and Hemming, 2005; Henehan et al., 2013; Chalk et al., 2017] and presented estimates of pCO₂ throughout portions of the Pliocene and Pleistocene [Hönisch et al., 2009; Bartoli et al., 2011; Henehan et al., 2013; Martínez-Botí et al., 2015a; Chalk et al., 2017]. Here we present estimates of pCO₂ based on new δ¹¹B measurements in planktic foraminifera shells within a time window spanning Marine Isotope Stages (MIS) 44–52 (1.38–1.54 Ma).

Published estimates of early Pleistocene pCO₂ are as high as 410 (±50) μatm as recorded at ODP Site 999 at 2.37 Ma [Martínez-Botí et al., 2015a] and as low as 167 (±19) μatm at 0.65 Ma [Hönisch et al., 2009]. Bartoli et al. [2011] observed that atmospheric pCO₂ decreased in a step-wise fashion at ~ 2.7 Ma, although that particular study did not measure a temperature proxy alongside each of the boron isotope analyses, and used modeled estimates of the carbonate ion concentration, [CO₃^2-], as the second parameter of the carbonate system to translate pH into reconstructed pCO₂. Here we present new high-resolution data from ODP 668B in the eastern tropical Atlantic, revise the dataset of Bartoli et al. [2011] with new temperature and geochemical constraints, and compile these records in a consistent manner with other published datasets of early Pleistocene pCO₂. By minimizing the differences in the way boundary conditions are treated among these records, we are able to compare the combined δ¹¹B and pCO₂ records and to describe coherent features of the pCO₂ decline from the late Pliocene through the Pleistocene.

2. Materials and Methods

The primary materials for this study come from ODP Site 668B in the eastern tropical Atlantic (4.77°N, 20.93°W, water depth 2693 m, average sedimentation rate 1.5 cm/kyr, Figure 1). The modern surface ocean at this location is near equilibrium with the atmosphere with respect to CO₂ [Takahashi et al., 2009], and previously published late Pleistocene boron isotope data from this site show good agreement with ice core pCO₂ over the past 0.8 Ma [Hönisch and Hemming, 2005; Hönisch et al., 2009], making this a promising location for extending the reconstruction of paleo-pCO₂. Sediment samples were taken from core 668B every 5 cm (3.3 kyr) and were selected to include glacial and interglacial extrema in planktic δ¹⁸O [Hönisch et al., 2009]. Samples were washed and picked for the planktic foraminiferal species Globigerinoides ruber (300–355 μm size fraction) and Trilobatus (formerly Globigerinoides) sacculifer (>500 μm size fraction), which both live in the surface mixed layer [Spero et al., 2003].

Figure 1.

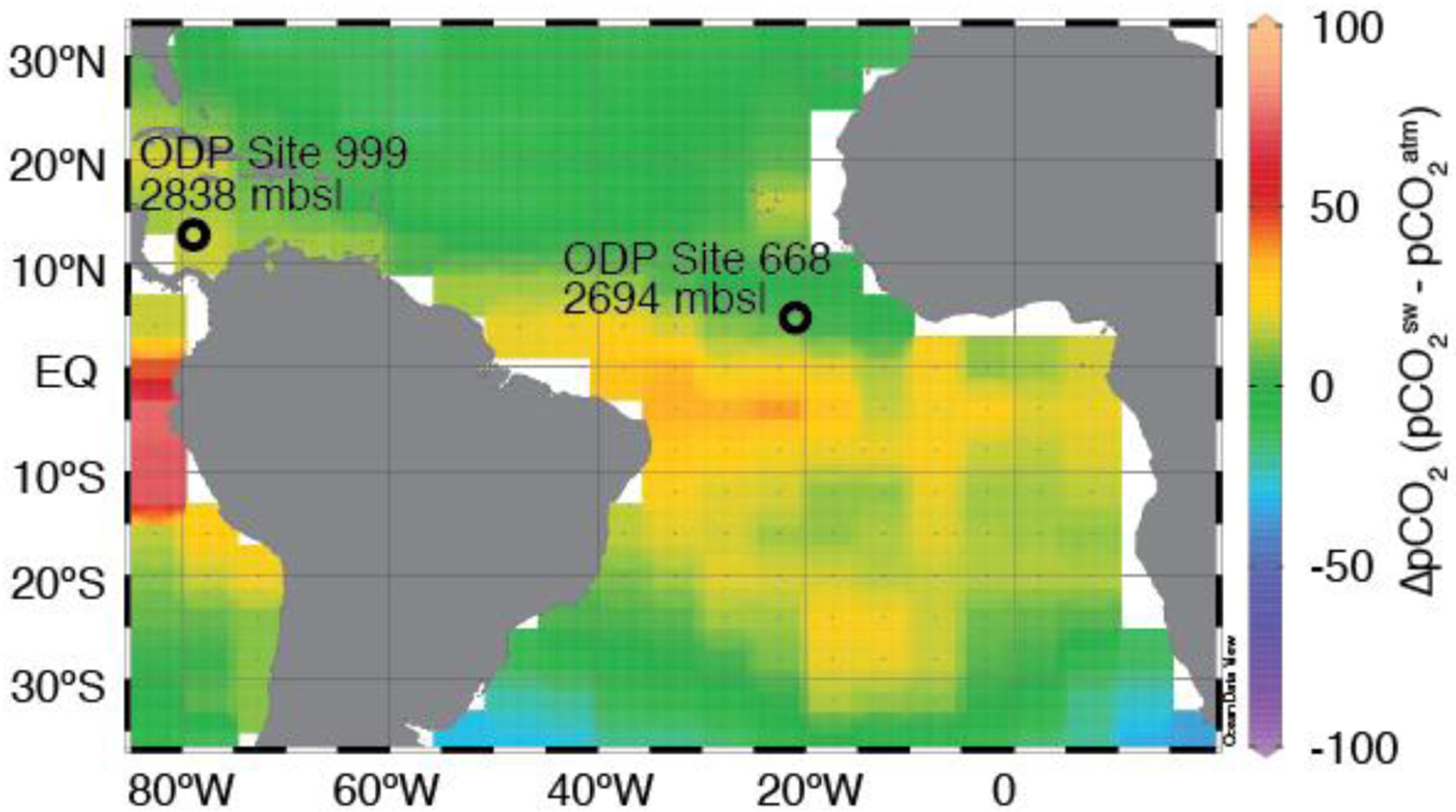
New geochemical data presented are from eastern equatorial Atlantic site ODP 668B and from Caribbean site ODP 999A. Background colors are modern mean annual ΔpCO₂ (seawater pCO₂ – atmosphere pCO₂) [Takahashi et al., 2009] and are plotted using Ocean Data View 4 [Schlitzer, 2017]. Today surface water pCO₂ in these locations is near equilibrium with the atmosphere.

2.1. δ¹¹B-based pCO₂ estimates

Tests of T. sacculifer from the >500 μm size fraction have been validated to reflect surface ocean conditions for pH and pCO₂ estimates [Hönisch and Hemming, 2004; 2005; Hönisch et al., 2009]. Although partial dissolution has the potential to lower foraminiferal δ¹¹B in corrosive bottom water, this effect is more pronounced in smaller foraminiferal test size classes [Hönisch and Hemming, 2004; Edgar et al., 2015]. The samples in this study come from the largest size fraction and from relatively shallow (2693 modern m depth) waters that are oversaturated with respect to calcite (Ώ_calcite = 1.5, Δ[CO₃^2-] ~35 μmol/kg). This depth is well above the regional lysocline and partial dissolution is unlikely [Regenberg et al., 2006]. For each δ¹¹B sample, ~30–50 T. sacculifer shells were picked, gently crushed and cleaned by repeated sonication in MilliQ water and methanol, oxidation in a buffered H₂O₂ solution to remove organic material, and a final weak acid leach [Barker et al., 2003]. Cleaned material was rinsed in MilliQ water, dried to determine the calcite mass after cleaning, and finally dissolved in 2N hydrochloric acid just before analysis. All δ¹¹B samples were measured at the Lamont-Doherty Earth Observatory using a TRITON thermal ionization mass spectrometer in negative mode (N-TIMS). Aliquots of the sample solution containing ≥1 ng boron were loaded onto outgassed zone-refined rhenium filaments, along with 1 μl of boron-free seawater to enhance ionization (see Hönisch et al. [2009] for details). Although analysis of boron isotopes in marine carbonates by the N-TIMS method yields ~1‰ higher δ¹¹B values compared to the alternative MC-ICP-MS technique, the relative variability between different samples is similar between the two methods and yield equivalent pH and pCO₂ results when technique-specific δ¹¹B_foraminifera vs. δ¹¹B_borate calibrations are applied [Foster et al., 2013; Farmer et al., 2016]. To minimize analytical uncertainty, each sample analysis was replicated 3–10 (average of 7) times. Of those replicates, individual analyses were rejected if excessive fractionation (δ¹¹B >1‰) occurred over the 40 minutes of data acquisition; 14% of analyses were rejected on this basis. The majority of samples yielded 5 or more replicates that met the acceptance criteria. Only one sample, at 1.436 Ma, could not be replicated due to low abundance of T. sacculifer shells. Uncertainty in the δ¹¹B measurement was determined as the larger of either: (1) the standard error in valid replicate analyses (i.e., 2σ = 2*standard deviation / √N, where N is the number of accepted replicates) or (2) the 2σ uncertainty of an equal number of repeat measurements of an in-house standard of NIST 951 precipitated in CaCO₃ matrix (vaterite). Average 2σ uncertainty of all δ¹¹B measurements is ±0.26‰.

The relative abundance of the two aqueous species of boron in seawater, borate ion (B(OH)₄⁻) and boric acid (B(OH)₃), is pH dependent [Dickson, 1990; Hemming and Hanson, 1992]. The isotopic fractionation between ¹¹B (natural abundance ~80%) and ¹⁰B (~20%) generates a constant δ¹¹B offset between these two aqueous boron species, such that δ¹¹B of borate increases with the relative abundance of borate at higher pH. Since the borate ion is the primary species incorporated into foraminiferal calcite [e.g., Hemming and Hanson, 1992; Branson et al., 2015], in-situ seawater pH can be estimated from the δ¹¹B of foraminiferal calcite. The boron isotopic composition of seawater (δ¹¹B_sw) must also be known; in the modern ocean δ¹¹B_sw is 39.61 (±0.04)‰ [Foster et al., 2010]. While this value likely increased over the Cenozoic through shifts in weathering and/or volcanic emissions [Lemarchand et al., 2000], attempts to reconstruct δ¹¹B_sw over the past 5 million years have yielded disparate results. The combined evidence, whether from benthic foraminiferal δ¹¹B alongside modeled ocean pH [Raitzsch and Hönisch, 2013] or paired δ¹¹B measurements in the water column coupled with assumptions about water column pH gradient [Pearson and Palmer, 2000; Greenop et al., 2017], shows no clear indication of a trend in δ¹¹B_sw over the past 5 Ma (Figure S1). As the residence time of boron in seawater is long (11–17 My), the maximum rate of change over this time period is likely <0.1‰ per million years [Lemarchand et al., 2000]; hence, we apply the modern δ¹¹B_sw value (39.61‰) to all Plio-Pleistocene samples and increase the uncertainty of this assumed value at a constant rate of 0.1‰/Myr (Figure S1). Ocean pH is then determined via:

$$\text{pH}=\text{p}{K}^{*}{}_{\text{B}}-log\left[-\left({\delta }^{11}{\text{B}}_{\text{sw}}-{\delta }^{11}{\text{B}}_{\text{borate}}\right)/\left\{{\delta }^{11}{\text{B}}_{\text{sw}}-\left({}^{11-10}{K}_{\text{B}}*{\delta }^{11}{\text{B}}_{\text{borate}}\right)-1000*\left({}^{11-10}{K}_{\text{B}}-1\right)\right\}\right]$$ (Eq. 1)

where pK*_B is the dissociation constant for boric acid at in situ temperature, salinity and pressure [Dickson, 1990; Millero, 1995], and the aqueous boron isotope fractionation factor is ^11–10K_B= 1.0272 (±0.0006) [Klochko et al., 2006]. Application of the boron isotope proxy also requires an understanding of any physiological or vital effects on the pH of the foraminiferal microenvironment, which have been documented for a variety of species. Here we use a calibration specifically established for T. sacculifer, which includes culture and core top sediment samples of T. sacculifer measured via N-TIMS at LDEO and Stony Brook [Sanyal et al., 2001; Hönisch and Hemming, 2004; 2005; Hönisch et al., 2009]. Values measured at Stony Brook have been cross-calibrated with N-TIMS [Hönisch et al., 2009] and a constant offset of −1.1‰ has been applied to all data measured in Stony Brook to shift them onto data measured on the N-TIMS at LDEO. A linear York fit [York et al., 2004] calculated for laboratory cultured specimens grown across a range of pH values includes uncertainties in the δ¹¹B_calcite measurement and the δ¹¹ B_borate calculation for experimental seawater. This regression is then adjusted by a constant intercept offset of −0.84‰ so as to pass through the average of core top T. sacculifer δ¹¹B_calcite data and the corresponding preindustrial δ¹¹B_borate (Figure 2 and Table S1). The offset accounts for the difference between cultured and sedimentary specimens, which is likely due to the gametogenic calcite crust that T. sacculifer secretes at greater water depths in the ocean [Bé, 1980]. The resulting calibration for T. sacculifer in the >500 μm size fraction (measured on N-TIMS), including 2σ uncertainty, is:

$${\delta }^{11}{\text{B}}_{\text{borate}}=\left[{\delta }^{11}{\text{B}}_{T.\mathit{\text{sacculifer}}\text{N}-\text{TIMS}}-6.42(\pm 1.64)\right]/0.73(\pm 0.08)$$ (Eq. 2)

Figure 2.

Calibration of δ¹¹B of T. sacculifer as measured by N-TIMS versus δ¹¹B of borate in seawater (data in Table S1). Culture data [Sanyal et al., 2001 and this study] define the slope of the relationship. Core top δ¹¹B data are offset from the culture relationship, where the offset can be explained by secretion of gametogenic calcite at greater water depth. This offset (0.84‰) is subtracted from the intercept of the culture regression to define the sedimentary calibration of δ¹¹B_{T. sacculifer} calcite to δ¹¹B borate. Linear regression is a York fit [York et al., 2004, Matlab script York_fit.m] which incorporates x and y uncertainty for each datum; slope and intercept uncertainties are 2σ.

In comparison, the published calibration for T. sacculifer using the MC-ICP-MS technique [Martínez-Botí et al., 2015b] is:

$${\delta }^{11}{\text{B}}_{\text{borate}}=\left[{\delta }^{11}{\text{B}}_{T.\mathit{\text{sacculifer}}\text{MC}-\text{ICP}-\text{MS}}-3.60(\pm 0.72)\right]/0.83(\pm 0.04)$$ (Eq. 3)

While the slope of the MC-ICP-MS δ¹¹B_borate calibration is steeper (0.83 vs. 0.73), the additional culture data points in our N-TIMS calibration (5 instead of 3) allow for a more precise calibration. The primary difference between these technique-specific calibrations is the intercept value, which is the most important factor in aligning pH estimates from N-TIMS and MC-ICP-MS δ¹¹B analyses [Foster et al., 2013].

2.2. Temperature, salinity, and pressure estimates

Here we present new Mg/Ca-based estimates of SST using G. ruber from Site 668B and T. sacculifer from Site 999A. Due to the limited availability of large T. sacculifer tests from Site 668B, tests of G. ruber (sensu stricto, white) were used to estimate surface ocean temperature for this site. Globigerinoides ruber shares the near-surface ocean habitat of large T. sacculifer specimens [Ravelo and Fairbanks, 1992; Spero et al., 2003; Farmer et al., 2007]. For Site 668B, 40–60 G. ruber tests were picked from the 300–355 μm size fraction. For Site 999A, 40 shells of T. sacculifer were picked from the 425–500 μm size fraction, the same species and size fraction of planktic foraminifera as the original δ¹¹B data [Bartoli et al., 2011]. Shells were then gently broken and cleaned following established protocol including both the oxidative and reductive steps [Boyle and Keigwin, 1985; Mashiotta et al., 1999]. Inclusion of the reductive step is generally preferred for Mg/Ca analysis as it is more effective at removing high-Mg contaminants such as authigenic metals precipitated after deposition in the sediment, even though it has been shown to lower Mg/Ca values beyond their original value [Martin and Lea, 2002; Weldeab et al., 2006]. Because the Mg/Ca-temperature calibration we use [Anand et al., 2003] is based on sediment trap samples and therefore did not apply reductive cleaning, we account for reductive cleaning bias by adding 10% to the measured Mg/Ca ratio of our samples [Martin and Lea, 2002]. Mg/Ca ratios were measured via ICPMS (iCAP-Q) at the Lamont-Doherty Earth Observatory. The 2σ standard error for repeated measurements of internal foraminifer reference standards is ±2.2%, or ~±0.08 mmol/mol. This SST calibration carries a larger uncertainty (±2.4 K, 2σ) than that of the Mg/Ca measurement uncertainty (~±0.24 K) and we adopt the larger calibration uncertainty for seawater temperature estimates. As our samples are derived from a time period when the Mg/Ca value of seawater (Mg/Ca_sw) was likely lower than the modern value of 5.2 mmol/mol, a correction is needed for this change in seawater constituents [Delaney et al., 1985; Fantle and DePaolo, 2005; 2006; Medina-Elizalde et al., 2008; O’Brien et al., 2014; Evans et al., 2016]. To facilitate this correction, Mg/Ca_sw values are taken from reported pore fluid chemistry and numerical modeling [Figure S7, Fantle and DePaolo, 2006]. This Mg/Ca_sw dataset is within the uncertainty of Mg/Ca_sw values estimated from fluid inclusions in marine evaporites, the most recent of which is Messinian in age (5–6 Ma, Mg/Ca_sw ~ 3.6 mmol/mol) [Horita et al., 2002; Brennan et al., 2013]. If data from marine evaporite fluid inclusions were considered alone, and Mg/Ca_sw values are linearly extrapolated from 5.5 Ma to present, the resulting SST would be ~0.7 K lower and calculated pCO₂ would be ~5 μatm higher. The SST calibration we use includes the power-law modification suggested by Evans and Müller [2012] and the T. sacculifer exponential H-value of 0.41 [Delaney et al., 1985; Evans and Müller, 2012]:

$$SST\left(°\text{C}\right)=\text{ln}\left[\left({(Mg/Ca)}_{\text{calcite}}*{\left({(Mg/Ca)}_{\text{sw}}{}^{\text{t}=0}\right)}^{\text{H}}\right)/\left(0.38*{\left({(Mg/Ca)}_{\text{sw}}{}^{\text{t}}\right)}^{\text{H}}\right)\right]/0.09$$ (Eq. 4)

where (Mg/Ca)^t_sw is the Mg/Ca ratio of seawater at time t. This approach is commonly used to reconstruct temperature in this time period [e.g., Martínez-Botí et al., 2015a; Chalk et al., 2017]. The correction for dissolution with depth [Dekens et al., 2002] is omitted for all records in this study, as all study sites are well above the regional tropical Atlantic lysocline (4200 m water depth), and bottom water is saturated with respect to calcium carbonate [Key et al., 2004; Regenberg et al., 2006]. Hönisch et al. [2013] have demonstrated that adjusting Mg/Ca data from sediments above the lysocline effectively overestimates actual calcification temperatures.

Pleistocene salinity was calculated as a function of relative mean sea level (RMSL) as determined via a numerical ice-ocean model [Bintanja and van de Wal, 2008]. The change in local salinity is approximately proportional to the change in global average salinity due to glacial-interglacial sea level change. The equation used is

$$\mathit{\text{Salinit}}{y}_{668\text{B}}=35.8{\%}_0+\mathit{\text{RMSL}}/3800\text{m}*34.8{\%}_0$$ (Eq. 5)

where 35.8‰ is the modern salinity of the mixed layer (50 m water depth) at Site 668B [Zweng et al., 2013], 3800 m is the average depth of the ocean and 34.8‰ is the average salinity of the modern ocean. These estimates agree (within uncertainty) with local salinity estimates derived from using Mg/Ca-based SST and calcite δ¹⁸O to estimate the δ¹⁸O of seawater (δ¹⁸O_sw, Figure 3) [Bemis et al., 1998; Legrande and Schmidt, 2006].

Figure 3.

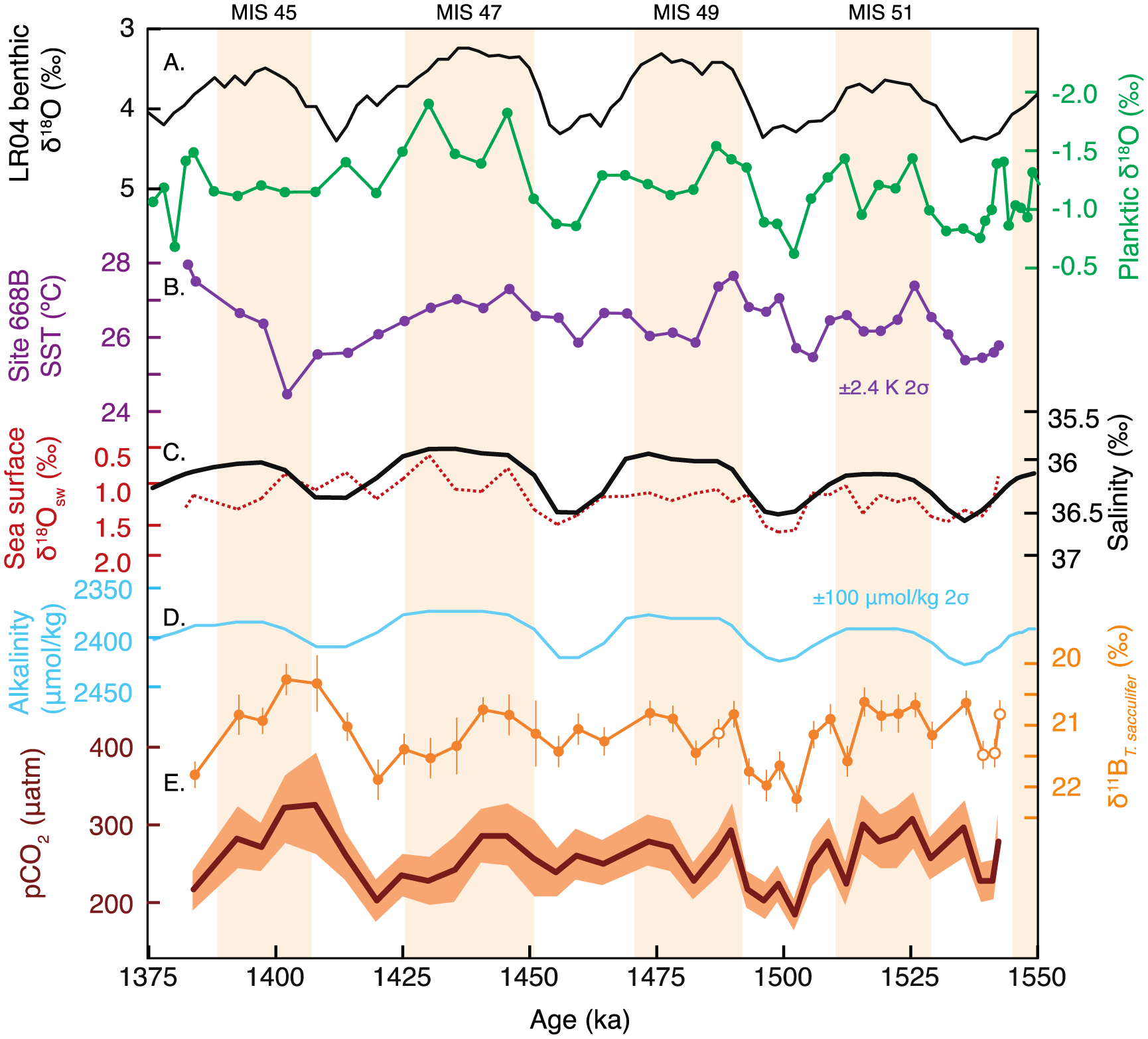
Site 668B orbital-scale records of the early Pleistocene from planktic foraminifera. (A) Site 668B planktic δ¹⁸O data [green, Hönisch et al., 2009] reflect local temperature and δ¹⁸O_sw. (B) SST based on planktic Mg/Ca (purple, uncertainty is ±2.4 K (2σ)). (C) Calculated δ¹⁸O_sw from planktic δ¹⁸O and Mg/Ca-based SST (red) and compared with salinity modeled from global sea level [black, Bintanja and van de Wal, 2008]. (D) Alkalinity based on local modern relationship with salinity. (E) Planktic δ¹¹B data contain minima and maxima in line with glacial and interglacial periods; uncertainty is 2σ and open circles are from Hönisch et al. [2009]. Surface ocean pCO₂ is calculated using pH (as estimated from δ¹¹B, SST, and salinity) and estimated alkalinity; the uncertainty band reflects the propagated 2σ uncertainty, the largest source of which is contributed by the analytical uncertainty of δ¹¹B_calcite.

In situ seawater pressure is also required and is a function of the foraminiferal calcification depth. Here we assume a calcification depth for both G. ruber and T. sacculifer of 50 m [Schiebel and Hemleben, 2005; Farmer et al., 2007] and a corresponding seawater pressure of 50 decibars. The pressure effect on equilibrium constants is small; an uncertainty of ±50 m water depth results in an uncertainty in calculated pH of ±0.002 and pCO₂ of ±1 μatm.

2.3. Alkalinity estimates

In order to calculate the partial pressure of CO₂ in seawater, a second variable of the ocean carbonate system is required [e.g., Zeebe and Wolf-Gladrow, 2001]. Here, alkalinity is estimated from the modern local alkalinity-to-salinity relationship following the ‘constant alkalinity’ scenario of previous studies, which assumes that total alkalinity in the ocean remained constant in the past [Hönisch and Hemming, 2005; Hönisch et al., 2009]. The local alkalinity-to-salinity relationship was developed using WOCE and GLODAP databases [Schlitzer, 2000; Key et al., 2004] covering the area 0–10°N and 10–20°W [Hönisch and Hemming, 2005; Hönisch et al., 2009].

$$\mathit{\text{Total}}\mathit{\text{Alkalinit}}{y}_{668\text{B}}=65.62*\mathit{\text{Salinit}}{y}_{668\text{B}}+22.84$$ (Eq. 6)

Over long timescales (tens to hundreds of thousands of years) the local alkalinity-to-salinity relationship could deviate from the modern relationship as a function of the Canadian Shield silicate weathering contribution to global weathering rates, where increased weathering would have added alkalinity to the ocean [Clark et al., 2006]. Even though the relative contribution of such differential weathering is weakly constrained, the absolute impact on paleo-alkalinity is relatively small. Models show that varying the contribution of Canadian Shield weathering to the total ocean alkalinity budget of between 0 and 8% (Figure S2) only change the total ocean alkalinity in the Pleistocene by ~50 μmol/kg [Clark et al., 2006]. To account for the potential effect of differential weathering on the local alkalinity-to-salinity ratio for past time periods, we include an alkalinity uncertainty of ±100 μmol/kg for the past 1.8 Ma.

2.4. Calculation of pCO₂

Aqueous CO₂ (differentiated as PCO₂) values are calculated from estimates of pH (total scale), alkalinity, salinity, temperature, and pressure using CO2SYS [version 2.3, Pierrot et al., 2006]. Within this program, we selected the recommended default values of pK₁ and pK₂ from Lueker et al. [2000], KHSO₄ from Dickson [1990], KHF from Perez and Fraga [1987], and [B]_T from Lee et al. [2010]. As described above, aqueous PCO₂ at site 668B is in equilibrium with the atmosphere in the modern ocean [Takahashi et al., 2009] and comparison of boron isotope estimates with ice core records suggests it was also in equilibrium over the past 800 kyr [Hönisch and Hemming, 2005; Hönisch et al., 2009]. We therefore interpret our aqueous paleo-PCO₂ estimates from Site 668B as equivalent to atmospheric paleo-pCO₂. In order to directly compare with δ¹¹B records from Site 999A, we translate δ¹¹B-based aqueous PCO₂ records from Site 999 to atmospheric pCO₂ by subtracting the annual average pre-industrial disequilibrium value (21 μatm) as justified by Henehan et al. [2013] who accounted for the modern seasonal ΔpCO₂ difference and a small correction for pre-industrial PCO₂ [Gloor et al., 2003; Takahashi et al., 2009].

2.5. Uncertainty

Uncertainty in the pH estimate is a function of the propagated 2σ uncertainties in the δ¹¹B measurement on δ¹¹B_borate, the uncertainty in δ¹¹ B_sw, and the effect of temperature and salinity uncertainties on the dissociation constants of boric and carbonic acid in seawater. We report uncertainty in pH as the root-mean-square error of the effect each parameter uncertainty has on pH: the δ¹¹B measurement and δ¹¹B_borate calibration (±0.03 pH units, ~80% coming from analytical uncertainty), the estimate of δ¹¹B_sw (±0.01 pH units at 1.5 Ma), the temperature constraints (calibration uncertainty equates to ±0.02 pH units) and salinity (±0.01 pH units). Uncertainty is calculated on a sample-by-sample basis; average total pH uncertainty of the Site 668B data is ±0.043 (2σ). Uncertainty in the pCO₂ calculation is likewise a function of uncertainty in the overall input parameters: the δ¹¹B measurement and calibration (±23 μatm), alkalinity (±12 μatm), and the effects of temperature (±19 μatm) and salinity (±3 μatm). Uncertainty in PCO₂ is similarly calculated on a sample-by-sample basis; average total PCO₂ uncertainty is ±33 μatm (2σ) for the newly estimated PCO₂ values at ~1.5 Ma.

2.6. Chronology

The age model for ODP Site 668B was initially constructed from microfossil occurrence data and estimates of the depths of geomagnetic reversals [Shipboard Scientific Party, 1988]. This initial chronology was later tuned through the alignment of glacial-interglacial cycles in the high-resolution planktic (G. ruber) δ¹⁸O values of Site 668B [Bird and Cali, 1998; 2002; Hönisch et al., 2009] with the well-dated planktic δ¹⁸O values of ODP Site 677 [Shackleton et al., 1990] and the LR04 benthic δ¹⁸O stack [Lisiecki and Raymo, 2005]. In order to resolve planktic δ¹⁸O mismatches between Sites 668B and 677 during MIS 48–52 (1.45–1.53 ka), we used AnalySeries software [Paillard et al., 1996] to add tie points which refine the planktic δ¹⁸O alignment. All ages younger than 1.3 Ma (19 m core depth) are unchanged from the previously published age model [Hönisch et al., 2009]. The revised age model for the period prior to 1.3 Ma (core depths 19–26 m) improves the planktic δ¹⁸O correlation coefficient (Pearson R²) between Sites 677 and 668B from ~0.31 to ~0.40 and reconstructed ages are up to 15% younger than previously estimated (Figure S3). The updated age model also conforms to the original ODP geomagnetic constraints, which placed the top of the Olduvai reversal (1.78 Ma) at 2.725 m core depth [Shipboard Scientific Party, 1988], just beyond the oldest available δ¹⁸O values from Site 668B (Figure S3). Unfortunately, the age uncertainty of the underlying benthic δ¹⁸O stack is ±6 kyr in the early Pleistocene [Lisiecki and Raymo, 2005]; this age uncertainty prevents the determination of leads or lags that are shorter than this confidence interval.

2.7. Comparison with other δ¹¹B-based PCO₂ records

For comparison between this new record and other previously published Pleistocene δ¹¹B-based PCO₂ records, we compile PCO₂ estimates from δ¹¹B data from Site 668B and Site 999A in the tropical Atlantic. These two sites present a good comparison as ocean-atmosphere disequilibrium is small at both locations. In order to rule out methodological differences, we calculated PCO₂ from each published record using equivalent input parameters and technique-specific calibrations. The original Site 668B δ¹¹B_{T. sacculifer} data [Hönisch et al., 2009] are used to recalculate pH and PCO₂ using the above methods (Section 2.1–2.6). The δ¹¹B calibration for this dataset is updated (Eq. 2) and δ¹¹B_sw is assumed to be 39.61‰ throughout. Temperature is calculated via the same Anand et al. [2003] calibration, after correcting for changes in seawater Mg/Ca (Eq. 4).

The δ¹¹B_{T. sacculifer} data of ODP 999A [Bartoli et al., 2011] were also revised using similar methods described above. To do so, we first generated new Mg/Ca data from the same or adjacent samples used for δ¹¹B analysis (see section 2.2). In the original study, SST was interpolated from T. sacculifer Mg/Ca values [Groeneveld, 2005] with a different temporal resolution than the δ¹¹B samples; our new temperature data reduce the interpolation of temperature estimates. Furthermore, the original SST record used the depth-based dissolution correction of Dekens et al. [2002], along with an outdated modern Mg/Ca_sw value of 4.96 mmol/mol. Due to omission of the depth correction, the SST estimated for this record is on average 1.8 K cooler than SST in the original publication (Figure S4) which places interglacial SST in agreement with modern SST at this location, whether taken from an annual average of modern direct measurements (27.7 °C) [Locarnini et al., 2013] or estimated from core top Mg/Ca values (28.2 °C) [Henehan et al., 2013]. Site 999A (water depth 2839 m) is situated well above the regional lysocline (4200 m) and T. sacculifer shells are not subject to preferential high-Mg calcite dissolution at this water depth [Regenberg et al., 2006]. Taken together, the omission of the depth correction thus appears well justified.

Additionally, Bartoli et al. [2011] used modeled surface ocean [CO₃^2-] estimates as the second parameter of the carbonate system and paired them with their δ¹¹B-pH estimates and to calculate PCO₂. Because pH and [CO₃²⁻] are closely related in carbonate equilibria, pairing them in carbon system calculations produces large variations in the calculated parameters. For instance, the pH and [CO₃^2-] estimates of Bartoli et al. [2011] combine to yield glacial-interglacial total alkalinity variations of up ~800 μmol/kg (Figure S5). Such a large change in ocean alkalinity is unlikely over these timescales as alkalinity is stabilized by the distribution of calcium carbonate accumulation and dissolution (carbonate compensation) in the deep sea on scales of thousands of years [Broecker, 1971; Broecker and Peng, 1987; Boyle, 1988]. Extrapolating from LGM estimates of alkalinity and lysocline depth, an 800 μmol/kg decrease in alkalinity would correspond to a >2 km shallower lysocline, which is difficult to reconcile with observations of relatively small changes (<0.5 km) in lysocline depth over the Pleistocene [Farrell and Prell, 1991]. Geochemical models also suggest smaller alkalinity adjustments, e.g. <400 μmol/kg over the past 10 million years [Figures 3d and 4d of Tyrrell and Zeebe, 2004] and <250 μmol/kg over the past 2.6 Ma [Clark et al., 2006]. We therefore revise the PCO₂ record of Bartoli et al. [2011] by using estimates of total alkalinity as the second carbonate system parameter; pH, salinity, and temperature are calculated in the same manner as for Site 668B (Sections 2.2, 2.4). Here alkalinity is calculated via the same regional relationship with salinity that was previously established for Site 999A [Foster, 2008].

$$\mathit{\text{Total}}\mathit{\text{Alkalinit}}{y}_{999\text{A}}=59.19*\mathit{\text{Salinit}}{y}_{999\text{A}}+229.08$$ (Eq. 7)

Figure 4.

Boron-based pCO₂ record compared with orbital-scale records of the early Pleistocene climate. (A) LR04 benthic oxygen isotope stack [black, Lisiecki and Raymo, 2005] reflects high-latitude temperature and ice volume changes on the dominant ~41-kyr ice age cycle during this interval. (B) Compilations of sea surface temperature records used to estimate change in global average surface temperature (dashed line from Martínez-Botí et al. [2015a] and solid line from Snyder [Snyder, 2016]). (C) Benthic carbon isotope gradients between Pacific and North Atlantic basins (solid light green line, Δδ¹³C_{Pacific-(North Atlantic)/2}) [Lisiecki, 2010] and between intermediate and deep water in the south Atlantic (dashed line) [Hodell and Venz-Curtis, 2006]. (D) Marine accumulation rate of Fe from ODP Site 1090 (solid line) [Martínez-Garcia et al., 2011]. (E) Calculated δ¹¹B-based surface ocean pCO₂ from Figure 3. (F, G) Summer insolation at 65°N (blue) and 65°S (red) and orbital parameters [Laskar et al., 2004].

To account for the potential impact of differential weathering on the local alkalinity-tosalinity ratio for these older samples, we increase the alkalinity uncertainty to ±175 μmol/kg for all samples older than 1.8 Ma. Older time periods (> ~2 Ma are less well constrained and so larger uncertainty estimates are used. In contrast to Chalk et al. [2017] who used constant alkalinity and therefore assumed the larger 175 μmol/kg uncertainty throughout, our uncertainty estimates are superimposed on the alkalinity changes based on sea level, and are therefore even more conservative than those use by Chalk et al. [2017].

Published boron isotope data are also available from G. ruber from Site 999A [Foster, 2008; Seki et al., 2010; Henehan et al., 2013; Martínez-Botí et al., 2015a; Chalk et al., 2017]. Boron-based PCO₂ reconstructions from both T. sacculifer and G. ruber have been extensively calibrated and both species provide convincing PCO₂ estimates compared to ice core records. Here we apply minor revisions to the published δ¹¹B_{G. ruber}-based PCO₂ calculations (namely, using a common SST calibration and assuming a constant δ¹¹B_sw over the past 5 Ma) with the goal of ensuring compatible comparisons among the results. All the published δ¹¹B_{G. ruber} values are translated to δ¹¹B_borate using the established species- and instrument-specific calibration of Henehan et al. [2013]:

$${\delta }^{11}{\text{B}}_{\text{borate }}=\left[{\delta }^{11}{\text{B}}_{G.\mathit{\text{ruber}}\text{MC-ICP-MS}}-8.87(\pm 1.52)\right]/0.60(\pm 0.09)$$ (Eq. 8)

In each case G. ruber specimens are from the 300–355 μm size fraction so any additional offset for size fraction is not required [Henehan et al., 2013].

The other parameters needed (temperature, salinity, δ¹¹B_sw, and alkalinity) are estimated consistently with Sections 2.1–2.6. In situ temperature is determined from Mg/Ca values as described by equation 4, except for the record of Seki et al. [2010] in which the alkenone unsaturation index is used for temperature reconstruction as in the original publication; alkenone-based temperatures are indistinguishable from Mg/Ca-based SST at this location. In all cases salinity is assessed from the modeled sea level estimates of Bintanja and van de Wal [2008], similar to equation 5, with modern salinity of the mixed layer (50 m water depth) at Site 999A of 36.2‰.

$$\mathit{\text{Salinit}}{y}_{999\text{A}}=36.2{\%}_0+\mathit{\text{RMSL}}/3800\text{m}*34.8{\%}_0$$ (Eq. 9)

For samples older than 3 Ma, the limit of the RMSL data set [Bintanja and van de Wal, 2008], the oldest value (S_{t=3.0 Ma} = 36.2‰) is used. An alternate method for calculating salinity used by previous publications is via the δ¹⁸O and Mg/Ca values of planktic calcite to find local δ¹⁸O_sw and then translate δ¹⁸O_sw to a salinity estimate. In practice, this method would result in average salinity ~0.4 lower than estimated above (Eq. 9), pH ~0.0002 lower, and PCO₂ ~1 μatm higher. Equations for this alternative salinity estimate can be found in the supplemental material.

3. Results

The ODP Site 668B boron-based PCO₂ record for the interval 1.38–1.54 Ma is presented in Figure 3. Within this time period δ¹¹B_{T. sacculifer} values range between a maximum of 22.19 (±0.21)‰ (1.502 Ma) and a minimum of 20.26 (±0.25)‰ (1.402 Ma) with an average δ¹¹B value of 21.14 (±0.16)‰. Calculated PCO₂ ranges between 183 (±21) μatm (at 1.502 Ma) and 327 (±61) μatm (at 1.408 Ma) with an average PCO₂ value of 258 (±29) μatm. The average amplitude of minimum glacial to maximum interglacial PCO₂ is 92 (±34) μatm (average of 4 interglacial maxima (304 (±46) μatm) minus average of 5 glacial minima (212 (±23) μatm); these uncertainties are based on the average uncertainty of the data points in question)).

The measured δ¹¹B_{T. sacculifer} value is the dominating parameter for the calculated PCO₂ record (Figure S6). To evaluate the respective effects of temperature, alkalinity, and salinity on the calculated PCO₂, we performed a simple sensitivity study in which δ¹¹B was held constant at the average value (21.15‰) while all other factors (temperature, alkalinity, salinity) varied as evaluated previously. When δ¹¹B_{T. sacculifer} is held constant, the secondary driver of the PCO₂ calculation is local SST, although even the full range of local SST (3.1 K) can only account for a maximum glacial-interglacial PCO₂ range of 24 μatm (Figure S6). Thus, the calculation of paleo-PCO₂ is driven primarily by changes in surface ocean pH as reflected in the raw δ¹¹B data; temperature, salinity, and alkalinity exert only a minor additional influence on the pH and PCO₂ estimates. This is in contrast to the potentially dominant effects other environmental parameters (i.e. [B(OH)₄⁻], [HCO₃⁻]) can have on B/Ca-based estimates of carbonate parameters [Tripati et al., 2011; Allen et al., 2012].

Published records of δ¹¹B-based PCO₂ were revised to be consistent with the given methodology above. Each parameter revision was tested individually to determine which parameter caused the greatest resulting PCO₂ shift from the original publication. In each instance, T. sacculifer δ¹¹B has been measured via N-TIMS and G. ruber δ¹¹B via MC-ICP MS. For the longer (0–1.8 Ma) Site 668B T. sacculifer dataset, average PCO₂ is +2 μatm higher than the published record [Hönisch et al., 2009]. This difference is composed of the assumption that δ¹¹B_sw was 39.61‰ rather than 39.5‰ (+6 μatm), the updated δ¹¹B_borate calibration (Eq. 2, −16 μatm), updated SST calibration (Eq. 4, +3 μatm), and alkalinity calculated via the ‘constant alkalinity scenario’ (Eq. 6, +14 μatm). For Site 999A (0–26 ka), average PCO₂ is also +12 μatm higher than the published record [Henehan et al., 2013], primarily due to the revised salinity and alkalinity estimations (Eq. 7 and 9). For Site 999A (0–1.24 Ma), average PCO₂ is +12 μatm higher than the published record [Chalk et al., 2017] also due to the revised salinity and alkalinity estimates. For the Site 999A study of Seki et al. [2010] (0–2.6 Ma), the revised average PCO₂ is +26 μatm higher than the published record [Seki et al., 2010], due to the updated calibration for the boron isotope proxy in G. ruber [Henehan et al., 2013]. For the Plio-Pleistocene (2.3–3.3 Ma) Site 999A G. ruber dataset, average PCO₂ is +12 μatm higher than the published record [Martínez-Botí et al., 2015b], primarily due to the revised assumption that seawater δ¹¹B_sw was constant at 39.61‰ over the past 5 Ma (Figure S1), whereas the original publication assumed a lower δ¹¹B_sw (~39.2‰) at the Plio-Pleistocene transition.

For the Plio-Pleistocene (1.97–4.6 Ma) Site 999A T. sacculifer dataset, average PCO₂ is 41 μatm lower than the published record [Bartoli et al., 2011], primarily due to the revised SST record which omits the depth-based dissolution correction (Eq. 4, SST 1.8 K cooler, −15 μatm) and the application of the pre-industrial disequilibrium value at this site (−21 μatm). The choice of alkalinity, rather than [CO₃^2-] as the second parameter of the carbonate system, reduces the glacial-interglacial PCO₂ amplitude of this record by 25% compared to the original publication (Figure S5). This finding highlights the volatile nature of the pH and [CO₃^2-] pair in constraining the carbonate system, i.e., a small uncertainty in [CO₃^2-] translates into a large shift in PCO₂ when paired with pH. The amplitude reduction is a result of both reducing the interglacial PCO₂ estimates and increasing the glacial PCO₂ estimates compared to the original record. All revisions were applied for consistency among calculations; the average PCO₂ change in all cases is smaller than the average 2σ uncertainty reported in the original studies.

4. Discussion

Given that late Pleistocene pCO₂ levels were closely correlated with both tropical SST [e.g., Lea, 2004; Herbert et al., 2010; Dyez and Ravelo, 2013] and high latitude surface temperatures [Petit et al., 1999; Jouzel et al., 2007], an equivalent relationship could be expected for early Pleistocene glacial-interglacial cycles. Here we add to the growing body of data evidence that a similar first-order relationship between global average temperature and pCO₂ also existed in the early Pleistocene, specifically in the interval 1.38–1.54 Ma (Figure 4). During interglacial periods δ¹¹B was lower (i.e., lower surface ocean pH and higher atmospheric pCO₂) and during glacial periods δ¹¹ B was higher (i.e., higher surface ocean pH and lower atmospheric pCO₂), in line with similar findings for the late Pleistocene period [Hönisch and Hemming, 2005; Henehan et al., 2013; Chalk et al., 2017]. To verify that our data are directly related to variation in atmospheric pCO₂, we need to evaluate a range of processes that could have biased our geochemical signals and interpretations.

First of all, ocean upwelling brings cooler and more CO₂-rich water to the surface; if upwelling had increased during glacial intervals at this location, we would expect to observe a larger glacial-interglacial SST amplitude than other open-ocean sites; if upwelling had increased during interglacial intervals, we would expect a smaller SST amplitude. The local temperature amplitude we measure from Mg/Ca values (i.e., average of 4 interglacial SST maxima minus average of 5 glacial SST minima) is 1.4 (±0.3) K, equivalent to other early Pleistocene tropical SST records, whether derived from the south China Sea [Site 1146; 1.4 K, Herbert et al., 2010], the western Pacific [Site 806; 1.2 K, Medina-Elizalde and Lea, 2005; Site 871; 1.2 K, Dyez and Ravelo, 2014], the south Pacific [MD06–3018; 1.3K, Russon et al., 2010], the tropical Atlantic [Site 662; 1.6 K, Herbert et al., 2010], or the Arabian Sea [Site 722; 1.1 K, Herbert et al., 2010]. The similarity of the SST amplitude at Site 668B to other tropical records implies that glacial-interglacial upwelling changes at this site were not substantial and did not preferentially influence either glacial or interglacial δ¹¹B values.

Secondly, shell diagenesis can occur after shells have been deposited on the ocean floor, potentially biasing our paleoenvironmental interpretations. However, in section 2 we already reasoned against potential dissolution at the sediment surface based on the shallow depth of the core tops and the much deeper Atlantic lysocline. Furthermore, the calcite saturation state of bottom water at this site is Ώ_CaCO3= 1.5 and bottom water Δ[CO₃^2-] = 34.5, both of which are higher than any site previously used for δ¹¹B-based pCO₂ estimates and above the range suggested for the onset of partial dissolution [de Villiers 2005; Dai et al., 2016]. If diagenesis lowered δ¹¹B values within the buried sediment, we would expect to also observe lower shell weights and higher planktic δ¹⁸O and δ¹³C values [e.g., Edgar et al., 2015]. We examined the correlations among these values and do not find any significant relationships to support the notion that diagenesis has occurred within the sediment column. Taken together with the expected range of glacial-interglacial SST presented above, we can reasonably infer that the δ¹¹B-based PCO₂ signal we measure is primary and has not been biased by incomplete preservation.

4.1. Early Pleistocene pCO₂ varied with obliquity-related climate cycles

To examine the glacial-interglacial linkages between pCO₂, temperature, and orbital climate parameters from the period 1.38–1.54 Ma, we created cross-plots of reconstructed pCO₂ with physiochemical measurements, orbital parameters, and global stacks of temperature and benthic δ¹⁸O (Figure 5). In this analysis, only data that are clearly associated with the broad maxima or minima in temperature and marine isotope stage are plotted, as determined by visual comparison with both a benthic δ¹⁸O values [Lisiecki and Raymo, 2005] and a global stack of surface temperatures [Snyder, 2016]. Omitted are intermediate data that fall between these climate extrema and, due to age model uncertainty, cannot be easily associated with a particular stage; the MIS intervals and maximum/minimum pCO₂ values are listed in Table S2.

Figure 5.

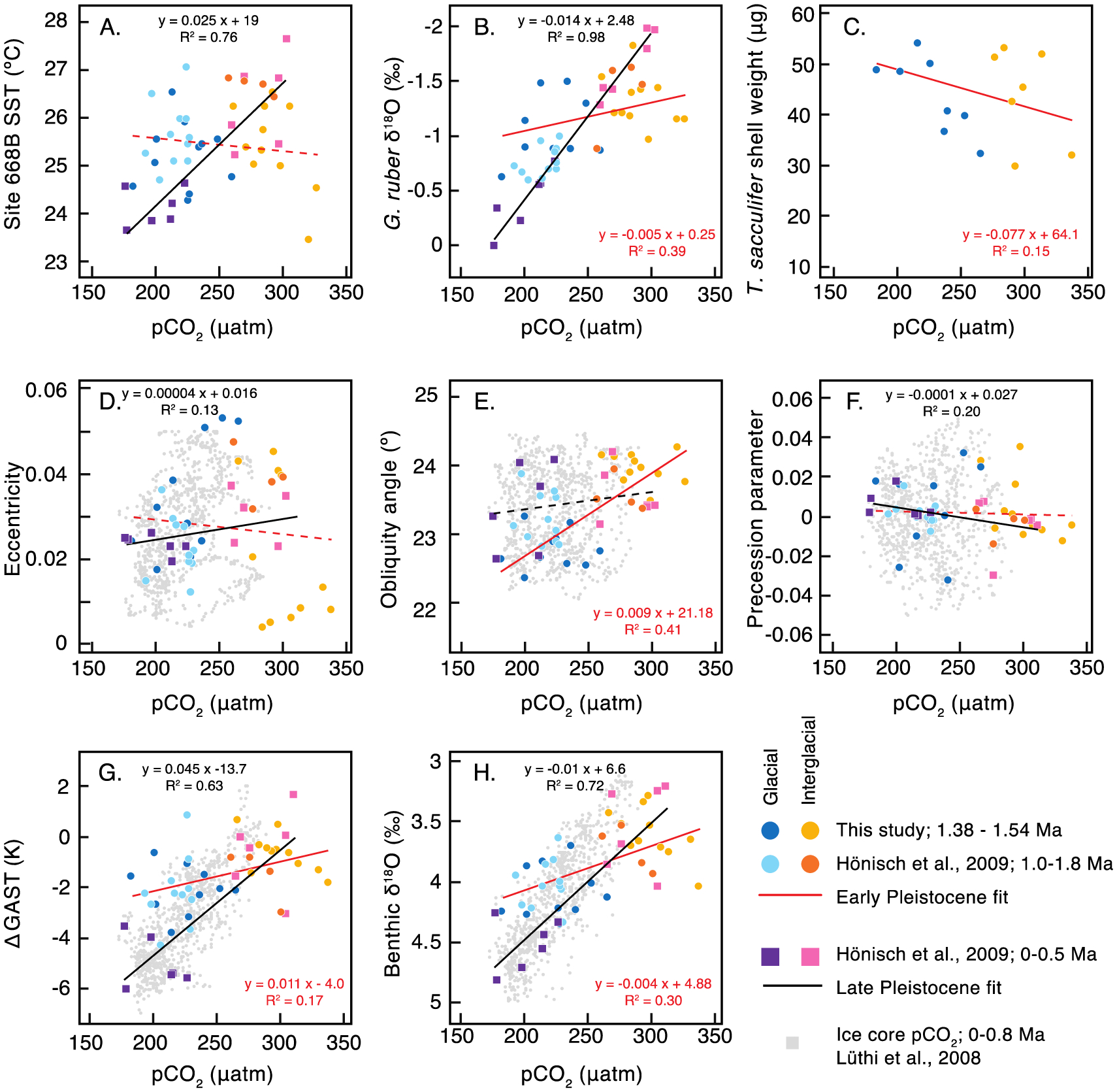
Cross plots of Site 668B peak MIS pCO₂ with Mg/Ca-based SST (A), G. ruber δ¹⁸O (B), T. sacculifer shell weight (C), coeval orbital parameters (D-F) [Laskar et al., 2004], surface temperature (G) and benthic δ¹⁸O (H). Late Pleistocene ice core pCO₂ is plotted for reference in gray [Bereiter et al., 2015], but not used for linear regressions. The linear fit of Early Pleistocene values (circles) is in red while the linear fit of late Pleistocene values (squares) is in black. Where R² > 0.1, regression equations are plotted and the linear fit is a solid line. Late Pleistocene pCO₂ is correlated with surface temperature and benthic δ¹⁸O, while early Pleistocene pCO₂ is associated with obliquity forcing. Precession parameter is calculated as the standard definition of precession (i.e., where ϖ is the angle between perihelion and vernal equinox on the orbital plane, precession is e*sin(ϖ)).

With which orbital cycle is pCO₂ most closely related in the early Pleistocene? Cross-plots show that in the late Pleistocene, periods of peak pCO₂ are associated with orbital eccentricity, but in the early Pleistocene peak interglacial pCO₂ is correlated with increased tilt (obliquity) in Earth’s rotation axis (Figure 5). The association of pCO₂ and obliquity supports the notion that pCO₂ was linked with the orbital insolation cycle and surface temperatures, even in the 41-kyr world before the mid-Pleistocene transition, but that the linkages took a different form, which resulted in climate that was in phase with obliquity. This finding is consistent with previously proposed hypotheses for maintaining ~41-kyr periodicity of glacial-interglacial change in the early Pleistocene, either through meridional temperature gradients or ice dynamics. In the early Pleistocene, the 41-kyr cycle could have been promoted by amplified equator-to-pole temperature gradients that carried additional moisture poleward to build ice sheets [Raymo and Nisancioglu, 2003] and/or by thinner, fast-spreading Laurentide ice sheets [Clark et al., 2006]. The glacial-interglacial temperature perturbations that drive glacial-interglacial climate would likely have been further amplified by obliquity-scale radiative pCO₂ feedbacks.

4.2. Glacial pCO₂ decreased through the Pleistocene

Site 668B δ¹¹B_{T. sacculifer} values indicate that early and late Pleistocene maximum interglacial pCO₂ did not change across the MPT (average interglacial peak pCO₂ at 1.2–1.8 Ma: 303 (±12) μatm, average interglacial peak pCO₂ at 0–0.5 Ma: 299 (±16) μatm (two-tailed t-test of all peak interglacial pCO₂ values, P>0.7). However, minimum glacial pCO₂ values declined by ~25 μatm between the early and late Pleistocene (average minimum pCO₂ at 1.2–1.8 Ma: 213 (±10) μatm, average minimum pCO₂ at 0–0.5 Ma: 187 (±10) μatm (two-tailed t-test of glacial minimum values, P<0.05). These pCO₂ estimates are congruent with proxy records of warmer glacial temperatures in the early Pleistocene than the late Pleistocene and support the initial observation that glacial pCO₂ declined across the MPT [Hönisch et al., 2009; Chalk et al., 2017]. While the collapse of North Atlantic deep-water formation around 900 ka coincides with this decrease in glacial pCO₂ [e.g., Pena and Goldstein, 2014], our atmospheric estimates do not allow us to determine the cause of the pCO₂ drawdown. However, the covariation of ocean circulation and pCO₂ shifts over the MPT to longer, colder glacial intervals highlights the close association of ocean dynamics, atmospheric circulation, and climate in the Pleistocene [e.g., Clark et al., 2006].

Glacial pCO₂ was higher in the early Pleistocene than the late Pleistocene, just as glacial temperatures were also 2–2.2 K warmer in the period 1.2–1.8 Ma than in the period 0–0.5 Ma based on multiple compilations of temperature change between the early and late Pleistocene [Herbert et al., 2010; Martínez-Botí et al., 2015a; Snyder, 2016]. If average surface temperature is due to the radiative pCO₂ forcing alone, an equilibrium response of global temperature to such forcing can be calculated. At its most basic, this calculation is commonly given in the form of S_[CO2] = ΔT/ΔF_[CO2] where ΔT (change in global average surface temperature) and ΔF_[CO2] (change in radiative forcing due to pCO₂) are millennial-scale averages and all other forcing mechanisms are regarded as internal feedbacks. Here the canonical radiative forcing due to CO₂ is used, where ΔF_[CO2] = 5.35 * ln(C/278 μatm) and C is atmospheric pCO₂ [Myhre et al., 1998]. For the early Pleistocene we thus calculate an equilibrium temperature response to radiative CO₂ forcing as S_[CO2] = 0.75 (±0.5) °C/Wm⁻². For the late Pleistocene, the parallel calculation yields S_[CO2] = 1.75 (±0.6) °C/Wm⁻² (Figure 6). To the first order, these relationships imply that climate sensitivity to radiative greenhouse gas forcing increased by a factor of ~2 between 1.2 and 0.5 Ma, largely driven by lower glacial-interglacial temperature amplitude in the early Pleistocene.

Figure 6.

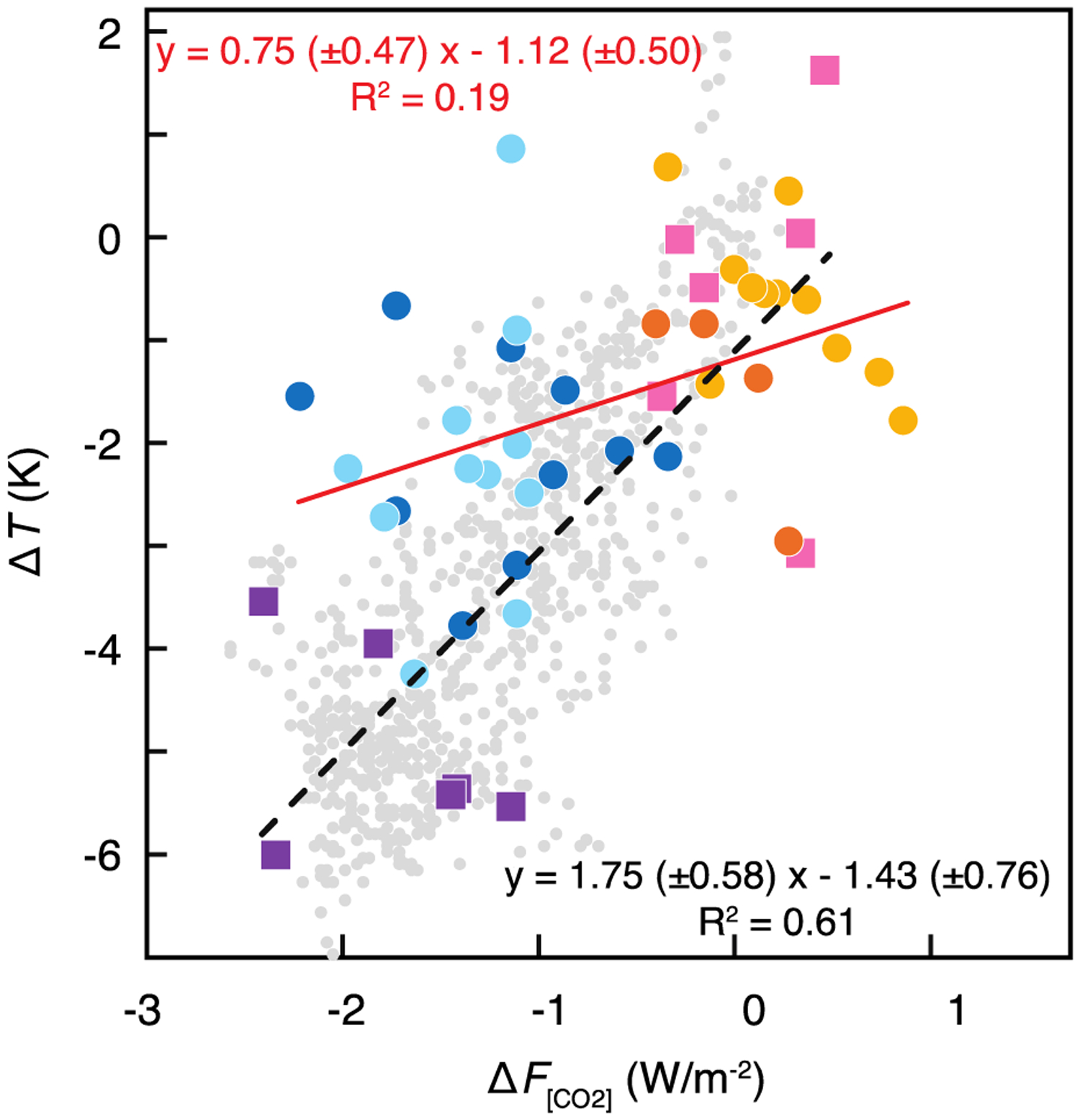
Cross plot of the change in global average surface temperature [ΔT; Snyder 2016] with the change in radiative pCO₂ forcing (ΔF_[CO2]; calculated after Myhre et al. [1998], relative to pre-industrial pCO₂ of 278 ppm). Colors are the same as in Figure 5, with fit through early Pleistocene (1.0–1.8 Ma) in red and fit through late Pleistocene data (0–0.8 Ma) in black. Note that this framework considers the contributions of other feedbacks as internal to the Pleistocene climate system.

In reality, however, climate feedbacks such as ice sheets and ocean circulation also amplify the range of global average temperature [e.g., Köhler et al., 2015; von der Heydt et al., 2016]. Recent studies have pointed out that in order to project the climate effects of rising pCO₂ levels in a warmer world with smaller ice sheets, climate sensitivity must account for the temperature response to each climate parameter separately (i.e., CO₂, ice sheets, etc.) [e.g., Köhler et al., 2015; Schmidt et al., 2017]. The lower early Pleistocene climate sensitivity calculated above is a result of comparing between time periods in which, at minimum, ice dynamics have changed [Raymo et al., 2006; Shakun et al., 2016]. Though this dataset does not allow us to quantify changes in albedo and atmospheric circulation, increased glacial ice volume (and vertical growth of ice sheets) at the MPT is an important change in the earth system that could have amplified glacial-interglacial temperature variability. Increased ice volume cools global temperature through two pathways: by increasing ice sheet extent, which increased global albedo, and through taller ice sheets, which deflected cold northern hemisphere atmospheric jets southward and compressed the subtropical atmospheric bands [Manabe and Broccoli, 1985; Shinn and Barron, 1989; Clark et al., 1999]. Qualitatively, then, these additional ice sheet and ocean feedbacks, in conjunction with lower atmospheric pCO₂, worked to cool glacial temperatures across the mid-Pleistocene transition.

4.3. Model comparison

We evaluate these reconstructions of early and late Pleistocene pCO₂ with a simple numerical box model that allows for an initial exploration of Pleistocene climate sensitivity given the available surface temperature and pCO₂ data. This model has three coupled components: ice sheets, temperature, and carbon dioxide levels. We force this model with atmospheric insolation over glacial cycles to explore the effect of Laurentide ice sheet changes for climate sensitivity. This model has been documented elsewhere [Schmidt et al., 2017]; briefly, this model includes coupling between ice sheet volume (L) and global average surface temperature (T) and between surface temperature and carbon dioxide levels (C) but does not incorporate 3D geography or topography. The model is initialized at the following mid-glacial values: T₀ = 285 K, C₀ = 230 μatm, L₀ = −60 m (meters of sea level equivalent). The sensitivity of ice sheets to temperature (a) and the non-Planck feedback (λ) are tested via 20×20 experiments (varying a = [0,30] mSL K⁻¹ and λ = [2.8,4.6] Wm⁻² K⁻¹). These parameters are consistent with the full range of late Pleistocene observations [Köhler et al., 2010].

We use this model to explore the qualitative impact of increasing ice volume on global climate at the MPT. Geochemical evidence and ice sheet models suggest that the Laurentide ice sheet of the early Pleistocene was thinner due to a “slippery” layer of weathered regolith over solid bedrock [Clark and Pollard, 1998; Clark et al., 2006], but that the spatial extent of land ice was similar to the late Pleistocene ice ages [Roy et al., 2004; Balco and Rovey, 2010]. Thus, the radiative forcing due to ice sheet albedo was roughly similar in the early and late Pleistocene, but the ice volume required (in equivalent meters of sea level fall) to acquire that forcing was smaller prior to ~1.0 Ma. We test the effect of radiative albedo forcing per ice sheet volume (μ) at 0.025 Wm⁻² mSL⁻¹ for the late Pleistocene such that late Pleistocene ice sheets cooled the global climate by 1 Wm⁻² for each 40 meters of equivalent sea level fall, consistent with what is assumed for ice-albedo cooling at the LGM [Köhler et al., 2010]. If the early Pleistocene Laurentide ice sheet was comparably expansive as in the late Pleistocene, but thinner, it can be thought of as more ‘efficient’ at radiative albedo cooling per unit volume of ice. We investigate this idea by testing the parameter μ (defined above) for the early Pleistocene at double and triple the late Pleistocene value: at 0.05 and 0.075 Wm⁻² mSL⁻¹. This exercise is not meant to fully simulate the climate system, but to explore elemental system sensitivity to a realistic range of radiative CO₂, insolation, and ice-sheet albedo forcing.

The results of this model suggest that if the efficiency of ice cooling (μ) were higher in the past, the amplitude of temperature variability and atmospheric CO₂ variability would also have been higher. When μ is doubled (or tripled), which simulates the large, but relatively thinner early Pleistocene northern hemisphere ice sheets, temperature and pCO₂ amplitude are ~40 (~80% for tripled μ) larger. However, we do not observe this phenomenon in the early Pleistocene geochemical datasets. Instead we observe lower temperature variability in the early Pleistocene, and a similar amplitude of atmospheric CO₂ variability as in the late Pleistocene. These observations could be a consequence of only considering northern hemisphere insolation and the impact on Laurentide ice. Out-of-phase insolation in the southern hemisphere could have driven Antarctic ice in the opposite direction and dampened overall atmospheric pCO₂ levels by modulating the Southern Ocean dynamics [Raymo et al., 2006]. Interhemispheric insolation differences tend to diminish the greater temperature variability that would be implied by greater northern hemisphere ice sheet efficiency in the early Pleistocene.

The simple model described above is also designed to explore the effect of changing Laurentide ice sheet dynamics on climate sensitivity. As the efficiency of ice sheet cooling per unit volume of ice was greater for the early Pleistocene conditions (model μ is increased from 0.025 to 0.075 Wm⁻²mSL⁻¹) the model suggests that earth system sensitivity (ESS) must be higher as well. This particular example indicates that a three-fold increase in μ would increase ESS from 3.0 to 5.1 K for a doubling of atmospheric CO₂. As stated previously, we observe the opposite in geochemical reconstructions of the early Pleistocene: because the early Pleistocene pCO₂ amplitude is only slightly smaller than the late Pleistocene pCO₂ amplitude, the associated temperature change with a climate sensitivity of 5.1 K per doubling of CO₂ would predict a temperature amplitude of ~4 K. In contrast, we observe a temperature amplitude of ~3 K and a correspondingly lower ESS in the early Pleistocene than in the late Pleistocene. This result simply suggests that earth’s surface temperature in the early Pleistocene is not solely determined by northern hemisphere ice sheets and CO₂ feedbacks. Rather, other forcing factors, which are not explicitly taken into account in this model (e.g., tropical and Southern Ocean dynamics, southern hemisphere insolation, Antarctic ice sheets) must be responsible for helping to dampen glacial-interglacial temperature amplitude in the early Pleistocene.

4.4. Species-specific differences; implications for Plio-Pleistocene pCO₂ drawdown

As the boron isotope proxy gains maturity and acceptance in the scientific community, the number of δ¹¹B-based datasets has increased, offering an opportunity to glean more detailed insight into the interplay between pCO₂ and climate. In Figure 7 we compile new pCO₂ estimates alongside ice-core records of late Pleistocene pCO₂ [Bereiter et al., 2015; Higgins et al., 2015] and six published records of δ¹¹B-based pCO₂. As described above, the δ¹¹ B-based pCO₂ data [Hönisch et al., 2009; Seki et al., 2010; Bartoli et al., 2011; Henehan et al., 2013; Martínez-Botí et al., 2015a; Chalk et al., 2017], have been recalculated to minimize differences in the chemical and physical boundary conditions estimated for each record (see Section 2.7). It is worth reiterating that the resulting pCO₂ values are primarily dependent on the published δ¹¹B measurements and that our minor revisions in boundary condition treatment do not shift average pCO₂ estimates outside of the published 2σ uncertainty bands.

Figure 7.

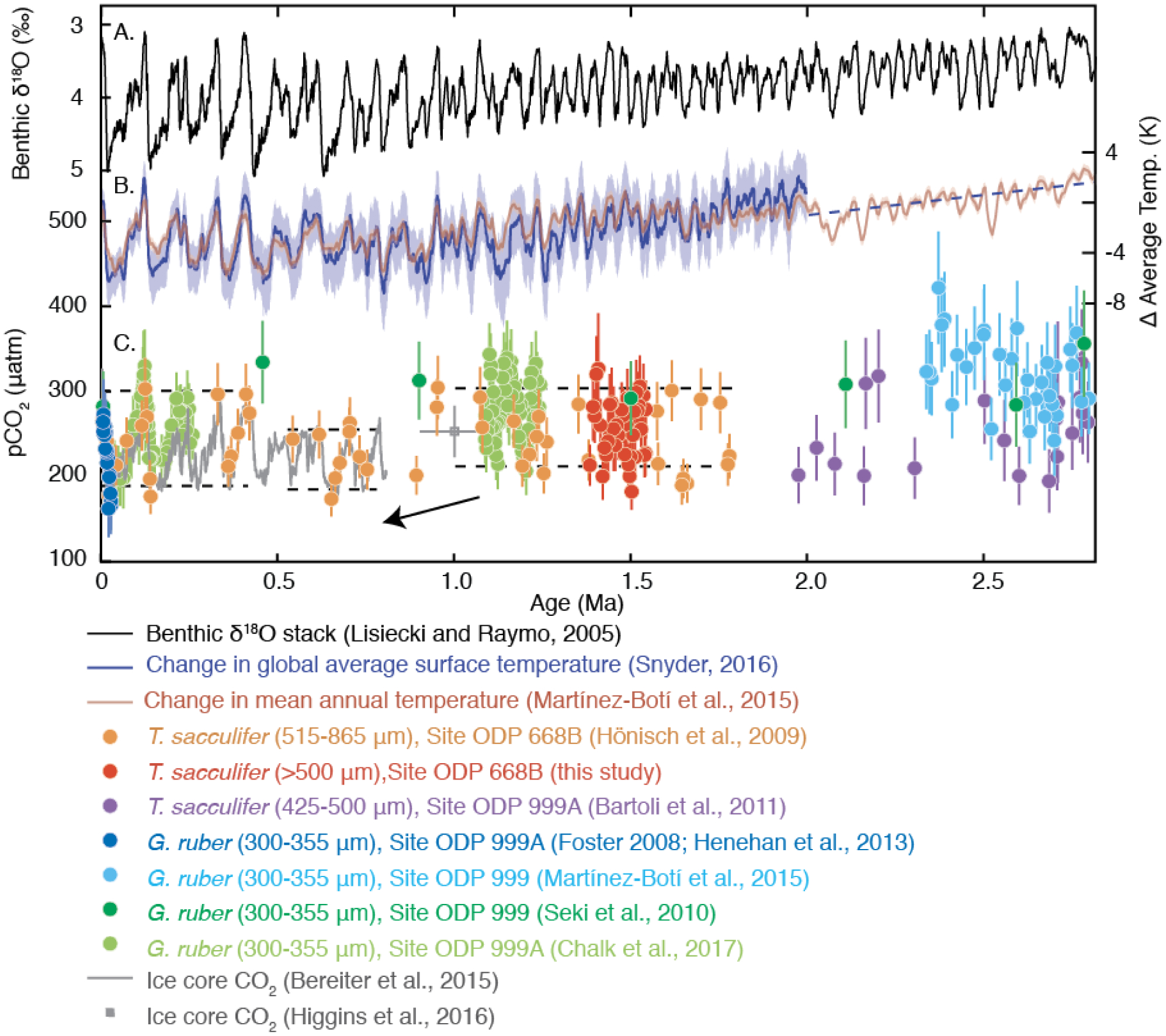
(A) Benthic δ¹⁸O [Lisiecki and Raymo, 2005] and (B) change in global average surface temperature (ΔGAST) [Snyder, 2016] compared with (C) pCO₂ derived from ice cores [Bereiter et al., 2015; Higgins et al., 2015] and boron isotope reconstructions [Hönisch et al., 2009; Seki et al., 2010; Bartoli et al., 2011; Henehan et al., 2013; Martínez-Botí et al., 2015a; Chalk et al., 2017]. Published pCO₂ records have been recalculated using consistent methods (see Methods) from the original δ¹¹B data. Late Pleistocene boron-based pCO₂ records from Sites 999A and 668B are in the same range as ice-core-based pCO₂ measurements. The largest resulting difference is the record of Bartoli et al. [2011], to which new temperature data have been applied and pCO₂ is calculated by pairing pH with alkalinity estimates rather than [CO₃^2-].

Paleo-pCO₂ estimates based on δ¹¹B values of either T. sacculifer or G. ruber [Bartoli et al., 2011; Martínez-Botí et al., 2015a] suggest that pCO₂ declined by 50–100 μatm between 2.8 and 2.6 Ma (Figure 8). This pCO₂ drawdown, coincident with the onset of northern hemisphere glaciation [Raymo, 1994; Haug et al., 1999] is thought to be the result of increased glacial dust load and greater biological productivity in high-nitrate low-chlorophyll regions [Bailey et al., 2011] or polar stratification which sequestered carbon in the deep ocean in both the north Pacific [e.g., Haug et al., 1999; Sigman et al., 2004] and the Southern Ocean [Hodell and Venz-Curtis, 2006; Waddell et al., 2009; Martínez-Garcia et al., 2011]. The pCO₂ initial drawdown at 2.8–2.6 Ma is implicated in the increased glaciation of Greenland and the northern hemisphere more broadly [Lunt et al., 2008].

Figure 8.

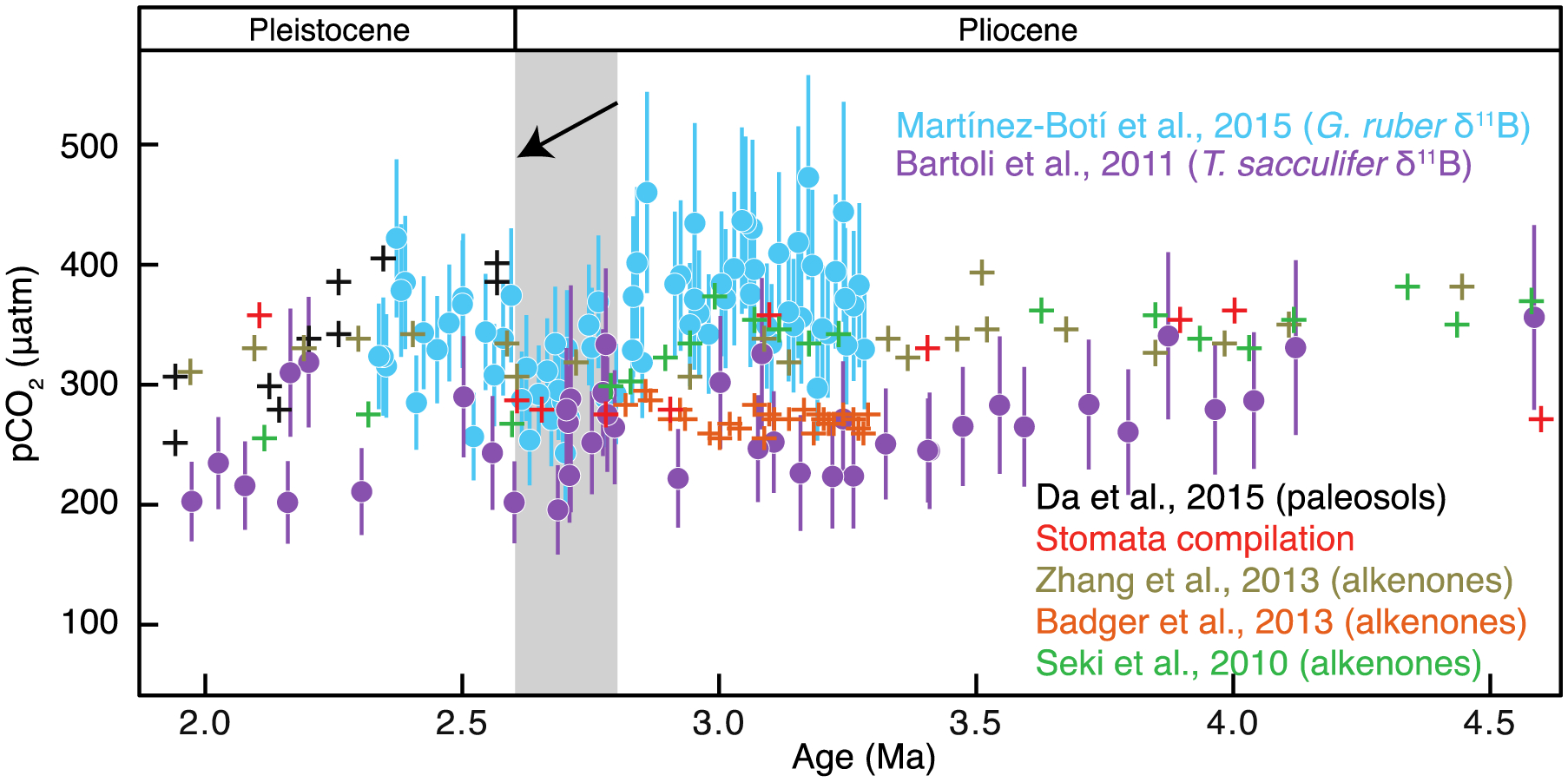
Revised pCO₂ values using δ¹¹ B from T. sacculifer [Bartoli et al., 2011] (purple) compared with pCO₂ from G. ruber [Martínez-Botí et al., 2015a] (blue). In the interval 2.8–2.6 Ma, G. ruber-based pCO₂ declines by >100 μatm, coincident with the onset of northern hemisphere glaciation (gray band, black arrow). Throughout the Pliocene, the T. sacculifer-based pCO₂ record is lower than G. ruber-based pCO₂ but also shifts to lower values at 2.7 Ma. The text discusses potential offsets due to evolutionary changes in foraminiferal physiology and consequent species-differences between pH and pCO₂ reconstructions. Paleo-pCO₂ reconstructions from paleosols [Da et al., 2015], stomatal indices [Kürschner et al., 1996; Retallack, 2009; Stults et al., 2011; Wang et al., 2015], and alkenone δ¹³C [Seki et al., 2010; Badger et al., 2013; Zhang et al., 2013] are intermediate between the estimates of Martínez-Botí et al. [2015a] and Bartoli et al. [2011].

Nonetheless, a distinct mismatch exists between the two δ¹¹B-based pCO₂ estimates from Site 999A (Figures 7, 8) for much of the late Pliocene. Where these two records overlap (from 3.3–2.3 Ma), the G. ruber-based pCO₂ estimates are on average 90 μatm higher than the T. sacculifer estimates (Figures 7, 8). This difference is apparent to a small degree even where G. ruber and T. sacculifer records overlap in the late Pleistocene, and as a mismatch between G. ruber and ice core records (Figure S8), although the species difference is larger further back in time. We can rule out discrepancies in environmental temperature as impacting the equilibrium constants because the Mg/Ca-based temperature reconstructions from the two datasets are indistinguishable (Figure S7–B). As we have already precluded inconsistent treatment of the physicochemical boundary conditions, the difference is more likely rooted in the underlying δ¹¹B data of G. ruber and T. sacculifer, where δ¹¹B_{G. ruber} decreases more strongly between the last glacial cycle and the late Pliocene than δ¹¹B_{T. sacculifer}. It is important to explore this discrepancy, which could be explained a biologically-mediated shift in the δ¹¹B_calcite to δ¹¹B_borate calibration (Figure S9), as differential pCO₂ results have important implications for Plio-Pleistocene climate research [e.g., Martínez-Botí et al., 2015a].

Differences in the pCO₂ reconstructions from these two surface dwelling foraminifera could in theory result from diagenetic alteration or incomplete sample cleaning. However, in the specific case of the late Pliocene data, evaluation of these factors is partly constrained by the fact that both species have been analyzed from the same sediment core. The first of these arguments relates to the potential bias due to partial dissolution, which typically lowers the δ¹¹B value by preferential removal of higher-δ¹¹B calcite [e.g., Hönisch and Hemming, 2004]. Both Pliocene data sets were measured using material from the same shallow core, so diagenetic alteration due to regional changes in the lysocline can reasonably be excluded. Could dissolution susceptibility be species-specific [e.g., Berger, 1967]? Higher pCO₂ estimates are based on relatively lower δ¹¹B values, suggesting that G. ruber would have to be relatively more dissolved that T. sacculifer. Shell-weight evidence indeed suggests that G. ruber is slightly more susceptible to partial dissolution than T. sacculifer based on in situ and laboratory work [e.g., Thunell and Honjo, 1981]. In actuality, however, studies of foraminiferal δ¹¹B from depth transects have suggested that G. ruber δ¹¹B values may be more robust and not greatly affected by partial dissolution [Ni et al., 2007; Seki et al., 2010; Henehan et al., 2013] and that the foraminiferal δ¹¹B signature is preserved even when the shell is visibly recrystallized [Edgar et al., 2015]. Another factor which could lower δ¹¹B values is contamination from pelagic clays, whose δ¹¹B values typically fall in the −7 to +5‰ range [Ishikawa and Nakamura, 1993] and are thus much lower than δ¹¹B of foraminiferal calcite. For the G. ruber pCO₂ estimates to agree with the T. sacculifer estimates, clay contamination would have to explain the −1‰ discrepancy in δ¹¹B_{G. ruber}. This would require the G. ruber samples to have contained ~5 wt % clay, which is unlikely given the robust cleaning protocol applied to remove impurities and the careful contaminant screening for aluminum and iron [e.g., Martínez-Botí et al., 2015a; Chalk et al., 2017].

At this point we have reasonably ruled out dissolution differences and clay contamination in addition to differential temperature calibrations, δ¹¹B_sw values, salinity, and alkalinity estimates. It is therefore more likely that the difference is biological. Although both foraminifera species and instrumental techniques have been calibrated using modern cultured and core top specimens and shown to replicate the ice-core pCO₂ record of the last glacial cycle [Hönisch and Hemming, 2004; 2005; Foster, 2008; Henehan et al., 2013; Chalk et al., 2017], one or both of the studied foraminifer species could have evolved prior to the last glacial cycle. One line of evidence for such an evolutionary shift has been described by Bartoli et al. [2011], who could not find enough Pliocene T. sacculifer specimens in the >500 μm test size fraction and instead substituted specimens in the 425–500 μm range. Hönisch and Hemming [2004] observed no significant difference in δ¹¹B_{T. sacculifer} between the 425–500 and >500 μm test size fraction, suggesting that the depth habitat and ecology is the same for both of the large size fractions. Indeed, if the overall smaller specimens of the largest size fraction in the early Pleistocene sediments had inhabited a deeper water depth, T. sacculifer should have recorded lower δ¹¹B, which would imply lower pH and elevated pCO₂. Instead, we observe the opposite pattern: T. sacculifer pCO₂ estimates are lower than those based on G. ruber [Seki et al., 2010; Martínez-Botí et al., 2015a; Chalk et al., 2017].

Could the response of G. ruber to ocean pH have evolved over the Plio-Pleistocene? Interestingly, in the modern Caribbean the pink variety of G. ruber is quite abundant, whereas the culture and global core top calibration of Henehan et al. [2013] is based on the white variety. The canonical G. ruber morphospecies represents up to five genetically distinct varieties each with non-unique ecological and biogeographic preferences. In contrast, T. sacculifer does not exhibit such cryptic diversity [Darling and Wade, 2008; André et al., 2012]. Confidence in the δ¹¹B proxy of pCO₂ in the Pliocene and early Pleistocene is strengthened by good proxy replication of pCO₂ with the ice core record (past 800 ka). In comparing the last two glacial cycles, average G. ruber δ¹¹B values are ~0.3‰ lower in MIS 6 even as pCO₂ derived from ice cores is nearly identical in MIS 2 and 6 [Chalk et al., 2017]. Using a consistent method for estimating temperature, in this case via Evans and Müller [2012], the pCO₂ calculated from G. ruber δ¹¹B is ~40 μatm higher in MIS 6 than in MIS 2. This result suggests that evolutionary differences in G. ruber could be as young as ~200 ka. Once again, the Mg/Ca-based temperatures derived from these two species do not diverge in the Plio-Pleistocene (3.3–2.3 Ma), which implies that the difference in reconstructed pCO₂ is less likely due to changes in habitat depth or seasonal preferences.

Finally, pCO₂ estimates from other proxy archives are at odds with the highest Pliocene G. ruber-based pCO₂ estimates (Figure 8). For example, evidence from the alkenone δ¹³C proxy suggests relatively lower (<350 μatm) levels of late Pliocene pCO₂, whether derived from Site 999A, (high resolution data: 270±40) [Badger et al., 2013], (low resolution data: 330±40) [Seki et al., 2010], or from Site 925 in eastern tropical Atlantic (320±40) [Zhang et al., 2013]. While different proxies have different uncertainties, the larger amplitude of Pliocene pCO₂ change in the G. ruber-based record (~150 μatm as opposed to ~100 μatm in the T. sacculifer-based record) is difficult to justify given the smaller amplitude of glacial-interglacial cycles in the Pliocene [Lisiecki and Raymo, 2005]. In summary, although we cannot unequivocally state which species may have changed behavior, it will be important to cross-calibrate the δ¹¹B proxy in the Pliocene with regard to potential physiological distinctions.

Importantly, both G. ruber and T. sacculifer record a pCO₂ decline through the Plio-Pleistocene (Figures 7, 8), but the extent of the pCO₂ decline is larger for G. ruber reconstructions and this has critical implications for estimates of climate sensitivity from these two species. If the Pliocene G. ruber-based pCO₂ estimate is correct, then late Pliocene (3.3–2.8 Ma) pCO₂ levels were relatively high (>350 μatm), and highly variable, and then dramatically declined at the onset of northern hemisphere glaciation. Martínez-Botí et al. [2015a] use this data to infer low sensitivity to radiative pCO₂ forcing in the Pliocene and higher sensitivity in the Pleistocene. They call out increased continental ice-albedo as the primary mechanism for this change in sensitivity and use, as one line of evidence, the inflection point at ~275 μatm in the relationship between benthic δ¹⁸O and forcing due to pCO₂ changes [Martínez-Botí et al., 2015a]. Here we replot this figure using all available datasets discussed herein, but we also separate the two species (Figure 9). Martínez-Botí et al. [2015a] originally excluded the data of Bartoli et al. [2011] from their plot to improve clarity, but it now emerges that the change in slope of the relationship observed by Martínez-Botí et al. [2015a] is only true for G. ruber but not for T. sacculifer (Figure 9). Explaining the larger Plio-Pleistocene CO₂ drawdown inferred by the G. ruber δ¹¹B record requires significant increases in ocean stratification, dust fertilization, and/or (potentially) silicate rock weathering since the Pliocene (e.g., Martinez-Garcia et al., 2011).

Figure 9.

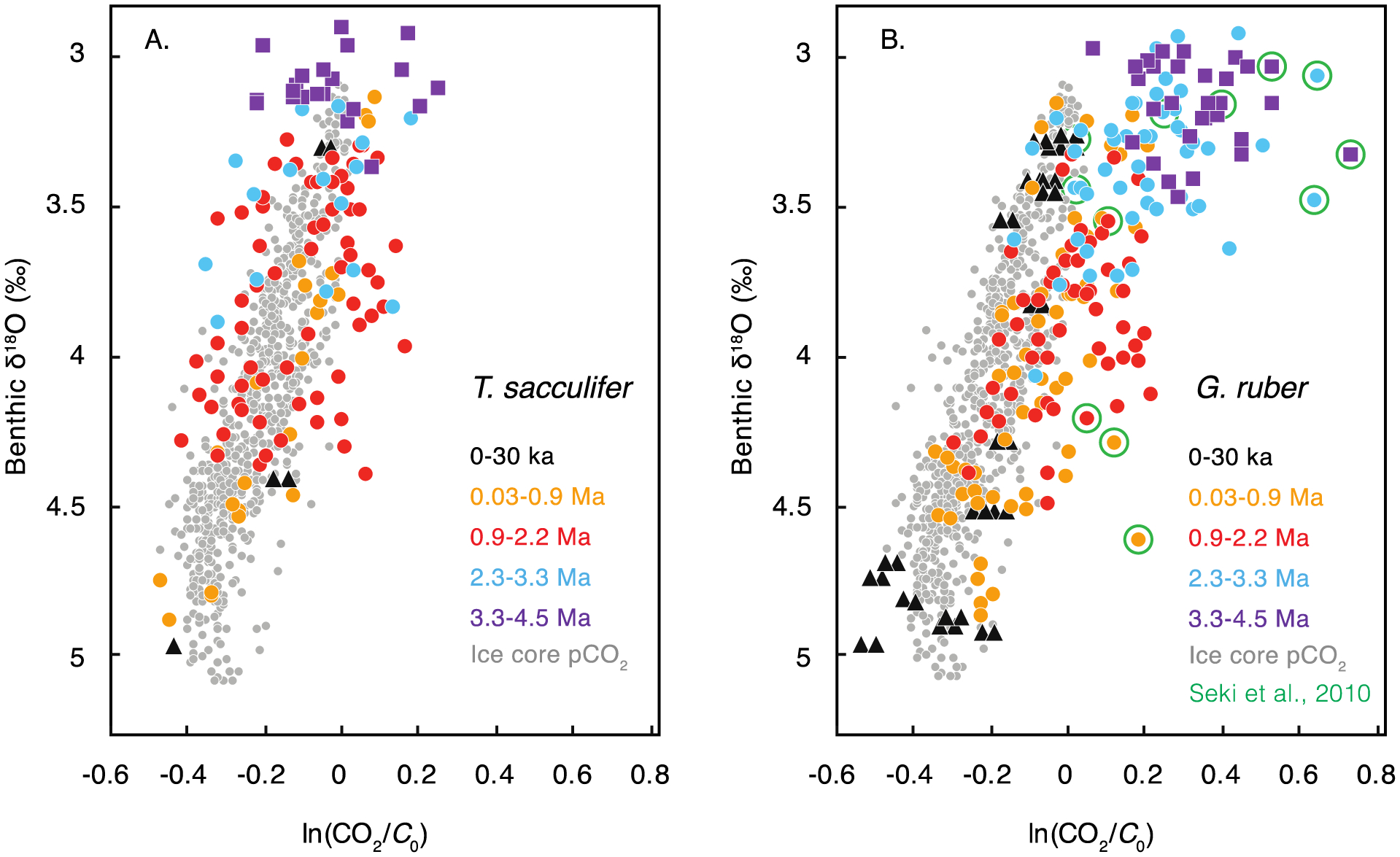
Relationship between benthic δ¹⁸O and climate forcing due to radiative CO₂ forcing (ln(CO₂/ C₀), where C₀ is 278 μatm), including all six δ¹¹B-based pCO₂ records presented in Figure 7. (A) Forcing derived from δ¹¹B_{T. sacculifer}-based pCO₂ compared with forcing from pCO₂ values derived from ice cores (gray). Time periods are coded by color, yet the overall benthic δ¹⁸O-to-ln(CO₂/C₀) relationship for boron-based pCO₂ data falls along the same relationship for pCO₂ as that derived from ice cores. (B) The corresponding relationship of boron-based CO₂ forcing compared with pCO₂ values from ice cores, this time using δ¹¹B values from G. ruber. Although Holocene and LGM pCO₂ values based on the foraminifer G. ruber are consistent with the ice-core pCO₂, the estimates deviate in earlier time periods, when pCO₂ values are higher than expected based on the general benthic δ¹⁸O : ln(CO₂/C₀) relationship derived from ice cores. This gives rise to the question of whether G. ruber and its vital effects evolved over time. Values derived from one early study are circled in green; these data are based on unusually low boron isotope values [Seki et al., 2010].

If, on the other hand, the Pliocene T. sacculifer-based pCO₂ estimates are correct, Pliocene pCO₂ was less elevated relative to early Pleistocene pCO₂ values and the linear relationship between benthic δ¹⁸O and pCO₂ forcing extended into the Pliocene (Figure 9A). The T. sacculifer-based estimates, with pCO₂ likely <350–400 μatm, support the evidence for lower Pliocene pCO₂ from other proxies (Figure 8): alkenone δ¹³C, stomatal indices, and paleosols [e.g., Badger et al., 2013; Da et al., 2015; Wang et al., 2015] and implies that atmospheric pCO₂ was relatively similar between the late Pliocene and early Pleistocene, despite the descent into cooler polar temperatures. If correct, this record implies that Arctic temperatures declined at the Plio-Pleistocene transition due to factors other than direct radiative pCO₂ forcing, such as the thickening of northern-hemisphere ice sheets or reduced poleward oceanic heat transport. Further work is warranted to improve our understanding of foraminiferal vital effects on δ¹¹B, and thereby improve confidence in paleo-pCO₂ estimates from this proxy.

5. Conclusions

Glacial-interglacial climate cycles in the early Pleistocene (>1 Ma) were shorter and less severe than the iconic 100-kyr cycles of the last 0.5 million years. Our new high-resolution record of atmospheric pCO₂ over three glacial cycles in the early Pleistocene (1.38–1.54 Ma) is closely linked with obliquity pacing, with an average pCO₂ amplitude of 92 (±13) μatm. Over the MPT, glacial pCO₂ declined, alongside glacial SST cooling in both the tropics and high latitudes. In contrast to an earlier assessment of climate sensitivity from δ¹¹B in G. ruber, our compilation of pCO₂ estimates from δ¹¹ B in T. sacculifer suggests apparent climate sensitivity in the early Pleistocene was lower compared to the late Pleistocene; the difference is likely due to changing ocean or ice sheet dynamics over the mid-Pleistocene. Using a simple model, we suggest that the lower climate sensitivity in the early Pleistocene was not directly related to the thinner, yet extensive, northern-hemisphere terrestrial ice sheets, but is rather a result of changing ocean dynamics in the southern hemisphere or tropics. The observed discrepancy in late Pliocene pCO₂ estimates based on G. ruber and T. sacculifer requires further study of potentially evolving species-specific vital effects in the past, so that paleo-pCO₂ estimates from the proxy can be appreciated with confidence.

Key points:

1. Early Pleistocene pCO₂ roughly varied with obliquity cycles.

2. Interglacial pCO₂ was similar in the early and late Pleistocene; glacial pCO₂ declined over the mid-Pleistocene transition.

3. Discrepancies between δ¹¹B values and corresponding pCO₂ estimates from G. ruber and T. sacculifer are observed and may indicate evolving vital effects.