Monitoring interannual variation in global crop yield using long-term AVHRR and MODIS observations

Abstract

Advanced Very High Resolution Radiometer (AVHRR) and Moderate Resolution Imaging Spectroradiometer (MODIS) data have been extensively applied for crop yield prediction because of their daily temporal resolution and a global coverage. This study investigated global crop yield using daily two band Enhanced Vegetation Index (EVI2) derived from AVHRR (1981–1999) and MODIS (2000–2013) observations at a spatial resolution of 0.05° (~5 km). Specifically, EVI2 temporal trajectory of crop growth was simulated using a hybrid piecewise logistic model (HPLM) for individual pixels, which was used to detect crop phenological metrics. The derived crop phenology was then applied to calculate crop greenness defined as EVI2 amplitude and EVI2 integration during annual crop growing seasons, which was further aggregated for croplands in each country, respectively. The interannual variations in EVI2 amplitude and EVI2 integration were combined to correlate to the variation in cereal yield from 1982–2012 for individual countries using a stepwise regression model, respectively. The results show that the confidence level of the established regression models was higher than 90% (P value < 0.1) in most countries in the northern hemisphere although it was relatively poor in the southern hemisphere (mainly in Africa). The error in the yield predication was relatively smaller in America, Europe and East Asia than that in Africa. In the 10 countries with largest cereal production across the world, the prediction error was less than 9% during past three decades. This suggests that crop phenology-controlled greenness from coarse resolution satellite data has the capability of predicting national crop yield across the world, which could provide timely and reliable crop information for global agricultural trade and policymakers.

1. Introduction

Global population continues to rise and will reach between 7.4 and 10.6 billion people on this planet by the year 2050 (United Nations, 2003). With growing population and rising per-capita consumption, the demand for cereals and grains is expected to increase 1.3% per year (Duvick and Cassman, 1999). During the twentieth century, agricultural productivity has greatly increased to keep pace with population growth through Green Revolution technologies, including the use of new high yielding varieties of rice, maize, and wheat, and through the application of fertilizers, irrigation, and pesticides (Kucharik and Ramankutty, 2005). With the increase of future food demand, the diminishing returns from advancements in agricultural technology, and the impacts of climate change on crop yield, global food security has become a great concern (Conway and Toenniessen, 1999; Rosegrant and Cline, 2003). Thus, monitoring of crop growing conditions and forecasting crop yield are significant for economic development and food security.

Satellite remote sensing has been demonstrated to be an effective tool in monitoring crop growth and yield over local, regional, national, and global extent (Alemu and Henebry, 2013; Beeri and Peled, 2009; Behmann et al., 2014; Gumma et al., 2014; Jiao et al., 2014; Steven, 1993; Tucker et al., 2005; Wagle et al., 2015; Wardlow and Egbert, 2008). The NOAA (National Oceanic and Atmospheric Administration) AVHRR (Advanced Very High Resolution Radiometer, available since 1981) and NASA (National Aeronautics and Space Administration) MODIS (Moderate Resolution Imaging Spectroradiometer, available since 2000) data are the most frequently used datasets for crop yield monitoring and predicting because of their daily observation and global coverage. Thus, such remote sensing data have been applied in various operational monitoring systems including the USAID Famine Early Warning System (FEWS-NET), the UN Food and Agriculture Organization (FAO) Global Information and Early Warning System (GIEWS), the Monitoring of Agriculture by Remote Sensing (MARS) Project of the Joint Research Centre in Europe (Csornai et al., 2003; ITA, 2002), Crop Watch Program in China, and the USDA Foreign Agricultural Service (FAS) Global Agriculture Monitoring (GLAM) System (Becker-Reshef et al., 2010).

Vegetation indices from satellites have been commonly used for the predication of crop production and yield because they provide a means for characterizing net primary productivity (NPP). Although various vegetation indices (such as ratio vegetation index, perpendicular vegetation index, and soil-adjusted vegetation index) have been investigated, Normalized Difference Vegetation Index (NDVI) is the most extensively used parameter to statistically correlate to crop growth and yield for spring and winter wheat, corn, rice, sorghum and soybeans across the world, such as the USA, Brazil, Argentina, Greece, Morocco, Zimbabwe, China, Mongolia, India, Poland and other countries (Groten, 1993; Gumma et al., 2014; Kogan et al., 2012; Maselli et al., 1993; Rasmussen, 1992; J.H. Zhang et al., 2014).

During a crop growing season, the integrated greenness and peak greenness are critical parameters in characterizing crop growth. The NDVI integrated during the crop growing season is an excellent measure of prevailing patterns of NPP, which is equivalent to a measure of the duration of green leaf area and gives a good description of the produced biomass and crop yield (Goward, 1987; Pinter et al., 1981; Tucker et al., 1983). NPP is a function of NDVI and photosynthetically active radiation (PAR) during a vegetation growing season because plant production of organic matter is proportionally related to both the absorbed radiation and reflected radiation by green vegetation (primarily leaves) (Running et al., 2000). Thus NDVI obtained over a growing season has been simply related to NPP (Chong et al., 1993; Loveland et al., 1991; Markon and Peterson, 2002; Paruelo et al., 1997). As a result, the NDVI integration during a growing season has been shown a better indicator of crop yield relative to the individual NDVI observations or average NDVI (Benedetti and Rossini, 1993; Esquerdo et al., 2011). On the other hand, several studies have demonstrated that the vegetation index reflecting peak greenness is the most effective parameter in forecasting crop yield (Bolton and Friedl, 2013; Groten, 1993; Rasmussen, 1992; Rembold et al., 2013). The crop peak NDVI occurs during the period between flowering and milky ripe (Shuai et al., 2013), which is a peak grain filling phase of crop growth (Funk and Budde, 2009). Moreover, some studies, such as Funk and Budde (2009), also suggest that the sum of NDVI increases during the mid-to-late season growing period should be a better indicator of crop yield. Evidently, the advantages of both NDVI integration and peak NDVI for crop yield prediction vary with crop types and geographic locations because parameters in statistical models are dependent on the quality of NDVI in representing crop growth and crop types in a given region (Rembold et al., 2013). Overall, AVHRR NDVI at a spatial resolution from 8 to 16 km and a temporal resolution from weekly to 16 days provided the crop yield predication with an accuracy of 8–15% at either entire country or administrative divisions (Dabrowska-Zielinska et al., 2002; Domenikiotis et al., 2004; Kogan et al., 2003, 2012, 2005; Liu and Kogan, 2002; Salazar et al., 2007; Singh et al., 2003). The limitation of the empirical prediction models is that it would be difficult to apply a model established in a specific geographic region across various environmental characteristics.

More recently, the Enhanced Vegetation Index (EVI), which is calculated from blue, red and near infrared reflectance (Huete et al., 2002), and a two-band variant of the Enhanced Vegetation Index (EVI2), which is calculated from red and near infrared reflectance (Jiang et al., 2008), have been demonstrated to be more effective in monitoring vegetation growth than NDVI. It is due to the fact that the EVI/EVI2 is less sensitive to different background soil reflectance and non-green winter land surface and remains sensitive to variation in dense canopy where NDVI becomes saturated (Huete et al., 2006; Rocha and Shaver, 2009). Specifically, EVI/ EVI2 is better than NDVI in discriminating land cover diversity (Mondal, 2011), monitoring maize area and yield (Bolton and Friedl, 2013; J.H. Zhang et al., 2014) and coffee yield in Brazil (Bernardes et al., 2012), estimating gross primary productivity (Xiao et al., 2005), capturing subtle change in vegetation condition and structure (Rocha and Shaver, 2009), and estimating the start of the green season (Zhang et al., 2004). From these studies, it is reasonable to suggest that EVI2 should be more effective in monitoring crop growth.

As the FAO indicated that timeliness is a major factor underlying agricultural statistics and associated monitoring systems globally (FAO, 2011), this study is expected to develop an approach for timely and reliable monitoring of global crop yield at national and international scales for global agricultural trade, policymakers, farmers, hedgers, and investors. Currently, the USDA FAS with its GLAM system is the only provider of regular, timely, objective crop production forecasts at a global scale (Becker-Reshef et al., 2010). The GLAM system is complex, which includes web-based technology, analysis tools, and satellite datasets, which enable FAS analysts to monitor crops and forecast yield and production of the major crops grown worldwide. On the other hand, simple models that directly link satellite vegetation indices to crop yield have been extensively established in a variety of local areas across the world (Bolton and Friedl, 2013; Dabrowska-Zielinska et al., 2002; Domenikiotis et al., 2004; Kogan et al., 2003, 2012, 2005; Liu and Kogan, 2002; Salazar et al., 2007; Singh et al., 2003). However, little study has been carried out to use the simple models for estimating crop yield across the world. Moreover, although crop phenology has been recognized as an effective index reflecting crop growth and yield, little research effort has been devoted to explicitly establishing crop growth trajectory for the accurate determination of crop greenness from daily satellite observation. Therefore, this study is to develop a simple approach for monitoring crop greenness which is a proxy of crop yield from long-term satellite data for individual countries across the world. To reach this goal, this study first simulated temporal trajectory of EVI2 from daily AVHRR (1981–1999) and MODIS (2000–2012) EVI2 data using a Hybrid Piecewise Logistic Model (HPLM), and then identified crop phenological metrics for each 0.05° (~5 km) pixel. The satellite crop phenology was further used to quantify interannual variation in both crop greenness at a peak season and integrated greenness during a growing season. By correlating satellite crop greenness to statistical crop yield data, the prediction models were finally established to predict national crop yield across the world.

2. Data and methods

2.1. Crop data

Cereal production and yield at a national scale from 1982–2012 were obtained from the World Bank (http://data.worldbank.org/indicator), which were originally from the FAO. The cereal crop types include wheat, rice, maize, barley, oats, rye, millet, sorghum, buckwheat, and mixed grains. Cereal yield is measured as kilograms per hectare of harvested land for dry grain only and production data are referred as to the total cereal crops harvested. Among the 214 counties or regions, there are 24 (such as Croatia, Estonia, Serbia, Russian Federation, and Ukraine) with data available after 1991–1999, respectively, and 39 without data (such as Singapore, Monaco, Kosovo, and Iceland).

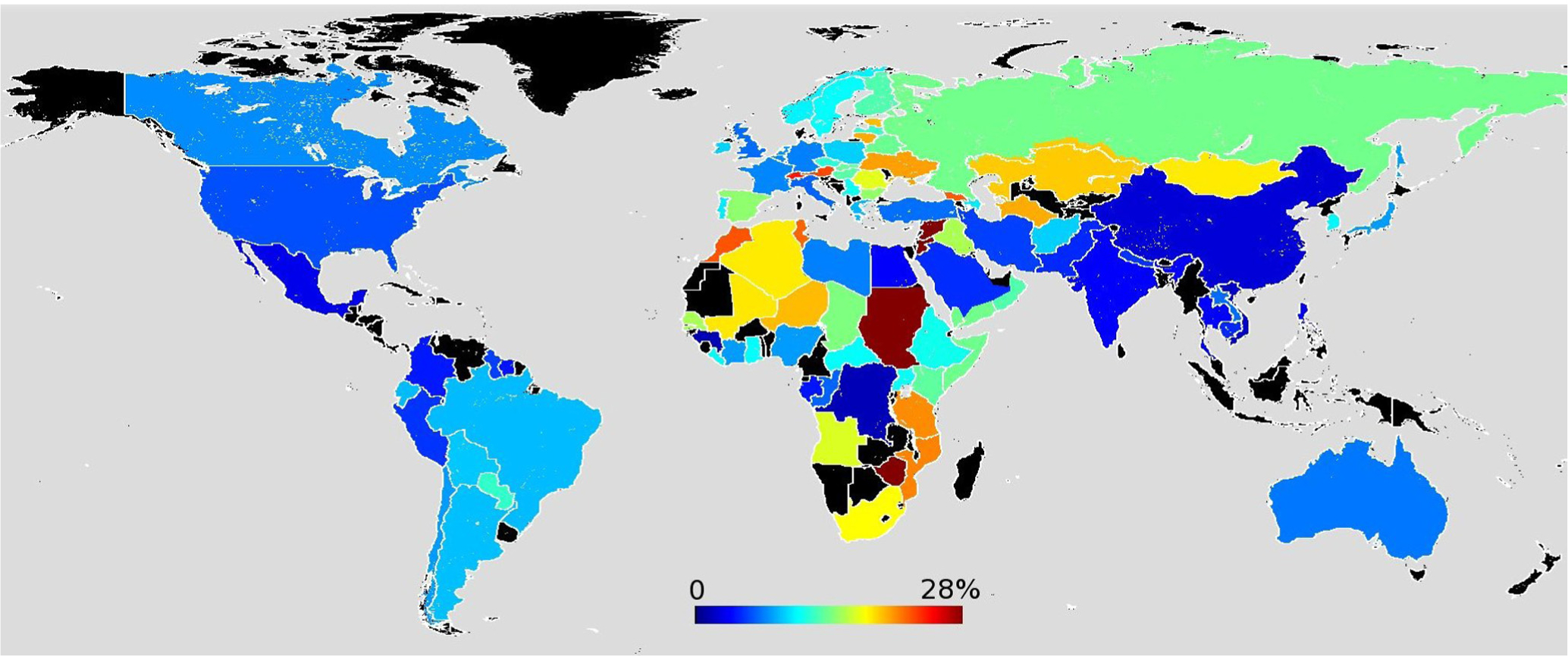
The global cereal production on average is mainly produced from China, the United States of America (USA) and India, which accounts for 51.8% of global production (Fig. 1). During last three decades, the cereal production increased steadily with a rate of 3.68 × 10⁶ tons/y, 4.34 × 10⁶ tons/y, 4.67 × 10⁶ tons/y, and 32.88 × 10⁶ tons/y for India, the USA, China, and the world, respectively. There were more than 80% and 14% of countries with an increase of cereal yield more than 20% and 80%, respectively (Fig. 2). However, the cereal yield varies greatly worldwide from 416 to 8742 kg/hectare at a national scale (Fig. 3).

Fig. 1.

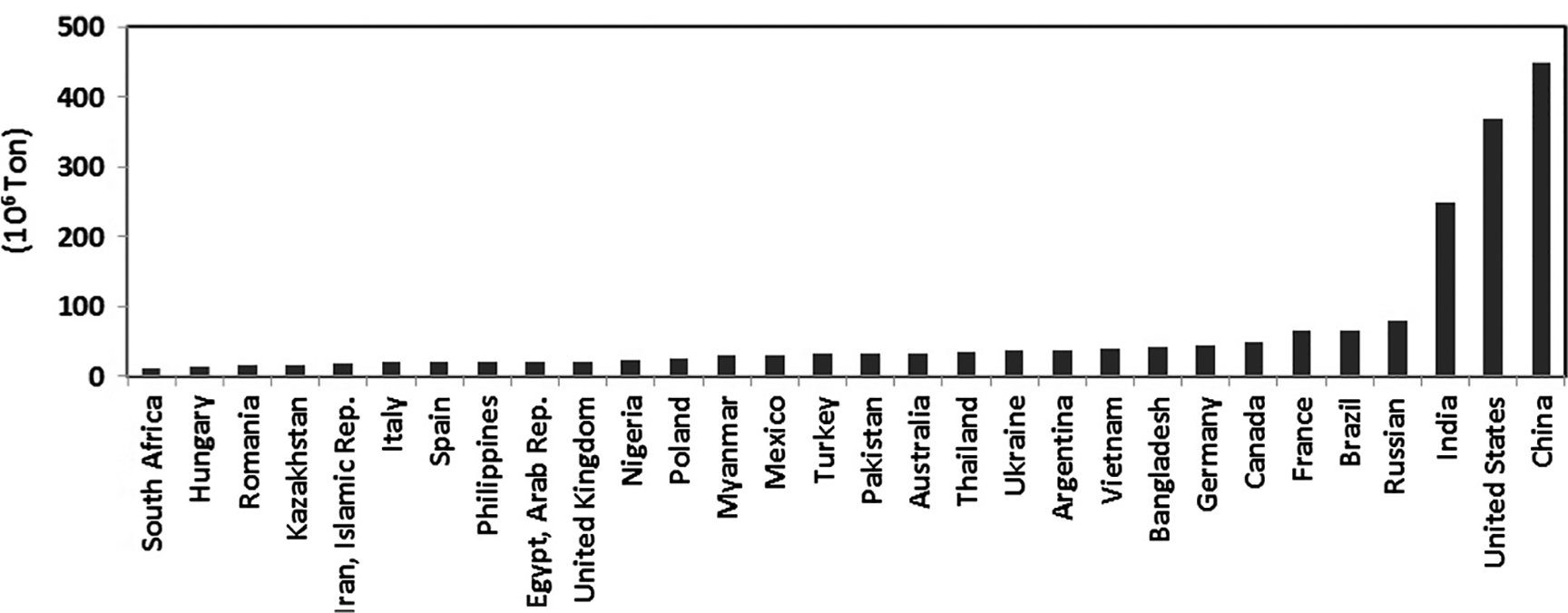
The 30 countries with largest cereal production in 2000 s.

Fig. 2.

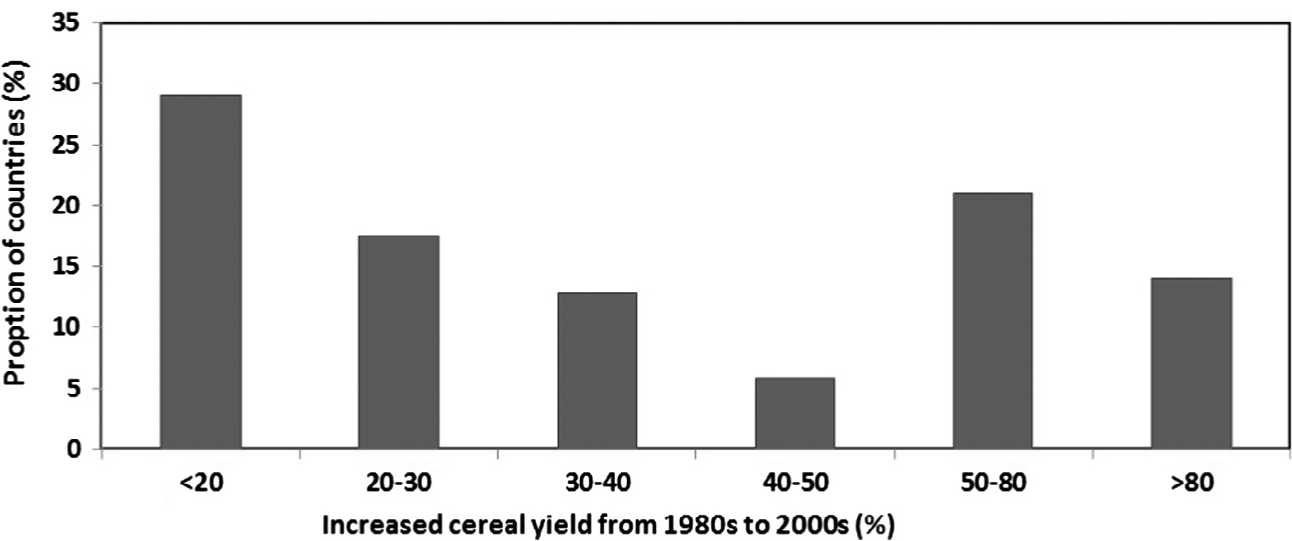
Proportion of countries varying with average increased rate of cereal yield from 1980 s to 2000 s.

Fig. 3.

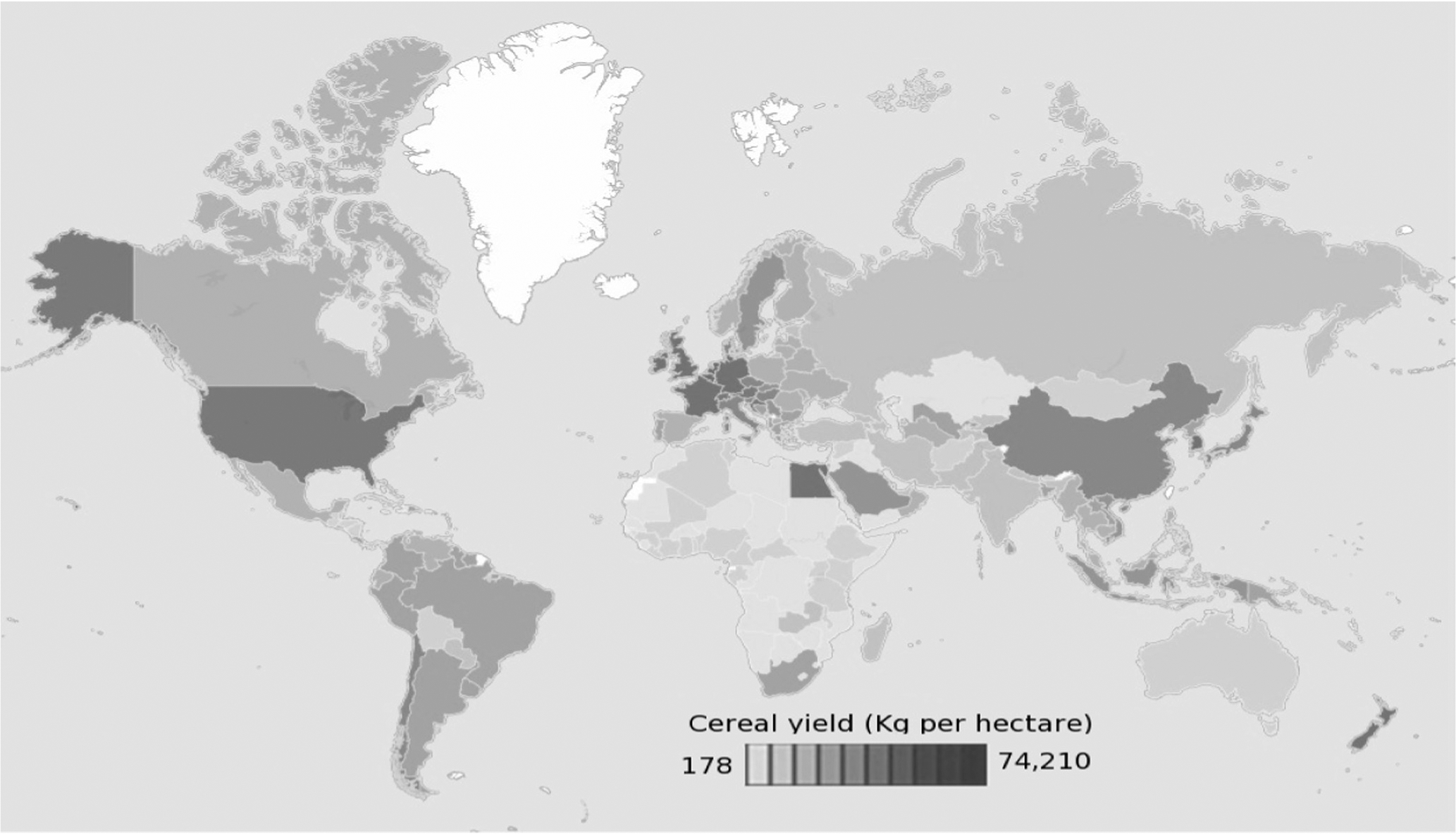
Spatial pattern of mean cereal yield across the countries from 2009–2012 (modified from http://data.worldbank.org/indicator).

Croplands were obtained from MODIS land cover product. This product provides croplands in 500 m pixels in 2010 s (Friedl et al., 2010). It could effectively delineate croplands for establishing models between vegetation index and crop yield (Bolton and Friedl, 2013). Since the MODIS land cover product does not differentiate crop types, this study included all pixels classified as agriculture and aggregated to a spatial resolution of 0.05° using a majority approach to match the spatial resolution of long-term AVHRR and MODS datasets.

2.2. Long-term satellite data and crop phenology detection

It has been demonstrated in previous studies that crop yield can be estimated and predicted using remote sensing data (e.g., Bolton and Friedl, 2013; Dabrowska-Zielinska et al., 2002; Domenikiotis et al., 2004; Kogan et al., 2012; Singh et al., 2003). The reliability of remotely-sensed estimation is strongly dependent on the quality of crop greenness extraction. This research was to calculate crop greenness from crop growth trajectory reconstructed from daily satellite observations according to the general structure summarized in Fig. 4.

Fig. 4.

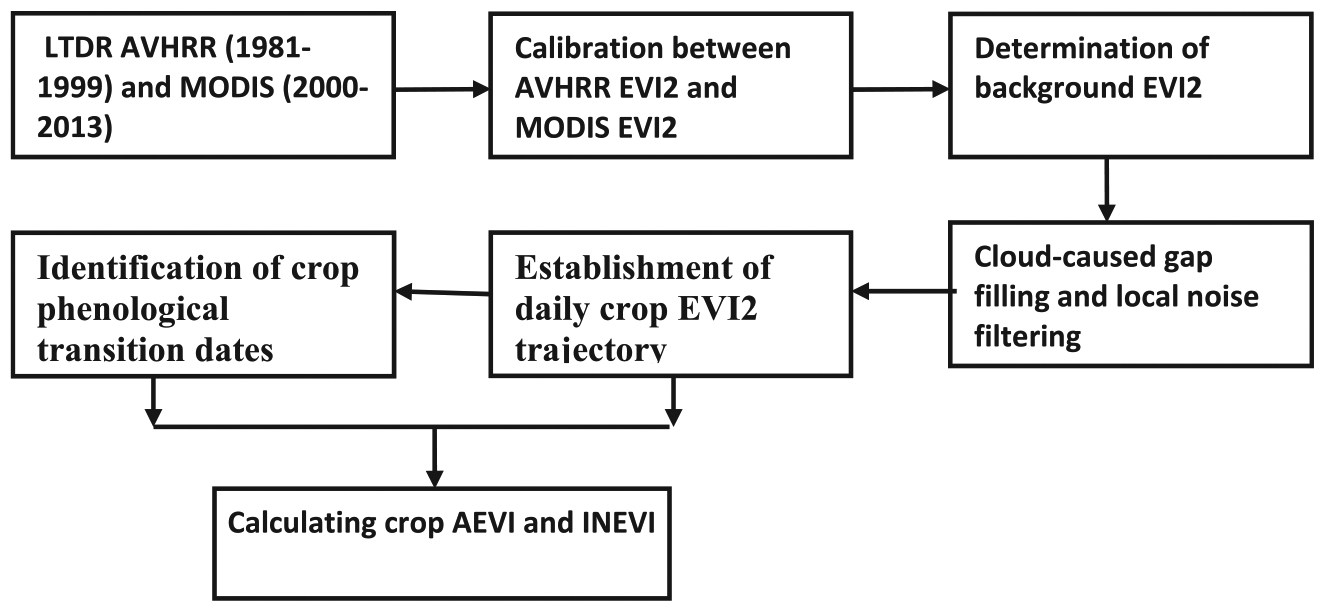
Flowchart of qualifying amplitude greenness and integrated greenness during a crop growing season.

2.2.1. Daily satellite vegetation index

AVHRR and MODIS data were collected from June 1981–June 2013 globally. AVHRR Long-Term Data Record (LTDR Version3) provides daily reflectance of 0.05° for the period from June 1981–December 1999. After the processing of atmospheric correction and sensor degradation calibration, the LTDR data were derived from a set of AVHRR sensors on NOAA-7, NOAA-9, NOAA-11, NOAA-14, and NOAA-16 (Vermote and Saleous, 2006). The MODIS CMG (Climate Modeling Grid) dataset provides daily surface reflectance (Collection 5.0) at a spatial resolution of 0.05°, which spans the period from March 2000 to June 2013 in this study. The CMG data were averaged from 250 m, 500 m, and 1 km on the basis of minimum values at band 3 (459–479 nm) after excluding pixels flagged for clouds and high solar zenith angles (Vermote and Kotchenova, 2011).

Daily EVI2 was calculated from red and near infrared reflectances using AVHRR LTDR and MODIS CMG. EVI2 remains functionally equivalent to EVI but can be derived from AVHRR data without blue band (Huete et al., 2006; Jiang et al., 2008). It is able to monitor vegetation phenology and activity across a variety of ecosystems (Rocha and Shaver, 2009), and is more effective than NDVI in crop yield monitoring (Bolton and Friedl, 2013). To bridge AVHRR and MODIS data, SPOT-4 VGT observations in 2001–2002 were calibrated to be comparable with MODIS data and then the calibrated SPOT-4 VGT data in 1998–1999 were used to adjust AVHRR NOAA-14 (Tsend-Ayush et al., 2012), because NOAA-14 AVHRR from 2000 to 2001 is not recommended for scientific uses due to significant orbital drift. After AVHRR LTDR dataset was calibrated to be continuous with MODIS data, the daily EVI2 during the last thirty years was generated by a NASA funded MEASURES project and is available at University of Arizona (http://vip.arizona.edu/viplab_data_explorer).

2.2.2. Detection of crop phenology

Crop phenology was detected using a Hybrid Piecewise Logistic Model (HPLM) based Land Surface Phenology Detection (LSPD) algorithm (Zhang et al., 2003, 2014), where the annual EVI2 time series was reconstructed using EVI2 observations from preceding half year, current year, and following half year. Briefly, the EVI2 time series was first smoothed after daily EVI2 data were composited to 3-day data by selecting the best quality data and using the maximum value composite. Then the observations of clouds and snow cover were removed from the temporal EVI2 data based on quality assurance. Specifically, the irregular snow cover EVI2 during a winter period was replaced using the background EVI2 value which represents the minimum EVI2 that consists of soil and seasonally-stable vegetation properties in an annual time series in each pixel. The data gaps caused by clouds were filled by linear interpolation using neighbour good quality data. The time series of EVI2 data at each pixel was finally smoothed using a Savitzky-Golay filter and a running local median filter. During data processing, EVI2 in preceding year was used to replace the data between September 1994 and February 1995 when the NOAA-11 AVHRR instrument unexpectedly failed. Similarly, EVI2 between January and March in 2000 was replaced using data in 2001 because MODIS data were not available until March 2000.

HPLM was developed to trace crop growth trajectory reflected from satellite vegetation index (Zhang, 2015). The logistic model was originally developed for monitoring crop growth based on field measurements (Ratkowsky, 1983; Richards, 1959) and adopted to simulate temporal satellite vegetation index (Zhang et al., 2003). By considering crop stress condition, HPLM was described as the followings:

$$\text{EVI2}\left(t\right)={\{}_{\frac{c_2+dt}{1+e^{a}21+{}_{}{}^{b}2{}^t}+{\text{EVI2}}_b\text{Crop}\text{stress}\text{condition}}^{\frac{c_1}{1+e^{a}1+{}_{}{}^{b}1{}^t}+{\text{EVI2}}_b\text{Favorable}\text{crop}\text{growth}\text{condition}}$$ (1)

where t is time in the day of year (DOY), a₁ and a₂ are related to the vegetation growth time, b₁ and b₂ are associated with the rate of plant leaf development, c₁ and c₂ are the amplitude of EVI2 variation, d is a vegetation stress factor, and EVI2_b is the background EVI2 value.

HPLM was then used to derive phenological transition dates based on the extreme points in curvature change rate of the modeled temporal trajectories (Zhang et al., 2006, 2003). Crop phenological metrics were defined according to crop seasonal growing cycles. Briefly, a seasonal cycle of vegetation growth consists of a greenup phase, a maturity phase, a senescent phase, and a dormant phase. These four phases are characterized using four phenological transition dates in the time series of greenness data: (1) greenup onset: the date of onset of greenness increase (GIN); (2) maturity onset: the date of onset of greenness maximum (GMA); (3) senescence onset: the date of onset of greenness decrease (GDE); and (4) dormancy onset: the date of onset of greenness minimum (GMI). These transition dates correspond well to the timing of wheat (corn) greening (emergence), heading (teaseling), grain-filling, and maturity (or harvest), separately (Shuai et al., 2013). The four transition dates correspond to the day-of-year on which the curvature change rate along the EVI2 data exhibits local minima or maxima (Zhang et al., 2003).

Two critical parameters of crop greenness were calculated from HPLM using the following formula:

$$\text{AEVI}\text{=}\text{EVI2}\left(\text{GMA}\right)-\text{EVI2}\left(\text{GIN}\right)$$ (2)

where AEVI is the growing season amplitude in EVI2; EVI2(GMA) and EVI2(GIN) are the EVI2 values at maturity onset and greenup onset, respectively, which were determined from HPLM.

Integrated EVI2 (IEVI) during a growing season was computed by summing the fitted daily EVI2 values throughout the period between the greenup onset and the dormancy onset:

$$\text{IEVI}\text{=}{\int }_{\text{GIN}}^{\text{GMI}}\left[\text{EVI2}\left(t\right)-\text{EVI2}\left(\text{GIN}\right)\right]dt$$ (3)

These two greenness parameters minimize the impact of systematic uncertainty in the long time series of EVI2 data and remove the influence of seasonal shifts. For the pixels with multiple crop growing cycles, AEVI was selected from largest value and IEVI was the sum from all cycles during a year.

Crop greenness at a national scale was averaged from all cropland pixels. Practically, country boundary and MODIS land cover product (Friedl et al., 2010) were used to extract crop area for individual countries. Then AEVI and IEVI for crop pixels were calculated and averaged for each country across the world.

2.3. Establishment of relationship between crop phenology and cereal yield at national scales

Relative variation in interannual crop greenness was used to associate with cereal yield in this study although the magnitude value of crop greenness has frequently been directly applied in crop yield monitoring in previous studies (Benedetti and Rossini, 1993; Bolton and Friedl, 2013; Esquerdo et al., 2011; Rembold et al., 2013). It is due to the following reasons. First, crop yield presents the increased trends during past decades (see Section 2.1) with the improvement of agricultural practices which include cultivar advances, fertilizers, breeding, and crop protection (Edgerton, 2009; Kogan et al., 2012; Salazar et al., 2007). These agricultural practices would result in the change of the proportion of crop biomass partitioning to the crop yield, so that the relationship between the crop greenness and crop yield does not necessarily remain constant in a long time period. Secondly, crop growth conditions and yield are often affected by abiotic and biotic factors which mainly include weather (particularly drought), insect population, and disease incidence. When crops are impacted by the biotic and abiotic factors, the biochemical constituent of the crop changes and so would be the spectral signatures and greenness (Mirik et al., 2007; Moshou et al., 2004; Sudbrink et al., 2003; Williams et al., 2012). Therefore, the drought severity and yield variation are effectively monitored using interannual variation in crop greenness (Kogan, 1995; Zhang, 2015). Moreover, the degree of disease infection is strongly correlated to crop greenness over time because diseased plants react with changes in greenness or canopy structure (Ashourloo et al., 2014; Hatfield and Pinter, 1993; Williams et al., 2012). Thirdly, the continuity of greenness across satellite sensors is still an open issue even with careful sensor inter-calibration because self-consistency in a signal sensor and inter-calibration for various sensors are sophisticated (Wu and Yan, 2011). Particularly, the discrepancy between AVHRR and MODIS may still remain to some degree although the calibration was carefully performed. However, interannual variation in greenness could reduce some of the uncertainties by assuming that the instrument-impacts are limited within two consecutive years. As a result, MODIS greenness in 2000 was not compared with AVHRR greenness in 1999 because AVHRR EVI2 and MODIS EVI2 were from two different instruments.

It was therefore supposed that the interannual variation in cereal yield could be effectively reflected from that of vegetation greenness. Thus, the interannually normalized greenness and crop yield was first defined as the follows:

$$Y{r}_{\left(i\right)}=\left(Y_{\left(i\right)}-Y_{\left(i-1\right)}\right)/\left(Y_{\left(i\right)}+Y_{\left(i-1\right)}\right)$$ (4)

$${\text{AEVIr}}_{\left(i\right)}=\left({\text{AEVI}}_{\left(i\right)}-{\text{AEVI}}_{\left(i-1\right)}\right)/\left({\text{AEVI}}_{\left(i\right)}\text{+}{\text{AEVI}}_{\left(i-1\right)}\right)$$ (5)

$${\text{IEVIr}}_{\left(i\right)}=\left({\text{IEVI}}_{\left(i\right)}-{\text{IEVI}}_{\left(i-1\right)}\right)/\left({\text{IEVI}}_{\left(i\right)}+{\text{IEVI}}_{\left(i-1\right)}\right)$$ (6)

where Y is yield; IEVI is the EVI2 integration during a crop growing season; AEVI is the growing season amplitude in EVI2; Yr is interannually normalized cereal yield; AEVIr and IEVIr are the interannually normalized AEVI2 and IEVI2, respectively; i and i − 1 are current year and preceding year, respectively.

Secondly, a stepwise regression model was established using an ordinary least squares (OLS) method:

$$Y{r}_{\left(i\right)}={\alpha }_0+{\alpha }_1{\text{AEVIr}}_{\left(i\right)}+{\alpha }_2{\text{IEVIr}}_{\left(i\right)}+e$$ (7)

where α₀, α₁, and α₂ are coefficients, and e is error.

Finally, the model of cereal yield prediction (Y_p) was generated based on Eqs. (4)–(7):

$$Y_{p\left(i\right)}=Y_{\left(i-1\right)}\left(1+{\alpha }_0+{\alpha }_1{\text{AEVIr}}_{\left(i\right)}+{\alpha }_2{\text{IEVIr}}_{\left(i\right)}\right)/\left(1+{\alpha }_0-{\alpha }_1{\text{AEVIr}}_{\left(i\right)}-{\alpha }_2{\text{IEVIr}}_{\left(i\right)}\right)$$ (8)

Model accuracy was evaluated using the average of absolute relative error (Re). To calculate Re, a leave-one-out cross-validation approach was used (Bolton and Friedl, 2013; Mkhabela et al., 2011; Schut et al., 2009). Using this approach, the regression model (Eq. (7)) was repeatedly refitted by leaving out a single year observation and then used to derive a prediction for the left-out observation. This approach gives estimates of the prediction error for each observation. The Re in the model prediction during past three decades was calculated by comparing to the observed cereal yield at a national level:

$$\mathit{\text{Re}}\text{=}\frac{1}{n}\sum _{i=1}^n\left|Y_{p\left(i\right)}-Y_{\left(i\right)}\right|/Y_{\left(i\right)}$$ (9)

where n is the total number of years, Y is the observation and Y_p is the prediction in year i.

2.4. Verification of relationship between crop phenology and crop yield using data at a state scale

The relationship between crop greenness and crop yield was verified in four states in the Central United States. Crop yield and planted area at a state scale were obtained from the USDA (US Department of Agriculture) National Agricultural Statistics Service (NASS) database site (http://www.nass.usda.gov/). The crop yield (bushels per acre) and planted area (acre) in the four states were collected for barley, corn, oats, soybeans, and sorghum from 1982 to 2012, where corn and soybean accounted for more than 90% of planted area in most of the states. The overall crop yield in a state was determined using the crop yield in a given crop type and weighted by the planted area. Correspondingly, crop greenness (AEVI and INEVI) in these states was averaged from cropland pixels. Finally, the interannual variation in crop yield was associated with the interannually normalized crop greenness using Eq. (7).

3. Results

3.1. Reconstructed crop EVI2 time series

EVI2 temporal trajectory was reconstructed for individual crop pixels from 1982–2012. Fig. 5 shows an example of the time series of crop EVI2 simulated from AVHRR data. The seasonal cycle was distinctive in croplands because EVI2 varies from bare soil before sowing to fully covered canopy during maturity phases. However, winter snow cover effects were evident in mid-high latitudes, which reduced the EVI2 value dramatically, such as the winter periods in 1984 and 1989 (Fig. 5). In these cases, the background value, which was the average from the good EVI2 during the period after snow melting and before crop germination, was used to replace the snow EVI2. The EVI2 variation below background value was considered as noise in analyzing crop growth.

Fig. 5.

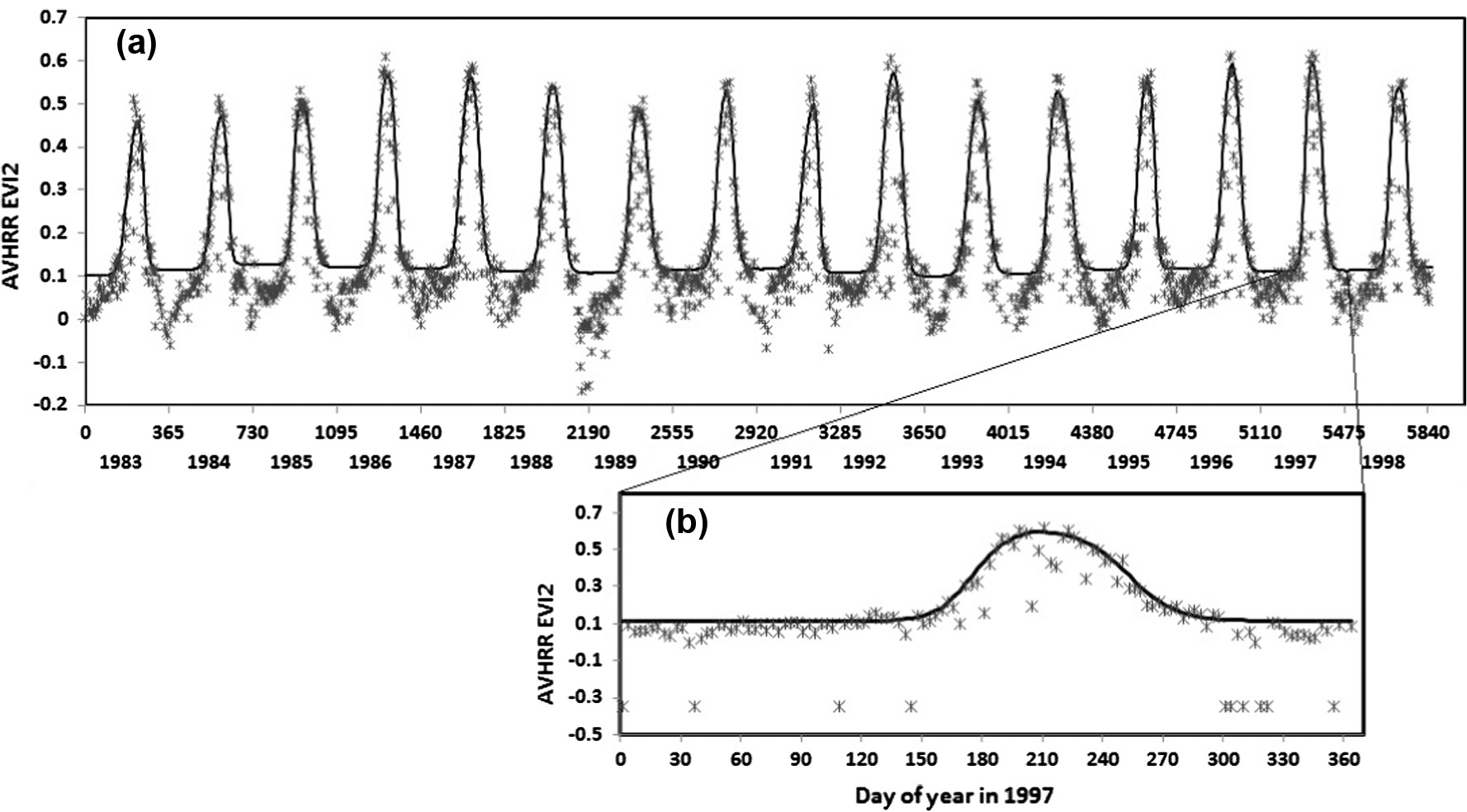
Resconstructed temporal trajectory of AVHRR EVI2 in a cropland pixel in the central United States. The solid line is the simulated curve using HPLM while the asterisks are original values (3-day composites). X-axis in (a) is the number days from January 1, 1983 (upper) and year (bottom), (b) is an example of an enlarged annual trajectory in 1997 for visualization purpose.

Fig. 6 presents examples of the reconstructed MODIS EVI2 temporal trajectories for double crops which are frequently planted in Asia such as China and India. However, daily satellite observations were noisy and missing observations always occurred because of cloud cover. The reconstructed temporal trajectories in double crop fields show that both the growing season amplitude in EVI2 and the growing season length varied greatly in individual cycles.

Fig. 6.

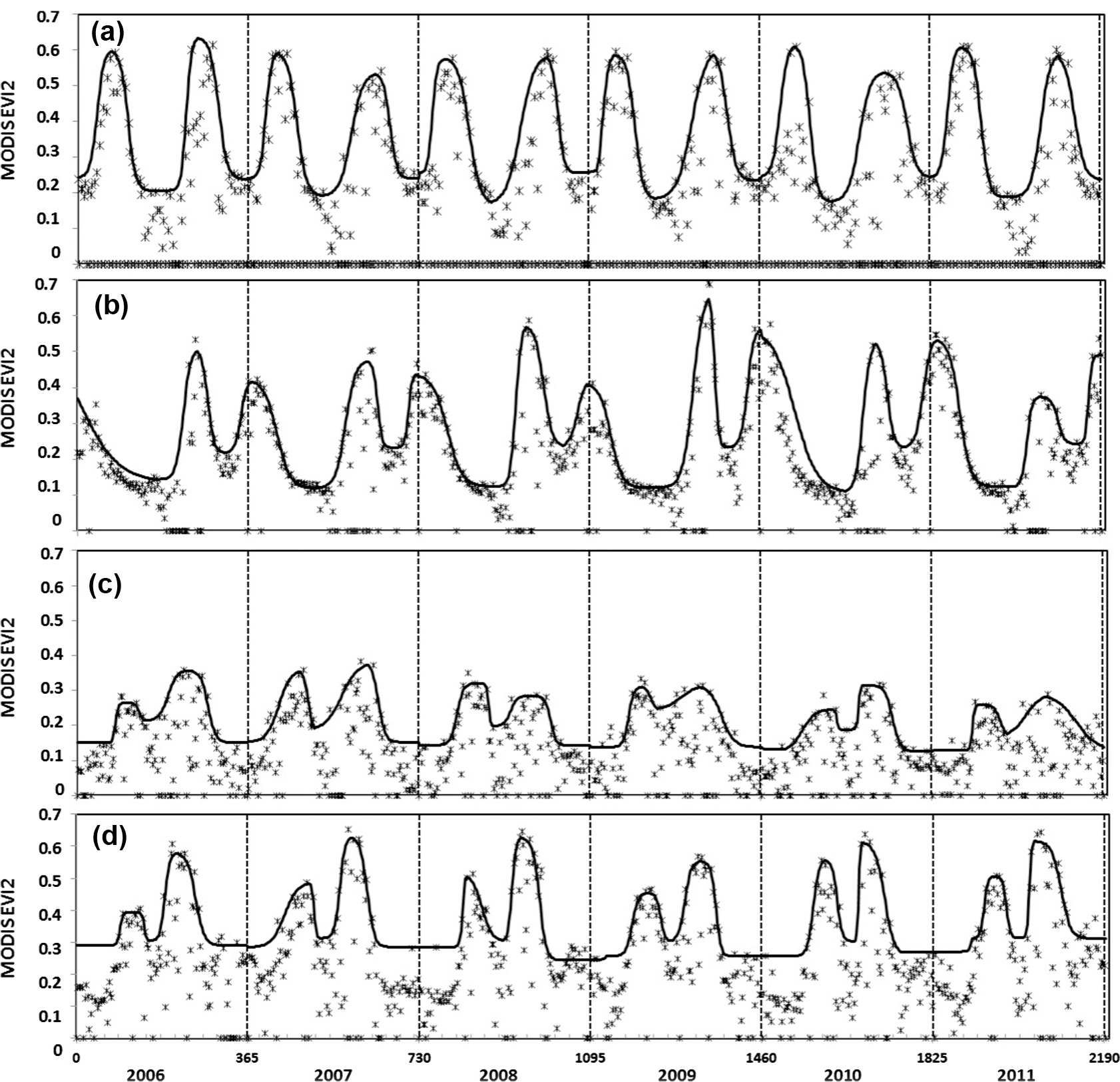
Resconstructed temporal trajectory of MODIS EVI2 in double cropland fields (randomly selected pixels). (a) Telangana in India (e.g. double rices), (b) Madhya Pradesh in India (e.g. maize and wheat or rice and wheat), (c) central China (double rices), (d) northern China (wheat and maize). The solid dark lines are reconstructed EVI2 trajectories while the asterisks are original values. All missing observations and negative EVI2 are set to zero. X-axis is the number days from Janurary 1, 2006 (upper) and year (bottom).

3.2. Temporal and spatial variation in AEVI2 and IEVI2

Fig. 7 presents the spatial pattern in average AEVI2 and IEVI2 in 2000s. The values were large in the central USA and northeastern China while they were smaller in Africa and South America. The histogram of pixels (5 km) indicates that the peak occurred at 0.2–0.25 AEVI2 in Europe, Asia, and Africa, 0.15–0.2 from South America, and 0.25–0.3 in North America (Fig. 8a). The proportion of pixel with AEVI2 larger than 0.25 was 67.6%, 86.8%, 65.6%,66.9%, 54.2%, and 38.9% in globe, North America, Europe, Asia, Africa, and South America, respectively (Fig. 8a). For IEVI2, the largest proportion of pixels appeared at 20–25 in Africa, 25–30 in Europe, Asia, and South America, 40–45 in North America (Fig. 8b). The pixel proportion with IEVI2 > 25 was 60.7% 74.1%, 57.5%,62.8%, 50.5%, 64.9% in globe, North America, Europe, Asia, Africa, and South America, respectively. Both IEVI2 and AEVI2 show that the largest value occurred in North America. Comparing the spatial pattern of cereal yield in Fig. 3, it was evident that large AEVI2 and IEVI2 values were in most cases associated with high cereal yield. This relationship from spatial pattern is consistent with previous findings that crop greenness performs well in reflecting crop yield (Benedetti and Rossini, 1993; Bolton and Friedl, 2013; Esquerdo et al., 2011) although agricultural practice could make it more complex.

Fig. 7.

Spatial pattern in crop greenness averaged from 2000–2010 at a spatial resolution of 0.05° (~5 km). (a) Greenness amplitude during a growing season (AEVI2), and (b) integrated crop greenness during growing seasons. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

Fig. 8.

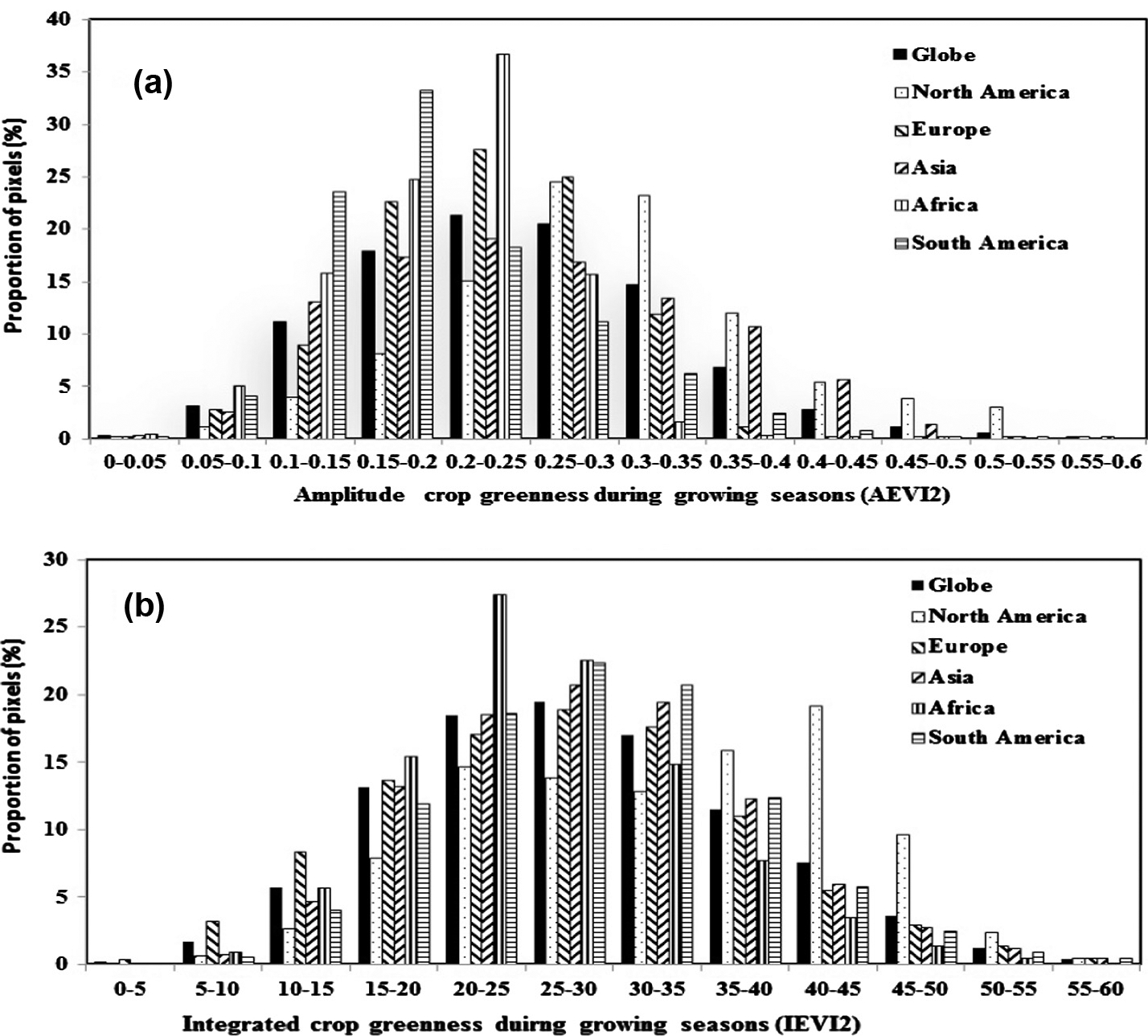
Proportion of crop pixels with the variation in AEVI2 (a) and IEVI2 (b) averaged from 2000–2010.

AEVI2 and IEVI2 varied considerably interannually during past 30 years. Fig. 9 illustrates the interannual variation in AEVI2 and IEVI2 for the three counties (the USA, China, and India) where cereal productions were the largest over the world. On average, both AEVI2 and IEVI2 were largest in the USA and followed by China and India. The greenness patterns were certainly associated with the variation in cereal yield which reflected the largest crop yield in the USA while smallest in India (Fig. 9b). The relationship between crop greenness and crop yield varies with countries considerably during past 30 years (Fig. 10). However, it is noted that EVI2 increase rapidly from 1990s to 2000s. It is likely that AVHRR data were not calibrated well with MODIS data although a set of equations were used to adjust AVHRR data (Tsend-Ayush et al., 2012). The discontinuity is likely related to the ineffective correction of water vapor which strongly absorbs LTDR AVHRR near infrared reflectance. Thus, the AVHRR EVI2 is considerably lower than MODIS EVI2 over humid regions. This systematic inconsistency would propagate some uncertainties in the models if cereal yield was directly correlated to the magnitude greenness (AEVI2 and IEVI2).

Fig. 9.

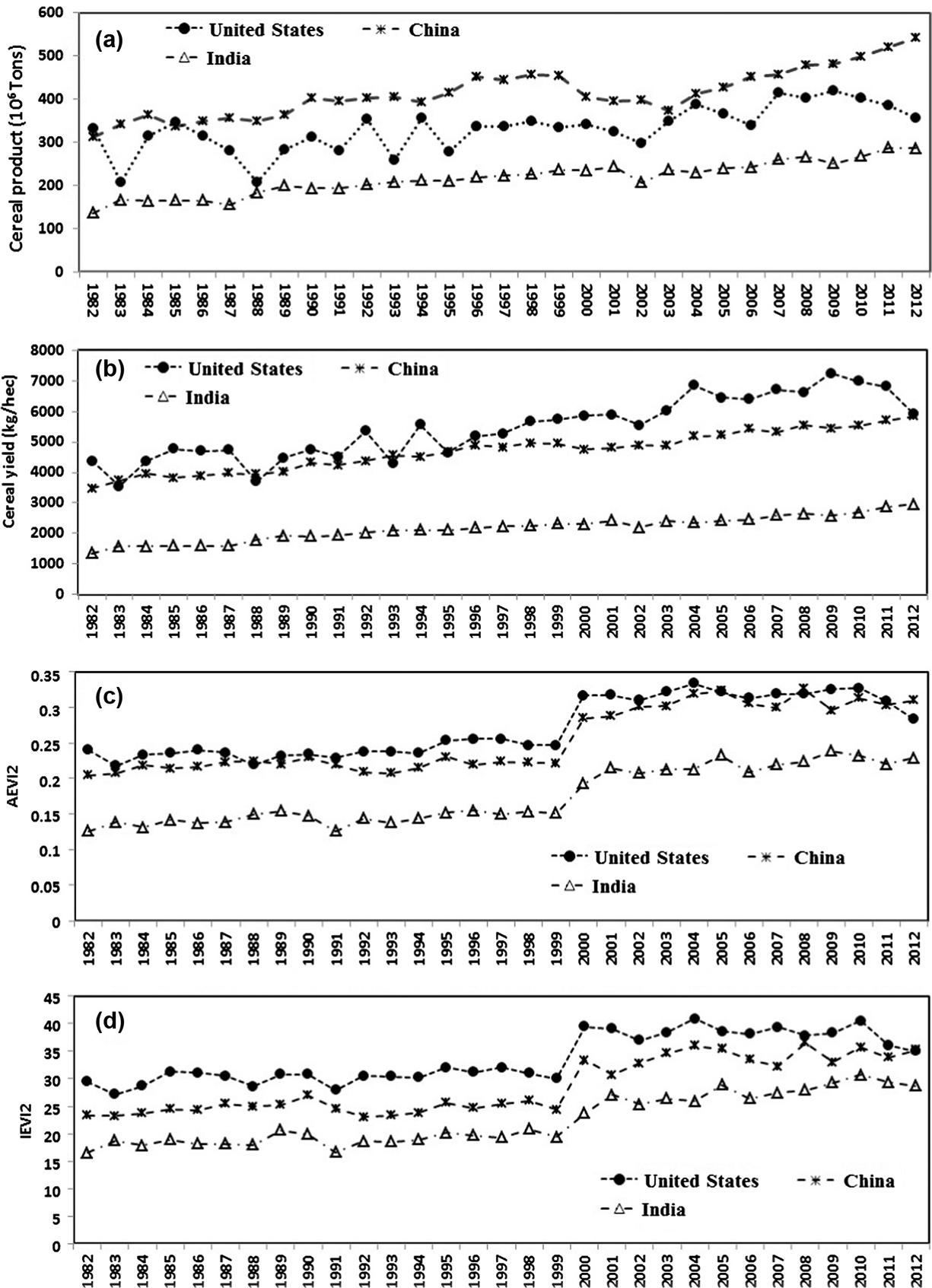
Interannual variation in cereal production (a), cereal yield (b), AEVI2 (c), and IEVI2 (d) in the United States, China, and India.

Fig. 10.

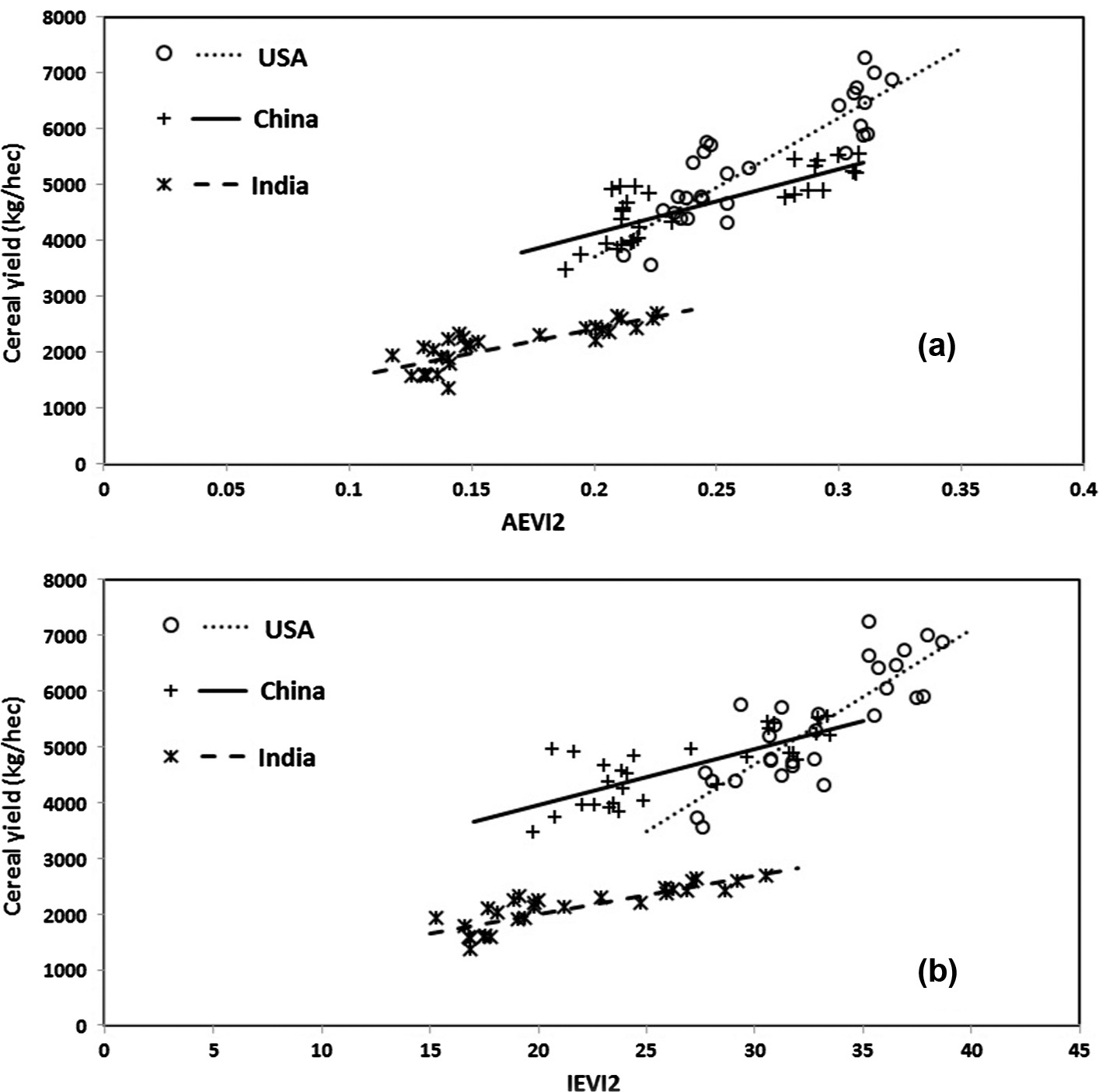
Correlation of cereal yield with (a) AEVI2 and (b) IEVI2. The lines show the linear regression values in USA, China, and India, respectively.

The correlation of cereal yield with AEVI2 and IEVI2 varied with time period and country (Table 1). The significant correlation (P value < 0.1) for both AEVI2 and IEVI2 appeared in two different periods for India, while it only occurred in 1982–1999 in the USA. In China, the significance only occurred for AEVI2 but not for IEVI2. In contrast, there was no significant correlation of cereal yield with either AEVI2 or IEVI2 in Brazil and Russia (except for AEVI2 in 1992–1999). This suggests that the magnitude greenness does not always reflect cereal yield well in a long time series.

Table 1.

Significance of correlation between crop greenness and crop yield (P values) in five countries with large cereal production. Note no data was included before 1992 in Russia.

	USA		India		China		Russia		Brazil
	AEVI2	IEVI2	AEVI2	IEVI2	AEVI2	IEVI2	AEVI2	IEVI2	AEVI2	IEVI2
1982–1999	0.001	0.009	0.002	0.007	0.073	0.165	0.085	0.214	0.522	0.558
2000–2012	0.074	0.252	0.031	0.004	0.077	0.112	0.929	0.468	0.197	0.189

3.3. Relationship between interannually normalized greenness and cereal yield

Interannually normalized greenness is strongly correlated to the variation in cereal yield. Fig. 11 displays the correlation in six countries where the largest cereal productions were produced. IEVIr and AEVIr varied between −0.1 and 0.1, which reflects about 20% (difference/mean) of the interannual variation in IEVI and AEVI. The interannually normalized cereal yield was largest in the USA, changing between −0.12 and 0.1, while it was smallest in China, ranging between −0.02 and 0.036 among the six countries. Because IEVIr and AEVIr represent different crop growing characteristics, the stepwise regression models show strongly significant correlations with interannual variation in cereal yield (P < 0.01). Note that Russia, which is the fourth largest cereal producer during recent years, is not listed here because the statistics crop yield/production is not available before 1992.

Fig. 11.

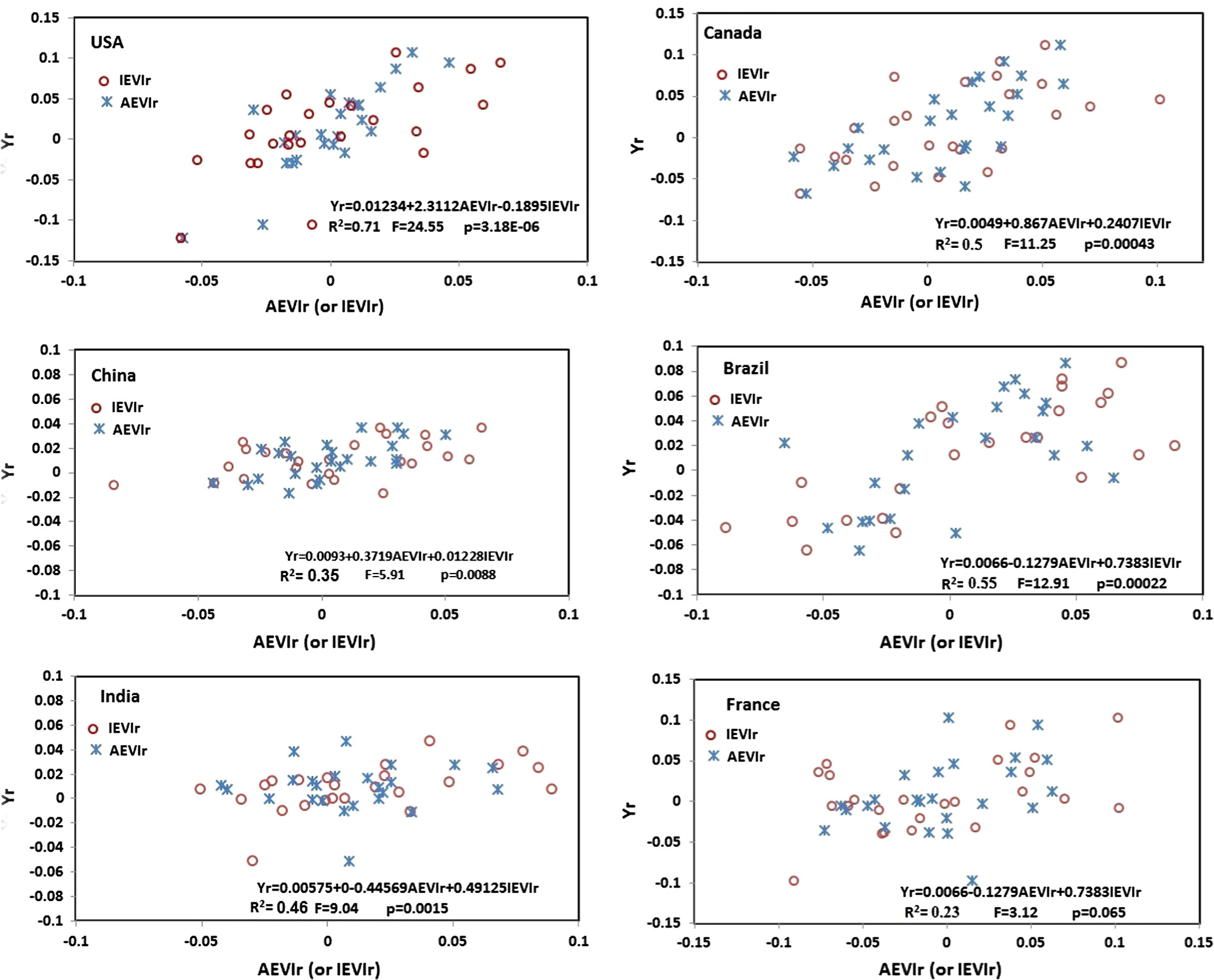
Scatter plots between Yr and both IEVIr and AEVIr for the countries with the largest cereal production across the globe.

Fig. 12 shows the spatial pattern in the relationship of interannually normalized cereal yield with IEVIr and AEVIr across the globe, respectively. The correlation was generally higher in the northern hemisphere than in the southern hemisphere (Fig. 12a and b). Overall, there were 38% and 35% of countries where the correlation coefficient was larger than 0.5 between Yr and AEVIr and between Yr and IEVIr, respectively. This suggests that AEVIr is generally a better indicator of cereal yield. The negative correlations between Yr and IEVIr or AEVIr also occurred in about 15 countries where the cereal production was low and located mainly in arid environment but correlation was generally insignificant. Clearly, a considerable amount of crop greenness in low-cropping density countries was not able to be detected accurately due to the mixed pixel effects in 0.05° satellite data and relatively poor cropland classification. In such regions, fine resolution data are certainly needed.

Fig. 12.

Correlation between interannually-normalized cereal yield and EVI2 greenness from 1982–2012. (a) Correlation coefficient (R²) between AEVI2 and cereal yield, (b) correlation coefficient (R²) between IEVI2 and cereal yield, (c) correlation coefficient (R²) between cereal yield and both IEVI2 and AEVI2, (d) Confidence level (%) of the stepwise regression models. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

The stepwise regression improves the correlation between cereal yield and both IEVIr and AEVIr (Fig. 12c and d). There were about 50% of countries where the correlation coefficient was larger than 0.5. The confidence level of the stepwise regression model was larger than 90% (P value < 0.1) in most countries in the northern hemisphere. It was over 95% in most of the countries with large cereal production. Poor correlation mainly appeared in Africa where croplands were basically sparsely distributed and hard to be captured from coarse resolution satellite data.

The average of absolute relative error in the yield predication was relatively smaller in America, Europe and East Asia (Fig. 13). In the countries of 10 largest cereal production, the prediction error was less than 9% during past three decades except Russia. For example, the prediction and observation of cereal yield from 1982–2012 were distributed along a 1:1 line in the USA, China, and India (Fig. 14). However, the model prediction was relatively poor in most of counties across Africa. This was likely associated the small areas in cereal croplands, where EVI2 at coarse resolution was contaminated by non-crop growth and was insufficient in extracting crop growth.

Fig. 13.

Average of absolute relative error from 1982–2012 calculated from a leave-one-out cross-validation approach.

Fig. 14.

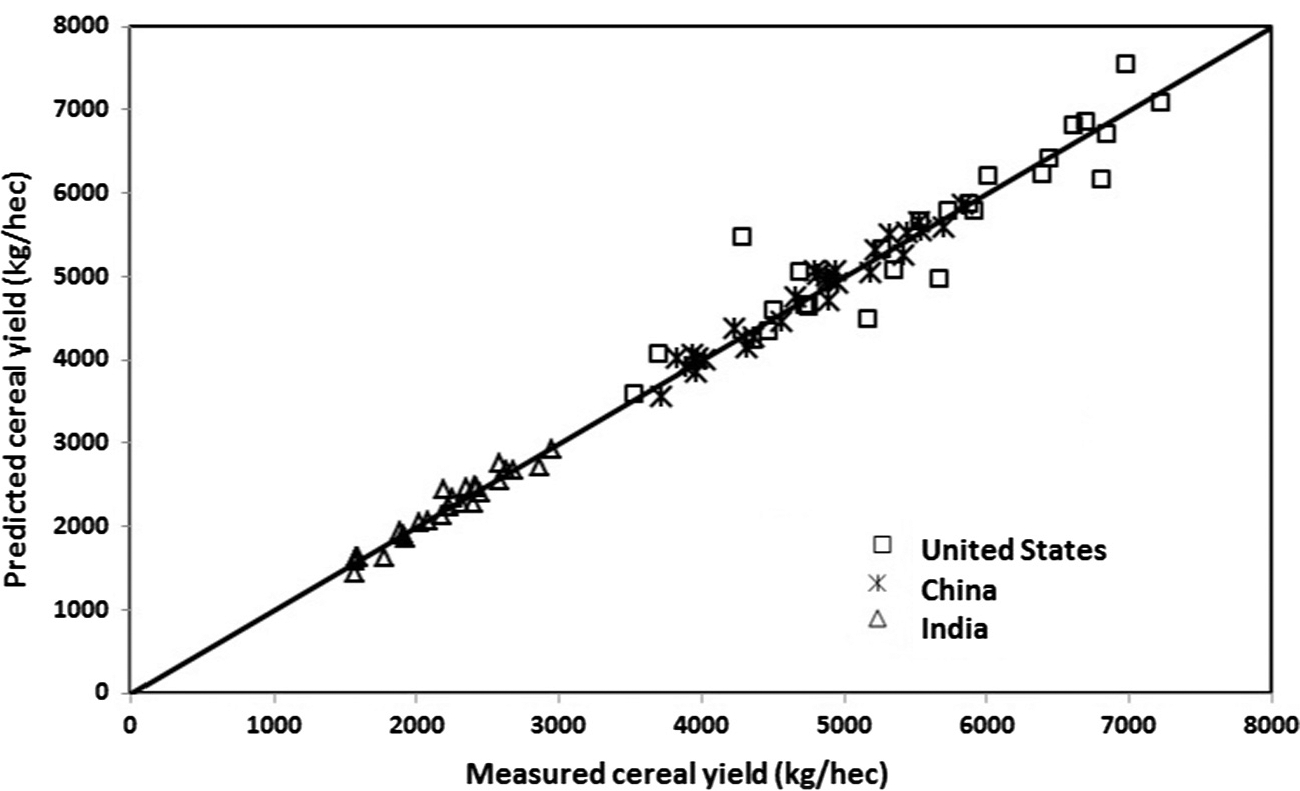
Scatterplot between observed and model predicted cereal yield from 1982–2012 in the USA, China, and India.

3.4. Evaluation of relationship between crop phenology and crop yield in the Central United States

Interannual variation in the crop greenness (AEVIr and IEVIr) effectively reflected the variation of crop yield in four states in the Central United States (Fig. 15). Specifically, the correlation models in Minnesota and Iowa were strongly significant (P < 0.0001) with the correlation coefficient higher than 0.8, respectively. When the established parameters were used for Eq. (8) to predict crop yield, the model in each state could produce a prediction accuracy of larger than 90%. Similarly, significant statistical models were found in Indiana and Ohio (P < 0.001), which were able to predict crop yield with an accuracy of 88%, respectively.

Fig. 15.

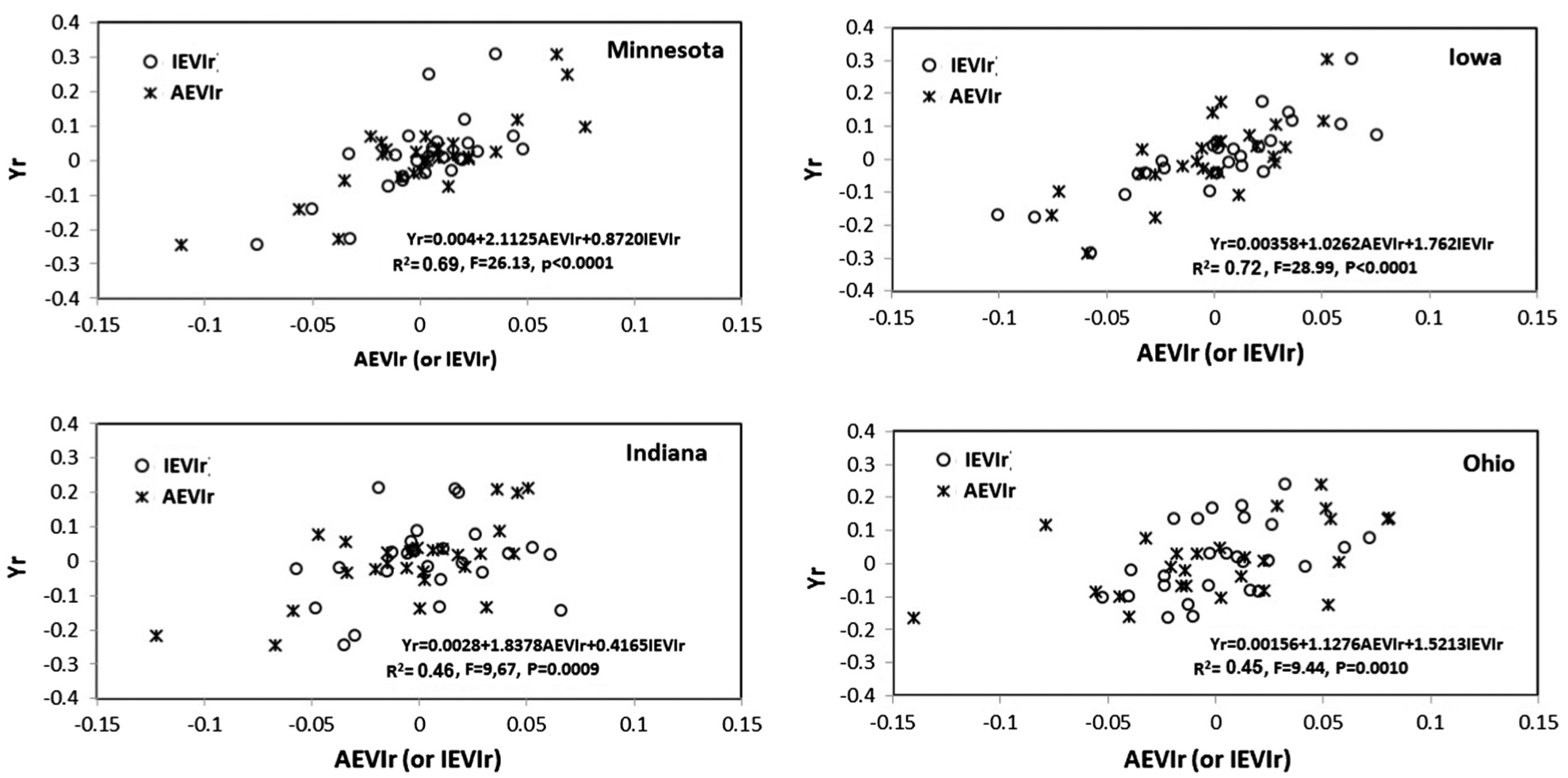
Scatter plots between interannual variations in crop yield (Yr) and vegetation greenness (IEVIr and AEVIr) at a state scale in central United States.

4. Discussion and conclusions

This study investigated global cereal yield using greenness derived from coarse resolution satellite data during last three decades. Crop greenness values in the EVI2 amplitude and EVI2 integration during a growing season were effectively calculated after temporal EVI2 trajectory had been reconstructed and crop phenological metrics had been detected. The crop phenology detection is particularly important to reduce effects from the noises in raw EVI2 data and the temporal shift in crop growing season spatially. The algorithm of reconstructing crop growth trajectory in this study has several advantages (Zhang, 2015) which include: (1) snow cover, cloud-caused gaps and local irregular EVI2 variation can be effectively removed; (2) HPLM provides a simple, bounded, continuous function for modeling growth and decay processes; (3) each parameter in HPLM can be assigned to a biophysical meaning related to crop growth; (4) the logistical model performs superiorly to both Fourier-based and asymmetric Gaussian functions for fitting remote sensing-based phenology development (Beck et al., 2006). Further, the phenological results detected from this approach have been verified in various studies. Indeed, the logistic model for detecting vegetation phenology has been validated using observations of forest leaf developments (Ahl et al., 2006; Ganguly et al., 2010; Liang et al., 2011; Zhang et al., 2006), where the satellite detections were closely related to field observations. Using MODIS EVI in croplands, this approach detected winter wheat turning green, heading, milky ripe, and harvest with an accuracy of less than 5 days in northern China (Shuai et al., 2013), and detected crop phenology from 2001–2009 which were comparable with ground observations in winter wheat (R² = 0.90) and summer maize (R² = 0.93) (Xiao et al., 2013). Moreover, the interannual variation in AVHRR EVI2 crop phenological trajectory at 0.05° was identical to the interannual tower-observed GPP trajectories in Bondville in Illinois (Zhang, 2015).

The results from this study suggest that interannual variation in EVI2 greenness is an effective indicator of interannual cereal yield changes although absolute satellite greenness is not always linearly correlated to cereal yield during last three decades. The EVI2 magnitude was a more effective predictor in cereal yield in some countries while EVI2 integration during annual growing seasons was better in other countries across the world. Combination of these two parameters significantly improved the predication of cereal yield, where the model confidence was generally higher than 95% and the prediction error was less than 9%, particularly in the countries with large cereal production. However, the model prediction was relatively poor in Africa, where crop greenness was difficult to extract accurately from coarse satellite data because croplands were sparsely distributed with small farm size and the census data of cereal yield for model establishment was also relatively poor.

The reliability of EVI2 greenness based models for monitoring crop yield is mainly affected by the following factors. First, the calculation of regional crop greenness is strongly dependent on the quality of cropland classification data. Currently, global croplands are commonly obtained from three land cover products which are the GLC2000 product (Bartholome and Belward, 2005), MODIS land cover product collection 5 (Friedl et al., 2010), and GlobCover (Arino et al., 2008). However, the overall accuracy of croplands from these products is less than 77% (Fritz et al., 2011) and the spatial discrepancy among these products is significant (Kaptue Tchuente et al., 2011; Ran et al., 2010; Vintrou et al., 2012; Wu et al., 2008). As a result, the accuracy of the crop yield models would vary with cropland data used.

Second, the purity of cropland in a pixel is closely related to the spatial resolution of satellite data. Crop yield has been successfully estimated in various studies using coarse resolution satellite images with high temporal frequency. However, each pixel at a coarse resolution (0.05°) generally represents mixed crop types or mixture between crops and natural vegetation, which would have considerable impacts on the estimation of crop yield. Certainly, the quality of crop monitoring will increase with the increase of the spatial resolution of satellite data. However, it is extremely difficult to quantitatively evaluate the impact of the spatial resolution of the crop phenology parameters on the capability of estimating crop yield at a global scale. It is due to the fact that spatial patterns in croplands play a fundamental role in defining the optimal resolution for a certain region (Rembold et al., 2013). In the Central United States, for example, crop is relatively homogeneously distributed, crop greenness in a 0.05° pixel is less contaminated by natural vegetation and the vegetation indices mainly reflect the crop growth condition. In contrast, for the crop areas with highly fragmented and heterogeneous patterns, such as African agriculture, parts of Europe, southern China and India, high resolution data would significantly reduce the pixels with mixed problem, which would improve greatly the estimation of crop yield. To monitor crop yield for specific crop types and locations precisely, high spatial and temporal resolution data are needed, but such data are currently not available. One potential approach is to fuse high spatial resolution Landsat observations and high temporal resolution MODIS data. In this study, crop yield was estimated by statistically linking to interannual variation in crop greenness. The statistic model of interannual variation could greatly minimize the influences from the coarse spatial resolution data on the predication of crop yield at state or national scales. It is because interannual variation (anomalies) of crop greenness relates to local meteorological condition (e.g., droughts), which limits the spatial resolution impacts on crop yield estimation.

Third, the reliability of crop yield varies with the choices of vegetation indices. Both NDVI and EVI/EVI2 are commonly used for monitoring crop growth and yield. NDVI could work more effectively in some regions or crop types while EVI/EVI2 might be better in others. Moreover, some other vegetation indices may also have advantages in specific regions. For example, Normalized Difference Water Index (NDWI) is more sensitive to irrigation in semi-arid areas with low-density agriculture than both EVI2 and NDVI (Bolton and Friedl, 2013).

The coarse resolution satellite data, particularly AVHRR and MODIS data, have been widely used for the estimation of crop yield in local areas (Doraiswamy et al., 2003; Kogan et al., 2013, 2012; Maselli and Rembold, 2001) and applied in a large number of operational national and international agricultural monitoring systems for providing critical agricultural information (Becker-Reshef et al., 2010). The estimation of crop yield from coarse resolution data is impacted by various factors and is incapable to provide detailed spatial pattern, but it can provide timely information on global crop production which is indispensable for combating the growing stress on the world’s crop production and for securing both short-term and long-term stable and reliable supply of food. The simple models established in this study have the capability of monitoring national cereal yield from coarse resolution satellite data with a reasonable accuracy for individual countries across the world. This approach is expected to monitor global crop growth and yield in near real time using Visible/Infrared Imager/Radiometer Suite (VIIRS) observations. VIIRS onboard the Suomi National Polar-orbiting Partnership (S-NPP) satellite was launched in October 2011 and is the primary instrument for a suite of Environmental Data Records (EDR), including vegetation indices. Daily global VIIRS products are operationally produced and available at NOAA’s Comprehensive Large Array-Data Stewardship System (CLASS) web site (http://www.class.ngdc.noaa.gov/saa/products/welcome) with a latency of 6 h (Vargas et al., 2013). The operational VIIRS data make it practicable to estimate crop yield in near real time. The timely prediction could provide critical information for worldwide crop monitoring, cereal trade and food management and it has direct impact on year-to-year national and international economies (Hayes and Decker, 1996).