Dynamic risk profiling using serial tumor biomarkers for personalized outcome Prediction

Summary

Accurate prediction of long-term outcomes remains a challenge in the care of cancer patients. Due to the difficulty of serial tumor sampling, previous prediction tools have focused on pretreatment factors. However, emerging non-invasive diagnostics have increased opportunities for serial tumor assessments. We describe the Continuous Individualized Risk Index, a method to dynamically determine outcome probabilities for individual patients utilizing risk-predictors acquired over time. Similar to ‘win probability’ models in other fields, CIRI provides a real-time probability by integrating risk-assessments throughout a patient’s course. Applying CIRI to patients with diffuse large B-cell lymphoma, we demonstrate improved outcome prediction compared to conventional risk-models. We demonstrate CIRI’s broader utility in analogous models of chronic lymphocytic leukemia and breast adenocarcinoma, and perform a proof-of-concept analysis demonstrating how CIRI could be used to develop predictive biomarkers for therapy selection. We envision that dynamic risk-assessment will facilitate personalized medicine and enable innovative therapeutic paradigms.

Graphical Abstract

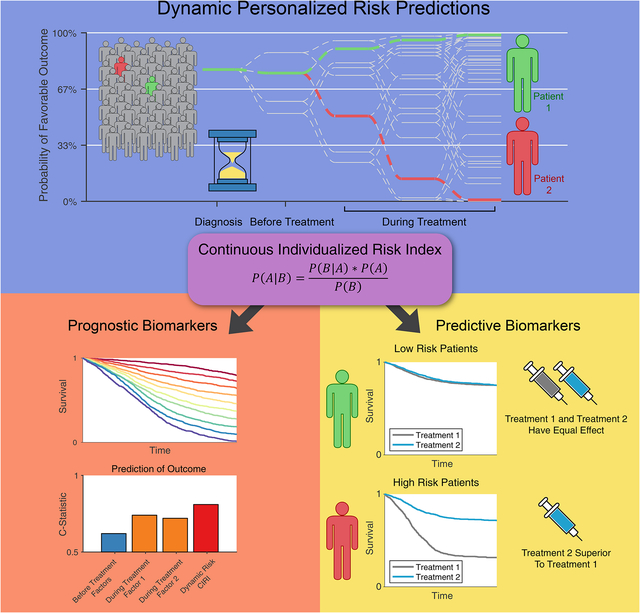
Current cancer biomarkers are obtained throughout a disease or treatment course Prognostic biomarkers can be integrated over time similar to ‘win probability’ models Dynamic risk profiling produces a personal risk model, outperforms traditional methods Dynamic risk profiling can potentially inform personalized therapy selection

eTOC:

A framework for the integration of cancer patient biomarker data over time improves prognostic accuracy and could inform personalized therapy selection.

Introduction

Biological and clinical heterogeneity between patients remain inherent barriers to improving cancer outcomes. Such variation contributes to dramatically different outcomes for patients nominally sharing the same disease. Over the past five decades, significant efforts have been made in unraveling this heterogeneity between patients through refined classifications that capture physical, anatomical, radiographic, histological, and molecular features of tumors. For example, by identifying patients with similar clinical phenotypes, anatomic staging systems have enabled more uniform treatment practices, leading to improvement in outcomes for patients (Edge and Compton, 2010; Gradishar et al., 2018; Horwitz et al., 2016; Wierda et al., 2017). Similarly, molecular dissection of differing biological features has resulted in the identification of targetable subtypes in diverse tumors, including HER2 amplifications in breast cancer and EGFR mutations in lung cancers, also leading to improved patient outcomes (Lynch et al., 2004; Paez et al., 2004; Piccart-Gebhart et al., 2005; Romond et al., 2005; Slamon et al., 1987).

Despite such advances, however, significant heterogeneity remains in most cancer subtypes (Bedard et al., 2013). For example, within the most common hematologic cancer, diffuse large-B cell lymphoma (DLBCL), systemic therapy cures the majority of patients; however, a significant minority will succumb to disease. Several prognostic tools to stratify DLBCL patients into risk groups are currently employed, utilizing clinical (International prognostic index, IPI), molecular (Cell-of-origin, COO) (Alizadeh et al., 2000; Rosenwald et al., 2002), or radiographic (Interim positron emission tomography, iPET) features (Fig 1A,B) (Safar et al., 2012; Thompson et al., 2014). However, prior studies utilizing these methods to select patients for intensified therapy have failed to improve overall survival (Duhrsen et al., 2018; El-Galaly et al., 2015; Moskowitz et al., 2010; Nowakowski et al., 2016).

Figure 1. Design and motivation for development of the Continuous Individualized Risk Index.

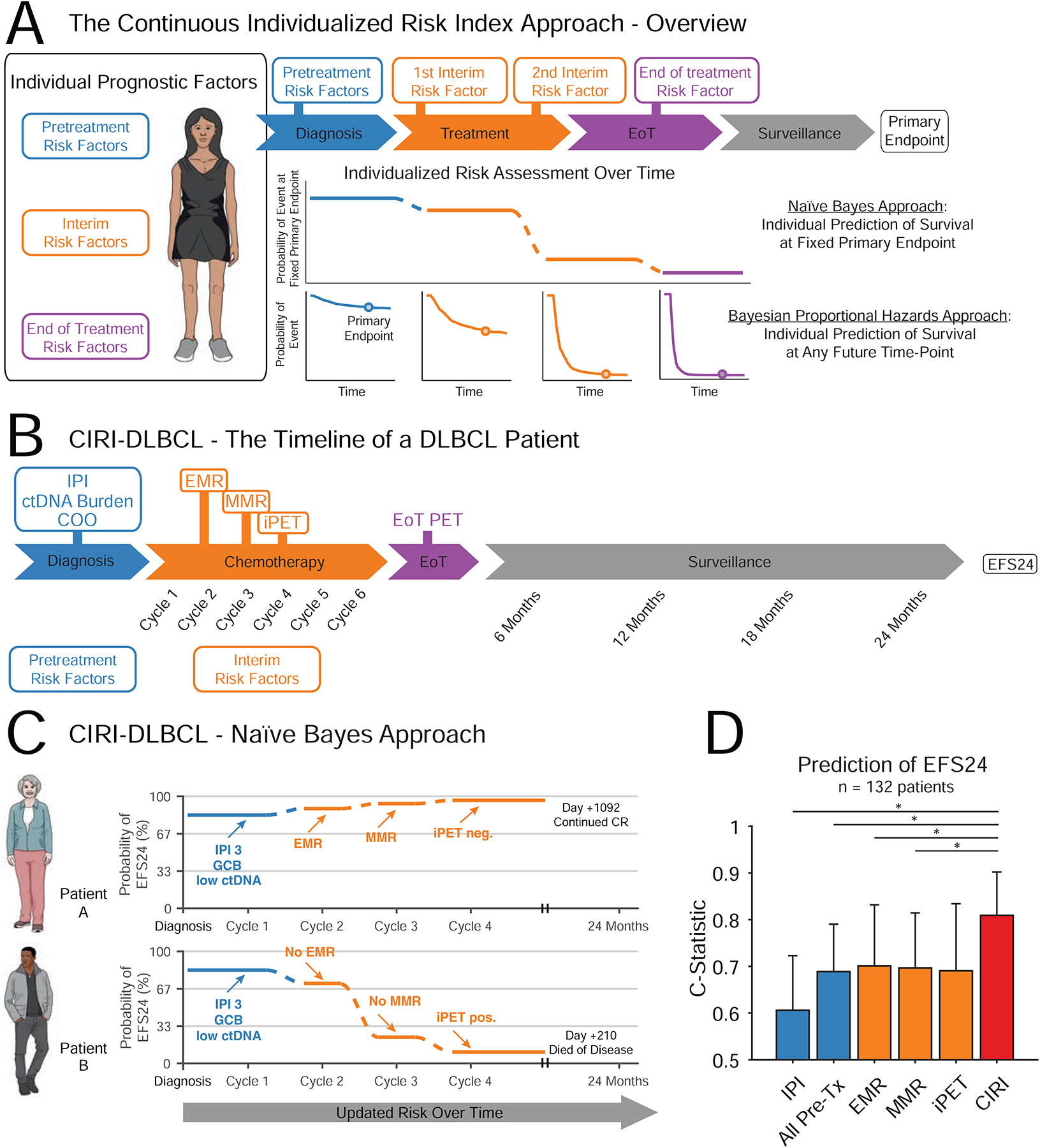
A) Patients with malignancies have a number of prognostic risk factors that can be evaluated throughout a course of therapy. CIRI integrates these to make a personalized prediction of treatment outcome. We describe two approaches; i) an initial naïve Bayes Approach, which produces the probability of event by a fixed primary endpoint, and ii) a Bayesian proportional hazards approach, which produces a prediction of survival at any future time-point. B) The course of a typical patient with DLBCL through therapy and surveillance is shown. Pretreatment risk factors (shown in blue) are obtained directly prior to therapy. Interim risk factors (shown in orange) are obtained early on during a course of therapy before the eventual clinical outcome. C) A graphical schema depicting CIRI-DLBCL is shown. The probability of achieving a desired clinical outcome (here, EFS24) at a given point in time is shown. As more information is obtained, this probability is updated. For example, both patient A (top) and B (bottom) have the same pretreatment risk factors. However, at the start of cycle 2, patient A has achieved a favorable EMR - therefore, her probability of reaching EFS24 increases. In contrast, patient B does not achieve an EMR at the start of cycle 2 - therefore, his probability of reaching EFS24 decreases. Similar changes are seen when MMR and interim PET/CT scans become available. D) A bar plot demonstrates the C-Statistic and 95% C.I. for predicting EFS24 by the IPI, all pretreatment factors, EMR, MMR, interim PET/CT, and CIRI; predictions from CIRI-DLBCL are made after integration of all data. * indicates P < 0.05. (DLBCL: diffuse large B cell lymphoma; IPI: international prognostic index; ctDNA: circulating tumor DNA; EMR: early molecular response; MMR: major molecular response; EFS24: event-free survival at 24 months; iPET: interim PET/CT scan; All Pre-Tx: All pretreatment factors). See also Figure S1.

Previous risk stratification tools have largely focused on pretreatment factors due to the difficulty of obtaining serial tumor biopsies. Despite this, an early response to systemic therapy is a strong prognostic factor in many cancers, including hematologic and solid tumors (Barrington et al., 2014; Cheson et al., 2014; Hahnen et al., 2017; Ommen, 2016). Innovative tools such as liquid biopsies are rapidly emerging and allow serial assessments of tumor burden with relative ease (Schwarzenbach et al., 2011). For example, our group recently reported the prognostic performance of circulating tumor DNA (ctDNA) after one or two cycles of systemic therapy (Early and Major Molecular Response; EMR/MMR) for predicting outcomes in patients with DLBCL (Kurtz et al., 2018). Similarly, other response-based surrogates of outcome have proven strongly predictive in other cancers. Circulating minimal residual disease (MRD) following therapy of chronic lymphocytic leukemia (CLL) is strongly associated with outcomes after diverse therapies (Bottcher et al., 2012; Kovacs et al., 2016a; Kwok et al., 2016). Separately, pathological complete responses (pCR) to neoadjuvant therapy have been suggested as predictive of ultimate outcomes in several cancer types, including invasive ductal carcinomas of the breast (Symmans et al., 2007; Symmans et al., 2017).

However, each of the above tools fundamentally separates patients into ‘risk categories’ based on an assessment at a fixed time-point either before or during therapy, leading to misclassification of certain patients. For example, over 50% of DLBCL patients in the ‘high-risk’ IPI category will ultimately be cured with frontline therapy (Ziepert et al., 2010). We therefore hypothesized that a method to accurately measure a given patient’s risk throughout the disease course - rather than solely identifying at-risk populations of patients prior to treatment - could better resolve clinical heterogeneity and provide superior outcome predictions. Here, we describe this new framework - the Continuous Individualized Risk Index (CIRI, http://ciri.stanford.edu) - as a dynamic risk model for integrating diverse outcome predictors into a single quantitative risk estimate for individual patients throughout their disease. We explore the utility of CIRI for dynamic outcome prediction in multiple diseases, including the most common lymphoma subtype (DLBCL), the most common leukemia (CLL), and the most common cancer in women (breast cancer). These cancers have diverse, established outcome predictors, including biomarkers assessed after therapy by noninvasive or invasive means as outlined above. We compare CIRI to proportional hazard modeling, the traditional tool for modeling survival with multiple predictors. We demonstrate that by integrating prior knowledge of the utility of each biomarker, CIRI can outperform proportional hazard modeling, with proportional hazard models demonstrating similar performance only when large amounts of training data are available. Finally, we perform a proof-of-concept analysis to explore how CIRI could be used to not only improve accuracy of prognostic models, but also identify subsets of patients who benefit from specific therapies.

Results

Development of a dynamic model for personalized disease risk in DLBCL

We initially conceptualized our risk tool after ‘win-probability’ models that have gained popularity in several fields, most notably in sports and politics for predicting the outcomes of football games and elections (Chen et al., 2008; Gelman, 2014; Linzer, 2013; Lock and Nettleton, 2014; Stern, 1991). Here, predictions are made in the context of time and are refined with serially collected, longitudinal data (Fig 1A). For example, in patients with DLBCL, not all risk predictors are available prior to therapy (Fig 1B). Therefore, risk-predictions are updated dynamically as additional information becomes available, such as measuring molecular response by ctDNA or interim imaging studies (Fig 1C).

Unlike win probability models in sports and elections where ample historical training data exists, large archives of case-level medical data are generally lacking. Even less common are complete datasets that include all predictors of interest. For example, few case-level data sources exist that capture both established DLBCL risk factors (such as the IPI, cell of origin, and interim PET) and novel predictors such as ctDNA (Sargent et al., 2017). We therefore initially developed CIRI using a naïve Bayes approach, allowing us to leverage group-level prior knowledge on the performance of established tools for risk stratification, which is commonly reported in the literature. This approach also allows serial integration of predictors over time, as described above (STAR Methods).

CIRI-DLBCL considers a total of six complementary risk predictors, including three established risk-factors (IPI (Sehn et al., 2007; Ziepert et al., 2010), molecular cell of origin (Scott et al., 2015), and interim imaging (Cashen et al., 2011; Micallef et al., 2011; Nols et al., 2014; Pregno et al., 2012; Safar et al., 2012; Yang et al., 2011; Yoo et al., 2011; Zinzani et al., 2011)), as well as three ctDNA risk-factors (pretreatment ctDNA levels, EMR, and MMR) (Kurtz et al., 2018). To assess CIRI-DLBCL, we attempted to predict event-free survival at 24 months (EFS24), a clinically relevant milestone and standard endpoint in this disease (Fig 1B) (Maurer et al., 2014). We determined the performance for established risk-factors from a total of 2558 patients in 11 previously published studies to serve as prior information for our model (STAR Methods, Fig S1A–F). No prior knowledge is available for ctDNA levels; thus, we determined the performance of ctDNA in a development set of patients receiving frontline immunochemotherapy (Table S1). The conditional probabilities for individual predictors are provided in Table S2.

A graphical schema for CIRI depicting its performance for two exemplar patients with similar baseline characteristics is shown in Fig 1C. When a new diagnosis of DLBCL is made, the IPI is typically assessed, providing an initial risk estimate. Additional risk factors, including cell-of-origin and pretreatment ctDNA, can further refine the pretreatment risk estimate. As therapy is introduced, further risk factors, including ctDNA measurements (i.e., EMR, MMR) and interim imaging (i.e., PET/CT) can be obtained and integrated, updating CIRI personalized risk estimates over time.

CIRI outcome predictions improve on the IPI and molecular response in DLBCL

We assessed the performance of CIRI-DLBCL in an independent validation cohort of 132 patients with available ctDNA data; the clinical characteristics of these patients are provided in Table S1. We evaluated our predictions for both quantitative accuracy (i.e., ‘model calibration’) as well as ability to accurately identify outcomes (i.e., ‘discrimination’). We assessed model calibration by comparing predicted and observed risks of the entire cohort (‘calibration-in-the-large’) as well as across subgroups of patients with similar risk profiles (via calibration plot and regression) (STAR Methods). Across the cohort, predictions made by CIRI-DLBCL were calibrated with clinical outcomes - the average predicted risk of event by 24 months was not different from the observed risk (25% vs 26% risk of event, or a 1% overestimate of risk [95% CI −3% to 4%]). Subgroups of patients with similar risk profiles also displayed adequate calibration to observed outcomes (n=528 predictions from 132 patients; Fig S1G). Importantly, prediction of EFS24 by CIRI significantly improved on the IPI when compared by C-statistic (Fig 1D, 0.81 vs 0.61; P<0.001), with similar improvements over EMR, MMR, and interim PET as individual predictors (C-statistic 0.70, 0.70, 0.69; P=0.022, 0.006, and 0.07 respectively). Moreover, while this initial approach was designed to predict EFS at 24 months, stratification of risk by CIRI-DLBCL also significantly improved on prediction of OS at 24 months compared to the IPI (Fig S1H; 0.86 vs 0.71; P=0.009).

Extension of CIRI to longitudinal survival data

The formulation of CIRI above predicts the probability of an event at a fixed time-point of interest (in the case of DLBCL, EFS at 24 months). However, in many situations, patients and clinicians may not be interested in survival at a fixed point in time, but rather in survival at any time during a course of therapy. We therefore extended CIRI to predict the survival of individual patients at any point over time by utilizing proportional hazard modeling and Bayesian analysis (STAR Methods). Similar to the fixed time-point CIRI above, we began by identifying parameters for the model based on previously established literature (Fig S2A–G). A schema for CIRI predicting survival over time for two patients with similar baseline characteristics is shown in Fig 2A. Similar to Fig 1C, a given patient’s probability of survival is updated as more information becomes available. However, a complete, personalized survival curve is produced, rather than a prediction at a fixed point in time. Notably, as this procedure includes predictors obtained after the start of therapy, this process can suffer from ‘guaranteed time bias’. To account for this, the personalized probability of survival beginning from the start of therapy remains at 100% - or ‘guaranteed’ - until the time of the most recently obtained risk predictor, as demonstrated in Fig 2A.

Figure 2. Extension of CIRI to survival data.

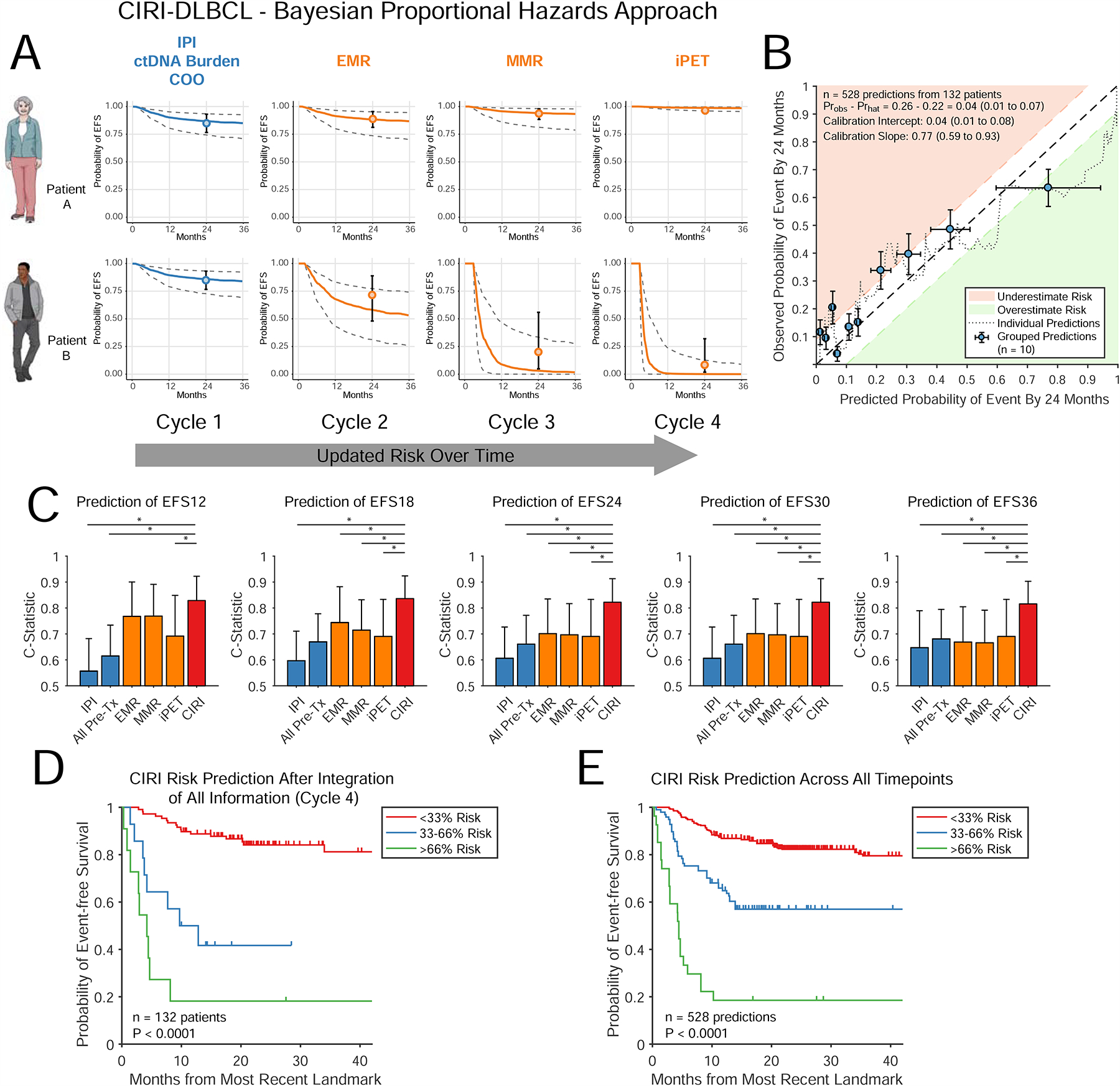
A) A schema for extending CIRI-DLBCL to patient-specific survival curve prediction. Similar to Fig 1C, the predicted survival function for a given patient is updated as more information becomes available. The survival curves are shown with 80% C.I.; predictions from the time-point specific CIRI-DLBCL in Fig 1 are also shown. B) Calibration plot of CIRI-DLBCL including predictions from all time-points, demonstrating predicted EFS24 (x-axis) and observed EFS24 (y-axis). See STAR Methods (Determination of model calibration) for details. The dotted line shows predicted versus observed risk (moving average) of event within 24 months. Patients were also grouped into deciles by predicted risk. The observed risk of each decile was calculated by the Kaplan-Meier method (blue dots). Areas of under and over prediction of risk by >10% are shown in red and green. Further calibration statistics are provided in the legend. C) Bar plots demonstrate the C-Statistic and 95% C.I. for predicting EFS at multiple time intervals by the IPI, all pretreatment risk factors, EMR, MMR, interim PET/CT, and CIRI; predictions from CIRI-DLBCL are made after integration of all data. D) A Kaplan-Meier estimate shows the EFS for patients stratified by CIRI-DLBCL risk-prediction of EFS24 split into three groups after integration of all information (i.e., at cycle 4, after interim PET/CT scan). E) Similar to panel D, a Kaplan-Meier estimate shows the event-free survival for patients stratified by CIRI-DLBCL into three groups. Here, risk-predictions across all time-points are shown. * indicates P < 0.05. See also Figure S2.

In our independent validation set, prediction of EFS24 demonstrated reasonable calibration-in-the-large, with only a 4% difference (95% C.I.: 1%–7%) between observed and predicted outcomes (Fig 2B). Moreover, CIRI-DLBCL demonstrated adequate calibration of predictions throughout the disease course, with a <5% difference between observed and predicted outcomes when considering event-free survival from 12 to 36 months (Fig. S2H). Importantly, CIRI-DLBCL generally outperformed the IPI, pretreatment risk factors, molecular response, and interim PET for prediction of EFS at multiple time-intervals throughout the disease course, ranging from 12 to 36 months (Fig 2C). Furthermore, while CIRI-DLBCL provides a quantitative risk estimate for each patient at each time-point, these predictions can also be separated into risk groups. When considering strata with <33%, 33%–66%, and >66% predicted risk of adverse event by 24 months - or low, medium, and high-risk - CIRI significantly stratified patients when considering either the final prediction after 3 cycles of immunochemotherapy or all risk-predictions in aggregate (Fig 2D–E). Additionally, we constructed a similar CIRI-DLBCL model for prediction of OS. Again, CIRI-DLBCL improved on prediction of OS at multiple time-intervals throughout the disease course as compared to the IPI and other individual predictors (Fig S2I–K).

Extension of CIRI to chronic lymphocytic leukemia

To further extend dynamic risk modeling and CIRI, we explored its utility in Chronic Lymphocytic Leukemia (CLL), an indolent malignancy and the most common leukemia in adults. Although CLL and DLBCL are both lymphoid malignancies, a distinct set of risk factors is used in each disease. In CLL, these include clinical and cytogenetic risk indices such as the CLL-IPI (The International CLL-IPI Working Group, 2016) and minimal residual disease (MRD) levels from peripheral blood cells (Bottcher et al., 2012; Kovacs et al., 2016a; Kwok et al., 2016). Furthermore, as treatment selection is a major prognostic factor in CLL (Eichhorst et al., 2016; Goede et al., 2014; Hallek et al., 2010), we explicitly considered the effect of therapy on outcomes in CIRI-CLL.

A timeline for a typical patient with CLL is shown in Fig 3A. The prognostic value of each of these features has been previously demonstrated in prior studies. We reanalyzed case-level data from three such studies from the German CLL Study Group - CLL8, CLL10, and CLL11 (Eichhorst et al., 2016; Goede et al., 2014; Hallek et al., 2010). These studies prospectively assessed the effect of therapy for CLL in a large population of patients. Notably, each study also had MRD data available at interim and final restaging assessed by flow cytometry (CLL8 and CLL10) or qPCR (CLL11). We identified 1426 patients from these 3 studies with at least one available MRD assessment after initiation of therapy (STAR Methods).

Figure 3. CIRI applied to chronic lymphocytic leukemia.

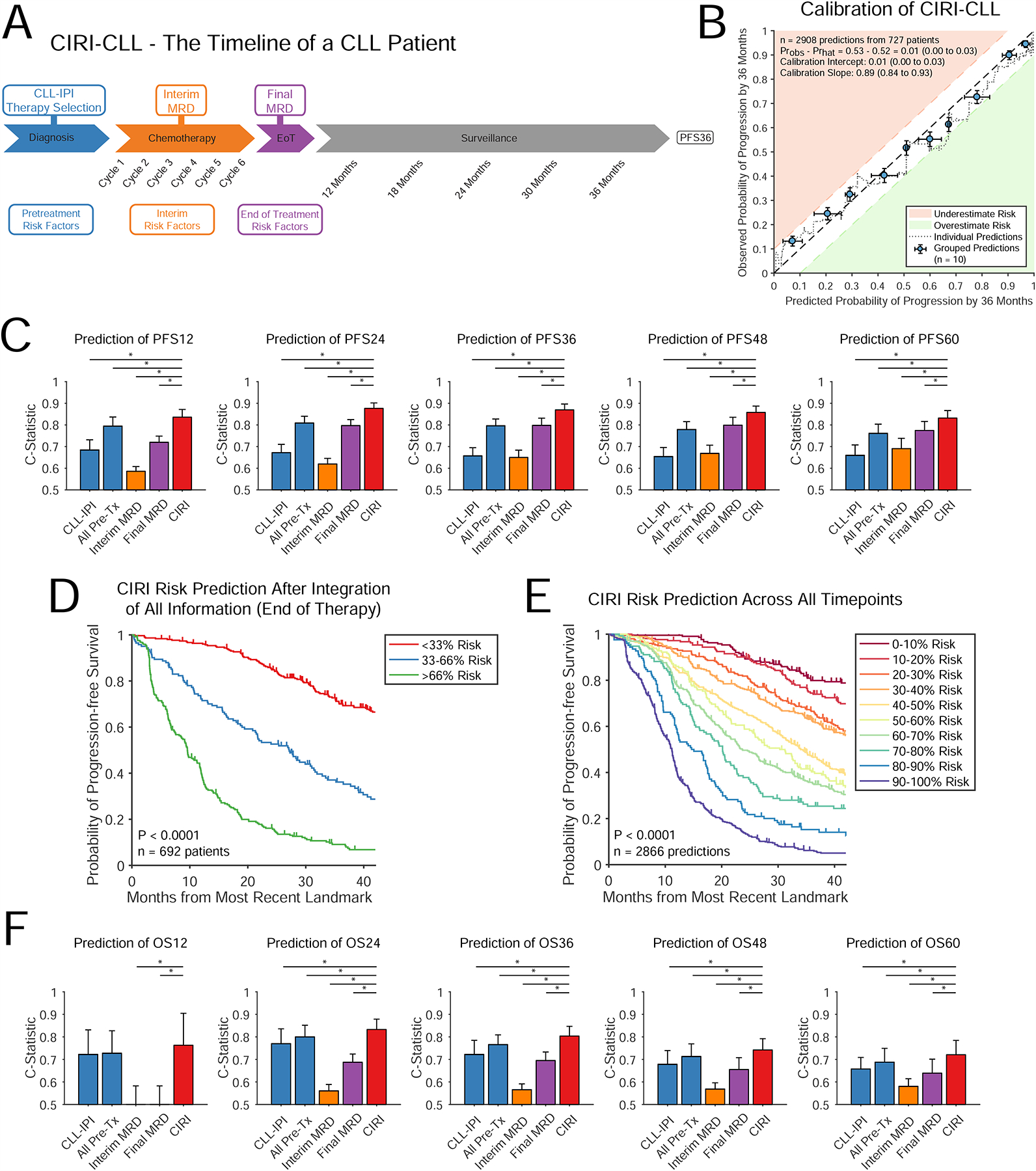
A) The course of a patient with CLL through therapy and surveillance is shown. Pretreatment risk factors (shown in blue) are obtained directly prior to therapy. Interim and end of therapy risk factors (shown in orange and purple) are obtained throughout a course of therapy, before the eventual clinical outcome (PFS36). B) Similar to Fig 2B, the displayed plot demonstrates the calibration of predictions from CIRI-CLL with observed patient outcomes across predictions from all time-points. C) Bar plots demonstrates the C-Statistic and 95% C.I. for predicting progression-free survival at various time-points using the CLL-IPI, all pretreatment risk factors, interim MRD, end of therapy MRD, and CIRI-CLL. Predictions from CIRI are made after integration of all data. D) A Kaplan-Meier estimate shows the PFS for patients stratified by CIRI-CLL risk-prediction of PFS36 split into three groups at the time of final restaging after integration of all information (i.e., at the end of therapy with knowledge of final MRD). To guard against guaranteed time bias, patients with progression prior to end of therapy MRD assessment (n=35, 5%) were excluded. E) Similar to panel D, a Kaplan-Meier estimate shows the PFS for patients stratified by CIRI-CLL. Here, risk-predictions across all time-points are shown; as many more individual risk-predictions are available, patients are split into 10-strata to demonstrate the power of this approach and model calibration at the desired endpoint (PFS at 36 months). To guard against guaranteed time bias, predictions utilizing information obtained after the progression event (n=42, 1%) were excluded. F) Bar plots demonstrates the C-Statistic and 95% C.I. for predicting OS at various time-points using the CLL-IPI, all pretreatment risk factors, interim MRD, end of therapy MRD, and CIRI. (PFS: progression-free survival; PFS36: progression-free survival at 36 months). * indicates P < 0.05. See also Figure S3.

We randomly assigned these patients into development and validation sets (STAR Methods); the characteristics of these patients are provided in Table S3. Using the development set to serve as our ‘prior knowledge’, we determined the parameters for CIRI-CLL, including the predictive value of CLL-IPI, interim and final MRD measurement, and choice of therapy, using our framework to predict a personalized probability of progression-free survival (PFS) over time (Fig S3A–E). We then assessed the performance of CIRI-CLL in the independent validation set. Similar to DLBCL, predictions made by CIRI-CLL were adequately calibrated with observed outcomes for predictions of PFS at 12, 24, 36, and 48 months (Fig 3B, S3F). Specifically, there was <5% difference between observed and predicted outcomes in the validation set at each of these time-points. Prediction of PFS by CIRI-CLL outperformed CLL-IPI and MRD assessment by C-statistic across all time-points considered (Fig 3C).

Similar to CIRI-DLBCL, when stratified based on predicted probability of reaching PFS36, CLL patients could be separated into risk strata with defined risk profiles (Fig 3D; P<0.0001). Given the larger number of subjects and predictions, this model provides an opportunity to further assess the ability of CIRI to stratify patients based on predicted risk. Considering all risk-predictions divided into ten groups, CIRI-CLL demonstrated robust and quantitative stratification of patient outcomes (Fig 3E; P<0.0001). We additionally constructed a CIRI-CLL model for prediction of OS. Similar to our model of PFS, stratification of risk by CIRI-CLL significantly improved on prediction of OS compared to the CLL-IPI and MRD assessment alone at all time horizons longer than 12 months, including an improvement in C-statistic from 0.72 to 0.80 for OS36 (P<0.001; Fig 3F, S3G–H).

Extension of CIRI to neoadjuvant chemotherapy in breast cancer

While detection of residual disease from either cell-free DNA or via cell-based approaches lends itself to dynamic risk assessment, this concept is more widely applicable to any longitudinal data that can be quantified during a course of therapy. To exemplify this, we constructed a CIRI risk model of localized breast adenocarcinomas (BRCA) treated with a combination of neoadjuvant chemotherapy followed by definitive surgical resection. A timeline for a typical patient with breast cancer receiving neoadjuvant chemotherapy prior to surgical resection is shown in Fig 4A. In this context, CIRI-BRCA again utilizes risk-factors obtained both prior to and during therapy; these indices include clinical stage, tumor grade, estrogen receptor and HER2 status (obtained pretreatment), as well as pathological response to neoadjuvant chemotherapy (i.e., residual cancer burden, assessed after neoadjuvant therapy and resection) (Symmans et al., 2017).

Figure 4. CIRI applied to breast adenocarcinoma.

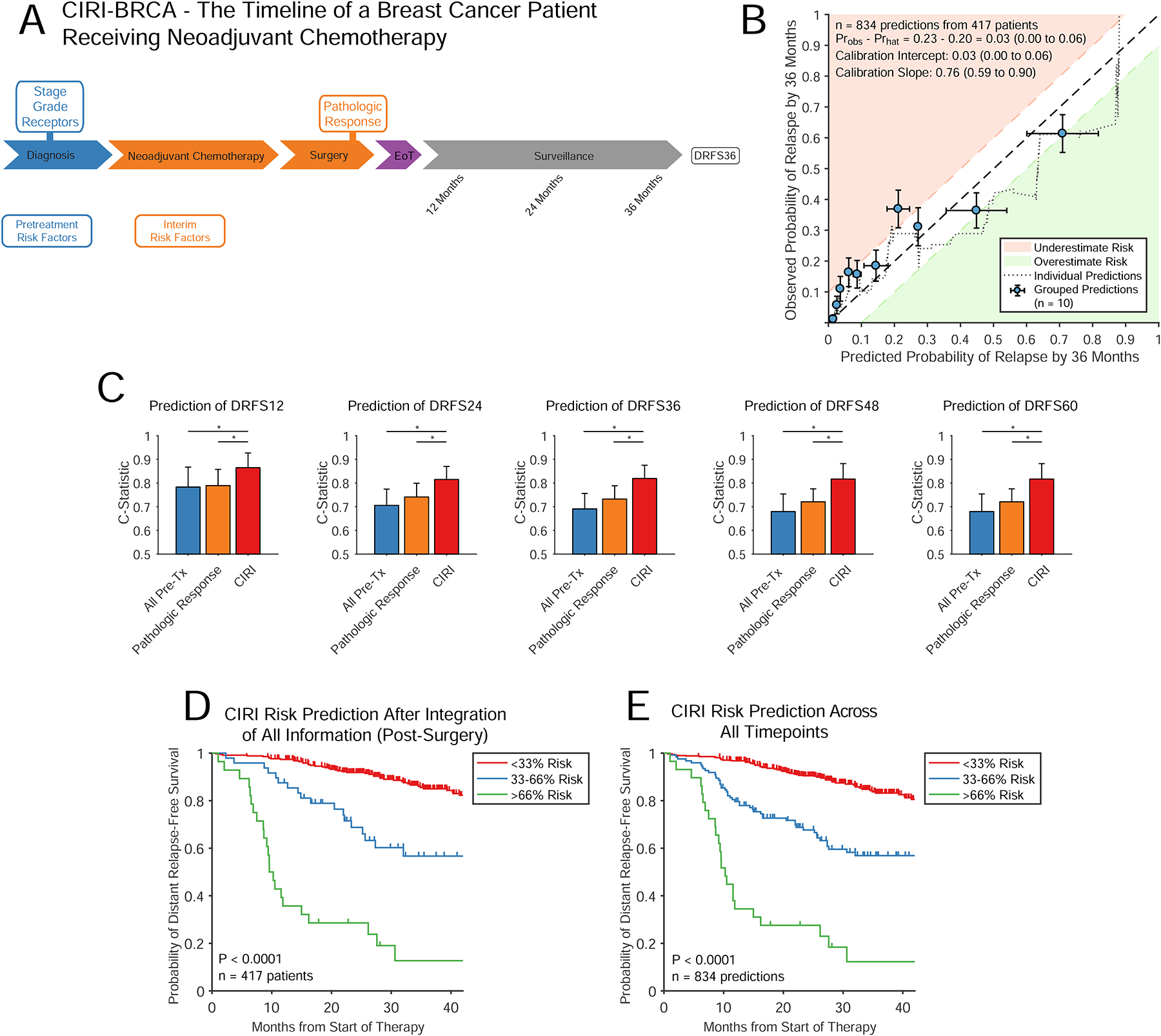
A) The course of a patient with breast cancer receiving neoadjuvant chemotherapy followed by surgery is shown. Pretreatment risk factors (shown in blue) are obtained directly prior to therapy. Interim risk factors (shown in orange) are obtained after surgery, but before the eventual clinical outcome (DRFS36). B) Similar to Fig 2B and 3B, the displayed plot demonstrates the calibration of predictions from CIRI-BRCA with observed patient outcomes across predictions from all time-points. C) Bar plot demonstrates the C-Statistic and 95% confidence interval for predicting DRFS at various time-points using pretreatment risk factors, residual cancer burden and CIRI. Predictions from CIRI-BRCA are made after integration of all data. D) A Kaplan-Meier estimate shows the DRFS for patients stratified by CIRI-BRCA risk-prediction of DRFS36 split into three groups at the time of final restaging after integration of all information (i.e., inclusive of pathologic response). E) Similar to panel D, a Kaplan-Meier estimate shows the DRFS for patients stratified by CIRI-BRCA. Here, risk-predictions across all time-points are shown; split into 3-strata. (DRFS: distant relapse-free survival; DRFS36: distant relapse free survival at 36 months). * indicates P < 0.05. See also Figure S4.

We established the parameters for CIRI-BRCA for each of these risk factors from published literature (Curtis et al., 2012; Symmans et al., 2007) (Fig. S4A–E); we then assessed the performance of our model in an independent, publicly available cohort of 417 patients (Hatzis et al., 2011). The characteristics of the patients used to develop and validate CIRI-BRCA are shown in Table S4. Similar to our DLBCL and CLL models, predictions made by CIRI-BRCA demonstrated acceptable calibration across endpoints from 12 to 60 months (Fig. 4B, S4F). Furthermore, predictions made by CIRI-BRCA improved on predictions made using pretreatment factors or pathologic response assessment alone (Fig. 4C). CIRI-BRCA significantly stratified patients with similar risk profiles for distant relapse-free survival both at the completion of therapy and throughout the course of treatment (Fig. 4D–E). Overall survival data was not available for this cohort.

Effect of correlated predictors on CIRI

One of the assumptions behind CIRI is the independence of the effects of individual risk predictors in the prior distribution. To test the robustness of CIRI using our Bayesian proportional hazard approach to correlation of these predictors, we simulated datasets containing an increasing amount of correlation between each risk factor (STAR Methods). We assessed the effect of increasing correlation on the performance of CIRI, both for classification of and quantitative calibration with observed outcomes. CIRI remained robust to increasing levels of correlation, with minimal change in classification performance (i.e., C-Statistic) and degradation of model calibration only at high levels of correlation (Fig. 5A–C).

Figure 5. Robustness of CIRI and comparisons with proportional hazard modeling.

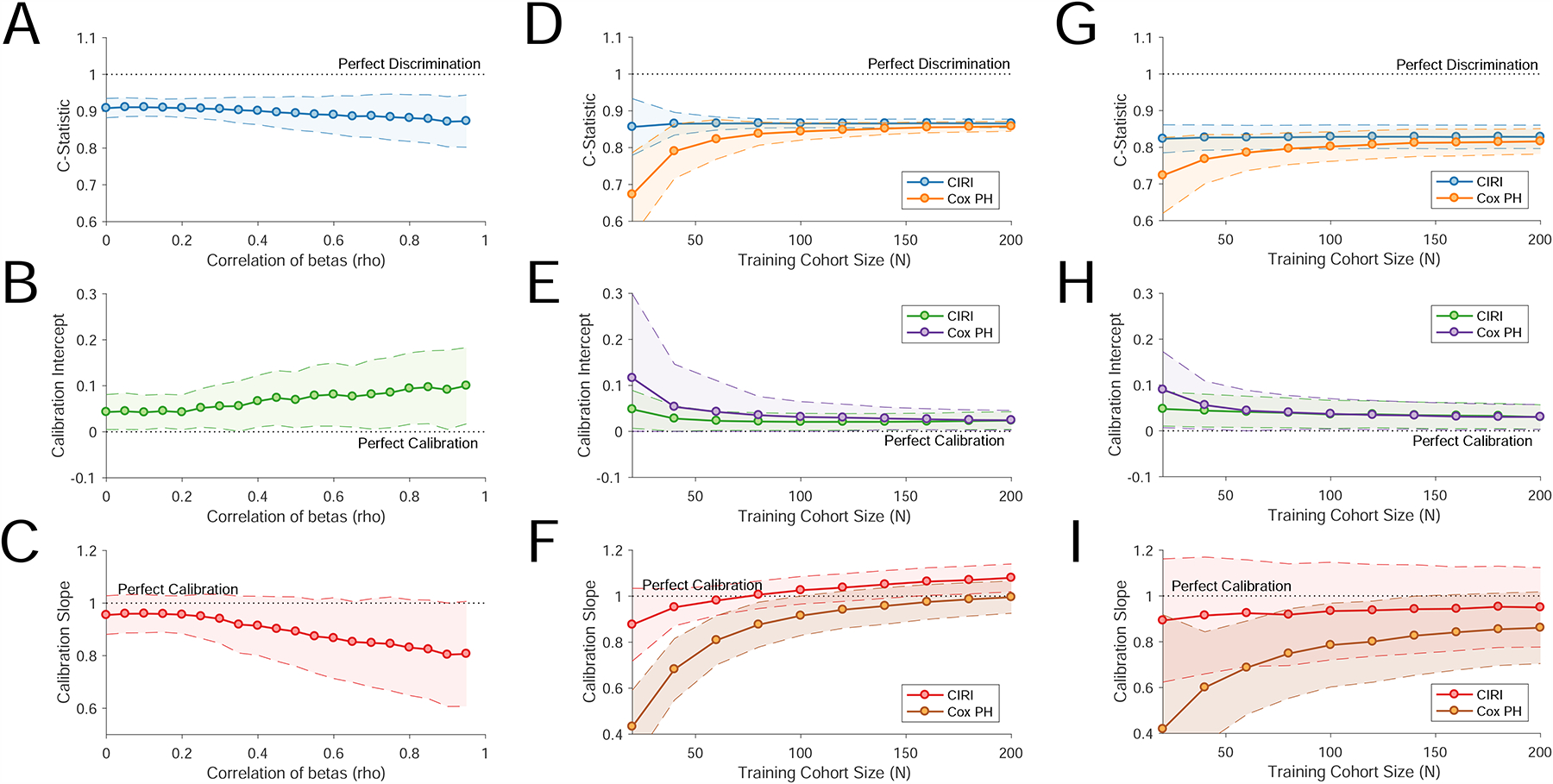
A–C) These plots demonstrate the effect of increasing levels of correlation of individual component risk predictors on CIRI in a simulated dataset. These include the effect of increasing correlation on discrimination of outcomes by C-Statistic (Panel A), calibration intercept (Panel B), and calibration slope (Panel C). D–I) To compare CIRI with Cox proportional hazard models, we trained Cox proportional hazard models starting from 20 to 200 cases drawn randomly from our validation set in CLL (D–F) and breast cancer (G–I). We then evaluated this model in independent cases (CLL, n=400; breast cancer n=150) drawn randomly from our validation set. The performance of the resulting model in this independent patient sets was compared to the performance of CIRI. Panels D–F demonstrate model performance in CLL. Panel D demonstrates the predictive performance of each model (i.e., C-Statistic) as a function of the number of training cases. Panel E demonstrates the calibration-in-the-large, or calibration intercept, of each model as a function of the number of training cases. Panel F demonstrates the calibration slope of each model as a function of the number of training cases. A perfect model has a calibration slope of 1. The confidence envelope (80%) of each statistic is shown as a shaded area, based on 250 samplings. Panels G–I are as per panels D–F, demonstrating performance in breast cancer.

Comparison of CIRI to proportional-hazard modeling

The CIRI framework outlined here has a number of advantages over alternative methods, including the ability to incorporate prior knowledge of the performance of each outcome predictor as established from prior literature or datasets. We compared the performance of CIRI to proportional hazard models that were not informed by prior knowledge in the CLL and breast cancer datasets. As proportional hazard models typically require case level training data, we utilized our validation set in each case to develop and cross-validate the model. Interestingly, when the amount of case-level training data was low (<100 cases), CIRI outperformed standard Cox proportional hazard models, both in terms of identifying clinical outcomes (Fig. 5D and 5G) and calibration with quantitative outcomes (Fig. 5E–F, 5H–I). However, as the number of cases increased, the predictive performance of proportional hazard modeling converged toward the performance of CIRI for both discrimination of clinical outcomes (i.e., C-Statistic) and model calibration.

Prediction of therapeutic-benefit within specific disease subgroups

While improvements in prognostication are useful on their own, developing biomarkers to identify patient subgroups who benefit from specific therapies is a major challenge and focus of intense investigation. Such so-called predictive biomarkers identify a differential effect of therapy between biomarker-positive and negative patients (Ballman, 2015). We wished to explore if CIRI could facilitate development of novel predictive biomarkers. To do so we focused on CLL, since our dataset contained multiple therapeutic regimens.

To utilize CIRI as a predictive biomarker, an ‘induction’ period of therapy must be given, followed by an assessment of response to therapy. Based on the combination of this dynamic evaluation and pretreatment risk factors, the best therapy for a specific patient could then be selected (Fig. 6A and 6D). To simulate this potential use-case, we constructed a CIRI-CLL model combining the CLL-IPI and interim MRD while blinding ourselves to the choice of initial therapy (STAR Methods). We applied this model to our CLL dataset in a 10-fold cross-validation framework to identify patients who preferentially benefit from FCR compared to alternative immuno-chemotherapies after the interim MRD time-point.

Figure 6. Prediction of therapeutic benefit in subsets of patients.

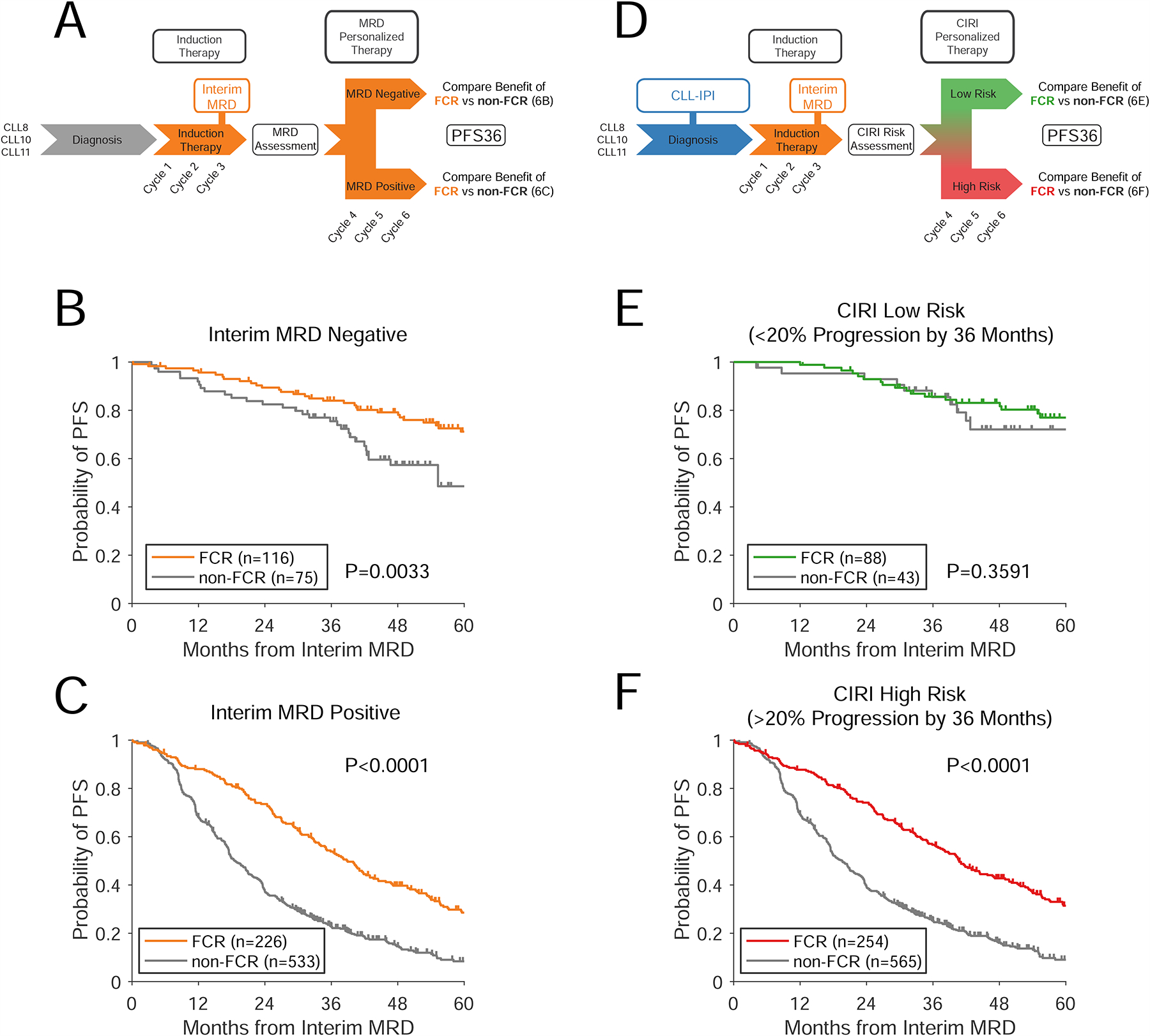
A) A schema for using interim MRD to guide therapy in CLL. Patients receive a period of induction therapy; after which interim MRD is assessed. The effect of different types of therapy can then be assessed in patients with interim MRD negative or positive disease. Here, we assessed this paradigm using patients from the CLL8, CLL10, and CLL11 clinical trials receiving chemo-immunotherapy (i.e., FCR, BR, R-chlorambucil, G-chlorambucil), blinding ourselves to the choice of therapy over the first 3 cycles. B–C) Kaplan-Meier estimates show the benefit of therapy with FCR vs alternative therapies for progression-free survival in interim MRD negative patients (Panel B) and interim MRD positive patients (Panel C). Survival is landmarked from the time of interim MRD assessment. D) A schema for using CIRI-CLL to discover predictive biomarkers to guide therapy. Patients receive a pretreatment risk-prediction (using the CLL-IPI), and then receive a period of induction therapy. At this point, interim MRD is assessed, allowing quantitative integration with CIRI. E–F) Kaplan-Meier estimates show the PFS of patients receiving FCR vs alternative therapies in patients with CIRI risk < 20% (Panel E) and patients with CIRI risk > 20% (Panel F). See also Figures S5–6.

Taken as a single biomarker (Fig 6A), interim MRD was prognostic, but not predictive of benefit from subsequent therapy. Specifically, MRD negative (MRD−) patients had superior outcomes to MRD positive (MRD+) patients; yet, both MRD− and MRD+ patients benefited from FCR over alternatives (Fig 6B–C). In contrast, CIRI-CLL provides each individual patient with a quantitative estimate of the probability of disease progression at 36 months, based on the combination of CLL-IPI and interim MRD (Fig 6D). Therefore, a range of thresholds are available to separate patients into low- and high-risk groups. CIRI-CLL establishes parameters for the benefit from each alternative therapy - this allows us to forecast the outcomes for patients receiving each potential therapy.

We performed this forecasting to estimate the likely benefit from FCR versus non-FCR therapy for groups of high vs low risk patients defined by CIRI at various thresholds (Fig. S5A–C). Interestingly, while patients with a probability of progression >20% at 36 months were predicted to benefit from FCR, patients with <20% probability of progression were not predicted to benefit. More importantly, these predictions were confirmed in patient outcomes (Fig. 6E–F) - patients with >20% probability of progression at 36 months significantly benefited from FCR therapy, while patients with <20% probability of progression did not. This differential effect between low- and high-risk patients indicates that CIRI-CLL is a predictive biomarker. Furthermore, the interaction between CIRI and choice of therapy was statistically significant for prediction of PFS at 36 months in multivariate models (Cox proportional hazards, P= 0.047; generalized linear model, P=0.0006), further indicating a predictive biomarker (Ballman, 2015). As compared to interim MRD, the improvement in predictive power by CIRI stems primarily from reclassifying MRD− patients. In total, 31% (60/191) of MRD− patients were reclassified as CIRI high-risk, due to high or very-high CLL-IPI scores. When comparing the predicted benefit of FCR versus alternate therapies from our model to the observed benefit at each threshold, the observed benefit of FCR in low- and high-risk populations largely agreed with the model predictions (Fig S5A–C, Supplementary Dataset).

We further explored the ability of CIRI to identify predictive biomarkers in the context of neoadjuvant chemotherapy for locally advanced HER2+ breast adenocarcinoma. We applied our CIRI-BRCA model to publicly available retrospective data from multiple clinical trials where neoadjuvant therapy was given (Esserman et al., 2012; Ignatiadis et al., 2019). We limited our analysis to only patients with HER2+ disease to examine the effect of dual HER2-targeted therapy with Trastuzumab and Pertuzumab. Similar to our example in CLL, we blinded ourselves to treatment and applied CIRI-BRCA to predict DFS at 36 months. Similar to interim MRD in CLL, pathologic response to therapy was not predictive of benefit from dual HER2 therapy (Fig S5D–F). In contrast, CIRI-BRCA with a threshold of > or < 15% probability of progression identified a group of high-risk patients who preferentially benefited from dual targeted therapy (Fig S5G–L and Supplementary Dataset).

Discussion

Over the last two decades, numerous prognostic biomarkers have been described throughout oncology, with particular emphasis on pretreatment clinical and molecular factors. Various statistical methods to integrate these biomarkers at a fixed time-point have been described resulting in clinically useful prognostic scores for a variety of cancers (International Non-Hodgkin’s Lymphoma Prognostic Factors, 1993; Sparano et al., 2015; The International CLL-IPI Working Group, 2016). Such fixed time-point risk models are routinely used to determine prognosis at multiple clinical landmarks, including at the time of initial diagnosis or at the time of second-line or salvage therapy (Chi et al., 2016; Hamlin et al., 2003; Moskowitz et al., 1999). Importantly, these models generally do not consider dynamic response to therapy as a feature. More recently, evoked biomarkers capturing a phenotypic response to therapy have been described using radiographic, pathologic, or molecular features. While these features are independently prognostic of outcomes, we hypothesized that integration with other predictors - including pretreatment factors - could improve and individualize outcome predictions.

Early heuristic efforts to combine response-based biomarkers with pretreatment factors have shown promise for improving outcome prediction (Fink et al., 2017; Fink et al., 2013). Moreover, physicians routinely utilize anatomical imaging, blood work, and clinical symptoms to monitor patients during therapy and qualitatively assess risk. Unfortunately, in the clinical care of individual patients, evoked and dynamic risk-factors do not easily lend themselves to multivariate analysis due to their collection over time and the possibility of missing data-points. Prior methods for predictive modeling with covariates that change over time based on proportional hazard models have been explored (Fisher and Lin, 1999); however, these often require complex functional forms and have difficulty dealing with missing data. The emergence of novel response-based biomarkers, along with the long-standing use of routine clinical testing during a patient’s treatment course, affords an opportunity to improve on existing prognostic tools by integration of diverse dynamic data.

We therefore developed CIRI, a method to integrate diverse outcome predictors collected over time, resulting in a quantitative, personalized prediction of clinical outcomes. Here, we demonstrate two approaches - an initial naïve Bayes method to predict outcomes at a fixed endpoint, and a method based on Bayesian analysis and proportional hazard assumptions to develop personalized predictions of outcomes over time. In each method, the model is updated as information is gathered over a disease course. Notably, CIRI is distinct from machine-learning approaches in two key aspects. First, rather than starting with a large number of possible features, CIRI leverages prior knowledge and utilizes only a handful of established risk-factors. Second, by limiting the number of predictors and applying simple Bayesian frameworks, a prognostic model can be constructed simply by establishing a small number of parameters. These parameters are easily obtained from prior studies or literature, thus removing the need for a large number of training cases. Indeed, the performance of CIRI was superior to proportional hazard modeling when the number of training cases available for model development was limited. This scenario is often encountered with emerging biomarkers such as liquid biopsies that are not long-established in the literature. Consequently, by estimating the prognostic impact of novel risk-factors from relatively limited external data, CIRI can be easily updated as new biomarkers emerge.

To demonstrate the performance of this method, we developed CIRI models to predict outcomes in three different malignancies, when using a diverse source of biomarkers to measure response to therapy. Specifically, we evaluated serial ctDNA levels as a measure of residual disease in a common aggressive lymphoma (DLBCL), minimal residual disease from circulating cells in a common leukemia (CLL), and histopathological evidence of microscopic residual cancer in resected breast tumors following neoadjuvant therapy. The predictive models for each of these three diseases are available at http://ciri.stanford.edu (Fig. S6A). In each case, CIRI produces a personalized, quantitative prediction of the probability of clinically relevant outcome that is updated as more information is made available. In independent validation cohorts, we demonstrate a sufficient degree of calibration in all three diseases - that is, the predicted probability of outcome produced by CIRI is close to the observed data. Calibration is an important consideration for any predictive model, and it is worth noting that the model with the most training and validation cases (CIRI-CLL) demonstrated the best calibration. We anticipate that the calibration of other models would improve with increased data to train the necessary parameters.

Importantly, CIRI demonstrated superior outcome prediction to current gold standard prognostic indices, including against validated risk models tailored for each disease. Indeed, the composite CIRI model in each disease improved on each individual component predictor by C-statistic, demonstrating the importance of considering a diverse source of data when making predictions. As noninvasive biomarkers to monitor disease burden (i.e., ctDNA and other MRD methods) become more common, we anticipate methods to produce a personalized, quantitative estimate of likely outcomes such as CIRI will become widely useful for both clinicians and patients.

We also note that we evaluated CIRI in patient cohorts with some element of case-level missing data; that is, not every risk-factor considered by CIRI was available for every patient. The fact that CIRI remains robust to missing data when making predictions for individuals is one of its key features, as missing data is commonplace in the clinic (Little et al., 2012). Moreover, we expect the performance of CIRI should only improve in cases where complete data are available.

When applying CIRI and other risk models, attention must be paid to the clinical scenario and specifically the choice of therapy. The performance of risk models trained in the context of a given therapy may degrade as more effective novel therapies emerge. Correspondingly, in the case of CLL, where the choice of frontline therapy can significantly impact expected PFS and OS, we explicitly consider the choice of therapy as an outcome predictor. As new therapies emerge, the effect of these on outcomes should be considered and integrated into CIRI. Doing so should maximize the discriminative performance of CIRI, although prognostication in a therapy-independent context may also be valuable.

While having a better tool for risk-stratification has potential utility by itself, how to use prognostic information in the clinic is not well established. Circulating tumor DNA and other circulating biomarkers have shown significant prognostic value at both early time-points and at the end of therapy (Bottcher et al., 2012; Chaudhuri et al., 2017; Garcia-Murillas et al., 2015; Jongen-Lavrencic et al., 2018; Tie et al., 2016), but how to act on this data remains unclear. In contrast, ‘predictive biomarkers’ that identify a differential therapeutic effect between patient subgroups can be used to select therapy. Previous predictive biomarkers often relate to qualitative differences between tumors - such as activating EGFR mutations in lung cancer and EGFR tyrosine kinase inhibitors (Lynch et al., 2004; Paez et al., 2004) - but these markers are limited to a handful of examples.

Here, we explored the possibility of using quantitative risk assessment through CIRI as an alternative approach for developing predictive biomarkers. In a proof-of-concept analysis in CLL utilizing CLL-IPI and interim MRD, we identified a high-risk group of patients who preferentially benefited from aggressive immunochemotherapy with FCR, as well as a low-risk group of patients who did not benefit from FCR over other evaluated therapies. A similar analysis in HER2+ breast adenocarcinomas revealed a group of high-risk patients who preferentially benefited from dual HER2-targeted therapy. These unplanned post hoc analyses have important limitations - most notably that selecting therapy based on CIRI requires a period of ‘induction therapy’ prior to personalized therapy selection. Most historic trials have not been performed in this manner, requiring us to ‘blind’ ourselves to choice of initial therapy in this proof-of-concept. Nevertheless, similar survival outcomes have been observed in scenarios where systemic treatment can be performed before or after surgery (e.g., adjuvant vs. neoadjuvant therapy for breast cancer (Early Breast Cancer Trialists’ Collaborative, 2018)), suggesting the feasibility of this approach. While these retrospective analyses must be confirmed by prospective clinical trials, this data suggests a shift in clinical paradigms to include an initial ‘induction phase’ where response to therapy can be assessed could facilitate a new class of predictive biomarkers.

CIRI furthermore provides a potential path forward to aid clinical decision-making by providing quantitative estimates of likely outcomes. To illustrate this, consider a current clinical challenge - selecting high-risk DLBCL patients for intensified therapy (Fig S6B–D, STAR Methods). While previous methods to select patients for early treatment intensification, such as the IPI and interim PET/CT scans, are able to identify a group with worse outcomes than the average patient, prior studies intensifying therapy for patients based on these factors alone have failed to improve overall survival (Chiappella et al., 2017; Duhrsen et al., 2018). This is potentially due to largely favorable outcomes for patients despite high-risk IPI or interim PET/CT scan, particularly in comparison to the efficacy of salvage therapy (Fig S6B). Indeed, 42% of patients with positive interim PET/CT scans remain disease-free at 24 months with continued RCHOP (Duhrsen et al., 2018), compared to ~30% EFS24 rate in unselected patients receiving salvage therapy (Crump et al., 2014). In contrast, CIRI considers the probability of outcome for each patient individually (Fig S6C); by doing so, CIRI can identify individual patients with extremely high-risk of treatment failure who are unlikely to benefit from their current treatment as compared to possible salvage approaches (Fig S6D). While this method does inherently identify a smaller fraction of patients than current approaches, we suggest that identifying small groups of individual patients likely to benefit from alternative therapy will be essential to truly implement personalized approaches.

In total, our data suggest that identification of personalized risk throughout a course of therapy is feasible and can improve upon established risk assessment tools. Dynamic risk modeling will facilitate novel clinical trial designs for personalized therapeutic approaches, with wide applicability in oncology and other areas of medicine.

STAR Methods

Contact for reagents and resource sharing

Further information and requests for resources and reagents should be directed to and will be fulfilled by the lead contact, Ash Alizadeh, MD/PhD (arasha@stanford.edu).

Experimental models and subject details

DLBCL patient data collection

We analyzed data from subjects with large B-cell lymphomas undergoing treatment at six institutions across North America and Europe with serial ctDNA measurements available. A total of 181 patients receiving anthracycline-based immunochemotherapy were enrolled at Stanford University (Stanford, CA, USA, n=49), MD Anderson Cancer Center (Houston, TX, USA, n=23), University of Eastern Piedmont (Novara, Italy, n=36), the National Cancer Institute (Bethesda, MD, USA, n=33), Essen University Hospital (Essen, Germany, n=15), and Center Hospitalier Universitaire Dijon (Dijon, France, n=25). Patients in this study were prospectively enrolled and provided written, informed consent. The clinical characteristics of these patients are provided in Table S1. Levels of ctDNA were measured prior to the first, second, and third cycles of therapy as previously described (Newman et al., 2014; Scherer et al., 2016). Circulating tumor DNA measurements were used to predict EFS as previously described (Kurtz et al., 2018).

CIRI-DLBCL model development and validation

To build CIRI-DLBCL, prior knowledge on the performance of included risk factors is required to determine the model parameters (for details on the necessary parameters, see “Design details of the Continuous Integrated Risk Index” section of the STAR Methods). CIRI-DLBCL considers a total of six risk factors, including the International Prognostic Index (IPI), molecular cell of origin, interim imaging, along with ctDNA measurements prior to cycles one, two, and three of therapy. We obtained estimates for the prior probability of event-free survival for the average patient with DLBCL, as well as the parameters for CIRI-DLBCL from previously established literature describing the IPI (Sehn et al., 2007; Ziepert et al., 2010), cell of origin (Scott et al., 2015), and interim imaging procedures (Cashen et al., 2011; Micallef et al., 2011; Nols et al., 2014; Pregno et al., 2012; Safar et al., 2012; Yang et al., 2011; Yoo et al., 2011; Zinzani et al., 2011). To determine the performance of ctDNA for predicting patient outcomes and the corresponding parameters, we utilized the 49 patients from Stanford University as a development set. The performance of CIRI-DLBCL was tested in the validation set consisting of the remaining 132 patients.

CLL patient data collection

We reanalyzed patient level clinical and peripheral blood MRD data from patients enrolled in three phase III clinical trials from the German CLL Study Group (GCLLSG) - CLL8: fludarabine and cyclophosphamide (FC) vs. FC plus rituximab (FCR); CLL10: FCR vs. bendamustine plus rituximab (BR); and CLL11: chlorambucil vs. chlorambucil plus rituximab vs. chlorambucil plus obinutuzumab (NCT00281918, NCT00769522, and NCT02053610) (Eichhorst et al., 2016; Goede et al., 2014; Hallek et al., 2010). Trial protocols were approved by the relevant institutional review board and ethics committee of each participating center. Patients provided written informed consent to participate in the trials and to undergo MRD testing. The clinical characteristics of these patients are provided in Table S3. A total of 1426 patients with either interim or final MRD measurement from peripheral blood were available. Interim MRD measurement was obtained after the first 3 cycles of therapy; final MRD measurement was obtained 3 months after the completion of therapy. MRD was measured either by four-color flow cytometry (CLL8 and CLL10) or by polymerase chain reaction (PCR, CLL11). MRD negativity was defined as a level of <10⁻⁴; this threshold was previously found to be predictive for both progression-free and overall survival (Bottcher et al., 2012; Kovacs et al., 2016b).

CIRI-CLL model development and validation

To build and parameterize CIRI-CLL, we divided our patients into separate development and validation sets. Patients were randomly assigned to either the development or validation set with a 50% chance of assignment to either group. CIRI-CLL considers four risk factors, including choice of first-line therapy, CLL-IPI (The International CLL-IPI Working Group, 2016), interim MRD, and final MRD. The prior probability of progression free survival and corresponding parameters for each risk factor was determined from the development set (n=699), providing the parameters for CIRI-CLL. This model was then evaluated in the independent validation set (n=727).

Breast adenocarcinoma patient collection

We obtained case-level data from a previous study of taxane and anthracycline based neoadjuvant chemotherapy for patients with resectable breast adenocarcinoma (GEO series GSE25066) (Hatzis et al., 2011). Patients in this study were prospectively enrolled and provided written, informed consent. Patients were treated with neoadjuvant anthracycline and taxane based chemotherapy, followed by surgical resection. Pathological response to chemotherapy was assessed using the residual cancer burden method as previously described (Symmans et al., 2007). A total of 417 patients with clinical data were available. The clinical characteristics of these patients are provided in Table S4. To explore the possibility of using CIRI to discover predictive biomarkers, we assessed CIRI-BRCA in two additional publicly available cohorts of patients with HER2+ breast adenocarcinoma in the context of neoadjuvant therapy (Esserman et al., 2012; Ignatiadis et al., 2019) (GEO series GSE22226 and GSE109710; see “Prediction of therapeutic benefit in subsets of patients” for additional details).

CIRI-BRCA model development and validation

To build CIRI-BRCA, we established our prior knowledge and the model parameters from two independent, previously published studies. CIRI-BRCA considers four separate risk factors - clinical stage, tumor grade, estrogen receptor / HER2 status, and pathological response to chemotherapy. The prior probability of survival, as well as the parameters based on stage, grade, and receptor status, were all determined from patient-level data from the METABRIC study (shown as the development set in Table S4) (Curtis et al., 2012). The likelihood of distant-relapse free survival based on pathological response to chemotherapy was derived from a separate, previously published study (Symmans et al., 2007). These values determined the parameters for the CIRI-BRCA model. The performance of CIRI-BRCA was tested in the validation set of 417 patients receiving neoadjuvant chemotherapy described above, which was independent of the patients used to parameterize our model.

Method Details

Design details of the Continuous Individualized Risk Index

This manuscript describes two separate approaches to dynamic risk modeling, collectively described as CIRI. The first utilized a naïve Bayesian framework to estimate the probability of a clinical outcome at a defined endpoint in time. This initial approach is used to describe the concept of CIRI, with data shown for CIRI-DLBCL in Fig. 1. The second method estimates a personalized probability of survival over time (i.e., a predicted survival curve) based on Cox proportional hazard modeling, and is used to construct the final CIRI-DLBCL model as well as CIRI-CLL and CIRI-BRCA (Fig. 2–4). We describe each of these two methods in the sections below.

CIRI for fixed-endpoints

We used a naïve Bayesian framework to predict the risk of clinical events at defined endpoints in time. To construct a CIRI model in this framework, a number of parameters need to identified. These include an initial probability of adverse outcome, P(event), which is applicable to our patient population without knowledge of any risk factors. Additionally, for a set of risk factors, {f₁, f₂, … f_n}, the conditional probabilities P(f_i|event) and P(f_i|no event) need to be determined as well. For details on the determination of these parameters for CIRI-DLBCL, please see the section on “Determination of model parameters in CIRI for fixed-endpoints” below.

Using these conditional probabilities, we applied our prognostic features for each patient to a baseline estimate via Bayes’ Theorem:

$$P(\mathit{\text{event}}\mid \mathit{\text{feature}})=\frac{P(\mathit{\text{event}})*P(\mathit{\text{feature}}\mid \mathit{\text{event}})}{P(\mathit{\text{feature}})}$$

where

$$P(\mathit{\text{feature}})=P(\mathit{\text{event}})*P(\mathit{\text{feature}}\mid \mathit{\text{event}})+(1-P(\mathit{\text{event}}))*P(\mathit{\text{feature}}\mid no\mathit{\text{ event}})$$

and P(event) is the prior probability of an event. Sequential prognostic features were added to determine the personalized probability of an event for each patient with increasing amounts of information.

Extending this framework to patients with multiple prognostic features, {f₁, f₂, … f_n}, we can state that:

$$P\left(\mathit{\text{event}}\mid f_1,f_2,\dots f_n\right)\propto P\left(f_1,f_2,\dots f_n\mid \mathit{\text{event}}\right)*P(\mathit{\text{event}})$$

We use the naïve Bayes approach that assumes independence of the features within each event or no-event group. Under these independence assumptions:

$$\begin{gathered} P\left(f_1,f_2,\dots f_n\mid \mathit{\text{event}}\right)=P\left(f_1\mid \mathit{\text{event}}\right)*P\left(f_2\mid \mathit{\text{event}}\right)*\dots *P\left(f_n\mid \mathit{\text{event}}\right) \\ =\prod _{i}P\left(f_i\mid \mathit{\text{event}}\right) \end{gathered}$$

Therefore,

$$P\left(\mathit{\text{event}}\mid f_1,f_2,\dots f_n\right)\propto P(\mathit{\text{event}})*\prod _{i}P\left(f_i\mid \mathit{\text{event}}\right)$$

Converting this proportionality to a probability results in:

$$P\left(\mathit{\text{event}}\mid f_1,f_2,\dots f_n\right)=\frac{P(\mathit{\text{event}})*{\prod }_{i}P\left(f_i\mid \mathit{\text{event}}\right)}{P(\mathit{\text{event}})*{\prod }_{i}P\left(f_i\mid \mathit{\text{event}}\right)+P(no\mathit{\text{ event}})*{\prod }_{i}P\left(f_i\mid no\mathit{\text{ event}}\right)}$$

This equation is mathematically equivalent to the naïve Bayes approach outlined above.

For CIRI, prognostic features are sequentially added, as information becomes available. For example, in the case of CIRI-DLBCL, the following prognostic features available prior to therapy are first added, with the allowed values for each feature listed in curly brackets: 1) International Prognostic Index {low, low-intermediate, high-intermediate, high, N/A}; 2) pretreatment ctDNA {low, high, N/A}; 3) cell-of-origin {GCB, non-GCB, N/A}. After the first cycle of therapy, cycle 2 ctDNA becomes available, with possible values {EMR, No EMR, N/A}. After the second cycle of therapy, cycle 3 ctDNA becomes available. {MMR, no MMR, N/A}. Finally, interim imaging measurements become available {residual disease, no residual disease, N/A}. Note that when data was missing or not available, the prognostic feature was considered non-informative and the prior probability was not updated.

To make the details clearer, the following example illustrates CIRI probabilities over time. Consider a patient, Patient B from Figure 1C, with a diagnosis of DLBCL. Without any information about his clinical features, his initial (prior) probability of event by two years (e.g.: P(event)) is estimated to be 21.8%, based on literature values for the disease (Table S2). Now, we learn that his IPI is 3, putting him in the high intermediate risk group. His probability of adverse event is therefore updated to:

$$P(\mathit{\text{event}}\mid IPI=3)=\frac{P(\mathit{\text{event}})*P(IPI=3\mid \mathit{\text{event}})}{P(IPI=3)}$$

which is equivalent to

$$P(\mathit{\text{event}}\mid IPI=3)=\frac{P(\mathit{\text{event}})*P(IPI=3\mid \mathit{\text{event}})}{P(\mathit{\text{event}})*P(IPI=3\mid \mathit{\text{event}})+(1-P(\mathit{\text{event}}))*P(IPI=3\mid no\mathit{\text{ event}})}$$

We can obtain all the probabilities on the right-hand side of this equation from our model parameters (Table S2), resulting in:

$$P(\mathit{\text{event}}\mid IPI=3)=\frac{0.218*0.305}{0.218*0.305+(1-0.218)*0.129}=0.40$$

or a 40% probability of relapse. Now suppose that prior to therapy, this patient has not one, but three risk-predictors - IPI = 3, low ctDNA, and GCB molecular subtype. His full expression for risk of an event is therefore:

$$P(\mathit{\text{event}}\mid IPI=3,low\mathit{\text{ctDNA}},GCB)=\frac{P(\mathit{\text{event}})*A}{P(\mathit{\text{event}})*A+P(no\mathit{\text{ event}})*B}$$

Where:

$$\begin{gathered} A=\prod _{i}P\left(f_i\mid \mathit{\text{event}}\right)=P(IPI=3\mid \mathit{\text{event}})*P(low\mathit{\text{ctDNA}}\mid \mathit{\text{event}})*P(GCB\mid \mathit{\text{event}}) \\ =\left(0.305\right)*\left(0.235\right)*\left(0.602\right)=0.042 \end{gathered}$$

And

$$\begin{gathered} B=\prod _{i}P\left(f_i\mid no\mathit{\text{ event}}\right)=P(IPI=3\mid no\mathit{\text{ event}})*P(low\mathit{\text{ctDNA}}\mid no\mathit{\text{ event}})*P(GCB\mid no\mathit{\text{ event}}) \\ =\left(0.129\right)*\left(0.563\right)*\left(0.369\right)=0.027 \end{gathered}$$

Therefore,

$$P(\mathit{\text{event}}\mid IPI=3,low\mathit{\text{ctDNA}},GCB)=\frac{0.218*0.042}{0.218*0.042+(1-0.218)*0.027}=0.148$$

which is equivalent to a 14.8% chance of event by 24 months, or an 85.2% probability of reaching EFS24, as shown in Fig. 1C.

After one cycle of therapy, however, the patient does not achieve an early molecular response (no EMR, second time-point, Fig. 1C). Upon learning this information, his expression for probability of event is:

$$P(\mathit{\text{event}}\mid IPI=3,low\mathit{\text{ctDNA}},GCB,NoEMR)=\frac{P(\mathit{\text{event}})*A}{P(\mathit{\text{event}})*A+P(no\mathit{\text{ event}})*B}$$

Where A and B are now:

$$\begin{gathered} A=\prod _{i}P\left(f_i\mid \mathit{\text{event}}\right)=P(IPI=3\mid \mathit{\text{event}})*P(low\mathit{\text{ctDNA}}\mid \mathit{\text{event}})*P(GCB\mid \mathit{\text{event}})*P(NoEMR\mid \mathit{\text{event}}) \\ =(0.305)*(0.235)*(0.602)*(0.429)=0.0027 \end{gathered}$$

And

$$\begin{gathered} B=\prod _{i}P\left(f_i\mid no\mathit{\text{ event}}\right)=P(IPI=3\mid no\mathit{\text{ event}})*P(low\mathit{\text{ctDNA}}\mid no\mathit{\text{ event}})*P(GCB\mid no\mathit{\text{ event}})*P(NoEMR\mid no\mathit{\text{ event}}) \\ =(0.129)*(0.563)*(0.369)*(0.190)=0.0068 \end{gathered}$$

Therefore,

$$P(\mathit{\text{event}}\mid IPI=3,low\mathit{\text{ctDNA}},GCB,NoEMR)=\frac{0.218*0.0027}{0.218*0.0027+(1-0.218)*0.0068}=0.282$$

which is equivalent to a 28.2% chance of event by 24 months, or a 71.8% probability of reaching EFS24, as shown in Fig. 1C (second step).

Subsequent measurements of ctDNA and interim imaging studies for this patient further update his probability of relapse. Note that for these subsequent measurements (e.g.: EMR, MMR, and interim imaging), we still estimate the two-year event probability for the patient from the time of diagnosis. That is, we do not account for the fact that the patient has been relapse-free for 21 days at cycle 2, day 1. This will suffer from some guarantee-time bias, which we believe may cause us to over-estimate the relapse probability. However, we feel that this bias is small, as evidenced by our calibration curve (i.e., Fig S1G).

An example of CIRI for fixed endpoint for two patients is given in Fig 1C. The expectation value for the probability of event-free survival at 24 months is shown as a solid line for each patient. For the analyses in Fig. 1 and S1, the expectation value from CIRI was used. A distribution of the posterior probability and confidence intervals can additionally be obtained. To perform this, the variance for each baseline and conditional probability used in CIRI was estimated (using Greenwood’s formula). A distribution of the posterior probability was then determined by sampling from the distribution of each conditional and prior probability and performing the naïve Bayes analysis 10,000 times (Markov Chain Monte Carlo). This distribution was used to create the 80% confidence intervals shown in Fig. 2A. This posterior distribution was also used to in the proposed framework for therapy selection utilizing CIRI shown in Fig. S6B–D and the Supplementary Note. (see “Framework for therapeutic selection from CIRI risk estimates” section of the methods).

Determination of model parameters in CIRI for fixed-endpoints

The goal of fixed-endpoint CIRI is to estimate the probability of adverse event for a given patient at a fixed point in time, given a set of n features (i.e., P(event) | f₁ … f_n)). To use the approach outlined above, a number of parameters need to be determined. These include an initial or baseline probability of adverse outcome, P(event), applicable to an entire patient population at large, as well as two conditional probabilities - P(f_i|event) and P(f_i|no event) - for all prognostic features f_i of interest.

To estimate the baseline probability of an event, P(event), we employed Kaplan-Meier estimates of the survival function (e.g., Fig. S1A). We used this to estimate the probability of survival, or ‘no event’, P(no event), with the knowledge that P(event) = 1 − P(no event). When patient level survival data was available, we constructed Kaplan-Meier survival estimates from this primary data. When patient level survival data was not available, survival functions were estimated from the literature (see methods section on “Estimation of survival functions from published literature”).

To determine the conditional probabilities P(f_i|event) and P(f_i|no event), a similar approach was employed. To identify these parameters for a given feature, F with possible values {f₁, f₂, … f_i … f_n}, we began with Kaplan-Meier survival estimates of subgroups of interest - i.e., P(no event | f_i) Using this survival function, we determine P(no event | f_i) and P(event | f_i) at our end-point of interest:

$$P\left(\mathit{\text{event}}\mid f_i\right)=1-P\left(no\mathit{\text{ event}}\mid f_i\right)$$

We then estimate the number of patients with and without events as follows:

$$\begin{gathered} n_{\left(f_i,\mathit{\text{event}}\right)}=n_{f_i}*P\left(\mathit{\text{event}}\mid f_i\right) \\ {n}_{\left(f_i,no\mathit{\text{ event}}\right)}=n_{f_i}*P\left(no\mathit{\text{ event}}\mid f_i\right) \end{gathered}$$

Where $n_{f_i}$ is the number of patients with a given risk feature. With this information, we can estimate:

$$\begin{gathered} P\left(f_i\mid \mathit{\text{event}}\right)=\frac{n_{\left(f_i,\mathit{\text{event}}\right)}}{{\sum }_i{n}_{\left(f_{i,\mathit{\text{event}}}\right)}} \\ P\left(f_i\mid no\mathit{\text{event}}\right)=\frac{n_{\left(f_i,no\mathit{\text{event}}\right)}}{{\sum }_i{n}_{\left(f_{i,no\mathit{\text{event}}}\right)}} \end{gathered}$$

For example, see Fig S1B, where we estimate these parameters for the IPI. Here, we estimate:

$$\begin{gathered} P(no\mathit{\text{ event}}\mid lowIPI)=0.891 \\ P(no\mathit{\text{ event}}\mid lowintIPI)=0.777 \\ P(no\mathit{\text{ event}}\mid \mathit{\text{high }}intIPI)=0.617 \\ P(no\mathit{\text{ event}}\mid \mathit{\text{high }}IPI)=0.599 \end{gathered}$$

Therefore,

$$\begin{gathered} n_{(low,no\mathit{\text{ event}})}=553*0.891=492.7 \\ {n}_{(lowint,no\mathit{\text{ event}})}=227*0.777=176.4 \\ {n}_{(low,no\mathit{\text{ event}})}=175*0.617=108.0 \\ {n}_{(low,no\mathit{\text{ event}})}=105*0.599=62.9 \end{gathered}$$

Finally,

$$P(lowIPI\mid no\mathit{\text{ event}})=\frac{492.7}{492.7+176.4+108.0+62.9}=0.587$$

Conditional probabilities for the other IPI groups and for patients having adverse events are calculated similarly.

CIRI for survival analysis

We extended the concept for dynamic risk-prediction to including prediction of a personalized survival function over time by utilizing the Cox proportional hazard model. This method was utilized to produce the results shown in Figs. 2–6, as well as Fig. S2–6. We note that the use of the proportional hazard assumption in CIRI-DLBCL, CIRI-CLL, and CIRI-BRCA was largely satisfied - after constructing a standard Cox proportional hazard model for each disease, we tested the proportional hazard assumption by Schoenfeld residuals, resulting in global P-values for the composite model of 0.08, 0.25, and 0.40 respectively. The individual P-values for the test of proportional hazards for each individual covariate are provided in Table S5. In the case of singularity (i.e., IPI values of {0–1,2,3,4–5}), one value has been removed from analysis to allow model convergence.

Having assessed the proportional hazard assumption, we next sought to identify model parameters for CIRI. In an ordinary Cox model, we start with a baseline survival function, denoted by S₀(t), a set of observed covariates, denoted by X, and a set of (regression) coefficients, β reflecting the deviation from the baseline survival given the observed covariates. These will lead to the final survival function $S(t)=S_0{(t)}^{\text{exp}(X^T\beta )}$. In this setting, the coefficients are often inferred, via maximum partial likelihood estimation, from a set of samples with joint covariate information, in which the accuracy of the estimated coefficients is highly dependent on the number of available samples. Moreover, although the inference can be done in the presence of missing values, the performance can significantly degrade.

In most cases where we deal with clinical survival data, the joint covariate information is extremely rare, due to either limited sample sizes or the absence of case-level reporting in the literature. In contrast, the univariate survival information can be straightforwardly extracted from the literature (see section on “estimation of survival functions from published literature”), which can be incorporated, as prior knowledge, into the survival prediction. Therefore, we propose to use a “Bayesian Cox model”, where Cox coefficients are governed by some “prior probability.” A natural choice for such prior probability is normal distribution, and therefore we set β ~ π(β) = N(μ, Σ). Due to the type of prior knowledge that we can collect we assume Σ to be a diagonal matrix. It should be noted that Σ can be a non-diagonal matrix if we have joint prior information (for a relatively large cohort); however, for practicality of the method we make this choice to let users incorporate their univariate survival data associated with all the desired covariates in the model.

Taking a Bayesian approach, we now define the final survival function as

$$S^{*}(t;X)=\int S_0{(t)}^{\text{exp}\left(X^T\beta \right)}\pi (\beta )d\beta$$

where π(β) is the prior probability of β. We use the Cox partial likelihood as the likelihood function, and employ Markov Chain Monte Carlo (MCMC) sampling to calculate the posterior survival function for each individual patient. In the cases where no sample is used for posterior calculation, it basically reduces to a model averaging schema. Next, we describe how to construct the prior probability π(β).

Parameter construction in CIRI for survival analysis

In order to estimate the mean and variance of the priors for the Bayesian Cox model, we used the uncertainty around the prior survival curves, as estimated by the total number of patients at risk at a given time point (see “Estimation of survival functions from published literature”). Therefore, the input to this step was a set of survival curves along with their confidence intervals. We also assume that all the covariates are converted into binary valued variables, i.e. dummy variables. We then inferred the hyper-parameters via an optimization framework which fits the final prior probability to the given curves.

Mathematically, we aim to satisfy Pr [S₀(t)^exp(β) ∈ [L_b, U_b]] ≈ 1 − α with α being a user parameter (α = 0.05 is used in CIRI) and β ~ N(μ, σ²). Note that here, we determine the function S₀(t), he survival of an unselected population of patients, from prior knowledge derived from the literature as described in the “Estimation of survival functions from published literature” section. Here, L_b and U_b are lower and upper bounds for the effect of individual risk-factors (i.e., beta-value). These bounds are estimated using the uncertainty of survival given each individual risk-factor using Greenwood’s formula (Greenwood. 1926).

The task is then to find μ and σ (here and for simplicity in notations we drop the subscript indexing the covariates). Hence, first we simplify the probability as follows:

$$\begin{gathered} \text{Pr}\left[S_0{(t)}^{\text{exp}(\beta )}\in \left[L_b(t),U_b(t)\right]\right]=\text{Pr}\left[e^{\beta }\text{log}{S}_0(t)\in \left[\text{log}{L}_b(t),\text{log}{U}_b(t)\right]\right]= \\ \text{Pr}\left[\text{log}-e^{\beta }\text{log}{S}_0(t)\in \left[\text{log}\left(-\text{log}{U}_b(t)\right),\text{log}\left(-\text{log}{L}_b(t)\right)\right]\right]= \\ \text{Pr}\left[\text{log}{e}^{\beta }+\text{log}\left(-\text{log}{S}_0(t)\right)\in \left[\text{log}\left(-\text{log}{U}_b(t)\right),\text{log}\left(-\text{log}{L}_b(t)\right)\right]\right] \\ =\text{Pr}\left[\beta \in \left[\text{log}\frac{\text{log}{U}_b(t)}{\text{log}{S}_0(t)},\text{log}\frac{\text{log}{L}_b(t)}{\text{log}{S}_0(t)}\right]\right] \\ =\Phi \left(\frac{\text{log}\frac{\text{log}{L}_b(t)}{\text{log}{S}_0(t)}-\mu }{\sigma }\right)-\Phi \left(\frac{\text{log}\frac{\text{log}{U}_b(t)}{\text{log}{S}_0(t)}-\mu }{\sigma }\right). \end{gathered}$$

We setup our optimization problem as follows:

$$\text{arg}\underset{\mu ,\sigma }{\text{min}}\frac{1}{\left|T\right|}\sum _{\text{t}\in \text{T}}\frac{1}{{\sigma }_t}|\Phi \left(\frac{\text{log}\frac{\text{log}{L}_b(t)}{\text{log}{S}_0(t)}-\mu }{\sigma }\right)-\Phi \left(\frac{\text{log}\frac{\text{log}{U}_b(t)}{\text{log}{S}_0(t)}-\mu }{\sigma }\right)-0.95{|}^2.$$

where σ(t) is the standard deviation of the target covariate’s prior survival curve at time point t, and Φ(.) is the cumulative distribution function of the standard normal distribution. In the equation above, T is the time horizon in which the fitting is desired, noting that the interval range can affect the fitting quality. This problem is non-convex, and therefore instead of using gradient-based methods, we take a brute-force approach and make a grid and find the “optimal” hyper-parameters. Once hyper-parameters are inferred for all the covariates, they will be used in our Bayesian Cox model described above.

To make this process clear, the results of parameter construction can be seen in Fig. S2A–G, S3A–E, and S4A–E. In each case, the baseline survival function S₀(t) is shown in panel A. The subsequent panels show both the underlying primary data (solid line + dashed line CIs) as well as S₀(t)^exp(β) - that is, the result of parameter optimization β ~ N(μ, σ²) for each given risk-factor. This shaded area is the 95% CI of the corresponding normal distribution of β. The μ and σ for each outcome predictor is shown as well.

Parameter calibration in CIRI for survival analysis

It is possible that different cohorts used for hyper-parameter inferences could have significantly different survival functions (compared to the baseline function) which can in turn affect the calibration to the observed risk. In order to address this issue, we introduce new coefficients, and call them “calibrating coefficients”. These calibrating coefficients are found using the same approach described above for covariates, where σ(t), L_b(t) and U_b(t) are instead “cohort baseline function”, and the difference being we will only employ the inferred mean (and ignore the variance). Once these means are inferred, we subtract them from all the coefficients corresponding to the covariates whose prior knowledge came from that same cohort.

As an example, suppose that we find the prior knowledge for Stage and Grade in breast cancer from one cohort. We first infer the hyper-parameters for dummy variables defined based on Stage and Grade categories. Without loss of generality, for Stage=1, first construct the prior as ${\beta }_{\mathit{\text{Stage}}1}~N({\mu }_{\mathit{\text{Stage}}1},{\sigma }_{\mathit{\text{Stage}}1}^2)$ and for Grade=1 as ${\beta }_{\mathit{\text{Grade}}1}~N({\mu }_{\mathit{\text{Grade}}1},{\sigma }_{\mathit{\text{Grade}}1}^2)$. Next, by pooling all the patients in the same cohort (regardless of stage or grade), we find σ(t), L_b(t) and U_b(t). Then, using the optimization above, we find a calibrating factor, denoted by μ_calibration. In the example outlined above, we adjust the prior centers for Stage=1 and Grade=1, respectively, as follows: ${\beta }_{\mathit{\text{Stage}}1}~N({\mu }_{\mathit{\text{Stage}}1}-{\mu }_{\mathit{\text{calibration}}},{\sigma }_{\mathit{\text{Stage}}1}^2)$ and ${\beta }_{\mathit{\text{Grade}}1}~N({\mu }_{\mathit{\text{Grade}}1}-{\mu }_{\mathit{\text{calibration}}},{\sigma }_{\mathit{\text{Grade}}1}^2)$.

Markov Chain Monte-Carlo Sampling in CIRI for survival analysis

In order to perform Markov Chain Monte Carlo (MCMC), we employed Metropolis-Hastings algorithm. The prior probability is defined as β ~ N(μ, Σ). In cases where there is no sample to update the prior, i.e. posterior is in fact the prior itself. However, one powerful characteristic of the proposed Bayesian model is the capability of updating the prior using a limited set of samples. In these scenarios one needs to add the likelihood function. There are two possibilities to add the likelihood function: (1) Cox partial likelihood function and (2) the exact likelihood function given the presumed baseline survival function. In order to make sure that the calibration is not affected we chose the latter. Therefore, the log-likelihood function becomes

$$\mathcal{l}\left(\beta \mid {\left\{\left(X_i,C_i\right)\right\}}_{i=1:n}\right)=\prod _{i=1}{\left\{\text{exp}\left\{{\beta }^T{Z}_i\right\}{\lambda }_0\left(T_i\right)\right\}}^{{\Delta }_i}\text{exp}\left\{-{\int }_0^{T_i}{\lambda }_0(t)dt\times e^{{\beta }^T{Z}_i}\right\}$$

where λ₀(.) Is the instantaneous hazard function, Δ_i is the event indicator variable. Writing it in log-transformed form, we have

$${\mathcal{l}}_l=\sum _i[{\Delta }_i[{\beta }^T{Z}_i+\text{log}{\lambda }_0\left(T_i\right)]-{\int }_0^{T_i}{\lambda }_0(t)dt\times e^{{\beta }^T{Z}_i}].$$

Now we have $S_0(t)=\text{exp}\left\{-{\int }_0^t{\lambda }_0(\tau )d\tau \right\}$ and therefore $\text{log}{\lambda }_0(t)=\text{log}(\frac{d}{dt}(-\text{log}{S}_0(t)))$. In our implementation we used spline fitting to the prior knowledge survival Kaplan-Meier curves to estimate the instantaneous hazard function.

In the MCMC sampling, we also tuned the proposal distribution such that the acceptance rate falls in [0.2,0.3] interval. Whenever we had prior updating samples, we used a linear combination of prior mean and Cox proportional hazard model with ridge regression as the initial sample. We used 500 burnin samples in the MCMC with 10,000 samples in the actual predictions and 2,000 samples for the simulations comparing traditional Cox proportional hazard models to CIRI (Figure 5).

Estimation of survival functions from published literature

As outlined above, a number of model parameters were required to develop CIRI. These parameters were derived from previously published datasets or literature, depending on their availability. Specifically, we determined these parameters from survival data in each disease of interest. For DLBCL, we estimated event-free survival or EFS (either at 24 months for fixed-endpoint analysis or over time in survival analysis); for CLL, we estimated progression-free survival or PFS (either at 36 months for fixed-endpoint analysis or over time in survival analysis); for BRCA, we estimated distant-relapse free survival or DRFS (either at 36 months for fixed-endpoint analysis or over time in survival analysis). To estimate these, information on survival was determined by one of three methods from established literature.

1. When patient-level data was available from a prior study or data-set, this was preferentially used to determine survival functions by the Kaplan-Meier method. In this study, parameters for the following risk-factors were determined from patient-level data:

   1. CIRI-DLBCL - pretreatment ctDNA level, early molecular response, major molecular response
   2. CIRI-CLL - baseline survival function, CLL-IPI, interim MRD, final MRD
   3. CIRI-BRCA - baseline survival function, clinical stage, tumor grade, estrogen receptor / HER2 status.

2. When patient-level data was not available, published Kaplan-Meier estimates of survival were used. Quantitative imaging analysis was performed on published survival curves to determine the survival function S(t), along with the number at risk (n_i), number of events (d_i), and probability of survival (p_i) during each time interval t_i (DataThief III, http://datathief.org); point estimates were manually reviewed against published survival outcomes to confirm accuracy. The probability of survival at the time of interest was then determined directly from the function S(t). When multiple survival estimates needed to be combined (either to combine multiple groups or to combine multiple literature sources, these were combined as follows:

   Given two Kaplan-Meier estimates of survival, S₁(t) and S₂(t) with equally spaced time intervals, the number at risk and number of events for the combined survival curve S_combined(t) for a given time interval t_i are:

   $$\begin{gathered} n_{i,\mathit{\text{combined }}}=n_{i,1}+n_{i,2} \\ {d}_{i,\mathit{\text{combined }}}=d_{i,1}+d_{i,2} \end{gathered}$$
   The probability of survival during the interval t_i, termed p_i,combined, is therefore:

   $$p_{i,\mathit{\text{combined}}}=\left(n_{i,\mathit{\text{combined}}}-d_{i,\mathit{\text{combined}}}\right)/n_{i,\mathit{\text{combined}}}$$
   In this study, parameters for the following risk-factors were determined from previously published Kaplan-Meier survival curves:

   1. CIRI-DLBCL - baseline survival function, IPI, and cell of origin
   2. CIRI-CLL - N/A
   3. CIRI-BRCA - residual cancer burden
3. When neither patient-level data nor Kaplan-Meier estimate of the survival function were available, estimates of the probability of survival at fixed points in time were used. In this study, parameters for the following risk-factors were determined from survival at fixed time-points:

   1. CIRI-DLBCL - interim imaging
   2. CIRI-CLL - N/A
   3. CIRI-BRCA - N/A

The above methods were used to determine the expectation value for each survival function. The variance, standard deviation, and 95% confidence intervals for survival were then estimated using Greenwood’s formula (Greenwood, 1926). These confidence intervals were used for parameter estimation in our CIRI model for survival analysis as described above.

Simulations to assess the effect of correlated coefficients on CIRI

In order to evaluate the effect of correlation between CIRI coefficients βs), we simulated a series of models with different degrees of correlation between coefficients. To generate synthetic model and draw samples from that model, we performed the following steps (using the part of the data sets which was used for prior construction): (1) for 1,000 bootstrap resampling of the full data, we solved the Cox proportional hazard model (i.e. inferred the corresponding regression coefficients), (2) built a covariance matrix using these 1,000 random realizations, (3) calculated the mean of the β vector, (4) fixed the diagonal elements of the matrix (i.e. individual variances), kept the direction of the off-diagonal elements (i.e. positive or negative correlation), changed the off-diagonal elements to the desired value, i.e. ${\sigma }_{\text{ij}}^{\text{new}}=\text{sign}\left({\sigma }_{\text{ij}}^{\text{old}}\right)*\left|\rho \right|*{\sigma }_{\text{i}}^{\text{old}}{\sigma }_{\text{j}}^{\text{old}}$, and denoted that by Σ_ρ, (5) randomly generated samples from a multivariate normal distribution with the mean and covariance matrix generated in (3) and (4), respectively. Associated with each β, we then took the original covariate matrix (matrix X), calculated the β^TX, and via the baseline and Cox proportional hazard model, generated random time of events. We also generated the same rate of censoring time by sampling from the censor value in the original data set. Note that step (4) might lead to negative definite matrix, where in those situations we added 1.01 × |λ_min| × I to the covariance matrix Σ_ρ where λ_min (< 0) is the minimum eigenvalue of Σ_ρ.

Comparison with Cox proportional hazard model

In order to evaluate CIRI, we compared it with the standard Cox proportional hazard model. We implemented a simulation setup for breast cancer and chronic lymphocytic leukemia, the two diseases for which we had a large number of samples in this paper. We considered three metrics for performance evaluation (1) area under receiver operating characteristic (ROC) curve or C-statistic, (2) the calibration-in-the-large intercept defined as $\left|\frac{1}{n_{\mathit{\text{test}}}}\sum _i{\text{Pr}}^{\mathit{\text{CIRI}}}(\mathit{\text{Surv}}\left|\mathit{\text{indiv}}.\#i)-{\text{Pr}}^{KM}(\mathit{\text{Surv}}\right|\mathit{\text{full cohort}})\right|$, and (3) the calibration slope. For the simulation setup, we used n_test = 150 for breast cancer, and 400 for CLL; however, we varied the number of training samples n_train ∈ {20, 40, …, 200}. For M = 250 iterations, the datasets were split into test set $S_{n_{\mathit{\text{test}}}}$, and train $S_{n_{\mathit{\text{train}}}}$. The training samples $S_{n_{\mathit{\text{train}}}}$ were used for inferring Cox model coefficients, and also updating CIRI framework via MCMC. We then applied both models to the test set $S_{n_{\mathit{\text{test}}}}$ and calculated the three metrics above. Metric # 1 was calculated using R package survivalROC (version 1.0.3) at T = 36 (months). In order to calculate metrics# 2 and 3 a baseline function is required, which is inherently part of the CIRI framework, however it is not so for the Cox model. Therefore, we further estimated the cumulative hazard function, H(t), after estimating the Cox coefficients (still using the training data) and plugged that in to obtain the corresponding baseline function S₀(t) = exp{−H(t)}.

Prediction of therapeutic benefit in subsets of patients

To explore the possibility of using CIRI to discover predictive biomarkers - i.e., patient subsets defined quantitatively by CIRI who preferentially benefit from specific therapies - we constructed proof-of-concept CIRI models agnostic to therapy selection, integrating pretreatment and interim predictors. For example, in the case of CLL, we constructed a CIRI model integrating only the CLL-IPI and interim MRD, that was not informed by choice of initial therapy (Fig. 6D). We then made predictions for the probability of outcome (PFS at 36 months) for each patient using only this data. Furthermore, we also made a “prediction” of the likely effect of each therapy on each patient - i.e., what the likely benefit of every possible therapy would be for each individual. This involved making a personalized outcome prediction for each patient for each possible immunochemotherapy (FCR, BR, R-chlorambucil, G-chlorambucil). In each case, we compared the predicted benefit from treatment for groups of patients defined by various CIRI thresholds to actual outcomes (e.g., in CLL, see Fig S5A–C), and assessed for specific thresholds of CIRI risk that could identify a selective therapeutic benefit in a patient subpopulation (e.g., in CLL, see Fig 6E–F and Supplementary Dataset). 95% confidence intervals for the predicted benefit of treatment (Fig S5A) was determined from 10,000 bootstrap resamplings of patients in each risk group; 95% confidence intervals for the observed benefit of treatment (Fig S5B) was obtained from Greenwood’s formula.

Existing literature does not well capture the full set of parameters relating to each individual therapy or therapeutic combination. Therefore, we adapted our data-driven approach to deriving priors as used in CIRI to identify parameters related to therapeutic selection. In the case of CLL, this consisted of the therapies used in the CLL8, CLL10, and CLL11 dataset; for breast cancer, this consisted of neoadjuvant chemotherapy +/− Trastuzumab as per the ISPY trial (Esserman et al., 2012), or neoadjuvant chemotherapy + Trastuzumab + Pertuzumab as per the TRYPHAENA trial (Ignatiadis et al., 2019). We used our previously established CIRI prognostic model priors for other shared covariates. Since the disease subsets within the existing cohorts with available prognostic covariates, treatment assignment, and outcome data are often small, to construct robust priors for treatment and other new covariates, we implemented a k-fold cross-validation (k-CV) framework. In each iteration of this CV framework, (k − 1) folds of patients were used to derive maximum-likelihood estimates of the survival probability (i.e. Kaplan-Meier curves) along with their 95% confidence bands. Next, we used our method described in the CIRI prognostic model to infer the hyper-parameters from these estimates. The final CIRI model built using these priors was then applied to the remaining “held out” patients in each fold to predict the outcome. In the case of CLL, this cross-validation framework was applied to patients from the CLL8, CLL10, and CLL11 trials (Eichhorst et al., 2016; Goede et al., 2014; Hallek et al., 2010), limiting our analysis to only patients with interim MRD assessment receiving immuno-chemotherapy. For breast cancer, we pooled patients from two clinical trials where neoadjuvant therapy was given (ISPY and TRYPHAENA) and where data was publicly available (Esserman et al., 2012; Ignatiadis et al., 2019). Here, we limited our analysis to HER2+ patients where survival data was available. In the ISPY dataset, RCB scores were available. In the TRYPHAENA dataset, only pathologic CR (pCR) status was available; therefore, for the purpose of the CIRI model, patients achieving a pCR were assigned an RCB score of 0, while patients not achieving pCR were assigned an RCB score of 3.

To assess the ability of CIRI to identify a subgroup of patients who preferentially benefit from a given therapy (i.e., act as a “predictive” biomarker), we should find a region $\mathcal{P}$ in which the treatment effect is significantly better than the average treatment effect. This subgroup is traditionally defined heuristically by constraining the covariates, e.g. $\mathcal{P}\left\{x_1\langle a,x_2\rangle b\right\}$ (Foster et al., 2011). Here, we employ our prognostic model CIRI to find this subgroup. Denoting CIRI prediction for covariate vector X at time t₀ by S_CIRI(t₀|X), e.g. t₀=36mo for CLL, we define a CIRI based subgroup as $\mathcal{P}{s}_0=\{X\in \mathcal{X}|S_{\mathit{\text{CIRI}}}(T_0|X)\rangle s_0\}$, where $\mathcal{X}$ is the entire covariate space. We then define two treatment benefit variables:

$$\begin{array}{l}{\Delta }_{\mathit{\text{CIRI}}}\left({\mathcal{P}}_{S_0}\right)=\widehat{\text{Pr}}\left(Y=1\mid T=1,X\in {\mathcal{P}}_{s_0}\right)-\widehat{\text{Pr}}\left(Y=1\mid T=0,X\in {\mathcal{P}}_{S_0}\right),\hfill \\ {\Delta }_{\mathit{\text{CIRI}}}\left(\mathcal{X}\backslash {\mathcal{P}}_{s_0}\right)=\widehat{\text{Pr}}\left(Y=1\mid T=1,X\notin {\mathcal{P}}_{s_0}\right)-\widehat{\text{Pr}}\left(Y=1\mid T=0,X\notin {\mathcal{P}}_{s_0}\right)\hfill \end{array}$$

which respectively quantify the benefit of the patients whose covariates satisfy $\mathcal{P}{s}_0$, and patients who do not. In these equations, $\widehat{\text{Pr}}(.)$ denotes the CIRI predictions, and Y denotes the binary outcome. We finally define the predictive threshold set as all CIRI thresholds leading to subgroup treatment benefit as follows

$$\Im =\left\{s_0\mid {\Delta }_{\mathit{\text{CIRI}}}\left({\mathcal{P}}_{s_0}\right){>}^{*}0and{\Delta }_{\mathit{\text{CIRI}}}\left(\mathcal{X}\backslash {\mathcal{P}}_{s_0}\right){<}^{*}0\right\}$$

where >* and <*, denote greater and less than in probability (i.e. evaluated by significance p-values), respectively.

Framework for therapeutic selection from CIRI risk estimates

In addition to identifying patients at high-risk of disease progression and associated mortality, prognostic biomarkers should ideally help make therapeutic decisions to overcome such risk. For example, previous studies have attempted to identify DLBCL patients for early treatment intensification using either the IPI or interim PET/CT scans. Unfortunately, these approaches have largely failed to improve survival (Duehrsen, 2014; El-Galaly et al., 2015; Moskowitz et al., 2010; Yoo et al., 2011).

Quantitative risk assessment with CIRI-DLBCL can lend insight into these results. A decision to change therapy could be considered as a test of two competing therapeutic strategies. In the case of DLBCL, alternative options are 1) to continue and complete frontline therapy, or 2) transition to a salvage regimen, typically high-dose chemotherapy followed by autologous hematopoietic stem cell transplantation (ASCT) (Hertzberg et al., 2017; Stiff et al., 2013). A statistical test between the probability of favorable outcome (i.e., event-free survival at 24 months) with each of these options could help identify the ideal treatment course. A quantitative distribution of likely outcomes with frontline therapy for a given patient can be obtained through the Bayesian analysis framework within CIRI. A conservative estimate of the probability of favorable outcome with salvage ASCT can be obtained from prior studies in the salvage setting (Crump et al., 2014).

To explore the predicted benefit from early ASCT in patients with high IPI or positive interim PET/CT scans, we considered two typical patients with these single risk-factors and their predicted probability of achieving EFS24 after frontline therapy (Fig S6B, red and blue profiles). We compared these two risk profiles to the average outcome probability for patients receiving salvage therapy and ASCT in the second line (grey). Remarkably, we observed that patients whose only unfavorable features relate to baseline clinical risk or poor radiographic responses are, on average, unlikely to benefit from such a change in therapy, as their predicted outcomes after first-line therapy are superior to the average patient receiving subsequent ASCT.

We next considered risk estimates from CIRI-DLBCL to identify individual patients likely to benefit from an early intervention with ASCT. Unlike with interim radiographic evaluation alone, CIRI identified individual patients where the predicted risk after first-like therapy that was inferior to the average outcome with second-line therapy (e.g., patient DLBCL103 in Fig S6C). By comparing the personalized predicted outcome after traditional frontline therapy versus ASCT for each patient over time, we used CIRI to estimate the statistical likelihood of the benefit of a change in therapy at this milestone (Fig S6D).

To perform this statistical test, we compared the personalized probability of EFS24 with frontline therapy to the probability of EFS24 for the average patient with salvage therapy - namely, autologous stem cell transplantation (ASCT) - determined from the LY.12 trial, established in prior literature (Crump et al., 2014) (this probability was determined as described in the “Estimation of survival functions from published literature” section). To evaluate the probability that an individual patient would benefit from a switch in therapy, we calculated the personalized value of:

$$P\left(EFS{24}_{\mathit{\text{RCHOP}}}\right)-P\left(EFS{24}_{\mathit{\text{salvage}}}\right)$$

which represents the difference in likely outcomes with RCHOP therapy vs salvage ASCT. The distribution of this posterior probability was calculated by 10,000 Markov Chain Monte Carlo samplings. This process is shown for an individual patient, DLBCL103, resulting in the probability density functions shown in Fig S6D. We then calculated empiric P-values for the probability that:

$$P\left(EFS{24}_{\mathit{\text{RCHOP}}}\right)-P\left(EFS{24}_{\mathit{\text{salvage}}}\right)<0$$

This P-value represents the probability that a switch in treatment - from RCHOP to salvage therapy - would represent a superior treatment option for patient DLBCL103.

Quantification and statistical analysis

Determination of model calibration

For any predictive model, determination of correct calibration is essential (Pencina et al., 2010; Steyerberg et al., 2010) - that is, if a patient is predicted to have a 25% risk of an event within 24 months of diagnosis, this patient should truly have a 25% risk. If the true risk is significantly higher or lower than this, the model is said to be poorly calibrated. As CIRI provides an updating risk-estimate for each patient as more information is obtained throughout a course of treatment, we sought to ensure that CIRI was calibrated at the time of each prediction - for example, in the case of CIRI-DLBCL, where a prediction is made for each patient at four times (before and after 1, 2, or 3 cycles of therapy), a total of 528 predictions across 132 patients were evaluated for calibration.

For CIRI-DLBCL, CIRI-CLL, and CIRI-BRCA, we assessed calibration-in-the-large, or the difference between the predicted and observed risk of an event (Pr(event, Observed) vs Pr(event, Predicted)) (Steyerberg, 2009). In each case, we calculated the predicted Pr(event) as the mean predicted risk at an endpoint of interest. For example, in the fixed-endpoint formulation of CIRI, we compared the observed and expected probability of an event by 24 months (Pr_obs − Pr_hat, Fig. S1G). To account for censoring, we calculated the observed Pr(event) by the Kaplan-Meier method. These probabilities and their difference are provided along with each calibration plot for each model. The 95% confidence interval for this assessment of calibration-in-the-large is also provided (via 2000 bootstraps).

Next, we assessed model calibration through calibration plots. Here, predictions were divided into deciles of estimated risk. Similar to above, the mean predicted risk was compared to the observed risk (calculated by Kaplan-Meier method) and is shown on the plots. Calibration was initially assessed visually, where each risk quantile should remain close to the line x=y (dashed line on each plot). Patient-level outcome data is also shown, plotting the predicted risk versus a moving-average smoothed observed risk for each patient. Both the patient-level and quantile-level data were visually calibrated.

Calibration can be assessed quantitatively via calibration plot by performing linear regression of the predicted vs. observed risk. Here, the intercept, given a slope of 1 (termed the ‘Calibration Intercept’ in this paper), provides another estimate of calibration-in-the-large (intercept should be 0 in perfect calibration) (Steyerberg, 2009). This metric and 95% confidence interval is provided in each calibration plot in this manuscript. Additionally, the slope of this linear regression (i.e., ‘Calibration Slope’) provides another assessment of calibration, where a slope of 1 represents perfect calibration. The Calibration Slope and 95% confidence intervals are also provided with each calibration plot.

Assessment of CIRI performance by C-statistic

In addition to the calibration of a prediction model, the predictive value of the model is also essential (i.e., the discrimination power of the model). We assessed our model’s performance using the area under receiver operator characteristic curve, or C-statistic. Given that we are interested in survival data that includes possible censorship, we calculated our C-statistic accounting for censored data as per Heagerty et al (Heagerty et al., 2000). This requires selection of a time-point of interest; in the case of CIRI-DLBCL for fixed-endpoint, this was EFS and OS at 24 months (Fig. 1D and S1H, respectively). In our CIRI-DLBCL model for survival analysis, this was EFS and OS from 12 to 36 months (Fig. 2C and S2I, respectively); for our CIRI-CLL model for survival analysis, this was PFS and OS from 12 to 60 months (Fig. 3C and 3F, respectively); finally, for our CIRI-BRCA for survival analysis, this was DRFS from 12 to 60 months (Fig. 4C). Confidence intervals and empiric P-values for comparison with each individual risk stratification tool were performed from 2000 bootstrap resamplings.

Additional statistical analyses

Survival probabilities were estimated using the Kaplan-Meier method; survival of groups of patients base on ctDNA levels were compared using the log-rank test. All analyses were performed with the use of MATLAB, version 2017a, R Statistical Software version 3.4.1, and GraphPad Prism, version 7.0a. Calculation of AUC accounting for censorship was performed using the R ‘survivalROC’ package version 1.0.3 with default settings.

Additional resources

Description: Web resource containing the CIRI models for DLBCL, CLL, and breast adenocarcinoma described in this paper.

URL: https://ciri.stanford.edu

Supplementary Material

2

Figure S1, Related to Figure 1. Determination of parameters, calibration, and prediction of OS for CIRI-DLBCL, fixed endpoint. A) Baseline EFS for the general population of patients with DLBCL (adapted from Sehn et al and Ziepert et al). B) EFS for subgroups of patients defined by IPI risk categories (adapted from Ziepert et al). C) EFS for subgroups of patients defined by cell of origin (adapted from Scott et al). D) EFS for subgroups of patients separated by pretreatment ctDNA levels; patients here are from the Development Set shown in Table S1. E) EFS for subgroups of patients from the Development Set separated by EMR at cycle 2, day 1. F) EFS for subgroups of patients from the Development Set separated by MMR at cycle 3, day 1. The endpoint of interest (24 months) is marked with a dotted line. To the right of each figure, the conditional probabilities used to develop CIRI-DLBCL are shown. G) The displayed plot demonstrates the calibration of predictions from CIRI-DLBCL for a fixed-endpoint (EFS24) with observed patient outcomes across predictions from all time-points during therapy. CIRI produces a numeric estimate of the risk of an adverse event within 24 months (EF2S4) for each individual patient; this risk is shown on the x-axis. The accuracy of these risk-predictions is demonstrated on these scatter plots in several ways as outlined in the STAR Methods (Determination of model calibration). A dotted line shows a plot of predicted versus observed risk of event within 24 months; observed risk is smoothed via moving average. Patients were further ranked according to observed risk and grouped into deciles. The observed risk of event at 24 months in each quantile was calculated by the Kaplan-Meier method (blue dots). The line x=y is plotted as a visual aid (thick dashed line); areas of under and over prediction of risk by >10% are shown in red and green. Further calibration statistics are also provided in the legend. H) A bar plot demonstrates the C-Statistic and 95% confidence interval for predicting overall survival at 24 months by the IPI, all pretreatment factors, EMR, MMR, interim PET, and CIRI-DLBCL for a fixed-endpoint; predictions from CIRI-DLBCL are made after integration of all data.* indicates P < 0.05. (EFS: event-free survival; GCB: Germinal-center B-cell like; ABC: Activated B-cell like; EMR: Early molecular response; MMR: Major molecular response.)

3

Figure S2, Related to Figure 2. Determination of parameters, calibration, and prediction of OS for CIRI-DLBCL, survival analysis. A–G) These plots show the results of parameter determination, or ‘construction of the prior knowledge’, for various risk factors in DLBCL for use in the CIRI-DLBCL survival analysis model. For each possible risk factor, a survival curve was estimated either from case-level data or from the literature as described in the supplemental methods - this represents the prior knowledge. This is shown as the line along with the 95% confidence interval (dashed line). We then identify parameters μ and σ to ‘best fit’ the prior knowledge survival curve in the context of a Cox proportional hazard model, starting from the baseline survival function shown in panel A (adapted from Sehn et al and Ziepert et al). This is performed for B) the IPI (adapted from Ziepert et al), C) cell of origin (adapted from Scott et al), D) pretreatment ctDNA levels (derived from the Development Set), E) early molecular response (derived from the Development Set), F) major molecular response (derived from the Development Set), and G) interim PET/CT scans (adapted from Safar et al). The results of this curve-fitting are shown with the shaded area. These figures demonstrate this process of parameter determination for EFS; the process for OS was performed in a similar manner. H) The calibration of CIRI-DLBCL for survival analysis is shown compared to event-free survival endpoints from 12 months to 36 months. These figures are shown in the same fashion as Fig. 2B, but for multiple endpoints. Additional calibration statistics are provided in the legends. I) Bar plots demonstrates the C-Statistic and 95% confidence interval for predicting overall survival at multiple time intervals by the IPI, all pretreatment factors, EMR, MMR, interim PET/CT, and CIRI; predictions from CIRI-DLBCL are made after integration of all data. J) A Kaplan-Meier estimate shows the overall survival for patients stratified by CIRI-DLBCL risk-prediction into three groups after 3 cycles of therapy (i.e., integration of all data). K) Similar to panel J, a Kaplan-Meier estimate shows the overall survival for patients stratified by CIRI-DLBCL into three groups. Here, risk-predictions across all time-points are shown. Patients in K and J are grouped based on prediction of OS at 36 months. * indicates P < 0.05.

4

Figure S3, Related to Figure 3. Determination of parameters, calibration, and prediction of OS for CIRI-CLL, survival analysis. A–E) These plots show the results of parameter determination, or ‘construction of the prior knowledge’, for various risk factors in CLL for use in the CIRI-CLL survival analysis model derived from the Development Set (Table S3). For each possible risk factor, a survival curve was estimated either from case-level data or from the literature as described in the supplemental methods - this represents the prior knowledge. This is shown as the line along with the 95% confidence interval (dashed line). We then identify parameters μ and σ to ‘best fit’ the prior knowledge survival curve in the context of a Cox proportional hazard model, starting from the baseline survival function shown in Panel A. This is performed for B) the CLL-IPI, C) choice of therapy, D) interim MRD detection, and E) final MRD Detection. The results of this curve-fitting are shown with the shaded area. These figures demonstrate this process of parameter determination for PFS; the process for OS was performed in a similar manner. F) The calibration of CIRI-CLL for survival analysis is shown compared to event-free survival endpoints from 12 months to 60 months. These figures are shown in the same fashion as Fig. 3B, but for multiple endpoints. Additional calibration statistics are provided in the legends. G) A Kaplan-Meier estimate shows the overall survival for patients stratified by CIRI-CLL risk-prediction into three groups after 3 cycles of therapy (i.e., integration of all data). H) Similar to panel G, a Kaplan-Meier estimate shows the overall survival for patients stratified by CIRI-CLL. Here, risk-predictions across all time-points are shown; as many more individual risk-predictions are available here, patients are split into 10-strata. Patients in G and H are grouped based on prediction of OS at 60 months. * indicates P < 0.05.

5

Figure S4, Related to Figure 4. Determination of parameters and calibration for CIRI-BRCA, survival analysis. A–E) These plots show the results of parameter determination, or ‘construction of the prior knowledge’, for various risk factors in breast cancer for use in the CIRI-BRCA survival analysis model. For each possible risk factor, a survival curve was estimated either from case-level data or from the literature as described in the supplemental methods - this represents the prior knowledge. This is shown as the line along with the 95% confidence interval (dashed line). We then identify parameters_μ and σ to ‘best fit’ the prior knowledge survival curve in the context of a Cox proportional hazard model, starting from the baseline survival function shown in Panel A (adapted from Curtis et al). This is performed for B) clinical stage (adapted from Curtis et al), C) ER and Her2 status (adapted from Curtis et al), D) tumor grade (adapted from Curtis et al), and E) pathological response to therapy (adapted from Symmans et al). The results of this curve-fitting are shown with the shaded area. F) The calibration of CIRI-BRCA for survival analysis is shown compared to distant-relapse free survival endpoints from 12 months to 60 months. These figures are shown in the same fashion as Fig. 4B, but for multiple endpoints. Additional calibration statistics are provided in the legends.

6

Figure S5, Related to Figure 6. Developing potential predictive biomarkers through CIRI. A) This plot shows the predicted benefit of FCR vs alternative immunochemotherapy for subsets of patients defined as “high” or “low” risk by various CIRI thresholds as outlined in Fig. 6D by 10-fold cross validation. For example, for patients with a CIRI risk of >20%, our model predicts a 34% benefit of FCR for improvement in PFS at 36 months, while patients with CIRI risk of <20%, our model predicts only a 5% benefit in PFS at 36 months. Error bars are generated by bootstrap resampling (STAR Methods), and represent a 95% C.I. B) Validation of model predictions in panel A. This plot shows the benefit of FCR for PFS at 36 months by Kaplan-Meier for patients with high or low CIRI risk defined at various thresholds - benefit of PFS at 36 months was defined as the difference between PFS36 for FCR-treated and non-FCR treated patients. 95% C.I.s were determined by Greenwood’s formula. C) A scatter plot shows the predicted vs observed benefit of FCR for PFS36 for CIRI low and high-risk patients for various thresholds, defined in panels A and B. D) A schema for using pathological response to therapy to guide therapy. Patients receive a period of neoadjuvant therapy. At this point, pathologic response to therapy is assessed. The effect of different types of therapy can then be assess in patients with or without a pathologic complete response. Here, we assessed this paradigm using HER2+ patients from two publicly available datasets (GSE22226 and GSE109710), blinding ourselves to the choice of therapy. E–F) Kaplan-Meier estimates show the benefit of neoadjuvant therapy containing Trastuzumab + Pertuzumab vs standard therapy for disease-free survival in patients achieving a pathological CR (Panel E) or not achieving a pathological CR (Panel F). G) A schema for using CIRI-BRCA to discover predictive biomarkers to guide therapy. Patients receive a pretreatment risk-prediction (using clinical stage, grade, and receptor status), and then receive a period of neoadjuvant therapy. At this point, pathologic response to therapy is assessed, allowing quantitative integration with CIRI. The effect of different types of therapy can then be assess in patients with high or low risk, assigned by CIRI, at various thresholds. H–I) Kaplan-Meier estimates show the DFS of patients receiving Trastuzumab + Pertuzumab vs standard therapy in patients with CIRI risk < 15% (Panel H) and patients with CIRI risk > 15% (Panel I). J–L) As per panels A–C, but for predicting the benefit of Trastuzumab + Pertuzumab containing neoadjuvant therapy in breast cancer with CIRI-BRCA. Predictions in panel J are performed via 20-fold cross-validation.

7

Figure S6, Related to Figure 6. CIRI web resource, and a proposed framework for CIRI-directed therapeutic selection. A) This figure shows a sample window from the web resource http://ciri.stanford.edu, which contains the CIRI-DLBCL, CIRI-CLL, and CIRI-BRCA risk models. This figure shows the CIRI-DLBCL risk model predicting PFS for Patient B from Fig 2A. B) The CIRI-DLBCL risk profile, predicting the probability of EFS24, for two exemplar patients with individual adverse risk-factors in DLBCL are shown - high IPI score (red) and a positive interim PET/CT scan (blue). Previous clinical trials have been performed utilizing these risk-factors to select patients for early treatment intensification to second-line therapy (i.e., autologous stem cell transplantation). The predicted outcomes for the typical patient with such second-line therapy is also shown (black dashed line). Shaded bands represent 95% confidence intervals. C) The CIRI-DLBCL risk profile, predicting the probability of EFS24, for a specific individual patient (DLBCL103) is shown as additional information is added. Similar to Panel B, the predicted outcomes for the typical patient with second-line therapy is shown as a black dashed line. D) These plots demonstrate probability density functions (PDF) for the patients shown in Panels A and B. The PDF measures the probability that continuing frontline RCHOP therapy is superior to salvage therapy, [or P(EFS24_RCHOP) − P(EFS24_Salvage)]. Probability distributions were calculated by Markov chain Monte Carlo sampling from the posterior distribution, as described in the STAR Methods. P-values represent the probability that salvage therapy gives the patient a superior P(EFS24) than frontline RCHOP therapy.

8

Supplementary Dataset 1, Related to Figure 6. Identifying patient subsets for therapy selection in CLL and BRCA via CIRI. Page 1: A–I) Kaplan-Meier survival estimates show the benefit of FCR vs alternative therapy for low and high-risk patients (left and right, respectively) as defined by CIRI thresholds of 10% to 90% risk of progression by 36 months. Page 2: J–S) Kaplan-Meier survival estimates show the benefit of Trastuzumab + Pertuzumab containing neoadjuvant therapy vs standard therapy for low- and high-risk patients (left and right, respectively) as defined by CIRI thresholds of 5% to 50% risk of progression by 36 months.