Abstract
The recent pandemic triggered by the outbreak of the novel coronavirus boosted the demand for medical services and protective equipment, causing the generation rate of infectious medical waste (IMW) to increase rapidly. Designing an efficient and reliable IMW reverse logistics network in this situation can help to control the spread of the virus. Studies on this issue are limited, and minimization of costs and the risks associated with the operations of this network consisting of different types of medical waste generation centers (MWGC) are rarely considered. In this research, a linear programming model with three objective functions is developed to minimize the total costs, the risk associated with the transportation and treatment of IMW, and the maximum amount of uncollected waste in MWGCs. Also, multiple functions that calculate the amount of generated waste according to the parameters of the current epidemic outbreak are proposed. Revised Multi-Choice Goal Programming method is employed to solve the multi-objective model, and a real case study from Iran is examined to illustrate the validation of the proposed model. The final results show that the model can create a balance between three considered objectives by determining the flow between centers, deciding to install two new temporary treatment centers, and allowing the network to only have uncollected waste in the first two periods in some MWGCs. Also, managerial insights for health organization authorities extracted from the final results and sensitivity analyses are presented for adequately handling the IMW network.
Keywords: Reverse supply chain, Medical waste, Multi-objective, Fuzzy Goal Programming, Infectious disease
Graphical abstract
Highlights
-
•
Proposing a model compatible with condition of epidemic outbreak or pandemic
-
•
Minimizing cost and risk of handling infectious medical waste in epidemic outbreak
-
•
Minimizing the maximum uncollected waste in medical waste generation centers
-
•
Designed functions that calculate amounts of waste based on parameters of the virus
-
•
Considering all potential centers that generate infectious medical waste
1. Introduction
Different kinds of catastrophes, like the outbreak of contagious diseases, can pose a threat to human lives alongside natural disasters. History indicates that epidemics and pandemics can cause tremendous agony and death (Dasaklis et al., 2012). Pandemics, which cause a global crisis, could stem from inefficiently controlled epidemics, which according to the World Health Organization (WHO), is defined as the case that the growth of diseases goes beyond the normal expectancy (WHO, 2020).
One of the most recent epidemic outbreaks that led to a pandemic and public health emergency is caused by the spread of the novel coronavirus (COVID-19), putting the whole population of the world in great danger and panic (Khan et al., 2020). In cases of epidemic outbreaks, the demand for medical equipment will increase dramatically. This increase would be an inevitable outcome of the spread of disease, calling for special attention to the network of this equipment in their lifecycle (Rowan and Laffey, 2020).
Alongside the importance of providing medical equipment, another equally vital issue is handling the infectious medical waste (IMW) generated in diagnosing patients and treating them. Due to the importance of finding patients, and the increasing number of patients needing medical attention, which turns to the use of more equipment, the amount of generated IMW will increase dramatically. IMW management is an essential part of controlling a contagious disease because improper collection and treatment of IMW can accelerate the spread of the disease, posing extra pressure on the medical community and patients (Madsen et al., 2020). For example, researchers revealed the severe ramifications of improperly managed waste infected by human immunodeficiency viruses (HIV), on medical staff (Marinković et al., 2008). Moreover, since most of this waste is plastic-based, it can threaten the environment, if it is released in nature (Ghayebzadeh et al., 2020). In general, handling products at the end of their lifecycle when they might harm the environment and humans is called reverse logistics.
To this extend, the waste management problem falls into the category of reverse logistics networks (Hu et al., 2002). Hence, the network for handling infectious medical waste of COVID-19 (IMWC-19) should be adequately designed to reduce its potential harms, one of which is the spread of the virus. Considering the real challenges posed to the authorities of infected cities that follow the regulations enforced by WHO for the collection and treatment of IMW in conditions of an epidemic outbreak, led to presenting a multi-objective and multi-period mathematical model. The presented model aims to consider all of the centers that might generate IMWC-19, and the amounts of generated waste in each center are calculated through proposed functions for illustrating more realistic conditions. Since the model is designed regarding these general rules, it could be confidently said that the model is a general model except for the regions that do not obey the WHO regulations, and it is not bound to the condition of a specific region or country. Finally, since Iran follows these regulations and the required data for solving the model in a specific region in the north of Iran was accessible, it has been used to validate the model.
2. Literature review
In this section, a concise literature review with the focus on studies related to the COVID-19, and waste management is presented to recognize the research gap regarding the current health-related issues. According to the scientific databases, there have been some studies related to the novel coronavirus, most of which were in the area of medicine. Alongside the importance of knowing the virus and finding a cure or remedy for it, when an epidemic outbreak or a pandemic happens, forecasting its trend and controlling measures in different parts of the problem that are directly or indirectly influences by it become necessary, too.
Madurai Elavarasan and Pugazhendhi (2020) tried to uncover the hidden role of technologies that ultimately could help to control the pandemic. Ivanov (2020) used a simulation-based analysis to predict the possible impacts of the current pandemic on the global supply chain. He presented an analysis approach for monitoring and predicting the possible impacts of epidemic outbreaks on supply chain risk. Klemeš et al. (2020) investigated the long-term and short-term effects of plastic waste, energy, and environmental footprints, and the emerging challenges regarding waste management during and after epidemic outbreaks. Severe challenges in the process of sustainable development were investigated by Pirouz et al. (2020) within a binary classification using regression analysis and artificial intelligence. Shirouyehzad et al. (2020) evaluated the performance of countries with the highest reported cases regarding their medical care and controlling the spread of the disease to predict the spreading trend of the virus. Zareie et al. (2020) presented a model for predicting the trend of COVID-19 in Iran based on the transmission, recovery, and death rate parameters. Govindan et al. (2020) developed a decision support scheme based on the knowledge of physicians and fuzzy inference system to assist with the demand management in the healthcare section, lessen the stress on community, and diminish the spread of the COVID-19. The environmental perspective of the current pandemic is evaluated by Saadat et al. (2020), and they concluded that air and water pollution decreased in some parts of the world.
Next to the more general studies mentioned above, few researchers studied the issues regarding the IMWC-19. Abu-Qdais et al. (2020) carried out statistical analysis to assess the generation rate of IMW during the treatment process of the novel coronavirus, considering a major hospital in Jordan. A discussion on the potential repercussions of the novel coronavirus pandemic on wastewater and waste service with a focus on crucial points where alternative operating processes or further relief measures might be fitting was presented by Nghiem et al. (2020). Hart and Halden (2020) used computational analysis and modeling to explore the feasibility, opportunities, and challenges of identifying active coronavirus infections, through wastewater-based epidemiology. Guidelines for collection, transport, treatment, and disposal of IMW generated in private houses or areas different from medical centers and hospitals that treat COVID-19 patients was established by Di Maria et al. (2020). In one of the most recent studies related to the waste and COVID-19, Kulkarni and Anantharama (2020) discussed the effects of the current pandemic on the municipal waste management system, such as the influence of IMW surge on current systems for municipal waste treatment and disposal.
Some researchers investigated waste management optimization problems in their studies, some of which are presented in the following. Taghipour and Mosaferi (2009) analyzed the quantity and quality, generation rate, and composition of medical waste generated in one of the major cities in the northwest of Iran. Budak and Ustundag (2017) presented a mixed-integer mathematical model to minimize the cost, focusing on collecting and treating the generated waste in Turkish health institutions. An optimization model for minimizing the cost of an infectious waste management network was formulated by Mantzaras and Voudrias (2017). The focus of their model was on finding the optimal location of transfer stations and treatment centers, their related capacities, and the optimal number, capacity, and transformation route of collecting vehicles. A mathematical model for reverse logistics of medical waste was presented by Kargar et al. (2020), where they considered sustainable selection of treatment technology as a part of their research. In one of the latest studies, Yu et al. (2020) proposed a mixed-integer mathematical model for an IMW management network in epidemic outbreak conditions.
2.1. Research gap
The literature review indicates that there is a lack of thorough and adoptable reverse logistics network design for IMW during epidemic outbreaks or pandemic in a specific region. Since most of the world is dealing with the current outbreak of COVID-19, the need for such a network is increasing, so the health authorities could control the spread of disease in this direction. There are indeed many studies in the area of reverse logistics waste management. As the research area gets narrowed down, there are fewer studies that optimize reverse logistics systems of medical waste. Most importantly, according to the literature review, there is only one study that presented an optimization model for IMWC-19, which had many limitations. A concise description of the current study and competitive advantages of the presented model to the existing one are discussed in the following.
The current study presents a model that reduces the cost and risk associated with the collection and treatment of IMWC-19, and the severe harm caused by uncollected waste in each medical waste generation center (MWGC), leading to a tri-objective mathematical model. This study considered all possible MWGC, including existing and temporary hospitals (EHs and THs), clinics, laboratories, residential areas (RAs), and cemeteries. Also, several functions that calculate the amount of generated waste in each MWGC are presented. The main contributions of this study are summarized in the following:
-
1.
Proposing a model compatible with the condition of an epidemic outbreak or pandemic.
-
2.
Considering the cost and risk associated with handling IMW in minimizing objective functions.
-
3.
Presenting an objective function for reducing the possible severe harms caused by uncollected waste in various MWGCs regarding their importance.
-
4.
Designing functions that calculate the amounts of generated waste regarding the parameters of the current epidemic outbreak.
-
5.
Considering all potential centers that generate IMW, especially laboratories, patients quarantined at home, and cemeteries.
-
6.
Evaluating the presented model by optimizing a real case problem.
3. Problem description
In order to design a reverse logistics model compatible with real conditions of the current pandemic and its outbreak in a specific region following assumptions and explanations are considered.
-
1.
Existing hospitals allocated a portion of their beds to the patients of COVID-19, and few temporary hospitals are established to meet the potential demand for beds.
-
2.
Few medical clinics are assigned for outpatient examinations of suspicious cases, so these centers generate IMW.
-
3.
Laboratories that can diagnose COVID-19 through testing kits and chest CT scans, also generate IMW.
-
4.
The treatment machine should have the efficacy inactivation Microbial Bacterial spores at least more than 6 log10. Due to that, the infectious waste of COVID-19 would be safe after being treated with Autoclave machine and could be buried with other waste.
-
5.
The patients diagnosed to be infected and are not in severe conditions are home quarantined. Since these patients also generate IMW, the health organization authorities asked families of these patients to separate their general waste from the waste generated by patients, so the collection and treatment of this waste would be easier. This waste is collected from RAs with a specified protocol. The authorities of the network are obliged to collect IMW of RAs and transport them to their related transfer stations, which are only used for transferring IMW of RAs to treatment centers, and then to one of the nearest treatment centers (Di Maria et al., 2020).
-
6.
Patients that are passed away due the COVID-19 are buried in cemeteries, and since their bodies still carry the virus, these centers generate IMW. This waste is transported to one of the nearest treatment centers.
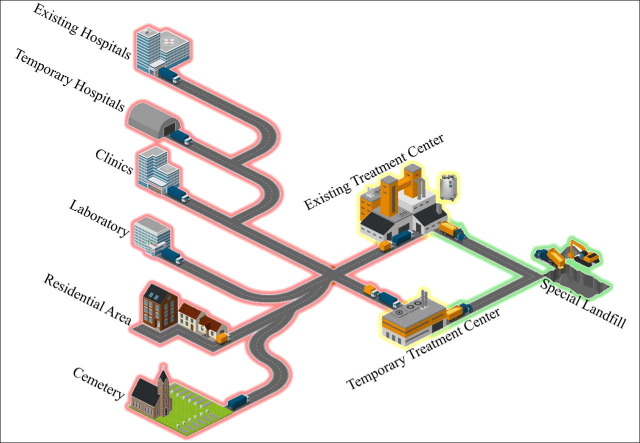
According to the mentioned explanations, the proposed reverse logistics network for IMWC-19 is consists of three major parts. These parts are generation, treatment, and burial of IMW. The generation part is consist of different medical center and centers that are somehow related to COVID19 patients, all of which are called MWGC. These centers are EHs, THs, clinics, laboratories, RAs, and cemeteries, generating different amounts of waste. All of the collected waste from different centers are transported to the second part of the network, which is treatment centers so that they could get treated according to specific protocols. After the treatment process, the trace of the virus would be eliminated from the waste, and it will not cause the disease. There are few existing treatment centers (ETC) in the specific region, so the network authorities can facilitate them with new machines or establish temporary treatment centers (TTC) to meet the demand of the network for treating the surplus waste. The final part of the network is burring the treated waste in special landfills (SLs). The treated waste is sent to the special landfills to get buried according to the sanitation protocols. The structure of the network is illustrated in Fig. 1 .
Fig. 1.
The structure of the proposed network.
3.1. The proposed mathematical model
The main decisions determined by the presented model are as follows:
-
1.
Finding the best location for installing temporary waste treatment centers.
-
2.
Specifying the number of temporary treatment centers.
-
3.
Determining the optimal flow between centers.
-
4.
Determining the optimal amount of uncollected waste in MWGCs.
Indices:
| i | Medical waste generation center (MWGC) |
| c | Existing treatment center (ETC) |
| j | Potential locations for temporary treatment center (TTC) |
| d | Special landfill (SL) |
| t | Period |
Parameters:
| CTc | Unit treatment cost in ETC c |
| CTTj | Unit treatment cost in TTC j |
| DCd | Unit burial cost in SL d |
| R | Unit transportation cost for IMW |
| RT | Unit transportation cost for treated MW |
| COi | Unit collection cost for collecting IMW from RA i and transferring it to its related transfer station |
| PbAic | Probability of accidental risk for transportation between MWGC i and ETC c |
| PbATij | Probability of accidental risk for transportation between MWGC i and TTC j |
| PbAAc | Probability of accidental risk at ETC c |
| PbAATj | Probability of accidental risk at TTC j |
| WUWi | Weight assigned to the severity of the harm of uncollected waste in MWGC i |
| Popric | Population exposure along the route from MWGC i to ETC c |
| Poprtij | Population exposure along the route from MWGC i to PTTC j |
| Popc | Population exposure around ETC c |
| Poptj | Population exposure around TTC j |
| INSj | Installation cost of TTC in location j |
| FICTj | Fixed operating cost of TTC j |
| FICc | Fixed operating cost of ETC c |
| DICic | Distance from MWGC i to ETC c |
| DITij | Distance from MWGC i to TTC j |
| DIDcd | Distance from ETC c to SL d |
| DIDTjd | Distance from TTC j to SL d |
| CACc | Maximum capacity of ETC c |
| CACTj | Maximum capacity of TTC j |
| DEit | Amount of generated waste in the MWGC i in period t |
Decision variables:
| Wj | 1 If TTC is installed in location j, 0 otherwise |
| ZCTjt | 1 If TTC j is utilized in period t; 0 otherwise |
| ZCct | 1 If ETC c is utilized in period t, 0 otherwise |
| Yict | Amount of waste transported from MWGC i to ETC c in period t |
| YTijt | Amount of waste transported from MWGC i to TTC j in period t |
| TQct | Amount of waste treated at ETC c in period t |
| TQTjt | Amount of waste treated at TTC j in period t |
| Qcdt | Amount of waste transported from ETC c to SL d in period t |
| QTjdt | Amount of waste transported from TTC j to SL d in period t |
| UQit | Amount of uncollected waste at MWGC i |
Objective functions:
| (1) |
In this model, the objective function (1) minimizes the total cost that is composed of the following components. The first and the second terms calculate fixed operating cost of ETCs and their operation cost for treating waste. The third and fourth terms compute the installation and fixed operating cost of TTCs, and the fifth term calculates the operation cost of treating waste in TTCs. The sixth term computes the transportation cost of waste from MWGCs to ETCs and TTCs, and the seventh term computes the transportation cost of treated waste from treatment centers to SLs. The final term calculates the collection cost of waste from RAs.
| (2) |
The objective function (2) minimizes the risk associated with the transportation and treatment of infectious waste. The first and second terms of the objective function compute the risk associated with the treatment of waste at ETCs and TTCs. The last two terms calculate the risk associated with the transportation of waste from MWGCs to ETCs and TTCs, respectively.
| (3) |
The objective function (3) minimizes the maximum amount of uncollected waste in MWGCs in all of the periods, resulting in minimizing the severe harm caused by the uncollected waste.
Constraints:
| (4) |
Eq. (4) balances the flow between MWGCs, ETCs, and TTCs.
| (5) |
| (6) |
| (7) |
| (8) |
Eqs. (5), (7) guarantee that the inflow of waste to ETCs and TTCs is less than or equal to their capacity. Equality of the inflow and outflow to and out of ETCs and TTCs are assured in Eqs. (6), (8), respectively.
| (9) |
| (10) |
Eqs. (9), (10) guarantee that the outflow of treated waste from ETCs and TTCs is equal to its inflow to SL, respectively.
| (11) |
Finally, Eq. (11) shows the characteristics of the decision variables.
3.2. Waste generation function
Predictions regarding the number of infected patinas became an important part of studies within which an epidemic outbreak or a pandemic happens. A precise and reliable method for forecasting this number can improve the efficiency of disease management measures (Moreira and Günther, 2013). Also, the amount of generated IMW in these conditions are influenced by this number and some other parameters. In order to present more realistic values for generated waste in these circumstances, several functions are introduced. Total urban population and accordingly population that is covered by each center are critical factors in these functions, which are computed through an assigned weight to each center. These weights are calculated regarding the capacity and service level of centers. The parameters used in the calculation of generated waste in each kind of MWGC and the functions are presented in the following:
| PopCi | Population that is covered by MWGC i |
| IRt | Infection rate for COVID-19 in period t |
| PRHt | Percentage of patients that attend to hospitals in period t |
| PHt | Probability of getting hospitalized in period t |
| NPHit | Number of patients that are under medical attention in hospital i and period t |
| Ret | Recovery rate in period t |
| Mut | Mortality rate in period t |
| Qpit | Amount of generated waste by each patient in MWGC i and period t |
| Pct | Percentage of patients that attend clinics in period t |
| MSt | Percentage of test that is done for diagnosing COVID-19 in period t |
| PAHit | Number of patients that are home quarantined in RA i and period t |
Eqs. (12), (13), (14), (15), (16) calculate the amount of generated waste in hospitals, clinics, laboratories, RAs, and cemeteries in each period, respectively.
| (12) |
| (13) |
| (14) |
| (15) |
| (16) |
The number of patients under medical attention in hospital i and period t and the number of patients that are home quarantined are computed by Eqs. (17), (18).
| (17) |
| (18) |
3.3. Linearization
The proposed model has two different kinds of non-linear terms. The first term is the third objective function of the model that is non-linear through the existence of a max function on the mentioned objective function. A new auxiliary variable should be added to the model, Eq. (3) should be substituted by Eq. (19), and a new constraint as Eq. (20) should be added to the model, so the problem regarding the first non-linear term get solved (Molladavoodi et al., 2020).
| (19) |
| (20) |
| (21) |
The second term is formed by multiplication of two binary variables in the right-hand side of constraint (7), which is transformed into a linear equation through substitution of a new binary variable as WZ jt instead of ZCT jt×W j. The non-linear constraint of the model is replaced by the constraints given in Eqs. (22), (23), (24), (25) (Paydar and Saidi-Mehrabad, 2015).
| (22) |
| (23) |
| (24) |
| (25) |
3.4. Solution approach
In real case problems, decision-makers intend to optimize problems in more than one aspect, leading to a multi-objective model. Each of the objectives can represent a distinct answer when the problem is solved just with that objective, so it will not give a thorough solution. Hence, the problem should be solved with multi-objective approaches to give an overall optimized answer. This study utilized the Revised Multi-Choice Goal Programming (RMCGP) in its solution process. Therefore, a brief background of the method and the approach itself are explored in the following.
The Goal Programming (GP) model was first presented by Charnes et al. (1955), and after that, researchers modified it in different ways to have more efficient and adaptable methods. The method itself and its extensions are used to solve many problems and showed their validations (Jones and Tamiz, 2016). One of the main steps of GP is specifying an aspiration level for each objective function, and the main goal of the method is minimizing the summation of deviations from the determined values (Tanino et al., 2003).
Determining an aspiration level for different objectives might be hard due to the lack of valid information. Chang presented a model within which decision-makers can set multiple aspiration levels for a single objective to reduce the adverse effects of ambiguous information (Chang, 2007). Chang extended his model and presented RMCGP, where decision-makers can assign a range to an objective instead of discrete numbers. In brief, the main goal of the model is minimizing the weighted summation of deviations from aspiration levels of all of the goals and deviations from the goals themselves (Chang, 2008). The parameters and variables of the RMCGP method are as follows:
| gi, min, gi, max | Lower and upper bound of aspiration level of objective i |
| Ri | Continuous variable with a lower bound of gi,min and upper bound of gi,max |
| wi | Weight of deviations from the goal of objective i |
| di+, di− | Positive and negative variation from aspiration level of objective i |
| pi | Weight of deviations from upper or lower bound of aspiration level for objective i |
| ei+, ei− | Positive and negative variation from upper or lower bound of aspiration level of objective i |
The configuration of the RMCGP has two cases regarding the type of objective functions. The first case is called “the less the better” which is presented as follows:
| (26) |
S. t.
| (27) |
| (28) |
| (29) |
| (30) |
| (31) |
f i (X) represents the objective function i, and X is the decision vector. Eq. (26) represents the goal of the RMCGP, minimizing the weighted summation of deviations from the aspiration level and the lower bund of aspiration level. Eq. (27) shows the constraints of the system, and Eq. (28) calculates the positive and negative variations from the aspiration level. Eq. (29) computes the positive and negative variations from the lower bound of the aspiration level. Eq. (30) guarantees that aspiration levels are bound to the lower and upper bound. The characteristics of the variables are presented in Eqs. (31).
The second case is called “the more the better”, and its only difference with the first case is that the right-hand side of Eq. (29) would be g i,max. Hence, the model minimizes the positive and negative deviations from the upper bound of the aspiration level.
3.5. The mathematical model of the proposed network
The proposed mathematical model after application of the RMCGP is as follows:
| (32) |
S. t.
Eqs. (4), (5), (6), (8), (9), (10), (11), (19), (20), (21), (22), (23), (24), (25)
| (33) |
| (34) |
| (35) |
| (36) |
| (37) |
| (38) |
| (39) |
| (40) |
| (41) |
| (42) |
Eq. (32) minimizes the normalized weighted positive and negative variations from the aspiration levels and their lower bounds. Eqs. (33), (34), (35), (36), (37), (38), (39), (40), (41) calculate the negative and positive variations from their related goals, and their lower bounds, and also guarantee that aspiration levels are bound to their related upper and lower bounds. Finally, the characteristics of the variables are presented in Eq. (42).
4. Case study
4.1. Case description
As mentioned before, the presented model has three parts, including MWGCs, treatment centers, and special landfills. The model optimizes the reverse logistics network of IMWC-19, regarding the economic and health-related issues of the network. The required data for modeling and solving the problem is collected from a real case in Babol city located in the north of Iran. This city is selected because the number of infected patients of this city increased rapidly, and composed a significant portion of patients in the province and the country.
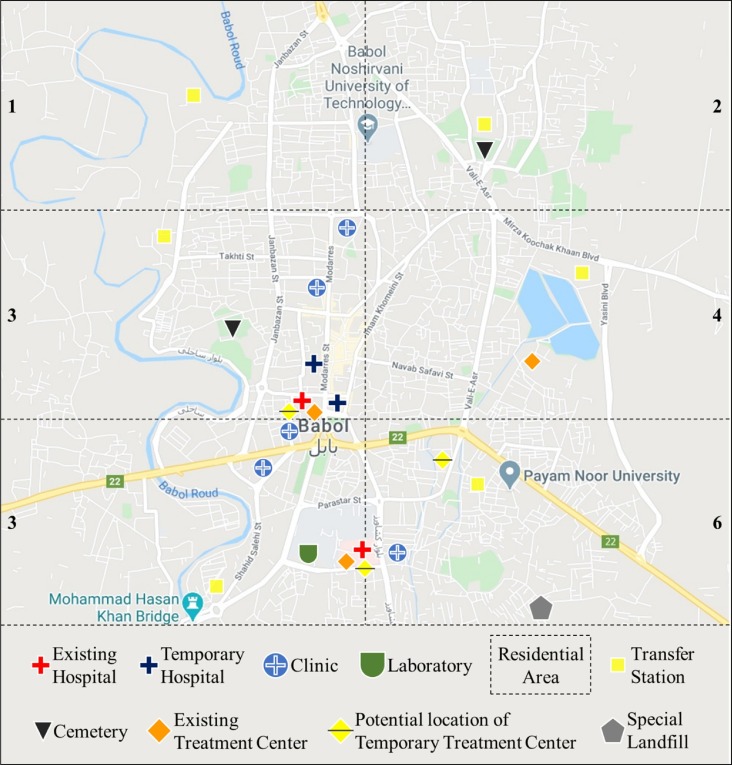
The first part of the model consists of different MWGCs, which are EHs, THs, clinics, laboratories, RAs, and cemeteries. In order to handle the waste generated in RAs, which are the waste generated by patients quarantined at home, managers of the network proposed to divide the considered region into several parts, each of which considered as a separate MWGC. The waste generated in each area is collected to its related transfer station and then sent to treatment centers. The planning horizon of the model is 48 h, which consists of six periods with 8-hour lengths. Fig. 2 illustrates the location of the mentioned centers. Since the considered case study has one landfill, and it is located in a remote place in the southeast forests of the city, it will not fit in the presented figure. Still, a figurative location is presented in the figure for the special landfill.
Fig. 2.
Location of the centers of the presented network.
4.2. Input parameters
In normal conditions, the generation rate of IMW in Iran is 0.68 kg per bed and day. However, regarding the current outbreak of the COVID-19, not only the generation rate of previous equipment is increased but also other necessary equipment for precautionary measures are added to the MW. In this regard, according to the evaluation of the considered medical centers of the case study, the generation rate of IMW is increased, and it is estimated at 5 kg per bed and day. One of the main reasons for this sudden increase is that according to the protocols, all of the equipment used in the centers that take care of COVID-19 patients is assumed to be infected by the virus. Also, the generation rate of infectious waste in clinics, laboratories, and RAs are about 0.5 kg, 0.3 kg, and 4 kg per patient and day, respectively. Moreover, the generation rate of waste for burring each passed away patient is approximately 5 kg per person and day. Since each day is divided into three working shifts, the mentioned numbers are divided into three equal parts.
According to the most recent demographic studies, the total population of the considered region is 250,217 people, and its population density is 6858 people/km2. In order to compute the population covered by a center, a weight is assigned to each center, which is calculated regarding the capacity and service level of centers. The population that is covered by each MWGC and other parameters related to the functions that calculate the generated waste are presented in Tables S1 and S2, respectively. The amount of generated IMW by each MWGC is presented in Table S3.
Three ETCs, which two of them are located in the EHs, are considered in the case study. Also, three TTCs are assumed to be available for treating the surplus waste. Two of the TTCs can be installed in the EHs, meaning that they need extra machines, so the capacity of treatment would be increased. All of the treatment centers use Autoclave machines with different capacities, which are mentioned in Table S4.
The consequence of accidental risk in each treatment center (Pop c , Popt i), which is the population exposure around it, is calculated with Eq. (44) (Zhao et al., 2016; Yu et al., 2020). The radius of effect is assumed to be 3 km, and the probability of risk for each treatment center (PbAA c, PbAAT j) is approximated about 0.0006. Also, for calculating the probability of risk associated with the transportation of IMW (PbA ic, PbAT ij), the Eq. (45) is presented. The first part Eq. (45) is calculated by multiplying two numbers that are the accident rate of trucks transporting IMW on inter-city routes, and the release probability given an accident of a truck with IMW. Eq. (46) is used for computing the consequence of risk in transportation, which is the population exposure along its route (Zhao et al., 2016; Yu et al., 2020).
| (44) |
| (45) |
| (46) |
The distances between the different centers of the network are presented in Table S5. The collection cost of IMW from homes in RAs (CO i) is 400 Toman/kg. The cost of treating (CT c, CTT j) and burring (DC d) the waste is 700 and 200 Toman/kg, respectively. The transportation cost of IMW (R) and treated waste (RT) are 530 and 22 Toman/kg*km, respectively. The installation cost of TTCs (INS j) is 20,000,000 Toman, and the fixed operating cost of each machine (FIXCT j, FIXC c) is 300,000 Toman.
5. Results
The presented model with the parameters extracted from the real case study is solved with Intel® Core™ i5 2410 CPU 4.00 GHz, 6.00 GB RAM, and LINGO 17.0 software package in 25 s. The code and data can be accessed at https://github.com/MoPourmehdi/COVID-19-waste-management. At first, each objective is considered separately, and the model is solved to obtain an upper and a lower bound for the aspiration level of each objective. Then the tri-objective model is solved with RMCGP, and given weights to the objectives are 0.3, 0.3, and 0.4, respectively. The value of each objective function is presented in Table 1 .
Table 1.
Value of objective functions.
| Objective | Z1 (million Toman) | Z2 | Z3 (kg) |
|---|---|---|---|
| Z1 | 2.280 | 0 | 25,068 |
| Z2 | 14.880 | 0 | 25,068 |
| Z3 | 107.936 | 1,262,641 | 0 |
| Goal Programming | 78.989 | 1,259,501 | 36 |
One million Tomans: Approximately 100 US dollars.
The amount of treated waste in each treatment center and each period is shown in Table S6. The data of the table shows that only TTC1 used its full capacity for treating waste, and since two of the TTCs are installed at the beginning of the first period, there would be no difference between ETCs and TTCs. Regarding this condition, the model decides between five treatment centers and treats IMW in the best way possible.
The uncollected waste in each MWGC in each period is presented in Table S7. As shown in the table, only the first two periods have uncollected waste, which shows the efficiency of the presented model, and it stems from the decreasing rate of generated waste in each NWGC. The different parts of the cost associated with the operation of the presented network and the percentage of each cost in the total cost are presented in Table 2 .
Table 2.
Different part of the cost of the presented network.
| Cost | Value (million Toman) | Percentage of each cost |
|---|---|---|
| Fixed operating cost of ETCs | 5.100 | 6.46 |
| Operation cost of treating waste in ETCs | 5.081 | 6.43 |
| Installation cost of TTCs | 40.000 | 50.64 |
| Fixed operating cost of TTCs | 4.000 | 5.06 |
| Operation cost of treating waste in TTCs | 2.478 | 3.14 |
| Transportation cost of infectious medical waste | 12.374 | 15.67 |
| Transportation cost of treated waste | 7.676 | 9.72 |
| Collection cost from RA | 2.280 | 2.89 |
One million Tomans: Approximately 100 US dollars.
ETC: Existing treatment center.
TTC: Temporary treatment center.
RA: Residential area.
6. Sensitivity analyses and discussion
Sensitivity analyses are done on some of the decision factors presented by decision-makers and the parameters of the model and the disease to evaluate the effects of potential changes on the proposed network. Different analyses and their effects on the final results are presented in the following.
6.1. Sensitivity analysis on given weights to objective functions
One of the most influential decision factors that have significant effects on the final results of the problem is the parameters of the solution approach. Four different cases for the given weights to the objective functions are considered to observe the effects of these changes on the final value of the objective functions. It should be mentioned that the economic objective is not the most important objective of this study, and the essential goal is controlling the disease, mostly by minimizing the risk associated with transportation and treatment of the waste, and the amount of uncollected wastes. Due to the mentioned explanations, the economic objective always gets the lowest weight and the weight of the second and third objectives are varied. Different cases and their final results are presented in Table 3 .
Table 3.
Sensitivity analysis of the parameters of the Goal Programming approach.
| Case | Given weight to objective |
Value of objective |
Installed TTC | ||||
|---|---|---|---|---|---|---|---|
| W1,P1 | W2,P2 | W3,P3 | Z1 (million Toman) | Z2 | Z3 (kg) | ||
| 1 | 0.3 | 0.3 | 0.4 | 78.989 | 1,259,501 | 36 | TTCs 1 and 2 |
| 2 | 0.333 | 0.333 | 0.333 | 78.989 | 1,259,501 | 36 | TTCs 1 and 2 |
| 3 | 0.25 | 0.25 | 0.5 | 99.208 | 1,259,426 | 0 | All TTCs |
| 4 | 0.2 | 0.5 | 0.3 | 77.785 | 1,222,223 | 90 | TTCs 1 and 2 |
One million Tomans: Approximately 100 US dollars.
TTC: Temporary treatment center.
A comparison between the first two cases shows that a small change in the given weight to objective functions will not change their final values. However, the last two cases show that giving the more significant weight to one of the second or third objectives will change the final results in their favor. The third case illustrates that by giving a bigger weight to the third objective, the model makes the amount of uncollected waste zero, and in doing so, the model suggests to install all potential TTCs.
6.2. Sensitivity analysis of the parameters of the disease
Parameters of the disease have a direct effect on the amount of generated waste and, accordingly, the final results of the problem. Since the most important objective is the amount of uncollected waste on the MWGCs, the effects of two different parameters of the disease, which are infection rate for COVID-19 and the recovery rate of patients, on the total amount of generated waste and uncollected waste are analyzed.
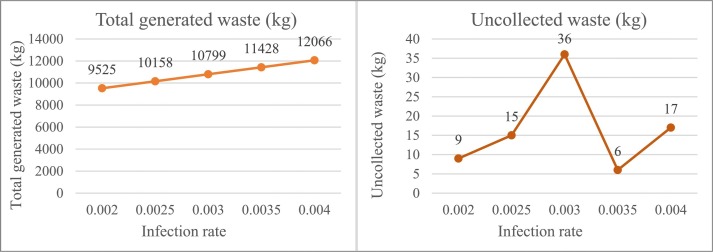
According to Fig. 3 and Table S8, the infection rate has a direct correlation with the total generated waste, so its amount increases by the increase of infection rate. Moreover, increasing the infection rate causes the amount of uncollected waste to increase, too. However, there is an anomaly in its trend, which happens because of a TTC installation.
Fig. 3.
Sensitivity analysis of total generated waste and uncollected waste regarding the changes in infection rate.
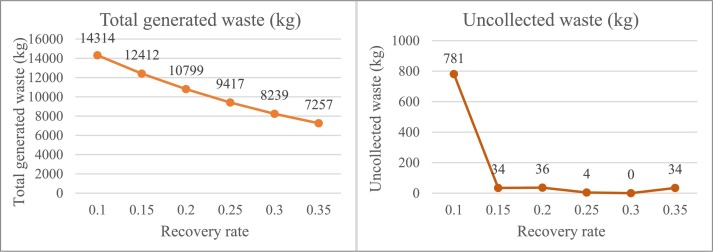
Since based on the data of Table S9 and Fig. 4 the total amount of generated waste decreases as the recovery rate increases, so they have an adverse correlation. Also, in general, the amount of uncollected waste decreases as the recovery rate increases, but similar to the case of infection rate, there are two anomalies in its trend, which happens when TTCs get installed.
Fig. 4.
Sensitivity analysis of total generated waste and uncollected waste regarding the changes in recovery rate.
6.3. Sensitivity analysis of the amount of generated waste
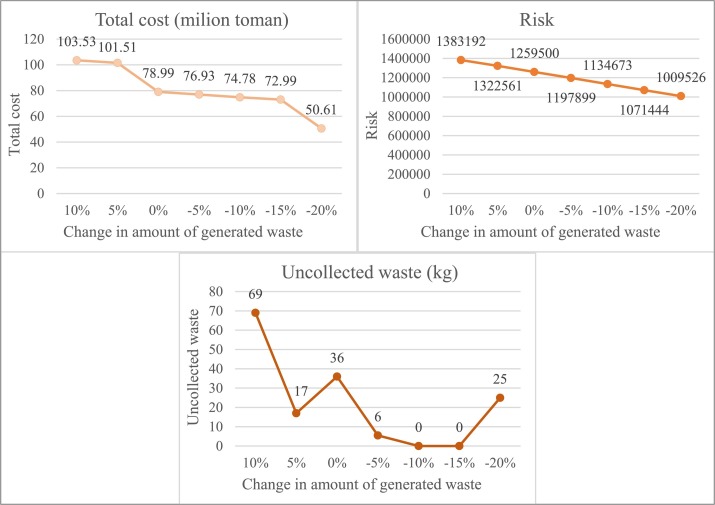
Even though the amount of generated waste in hospitals has been estimated thorough evaluation of the case study, it might be unrealistic to assume that this amount is a fixed value and does not change. Several cases are taken into account to observe the consequences of these changes on the total cost, risk, and amount of uncollected waste.
Based on the data of Table S10 and Fig. 5 , the change in the amount of generated waste per person and period has a direct correlation with the total cost and risk with different ratios. It also has a direct correlation with the amount of uncollected waste with two special cases that relate to the installation of TTCs. This data shows that small changes in the amount of generated waste per person and period can have a positive effect on almost all of the objectives.
Fig. 5.
Sensitivity analysis of total cost, risk, and uncollected waste regarding the changes in the amount of generated waste per patient and period.
6.4. Managerial insights
The main goal of this study is to properly manage the IMWC-19 to minimize the transmission rate of the disease by minimizing the risk associated with transporting and treating the generated waste and minimizing the amount of uncollected waste. Also, minimizing the total cost of the operations related to collection, treatment, and burial were considered in the proposed model.
Regarding the characteristics of the study, it can present insights to the managers of health organizations for efficient management of the IMW network. Some of the recommendations extracted from the result and sensitivity analyses of the case study are presented in the following:
-
1.
One of the essential factors in handling the generated waste and trying to reduce its harmful effects is an efficient forecast of the amount of generated waste. Hence, attempts to improve the performance of the waste generation functions, and trying to use real-time data to have a precise prediction of generated waste can help managers to handle this waste efficiently.
-
2.
Improper management of the IMWC-19 can accelerate the transmission of the disease and infected more people and medical staff, making the problem bigger than it was at the beginning of the outbreak. The beginning of the management process might have an extra cost for the managers, but the reduction in risk associated with IMW and the reduction in cost for the long run is one of the promising outcomes of proper management. Additionally, another more significant outcome is controlling the disease and saving many lives.
-
3.
Using experts to calculate the specific risk associated with transporting and treating IMW can help managers adequately reduce the potential hazards of IMW by finding the best route for transporting waste and determining the best location for treating them. Moreover, using portable treatment equipment can eliminate the risk associated with transporting waste. These portable machines can be quickly sent to centers that are predicted to have surplus waste.
-
4.
According to Table 3, in cases that the managers do not care so much about the total cost of the network, they can reduce the risk associated with the processes of the network and the amount of uncollected waste, reducing the hazards of IMW. The managers can ask the government or philanthropists for funds to control the disease without worrying about its cost.
-
5.
If people obey the protocol given to them for precautionary measures, the infection rate of the disease will decrease, or if medical society finds a cure of remedy that can improve the recovery rate of patients, according to Fig. 3, Fig. 4, the amount of total generated waste will decrease. This decrease will result in the more efficient control of the disease. Moreover, the analysis of the amount of generated waste per person and period shows that if in some way medical staff manage to decrease this amount as 15%, the total cost and the risk decrease about 7.5 and 15%, respectively. Also, the amount of uncollected waste would be zero.
7. Conclusions
According to the novelty of the COVID-19, its outbreak all around the world, which led to a pandemic, and its rapid transmission rate, there is no specific approach for controlling it. One of the outcomes of pandemics is the sudden increase in the amount of generated MW, which itself can be problematic in case of improper management. Like every other country, Iran is dealing with this problem, so finding an efficient strategy for handling this problem can help Iran and set an example for other countries with the same condition to using this strategy so they would be able to control the spread of the disease. Hence, designing a reverse logistics network for properly managing IMWC-19 is a necessity. In this regard, this study presented a tri-objective mathematical model to minimize the total cost, the risk associated with the operations of the network, and the maximum amount of uncollected waste in MWGCs through determining the flow of material and the location of TTCs and whether they should be installed or not. The RMCGP approach was used to solve the presented model. The model was shown to be compatible with the condition of the current pandemic. Also, it incorporated all of the potential centers that might generate IMWC-19.
The final results showed that the model created a balance between three considered objectives by determining the flow between centers, installing two TTCs, and only allowing the network to have uncollected waste in the first two periods of some MWGCs. It showed that the most significant portion of the cost is the cost of installing TTCs with about 50% of the total cost. The next significant portions are the transportation cost of IMW and treated waste with about 16% and 10%, respectively. Sensitivity analyses showed that when the decision-makers gave the weight of 0.5 to the second and third objectives, the model reduced the cost about 1.5% and the risk, about 3% in the first case, and diminished the amount of uncollected waste to zero in the second case, respectively. This is a realistic assumption because if the disease and its waste, which in case of improper management can accelerate the spread of the disease, are adequately managed, other potential future costs, health-related problems, and possible deaths would be decreased or eliminated. The sensitivity analyses showed that cooperation of society in precautionary measures, finding a remedy or cure, and reduction in the amount of generated waste per person and period could have significant effects on the final results of the model.
For future research, uncertainty is some parameters regarding the calculation of the generated waste in different MWGCs can be considered. Considering different working shift durations and evaluating their influence on the model could be a suggestion for future research. Also, taking into account bigger examples, the possible changes that might be made to the model, and the need for a meta-heuristic approach for solving the potential NP-hard problem could be a future extension. Moreover, calculating precise traffic loads of potential routes for future research can result in evaluating the risk associated with the transportation of IMW in a more realistic way.
CRediT authorship contribution statement
Saeed Kargar: Conceptualization, Software, Investigation, Methodology. Mohammad Pourmehdi: Conceptualization, Methodology, Validation, Formal analysis, Writing - original draft, Writing - review & editing, Visualization. Mohammad Mahdi Paydar: Supervision, Methodology, Validation, Writing - review & editing.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Editor: Huu Hao Ngo
Footnotes
Supplementary data to this article can be found online at https://doi.org/10.1016/j.scitotenv.2020.141183.
Appendix A. Supplementary data
Supplementary tables
References
- Abu-Qdais H.A., Al-Ghazo M.A., Al-Ghazo E.M. Statistical analysis and characteristics of hospital medical waste under novel coronavirus outbreak. Glob. J. Environ. Sci. Manag. 2020;6:1–10. doi: 10.22034/gjesm.2020.04.0. [DOI] [Google Scholar]
- Budak A., Ustundag A. Reverse logistics optimisation for waste collection and disposal in health institutions: the case of Turkey. Int. J. Logist. Res. Appl. 2017;20:322–341. doi: 10.1080/13675567.2016.1234595. [DOI] [Google Scholar]
- Chang C.-T. Multi-choice goal programming. Omega. 2007;35:389–396. doi: 10.1016/j.omega.2005.07.009. [DOI] [Google Scholar]
- Chang C.-T. Revised multi-choice goal programming. Appl. Math. Model. 2008;32:2587–2595. doi: 10.1016/j.apm.2007.09.008. [DOI] [Google Scholar]
- Charnes A., Cooper W.W., Ferguson R.O. Optimal estimation of executive compensation by linear programming. Manag. Sci. 1955;1:138–151. doi: 10.1287/mnsc.1.2.138. [DOI] [Google Scholar]
- Dasaklis T.K., Pappis C.P., Rachaniotis N.P. Epidemics control and logistics operations: a review. Int. J. Prod. Econ. 2012;139:393–410. doi: 10.1016/j.ijpe.2012.05.023. [DOI] [Google Scholar]
- Di Maria F., Beccaloni E., Bonadonna L., Cini C., Confalonieri E., La Rosa G., Milana M.R., Testai E., Scaini F. Minimization of spreading of SARS-CoV-2 via household waste produced by subjects affected by COVID-19 or in quarantine. Sci. Total Environ. 2020;743 doi: 10.1016/j.scitotenv.2020.140803. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ghayebzadeh M., Taghipour H., Aslani H. Estimation of plastic waste inputs from land into the Persian Gulf and the Gulf of Oman: an environmental disaster, scientific and social concerns. Sci. Total Environ. 2020 doi: 10.1016/j.scitotenv.2020.138942. [DOI] [PubMed] [Google Scholar]
- Govindan K., Mina H., Alavi B. A decision support system for demand management in healthcare supply chains considering the epidemic outbreaks: a case study of coronavirus disease 2019 (COVID-19) Transp. Res. Part E Logist. Transp. Rev. 2020;138 doi: 10.1016/j.tre.2020.101967. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hart O.E., Halden R.U. Computational analysis of SARS-CoV-2/COVID-19 surveillance by wastewater-based epidemiology locally and globally: feasibility, economy, opportunities and challenges. Sci. Total Environ. 2020;730 doi: 10.1016/j.scitotenv.2020.138875. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hu T.L., Sheu J.B., Huang K.H. A reverse logistics cost minimization model for the treatment of hazardous wastes. Transp. Res. Part E Logist. Transp. Rev. 2002;38:457–473. doi: 10.1016/S1366-5545(02)00020-0. [DOI] [Google Scholar]
- Ivanov D. Predicting the impacts of epidemic outbreaks on global supply chains: a simulation-based analysis on the coronavirus outbreak (COVID-19/SARS-CoV-2) case. Transp. Res. Part E Logist. Transp. Rev. 2020;136 doi: 10.1016/j.tre.2020.101922. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jones D., Tamiz M. International Series in Operations Research and Management Science. Springer; 2016. A review of goal programming; pp. 903–926. [DOI] [Google Scholar]
- Kargar S., Paydar M.M., Safaei A.S. A reverse supply chain for medical waste: a case study in Babol healthcare sector. Waste Manag. 2020;113:197–209. doi: 10.1016/j.wasman.2020.05.052. [DOI] [PubMed] [Google Scholar]
- Khan S., Ali A., Siddique R., Nabi G. Novel coronavirus is putting the whole world on alert. J. Hosp. Infect. 2020;104:252–253. doi: 10.1016/j.jhin.2020.01.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klemeš J.J., Fan Y. Van, Tan R.R., Jiang P. Minimising the present and future plastic waste, energy and environmental footprints related to COVID-19. Renew. Sust. Energ. Rev. 2020;127 doi: 10.1016/j.rser.2020.109883. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kulkarni B.N., Anantharama V. Repercussions of COVID-19 pandemic on municipal solid waste management: challenges and opportunities. Sci. Total Environ. 2020 doi: 10.1016/j.scitotenv.2020.140693. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Madsen A.M., Frederiksen M.W., Bjerregaard M., Tendal K. Measures to reduce the exposure of waste collection workers to handborne and airborne microorganisms and inflammogenic dust. Waste Manag. 2020;101:241–249. doi: 10.1016/j.wasman.2019.10.023. [DOI] [PubMed] [Google Scholar]
- Madurai Elavarasan R., Pugazhendhi R. Restructured society and environment: a review on potential technological strategies to control the COVID-19 pandemic. Sci. Total Environ. 2020 doi: 10.1016/j.scitotenv.2020.138858. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mantzaras G., Voudrias E.A. An optimization model for collection, haul, transfer, treatment and disposal of infectious medical waste: application to a Greek region. Waste Manag. 2017;69:518–534. doi: 10.1016/j.wasman.2017.08.037. [DOI] [PubMed] [Google Scholar]
- Marinković N., Vitale K., Holcer N.J., Džakula A., Pavić T. Management of hazardous medical waste in Croatia. Waste Manag. 2008;28:1049–1056. doi: 10.1016/j.wasman.2007.01.021. [DOI] [PubMed] [Google Scholar]
- Molladavoodi H., Paydar M.M., Safaei A.S. A disaster relief operations management model: a hybrid LP–GA approach. Neural Comput. Appl. 2020;32:1173–1194. doi: 10.1007/s00521-018-3762-0. [DOI] [Google Scholar]
- Moreira A.M.M., Günther W.M.R. Assessment of medical waste management at a primary health-care center in São Paulo, Brazil. Waste Manag. 2013;33:162–167. doi: 10.1016/j.wasman.2012.09.018. [DOI] [PubMed] [Google Scholar]
- Nghiem L.D., Morgan B., Donner E., Short M.D. The COVID-19 pandemic: considerations for the waste and wastewater services sector. Case Stud. Chem. Environ. Eng. 2020 doi: 10.1016/j.cscee.2020.100006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paydar M.M., Saidi-Mehrabad M. Revised multi-choice goal programming for integrated supply chain design and dynamic virtual cell formation with fuzzy parameters. Int. J. Comput. Integr. Manuf. 2015;28:251–265. doi: 10.1080/0951192X.2013.874596. [DOI] [Google Scholar]
- Pirouz B., Haghshenas Sina Shaffiee, Haghshenas Sami Shaffiee, Piro P. Investigating a serious challenge in the sustainable development process: analysis of confirmed cases of COVID-19 (new type of coronavirus) through a binary classification using artificial intelligence and regression analysis. Sustain. (United States) 2020;12 doi: 10.3390/su12062427. [DOI] [Google Scholar]
- Rowan N.J., Laffey J.G. Challenges and solutions for addressing critical shortage of supply chain for personal and protective equipment (PPE) arising from coronavirus disease (COVID19) pandemic – case study from the Republic of Ireland. Sci. Total Environ. 2020;725 doi: 10.1016/j.scitotenv.2020.138532. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saadat S., Rawtani D., Hussain C.M. Environmental perspective of COVID-19. Sci. Total Environ. 2020;728 doi: 10.1016/j.scitotenv.2020.138870. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shirouyehzad H., Jouzdani J., Khodadadi Karimvand M. Fight against COVID-19: a global efficiency evaluation based on contagion control and medical treatment. J. Appl. Res. Ind. Eng. 2020;7:109–120. doi: 10.22105/JARIE.2020.225087.1146. [DOI] [Google Scholar]
- Taghipour H., Mosaferi M. Characterization of medical waste from hospitals in Tabriz, Iran. Sci. Total Environ. 2009;407:1527–1535. doi: 10.1016/j.scitotenv.2008.11.032. [DOI] [PubMed] [Google Scholar]
- Tanino T., Tanaka T., Inuiguchi M. Springer Science & Business Media; 2003. Multi-Objective Programming and Goal Programming, Multi-Objective Programming and Goal Programming. [DOI] [Google Scholar]
- WHO Definitions: emergencies. 2020. https://www.who.int/hac/about/definitions/en/ [WWW Document]. URL.
- Yu H., Sun X., Solvang W.D., Zhao X. Reverse logistics network design for effective management of medical waste in epidemic outbreaks: insights from the coronavirus disease 2019 (COVID-19) outbreak in Wuhan (China) Int. J. Environ. Res. Public Health. 2020;17 doi: 10.3390/ijerph17051770. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zareie B., Roshani A., Mansournia M.A., Rasouli M.A., Moradi G. A model for COVID-19 prediction in Iran based on China parameters. Arch. Iran. Med. 2020;23:244–248. doi: 10.34172/aim.2020.05. [DOI] [PubMed] [Google Scholar]
- Zhao J., Huang L., Lee D.-H., Peng Q. Improved approaches to the network design problem in regional hazardous waste management systems. Transp. Res. Part E Logist. Transp. Rev. 2016;88:52–75. doi: 10.1016/j.tre.2016.02.002. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary tables