Exposing Hidden High-Affinity RNA Conformational States

Abstract

RNA recognition frequently results in conformational changes that optimize intermolecular binding. As a consequence, the overall binding affinity of RNA to its binding partners depends not only on the intermolecular interactions formed in the bound state but also on the energy cost associated with changing the RNA conformational distribution. Measuring these “conformational penalties” is, however, challenging because bound RNA conformations tend to have equilibrium populations in the absence of the binding partner that fall outside detection by conventional biophysical methods. In this study we employ as a model system HIV-1 TAR RNA and its interaction with the ligand argininamide (ARG), a mimic of TAR’s cognate protein binding partner, the transactivator Tat. We use NMR chemical shift perturbations and relaxation dispersion in combination with Bayesian inference to develop a detailed thermodynamic model of coupled conformational change and ligand binding. Starting from a comprehensive 12-state model of the equilibrium, we estimate the energies of six distinct detectable thermodynamic states that are not accessible by currently available methods. Our approach identifies a minimum of four RNA intermediates that differ in terms of the TAR conformation and ARG occupancy. The dominant bound TAR conformation features two bound ARG ligands and has an equilibrium population in the absence of ARG that is below detection limit. Consequently, even though ARG binds to TAR with an apparent overall weak affinity $\left(K_{\text{d}}^{\text{app}}\approx 0.2\text{mM}\right)$, it binds the prefolded conformation with a K_d in the nM range. Our results show that conformational penalties can be major determinants of RNA-ligand binding affinity as well as a source of binding cooperativity, with important implications for a predictive understanding of how RNA is recognized and for RNA-targeted drug discovery.

Graphical Abstract

INTRODUCTION

The ability of non-coding RNAs to adopt a multitude of conformations underlies their cellular roles in gene expression and regulation.^1–6 These dynamic transitions occur on time scales ranging from picoseconds to tens of seconds and can feature global changes in the orientation of helical elements and local base pair reshuffling that remodel both secondary and tertiary structure.^5,7 Although such alternative conformational states can be short-lived and/or poorly populated in the isolated RNA, they can become long-lived and appreciably populated to play regulatory roles through interactions with binding partners.⁸ The high prevalence of conformational changes in RNA on molecular recognition^9–11 implies that binding energies are highly dependent on RNA conformational penalties.^12,13 However, the relative magnitudes of these energetic penalties are difficult to experimentally quantify due to challenges in detecting extremely low population species in the absence of ligand. Detection and characterization of such transient species is further complicated by highly cooperative interactions that can deceivingly appear two-state.^14,15 Significant advances in nuclear magnetic resonance (NMR) spectroscopy^16–20 have allowed characterization of protein and more recently RNA conformational dynamics occurring on the microsecond to millisecond time scale by relaxation dispersion (RD) techniques including R_1ρ,^21–23 CPMG,^24,25 and CEST,^8,26 but challenges remain with respect to detection limitations and complicated data analysis. Developing a predictive understanding regarding the role of RNA conformational thermodynamics is of critical importance²⁷ for RNA-targeted drug discovery^28–30 and bioengineering.^31–33

Prior studies have successfully determined complex mechanisms by globally fitting data collected as a function of multiple independent variables in order to reshape the population distribution of relevant conformational states.^34–38 We apply this strategy in our study of trans-activation response element (TAR) RNA from human immunodeficiency virus type-1 (HIV-1), which is one of the first paradigmatic examples of RNA adaptive recognition. Its conformation-dependent binding interaction with the viral protein Tat is required for full-length transcription elongation^39–41 and has therefore been the subject of numerous studies aimed at understanding the principles behind dynamic ligand recognition. TAR is also a drug target for the development of anti-HIV therapeutics and it has been shown that the ligand-bound RNA conformation is an important determinant of the ligand’s inhibitory activity.^42–44 Previous NMR-derived structures show that unliganded TAR adopts a mainly bent (average bend angle ~47°) and flexible inter-helical conformation in which bulge residue U23 stacks on A22, while spacer bulge residues C24 and U25 are looped out and flexible.^45–48 The ligand argininamide (ARG) has been used extensively in TAR binding studies because it recapitulates the functional structural changes that TAR undergoes upon binding to the HIV-1 Tat arginine-rich motif (ARM).^45,49–53 ARG binding arrests inter-helical motions and stabilizes a coaxial conformation in which bulge residue U23 forms a base triple with helical residues A27 and U38, and junctional residues A22 and U40 become stably hydrogen bonded.^49,53

Several studies measuring TAR binding to Tat-like peptides or ARG-derived compounds have reported evidence for two binding sites,^43,54–57 while others report single apparent affinities,^{44,50,58–61} and it remains unclear what role the other Tat arginine residues located in the arginine-rich RNA binding domain (RBD, residues G48-R57)⁶² play in vivo. Overall, the results in the literature hint at conformational heterogeneity present in the TAR·ARG bound state that has not been fully explored. Here, we show that bulge-dependent binding occurs at two sites on TAR and that the tightest affinity occurs on the base tripled TAR state. The apical loop of the TAR construct used for all experiments in this study is replaced with a UUCG loop to simplify the analysis and ensure that no dispersion is present in the unliganded state.⁶³ This substitution has been shown to have minimal effects on ARG binding or ARG-dependent conformational equilibria.^53,64 We globally fit NMR chemical shift perturbation (CSP) data to a six-state model and then test the predictions generated from our model using NMR RD in the presence of ligand.

RESULTS AND DISCUSSION

Qualitative Inspection of Chemical Shift Perturbations′ Ligand and Temperature Dependence Reveals Three Conformations and Two Binding Sites.

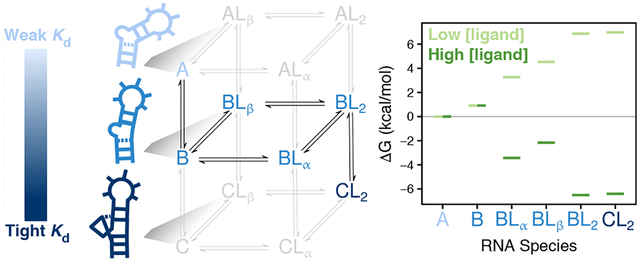
We carried out NMR 2D HSQC experiments as a function of both ligand concentration and temperature to quantitatively dissect the coupled conformational change and binding reactions that occur when the small-molecule ligand, ARG (Figure 1B), binds to TAR RNA (Figure 1A). Chemical shifts are exceptionally sensitive to local electronic environment, making them excellent reporters of conformational change and proximity to ligands, although distinguishing the two can be challenging. Close inspection of the raw CSP data (Figure 1C) enables us to build basic elements of a binding model on the basis of the following three criteria.

1. Nonlinear trajectories observed in the 2D HSQC spectra⁶⁵ in Figure 1C under the fast-exchange limit are indicative of multi-site binding.^66–68 The data is consistent with fast exchange because no significant line broadening is observed at any of the ligand concentrations and temperatures tested (Figures 1C and S2).

2. Temperature-dependent chemical shifts^69–72 at low ligand concentration (see residue U23-C1′ in Figure 1C) are indicative of conformational equilibria between multiple unliganded RNA species.

3. Temperature-dependent chemical shifts at high ligand concentration (see residue G28-C8 in Figure 1C) are indicative of conformational equilibria between multiple ARG-bound RNA species.

Figure 1.

NMR evidence for multi-site binding coupled with conformational equilibria. (A) Secondary structure of TAR construct used in this work. Red asterisk highlights residues that are particularly sensitive to temperature-dependent conformational equilibria and green asterisk highlights residues that show curved CSP trajectories indicating multiple binding sites. (B) Chemical structure of argininamide (ARG). (C) Chemical shifts as a function of ARG concentration at varying temperatures (blue, 1 °C to red, 25 °C) for representative resonances. Examples are shown for residues sensitive to multiple binding sites (A27-C8 and G28-C8) evidenced by curved CSP trajectories, and residues sensitive to conformational equilibria (U23-C1′ and G28-C8) evidenced by CSPs that vary significantly with temperature. Note that G28-C8 is sensitive to the BL₂ ⇌ CL₂ equilibria in addition to multi-site binding, while U23-C1′ reports on A ⇌ B but is almost entirely insensitive to BL₂ ⇌ CL₂. Shown are the aromatic C6/C8-H6/H8 (left) and sugar C1′-H1′ (right) spectra at 25 °C as a function of increasing ARG concentration showing that the peaks shift in accordance with fast exchange. Spectra of all raw data can be found in Figure S2. (D) Minimal six-state model consistent with the observed CSP trends. In lighter gray are the equilibria that complete the statistical thermodynamic description for a system with three conformations and two independent binding sites per conformation, giving a total of 12 possible RNA species. (E) Cartoon depictions of the three TAR conformational states discussed in the text.

In addition to the perturbations addressed by these observations, ARG-dependent perturbations are also observed across a wide variety of residues including helical regions outside the apparent binding sites, raising the immediate question of whether these distant perturbations are due to long-range conformational effects or whether they reflect weak interaction with three or more ARG molecules. Strong temperature but no ligand dependencies are observed in the chemical shifts of resonances in the UUCG loop even though bulge-dependent equilibria are expected to be independent of the apical loop for the TAR sequence used here.⁶⁴ This observation suggests that more than two conformational equilibria may contribute to the observed chemical shifts. A model that accounts for all of these additional RNA species would be under-determined without a substantial amount of additional data, and the equations may not have analytical solutions (for ligand binding to ≥ two non-identical sites).⁷³ To circumvent this issue and focus on ligand-dependent CSPs that probe ARG binding, we used a bulgeless TAR variant to help identify the resonances reporting only on bulge-dependent ARG binding and conformational change.

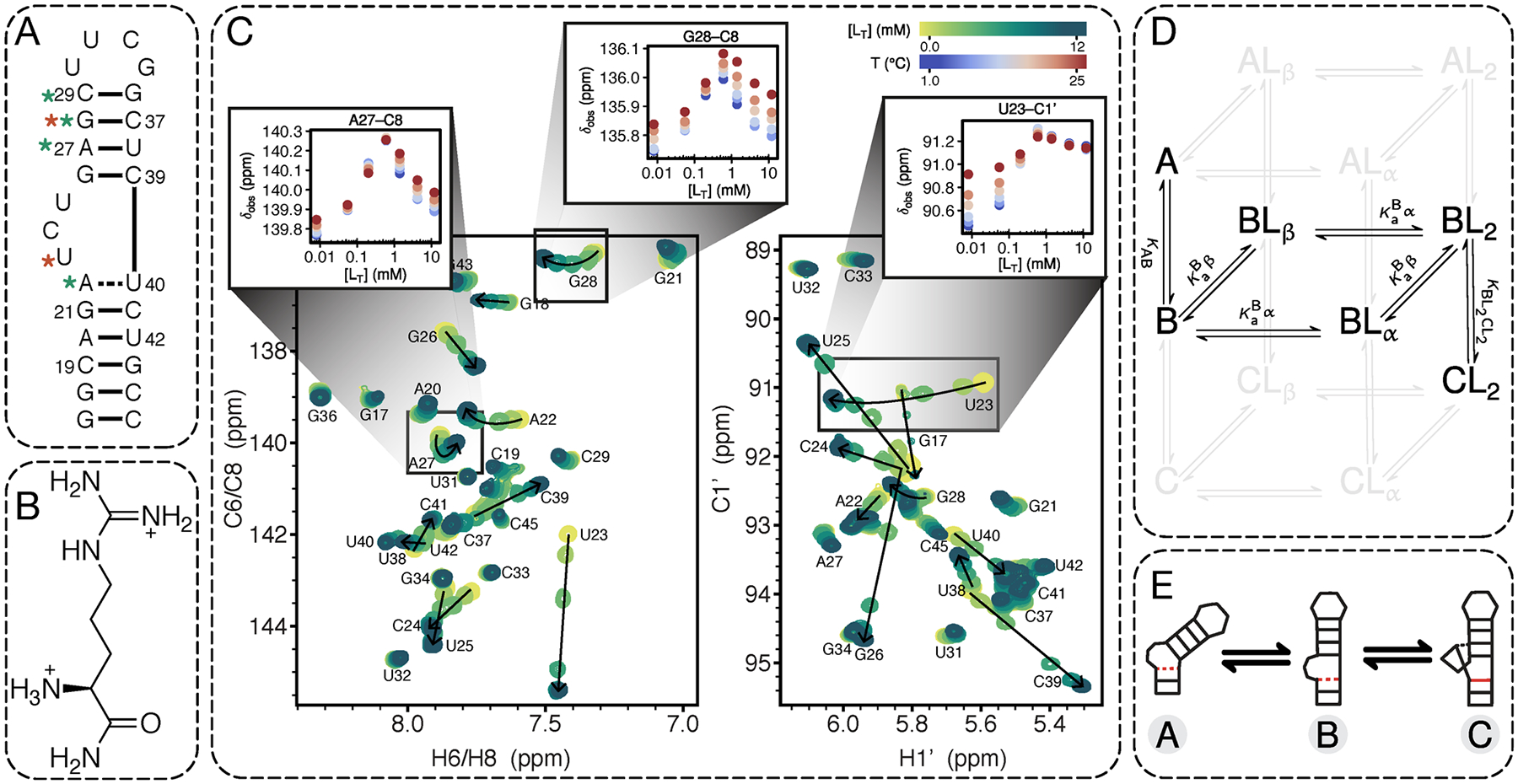
Bulge Deletion Identifies Chemical Shifts Not Perturbed by Two Primary Binding Sites.

Quantitative interpretation of the observed CSP temperature and ligand dependencies depends on the assumption that the underlying data reports on the explicit equilibria included in the binding model. Ideally, the binding model would include all equilibria but due to experimental and computational limitations, we are forced to build minimal complexity models. Because we have chosen to model the bulge-dependent binding and conformational equilibria presumed to be critical for functionally important TAR-Tat interactions in the cell,^39,40,74,75 it is important for accurate modeling that we exclude CSPs from global fitting that are bulge-independent. To identify these resonances, we carried out NMR CSP mapping experiments on a construct lacking the UCU bulge (ΔbulgeTAR) as a function of temperature and ARG concentration. Specifically, comparison of the NMR spectra between the two constructs both in the absence (Figure S3A) and presence (Figure S3B) of ARG reveals that ARG-induced perturbations in the lower helix do not depend on the bulge. Importantly, when we compare the NMR spectra of TAR and ΔbulgeTAR in the presence of ARG, any peaks in the ARG-bound spectra that do not overlay between TAR and ΔbulgeTAR identify a specific bulge-dependent binding site or a binding-dependent conformational change that can only occur in the construct with the trinucleotide bulge. The aromatic resonances for A20 and G21 are nearly identical for both RNA variants under ARG-saturating conditions (Figure S3B), which indicates that the lower helix does not report on bulge-dependent binding. As expected, resonances near the bulge that are known to play a role in ARG recognition (A22, G26, A27, U38, C39, U40)⁴⁹ have large chemical shift differences (Δδ = δ_Δbulge·ARG − δ_TAR·ARG) in the presence of ARG. More interesting, however, are resonances located farther away from the bulge that do not overlay well in the ARG-bound spectra, namely G28-C8 and C29-C6. This result provides support for a second bulge-dependent binding site in the upper helix above the bulge, (Figure 2B and Figure S4) consistent with a recently published NMR study that showed the TAR·Tat RBD complex was stabilized by two arginine residues: R52 below the bulge and R49 above the bulge.⁷⁶ Additionally, these results suggest that using a simplified small-molecule system to study RNA–protein binding can faithfully capture key features of the larger system and is an effective approach for dissecting complex binding equilibria. For the purpose of accurately modeling the TAR bulge-dependent binding equilibria, we exclude resonances from global fitting whose chemical shifts are sensitive to bulge-independent binding or to melting as discussed further in the Supporting Information.

Figure 2.

Evidence for bulge-dependent secondary binding site in the TAR upper helix. (A) Comparison of secondary structures of the TAR and the bulgeless mutant in the absence of ligand. Resonances colored in yellow correspond to the putative secondary binding site. (B) CSPs as a function of ARG concentration and temperature for residues that are sensitive to the bulge-dependent secondary binding site on TAR that is abolished in the bulgeless mutant. Color coding of temperatures follows that of Figure 1C. The data supports that the secondary binding site is localized to the upper helix region between residues A27 and G36. The curved trajectories seen for A27-C8 and G28-C8 in TAR indicate they are sensitive to both the α and β sites. This is consistent with previous results that the α site ARG is stacked above A22 and contacts G26 just below A27. Note that the chemical shifts for G36-C1′ and G36-C8 in TAR are only sensitive to the β site ligand.

Global Bayesian Fitting Provides Posterior Probability Distributions of Thermodynamic and Structural Parameters.

Global fitting of the TAR CSPs caused by changes in ligand concentration and temperature to a thermodynamic model can provide estimates of reaction energies and chemical shift fingerprints (i.e., structural information) of the various populated RNA species. Each data point collected at a given temperature and ARG concentration for a given resonance is modeled as the observed chemical shift position δ_obs. For systems exchanging between n states on the fast NMR time scale, the δ_obs at a given ligand concentration and temperature is an ensemble-averaged value given by

$${\delta }_{\text{obs}}=\sum _{i=1}^n{p}_i{\delta }_i$$ (1)

for states i = 1, …, n. The population of a given species p_i, expressed as

$$p_i=\frac{{\text{e}}^{-\Delta G_i/RT}}{Q}=\frac{{\text{e}}^{-\Delta G_i/RT}}{{\sum }_{i=1}^n{\text{e}}^{-\Delta G_i/RT}}$$ (2)

is the probability of the system being in state i, where ${\sum }_{i=1}^n{p}_i=1$, R is the ideal gas constant, T is the absolute temperature in Kelvin, and ΔG_i is the Gibbs free energy difference between state i and a reference state. The partition function $Q={\sum }_{i=1}^n{\text{e}}^{-\Delta G_i/RT}$ represents the sum of the statistical weights of all microstates distinguishable by binding site occupancy and cooperatively formed conformational minima (see Methods for model-dependent Q derivations).

Because the raw data establish a mechanism that involves multiple RNA conformational states and multiple liganded states, we employed a Bayesian approach that has several advantages over least-squares fitting methods, particularly for estimation of correlated parameters in multi-component biophysical models.^77–80 Least-squares methods that obtain point estimates for parameter values rely on the assumption that the error in the data is normally distributed around the mean value, but this assumption need not be true for more complicated systems in which the variance in the data has complex sources (Methods) and parameters are often correlated. A Bayesian approach, by contrast, estimates complete joint probability distributions for each parameter and in so doing estimates the associated uncertainty over all potential parameter space, providing more reliable estimates of parameter uncertainty. Additionally, Bayesian inference has the advantage over standard approaches in its ability to formally incorporate prior knowledge with the observed data, which together are used to maximize the log likelihood of the proposed model, or the conditional probability of observing the data given the model. This approach is represented by Bayes’s rule, p(θ|y) ∝ p(y|θ) p(θ), where p(θ|y) is the posterior probability distribution, p(y|θ) is the likelihood, and p(θ) is the prior probability distribution for a specified model with parameters θ and data y. Our implementation of Bayesian fitting is described in Methods.

A Six-State Thermodynamic Model Matches the Information Content of the CSP Data.

The model we developed for data fitting assumes explicit conformational changes and binding equilibria to quantitatively interpret the observed CSP temperature and ligand dependencies. As noted earlier, the curvature observed in the ligand-dependent 2D CSP trajectories provides evidence for at least two binding sites, and the temperature-dependent CSPs at both low and high ligand concentrations indicate conformational equilibria between at least three species. Taken together, these observations suggest the existence of a minimum of 12 distinct RNA species: three conformational states (referred to herein as states A, B, and C) and three bound forms of each conformational state, corresponding to ARG bound to site α or β, or both. This scheme is depicted in Figure 1D.

Ideally, there would be sufficient information in the experimental data to determine all of the equilibrium constants. Unfortunately, because some states are insufficiently populated to allow estimation of their contributions to observed CSPs, we are forced to reduce the complexity of the model to six RNA species: only the unliganded form of the A conformation (A), only the fully liganded form of the C conformation (CL₂), and all possible liganded states of the B conformation (B, BL_α, BL_β, and BL₂). Our rationale for including these states and not the other six is described in detail in the Supporting Information. Although our model-fitting approach does not strictly require any prior assumptions regarding the structural identities of the A, B and C conformations, we propose that they correspond to the flexible, bent inter-helical form of TAR^10,46,47,81 (state A); the coaxially stacked state observed at high Mg²⁺ concentration^82–85 where junctional residues A22 and U40 below the bulge remain unpaired (state B); and the coaxially stacked state stabilized with a A22·U40 base pair and U23-A27·U38 base triple⁴⁹ (state C), as depicted in Figure 1E. These predictions are based on earlier NMR studies that report hydrogen bond alignments between A22-U40 and U23-A27 in excess ARG but not in Mg²⁺,⁵³ where both ARG and Mg²⁺ similarly reduce the TAR helix bend angle relative to the unliganded state according to transient electric birefringence, NMR, and circular dichroism studies.^47,59,84,86

At intermediate ARG concentrations there must be significantly populated singly bound species, which must have either the B or C conformations, or both. As noted above, the minimal model must include one or more singly bound species in the same conformational state as the doubly bound species. The non-sigmoidal binding curves observed for several resonances would not be observed if the two binding sites were on different conformational states. Given the assumption that the unliganded C state is negligible, the B conformation is the best candidate for the singly bound species, i.e., BL_α and/or BL_β as opposed to CL_α and/or CL_β. We fit for $K_{\text{a}}^{{\text{B}}_{\alpha }}$ and ${\text{K}}_{\text{a}}^{{\text{B}}_{\beta }}$ distributions but also consider the possibility that CL_α and/or CL_β become sufficiently populated to contribute to the observed CSPs and therefore also test fits including $K_{\text{a}}^{{\text{C}}_{\alpha }}$ and/or $K_{\text{a}}^{{\text{C}}_{\beta }}$. We conclude that the models including CL_α and/or CL_β do not fit the data significantly better than the simpler and less parametrized model with only BL_α and BL_β. This conclusion is consistent with our preference for a model whose complexity is matched to the information content of the data. Additional experiments beyond the scope of the present study might provide sufficient information to determine the populations of some of the six species not included in our minimal model. An example of such an experiment would be relaxation kinetics, which have the capacity to detect transiently populated species whose equilibrium populations are undetectable.³⁷

The Unliganded C Conformation of TAR Is Poorly Populated But Has High Affinity for ARG.

For the six-state model, the fitting equation is given by

$${\delta }_{\text{obs}}=\sum _{i=1}^{n=6}{p}_i{\delta }_i={\delta }_{\text{A}}{p}_{\text{A}}+{\delta }_{\text{B}}{p}_{\text{B}}+{\delta }_{{\text{BL}}_{\alpha }}{p}_{{\text{BL}}_{\alpha }}+{\delta }_{{\text{BL}}_{\beta }}{p}_{{\text{BL}}_{\beta }}+{\delta }_{{\text{BL}}_2}{p}_{{\text{BL}}_2}+{\delta }_{{\text{CL}}_2}{p}_{{\text{CL}}_2}$$ (3)

where the population of each species is found as described in Methods. The populations and therefore the observed chemical shifts are a function of the site binding affinities for ${\text{BL}}_{\alpha }\left(K_{\text{a}}^{{\text{B}}_{\alpha }}=1/K_{\text{d}}^{{\text{B}}_{\alpha }}\right)$ and ${\text{BL}}_{\beta }\left(K_{\text{a}}^{{\text{B}}_{\beta }}=1/K_{\text{d}}^{{\text{B}}_{\beta }}\right)$ and equilibrium constants for A ⇌ B (K_AB) and ${\text{BL}}_2\rightleftharpoons {\text{CL}}_2\left(K_{{\text{BL}}_2{\text{CL}}_2}\right)$. Because the slopes of chemical shifts versus ligand concentration do not vary significantly with temperature for all resonances, (representatives shown in inset in Figure 1C), we assume that the site binding constants are insensitive to temperature at the experimental conditions tested and the only detectable temperature dependency arises from conformational equilibria given by

$$K_{\text{eq}}={\text{e}}^{\Delta H/R\left(1/T_{\text{m}}-1/T\right)}$$ (4)

where ΔH is the enthalpy change and T_m is the melting temperature in Kelvin for a given conformational transition. Here, the parameter vector θ is given by $\theta =\left(K_{\text{a}}^{{\text{B}}_{\alpha }},K_{\text{a}}^{{\text{B}}_{\beta }},\Delta H_{\text{A}\text{B}},\Delta H_{{\text{BL}}_2{\text{CL}}_2},T_{\text{m}}^{\text{AB}},T_{\text{m}}^{{\text{BL}}_2{\text{CL}}_2},{\delta }_{r,i},{ϵ}_j\right)$ where δ_r,i represents the vector of basis chemical shifts for species i (i = A, B, BL_α, BL_β, BL₂, and CL₂) per resonance r, and ϵ_j is the measurement error in δ_obs in units of ppm for chemical shift groups j (j = C6/C8, C1′, C2, H2/H6/H8/H1′, H1/H3, and overlapped resonances). The error terms were grouped according to scale of raw chemical shift values, as described in Methods.

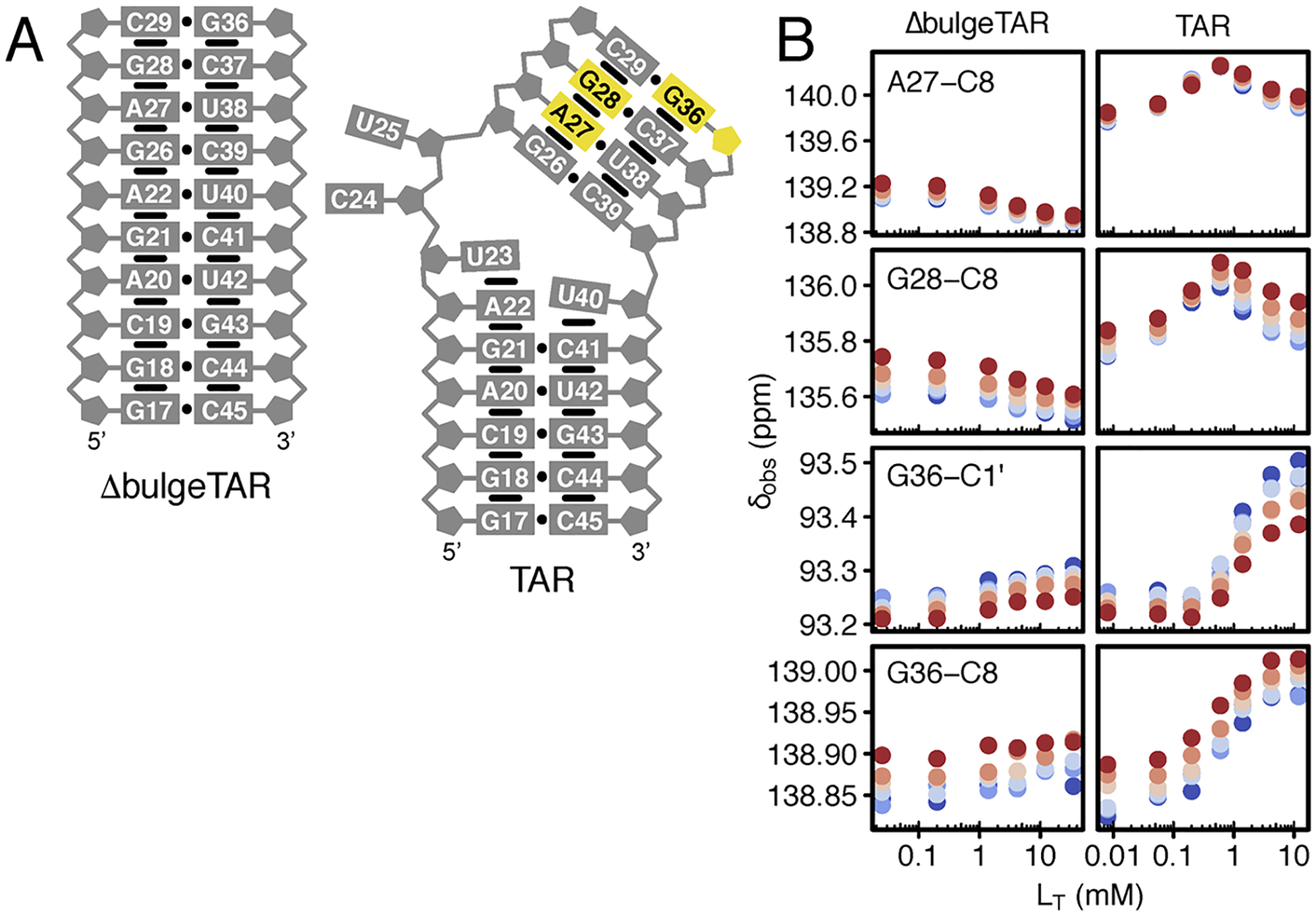
As listed in Table 1, the site binding affinities estimated from the marginal posterior distributions are 66 (+7/−6) μM and 550 (+50/−40) μM for the α and β sites on state B, respectively. The enthalpy change of the stacking equilibrium (A ⇌ B) is estimated to be −7.9 (+0.5/−0.4) kcal mol⁻¹, while the derived entropy change for the same reaction is quite unfavorable at −29.4 (+0.4/−1.2) cal mol⁻¹ K⁻¹. This reduction in entropy is expected for a stacking reaction. The BL₂ ⇌ CL₂ equilibrium is slightly less exothermic at −2.9 (+0.4/−0.4) kcal mol⁻¹ and also less entropically unfavorable at 9.9 (+1.6/−1.3) cal mol⁻¹ K⁻¹. The derived free energy change for both reactions is slightly positive (unfavorable) at 25 °C (Figure 3C, red), but as depicted in Figure 4, both A and B are significantly populated in the absence of ligand and both BL₂ and CL₂ are significantly populated at high ARG concentrations. Figure 4 also shows that the only other significantly populated species is BL_α, whose population reaches ~35% at the midpoint of the apparent binding curve, but is poorly populated at low and high ARG concentrations.

Table 1.

Thermodynamic Parameter Estimates and Their 5% and 95% Confidence Intervals

Parameter	estimate	5% C.I.	95% C.I.
ΔHAB (kcal mol−1)	−7.86	−8.33	−7.45
$\Delta H_{{\text{BL}}_2{\text{CL}}_2}\left(\text{kcal }{\text{mol}}^{-1}\right)$	−2.85	−3.27	−2.47
$T_{\text{m}}^{\text{AB}}\left({}^{°}\text{C}\right)$	−6.08	−9.63	−2.46
$T_{\text{m}}^{{\text{B}}_2{\text{CL}}_2}\left({}^{°}\text{C}\right)$	14.55	6.92	22.05
ΔSAB (cal mol−1K−1)a	−29.44	−30.83	−28.23
$\Delta S_{{\text{BL}}_2{\text{CL}}_2}\left({\text{ cal mol}}^{-1}{\text{K}}^{-1}\right)$a	−9.90	−11.45	−8.55
ΔGAB (kcal mol−1)a,b	0.91	0.84	0.99
$\Delta G_{{\text{BL}}_2{\text{CL}}_2}\left(\text{kcal }{\text{mol}}^{-1}\right)$a,b	0.11	0.03	0.19
$K_{\text{d}}^{{\text{B}}_{\alpha }}(\text{mM})$	0.066	0.060	0.073
$K_{\text{d}}^{{\text{B}}_{\beta }}(\text{mM})$	0.55	0.51	0.60

^aDerived parameter.

^bAt 25 °C.

Figure 3.

Bayesian global fitting of CSPs. (A) Representative fits to 10 resonances out of a global fitting set containing 54 resonances. Shown are the 95% confidence interval regions at each temperature. Fits for all 54 resonances included in the global fit are shown in Figure S8. The points and curves are colored from 1 °C (blue) to 25 °C (red). (B) Joint posterior distributions of thermodynamic parameters with marginal posterior distributions down the diagonal. (C) Marginal posterior distributions of ΔG values for the A ⇌ B and BL₂ ⇌ CL₂ reactions at each temperature. They are colored using the same color scheme used in panel A.

Figure 4.

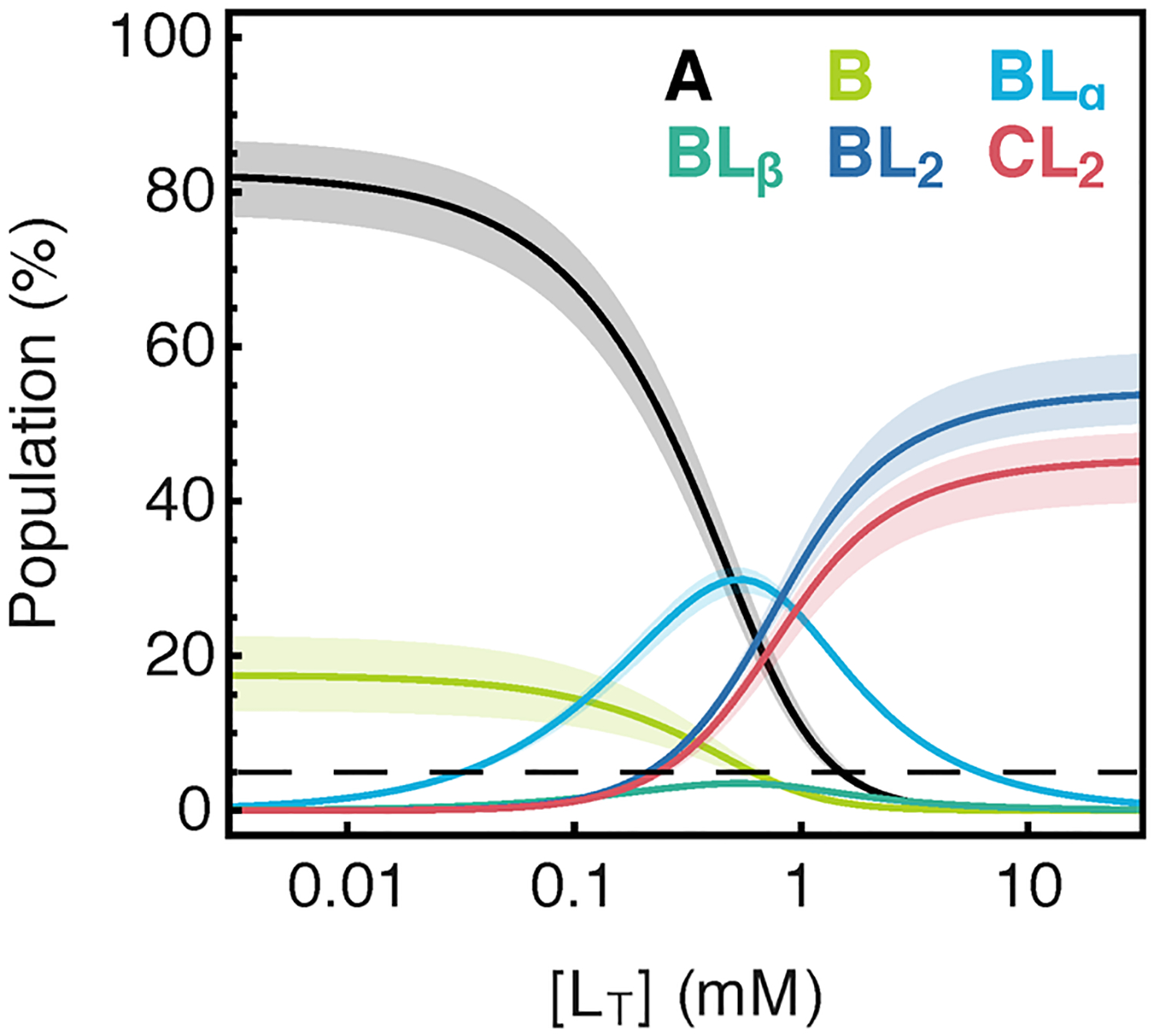
Populations vs [ARG] for all species in the six-state model calculated using fitted parameter confidence intervals at 25 °C. The dotted line refers to the ~5% population cutoff for detection of species by the CSP titration method.

In addition to the six-state model, we tested several models (Figure S5) as potential fits to the data. Although fits to models with species n ≥ 7 were not statistically superior to the simpler, less parametrized six-state model, they provide additional support for the existence of tight binding to an undetectable C species. For instance, the K_d to at least one site on the C conformation was consistently estimated to be below 0.009 mM for fits to n ≥ 7-state models. Under such conditions, the population of the singly bound C conformation would be below 5%, so its contribution to δ_obs would be negligible and largely indeterminable, which is consistent with the highly uncertain distributions obtained for δ_CLα and/or δ_CLβ in those fits. Overall, these results are consistent with a model in which binding to at least one of the sites on the C conformation is much tighter than binding to that site in the B conformation.

Fitted CSPs Give Insight into Structures of Intermediate Species.

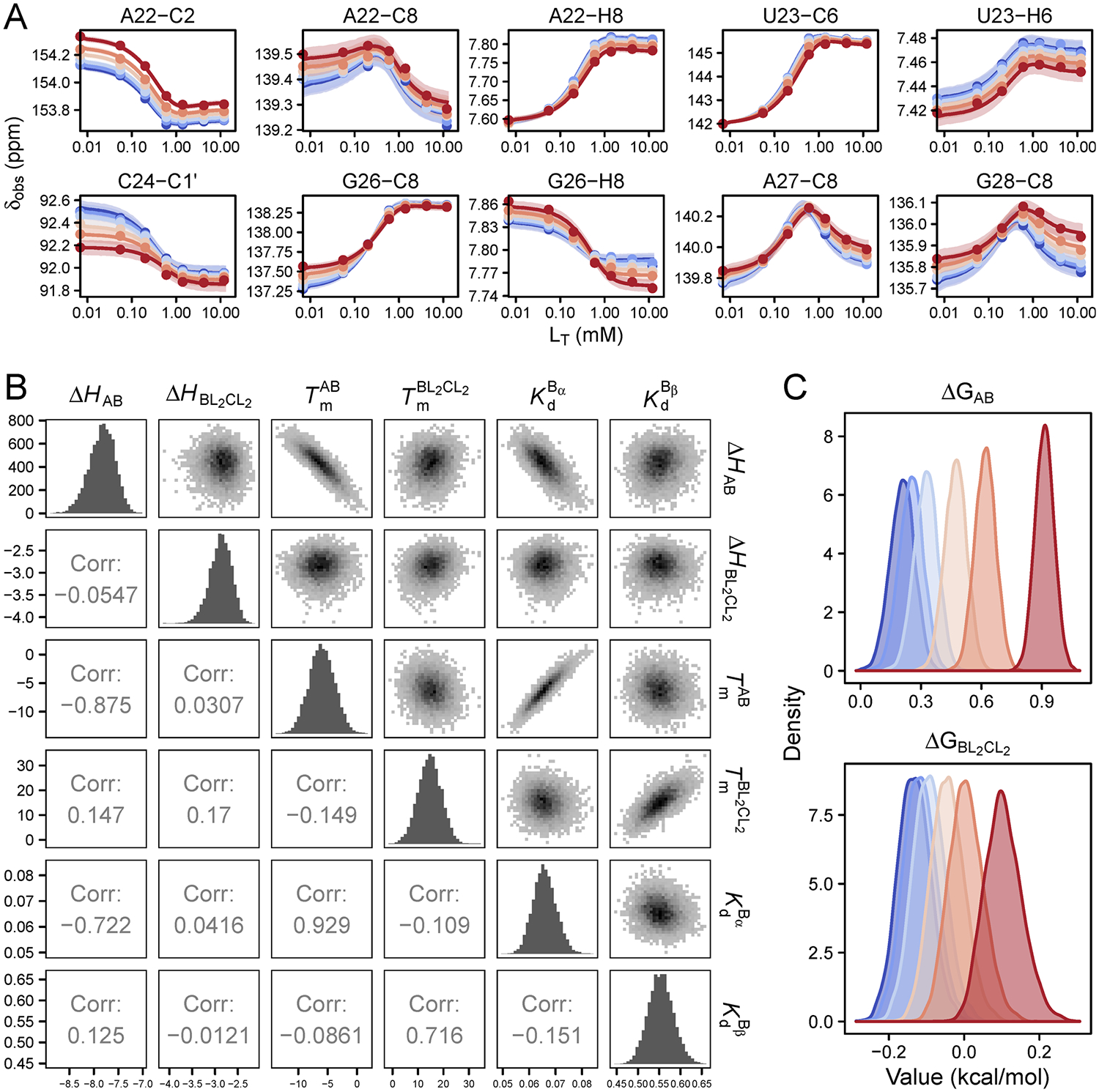
To answer the question of whether the A ⇌ B equilibrium reports on coaxial stacking, we compared the fitted chemical shifts for the B state with measured chemical shifts for TAR in Mg²⁺ and additionally for ΔbulgeTAR in ionic strength conditions comparable to those in the CSP titration (Figure 5A). It is known that Mg²⁺ shifts the equilibrium to >90% stacked,^84,85,87 so we would expect the chemical shifts of the fitted B state to match those seen in Mg²⁺ if temperature perturbs the same stacking equilibrium. However, a complication with this previously used assumption is that Mg²⁺ also makes direct contacts with resonances near the bulge, so it may be difficult to separate the chemical shift contributions due to stacking/unstacking versus those due to localization of Mg²⁺. The bulgeless variant, however, provides a cleaner fingerprint of the chemical shift for the stacked state since it is presumably never unstacked. The disadvantage of this comparison is that it provides no information on the stacked chemical shift for bulge residues U23, C24, and U25 because they are absent in the variant. As shown in Figure 5A, many of the B-state shifts agree in direction and approximate magnitude with shifts for ΔbulgeTAR, supporting the hypothesis that the A ⇌ B equilibrium is the unstacked ⇌ stacked equilibrium. Interestingly but perhaps not surprisingly, the chemical shifts of resonances thought to be in close contact with Mg²⁺ ions (C24-C1′, C24-C6, U25-C1′, U25-C6, G26-C8, A27-C8) are in opposite direction to the chemical shifts for TAR·Mg²⁺. Relative to the A state, C39-C6 shifts upfield and C39-C1′ shifts downfield in B, consistent with the base becoming more stacked and the sugar pucker becoming more A-form, as would be expected for residues directly above the bulge in the coaxially stacked B state.

Figure 5.

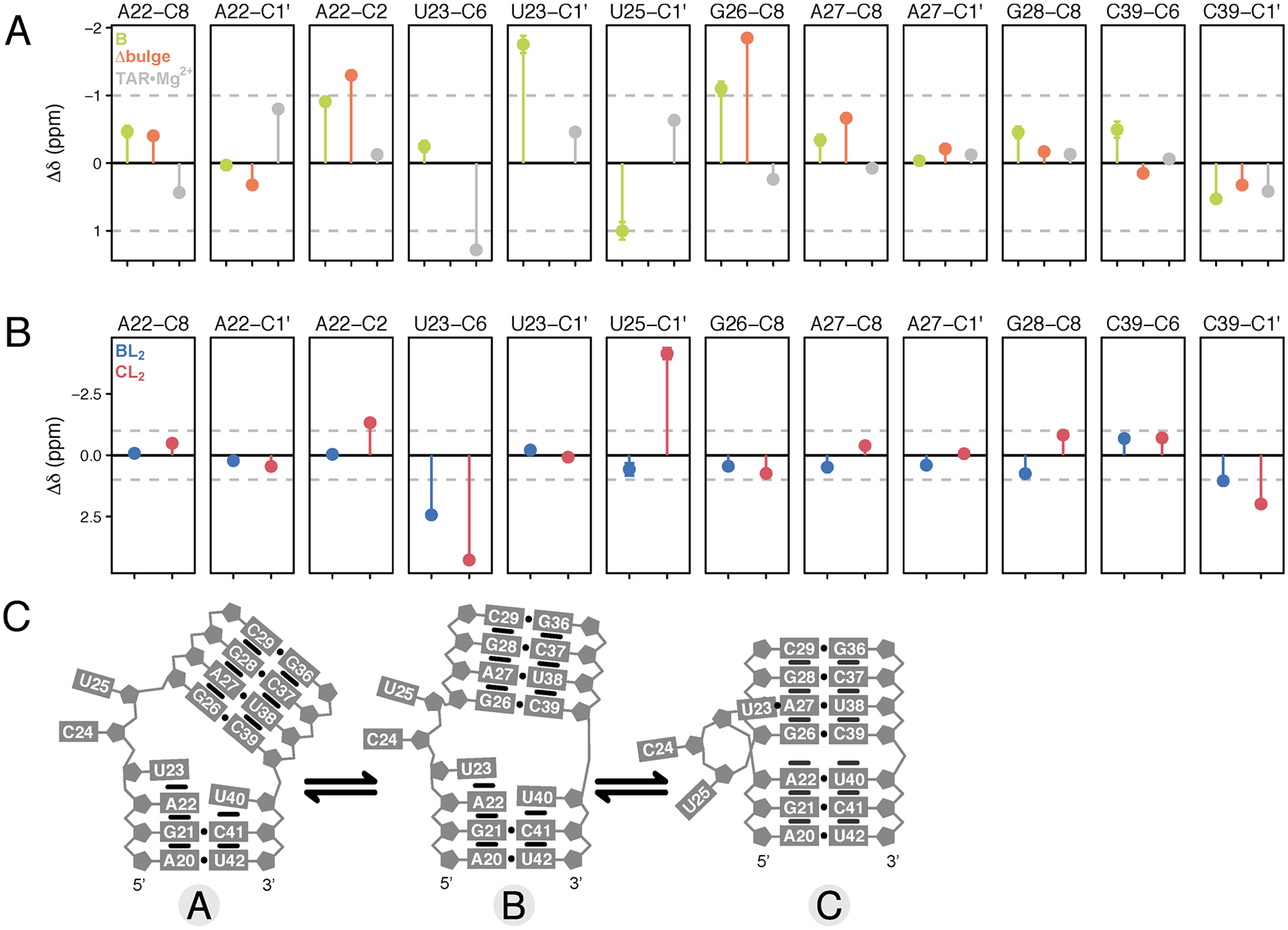
Bayesian-fitted chemical shifts of intermediate species. (A) Comparison of chemical shift changes Δδ obtained for species B by Bayesian global fitting (green) with chemical shifts measured for ΔbulgeTAR in 25 mM NaCl (orange) and TAR in 25 mM NaCl plus 3 mM free MgCl₂ (buffer exchanged) (gray) for representative resonances. (B) Comparison of Δδ between species BL₂ (blue) and CL₂ (red) by Bayesian global fitting. The reference state is the unliganded A state and all Δδ are shown relative to the Bayesian-fitted δ_A values. Error bars represent the standard deviation determined by Bayesian fitting. (C) Schematic of the structural changes between the three different conformational states.

Comparing the chemical shifts for CL₂ relative to BL₂ gives insight into the structural differences between the stacked/base triple state and the stacked state. Relative to the BL₂ state, resonances in CL₂ that lose stacking interactions on the basis of downfield chemical shifts include U23-C6, G26-C8, G28-C8/H8, C29-H6, while resonances that become more stacked in the base-tripled state include A22-H2, C24-C6, U25-C6, and C29-C6 (Figure 5B). U25-C1′ has a large upfield chemical shift in CL₂ indicating a shift from C3′-endo to C2′-endo (deviating away from RNA A-form geometry). C39-C6 remains unchanged between the BL₂ and CL₂ states, while its sugar (C39-C1′) becomes slightly more helical (downfield chemical shift), although it is already adopting a more A-form geometry in BL₂ relative to unliganded A and B. The upfield shift in H2 of A22 is consistent with increased stacking and stabilization of the A22-U40 base pair in CL₂.

Testing the Model and Characterizing a Binding Intermediate by NMR RD.

Our model predicts detectable populations of the intermediate species BL_α at intermediate ligand concentrations, so we can exploit this information to gain insight into the kinetics of ligand binding using NMR R_1ρ RD. Additionally, R_1ρ experiments allow independent determination of chemical shifts for comparison to those obtained from analysis of the CSPs. Measurements were first carried out in the absence of ARG. Consistent with previous results,⁶³ no dispersion is observed in the free TAR construct at temperatures between 5 and 25 °C. Because our model predicts populations of roughly 30% and 15% for the unliganded B state at 5 and 25 °C, respectively (Figure 6A), and sufficiently large ¹³C chemical shifts (Δω = ω_B − ω_A > 1 ppm) for several resonances (Figure 5A), the absence of dispersion indicates that the A ⇌ B transition must be fast (τ = 1/k_ex ≤ 1 μs) and outside the detection limits. Our CSP experiments revealed that binding occurs on the fast exchange NMR time scale (k_ex (s⁻¹) > Δω (rad s⁻¹))⁶⁸ at all tested temperatures and therefore we can predict that for average chemical shift differences of 2 ppm in ¹³C on a 700 MHz spectrometer, the exchange process (k_ex = k₁ + k₋₁) will be faster than ~2000 s⁻¹. A simplified description of ligand binding between one ligand and one receptor with a single site yields k₁ = k_on[L] and k₋₁ = k_off. Thus, the total observed exchange (k_ex = k_on[L] + k_off) scales with increasing free ligand concentration [L]. Experiments were carried out at low ligand concentration to avoid reaching exchange rates too fast to be detected by RD.

Figure 6.

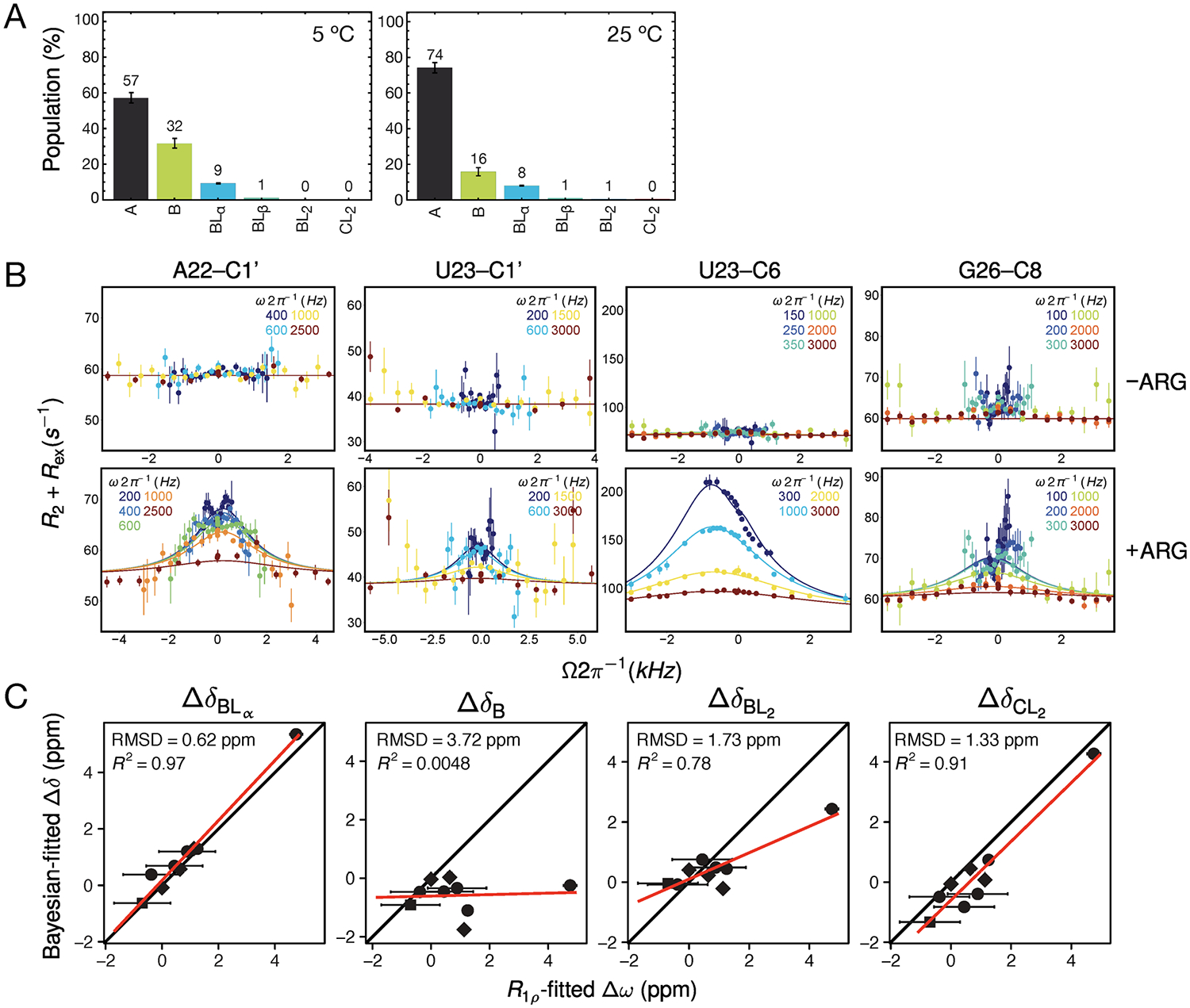
Testing the model by NMR RD. (A) The predicted distribution of RNA states at the conditions under which the RD measurements were run (0.2 mM ARG, 1.5 mM RNA) at 5 and 25 °C. (B) Off-resonance RD data for the resonances with detectable chemical exchange at 5 °C. Lines represent global fit to BM equations. (C) Comparison of fitted chemical shifts obtained by RD with the chemical shifts obtained by Bayesian fitting to CSP data. Closest agreement is with chemical shifts for state BL_α, consistent with RD reporting on the binding to the α site in the B conformation.

To test the predictions from the CSP analysis, we carried out off-resonance R_1ρ measurements at 1.5 mM RNA and 0.2 mM ARG which should give rise to chemical exchange corresponding to 9% of the BL_α species and 1% of the BL_β species for resonances with large enough ¹³C chemical shifts relative to the ground state (Δω = ω_BLα − ω_GS> 1 ppm and Δω = ω_BLβ − ω_GS > 1 ppm). We note here that because the observed ground state (GS) is in fast exchange between A ⇌ B as described above, the GS chemical shift is not simply ω_A; rather it is given by ω_GS = ω_A(1 − p_B) + ω_Bp_B, where p_B is calculated from the Bayesian-fitted parameters according to

$$p_{\text{B}}=\frac{K_{\text{AB}}}{1+K_{\text{AB}}}=\frac{{\text{e}}^{\Delta H_{\text{AB}}/R\left(1/T_{\text{m}}^{\text{AB}}-1/T\right)}}{1+{\text{e}}^{\Delta H_{\text{AB}}/R\left(1/T_{\text{m}}^{\text{AB}}-1/T\right)}}$$ (5)

At 5 °C, we observe apparent two-state dispersion profiles at four resonances located near the primary bulge binding site (Figure 6B). No ligand-dependent dispersion was observed at 25 °C, likely because the reaction is too fast for detection by R_1ρ, as reaction rates scale with increasing temperature. Global fitting of the data at 5 °C revealed the apparent on-rate constant to be 3 × 10⁶ M⁻¹ s⁻¹ and the apparent off-rate for binding to be about 8000 s⁻¹. The $k_{\text{on}}^{\text{app}}$ and $k_{\text{off}}^{\text{app }}$ values were calculated using eq 19 and eq 20 as described in Methods. The population obtained by RD (5.4 ± 0.5%) is in fairly close agreement with the predicted 9%, although it is important to note that there is no RD evidence for the 1% predicted exchange with a third species. This could be explained by the chemical shifts for the BL_β state being too small (<1 ppm) for RD detection, as we do not have accurate estimations for the BL_β chemical shifts from the global fitting of the CSP data (Supporting Information). Nevertheless, the chemical shifts obtained by RD are in strikingly good agreement with the chemical shifts for species BL_α determined from the CSP fitting (Figure 6C), further supporting that the RD is reporting on the binding to the α site on the B conformation.

Furthermore, the apparent dissociation constant $K_{\text{d}}^{\text{app }}$ can be calculated from the RD fitted parameters using $K_{\text{d}}^{\text{app}}=k_{\text{off}}^{\text{app }}/k_{\text{on}}^{\text{app }}$ for a two-state system. In this case, because of the fast A ⇌ B pre-equilibrium, the $K_{\text{d}}^{\text{app}}$ is scaled by the population of the B state, so $K_{\text{d}}^{\text{app}}=K_{\text{AB}}{k}_{\text{off}}^{\text{app}}/\left(\left(1+K_{\text{AB}}\right)k_{\text{on}}^{\text{app}}\right)$, where K_AB (at 5 °C) is obtained from the CSP results. The result for $K_{\text{d}}^{\text{app}}$ obtained by RD (0.22 ± 0.05 mM) is in fairly good agreement with the 0.1 mM measured for $K_{\text{d}}^{{\text{B}}_{\alpha }}$ by the global CSP analysis. Measure ments were also carried out at high ligand concentration (10 mM ARG) to probe the kinetics for base triple formation (BL₂ ⇌ CL₂) since our model predicts a sufficiently high population of ${\text{CL}}_2\left(p_{{\text{CL}}_2}\approx 40-60\%\right)$, but no dispersion was observed at all tested temperatures (Figure S11). It is possible that base triple formation is too fast and outside the detection limits of RD, and more experiments in the future will be needed to explore this hypothesis further.

CONCLUSION

Returning to the complete 12-state model introduced earlier, we can begin to make predictions about this more detailed mechanism based on the analysis of our simpler six-state model. As a consequence of thermodynamic linkage and free energy conservation, not all equilibrium constants in the full 12-state model are independent, i.e.,

$$K_{\text{a}}^{{\text{C}}_{\alpha }}{K}_{\text{a}}^{{\text{C}}_{\beta }}=\frac{K_{\text{a}}^{{\text{B}}_{\alpha }}{K}_{\text{a}}^{{\text{B}}_{\beta }}{\beta }_{{\text{BL}}_2{\text{CL}}_2}}{K_{\text{BC}}}$$ (6)

Our fitted minimal model provides estimates at 25 °C for $K_{\text{a}}^{{\text{B}}_{\alpha }}$, $K_{\text{a}}^{{\text{B}}_{\beta }}$, and ${\beta }_{{\text{BL}}_2{\text{CL}}_2}$ (1.4 × 10⁴ M⁻¹, 1.8 × 10³ M⁻¹ and 0.84, respectively). Our inability to detect any form of C except CL₂ gives an upper limit for K_BC of 0.05, and substitution of these estimates into eq 6 gives an estimate for the product of the two C-state binding constants of at least 3 × 10¹² M⁻². This estimate implies that the upper limit for both binding dissociation constants $K_{\text{d}}^{{\text{C}}_{\alpha }}$ and $K_{\text{d}}^{{\text{C}}_{\beta }}$ must be 0.6 μM, assuming that they are equal. If they are not the same, then one of the C sites must be even tighter (Figure S12).

Because this affinity is much tighter than that of the B conformation ($K_{\text{d}}^{{\text{C}}_{\alpha }}{K}_{\text{d}}^{{\text{C}}_{\beta }}<K_{\text{d}}^{{\text{B}}_{\alpha }}{K}_{\text{d}}^{{\text{B}}_{\beta }}$ by 4 orders of magnitude), the probability of finding a doubly bound C species (CL₂) is much higher than finding a singly bound C species (CL_α or CL_β). In other words, it is much more thermodynamically favorable for ARG to bind to both sites on conformation C than it is to have only one ligand bound. The same is not true for the B conformation, whose ligand binding is sufficiently weak that the most energetically favorable species is the singly bound B state (BL_α) at intermediate ARG concentrations (see population of BL_α in Figure 4).

Considering our results in the context of energetic penalties previously measured for RNA systems, the enthalpy we measure for A ⇌ B (ΔH_AB ≈ −7.9 kcal mol⁻¹) is in fairly close agreement with the enthalpy reported for formation of a single terminal AU-AU base stack (ΔH_stack = −6.82 ± 0.72 kcal mol⁻¹).⁸⁸ Since formation of the TAR B state involves coaxial stacking between the upper and lower helix, our data is consistent with the conclusion that the ΔH measured for A ⇌ B reflects the enthalpy of stacking. This occurs between junctional bases at the bulge that are likely to be as flexible as the terminal bases studied previously.⁸⁸ Additionally, consistent with our results of ~ 7 kcal mol⁻¹ penalty for forming the C conformation in the absence of ligand (Figure 7), no evidence has ever been observed suggesting the base triple is detectable in the free RNA, and an RDC-informed MD ensemble also never observed the base triple for either HIV-1 or HIV-2 TAR.^89,90

Figure 7.

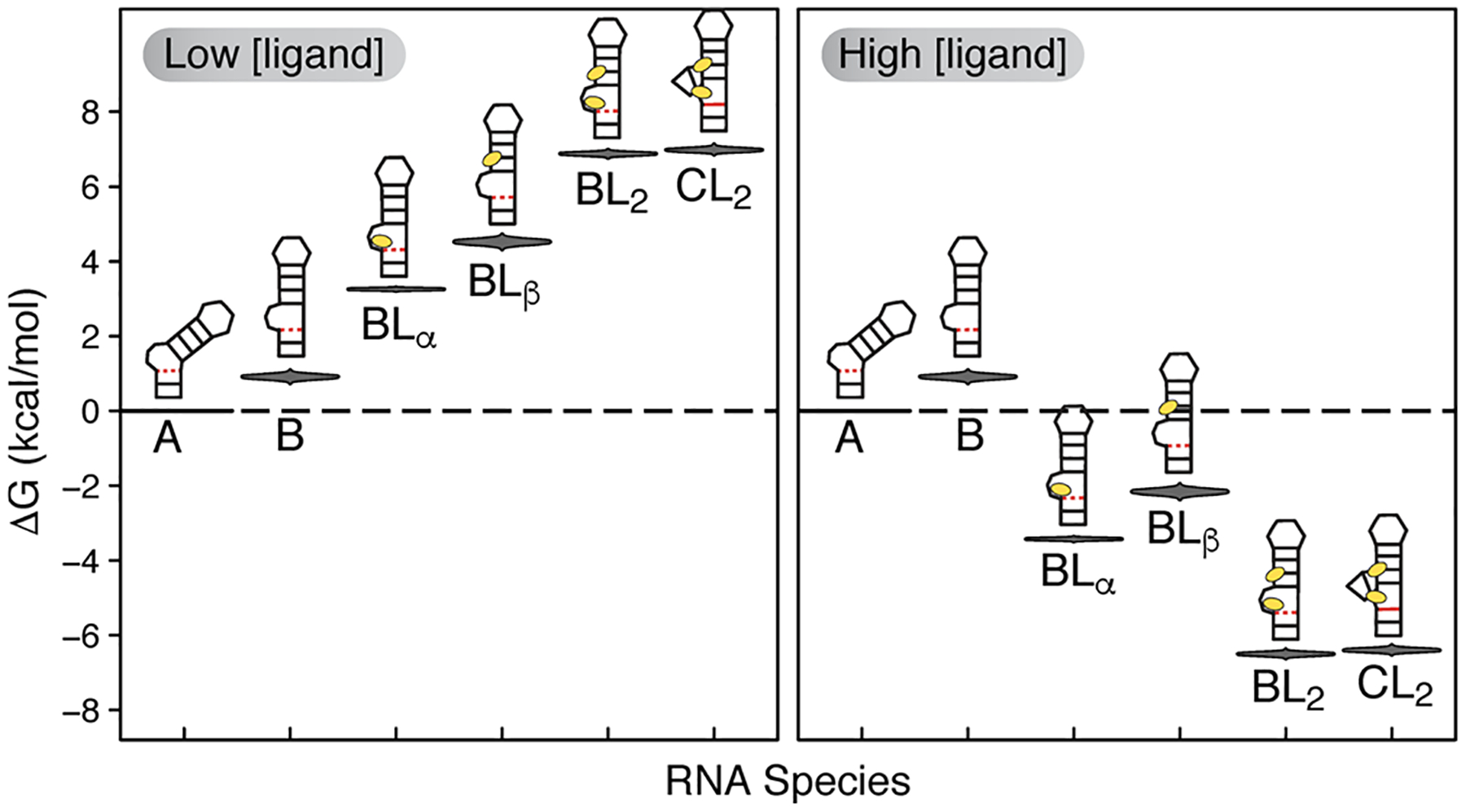
Energetic distributions of the six detectable RNA species showing the effect of ligand concentration on the RNA energy landscape. The violin plots show the ΔG posterior distributions calculated at 25 °C relative to the A state.

Our results suggest that preferentially tight affinity to high-energy RNA states may be a ubiquitous mechanism by which ligands confer selectivity to otherwise promiscuous RNA binding partners. The binding energy from binding to a tight-affinity ligand can explain how the RNA overcomes the high conformational energetic penalty for formation of the binding-competent conformation. Lack of selectivity is among the main challenges in RNA drug design and in understanding processes regulated by RNA. Our study provides direct evidence that undetectable RNA species are the key thermodynamic players in a paradigmatic example of RNA adaptive recognition and underscores the importance of developing methods to study low-populated states that have gone undetected. While the presented approach only provides thermodynamic information regarding binding intermediates, its integration with other methods such as NMR RD and stopped-flow techniques may afford a deeper and more complete kinetic characterization of the binding reaction. In addition, extending NMR measurements to other sugar resonances should be straightforward, and this will afford the opportunity to structurally characterize the intermediates to higher resolution.^91,92 We predict that the mechanism uncovered here is not limited to TAR and anticipate that further experiments using the approach outlined here can help to quantitatively characterize multi-state RNA–ligand interactions.

METHODS

Sample Preparation.

HIV-1 TAR RNA capped with a UUCG loop (sequence GGCAGAUCUGAGCUUCGGCUCUCUGCC) and bulgeless mutant (sequence GGCAGAGAGCUUCGGCUCUCUGCC) were prepared by in vitro transcription using DNA templates containing the T7 promoter (Integrated DNA Technologies). DNA templates were annealed in 3 mM MgCl₂ by heating to 95 °C for 5 min and cooling on ice for 30 min. The transcription reaction was carried out at 37 °C for 12 h with T7 RNA polymerase (New England BioLabs) using ¹³C/¹⁵N-labeled nucleotide triphosphates (Cambridge Isotope Laboratories, Inc.). RNA was purified using 20% (w/v) denaturing polyacrylamide gel electrophoresis (PAGE) with 8 M urea and 1× TBE buffer followed by excision from the gel by electroelution in 1× TAE buffer and further purified by ethanol precipitation overnight at −20 °C. Purified RNA was dissolved in water to 50 μM RNA and annealed by heating to 95 °C for 5 min and cooling on ice for 1 h. Prior to NMR experiments, ¹³C/¹⁵N-labeled RNA samples were exchanged into phosphate NMR buffer (15 mM NaH₂PO₄/Na₂HPO₄, 25 mM NaCl, 0.1 mM EDTA, 10% (v/v) D₂O at pH 6.4) to the desired RNA concentrations (0.2 mM for HSQC titrations and 1.5 mM for RD). Concentrations were measured using a nanodrop UV spectrometer by the absorbance reading of heat-denatured RNA at 260 mm.

NMR CSP Experiments.

NMR experiments were carried out on Bruker Avance III 600 MHz and Bruker Avance III 700 MHz spectrometers equipped with a 5 mm triple resonance cryogenic probe. Assignments for TAR in the unbound and ARG-bound states were previously published.⁹³ CSPs as a function of temperature and ligand concentration were monitored for aromatic and aliphatic resonances using 2D [¹³C,¹H] heteronuclear single quantum coherence (HSQC) spectra and for imino resonances using 1D [¹H] SOFAST spectra. For each titration point, successive additions of ARG (l-argininamide dihydrochloride, Sigma) from a concentrated stock dissolved in phosphate NMR buffer were added directly to an NMR sample tube containing 450 μL of 0.2 mM ¹³C/¹⁵N-labeled RNA, and the tube was inverted at least six times to ensure homogeneous mixing. The increase in total sample volume due to ARG addition remained less than 5% of the starting volume and therefore had a negligible effect on the RNA concentration. A total of seven titration points per temperature were used for the TAR titration and six for the bulgeless mutant titration. Experiments for both constructs were carried out at six different temperatures (1, 2.5, 5, 10, 15, and 25 °C). The temperature of the NMR probe was calibrated using a methanol sample and spectra was internally referenced relative to a trace amount of 2,2-dimethyl-2-silapentane-5-sulfonate (DSS). Spectra were processed using NMRPipe,⁹⁴ and peak positions were measured using Sparky.⁹⁵

NMR RD Experiments.

¹³C R_1ρ measurements were carried out at 25 and 5 °C on a Bruker Avance III 700 MHz spectrometer using 1.5 mM ¹³C/¹⁵N-labeled RNA. On- and off-resonance measurements were collected at the spin lock powers (Ω) and spin lock offsets (ω₁) listed in Table S1 using a 1D acquisition scheme which uses Hartmann–Hahn cross-polarization transfer to selectively excite a single peak at a time as described previously.^22,63,92 To account for sample heating effects due to high-power spin locks,⁹⁶ the pulse sequence contains a heat-compensation element that applies far off-resonance ¹³C spin locks during the recycle delay after acquisition at the highest field strength for a time $T_{\text{relax }}^{\text{max}}-T_{\text{relax }}$ such that the net amount of radiofrequency (RF) introduced into the sample is constant across all relaxation delay times.^21,64 For preparation of samples, ARG from a concentrated stock dissolved in phosphate NMR buffer was added directly to the NMR sample tube containing 1.5 mM ¹³C/¹⁵N-labeled RNA following the procedure used for titration experiments to achieve the desired ARG concentrations (0.2 and 10 mM). Raw data was processed using NMRPipe to determine peak intensities at each delay time point, which were then fit to a mono-exponential function to estimate the R_1ρ values needed for further analysis via eq 18.

Statistical Thermodynamic Framework.

As described in the Results and Discussion section, qualitative analysis of the CSP data led us to conclude that the minimum complexity system necessary to explain the temperature and ligand dependencies must include three conformational states (A, B, C) each potentially capable of binding two ligands. To further minimize complexity, the two binding sites (α and β) are assumed to be independent; that is, occupancy at one site does not detectably influence the intrinsic affinity at the other site. The partition function Q for such a system can be derived by rewriting the following microscopic association and conformational equilibrium constants:

$$\begin{array}{ll}{K}_{\text{a}}^{{\text{A}}_{\alpha }}=\frac{\left[\text{A}{\text{L}}_{\alpha }\right]}{[\text{A}][\text{L}]}=\frac{\left[\text{A}{\text{L}}_2\right]}{\left[\text{A}{\text{L}}_{\beta }\right][\text{L}]}\hfill & K_{\text{a}}^{{\text{A}}_{\beta }}=\frac{\left[\text{A}{\text{L}}_{\beta }\right]}{[\text{A}][\text{L}]}=\frac{\left[\text{A}{\text{L}}_2\right]}{\left[\text{A}{\text{L}}_{\alpha }\right][\text{L}]}\hfill \\ K_{\text{a}}^{{\text{B}}_{\alpha }}=\frac{\left[\text{B}{\text{L}}_{\alpha }\right]}{[\text{B}][\text{L}]}=\frac{\left[\text{B}{\text{L}}_2\right]}{\left[\text{B}{\text{L}}_{\beta }\right][\text{L}]}\hfill & K_{\text{a}}^{{\text{B}}_{\beta }}=\frac{\left[\text{B}{\text{L}}_{\beta }\right]}{[\text{B}][\text{L}]}=\frac{\left[\text{B}{\text{L}}_2\right]}{\left[\text{B}{\text{L}}_{\alpha }\right][\text{L}]}\hfill \\ K_{\text{a}}^{{\text{C}}_{\alpha }}=\frac{\left[\text{C}{\text{L}}_{\alpha }\right]}{[\text{C}][\text{L}]}=\frac{\left[\text{C}{\text{L}}_2\right]}{\left[\text{C}{\text{L}}_{\beta }\right][\text{L}]}\hfill & K_{\text{a}}^{{\text{C}}_{\beta }}=\frac{\left[\text{C}{\text{L}}_{\beta }\right]}{[\text{C}][\text{L}]}=\frac{\left[\text{C}{\text{L}}_2\right]}{\left[\text{C}{\text{L}}_{\alpha }\right][\text{L}]}\hfill \\ K_{\text{AB}}=\frac{[\text{B}]}{[\text{A}]}\hfill & K_{\text{B}\text{C}}=\frac{[\text{C}]}{[\text{B}]}\hfill \end{array}$$ (7)

in terms of RNA concentrations, summing together all 12 RNA forms,

$$\left[{\text{R}}_{\text{T}}\right]=[\text{A}]+\left[{\text{AL}}_{\alpha }\right]+\left[{\text{AL}}_{\beta }\right]+\left[{\text{AL}}_2\right]+[\text{C}]+\left[{\text{CL}}_{\alpha }\right]+\left[{\text{CL}}_{\beta }\right]+\left[{\text{CL}}_2\right]+[\text{B}]+\left[{\text{BL}}_{\alpha }\right]+\left[{\text{BL}}_{\beta }\right]+\left[{\text{BL}}_2\right]$$ (8)

and dividing by a chosen reference state (most simply set as the free A state) to obtain

$$Q=1+K_{\text{a}}^{{\text{A}}_{\alpha }}[\text{L}]+K_{\text{a}}^{{\text{A}}_{\beta }}[\text{L}]+K_{\text{a}}^{{\text{A}}_{\alpha }}{K}_{\text{a}}^{{\text{A}}_{\beta }}{[\text{L}]}^2+K_{\text{AB}}+K_{\text{AB}}{K}_{\text{a}}^{{\text{B}}_{\alpha }}[\text{L}]+K_{\text{AB}}{K}_{\text{a}}^{{\text{B}}_{\beta }}[\text{L}]+K_{\text{AB}}{K}_{\text{a}}^{{\text{B}}_{\alpha }}{K}_{\text{a}}^{{\text{B}}_{\beta }}{[\text{L}]}^2+K_{\text{AB}}{K}_{\text{BC}}+K_{\text{AB}}{K}_{\text{BC}}{K}_{\text{a}}^{{\text{C}}_{\alpha }}[\text{L}]+K_{\text{AB}}{K}_{\text{BC}}{K}_{\text{a}}^{{\text{C}}_{\beta }}[\text{L}]+K_{\text{AB}}{K}_{\text{BC}}{K}_{\text{a}}^{{\text{C}}_{\alpha }}{K}_{\text{a}}^{{\text{C}}_{\beta }}{[\text{L}]}^2$$ (9)

Although this 12-state model (Figure 1D) was used for simulations, extensive testing revealed that the information content of the data is insufficient to fit more parameters than those necessary to quantify the interconversion of the six states highlighted in Figure 1D. The summation of all RNA forms in the six-state model is

$$\left[{\text{R}}_{\text{T}}\right]=[\text{A}]+[\text{B}]+\left[{\text{BL}}_{\alpha }\right]+\left[{\text{BL}}_{\beta }\right]+\left[{\text{BL}}_2\right]+\left[{\text{CL}}_2\right]$$ (10)

which gives the partition function

$$Q=1+K_{\text{AB}}+K_{\text{AB}}{K}_{\text{a}}^{{\text{B}}_{\alpha }}[\text{L}]+K_{\text{AB}}{K}_{\text{a}}^{{\text{B}}_{\beta }}[\text{L}]+K_{\text{AB}}{K}_{\text{a}}^{{\text{B}}_{\alpha }}{\text{K}}_{\text{a}}^{{\text{B}}_{\beta }}{[\text{L}]}^2+K_{\text{AB}}{K}_{{\text{BL}}_2{\text{CL}}_2}{K}_{\text{a}}^{{\text{B}}_{\alpha }}{K}_{\text{a}}^{{\text{B}}_{\beta }}{[\text{L}]}^2$$ (11)

The population term for each species is found by taking its statistical weight and dividing by the partition function. Note that the equilibrium constants K_BC and $K_{{\text{BL}}_2{\text{CL}}_2}$ are related through

$$K_{\text{BC}}=\frac{K_{\text{a}}^{{\text{B}}_{\alpha }}{K}_{\text{a}}^{{\text{B}}_{\beta }}{K}_{{\text{BL}}_2{\text{CL}}_2}}{K_{\text{a}}^{{\text{C}}_{\alpha }}{K}_{\text{a}}^{{\text{C}}_{\beta }}}$$ (12)

The free ligand concentration term [L] is a solution to a cubic equation of the form

$$a{[\text{L}]}^3+b{[\text{L}]}^2+c[\text{L}]+d=0$$ (13)

where the coefficients a, b, c, and d are defined as

$$\begin{gathered} a=-K_{\text{a}}^{{\text{A}}_{\alpha }}{K}_{\text{a}}^{{\text{A}}_{\beta }}-K_{\text{AB}}\left(K_{\text{a}}^{{\text{B}}_{\alpha }}{K}_{\text{a}}^{{\text{B}}_{\beta }}+K_{\text{a}}^{{\text{C}}_{\alpha }}{K}_{\text{a}}^{{\text{C}}_{\beta }}{K}_{\text{BC}}\right) \\ b=K_{\text{a}}^{{\text{A}}_{\alpha }}\left(K_{\text{a}}^{{\text{A}}_{\beta }}\left(\left[{\text{L}}_{\text{T}}\right]-2\left[{\text{R}}_{\text{T}}\right]\right)-1\right)-K_{\text{a}}^{{\text{A}}_{\beta }}+K_{\text{AB}}(K_{\text{a}}^{{\text{B}}_{\alpha }}\left(K_{\text{a}}^{{\text{B}}_{\beta }}\left(\left[{\text{L}}_{\text{T}}\right]-2\left[{\text{R}}_{\text{T}}\right]\right)-1\right)-K_{\text{a}}^{{\text{B}}_{\beta }}+K_{\text{a}}^{{\text{C}}_{\alpha }}{K}_{\text{BC}}\left(K_{\text{a}}^{{\text{C}}_{\beta }}\left(\left[{\text{L}}_{\text{T}}\right]-2\left[{\text{R}}_{\text{T}}\right]\right)-1\right)-K_{\text{a}}^{{\text{C}}_{\beta }}{K}_{\text{BC}}) \\ c=K_{\text{a}}^{{\text{A}}_{\alpha }}\left(\left[{\text{L}}_{\text{T}}\right]-\left[{\text{R}}_{\text{T}}\right]\right)+K_{\text{a}}^{{\text{A}}_{\beta }}\left[{\text{L}}_{\text{T}}\right]-K_{\text{a}}^{{\text{A}}_{\beta }}\left[{\text{R}}_{\text{T}}\right]+K_{\text{AB}}(K_{\text{a}}^{{\text{B}}_{\alpha }}\left[{\text{L}}_{\text{T}}\right]-K_{\text{a}}^{{\text{B}}_{\alpha }}\left[{\text{R}}_{\text{T}}\right]+K_{\text{a}}^{{\text{B}}_{\beta }}\left[{\text{L}}_{\text{T}}\right]-K_{\text{a}}^{{\text{B}}_{\beta }}\left[{\text{R}}_{\text{T}}\right]+K_{\text{BC}}\left(K_{\text{a}}^{{\text{C}}_{\alpha }}\left[{\text{L}}_{\text{T}}\right]-K_{\text{a}}^{{\text{C}}_{\alpha }}\left[{\text{R}}_{\text{T}}\right]+K_{\text{a}}^{{\text{C}}_{\beta }}\left[{\text{L}}_{\text{T}}\right]-K_{\text{a}}^{{\text{C}}_{\beta }}\left[{\text{R}}_{\text{T}}\right]-1\right))-1 \\ d=\left[{\text{L}}_{\text{T}}\right]\left(K_{\text{AB}}+K_{\text{AB}}{K}_{\text{BC}}+1\right) \end{gathered}$$ (14)

for the 12-state model and

$$\begin{gathered} a=-K_{\text{a}}^{{\text{B}}_{\alpha }}{K}_{\text{a}}^{{\text{B}}_{\beta }}{K}_{\text{AB}}-\left(1+K_{{\text{BL}}_2{\text{CL}}_2}\right) \\ b=K_{\text{AB}}\left(-K_{\text{a}}^{{\text{B}}_{\beta }}+K_{\text{a}}^{{\text{B}}_{\alpha }}\left(-1+K_{\text{a}}^{{\text{B}}_{\beta }}\left(1+K_{{\text{BL}}_2{\text{CL}}_2}\right)\left(\left[{\text{L}}_{\text{T}}\right]-2\left[{\text{R}}_{\text{T}}\right]\right)\right)\right) \\ c=-1+K_{\text{AB}}\left(-1+\left(K_{\text{a}}^{{\text{B}}_{\alpha }}+K_{\text{a}}^{{\text{B}}_{\beta }}\right)\left(\left[{\text{L}}_{\text{T}}\right]-\left[{\text{R}}_{\text{T}}\right]\right)\right) \\ d=\left[{\text{L}}_{\text{T}}\right]\left(1+K_{\text{AB}}\right) \end{gathered}$$ (15)

for the six-state model. The general, model-independent algebraic solution^97,98 for free ligand concentration [L] is given by

$$[\text{L}]=\{\begin{array}{l}\begin{array}{ll}{c}_0+s_c\text{ sinh}\left(\frac{1}{3}{\text{sinh}}^{-1}(\chi )\right)\hfill & \text{ if }p>0\hfill \\ c_0+s_c\text{ cosh}\left(\frac{1}{3}{\text{cosh}}^{-1}(\chi )\right)\hfill & \text{ if }p<0\wedge \chi \ge 1\hfill \\ c_0-s_c\text{ cosh}\left(\frac{1}{3}{\text{cosh}}^{-1}(-\chi )\right)\hfill & \text{ if }p<0\wedge \chi \le 1\hfill \end{array}\hfill \\ \text{max}\left(\begin{array}{l}{c}_0+s_c\text{ cos}\left(\frac{1}{3}{\text{cos}}^{-1}(\chi )\right)\hfill \\ c_0-s_c\text{ sin}\left(\frac{\pi }{6}-\frac{1}{3}{\text{cos}}^{-1}(\chi )\right)\hfill \\ c_0-s_c\text{ sin}\left(\frac{\pi }{6}+\frac{1}{3}{\text{cos}}^{-1}(\chi )\right)\hfill \end{array}\right)\text{ if }p<0\wedge |\chi |<1\hfill \end{array}$$ (16)

where

$$\begin{gathered} c_0=-\frac{b}{3a} \\ p=\frac{c}{a}-\frac{b^2}{3a^2} \\ {s}_c=\frac{2\sqrt{\left|p\right|}}{\sqrt{3}} \\ \chi =\frac{3\sqrt{3}\left(-\frac{2b^3}{27a^3}+\frac{bc}{3a^2}-\frac{d}{a}\right)}{2|p{|}^{3/2}} \end{gathered}$$ (17)

and a, b, c, and d are model-dependent terms as shown in eqs 14 and 15.

Bayesian Analysis of CSP Data.

Bayesian inference was used to fit the CSP data. This fitting method applies Bayes’s rule, p(θ|y) = p(y|θ) p(θ)/p(y), which states that for a specified mathematical model of the data y based on parameters θ, the probability distributions of parameter values given the data, p(θ|y) (called the posterior distributions), are the product of the likelihood of the data given the parameters, p(y|θ) (a measure of goodness-of-fit), and user-specified prior probability distributions, p(θ), normalized by the probability of the data, p(y). In simpler terms, the posterior ∝ prior × likelihood. The calculation of the p(y) term needed for calculating the likelihood involves a multivariate integral that does not have an analytical solution except in the simplest of cases such as single-parameter models,^80,99 so Bayesian techniques have been developed that use Markov-chain Monte Carlo (MCMC) rejection sampling to approximate the likelihood function and respective posterior distributions. Here, we use the software package Stan, which employs a version of MCMC sampling known as the no-U-turn (NUTS) Hamiltonian Monte Carlo (HMC) sampler which is efficient and robust for models with complicated posteriors.^100,101 The analysis was carried out using in-house scripts written in the Stan statistical programming language run under the R programming interface (RStan).

The Stan interface allows the user to define a likelihood function given by the model equations and conditioned on the data. For each unknown parameter, a prior distribution is specified with a corresponding mean μ and standard deviation σ. Briefly, at each sampling iteration, the algorithm takes a number of discretized leapfrog parameter steps to simulate the trajectory of a particle along a potential energy field. The parameter values at a point in this field correspond to the log of the posterior density we wish to maximize. Essentially, the leapfrog steps are a discrete way to approximate the continuous function represented by the model’s equations. Highly curved posteriors (i.e., complicated nonlinear functions) are especially difficult to sample from, partly because an infinite number of steps would be required to accurately traverse the trajectory. In the work here, the polynomial terms in the free ligand expression (eq 16) give rise to a highly nonlinear dependence of the model on free ligand concentration. This variable is model-dependent and based on the combination of binding and equilibrium constants (as shown in eqs 7–17), which makes the selection of informative priors very important.

The Bayesian fitting algorithm aims to maximize the log-likelihood for master eq 1 and in doing so treats each model parameter as a random variable with its own probability distribution for parameter vector θ. The general parameter vector for all models tested can be expressed as $\theta =\left(K_{\text{d}}^{{\text{X}}_{\text{s}}},\Delta H_{{\text{Y}}_1\rightleftharpoons {\text{Y}}_2},T_{\text{m}}^{{\text{Y}}_1\rightleftharpoons {\text{Y}}_2},{\delta }_{r,i},{ϵ}_j\right)$, where superscript X refers to a conformational state (A, B, or C), subscript s refers to a binding site (α or β), Y₁ ⇌ Y₂ refers to a given conformational equilibrium (such as A ⇌ B), δ_r,i represents the vector of basis chemical shifts for species i per resonance r, and ϵ_j is the measurement error for chemical shift categories discussed in the following paragraph.

For all thermodynamic parameters, Gaussian prior distributions were used with standard deviations up to 50% of their means. Gaussian priors were also used for chemical shift parameters with standard deviations of 1.0 ppm for carbon and 0.25 ppm for proton. For a given resonance, the prior distributions used for all species’ chemical shifts were identical to avoid biasing the posteriors. In addition to the thermodynamic and chemical shift parameters, the Bayesian fitting algorithm treats the measurement error as a random unknown variable and therefore fits for the an error term referred to as ϵ_j. As mentioned in the Results and Discussion, Bayesian techniques are suitable for handling data whose variance may have several sources. Because our fitting approach uses the raw measured chemical shift values of all included resonance types and avoids scaling or normalizing the data, the scale of the measurement error varies depending on the nucleus type (¹³C vs ¹H) and even atom position (C6/C8 vs C1′). For this reason, we fit for six error terms corresponding to the following categories of chemical shifts: C6/C8, C1′, C2, non-exchangeable protons, exchangeable protons, and resonances with significant overlap at any point in the titration. An Inverse-Gamma distribution with shape and scale parameters (α, β) was chosen for the error priors, where the shape and scale terms are related to the mean μ and standard deviation σ by α = (μ² + 2σ²)/σ² and β = μ(μ² + σ²)/σ².

MCMC sampling was carried out using four independent chains and 4000 iterations per chain, the first half of which comprise the initial warm-up phase where the algorithm optimizes for sampling efficiency and are therefore discarded before posterior analysis. The post-warm-up samples used for approximating the parameter posterior distributions consist of 2000 draws per chain, i.e., 8000 total draws. Convergence was assessed (Figure S6) via the potential scale reduction factor $\widehat{R}$ ¹⁰² for each parameter where $\widehat{R}$ values approaching 1 but ≤1.05 are ideal and $\widehat{R}\ge 1.2$ indicate lack of convergence.¹⁰³ Prior to data fitting, the model was extensively tested for robustness by subjecting simulated data to the fitting procedure and evaluating the effects of various prior distributions on posterior distributions. As a benchmark, data with noise were simulated for 20 resonances under experimental conditions identical to that of the collected data (seven ligand concentrations and six temperatures), and the simulated data was subjected to global fitting using the equations described above. The fitting was able to converge within 2000 iterations only when the correct parameter distributions were found. Setting priors very far from simulated values prevented convergence, indicating that the algorithm did not falsely converge to incorrect parameter values.

We note that using a Bayesian approach was not only advantageous to a standard nonlinear least-squares approach but it was integral for quantitative analysis of a model that matched the level of complexity present in the raw data described here. For data sets simulated to the six-state model both with and without noise, least-squares global fitting failed to recover the simulated parameters, whereas Bayesian global fitting correctly recovered the parameter distributions for converged fits.

Analysis of RD Data.

Data for two-state exchange were fit to

$$R_{1\rho }=R_1{\text{cos}}^2\theta +R_2{\text{sin}}^2\theta +\frac{{\text{sin}}^2\theta p_{\text{GS}}{p}_{\text{ES}}\Delta {\omega }_{\text{ES}}^2{k}_{\text{ex}}}{\left\{\frac{{\omega }_{\text{GS}}^2{\omega }_{\text{ES}}^2}{{\omega }_{\text{eff}}^2}+k_{\text{ex}}^2-{\text{sin}}^2\theta p_{\text{GS}}{p}_{\text{ES}}\Delta {\omega }_{\text{ES}}^2\left(1+\frac{2k_{\text{ex}}^2\left(p_{\text{GS}}{\omega }_{\text{GS}}^2+p_{\text{ES}}{\omega }_{\text{ES}}^2\right)}{{\omega }_{\text{eff}}^2{k}_{\text{ex}}^2}\right)\right\}}$$ (18)

where R₁ and R₂ are the longitudinal and transverse relaxation rates, Δω is the change in chemical shift between the low population excited state (ES) and highly populated ground state (GS), expressed as Δω = ω_ES − ω_GS. The strength of the carrier spinlock power is ω_SL and the tilt angle in the rotating frame is defined as θ = tan⁻¹(ω_SL/ΔΩ) given by ΔΩ = Ω − ω_rf, the difference between average spin lock offset (Ω_ave) and reference frequency (ω_rf). Average spin lock offset is calculated by Ω_ave = p_GSω_GS + p_ESω_ES where p_GS and p_ES are populations of the GS and ES, respectively. The spinlock strengths at the GS and ES are given by ${\omega }_{\text{GS}}^2={\left({\omega }_{\text{GS}}+{\omega }_{\text{rf}}\right)}^2+{\omega }_{\text{SL}}^2$ and ${\omega }_{\text{ES}}^2={\left({\omega }_{\text{ES}}+{\omega }_{\text{rf}}\right)}^2+{\omega }_{\text{SL}}^2$, respectively, and their resonance offsets from the spinlock carrier correspond to ω_GS and ω_ES. Δω_ES = ω_ES − Ω_GS defines the difference in offset for transitions from ES to GS. The effective spinlock field strength is calculated as ${\omega }_{\text{eff}}^2=\Delta {\Omega }^2+{\omega }_{\text{SL}}^2$. Finally, the exchange rate constant is expressed as k_ex = k₁ + k₋₁ = p_ESk_ex + p_GSk_ex and can be converted to the form $k_{\text{ex}}=k_{\text{on}}^{\text{app}}[\text{L}]+k_{\text{off}}^{\text{app}}$ to determine the on and off rate constants. Free ligand concentration [L] is calculated from the relation [L] = [L_T] − p_bound[R_T], where the total ligand and RNA concentrations are known a priori, and the population of bound RNA (p_bound) is obtained from the RD fitted value for p_ES in the case of low ligand concentration where the excited species is the bound state, or p_GS in the case of excess ligand where the excited state is the free RNA. This allows us to rewrite $k_{\text{on}}^{\text{app}}$ and $k_{\text{off}}^{\text{app}}$ as

$$k_{\text{on}}^{\text{app}}=\frac{p_{\text{bound}}{k}_{\text{ex}}}{\left[{\text{L}}_{\text{T}}\right]-p_{\text{bound}}\left[{\text{R}}_{\text{T}}\right]}$$ (19)

and

$$k_{\text{off}}^{\text{app}}=k_{\text{ex}}\left(1-p_{\text{bound}}\right)$$ (20)

Note that the rate constants are considered apparent rather than intrinsic due to the presence of RD-invisible $\text{A}\underset{\left[k_{\text{BA}}\right]}{\overset{\left[k_{\text{AB}}\right]}{\rightleftharpoons }}\text{B}$ pre-equilibrium. The apparent association and dissociation rate constants $k_{\text{on}}^{\text{app}}=k_{\text{on}}{k}_{\text{AB}}/\left(k_{\text{off}}+k_{\text{AB}}\right)$ and $k_{\text{of}}^{\text{app}}=k_{\text{off}}{k}_{\text{BA}}/\left(k_{\text{off}}+k_{\text{AB}}\right)$¹⁰⁴ are measured, whereas the intrinsic k_on and k_off cannot be determined here because k_AB and k_BA are unknown.