Where do bike lanes work best? A Bayesian spatial model of bicycle lanes and bicycle crashes

Abstract

US municipalities are increasingly introducing bicycle lanes to promote bicycle use, increase roadway safety and improve public health. The aim of this study was to identify specific locations where bicycle lanes, if created, could most effectively reduce crash rates. Previous research has found that bike lanes reduce crash incidence, but a lack of comprehensive bicycle traffic flow data has limited researchers’ ability to assess relationships at high spatial resolution. We used Bayesian conditional autoregressive logit models to relate the odds that a bicycle injury crash occurred on a street segment in Philadelphia, PA (n = 37,673) between 2011 and 2014 to characteristics of the street and adjacent intersections. Statistical models included interaction terms to address the problem of unknown bicycle traffic flows, and found bicycle lanes were associated with reduced crash odds of 48% in streets segments adjacent to 4-exit intersections, of 40% in streets with one- or two-way stop intersections, and of 43% in high traffic volume streets. Presence of bicycle lanes was not associated with change in crash odds at intersections with less or more than 4 exits, at 4-way stop and signalized intersections, on one-way streets and streets with trolley tracks, and on streets with low-moderate traffic volume. The effectiveness of bicycle lanes appears to depend most on the configuration of the adjacent intersections and on the volume of vehicular traffic. Our approach can be used to predict specific street segments on which the greatest absolute reduction in bicycle crash odds could occur by installing new bicycle lanes.

1. Introduction

Over the last several years, bicycle traffic has increased dramatically in the US, and calls to improve bicycle safety and bicycle infrastructure have followed. Bicycle lanes are the main form of infrastructure implemented in the US to support bicycle use. First introduced in the US in the late 1960 s, there are now an estimated 9931 miles of unprotected bicycle lanes (a designated space on the right side of motor vehicle traffic, demarcated by painted striping) and an additional 674 miles of protected bicycle lanes (with a physical barrier in-between cyclists and motor-vehicle traffic) in 69 of the most populous US cities (Alliance for Biking and Walking, 2016). A growing body of evidence suggests that installing bicycle lanes is an effective and low-cost approach to reduce the crash risk for cyclists in a given city (Gu et al., 2016; Harris et al., 2013; Pedroso et al., 2016; Poulos et al., 2015; Pucher and Buehler, 2016; Reynolds et al., 2009; Teschke et al., 2012; Thomas and DeRobertis, 2013).

It is increasingly recognized that perceived roadway safety is one of the strongest predictors of bicycle traffic volume (Pucher et al., 2010; Thomas and DeRobertis, 2013; Winters et al., 2011), and that cycling has demonstrated benefits for cyclists, for example due to improved cardiovascular and metabolic function (Götschi et al., 2016; Oja et al., 2011), and for the general public, for example due to reduced air pollution. Municipalities are therefore increasingly introducing bicycle lanes into their roadway infrastructure as part of a suite of approaches to promote bicycle use, increase roadway safety, and improve public health. In areas without bicycle lanes, cyclists most commonly ride on roadways that are thought or known to be safest (Pucher et al., 2010; Thomas and DeRobertis, 2013; Winters et al., 2011). That scenario is suboptimal, given that riders face an elevated risk of crashing in areas without designated bicycle lanes. A research approach that empirically identifies the specific locations where bicycle lanes could most substantially reduce crash incidence could provide a timely and valuable resource to officials that seek to introduce or improve bicycle infrastructure.

Previous studies used two main approaches to identify geographic correlates of bicycle crashes. First, individual studies in Belgium (de Geus et al., 2012), Australia (Beck et al., 2016; Poulos et al., 2015), Portland, Oregon (Hoffman et al., 2010), and Canada (Harris et al., 2013; Teschke et al., 2014; Teschke et al., 2012) provided important information on the types of cyclists at greatest risk of crashing, the locations where these individuals are most likely to ride, and the locations they are most likely to crash. Because bicycle crashes are statistically rare events, this approach requires access to registries describing a census of crashes within a study region, very large survey samples, or carefully selected samples for case-control or case-crossover analyses, for example recruited from emergency rooms or hospitals (de Geus et al., 2012; Hoffman et al., 2010; Poulos et al., 2015). Such studies found that relative risks for injury crashes are higher at intersections (especially at intersections of more than two streets) (Harris et al., 2013), in traffic circles (Harris et al., 2013), on downhill grades (Harris et al., 2013; Teschke et al., 2012), in streets with parked cars (Teschke et al., 2014; Teschke et al., 2012), streets with train or streetcar tracks (Teschke et al., 2014; Teschke et al., 2012), for women, and less-experienced riders and commuters (Poulos et al., 2015). However, these studies have not identified locations for infrastructure interventions that could reduce risk of bicycle crashes.

Second, spatial analyses have related crash incidence to aggregate measures of social and environmental characteristics within geographic areas to identify general factors (sometimes relating to the built environment) that explain bicycle crash frequencies. Such studies have been conducted at numerous spatial scales, such as cities, Traffic Analysis Zones, Census areas, street intersections, or street networks (Chen, 2015; Loidl et al., 2016; Siddiqui et al., 2012; Strauss et al., 2013; Vandenbulcke et al., 2014; Wang and Nihan, 2004). This approach has the advantage that the requisite data are often publicly available, and that researchers can estimate crash risks for all locations within a study region. Spatial analyses have identified that bicycle crashes (or specifically severe-injury crashes in the case of Kim et al. (2007)) occur more commonly at intersections (or in areas with more intersections) (Loidl et al., 2016; Reynolds et al., 2009; Siddiqui et al., 2012; Strauss et al., 2013; Vandenbulcke et al., 2014; Wang and Nihan, 2004), and are associated with vehicular traffic conditions (Anderson, 2009; Kim et al., 2007; Wang and Nihan, 2004) including speed limits (Siddiqui et al., 2012) and count of automobile trips (Chen, 2015), bicycle traffic volume (Loidl et al., 2016; Strauss et al., 2013), physical street characteristics such as presence of trolley tracks, parked cars, street signs and driveways (Chen, 2015; Vandenbulcke et al., 2014), presence of bicycle facilities (Chen, 2015; Thomas and DeRobertis, 2013; Vandenbulcke et al., 2014), population density (Siddiqui et al., 2012) factors such as weather and lighting (Kim et al., 2007) and characteristics of the cyclist (Kim et al., 2007). However, with some notable exceptions (Strauss et al., 2013; Vandenbulcke et al., 2014), these studies primarily identified environmental correlates of bicycle crashes, rather than specific locations of highest relative risk.

A problem common to both individual analyses and spatial analyses of vehicular crashes is that the volume of traffic through a given location is often unknown. This problem is non-trivial for studies of bicycle crashes, because analyses that do not adequately account for traffic flow may erroneously find positive relationships between crash risks and roadway features that attract greater volumes of cyclists (e.g. bicycle lanes). The optimal solution would be to collect detailed diurnal inventories of bicycle traffic flow through each location (Vanparijs et al., 2015), however such information becomes increasingly expensive and impractical to collect as sample sizes increase. Bicycle traffic volumes are therefore often estimated from household travel surveys (Blaizot et al., 2013), census data (Siddiqui et al., 2012), or travel diaries (de Geus et al., 2012; Poulos et al., 2015), but these rates cannot be interpreted at a fine scale. Importantly, this denominator problem is inversely related to the problem of aggregation bias. That is, as the size of the spatial units decreases, the likelihood that results are affected by underlying crash risks due to local variation in the traffic flows increases (i.e. the denominator problem), but the certainty that crashes co-occur in physical space with roadway features to which they are statistically related decreases (i.e. aggregation bias).

The aim of the study was to identify the locations where bicycle lanes most effectively reduce crash rates. To overcome the challenges inherent in this field, we applied a Bayesian conditional autoregressive (CAR) spatial analytic approach (Besag, 1974) to cross sectional data describing bicycle crash locations and roadway characteristics for 2011–2014 in Philadelphia, Pennsylvania. Philadelphia has invested in substantial new infrastructure, has an increasing volume of cyclists, a variety of road types, and a relatively high number of collision across a variety of types of road conditions. Our novel approach minimized aggregation bias by using street segments as the units of analysis, and addressed the denominator problem using interaction terms between bicycle lanes and other roadway features.

2. Methods

2.1. Study setting and spatial structure

The oldest parts of Philadelphia, those areas in the central or downtown area, were developed in the 1600s prior to automobiles, while more modern areas grew around trolley lines in the first half of the 20th century. Most parts of the city are characterized by a grid of narrow collector streets (typically 35 feet wide with parking on both sides and a single one way traffic lane with a speed limit 25 miles per hour) with intermittent arterial streets (typically 65 feet wide, speed limit 30 miles per hour). The terrain throughout the city is generally flat with mild slopes and few hills. Traffic flow is mediated by stop signs and signalized intersections, rather than roundabouts and traffic circles. Since the first bicycle lanes opened in 1995, the city has added over 250 miles of bike lanes and regularly features on lists of the best biking cities in the US. At the time of this study, according to the American Community Survey 5-Year study for 2011–2015, 2.1 percent of commute trips to work were by bicycle, relative to 59 percent of commute trips by personal vehicle. Also at this time, there were 285 miles of bicycle lanes in various forms within the city of Philadelphia. These consisted primarily of conventional bicycle lanes, a 3-foot lane for bicycles indicated by white painted striping and bicycle symbol (227 miles), in some cases painted green (17 miles), and “sharrows” reminding vehicle drivers to share the lane with cyclists 34 miles) (see Fig. 1). As shown in Fig. 1, bicycle lane striping does not run continuously through intersections.

Fig. 1.

Bicycle lane typologies in Philadelphia, including (A) traditional bicycle lane, (B) traditional bicycle lane with green shading, and (C) a sharrow lane. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

Street segments in the city of Philadelphia served as the unit of analysis. We built the unit of analysis dataset from a street centerline spatial dataset (Philadelphia Streets Department, 2016) that represented the location and length of every street in the city of Philadelphia present in 2011. We removed all freeways from the dataset used for analysis because bicycles are prohibited from using these sections of the roadway network. This procedure yielded a sample of 37,673 street segments. All spatial processes were conducted in ArcGIS v10.3.1 (ESRI, Inc.; Redlands, CA).

2.2. Dependent variable

The dependent variable was a dichotomous measure for the presence or absence of a bicycle injury crash for a given street segment during the study period. We defined bicycle injury crashes as all road crashes between 2011 and 2014 in which a cyclist was injured requiring medical attention (excluding 9 reported bicycle crashes in which no cyclists were injured). These event-level data were provided to us geocoded to the internal centroid of each street centerline, and therefore we were not able to model intersection crashes separately. We omitted the 25 (1.2%) crashes that were geocoded to locations more than 45 feet from the street segments identified as the units of analysis. We judged based on visual inspection of the crash and street segments maps that a buffer of 45 feet would maximize the number of crashes spatially joined to intersections, while minimizing misclassification of crashes that were geocoded to locations away from the roadway network or to streets that were omitted from the analysis (e.g. freeways).

2.3. Street characteristics

Multiple street characteristics served as independent variables. The City of Philadelphia’s street centerline file identified whether the segments formed major arterials, minor arterials, collector streets, local streets, or whether they were designated pedestrian or off-street paths from which motor vehicles were prohibited. There were very few pedestrian or off-street paths, so we combined these street segments with local streets for analysis. We also assigned dichotomous variables to each street segment based on the presence or absence of trolley tracks, bicycle lanes and one-way traffic flows. We obtained vehicular traffic volume indicators from the State of Pennsylvania Department of Transportation’s estimates of annual average daily traffic volume (AADT) for major roadways. AADT estimates were available for 8680 (31.4%) of the street segments. We calculated tertiles of the estimated volume in these segments and produced dummy variables indicating low volume, moderate volume, or high volume. We also produced an indicator for the 28,993 segments where no AADT estimate was available. Finally, we calculated the length of each segment in meters.

2.4. Intersection characteristics

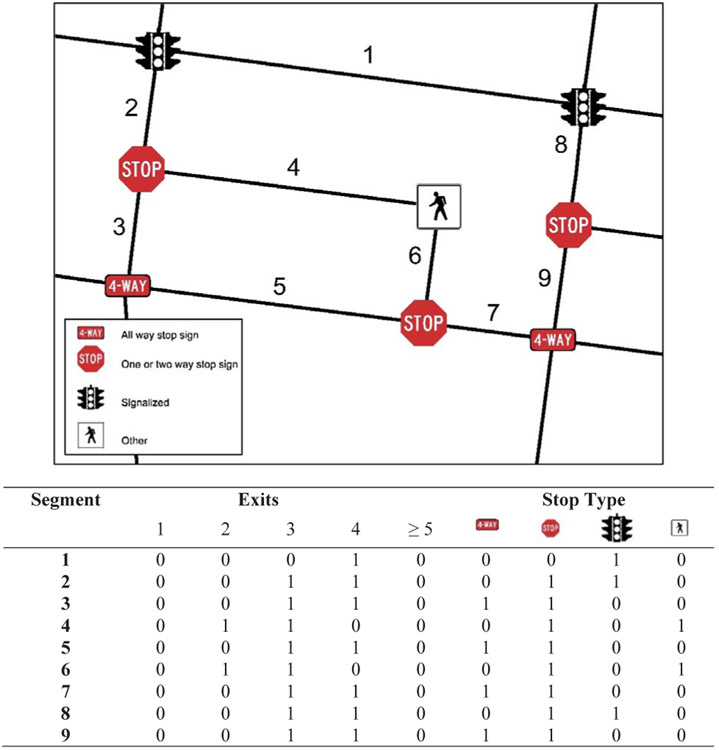
We used two groups of independent measures to characterize the intersections that formed the endpoints of the street segments: the number of exits and the stop type. We identified the number of exits (though in the case of one-way streets, exits may actually only be entrances) by taking a count of the street centerlines that overlapped each intersection. We identified the stop type as all-way stop signs, one- or two- way stops signs, signalized, or other (including pedestrian crossings, unmarked crossings, and stops of unknown type).

Fig. 2 demonstrates our method of assigning intersection characteristics to the street segments. We constructed dummy variables for each of the exit count and stop type categories, then assigned street segments a value of 1 where either of the intersections to which they were connected had that attribute, and 0 otherwise. For example, segment 1 is connected to two signalized intersections that both have 4 exits. Segment 6 is connected to a pedestrian intersection with 2 exits, and an intersection with a one or two-way stop sign and 3 exits.

Fig. 2.

Intersection exit counts and stop types.

2.5. Bicycle traffic index

We addressed the denominator problem analytically using the method described in the Statistical Analysis section below, however we also wished to assess whether bicycle lanes would be most effective where bicycle traffic volume was greatest. To address this specific question, we constructed a bicycle traffic index using a novel approach (see Kondo et al., (submitted)). Briefly, our four-step approach assumed bicycle traffic would occur between origins and destinations along a roadway network. First, the origins were the Census blocks within the Philadelphia city limits (n = 18,872). We estimated the number of cyclists in these polygons by combining the Census demographic characteristics (sex, age, racial/ethnic composition) with the results of a logistic regression model from the 2009 National Household Travel Survey for the odds of cycling to work. Second, the destinations were all tax parcels in the city categorized as industrial, commercial or civic use. Third, the roadway network was the street centerline file excluding freeways, with a network hierarchy reflecting the street segments used most frequently by cyclists. We calculated the hierarchy using quintiles of street segments based on maps of bicycle journeys for a convenience sample of cyclists in the city (CyclePhilly, 2016). Finally, from each of the 18,872 origins in the city we modeled journeys to 100 destinations randomly selected in the city, weighted by a 2010 estimate of daytime population (Delaware Valley Regional Planning Commission, 2016). We further weighted each journey by the estimated number of cyclists at the origin as well as a distance decay function for bicycle journeys calibrated using the 2009 National Household Travel Survey data. The sum of the weighted journeys that passed through each line segment was used as an estimate of bicycle traffic volume. We standardized these values to make model estimates more easily interpretable.

2.6. Statistical analysis

We estimated the odds of a bicycle crash occurring on a street segment using Bayesian conditional autoregressive logit models. To identify the characteristics of segments on which crashes were most likely to occur, we first specified a model including all independent variables (Model 1). Although the bicycle traffic index partially accounts for local variation in bicycle traffic volume, this approach does not fully address the denominator problem, and thus the parameter estimates for the independent variables will reflect both the volume of bicycle traffic through each segment and the risks associated with these variables. To address the denominator problem we added interaction terms between bicycle lanes and the independent variables (Model 2). Because the independent variables account for the underlying risk of bicycle crashes (i.e. due to the presence or absence of bicycle lanes and the other street segment and intersection attributes), a negative parameter estimate for an interaction term can be interpreted as the relative benefit of placing a bicycle lane on a street segment with a given characteristic. Finally, we estimated the absolute benefit for installing new bicycle lanes. We calculated the model, predicted odds of observing a crash for all street segments from Model 1, then for street segments that did not already have bicycle lanes, we multiplied these odds by the parameter estimates for the interaction terms from Model 2 and the binary indicators for the relevant attribute.

Spatial autocorrelation is a potential problem for our analyses. If crash risks are more alike on nearby street segments than on distant street segments, the assumptions of unit independence common to standard regression analyses will be violated and the likelihood of Type I error will increase. To address this problem, we partitioned the model residuals into a conditional autoregressive (CAR) random effect and a non-spatial noise term (Lord et al., 2005; Waller and Gotway, 2004). We fit the model to the data in WinBUGS v14 using a Bayesian procedure with non-informed priors, discarding the first 150,000 iterations of a Markov Chain Monte Carlo, before sampling 50,000 iterations to provide model estimates. We interpreted the exponent of the median estimated value as the odds ratio, and the exponents of the 2.5th and 97.5th percentile values as a 95% credible interval (CI; which is analogous to a 95% confidence interval in conventional regression analyses).

3. Results

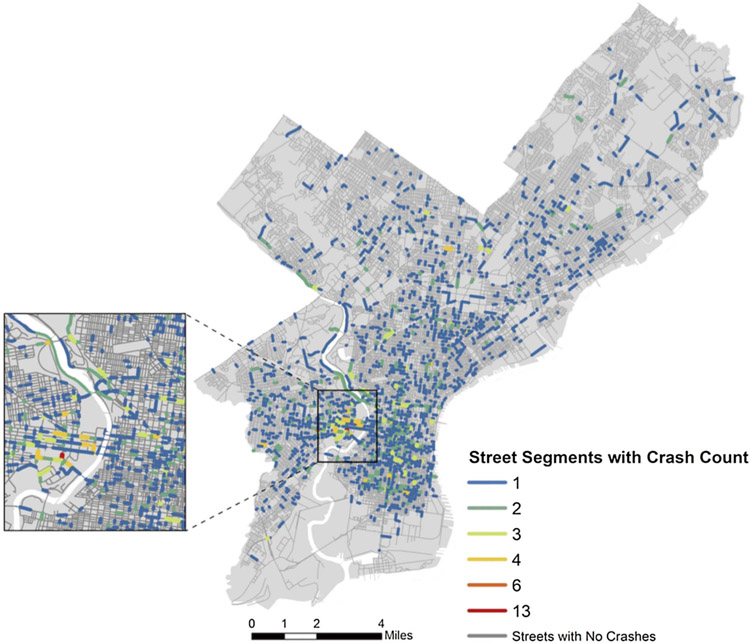
A total of 2052 bicycle injury crashes observed during 2011 to 2014 occurred on 1744 (4.6%) of the 37,673 street segments in Philadelphia. The median number of crashes on segments where crashes occurred was 1 (range 1–16), and only 220 (0.6%) segments had ≥ 2 crashes. The median street segment length was 84.9 ms. Crashes were geographically concentrated in the center city area (Fig. 3).

Fig. 3.

Observed injury crashes on Philadelphia street segments, 2011–2014.

There were 3851 (10.2%) segments with a bike lane. Approximately two-thirds of the segments were connected to at least one intersection with 3 exits (66.8%) or 4 exits (66.8%), and around two-thirds were connected to at least one intersection with a one or two-way stop sign (65.9%). Because street segments can have up to two intersections or stop types, these proportions will not necessarily sum to 100%. Other characteristics are presented in Table 1.

Table 1.

Characteristics of Philadelphia street segments, stratified by bicycle injury crashes 2011–2014.

	Injury crash (n = 1774)		No injury crash (n = 35,929)
	n	%	n	%
Intersections – number of exits
2	73	4.2	2191	6.1
3	819	47.0	21,955	61.1
4	1363	78.2	23,810	66.3
≥5	396	22.7	5565	15.5
Intersections – stop type
All way stop signs	480	27.5	11,886	33.1
One or two way stop signs	878	50.3	23,935	66.6
Signalized	1053	60.4	9233	25.7
Other (incl. pedestrian crossing)	456	26.1	13,142	36.6
Street – class code
2 (Major arterial)	366	21.0	2387	6.6
3 (Minor arterial)	511	29.3	4855	13.5
4 (Collector)	638	36.6	14,183	39.5
5 (Local)	229	13.1	14,482	40.3
Street – vehicular traffic
No estimate available	850	48.7	28,143	78.3
Low volume	235	13.5	2666	7.4
Moderate volume	317	18.2	2573	7.2
High volume	342	19.6	2547	7.1
Street – characteristics
Length (meters) [mean, SD]	[1.159	1.053]	[1.073	0.886]
One way	890	51.0	16,149	44.9
Bicycle traffic index [mean, SD]	[0.608	1.746]	[−0.029	0.939]
Trolley	208	11.9	1829	5.1
Any bicycle lane	442	25.3	3409	9.5

Cross tabulations between the independent variables identified that street class code was correlated strongly with street vehicular traffic, or AADT. Systematically removing class code and AADT from the models produced inconsistent results for these variables, providing further evidence of collinearity. Relationships for class code were not supported in models with AADT omitted, but relationships for AADT were supported in models with class code omitted. Therefore, we present the models with AADT only included.

Results of the Bayesian logit models are presented in Table 2. Findings of Model 1 indicated that bicycle lanes were associated with increased odds of a crash occurring on a given street segment. Specifically, street segments with bicycle lanes had 43.6% increased odds of having a bicycle injury crash between 2011 and 2014 compared to street segments with no bicycle lane. The 95% credible interval (1.239, 1.661) provides a lower bound of 23.9% and an upper bound of 66.1% for this estimate, and importantly, does not include the null value of OR = 1.00. Other characteristics associated with increased odds of bicycle injury crashes were segments with greater length (OR = 1.21; 95% CI: 1.14; 1.28), higher scores on the bicycle traffic index (OR = 1.10; 95% CI: 1.06; 1.14), and those with signalized intersections (OR = 2.28; 95% CI: 1.96; 2.66), 4-exit intersections (OR = 1.32; 95% CI: 1.12, 1.54) and ≥5 exit intersections (OR = 1.21; 95% CI: 1.4, 1.40) compared to those without these intersection configurations.

Table 2.

Bayesian conditional autoregressive logit models, Odds Ratios (OR) with Credible Intervals (CI) for the odds of an injury crash occurring on a street segment from 2011 to 2014, Philadelphia (n = 37,673). A CI that includes the null value of 1.00 provides evidence against an association.

	Model 1			Model 2
	IRR	(95% CI)		IRR	(95% CI)
Intersections – EXITS
2	0.930	0.694	1.231	0.811	0.560	1.148
3	1.003	0.878	1.145	1.022	0.878	1.187
4	1.315	1.124	1.539	1.531	1.279	1.829
≥5	1.206	1.038	1.400	1.147	0.967	1.355
Intersections – stop type
All way stop signs	1.166	0.999	1.365	1.190	1.006	1.408
One or two way stop signs	0.769	0.669	0.884	0.878	0.749	1.033
Signalized	2.281	1.957	2.657	2.326	1.965	2.757
Other (incl. pedestrian crossing)	0.679	0.579	0.795	0.721	0.602	0.864
Street – vehicular traffic
No estimate available [reference]
Low volume	1.447	1.213	1.720	1.509	1.230	1.844
Moderate volume	2.062	1.725	2.466	2.122	1.711	2.618
High volume	2.389	1.996	2.855	2.768	2.239	3.404
Street - Characteristics
Length (100 m)	1.208	1.144	1.278	1.206	1.142	1.275
One way	1.079	0.944	1.232	1.119	0.972	1.291
Bicycle traffic index	1.100	1.061	1.141	1.100	1.053	1.147
Trolley	0.969	0.806	1.158	0.962	0.754	1.213
Bicycle lane	1.436	1.239	1.661	4.568	2.425	8.593
Interactions
Bike lane * 2 exits				1.537	0.822	2.855
Bike lane * 3 exits				0.902	0.654	1.243
Bike lane * 4 exits				0.524	0.363	0.756
Bike lane * ≥5 exits				1.217	0.855	1.728
Bike lane * All way stop signs				1.043	0.651	1.658
Bike lane * One or two way stop signs				0.601	0.439	0.824
Bike lane * Signalized				0.981	0.658	1.496
Bike lane * Other (incl. pedestrian crossing)				0.812	0.563	1.170
Bike lane * Class code 2
Bike lane * Class code 3
Bike lane * One Way				0.769	0.572	1.028
Bike lane * Bicycle traffic index				1.000	0.925	1.081
Bike lane * Trolley				1.008	0.699	1.452
Bike lane * Low volume				0.735	0.477	1.146
Bike lane * Moderate volume				0.788	0.518	1.210
Bike lane * High volume				0.572	0.373	0.885

The key feature of Model 2 is the interaction terms between bicycle lanes and the street segment and intersection characteristics. Because the main independent variables control for the underlying crash risks associated with these attributes (i.e. the denominator problem), the interaction term estimates the benefit or hazard of locating bicycle lanes on street segments with these features. The interactions with bicycle lanes revealed a protective effect for intersections with 4 exits (OR = 0.52; 95% CI: 0.36; 0.76) and those with one- or two-way stop signs (OR = 0.60; 95% CI: 0.44; 0.82), suggesting that, compared to similar segments with no bike lanes, street segments with these characteristics have 47.6% and 39.9% fewer injury crashes when bike lanes are present, respectively. In addition, there was a negative association with high-volume vehicular traffic roadways (OR = 0.57; 95% CI: 0.37; 0.89), suggesting that compared to similar segments with low-volume traffic, high-volume traffic street segments have 42.8% fewer injury crashes when bike lanes are present.

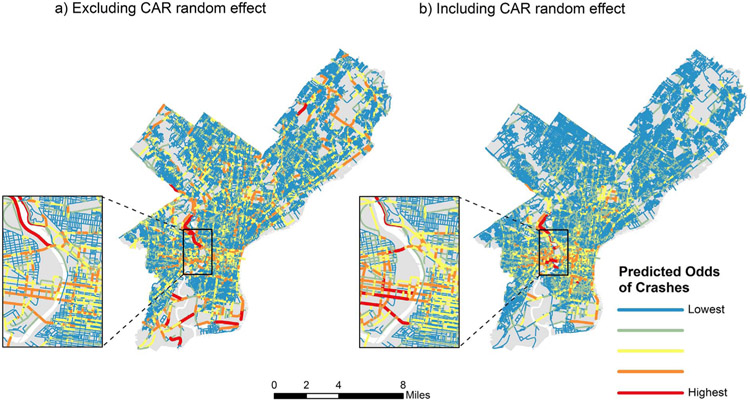
Model diagnostics indicate that the data were highly spatially autocorrelated, and that failing to account for this spatial structure would likely produce biased estimates. The conditional autoregressive (CAR) random effect explained over 99% of error variance in both models, suggesting that the independent variables captured very little of the dependent variable’s spatial structure. Fig. 4a shows the predicted odds of bicycle injury crashes based only on the main variables for Model 1. Major arterials and minor arterials form a clear grid pattern across the city, and much of the spatial clustering evident in the observed crash locations (Fig. 2) is not replicated here. By contrast, Fig. 4b shows that the full model predictions, including the conditional autoregressive random effect, substantially improve the predictive power of the model. Predicted odds are greatly spatially smoothed in Fig. 4b compared to Fig. 4a, and the geographic clustering of crashes in the center city region is clearly evident.

Fig. 4.

(a and b). Predicted odds of an injury crash on Philadelphia street segments, Model 1.

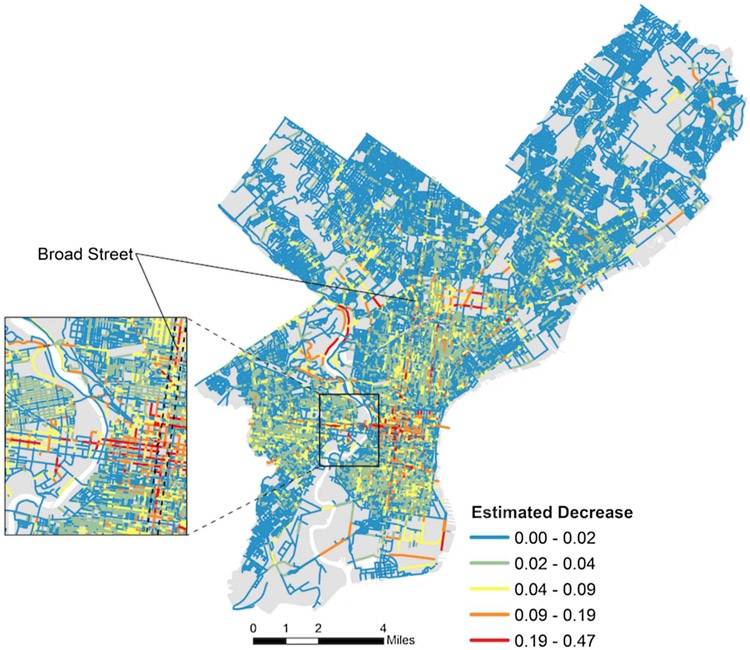
Fig. 5 combines the relative benefit of bicycle lanes identified in the interaction terms for Model 2 with the predicted absolute odds of bicycle crashes from Model 1. Results suggest that the greatest absolute reduction in bicycle crash odds could be obtained from bicycle lanes installed in street segments in and around the center city area. For example, South Broad Street (Fig. 6) is a major arterial in the city’s inner south that we estimate would produce the greatest benefit if bicycle lanes were added. The street is characterized by numerous 4-exit intersections, no bicycle lane, heavy vehicular traffic, and a center city location.

Fig. 5.

Estimated decrease in absolute odds of observing a crash if new bicycle lanes were installed.

Fig. 6.

South broad street at chestnut street intersection.

4. Discussion

Our study indicates that in Philadelphia, bicycle lanes are most effective at reducing risk of bicycle crashes at intersections, particularly 4-exit intersections and one- and two-way stop signs. Namely, compared to similar segments with no bike lanes, street segments with these characteristics have 47.6% and 39.9% fewer injury crashes when bike lanes are present, respectively. In addition, bicycle lanes are most effective on high-volume vehicular traffic roadways; high-volume traffic street segments have 42.8% fewer injury crashes when bike lanes are present, compared to similar segments with low-volume traffic. By using interaction terms in Model 2, we have minimized spurious positive associations between presence of bicycle lanes and increased risk of crashes. These findings concur with recent studies that show bicycle infrastructure’s greatest effect at intersections (Strauss et al., 2013; Thomas and DeRobertis, 2013; Vandenbulcke et al., 2014) and on busy streets (Thomas and DeRobertis, 2013). Given that intersections are “black spots” that generate the vast majority of motor vehicle, pedestrian, and bicycle crashes (Reynolds et al., 2009; Wang and Nihan, 2004), the protective effect of bicycle lanes at intersections is particularly valuable, even though bicycle lanes necessarily cross vehicular traffic at these junctions.

There are several possible mechanisms by which bicycle lanes might reduce relative risk most at 4-exit intersections and at one- and two-way stop signs. Bicycle lanes may increase driver awareness of the presence of bicycles in complex traffic situations. A bicycle lane adjacent to motor vehicle traffic lane allows the bicyclist to stop at intersections or wait for light signals at the entrance of the intersection, which can improve cyclists’ visibility by motorists, and cyclists’ view of the transition of vehicular traffic flow. In addition, presence of a demarcated bicycle lane might signal to motorists approaching yellow lights that they do not have adequate space or safety to speed up in order to “make it” through an intersection before or during a red light.

Our results suggest street segments with greater estimated bicycle traffic (i.e. the bicycle traffic index) have greater crash incidence, but that bicycle lanes do not necessarily reduce crashes in these locations. Previous research may explain this finding. Crashes are more likely to occur where there are more cyclists, however prior studies have identified a non-linear relationship between bicycle traffic volume and injury rates, or a “safety in numbers” effect (Jacobsen, 2003; Nordback et al., 2014). For example, Elvik (2009) calculated that the frequency of bicycle accidents increases by 3–6.5% when bicycle flows increase by 10%. On busy streets, it is possible that the protection afforded by bicycle lanes is negligible compared with the protection afforded by the presence of more cyclists. Alternatively, although our bicycle traffic index is similar to that employed in other studies (Vandenbulcke et al., 2014), it is clear that the measure accounts for very little of the variance in crash risks between street segments; it may also be a poor measure of actual bicycle traffic volume.

Certain limitations should be considered when interpreting our findings. First, our study is cross-sectional and therefore does not account for dynamics associated with installation of new bike lanes, including spatial or temporal patterns and shifts in bicycle traffic that might occur during the study period. Therefore, adding a bicycle lane to South Broad Street would have the predicted effect based on observed data between 2011 and 2014, and would change bicycle traffic in ways that our models do not account for. Second, some important data were unavailable for our study, including dates of bicycle lane installation, street characteristics such as width, number of lanes, and speed limits. Bicycle lanes have been installed on streets wide enough to accommodate them, or in some cases parking has been eliminated to make space. As such bicycle lanes could also indicate a greater distance between street curb and centerline. However, street width information was not available at the time of the study.

Lack of bicycle traffic flows or counts by street segment, whether commuter or recreational, was a major limitation to calculating predictors of rate of bicycle crash. While an increasing supply of data about cycling behaviors exists due to mobile-phone technology, these data sets are incomplete because not all cyclists use mobile phones, and not all cyclists with mobile phones use sports-behavior apps. Monitoring of bicycle traffic, and cycling purpose, is expensive and technically difficult, and therefore these data sets largely do not yet exist. However, our index provides the best available estimation of bicycle traffic volume given available data sources.

Another limitation is that geocoding crashes to street segment centroids could be problematic, especially on longer street segments. Bicycle crashes are underreported (Juhra et al., 2012; Watson et al., 2015); crashes are often reported only in the case of damage to property, hospital admission, or fatality. If missing crashes are spatially structured, our results could be biased in either direction.

Finally, AADT estimates were available for only 8680 out of 37,673 study streets. These 28,993 segments received the indicator for “No estimate available,” and the remaining 8680 segments were separated into tertiles according to the AADT value. The Pennsylvania Department of Transportation deliberately makes its assessments of AADT for streets that it estimates will have the greatest traffic volume, and typically omits residential and local roads. This may or may not be the case, but it is important to note that the consequences of any misclassification would be to shift credible intervals closer to 1.

5. Conclusions

Our findings indicate that indeed bicycle lanes in a city such as Philadelphia are associated with reduced bicycle crash risk. Though our model identified relative risk to be reduced at segments with 4-exit and at one- and two-way stop intersections with bicycle lanes, and on high-volume traffic roadways, our calculations indicate specific locations, shown in Fig. 4, at which bicycle lanes could most reduce absolute risk (Rose, 1992). Our approach, if not our specific findings, would transfer readily to other municipalities. As our cities continue to expand use of bicycle infrastructure, we have the opportunity to study its impact in a rigorous, prospective way. Researchers can collaborate with municipal agencies to plan staged, and even randomized, introduction of bicycle lanes or other infrastructure, and can collect pre- and post-intervention crash data. This would allow us not only to demonstrate the value of bicycle lanes, but also to examine differential impact of bicycle infrastructure design innovation (Hutchinson, 2007).