Abstract
Mayer waves may synchronize overlapping propriobulbar interneuronal microcircuits constituting the respiratory rhythm and pattern generator, sympathetic oscillators, and cardiac vagal preganglionic neurons. Initially described by Sir Sigmund Mayer in the year 1876 in the arterial pressure waveform of anesthetized rabbits, authors have since extensively observed these oscillations in recordings of hemodynamic variables, including arterial pressure waveform, peripheral resistance, and blood flow. Authors would later reveal the presence of these oscillations in sympathetic neural efferent discharge and brainstem and spinal zones corresponding with sympathetic oscillators. Mayer wave central tendency proves highly consistent within, though the specific frequency band varies extensively across, species. Striking resemblance of the Mayer wave central tendency to the species-specific baroreflex resonant frequency has led the majority of investigators to comfortably presume, and generate computational models premised upon, a baroreflex origin of these oscillations. Empirical interrogation of this conjecture has generated variable results and derivative interpretations. Sinoaortic denervation and effector sympathectomy variably reduces or abolishes spectral power contained within the Mayer wave frequency band. Refractorines of Mayer wave generation to barodeafferentation lends credence to the hypothesis these waves are chiefly generated by brainstem propriobulbar and spinal cord propriospinal interneuronal microcircuit oscillators and likely modulated by the baroreflex. The presence of these waves in unitary discharge of medullary lateral tegmental field and rostral ventrolateral medullary neurons (contemporaneously exhibiting fast sympathetic rhythms [2–6 and 10 Hz bands]) in spectral variability in vagotomized pentobarbital-anesthetized and unanesthetized midcollicular (i.e., intercollicular) decerebrate cats supports genesis of Mayer waves by supraspinal sympathetic microcircuit oscillators. Persistence of these waves following high cervical transection in vagotomized unanesthetized midcollicular decerebrate cats would seem to suggest spinal sympathetic microcircuit oscillators generate these waves. The widespread presence of Mayer waves in brainstem sympathetic-related and non-sympathetic-related cells would seem to betray a general tendency of neurons to oscillate at this frequency. We have thus presented an extensive and, hopefully cohesive, discourse evaluating, and evolving the interpretive consideration of, evidence seeking to illumine our understanding of origins of, and insight into mechanisms contributing to, the genesis of Mayer waves. We have predicated our arguments and conjectures in the substance and matter of empirical data, though we have occasionally waxed philosophical beyond these traditional confines in suggesting interpretations exceeding these limits. We believe our synthesis and interpretation of the relevant literature will fruitfully inspire future studies from the perspective of a more intimate appreciation and conceptualization of network mechanisms generating oscillatory variability in neuronal and neural outputs. Our evaluation of Mayer waves informs a novel set of disciplines we term quantum neurophysics extendable to describing subatomic reality. Beyond informing our appreciation of mechanisms generating sympathetic oscillations, Mayer waves may constitute an intrinsic property of neurons extant throughout the cerebrum, brainstem, and spinal cord or reflect an emergent property of interactions between arteriogenic and neuronal oscillations.
Keywords: Mayer waves, genesis, origins, sympathetic, baroreceptor
Introduction
Vasomotor waves were initially recorded by Stephan Hales (1981) in 1733 in crural arterial pressure of a bound mare using a glass tube. Traube (1865) and Hering (1869) would successively characterize respirophasic oscillations in arterial pressure waveform, termed Traube–Hering waves, greater than a century later (Traube, 1865; Hering, 1869; see Fredericq, 1882). Oscillations of, and coherent between, mammalian (foxhound, cat, and rabbit) dynamic arterial blood pressure and changes in organ (spleen, kidney, and/or intestine) volume were successively demonstrated by several investigators in the 19th century (Figure 1; Traube, 1865; Hering, 1869; Mayer, 1876; Roy, 1881; Strasser and Wolf, 1905; Bottazzi, 1906). The very low frequency oscillations observed by Roy, Bunch, Strasser and Wolf, Bayliss and Bradford in foxhounds and cats exhibiting a frequency failing to exceed 0.04 Hz likely reflect similar phenomena, distinct from asphyxia-induced waves observed by Traube, Hering, and Mayer exhibiting frequencies typically exceeding 0.14 Hz (Henle, 1852; Schäfer and Moore, 1896). Very low frequency oscillations of splenic volume were observed by Wagner and Henle, in foxhounds and humans, in 1849 and 1852, respectively, spontaneously, and successively, shown to occur in rabbits in response to stimulation of the splanchnic nerve or semilunar ganglion by Schiff (1867) and Sabinsky in 1867 and in response to stimulation of the proximal or distal transected ends of vagal nerves in foxhounds, rabbits, and cats by Oehl in 1869. Tarchanoff elicited contractions of the spleen by stimulating what at the time was termed the vasomotor center of the medulla oblongata in 1874. Bulgak (1877), under the mentorship of Babuchin, elicited oscillations of splenic volume exhibiting very low frequency in response to administration of quinine (though not in response to administration of ergot), stimulation of the distal transected end of the splanchnic nerve, stimulation of the spinal cord between the first through fourth cervical, and fourth cervical through eleventh thoracic, spinal cord segments, in morphine-anesthetized foxhounds. Roy (1881) observed oscillations of arterial blood pressure exhibiting a frequency of 0.016 Hz in foxhounds and cats, elicitable by delivery of a train of sub-tetanic electrical stimuli of any peripheral sensory nerve, perhaps conveyed to the sympathetic nerves innervating the vasculature through retro-arterial propagation and distribution to a common propriospinal interneuronal network of bulbospinal premotoneurons conveying excitatory axodendritic and axosomatic synaptic drive to preganglionic sympathetic neurons or through spinoreticulospinal pathways relaying through supraspinal sympathogenic centers (Figures 2, 3). Elicitability of very low frequency oscillations of the splenic volume by stimulation of the distal ends of transected vagi and/or splanchnic nerves or vasomotor center remaining refractory to transection of both the vagal and splanchnic nerves bilaterally successively indicates generation by autochthonous, and amplifiability by intra-neuraxial, mechanisms and amplifiability by central mechanisms. Roy (1881) revealed cross-clamping the aorta below the diaphragmatic hiatus reduces splenic blood volume less rapidly than blood volume of kidneys, intestine, and limb.
FIGURE 1.
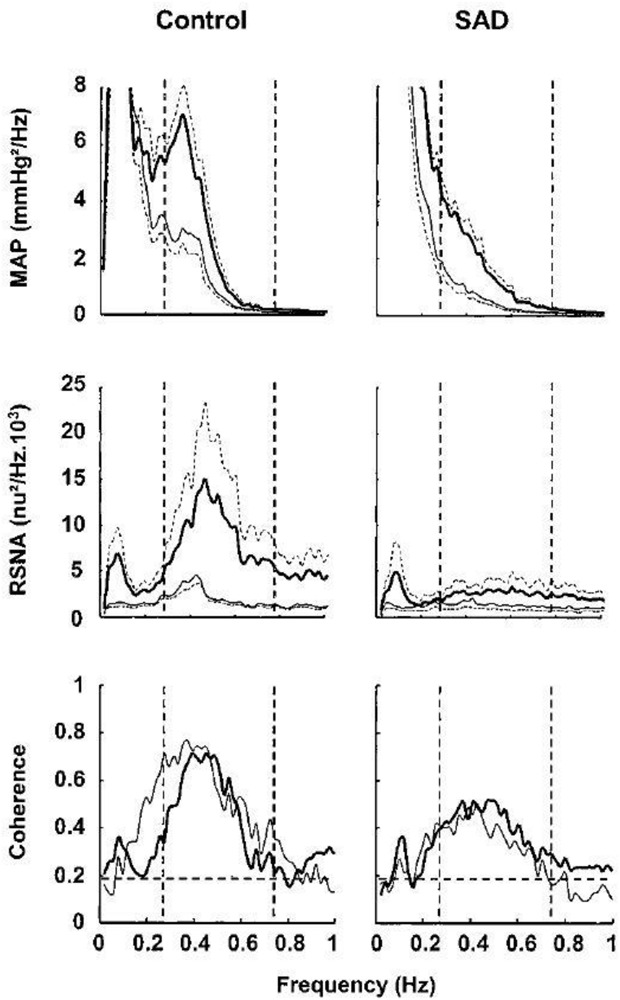
Sinoaortic denervation reduces spectral power of Mayer waves in mean arterial pressure (MAP) and renal sympathetic nerve activity (RSNA) in conscious rats. Central tendency of Mayer waves (low-frequency oscillations) varies across species and approximates 0.4 Hz in rats (range 0.2–0.8 Hz; dashed lines). Recordings of mean arterial pressure and renal sympathetic nerve activity were contemporaneously performed in sham-operated (CONTROL) (n = 10; heavy lines) and sinoaortic-denervated (SAD) (n = 10; thin lines) conscious rats. Fast Fourier transformation (34 periods of 204.8-s duration, representing 2048 data points, overlapping by half the recorded epoch) was employed to determine power spectral density and coherence. Renal sympathetic nerve activity constituent spectral bands were normalized to mean burst power determined in precession to spectral analysis. Hz, hertz (cycles/s); n.u., normalized units. Modified with permission from Figure 1 of Julien (2006).
FIGURE 2.
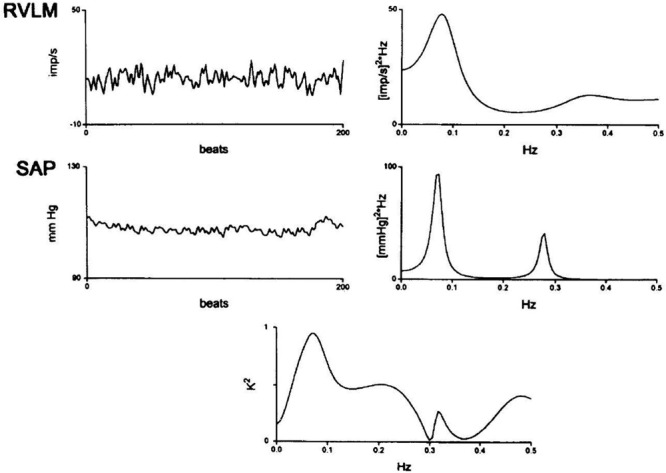
Rostral ventrolateral medullary (RVLM) neuronal firing spectra. Rostral ventrolateral medullary extracellular single neuronal recordings were conducted in unanesthetized midcollicularly decerebrate cats contemporaneously with systolic arterial pressure (SAP). Rostral ventrolateral medullary neuronal spectra reveal a spectral peak correlating with Mayer waves at slightly less than 0.1 Hz and a spectral peak at approximately 0.36 Hz, likely corresponding with Traube–Hering waves. Systolic arterial pressure spectra reveal a correlated Mayer spectral peak approximating 0.08 Hz and respirophasic oscillations exhibiting a lower amplitude and higher frequency corresponding with Traube–Hering waves a central tendency of 0.28 Hz. RVLM-SAP power spectral cross correlogram reveals prominent oscillatory correspondence at several spectral bands. Modified with permission from Montano et al. (1996).
FIGURE 3.
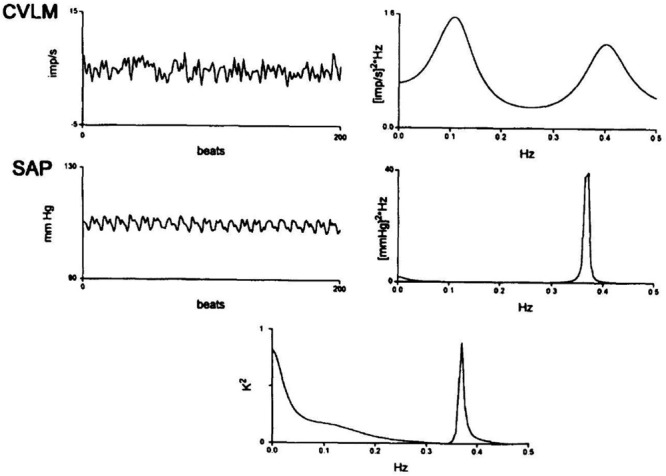
Caudal ventrolateral medullary (CVLM) neuronal spectra. Caudal ventrolateral medullary extracellular neuronal recordings were conducted in unanesthetized decerebrate cats contemporaneously with systolic arterial pressure (SAP). Caudal ventrolateral medullary neuronal spectra reveal a spectral peak at just less than 0.1 Hz, corresponding with Mayer waves, and a spectral peak at approximately 0.40 Hz, likely corresponding with Traube–Hering waves. Systolic arterial pressure spectra reveal a lower amplitude, higher frequency spectral peak corresponding with respirophasic Traube–Hering waves approximating a central tendency of 0.37 Hz and the absence of a correlated Mayer wave spectral peak. The CVLM-SAP power spectral cross correlogram reveals oscillatory correspondence at very-low-frequency and Traube–Hering high-frequency spectral peaks. Modified with permission from Montano et al. (1996).
Bunch (1899) observed very low frequency oscillations of dynamic arterial blood pressure coherent with changes in intestinal (though neither spleen nor kidney) blood volume in cats. Bayliss and Bradford (1894) would later indicate oscillations of blood volume of the kidney may generate corresponding oscillations of frequency of dynamic arterial blood pressure magnitude, consistent with the suggestion by Roy (1881) just greater than a decade prior, though later challenged by Barcroft and Nisimaru (1932) in their investigations conducted upon urethane-anesthetized cats. Schäfer and Moore (1896) debated the relative merits of synchrony between dynamic arterial blood pressure magnitude and organ volume waveforms reflecting coincidental versus physiologically-relevant behavior. Gorjajew et al. (1931) sought to explain mechanisms emergently generating coherence between oscillations of dynamic arterial blood pressure and splenic volume without success. Barcroft and Nisimaru (1932) observed coherent fluctuations of dynamic arterial blood pressure magnitude and splenic volume varying between ∼0.022 and 0.040 Hz in urethane-anesthetized cats not having undergone decerebrative encephalotomy (see Figure 2C of paper by Barcroft and Nisimaru, 1932), with visually-evident correspondence between maxima of the former, with minima of the latter, waveform. Lower dynamic arterial blood pressure magnitude correlated with less magnitude of very low frequency oscillations. Occlusive ligation of the splenic vessels, though neither sympathetic denervation nor complete resective removal of the spinal cord between the fourth and twelfth myelic thoracic segments, abolished these waves. Barcroft and Nisimaru (1932) successfully elicited oscillations of, and coherent between, dynamic arterial pressure magnitude and volume of the spleen by stimulation of the splanchnic nerve or adrenal gland, tracheal occlusion, parenteral administration of tubocurarine (see Figure 6 of paper by Barcroft and Nisimaru, 1932) or adrenaline, or precipitous rises of dynamic arterial blood pressure magnitude. Splenic volume waves successfully induced by successively sequentially clamping and unclamping the splenic artery dynamically faded with coordinately generated oscillations of dynamic arterial blood pressure magnitude (see Figure 10 of Barcroft and Nisimaru, 1932). Gain of dynamic arterial blood pressure magnitude with respect to those of splenic volume varied between 2.25 and 8.25 mmHg/mL across animals. We propose arteriogenic oscillations of the microvasculature irrigating and draining the splenic tissue coordinately and coherently generate large amplitude oscillations en masse retro-arterially transmitted to hemodynamic variables. Magnitude of dynamic arterial blood pressure oscillations were relatively attenuated in the presence of low mean integrated arterial pressure, significant irregularity of the cardiac interval or breathing cycle period, or by intravenous administration of hemoglobin.
Several decades successive to the initial characterization of very low frequency oscillations of dynamic arterial blood pressure magnitude and splenic volume by Wagner in 1849 and Henle in 1852 and less than a decade successive to the discovery of respirophasic oscillations of dynamic arterial blood pressure magnitude by Traube (1865) and Hering (1869) and Mayer (1876) would describe oscillations possessing a lower central frequency ranging between 0.10 and 0.15 Hz in dynamic arterial blood pressure magnitude of anesthetized rabbits (Mayer, 1876). The precise central frequency of these rhythms varies between, though proves highly consistent within, any given species, ranging between 0.1 and 0.4 Hz (Julien, 2006). The central tendency of Mayer waves approximates 0.1 Hz in humans (Julien, 2006), conscious (Pagani et al., 1986) and anesthetized (Cevese et al., 1995) dogs, and cats (Di Rienzo et al., 1991), 0.3 Hz in rabbits (Janssen et al., 1997), and 0.4 Hz in rats (Cerutti et al., 1991a, b, 1994; Bertram et al., 2000; Julien, 2006; Table 1). Authors would successively observe congruent oscillations occurring throughout units residing within sympathetic- and respiratory-related propriobulbar interneuronal microcircuit oscillators (Montano et al., 1995, 1996; Morris et al., 2010; Ott et al., 2011), sympathetic neural efferent discharge (Cerutti et al., 1991a, b, 1994; Janssen et al., 1997), dynamic arterial pressure magnitude (Andersson et al., 1950; Guyton et al., 1951; Guyton and Satterfield, 1952; Guyton and Harris, 1961; Cerutti et al., 1991a, b, 1994), peripheral arterial resistance (Killip, 1962), blood flow (Killip, 1962), and cardiac interval (Cerutti et al., 1991a, b, 1994). Rieger et al. (2018) would successively reveal coherence among oscillations of dynamic arterial pressure magnitude and retinal arteriolar and venular diameter at the Mayer wave spectral band in human subjects. Transcalvarial optical imaging of mouse cerebral blood flow identified successive Mayer wave and very low frequency spectral bands exhibiting central tendencies of 0.2 and 0.01 Hz, respectively (Bumstead et al., 2017). Mayer waves may occur in nonmammalian species, demonstrated in a teleost fish by Wood (1974) several decades precessively. We provide an operant set of criteria defining Mayer wave oscillations in Table 2. The origins of Mayer waves remain a nebulous mystery (see Julien, 2006). Our best interpretation of the literature would seem to indicate Mayer waves constitute an intra-neuraxially generated, sympathomodulated, baromodulated, and inter-heterologously coherent oscillatory deflection (Table 3) exhibiting central frequency peak immediately beneath respirophasic Traube–Hering waves and above arteriogenic oscillations (Siegel et al., 1976, 1984; Fuji et al., 1990; Ursino et al., 1992) present in individual unitary recordings of propriobulbar and/or bulbospinal neuronal somata constituting supraspinal sympathetic-related interneuronal microcircuit oscillators, propriospinal and/or spinobulbar neuronal somata constituting myelic sympathetic-related microcircuit oscillators, and pre- and post-ganglionic sympathetic neurons and dynamic arterial pressure magnitude, peripheral arterial resistance, and blood flow present natively (Figure 4 and Table 2). The works of Andersson, Guyton, and Harris in the 1950’s provided us with a set of data which would seem to indicate oscillations of, and between, discharge of baroreceptor and chemoreceptor cells, chiefly generate oscillations of arterial pressure possessing a frequency corresponding with the central tendency of Mayer waves (Andersson et al., 1950; Guyton et al., 1951). According to this set of findings and derivative interpretations, it would seem a most plausible, intuitive, and astute hypothesis oscillations of dynamic arterial pressure magnitude may be chiefly generated and synchronized by the baroreflex, effectively conveying a modulatory influence upon sympathetic neural efferent discharge and blood pressure magnitude successive to time variant oscillatory fluctuations of dynamic force density exerted against the carotid sinus and aortic arch (Armstrong and Moore, 2019). Myriad experimental findings accordingly indicate the baroreflex modulates, and/or inter-heterologously synchronizes, Mayer wave properties (Barrès et al., 2004; Bertram et al., 2005). Empirical studies conducted by Andersson et al. (1950) and Guyton et al. (1951) have variably implicated oscillations of, and between, discharge of baroreceptors and chemoreceptors generate Mayer waves (Andersson et al., 1950; Guyton et al., 1951). The existence of oscillations exhibiting a frequency corresponding with the central tendency of Mayer waves evident in dynamic arterial pressure magnitude and variably induced, augmented, or abolished by distinct sets of experimental interventions and lesioning constitutes evidence underscoring variable dependence of oscillatory genesis and dynamic modulation of these waves upon catory and inhibitory interactions between propriobulbar interneurons, constituting sympathetic-related microcircuit oscillators, receiving axodendritic and/or axosomatic drive from afferents conveying oscillations of baroreceptor and/or chemoreceptor discharge (Andersson et al., 1950).
TABLE 1.
Mayer wave central tendency in different species.
| Species | Mayer Wave Central Frequency |
| Rats | ∼0.4 Hz |
| Rabbits | ∼0.3 Hz |
| Cats | ∼0.1 Hz |
| Dogs | ∼0.1 Hz |
| Humans | ∼0.1 Hz |
| Mice | Unknown |
Traube–Hering central tendency corresponds with the frequency of the breathing impulse. Very low frequency oscillation central tendency corresponds with the frequency of the vasogenic autorhythmicity, typically cited to range between 0.025 and 0.075 Hz, though 0.01–0.1 Hz may represent a more inclusive, though les specific, range.
TABLE 2.
Mayer wave criteria.
| Mayer wave criteria |
| Spectral peak immediately below the respirophasic Traube–Hering wave variation |
| Spectral peak with central tendency above the vasogenic autorhythmicity very- low-frequency oscillations |
| Present in arterial pressure waveform |
| Present in cardiac interval |
| Present in sympathetic discharge |
| Present in supraspinal sympathetic neuronal firing |
| Present in spinal sympathetic neuronal firing |
| Present in sympathetic neural efferent discharge |
| Sympathomodulated |
| Baromodulated |
Criteria that must be satisfied to indicate that a set of oscillations in recorded physiological variables truly constitutes Mayer waves. The Mayer wave spectral band has a central tendency interposed between high-frequency oscillations corresponding with Traube–Hering waves and very-low-frequency oscillations corresponding with the vasogenic autorhythmicity. Mayer waves characteristically exhibit coherence or correlation between heterologous neuronal, neural, and hemodynamic outflows. Levels of sympathoexcitation, hypercarbia, hypoxia, or barounloading amplify, and hypocapnia and baroloading attenuate, Mayer wave amplitude and spectral power. Mayer wave oscillations may be generated following interruption of the baroreflex.
TABLE 3.
Mechanisms contributing to the genesis of Mayer Waves.
| Proposed Mechanism of Mayer Wave Genesis | Mechanistic Details |
| Supraspinal sympathetic microcircuit oscillators | Autochthonous supraspinal sympathetic-related interneuronal generation of Mayer waves |
| Spinal thoracolumbar intermediolateral cell column interneuronal spinal sympathetic oscillators | Autochthonous spinal sympathetic-related neuronal generation of Mayer waves |
| Baroreceptor time delay and resonant frequency | Baroreflex input-output-conduction time delay → generated by conduction delay across interneuronal central processing and afferent and efferent arms of the baroreflex arc → generated by vascular neuroeffector junction delay Baroreflex time delay generates resonance frequency → phase angle at which transfer function falls to zero → congruous with Mayer-wave central tendency in any given species |
| Arteriogenic oscillations | Correspond with vasogenic autorhythmicity Correspond with very-low-frequency oscillations Mechaotransduced through neural interstitium Conveyed to supraspinal and spinal sympathetic-related interneuronal microcircuit oscillators Conveyed to supraspinal and spinal sympathetic-unrelated interneuronal microcircuit oscillators Retro-arterially propagate by generating oscillations of dynamic arterial pressure magnitude, peripheral resistance, and blood flow |
Oscillatory perturbations generated by diffusely distributed supraspinal and spinal oscillators generate rhythmic Mayer wave variability. Arteriolar oscillations propagate through intra-neuraxial supraspinal and spinal interneuronal microcircuit oscillators via baroreflex mechanisms or neural interstitial mechanotransduction. The variabilities express the analogous base rhythm or generate an integer pseudo-harmonics thereof, entraining oscillatory central tendency and contributing to generating power within, and synchronization by, the spectral band. Baroreflex mechanisms transduce oscillatory fluctuations of dynamic arterial pressure magnitude centrally to the sympathetic oscillators via barosensitive nucleus tractus solitarius neurons.
FIGURE 4.
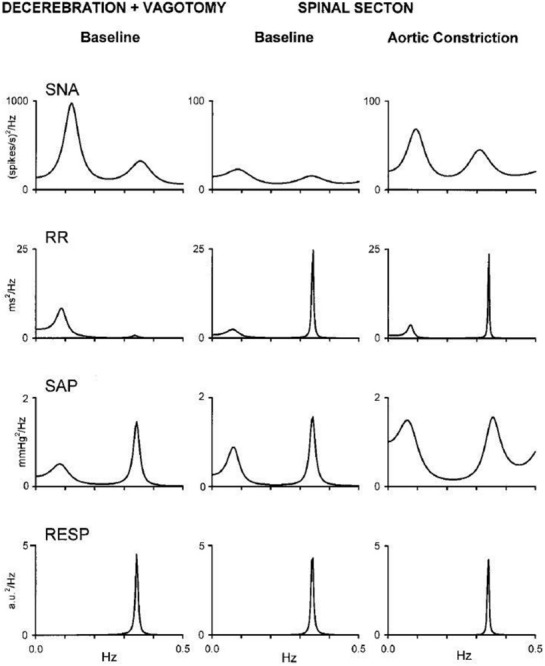
Cervical transection and aortic constriction elicits dynamic changes in cardiovascular spectral variabilities in a vagotomized unanesthetized midcollicular decerebrate cat. Spectral analysis of sympathetic nerve activity (SNA), cardiac interval (R–R interval), and systolic arterial pressure (SAP) reveal a low-frequency (i.e., LF) spectral peak corresponding with Mayer waves and a high-frequency (i.e., HF) spectral peak corresponding with Traube–Hering waves. Ventilatory frequency reveals high frequency oscillations corresponding with Traube–Hering waves. Spectral peaks corresponding with Traube–Hering and Mayer waves persisted in recorded cardiovascular variabilities following cervical spinal transection and mechanical constriction of the aortic lumen (i.e., eliciting the soi-disant spinospinal sympathetic reflex) augmented amplitude of Traube–Hering and Mayer waves in sympathetic neural efferent activity and arterial pressure, indicating native capacity of the spinal cord to generate Mayer waves exhibiting oscillatory properties subject to peripheral modulation. Modified with permission from Figure 2 of Montano et al. (2000).
Hemorrhage-induced emergence of Mayer waves in dynamic arterial pressure magnitude exhibiting marked amplitude may be generated by mechano-unloading of baroreceptors and ensuant disinhibition of supraspinal sympathetic-related microcircuit oscillators residing within the medullary lateral tegmental field and rostral ventrolateral medulla (RVLM; Andersson et al., 1950), hydrogen ions generated by hemorrhage-related tissue hypoxia enhancing carotid body and discharge frequency of chemosensitive-cells residing within the brainstem, and/or contraction of the perivascular fluid compartment promoting facile propagation of arteriolar oscillations through the neural interstitium. Mechanically interrupting nerve branches innervating the carotid sinus in animals having undergone vagal transection or conducting vagotomy or vagal cooling in animals having precedingly undergone carotid sinus nerve transection markedly attenuates amplitude of hemorrhage-induced Mayer waves (Andersson et al., 1950), consistent with a model whereby crossmodal interaction between baro-unloading-mediated augmentation of amplitude and/or frequency of sympathetic oscillations with neural interstitium contraction-mediated augmentation of mechanotransductive propagation of arteriolar oscillations to successive neural nets emergently contributes to generating augmentation of the natively extant behavior. Selectively interrupting the influence of chemoreceptors residing within the carotid body upon supraspinal interneuronal microcircuit oscillators generating sympathetic rhythms via acetic acid lesioning effectively prevents the development of Mayer waves exhibiting large amplitude in dynamic arterial pressure magnitude successive to experimental hemorrhage (Andersson et al., 1950), corroborating the derivative mechanistic and corollary interpretations. Occlusion of the common carotid artery generates Mayer waves exhibiting large amplitude, an effect likely mediated by augmentation of amplitude and/or frequency of discharge of symapthetic-related propriobulbar interneuronal microcircuit oscillators by barounloading (i.e., sympathoexcitation), variably elicited in animals with preserved and mechanically-severed vagal and Hering’s nerve and intact or lesioned carotid body chemoreceptors (Andersson et al., 1950), prevented by vagal nerve cooling and occlusion of the external carotid artery, the latter maneuver enhancing flow of a dynamic column of blood through the carotid sinus and internal carotid artery irrigating the cerebrum (Andersson et al., 1950). Administration of the highly lipid-soluble barbiturate agonist of γ-amino butyric acid receptor modulated signaling phenobarbital significantly attenuates dynamic arterial pressure magnitude and Mayer wave amplitude, indicating crossmodal modulation among oscillations of baroreceptors and chemoreceptors may chiefly generate Mayer waves evident in dynamic arterial pressure magnitude (Andersson et al., 1950). Guyton et al. (1951) similarly revealed spontaneous, as well as hemorrhage-induced, large amplitude Mayer waves in adult dogs subjected to the influence of anesthetics. Though Mayer waves exhibiting large amplitude were effectively induced in dynamic arterial pressure magnitude by hypotension (Andersson et al., 1950; Guyton et al., 1951) and hypoxia (Janssen et al., 1997) in early reports, Mayer waves constitute physiological oscillations manifesting in spectra of respiratory- and sympathetic-related interneuronal microcircuit oscillators (Montano et al., 1995, 1996, 2000; Morris et al., 2010; Ott et al., 2011), sympathetic neural efferent discharge (Stauss et al., 1997), and hemodynamic variables (Killip, 1962) in animals with otherwise intact continuity of carotid sinus and vagal nerves (Figure 1).
Investigators have provided data suggesting Mayer waves may be generated via dynamic interactions occurring amongst sympathetic-related propriobulbar interneuronal microcircuit oscillators residing within the confines of the brainstem (Montano et al., 1995, 1996), sympathetic-related propriospinal interneuronal microcircuit oscillators residing within the confines of the myelic substance (Montano et al., 2000), oscillations of discharge of baroreceptors and/or chemoreceptors (Andersson et al., 1950; Guyton et al., 1951; Bertram et al., 2005), and/or intra-neuraxial mechanisms (Table 3; Julien, 2006). Retrograde arterio-aorto-ventricular propagation of autochthonous vasogenic arteriolar oscillations (Siegel et al., 1976, 1984; Fuji et al., 1990; Ursino et al., 1992), or a complex and dynamic interplay amongst these oscillations, may putatively contribute to incipiently generating or dynamically modulating Mayer waves. Persistence of Mayer waves successive to sinoaortic denervation and/or high cervical transection indicates propriobulbar interneuronal microcircuit oscillators residing within the bulb (Figures 2, 3; Montano et al., 1995, 1996; Morris et al., 2010; Ott et al., 2011) or myelic substance (Montano et al., 2000) may generate very low frequency oscillations and/or Mayer waves exclusively or in unison, respectively (Figure 4). Oscillations of arteriolar diameter propagating to interneuronal microcircuit oscillators residing within the bulb and/or spinal cord through the neural interstitium may emergently generate Mayer waves, through spatiotemporal integration of coupled phase-related oscillations (soi-disant out-of-phase summation). Mechanical propagation of oscillations of the vasa vasorum to arteriomural baroreceptors exhibiting highest density within the carotid sinus and/or aortic arch may be centrally-conveyed and imposed upon respiratory- and sympathetic-related interneuronal microcircuitry and distribute to electrically-excitable cells throughout the neuraxis. Retro-arterial propagation of arteriolar oscillations may convey coherent oscillatory dynamics upon peripheral arterial resistance, dynamic arterial blood pressure magnitude, and/or blood flow. Hysteresis within intra-neuraxial, and between intra-neuraxial and extra-neuraxial, microcircuits exhibiting complex resonant frequencies and derivative oscillations may emergenty generating very low frequency oscillations and fast sympathetic rhythms. Successive cycle-skipping and out-of-phase summation may generate integer pseudo-harmonics of vasogenic autorhythmicity corresponding with the central frequency of Mayer waves (see Table 4). We synthesize findings generated across legion studies in order to develop a cohesive integrated model explaining the disparate and multivariately interacting mechanisms underlying the neurogenesis of Mayer waves and illumine a fundamentally novel discipline we term dynamic and quantum neurophysiology and neurophysics (Julien, 2006).
TABLE 4.
Arteriogenic oscillations and neuronal vascular interactions may contribute to the genesis of Mayer Waves.
| Neuronal-vascular interaction-mediated genesis of Mayer waves | Detailed pathway |
| Intra-neuraxial rhombomyelic microvascular arteriogenic neuronal oscillations | → Intra-neuraxial (rhombomyelic) radial and longitudinal microvascular oscillations → Generate sympathetic propriobulbar interneuronal oscillations → Generate presympathetic bulbospinal neuronal oscillations → Generate preganglionic sympathetic neuronal oscillations → Generate postganglionic sympathetic neuronal oscillations → Generate oscillations of neurotransmitter release from postganglionic sympathetic neuronal endplate upon vascular smooth muscle cells → Modulate autochthonous arteriolar oscillations |
| Arteriogenic baroreceptor oscillations | → Carotid sinus and/or aortic arch vasa vasorum oscillations → Generate oscillations of baroreceptor cell firing → Generate nucleus tractus solitarius neuronal firing oscillations → Generate caudal ventrolateral medullary interneuronal firing oscillations → Generate rostral ventrolateral medullary presympathetic neuronal firing oscillations → Generate preganglionic sympathetic neuronal firing oscillations → Generate postganglionic sympathetic neuronal firing oscillations → Generate oscillations of neurotransmitter release from postganglionic sympathetic neuronal endplate upon vascular smooth muscle cells → Modulate autochthonous arteriolar oscillations |
| Retro-arterially propagated arteriogenic oscillations | → Retro-arterial propagation of oscillations of arteriolar diameter → Generate oscillations of arterial resistance → Generate oscillations of arterial pressure → Generate oscillations of blood flow → Generate oscillations of baroreceptor cell discharge → Generate nucleus tractus solitarius neuronal firing oscillations → Generate caudal ventrolateral medullary neuronal firing oscillations → Generate rostral ventrolateral medullary presympathetic neuronal firing oscillations → Generate preganglionic sympathetic neuronal oscillations → Generate postganglionic sympathetic neuronal oscillations → Generate oscillations of neurotransmitter release from postganglionic sympathetic neuronal endplate upon vascular smooth muscle cells → Modulate autochthonous arteriolar oscillations |
We propose that arteriogenic oscillations may emergently generate oscillations manifest in neuronal, neural, and hemodynamic spectra through several mechanisms. Arteriogenic oscillations may propagate through the neural interstitium to supraspinal and spinal interneuronal microcircuit oscillators and through vasa vasorum to carotid sinus and aortic arch baroreceptors. Arteriogenic oscillations may retro-arterially propagate to generate oscillations of arteriolar and arterial resistance, arterial pressure, and blood flow. Hysteresis between disparately distributed, though inter-neuronally synchronizable, oscillations may generate conduction delays within intra-neuraxial circuits and between centrogenic oscillators and baroreflex elements, modulating Mayer wave amplitude and/or frequency.
Very Low Frequency Oscillations in Human Electroencephalogram and Supratentorial Cerebral Blood Flow
Human cerebral hemodynamics and oxygenation indices exhibit Mayer waves with a central tendency approximating 0.1 Hz (Yucel et al., 2016). Mayer waves and very low frequency oscillations in dynamic electroencephalographic activity, cerebral blood oxygenation, and arterial blood pressure in otherwise healthy individuals may interact multivariately and reciprocally, behavior revealed through use of autoregressive models and a directed transfer function premised upon the Granger causality principle, lending credence to our hypothesis Mayer waves may be generated by retro-arterial propagation of arteriogenic oscillations or mechanotransduction of these rhythms to generative propriobulbar interneuronal microcircuits through the perivascular fluid compartment and neural interstitium. Functional near infrared spectroscopy (fNIRS) reveals very low frequency oscillations (0.029 Hz; 0.012–0.018 Hz) in frontal eye fields during vergence eye movements in otherwise healthy individuals (Yaramothu et al., 2020). Patients suffering from attention deficit hyperactivity disorder exhibit increased very low frequency band spectral power in parietal electroencephalogram, attenuable by treatment with the dopamine and norepinephrine potentiator methylphenidate (Cooper et al., 2014). In migraineurs, waves of cortical spreading depression generate neuronal and astrocytic swelling, which may successively collapse the perivascular fluid compartment to influence oscillatory amplitude of cerebrovascular pulsatility (Schain et al., 2017). Müller et al. (2003) identified mean very low frequency oscillation spectral peak of 0.021 Hz in transcranial Doppler (TCD) flow. Arteriogenic oscillations exhibiting central frequencies of 0.033 and 0.066 (0.045) Hz analogous to waves observed in middle cerebral artery-derived cerebral blood flow may be observed in rabbit external ophthalmic artery (Delgado et al., 2013). Acute hypoxia (15% O2) enhanced spectral power of very low frequency oscillations in cerebral blood flow volume and mean arterial blood pressure in otherwise healthy subjects (Iwasaki et al., 2007), perhaps through acidosis-mediated relaxation of vascular smooth muscle and vasodilation, amplifying oscillatory trough dips. Patients suffering from traumatic brain injury may experience enhancement of very low frequency spectral power in middle cerebral artery cerebral blood flow velocity and dynamic arterial blood pressure magnitude (Turalska et al., 2008).
Baroreflex Mechanisms Modulate Mayer Wave Properties
Oscillations of dynamic arterial blood pressure magnitude convey to neurons residing within the nucleus tractus solitarius (Jhamandas and Harris, 1992; Rogers et al., 1993, 1996, 2000; Vitela and Mifflin, 2001; Becker et al., 2016) via oscillatory inputs conveyed through baroreceptors and baroafferents (Armstrong and Moore, 2019). Propriobulbar interneuronal microcircuit oscillators residing within the nucleus tractus solitarius successively and coordinately filter (Titz and Keller, 1997; Young et al., 2003) and integrate (Rogers et al., 2000; Young et al., 2003) oscillatory discharge of baroreceptors. Divergence of axodendritic and axosomatic inputs conveyed to multiple neural nets residing within the medial and interstitial divisions of the nucleus tractus solitarius by baroafferents successively amplifies and synchronizes the discharge of propriobulbar interneuronal microcircuits oscillators (Becker et al., 2016). Ascending oscillatory baroreceptor inputs undergo low-pass filtering by neurons residing within the nucleus tractus solitarius to alternately admit, preclude, or modify caudorostral relay of constituent spectral frequencies from reaching higher order neurons emergently constituting supraspinal sympathetic-related and parasympathetic-related propriobulbar interneuronal microcircuit oscillators (Titz and Keller, 1997; Young et al., 2003). Elimination of Mayer waves by sinoaortic denervation (Barrès et al., 2004), biophysical properties of the baroreflex arc (Seydnejad and Kitney, 2001), posture-dependent enhancement of Mayer waves in muscle sympathetic neural efferent activity (Marchi et al., 2016a, b), and a most striking equivalence of resonant frequency of the baroreflex with central frequency of Mayer waves (Cerutti et al., 1991a, b, 1994) may support the set of hypotheses the baroreflex chiefly generates these oscillations. Authors have accordingly developed several successive conceptual and mathematical models seeking to explain genesis of Mayer waves by biophysical properties of the baroreflex (Seydnejad and Kitney, 2001). Phase-lagged dynamic input and output of the baroreflex, a feature common to any closed negative feedback loop exhibiting non-linear dynamics, summating successive delays interposed between oscillatory arterial pressure inputs conveyed through baroreceptors residing within the walls of the carotid sinus and aortic arch, transduction across pauci-synaptic neuronal pathways, and ultimate set of physiological effects conspiring to mediate corrective changes in dynamic arterial pressure magnitude emergently generates self-sustaining oscillations corresponding with the resonant frequency of the baroreflex (Seydnejad and Kitney, 2001). Mayer wave properties may thus reflect differential resonance frequencies and latencies of distinct effector components comprising the baroreflex (Marchi et al., 2016a, b). Thus, spatiotemporally dynamic oscillatory discharge of baroreceptors residing within the carotid sinus and aortic arch generates a substantial fraction of the power contained within the Mayer wave spectral band and coherence amongst heterologous neurons and nerves (Cerutti et al., 1991b; Just et al., 1995).
We presume centrally-conveyed oscillations of discharge by baroreceptors cells electrochemically transducing dynamic arterial pressure magnitude (see Rogers et al., 1993, 1996, 2000; Armstrong and Moore, 2019) modulate and synchronize (Julien, 2006), though do not chiefly initiate, Mayer waves (Armstrong and Moore, 2019), a set of presumptions exclusively conforming to Truth should sectioning of the glossopharyngeal and vagal nerves successively exclude oscillations of arterial pressure from intra-neuraxial first-order neuronal relays residing within the nucleus tractus solitarius and distally-related integrative neural circuits, rendering mechanisms generating Mayer wave oscillations manifest in sympathetic-related and parasympathetic-related propriobulbar interneuronal microcircuit oscillators and neural spectra independent of, though modulated by, dynamic changes in force density exerted upon the luminal surface of the vessel wall by the pulse-synchronous column of blood (i.e., arterial blood pressure) (Cerutti et al., 1991a, 1994). Laudable persistence of oscillations exhibiting a central frequency downshifted from Mayer waves and consistent with very low frequency oscillations of vasogenic autorhythmicity successive to cervicomedullary transection (Montano et al., 2000) somewhat undermines the merit of the preceding set of suppositions. Nevertheless, innervation of extra-sinoaortic baroreceptors, present in medial proximal internal carotid, subclavian (Chevalier-Cholat and Friggi, 1976a, b), and vertebral (Kupriyanov, 2009) arteries conveyed via axons not transmitted in the vagus or glossopharyngeus nerves would experimentally validate and substantiate the conjecture interactions amongst interneuronal microcircuit oscillators residing within the bulb and spinal cord (see Montano et al., 1995, 1996), rhythmically fluctuating dynamic baroreceptor cell spiking (see Cerutti et al., 1991b, 1994; Julien, 2006), and oscillations of arteriolar diameter (Barcroft and Nisimaru, 1932; Nisimaru, 1984; Siegel et al., 1984; Fuji et al., 1990; Ursino et al., 1992) generate Mayer waves by amplifying pseudo-harmonics of integratively summated out-of-phase very low frequency oscillations (Martín et al., 1981; Vanni et al., 2010).
Brainstem and Spinal Sympathetic Propriospinal Microcircuit Oscillators Generate Mayer Waves
Dittmar demonstrated precipitous reductions of dynamic arterial pressure magnitude successive to bilateral lesioning of the RVLM in anesthetized animals in 1873. Authors have since provided evidence underscoring propriobulbar interneuronal microcircuits residing within the brainstem likely convey excitatory axodendritic and axosomatic synaptic drive to propriospinal interneuronal microcircuit oscillators modulating the discharge of preganglionic sympathetic neurons residing within the intermediolateral cell column thoracic and upper lumbar segments of the spinal cord (Ghali, 2017a,b). Accordingly, propriobulbar, bulbospinal, propriospinal, and spinobulbar neurons forming successive nets brainstem (Figures 5, 6) [e.g., medullary division of the lateral tegmental field (mLTF) and RVLM] (Ghali, 2017a, b) and intermediolateral cell column of the spinal cord (Ghali, 2019) constitute microcircuit oscillators emergently generating sympathetic activity manifest in neural efferent discharge (Sun and Guyenet, 1986; Sun et al., 1988; Dampney, 1994; Lipski et al., 1996; Ghali, 2017a, b, 2019), which may analogously generate Mayer waves, putatively constituting a common rhythm propagating throughout brainstem or spinal neural networks, either generated chiefly in, or conveyed to, sympathetic interneuronal microcircuit oscillators. Persistence (Cerutti et al., 1991a, b, 1994; Montano et al., 1995, 1996, 2000) or paradoxical enhancement (Di Rienzo et al., 1991; Mancia et al., 1999) of Mayer wave spectral power and non-modulation of Mayer wave central frequency by mechanically interrupting afferent or efferent arms of the baroreflex, pharmacological antagonism of the paravertebral chain ganglia (Cerutti et al., 1994; Bertram et al., 1998), guanethidine-induced chemical sympathectomy (Cerutti et al., 1991b; Julien et al., 1995), and α adrenergic antagonism (Japundzic et al., 1990; Cerutti et al., 1991b; Rubini et al., 1993; Julien et al., 1995) indicates emergent, correlated, and synchronous discharge amongst brainstem propriobulbar and propriospinal interneuronal microcircuit oscillators generate Mayer waves modified by the baroreflex (Montano et al., 1995, 1996, 2000). Though several authors have espoused models indicating Mayer wave genesis chiefly reflects an emergent behavior of transduction properties of the baroreflex loop (see Seydnejad and Kitney, 2001), we believe a more parsimonious dynamic interplay amongst propriobulbar interneuronal microcircuit oscillators residing within the bulb (Montano et al., 1995; Julien, 2006)and spinal cord (Montano et al., 2000), with oscillations of baroreceptors (Andersson et al., 1950; Guyton et al., 1951), chemoreceptors (Andersson et al., 1950; Guyton et al., 1951) and arteriolar diameter (Siegel et al., 1976, 1984; Fuji et al., 1990; Ursino et al., 1992) generate Mayer waves in spectra of neurons generating, and nerves relaying, sympathetic discharge (Julien, 2006).
FIGURE 5.
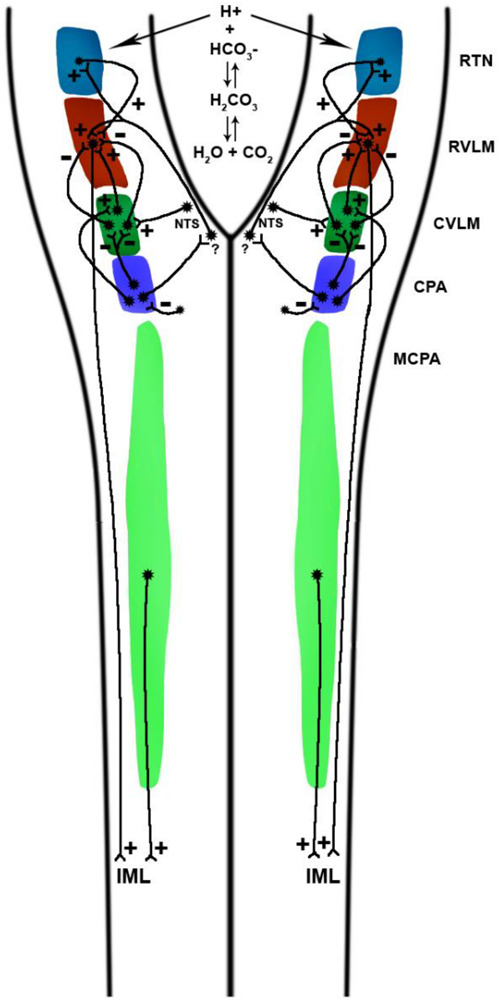
Neuroanatomical organization of medullary and cervical zones from which pressor and depressor responses may be elicited by glutamate microinjections. The chief medullary pre-sympathetic units conveying axodendritic and axosomatic synaptic drive to preganglionic sympathetic neurons residing within the intermediolateral cell column reside in the rostral ventrolateral medulla and the medullocervical pressor area, the latter projecting at least as far caudal as the C3 segment of the cervical spinal cord. The discharge of GABAergic propriobulbar interneurons constituting inhibitory CVLM (I-CVLM) attenuates RVLM pre-sympathetic neuronal firing via GABAergic mechanisms. A few I-CVLM units driven by the baroreflex arc are putatively activated by second-order barosensitive NTS units, which are, in turn, activated by barosensitive afferents conveyed from the carotid sinus and aortic arch, relaying via the glossopharyngeal and vagus nerves, respectively. A distinct group of GABAergic I-CVLM units exhibit baro-independence and tonically attenuate RVLM pre-sympathetic neuronal firing frequency. Glutamatergic units constituting the excitatory CVLM (E-CVLM) convey axodendritic and axosomatic synaptic drive to RVLM pre-sympathetic units via glutamate receptor-modulated signaling. Chemoreceptor afferents terminate upon second-order neurons residing within the commissural nucleus tractus solitarius, which in turn convey excitatory axodendritic and axosomatic synaptic drive to RVLM units monosynaptically and/or polysynaptically. The NTS also conveys axodendritic and axosomatic synaptic drive to retrotrapezoid nucleus neurons, which convey excitatory axodendritic and axosomatic synaptic drive to RVLM neurons. Water reacts with carbon dioxide in a reaction catalyzed by carbonic anhydrase to form carbonic acid, which dissociates into bicarbonate anion and hydrogen cations, the latter potentiating the firing frequency of chemosensitive neurons residing within the retrotrapezoid nucleus, medullary raphé, and nucleus tractus solitarius firing, among other central chemoreceptor sites. Experimental excitatory stimulation of the caudal pressor area, caudally-related with respect to RVLM-projecting CVLM interneurons, elicits sympathoexcitation by preventing GABAergic CVLM units from attenuating RVLM neuronal spiking and by activating sympathoexcitatory E-CVLM units. Axonal efferents from GABAergic interneurons residing within the caudal pressor area conveyed to units residing within the midline commissural division of the nucleus tractus solitarius units, though demonstrated, possess a neurochemical phenotype which remains unsettled, with one study demonstrating commissural NTS-dependence of pressor responses to stimulation of the caudal pressor area. Experimental excitatory stimulations of the caudal and medullary and cervical pressor areas elicit RVLM-dependent and RVLM-independent pressor responses, respectivelysee Fig. 2). Though MCPA-mediated pressor responses do not require efferents to RVLM, reciprocal connections between both structures likely exist. CPA-dependence of raphé-mediated pressor responses remains to be illustrated. RTN, retrotrapezoid nucleus; RVLM, rostral ventrolateral medulla; CVLM, caudal ventrolateral medulla; CPA, caudal pressor area; MCPA, medullocervical pressor area; NTS, nucleus tractus solitarius.
FIGURE 6.
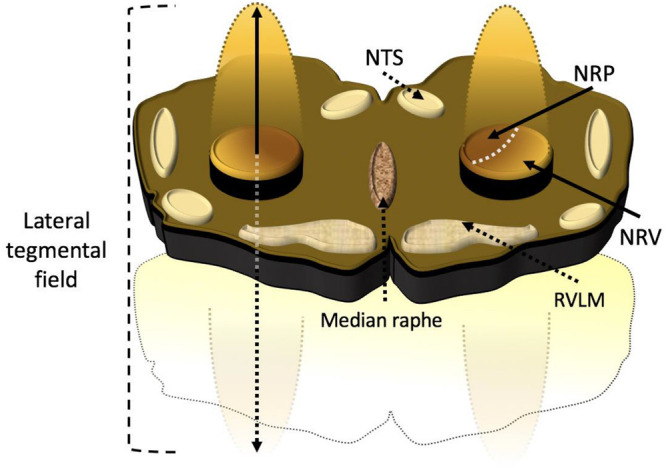
Artist rendition of a transverse slab of medulla the anatomic relationship between the medullary lateral tegmental field and rostral ventrolateral medulla. Propriobulbar interneuronal microcircuit oscillators constituting the medullary lateral tegmental field residing within the caudolateral medulla extend in line with rostromedial ascent toward the tip of the rostral ventrolateral medulla, thus presenting the architectonic appearance of the cometary tail of the rostral ventrolateral medulla in vivo. The medullary lateral tegmental field contains barosensitive units providing sympathoexcitatory and sympathoinhibitory propriobulbar inputs to the rostral ventrolateral medulla. The discharge of medullary lateral tegmental field neurons precedes unitary activity of rostral ventrolateral medullary units and exhibits correlation with bulbospinal presympathetic neuronal and cardiac sympathetic neural efferent discharge. The medullary lateral tegmental field contributes prominently to basal sympathoexcitation and reflexive changes in sympathetic tone, mediating baroreceptor, chemoreceptor, Bezold-Jarisch, somatoautonomic, and visceroautonomic reflexes via N-methyl-D-aspartate and non-N-methyl-D-aspartate-dependent mechanisms. NRP, nucleus reticularis paragigantocellularis; NRV, nucleus reticularis ventralis; NTS, nucleus tractus solitarius; RVLM, rostral ventrolateral medulla.
Persistence of Mayer waves in the discharge of neurons residing within the RVLM (Figure 2), caudal ventrolateral medulla (CVLM; Figure 3), mLTF, and caudal raphe in phenobarbital-anesthetized and unanesthetized intercollicularly decerebrated cats having undergone sinoaortic denervation and mechanical interruption of vagal continuity supports intra-neuraxial originate genesis of these oscillations (Montano et al., 1995, 1996). Neurons residing within the medullary raphé, metencephalon, retrotrapezoid nucleus, parafacial respiratory group, Bötzinger complex (BötzC), and ventral respiratory group (VRG) exhibit dynamic oscillations possessing nested central frequencies corresponding with those typifying the Mayer wave spectral band, synchronous with arterial blood pressure oscillations, coupled to the respiratory rhythm sans vagal continuity (Tables 5, 6; Morris et al., 2010; Ott et al., 2011; see Guyenet and Mulkey, 2010; Sobrinho et al., 2014; Guyenet et al., 2019). The retrotrapezoid nucleus transduces hydrogen ion concentrations and carbon dioxide tension into spike trains modulating the respiratory rhythm and pattern generator, sympathetic-related propriobulbar interneuronal microcircuit oscillators, and cardiovagal premotoneuronal discharge. These data indicate propriobulbar interneuronal microcircuit oscillators residing within the bulb may generate Mayer waves independently of the baroreflex. Mayer waves persist in dynamic arterial pressure magnitude and lumbar sympathetic neural efferent discharge successive to mechanical interruption of cervicomedullary continuity in pentobarbital-anesthetized Beagle dogs (Kaminski et al., 1970) and in cardiac interval, dynamic arterial pressure magnitude, blood flow, and sympathetic neuronal spiking successive to high cervical transection in unanesthetized mid-collicularly decerebrate cats having undergone transection of the vagi bilaterally (Figure 4; Montano et al., 2000), though reduction of central frequency of the Mayer wave spectral band from 0.11 to 0.09 in sympathetic neural efferent discharge and from 0.08 to 0.05 Hz in systolic arterial pressure successive to spinal transection (Montano et al., 2000) underscores the existence of propriospinal interneuronal microcircuit oscillators independently capable of generating Mayer waves or Mayer wave-like oscillations, with supraspinal neuronal microcircuit oscillators conveying axodendritic and axosomatic drive augmenting central frequencies of the oscillations by enhancing the gain of propriospinal interneuronal somatodendritic membranes postsynaptic to bulbospinal axonal terminals emergently constituting the chief generative neuronal ensembles (Figure 4; Montano et al., 2000). Mayer waves generated by neural microcircuits residing within the myelic substance or fractional integer subharmonics thereof may constitute autochthonous neuronal oscillations, arteriolar oscillations mechanotransduced through neural circuits of the myelic parenchyma, and/or propagation of arteriolar oscillations of the dorsal root ganglia throughout the neuraxis (Siegel et al., 1976, 1984; Fuji et al., 1990; Ursino et al., 1992; Montano et al., 2000). Low-frequency oscillations generated by the spinal cord may synchronize sympathetic-related propriospinal activity, amplifying amplitude and total spectral power of sympathetic neural efferent discharge conveyed to the vasculature, putatively hastening dynamic arterial pressure magnitude recovery successive to reductions of sympathetic neural efferent discharge successive to mechanical interruption of spinomedullary continuity (see Sherrington, 1906; Ghali, 2019). Mayer waves generated by supraspinal and spinal sympathetic-related interneuronal microcircuit oscillators via coherent and out-of-phase spatiotemporally integrated activity of mechanotransductively propagated arteriolar oscillations, correlated sympathetic-related neuronal spiking, and coherent oscillations of baroreceptor discharge (Montano et al., 1995, 1996) propagate to and “permeate” through surrounding propriobulbar neural network arrays (Morris et al., 2010; Ott et al., 2011). We do not exclude brainstem and spinal cord interneuronal microcircuit oscillators (Montano et al., 1995, 1996, 2000; Morris et al., 2010; Ott et al., 2011), the baroreflex (Seydnejad and Kitney, 2001), and arteriolar oscillations (Barcroft and Nisimaru, 1932; Siegel et al., 1976, 1984; Fuji et al., 1990; Ursino et al., 1992) independently contribute to emergently generating Mayer waves.
TABLE 5.
Mayer waves and very low frequency oscillations in neural and hemodynamic spectra.
| Zone | Very low frequency oscillations | Mayer waves |
| Retrotrapezoid nucleus | See Figure 3A of Ott et al., 2011 | See Figure 3A of Ott et al., 2011 |
| Parafacial respiratory group | cell 404, RTN I-Dec, ∼0.02 Hz | cell 407, RTN E-Dec, ∼0.083 Hz |
| cell 406, RTN NRM, ∼0.02 Hz | cell 412, RTN I-Aug, ∼0.083 Hz | |
| cell 462, RTN NRM, ∼0.02 Hz | cell 417, RTN E-Dec, ∼0.083 Hz | |
| cell 497, RTN E-Dec, ∼0.02 Hz | cell 418, RTN NRM, ∼0.083 Hz | |
| cell 420, RTN I-Aug, ∼0.083 Hz | ||
| cell 424, RTN E-Aug, ∼0.083 Hz | ||
| Botzinger complex | See Figure 3A of Ott et al., 2011 | See Figure 3A of Ott et al., 2011 |
| Ventral respiratory group | cell 810, Bot I-Dec, ∼0.033 Hz | cell 899, Bot E-Dec, ∼0.083 Hz |
| cell 810, Bot NRM, ∼0.02 Hz | ||
| cell 816, Bot E-Dec, ∼0.025 Hz | ||
| cell 892, Bot E-Aug, ∼0.025 Hz | ||
| Pontine nuclei | See Figure 4 of Morris et al., 2010 | Morris et al. (2010) describe the presence of Mayer wave oscillations in pontine nulcei, though visual inspection more consistently evidences a central tendency conforming to that of VLF |
| cell 509 ∼0.075 Hz | ||
| cell 554 ∼0.06 Hz | ||
| cell 555 ∼0.075 Hz | ||
| cell 556 ∼0.075 Hz | ||
| Medullary raphe nuclei | See Figure 4 of Morris et al., 2010 | Morris et al. (2010) describe the presence of Mayer wave oscillations in medullary raphe nuclei, though visual inspection more consistently evidences a central tendency conforming to that of VLF |
| cell 914 0.07 Hz | ||
| cell 915 0.075 Hz | ||
| Medullary lateral tegmental field | YTBR | Montano et al., 1995, 1996 |
| Rostral ventrolateral medulla | YTBR | Montano et al., 1995, 1996 |
| Caudal ventrolateral medulla | YTBR | Montano et al., 1995, 1996 |
| ∼0.105 Hz | ||
| Caudal Raphe | YTBR | Montano et al., 1995, 1996 |
| Described mean ∼0.12 Hz | ||
| T1 and T2 preganglionic sympathetic neurons | Preiss and Polosa, 1974 | Montano et al., 1992 |
| ∼0.03 Hz; group termed these Mayer waves, but significantly less cycle frequency | ||
| Renal sympathetic nerve | Murasato et al., 1998 | Cerutti et al., 1991a, b, 1994; Julien et al., 2003; Barrès et al., 2004 |
| Arterial Blood Pressure | Di Rienzo et al., 1991; Just et al., 1995 | See Julien, 2006 for review |
| Peripheral Resistance | Mal’tsev et al., 2010 | Killip, 1962 |
| Peripheral organ blood flow | Barcroft and Nisimaru, 1932 | Killip, 1962 |
| Cerebral Blood Flow | Vermeij et al., 2014 | Lachert et al., 2019 |
| Vaginal Blood flow | Allers et al., 2010 | Allers et al., 2010 |
| Electroencephalographic activity | Cooper et al., 2014 | Blinowska et al., 2020 |
| Cardiac Interval | Tripathi, 2011 | Japundzic et al., 1990; Montano et al., 1992; Rubini et al., 1993; Mancia et al., 1999; Van de Borne et al., 2001 |
| Cerebral vasomotion | Bosch et al., 2017 | Bumstead et al., 2017 |
| Organ volume | Barcroft and Nisimaru, 1932∼0.02–0.04 Hz | Killip, 1962 |
YTBR, yet to be revealed.
TABLE 6.
Effects of empirical interventions upon Mayer wave properties.
| Author(s) | Animal preparation | Intervention | Major findings |
| Preiss and Polosa, 1974 | Pentobarbital-anesthetized cats | Bilateral mechanical interruption of cervical vagal continuity | Mayer waves present in preganglionic neuronal recordings and cervical sympathetic fibers |
| intercollicularly decerebrate cats | Bilateral mechanical interruption of the aortic depressor nerve | Persisted successive to sinoaortic denervation | |
| Central frequency more consistent with vasogenic autorhythmicity | |||
| Japundzic et al., 1990 | Conscious rats | Atropine Atenolol Prazosin | Spectral power of oscillations of cardiac interval at the Mayer wave spectral band (0.2 to 0.605 Hz) reduced by atropine and atenolol sympathetic antagonism |
| Cardiac interval Traube–Hering (1.855 Hz) waves abolished by atropine | |||
| Mayer waves in arterial pressure waveform attenuated by prazosin | |||
| Traube–Hering waves in arterial pressure waveform attenuated by prazosin | |||
| Di Rienzo et al., 1991 | Unanesthetized decerebrate cats | Mechanical interruption of the baroreflex (acute) | Spectral variabilities in arterial pressure included very low frequency (0.0012 to 0.0025), low frequency (0.025 to 0.07), medium frequency (0.07 to 0.14), and high frequency waves |
| Spectral power of VLF and LF augmented by sinoaortic denervation | |||
| Spectral power of MF reduced by sinoaortic denervation | |||
| Spectral power of HF unaffected by sinoaortic denervation | |||
| Mancia et al., 1999 | Conscious cats | Mechanical interruption of the baroreflex (chronic) | Systolic blood pressure variability augmented by sinoaortic denervation |
| Spectral power of Mayer and Traube–Hering waves in arterial blood pressure and cardiac interval augmented by sinoaortic denervation | |||
| Coherence between dynamic arterial blood pressure and cardiac interval at the Mayer wave spectral band reduced by sinoaortic denervation | |||
| Coherence between blood pressure and cardiac interval at the Traube–Hering spectral band reduced by sinoaortic denervation | |||
| Cerutti et al., 1991a | Conscious normotensive and hypertensive Lyon rats | Mechanical interruption of the baroreflex | Mayer waves in dynamic arterial pressure magnitude and cardiac interval (0.38–0.45 Hz) abolished by sympathetic denervation and successive antagonism of b and a adrenergic receptors |
| Traube–Hering waves present in dynamic arterial pressure enhanced by atropine and in cardiac interval abolished by atropine (1.04–1.13 Hz) Hypertensive rats exhibited less basal sympathetic activity and less distinct Mayer wave spectral peaks | |||
| Cerutti et al., 1991b | Normotensive Lyon rats | Mechanical interruption of the baroreflex (chronic) Guanethidine α adrenergic antagonism | Mayer waves present in dynamic arterial pressure magnitude (0.27–0.74 Hz, central tendency 0.38–0.45 Hz) |
| abolished by guanethidine sympathectomy and successive concurrent pharmacological antagonism of b and a adrenergic receptors | |||
| Spectral power of Mayer waves present in dynamic arterial pressure magnitude (0.27–0.74 Hz, central tendency 0.38–0.45 Hz) by treatment with phentolamine or propranolol | |||
| Traube–Hering and Mayer waves present in cardiac interval abolished by combined phentolamine and propranolol | |||
| Persson et al., 1992 | Conscious Wistar Kyoto rats Conscious spontaneously hypertensive rats | Prazosin Methylscopolamine | Mayer (0.06–0.15 Hz) and Traube–Hering waves present in splanchnic sympathetic nerve and blood pressure |
| Arterial pressure oscillations lagged those of splanchnic sympathetic nerve by 200 ms | |||
| Spectral band frequency ranges similar between splanchnic sympathetic nerve and blood pressure | |||
| Spectral band frequency ranges similar between Wistar Kyoto and spontaneously hypertensive rats | |||
| Traube–Hering waves coherent between splanchnic sympathetic nerve and blood pressure | |||
| Prazosin reduced the fractional contribution of Mayer waves to total spectral power | |||
| Methylscopolamine failed to modify fractional contributions of Mayer and Traube–Hering waves | |||
| Montano et al., 1992 | Vagotomized unanesthetized decerebrated cats | Obstruction of the aorta or vena cava | Mayer (0.1 Hz) and Traube–Hering (0.32 Hz) waves present in cardiac interval, dynamic arterial blood pressure, and thoracic sympathetic preganglionic neurons |
| Spectral power of Mayer waves in cardiac interval and thoracic sympathetic preganglionic neurons enhanced by aortic of vena caval obstruction | |||
| Spectral power of Traube–Hering wave in cardiac interval and thoracic sympathetic preganglionic neurons reduced by aortic or vena caval obstruction | |||
| Spectral power of Mayer waves in cardiac interval reduced by sympathoinhibition | |||
| Spectral power of Traube–Hering waves in cardiac interval and thoracic sympathetic preganglionic neurons augmented by sympathoinhibition | |||
| Rubini et al., 1993 | Conscious freely-exploring rats | Phentolamine | High coherence between arterial pressure and cardiac interval at the very low frequency (0.08 Hz), Mayer wave (0.43 Hz) and Traube–Hering wave (1.36 Hz) spectral bands in systolic and diastolic arterial blood pressure and cardiac interval |
| Spectral power of Mayer waves in dynamic arterial blood pressure magnitude abolished by phentolamine | |||
| Spectral power of Mayer waves in cardiac interval significantly reduced by phentolamine | |||
| Cerutti et al., 1994 | Conscious Sprague-Dawley rats with preserved baroreflex Conscious rats having preceding undergone sinoaortic denervation Previous studies by this group conducted upon Lyons rats | Mechanical interruption of the baroreflex (chronic) Ganglionic antagonism in rats not having undergone mechanical interruption of the baroreflex | Spectral power of Mayer waves in arterial pressure reduced by sinoaortic denervation |
| Spectral power of Mayer waves in arterial pressure reduced by pharmacological antagonism of sympathetic ganglia using chlorisondamine in sinoaortic-intact rats | |||
| Coherence of between cardiac interval and dynamic arterial blood pressure magnitude at the Mayer wave spectral band abolished by sinoaortic denervation | |||
| Coherence between cardiac interval and dynamic arterial pressure magnitude at the Mayer wave spectral band refractory to sinoaortic denervation | |||
| Just et al., 1995 | Conscious dogs | Mechanical interruption of the baroreflex (chronic) Cardiopulmonary deafferentation | Spectral power of low-frequency oscillations < 0.1 Hz augmented by sinoaortic denervation and cardiopulmonary deafferentation |
| Hexamethonium | Spectral power of low-frequency oscillations unmodified by treatment with hexamethonium or prazosin Hexamethonium and prazosin prevented augmentation of spectral power of low frequency oscillations successive to sinoaortic denervation and cardiopulmonary deafferentation | ||
| Prazosin | |||
| Stauss et al., 1995 | Normotensive Wistar-Kyoto and Sprague-Dawley rats Spontaneously hypertensive rats (SHR) Transgenic rats (TGR) subjected to mutation of the Ren-2 gene | Splanchnic sympathetic neural efferent discharge and dynamic arterial blood pressure Pharmacological antagonism of a1 adrenergic receptors | Mean arterial pressure and resting sympathetic activity varied across rat strains |
| Mean arterial pressure higher in spontaneously-hypertensive compared with transgenic rats | |||
| Resting sympathetic activity higher in spontaneously hypertensive compared with Wistar Kyoto rats | |||
| Resting sympathetic activity lower in transgenic compared with Sprague-Dawley rats | |||
| Mayer and Traube–Hering waves present in dynamic arterial pressure magnitude and splanchnic sympathetic nerve activity | |||
| Spectral power of Mayer and Traube–Hering waves in arterial blood pressure and sympathetic neural efferent discharge reduced by pharmacological antagonism of a adrenergic receptor antagonism in Wistar Kyoto, Sprague Dawley, and transgenic rats possessing Ren-2 mutation | |||
| Spectral power of Mayer and Traube–Hering waves unmodified by pharmacological antagonism of a adrenergic receptors | |||
| Spectral power of Mayer and Traube–Hering waves uncorrelated with resting sympathetic neural efferent discharge | |||
| Jacob et al., 1995 | Ketamine acepromazine maleate-anesthetized rats | Mechanical interruption of baroreflex (i.e., sinoaortic denervation) Pharmacological ganglionic antagonism by chlorisondamine | Mayer and Traube–Hering waves evident and prominent in arterial pressure spectra |
| Mayer wave peak abolished by sinoaortic denervation | |||
| Mayer wave peak abolished by pharmacological antagonism of ganglia with chlorisondamine in rats not having undergone sinoaortic denervation | |||
| Julien et al., 1995 | Conscious rats | Mechanical interruption of the baroreflexGuanethidine sympatholysis | Spectral power of Mayer and Traube–Hering waves in dynamic arterial pressure magnitude |
| reduced 54% by sinoaortic denervation | |||
| Spectral power of Mayer and Traube–Hering waves in dynamic arterial pressure magnitude reduced 85% by sympatholysis induced by treatment with guanethidine | |||
| Traube–Hering waves unmodified by sinoaortic denervation or sympatholysis | |||
| Montano et al., 1995 | Unanesthetized decerebrate cats having undergone sinoaortic denervation | Mechanical interruption of the baroreflex | Mayer and Traube–Hering waves variably present in sympathetic-related neurons residing within the medullary division of the lateral tegmental field, |
| rostral ventrolateral medulla, caudal ventrolateral medulla, and caudal raphe | |||
| Mayer and Traube–Hering waves present in dynamic arterial blood pressure magnitude | |||
| Coherence between sympathetic-related neuronal discharge and dynamic arterial pressure at at Mayer and Traube–Hering spectral bands | |||
| Montano et al., 1996 | Unanesthetized decerebrate cats having undergone sinoaortic denervation Urethane-anesthetized cats Having undergone sinoaortic denervation | Mechanical interruption of the baroreflex | Mayer and Traube–Hering waves variably present in sympathetic-related neurons residing within the medullary division of the lateral tegmental field, |
| rostral ventrolateral medulla, caudal ventrolateral medulla, and caudal raphe | |||
| Mayer and Traube–Hering waves present in dynamic arterial blood pressure magnitude | |||
| Coherence between sympathetic-related neuronal discharge and dynamic arterial pressure at at Mayer and Traube–Hering spectral bands | |||
| Stauss and Kregel, 1996 | Conscious rats | Stimulation of transected distal end of the splanchnic nerve Recordings of mesenteric artery resistance and blood pressure | Stimulating the transected distal end of the splanchnic nerve generated spectra in mesenteric arterial resistance with central tendencies corresponding with stimulation frequency |
| The greatest response occurred with stimulation frequencies between 0.2 and 0.5 Hz | |||
| Oscillations of mesenteric resistance generated corresponding oscillations of dynamic arterial blood pressure magnitude | |||
| Stimulating degenerated segments of nerve failed to modify mesenteric arterial resistance | |||
| Stauss et al., 1997 | Conscious rats | Delivery of tetanic stimuli to neurons residing within the paraventricular nucleus β adrenergic receptor antagonists Muscarinic antagonists | Authors demonstrated differential responsivity of splanchnic sympathetic neural efferent discharge, dynamic arterial blood pressure magnitude, mesenteric arterial blood flow, and heart rate by different levels of stimulation of the paraventricular nucleus in the presence or absence of ganglionic antagonism |
| Optimal stimulation frequencies to generate oscillations of blood pressure, mesenteric arterial resistance, mesenteric arterial blood flow, and splanchnic nerve in the presence of intact ganglionic transmission were 0.2, 0.5, 0.5, and 1.0 Hz, respectively | |||
| Pharmacological antagonism of paravertebral ganglia abolished the development of oscillations in mesenteric arterial blood pressure, mesenteric arterial blood flow, and mesenteric arterial resistance | |||
| Stimulation of neurons residing within the paraventricular nucleus induced oscillations of splanchnic sympathetic neural efferent discharge in the presence or absence of pharmacological antagonism | |||
| Janssen et al., 1997 | Conscious rabbits possessing, or having undergone mechanical interruption of, continuity of renal sympathetic nerve | Moderate hypoxia | Amplitude of renal sympathetic neural efferent discharge and renal arteriolar tone augmented by moderate hypoxia in rats not having undergone renal denervation Renal blood flow reduced by moderate hypoxia |
| Amplitude of renal sympathetic neural efferent discharge, though not renal arteriolar tone, augmented by moderate hypoxia in rats having undergone renal denervation | |||
| Oscillations exhibiting a central frequency approximating 0.3 Hz correlated between renal sympathetic neural efferent discharge and renal blood flow induced by moderate hypoxia | |||
| Oscillations of the renal sympathetic neural efferent discharge transmitted to renal blood flow exhibiting a transfer function gain of 0.1 at frequencies exceeding 0.5 Hz | |||
| Bertram et al., 1998 | Urethane-anesthetized rats | Stimulation of the aortic depressor nerve Pharmacological antagonists of a adrenergic receptors Pharmacological antagonism of ganglia | Mayer waves induced in dynamic arterial pressure magnitude by sub-tetatnic delivery of electrical stimuli to the aortic depressor nerve |
| Amplitude of Mayer waves in dynamic arterial pressure magnitude attenuated by pharmacological antagonism of a adrenergic receptors and abolished by pharmacological antagonism of paravertebral chain sympathetic ganglia | |||
| Montano et al., 2000 | Unanesthetized intercollicularly decerebrated cats having undergone vagotomy | Mechanical interruption of the baroreflex Mechanical interruption of spinomedullary continuity | Mayer waves in sympathetic neural efferent discharge and dynamic arterial pressure magnitude proved recalcitrant to mechanical interruption of the baroreflex and cervicomedullary continuity |
| Van de Borne et al., 2001 | Recipients of heart transplants of the family Homo, genus sapiens, and species sapiens Hypertensive individuals not having undergone transplantation | Recordings of dynamic arterial blood pressure and cardiac interval | Restoration of coherence between cardiac interval and arterial pressure at the Mayer wave spectral band |
| Progressive dynamic augmentation of sympathetic neural efferent discharge successive to transplantation of cardiac allograft likely reflecting sympathetic reinnervation of sinoatrial node | |||
| Julien et al., 2003 | Conscious rats possessing, or having undergone mechanical interruption of, continuity of the vagus and carotid sinus nerves | Mechanical interruption of the baroreflex | High coherence between renal sympathetic neural efferent discharge and dynamic arterial blood pressure magnitude at the Mayer wave spectral band |
| Spectral power of Traube–Hering waves in renal sympathetic neural efferent discharge and dynamic arterial blood pressure magnitude unmodified by chronic mechanical interruption of the baroreflex | |||
| Spectral power of Mayer waves in renal sympathetic neural efferent discharge and dynamic arterial blood pressure magnitude | |||
| significantly reduced by chronic mechanical interruption of the baroreflex | |||
| Transfer function between renal sympathetic neural efferent discharge and dynamic arterial blood pressure magnitude consistent with a second-order low-pass filter in rats having undergone mechanical interruption of the baroreflex | |||
| Barrès et al., 2004 | Conscious rats possessing, or having undergone mechanical interruption of, continuity of the vagus and carotid sinus nerves | Jetted streams of air | Mayer waves (0.27–0.74 Hz band) present in arterial pressure and renal sympathetic nerve activity in sinoaortic intact condition |
| Non-zero coherence between dynamic arterial pressure and renal sympathetic neural efferent discharge at the Mayer wave spectral band present in rats not having undergone mechanical interruption of the baroreflex | |||
| Spectral power of, and coherence between dynamic arterial blood presure magnitude and renal sympathetic neural efferent discharge at, Mayer waves augmented by jetted streams of air | |||
| Spectral power at the Mayer wave spectral band reduced by mechanical interruption of the baroreflex and augmented by jetted streams of air | |||
| Kanbar et al., 2008 | Conscious freely-exploring rats | Intravenous bolus injection of phenylephrine (i.e., baroloading) | Baroreflex sensitivity greater in renal, compared with lumbar, sympathetic neural efferent discharge |
| Intravenous bolus injection of nitroprusside (i.e., barounloading) | Mayer waves present in renal and lumbar sympathetic neural efferent discharge exhibited an approximate central tendency of 0.4 Hz | ||
| Morris et al., 2010 | Vagus intact and Vagotomized unanesthetized decerebrate cats having undergone mechanical interruption of the vagus nerve | Mechanical interruption of vagal continuity | Mayer waves present in the spectra of recordings of neurons residing within the medullary raphe and metencephalon |
| Ott et al., 2011 | Unanesthetized decerebrate cats having undergone mechanical interruption of vagal continuity | Mechanical interruption of vagal continuity | Mayer waves present in the spectra of recordings of neurons residing within the retrotrapezoid nucleus, parafacial respiratory group, Botzinger complex, and ventral respiratory group |
CVLM, caudal ventrolateral medulla; mLTF, medullary division of the lateral tegmental field; RVLM, rostral ventrolateral medulla; SHR, spontaneously hypertensive rat; TGR, transgenic rat.
Stringent coupling amongst sympathetic-related propriobulbar interneuronal microcircuit oscillators and cardiac vagal preganglionic neurons may synchronize Mayer waves distributing to disparate sympathetic and parasympathetic neural efferent discharge (Montano et al., 1995, 1996, 2000). Common genesis and presence of Mayer waves by neurons exhibiting unitary discharge correlated or uncorrelated with dynamic arterial pressure magnitude residing within the bulb indicates the set of oscillations may be emergently generated by distinct sets of neural circuits. Correlation of dynamic arterial pressure magnitude with phrenic and locomotor neural efferent discharge at the Mayer wave frequency band in unanesthetized decerebrate cats indicates supraspinal sympathetic-related interneuronal microcircuit oscillators must dynamically interact with propriospinal interneuronal microciruict oscillators generating the locomotor rhythm (Wienecke et al., 2015). Inducibility of Mayer waves by hypercapnia, hypoxia, and topical application of substance P, neurokinin A, and neurotensin suggests disturbing a linear or non-linear entity, interactions by which amongst each other, provokes or amplifies neural circuit hysteresis chiefly generative de la oscillations (Haxhiu et al., 1989; Wienecke et al., 2015). To the end of ontogenically recapitulating very low frequency oscillations of dynamic arterial blood pressure magnitude in cats (Figure 7; Preiss and Polosa, 1974), synchronously-correlated phase-shifted oscillations of dynamic arterial pressure magnitude and respiratory-related neural discharge were revealed in an unanesthetized supracollicularly decerebrated adult rat having undergone interruption of chemoreceptor and baroreceptor inputs (Figure 8), characterized by potent and short-lived pressor responses and correlated rapid-onset prominent transient tachypneic hyperpnea with exceptionally consistent regularity, suggesting emergent derivative genesis of Mayer waves by agitation of crossmodal coupling among respiratory-related, sympathetic-related, parasympathetic-related, and locomotor pattern generators. Contemporaneous recordings of sympathetic- and parasympathetic-related neuronal and neural efferent discharge may allow us to successively dissect the experimentally-evident behavior contributing to autonomorespiratory coupling in intra-neuraxially-extant sympathetic-related and parasympathetic-related interneuronal microcircuit oscillators.
FIGURE 7.
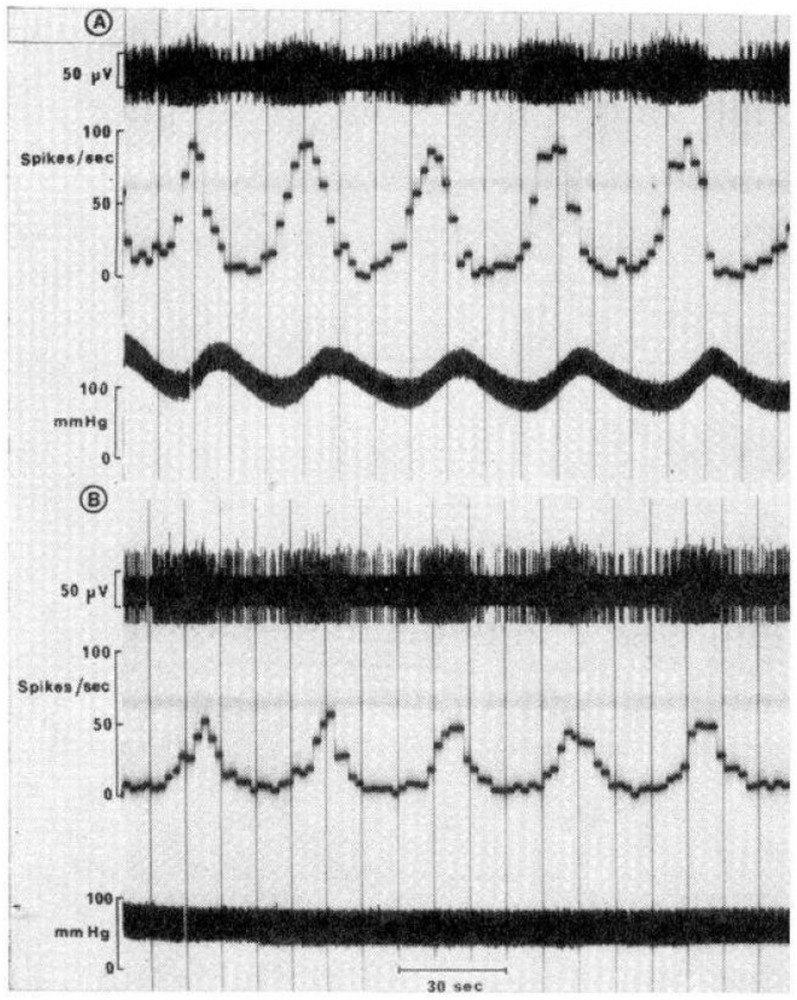
Very-low-frequency oscillations of upper thoracic preganglionic sympathetic neurons and arterial pressure in a Nembutal-anesthetized cat. (A) Recordings of an intermediolateral cell column preganglionic sympathetic neuron conducted contemporaneously with the acquisition of dynamic arterial pressure magnitude. Unitary recordings of the preganglionic sympathetic neuron reveal regular fluctuations oscillating with a frequency corresponding with vasogenic autorhythmicity. Time constant integration of unitary discharge of action potentials expressed as frequency readily evidences regularly rhythmic oscillatory pattern of the discharge. The oscillations are synchronized, though out-of-phase, with the arterial pressure waveform recording. Peaks of preganglionic sympathetic neuronal firing frequency precede peaks of dynamic arterial pressure magnitude by a time delay corresponding with the delay of neurosynaptic transmission across the vascular neuroeffector junction and propagation of changes of net arteriolar tone throughout the vascular tree. (B) Pharmacological antagonism of a adrenergic receptors utilizing phentolamine effectively eliminates oscillations from dynamic arterial pressure magnitude, though these waves persist in preganglionic sympathetic neuronal discharge, exhibiting a central frequency approximating that of vasogenic autorhythmicity. Thus, interfering with vascular neuroeffector electrochemical transduction prevents very low frequency oscillations from becoming manifest in hemodynamic variabilities peripherally. Modified with permission from Preiss and Polosa (1974).
FIGURE 8.
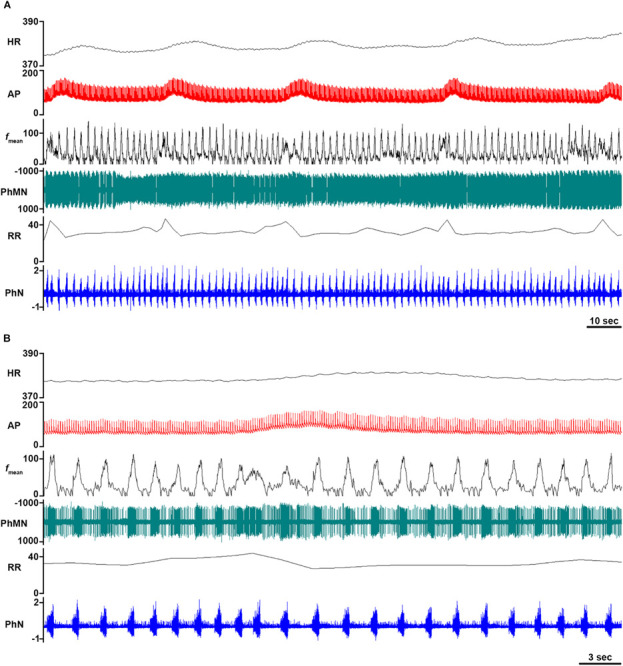
Very-low-frequency oscillations in an unanesthetized supracollicularly decerebrate rat. (A) Oscillations exhibiting a frequency corresponding with vasogenic autorhymicity are manifest within dynamic arterial pressure magnitude, phrenic motoneuronal recordings, and phrenic nerve discharge in an unanesthetized decerebrate rat. Heart rate, arterial blood pressure, and phrenic nerve bursting frequency and amplitude exhibit concurrent oscillatory augmentations. (B) Magnified epoch from panel (A). AP, arterial pressure; fmean, mean PhMN unit neuronal dischargefrequency; HR, heart rate; RR, respiratory rate; PhMN, phrenic motoneuron; PhN, phrenic nerve. Neurogram amplitude in volts. Timescale bars (seconds) shown in lower right-hand corner of each panel.
Modeling Mayer Wave Generation, Modulation, and Propagation
The presence of Mayer waves in hemodynamic spectra ontogenically recapitulates biophysical features of the baroreflex, including nonlinearity, negative feedback control, time delay, and emergent resonant frequency of the baroreflex (Figures 9, 10; Myers et al., 2001; Seydnejad and Kitney, 2001). Baroreflex instability occurring when gain conforms to unity at the resonant frequency generates autochthonous oscillations in sympathetic neural efferent discharge, hemodynamic variables, and cardiac interval (Myers et al., 2001; Vielle, 2005; Julien, 2006). Should gain at the baroreflex resonant frequency exceed unity, oscillatory amplitude of feedback modulatory input (i.e., carotid sinus pressure) progressively increases (Seydnejad and Kitney, 2001). Biophysical properties of the baroreflex emergently generate non-linearities imposing limits upon Mayer wave amplitude deflections and restrain baroreflex gain from increasing beyond unity (Seydnejad and Kitney, 2001). A simple model precisely explaining genesis, and recapitulating dynamics, of Mayer waves predicated upon baroreflex mechanisms, though wholly insufficient, utilizes linear methods exhibiting dual input and output variables (i.e., heart rate and sympathetic-related activity) derived from Poiseuille’s law (Myers et al., 2001). The model incorporates two weighted inputs, each with a single time lead, and allows direct assessment of time relations between, and relative contributions of, oscillations of cardiac interval and sympathetic-related activity to generate and amplify power at the Mayer wave spectral band. The model characterizes trait and state differences in the genesis of Mayer waves and effectively explains approximately half of the power contained within the Mayer wave spectral band (Myers et al., 2001). According to the chief tenets presented by this model, sympathetic neural efferent discharge modulates amplitude of Mayer waves present within dynamic arterial pressure magnitude most powerfully at relatively augmented levels of basal sympathoexcitation. The model developed by Myers et al. (2001) accurately predicts behavior of Mayer waves, indicating a simple bivariate linear autoregressive model may reasonably predict nonlinear behavior despite the inherent limitations inherent to a linear model and fruitful hypotheses subject to empirical interrogation. Accordingly, the mathematical relationships representing emergent genesis and dynamic properties of Mayer waves may be expressed in the form of nonlinear differential equations (Cavalcanti and Belardinelli, 1996; Czosnyka et al., 2018), difference equations (Cushing, 2019), non-linear oscillators (Zhu et al., 2019), regularization theory (Chen and Haykin, 2002), non-linear fluid dynamics (Olufsen et al., 2012), non-linear time series analysis (de la Cruz et al., 2019), and systems identification, in order to investigate interactions amongst the oscillations (Plakias and Boutalis, 2019).
FIGURE 9.
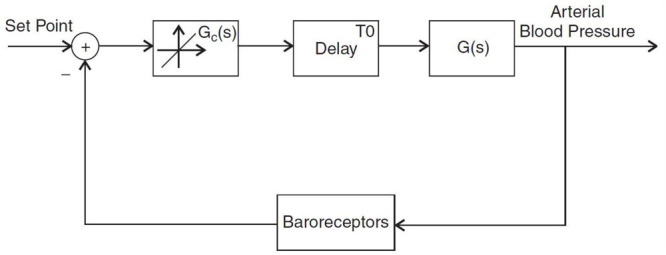
Linear model of the baroreflex. Arterial pressure inputs relay through an element representing a constant gain with respect to the set point with a time delay imposed upon the circuit. The resonant frequency represents the frequency at which the phase angle falls to zero. The baroreceptor emergently generates corrective modulation of dynamic arterial pressure magnitude according to baroreflex- and crossmodally-modulated sympathetic and parasympathetic discharge. Modified with permission from Seydnejad and Kitney (2001).
FIGURE 10.
Dual input model. Ascribing differential weighing to waveform variabilities successively follows filtering and normalizing heart rate (HR) and muscle sympathetic nerve activity (SNA) and arithmetic summation to generate estimations of dynamic mean arterial pressure (MAP). Modified with permission from Myers et al. (2001).
We present a conceptual neurobiological framework through which to apprehend the development of a centrogenic model explaining initiation, maintenance, and propagation of Mayer waves, multivariately modulated by baroreflex mechanisms and retro-arterially propagated and neuro-interstitially mechanotransductively conveyed oscillations of arteriolar diameter (Seydnejad and Kitney, 2001). A model predicated upon generation of Mayer waves by propriobulbar and propriospinal interneuronal microcircuit oscillators residing within the brainstem and spinal cord essentially becomes a modified form of a composite of the constituent nonlinear transforms. Signaling techniques developed by Baselli et al. (2002) identified oscillations independent of the baroreceptor resonant frequency, putatively ontogenically recapitulating the behavior of rhombomyelic (brainstem and spinal cord) propriobulbar interneuronal microcircuits underlying the emergent genesis of Mayer waves. According to a simple framework, brainstem and spinal cord Mayer wave microcircuit generators oscillate with a frequency conforming to the species-specific Mayer wave central tendency. The oscillations propagate through propriobulbar and propriospinal interneuronal microcircuit oscillators, sympathetic neural efferent activity, and vascular smooth muscle cell discharge and are successively modulate amplitude and period of hemodynamic variables (i.e., arterial pressure, peripheral arterial resistance, and blood flow). Excitatory and inhibitory axodendritic and/or axosomatic inputs from proximal and distal neuronal elements emergently constituting Mayer wave generators amplify inter-neuronal, intra-microcircuit, and inter-microcircuit dynamic emergent network synchrony (see Montano et al., 1995, 1996, 2000), modulated by oscillations of baroreceptor discharge (Barrès et al., 2004) and the influences of intra-neuraxial and intra-neuraxial-extra-neuraxial hysteresis of correlated oscillations (Julien, 2006).
Mayer waves manifest in neuronal recordings of propriobulbar and propriospinal interneuronal microcircuit oscillators are chiefly generated by oscillations of arteriolar diameter conveyed upon neuronal membranes and biophysical properties (i.e., somatodendritic propagation and axonal micro-propagation of electrotonic graded potentials, activation and inactivation kinetics of membrane ion channels) via mechanotransductive propagation through the neural interstitium (see Barcroft and Nisimaru, 1932; Siegel et al., 1976, 1984; Fuji et al., 1990; Ursino et al., 1992). These waves are subject to modulation by the baroreflex and retro-arterial propagation of oscillations of arteriolar diameter (Julien, 2006). Let us consider an aggregate of arteriolar oscillations generated by the microvasculature mechanotransductively propagating through the neural interstitium and conveyed upon, and successively creating dynamic ripples of, somatodendritic membranes and axonal spiking. The dynamic and multivariate integration of arteriogenic oscillations creates analogous and pseudo-harmonic frequency bands manifest in individual and population neuronal spectra. In a manner of reference, “the rhythmic beating of the vessels generates beating of the neurons.” A set of transfer functions may express dynamic mechanotransductive propagation of these waves throughout the neural interstitium and modulation of supraspinal and spinal sympathetic interneuronal microcircuit oscillators by barosensitive units residing within the medial and interstitial divisions of the nucleus tractus solitarius. The entire model assumes a set of multimodally interacting multivariate differential equations expressing empirically determined transfer functions and oscillatory interactions multivariately reciprocally influencing the spectral oscillations.
Neuronally Conveyed Arteriolar Oscillations May Generate Mayer Waves
Autochthonously generated neural oscillations insufficiently explain emergent genesis of Mayer waves. The majority of investigators concur oscillations of arteriolar diameter (i.e., vasogenic autorhythmicity; see Siegel et al., 1976, 1984; Fuji et al., 1990; Ursino et al., 1992; Rembold and Chen, 1998), an intrinsic property of vessels obviating the necessity of neural inputs, generates very low frequency oscillations manifest in dynamic arterial blood pressure magnitude, peripheral arterial resistance, and blood flow waveforms (see Barcroft and Nisimaru, 1932; Nisimaru, 1984; Ursino et al., 1992). Authors typically cite the central tendency of these waves to range between 0.025 and 0.075 Hz (∼0.01 to <0.1 Hz) (Seydnejad and Kitney, 2001). Jacob et al. (1995) conducted time epoch and frequency “kernel-binned” Wigner-Ville distribution time frequency spectral representations of arterial pressure spectra in ketamine acepromazine maleate-anesthetized rats to reveal a spectral band in arterial pressure waveform exhibiting a frequency approximating 0.05 Hz (see Marchenko and Rogers, 2006a, b, 2007, 2009; Marchenko et al., 2012; Ghali and Marchenko, 2013), analogous with the central tendency of the frequency of the spectral band generated by vasogenic autorhythmicity (Barcroft and Nisimaru, 1932; Siegel et al., 1976, 1984; Nisimaru, 1984; Fuji et al., 1990; Ursino et al., 1992). Spectra of cerebral hemodynamics and oxygenation indices in human subjects exhibit Mayer waves with a central frequency tending toward 0.1 Hz (Yucel et al., 2016).
Lachert et al. (2019) conducted an elegant study contemporaneously recording electroencephalographic activity, cerebral blood oxygenation, arterial blood pressure, and electrocardiographic signals in human subjects, providing evidence indicating interactions between low frequency oscillations corresponding with Mayer waves and very low frequency oscillations corresponding with arteriolar oscillaitons by utilizing multivariate autoregressive models and a directed transfer function premised upon the Granger causality principle, indicating arterial pressure oscillations reciprocally modulate analogous oscillations of cardiac interval. The work of Lachert et al. (2019) thus provides a logical framework guiding the inspired efforts of appropriately enthused investigators seeking to evaluate emergent neural network generation of, and interactions amongst, Mayer waves and oscillations of arteriolar diameter amongst disparately distributed neuronal and vascular arrays. Authors have also observed very low frequency oscillations in astrocytes, pancreatic β islet cells, retinal arteriolar vascular smooth muscle cells (Jeffries et al., 2010), and retinal ganglion cells. Astrocytic calcium oscillations characteristically exhibit a frequency approximating 0.03 Hz, consistent with the range of the central tendency of oscillations of arteriolar diameter (Jeffries et al., 2010). Accordingly, vasogenic autorhythmicity may be generated by oscillations of cytosolic concentrations of cyclic adenosine monophosphate and calcium within vascular smooth myocytes (see Siegel et al., 1976, 1984; Fuji et al., 1990; Ursino et al., 1992).
A tenable theory posits Mayer waves may be chiefly generated by oscillations of arteriolar diameter propagating to, and permeating to supraspinal sympathetic-related interneuronal microcircuit oscillators through successive propagation of the oscillations successively through the perivascular fluid compartment and neural interstitium (Figure 11 and Table 4; Siegel et al., 1976, 1984; Fuji et al., 1990; Ursino et al., 1992). Arteriogenic neuronal oscillations propagating through supraspinal sympathetic-related interneuronal microcircuit oscillators (e.g., medullary lateral tegmental field, RVLM) may be successively pauci-synaptically-conveyed to preganglionic and postganglionic sympathetic-related neurons and effector sinoatrial and atrioventricular nodes, atrial and ventricular cardiomyocytes, and vascular neuroeffector junctions at arterial, arteriolar, and venular media, and sparsely-innervated venous media to generate Mayer wave oscillations of arteriolar diameter, peripheral resistance, blood flow, and arterial blood pressure. Endogenously-generated oscillations of arteriolar diameter and resistance retro-arterially propagate to generate analogous oscillations of dynamic arterial blood pressure magnitude and blood flow, coordinately conveyed to sympathetic-related propriobulbar interneuronal microcircuit oscillators through the cerebral microvasculature via the neural interstitium and central sympathetic-related interneuronal microcircuit oscillators via barosensitive nucleus tractus solitarius units. These mechanisms generate reverberating oscillatory loops conducted through neural circuits in parallel and in series. Integer pseudo-harmonics of retro-arterially propagated oscillations of arteriolar diameter may entrain, be relayed to, and amplify spectral power of sympathetic-related and parasympathetic-related interneuronal microcircuit oscillators residing within the bulb via oscillations of baroreceptor discharge (Julien, 2006). Oscillations of dynamic arterial blood pressure magnitude are conveyed centrally to propriobulbar interneurons emergently constituting sympathetic interneuronal microcircuit oscillators in parallel through the regularly rhythmic discharge of afferent oscillatory barosensitive nucleus tractus solitarius unitary inputs.
FIGURE 11.
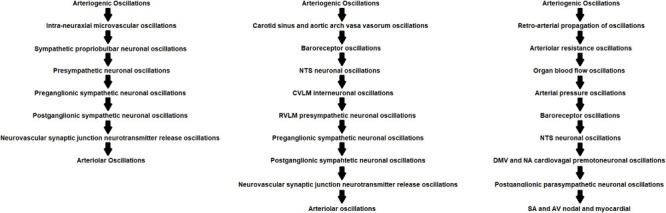
Neuronal-vascular interactions may generate Mayer waves. CVLM, caudal ventrolateral medulla; DMV, dorsal motor nucleus of the vagus; RVLM, rostral ventrolateral medulla; NA, nucleus ambiguus; NTS, nucleus tractus solitarius.
The set of findings collectively lends credence to the hypothesis emergent generation of Mayer waves by intra-neuraxial vasomotion via mechanotransduction of the rhythms propagated and conducted through the neural interstitium to propriobulbar interneuronal microcircuits and by extra-neuraxial vasomotion through retro-arterial propagation of oscillations of arteriolar diameter. Though duality of Mayer wave persistence in unitary discharge of sympathetic-related neuronal recordings and sympathetic-related neural efferent activity recalcitrant to sinoaortic denervation constitutes powerful inferential evidence indicating chief genesis by supraspinal interneuronal microcircuit oscillators, we believe presence of Mayer waves in neural networks (Montano et al., 1996) indicates a generalized tendency of supraspinal and spinal neural networks to oscillate at the Mayer wave central tendency, consistent with the tenet arteriolar oscillations mechanotransduced and propagated through the neural interstitium to neurons residing within the bulb generate oscillations of neuronal spiking (Montano et al., 1992, 1995, 1996, 1998, 2000; Morris et al., 2010; Ott et al., 2011), distributing diffusely throughout rhombomyelic neural networks (see Scarr, 2016 for precedence of these tenets). Emergently generated dynamic oscillatory synchrony presumably contributes to maintaining sympathetic-related vasoconstrictor tone and differentially regulating blood flow conveyed to tissues, though the execution of further studies are necessary in order to evaluate this set of conjectures and hypotheses and thus deduce the functional role of these most enigmatic of oscillations. Theoretically-extant intermediate integer pseudo-harmonics of oscillations of arteriolar diameter, characteristically absent from discharge variability spectra of empirically-recorded sympathetic-related neuronal activity, may be extant though inferior to the experimentally-discriminable threshold, with low spectral power insufficient to generate a distinct spectral peak. Some mechanism may thus specifically amplify higher-order pseudo-harmonics of very low frequency oscillations corresponding with Mayer waves, though lower order pseudo-harmonics remain indistinct from background spectral power.
Multimechanistic Dynamic Emergent Generation of Mayer Waves
Let us accordingly take the liberty of venturing beyond the limits of directly empirically-supported hypotheses, tenets, and conjectures. We have consequently proposed oscillations of arteriolar diameter (i.e., vasogenic autorhythmicity) may be conveyed to neurons constituting the sympathetic-related microcircuit oscillators and conveyed to sympathetic neural efferent discharge and hemodynamic oscillations incipiently generate Mayer waves (Figure 11). Interspecies variability of vascular smooth muscle cell contraction and relaxation kinetics may contribute to generating differences in time delay across the baroreflex loop, Mayer wave central frequency (Seydnejad and Kitney, 2001), and frequency of oscillations of arteriolar diameter (Siegel et al., 1976, 1984; Fuji et al., 1990; Ursino et al., 1992), exhibiting a frequency congruous with that of very low frequency oscillations present in, and correlated between, dynamic arterial blood pressure and splenic volume (see Barcroft and Nisimaru, 1932; Iriuchijima, 1984; Nisimaru, 1984). Differential vessel response latency to noradrenergic (Christ, 1995; Seyrek et al., 2011), purinergic (Alexander et al., 1999; Böhmer et al., 2010; Dǎnilǎ et al., 2017), and peptidergic excitatory sympathetic “neurono-vascular” synaptic drive may reflect differences in arteriolar diameter, architecture of the vascular tree, and mediator utilized at the smooth neuromuscular end-plate junction. Arterioloconstriction and venuloconstriction elicited by adenosine triphosphate elaborated from presynaptic end plates exhibit more rapid kinetics, compared with noradrenergic signaling. Saturation of vascular responses to sympathetic-related “neurono-vascular” synaptic inputs, the magnitude and dynamics of which may be coordinately determined by propriobulbar interneuronal microcircuit oscillators, and influenced by oscillatory baroreceptor discharge (Stauss et al., 1997; Bertram et al., 1998), curtails amplitude of Mayer wave oscillations (Julien, 2006).
Interpreting the findings collectively generated by investigations interrogating mechanisms contributing to the genesis of Mayer waves and oscillations of arteriolar diameter in the context of remarkable findings by Preiss and Polosa (1974) (Figure 7) and our experimental observations (Figure 8) would seem to confirm arteriolar oscillations (i.e., vasogenic autorhythmicity; see Siegel et al., 1976, 1984; Fuji et al., 1990; Ursino et al., 1992) generate very low frequency oscillations and integer pseudo-harmonic Mayer waves of dynamic arterial pressure magnitude. We have observed rhythmic oscillatory fluctuations of dynamic arterial pressure magnitude exhibiting a frequency approximating 0.05 Hz commensurately evident in continuous recordings conducted on-line of phrenic motoneuronal firing rate and frequency and amplitude of phrenic nerve discharge (Figure 8), corresponding with the central tendency of the vasogenic autorhythmicity (∼0.05 Hz) in our experiments conducted upon trephined unanesthetized supracollicularly decerebrate rats, with continuity of Hering’s and vagal nerves preserved bilaterally. Preiss and Polosa (1974) analogously observed hemorrhage-induced rhythmic fluctuations of dynamic arterial pressure magnitude and discharge of thoracic T1 and T2 sympathetic preganglionic neuronal somata in Nembutal-anesthetized and unanesthetized midcollicularly decerebrated cats, though misinterpreted their data to indicate these oscillations represent Mayer waves. Analogous to our observations, these arterial pressure oscillations exhibited a central frequency significantly less than the central tendency of Mayer waves in cats (∼0.1 Hz), more closely approximated to the frequency of vasogenic autorhythmicity (∼0.03 Hz) (cf., Siegel et al., 1976, 1984; Fuji et al., 1990; Ursino et al., 1992).
Vasogenic autorhthmicity and multiplicative pseudo-harmonics thereof may consequently emergently generate analogous oscillations propagating through the perivascular fluid compartment and neural interstitium to neural elements to generate corresponding fluctuations of the somatodendritic membrane, axon hillock, axonal membrane, and neurosynaptic machinery (see Siegel et al., 1976, 1984; Fuji et al., 1990; Ursino et al., 1992). Mechano-oscillatory transduction of oscillations of arteriolar diameter to somatodendritic neurolemmal membranes varies according to visco-elastic properties of the neural interstitium. We suggest hemorrhage-induced generation and amplification of Mayer waves (see Andersson et al., 1950; Preiss and Polosa, 1974) may reflect amplification of vibrations propagating throughout the interstitial tissue or loss of tissue fluid-mediated buffering of neural interstitial tissue oscillations dynamically generated by oscillations of arteriolar diameter resulting from contraction of the neural tissue. Neural nets constituted by sympathetic-related interneuronal microcircuit oscillators transduce and integrate neural interstitial oscillations generated by oscillations of arteriolar diameter and/or generate integer pseudo-harmonics thereof, propagateing throughout propriobulbar interneuronal and presympathetic bulbospinal neuronal microcircuit oscillators extant throughout the rhombomyelic neuraxis, generating fluctuations exhibiting a central frequency approximating that of the vasogenic autorhtyhmicity in dynamic arterial blood pressure magnitude, demonstrated in Nembutal-anesthetized cats (Preiss and Polosa, 1974; Figure 7) and by in rats having undergone supracollicular decerebration and successful weaning from anesthesia (unpublished results; Figure 8). A given neuron perturbed by arteriogenic neural interstitial oscillations may transduce analogous frequency components or emergently generate a pseudo-harmonic derivative thereof, a hypothesis presented and espoused by van Brederode and Berger (2008) to explain generation of high frequency oscillations in respiratory-related neural spectra through spatiotemporal integration of out-of-phase synchronous medium-frequency oscillations. Hysteresis generated by autochthonously generated arteriolar oscillations and oscillatory perturbations imposed upon vascular smooth myocytes by sympathetic innervation may contribute to emergent genesis of Mayer waves and complex frequency components of neural and vascular spectral variability. In order to validate these mechanistic conjectures, it shall thus prove requisite to initially empirically demonstrate these waves are indeed generated endogenously by autochthonous oscillations of the vessels and vascular smooth myocytes, by demonstrating rhythmic oscillations of the arterioles persist successive to sympathetic denervation and denudation of the adventitia. Subsequently, we must empirically detect and/or visualize micro-oscillations of the neural interstitium and neuronal membranes. Simulation studies may prove especially illuminative in evolving our understanding of the effects of somatodendritic neurolemmal oscillations upon membrane biophysical properties.
Arteriogenic Oscillations of Neuronal Membranes and Neuronal Biophysical Properties
Arteriogenic neuronal oscillations deflecting somatodendritic and axonal neuronal membranes may generate nano-oscillatory or micro-oscillatory variability of electrotonically-propagated graded somatodendritic and axonal potentials, by conferring an oscillatory perturbation upon somatodendritic space and time constants (cf., Hodgkin and Huxley, 1945, 1952a,b). If true, time-dependent decay of electrotonically-propagated graded excitatory and inhibitory postsynaptic potentials and currents may be governed by biophysical membrane properties and micro-oscillatory perturbations of somatodendritic space and time values. We venture to propose arteriogenic neuronal oscillations have their chief effect upon neuronal spiking by conferring upon voltage-gated sodium channels an oscillatory perturbation of activation, inactivation, and deinactivation bio-organic mechanisms and kinetics. Flux through voltage-gated sodium channels generates the rising phase of successive action potentials (Hodgkin and Huxley, 1945, 1952a,b). Rapid inactivation of the voltage-gated sodium channel occurs via the swinging action of a side chain constituted by amino acid residues configured in the form of a ball-and-chain physically impeding the flow of charged monovalent sodium cations through the membrane ion channel pore and, in conjunction with the opening of repolarizing potassium channels, generates the falling phase of the action potential (Hodgkin and Huxley, 1945, 1952a,b). Membrane voltage hyperpolarizes to values more negative than dynamic resting undulations and gradually returns to baseline as repolarizing potassium currents inactivate (Hodgkin and Huxley, 1945, 1952a,b). The electrogenic sodium potassium adenosine triphosphatase contributes to maintaining electronegativity of the resting transmembrane voltage gradient (Hodgkin and Huxley, 1945, 1952a,b) (N.B. Our use of the term membrane voltage refers to transmembrane voltage difference at the cytosolic side of the neurolemmal membrane with respect to an extracellular matrix voltage of zero millivolts). The neuronal tendency to generate action potentials successive to suprathreshold membrane voltage occurs in parallel with voltage-gated sodium channel de-inactivation, a process exhibiting slower kinetics compared with channel activation or inactivation (Hodgkin and Huxley, 1945, 1952a,b).
Arteriogenic oscillations propagating through somatodendritic and axonal membranes amplify decomposable nested spectral power through vibrations of cytoskeletal elements, generating powerful oscillations of membrane ion channels and their activation and inactivation kinetics, through vibratory oscillations of covalent bonds and molecular orbitals linking amino acid residues. We accordingly suggest oscillations of the ball-and-chain-like string of amino acid residues inactivatingly gating the voltage-gated sodium channel specifically generates oscillatory perturbations contributing quite powerfully to emergently generating oscillations of action potential discharge by neurons. Arteriogenic neuronal oscillations may generate micro-oscillatory variability of distinct conductances perpendicularly traversing the membrane via hydrophilic channel pores, in effect generating oscillations of dynamic current traversing the neurolemmal phopspholipid bilayer and frequency of action potentials propagating from axon hillock to axon terminal. Current, voltage, and membrane conductances vary interdependently and time-dependently. The presence of distinct isoforms of membrane ion channels belonging within the same family (e.g., voltage-gated sodium channels) subjectable to differential modulation by neurolemmal oscillations may constitute a biomolecular substrate by which out-of-phase summation of the oscillations may generate integer pseudo-harmonics of conveyed oscillatory frequency (i.e., Mayer waves generated by oscillations of arteriolar diameter). Let us consider the activation-inactivation-deinactivation cycle time of the voltage gated sodium channel, †(VGNa+) reflecting the sum of activation †act, inactivation (†inact), and deinactivation (†deinact) time constants:. †(VGNa +)=†act + †inact + †deinactThe dynamic voltage-gated sodium channel time value, Λ(VGNa +)(τ)oscillates according to the frequency of oscillations of arteriolar diameter, γ and a subtended amplitude modifiable by the Yaşargilian modulus operator, Д expressing the visco-elastic properties of the neural interstitium, Λ(VGNa +)(τ) = Д[†(VGNa +)]sin(2πγτ) + [†(VGNa +)]. Oscillations of voltage-gated sodium channel activation, inactivation, and deinactivation time values, traditionally believed to be invariant, in turn, generate oscillations of maximal neuronal spiking frequency, ψ(τ)max according to. Oscillations conferred upon membrane ion channels studding the phospholipid bilayer of the axon terminal may contribute to hysteresis underlying the proposed set of neuronal dynamics. Net current flow across, and perpendicular with respect to, the neurolemmal membrane generates a wavefront of depolarization of the membrane voltage propagating parallel, and unidirectionally across, the membrane. The full evolution of the mathematical formalism employing multivariate, matrix, vector, and tensor calculus constitutes the subject of our current efforts (Hubbard and Hubbard, 2015). These conjectures are enchantingly beautiful, empirically interrogable, and plausible and elegantly recapitulate the experimental findings describing oscillatory variability in neural, cardiac interval, and hemodynamic spectra. These mechanisms may contribute to generating coherence amongst propriobulbar interneuronal microcircuit oscillators generating the respiratory rhythm and pattern, sympathetic oscillations, and ambiguual and dorsal medullary cardiovagal premotoneuronal spiking.
Somatodendritic Space and Time Constants
Mechanisms underlying the generation of Mayer Waves inform quantum neurophysiology. In evolving our mathematical formalism describing oscillations of the somatodendritic and axonal membranes of neurons and its biophysical properties, let us accordingly provide operant definitions of each of the entities and the units utilized to express the generated scalar values and magnitudes of the generated vectors. We express charge using Coulombs, (C) current (i.e., flux of charge per unit time) using amperes(A), voltage using volts (i.e., current multiplied by resistance)(V), resistance (i.e., voltage divided by resistance) using Ohms (Ω), resistivity (i.e., resistance per unit distance) using Ohms per meter (Ω/m), magnetic force (i.e., the permeability in a vacuum multiplied by the length of the wire divided by(2πr)) using Tesla, mass using grams or kilograms, force using Newtons or kilograms multiplied by meters divided by seconds squared (kgm/s2), velocity (i.e., change in distance per unit time) using meters per second (m/s), acceleration (i.e., change in velocity per unit time) using meters per seconds squared (m/s2), momentum (i.e., mass times velocity) using kilograms multiplied by meters divided by seconds (kgm/s), frequency (i.e., complete oscillatory cycles of a regular rhythm per unit time) using Hertz (Hz), period (i.e., duration of one complete oscillatory cycle of a regular rhythm) using inverse seconds (s−1), wavelength (i.e., wave velocity divided by wave frequency) using meters, (m) distance (i.e., change in position) using meters (m), time (i.e., duration between onset and offset events) using seconds (s), and energy (i.e., work or the potential to do work) using Joules (J). Any of these entities may be expressed as a scalar value, vector, set of vectors, vector field, or set of vector fields. Authors have classically used the dendritic length constant to represent the length along the neurolemmal membrane of the somatodendritic compartment an electrical potential will travel prior to decaying to nil may be represented by the dendritic length constant. This value may be more appropriately termed the somatodendritic length constant,λ (Kandel et al., 2000), varying in accordance with, and expressible as an operation of, membrane resistance, σm extracellular resistance, σo and cytosolic resistance, σiaccording to the following mathematical relationship:
Where ƛ represents the somatodendritic length constant, σm represents neuronal membrane σi resistance, represents intraneuronal cytoplasmic resistance, and σorepresents extracellular matrix resistance (Kandel et al., 2000). The equation expresses the somatodendritic space constant, ƛin terms of the square root of the arithmetic ratio of the membrane resistance, σm to the arithmetic sum of the intraneuronal cytoplasmic resistance, σi and extracellular matrix resistance,σo. The convention indicates the distance an electrotonically propagated potential will travel prior to decaying to nil is a constant scalar value. If we consider the extracellular matrix resistance, σo negligible, we generate the following proportionality accordingly:
The equation expresses the somatodendritic length constant, ƛ in terms of the square root of the arithmetic ratio of the membrane resistance, σm, to the intraneuronal cytoplasmic resistance, σi). The equation asserts the distance an electrotonically propagated potential, ƛ will travel prior to decaying to zero is constant. We may alternatively express the somatodendritic length constant, ƛ in terms of the square root of the arithmetic ratio of the product of the neuronal radius, r, and the neuronal membrane resistivity,ρm to the scalar double of the intraneuronal cytoplasmic resistivity,ρi:
Where ƛ represents the somatodendritic length constant, ρm represents neuronal membrane resistivity, and ρi represents the intraneuronal cytoplasmic resistivity (Kandel et al., 2000). The duration an electrotonically propagated potential will travel prior to decaying to zero may be represented by the product of the neuronal membrane resistance and the neuronal membrane capacitance:
Where the somatodendritic time constant, τ represents the duration an electrotonically conducted potential will travel prior to decaying to nil to vary according to the product of the membrane resistance σm, and the membrane capacitance,cm. The time constant, τ expresses the duration an electrotonically conducted potential will travel prior to decaying to nil. The resistivity of a material expresses the resistance density or units of resistance per units of surface area or volume. The presented formalism thus expresses the somatodendritic space constant in terms of the square root of the arithmetic ratio of the product of the neuronal radius and membrane resistivity with the scalar double of the intraneuronal cytoplasmic resistivity. The proportionality asserts constancy of the distance an electrotonically propagated potential will travel prior to decaying to nil. Neuronal membrane resistivity may be expressed as the ratio of membrane resistance to neuronal circumference:
Where ρm represents neuronal membrane resistivity and σm represents neuronal membrane resistance (Kandel et al., 2000). Neuronal membrane resistivity varies according to intraneuronal cytoplasmic resistance, σi divided by neuronal cross sectional area, effectively representing a measure of intraneuronal cytoplasmic resistance density. Accordingly:
Where ρi represents intraneuronal cytoplasmic resistivity and σi represents intraneuronal cytoplasmic resistance (Kandel et al., 2000). The intraneuronal cytoplasmic resistivity thus varies in proportion with the arithmetic ratio of intraneuronal cytoplasmic resistance σi to neuronal cross sectional area πr2 and represents a measure of intraneuronal cytoplasmic resistance density.
Monovariate Oscillations of the Somatodendritic Space Value
Arteriolar oscillations constituting the vasogenic autorhythmicity (Barcroft and Nisimaru, 1932) generate corresponding oscillations of the neural interstitium which propagate toward, and generate physical oscillations of, the somatodendritic and axonal membranes and neuronal biophysical properties. Let us accordingly preface our exposition of physical oscillations of the neuronal membrane and its biophysical properties generated by the vasogenic autorhythmicity mechanotransduced through the interstitium by presenting a mathematical relationship describing and characterizing vasogenic autorhythmicity generated oscillations of the somatodendritic space and time values and neurolemmal membrane and intraneuronal cytoplasmic resistivities. A sinusoidal wave oscillating in bidimensional Euclidean Cartesian coordinate space (Γ,τ) about the horizontal τ axis of zero takes the form, Γ(τ) = αsin(βτ) + μ where α represents wave amplitude, represents periodicity, and Γ = μ represents the Ψ intercept. Consequently, we seek to represent the somatodendritic space value as a function oscillating about a central tendency equal to the somatodendritic space constant, ƛ derived according to the classic equation, with an amplitude equivalent to the product of the Yaşargilian modulus operator, Υ, and the central tendency of the somatodendritic space constant, ƛ, and a frequency γ equivalent to the vasogenic autorhythmicity. We substitute the terms accordingly:
Where Γ(τ) is the time variant somatodendritic space function, yielding a time variant somatodendritic space value, Γ ƛ represents the classically derived somatodendritic space constant and central tendency of the oscillations, γ represents the frequency of the vasogenic autorhythmicity. The amplitude of the oscillations varies according to the product of the viscoelasticity Yaşargilian modulus operator, Y and the somatodendritic space value central tendency ƛ. The Yaşargilian modulus operator reflects biophysical mechanotransduction properties of the neural interstitium. Alternatively
We fix the wave with an amplitude ƛ of at time zero. We substitute for ƛ to generate the time variant somatodendritic space value accordingly:
We have accordingly generated a continuous monovariate function expressible in two-dimensional Euclidean Cartesian space yielding a time variant somatodendritic space value. Alternatively:
The rate of change of the somatodendritic space value with respect to time may be expressed as the first order derivative of the monovariate somatodendritic space function with γ stabilized as a constant:
Where 2πγcos(2πγτ)represents the first order derivative of the termsin(2πγτ). Alternatively:
The somatodendritic space function, Γ(τ) may accordingly be expressed simply as the improper integral of the first order derivative of the somatodendritic space function with respect to time, τ:
Alternatively:
Alternatively, presuming negligible extracellular matrix resistance, σo we may express the somatodendritic space function accordingly:
Alternatively:
The first order derivative expressing rate of change of the monovariate somatodendritic space function may be expressed accordingly:
Alternatively:
The somatodendritic space function,Γ(τ) assuming conditions of negligible extracellular matrix resistance, may alternatively be expressed as the integral of the first order derivative of the somatodendritic space wave function:
Alternatively:
The somatodendritic space function, Γ(τ) may alternatively be expressed in terms of the neurolemmal membrane and intraneuronal cytoplasmic resistivities:
Alternatively:
We generate the first order derivative of the somatodendritic space function in terms of neuronal membrane and intraneuronal cytoplasmic resistivities accordingly:
Alternatively:
The somatodendritic space wave function, Γ(τ) may thus alternatively be represented as the integral of the first order derivative of the somatodendritic space wave function:
Alternatively:
Monovariate Oscillations of the Somatodendritic Time Value
A sinusoidal wave oscillating in Euclidean Cartesian coordinate space (Ŧ,τ) about the horizontal τ axis of zero takes the form, Ŧ(τ) = asin(bτ) + m where a represents wave amplitude, represents periodicity, and (0,τ) represents the Ŧ intercept. Consequently, we seek to represent the somatodendritic time value as a function oscillating about a central tendency with a value equal to the somatodendritic time constant, τ, derived using the classic equation, with an amplitude equivalent to the product of the Yaşargilian modulus operator, Υ, and the central tendency of the somatodendritic time constant, τ and a frequency γ equivalent to the vasogenic autorhythmicity. We substitute the terms accordingly:
Where Ŧ(τ) expresses the time variant somatodendritic time function, yielding a time variant somatodendritic time value, Ŧ(τ), τ represents the classic somatodendritic time constant and central tendency of the oscillations, γ represents the frequency of the arteriolar oscillations. Oscillatory amplitude varies according with the product of the viscoelasticity Yaşargilian modulus operator, and the somatodendritic time value central tendency τ. The Yaşargilian modulus operator reflects biophysical mechanotransduction properties of the neural interstitium. Alternatively:
We fix the wave with an amplitude of τ at τ = 0. We substitute for τ to generate the time variant somatodendritic time value accordingly:
We have thus generated a continuous monovariate function expressible in two-dimensional Euclidean Cartesian space yielding a time variant somatodendritic time value. Alternatively:
Rate of change of the somatodendritic time value with respect to time may be expressed as the first order derivative of the monovariate somatodendritic with γ stabilized constant:
Alternatively:
Where 2πγcos(2πγτ) represents the first order derivative of the term sin(2πγτ). The somatodendritic time value function, Ŧ(τ) may accordingly be expressed simply as the line integral of the first order derivative of the somatodendritic time wave function with respect to time,τ:
Alternatively:
The somatodendritic time value function, Ŧ(τ) may alternatively be expressed in terms of the neurolemmal membrane and intraneuronal cytoplasmic resistivities:
Alternatively:
We derive the first order derivative of the somatodendritic time function in terms of the neuronal membrane and intraneuronal cytoplasmic resistivities accordingly:
Alternatively:
The somatodendritic time function, Ŧ(τ) may thus alternatively be represented as the line integral of the first order derivative of the somatodendritic time function:
Alternatively:
The somatodendritic time function Ŧ(τ), may alternatively be expressed in terms of neurolemmal membrane resistivity:
Alternatively:
We derive the first order derivative of the somatodendritic time function in terms of neuronal membrane and intraneuronal cytoplasmic resistivities accordingly:
Alternatively:
The somatodendritic time function, Ŧ(τ) may alternatively be represented as the line integral of the first order derivative of the somatodendritic time function:
Alternatively:
Summary and Synthesis
Mayer waves may synchronize overlapping propriobulbar interneuronal microcircuits constituting the respiratory rhythm and pattern generator, sympathetic oscillators, and cardiac vagal preganglionic neurons (Julien, 2006). Initially described by Sir Sigmund Mayer in the year 1876 in the arterial pressure waveform of anesthetized rabbits (Mayer, 1876), authors have since extensively observed these oscillations in recordings of hemodynamic variables, including the arterial pressure waveform, peripheral resistance, and blood flow (Killip, 1962; Cerutti et al., 1991a, b, 1994). Further authors would later reveal the presence of these oscillations in sympathetic neural efferent discharge and brainstem and spinal zones corresponding with sympathetic oscillators (e.g., mLTF, RVLM, CVLM, caudal raphe; Montano et al., 1995, 1996). The Mayer-wave central tendency proves highly consistent within, though the specific frequency band varies extensively across, species (Julien, 2006). The striking resemblance of the Mayer-wave central tendency to the species-specific baroreflex resonant frequency has led the majority of investigators to comfortably presume, and generate computational models premised upon, a baroreflex origin of these oscillations. Empirical interrogation of this conjecture has generated variable results and derivative interpretations. Sinoaortic denervation and effector sympathectomy variably reduces or abolishes spectral power contained within the Mayer wave frequency band. Refractoriness of Mayer-wave generation to barodeafferentation (Cerutti et al., 1994) lends credence to the hypothesis that these waves are chiefly generated by brainstem propriobulbar and spinal cord propriospinal interneuronal microcircuit oscillators and are likely modulated by the baroreflex (Julien, 2006). The presence of these waves in unitary discharge of medullary lateral tegmental field and RVLM neurons (contemporaneously exhibiting fast sympathetic rhythms [2–6 and 10 Hz bands]) in spectral variability in vagotomized pentobarbital-anesthetized and unanesthetized midcollicular (i.e., intercollicular) decerebrate cats supports the genesis of Mayer waves by supraspinal sympathetic microcircuit oscillators (Montano et al., 1995, 1996). Persistence of these waves following high cervical transection in vagotomized unanesthetized midcollicular decerebrate cats would seem to suggest that spinal sympathetic microcircuit oscillators generate these waves (Montano et al., 2000). The widespread presence of Mayer waves in brainstem sympathetic-related and non-sympathetic-related cells would seem to indicate a general tendency of neurons to oscillate at this frequency (Morris et al., 2010; Ott et al., 2011).
Conclusion
Sir Sigmund Mayer described oscillations of arterial pressure magnitude in anesthetized rabbits exhibiting a lesser frequency compared with respirophasic variations of blood pressure described a few years earlier by Traube in 1865 and Hering in 1869. The origins of Mayer waves remain a mystery. The works of Guyton, Harris, and Andersson in the 1950’s suggested baroreflex or chemoreflex mechanisms may chiefly generate of these oscillations. Authors would later demonstrate spectral power reduction, though persistence, of Mayer waves following sinoaortic denervation or pharmacological ganglionic antagonism, in most experiments, indicating supraspinal and/or spinal microcircuits oscillators may generate this rhythmic activity. Zones which may chiefly generate these oscillations include the medullary lateral tegmental field and RVLM, though our impression lead us to deduce these oscillations may constitute a rhythm expressed by most neurons. Persistence of these dynamic oscillations following cervicomedullary transection, indicates the myelic propriospinal interneuronal circuits may be independently capable of generating Mayer wave-like oscillations. Mayer waves generated intra-neuraxially propagate throughout propriospinal interneurons constituting brainstem and spinal cord microcircuits oscillators and are conveyed via sympathetic nerves to sympathetically innervated arterioles, becoming manifest in dynamic arterial pressure magnitude, peripheral resistance, and blood flow. We propose autochthonous arteriogenic oscillations propagating throughout the neural interstitium generate oscillations of neuronal membranes and neuronal biophysical properties leading to oscillations of electrotonically propagated graded somatodendritic and axonal potentials and neuronal spiking frequency. Out-of-phase summation of arteriogenic very low frequency oscillations may generate integer pseudo-harmonic Mayer waves. We have extended the formalism to characterize the novel subdisciplines of dynamic and quantum neurophysics and describe the behavior of entitities constituting invisible reality. In the words of Emeritus Professor Dr. V. Marchenko, “Everything is Waves.”
Data Availability Statement
All datasets generated for this study are included in the article/supplementary material.
Ethics Statement
All studies were in accordance with Karolinska Institutet, Stockholm, and Linköping ethical committee and with the 1964 Helsinki Declaration and its later amendments or comparable ethical standards.
Author Contributions
MG and GG: conception and design, acquisition of data, analysis and interpretation of data, drafting the article and critically revising for intellectual content, and approval of the final version of the manuscript.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Footnotes
Funding. This work was supported by the Vetenskapsrådet (#201900973, MG), Karolinska Institutet, och the United States Environmental Protection Agency.
References
- Alexander B., Gryf-Lowczowski J. V., Sherlock D., Salisbury J., Benjamin I. S. (1999). Paradoxical cholinergic and purinergic vascular reactivity of rabbit thoracic aorta cold-stored in University of Wisconsin solution. J. Pharm. Pharmacol. 51 623–630. 10.1211/0022357991772736 [DOI] [PubMed] [Google Scholar]
- Allers K. A., Richards N., Sultana S., Sudworth M., Dawkins T., Hawcock A. B., et al. (2010). Slow oscillations in vaginal blood flow: alterations during sexual arousal in rodents and humans. J. Sex Med. 7 1074–1087. 10.1111/j.1743-6109.2009.01465.x [DOI] [PubMed] [Google Scholar]
- Andersson B., Kenney R. A., Neil E. (1950). The role of the chemoceptors of the carotid and aortic regions in the production of the Mayer waves. Acta Physiol. Scand. 20 203–220. 10.1111/j.1748-1716.1950.tb00699.x [DOI] [PubMed] [Google Scholar]
- Armstrong M., Moore R. A. (2019). Physiology, Baroreceptors. StatPearls [Internet]. Treasure Island, FL: StatPearls Publishing. [PubMed] [Google Scholar]
- Barcroft J., Nisimaru Y. (1932). Rhythmical contraction of the spleen. J. Physiol. 74 294–298. 10.1113/jphysiol.1932.sp002848 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barrès C., Cheng Y., Julien C. (2004). Steady-state and dynamic responses of renal sympathetic nerve activity to air-jet stress in sinoaortic denervated rats. Hypertension 43 629–635. 10.1161/01.hyp.0000115384.01463.61 [DOI] [PubMed] [Google Scholar]
- Baselli G., Caiani E., Porta A., Montano N., Signorini M. G., Cerutti S. (2002). Biomedical signal processing and modeling in cardiovascular systems. Crit. Rev. Biomed. Eng. 30 55–84. 10.1615/critrevbiomedeng.v30.i123.40 [DOI] [PubMed] [Google Scholar]
- Bayliss W. M., Bradford J. R. (1894). The innervation of the vessels of the limbs. J Physiol. 16 10–158. 10.1113/jphysiol.1894.sp000491 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Becker B. K., Tian C., Zucker I. H., Wang H. J. (2016). Influence of brain-derived neurotrophic factor-tyrosine receptor kinase B signalling in the nucleus tractus solitarius on baroreflex sensitivity in rats with chronic heart failure. J. Physiol. 594 5711–5725. 10.1113/jp272318 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bertram D., Barrès C., Cheng Y., Julien C. (2000). Norepinephrine reuptake, baroreflex dynamics, and arterial pressure variability in rats. Am. J. Physiol. Regul. Integr. Comp. Physiol. 279 R1257–R1267. [DOI] [PubMed] [Google Scholar]
- Bertram D., Barrès C., Cuisinaud G., Julien C. (1998). The arterial baroreceptor reflex of the rat exhibits positive feedback properties at the frequency of Mayer waves. J. Physiol. 513 251–261. 10.1111/j.1469-7793.1998.251by.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bertram D., Orèa V., Chapuis B., Barre‘s C., Julien C. (2005). Differential responses of frequency components of renal sympathetic nerve activity to arterial pressure changes in conscious rats. Am. J. Physiol. Regul. Integr. Comp. Physiol. 289 R1074–R1082. [DOI] [PubMed] [Google Scholar]
- Blinowska K. J., Lachert P., Zygierewicz J., Janusek D., Sawosz P., Kacprzak M., et al. (2020). Characteristic of mayer waves in electrophysiological, hemodynamic and vascular signals Int. J. Neural. Syst. 30:2050003 10.1142/S0129065720500033 [DOI] [PubMed] [Google Scholar]
- Böhmer A. E., Brum L. M., Souza D. G., Corrêa A. M., Oses J. P., Viola G. G., et al. (2010). Chronic treatment with cyclosporine affects systemic purinergic parameters, homocysteine levels and vascular disturbances in rats. Chem. Biol. Interact. 188 15–20. 10.1016/j.cbi.2010.06.011 [DOI] [PubMed] [Google Scholar]
- Bosch B. M., Bringard A., Ferretti G., Schwartz S., Iglói K. (2017). Effect of cerebral vasomotion during physical exercise on associative memory, a near-infrared spectroscopy study. Neurophotonics 4:041404 10.1117/1.nph.4.4.041404 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bottazzi F. (1906). Genese der Blutdruckschwankungen III. Ordnung. Z. Biol. 47:487. [Google Scholar]
- Bulgak J. (1877). Ueber die Contractionen und die Innervation der Milz. Arch. Pathol. Anat. Physiol. Klinische Med. 69 181–213. 10.1007/bf02326115 [DOI] [Google Scholar]
- Bumstead J. R., Bauer A. Q., Wright P. W., Culver J. P. (2017). Cerebral functional connectivity and Mayer waves in mice: phenomena and separability. J. Cereb. Blood Flow Metab. 37 471–484. 10.1177/0271678x16629977 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bunch J. L. (1899). On the vaso-motor nerves of the small intestines. J. Physiol. 24 72–98. 10.1113/jphysiol.1899.sp000751 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cavalcanti S., Belardinelli E. (1996). Modeling of cardiovascular variability using a differential delay equation. IEEE Trans. Biomed. Eng. 43 982–989. 10.1109/10.536899 [DOI] [PubMed] [Google Scholar]
- Cerutti C., Barres C., Paultre C. Z. (1994). Baroreflex modulation of blood pressure and heart rate variabilities in rats: assessment by spectral analysis. Am. J. Physiol. 266 H1993–H2000. [DOI] [PubMed] [Google Scholar]
- Cerutti C., Gustin M. P., Paultre C. Z., Lo M., Julien C., Vincent M., et al. (1991a). Autonomic nervous system and cardiovascular variability in rats: a spectral analysis approach. Am. J. Physiol. 261 H1292–H1299. [DOI] [PubMed] [Google Scholar]
- Cerutti C., Lo M., Julien C., Paultre C. Z., Vincent M., Sassard J. (1991b). [Role of sympathetic nervous system on blood pressure and heart rate variabilities in the rat: spectral analysis]. Arch. Mal. Coeur. Vaiss. 84 1235–1238. [PubMed] [Google Scholar]
- Cevese A., Grasso R., Poltronieri R., Schena F. (1995). Vascular resistance and arterial pressure low-frequency oscillations in the anesthetized dog. Am. J. Physiol. 268 H7–H16. [DOI] [PubMed] [Google Scholar]
- Chen Z., Haykin S. (2002). On different facets of regularization theory. Neural Comput. 14 2791–2846. 10.1162/089976602760805296 [DOI] [PubMed] [Google Scholar]
- Chevalier-Cholat A. M., Friggi A. (1976a). Carotid sinus, aortic and subclavian baroreceptor activities during cardiopulmonary bypass in rabbits. J. Physiol. 72 971–986. [PubMed] [Google Scholar]
- Chevalier-Cholat A. M., Friggi A. (1976b). [The reactivity of the sinocarotid, aortic, and subclavian baroreceptors during artificial circulation in the rabbit]. C. R. Acad. Sci. Hebd. Seances Acad. Sci. D 282 1191–1193. [PubMed] [Google Scholar]
- Christ G. J. (1995). Modulation of alpha 1-adrenergic contractility in isolated vascular tissues by heptanol: a functional demonstration of the potential importance of intercellular communication to vascular response generation. Life Sci. 56 709–721. 10.1016/0024-3205(95)00001-m [DOI] [PubMed] [Google Scholar]
- Cooper R. E., Skirrow C., Tye C., McLoughlin G., Rijsdijk F., Banaschweski T., et al. (2014). The effect of methylphenidate on very low frequency electroencephalography oscillations in adult ADHD. Brain Cogn. 86 82–89. 10.1016/j.bandc.2014.02.001 [DOI] [PubMed] [Google Scholar]
- Cushing J. M. (2019). Difference equations as models of evolutionary population dynamics. J. Biol. Dyn. 13 103–127. 10.1080/17513758.2019.1574034 [DOI] [PubMed] [Google Scholar]
- Czosnyka Z., Kim D. J., Balédent O., Schmidt E. A., Smielewski P., Czosnyka M. (2018). Mathematical Modelling of CSF pulsatile flow in aqueduct cerebri. Acta Neurochir. Suppl. 126 233–236. 10.1007/978-3-319-65798-1_47 [DOI] [PubMed] [Google Scholar]
- Dampney R. A. L. (1994). Functional organization of central pathways regulating the cardiovascular system. Physiol. Rev. 74 323–364. 10.1152/physrev.1994.74.2.323 [DOI] [PubMed] [Google Scholar]
- Dǎnilǎ M. D., Privistirescu A., Duicu O. M., Raţiu C. D., Angoulvant D., Muntean D. M., et al. (2017). The effect of purinergic signaling via the P2Y11 receptor on vascular function in a rat model of acute inflammation. Mol. Cell Biochem. 431 37–44. 10.1007/s11010-017-2973-5 [DOI] [PubMed] [Google Scholar]
- de la Cruz F., Schumann A., Köhler S., Reichenbach J. R., Wagner G., Bär K. J. (2019). The relationship between heart rate and functional connectivity of brain regions involved in autonomic control. Neuroimage 196 318–328. 10.1016/j.neuroimage.2019.04.014 [DOI] [PubMed] [Google Scholar]
- Delgado E., Marques-Neves C., Rocha I., Sales-Luís J., Silva-Carvalho L. (2013). Myogenic oscillations in rabbit ocular vasculature are very low frequency. Ophthalmic Res. 50 123–128. 10.1159/000351629 [DOI] [PubMed] [Google Scholar]
- Di Rienzo M., Parati G., Castiglioni P., Omboni S., Ferrari A. U., Ramirez A. J., et al. (1991). Role of sinoaortic afferents in modulating BP and pulse-interval spectral characteristics in unanesthetized cats. Am. J. Physiol. 261 H1811–H1818. [DOI] [PubMed] [Google Scholar]
- Fredericq L. (1882). De l’influence de la respiration sur la circulation. Les oscillations respiratoires de la pression arterielle chez le chien. Arch. Biol. 3 55–100. [Google Scholar]
- Fuji K., Heistad D. D., Faraci F. M. (1990). Vasomotion in basilar arteries in vivo. Am. J. Physiol. 258 H1829–H1834. [DOI] [PubMed] [Google Scholar]
- Ghali M. G. (2017a). Role of the medullary lateral tegmental field in sympathetic control. J. Integr. Neurosci. 16 189–208. 10.3233/jin-170010 [DOI] [PubMed] [Google Scholar]
- Ghali M. G. (2017b). The brainstem network controlling blood pressure: an important role for pressor sites in the caudal medulla and cervical cord. J. Hypertens. 35 1938–1947. 10.1097/hjh.0000000000001427 [DOI] [PubMed] [Google Scholar]
- Ghali M. G., Marchenko V. (2013). Fast oscillations during gasping and other non-eupneic respiratory behaviors: clues to central pattern generation. Respir. Physiol. Neurobiol. 187 176–182. 10.1016/j.resp.2013.03.010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ghali M. G. Z. (2019). Dynamic changes in arterial pressure following high cervical transection in the decerebrate rat. J. Spinal Cord Med. 16 1–12. 10.1080/10790268.2019.1639974 [DOI] [PMC free article] [PubMed] [Google Scholar] [Retracted]
- Gorjajew N. K., Sergijewsky N. K., Zwetkow J. (1931). Zur Frage des Ursprungs der Traube-Heringschen Wellen. Pflüger’s Arch. Gesamte Physiol. Menschen Tiere 227, 45–56. 10.1007/BF01755524 [DOI] [Google Scholar]
- Guyenet P. G., Mulkey D. K. (2010). Retrotrapezoid nucleus and parafacial respiratory group. Respir. Physiol. Neurobiol. 173 244–255. 10.1016/j.resp.2010.02.005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guyenet P. G., Stornetta R. L., Souza G. M. P. R., Abbott S. B. G., Shi Y., Bayliss D. A. (2019). The retrotrapezoid nucleus: central chemoreceptor and regulator of breathing automaticity. Trends Neurosci. 42 807–824. 10.1016/j.tins.2019.09.002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guyton A. C., Batson H. M., Smith C. M., Armstrong G. G. (1951). Method for studying the competence of the body’s blood pressure regulatory mechanisms and effect of pressoreceptor denervation. Am. J. Physiol. 164 360–368. 10.1152/ajplegacy.1951.164.2.360 [DOI] [PubMed] [Google Scholar]
- Guyton A. C., Harris J. W. (1961). Pressorecoptor-autonoinic oscillation: A probable cause of vaaomotor waves. Am. J. Physiol. 165:158 10.1152/ajplegacy.1951.165.1.158 [DOI] [PubMed] [Google Scholar]
- Guyton A. C., Satterfield J. H. (1952). Vasomotor waves possibly resulting from CNS ischemic reflex oscillation. Am. J. Physiol. 170 601–605. 10.1152/ajplegacy.1952.170.3.601 [DOI] [PubMed] [Google Scholar]
- Hales S. (1981). Statical Essays: concerning Haemastaticks; or, An Account of some Hydraulick and Hydrostatical Experiments made on the Blood and Blood-vessels of Animals, eds Innys W., Manby R. (London: Pfizer Laboratories; ). [Google Scholar]
- Haxhiu M. A., van Lunteren E., Deal E. C., Cherniack N. S. (1989). Role of the ventral surface of medulla in the generation of Mayer waves. Am. J. Physiol. 257 R804–R809. [DOI] [PubMed] [Google Scholar]
- Henle J. (1852). Zeitschrift für Rationelle. Medicine 2 299–313. [Google Scholar]
- Hering E. (1869). Uber den EinfluB der Atmung auf den Kreislauf. Akad. Wiss. Wien Math-Nat. KI. 60 829–856. [Google Scholar]
- Hodgkin A. L., Huxley A. F. (1945). Resting and action potentials in single nerve fibres. J. Physiol. 104 176–195. 10.1113/jphysiol.1945.sp004114 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hodgkin A. L., Huxley A. F. (1952a). A quantitative description of membrane current and its application to conduction and excitation in nerve. J. Physiol. 117 500–544. 10.1113/jphysiol.1952.sp004764 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hodgkin A. L., Huxley A. F. (1952b). The components of membrane conductance in the giant axon of Loligo. J. Physiol. 116 473–496. 10.1113/jphysiol.1952.sp004718 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hubbard J., Hubbard B. B. (2015). Vector Calculus, Linear Algebra, and Differential Forms: A Unified Approach, 5th Edn United States: Matrix Editions. [Google Scholar]
- Iriuchijima J. (1984). “Role of cardiac output and total peripheral resistance in the generation of splenic blood pressure wave,” in Mechanisms of Blood Pressure Waves, eds Miyakawa K., et al. (New York, NY: Springer Verlag; ), 347–348. [Google Scholar]
- Iwasaki K., Ogawa Y., Shibata S., Aoki K. (2007). Acute exposure to normobaric mild hypoxia alters dynamic relationships between blood pressure and cerebral blood flow at very low frequency. J. Cereb. Blood Flow Metab. 27 776–784. 10.1038/sj.jcbfm.9600384 [DOI] [PubMed] [Google Scholar]
- Jacob H. J., Ramanathan A., Pan S. G., Brody M. J., Myers G. A. (1995). Spectral analysis of arterial pressure lability in rats with sinoaortic deafferentation. Am. J. Physiol. 269 R1481–R1488. [DOI] [PubMed] [Google Scholar]
- Janssen B. J., Malpas S. C., Burke S. L., Head G. A. (1997). Frequency-dependent modulation of renal blood flow by renal nerve activity in conscious rabbits. Am. J. Physiol. 273 R597–R608. [DOI] [PubMed] [Google Scholar]
- Japundzic N., Grichois M. L., Zitoun P., Laude D., Elghozi J. L. (1990). Spectral analysis of blood pressure and heart rate in conscious rats: effects of autonomic blockers. J. Auton. Nerv. Syst. 30 91–100. 10.1016/0165-1838(90)90132-3 [DOI] [PubMed] [Google Scholar]
- Jeffries O., McGahon M. K., Bankhead P., Lozano M. M., Scholfield C. N., Curtis T. M., et al. (2010). cAMP/PKA-dependent increases in Ca Sparks, oscillations and SR Ca stores in retinal arteriolar myocytes after exposure to vasopressin. Invest. Ophthalmol. Vis. Sci. 51 1591–1598. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jhamandas J. H., Harris K. H. (1992). Influence of nucleus tractus solitarius stimulation and baroreceptor activation on rat parabrachial neurons. Brain Res. Bull. 28 565–571. 10.1016/0361-9230(92)90104-6 [DOI] [PubMed] [Google Scholar]
- Julien C. (2006). The enigma of Mayer waves: facts and models. Cardiovasc. Res. 70 12–21. 10.1016/j.cardiores.2005.11.008 [DOI] [PubMed] [Google Scholar]
- Julien C., Chapuis B., Cheng Y., Barre‘s C. (2003). Dynamic interactions between arterial pressure and sympathetic nerve activity: role of arterial baroreceptors. Am. J. Physiol. Regul. Integr. Comp. Physiol. 285 R834–R841. [DOI] [PubMed] [Google Scholar]
- Julien C., Zhang Z. Q., Cerutti C., Barre‘s C. (1995). Hemodynamic analysis of arterial pressure oscillations in conscious rats. J. Auton. Nerv. Syst. 50 239–252. 10.1016/0165-1838(94)00095-2 [DOI] [PubMed] [Google Scholar]
- Just A., Wagner C. D., Ehmke H., Kirchheim H. R., Presson P. B. (1995). On the origin of low frequency blood pressure variability in the conscious dog. J. Physiol. 489 215–223. 10.1113/jphysiol.1995.sp021043 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kaminski R. J., Meyer G. A., Winter D. L. (1970). Sympathetic unit activity associated with Mayer waves in the spinal dog. Am. J. Physiol. 219 1768–1771. 10.1152/ajplegacy.1970.219.6.1768 [DOI] [PubMed] [Google Scholar]
- Kanbar R., Chapuis B., Oréa V., Barrès C., Julien C. (2008). Baroreflex control of lumbar and renal sympathetic nerve activity in conscious rats. Am. J. Physiol. Regul. Integr. Comp. Physiol. 295 R8–R14. [DOI] [PubMed] [Google Scholar]
- Kandel E. R., Schwartz J. H., Jessell T. M. (2000). Principles of Neural Science 4/e. New York, NY: McGrawHill. [Google Scholar]
- Killip I. I. I. T. (1962). Oscillation of blood flow and vascular resistance during Mayer waves. Circ. Res. 11 987–993. 10.1161/01.res.11.6.987 [DOI] [PubMed] [Google Scholar]
- Kupriyanov S. V. (2009). Role of baroreceptors in the zone of vertebral arteries in the reflex regulation of venous tone in the splanchnic basin. Bull. Exp. Biol. Med. 148 9–11. 10.1007/s10517-009-0635-7 [DOI] [PubMed] [Google Scholar]
- Lachert P., Zygierewicz J., Janusek D., Pulawski P., Sawosz P., Kacprzak M., et al. (2019). Causal coupling between electrophysiological signals, cerebral hemodynamics and systemic blood supply oscillations in mayer wave frequency range. Int. J. Neural Syst. 29:1850033 10.1142/S0129065718500338 [DOI] [PubMed] [Google Scholar]
- Lipski J., Kanjhan R., Kruszewska B., Rong W. (1996). Properties of presympathetic neurones in the rostral ventrolateral medulla in the rat: an intracellular study ‘in vivo’. J. Physiol. 490 729–744. 10.1113/jphysiol.1996.sp021181 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mal’tsev A. I., Mel’nikov A. A., Vikulov A. D., Gromova K. S. (2010). [The State of central hemodynamics and variability of hearty rate in sportsmen with various direction of training process]. Fiziol. Cheloveka 36, 112–118. [PubMed] [Google Scholar]
- Mancia G., Parati G., Castiglioni P., di Rienzo M. (1999). Effect of sinoaortic denervation on frequency domain estimates of baroreflex sensitivity in conscious cats. Am. J. Physiol. Heart Circ. Physiol. 276 H1987–H1993. [DOI] [PubMed] [Google Scholar]
- Marchenko V., Ghali M. G., Rogers R. F. (2012). Motoneuron firing patterns underlying fast oscillations in phrenic nerve discharge in the rat. J. Neurophysiol. 108 2134–2143. 10.1152/jn.00292.2012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marchenko V., Rogers R. F. (2006a). Selective loss of high-frequency oscillations in phrenic and hypoglossal activity in the decerebrate rat during gasping. Am. J. Physiol. Regul. Integr. Comp. Physiol. 291 R1414–R1429. [DOI] [PubMed] [Google Scholar]
- Marchenko V., Rogers R. F. (2006b). Time-frequency coherence analysis of phrenic and hypoglossal activity in the decerebrate rat during eupnea, hyperpnea, and gasping. Am. J. Physiol. Regul. Integr. Comp. Physiol. 291 R1430–R1442. [DOI] [PubMed] [Google Scholar]
- Marchenko V., Rogers R. F. (2007). Temperature and state dependence of dynamic phrenic oscillations in the decerebrate juvenile rat. Am. J. Physiol. Regul. Integr. Comp. Physiol. 293 R2323–R2335. [DOI] [PubMed] [Google Scholar]
- Marchenko V., Rogers R. F. (2009). GABAAergic and glycinergic inhibition in the phrenic nucleus organizes and couples fast oscillations in motor output. J. Neurophysiol. 101 2134–2145. 10.1152/jn.91030.2008 [DOI] [PubMed] [Google Scholar]
- Marchi A., Bari V., De Maria B., Esler M., Lambert E., Baumert M., et al. (2016a). Calibrated variability of muscle sympathetic nerve activity during graded head-up tilt in humans and its link with noradrenaline data and cardiovascular rhythms. Am. J. Physiol. Regul. Integr. Comp. Physiol. 310 R1134–R1143. [DOI] [PubMed] [Google Scholar]
- Marchi A., Bari V., De Maria B., Esler M., Lambert E., Baumert M., et al. (2016b). Simultaneous characterization of sympathetic and cardiac arms of the baroreflex through sequence techniques during incremental head-up tilt. Front. Physiol. 7:438 10.3389/fphys.2016.00438 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martín G., Gimeno J. V., Ramirez A., Cosín J., Báguena J. (1981). Effects of high-frequency harmonics on cardiac relaxation indices. Am. J. Physiol. 240 H669–H675. [DOI] [PubMed] [Google Scholar]
- Mayer S. (1876). Studien zur Physiologie des Herzens und der Blutgefässe. Sitzungsberichte Kaiser Akad. Wissenschaften 74 281–307. [Google Scholar]
- Montano N., Barman S. M., Gnecchi-Ruscone T., Porta A., Lombardi F., Malliani A. (1995). Role of low frequency neuronal activity in the medulla in the regulation of the cardiovascular system. Cardiologia 40 41–46. [PubMed] [Google Scholar]
- Montano N., Cogliati C., da Silva V. J., Gnecchi-Ruscone T., Massimini A., Porta A., et al. (2000). Effects of spinal section and of positive-feedback excitatory reflex on sympathetic and heart rate variability. Hypertension 36 1029–1034. 10.1161/01.hyp.36.6.1029 [DOI] [PubMed] [Google Scholar]
- Montano N., Cogliati C., Porta A., Pagani M., Malliani A., Narkiewicz K., et al. (1998). Central vagotonic effects of atropine modulate spectral oscillations of sympathetic nerve activity. Circulation 98 1394–1399. 10.1161/01.cir.98.14.1394 [DOI] [PubMed] [Google Scholar]
- Montano N., Gnecchi-Ruscone T., Porta A., Lombardi F., Malliani A., Barman S. M. (1996). Presence of vasomotor and respiratory rhythms in the discharge of single medullary neurons involved in the regulation of cardiovascular system. J. Auton. Nerv. Syst. 57 116–122. 10.1016/0165-1838(95)00113-1 [DOI] [PubMed] [Google Scholar]
- Montano N., Lombardi F., Gnecchi Ruscone T., Contini M., Finocchiaro M. L., Baselli G., et al. (1992). Spectral analysis of sympathetic discharge, R-R interval and systolic arterial pressure in decerebrate cats. J. Auton. Nerv. Syst. 40 21–31. 10.1016/0165-1838(92)90222-3 [DOI] [PubMed] [Google Scholar]
- Morris K. F., Nuding S. C., Segers L. S., Baekey D. M., Shannon R., Lindsey B. G., et al. (2010). Respiratory and Mayer wave-related discharge patterns of raphe and pontineneurons change with vagotomy. J. Appl. Physiol. 109 189–202. 10.1152/japplphysiol.01324.2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Müller T., Timmer J., Reinhard M., Oehm E., Hetzel A. (2003). Detection of very low-frequency oscillations of cerebral haemodynamics is influenced by data detrending. Med. Biol. Eng. Comput. 41, 69–74. [DOI] [PubMed] [Google Scholar]
- Murasato Y., Hirakawa H., Harada Y., Nakamura T., Hayashida Y. (1998). Effects of systemic hypoxia on R-R interval and blood pressure variabilities in conscious rats. Am. J. Physiol. 275, H797–H804. 10.1152/ajpheart.1998.275.3.H797 [DOI] [PubMed] [Google Scholar]
- Myers C. W., Cohen M. A., Eckberg D. L., Taylor J. A. (2001). A model for the genesis of arterial pressure Mayer waves from heart rate and sympathetic activity. Auton. Neurosci. 91 62–75. 10.1016/s1566-0702(01)00289-2 [DOI] [PubMed] [Google Scholar]
- Nisimaru Y. (1984). “A story of the spleen, the fourth grade blood pressure change,” in Mechanisms of Blood Pressure Waves, eds Miyakawa K., Koepchen H. P., Polosa C. (New York, NY: Springer-Verlag; ), 341–346. [Google Scholar]
- Olufsen M. S., Hill N. A., Vaughan G. D., Sainsbury C., Johnson M. (2012). Rarefaction and blood pressure in systemic and pulmonary arteries. J. Fluid Mech. 705 280–305. 10.1017/jfm.2012.220 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ott M. M., Nuding S. C., Segers L. S., Lindsey B. G., Morris K. F. (2011). Ventrolateral medullary functional connectivity and the respiratory and central chemoreceptor-evoked modulation of retrotrapezoid-parafacial neurons. J. Neurophysiol. 105 2960–2975. 10.1152/jn.00262.2010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pagani M., Lombardi F., Guzzetti S., Rimoldi O., Furlan R., Pizzinelli P., et al. (1986). Power spectral analysis of heart rate and arterial pressure variabilities as a marker of sympatho-vagal interaction in man and conscious dog. Circ. Res. 59 178–193. 10.1161/01.res.59.2.178 [DOI] [PubMed] [Google Scholar]
- Persson P. B., Stauss H., Chung O., Wittmann U., Unger T. (1992). Spectrum analysis of sympathetic nerve activity and blood pressure in conscious rats. Am. J. Physiol. 263 H1348–H1355. [DOI] [PubMed] [Google Scholar]
- Plakias S., Boutalis Y. S. (2019). Lyapunov theory-based fusion neural networks for the identification of dynamic nonlinear systems. Int. J. Neural. Syst. 29:1950015 10.1142/s0129065719500151 [DOI] [PubMed] [Google Scholar]
- Preiss G., Polosa C. (1974). Patterns of sympathetic neuron activity associated with Mayer waves. Am. J. Physiol. 226 724–730. 10.1152/ajplegacy.1974.226.3.724 [DOI] [PubMed] [Google Scholar]
- Rembold C. M., Chen X. L. (1998). The buffer barrier hypothesis, [Ca2+]i homogeneity, and sarcoplasmic reticulum function in swine carotid artery. J. Physiol. 513 477–492. 10.1111/j.1469-7793.1998.477bb.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rieger S., Klee S., Baumgarten D. (2018). Experimental characterization and correlation of mayer waves in retinal vessel diameter and arterial blood pressure. Front. Physiol. 9:892 10.3389/fphys.2018.00892 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rogers R. F., Paton J. F., Schwaber J. S. (1993). NTS neuronal responses to arterial pressure and pressure changes in the rat. Am. J. Physiol. 265 R1355–R1368. [DOI] [PubMed] [Google Scholar]
- Rogers R. F., Rose W. C., Schwaber J. S. (1996). Simultaneous encoding of carotid sinus pressure and dP/dt by NTS target neurons of myelinated baroreceptors. J. Neurophysiol. 76 2644–2660. 10.1152/jn.1996.76.4.2644 [DOI] [PubMed] [Google Scholar]
- Rogers R. F., Rybak I. A., Schwaber J. S. (2000). Computational modeling of the baroreflex arc: nucleus tractus solitarius. Brain Res. Bull. 51 139–150. 10.1016/s0361-9230(99)00242-7 [DOI] [PubMed] [Google Scholar]
- Roy C. S. (1881). The elastic properties of the arterial wall. J. Physiol. 3 125–159. 10.1113/jphysiol.1881.sp000088 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rubini R., Porta A., Baselli G., Cerutti S., Paro M. (1993). Power spectrum analysis of cardiovascular variability monitored by telemetry in conscious unrestrained rats. J. Auton. Nerv. Syst. 45 181–190. 10.1016/0165-1838(93)90050-5 [DOI] [PubMed] [Google Scholar]
- Scarr G. (2016). Fascial hierarchies and the relevance of crossed-helical arrangements of collagen to changes in shape; part II: The proposed effect of blood pressure (Traube-Hering-Mayer) waves on the fascia. J. Bodyw. Mov. Ther. 20 629–638. 10.1016/j.jbmt.2015.10.008 [DOI] [PubMed] [Google Scholar]
- Schäfer E. A., Moore B. (1896). On the contractility and innervation of the spleen. J. Physiol. 20, 1–50. 10.1113/jphysiol.1896.sp000609 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schain A. J., Melo-Carrillo A., Strassman A. M., Burstein R. (2017). Cortical spreading depression closes paravascular space and impairs glymphatic flow: implications for migraine headache. J. Neurosci. 37 2904–2915. 10.1523/jneurosci.3390-16.2017 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schiff M. M. (1867). Lecons Sur La Physiologie de La Digestion: Faites Au Museum D’Histoire Naturelle de Florence. Hirschwald: Libraire. [Google Scholar]
- Seydnejad S. R., Kitney R. I. (2001). Modeling of Mayer waves generation mechanisms. IEEE Eng. Med. Biol. Mag. 20 92–100. 10.1109/51.917729 [DOI] [PubMed] [Google Scholar]
- Seyrek M., Halici Z., Yildiz O., Ulusoy H. B. (2011). Interaction between dexmedetomidine and α-adrenergic receptors: emphasis on vascular actions. J. Cardiothorac. Vasc. Anesth. 25 856–862. 10.1053/j.jvca.2011.06.006 [DOI] [PubMed] [Google Scholar]
- Sherrington C. (1906). The Integrative Action of the Nervous System. New Haven: Yale University Press, 241–243. [Google Scholar]
- Siegel G., Ebeling H. W., Hofer H. W., Nolte J., Roedel H., Klubendorf D. (1984). “Vascular smooth muscle rhythmicity,” in Mechanisms of Blood Pressure Waves, eds Miyakawa K., Koepchen H. P., Polosa C. (New York, NY: Springer-Verlag; ), 319–340. [Google Scholar]
- Siegel G., Roedel H., Hofer H. W. (1976). “Basic rhythms in vascular smooth muscle,” in Smooth Muscle Pharmacology and Physiology, eds Worcel M., Vassort G. (Paris: INSERM; ), 215–231. [Google Scholar]
- Sobrinho C. R., Wenker I. C., Poss E. M., Takakura A. C., Moreira T. S., Mulkey D. K. (2014). Purinergic signalling contributes to chemoreception in the retrotrapezoid nucleus but not the nucleus of the solitary tract or medullary raphe. J. Physiol. 592 1309–1323. 10.1113/jphysiol.2013.268490 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stauss H. M., Kregel K. C. (1996). Frequency response characteristic of sympathetic-mediated vasomotor waves in conscious rats. Am. J. Physiol. 271(4 Pt 2), H1416–H1422. [DOI] [PubMed] [Google Scholar]
- Stauss H. M., Mrowka R., Nafz B., Patzak A., Unger T., Persson P. B. (1995). Does low frequency power of arterial blood pressure reflect sympathetic tone? J. Auton. Nerv. Syst. 54 145–154. 10.1016/0165-1838(94)00000-a [DOI] [PubMed] [Google Scholar]
- Stauss H. M., Persson P. B., Johnson A. K., Kregel K. C. (1997). Frequency—response characteristics of autonomic nervous system function in conscious rats. Am. J. Physiol. 273 H786–H795. [DOI] [PubMed] [Google Scholar]
- Strasser A., Wolf H. (1905). Über die Blutversorgung der Milz. Pflüger Arch. 108 590–626. 10.1007/bf01682460 [DOI] [Google Scholar]
- Sun M. K., Guyenet P. G. (1986). Hypothalamic glutamatergic input to medullary sympathoexcitatory neurons in rats. Am. J. Physiol. 251 R798–R810. [DOI] [PubMed] [Google Scholar]
- Sun M. K., Young B. S., Hackett J. T., Guyenet P. G. (1988). Reticulospinal pacemaker neurons of the rat rostral ventrolateral medulla with putative sympathoexcitatory function: an intracellular study in vitro. Brain Res. 442 229–239. 10.1016/0006-8993(88)91508-9 [DOI] [PubMed] [Google Scholar]
- Titz S., Keller B. U. (1997). Rapidly deactivating AMPA receptors determine excitatory synaptic transmission to interneurons in the nucleus tractus solitarius from rat. J. Neurophysiol. 78 82–91. 10.1152/jn.1997.78.1.82 [DOI] [PubMed] [Google Scholar]
- Traube L. (1885). Ueber periodische thatigkeits-aeusserungen des vasomotorischen und hemmungs-nervencentrums. Medizin Wissenschaft 56 881–885. [Google Scholar]
- Tripathi K. K. (2011). Very low frequency oscillations in the power spectra of heart rate variability during dry supine immersion and exposure to non-hypoxic hypobaria. Physiol. Meas. 32 717–729. 10.1088/0967-3334/32/6/008 [DOI] [PubMed] [Google Scholar]
- Turalska M., Latka M., Czosnyka M., Pierzchala K., West B. J. (2008). Generation of very low frequency cerebral blood flow fluctuations in humans. Acta Neurochir. Suppl. 102 43–47. 10.1007/978-3-211-85578-2_9 [DOI] [PubMed] [Google Scholar]
- Ursino M., Fabbri G., Belardinelli E. (1992). A mathematical analysis of Vasomotion in the peripheral vascular bed. Cardioscience 3 13–25. [PubMed] [Google Scholar]
- van Brederode J. F., Berger A. J. (2008). Spike-firing resonance in hypoglossal motoneurons. J. Neurophysiol. 99 2916–2928. 10.1152/jn.01037.2007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van de Borne P., Rahnama M., Mezzetti S., Montano N., Porta A., Degaute J. P., et al. (2001). Contrasting effects of phentolamine and nitroprusside on neural and cardiovascular variability. Am. J. Physiol. 281 H559–H565. [DOI] [PubMed] [Google Scholar]
- Vanni M. P., Provost J., Lesage F., Casanova C. (2010). Evaluation of receptive field size from higher harmonics in visuotopic mapping using continuous stimulation optical imaging. J. Neurosci. Methods. 189 138–150. 10.1016/j.jneumeth.2010.03.013 [DOI] [PubMed] [Google Scholar]
- Vermeij A., Meel-van den Abeelen A. S., Kessels R. P., van Beek A. H., Claassen J. A. (2014). Very-low-frequency oscillations of cerebral hemodynamics and blood pressure are affected by aging and cognitive load. Neuroimage 85(Pt 1), 608–615. 10.1016/j.neuroimage.2013.04.107 [DOI] [PubMed] [Google Scholar]
- Vielle B. (2005). Mathematical analysis of Mayer waves. J. Math. Biol 50 595–606. 10.1007/s00285-004-0305-3 [DOI] [PubMed] [Google Scholar]
- Vitela M., Mifflin S. W. (2001). gamma-Aminobutyric acid(B) receptor-mediated responses in the nucleus tractus solitarius are altered in acute and chronic hypertension. Hypertension 37 619–622. 10.1161/01.hyp.37.2.619 [DOI] [PubMed] [Google Scholar]
- Wienecke J., Enríquez Denton M., Stecina K., Kirkwood P. A., Hultborn H. (2015). Modulation of spontaneous ocomotor and respiratory drives to hindlimb motoneurons temporally related to sympathetic drives as revealed by Mayer waves. Front. Neural Circ. 9:1 10.3389/fncir.2015.00001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wood C. M. (1974). Mayer waves in the circulation of a teleost fish. J. Exp. Zool. 189 267–274. 10.1002/jez.1401890216 [DOI] [PubMed] [Google Scholar]
- Yaramothu C., Li X., Morales C., Alvarez T. L. (2020). Reliability of frontal eye fields activation and very low frequency oscillations observed during vergence eye movements: an fNIRS study. Sci. Rep. 10:712 10.1038/s41598-020-57597-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Young D. L., Eldridge F. L., Poon C. S. (2003). Integration-differentiation and gating of carotid afferent traffic that shapes the respiratory pattern. J. Appl. Physiol. 1985 1213–1229. 10.1152/japplphysiol.00639.2002 [DOI] [PubMed] [Google Scholar]
- Yucel M. A., Selb J., Aasted C. M., Lin P.-Y., Borsook D., Becerra L., et al. (2016). Mayer Waves Reduce the Accuracy of Estimated Hemodynamic Response Functions in Functional Near-Infrared Spectroscopy. Biomed. Opt. Express 7 3078–3088. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu Y., Zhou S., Gao D., Liu Q. (2019). Synchronization of non-linear oscillators for neurobiologically inspired control on a bionic parallel waist of legged robot. Front. Neurorobot. 2:59 10.3389/fnbot.2019.00059 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
All datasets generated for this study are included in the article/supplementary material.


