Experience-dependent reorganization drives development of a binocularly unified cortical representation of orientation

Summary

Across sensory areas, neural microcircuits consolidate streams of information into unified representations of the external world. In the carnivore visual cortex, where eye-specific inputs first converge, it has been posited that a single, binocularly aligned modular orientation representation develops independent of sensory experience. In this study of ferret visual cortex using in vivo calcium imaging, we find evidence for a different developmental process. Early in development, contralateral, ipsilateral or binocular stimulation each yield well-organized modular representations of orientation that display features of mature cortex. However, comparison of these representations reveals considerable misalignment that is evident at both modular and cellular scales. Experience-dependent processes drive reorganization of these three representations towards a single binocularly-aligned representation resembling the early binocular representation through shifts in cellular orientation preference. Thus, while orderly modular networks of orientation preference initially arise independent of visual experience, experience is critical for the alignment of these early representations.

eTOC

Chang et al. demonstrate that at eye opening three distinct representation of orientation exist in the ferret visual cortex: one each for monocular stimulation and a third for binocular stimulation. Through experience-dependent processes, a unified binocularly aligned orientation representation develops, driven by concerted shifts in monocular orientation preferences.

Introduction

A critical function of neural circuits that represent sensory stimuli is the integration of information from different sources to build coherent representations of the external world (Duhamel et al., 1998; King and Hutchings, 1987; Knudsen and Brainard, 1991; Wallace and Stein, 1997). The binocular representation of orientation in visual cortex provides an excellent example of this integrative process, with segregated inputs from the two eyes coming together to yield a unified binocular representation, such that visual stimuli presented to either eye yield similar population responses (Bridge and Cumming, 2001; Sarnaik et al., 2014) (Bridge and Cumming, 2001; Crair et al., 1998; Wang et al., 2010).

Early studies that probed the development of modular networks of orientation preference in carnivore visual cortex using intrinsic signal imaging concluded that a binocularly unified modular representation of orientation arises without the need of visual experience (Chapman et al., 1996; Crair et al., 1998; Godecke and Bonhoeffer, 1996; Godecke et al., 1997; Sengpiel et al., 1998; White et al., 2001). In contrast, recent studies in mice, which lack a modular-scale organization, have highlighted the necessity of visual experience for the development of feature-specific connectivity (Ko et al., 2013; Ko et al., 2014) and binocularly matched orientation preferences of single neurons (Gu and Cang, 2016; Wang et al., 2010). The lack of consensus across species for the role of experience in such a fundamental process remains puzzling and led us to reexamine the development of the binocular representation of orientation preference in ferret visual cortex at both the cellular- and network-scales using widefield and two-photon in vivo calcium imaging.

Consistent with earlier work, we find that orientation-selective responses are spatially clustered into distributed, modular network representations early in postnatal development, even before the onset of patterned visual experience. Despite the appearance of a high degree of order in the visually-evoked modular network structure, detailed comparison of the activity patterns arising from monocular and binocular stimulation revealed mismatches in the representations of orientation preference at eye-opening at both network and cellular scale. In fact, our analysis suggests the presence of three distinct modular representations at eye opening: a monocular representation for each eye, and a third representation revealed through binocular stimulation. Furthermore, we demonstrate that shared binocular experience is necessary to drive network-scale alignment of these orientation representations towards a single binocularly unified representation. The absence of binocular experience during this period not only prevents network-scale alignment, but degrades the intrinsic modular organization of orientation preference into a state resembling the salt-and-pepper functional architecture of rodents. Finally, we observed substantial changes in orientation preference, evident at both cellular- and network-scales, that are a critical part of a dynamic process that leads to a unified representation of orientation preference resembling the early binocular representation. We propose that the emergence of a binocularly unified orientation representation in visual cortex reflects the experience-driven alignment of three distinct representations of orientation which arise independent of sensory experience.

Results

Naive animals exhibit mismatched monocular orientation preference representations that become aligned with age

To measure monocular orientation preferences in ferret visual cortex, we utilized viral expression of GCaMP6s with widefield epifluorescence imaging (Figure 1A–B). In ferrets, orientation selective responses are first observed around eye-opening (~P30) and reach mature levels within one week (Chapman and Stryker, 1993; Chapman et al., 1996; Clemens et al., 2012; White et al., 2001). We first investigated the similarity of trial-averaged activity patterns evoked by oriented stimuli presented to either eye in visually experienced animals (experienced, P36–42). Activity patterns evoked by the same stimulus were similar (Figure 1C) and produced a binocularly unified modular representation of orientation preference (Figure 1E). Responses to grating stimuli in visually naive animals (prior to natural eye-opening, naive, P27–31), were strikingly different (Figure 1D). In visually naive animals, identical stimuli presented to each of the open eyes evoked distinct modular patterns of trial-averaged activity (Figure 1G, Pearson’s correlation: Naive r=0.31±0.09 vs Experienced r=0.79±0.03 (Mean±SEM), n=6 vs 7 animals, p<0.001, unpaired permutation test). These differences resulted in modular representations of orientation preference that are different for each eye, with regions of cortex that display prominent differences in orientation preference rarely seen in experienced animals (Figure 1F,G, Mean monocular mismatch: Naive 27.91±4.19° vs Experienced 11.04±1.57° (Mean±SEM), n=6 vs 7 animals, p<0.001, unpaired permutation test).

Figure 1: Mismatched monocular orientation preference is reduced across development.

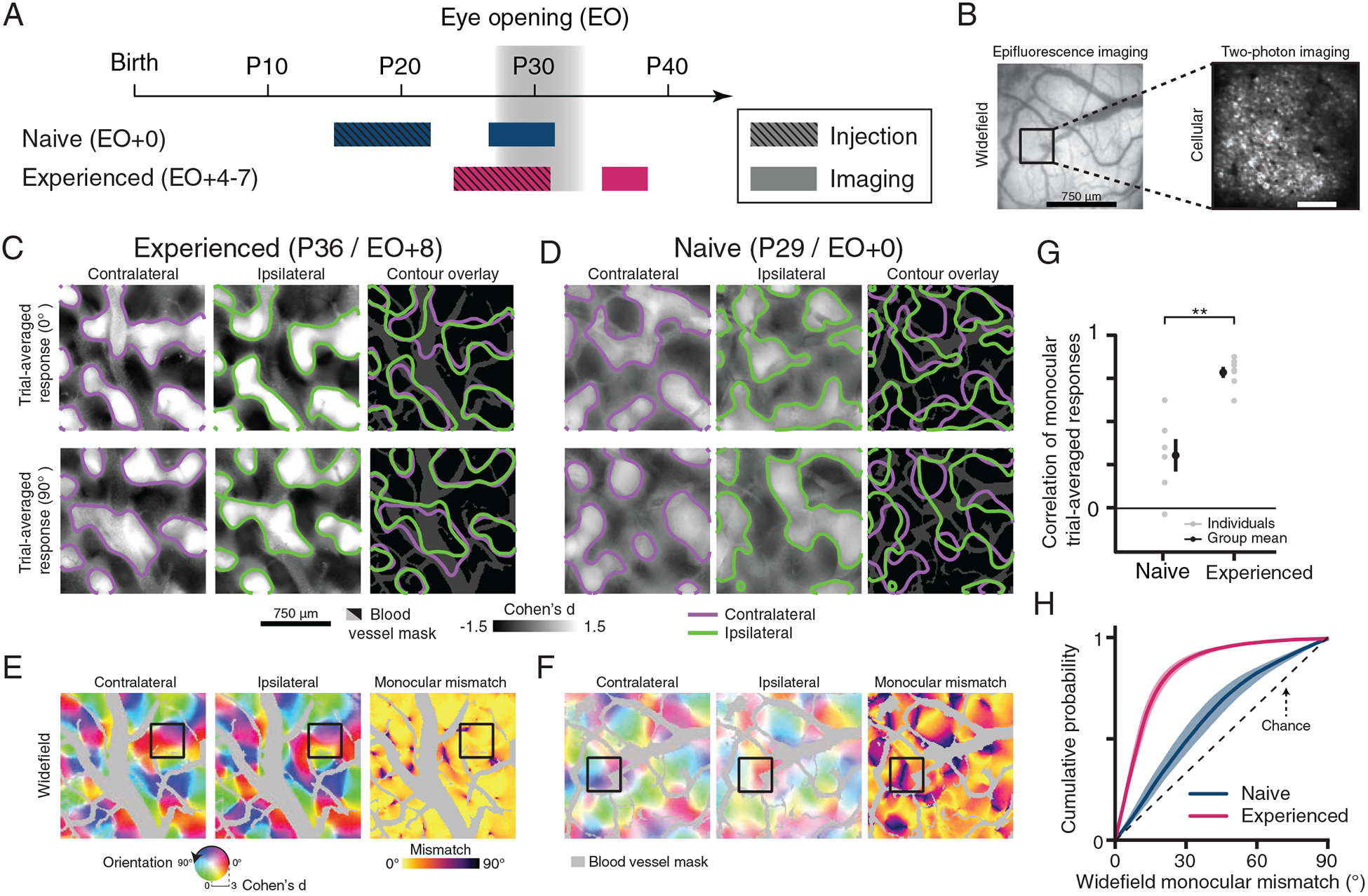
(A) Experimental timeline.

(B) Widefield and two-photon images from the naive animal in (D,F).

(C) Trial-averaged, cocktail-blank subtracted response maps evoked by monocular presentation of drifting gratings for an experienced animal and contour overlay of active domains. Active domains were defined as regions where the relative activity of z-scored trial-average response maps was >0.25 after applying a 10×10 median filter.

(D) Same as (C), but for a naive animal. For all widefield images, grayed or blacked out regions represent blood vessels.

(E-F) Widefield orientation preference maps for experienced (E) and naive animals (F). Far right column is monocular mismatch and grayed out regions represent blood vessels. Preferred orientation and selectivity (or monocular mismatch) are represented by image hue and saturation (or image color).

(G) Pearson’s correlation between monocular trial-averaged responses. Gray and black dots reflect individual or grouped measurements respectively.

(H) Cumulative distributions of widefield monocular mismatch for naive and experienced animals (mean±SEM).

Scale bars for widefield imaging (B) apply to (C-F). Asterisks denote significance between groups in (G) (**: p<0.01). Animal experiments: naive (n=6) and experienced (n=7).

Could this mismatch in orientation preference be due to torsional differences in the position of the eyes? This is unlikely for two reasons. First, if the mismatch was due to an angular rotation of one eye relative to the other, then this would result in a uniform offset of orientation preference throughout the imaging field and this is not what we observed. Instead we find a range of different angular differences in preferred orientations, expressed as regions with matched orientation preference and regions with mismatched preferences (Figure 1F,H). Second, we specifically tested the impact of rotating the orientation preference of the ipsilateral representation relative to the contralateral representation and found that the minimum mismatch produced by the rotational offsets was not significantly different from the actual acquired data (Δθmismatch in Naive: −2.48°±1.66° (Mean±SEM), n=6, p=0.19, one-sample t-test), and the degree of mismatch in naive and experienced animals remained high (Figure S1A–C,: Naive 25.19±4.55° vs Experienced 9.23±1.03° (Mean±SEM), n=6 vs 7 animals, p<0.001, unpaired permutation test). Together these data rule out the possibility that monocular mismatch is attributable to torsional differences in the position of the eyes.

Next, we wanted to understand how the monocular mismatch in orientation preference that we had observed at the level of wide-field imaging--which represents the average responses of large numbers of neurons--was represented at the scale of individual neurons. In principle, the mismatch at the population scale in naive animals could reflect the responses of binocular neurons that exhibit monocular responses with mismatched orientation preference, similar to what has been described in the mouse (Wang et al., 2010) Alternatively, the mismatch in naive animals could reflect the responses of individual neurons that are strictly monocular, forming spatially intermingled monocular neural populations with different modular patterns of orientation preference. To distinguish between these possibilities, we used two-photon calcium imaging to measure responses to oriented stimuli in layer 2/3 putatively excitatory neurons of visual cortex. We discovered that most neurons in both naive and experienced animals were binocularly responsive (Fraction of binocularly responsive cells: Naive 100±0% vs Experienced 96.27±1.57% (Mean±SEM), n=3 animals). Consistent with our widefield findings, binocularly responsive neurons in naive animals often displayed different monocular orientation preferences, whereas preferences were similar in experienced animals (Figure 2A–E, Figure S2, Cellular monocular mismatch: Naive 26.87±2.90° vs Experienced 13.11±1.03° (Mean±SEM), n=3 animals, p=0.002, unpaired bootstrap test). Furthermore, binocularly responsive neurons from naive animals did not display an obvious dominance in strength of response to the ipsilateral or contralateral eye that is prominent in experienced animals (Figure 2F, Cellular ODI: Naive 0.05±0.03 vs Experienced 0.23±0.06 (Mean±SD), Monocularity: Naive 0.09±0.04 vs Experienced 0.47±0.09 (Mean±SD), n=3 animals, p=0.04 for ODI and p=0.01 for Monocularity, unpaired bootstrap test) suggesting that ocular dominance only becomes pronounced after eye-opening. Together, our results demonstrate that neurons at eye-opening are highly binocular and frequently exhibit monocular mismatches in orientation preference that are rectified over the first week of visual experience.

Figure 2: Cellular mismatched monocular orientation preference is reduced across development.

(A-B) Cellular response traces (left panel, mean±SEM) and orientation tuning curves fit to trial-averaged responses (right panel, median) for experienced (A) and naive (B) animals. The black line under each trace indicates visual stimulation.

(C-D) Cellular orientation preference and monocular mismatch maps for the boxed regions in (Figure 1E) and (Figure 1F). Circles are cells and color represents the preferred orientation or monocular mismatch.

(E) Cumulative distributions of cellular monocular mismatch for naive and experienced animals (mean±SEM).

(F) Cumulative distribution of ocular dominance index for naive and experienced animals (mean±SEM).

(G) Pairwise cellular distance-dependent, difference in preferred orientation for contralateral or ipsilateral stimuli naive and experienced animals (mean±SEM).

Two-photon field of view in (D) corresponds to that shown in Figure 1B. Asterisks denote significance where difference in orientation preference is significantly lower than chance (G) (*: p<0.05, **:p<0.01). Animal experiments: naive (n=3) and experienced (n=3).

One concern that could be raised is the degree to which differences in the strength of orientation tuning between naive and experienced animals could account for the greater mismatch in orientation preference in naive animals. To be sure, the fraction of well-tuned cells and well-tuned pixels (see Methods) is greater in experienced than in naive animals (Naive 56.76±3.94% vs Experienced 71.32±7.75% (Mean±SEM), n=3 animals; Fraction of well-tuned pixels: Naive 35.54±4.64% vs Experienced 80.87±2.33% (Mean±SEM), n=6 vs 7 animals). Our analysis, however, was limited to comparably tuned binocularly responsive neurons and pixels that exhibited well-tuned orientation responses, and we found a very weak correlation between the degree of cellular mismatch and monocular orientation selectivity (Pearson’s Correlation of cellular Cohen’s d and monocular mismatch: Contralateral Naive −0.26±0.08 vs −0.23±0.04 Experienced; Ipsilateral Naive −0.20±0.13 vs −0.22±0.04 Experienced (Mean±SEM), n=3 vs 3 animals). To further rule out the contribution of weak orientation selectivity, we compared monocular mismatch to the degree of uncertainty for the preferred orientation for the monocular responses. For each monocular representation, where orientation preference is known to be the same, we bootstrap resampled orientation specific responses to calculate a confidence interval for the orientation preference. The observed monocular mismatch in naive animals was higher than this interval for either eye, while the observed monocular mismatch and expected mismatch was comparable for experienced animals (Difference in observed monocular mismatch and 95^th percentile bootstrapped measurement error for cells: Naive contralateral 13.23° and ipsilateral 5.98° vs Experienced contralateral −1.17° and ipsilateral −0.15°, n=3 animals; for pixels: Naive contralateral 17.68° and ipsilateral 15.60° vs Experienced contralateral 2.80° and ipsilateral 3.66° (Mean), n=6 or 7 animals). Therefore, at the network and cellular scales, weak orientation selectivity alone cannot explain the observed orientation preference mismatch in naive animals.

Monocular mismatch in naive animals reflects topologically distinct monocular orientation representations

The modular patterns evident in the population responses of naive animals in widefield (Figure 1C–D) and two-photon imaging (Figure 2C–D), appear similar to those in the experienced animals and suggest that spatial clustering of cellular orientation preferences exists before eye opening. To test this possibility, we quantified the spatial clustering by computing the cellular pairwise difference in preferred orientation as a function of distance. For monocular stimulation, naive and experienced animals displayed a similar degree of cellular orientation preference similarity for neighboring cells (Figure 2G, p<0.05 within 100μm unpaired bootstrap test for both Naive and Experienced), consistent with the previously observed early columnar organization of spontaneous activity (Smith et al., 2018). Thus, the hallmarks of the mature visual cortex, such as orientation selectivity, binocular responsiveness, and a modular architecture, are already present in visually naive ferrets.

This high degree of functional maturity in network organization prior to eye-opening makes the differences in monocular orientation preference, evident at the network and cellular scale, even more surprising. The presence of monocular mismatch within a cortical network displaying orderly fine-scale spatially clustered monocular orientation representations suggests that early binocular cortical networks harbor modular representations of orientation for each eye, which have not achieved mature alignment (Figure 3A). To quantify whether the spatial layout of the preferred orientation is different for the monocular representations in naive animals, we computed the circular correlation of the monocular preferred orientations, a measure of the similarity of orientation preference, using widefield imaging. Consistent with our hypothesis, we found that the circular correlation of monocular preferred orientations was substantially lower in naive animals suggesting that the monocular representations are each arranged in an orderly fashion but are spatially distinct (Figure 3B, Circular correlation of monocular preferred orientations: Naive: r=0.44±0.11 vs Experienced: r=0.87±0.03 (Mean±SEM), n=6 vs 7 animals, p<0.001, unpaired permutation test).

Figure 3: Monocular orientation representations are distinct before eye-opening.

(A) Widefield orientation preference maps for naive (top) and experienced (bottom) animals for contralateral (left) and ipsilateral (right) visual stimuli. Overlay of the corresponding homogeneity maps for each eye is shown middle. Preferred orientation and selectively are represented by image hue and saturation. Grayed or blacked out regions represent blood vessels.

(B-C) Circular correlation of preferred orientation (B) and Pearson’s correlation of fine-network structure (C, homogeneity index) for monocular orientation preference maps in naive and experienced animals (mean±SEM). Gray and black dots reflect individual or grouped measurements.

(D) Pairwise cellular distance-dependent, difference in the cellular monocular mismatch for naive and experienced animals (mean±SEM).

Asterisks denote significance between groups in (B-C) and distances where clustering is significantly lower than chance in (D) (*: p<0.05, **:p<0.01). Animal experiments: naive (n=3 cellular and n=6 widefield) and experienced (n=3 cellular and n=7 widefield).

A characteristic topological feature of mature modular orientation representations is heterogeneity in the rate of change of orientation preference change across visual cortex: large regions of gradual orientation preferences change are interrupted by smaller regions of rapid change (fractures or pinwheels) (Bonhoeffer and Grinvald, 1993). If the monocular mismatch in naive animals arises from orderly but distinct monocular representations, we would expect to find evidence for fractures and pinwheels in the monocular representations, and that these features would also exhibit better spatial alignment for the monocular representations in mature animals. Because regions of low-homogeneity reflect pinwheels and linear fractures, we compared the homogeneity index (HI), which measures the local similarity of orientation preference within 100μm, for monocular orientation preference maps obtained with widefield imaging. Consistent with our hypothesis, we observed that the fine-network structures of the monocular representations, were less similar in naive animals (Figure 3C, Pearson’s correlation of monocular HI: Naive: r=0.41±0.11 vs Experienced: r=0.74±0.03 (Mean±SEM), n=6 vs 7 animals, p<0.001, unpaired permutation test).

If the mismatch in preference arises from well-organized, smoothly varying, but spatially misaligned monocular representations, it leads to another prediction: the pattern of monocular mismatch at the network scale should exhibit spatial clustering—smooth variation in the degree of mismatch such that neighboring cells exhibit similar mismatch. Indeed, we noticed that the spatial distribution of monocular mismatch appears to form clusters (Figure 1F, 2D) in naive animals. To formally test whether the degree of orientation preference mismatch varies in a clustered manner across cortex, we calculated the difference in observed monocular mismatch for cell pairs as a function of distance. We observed that cells from naive animals displayed significantly similar monocular mismatch in a region within 100μm (Figure 3D p<0.05 within 100μm unpaired bootstrap test).

While the spatial clustering of monocular mismatch is consistent with well-organized but spatially misaligned monocular representations, we thought it was important to address whether the clusters of cellular monocular mismatch would align with pinwheels and linear fractures within the map and found only a weak correlation (Pearson’s correlation of cellular HI vs cellular monocular mismatch: Naive Contralateral −0.15±0.07, Naive Ipsilateral −0.06±0.03 (Mean±SEM), n=3 animals). Even when considering large areas using widefield epifluorescence imaging, the relationship between monocular mismatch and low map homogeneity was substantially weaker in naive animals than experienced animals (Pearson’s correlation of HI vs monocular mismatch: Naive Contralateral −0.14±0.04 vs Experienced Contralateral −0.43±0.04, Naive Ipsilateral −0.13±0.04 vs Experienced Ipsilateral −0.38±0.03, n=6 vs 7 animals, p<0.001 for each comparison, unpaired permutation test) indicating that the spatial clustering of monocular mismatch in naive animals, unlike in experienced animals, was not consistently predicted by rapid transitions of orientation preference in either monocular representation. Together our findings suggest that innate factors before eye-opening establish distinct monocular representations of orientation, exhibiting unique topological structure, within the modularly, distributed networks of visual cortex.

Although there are substantial differences in the early monocular representations, these differences do not rule out that experience-independent mechanisms, such as known interocular correlations in retinal waves (Ackman et al., 2012; Burbridge et al., 2014), could partially coordinate the early development of the monocular representations before eye-opening. If experience-independent mechanisms contribute to an early co-development of the monocular representations, then the monocular representations in visually naive animals should be more similar than would be expected from statistically independent representations. To assess this possibility, we compared the similarity of the monocular representations in visually naive animals to a surrogate dataset of statistically independent orientation maps. Modular synthetic orientation preference maps were generated by low-pass filtering random-noise images at the approximate wavelength of ferret orientation columns (~1mm) (Smith et al., 2015). As would be expected from independent representations, the preference mismatch between pairs of synthetic orientation maps in our surrogate distribution is nearly 45° (45.11° [41.36° 48.75°], Mean [CI], n=1,000 bootstraps) and the circular correlation is nearly 0 (0.0001 [−0.0176 0.0197], Mean [CI], n=1,000 bootstraps). The mean monocular mismatch and circular correlation for monocular orientation maps in visually naive animals lie significantly outside the range of our surrogate dataset (p<0.001, simple bootstrap test to control distributions) demonstrating that the monocular representations are more similar than would be expected from representations that emerge independently. These results suggest that experience-independent mechanisms may produce partially aligned monocular representations before eye-opening. However, because visually naive animals still display lower levels of monocular matching than visually experienced animals, there appear to be limitations to the extent that experience-independent mechanisms can achieve optimal alignment of the monocular representations. Thus, experience-dependent mechanisms after eye-opening may be crucial for reaching a mature, binocularly unified layout.

Network-scale alignment of orientation representations requires patterned visual experience

Since the monocular preferred orientations are matched during the first week after eye-opening, we investigated whether this process requires patterned visual experience. We employed binocular eyelid suturing in a cohort of animals to delay eye-opening, depriving animals of patterned visual experience (deprived, P35–36, Figure 4A). Neurons from deprived animals demonstrated higher monocular mismatches in orientation preference than experienced animals (Figure 4B–D, Deprived 37.75±2.43° vs Experienced 13.11±1.03° (Mean±SEM), n=3 animals, p=.008, unpaired bootstrap test). Consistent with previous studies (Chapman and Stryker, 1993; White et al., 2001), we also found that orientation selectivity in neurons from deprived animals was impaired (Figure 4E, p<0.05, unpaired bootstrap tests). Thus, patterned visual experience plays a dual role in the alignment of the monocular representations and the proper maturation of orientation selectivity.

Figure 4: Network-scale alignment of orientation representations requires patterned visual experience.

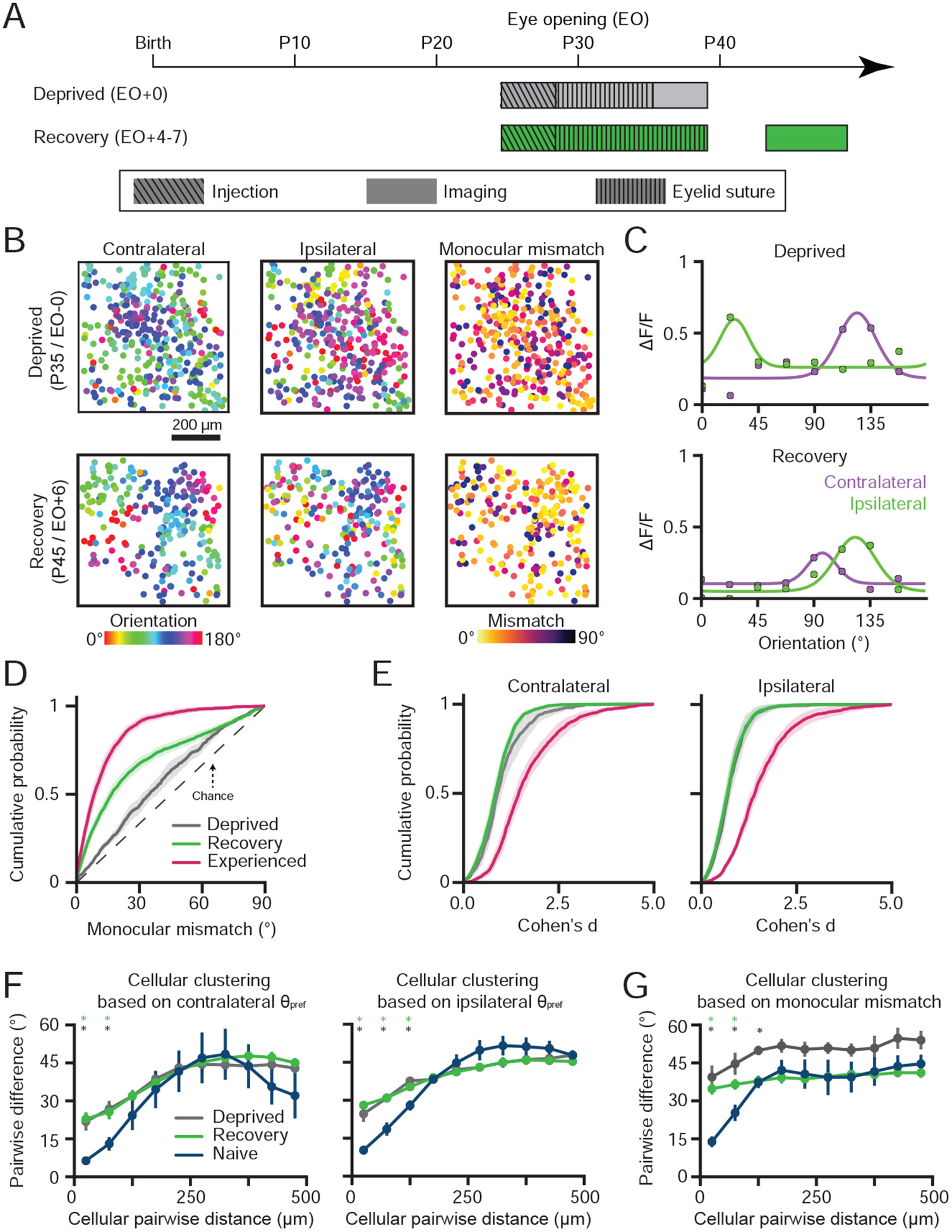
(A) Experimental timeline for deprivation and recovery.

(B) Cellular orientation preference maps and monocular mismatch maps for deprived animals (top row) and recovery animals (bottom row). Circles are cells and color represents either the preferred orientation or monocular mismatch.

(C) The trial-average response (median) and fit orientation tuning curves for cells from either a deprived animal (top row) or recovery animal (bottom row).

(D) Cumulative distribution of cellular monocular mismatch for experienced, deprived, and recovery animals (mean±SEM).

(E) Cumulative distributions of monocular orientation selectivity (Cohen’s d) for experienced, deprived, and recovery animals (mean±SEM).

(F) Pairwise cellular distance-dependent, difference in preferred orientation for monocular stimulation in naive, deprived, and recovery animals (mean±SEM).

(G) Pairwise cellular distance-dependent, difference in monocular mismatch for naive, deprived, and recovery animals (mean±SEM).

Asterisks in (F-G) denote distances where clustering is significant (*: p<0.05). Animal experiments: deprived (n=3), recovery (n=5), naive (n=3), and experienced (n=5).

Next, we investigated whether patterned visual experience during the normal first week of experience (P30–37) is critical for producing a binocularly aligned orientation representation. In a cohort of animals, we delayed eye-opening by 9 days with binocular eyelid suturing, and then provided 4–7 days of patterned visual experience (recovery, P43–46, Figure 4A). Notably, recovery animals displayed deficits compared to normally reared animals, despite access to comparable amounts of patterned visual experience. Neurons from recovery animals displayed lower levels of orientation mismatch than deprived animals (Figure 4B–D, Recovery 27.00±1.43° vs Deprived 37.75±2.43° (Mean±SEM), n=5 vs 3 animals, p<0.05, unpaired bootstrap test), but orientation mismatches were significantly higher than from experienced animals (Figure 4D, Recovery 27.00±1.43° vs Experienced 13.11±1.03° (Mean±SEM), n=5 vs 3 animals, p<0.05, unpaired bootstrap test). Furthermore, cellular orientation selectivity in the recovery animals was indistinguishable from deprived animals (Figure 4E, p>0.05, unpaired bootstrap tests). Therefore, we conclude that visual experience, during the first week after natural eye-opening, plays an important role in the development of orientation selectivity and the alignment of monocular preferences, which cannot be recovered through comparable experience at a later developmental stage.

In addition to single-cell impairments, we observed that the monocular representations of deprived and recovery animals showed impaired spatial clustering of preferred orientation (Figure 4F–G, p<0.05 within 100μm unpaired bootstrap test vs Naive). Weakened spatial clustering implies that abnormal experience after P30 induces a dramatic transformation of the representational network-structure in ferret visual cortex: from the highly modular functional organization characteristic of carnivores and primates into a more scattered functional organization reminiscent of the salt-and-pepper organization present in rodents. Alteration to circuit-level representations by abnormal experience is consistent with the underlying cortical circuitry becoming susceptible to visual experience at critical period onset (~P30–35)(Issa et al., 1999). Thus, the transition from closed-eye visual experience to patterned vision at ~P30 is critically important for both the proper maintenance of spatially-clustered, columnar representations of orientation and the binocular alignment of preferred orientation.

Binocular stimulation yields a third orientation representation before eye-opening

Sensitivity of the matching process to visual experience raises the possibility that binocular experience plays a crucial role in establishing the aligned representation of orientation preference. This led us to wonder how the patterns of activity induced by binocular and monocular stimulation would compare. To probe this issue, we recorded responses to binocular and monocular stimulation using two-photon calcium imaging in naive and experienced animals (Figure 5A–D). As expected, in experienced animals the monocular and binocular cellular orientation preferences were well matched (Figure 5E–F, Mean orientation preference difference with binocular: Contralateral 10.44±1.10°, Ipsilateral 12.73±0.40° (Mean±SEM), n=3 animals).

Figure 5: Binocular stimulation yields a third orientation representation before eye-opening.

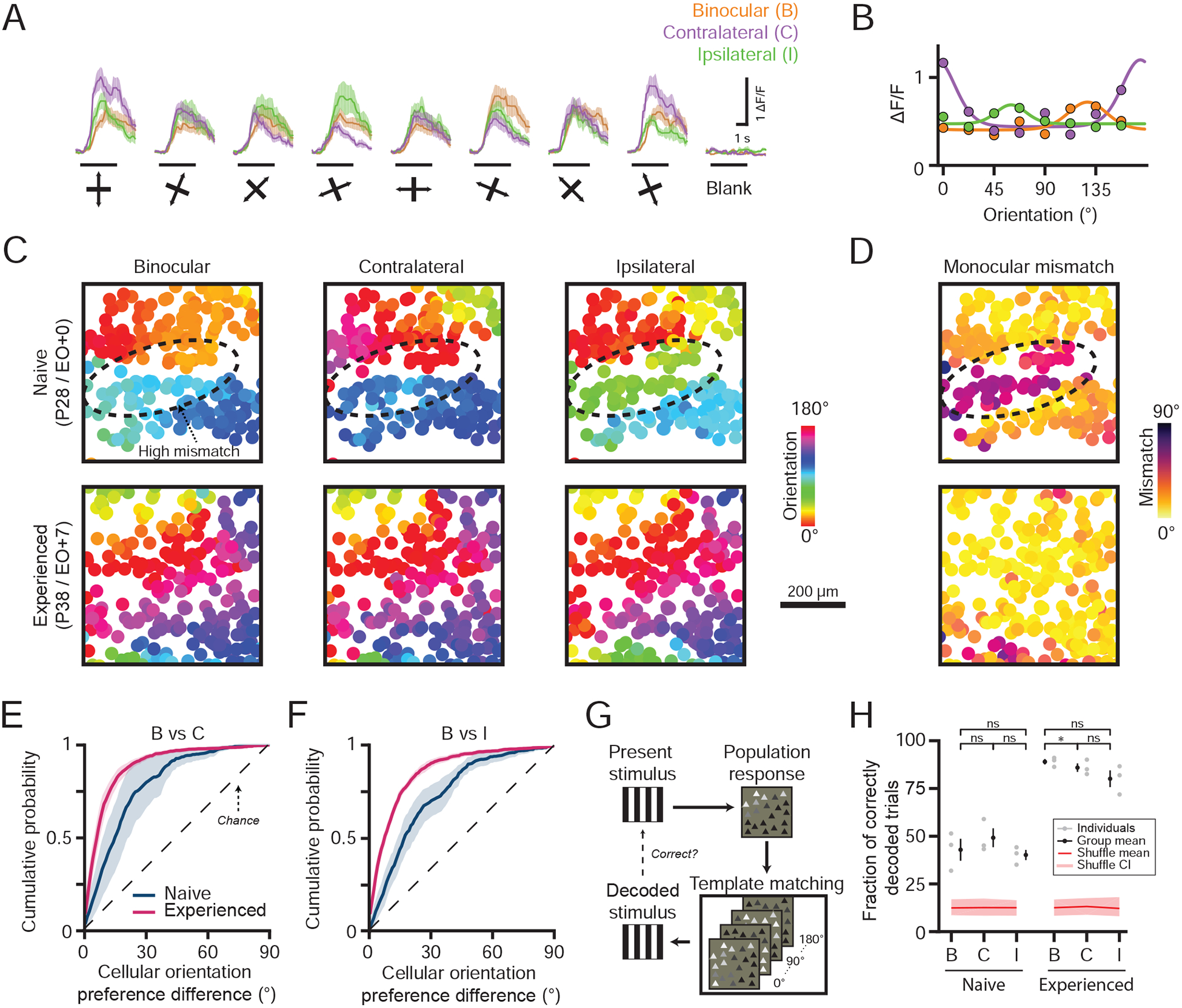
(A-B) Cellular response traces (A, mean±SEM) and orientation tuning curves fit to trial-averaged responses (B, median) in a naive animal. The black line under each trace indicates visual stimulation.

(C-D) Cellular orientation preference (C) and monocular mismatch (D) maps for naive (top) and experienced (bottom) animals. Circles are cells and color represents the preferred orientation or monocular mismatch. Dashed ellipse denotes a region of high monocular mismatch.

(E-F) Cumulative distributions of cellular orientation preference difference between the binocular and monocular preferred orientations (mean±SEM).

(G) Template-matching decoder schematic.

(H) Fraction of correctly decoded trials to binocular and monocular stimulation (mean±SEM). Red line and shaded regions indicate the mean and 95% confidence intervals for shuffled data. Asterisks denote significance between groups (*:p<0.05, ns: p>0.05). Animal experiments: naive (n=3) and experienced (n=3).

In naive animals, binocular stimulation drove robust orientation selective responses (Figure 5B–C), even in neurons where the monocular mismatch was high (Figure 5D–F). If the binocular representation simply reflected the co-activation of differently tuned monocular inputs, then we would expect to find a degraded binocular representation of orientation in regions of high monocular mismatch. Signatures of a degraded binocular representation would include reduced binocular orientation selectivity and reduced spatial clustering of preferred orientation. Cellular-scale spatial clustering of the binocular preferred orientation was comparable between naive and experienced animals (Figure S3A, p<0.05 within 100μm for Naive and Experienced, unpaired bootstrap test), and smoothly mapped across the cortex (Figure 5C). Furthermore, we failed to find any systematic difference between binocular and monocular orientation selectivity in either naive or experienced animals (Figure S3B, p>0.05 for all comparisons, paired bootstrap test), and binocular orientation selectivity was only weakly correlated to the amount of monocular mismatch (Figure S3C, Pearson’s correlation: Naive r=−0.25±0.12 vs Experienced r=−0.21±0.02 (Mean±SEM), n= 3 animals). Thus, we conclude that in naive animals cortical circuits generate a coherent representation of orientation preference in response to simultaneous binocular stimulation in spite of the mismatch in the monocular representations.

One possible explanation for the coherence in the naive binocular representation in spite of monocular mismatch is that the binocular representation is simply identical to one of the monocular representations. The binocular cellular preferred orientation in naive animals was not biased to either of the monocular preferred orientations (Figure 5E–F, Cellular orientation preference difference with binocular: Contralateral 19.12±6.83°, Ipsilateral 23.40±4.29° (Mean±SEM), n=3 animals; Naive vs Experienced comparison: Binocular vs Contralateral p=0.104, Binocular vs Ipsilateral p=0.052, unpaired bootstrap test). We also considered the possibility that the binocular orientation preference of neurons in naive animals simply reflects the relative strength of the monocular responses. However, binocular and monocular preferred orientation similarity was only weakly correlated to a cell’s ocular dominance (Figure S3D, Pearson’s correlation with ODI in naive animals: Binocular vs Contralateral r=−0.20, p<0.001, Binocular vs Ipsilateral r=−0.20, p<0.001, n=3 animals). These results at the cellular level suggest that the binocular representation of orientation preference in naive animals is not related in a simple way to either of the monocular representations.

Wide-field imaging experiments also confirmed prominent differences between the network structures of binocular and monocular representations in naive animals. In experienced animals, network-scale binocular orientation representations were well-matched with monocular representations (Figure 6A, Circular correlation with binocular: Contralateral r=0.93±0.01, Ipsilateral: r=0.93±0.02; Pearson’s correlation of homogeneity index with binocular: Contralateral: r=0.77±0.03, Ipsilateral: r=0.76±0.05 (Mean±SEM), n=7 animals). In contrast, both contralateral and ipsilateral representations were less correlated with the binocular representation in naive animals. (Figure 6C, Circular correlation of preferred orientation with binocular in naive animals: Contralateral r=0.79±0.05, Ipsilateral r=0.59±0.07 (Mean±SEM), n=6 animals, p=0.07, paired permutation test). Interestingly, the contralateral and ipsilateral representations differed in the degree of network structure correlation with the binocular representation in naive animals (Figure 6B,D, Pearson’s correlation of HI with binocular in naive animals: Contralateral r=0.71±0.05, Ipsilateral r=0.46±0.07 (Mean±SEM), n=6, p=0.04, paired permutation test).

Figure 6: Binocular representations of orientation preference are not trivially related to the monocular representations.

(A-B) Widefield maps of orientation preference (A) and homogeneity index maps (B) for naive (top row) and experienced (bottom row) animals. Preferred orientation and selectively (or homogeneity index) are represented by image hue and saturation (or image color). Grayed or blacked out regions represent blood vessels.

(C-D) Circular correlation of the binocular to monocular orientation preference maps (J) and Pearson’s correlation of fine-network structure (homogeneity index) for the binocular to monocular preferred orientation maps (K) (mean±SEM).

Asterisks denote significance between groups (*:p<0.05,**:p<0.01, ns: p>0.05). Animal experiments: naive (n=6) and experienced (n=7 widefield).

Having demonstrated a binocular representation that appears to be well-organized and distinct from the two mismatched monocular representations, we wondered whether there might be differences in the ability of these representations to encode orientation-specific information that might provide clues to their capacity to contribute to vision in naive animals. To probe this, we employed a template matching decoder to predict the stimulus orientation by comparing trial-evoked population activity patterns to the trial-averaged response pattern (Figure 5G)(Montijn et al., 2014). In naive animals, we could decode population responses from binocular and monocular stimulation at a rate higher than chance indicating that all three representations principally contribute to stimulus encoding (Figure 5H, Decoding performance in naive animals: Binocular 42.9±5.8%, Contralateral 49.5±5.0%, Ipsilateral 40.2±2.7% (Mean±SEM) vs chance 12.5%). Importantly, none of the orientation representations outperformed the others (p>0.05, paired bootstrap test), suggesting that the binocular and monocular representations are comparable in their capacity to deliver reliable information about the stimulus orientation in naive animals.

Shifts in cellular orientation preferences reduce monocular mismatch

How are monocular mismatches in binocularly responsive neurons reduced across development? One possibility is that highly mismatched cells in naive animals could become strongly dominated by one eye, such that our sample of binocularly responsive cells exhibit reduced monocular mismatch. Another change in responsiveness that could account for the reduction in monocular mismatch is a loss of orientation tuning for cells that exhibited mismatch prior to eye-opening. Finally, the reduction in monocular mismatch could result from shifts in the preferred orientation for one or more of the orientation representations. To investigate which of these mechanisms contribute, in a cohort of animals we chronically tracked L2/3 neurons using two-photon calcium imaging to monitor how the three orientation representations changed between eye-opening (naive) and four days after eye-opening (experienced) (Figure 7A–B, n=4 animals).

Figure 7: Shifts in cellular orientation preferences reduce monocular mismatch.

(A) Experimental timeline for chronic imaging.

(B) An example field-of-view of chronically tracked cells before and after eye-opening.

(C) The trial-average response (median) and fit orientation tuning curves for chronically tracked cells.

(D) Cumulative distributions of monocular mismatch for chronically tracked cells before and after eye-opening (mean±SEM).

(E) Scatter plot of the monocular mismatch for chronically tracked cells before and after eye-opening. The error bars represent the Median±MAD for each animal (n=4 animals), while the color of each dot or error bar represents the animal.

(F) Cumulative distributions of monocularity (or |ODI|) for chronically tracked cells before and after eye-opening (mean±SEM).

First we sought to evaluate whether neurons with high mismatch were selectively eliminated from our analysis. We found that binocularly responsive neurons only modestly increased in monocularity after four days of visual experience, suggesting that the maturation of ocular dominance occurs after the matching of orientation preference (Figure 7F, Monocularity: Naive 0.136±0.009 vs Experienced 0.154±0.003 (Mean±SEM), p<0.05, paired bootstrap test). Moreover, the degree of cellular monocular mismatch at eye-opening did not predict the monocularity recorded days later (Bootstrapped Pearson’s correlation: actual r=0.03 [−0.12, 0.17] vs surrogate r=0.14 [−0.02, 0.30], Median [CI]). We also failed to find a difference in the fraction of chronically tracked neurons that did not display well-fit orientation selective responses before and after eye-opening (Fraction of well-tuned chronically tracked cells: Naive 14.0±3.3% vs Experienced 24.7±9.0% (Mean±SEM), p=0.38, paired bootstrap test). Therefore, the reduction in monocular mismatch could not be accounted for by the selective elimination of highly mismatched cells from our analysis.

To assess whether individual neurons shifted in orientation preference, we restricted our analysis to chronically tracked cells. Neurons that maintained orientation selective responses across imaging sessions (73.53±7.97% of chronically tracked cells, Mean±SEM) displayed systematic reductions in monocular mismatch (Figure 7C–E, Mean monocular mismatch: Naive 35.47±6.09° vs Experienced 12.73±0.94° (Mean±SEM), p<0.001, paired bootstrap test). In addition to reduction in monocular mismatch, binocular and monocular orientation preference was better matched in experience animals (Figure S4). Together these results suggest that alignment is driven primarily by systematic reorganization of the preferred orientation such that monocular and binocular orientation preferences in experienced animals are matched.

Early orientation representations reorganize to a unified representation resembling the early binocular representation.

We have demonstrated that there are three distinct representations of orientation at eye-opening that reorganize into a single coherent representation through changes in the orientation preference of individual neurons. In principle, the mature coherent representation could reflect a radical reorganization that leaves little trace of the naive representations. To probe the nature of the reorganization, we asked whether the cellular-scale activity patterns at eye-opening exhibit any similarity to the binocularly unified representation that becomes evident days later. Our approach was to test whether a template matching decoder based on the trial-averaged response of the binocularly unified representation could be used to decode the stimulus identity using trial-evoked population responses recorded at eye-opening. Under these conditions we found the decoder performed at rates that were above chance levels (Figure S5, Fraction of correctly decoded trials: Binocular 21.5±3.1%, Contralateral 17.92±2.0%, Ipsilateral 20.82±2.4% (Mean±SEM) vs Shuffles 12.5% [8.13, 16.88], Mean [CI]), although the decoding accuracy based on the experienced representation was worse than the naive trial-average responses (p<0.001 for all comparisons, paired bootstrap test). Nevertheless, these results suggest that at the cellular-scale, experienced animals’ binocularly aligned representations bear a coarse resemblance to the representations evident at eye-opening.

Next we asked whether there were any differences in the relative stability of the three representations during this period of reorganization. Interestingly, using widefield imaging, we observed that the layout of the binocular orientation representation was significantly more stable than either of the monocular representations (Figure 8A,D, Circular correlation of the preferred orientation: Binocular r=0.40±0.04, Contralateral r=0.30±0.04, Ipsilateral r=0.16±0.04 (Mean±SEM), n=12 animals; Binocular vs Contralateral: p=0.02, Binocular vs Ipsilateral: p<0.01, Contralateral vs Ipsilateral: p=0.06, paired permutation test). If the binocular representation is more stable than the monocular representations, the fine-network structure of the binocular representation should remain more stable. Indeed, as assessed by HI, the fine-network structure of the binocular representation changes less than the monocular representations (Figure 8B,E, Pearson’s correlation of HI: Binocular r=0.40±0.06, Contralateral r=0.26±0.04, Ipsilateral r=0.12±0.07 (Mean±SEM); Binocular vs Contralateral: p=0.01, Binocular vs Ipsilateral: p<0.01, Contralateral vs Ipsilateral p=0.10, paired bootstrap test). These results demonstrate that the naive binocular representation is more stable than the monocular representations and suggests that after eye-opening the binocular unified representation might more closely resemble the naive binocular representation.

Figure 8: Early orientation representations reorganize to a unified representation resembling the early binocular representation.

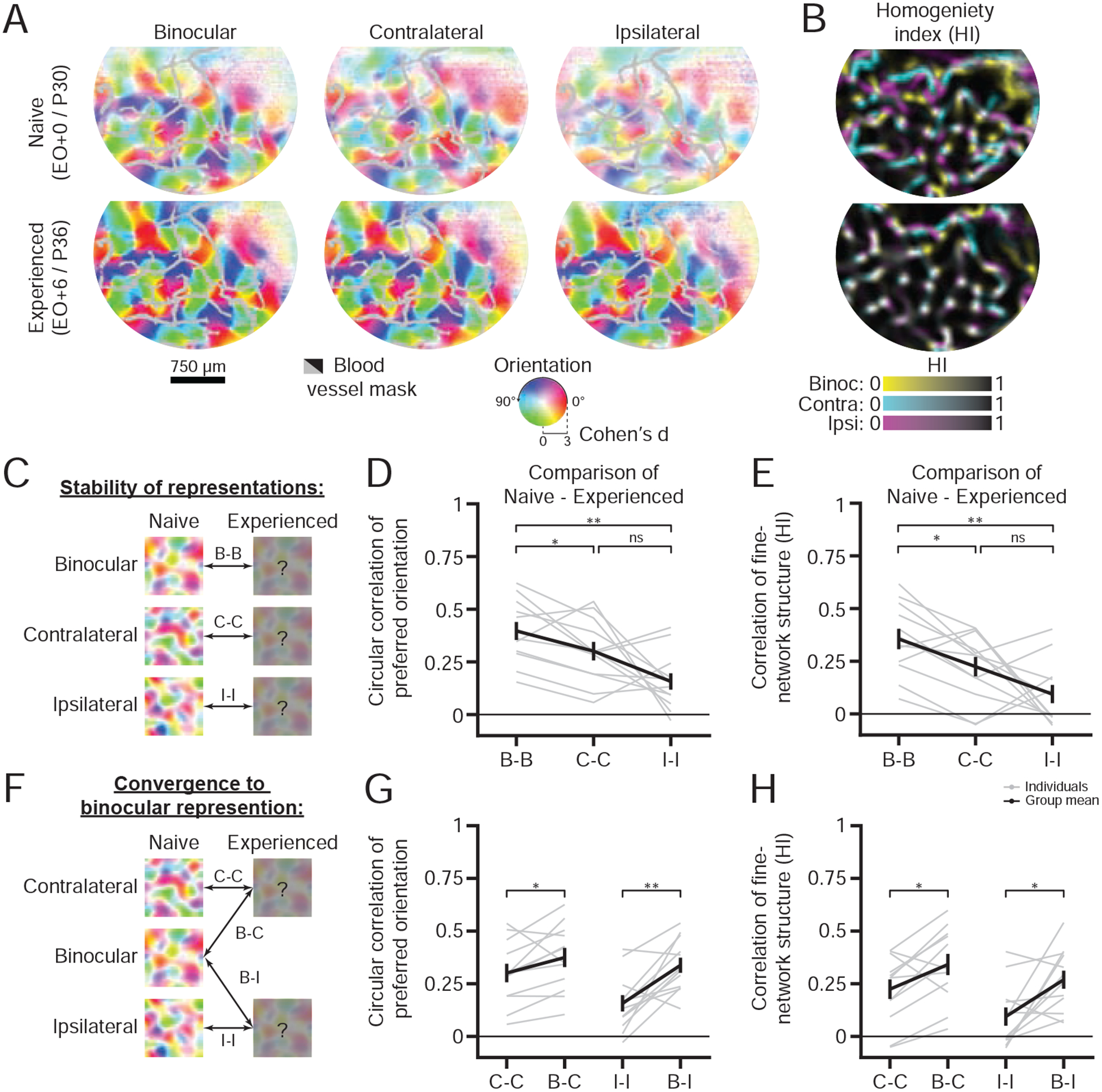
(A-B) Widefield maps of orientation preference (A) and homogeneity index maps (B) before and after eye-opening from a chronically imaged animal (top and bottom rows). Preferred orientation and orientation selectively (or homogeneity index) are represented by image hue and saturation (or image color). Grayed or blacked out regions represent blood vessels.

(C) Schematic for determining the stability of the monocular and binocular representations before and after eye-opening.

(D-E) Circular correlation of the preferred orientation (D) and Pearson’s correlation of fine-network structure (homogeneity index) (E) for comparing the stability of the binocular and monocular orientation preference maps before and after eye-opening (mean±SEM).

(F) Schematic for determining if the experienced monocular orientation preference maps are more similar to the naive binocular or naive monocular orientation preference maps.

(G-H) Circular correlation of the preferred orientation (G) and Pearson’s correlation of fine-network structure (homogeneity index) (H) for comparing the experienced monocular orientation preference maps either to the naive binocular or naive monocular orientation preference maps (mean±SEM).

Gray and black lines/dots in (D-E, G-H) reflect either individual or grouped measurements (n=12 animals), while asterisks denote significance between groups (*:p<0.05,**:p<0.01, ns:p>0.05).

To directly test this hypothesis, we compared the experienced monocular representations to the naive binocular representation or corresponding naive monocular representation (Figure 8F). Indeed, we found that both the layout of preferred orientation and fine-network structure for the naive binocular representation was more similar to the experienced monocular representations (Figure 8G–H, Circular correlation of the preferred orientation: Experienced Contralateral vs Naive Contralateral r=0.30±0.04 or Naive Binocular r=0.38±0.05, p=0.048, Experienced Ipsilateral vs Naive Ipsilateral r=0.16±0.04 or Naive Binocular r=0.34±0.04, p<0.01; Pearson’s correlation of HI: Experienced contralateral vs Naive contralateral r=0.22±0.05 or Naive binocular r=0.34±0.05, p=0.02, Experienced ipsilateral vs Naive ipsilateral r=0.16±0.04 or Naive binocular r=0.34±0.05, p=0.02, paired bootstrap test). Taken together our results suggest that the naive binocular representation plays a dominant role in the experience-dependent reshaping of the orientation representations, likely reflecting the onset of coherent binocular experience that accompanies eye-opening.

Discussion

Three well-organized representations of orientation develop independent of experience

The prevailing view of visual cortex in mammals that exhibit a modular architecture for orientation preference is that the basic modular structure is present at or before eye-opening, although patterns of activity become more distinct with experience, as visualized with intrinsic signal imaging (Chapman and Stryker, 1993; Chapman et al., 1996; Crair et al., 1998; White et al., 2001; Wiesel and Hubel, 1974). Our results using calcium imaging strengthen this view, demonstrating that well-organized columnar networks are present at eye-opening in ferret visual cortex, and that the fine-scale modular organization is evident across both cellular- and network-scales. While the presence of early modular structure was anticipated, we were surprised to find that the early modular representations of orientation preference derived from monocular and binocular stimulation exhibited misalignment. Previous studies had concluded that segregated inputs from the eyes converge in visual cortex early in development to yield a coarse, but stable, binocularly aligned representation (Crair et al., 1998; Godecke and Bonhoeffer, 1996). Multiple factors may contribute to the different conclusions reached, such as species differences or reliance on intrinsic signal imaging, a less-sensitive technique for assessing preferred orientation. Regardless, no previous study has suggested that there could be an early developmental misalignment of organized columnar network structures. Our findings highlight the complex interaction of eye-specific inputs during development, and the reorganization in network structure that is necessary for alignment of monocular and binocular representations of orientation.

Early binocular interactions are necessary for the development and maintenance of a single orientation representation

The presence of separate monocular and binocular representations of orientation selectivity before eye-opening suggests the developing cortex treats monocular inputs as separate streams of sensory information, and that shared binocular experience serves as an important catalyst for functional reorganization of monocular representations towards a binocularly aligned representation. Our findings highlight the cooperative nature of ocular interactions in the generation of a binocularly unified orientation representation, which contrasts with other studies that have focused on the competition of monocular inputs in the development of ocular dominance (Bienenstock et al., 1982; Blakemore and Van Sluyters, 1974; Katz and Shatz, 1996; Miller et al., 1989; Trachtenberg, 2015). Our deprivation experiments show that patterned binocular visual experience is important for the alignment of the orientation representations, as well as the maintenance of spatially-clustered responses. This is consistent with growing evidence that binocular visual experience both during and after the critical period of visual development can correct amblyopia related deficits (Birch et al., 2015; Hess et al., 2010; Murphy et al., 2015), and computational studies suggesting that interocular correlations arising from binocular experience could play a role in the alignment of the monocular orientation representations (Erwin and Miller, 1998; Miller and Erwin, 2001). Thus, shared sensory experience appears crucial for the proper maturation of binocular interactions and the normal development of visual responses.

Importantly, binocular alignment of monocular representations occurs during a critical window when neural responses are highly binocular. In the ferret, the critical period for ocular dominance begins about one week after eye-opening (Issa et al., 1999), suggesting that binocular alignment of orientation representations precedes the establishment of mature ocular dominance. Consistent with this hypothesis, we did not observe a dependence of binocular alignment on cellular monocularity. These results contrast with experiments in environmentally-enriched and monocularly deprived mice, where rescue of the monocular matching process depends on ocular dominance (Levine et al., 2017). Similarly, reverse-lid suture experiments in young kittens suggest that binocularly visual experience is unnecessary to develop matched monocular representations (Godecke and Bonhoeffer, 1996). Together these studies suggest that alignment of the preferred orientation in animals recovering from monocular deprivation, during a later developmental stage when cells are strongly monocular, benefit from the establishment of the dominant eye’s orientation representation. In contrast, over the course of normal development, monocular inputs cooperatively interact to achieve aligned orientation preference in an experience-dependent manner during the first week of visual experience.

Experience-dependent reorganization across large-scale networks underlies alignment of orientation representation

Our data demonstrating experience-dependent development of a binocularly unified representation of orientation selectivity in ferret visual cortex appears similar to the binocular matching process reported in the developing mouse (Gu and Cang, 2016; Wang et al., 2010; Yaeger et al., 2019). However, characterization in the mouse has been limited to single-cells, and has not yet evaluated how the ocular mismatch evident at the scale of individual neurons is related to the organization state of intracortical networks. While, refinement of intracortical connectivity has been implicated as an important contributor to the matching of orientation preference (Gu and Cang, 2016), it remains to be seen whether these changes reflect the refinement of existing orderly functional networks or the emergence of feature-specific network connectivity (Ko et al., 2013; Ko et al., 2014). By leveraging a model species with a modular functional network, we have been able to demonstrate a binocular matching process that proceeds via a systematic reorganization of pre-existing orderly network representations.

Furthermore, the changes in the responses of individual neurons that are responsible for the binocular alignment of orientation preference have remained a mystery. To the best of our knowledge, this is the first study to chronically track the cellular changes underlying the normal alignment of sensory representations. We show that chronically tracked cells display shifts in preferred orientation reflecting reorganization of the orientation representations, rather than changes in other properties (e.g. ocular dominance or orientation tuning) that could have accounted for the alignment.

While studies in the mouse have provided clear evidence that binocular visual experience is critical for the development of binocularly matched orientation preference in individual cortical neurons (Gu and Cang, 2016; Levine et al., 2017; Wang et al., 2010), what could not be envisioned from these studies is the existence of a distinct binocular network representation, one that could serve as the template for alignment of the monocular representations. This possibility derives from our observations at the network scale that the monocular representations undergo substantially more reorganization than the binocular representation during the alignment process. Previous studies that have explored the experience-dependent alignment of spatially-organized, sensory representations have naturally focused on direct interactions between the independent sensory representations as the basis for the alignment (Cang and Feldheim, 2013; Hyde and Knudsen, 2001; Knudsen and Knudsen, 1989; Smith and Trachtenberg, 2007; Triplett et al., 2009). Our results suggest a different possibility for large-scale mapped sensory representation alignment, one in which constructive interactions between segregated inputs lead to a third distinct representation, which serves as a template for the construction of a single unified representation.

STAR*Methods

RESOURCE AVAILABILITY

Lead Contact

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, David Fitzpatrick (david.fitzpatrick@mpfi.org).

Material Availability

This study did not generate new unique reagents.

Data and Code Availability

Custom-written MATLAB and Python code and date for this study are available from the lead contact upon request.

EXPERIMENTAL MODEL AND SUBJECT DETAILS

All experimental procedures were approved by the Max Planck Florida Institute for Neuroscience Institutional Animal Care and Use committee and were performed in accordance with guidelines from the U.S. National Institute of Health. Juvenile female ferrets from Marshal Farms were co-housed with jills on a 16-h light/8-h dark cycle.

METHOD DETAILS

Viral injections and Eyelid Suturing.

Viral injections were performed as previously described (Smith et al., 2018). Briefly we expressed GCaMP6s by microinjection of AAV2/1-hSyn-GCaMP6s-WPRE-SV40 (University of Pennsylvania Vector Core) into the visual cortex 6–14 days before imaging experiments. In developing ferrets, viral expression using the hSyn promoter has previously been demonstrated to primarily label excitatory neurons (Wilson et al., 2017) and yield multiple millimeters of roughly uniform labeling of GCaMP6s (Smith et al., 2018). Anesthesia induction was performed using either ketamine (50mg/kg, IM) and/or isoflurane (1–3%) delivered in O₂ and then maintained with isofluorane (1–2%). Atropine (0.2mg/kg, IM) was administered to reduce secretions, while Buprenorphine (0.01mg/kg, IM) and a 1:1 mixture of lidocaine and bupivacaine (injected directly into the scalp) were administered as analgesics. Animal temperatures were maintained at 37°C using a homeothermic heating blanket. Animals were also mechanically ventilated and both heart rate and end-tidal CO2 were monitored throughout the surgery. Under aseptic surgical technique, a small craniotomy was made over visual cortex 6.5–7 mm lateral and 2mm anterior to lambda. Approximately 1μL of virus was pressure infused into the cortex through a pulled glass pipette across two depths (~200μm and 400μm below the surface). This procedure reliably produced robust and widespread GCaMP6s expression in excitatory neurons over an area >3 mm in diameter (Smith et al., 2018). To improve the uniformity of the GCaMP6s expression, sometimes an additional injection of 1μL of virus was pressure injected into a separate region of cortex displaced ~1–1.5mm away from the first injection site.

Eyelid Suture Procedure.

In deprivation and chronic imaging experiments, eyelids were binocularly sutured during a short surgical procedure between P26–30. Anesthesia was induced with isoflurane (2–5%) and Buprenorphine (0.01mg/kg, IM) was administered. Using aseptic technique, both eyelids were sutured shut using continuous sutures (6–0 Ethilon suture). During recovery, antibiotic ointment was applied to the suture eyelid margins. Eyelid sutures were monitored daily until removed during an imaging experiment as noted in the main text.

Cranial window surgery.

All animals were anesthetized and prepared for surgery as described above. In acute imaging experiments, skin and muscle overlying visual cortex were reflected and a custom-designed metal headplate (8mm DIA) was implanted over the injected region with MetaBond (Parkell Inc.). Then a craniotomy and a subsequent durotomy were performed, and the underlying brain stabilized with a custom-designed titanium metal cannula (4.5mm DIA, 1.5mm height) adhered to a thin 4mm coverslip (Warner Instruments) with optical glue (#71, Norland Products, Inc). The headplate was hermetically sealed with a stainless-steel retaining ring (5/16” internal retaining ring, McMaster-Carr) and glue (VetBond, 3M or Krazy Glue).

To allow repeated access to the same imaging field in chronic imaging experiments, cranial windows were implanted in each animal 2 days prior to the first imaging session. Using aseptic surgical technique, we adhered a metal headpost (7×7mm) to the skull ~3.5mm anterior of bregma and a separate custom-designed, chamber implant overlying the injected region using MetaBond and black dental acrylic. At the end of the survival cranial window implant surgery, the metal cannula was sealed with a silicone polymer plug (Kwik-kast, World Precision Instruments) to protect the imaging window between imaging experiments. Whenever the imaging quality of the chronic cranial window was found to be suboptimal for imaging, the chamber was opened under aseptic conditions, any regrown tissue/neomembrane was removed, and a new coverslip was inserted.

Imaging experiments fell into two broad categories: acute and survival imaging experiments. Acute imaging experiments began immediately after the cranial window surgery. For survival imaging experiments, where animals had a cranial window implanted days earlier, anesthesia was induced with isoflurane (2–5%) and atropine (0.2mg/kg) was administered. Animals were intubated and ventilated, and an IV catheter was placed in the cephalic vein. The silicon polymer plug overlying the sealed imaging chamber was gently peeled off. Whenever the imaging quality of the chronic cranial window was found to be suboptimal for imaging, the chamber was opened under aseptic conditions, any regrown tissue/neomembrane was removed, and a new coverslip was inserted.

For both acute and survival imaging experiments, eyelid sutures were removed or eyelids were separated where applicable to ensure visual stimulation was always presented to open eyes. Phenylephrine (1.25–5%) and tropicamide (0.5%) were applied to the eyes to retract the nictitating membrane and dilate the pupil, and the cornea was protected with regular application of eye drops (Systane Ultra, Alcon Laboratories). Prior to imaging, isoflurane levels were reduced from a surgical plane to ~1–1.5%. After reaching a stable, anesthetic baseline for 30 minutes (~280–300bpm), animals were paralyzed with pancuronium bromide (0.1 mg/kg/hr in lactated Ringer’s with 5% dextrose, delivered IV). Upon completion of imaging in acute experiments, isoflurane was raised to 5% and given Euthasol (0.5ml, IV). In survival experiments, animals were instead recovered from anesthesia and returned to their home cages. During recovery, up to 3 repeated doses of neostigmine (0.06mg/kg/hr, IV) and atropine (0.05mg/kg/hr, IV) were used to reverse paralysis.

Calcium Imaging Experiments.

Widefield epifluoresence imaging of GCaMP6s was achieved with a Zyla 5.5 sCMOS camera (Andor) controlled by μManager (Edelstein et al., 2010). Images were acquired at 15Hz with 4×4 binning to yield 640×540 pixels through a 4x air-immersion objective (Olympus, UPlanFL 4x N/0.13NA). For analysis, images were spatially downsampled by a factor of 2x to yield 320×270 pixels at a spatial resolution of 11.63μm/pixel. Two-photon imaging of GCaMP6s was performed with a B-Scope microscope (ThorLabs) driven by a Mai-Tai DeepSee laser (Spectra Physics) at 940nm. The B-Scope microscope was controlled by ScanImage (Pologruto et al., 2003) in a resonant-galvo configuration with multi-plane images (512×512 pixels) being sequentially collected across either one or four imaging planes using a piezoelectric actuator for an effective frame rate of 30Hz or 6Hz respectively. Images were acquired at 2x zoom through a 16x water immersion objective (Nikon, LWD 16X W/0.80NA) yielding cellular fields-of-views of ~0.7mm on each side (1.36μm/pixel). The location of the two-photon calcium imaging ROIs was primarily determined by finding a location with strong GCaMP6s expression and not occluded by large superficial vessels.

To locate the same cellular field-of-views between chronic imaging sessions, we acquired a series of z-stack images across different depths incremented at 5μm steps during each experiment. For each chronic experiment, the original field-of-view was carefully compared to the different z-locations, and a matched location was chosen based on the relative similarity of physical landmarks, such as penetrating blood vessels and cells. However, because of natural warping in the field-of-view arising from brain growth, we carefully only chose cells for analysis that were obviously common to both sessions. To aid the experimenter in selecting common cells, all fields-of-view were registered into a common reference frame using an affine transform or a 2D elastic deformation (BUnwarpJ plug-in in ImageJ). The optimal geometric transformation was inferred from control point pairs of common physical landmarks between imaging sessions. To determine whether a pair of cell ROIs across chronic experiments corresponded to the same cell, we putatively required that the centroid of the candidate cell pairs were located within 4–5μm and overlapped >25%. The experimenter then manually decided whether the match was reasonable based on similarity of the local neighborhood and physical shape of the cell ROIs.

Visual stimulation.

Visual stimuli were delivered on a LCD screen placed approximately 25–30cm in front of the eyes using PsychoPy (Peirce, 2007). To evoke orientation responses, full-field square gratings at 100% contrast, at 0.015 or 0.06 cycles per degree and drifting at 1 or 4 Hz were presented at 8 or16 directions. For optimal responsivity, a single paired spatial and temporal frequency was used for each animal to assess both monocular and binocular orientation-specific responses. In addition, “blank” stimuli of 0% contrast were also presented. Stimuli were randomly interleaved and presented for 3–4s followed by 3–6s of gray screen.

QUANTIFICATION AND STATISTICAL ANALYSIS

General preprocessing for widefield and two-photon imaging.

All data analysis was performed using custom written scripts in either Python, Matlab, or ImageJ. Widefield and two-photon imaging were corrected for in plane motion to a common reference field of view via a 2D cross correlation-based approach within days. Periods with excessive or out of plane motion were excluded from further analysis. ROI segmentation was performed manually in widefield epifluorescence imaging by manually drawing around cortical regions with robust visually evoked activity, while cellular ROIs were drawn using custom software in ImageJ (Cell Magic Wand)(Wilson et al., 2017). The baseline F₀ for each pixel/cell was obtained by applying a rank-order filter to the raw fluorescence trace (25–30^th percentile) with a time window of 60s. The baseline corrected evoked activity was calculated as (F-F₀)/F₀ = ΔF/F₀. Grating evoked responses were then calculated as the difference of the average of the fluorescence ΔF/F₀ over the full stimulus period (3–4s) and the average of the fluorescence ΔF/F₀ over the pre-stimulus period (1.5–2s). Trial-averaged responses were calculated by taking the median across repeated trials to the same stimulus orientation.

Widefield Epifluorescence Imaging.

After performing general pre-processing (see earlier section), we analyzed the widefield epifluorescence imaging data. For analysis of the wide-field epifluorescence imaging data, spatial filtering was necessary to eliminate signal strength variations and measurement noise. To determine an appropriate high-pass filter cutoff that did not fundamentally alter the underlying modular response, we first computed the average size (i.e. wavelength) of orientation hypercolumns for each imaging experiment using an established wavelet technique (Kaschube et al., 2010; Smith et al., 2015). We then spatially filtered each trial-evoked response image using a bandpass fermi-filter, where the low-pass filter cutoff was defined as 50μm and the high-pass filter cutoff was defined as the mean orientation hypercolumn wavelength across monocular and binocular stimulation. A spatial filter was applied to each image in the Fourier Domain, using a filter kernel based on the Fermi-Dirac distribution:

$$\mathit{\text{Filtered Image}}(x)={\mathcal{F}}^{-1}\left(\mathcal{F}[\mathit{\text{Image}}(x)]*\mathit{\text{Filter}}\left(k_{lp},k\right)*\left[1-\mathit{\text{Filter}}\left(k_{hp},k\right)\right]\right)$$

$$\mathit{\text{Filter}}\left(k_{\mathit{\text{cutoff}}},k\right)=\frac{1}{1+e^{\frac{\left|k\right|-k_{\mathit{\text{cutoff}}}}{\beta *k_{\mathit{\text{cutoff}}}}}}$$

where $\mathcal{F}$ denotes the forward Fourier transform, ${\mathcal{F}}^{-1}$ denotes the inverse Fourier transform, k is the spatial wave-number (k = 2π/λ), k_cutoff is the filter cutoff (low-pass cutoff (l_lp): 2π/0.25mm, high-pass cutoff (l_hp): 2π/1.6mm), and β is the steepness parameter of the fermi-filter (T = 0.05). To maintain the original response amplitude of the population responses, spatially filtered images were ranged-fitted, such that the 5^th and 95^th percentiles intensity values matched the original, unfiltered images.

To evaluate orientation selective responses, we computed normalized single-condition response maps using the Cohen’s d metric, to account for response variance across trials:

$${\mathit{\text{Cohen}}}^{\prime }sd(\theta ,x)=\frac{\mu (x,\theta )-\mu (x)}{\sqrt{\frac{\left(n_{\mathit{\text{trials }}}-1\right)\sigma {(x,\theta )}^2-\left(n_{\theta }*n_{\mathit{\text{trials }}}-1\right)\sigma {(x)}^2}{\left(n_{\theta }+1\right)*n_{\mathit{\text{trials }}}-2}}}$$

$$\mu (\theta ,x)=\sum _{i=1}^{n_{\mathit{\text{trials}}}}{R}_i(x,\theta )/n_{\mathit{\text{trials}}}$$

$$\mu (x)=\sum _{\theta =0^{°}}^{{180}^{°}}\mu (x,\theta )/n_{\theta }$$

$$\sigma (\theta ,x)=\sqrt{\sum _{i=1}^{n_{\mathit{\text{trials}}}}{\left(R_i(x,\theta )-\mu (x,\theta )\right)}^2/\left(n_{\mathit{\text{trials}}}-1\right)}$$

$$\sigma (x)=\sqrt{{\sum }_{\theta =0^{°}}^{{180}^{°}}{\sum }_{i=1}^{n_{\mathit{\text{trials}}}}{\left(R_i(x,\theta )-\mu (x)\right)}^2/\left(n_{\theta }*n_{\mathit{\text{trials}}}-1\right)}$$

where n_trials is the number of trials, and n_θ is the number of stimulus conditions, and R_i(x, θ) is the evoked response to an oriented, drifting grating (θ) for trial i at pixel (θ). Preferred orientation (θ_pref(x), ranging from 0 to 180°) and orientation selectivity (r) was computed as the vector sum of the Cohen’s d (θ ,x)single-condition maps:

$$z(x)=\sum _{\theta =0^{°}}^{{360}^{°}}{\mathit{\text{Cohen}}}^{\prime }sd(\theta ,x)*e^{i*2\pi *\theta /{180}^{°}}$$

$${\theta }_{\mathit{\text{pref}}}(x)=\text{arg}(z(x))={\text{tan}}^{-1}\frac{\mathit{\text{real}}(z(x))}{\mathit{\text{imag}}(z(x))}$$

$$r=|z|=\sqrt{\mathit{\text{real}}{(z(x))}^2+\mathit{\text{imag}}{(z(x))}^2}$$

For each pixel, a permutation test (n=100) was used to evaluate if orientation selectivity was significant (p>0.05). Pixels were considered well-tuned if they exhibited statistically significant orientation selectivity for both monocular and binocular stimulation using a permutation test. We excluded any pixels overlying blood-vessels that could be observed in the raw fluorescence images. Monocular mismatch was computed as the absolute angular difference between the contralateral and ipsilateral preferred orientations:

$$\mathit{\text{Monocular mismatch}}(x)=\left|{\theta }_{\mathit{\text{contra}}}(x)-{\theta }_{\mathit{\text{ipsi}}}(x)\right|=\left(\frac{{180}^{°}}{2\pi }\right)\left|\text{arg}\left(\frac{e^{i*2\pi *{\theta }_{\mathit{\text{contra}}}/{180}^{°}}}{e^{i*2\pi *{\theta }_{\mathit{\text{ipsi}}}/{180}^{°}}}\right)\right|$$

where θ_contra and θ_ipsi are the preferred orientations for each eye at pixel (x). To ensure that the measured monocular mismatch for the population could not be artifactually explained by high variation in the preferred orientation, we evaluated the worst-case measurement error. Here we bootstrap resampled trial-averaged responses using replacement and recomputed the preferred orientation (n=1,000). The measurement error for each pixel was defined as the median error of the bootstrapped preferred orientations with the measured preferred orientation. We then defined our worst case measurement error as the value of the pixel exhibiting large measurement error (95^th percentile).

Orientation preference differences between the monocular and binocular preferred orientations were computed using a similar formula to the monocular mismatch. The circular correlation was used to assess differences in the layout of preferred orientation for monocular and binocular orientation maps. For computing the similarity of the fine network structure in orientation preference maps, we computed the Homogeneity Index (Wilson et al., 2017). We then quantified the similarity between the Homogeneity Index maps for the monocular and binocular orientation maps using Pearson’s correlation.

Two-Photon Imaging

After performing general pre-processing (see earlier section), we analyzed the two-photon imaging data. Cells were considered responsive if the trial-averaged response to any stimulus orientation for either monocular or binocular stimulation was greater than two standard deviations of the response to a blank stimulus. The preferred orientation for responsive cells was assessed by fitting a Von Mises function to the trial-averaged responses:

$$R(\theta )=\frac{e^{\kappa \text{cos}\left(\theta -{\theta }_{\mathit{\text{pref}}}\right)}}{2\pi I_0(\kappa )}$$

where R(θ) is the trial-averaged response, θ is the stimulation orientation, θ_pref is the preferred orientation, κ controls the orientation width, and I₀(κ) is a zero-order Bessel function. Cells were considered well-tuned if the R² value of the orientation fits to monocular and binocular stimulation were all ≥0.5. To evaluate a cell’s orientation selectivity, we used the Cohen’s d metric and compared the responses of the preferred and orthogonal orientations. The unbounded metric Cohen’s d, was chosen as a metric for orientation selectivity, as it takes into account both the differences in mean response and the underlying distribution (or variability) of responses and eliminates ceiling effects that could be encountered using other metrics of orientation selectivity. Spatial clustering of the preferred orientation or monocular mismatch was assessed by calculating the pairwise correlation for cells located within a fixed range from each other, ranging from distances of 50 μm to 500 μm. To evaluate the degree that all preferred orientations are represented uniformly within each of our cellular fields, we estimated the normalized difference from a uniform distribution using the following metric:

$$\mathit{\text{Normalized difference }}=\sum _{i=1}^n\frac{|\mathit{\text{Histogram}}(i)-1|}{2n}$$

where n is the number of cells, histogram (i) is the indexed histogram of preferred orientations, ranging from 0° to 180° with a bin size equal to n, i is the index for the histogram bins. Monocular mismatch, orientation preference differences, measurement error, and the homogeneity index were computed using the same formulas previously described used for pixels (see widefield imaging section).

To evaluate the degree that monocular input from one eye consistently drove stronger responses, we computed the ocular dominance index (ODI):

$$ODI=\frac{{\sum }_{\theta =0^{°}}^{{180}^{°}}\left(R_{\mathit{\text{contra}}}(\theta )-R_{\mathit{\text{ipsi}}}(\theta )\right)}{{\sum }_{\theta =0^{°}}^{{180}^{°}}\left(R_{\mathit{\text{contra}}}(\theta )+R_{\mathit{\text{ipsi}}}(\theta )\right)}$$

where R_conta(θ) and R_ipsi(θ) are the trial-averaged responses to contralateral and ipsilateral stimulation and θ is the stimulation orientation. ODI values range from −1 to +1, where 0 indicates a lack of bias and −1 and +1 values indicate complete dominance from either the ipsilateral or contralateral eyes respectively. Monocularity was defined as the magnitude of the ODI, with values ranging from +0 (binocular) to +1 (monocular).

To decode the stimulus orientation from the population activity vectors recorded during each trial, we used a normalized template matching algorithm (Montijn et al., 2014). In an effort to evaluate the decoding based on the relative responsiveness of each cell, the trial evoked ΔF/F₀ responses of each cell were first individually z-scored:

$$Z(\theta ,\text{n},\text{i})=\frac{R(\theta ,\text{n},\text{i})-\mu }{\sigma }$$

Where i indexes the N^th neuron, θ is the stimulation orientation, n is the trial number, Z(θ, n, i) is the z-scored response, R(θ, n, i)is the actual ΔF/F₀ response, μ is the mean ΔF/F₀ value over the monocular or binocular recording period, and σ is the standard deviation from the mean ΔF/F₀ value. Template population responses for each stimulation condition (φ) were generated by computing the median across repeated trials to the same stimulus orientation for the z-scored responses. Similarity between the actual trial evoked population vector and each template was defined as:

$${\Theta }_{\theta }(\theta ,n)=\frac{{\sum }_{\text{i}=1}^{\text{n}}\left(Z\left(\theta ,\text{n},\text{i}\right)\cdot \mathit{\text{Template}}(\phi ,\text{i})\right)}{\Vert Z(\theta ,\text{n})\Vert \Vert \mathit{\text{Template }}(\phi )\Vert }$$

where φ is the stimulus orientation for the template and ∙ indicates multiplication. To ensure our analysis was comparable across different fields-of-view where the number of cells present varies widely, we limited the number of cells to 50 at any time for our decoder. The similarity metric computed for each template was bootstrap resampled without replacement, but a different subset of cells was used for each resampling procedure (n=1,000). The decoded stimulation orientation was defined as the stimulus orientation for the template showing the highest median similarity across bootstrap resampling to the population activity vector.

Statistics

Unless otherwise noted, hypothesis testing was performed using either a permutation or bootstrapping test. We deliberately chose to use resampling methods for hypothesis testing, rather than relying on standard parametric or non-parametric tests, to avoid confounds that could arise from making assumptions on the underlying sampling distributions present in our data. Statistical significance was assessed by ranking if the observed difference between group averages (i.e. mean or median) was more extreme than the 95^th percentile from a surrogate distribution, where the null hypothesis is true. All statistical tests were two-tail, except when assessing if the performance of the normalized template matching decoder was above chance-levels (one-tail). For each hypothesis test, we produced a relevant surrogate distribution by pooling data between groups, bootstrapped new group averages from the pooled data using replacement (n=1,000), and then computed a distribution of differences between surrogate group averages. Unequal group sizes were maintained for unpaired tests, while resampling was restricted between paired measurements for any paired test. Permutation tests were performed similarly, but data was only exchanged between tested groups, rather than resampled with replacement.

KEY RESOURCES TABLE

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Bacterial and Virus Strains
AAV2/1-hSyn-GCaMP6s-WPRE-SV40	Penn Vector Core	RRID:Addgene_1100843
Experimental Models: Organisms/Strains
Ferret	Marshall Farms	n/a
Software and Algorithms
MATLAB	MathWorks	https://www.mathworks.com/products/matlab.html
Python	Anaconda	https://www.anaconda.com/
ImageJ	NIH	https://imagej.nih.gov/ij/
Cell Magic Wand Tool	Wilson et al., 2017	https://github.com/fitzlab/CellMagicWand
PsychoPy	Peirce, 2007	http://www.psychopy.org
ScanImage	Vidrio Technologies	http://scanimage.vidriotechnologies.com
Micromanager	Edelstein et al., 2010	https://micro-manager.org/

Highlights.

• Monocular stimulation at eye opening yields two distinct orientation representations

• Binocular stimulation at eye opening yields a third distinct orientation representation

• Experience-dependent processes drive development of a single unified representation

• Shifts in cellular preferred orientation contribute to this functional reorganization