Electric fans: A potential stay-at-home cooling strategy during the COVID-19 pandemic this summer?

Abstract

Current public health guidance designed to protect individuals against extreme heat and the ongoing COVID-19 pandemic is seemingly discordant, yet during the northern hemisphere summer, we are faced with the imminent threat of their simultaneous existence. Here we examine the environmental limits of electric fan-use in the context of the United States summer as a potential stay-at-home cooling strategy that aligns with existing efforts to mitigate the spread of SARS-COV-2.

Graphical abstract

Highlights

• •Public cooling centers are recommended for those without access to air-conditioning.
• •At home cooling reduces risk of SARS-COV-2 transmission among vulnerable individuals.
• •Fan-use with water spraying gives effective cooling 100% of time in 80 of 105 US cities.
• •In only 10 of 105 cities fan-use with water spraying is not effective >0.5% summer days.
• •Alternative COVID-compatible cooling methods must be found for Southwest US states.

1. Introduction

In the northern hemisphere summer, the United States faces two simultaneous threats to public health: heat waves and the COVID-19 pandemic. The intersection of these health threats is particularly salient given those most susceptible to the adverse outcomes of COVID-19 both clinically (e.g. older adults and those with cardiovascular and respiratory diseases) (Xie et al., 2020) and socioeconomically (i.e. poor and marginalized) (Bibbins-Domingo, 2020), mirror those most at risk during periods of extreme heat. Over the coming months, public health advice designed to protect against heatwaves must be compatible with the guidance issued to combat the further spread of COVID-19.

On average, 65,000 Americans visit the emergency room every summer for heat illness (Hess et al., 2014). As US healthcare continues to be stretched to capacity by the demands of COVID-19, the provision of effective interventions for preventing heat-related illness has never been more important. However, resources from Centers for Disease Control and Prevention (CDC) developed prior to the current pandemic (Centers for Disease Control and Prevention, 2017; Centers for Disease Control and Prevention, 2016), provide recommendations that could increase the risk of community transmission of SARS COV-2 — especially among those most at risk of its detrimental effects. For example, CDC urge people to “visit older adults or others at risk at least twice a day and closely watch them for signs of heat exhaustion or heat stroke” (Centers for Disease Control and Prevention, 2017; Centers for Disease Control and Prevention, 2016). Moreover, those without access to air-conditioning, or those who cannot afford to use it, are encouraged to congregate in local “cooling centers” (e.g. heat-relief shelters, shopping malls and public libraries) (Centers for Disease Control and Prevention, 2017; Centers for Disease Control and Prevention, 2016). The proportion of the population for which this applies is also likely to increase as COVID-19 exacerbates the financial strain experienced by many at a time of nationwide instability. These concerns have received some attention from mainstream media (Flavelle, 2020; Yuan et al., 2020) and in light of the current pandemic CDC have acknowledged that community cooling centers could in fact facilitate the spread of SARS-COV-2 among at-risk individuals, and have therefore issued interim guidance specifically aimed at reducing the risk of virus transmission in these centers (Centers for Disease Control and Prevention, 2020). This guidance emphasises the importance of physical distancing and personal hygiene at public cooling centers (Centers for Disease Control and Prevention, 2020), yet no alternative stay-at-home cooling solutions to air-conditioning are provided, that eliminate the need to seek refuge from the heat in public spaces and align with existing efforts to limit the spread of COVID-19 in the community.

A growing body of scientific evidence strongly supports the efficacy of several low-resource home-based cooling solutions. For example, skin-wetting has been shown to reduce physiological heat strain, dehydration, and thermal discomfort at temperatures up to 47 °C, irrespective of humidity (Morris et al., 2019a). Electric fans are another low-cost, low-energy demand (i.e. ~20–50-times less A/C) (Jay et al., 2019; Bachar et al., 2012) cooling strategy. However, their cooling effect during a heatwave is dependent on the prevailing combination of temperature and humidity (Morris et al., 2019b), which can vary greatly across the United States. Fans improve skin surface evaporation in humid conditions, but in low humidity conditions sweat evaporates readily, even without a fan, and therefore fans provide no additional benefit (Morris et al., 2019b). When air temperature exceeds skin temperature (~35 °C/95 °F) fans also accelerate dry heat transfer towards the body, via convection (Cramer and Jay, 2019). A recent clinical trial (Morris et al., 2019b) showed that increases in physiological heat strain and thermal discomfort were lower with fan use during an acute exposure to the peak conditions of the most deadly hot/humid heat wave in recent US history (Chicago, 1995; 40 °C/104 °F, 50%RH). While in very hot/arid heat wave conditions (e.g. Los Angeles, 2018; 47 °C/117 °F, 10%RH) fan-use was clearly detrimental, accelerating body heating and exacerbating cardiovascular strain and discomfort relative to a no-fan control condition. Other studies have shown that fans can provide physiological cooling up to air temperatures of 42 °C/108 °F with ~50%RH (Ravanelli et al., 2015). Heat loss may also be compromised by a reduced physiological capacity to secrete sweat, common in older adults (Gagnon et al., 2016; Inoue et al., 1991) and individuals taking certain medications (e.g. anticholinergics) (Cheshire and Fealey, 2008), effectively reducing the range of conditions under which a fan is beneficial (Gagnon et al., 2016). However, any potential decrements in sweating can be compensated by externally applying water directly to the skin with a spray bottle (Morris et al., 2019a). Therefore, our aim was assess the potential utility of electric fan-use with light water-spraying as a stay-at-home cooling solution across the United States this summer, by comparing the biophysically modelled humidity-dependent temperature limits for this strategy to peak historical summer weather conditions.

2. Methods

Employing a standard conceptual human heat balance model, we assessed the difference between the increased convective heat transfer towards the body and increased evaporative heat loss potential away from the body, with and without an electric fan (Morris et al., 2019b). A detailed description of the model methodology, including partitional calorimetry equations used with reference to the supporting evidence base can be found in Appendix A. Assessments were performed at 25–50 °C with a relative humidity of 0–60%. These ranges were chosen to capture all peak combinations of temperature and humidity naturally occurring across all regions of the mainland United States. The air velocity of 4.5 m·s⁻¹ was equivalent to an 18″ diameter fan at maximum speed, at 1.0 m distance positioned at waist height. A metabolic rate of 65 W·m⁻², body surface area of 1.8 m², mean skin temperature of 35.5 °C, and the dry insulation and evaporative resistance of clothing for a summer ensemble were used (Morris et al., 2019b).

The model yielded threshold combinations of air temperature and relative humidity (RH) at which the increase in convective heat load with fan-use exceeded the increase in evaporative potential assuming the maximum sweat rate of an older adult (440 mL·h⁻¹) (Inoue et al., 1991) spraying an additional 115 mL (~0.5 cup) of water onto the skin every hour (Morris et al., 2019a). Based on our pilot laboratory work this is equivalent to an individual that is wearing shorts and a sleeveless shirt spraying their exposed limbs (in 8 sweeping sprays) every 5 min. These temperature/humidity thresholds were subsequently compared to the highest hourly ambient temperature and associated humidity from May-to-July recorded over the last 20 years (2000–2019, inclusive) for 105 separate metropolis areas (100 most populous metropolises + top metropolis in each conterminous state not represented) across the United States.

3. Results

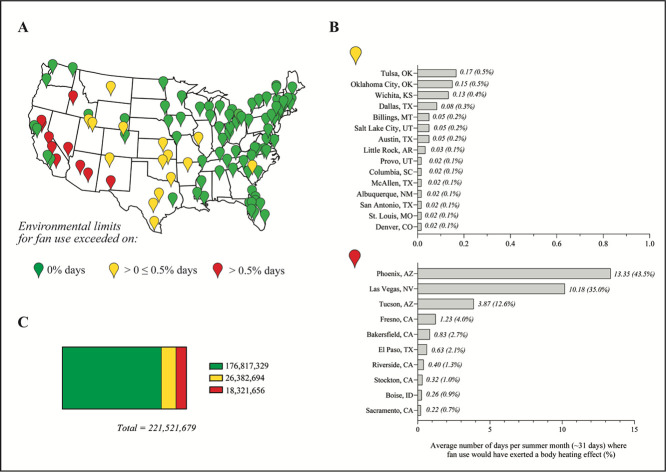
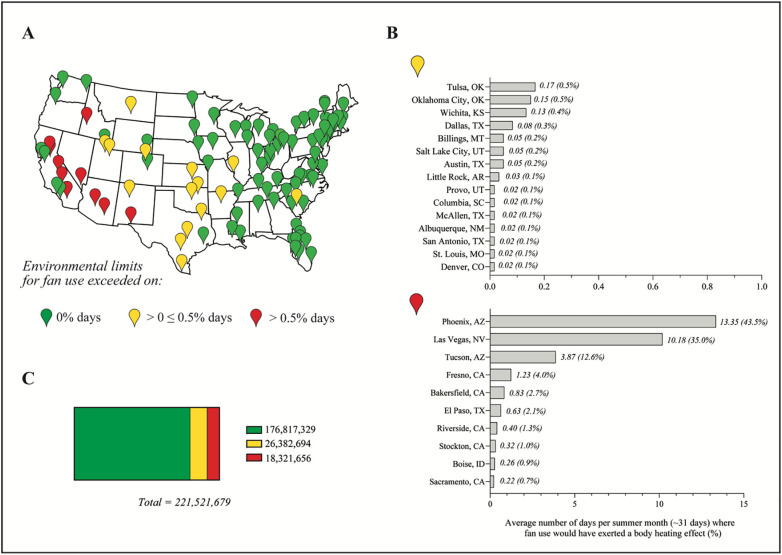
The modelled air temperature limit for fan-use was 37.2 °C at the lowest RH (0%), rising to 42.3 °C at 20%RH and then reducing to 39.9 °C at 50%RH (Fig. 1 ). Historically, fan-use would have been detrimental (i.e. exerted a heating effect) on 0% of summer days in 80 of 105 of the metropolises examined (home in 2018 to ~176 million individuals) (Fig. 2C). These metropolis areas are predominantly located in the Northeast, Southeast and Midwest regions of the United States, as well as the West Coast (Fig. 2A). According to our model, electric fan use would have been detrimental in a further 15 metropolises, mainly in the South (e.g. Austin, TX), on <0.5% of summer days; equivalent to 1–10 days in 20 years (Fig. 2B). In the remaining 10 metropolises, mostly in the hot-arid interior of the Southwest, fan use would have exerted a heating effect on up to 43.5% of summer days (Phoenix, AZ; Fig. 2B).

Fig. 1.

Biophysically modelled humidity-dependent threshold temperatures at which electric fan-use and modest skin-wetting becomes detrimental; above the line fans exert a heating effect, below the line fans exert a cooling effect. Individual data points represent the highest 1-h ambient temperature and associated relative humidity recorded between 2000 and 2019 (inclusive) for each of the 105 metropolises analyzed. Data points are colour-coded to identify percentage of summer days in last 20 years on which environmental limits were exceeded where green: 0%; yellow: >0% but ≤0.5%; red: >0.5%. (For interpretation of the references to colour in this figure legend, the reader is directed to the web version of this article.)

Fig. 2.

A) Map of the conterminous United States identifying the 105 metropolises examined, with markers colour-coded to identify percentage of summer days between 2000 and 2019 (inclusive) that exceeded the biophysically-modelled environmental limits for fan use coupled with modest skin wetting (green: 0%; yellow: >0%, but ≤0.5%; red: >0.5% days); B) average number of days per summer month that fan-use would have exerted a body heating effect for each individual metropolis that exceeded the environmental limit for fan use on >0%, but ≤0.5% (top); and on >0.5% (bottom) of summer days; C) total population examined across 105 metropolises, based on 2018 census estimates, split to identify number of inhabitants for which fan-use exceeded environmental limits on 0% (green); >0%, but ≤0.5% (yellow); >0.5% (red) summer days in the last 20 years. (For interpretation of the references to colour in this figure legend, the reader is directed to the web version of this article.)

4. Discussion

The present analysis indicates that electric fan-use with light water-spraying potentially offers a feasible stay-at-home cooling strategy during heat extremes for large parts of the US historically experiencing hot-humid summer conditions. In comparison to existing experimental data that demonstrates fan-use providing physiological cooling up to air temperatures of 42 °C/108 °F with ~50%RH (Ravanelli et al., 2015) our modelled thresholds appear conservative. The aforementioned study (Ravanelli et al., 2015) and others (Morris et al., 2019b) were undertaken using young, healthy participants, but it is known that other factors such as age alter the environmental limits for fan-use (Gagnon et al., 2016) likely due to age-related decrements in sweating (Inoue et al., 1991), that limit the potential increase in evaporative heat loss a fan can provide. To establish environmental limits more generalizable to the American public that can be easily adopted in at-home settings we chose to incorporate several conservative components in the current model. Examples include the assumption of a low maximal sweat rate (440 mL·h⁻¹), more representative of an older adult (Inoue et al., 1991) and considerably lower than sweat rates reported in previous experimental research examining fan effectiveness (i.e. average sweat rate in 47 °C/117 °F, 10%RH fan condition = 691 mL·h⁻¹ (Morris et al., 2019b)) and a low volume of water used for skin-wetting (115 mL⸱h⁻¹/0.5 cup⸱h⁻¹), relative to previously reported self-dousing values (i.e. =698 mL⸱h⁻¹ (Morris et al., 2019a)).

There are several important considerations when interpreting our model. Firstly, air temperatures used in the model were recorded from outdoor locations rather than from indoor locations, such as a home. Although, given the heterogeneity of building characteristics (i.e. thermal mass, ventilation rate, and insulation) known to influence the relationship between indoor and outdoor air temperatures (Nguyen and Dockery, 2016) we opted to use outdoor environmental conditions in the current model. Secondly, this cooling strategy is targeted as a stay-at-home cooling solution, rather than for use in public spaces. There is a lack of evidence suggesting fan-use may aid virus transmission, but given the suggested occurrences where air ventilation systems may have acted as a vector for virus transmission (Li et al., 2005; Yu et al., 2004) and our constantly developing knowledge of the nature of its spread (Van Doremalen et al., 2020; World Health Organization, 2020), it is possible that fan-use may accelerate the distribution of virus particles present in the home. There is indeed inherent transmission risk associated with co-habitation (Li et al., 2020; Wang et al., 2020). Importantly though, fan use during heat extremes in the home prevents people seeking cooling in public places among individuals whose virus status is less likely to be known than co-habitants, thus limiting personal risk of transmission and further spread in the community. Finally, our model identifies the point at which using a fan is better than not using a fan, and therefore does not quantify the amount of cooling, and whether it is sufficient to maintain body temperature within safe limits. Nevertheless, even with the conservative approach taken in developing the current model, for 200 million of the ~221.5 million residents (according to 2018 census estimates) in the 105 metropolis areas assessed, fan-use with light water-spraying would have been beneficial (i.e. exerted a cooling effect) relative to not using a fan on more than 199 of every 200 summer days in the past 20 years (Fig. 2C). It is therefore clear that public health officials should not advise people to turns fans off during heat waves as is current practice in a range of jurisdictions (New York State Department of Health, 2017; Department of Homeland Security, 2020).

While public health officials strive to protect all citizens during the current pandemic, parallel efforts are also required to proactively prepare for the likely overlap of COVID-19 with extreme heat. Heatwave preparation plans are increasingly centered on building community resilience and protecting the most vulnerable members of society (Manangan et al., 2020; Abbinett et al., n.d.; Fox et al., 2019). While this approach must continue, we require adaptive, yet evidence-based, efforts to protect against the ill-effects of extreme heat that align with current public health recommendations, such as physical distancing and stay-at-home orders, that are crucial to mitigating the spread of SARS-COV-2 this summer. Collectively, this analysis highlights how a stay-at-home fan-use with skin-wetting approach could better enable the simultaneous mitigation of heat stress and the spread of SARS-COV-2 across much of the United States. The widespread utility of this method also provides evidence for this alternative, low-cost, low-energy cooling strategy in a post-COVID climate. While, in hot-arid regions, environmental conditions have regularly exceeded the threshold for a heating effect with fan use, so alternative at-home cooling strategies, e.g. water-dousing without fans and/or cold-water foot immersion (Morris et al., 2019a), could be considered.

CRediT authorship contribution statement

Lily Hospers: Conceptualization, Data curation, Visualization, Writing - original draft, Writing - review & editing. James W. Smallcombe: Conceptualization, Data curation, Writing - original draft, Writing - review & editing. Nathan B. Morris: Methodology, Data curation. Anthony Capon: Supervision, Writing - review & editing. Ollie Jay: Conceptualization, Methodology, Supervision, Writing - review & editing.

Declaration of competing interest

This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.

Editor: SCOTT SHERIDAN

Appendix A

A.1. Methodological overview

The present model was created based around an elderly adult (+65 years), with a body mass of 70 kg, a height of 1.73 m, and a calculated body surface area (BSA) (DuBois, 1916) of 1.83 m², seated at rest, in light clothing, while wetting their skin either with or without the use of an electric fan in a variety of heatwave conditions. The model was created using standard partitional calorimetry equations (Cramer and Jay, 2019; Gagge et al., 1937) and has been updated from an earlier model (Jay et al., 2015) based upon the findings of several clinical laboratory experiments (Morris et al., 2019a; Morris et al., 2019b; Ravanelli et al., 2015; Gagnon et al., 2016; Gagnon et al., 2017). The partitional calorimetry method relies upon first principles thermodynamic heat transfer equations, which determine the body's net heat flow by comparing the total amount of heat produced within the body to the total amount of heat gained or lost to the environment, through all available avenues of heat transfer (i.e. conduction, convection, radiation and evaporation) (Kenny and Jay, 2013). Accordingly, fan use was determined to be detrimental when the net amount of heat lost to the environment was greater with the fan off compared to having the fan on. Below are the detailed equations and assumptions used to produce the model.

A.2. Partitional calorimetry equations – determining the required amount of evaporation

The primary argument informing this model is that, once ambient air temperature exceeds skin temperature, fan use will increase heat gain from the environment through dry heat transfer via convection (i.e. like a convection oven), necessitating a greater required amount of evaporation to maintain heat balance. However, fan use will simultaneously increase the maximal amount of heat that can be lost to the environment through evaporation, as well as improve sweating efficiency (Kenny and Jay, 2013). Accordingly, to determine whether fan use is overall beneficial or detrimental during a heatwave, the amount of total heat gain and loss from fan use needs to be assessed. This was done using the conceptual heat balance equation (Gagge et al., 1937):

$$S=M-W-\left(C+R\right)-\left(C_{\mathit{res}}+E_{\mathit{res}}\right)-E\left(\text{in}\mathrm{W}·{\mathrm{m}}^{-2}\right)$$ (1)

where S is heat storage, M is metabolic heat production, W is external work, C is convection, R is radiation, C_res and E_res are convection and evaporation (respectively) by respiration, and E is evaporation.

As evaporation is the primary method by which humans lose heat during moderate and more severe heat stress conditions (Kenny and Jay, 2013), and that this is the primary heat loss avenue controlled by the autonomic nervous system (Ravanelli et al., 2020), this equation was subsequently reorganized to determine the required amount of evaporation (E_req) to maintain heat balance (i.e. establish a steady-state core temperature):

$$E_{\mathit{req}}=M-W-\left(C+R\right)-\left(C_{\mathit{res}}+E_{\mathit{res}}\right)\left(\text{in}\mathrm{W}·{\mathrm{m}}^{-2}\right)$$ (2)

Here, when all other variables are held constant (as they would be at rest), an increase in dry heat transfer (primarily via convection) would necessitate an increase in E_req. Within the present model (seated rest) W can be eliminated as no external work is performed. For M, we assumed a resting metabolic rate of 65 W·m⁻², which is equivalent to a person standing (Parsons, 2003). A typical value for M when seated could be as low as 58 W·m⁻², however, the highest potential value was selected to represent the worst-case scenario in terms of metabolic heat that must be dissipated to maintain a stable body temperature (Parsons, 2003). In order to account for heat loss due to respiration, the following equation was used (Handbook, 1993):

$$C_{\mathit{res}}+E_{\mathit{res}}=\left[0.0014M\left(34-t_a\right)+0.0173M\left(5.87-P_a\right)\right]\left(\text{in}\mathrm{W}·{\mathrm{m}}^{-2}\right)$$ (3)

where P_a is the partial pressure of water vapor of ambient air in kP_a and t_a is ambient air temperature in °C. Next, dry heat transfer (the combined effect of convection and radiation) was accounted for (Gagge and Gonzalez, 1996):

$$C+R=\frac{\left(t_{\mathit{sk}}-t_o\right)}{\left(R_{cl}+\frac{1}{f_{cl}h}\right)}\left(\text{in}\mathrm{W}·{\mathrm{m}}^{-2}\right)$$ (4)

where t_sk is mean skin temperature in °C (assumed to be 35.5 °C based on the literature (Drinkwater et al., 1982; Zahorska-Markiewicz, 1982)); t_o is operative temperature in °C, which in this case was equal to ambient air temperature; R_cl is dry heat transfer resistance of clothing in m²·K·W⁻¹; f_cl is the unitless clothing area factor (see Eq. (5)) and h is the sum of the convective heat transfer coefficient (h_c; see Eq. (6)) and the radiative heat transfer coefficient (h_r; see Eq. (7)). For the “fan on” condition, a dry heat transfer resistance of clothing (R_cl) value of 0.0497 m²·K·W⁻¹ (front, facing fan; 50% of BSA) and 0.0844 m²·K·W⁻¹ (rear; 50% of BSA), equivalent to a typical summer ensemble of underwear, a light cotton shirt (with sleeves rolled up to the elbow) and light cotton shorts, and included the insulative effect of air layers and alterations in insulation due to different levels of air flow, was employed (ISO I, 2007). For the “fan off” condition, an R_cl value of 0.1291 m²·K·W⁻¹ was used across the whole body (ISO I, 2007). Subsequently, f_cl can be determined (McCullough et al., 1985) using the following equation:

$$f_{\mathit{cl}}=1.0+\frac{0.31R_{\mathit{cl}}}{0.155}\left(\mathrm{no}\text{units}\right)$$ (5)

Further, h_c can be determined by the equation (Mitchell, 1974):

$$h_c=8.3v^{0.6}\left(\text{in}\mathrm{W}·{\mathrm{m}}^{-2}·{\mathrm{K}}^{-1}\right)$$ (6)

where v is air velocity in m·s⁻¹. For the “fan on” condition, v was estimated by employing a free space air velocity of 4.5 m·s⁻¹, which was determined using a hot-wire anemometer (VelociCalc 9535, TSI Inc., Shoreview MN, USA) during pilot testing of an 18″ diameter standard electrical floor fan (High velocity orbital air circulator, Whirlpool, Benton Harbor, MI, USA) at waist height set at maximum speed and at a distance of 1.0 m. The air flow profile around the body was then determined using a cylindrical model proposed by Kerslake (1972), and mean h_c values were separately determined for the front (16.28 W·m⁻²·K⁻¹; 50% of BSA) and back (8.04 W·m⁻²·K⁻¹; 50% of BSA) halves of the body. For the “no fan” condition, an air velocity of 0.2 m·s⁻¹ was employed across the front and back of the body (h_c = 3.16 W·m⁻²·K⁻¹), which accounted for any effects of natural convection. Additionally, h_r was determined (Parsons, 2003; De Dear et al., 1997) as:

$$h_r=4\mathit{\epsilon \sigma }\frac{A_r}{\mathit{BSA}}{\left[273.2+\frac{\left(t_{\mathit{sk}}+t_r\right)}{2}\right]}^3\left(\text{in}\mathrm{W}·{\mathrm{m}}^{-2}·{\mathrm{K}}^{-1}\right)$$ (7)

where ε is the area weighted emissivity of the clothing body surface (assumed to be 1.0); σ is the Stefan-Boltzmann constant, 5.67·10⁻⁸ W·m⁻²·K⁻⁴; A_r/BSA is the effective radiative area of the body (assumed to be 0.70 for seated individuals (Fanger, 1967)); t_r is mean radiant temperature in °C, which was assumed to be equal to ambient air temperature, since indoor environments are assumed to be uniform spaces with no sources of direct radiation (Parsons, 2003).

A.3. Addition of skin wetting component

In addition to standard partitional calorimetric terms outlined above, an additional term was added to characterize exogenous skin wetting (E_xsw):

$$E_{\mathit{req}}=M-W-\left(C+R\right)-\left(C_{\mathit{res}}+E_{\mathit{res}}\right)-E_{\mathit{xsw}}\left(\text{in}\mathrm{W}·{\mathrm{m}}^{-2}\right)$$ (8)

This term was added as previous research has demonstrated that skin wetting is beneficial for reducing thermal and cardiovascular strain, as well as dehydration, regardless of the environmental conditions (Morris et al., 2019a), and should therefore be considered as the baseline cooling intervention, regardless of fan use. E_xsw was determined by multiplying the amount of water spread over the skin by the latent heat of evaporation of water (2426 J·g⁻¹) (Wenger, 1972) and then corrected for the evaporative efficiency and divided by BSA. The amount of water used to wet the skin was 116 mL (i.e. approximately half a cup of water) every hour, based upon preliminary data from two of our clinically registered trials on cooling interventions in the elderly (ACTRN12619000938101 and ACTRN12618001913268). For similar reasons, the evaporative efficiency was assumed to be 0.70 for the “fan on” condition and 0.50 for the “fan off condition”.

A.4. Partitional calorimetry equations – determining the maximum amount of evaporation

As discussed above, fan use not only increases convective heat gain but also increases the maximum amount of evaporation (E_max) possible in a given environment. Using the following equation, E_max was calculated (Handbook, 1993):

$$E_{\max }=\frac{\omega \left(P_{\mathit{sk},s}-P_a\right)}{\left[R_{e,\mathit{cl}}+\frac{1}{f_{\mathit{cl}}{h}_e}\right]}\left(\text{in}\mathrm{W}·{\mathrm{m}}^{-2}\right)$$ (9)

where ω is skin wettedness (i.e. proportion (0 through to 1) of BSA covered with sweat (Gagge, 1937); P_a the water vapor pressure in the ambient air in kPa; P_sk,s is the partial water vapor pressure at the skin in kPa (equal to saturated water vapor pressure at skin temperature (35.5 °C), i.e. 5.78 kPa); R_e,cl is the evaporative resistance of clothing in m²·kPa⁻¹·W⁻¹; f_cl is clothing area factor (see Eq. (2)); h_e is the evaporative heat transfer coefficient (in W·m⁻²·kPa⁻¹) calculated using the Lewis Relation (Gagge and Gonzalez, 1996):

$$h_e=16.5h_c\left(\text{in}\mathrm{W}·{\mathrm{m}}^{-2}·{\mathrm{kPa}}^{-1}\right)$$ (10)

Critical values for skin wettedness (ω) were adjusted for fan use and age. Based on the data of McConnell et al. (1924), a critical ω value of 0.65 was employed for the physiological compensation of all endogenous heat and any exogenous heat in the “fan on” condition in the young adult predictions. This value was reduced to 0.50 for elderly adult predictions to account for the age-related decrements in sweat output of ~25% observed in hot/dry environments (Anderson and Kenney, 1987) due to a decreased peripheral sensitivity of the sweating mechanism (Dufour and Candas, 2007).

For the “fan off” condition, the critical ω values used for the physiological compensation of endogenous and exogenous heat were 0.85 for young adult predictions (Candas et al., 1979); this was reduced to 0.65 for the elderly adult predictions. Using the equation reported by Berglund and Gonzalez (1977), the critical ω value at which an elevated cardiovascular strain (i.e. heart rate) would occur in both young and old adults was estimated to be 0.35 in the “fan on” condition. A value of 0.50 was employed for the “fan off” condition. For the “fan on” condition, an evaporative resistance of clothing (R_e,cl) value of 0.0112 m²·kPa⁻¹·W⁻¹ (front, facing fan; 50% of BSA) and 0.0161 m²·kPa⁻¹·W⁻¹ (rear; 50% of BSA) were employed. Similarly to R_cl, this value was determined using ISO 9920 (2007) and was equivalent to a typical summer ensemble, inclusive of air layers. For the “fan off” condition, an R_e,cl value of 0.0237 m²·kPa⁻¹·W⁻¹ was used for the whole body.

In addition to E_max, which is determined by the physical properties (i.e. temperature, water vapor content and air speed) of the skin and the surrounding the environment as well as alterations in attainable skin wettedness, the actual attainable E_max will be dictated by the maximum amount of sweat which can be produced. For the purpose of our model this was assumed to be 440 mL·h⁻¹ based upon the literature (Inoue et al., 1991), and subsequently, a maximum evaporative heat loss from sweating (SW_max) was determined (ISO, 2004):

$${\mathit{SW}}_{\max }=\frac{\left[\frac{\mathit{SR}\times {\mathit{SW}}_{\mathit{latent}}}{3600}\right]{\mathit{SW}}_{\mathit{eff}}}{\mathit{BSA}}\left(\text{in}\mathrm{W}·{\mathrm{m}}^{-2}\right)$$ (11)

where SR is the sweat rate (in our model assumed to be 440 mL·h⁻¹), SW_latent is the latent heat of the vaporization of sweat (2426 J·g⁻¹) (Wenger, 1972), 3600 is the factor needed to convert mL·h⁻¹ to g·s⁻¹ and SW_eff is the sweating efficiency, i.e. the proportion of sweat produced that is evaporated from the skin surface (thereby contributing to evaporative heat loss) as opposed to sweat that drips off the body and does not contribute to heat loss. Sweating efficiency is calculated by (ISO, 2004):

$${\mathit{SW}}_{\mathit{eff}}=1-\frac{{{\omega }_{\mathit{req}}}^2}{2}\left(\mathrm{no}\text{units}\right)$$ (12)

where ω_req is the skin wettedness required for heat balance determined by (Gagge, 1937):

$${\omega }_{\mathit{req}}=\frac{E_{\mathit{req}}}{E_{\max }}\left(\mathrm{no}\text{units}\right)$$ (13)

A.5. Weather data analysis

Finally, to determine whether (in conjunction with exogenous skin wetting) an electric fan should be used in given environmental conditions, a final equation was generated:

$$S=\left(E_{\mathit{req}-\mathit{off}}-E_{\mathit{req}-\mathit{on}}\right)-\left(E_{maxl-\mathit{off}}-E_{maxl-\mathit{on}}\right)\left(\text{in}\mathrm{W}·{\mathrm{m}}^{-2}\right)$$ (14)

where E_{req – off} and E_{req – on} are the required amount of evaporation with a fan off or on, respectively, and E_{maxl – off} and E_{maxl – on} was the lower value of the calculated E_max and SW_max terms with fan off or on, respectively. This equation was subsequently entered into an environmental conditions matrix that ranged from 30 °C to 50 °C in 2 °C increments and from 5% to 100% relative humidity in 10% increments (with the exception of 5% to 10% relative humidity). The resultant values of this equation were heat storage values, with negative heat storage values denoting heat loss and positive values denoting heat gain. From these values, the exact temperature at which fan use became detrimental could be determined.

These values were subsequently analyzed with a 4th order polynomial using GraphPad Prism (version 8.0, GraphPad Software, LaJolla, CA). The resultant equation for determining the upper temperature limit for fan use at a given relative humidity value was as follows:

$$\mathit{Upper}{t}_a=37.34+\left(0.4924\mathit{RH}\right)+\left(-0.01522{\mathit{RH}}^2\right)+\left(1.552\times {10}^{-4}{\mathit{RH}}^4\right)+\left(-5.413\times {10}^{-7}{\mathit{RH}}^4\right)\left(\text{in}°\mathrm{C}\right)$$ (15)

where upper t_a is the temperature above which fan use becomes detrimental and RH is the relative humidity. The resultant R squared of this model was 0.9940. The model was further verified by calculating an additional 20 points using Eq. (14) and plotting them against the model. None of the upper limit temperature data points generated by the 4th order polynomial differed from the partitional calorimetry derived values by more than 0.2 °C.

A.6. Weather data

To perform the weather data analysis, hourly weather data for the 100 most populous metropolitan areas in the contiguous United States, plus the top metropolis in each contiguous state, not represented in top 100, was purchased from CustomWeather (CustomWeather, Inc., 271 Miller Avenue Mill Valley, CA, USA 94941). The weather data spanned from January 1st, 2000 to December 31st, 2019. In order to ensure only the hottest weather was included in the analysis, only weather from daylight hours during the months of June, July and August were analyzed. From this data, the following metrics were ascertained: the peak temperature and corresponding relative humidity, the number of days where recorded temperatures exceed the calculated upper temperature limit at which point fan use is no longer beneficial and the total number of days included in the analysis (typically 1839 days, but this differed slightly due to missing data from select weather stations). These data are displayed in supplementary table A1 as well as within the manuscript Fig. 1.

Table A1.

Weather analysis by city using summer (June–August) weather data (CustomWeather, Inc., 271 Miller Avenue Mill Valley, CA, USA 94941) from 2000 to 2019.

Metropolitan statistical area	Peak temperature (ºC)	Peak relative humidity (%)	Total days fans detrimental	Total days in analysis	Average detrimental days per summer	Detrimental days (%)
Phoenix, AZ	48.3	6	801	1839	40.1	43.5
Las Vegas, NV	47.0	2	611	1747	30.6	35.0
Tucson, AZ	46.1	7	232	1839	11.6	12.6
Fresno, CA	44.4	19	74	1839	3.7	4.0
Bakersfield, CA	44.0	16	50	1839	2.5	2.7
El Paso, TX	43.0	10	38	1839	1.9	2.1
Riverside, CA	45.0	13	24	1839	1.2	1.3
Stockton, CA	46.0	16	19	1838	1.0	1.0
Boise City, ID	43.0	9	16	1839	0.8	0.9
Sacramento, CA	43.0	17	13	1839	0.7	0.7
Tulsa, OK	44.4	19	10	1839	0.5	0.5
Oklahoma City, OK	43.9	14	9	1839	0.5	0.5
Wichita, KS	43.3	19	8	1839	0.4	0.4
Dallas, TX	42.8	22	5	1839	0.3	0.3
Austin, TX	43.3	15	3	1839	0.2	0.2
Salt Lake City, UT	41.1	11	3	1839	0.2	0.2
Billings, MT	41.1	12	3	1839	0.2	0.2
Little Rock, AR	45.0	19	2	1839	0.1	0.1
Denver, CO	39.4	9	1	1839	0.1	0.1
St. Louis, MO	42.2	13	1	1839	0.1	0.1
San Antonio, TX	42.8	16	1	1839	0.1	0.1
Albuquerque, NM	40.0	5	1	1839	0.1	0.1
McAllen, TX	43.9	19	1	1839	0.1	0.1
Columbia, OH	42.2	17	1	1839	0.1	0.1
Provo, UT	41.0	9	1	1839	0.1	0.1
New York, NY	39.4	31	0	1812	0.0	0.0
Los Angeles, CA	34.0	26	0	1839	0.0	0.0
Chicago, IL	39.4	31	0	1793	0.0	0.0
Houston, TX	42.2	20	0	1747	0.0	0.0
Washington, DC	40.6	35	0	1839	0.0	0.0
Miami, FL	36.7	38	0	1839	0.0	0.0
Philadelphia, PA	39.0	24	0	1839	0.0	0.0
Atlanta, GA	40.6	25	0	1839	0.0	0.0
Boston, MA	38.9	30	0	1839	0.0	0.0
San Francisco, CA	39.4	19	0	1747	0.0	0.0
Detroit, MI	38.3	32	0	1839	0.0	0.0
Seattle, WA	39.4	20	0	1840	0.0	0.0
Minneapolis, MN	38.9	32	0	1839	0.0	0.0
San Diego, CA	36.0	39	0	1839	0.0	0.0
Tampa, FL	36.0	47	0	1839	0.0	0.0
Baltimore, MD	41.0	20	0	1839	0.0	0.0
Orlando, FL	37.2	39	0	1839	0.0	0.0
Charlotte, NC	39.4	27	0	1839	0.0	0.0
Portland, OR	41.0	20	0	1748	0.0	0.0
Pittsburgh, PA	36.1	43	0	1839	0.0	0.0
Cincinnati, OH	39.4	31	0	1839	0.0	0.0
Kansas City, MO	41.7	26	0	1839	0.0	0.0
Columbus, SC	37.2	38	0	1839	0.0	0.0
Cleveland, OH	36.7	35	0	1835	0.0	0.0
Indianapolis, IN	40.6	25	0	1839	0.0	0.0
San Jose, CA	41.0	23	0	1839	0.0	0.0
Nashville, TN	41.7	17	0	1839	0.0	0.0
Virginia Beach, VA	38.3	44	0	1836	0.0	0.0
Providence, RI	38.3	33	0	1839	0.0	0.0
Milwaukee, WI	38.3	29	0	1839	0.0	0.0
Jacksonville, FL	38.3	42	0	1839	0.0	0.0
Raleigh, NC	40.6	30	0	1839	0.0	0.0
Memphis, TN	41.1	25	0	1839	0.0	0.0
Richmond, VA	41.0	23	0	1839	0.0	0.0
Louisville, KY	40.0	22	0	1839	0.0	0.0
New Orleans, LA	38.0	37	0	1839	0.0	0.0
Hartford, CT	39.0	29	0	1839	0.0	0.0
Birmingham, AL	41.0	17	0	1839	0.0	0.0
Buffalo, NY	35.0	37	0	1839	0.0	0.0
Rochester, NY	36.1	46	0	1839	0.0	0.0
Grand Rapids, MI	40.0	30	0	1839	0.0	0.0
Worcester, MA	39.4	17	0	1826	0.0	0.0
Bridgeport, CT	38.3	38	0	1839	0.0	0.0
Omaha, NE	40.6	25	0	1839	0.0	0.0
Greenville, SC	40.6	30	0	1836	0.0	0.0
Knoxville, TN	40.6	22	0	1839	0.0	0.0
Albany, NY	37.2	41	0	1839	0.0	0.0
New Haven, CT	38.0	37	0	1838	0.0	0.0
Oxnard, CA	30.0	45	0	1839	0.0	0.0
Allentown, PA	39.4	36	0	1838	0.0	0.0
Baton Rouge, LA	39.4	30	0	1747	0.0	0.0
North Port, FL	37.2	42	0	1839	0.0	0.0
Dayton, OH	38.9	30	0	1839	0.0	0.0
Charleston, SC	38.3	33	0	1839	0.0	0.0
Greensboro, NC	38.3	33	0	1839	0.0	0.0
Cape Coral, FL	37.0	37	0	1839	0.0	0.0
Colorado Springs, CO	37.2	18	0	1839	0.0	0.0
Lakeland, FL	39.0	33	0	1839	0.0	0.0
Akron, OH	37.8	37	0	1839	0.0	0.0
Poughkeepsie, NY	39.0	29	0	1837	0.0	0.0
Ogden, UT	39.0	14	0	1834	0.0	0.0
Winston, NC	38.9	30	0	1838	0.0	0.0
Madison, WI	39.4	30	0	1839	0.0	0.0
Deltona, FL	36.7	34	0	1839	0.0	0.0
Des Moines, IA	41.1	26	0	1839	0.0	0.0
Syracuse, NY	38.0	27	0	1839	0.0	0.0
Springfield, MA	38.3	26	0	1838	0.0	0.0
Augusta, GA	42.0	25	0	1839	0.0	0.0
Toledo, OH	38.9	32	0	1839	0.0	0.0
Palm Bay, FL	37.0	47	0	1839	0.0	0.0
Jackson, MS	41.1	25	0	1839	0.0	0.0
Durham, NC	40.6	30	0	1839	0.0	0.0
Harrisburg, PA	38.9	40	0	1839	0.0	0.0
Spokane, WA	40.6	13	0	1839	0.0	0.0
Chattanooga, TN	41.1	21	0	1839	0.0	0.0
Portland, ME	37.8	30	0	1839	0.0	0.0
Fargo, ND	39.0	33	0	1839	0.0	0.0
Sioux Falls, SD	39.4	26	0	1839	0.0	0.0
Burlington, VT	36.7	32	0	1839	0.0	0.0
Cheyenne, WY	36.7	13	0	1839	0.0	0.0