Optimal strategies for vaccination and social distancing in a game-theoretic epidemiologic model

Highlights

• •We propose a game-theoretic model for infectious disease transmission.
• •Vaccination and social distancing are considered as control strategies.
• •We identify individual optimal strategies by considering group behavior.
• •We determine the threshold costs at which either vaccination or social distancing is preferred.

Abstract

For various infectious diseases, vaccination has become a major intervention strategy. However, the importance of social distancing has recently been highlighted during the ongoing COVID-19 pandemic. In the absence of vaccination, or when vaccine efficacy is poor, social distancing may help to curb the spread of new virus strains. However, both vaccination and social distancing are associated with various costs. It is critical to consider these costs in addition to the benefits of these strategies when determining the optimal rates of application of control strategies. We developed a game-theoretic epidemiological model that considers vaccination and social distancing under the assumption that individuals pursue the maximization of payoffs. By using this model, we identified the individually optimal strategy based on the Nash strategy when both strategies are available and when only one strategy is available. Furthermore, we determined the relative costs of control strategies at which individuals preferentially adopt vaccination over social distancing (or vice versa).

1. Introduction

Infectious diseases represent an ongoing threat to global health, and their prevention can significantly reduce economic and epidemiological burdens. Worldwide, an estimated 14.7 million individuals are killed by infectious diseases each year, with the vast majority of death occurring in developing regions (14.2 million out of 14.7 million) (Michaud, 2009). Specifically, the mortality from infectious diseases is the highest in sub-Saharan Africa with 6.8 million annual deaths and South Asia with 4.4 million annual deaths (Michaud, 2009). It is estimated that over 400 million disability-adjusted life years (DALYs) are lost each year as a result of infectious diseases, representing 26.9% of total DALYs (Michaud, 2009). Additionally, the disease burden of infections largely rests on populations in low- and middle-income countries, which account for 98.6% of the total burden of infections (Michaud, 2009). Specifically, lower respiratory infections (3.4 million deaths), HIV/AIDS (2.6 million deaths), diarrheal diseases (1.8 million deaths), tuberculosis (1.6 million deaths), and malaria (1.1 million deaths) are the top five infections that are responsible for the greatest numbers of deaths in low- and middle-income countries (Michaud, 2009). Emerging global challenges related to infectious diseases and the associated social and economic risks have been highlighted by the ongoing pandemic of coronavirus disease-19 (COVID-19). Since the first reports from Wuhan, China in December of 2019, more than 85,600 COVID-19 cases have been reported in China. Outside China, ongoing local transmission and more than 12.9 million cases have been reported in numerous countries, including the US, Brazil, India, Russia, and Peru (WHO, 2020). In addition to newly emerging infectious diseases, seasonal diseases such as influenza jeopardize not only human health, but also various levels of social and economic wellbeing. Annual epidemics of influenza result in 3–5 million cases of severe illness and 290,000–650,000 deaths worldwide (WHO).

Prevention and control can minimize the negative impact of infectious diseases on society, meaning that such measures are important for public health and welfare. Specifically, it is noteworthy that behavioral changes during disease outbreaks reflect individual choices regarding preventive measures for effectively reducing the chance of contracting diseases. For example, during the severe acute respiratory syndrome outbreak in 2003, precautionary actions, such as wearing face masks, hand washing, and avoiding public transportation and crowded areas, contributed to reducing transmission in Hong Kong and Beijing (Beutels et al., 2009, Lau et al., 2004). Additionally, it was noted that a significant proportion of the population adapted their behavior and took preventive measures, such as social distancing, during the 2009 A/H1N1 influenza pandemic (Jones and Salathe, 2009, Rubin et al., 2009). Similarly, during the ongoing COVID-19 pandemic, extensive social distancing policies, wearing facial masks, and delaying the opening of schools have effectively reduced the transmission of the disease in South Korea (Shim et al., 2020).

Overall, human behavior plays an important role in the spread of infectious diseases. Therefore, understanding the influence of behavior on the spread of diseases could be a key aspect of improving control efforts (Funk et al., 2010a). In recent years, the behavioral epidemiology of infectious diseases has emerged as a new subfield of epidemiology (d’Onofrio and Manfredi, 2020, d’Onofrio et al., 2016, Funk et al., 2010a, Manfredi and D'Onofrio, 2013, Manfredi et al., 2009, Wang et al., 2016). Behavioral epidemiology is an inherently multidisciplinary field combining classical epidemiological modeling with behavioral sciences, such as sociology, psychology, economics, and anthropology, to understand the connection between human mechanics and infection mechanics (d’Onofrio and Manfredi, 2020). Frameworks for the computational modeling of behavioral epidemiology range from classical models assuming homogeneously mixing (mean-field) populations to complex models that account for behavioral feedback and population spatial/social structures. Many of these methods originated from statistical physics models, such as lattice and network models (Wang et al., 2016).

The key issue in behavioral epidemiology is to understand the relationships between behavioral changes and the dynamics of infectious diseases. For example, a past study quantified how increases in population awareness can reduce disease transmission in well-mixed populations (Funk et al., 2010b). In another study on behavior epidemiology, a behavior-implicit susceptible-infectious-recovered (SIR) model with prevalence-dependent vaccination and prevalence-dependent contact rates was developed (d’Onofrio and Manfredi, 2020). This study presented the baseline perceived risk conditions under minimal infection circulation at which the elimination of a disease can be achieved.

Among the behavioral changes that can be used as strategies to limit the spread of infectious diseases, we consider vaccination and social distancing, and incorporate these strategies into a mathematical model of disease transmission. Specifically, a game-theoretic model was developed to consider both the costs and benefits associated with disease intervention strategies to identify the individually optimal strategy. By using game-theoretic models, one can not only examine the transmission dynamics of infectious diseases, but also determine how individual decision-making is affected by the perceived costs of actions and the resulting benefits.

Game theory is an established approach for modeling biological phenomena (Broom and Rychtar, 2013, Hofbauer and Sigmund, 1998, Maynard-Smith, 1982, Mesterton-Gibbons, 2000). Recently, game theory has emerged as a leading methodology for quantitatively describing the decision making of individuals presented with various intervention options. Specifically, there have been numerous studies on game-theoretic models focused on preventative measures, particularly vaccination and behavioral changes (Bauch and Earn, 2004, Bauch et al., 2003, Cornforth et al., 2011, Reluga, 2010, Reluga, 2013, Reluga and Li, 2013, Shim et al., 2011, Shim et al., 2012a, Shim et al., 2012b, Verelst et al., 2016). Regardless, the majority of these game-theoretic studies on disease modeling have considered a single strategy and have not facilitated multiple intervention options. One notable exception is the study by Kobe et al., where two options for protection strategies for cholera, namely vaccination and the use of clean water, were considered (Kobe et al., 2018). In our study, we aimed to derive individually optimal protection strategies in the event of a disease outbreak under the assumption that individuals have the options of being vaccinated or practicing social distancing. We formulated a game model for an endemic infection to account for both the individual and community costs of intervention and infection. Numerical methods were used to investigate the ranges of costs associated with these options. The resulting cost measures were used to determine which strategy is preferable from an individual perspective.

2. Methods

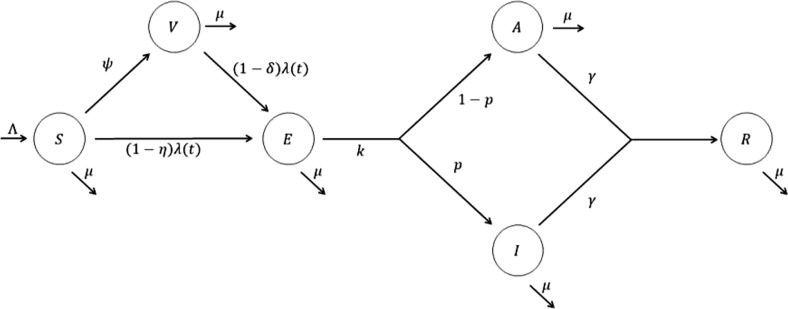
We developed a mathematical model of disease transmission considering vaccination and social distancing as personal protection strategies (Fig. 1 ). We extended a SIR-type model, and our model classifies individuals based on several epidemiological statuses, namely susceptible $(S)$, vaccinated $(V)$, exposed $(E)$, symptomatic $(I)$, asymptomatic $(A)$, and recovered $(R)$. Disease-free individuals enter the susceptible class through birth or immigration at a constant rate $\Lambda$ and their natural death rate is denoted by $\mu$. It is assumed that susceptible individuals become infected at a rate of $\lambda (t)$, where the force of infection is calculated as $\lambda \left(t\right)=\frac{{\beta }_0\left(I\left(t\right)+bA(t)\right)}{N\left(t\right)}$. Here, ${\beta }_0$ is the transmission rate, $b$ is the rate of relative infectiousness of asymptomatic cases compared to symptomatic cases, and $N\left(t\right)$ is the total population size ($N\left(t\right)=S\left(t\right)+V\left(t\right)+E\left(t\right)+I\left(t\right)+A\left(t\right)+R(t)).$ We define $1/k$ as the duration of the latent period, and assume that a proportion $p$ of infected individuals will become symptomatic. Both symptomatic and asymptomatic individuals are assumed to recover at a rate of $\gamma$.

Fig. 1.

Flow chart of the model of disease transmission with vaccination and social distancing as personal protection strategies.

To describe social distancing in the proposed model, we assume that susceptible individuals reduce the contact rate by a fraction $\eta$ ($0\le \eta \le 1$). As another prevention strategy, we incorporate vaccination into our model using a vaccination rate $\psi$. We assume that the infection rate among vaccinated individuals is reduced by the vaccine efficacy $\delta$ compared to unvaccinated individuals (Table 1 ).

Table 1.

Summary of model parameters and baseline values used in numerical simulations.

Parameter	Description	Value	References
$\mu$	Natural death rate (${\mathrm{d}}^{-1}$)	1/(75*365)	(Longini et al., 2004)
${\beta }_0$	Infection transmission rate (${\mathrm{d}}^{-1}$)	Varies	NA
$\psi$	Vaccination rate (${\mathrm{d}}^{-1}$)	Varies	NA
$\delta$	Vaccine efficacy	0.45	(Dawood, 2020)
$1/\gamma$	Infectious period (d)	4.5	(Galvani et al., 2007)
$b$	Relative infectiousness of asymptomatic cases compared to symptomatic cases	0.5	(Longini et al., 2004)
$\eta$	Fraction by which susceptible individuals reduce their contact rate	Varies	NA
$1/k$	Duration of latent period (d)	1.2	(Galvani et al., 2007)
$p$	Probability that exposed individuals progress to the symptomatic infectious compartment	0.67	(Longini et al., 2004)

Given the definitions and assumptions presented above, the transmission dynamic model is described by the following differential equations:

$$\begin{array}{c}{S}^{\prime }\left(t\right)=\mathrm{\Lambda }-\left(1-\eta \right)\lambda \left(t\right)S\left(t\right)-\left(\psi +\mu \right)S\left(t\right),\hfill \\ V^{\prime }\left(t\right)=\psi S\left(t\right)-\left(1-\delta \right)\lambda \left(t\right)V\left(t\right)-\mu V\left(t\right),\hfill \\ E^{\prime }\left(t\right)=\lambda \left(t\right)\left(\left(1-\eta \right)S\left(t\right)+\left(1-\delta \right)V\left(t\right)\right)-\left(k+\mu \right)E\left(t\right),\hfill \\ I^{\prime }\left(t\right)=kpE\left(t\right)-\left(\gamma +\mu \right)I\left(t\right),\hfill \\ A^{\prime }\left(t\right)=k\left(1-p\right)E\left(t\right)-\left(\gamma +\mu \right)A\left(t\right),\hfill \\ R^{\prime }\left(t\right)=\gamma A\left(t\right)+\gamma I\left(t\right)-\mu R\left(t\right).\hfill \end{array}$$ (1)

We assume that the total population is asymptotically constant, meaning $N\left(t\right)=K=\frac{\mathrm{\Lambda }}{\mu }$. Therefore, the model in (1) can be reduced to a lower-dimensional system by replacing $S$ with $K-V-E-I-A-R$.

The use of dimensionless variables $\left(v=\frac{V}{K},e=\frac{E}{K},i=\frac{I}{K},a=\frac{A}{K},r=\frac{R}{K}\right)$ leads to further simplifications and the model in (1) can be replaced with

$$\begin{array}{c}{v}^{\prime }\left(t\right)=\psi \left\{1-e\left(t\right)-i\left(t\right)-a\left(t\right)-r\left(t\right)\right\}-\left(1-\delta \right){\beta }_0\left\{i\left(t\right)+ba\left(t\right)\right\}v\left(t\right)-\left(\psi +\mu \right)v\left(t\right),\hfill \\ e^{\prime }\left(t\right)={\beta }_0\left\{i\left(t\right)+ba\left(t\right)\right\}\left\{\left(1-\eta \right)\left(1-e\left(t\right)-i\left(t\right)-a\left(t\right)-r\left(t\right)\right)+\left(\eta -\delta \right)v\left(t\right)\right\}-\left(k+\mu \right)e\left(t\right),\hfill \\ i^{\prime }\left(t\right)=kpe\left(t\right)-\left(\gamma +\mu \right)i\left(t\right),\hfill \\ a^{\prime }\left(t\right)=k\left(1-p\right)e\left(t\right)-\left(\gamma +\mu \right)a\left(t\right),\hfill \\ r^{\prime }\left(t\right)=\gamma a\left(t\right)+\gamma i\left(t\right)-\mu r\left(t\right).\hfill \end{array}$$ (2)

The model in (2) permits the following disease-free equilibrium (DFE):

$$E_0=\left(v_0,e_0,i_0,a_0,r_0\right)=\left(\frac{\psi }{\psi +\mu },0,0,0,0\right).$$

By using this DFE, we can obtain the control reproduction number ${\mathcal{R}}_c(\psi ,\eta )$ of the model by using the next-generation method (van den Driessche and Watmough, 2002). Here, the control reproduction number is defined as the number of secondary infections caused by a single infective individual in a population with control measures in place. We computed the control reproduction number under the assumption that the control parameters ($\psi ,\eta$) are fixed at constant values. To obtain ${\mathcal{R}}_c(\psi ,\eta )$, we introduce matrices $\mathcal{F}$ and $\mathcal{V}$ corresponding to transmission and transition, respectively. In other words, all epidemiological events leading to new infections are incorporated into the model through $\mathcal{F}$ and all other events are incorporated through $\mathcal{V}$, where

$$\mathcal{F}=\left[\begin{array}{c}{\beta }_0\left\{i\left(t\right)+ba\left(t\right)\right\}\left\{\left(1-\eta \right)\left(1-e\left(t\right)-i\left(t\right)-a\left(t\right)-r\left(t\right)\right)+\left(\eta -\delta \right)v\left(t\right)\right\}\\ 0\\ 0\end{array}\right]$$

And

$$\mathcal{V}=\left[\begin{array}{c}(k+\mu )e(t)\\ -kpe\left(t\right)+(\gamma +\mu )i(t)\\ -k\left(1-p\right)e\left(t\right)+\left(\gamma +\mu \right)a(t)\end{array}\right].$$

By using $\mathcal{F}$ and $\mathcal{V}$ in a linearized system, we can evaluate the sensitivity matrix for the appearance of new infections ($F$) and the sensitivity matrix of transitions ($V$) as

$$F=\left[\begin{array}{ccc}0& {\beta }_0(\left(1-\eta \right)+\frac{\psi \left(\eta -\delta \right)}{\psi +\mu })& {\beta }_{0}b(\left(1-\eta \right)+\frac{\psi \left(\eta -\delta \right)}{\psi +\mu })\\ 0& 0& 0\\ 0& 0& 0\end{array}\right]$$

And

$$V=\left[\begin{array}{ccc}k+\mu & 0& 0\\ -kp& \mu +\gamma & 0\\ -k(1-p)& 0& \mu +\gamma \end{array}\right]$$

By using the spectral radius of the matrix ${\mathit{FV}}^{-1}$, we can obtain the control reproduction number ${\mathcal{R}}_c(\psi ,\eta )$ as follows:

$${\mathcal{R}}_{\mathrm{c}}(\psi ,\eta )=\frac{k\beta }{\left(k+\mu \right)\left(\gamma +\mu \right)}\frac{\left(\left(1-\delta \right)\psi +\left(1-\eta \right)\mu \right)}{\psi +\mu }$$

where $\beta ={\beta }_0\left(p+b\left(1-p\right)\right)$. Here, $\beta$ indicates the weighted transmission rate considering both symptomatic and asymptomatic cases.

By assuming there are no control measures (i.e., $\psi =\eta =0$), we can derive the basic reproduction number ${\mathcal{R}}_0$, meaning the number of infected individuals that one infected individual would produce within an entire susceptible population in the absence of control measures. The first factor of ${\mathcal{R}}_{\mathrm{c}}\left(\psi ,\eta \right)$ is the basic reproduction number (${\mathcal{R}}_0$), where

$${\mathcal{R}}_0={\mathcal{R}}_c\left(0,0\right)=\frac{\beta k}{\left(k+\mu \right)\left(\gamma +\mu \right)}.$$ (3)

The second factor $\frac{\left(1-\delta \right)\psi +\left(1-\eta \right)\mu }{\psi +\mu }$ represents the reduction in ${\mathcal{R}}_0$ caused by control measures. This simplifies the control reproduction number as follows:

$${\mathcal{R}}_{\text{c}}\left(\psi ,\eta \right)=\frac{\left(\left(1-\delta \right)\psi +\left(1-\eta \right)\mu \right)}{\left(\psi +\mu \right)}{\mathcal{R}}_0$$ (4)

It should be noted that the control reproduction number generally decreases with the social distancing level $\left(\frac{{\partial \mathcal{R}}_{\mathrm{c}}\left(\psi ,\eta \right)}{\partial \eta }<0\right)$, but it decreases with the vaccination rate only when $\delta >\eta \mathrm{b}\mathrm{e}\mathrm{c}\mathrm{a}\mathrm{u}\mathrm{s}\mathrm{e}\frac{\partial {\mathcal{R}}_{\mathrm{c}}\left(\psi ,\eta \right)}{\partial \psi }$ =$\frac{(\eta -\delta )\mu }{{\left(\psi +\mu \right)}^2}{\mathcal{R}}_0$(Figs. 2 and S1). If vaccine efficacy is not sufficiently high (i.e., $\delta <\eta$), then the control reproduction number increases as additional individuals choose a vaccination strategy, indicating the increased risk of infection when vaccination is selected over social distancing.

Fig. 2.

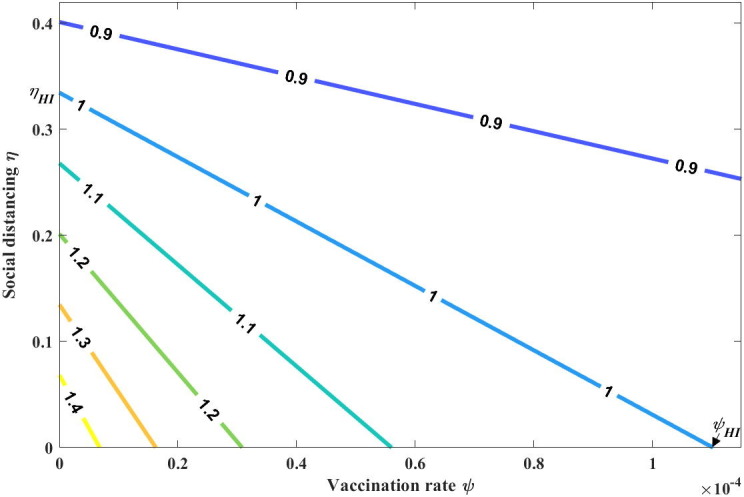
Contour plot of ${\mathcal{R}}_{\mathrm{c}}$ as a function of both the vaccination rate $\psi$ and social distancing level $\eta$.

When ${\mathcal{R}}_c>1$, a disease remains endemic in the population, and we can find the endemic equilibrium of the model in (2). By setting $i^{\text{'}}=0$, $a^{\text{'}}=0$, and $r^{\text{'}}=0$ in these equations, the endemic equilibrium can be calculated as

$$E^{\ast }=\left(v^{\ast },e^{\ast },i^{\ast },a^{\ast },r^{\ast }\right)=\left(v^{\ast },\frac{\gamma +\mu }{\mathit{kp}}{i}^{\ast },i^{\ast },\frac{1-p}{p}{i}^{\ast },\frac{\gamma }{p\mu }{i}^{\ast }\right).$$

By substituting $E^{\ast }$ into $v^{\text{'}}=0$ and setting $e^{\text{'}}=0$ in (2), it can be derived that the endemic level $i^{\ast }$ satisfies $H_1\left(i^{\ast }\right)=0$, where

$$H_1\left(i^{\ast }\right)=\left(1-\delta \right)\left(1-\eta \right){\left(\frac{\beta }{p\mu }\right)}^2{i^{\ast }}^2+\frac{\beta }{p\mu }\left\{\frac{\left(1-\delta \right)\left(\psi +\mu \right)}{\mu }+\left(1-\eta \right)\left(1-\left(1-\delta \right){\mathcal{R}}_0\right)\right\}{i}^{\ast }+\frac{\left(\psi +\mu \right)\left(1-{\mathcal{R}}_c\right)}{\mu }$$ (5)

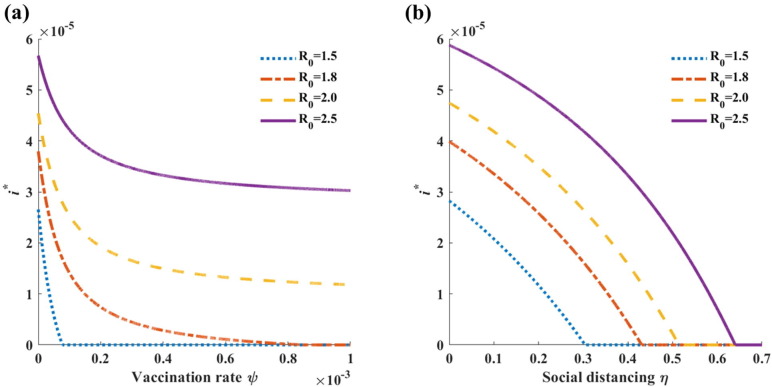
Here, we note that $H_1\left(0\right)<0$ when ${\mathcal{R}}_c>1$ and $H_1\left(\frac{p{\mu \mathcal{R}}_0}{\beta }\right)=\left(1-\delta \right){\mathcal{R}}_0+\frac{\left(\psi +\mu \right)}{\mu }>0$. Because $\frac{p{\mu \mathcal{R}}_0}{\beta }=\frac{pk\mu }{\left(k+\mu \right)\left(\gamma +\mu \right)}<1$, it follows that $H_1\left(i^{\ast }\right)=0$ has a solution $i^{\ast }$ with $0<i^{\ast }<\frac{p{\mu \mathcal{R}}_0}{\beta }$ when ${\mathcal{R}}_c>1$. Fig. 3 presents the variation in the endemic equilibrium level ($i^{\ast }$) with the vaccination rate ($\psi$) and social distancing level ($\eta$).

Fig. 3.

Sensitivity of the endemic level ($i^{\ast }$) to varying levels of control measures (i.e., vaccination and social distancing) varies. Other parameters are set to the baseline values listed in Table 1. (a) Endemic level as a function of the vaccination rate $\psi$ with $\eta =0.1$. (b) Endemic level as a function of the social distancing level $\eta$ with $\psi =0.00001$.

3. Results

3.1. Vaccination as a personal protection strategy

In this section, we consider vaccination as the sole personal protection strategy against infectious diseases ($\eta =0$). When it is available, vaccination functions as a primary prevention strategy, potentially leading to herd immunity. Specifically, vaccination provides direct protection by increasing the resistance of uninfected individuals to the pathogens from which a vaccine was prepared. Furthermore, vaccination can reduce the proportion of infected individuals, who could potentially transmit an infection, meaning that it also provides indirect protection. To analyze the role of vaccination and its optimal application strategy from an individual perspective, we consider the following model by setting $\eta =0$ in the model in (2):

$$\begin{array}{c}{v}^{\prime }\left(t\right)=\psi \left\{1-e\left(t\right)-i\left(t\right)-a\left(t\right)-r\left(t\right)\right\}-\left(1-\delta \right){\beta }_0\left\{i\left(t\right)+ba\left(t\right)\right\}v\left(t\right)-\left(\psi +\mu \right)v\left(t\right),\hfill \\ e^{\prime }\left(t\right)={\beta }_0\left\{i\left(t\right)+ba\left(t\right)\right\}\left\{1-e\left(t\right)-i\left(t\right)-a\left(t\right)-r\left(t\right)-\delta v\left(t\right)\right\}-\left(k+\mu \right)e\left(t\right),\hfill \\ i^{\prime }\left(t\right)=kpe\left(t\right)-\left(\gamma +\mu \right)i\left(t\right),\hfill \\ a^{\prime }\left(t\right)=k\left(1-p\right)e\left(t\right)-\left(\gamma +\mu \right)a\left(t\right),\hfill \\ r^{\prime }\left(t\right)=\gamma a\left(t\right)+\gamma i\left(t\right)-\mu r\left(t\right).\hfill \end{array}$$ (6)

3.1.1. Reproduction number and endemic equilibrium

In this vaccination model, the control reproduction number is calculated as

${\mathcal{R}}_{\psi }$ =$\frac{\left(\left(1-\delta \right)\psi +\mu \right)}{\left(\psi +\mu \right)}{\mathcal{R}}_0$.

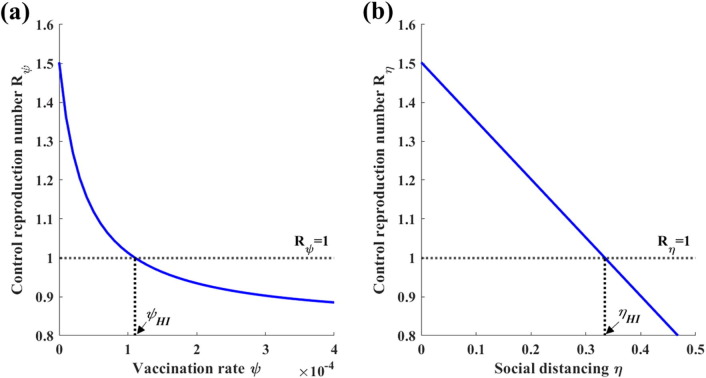
Fig. 4 (a) presents ${\mathcal{R}}_{\psi }$ as a function of the vaccination rate $\psi$. To analyze the threshold value for the vaccination rate that is required to achieve herd immunity, we set ${\mathcal{R}}_{\psi }=1$ and solve for $\psi$. This threshold vaccination rate is denoted as ${\psi }_{\mathit{HI}}$ and is calculated as

$${\psi }_{\mathit{HI}}=\frac{\mu \left\{{\mathcal{R}}_0-1\right\}}{1-\left(1-\delta \right){\mathcal{R}}_0},$$

where we assume that $1<{\mathcal{R}}_0<\frac{1}{1-\delta }$. If ${\mathcal{R}}_0>\frac{1}{1-\delta }$, then the disease cannot be eradicated by vaccination alone. Similarly, for values of $\psi$ less than ${\psi }_{\mathit{HI}}$, the disease remains endemic. Otherwise, the disease can be eradicated.

Fig. 4.

(a) Graph of the control reproduction number ${\mathcal{R}}_{\psi }$ when vaccination is the sole personal protection strategy ($\eta =0$). The threshold value for the vaccination rate that is required to achieve herd immunity is denoted as ${\psi }_{HI}$. (b) Graph of the control reproduction number ${\mathcal{R}}_{\eta }$ when social distancing is the sole personal protection strategy ($\psi =\delta =0$). The threshold value for the social distancing level that is required to achieve herd immunity is denoted as ${\eta }_{HI}$.

The endemic equilibrium in (6) is denoted as ${E_{\psi }}^{\ast }$ and exists when ${\mathcal{R}}_{\psi }>1$, where ${E_{\psi }}^{\ast }=\left(v_{\psi }^{\ast },e_{\psi }^{\ast },i_{\psi }^{\ast },a_{\psi }^{\ast },r_{\psi }^{\ast }\right)$ with

$$\begin{array}{c}{i}_{\psi }^{\ast }=\frac{-p\left\{\left(1-\delta \right)\left(\psi +\mu -\mu {\mathcal{R}}_0\right)+\mu \right\}+p\sqrt{{\left\{\left(1-\delta \right)\left(\psi +\mu {\mathcal{R}}_0\right)-\delta \mu \right\}}^2+4{\mathcal{R}}_0\delta \left(1-\delta \right){\mu }^2}}{2\left(1-\delta \right)\beta },\hfill \\ v_{\psi }^{\ast }=\frac{\psi \left(p\mu {\mathcal{R}}_0-\beta i_{\psi }^{\ast }\right)}{\mu {\mathcal{R}}_0\left(\left(1-\delta \right)\beta i_{\psi }^{\ast }+p\left(\psi +\mu \right)\right)},\hfill \\ e_{\psi }^{\ast }=\frac{\gamma +\mu }{\mathit{kp}}{i}_{\psi }^{\ast },\hfill \\ a_{\psi }^{\ast }=\frac{1-p}{p}{i}_{\psi }^{\ast },\hfill \\ r_{\psi }^{\ast }=\frac{\gamma }{p\mu }{i}_{\psi }^{\ast }.\hfill \end{array}$$ (7)

Here, the endemic level $i_{\psi }^{\ast }$ decreases with $\psi$ as

$$\frac{\partial \left(i_{\psi }^{\ast }\left(\psi \right)\right)}{\partial \psi }=\frac{p}{2\beta }\left\{\frac{\left(1-\delta \right)(\frac{\psi }{\mu }+{\mathcal{R}}_0)-\delta }{\sqrt{{\{\left(1-\delta \right)(\frac{\psi }{\mu }+{\mathcal{R}}_0)-\delta \}}^2+4{\mathcal{R}}_0\delta \left(1-\delta \right)}}-1\right\}<0.$$

Therefore, the endemic level attains its maximum value (denoted by $i_{\psi ,max}^{\ast }$) when $\psi$ is zero, meaning $i_{\psi ,max}^{\ast }=i_{\psi }^{\ast }\left(\psi =0\right)=\frac{p\mu ({\mathcal{R}}_0-1)}{\beta }$.

3.1.2. Application of game theory

Based on the endemic equilibrium, we now examine the individual payoff of vaccination strategies. We use the notations $v$ and $\mathit{nv}$ to denote individuals who choose vaccination and reject vaccination, respectively. The probabilities of infection among vaccinated and unvaccinated individuals, which are denoted as ${\pi }_v$ and ${\pi }_{\mathit{nv}}$, respectively, can be expressed as the proportions of susceptible individuals becoming infected versus dying during any unit of time (Bauch and Earn, 2004) as follows:

$${\pi }_v=\frac{\left(1-\delta \right){\beta }_0(i_{\psi }^{\ast }+b{a}_{\psi }^{\ast })}{\left(1-\delta \right){\beta }_0\left(i_{\psi }^{\ast }+b{a}_{\psi }^{\ast }\right)+\mu }\text{and}{\pi }_{\mathit{nv}}=\frac{{\beta }_0(i_{\psi }^{\ast }+b{a}_{\psi }^{\ast })}{{\beta }_0\left(i_{\psi }^{\ast }+b{a}_{\psi }^{\ast }\right)+\mu }$$ (8)

Here, ${\pi }_{V,N}$ is defined as the increased risk of infection among unvaccinated individuals compared to vaccinated individuals as follows:

$${\pi }_{V,N}\left(i_{\psi }^{\ast }\right)={\pi }_{\mathit{nv}}-{\pi }_v=\frac{\delta p\mu \beta i_{\psi }^{\ast }}{\left[\left(1-\delta \right)\beta i_{\psi }^{\ast }+p\mu \right]\left[\beta i_{\psi }^{\ast }+p\mu \right]}$$ (9)

By using the general game-theoretic framework (Bauch and Earn, 2004, Reluga and Galvani, 2011), the expected payoffs associated with each strategy can be defined as

$$E_v=-C_v-{\pi }_v{C}_i\text{and}{E}_{\mathit{nv}}=-{\pi }_{\mathit{nv}}{C}_i$$

where $C_v$ is the cost of vaccination, and $C_i$ is the cost associated with infection. To scale payoff without changing the outcome of the game, we divide both equations by $C_i$ to obtain

$$E_v=-C^v-{\pi }_v\text{and}{E}_{\mathit{nv}}=-{\pi }_{\mathit{nv}}$$ (10)

where $C^v$ is the relative cost of vaccination compared with the cost of infection, that is, $C^v=C_v/C_i$.

To analyze expected individual marginal payoffs, we denote the vaccination rate for the entire population as ${\psi }_{\mathit{POP}}$. If ${\psi }_{\mathit{POP}}>{\psi }_{\mathit{HI}}$, then ${\mathcal{R}}_{\psi }<1$ and the population reaches a disease-free equilibrium. In this case, the probability of infection becomes zero, meaning ${\pi }_v={\pi }_{\mathit{nv}}=0$. Therefore, there is no incentive for individuals to be vaccinated.

In contrast, if ${\psi }_{\mathit{POP}}<{\psi }_{\mathit{HI}}$, then ${\mathcal{R}}_{\psi }>1$, and the population reaches an endemic equilibrium ${E_{\psi }}^{\ast }$. An individual considers the expected marginal payoffs associated with switching from the non-vaccination strategy to the vaccination strategy as

$${\mathrm{\Delta }E(i_{\psi }^{\ast })=E}_v-E_{\mathit{nv}}={\pi }_{V,N}\left(i_{\psi }^{\ast }\right)-C^v.$$ (11)

In the presence of an endemic equilibrium (${E_{\psi }}^{\ast }$), an individual chooses a vaccination strategy when the relative benefit of vaccination versus non-vaccination is greater than the cost of vaccination, meaning $\mathrm{\Delta }E(i_{\psi }^{\ast })>0$, or equivalently, ${\pi }_{V,N}\left(i_{\psi }^{\ast }\right)>C^v$. In contrast, non-vaccination is favored when ${\pi }_{V,N}\left(i_{\psi }^{\ast }\right)<C^v$.

From a game-theoretic perspective, an individual adopts a vaccination strategy that will maximize personal payoff by considering the risk of infection, which is determined by the vaccination decisions made by the rest of the population (Reluga and Galvani, 2011, Shim et al., 2011). The Nash vaccination strategy, denoted as ${\psi }_{\mathrm{N}\mathrm{E}}$, where the payoff to an individual does not change regardless of whether one accepts or rejects vaccination, is governed by the equation ${\pi }_{V,N}\left(i_{\psi }^{\ast }\right)=C^v.$ By substituting the endemic level $i_{\psi }^{\ast }$ into the equation ${\pi }_{V,N}\left(i_{\psi }^{\ast }\right)=C^v$, we can obtain the following equation that the Nash vaccination strategy ${\psi }_{\mathrm{N}\mathrm{E}}$ must satisfy:

$$G\left(\psi \right)={\left(1-\delta \right)}^2{C}^v\left\{Z-\delta \left(1-\delta \right)C^v{\mathcal{R}}_0\right\}{\psi }^2+\left(1-\delta \right)\mu \left\{\delta \left(1+C^v\right)Z-2{\delta }^2{C}^v\right\}\psi +\delta {\mu }^2\left\{Z-{\delta }^2+\delta C^v\left(1-\delta \right){\mathcal{R}}_0\right\}=0,$$ (12)

where $Z=\left\{1-\left(1-\delta \right){\mathcal{R}}_0\right\}\delta +{\left\{\left(1-\delta \right){\mathcal{R}}_0\right\}}^2{C}^v$.

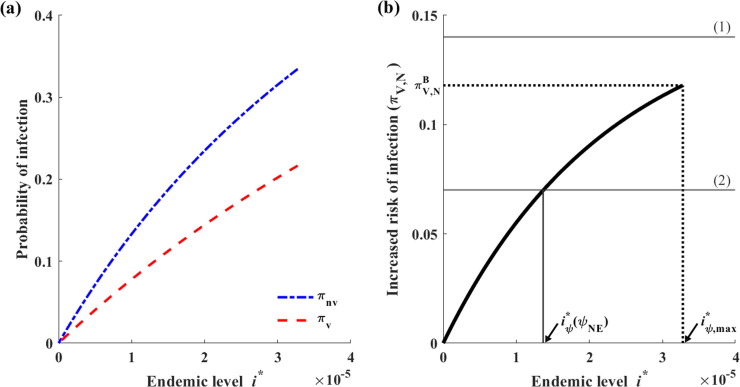
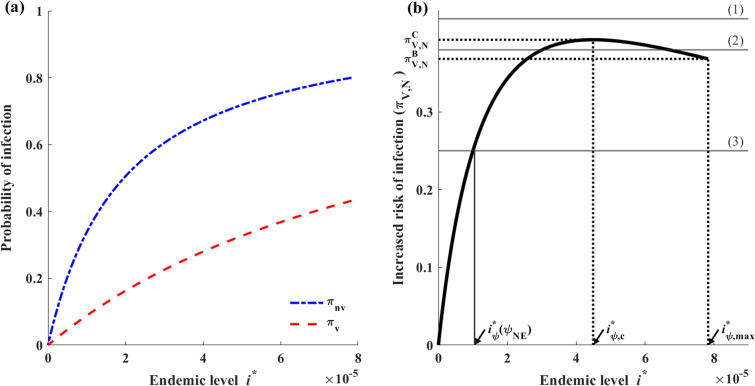
To analyze the existence of the Nash vaccination strategy ${\psi }_{\mathrm{N}\mathrm{E}}$, we examine the potential real roots of (12), which are denoted as ${\psi }_1$ and${\psi }_2$, where ${\psi }_1\le {\psi }_2<{\psi }_{\mathit{HI}}$ (Fig. S2). Additionally, it should be noted that $i_{\psi }^{\ast }\left({\psi }_1\right)\ge i_{\psi }^{\ast }\left({\psi }_2\right)$ because $\frac{\partial \left(i_{\psi }^{\ast }\left(\psi \right)\right)}{\partial \psi }<0$.

To analyze the Nash vaccination strategy, we first examine the maximum and minimum values of ${\pi }_{V,N}\left(i_{\psi }^{\ast }\right)$. Based on (9), we note that ${\pi }_{V,N}\left(i_{\psi }^{\ast }\right)$ increases with $i_{\psi }^{\ast }$ when $0<i_{\psi }^{\ast }<i_{\psi ,C}^{\ast }$ and decreases when $i_{\psi }^{\ast }>i_{\psi ,C}^{\ast }$, attaining its maximum value at $i_{\psi }^{\ast }=i_{\psi ,C}^{\ast }$, where $i_{\psi ,C}^{\ast }=\frac{\mu p}{\beta \sqrt{1-\delta }}$. Interestingly, it is feasible that $i_{\psi ,C}^{\ast }>i_{\psi ,max}^{\ast }$, which is equivalent to ${\mathcal{R}}_0\le 1+\frac{1}{\sqrt{1-\delta }}$. This case would correspond to the non-existence of $i_{\psi ,C}^{\ast }$.

The value of ${\pi }_{V,N}\left(i_{\psi }^{\ast }\right)$ when $i_{\psi }^{\ast }=i_{\psi ,C}^{\ast }$is denoted as ${\pi }_{V,N}^{\mathrm{C}}$. If this value exists, then ${\pi }_{V,N}^{\mathrm{C}}$ is calculated as

$${\pi }_{V,N}^{\mathrm{C}}={\left({\pi }_{V,N}\right|}_{i_{\psi }^{\ast }=i_{\psi ,C}^{\ast }}=\frac{\delta }{{\left(1+\sqrt{1-\delta }\right)}^2}$$ (13)

We also define ${\pi }_{V,N}^{\mathrm{B}}$ as the value of ${\pi }_{V,N}(i_{\psi }^{\ast })$ when the endemic level reaches its maximum value (i.e., when $\psi =0$) as follows:

$${\pi }_{V,N}^{\mathrm{B}}={\left({\pi }_{V,N}\right|}_{i_{\psi }^{\ast }=i_{\psi ,max}^{\ast }}=\frac{\delta \left({\mathcal{R}}_0-1\right)}{\left\{\left(1-\delta \right){\mathcal{R}}_0+\delta \right\}{\mathcal{R}}_0}$$ (14)

According to the calculations above, we arrive at the following results regarding the existence of the Nash strategy.

Case 1. We consider the case where ${\mathcal{R}}_0\le 1+\frac{1}{\sqrt{1-\delta }}$, which would indicate the non-existence of $i_{\psi ,C}^{\ast }$ (Fig. 5 ). The existence of a Nash vaccination strategy now depends on the value of $C^v$.

• ① If $C^v>{\pi }_{V,N}^{\mathrm{B}}$, then there is no Nash vaccination strategy. This is because $\mathrm{\Delta }E<0$ for all $i_{\psi }^{\ast }>0$ when $C^v>{\pi }_{V,N}^{\mathrm{B}}$, indicating that the relative cost of vaccination exceeds the corresponding marginal benefit.

• ② If $C^v<{\pi }_{V,N}^{\mathrm{B}}$, then there exists a unique Nash vaccination strategy ${\psi }_{\mathrm{N}\mathrm{E}}$ that is obtained when $C^v={\pi }_{V,N}$.

Fig. 5.

Case where ${\mathcal{R}}_0\le 1+\frac{1}{\sqrt{1-\mathit{\delta }}}$ (Case 1). Here, we set ${\mathcal{R}}_0=1.5$ and $\mathit{\delta }=0.45$. (a) Graph of the probabilities of infection among individuals who accept or reject vaccination. (b) Graph of the differences between two probabilities of infection: (1) When $C^v>{\pi }_{V,N}^{\mathrm{B}}$, there is no Nash vaccination strategy, (2) when $C^v={\pi }_{V,N}$, there is a unique Nash vaccination strategy ${\psi }_{\mathrm{NE}}$.

Case 2. We consider the case where ${\mathcal{R}}_0>1+\frac{1}{\sqrt{1-\delta }}$, which would allow $i_{\psi ,C}^{\ast }<i_{\psi ,max}^{\ast }$ (Fig. 6 ). Depending on the value of $C^v$, the following four cases can be identified. Here, we consider vaccine efficacy.

• ① If $C^v>{\pi }_{V,N}^{\mathrm{C}}$, then there is no Nash vaccination strategy. This is because $\mathrm{\Delta }E<0$ for all $i_{\psi }^{\ast }>0$ when $C^v>{\pi }_{V,N}^{\mathrm{C}}$.

• ② If $C^v={\pi }_{V,N}^{\mathrm{C}}$, then $\mathrm{\Delta }E=0$ only when $i_{\psi }^{\ast }=i_{\psi ,C}^{\ast }$. A unique Nash vaccination strategy is obtained in the scenario where the relative benefit of vaccination is maximized, facilitating the highest possible cost of vaccination.

• ③ If ${\pi }_{V,N}^{\mathrm{B}}<C^v<{\pi }_{V,N}^{\mathrm{C}}$, then $\mathrm{\Delta }E=0$ at two distinct endemic levels, resulting in two Nash vaccination strategies (i.e., ${\psi }_1$ and ${\psi }_2$). These strategies emerge when the cost of vaccination is intermediate and the disease transmissibility is relatively high with low vaccination coverage $({\psi }_{\mathit{POP}}<{\psi }_1)$. The expected marginal payoffs become zero at two distinct endemic levels, which correspond to two Nash vaccination strategies. This phenomenon was not identified in a prior study using a simple SIR vaccination game model (Bauch and Earn, 2004).

• ④ If $C^v\le {\pi }_{V,N}^{\mathrm{B}}$, then there is a unique Nash vaccination strategy ${\psi }_{\mathrm{N}\mathrm{E}}$. This scenario occurs when the cost of vaccination is relatively low, which promotes vaccination and reduces the endemic level at the Nash equilibrium.

Fig. 6.

Case where ${\mathcal{R}}_0>1+\frac{1}{\sqrt{1-\mathit{\delta }}}$ (Case 2). Here, we set ${\mathcal{R}}_0=5$ and $\mathit{\delta }=0.8$. (a) Graph of the probabilities of infection among individuals who accept or reject vaccination. (b) Graph of the differences between two probabilities of infection. If it exists, the Nash vaccination strategy can be obtained when $C^v={\pi }_{V,N}$: (1) there is no Nash strategy when $C^v>{\pi }_{V,N}^{\mathrm{C}}$, (2) two Nash strategies when ${\pi }_{V,N}^{\mathrm{B}}<C^v<{\pi }_{V,N}^{\mathrm{C}}$, and (3) one Nash strategy when $C^v={\pi }_{V,N}^{\mathrm{C}}$ or $C^v\le {\pi }_{V,N}^{\mathrm{B}}$.

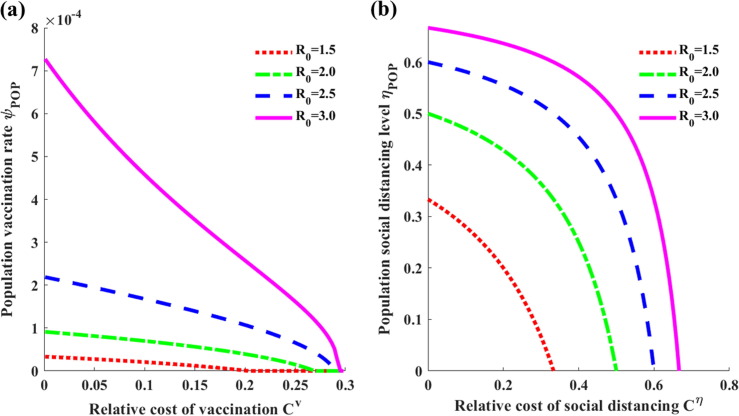
The Nash vaccination rate ${\psi }_{\mathrm{N}\mathrm{E}}$ is presented in Fig. 7 (a) as a function of the relative cost of vaccination $C^v$ when the value of ${\mathcal{R}}_0$ varies. One can seen that ${\psi }_{\mathrm{N}\mathrm{E}}$ decreases with $C^v$ and has a higher sensitivity to increasing costs when ${\mathcal{R}}_0$ is greater.

Fig. 7.

(a) Graph of the optimal vaccination rate ${\psi }_{NE}$ as a function of the relative cost of vaccination $C^v$ when the basic reproduction number ${\mathcal{R}}_0$ is $1.5,2,2.5,\mathrm{and}3$, where $\mathit{\delta }=0.7$. (b) Graph of the optimal level of social distancing ${\eta }_{NE}$ as a function of the relative cost of social distancing $C^{\eta }$.

3.2. Social distancing as a personal protection strategy

We now examine the case where individuals consider social distancing as the sole strategy for preventing infectious diseases. In the absence of vaccination, large-scale social distancing measures (including workplace non-attendance, school closures, and travel restrictions) appear to be the most effective means of mitigation. It has been reported that although social distancing alone may be insufficient to eliminate disease transmission, it can flatten the epidemic curve, thereby reducing the burden on the healthcare system and providing additional time to prepare for a subsequent epidemic (Anderson et al., 2020). To analyze the optimal social distancing at an individual level, we let $\psi =0$ in (2). This yields

$$\begin{array}{c}{e}^{\prime }\left(t\right)=\lambda \left(t\right)\left(1-\eta \right)\left(1-e\left(t\right)-i\left(t\right)-a\left(t\right)-r\left(t\right)\right)-\left(k+\mu \right)e\left(t\right),\hfill \\ i^{\prime }\left(t\right)=kpe\left(t\right)-\left(\gamma +\mu \right)i\left(t\right),\hfill \\ a^{\prime }\left(t\right)=k\left(1-p\right)e\left(t\right)-\left(\gamma +\mu \right)a\left(t\right),\hfill \\ r^{\prime }\left(t\right)=\gamma a\left(t\right)+\gamma i\left(t\right)-\mu r\left(t\right).\hfill \end{array}$$ (15)

where the force of infection is calculated as $\lambda \left(t\right)={\beta }_0\left\{i\left(t\right)+ba\left(t\right)\right\}$.

3.2.1. Reproduction number and endemic equilibrium

The proportion $\eta$ represents the social distancing level for a particular individual who can reduce their contact rate by staying home, refraining from attending public events, or cancelling appointments during outbreaks. The control reproduction number associated with this model is defined as

$${\mathcal{R}}_{\eta }=\left(1-\eta \right){\mathcal{R}}_0$$ (16)

To obtain the threshold value for the social distancing level that is required to achieve herd immunity (${\eta }_{\mathit{HI}}$), we set ${\mathcal{R}}_{\eta }=1$ and solve for $\eta$ as follows:

$${\eta }_{\mathit{HI}}=1-\frac{1}{{\mathcal{R}}_0}$$ (17)

Fig. 4(b) presents a graph of ${\mathcal{R}}_{\eta }$ as a function of the social distancing $\mathrm{l}\mathrm{e}\mathrm{v}\mathrm{e}\mathrm{l}\eta$. The disease remains endemic if $\eta <{\eta }_{\mathit{HI}}$ and is eradicated if $\eta >{\eta }_{\mathit{HI}}$. In this analysis, we consider the endemic settings by assuming that $\eta <{\eta }_{\mathit{HI}}$, which is equivalent to ${\mathcal{R}}_{\eta }>1$ or ${\mathcal{R}}_0>\frac{1}{1-\eta }$.

Given the value of ${\mathcal{R}}_0$, we can determine the corresponding endemic level by setting Eq (15) equal to zero. This resulted in $H_2\left(i_{\eta }^{\ast }\right)=0$, where

$$H_2\left(i_{\eta }^{\ast }\right)=\left(1-\eta \right){\left(\frac{\beta }{p\mu }\right)}^2{i_{\eta }^{\ast }}^2+\frac{\beta }{p\mu }\left\{1+\left(1-\eta \right)\left(1-{\mathcal{R}}_0\right)\right\}{i}_{\eta }^{\ast }+\{1-\left(1-\eta \right){\mathcal{R}}_0\}.$$ (18)

By $H_2\left(i_{\eta }^{\ast }\right)=0$, the endemic equilibrium is obtained as

$$i_{\eta }^{\ast }=\frac{p\mu ({\mathcal{R}}_{\eta }-1)}{\left(1-\eta \right)\beta }$$ (19)

It should be noted that $i_{\eta }^{\ast }=i_{\eta }^{\ast }({\eta }_{\mathit{pop}})$, where ${\eta }_{\mathit{pop}}$ is defined as the social distancing probability for the entire population.

3.2.2. Application of game theory

In the presence of an endemic equilibrium, we define $\varphi (\eta ,{\eta }_{\mathit{pop}})$ as the probability that a susceptible individual becomes infected, where

$$\varphi \left(\eta ,{\eta }_{\mathit{pop}}\right)=\frac{(1-\eta ){\lambda }_{\eta }^{\ast }({\eta }_{\mathit{pop}})}{(1-\eta ){\lambda }_{\eta }^{\ast }({\eta }_{\mathit{pop}})+\mu }$$ (20)

Here, $\eta$ represents the social distancing strategy of a target individual, and the force of infection (${\lambda }_{\eta }^{\ast }(t)$) is calculated as

$${\lambda }_{\eta }^{\ast }={\lambda }_{\eta }^{\ast }\left({\eta }_{\mathit{pop}}\right)={\beta }_0\left\{i_{\eta }^{\ast }+b{a}_{\eta }^{\ast }\right\}=\frac{\beta }{p}{i}_{\eta }^{\ast }=\frac{\mu \left({\mathcal{R}}_{\eta }-1\right)}{1-{\eta }_{\mathit{pop}}}$$ (21)

It should be noted that if the background social distancing level ${\eta }_{\mathit{pop}}$ increases, then the probability that an infected individual will encounter a susceptible individual decreases, and the force of infection ${\lambda }_{\eta }^{\ast }(t)$ also decreases, which demonstrates the dependence of ${\lambda }_{\eta }^{\ast }(t)$ on the background social distancing level ${\eta }_{\mathit{pop}}$. Furthermore, the social distancing strategy of a target individual can reduce their risk of infection $\varphi (\eta ,{\eta }_{\mathit{pop}})$. Therefore, the probability of infection is affected by both the background social distancing level ${\eta }_{\mathit{pop}}$ and the social distancing strategy $\eta$ of a target individual.

We now calculate the payoff for an individual who adopts a social distancing strategy $\eta$ in the presence of a background social distancing strategy ${\eta }_{\mathit{pop}}$ as follows:

$$E\left(\eta ,{\eta }_{\mathit{pop}}\right)=-\frac{\left(1-\eta \right){\lambda }_{\eta }^{\ast }\left({\eta }_{\mathit{pop}}\right)}{\left(1-\eta \right){\lambda }_{\eta }^{\ast }\left({\eta }_{\mathit{pop}}\right)+\mu }-\eta C^{\eta }=-\frac{\left(1-\eta \right)\left({\mathcal{R}}_{\eta }-1\right)}{\left(1-\eta \right)\left({\mathcal{R}}_{\eta }-1\right)+\left(1-{\eta }_{\mathit{pop}}\right)}-\eta C^{\eta },$$ (22)

where $C^{\eta }=\frac{C_{\eta }}{C_i}$ is the relative cost of social distancing $C_{\eta }$ compared to the cost of infection $C_i$.

Without loss of generality, we assume that the relative cost of social distancing is less than that of infection, meaning $C^{\eta }<1$. Therefore,

$$\frac{\partial E(\eta ,{\eta }_{\mathit{pop}})}{\partial \eta }=\frac{{\mathcal{R}}_{\eta }-1}{{\left\{\left(1-\eta \right)\left({\mathcal{R}}_{\eta }-1\right)+\left(1-{\eta }_{\mathit{pop}}\right)\right\}}^2}-C^{\eta }\text{and}\frac{{\partial }^{2}E(\eta ,{\eta }_{\mathit{pop}})}{\partial {\eta }^2}=\frac{2{\left({\mathcal{R}}_{\eta }-1\right)}^2}{{\left\{\left(1-\eta \right)\left({\mathcal{R}}_{\eta }-1\right)+\left(1-{\eta }_{\mathit{pop}}\right)\right\}}^3}$$ (23)

When $\frac{{\partial }^{2}E(\eta ,{\eta }_{\mathit{pop}})}{\partial {\eta }^2}>0$, $E\left(\eta ,{\eta }_{\mathit{pop}}\right)$ is a convex function of $\eta$ that attains its global maximum value at either $\eta =0$ or $\eta =1$. The corresponding payoff when $\eta =0$ is

$$E\left(0,{\eta }_{\mathit{pop}}\right)=-\frac{{\mathcal{R}}_{\eta }-1}{{\mathcal{R}}_{\eta }-{\eta }_{\mathit{pop}}}$$ (24)

where the focal individual does not practice social distancing at all and depends entirely on the social distancing of the background population. The payoff when $\eta =1$ is

$$E\left(1,{\eta }_{\mathit{pop}}\right)=-C^{\eta }$$ (25)

where the target individual practices social distancing exclusively and is protected against infection at the full cost of social distancing.

The optimal individual strategy ${\eta }_{\mathit{NE}}$ is obtained in the scenario where the individual payoff is consistent regardless of whether or not one adopts a social distancing strategy. In other words, ${\eta }_{\mathit{NE}}$ is the solution to the equation $E\left(0,{\eta }_{\mathit{pop}}\right)=E\left(1,{\eta }_{\mathit{pop}}\right)$, or equivalently,

$$\frac{{\mathcal{R}}_{\eta }-1}{{\mathcal{R}}_{\eta }-{\eta }_{\mathit{pop}}}=C^{\eta }.$$ (26)

By using (16), this expression can be rewritten as

$$\frac{\left(1-{\eta }_{\mathit{pop}}\right){\mathcal{R}}_0-1}{\left(1-{\eta }_{\mathit{pop}}\right){\mathcal{R}}_0-{\eta }_{\mathit{pop}}}=C^{\eta }.$$ (27)

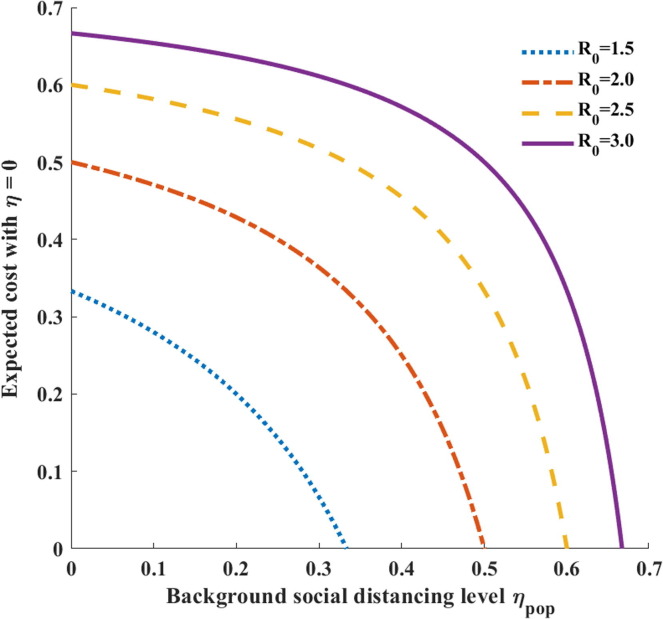
It should be noted that $\frac{\left(1-{\eta }_{\mathit{pop}}\right){\mathcal{R}}_0-1}{\left(1-{\eta }_{\mathit{pop}}\right){\mathcal{R}}_0-{\eta }_{\mathit{pop}}}$ is a decreasing function of ${\eta }_{\mathit{pop}}$ ($0\le {\eta }_{\mathit{pop}}<{\eta }_{\mathit{HI}}$) that attains its maximum value $1-\frac{1}{{\mathcal{R}}_0}$ when ${\eta }_{\mathit{pop}}=0$ (Fig. 8 ). Therefore, ${\eta }_{\mathit{NE}}$ never exceeds the herd immunity threshold ${\eta }_{\mathit{HI}}$ and equality is attained only when the relative cost of social distancing is zero ($C^{\eta }=0$). Furthermore, if $C^{\eta }>C_{\mathit{max}}^{\eta }$, then the resulting optimal social distancing strategy is zero (${\eta }_{\mathit{NE}}=0)$ when $C_{\mathit{max}}^{\eta }=1-\frac{1}{{\mathcal{R}}_0}$. When ${0<C}^{\eta }<C_{\mathit{max}}^{\eta }$, the optimal social distancing level ${\eta }_{\mathit{NE}}$ is computed as

$${\eta }_{\mathit{NE}}=1-\frac{1-C^{\eta }}{{\mathcal{R}}_0-(1+{\mathcal{R}}_0)C^{\eta }}$$ (28)

Fig. 8.

Expected cost when there is no individual social distancing, meaning $\frac{\left(1-{\eta }_{pop}\right){\mathcal{R}}_0-1}{\left(1-{\eta }_{pop}\right){\mathcal{R}}_0-{\eta }_{pop}}$, as a function of the background social distancing level ${\eta }_{pop}$. The basic reproduction number ${\mathcal{R}}_0$ takes on values of $1.5,2,2.5,$ and 3. If it exists, the optimal social distancing level can be obtained when the relative cost of social distancing $C^{\eta }$ is equal to the expected cost and the individual social distancing level is zero.

Graphs of the optimal social distancing level ${\eta }_{\mathit{NE}}$ as a function of the relative cost of social distancing $C^{\eta }$ in terms of the value of ${\mathcal{R}}_0$are presented in Figs. 7(b) and S2.

3.3. Combining vaccination and social distancing

Finally, we consider the case where individuals can adopt a combined strategy of vaccination and social distancing for personal protection against infectious diseases. When both strategies are available, the Nash vaccination strategy becomes a function of the social distancing level ${\psi }_{\mathit{NE}}\left(\eta \right)$. Similarly, the optimal social distancing strategy becomes a function of the vaccination rate ${\eta }_{\mathit{NE}}\left(\psi \right)$. By substituting the expression for $i^{\ast }$ from (5) into $-C^v+{\pi }_{V,N}\left(i^{\ast }\right)=0$ (see (11)), we can obtain the equation that the Nash vaccination strategy ${\psi }_{\mathit{NE}}\left(\eta \right)$ satisfies as follows:

$$\left\{Z-\delta {\mathcal{R}}_0\left(1-\delta \right)C^v\right\}{C}^v{\psi }^2+\frac{\mu }{1-\delta }\left\{\left(1-\delta \right)A+\left(1-\eta \right)B\right\}\psi +\frac{\delta {\mu }^2}{1-\delta }\left\{(1-\delta )C^v+\left(1-\eta \right)D\right\}=0$$ (29)

where

$$A=C^{v}Z+\delta C^v-\left(\left(1-\delta \right){\mathcal{R}}_0+\delta \right)\left(1-\delta \right){\mathcal{R}}_0{C^v}^2,$$

$$B=\delta Z+\left(2\delta -1\right)C^{v}Z-\left(1+\delta \right)\delta C^v+{\left(1-\delta \right)}^2\left(\delta +\left(1-\delta \right){\mathcal{R}}_0\right){\mathcal{R}}_0{C^v}^2,$$

$$D=\delta +\left(\delta -2-2{\mathcal{R}}_0\left(1-\delta \right)\right)C^v+\left(1-\eta \right)\left(\left(1-\delta \right)C^v{\mathcal{R}}_0^2+\left(\left(2-\delta \right)C^v-\delta \right){\mathcal{R}}_0+C^v\right),$$

and

$$Z=\left\{1-{\mathcal{R}}_0\left(1-\delta \right)\right\}\delta +{\left\{{\mathcal{R}}_0\left(1-\delta \right)\right\}}^2{C}^v.$$

Similarly, we can obtain the optimal social distancing strategy by solving (26) for $\eta$ as follows:

$${\eta }_{\mathit{NE}}\left(\psi ,\delta \right)=1-\frac{\left(1-C^{\eta }\right)\left\{1-{\mathcal{R}}_0\left(1-\delta \right)+\left(\left(1-\delta \right){\mathcal{R}}_0-\delta \right)C^{\eta }\right\}}{\left({\mathcal{R}}_0-C^{\eta }\left(1+{\mathcal{R}}_0\right)\right)\left(1-\delta C^{\eta }\right)\mu }\psi -\frac{1-C^{\eta }}{{\mathcal{R}}_0-\left(1+{\mathcal{R}}_0\right)C^{\eta }}.$$ (30)

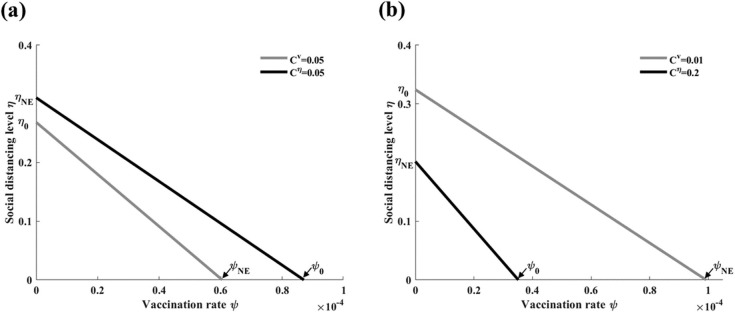
In this analysis, we consider $C^v\le {\pi }_{V,N}^{\mathrm{B}}$, which is the case where there is a unique Nash vaccination strategy. We denote the maximum threshold value for the relative cost of vaccination as $C_{\mathit{max}}^v$, where $C_{\mathit{max}}^v={\pi }_{V,N}^{\mathrm{B}}$. We let ${\eta }_0$ be the social distancing level where ${\psi }_{\mathit{NE}}\left({\eta }_0\right)=0$ and ${\psi }_0$ be the vaccination rate where ${\eta }_{\mathit{NE}}\left({\psi }_0\right)=0$. Numerical simulations demonstrate that there are two cases, namely (1) ${\eta }_0<{\eta }_{\mathit{NE}}\mathrm{a}\mathrm{n}\mathrm{d}{\psi }_0>{\psi }_{\mathit{NE}}$, and (2) ${\eta }_0>{\eta }_{\mathit{NE}}$ and ${\psi }_0<{\psi }_{\mathit{NE}}$, for the baseline parameter values (Table 1).

• -If ${\eta }_0<{\eta }_{\mathit{NE}}$ and ${\psi }_0>{\psi }_{\mathit{NE}}$, then the black line (optimal level of social distancing) remains above the gray line (optimal vaccination line). Therefore, social distancing is the dominant strategy (Fig. 9 (a)).
• -If ${\eta }_0>{\eta }_{\mathit{NE}}$ and ${\psi }_0<{\psi }_{\mathit{NE}}$, then the gray line remains above the black line. Therefore, vaccination is the dominant strategy (Fig. 9(b)).

Fig. 9.

Combined vaccination and social distancing strategies. When both strategies are available, the optimal vaccination rate (gray lines) and optimal social distancing level (black lines) are compared. (a) Social distancing is the dominant strategy. (b) Vaccination is the dominant strategy.

By setting $\psi$ equal to zero in (29) and solving for $\eta$, we obtain

$${\eta }_0=1+\frac{\delta +\left(\delta -2-2{\mathcal{R}}_0\left(1-\delta \right)\right)C^v+\sqrt{{\delta }^2+\left(2{\delta }^2-4\delta \right)C^v+{\delta }^2{C^v}^2}}{\left(2-2\delta \right)C^v{\mathcal{R}}_0^2+\left((4-2\delta )C^v-2\delta \right){\mathcal{R}}_0+2C^v}.$$

Similarly, setting (30) equal to zero and solving for $\psi$ yeilds

$${\psi }_0=\frac{({\mathcal{R}}_0-1)\left(1-\delta C^{\eta }\right)\mu }{1-{\mathcal{R}}_0\left(1-\delta \right)+\left(\left(1-\delta \right){\mathcal{R}}_0-\delta \right)C^{\eta }}.$$

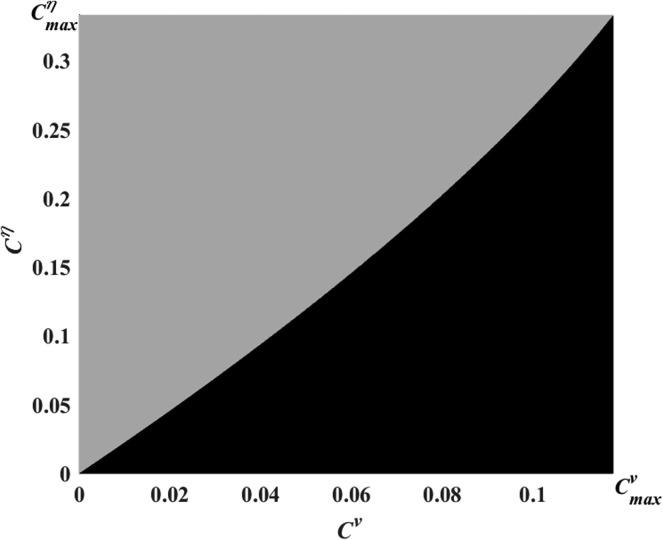
Vaccination is the dominant strategy (gray region) when ${\eta }_0>{\eta }_{\mathit{NE}}$, which is defined as

$$1+\frac{\delta +\left(\delta -2-2{\mathcal{R}}_0\left(1-\delta \right)\right)C_v+\sqrt{{\delta }^2+\left(2{\delta }^2-4\delta \right)C^v+{\delta }^2{C^v}^2}}{\left(2-2\delta \right)C^v{\mathcal{R}}_0^2+\left((4-2\delta )C^v-2\delta \right){\mathcal{R}}_0+2C^v}>1-\frac{1-C^{\eta }}{{\mathcal{R}}_0-\left(1+{\mathcal{R}}_0\right)C^{\eta }}\text{.}$$

Social distancing is the dominant strategy (black region) when ${\psi }_0>{\psi }_{\mathit{NE}},\mathrm{w}\mathrm{h}\mathrm{i}\mathrm{c}\mathrm{h}\mathrm{i}\mathrm{s}\mathrm{d}\mathrm{e}\mathrm{f}\mathrm{i}\mathrm{n}\mathrm{e}\mathrm{d}\mathrm{a}\mathrm{s}$

$$\frac{({\mathcal{R}}_0-1)\left(1-\delta C^{\eta }\right)\mu }{1-{\mathcal{R}}_0\left(1-\delta \right)+\left(\left(1-\delta \right){\mathcal{R}}_0-\delta \right)C^{\eta }}>\frac{-\mu \left(\delta \left(1+C^v\right)Z-2{\delta }^2{C}^v\right)+\mu \sqrt{\left\{{\delta }^2-2\left(2-\delta \right)\delta C^v+{\left(\delta C^v\right)}^2\right\}{Z}^2}}{2(1-\delta )C^v(Z-\delta \left(1-\delta \right){\mathcal{R}}_0{C}^v)}.$$

The cutoff values for the relative costs in the graph in Fig. 10 are the maximum threshold costs for the vaccination and social distancing strategies. If the relative cost of social distancing $C^{\eta }$ exceeds the maximum threshold value $C_{\mathit{max}}^{\eta }$, then the social distancing strategy is not selected, meaning vaccination is the dominant strategy. Similarly, if the relative cost of vaccination $C^v$ approaches the maximum threshold value $C_{\mathit{max}}^v$, then social distancing is the dominant strategy. If both of the relative costs $C^v$ and $C^{\eta }$ exceed their corresponding thresholds, then neither strategy is selected by the population because the corresponding costs are excessively high relative to the corresponding benefits.

Fig. 10.

Regions in $(C^v,C^{\eta })$ showing the cutoff values as the maximum threshold costs for the vaccination and social distancing strategies. Black: social distancing only, gray: vaccination only.

4. Discussion

In this study, we constructed a game-theoretic model for disease transmission and control measures (i.e., vaccination and social distancing) to determine the optimal individual strategies for preventing infectious diseases. We generated a payoff function associated with each control strategy for susceptible individuals, and the resulting payoffs were calculated based on the decisions of the rest of the population. When both vaccination and social distancing are available to a population, the relative cost of each strategy determines which strategy is more likely to be adopted by the population. For baseline parameter values, it was demonstrated that social distancing is more likely to be the dominant strategy. This is partially based on its superior efficacy compared to an imperfect vaccine. Social distancing directly reduces the per capita rate at which susceptible individuals are infected by reducing the contact rate, whereas vaccines may still permit infection based on poor efficacy. Therefore, when both strategies have the same cost, the social distancing strategy is more likely to be selected. If the relative costs of both strategies exceed the corresponding maximum threshold values, then neither strategy will be selected, because marginal payoffs of the control strategies will be minimal. These results indicate that when vaccine efficacy is not sufficiently high for a basic reproduction number, a disease cannot be eradicated by vaccination alone. In contrast, extreme social distancing has the potential to fully protect individuals from infection by minimizing the force of infection. However, a high social distancing level can result in economic loss not only for individuals, but also for communities based on the discontinuation of economic activity. Furthermore, the herd immunity threshold for social distancing cannot be achieved through voluntary participation alone (e.g., school or work attendance and using public transportation). Therefore, public health agencies should establish policies considering both social distancing and vaccination, such as subsidized vaccination, school closure, and cancellation of public events.

Vaccine coverage can be affected by psychological factors, such as epidemic scares, rumors of disease, the perceived effectiveness of vaccination by the media, or word of mouth (Bhattacharyya et al., 2015, Breban, 2011, d’Onofrio and Manfredi, 2020, d’Onofrio et al., 2016, Shim et al., 2012b, Tchuenche et al., 2011). In particular, when a vaccine for a newly emerging infectious disease, such as COVID-19, is under development, there is insufficient information available regarding its effectiveness. This study can provide guidance regarding preferred prevention strategies according to the perceived effectiveness and relative cost of new vaccines because it can identify an appropriate relative cost for vaccination for voluntary participation. If the cost of vaccination is relatively high compared to its efficacy, then individual adoption of vaccination may be reduced. In a prior study, it was also suggested that voluntary vaccination in the presence of a behavior-dependent contact rate can reduce infection prevalence, but may also induce recurrent epidemics (d’Onofrio and Manfredi, 2020). Public intervention was shown to have a stabilizing role which can reduce the strength of imitation-induced oscillations, and even facilitate disease elimination (d'Onofrio et al., 2012).

One limitation of our model is that it does not consider age heterogeneity in terms of disease susceptibility or age-dependent mixing patterns. Additionally, our model assumes that the costs associated with social distancing are limited to the personal costs, even though there are social costs associated with a malfunctioning society (e.g., food supply and healthcare services breakdowns) when social distancing is practiced by a relatively large fraction of a population over an extended period of time. Furthermore, our analysis was conducted under the assumption that a system has already reached an endemic state when individuals begin selecting protection strategies. In the real world, the infection probability changes dynamically with disease prevalence and age-dependent susceptibility. For example, the optimal vaccination rates for all age groups are the highest at the beginning of a seasonal influenza epidemic, and the optimal vaccination coverage differs between age groups (Shim, 2013). Additionally, if the severity of a disease increases, and government interventions, such as school closures and travel restrictions, are present, then individuals may choose to increase their social distancing level. For a more detailed analysis of optimal personal strategies, the vaccination rate and social distancing level should be defined as state variables.

In this paper, we presented the first study on a game-theoretic model for infectious diseases considering vaccination and social distancing simultaneously. Our findings highlight the optimal protection strategies from an individual perspective in the event of a disease outbreak. Our game-theoretic model can also be extended and applied to various infectious diseases to provide insights into the interplay between disease dynamics and individual adherence to protection strategies.

Funding

This work was supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIT) (No. 2018R1C1B6001723).

CRediT authorship contribution statement

Wongyeong Choi: Methodology, Formal analysis, Visualization, Writing - original draft, Writing - review & editing. Eunha Shim: Conceptualization, Methodology, Formal analysis, Visualization, Writing - original draft, Writing - review & editing, Supervision, Funding acquisition.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A.

Endemic equilibrium

By solving (5) and setting the equations in (2) equal to zero, we can obtain the endemic equilibrium as $E^{\ast }=\left(v^{\ast },e^{\ast },i^{\ast },a^{\ast },r^{\ast }\right)$, where

$$i^{\ast }=\frac{-p\mu \left(\psi +\mu +xy\right)+p\mu \sqrt{{\left(\psi +\mu -xy\right)}^2+4\left(1-x\right)y(y-\mu )}}{2\beta \left(1-\delta \right)y},$$

$$v^{\ast }=\frac{\psi (p\mu {\mathcal{R}}_0-\beta i^{\ast })}{\mu {\mathcal{R}}_0(\left(1-\delta \right)\beta i^{\ast }+p(\psi +\mu ))},$$

$$e^{\ast }=\frac{\gamma +\mu }{\mathit{kp}}{i}^{\ast },$$

$$a^{\ast }=\frac{1-p}{p}{i}^{\ast },$$

$$r^{\ast }=\frac{\gamma }{p\mu }{i}^{\ast },$$

where $x=1-{\mathcal{R}}_0\left(1-\delta \right)$and $y=\frac{\mu \left(1-\eta \right)}{1-\delta }.$

Appendix B.

Nash equilibrium$({\psi }_{\mathrm{N}\mathrm{E}})$

To study the existence of a Nash equilibrium ${\psi }_{\mathrm{N}\mathrm{E}}$, we solve (12), which has the following two possible real roots:

$${\psi }_1=\frac{-\mu \left(\delta \left(1+C^v\right)Z-2{\delta }^2{C}^v\right)-\mu \sqrt{\left\{{\delta }^2-2\left(2-\delta \right)\delta C^v+{\left(\delta C^v\right)}^2\right\}{Z}^2}}{2(1-\delta )C^v(Z-\delta \left(1-\delta \right){\mathcal{R}}_0{C}^v)}$$

and

$${\psi }_2=\frac{-\mu \left(\delta \left(1+C^v\right)Z-2{\delta }^2{C}^v\right)+\mu \sqrt{\left\{{\delta }^2-2\left(2-\delta \right)\delta C^v+{\left(\delta C^v\right)}^2\right\}{Z}^2}}{2(1-\delta )C^v(Z-\delta \left(1-\delta \right){\mathcal{R}}_0{C}^v)},$$

where $Z=\left\{1-\left(1-\delta \right){\mathcal{R}}_0\right\}\delta +{\left\{\left(1-\delta \right){\mathcal{R}}_0\right\}}^2{C}^v$.

Appendix C. Supplementary data

The following are the Supplementary data to this article: