Shipping markets in turmoil: An analysis of the Covid-19 outbreak and its implications

Abstract

In the current study, we examine, for the first time in the literature, the impact of exogenous effects in the shipping industry by employing data from the recent Covid-19 pandemic outbreak and explore the reactions of freight rates for dry bulk, clean, and dirty tankers. Our results, using both GARCH (1,1) and VAR specifications, suggest that such events are directly affecting the dry bulk and the dirty tanker segments. In addition, the results also suggest that second round effects, mostly via the decline in oil prices and, in some cases, third round effects via the impact from the stock market, also exist. Finally, by employing daily port calls a proxy variable for the demand for transportation services, we show that both the dry bulk and clean tankers are highly affected by the demand side of the economy, while vessels which transport crude oil do not register such a relationship.

Highlights

• •We study the impact of the Covid-19 pandemic on the shipping freight rates.
• •We find that the pandemic has directly affected dry bulks and dirty tankers.
• •Second round (oil prices) and third round (stock market) effects exist.
• •Demand affects freight rates in dry-bulk and clean tanker segments more
• •Results underline the potential use of tankers for storage when oil prices are low.

1. Introduction

The shipping industry is not only renowned for its main part in the global supply chain, since it accounts for 80% of the total transportations that are taking place globally (UNCTAD, 2019) but also for its high volatility when it comes to its freight rates (Theodossiou et al., 2020). While the average business cycle in the economy lasts for 14 years (Stock, 1987), the business cycle of the shipping industry lasts for only 7 years (Stopford, 2013). Nevertheless, despite the difference that exists between the rest of the economic sectors and shipping, little attention has been given up to now to the factors that are make the shipping cycles so short-spanned.

While the literature has focused on macro-variables that affect the sector (Grammenos and Arkoulis, 2002; Drobetz et al., 2010; Papapostolou et al., 2014; Michail, 2020), there has not been a research that investigates how the industry reacts to specific events. Given the latter, in the current paper, we examine how a global exogenous event is affecting the industry by quantifying the relationship between an epidemic outbreak and the freight rates of the tanker and the bulk shipping segments.

We are building our model not only by introducing for the first time a quantifiable variable for the exogenous event but also by using additional variables that are acting as proxies for the global supply and demand of the shipping markets. Additionally, so as to exclude any potential spillovers that may have erupted between economy and the shipping markets, we are including variables of that are connecting the outcome of the event to the financial markets, since the relationship that exists between the two is already well-established (Kavussanos et al., 2014; Papapostolou et al., 2016).

This research contributes to the current literature in various ways. First, it is the first time that a shipping cycle collapse is examined in the short run rather than as a point of a longer-duration cycle, allowing us to have a closer look at how freight rates are affected by rapid changes in the macroeconomic environment. Moreover, we employ, for the first time, what appears to be one of the best proxies for demand available, namely vessel port calls, which are able to better assist us in capturing the demand-side changes in the shipping. Finally, through the use of the coronavirus variable in a Vector Autoregression (VAR) model, we effectively turn an event-study methodology into an endogenous reaction, allowing us to observe how the whole system is affected when an unexpected shock occurs, and not just rely on how a variable reacts in a simple OLS framework.

The results of our research are important both for practitioners of the industry as well as academics, as they shed light on how shipping markets react on crisis periods as well as the pass-through channels through which it is affected. Shipowners, charterers, operators, and policymakers are all affected from the pandemic. As the results suggest, the excess drop in the industry's returns that hits the market in such exogenous events affect largely the cash flow generating abilities of shipping companies. This leaves companies with income problems that affect the companies themselves and consequently their investors, management, and employees. Moreover, on a broader perspective, extended stakeholders are affected by such events, like governments on a tax perspective. To address this issue, market participants could try to reduce losses and limit volatility in freight rates by entering into paper markets (FFAs, Futures) and engage in chartering activities. For policymakers, especially in locations which have been traditionally considered shipping hubs (Greece, Cyprus, Singapore, Shanghai, etc.), adverse changes in shipping companies' cash flows can potentially mean reductions in output as well as job losses, which could hurt the local economy, and thus they may need to use targeted measures to account for that.

The remainder of this paper is organized as follows: Section 2 provides a critical review of the literature on the issue; Section 3 described the methodology and data used; Section 4 discusses the empirical results obtained, and Section 5 concludes on the findings.

2. Review of the related literature

In December 2019, an unknown virus, later named “Covid-19” erupted in Wuhan district of China, in the city of Hubei (Sohrabi et al., 2020). Its fatality rate accounted for 2.5% of the cases (Xu et al., 2020), a percentage that is equivalent to previous pandemics (Grant and Giovannucci, 2009). While this research is written, researches have not concluded on the origin of the virus, however, the most prominent theories are that it came from a human interaction either with bats (Rothan and Byrareddy, 2020) or with pangolins (Zhang et al., 2020).

Despite its origin though, the latter virus has erupted faster when compared to previous diseases mainly because of the high transportation connectivity of today's world (Liu et al., 2020) and it has affected most countries of the world. The response to the latter threat by mostly all the national governments was a lockdown of all the citizens and businesses so as social distancing to act as a diminisher of the out-break (Lau et al., 2020). Thus, the world economy has been hit and a new economic crisis erupted. Researches show that coronavirus has affected both the financial markets (Ramelli and Wagner, 2020) as well as the national economies (Atkeson, 2020). Consequently, world trade has been hit as well.

While the shipping markets were still recovering from the new desulphurization legislation (Zis and Cullinane, 2020), the new virus has hit the markets hard.1 The freight rates have dropped by 73% for the dry bulk segment, by 36% for the dirty tankers segment and by 30% for the clean tanker segment, as it can be observed from Fig. 1

Fig. 1.

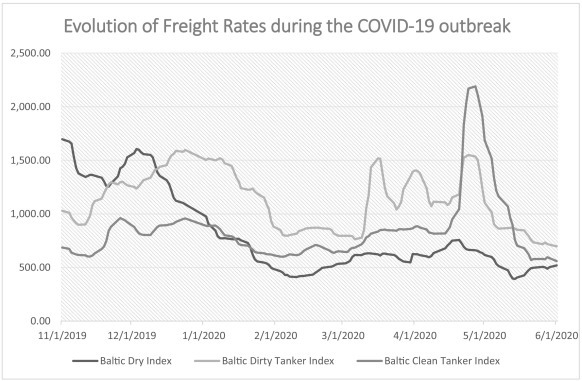
Evolution of Freight Rates during the COVID-19 outbreak.

Data from Clarksons Shipping Intelligence.

The latter changes affected negatively the cash flow of the shipping companies and given the strong substitution effect that exists between the different shipping segments (Kavussanos and Visvikis, 2016) as well as between the different vessel sizes (Tsouknidis, 2016), left both ship owners and the financiers exposed.

Nevertheless, despite the fact that an exogenous event can have such a strong influence on shipping companies cash flows, literature has not focused extensively on event studies for the industry. The latter method while it is heavily used in the finance, economics, and management literature, it has not been explored adequately in the shipping literature. The researches that have used event studies in the industry are mainly driven from the equivalent alike research of the finance literature that looks into the cumulative abnormal return of a company's stock, when an endogenous effect takes place (see Kothari and Warner, 2007 for a in-depth description of the method). Such a research is the seminal work conducted by Panayides and Gong (2002) were they have shown that mergers and acquisitions have a positive impact for the liner shipping companies. In a similar manner, Samitas and Kenourgios (2007) and Syriopoulos and Theotokas (2007) show that the results are also consistent for listed companies that operate in the dry bulk and the tanker segments. Alexandrou et al. (2014) on a more extended research conclude on the positive impact of mergers and acquisitions. In a different perspective, Marín and Sicotte (2003) has shown that some oligopolistic practices that have been apparent in the shipping industry in the 50's and the 60's were having a positive effect on the stocks of the companies.

On a macro-level, research is more extensive. Grammenos and Arkoulis (2002) have shown that oil prices, laid up tonnage and exchange rates affect the shipping industry. Likewise, Papapostolou et al., 2014, Papapostolou et al., 2016 show that industrial production and cumulative crisis periods in Asia and in the G7 countries are acting as indicators of the international demand for shipping services. Finally, oil prices have extensively being linked with the shipping markets as they have a lead-lag relationship with the freight rates (Angelopoulos et al., 2020) and thus they can provide better forecasts for the tanker and the dry bulk market (Gavriilidis et al., 2018; Michail, 2020).

However, while event studies and macroeconomic research has been conducted in the literature, there has not been an attempt yet to examine how exogenous macroeconomic events are affecting the shipping markets. Thus, the current paper comes to fill in this gap by exploring how a pandemic affects freight rates for the ocean-going vessels.

3. Methodology and dataset

To examine the impact of the coronavirus on freight rates, we employ a regression model with GARCH errors, as first presented by Bollerslev (1986). Formally, the GARCH (p,q) model can be formulated through a mean equation:

$${\mathit{Freight}}_t=c+{\mathit{WCalls}}_t+{\mathit{CCalls}}_t+{\mathit{Coronavirus}}_{t-1}+{\mathit{Oil}}_t+{\mathit{Markets}}_t+{\mathit{VIX}}_t+{\epsilon }_t$$ (1)

where Freight _t denotes credit standards, Wcalls _t are the world port calls, CCalls _t are the port calls in China, Coronavirus _t is a variable measuring coronavirus cases, Oil _t refers to the price of Brent oil, and Markets _t refers to a set of stock market variables (notably the S&P500 to capture the global macro impact and the Shanghai Composite Index to capture the Chinese impact), which would capture the change in the macroeconomic outlook. Similarly, the VIX _t index would capture any changes in the economy-wide (and worldwide) risk sentiment. The benefit of using the above-mentioned variables is that it allows us to use a higher frequency, given that they are all available on a daily basis. Furthermore, as the variables are in a daily frequency and there has undoubtedly been some noise embedded in them, the error term, ε _t, is allowed to evolve according to the following process in order to obtain better estimates (Hamilton, 2008; Michail, 2019):

$${\epsilon }_t\mid {\Omega }_t~N\left(0,h_t\right)$$ (2)

$$h_t={\beta }_0+\sum _{k=1}^q{\beta }_k{\epsilon }_{t-k}^2+\sum _{j=1}^p{\gamma }_j{h}_{t-j}$$ (3)

In Eq. (3), ε _t−k ² represents past squared values of the errors which can be interpreted as the feedthrough of shocks to the variance and h _t−j represents past values of the error variance (interpreted as the persistence of shocks to the error variance).2 p and q are the orders of ARCH and GARCH terms respectively. As in other studies in the literature, we limit the scope of the estimation to the GARCH (1,1) which has been shown to perform well in previous applications (see Andersen and Bollerslev, 1998; Javaheri et al., 2004; Hansen and Lunde, 2005; Gazola et al., 2008; Gazola et al., 2008; Michail, 2019). In addition to the fact that this has been the prevalent workhorse of the literature, the GARCH (1,1) is also the best fit model for the BDTI and the BCT case. For the BDI, the ARCH (1) model has been found to be the best fit and we have thus proceeded with that specification.

The use of a daily frequency has the important benefit of allowing us to utilize all the available data until very recently, without having to wait for GDP data to be released. Our expectations are that port calls should in general have a positive relationship with freight rates, given that they are a very good proxy for demand; the higher the number of vessels entering a port, the larger the demand for goods. On the other hand, the stock market impact is less clear as we expect it to be either positive or zero, given the fact that changes in the stock market which are unrelated to the macro environment but due to company earnings announcements should not affect freight rates.

A similar case can be made for Brent oil, given that higher oil prices should mean higher freight rates, but, longer-term contracts regarding fuels and lubricants could prevent the freight rate being affected in the short run. Finally, we expect the coronavirus variable to have either a negative or a zero impact on the freight rates. This is because, as the equation is specified, the number of cases can only be interpreted as an additional impact to the deterioration in the overall business environment. In other words, in this specification, the variable would capture something like a “sentiment effect” which would measure the additional reaction to the virus. It should be noted here that we employ the lag of the change in coronavirus cases, given that these values are usually reported for the previous day.

While a regression with GARCH(1,1) errors can provide an initial overview of the impact of the coronavirus on freight rates, it is limiting to the inferences it can provide. In particular, it does not allow us to capture any second round effects, and, even more importantly it does not allow for the coronavirus variable to be the first that is being shocked in a system of equations containing the above variables. In particular, the impact from the coronavirus is limited to the direct effect the variable can have on freight rates, and does not capture the full, systemic effects that a coronavirus can have on the other variables. To this end, we also employ a Vector AutoRegressive (VAR) specification, as first introduced by Sims (1980).

The benefit of the VAR is that it allows us to capture the full extent of the coronavirus impact and not just the additional impact which is captured in a regression estimate. In the coronavirus case, the impact from the lockdown and containment measures hits consumer activity which then has an impact on industrial activity. A reduction in industrial activity has an effect on the amount of goods traded and hence transported, lowering the derived demand for shipping services. As such, with demand declining, freight rates drop. This impact can be quantified in our estimates, with the stock market acting as a proxy for industrial and consumer activity, given that it is quick to capture changes in corporate profits and future potential. Then, this effect is passed on to oil prices and then to freight rates. The VAR model assists in capturing the effects of this ripple process as it allows for a shock in one variable to be passed on to the system of variables and thus allows us to observe the stream of changes.

Econometrically, it should be mentioned that there is no point in employing a cointegration setup like Johansen and Juselius (1990), given the fact that the coronavirus variable has a limited lifetime and is also trend-stationary. Thus, we proceed with the estimation of a VAR in growth rates. In particular, the setup employed can be expressed such that:

$$Y_t=c+\sum _{j=1}^J{\mathit{A}Y}_{t-j}+{\epsilon }_t$$ (4)

where Y _t is a matrix of all the variables employed in the estimation, as expressed in Eq. (1), and c is a vector of constants. The benefit of this specification is that it allows for any lagged effects to enter the equation and provides a better interpretation of the shocks as they are forced to be exogenous to the system of equations. This allows us to better capture the question at hand, namely, what is the response of freight rates and demand for shipping (port calls) from a shock to coronavirus cases.

To estimate the model, data from Clarksons Research Intelligence database have been used for freight rates, and notably for the Baltic Clean Tanker Index (BCT), the Baltic Dry Index (BDI), and the Baltic Dirty Tanker Index (BDTI).3 The same source was used for port calls, while stock market data and data for the Brent oil prices were obtained from the Federal Reserve of St. Louis Database (FRED). The number of coronavirus cases was obtained from the ourworldindata.com website, in association with World Health Organization data (www.who.int). The data range from the January 3, 2019 to June 1, 2020, on a daily basis. The data range is limited by the availability of the port calls data, while the coronavirus variable is denoted at zero prior to 2020. More details on the data sources can be found in Table 1 .

Table 1.

Variables description.

Variable	Description	Source	Units of Measurement
BCT	Baltic Clean Tanker Index	Clarksons Shipping Intelligence Network	Index
BDI	Baltic Dry Index	Clarksons Shipping Intelligence Network	Index
BDTI	Baltic Dirty Tanker Index	Clarksons Shipping Intelligence Network	Index
Global Calls	Global Port Calls - Total, 7-day average	Clarksons Shipping Intelligence Network	Number of Calls
China Calls	China Port Calls - Total, 3-day average	Clarksons Shipping Intelligence Network	Number of Calls
Coronavirus	Total Confirmed Cases - World	ourworldindata.org	Number of People
Shanghai	Shanghai Composite Index	Federal Reserve Bank of St. Louis	Index
SP500	Standard and Poor's 500 Index	Federal Reserve Bank of St. Louis	Index
Brent	Brent Oil Price	Federal Reserve Bank of St. Louis	Dollars
VIX	Option-Implied Volatility Index	Federal Reserve Bank of St. Louis	Level

Before we move on to the estimation, Table 2 offers the descriptive statistics of the variables we are employing. In particular, it can be seen that the BCT and the BDTI had positive average growth in the last year, while the BDI had recorded negative growth. Global calls also registered a small positive growth rate, at 0.02%, while the market indices were also positive. The largest positive value was recorded in the coronavirus dummy, which grew on average 2.37% for each day in the three months of its existence.

Table 2.

Descriptive statistics.

	BCT	BDI	BDTI	Global Calls	China Calls	Coronavirus	Shanghai	SP500	VIX	Brent
Mean	0.12	−0.23	0.13	0.02	0.12	2.37	0.05	0.02	0.66	−0.24
Median	−0.32	−0.15	−0.16	0.02	0.11	0.00	0.00	0.09	−0.46	0.09
Maximum	22.92	10.73	24.65	4.23	14.51	64.02	5.60	9.38	46.5	11.71
Minimum	−7.37	−11.51	−10.71	−12.05	−12.97	0.00	−7.72	−11.98	−23.37	−22.52
Std. Dev.	2.84	2.95	3.62	1.08	3.89	8.44	1.29	1.74	9.46	3.01
Skewness	2.84	−0.25	2.73	−4.18	−0.10	5.07	−0.70	−0.82	1.71	−1.95
Kurtosis	21.04	4.64	20.20	53.48	4.80	31.80	9.55	19.39	8.37	16.02
Jarque-Bera	46.2 (0.00)	37.7 (0.00)	42.4 (0.00)	33.8 (0.00)	42.3 (0.00)	19.0 (0.00)	57.8 (0.00)	35.1 (0.00)	52.5 (0.00)	58.7 (0.00)
Observations	351	351	351	351	351	351	351	351	351	351

Notes: See Table 1 for definitions of variables. All data are in log differences. Min and max are the minimum and maximum values of the sample data, respectively. Skewness and kurtosis are the estimated centralized third and fourth moments of the data. J-B is the Jarque and Bera (1980) test for normality; the statistic is χ2 distributed. Numbers in parentheses (.) report p-values.

The virus variable was also the one with the highest standard deviation, at 8.44%, while global calls had understandably the lowest. At is can be seen, the values of the variables fluctuated significantly through the year, ranging from −10 to +10 in the majority of cases, with the virus cases recording an impressive 64% growth at maximum, even though this was associated with the early days when the number of cases was still small. As also expected, the hypothesis of normality is rejected according to the Jarque and Bera (1980). Finally, the common sample has 310 observations which have been used to estimate the impact on the basis of the above two methodologies. The results from the estimations can be found the section which follows.

4. Estimating the impact of the coronavirus

Starting from the regression with GARCH (1,1) errors, as described in Eqs. (1), (2), Table 3 offers the results for the BDI index. Firstly, it should be noted that the regression used ARCH errors, given that the GARCH term proved to be statistically insignificant, suggesting that past values of the variance do not have an impact in current variance. In other words, it appears that long-term variance shocks are not as important as short-term shocks (Alexander, 2008).4

Table 3.

BDI results.^a

BDI	(1)	(2)	(4)	(4)	(5)
Mean equation
BDI [−1]	0.679*** (0.06)	0.663*** (0.05)	0.660** (0.05)	0.660** (0.04)	0.660** (0.04)
Coronavirus [−1]	−0.03** (0.01)	−0.03** (0.01)	−0.03** (0.01)	−0.03** (0.01)	−0.03** (0.01)
Global Calls	0.452*** (0.06)	0.450*** (0.06)	0.445*** (0.05)	0.445*** (0.05)	0.442*** (0.05)
China Calls	0.000 (0.03)
Brent [−1]	−0.161 (0.05)
S&P 500	−0.037 (0.07)	−0.037 (0.07)
S&P 500 [−1]			0.003 (0.07)
Shanghai	0.008 (0.07)	0.008 (0.07)
VIX [−1]					0.004 (0.01)
Constant	−0.00 (0.00)	−0.00 (0.00)	−0.00 (0.00)	−0.00 (0.00)	−0.00 (0.00)
ARCH equation
Constant	2.903*** (0.28)	2.919*** (0.28)	2.92*** (0.28)	2.91*** (0.27)	2.903*** (0.27)
ARCH	0.232*** (0.10)	0.234*** (0.09)	0.234*** (0.09)	0.234*** (0.09)	0.240*** (0.09)
R-squared	0.57	0.57	0.57	0.57	0.57
Durbin-Watson	1.75	1.75	1.74	1.75	1.74
Observations	350	350	350	350	350

Notes: Figures in parentheses (.) indicate t-statistics. ***, ** and * indicate significance at the 1%, 5% and 10% significance levels, respectively. Figures in brackets [.] indicate lagged values, where [−n] is the nth day before the day examined.

^aThe GARCH term was found to be statistically insignificant.

As the results show, the dry bulk index has a strong relationship with global calls, standing at around 0.45 throughout specifications (1) to (5). The BDI is also dependent on its previous values, but not to a very large extent, at 0.66. Other lags of the BDI were not found to be statistically significant. Interestingly, the coronavirus impact is statistically significant, with a 1% change in virus cases implying an additional impact of −0.03% on the BDI. It should be again underlined that due to the nature of this regression, the coronavirus impact is interpreted as additional to the drop in global port calls. Finally, it should be noted that the remaining variables, including the stock market indices and Brent oil, are not statistically significant.

In the BCT case (Table 4 ), clean tanker rate changes are less affected by global calls, at 0.28, but similarly have an autoregressive relationship with their previous day's values, at 0.63. In this case, the coronavirus variable does not have any important impact on the freight rates, with the impact remaining insignificant across all specifications. Interestingly, the Brent oil price is also insignificant for the BCT case. In the BCT case, it appears that the GARCH term is larger than the ARCH term, suggesting that shocks are kept in the variance for longer.

Table 4.

BCT results.

BCT	(1)	(2)	(3)	(4)	(5)
Mean equation
BCT [−1]	0.583*** (0.04)	0.589*** (0.04)	0.589*** (0.04)	0.589*** (0.04)	0.582*** (0.05)
Coronavirus	−0.002 (0.02)	−0.002 (0.02)	−0.002 (0.02)	−0.002 (0.02)	−0.001 (0.02)
Global Calls	0.300*** (0.04)	0.300*** (0.04)	0.295*** (0.04)	0.295*** (0.04)	0.294*** (0.04)
China Calls	0.008 (0.02)
Brent [−1]	−0.019 (0.03)
S&P 500	−0.030 (0.06)	−0.020 (0.05)
S&P 500 [−1]			−0.00 (0.05)
Shanghai	−0.063 (0.059)	−0.060 (0.063)
VIX [−1]					−0.003 (0.01)
Constant	−0.001 (0.001)	−0.001 (0.001)	−0.001 (0.001)	−0.001 (0.001)	−0.09 (0.10)
GARCH equation
Constant	0.000*** (0.00)	0.000*** (0.00)	0.000*** (0.00)	0.000*** (0.00)	0.357*** (0.07)
ARCH	0.305*** (0.07)	0.300*** (0.07)	0.301*** (0.07)	0.301*** (0.07)	0.301*** (0.07)
GARCH	0.615*** (0.06)	0.624*** (0.06)	0.617*** (0.06)	0.617*** (0.06)	0.617*** (0.06)
R-squared	0.44	0.57	0.57	0.58	0.58
Durbin-Watson	1.69	1.76	1.76	1.77	1.78
Observations	350	350	350	350	350

See notes in Table 3.

Figures in parentheses (.) indicate t-statistics. ***, ** and * indicate significance at the 1%, 5% and 10% significance levels, respectively.

For Dirty Tankers, Table 5 provides perhaps the most intriguing results. In this case, the coronavirus variable has the strongest negative impact, perhaps also due to the fact that port calls do not have an important bearing on the freight rates. This should be inherent to the nature of this category, given that, as our results show, macro variables, namely the stock market, risk sentiment as captured from the VIX index, and oil prices, have a statistically significant impact on the prices. Interestingly, Brent oil has the opposite relationship to the BDTI than the once anticipated: the results in Table 5 suggest that Brent oil is negatively related to the BDTI.

Table 5.

BDTI results.

BDTI	(1)	(2)	(3)	(4)	(5)
Mean equation
BDTI [−1]	0.635*** (0.04)	0.693*** (0.04)	0.689*** (0.04)	0.692*** (0.04)	0.693*** (0.04)
Coronavirus	0.006 (0.01)	−0.041*** (0.01)	−0.043*** (0.01)	−0.043*** (0.01)	−0.041*** (0.01)
Global Calls	0.076 (0.06)	0.078 (0.06)
China Calls	0.027 (0.03)
Brent [−1]	−0.042* (0.02)	−0.042** (0.025)	−0.081*** (0.02)	−0.080*** (0.02)	−0.076*** (0.02)
S&P 500	−0.128*** (0.05)	−0.135*** (0.05)
S&P 500 [−1]			0.162*** (0.04)	0.16*** (0.10)	0.41*** (0.10)
Shanghai	0.084** (0.04)	0.076* (0.04)	0.041 (0.04)
VIX [−1]					0.036*** (0.01)
Constant	−0.047 (0.08)	−0.011 (0.08)	−0.017 (0.07)	−0.018 (0.07)	−0.021 (0.08)
GARCH equation
Constant	0.220*** (0.06)	0.207*** (0.06)	0.202*** (0.07)	0.204*** (0.06)	0.204*** (0.07)
ARCH	0.662*** (0.09)	0.650*** (0.08)	0.720*** (0.09)	0.684*** (0.09)	0.754*** (0.11)
GARCH	0.487*** (0.06)	0.500*** (0.05)	0.467*** (0.05)	0.482*** (0.05)	0.421*** (0.06)
R-squared	0.40	0.41	0.42	0.43	0.43
Durbin-Watson	2.03	2.16	2.12	2.13	2.18
Observations	350	350	350	350	350

See notes in Table 3.

Figures in parentheses (.) indicate t-statistics. ***, ** and * indicate significance at the 1%, 5% and 10% significance levels, respectively.

While the relationship between the BDTI and oil may seem to be counterintuitive at first, there are a few reasons with regards to how this is justified. To begin with, lower oil prices can mean higher freight rates as tankers can serve as oil storage for some amount of time, as was the case in the 1990s oil crisis (Stopford, 2013). This has also been the case during the coronavirus crisis, where reports suggest that floating storage volumes have increased by 37% in just two months during the pandemic period.5 Additionally, current research has provided evidence of a floating storage arbitrage opportunity when the future oil curve is in contango (Regli and Adland, 2019). Furthermore, it should also be mentioned that Brent oil is transported with dirty tankers. This means that oil here is not only an operating expense but also the commodity that drives the demand for the transportation services. Thus, as per the law of demand in classical economics, the higher the price of oil the lower the demand will be.

Perhaps even more intriguing is the fact that the lag of the stock market prices has a positive sign, while its contemporaneous value has a negative sign. We attribute this to a mean-reverting behavior, one that still emphasizes the importance of the macroeconomic environment for the BDTI. Our results, are in accordance with Erdogan et al. (2013) and Gong et al. (2020) who show that the relationship between stock markets and freight markets is inter-changeable and also is stronger during the busts of the cycles. Finally, in this case the ARCH term is higher than the GARCH term, and thus past errors have a stronger impact on the variance and that these are not very persistent across time.

As discussed in the previous section, while the GARCH regression estimates provide an overview of the relationships between the variables, they are not showing the full picture which would allow us to examine not partial correlations but shocks to whole system. To alleviate this issue, we proceed with estimating a VAR model, in which all the variables are endogenous so as to observe the impact from an exogenous shock to the system. Fig. 2 provides the results of this exercise, using impulse responses. It should be remembered that impulse responses provide the response of a variable following an exogenous one standard deviation (from the errors distribution) shock in the system, after the shock has been fed through to the whole system. In other words, for a shock in Brent oil, we would observe the change to global calls, which would then also impact e.g. the BCT index, which would again impact oil prices and so on. As such, it allows us to obtain a more holistic view of the impact from a shock.6

Fig. 2.

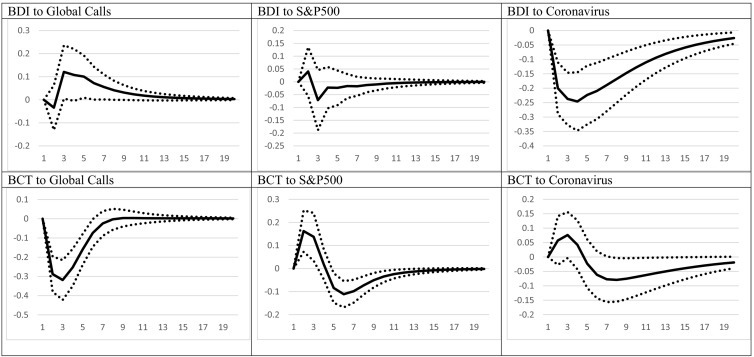
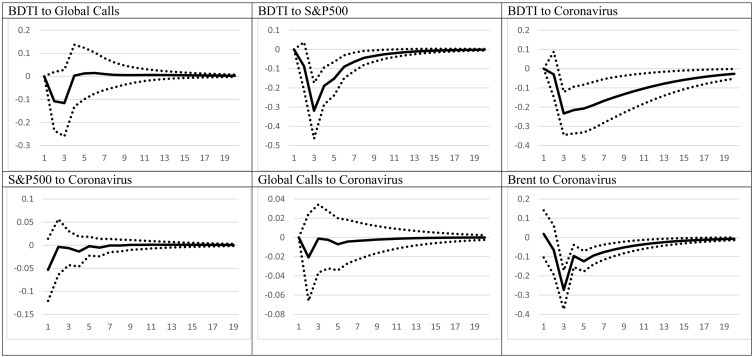
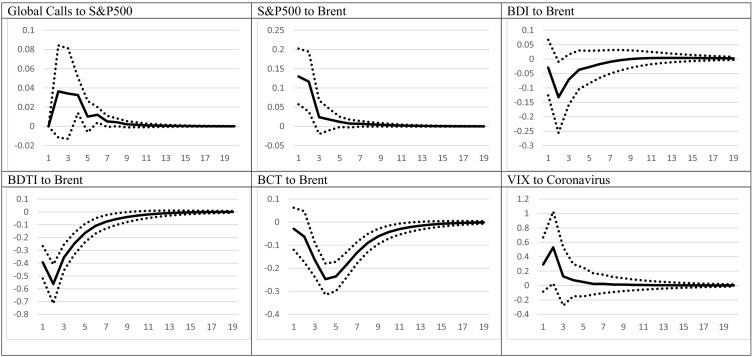
Impulse responses.

Notes: Fig. 2 reports the impulse responses from the VAR model, as specified in Section 3. BDI to Global Calls refers to the response of the BDI to a shock in Global Calls. Vertical axis reports the magnitude of the variable response in percentage points. For example, a 1% increase in global calls would case a maximum of 0.1% increase in the BDI. Dotted lines are the 68% confidence interval. Horizontal axis refers to the periods (days) ahead after the shock took place. For example, the BCT response to a shock in Global Calls is zero after 10 days.

As Fig. 2 suggests, the response of BDI to a shock in the coronavirus growth rate is strong, as it decreases by almost 0.25%, while the response is significant in all periods of time. The cumulative impact from a shock which increases coronavirus cases by about 5%, amounts to a drop of more than 1% within 6 days and to more than 2.30% within 20 days. Naturally, the impact from consecutive shocks in the system, i.e. when coronavirus cases increase for 2 or more consecutive days, would be even larger. For comparison purposes, the BDI is “only” affected by a maximum of 0.12% in the case of a rise in global port calls, while the S&P500 does not have a significant impact.

The BCT, on the other hand, registers a negative response when global port calls are increasing. On the other hand, an improvement in the global macroeconomic environment causes an increase in the BCT, even though this is later reversed as the movement moves to negative, showing a mean-reverting behavior. With regards to the coronavirus, the impact is delayed, as it takes around 6 days for the freight rate to respond to an increase in virus cases. As a result, the cumulated impact is also much smaller, reaching −0.50% in about 16 days.

For BDTI, the responses are quite different with regards to the macro variable and port calls. In particular, port calls do not appear to have an impact on the variable, as the response is insignificant throughout time. On the other hand, an increase in the S&P500 index causes a negative response from the BDTI, in accordance with the bi-directional lead-lag relationship as described by Gong et al. (2020). Most importantly, BDTI strong reacts to a shock in coronavirus cases, with the response reaching −0.23% in period 3, and accumulating to −1% after 7 days. By the end of the 20-day horizon of the impulse responses, the accumulated response stands at −2%. The reason for the latter is, as also elaborated upon previously, that Brent oil is not only acting as an operating expense fort this type of vessels but also as the commodity that they transport.

To examine how the pass-through of the virus takes place, the fourth row of Fig. 2 presents the responses of the variables to the coronavirus. In particular, a rise in coronavirus cases would mean a negative reaction from the stock market, even though this is not statistically significant, perhaps due to the increase in volatility during the crisis period. Similarly, global calls remain relatively unmoved from the coronavirus impact. On the other hand, Brent oil drops significantly after an increase in coronavirus cases, underlying one of the most important channels through which the increase in coronavirus cases can affect freight rates.

Moving to the fifth and sixth row of Fig. 2, we can see that global calls appear to have a positive relationship with the S&P, albeit not always statistically significant. Interestingly, in our sample, the S&P and Brent oil have a positive and significant relationship, perhaps due to the large presence of oil companies in the index. The remaining responses show that, as expected, the BDI does not record a statistically significant relationship with Brent oil, while BDTI responds negatively. BCT on the other hand registers a mildly negative response. Reasons for these reactions have been elaborated previously in the text. Finally, the coronavirus itself does not appear to have had any impact on risk, and as such suggesting that the impact could be most likely indirect, i.e. through lockdown and containment measures.

It should be noted here that the results from the VAR complement and support the GARCH results of Table 2, Table 3, Table 4, while, in addition, they present a fuller background story. The increase in coronavirus cases are usually followed by lockdown periods, which justifies the strong impact of the coronavirus on Brent oil prices as the VAR results imply. Still, it should be mentioned here that given that we employ the global coronavirus cases, lockdown periods are not the sole justification for the decline in oil prices, but most likely the coordinated efforts of people, firms, and governments across the world to minimize the movement of people. Thus, even though the coronavirus does not have a direct impact on the stock market as firms continue to operate via work, it does have an indirect effect via the decrease in Brent prices which would negatively affect the stock price, given the positive relationship between the two, as the results indicate.

Concerning the impact on freight rates, the rise in coronavirus cases has a strong effect on them, via the decline in the amount of goods transported and is more evident and direct in the BDI case. On the other hand, for BCT, the direct impact is much milder, while BCT rates are expected to decline due to the drop in the stock market, as the BCT is positively related to the S&P500. Finally, for the BDTI, the impact comes via three channels, namely the coronavirus itself, the stock markets, and the price of oil.

Overall, the results of this section show that there exists a strong relationship between freight rates and the coronavirus cases. In addition, second round effects, mostly via the decline in oil prices and, in some cases, third round effects via the impact from the stock market, have further affected freight markets in pushed them in a downwards spiral, from which they can only escape once cases start to decline and oil prices pick up again.

5. Conclusion

In this study, we have tried to capture how the shipping markets are reacting to an exogenous shock by employing GARCH regressions and impulse responses from a VAR model. By employing data from the on-going coronavirus disease, Covid-19, we have examined the reaction of the dry bulk, the clean tanker and the dirty tanker markets. The main findings are as follows.

First, the pandemic outbreak has negatively affected the dry bulk and the dirty tanker segments by more than what the decline in port calls would imply, while it has not affected the clean tanker segment. More precisely, an increase of 1% of the cases of the coronavirus reported globally, would decrease the Baltic Dry Index by 0.03% and the Baltic Dirty Tanker Index by 0.046%. While, the latter decreases do not seem large, one should consider both the daily nature of the data as well as the cumulative effect during the period of the pandemic.

Second, by employing a proxy variable for the demand of transportation services, namely the daily number of calls of vessels in ports, we show that both the Baltic Dry Index and the Clean Tanker Index are highly affected by the demand side of the economy, while vessels which transport crude oil do not register such a relationship. This supports the importance of using tankers as storage capacity during periods of oil market distress and the oil future curve is in contango (Regli and Adland, 2019): while commodities transported by dry bulk vessels and clean tankers cannot be easily stored given both their nature and the need for specific facilities, crude oil can be stored much more easily given that it can simply remain in the vessel.

Third, in accordance with previous researches (Erdogan et al., 2013; Gong et al., 2020), we confirm the bi-directional lead-lag relationship between stock markets and freight markets as contemporaneously S&P500 has a negative relationship with the Baltic Dirty Tanker Index while the 1 day lag relationship has a positive sign.

In general, the results from both the GARCH (1,1) and the VAR exercises show that there exists a strong relationship between freight rates and the coronavirus cases. Furthermore, second-round effects, mostly via the decline in oil prices and, in some cases, third round effects via the impact from the stock market, also exist. Via a combination of these effects, freight markets have been pushed in a downwards spiral, from which they can only escape once cases start to decline and oil prices pick up again.

Our results, which are the first to quantify the aforementioned relationships in the literature, should be of great assistance to ship-owners, charterers, shipping financiers, investors, and policy makers, as they shed light on how shipping markets react on crisis periods as well as the pass-through channels through which it is affected. Shipowners, charterers, operators could try to reduce losses and limit volatility in freight rates by entering into paper markets (FFAs, Futures) and engage in chartering activities. Furthermore, as the shipping industry has already been notoriously volatile due to its relationship with world trade and output, we expect that this will further add to this volatile nature, and the impact will highly affect shipping companies' cash flows, leaving both ship-owners and the industry's stakeholders exposed to potential losses. For policymakers, especially in locations which have been traditionally been considered shipping hubs (Greece, Cyprus, Singapore, Shanghai, etc.), adverse changes in shipping companies' cash flows can potentially mean reductions in output as well as job losses, which could hurt the local economy, and thus they may need to use targeted measures to account for that.

Naturally, and as a caveat to the current results, it should be mentioned that the current research has been written during the Covid-19 pandemic period and thus the final results of this situation cannot be fully fathomed. More research is needed in the future so as to fully capture the results of such an extraordinary event to its full extent. Future research can extend our current understanding of such exogenous shocks by examining the specification of vessels that are mainly affected from such events, taking into consideration factors such as size, age, and the different types of goods transported.

Credit

Kostis D. Melas: Conceptualization; Investigation; Methodology; Writing - original draft.

Nektarios A. Michail: Methodology; Resources; Software; Investigation; Writing - original draft.