Skip to main content
NCBI home page
Elsevier - PMC COVID-19 Collection logoLink to Elsevier - PMC COVID-19 Collection
. 2020 Jul 25;38:101701. doi: 10.1016/j.frl.2020.101701

Deaths, panic, lockdowns and US equity markets: The case of COVID-19 pandemic

Ahmed S Baig a, Hassan Anjum Butt b,⁎, Omair Haroon a, Syed Aun R Rizvi a
PMCID: PMC7381907  PMID: 32837381

Abstract

This study investigates the impact of COVID-19 pandemic on the microstructure of US equity markets. In particular, we explain the liquidity and volatility dynamics via indexes that capture multiple dimensions of the pandemic. Our results suggest that increases in confirmed cases and deaths due to coronavirus are associated with a significant increase in market illiquidity and volatility. Similarly, declining sentiment and the implementations of restrictions and lockdowns contribute to the deterioration of liquidity and stability of markets.

Keywords: COVID-19, Liquidity, Volatility, Pandemic, Lockdowns, Sentiment

1. Introduction

The recent outbreak of coronavirus (COVID-19), originating in December 2019 from Wuhan (China), has infected over ten million people and has resulted in more than 580,000 deaths worldwide. Early estimates have put the global economic costs of the pandemic at around $8.8 trillion.1 Given its immense human and economic impacts, the COVID-19 outbreak has spurred a deluge of news and opinions. It has also triggered government policy responses such as mandatory closures and lockdowns. Major events like the pandemic often overshadow all other events in the media (Blendon et al., 2004; Mairal, 2011; Young et al., 2013). A consistent influx of pandemic-related news can cause anxiety among investors, influencing their investment decisions (Ederington and Lee, 1996; Klibanoff et al., 1998; Tetlock, 2007). Such sentiment related influences have a significant impact on trading in financial markets (Tetlock, 2007; Kaplanski and Levy, 2010; Su et al., 2017). Similarly, restrictive government policies can cause uncertainty which may stimulate portfolio reconstructions and abnormal trading activity (Zaremba et al., 2020) and destabilize the markets (Blau et al., 2014).

Liquidity and stability are important features of financial markets.2 These factors tend to deteriorate under adverse market conditions such as crises and pandemics. Liquidity is being cited as a major concern during the COVID-19 pandemic (Adrian and Natalucci, 2020; Wilkes, 2020). Economic theory suggests that bid-ask spreads tend to increase in the presence of risk and uncertainty (Glosten and Milgrom, 1985; Hasbrouck, 1988), which in turn leads to the deterioration of liquidity in the markets. Liquidity in financial markets is affected by investors’ ability to process information (Boubaker et al., 2019). Liquidity also becomes a crucial policy area during financial crises (Brunnermeier, 2009). Similarly, uncertainty has been known to adversely impact the volatility of stock markets (Veronesi, 1999; Pastor and Veronesi, 2012). Recent studies find increased systematic risk and volatility in response to COVID-19 (Zhang et al., 2020; Albulescu, 2020; Zaremba et al., 2020). However, none of these studies analyze stock-level liquidity and volatility. We focus on three dimensions of the coronavirus pandemic and study their impact on stock-level liquidity and volatility in US equity markets. These dimensions are: 1) human costs i.e. cases and deaths associated with the virus, 2) general sentiment and the panic associated with the pandemic, 3) restrictive measures implemented by governments in the form of social distancing and lockdowns.

We find that reported number of confirmed coronavirus cases and deaths, general negative sentiment generated by news, reduced mobility and restrictive government regulations have an adverse impact on the liquidity and volatility of the stock market at the individual stock level. Our study contributes to the literature along the following dimensions. First, it adds to the evolving literature on market response to pandemics (Akhtaruzzaman et al., 2020; Al-Awadhi et al., 2020; Albulescu, 2020; Zhang et al., 2020; Haroon and Rizvi, 2020a, 2020b). Second, we add to the literature on the association of media/news originated sentiment with stock market liquidity and volatility (Barberis et al., 1998; Tetlock, 2007; Uhl et al., 2015). And finally, we extend the understanding of the impact of restrictive government policies on the stability and efficiency of financial markets (Blau et al., 2014; Blau, 2017; Baig et al., 2019, 2020).

The rest of this study is outlined as follows. Section 2 discusses data and methodology; Section 3 presents empirical results and Section 4 concludes.

2. Data and methodology

We obtain data from five different sources. Stock market information for the S&P 500 constituent stocks is obtained from Thomson Reuters Datastream. Our final data is a firm-day panel that consists of all the constituent stocks of the S&P 500 index for the period January 13th, 2020 to April 17th, 2020. US mobility trends report consisting of indexes on driving, walking, and transit is obtained from Apple,3 we sum all these three individual indexes and utilize the aggregate index that we denote as USDWT. Stringency index is obtained from Oxford COVID-19 Government Response Tracker (OxCGRT) ,4 we denote it in our study as STRINGENCY. We also obtain data on confirmed CASES and DEATHS in the U.S. from OxCGRT website and match it with John's Hopkins database. Coronavirus worldwide sentiment index is obtained from RavenPack,5 we denote it as GSENT in our study. Google trends data based on the search for the word “coronavirus deaths” in the US is obtained from Google Trends website,6 we denote it as GTREND. We choose to begin our sample on January 13th because our mobility data is available from that date.

From the stock level information, we create various variables following the prior literature (e.g. Blau et al., 2014; Blau, 2018a, 2018b; Baig and Sabah, 2020). PRICE is the closing share price. SIZE is the market capitalization computed by multiplying closing price with shares outstanding. SPREAD is the bid-ask spread calculated as the difference between ask and bid prices scaled by their midpoint. VOLUME is traded share volume. ILLIQUIDITY is the Amihud (2002) illiquidity measure computed as the absolute returns divided by dollar volume (scaled up by ten million). VOLT is the range-based volatility measure computed following Alizadeh et al. (2002) as the natural log of maximum price minus the natural log of the minimum price. GVOLT is the conditional volatility computed by estimating a GARCH (1,1) model using the first difference of daily returns. S&P represents the daily returns series for the S&P 500 index.

To control for outliers, we trim our stock-level variables at the 1st and 99th percentile, though it does not qualitatively impact our conclusions. For our regressions, we log transform all our five indexes. We add one to the number of cases, the number of deaths, stringency and google trends indexes and then take the natural log to avoid excluding zero values. Our RavenPack sentiment index has a negative value throughout our sample. We take the absolute value of our sentiment series and then take its natural log which makes this variable increasing in negative sentiment. Table 1 provides summary statistics for our sample. These descriptive statistics provide us with a background and basic understanding of our sample and allow for a better interpretation of the significance of empirical results. We find that the average value of USDWT index is 255.6, GSENT is −48.6, GTREND is 36.1, and the STRINGENCY index is 31.9. An average stock in our sample has a PRICE of $111, Market capitalization (SIZE) of about USD 57 billion, VOLUME of about 5.4 million, ILLIQUIDITY of about 0.002, VOLT of about 4.8%, GVOLT of about 0.7%. S&P 500 index has an average return of about −0.2%, the minimum return of about −13% and a maximum return of about 9% during our sample period.

Table 1.

Summary statistics.

Variable Mean Standard deviation Minimum 25th percentile Median 75th percentile Maximum
[1] [2] [3] [4] [5] [6] [7] [8]
CASES 91,948.760 185,749.400 0.000 11.000 74.500 55,231.000 709,735.000
DEATHS 3529.771 8548.607 0.000 0.000 1.000 801.000 37,147.000
USDWT 255.622 89.631 122.710 140.150 298.925 314.330 412.280
GSENT −48.606 14.732 −69.940 −59.150 −52.195 −38.850 −8.040
GTREND 36.086 33.664 0.000 5.000 25.000 72.000 100.000
STRINGENCY 31.904 31.293 0.000 9.520 11.905 76.190 76.190
PRICE 111.045 109.610 8.320 43.360 81.605 141.000 1136.600
SIZE 57.288 107.776 0.902 10.557 23.090 55.206 1041.719
SPREAD 0.0004 0.0005 0.0000 0.0001 0.0003 0.0005 0.0032
VOLUME 5,402,082 7,574,398 255,400 1,401,100 2,777,500 5,994,100 59,600,000
ILLIQUIDITY 0.002 0.002 0.000 0.000 0.001 0.002 0.017
VOLT 0.048 0.037 0.007 0.019 0.037 0.064 0.202
GVOLAT 0.007 0.012 0.000 0.001 0.002 0.007 0.081
S&P −0.002 0.036 −0.128 −0.016 0.000 0.010 0.090
Open in a new tab

This table provides the statistics that summarize our sample. CASES represent the number of people infected with coronavirus. DEATHS represent the number of people who lost their lives due to coronavirus related complications. USDWT is the sum of US driving, walking and transit mobility trends indexes of Apple Inc. STRINGENCY is the stringency index obtained from Oxford COVID-19 Government Response Tracker (OxCGRT). GSENT is the coronavirus worldwide sentiment index of RavenPack. GTREND is the google trends index based on the search for the word “coronavirus deaths” in the US. PRICE is the closing share price. SIZE is the market capitalization computed by multiplying closing price with shares outstanding. SPREAD is the bid-ask spread calculated as the difference between ask and bid prices scaled by their midpoint. VOLUME is share volume. ILLIQUIDITY is the Amihud (2002) illiquidity measure computed as the absolute returns divided by dollar volume (scaled up by ten million). VOLT is the range-based volatility measure computed following Alizadeh et al. (2002) as the natural log of maximum price minus the natural log of minimum price. GVOLT is the conditional volatility computed using the GARCH (1,1) model. S&P represents the daily returns series for the S&P 500 index.

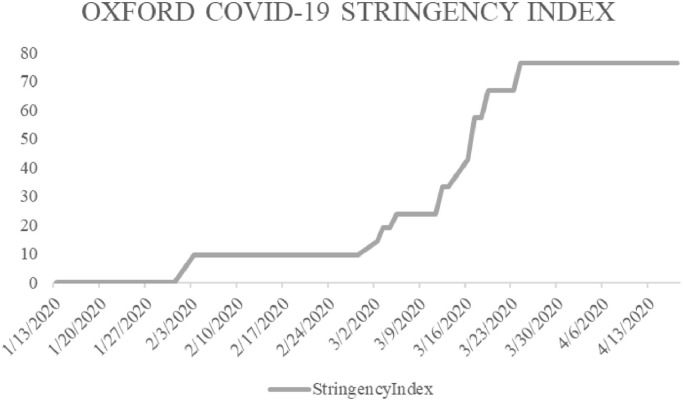
Fig. 1 provides the time series plot of the S&P 500 index closing prices. The index witnessed a steep decline beginning in March 2020 corresponding to the rise in cases and deaths as plotted in Fig. 2 . The S&P index reached its trough on March 23rd followed by a rebound as the government's response started to kick in as evident from the government policy stringency index in Fig. 5. Fig. 3 presents the time series plot of the mobility index. The plot suggests that mobility sharply decreased from mid-March surrounding the spike in cases and deaths. Fig. 4 presents the time series plot of the RavenPack sentiment index. The index has a general negative trend suggesting an overall decline in sentiment. Finally, Fig. 6 reports the time series plot of the google trends index. The index has a sharp increase surrounding the rise in cases and deaths due to coronavirus. The index also has a strong (negative) correlation with the RavenPack sentiment index. Baig et al. (2019) have used google trends indexes as a measure of sentiment. Accordingly, we utilize the “coronavirus deaths” google trends index as an additional measure of (negative) sentiment in the market.

Fig. 1.

Fig. 1

Open in a new tab

Time series plot of S&P 500 Index closing prices.

Fig. 2.

Fig. 2

Open in a new tab

Time series plot of COVID-19 related cases and deaths in the US.

Fig. 5.

Fig. 5

Open in a new tab

Time series plot of Oxford COVID-19 stringency index capturing lockdown related policies in the US.

Fig. 3.

Fig. 3

Open in a new tab

Time series plot of Apple mobility trends on driving, walking and transit in the US.

Fig. 4.

Fig. 4

Open in a new tab

Time series plot of RavenPack COVID-19 related global news sentiment index.

Fig. 6.

Fig. 6

Open in a new tab

Time series plot of google trends index for the search word “Coronavirus Deaths” in the US.

3. Empirical results

In the first set of tests, we examine the relation of various pandemic related indexes with our stock-level liquidity measures. Our analysis is based on regression models used in prior studies (e.g. Blau, 2017, 2018a). We estimate the following OLS regression specification with robust standard errors clustered at the firm-level. The impact of COVID-19 is likely to vary across different industries. Therefore, we include industry fixed effects based on Fama-French 48 industry classifications in all our specifications.7

LN(ILLIQUIDITYMEASURE)i,t=β0+β1LN(PANDEMICINDEX)i,t+β2PRICEi,t+β3SIZEi,t+β4VOLUMEi,t+β5S&Pi,t+β6VOLTi,t+εi,t (1)

Table 2 reports the results from the estimation of Eq. (1). Our dependent variable is the natural log of Amihud (2002) illiquidity (ILLIQUIDITY) in columns [1] to [6] while it is the natural log of bid-ask spreads (SPREAD) in columns [7] to [12]. The log-log model allows for better economic interpretation of the coefficients on the pandemic indexes.8

Table 2.

Illiquidity regressions.

LNILLIQ LNILLIQ LNILLIQ LNILLIQ LNILLIQ LNILLIQ LNSPREAD LNSPREAD LNSPREAD LNSPREAD LNSPREAD LNSPREAD
[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12]
LNCASES 0.041*** 0.038***
(16.957) (16.350)
LNDEATHS 0.045*** 0.040***
(16.789) (15.634)
LNUSDWT −0.222*** −0.420***
(−9.342) (−18.087)
LNGSENT 0.208*** 0.152***
(12.284) (11.856)
LNGTREND 0.163*** 0.110***
(18.241) (13.853)
LNSTRINGENCY 0.110*** 0.095***
(16.960) (15.062)
PRICE −0.004*** −0.004*** −0.004*** −0.004*** −0.004*** −0.004*** −0.002*** −0.002*** −0.002*** −0.002*** −0.002*** −0.002***
(−6.861) (−6.842) (−6.825) (−6.867) (−6.926) (−6.884) (−4.049) (−4.027) (−3.996) (−4.097) (−4.127) (−4.096)
SIZE −0.001** −0.001** −0.001** −0.001** −0.001** −0.001** −0.000 −0.000 −0.000 −0.000 −0.000 −0.000
(−2.476) (−2.475) (−2.453) (−2.430) (−2.470) (−2.459) (−0.086) (−0.079) (−0.110) (−0.025) (−0.067) (−0.065)
VOLUME −0.000*** −0.000*** −0.000*** −0.000*** −0.000*** −0.000*** 0.000 0.000 0.000 0.000 0.000 0.000
(−18.834) (−18.852) (−18.843) (−18.872) (−18.825) (−18.849) (1.245) (1.315) (1.494) (1.228) (1.067) (1.199)
S&P −1.240*** −1.329*** −1.070*** −0.631*** −0.784*** −0.988*** 0.252* 0.187 −0.067 0.838*** 0.733*** 0.515***
(−7.347) (−7.736) (−6.095) (−3.915) (−5.001) (−6.048) (1.715) (1.258) (−0.440) (5.961) (5.203) (3.574)
VOLATILITY 15.756*** 16.436*** 17.419*** 17.541*** 14.162*** 15.807*** 2.874*** 3.538*** 3.241*** 4.739*** 2.542*** 3.107***
(42.107) (46.061) (47.784) (49.364) (33.942) (41.764) (10.527) (13.647) (12.090) (17.475) (8.075) (11.005)
CONSTANT −7.319*** −7.246*** −5.932*** −7.941*** −7.455*** −7.361*** −8.425*** −8.357*** −5.919*** −8.856*** −8.486*** −8.454***
(−100.050) (−100.835) (−43.669) (−80.325) (−99.264) (−99.676) (−152.086) (−154.672) (−46.907) (−117.545) (−148.236) (−150.281)
ROBUST SE YES YES YES YES YES YES YES YES YES YES YES YES
INDUSTRY FE YES YES YES YES YES YES YES YES YES YES YES YES
OBSERVATIONS 29,965 29,965 29,965 29,965 29,965 29,965 29,932 29,932 29,932 29,932 29,932 29,932
R-SQUARED 0.409 0.408 0.400 0.400 0.412 0.407 0.146 0.143 0.148 0.128 0.139 0.140
Open in a new tab

This table provides the results from the estimation of the following OLS regression specification.

LN(ILLIQUIDITYMEASURE)i,t=β0+β1LN(PANDEMICINDEX)i,t+β2PRICEi,t+β3SIZEi,t+β4VOLUMEi,t+β5S&Pi,t+β6VOLTi,t+εi,t

Dependent variable LN(ILLIQUIDITY MEASURE) is the natural log of Amihud (2002) illiquidity in columns [1] to [6] while it is the natural log of bid-ask spreads in columns [7] to [12]. The independent variable LN(PANDEMIC INDEX) represents the is natural log of the COVID-19 pandemic related index. These indexes include the following. LNCASES represents the natural log of coronavirus cases. LNDEATHS represent the natural log of coronavirus related deaths. LNUSDWT is the natural log of sum of US driving, walking and transit mobility trends indexes of Apple Inc. LNSTRINGENCY is the natural log of the stringency index obtained from Oxford COVID-19 Government Response Tracker (OxCGRT). LNGSENT is the natural log of the absolute value of coronavirus worldwide sentiment index of RavenPack. LNGTREND is the natural log of google trends index based on the search for the word “coronavirus deaths” in the US. We add one to the number of cases, number of deaths, stringency and google trends indexes and then take the natural log to avoid excluding zero values. For the definitions of control variables please refer to Table 1. All specifications include industry fixed effects based on Fama-French 48 Industry classifications. Robust standard errors are clustered at the firm level. T-stats are in parentheses below the coefficient estimates. *, **, *** denote statistical significance at the 0.1, 0.05, and the 0.01 levels, respectively.

In general, our results are in line with prior literature connecting fear-inducing news regarding infectious diseases (Ichev and Marinč, 2018; Donadelli et al., 2017) and restrictive government policies (Blau and Thomas, 2015) with liquidity in financial markets. For our independent variable LNCASES, we observe a strong and statistically significant relationship between coronavirus cases and the stock market liquidity. In economic terms, a one percent increase in cases is associated with about 0.041% increase in illiquidity measured using the Amihud (2002) measure while about 0.038% increase in illiquidity measured using bid-ask spreads. Similarly, for LNDEATHS, we observe about 0.04% to 0.045% decrease in liquidity using both our measures which suggest that an increase in both cases and deaths erode liquidity in the stock market. Moreover, an increase in the number of coronavirus cases by 10,000 is associated with about a 0.06% decrease in market liquidity measured via Amihud (2002) measure while 0.05% decrease in liquidity using bid-ask spreads. Similarly, an increase in the number of deaths by 1000 is associated with a decrease in market liquidity by about 0.12% measured via Amihud (2002) measure while 0.11% decrease in liquidity using bid-ask spreads. For LNUSDWT, the coefficient is economically and statistically significant for both liquidity measures. In economic terms, one percent decrease in mobility is associated with about 0.22% increase in the Amihud (2002) illiquidity measure while about 0.42% increase in bid-ask spreads. It suggests that a decrease in mobility due to increased uncertainty, social distancing, and lockdowns have a significant negative impact on market liquidity. In columns [4] and [10] our independent variable of interest is LNGSENT. A higher value of this variable suggests a more negative global sentiment. Said differently, LNGSENT index indicates the extent of global panic. The coefficient on LNGSENT is statistically and economically significant in both columns. We find that a one percent increase in negative global sentiment is associated with a decline in market liquidity of about 0.15% using Amihud (2002) measure and 0.21% using the bid-ask spread measure. We use LNGTREND as our main independent variable in columns [5] and [11]. Like LNGSENT, our LNGTREND index is also a measure of (negative) sentiment. Similar to LNGSENT, we find that a one percent increase in GTREND is associated with an increase in market liquidity by about 0.16% when measured using the Amihud (2002) measure, and about 0.10% when measured using bid-ask spreads. This suggests that increased panic and negative sentiments contributed to market illiquidity. Finally, in columns [6] and [12] we use LNSTRINGENCY index as our main explanatory variable. In both specifications, we observe a strong positive relationship with market illiquidity. In economic terms, a one percent increase in stringency is associated with about 0.11% increase in Amihud (2002) measure and about 0.10% increase in bid-ask spread suggesting that government policies such as the closure of workplaces and non-essential businesses had a negative impact on market liquidity.

For our second set of tests, we follow prior literature (e.g. Blau et al., 2014; Blau, 2017) and estimate the following regression specification:

LN(VOLATILITYMEASURE)i,t=β0+β1LN(PANDEMICINDEX)i,t+β2SIZEi,t+β3PRICEi,t+β4VOLUMEi,t+β5S&Pi,t+β6ILLIQUIDITYi,t+β7SPREADi,t+εi,t (2)

Table 3 presents the results of this specification. Our dependent variable is the natural log of the range volatility measure (VOLT) in columns [1] to [6] while it is the natural log of GARCH (1,1) volatility measure (GVOLT) in columns [7] to [12].

Table 3.

Volatility regressions.

LNVOLT LNVOLT LNVOLT LNVOLT LNVOLT LNVOLT LNGVOL LNGVOL LNGVOL LNGVOL LNGVOL LNGVOL
[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12]
LNCASES 0.085*** 0.206***
(62.458) (75.847)
LNDEATHS 0.083*** 0.217***
(52.979) (67.143)
LNUSDWT −0.707*** −1.906***
(−52.410) (−67.884)
LNGSENT 0.645*** 1.157***
(66.950) (60.436)
LNGTREND 0.347*** 0.765***
(84.572) (96.363)
LNSTRINGENCY 0.252*** 0.604***
(71.243) (86.121)
SIZE −0.000** −0.000** −0.000** −0.000** −0.000** −0.000** −0.000** −0.000** −0.000** −0.000* −0.000* −0.000**
(−2.397) (−2.405) (−2.371) (−2.147) (−2.232) (−2.265) (−2.278) (−2.329) (−2.288) (−1.761) (−1.919) (−2.100)
PRICE 0.000*** 0.000*** 0.001*** 0.000*** 0.000** 0.000*** 0.001*** 0.001*** 0.001*** 0.001*** 0.000 0.000***
(4.245) (4.694) (5.096) (3.992) (2.269) (3.701) (3.760) (4.308) (5.124) (3.418) (1.198) (2.974)
VOLUME 0.000*** 0.000*** 0.000*** 0.000*** 0.000*** 0.000*** 0.000*** 0.000*** 0.000*** 0.000*** 0.000*** 0.000***
(9.654) (9.917) (10.047) (9.982) (8.661) (9.707) (10.760) (10.938) (11.072) (11.002) (9.210) (10.967)
S&P −1.694*** −1.785*** −1.940*** −0.555*** −0.658*** −1.245*** −3.597*** −4.094*** −4.591*** −0.788*** −0.996*** −2.466***
(−26.672) (−25.558) (−26.651) (−8.091) (−12.385) (−20.280) (−30.279) (−31.510) (−34.128) (−5.572) (−9.498) (−21.163)
ILLIQUIDITY 95.381*** 108.844*** 116.009*** 121.194*** 71.285*** 94.697*** 106.448*** 131.013*** 147.071*** 183.460*** 64.148*** 105.563***
(27.529) (28.535) (30.036) (30.555) (25.853) (28.732) (20.790) (22.873) (25.405) (27.325) (15.890) (22.225)
SPREAD 152.336*** 209.860*** 204.233*** 279.026*** 104.721*** 162.371*** 264.198*** 367.778*** 342.231*** 626.706*** 209.177*** 294.290***
(15.534) (20.275) (19.352) (27.677) (12.671) (17.583) (13.087) (17.193) (16.234) (26.542) (11.398) (15.176)
CONSTANT −4.245*** −4.066*** 0.044 −6.313*** −4.614*** −4.395*** −7.922*** −7.507*** 3.570*** −11.456*** −8.674*** −8.279***
(−240.404) (−214.371) (0.528) (−184.739) (−274.352) (−257.576) (−275.812) (−243.362) (21.157) (−169.476) (−305.829) (−288.963)
ROBUST SE YES YES YES YES YES YES YES YES YES YES YES YES
INDUSTRY FE YES YES YES YES YES YES YES YES YES YES YES YES
OBSERVATIONS 29,454 29,454 29,454 29,454 29,454 29,454 29,321 29,321 29,321 29,321 29,321 29,321
R-SQUARED 0.544 0.479 0.458 0.468 0.673 0.561 0.539 0.482 0.457 0.352 0.644 0.558
Open in a new tab

This table provides the results from the estimation of the following OLS regression specification.

LN(VOLATILITYMEASURE)i,t=β0+β1LN(PANDEMICINDEX)i,t+β2SIZEi,t+β3PRICEi,t+β4VOLUMEi,t+β5S&Pi,t+β6ILLIQUIDITYi,t+β7SPREADi,t+εi,t

Dependent variable LN(VOLATILITY MEASURE) is the natural log of the range volatility measure in columns [1] to [6] while it is the natural log of GARCH (1,1) volatility measure in columns [7] to [12]. The independent variable LN(PANDEMIC INDEX) represents the is natural log of the COVID-19 pandemic related index. These indexes include the following. LNCASES represents the natural log of coronavirus cases. LNDEATHS represent the natural log of coronavirus related deaths. LNUSDWT is the natural log of sum of US driving, walking and transit mobility trends indexes of Apple Inc. LNSTRINGENCY is the natural log of the stringency index obtained from Oxford COVID-19 Government Response Tracker (OxCGRT). LNGSENT is the natural log of the absolute value of coronavirus worldwide sentiment index of RavenPack. LNGTREND is the natural log of google trends index based on the search for the word “coronavirus deaths” in the US. We add one to the number of cases, number of deaths, stringency and google trends indexes and then take the natural log to avoid excluding zero values. For the definitions of control variables please refer to Table 1. All specifications include industry fixed effects based on Fama-French 48 Industry classifications. Robust standard errors are clustered at the firm level. T-stats are in parentheses below the coefficient estimates. *, **, *** denote statistical significance at the 0.1, 0.05, and the 0.01 levels, respectively.

Our results are in conformity with prior strands of literature that connect distress and anxiety causing news (Mehra and Sah, 2002; Donadelli et al., 2017) and restrictive government policies (Blau et al., 2014; Zaremba et al., 2020) with volatility in financial markets. The number of coronavirus cases are significantly positively associated with both volatility measures and we find that a one percent increase in cases is associated with about 0.09% increase in volatility measured via range volatility measure and about 0.21% increase in volatility measured via GARCH (1,1) measure. Similarly, a one percent increase in the number of deaths is associated with 0.083% increase in VOLT while about 0.22% increase in GVOLT suggesting that increases in both cases and deaths led to the instability of the markets. Moreover, an increase in the number of coronavirus cases by 10,000 is associated with about a 0.12% increase in market volatility when measured using the range volatility measure and an increase of about 0.29% using the GARCH (1,1) volatility measure. Similarly, an increase in the number of deaths by 1000 is associated with a 0.22% increase in volatility using the range volatility measure while an increase of about 0.58% using the (1,1) measure. The mobility measure LNUSDWT is very strongly negatively associated with both volatility measures with coefficients ranging from −0.071 in column [3] to −1.91 in column [9]. Similarly, both our (negative) sentiment indexes have a strong positive relationship with market volatility. In economic terms, a one percent increase in GSENT index (i.e. decrease in global sentiment) is associated with about 0.65% increase in VOLT and about 1.16% increase in GVOLT. Similarly, a one percent increase in GTREND index is associated with about 0.35% increase in VOLT and about 0.77% increase in GVOLT suggesting that growing panic and increasing negative sentiments contributed to stock market volatility. Finally, our LNSTRINGENCY variable is also significantly positively related to both market volatility measures. A one percent increase in stringency index is associated with about 0.25% increase in VOLT and about 0.60% increase in GVOLT suggesting that government regulatory responses such as mandatory lockdowns had a negative impact on market volatility.

Overall, the results of our empirical tests support the notion that COVID-19 related human costs, panic, and subsequent regulatory responses had an adverse impact on the liquidity and volatility of US equity markets. Our results are generally inline with prior literature connecting pandemics and fear-inducing news with equity market dynamics (Mehra and Sah, 2002; Ichev and Marinč, 2018; Donadelli et al., 2017; Haroon and Rizvi, 2020b). Our results are also consistent with the stream of research which suggests that regulatory restrictions can potentially harm the quality of financial markets (Blau et al., 2014; Baig et al., 2019, 2020).

4. Conclusion

We investigate the impact of multiple dimensions of COVID-19 pandemic on the liquidity and volatility of US equity markets. We are motivated by the nearly 580% rise in the CBOE VIX index during the month of April from its January levels and by the market-wide deterioration of liquidity (Adrian and Natalucci, 2020) corresponding with the rapid spread of coronavirus. Our results suggest that increases in confirmed cases and deaths due to coronavirus are associated with a significant deterioration of market liquidity and stability. Similarly, public fear and the implementation of restrictions and lockdowns seem to contribute to the illiquidity and instability of the markets.

CRediT authorship contribution statement

Ahmed S. Baig: Conceptualization, Data curation, Formal analysis, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing - original draft, Writing - review & editing. Hassan Anjum Butt: Conceptualization, Formal analysis, Investigation, Methodology, Project administration, Resources, Supervision, Validation, Visualization, Writing - original draft, Writing - review & editing. Omair Haroon: Data curation, Methodology, Project administration, Supervision, Visualization, Writing - original draft, Writing - review & editing. Syed Aun R. Rizvi: Data curation, Methodology, Project administration, Supervision, Visualization, Writing - original draft, Writing - review & editing.

Footnotes

3

Beginning January 13, 2020, Apple has published daily mobility trends that are based on requests for directions in Apple Maps. More at “https://www.apple.com/covid19/mobility”.

4

OxCGRT obtains publicly available information on 18 indicators of government response. A subset of these indicators consists of restrictive policies such as school closures, travel bans, etc. The containment and closure-policy related scores are then aggregated into a common ‘Stringency Index’ (Hale, Petherick, Phillips and Webster, 2020). More information is available at “https://www.bsg.ox.ac.uk/research/research-projects/coronavirus-government-response-tracker”.

5

The sentiment index computes the level of sentiment across all entities mentioned in the news alongside coronavirus. More details at “https://coronavirus.ravenpack.com”.

6

We note that our results are consistent if we use other variations of the search word “coronavirus deaths”. Our results also hold if we just use the google trends index for the word “coronavirus”.

7

As a robustness test, we compute the regression models (1) and (2) with firm fixed effects and find consistent results. Results are available upon request.

8

In log-log models, a percent change in the independent variable is equal to a percent change in dependent variable times the beta coefficient associated with the independent variable. This allows for easier computation of economic significance.

Supplementary material associated with this article can be found, in the online version, at doi:10.1016/j.frl.2020.101701.

Appendix. Supplementary materials

mmc1.xml (210B, xml)

References

  1. Adrian, T., Natalucci, F. (2020, April 15). COVID-19 crisis poses threat to financial stability. Retrieved fromhttps://blogs.imf.org/2020/04/14/COVID-19-crisis-poses-threat-to-financial-stability/.
  2. Akhtaruzzaman M., Boubaker S., Sensoy A. Financial contagion during COVID–19 crisis. Finance Res. Lett. 2020 doi: 10.1016/j.frl.2020.101604. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Al-Awadhi A.M., Al-Saifi K., Al-Awadhi A., Alhamadi S. Death and contagious infectious diseases: impact of the COVID-19 virus on stock market returns. J. Behav. Exp. Finance. 2020 doi: 10.1016/j.jbef.2020.100326. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Albulescu, C., 2020. Coronavirus and financial volatility: 40 days of fasting and fear. arXiv preprint arXiv:2003.04005.
  5. Alizadeh S., Brandt M.W., Diebold F.X. Range‐based estimation of stochastic volatility models. J. Finance. 2002;57(3):1047–1091. [Google Scholar]
  6. Amihud Y. Illiquidity and stock returns: cross-section and time-series effects. J. Financ. Mark. 2002;5(1):31–56. [Google Scholar]
  7. Arouri M.E.H., Boubaker S., Nguyen D.K., editors. Emerging Markets and the Global economy: a Handbook. Academic Press; 2013. [Google Scholar]
  8. Baig A., Blau B.M., Sabah N. Price clustering and sentiment in bitcoin. Finance Res. Lett. 2019;29:111–116. [Google Scholar]
  9. Baig A.S., Blau B.M., Sabah N. Free trade and the efficiency of financial markets. Glob. Finance J. 2020 [Google Scholar]
  10. Baig A.S., Blau B.M., Whitby R.J. Price clustering and economic freedom: the case of cross-listed securities. J. Multinat. Financ. Manag. 2019;50:1–12. [Google Scholar]
  11. Baig A.S., Sabah N. Does short selling affect the clustering of stock prices? Q. Rev. Econ. Finance. 2020;76:270–277. [Google Scholar]
  12. Barberis N., Shleifer A., Vishny R. A model of investor sentiment. J. Financ. Econ. 1998;49(3):307–343. [Google Scholar]
  13. Blau B.M. Social trust and the liquidity of cross-listed securities. J. Bus. Res. 2017;78:155–171. [Google Scholar]
  14. Blau B.M. Does religiosity affect liquidity in financial markets? J. Behav. Exp. Finance. 2018;19:72–83. [Google Scholar]
  15. Blau B.M. Exchange rate volatility and the stability of stock prices. Int. Rev. Econ. Finance. 2018;58:299–311. [Google Scholar]
  16. Blau B.M., Brough T.J., Thomas D.W. Economic freedom and the stability of stock prices: a cross-country analysis. J. Int. Money Finance. 2014;41:182–196. [Google Scholar]
  17. Blau, B.M., Thomas, D.W., 2015. Economic freedom and financial market liquidity: evidence from ADRs. Available at SSRN 2708519.
  18. Blendon R.J., Benson J.M., DesRoches C.M., Raleigh E., Taylor-Clark K. The public's response to severe acute respiratory syndrome in Toronto and the United States. Clin. Infect. Dis. 2004;38(7):925–931. doi: 10.1086/382355. [DOI] [PubMed] [Google Scholar]
  19. Boubaker S., Buchanan B., Nguyen D.K. Emerald Group Publishing; England: 2016. Risk Management in Emerging Markets: Issues, Framework and Modelling. [Google Scholar]
  20. Boubaker S., Gounopoulos D., Rjiba H. Annual report readability and stock liquidity. Financ. Mark. Inst. Instrum. 2019;28(2):159–186. [Google Scholar]
  21. Brunnermeier M.K. Deciphering the liquidity and credit crunch 2007-2008. J. Econ. Perspect. 2009;23(1):77–100. [Google Scholar]
  22. Donadelli M., Kizys R., Riedel M. Dangerous infectious diseases: bad news for main street, good news for wall street? J. Financ. Mark. 2017;35:84–103. [Google Scholar]
  23. Ederington L.H., Lee J.H. The creation and resolution of market uncertainty: the impact of information releases on implied volatility. J. Financ. Quant. Anal. 1996;31(4):513–539. [Google Scholar]
  24. Glosten L.R., Milgrom P. Bid, ask and transaction prices in a specialist market with heterogeneously informed traders. J. Financ. Econ. 1985;14(1):71–100. [Google Scholar]
  25. Haroon, O., Rizvi, S.A.R., 2020a. #Flattenthecurve and stock market liquidity – an inquiry into emerging economies. Emerg. Mark. Finance Trade. In Press.
  26. Haroon O., Rizvi S.A.R. COVID-19: media coverage and financial markets behavior-A sectoral inquiry. J. Behav. Exp. Finance. 2020 doi: 10.1016/j.jbef.2020.100343. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Hasbrouck J. Trades, quotes, inventories, and information. J. Financ. Econ. 1988;22(2):229–252. [Google Scholar]
  28. Ichev R., Marinč M. Stock prices and geographic proximity of information: evidence from the Ebola outbreak. Int. Rev. Financ. Anal. 2018;56:153–166. doi: 10.1016/j.irfa.2017.12.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Kaplanski G., Levy H. Exploitable predictable irrationality: the FIFA world cup effect on the US stock market. J. Financ. Quant. Anal. 2010;45(2):535–553. [Google Scholar]
  30. Klibanoff P., Lamont O., Wizman T.A. Investor reaction to salient news in closed‐end country funds. J. Finance. 1998;53(2):673–699. [Google Scholar]
  31. Mairal G. The history and the narrative of risk in the media. Health Risk Soc. 2011;13(1):65–79. [Google Scholar]
  32. Mehra R., Sah R. Mood fluctuations, projection bias, and volatility of equity prices. J. Econ. Dyn. Control. 2002;26(5):869–887. [Google Scholar]
  33. Pastor L., Veronesi P. Uncertainty about government policy and stock prices. J. Finance. 2012;67(4):1219–1264. [Google Scholar]
  34. Su Z., Fang T., Yin L. The role of news-based implied volatility among US financial markets. Econ. Lett. 2017;157:24–27. [Google Scholar]
  35. Tetlock P.C. Giving content to investor sentiment: the role of media in the stock market. J. Finance. 2007;62(3):1139–1168. [Google Scholar]
  36. Uhl M.W., Pedersen M., Malitius O. What's in the news? Using news sentiment momentum for tactical asset allocation. J. Portf. Manag. 2015;41(2):100–112. [Google Scholar]
  37. Veronesi P. Stock market overreactions to bad news in good times: a rational expectations equilibrium model. Rev. Financ. Stud. 1999;12(5):975–1007. [Google Scholar]
  38. Wilkes, T. (2020, March 15). The plumbing behind world's financial markets is creaking Loudly. Retrieved fromhttps://www.reuters.com/article/us-health-coronavirus-markets-crisis-ana/the-plumbing-behind-worlds-financial-markets-is-creaking-loudly-idUSKBN2120NJ.
  39. Young M.E., King N., Harper S., Humphreys K.R. The influence of popular media on perceptions of personal and population risk in possible disease outbreaks. Health Risk Soc. 2013;15(1):103–114. [Google Scholar]
  40. Zaremba A., Kizys R., Aharon D.Y., Demir E. Infected Markets: novel Coronavirus, government interventions, and stock return volatility around the globe. Finance Res. Lett. 2020 doi: 10.1016/j.frl.2020.101597. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Zhang D., Hu M., Ji Q. Financial markets under the global pandemic of COVID-19. Finance Res. Lett. 2020:1015. doi: 10.1016/j.frl.2020.101528. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

mmc1.xml (210B, xml)

Articles from Finance Research Letters are provided here courtesy of Elsevier

RESOURCES