The dual nature of the dead-water phenomenology: Nansen versus Ekman wave-making drags

Significance

A ship evolving in a stratified fluid is sometimes slowed down in comparison to a homogeneous case. This dead-water phenomenon was reported by the Norwegian explorer Fridtjöf Nansen during his North polar expedition in 1893. The physicist and oceanographer Vagn Walfrid Ekman was the first to study in the laboratory the physical origin of dead-water phenomenon in 1904: at the interface between saline water and freshwater, internal gravity waves appear, propagate, and generate a wave-making drag. Here we show that the velocity oscillations of pulled ships models à la Ekman caught in dead water are due to a transient internal dispersive undulating depression produced during the initial acceleration of the ship that we predict with a linear analytical model.

Abstract

A ship encounters a higher drag in a stratified fluid compared to a homogeneous one. Grouped under the same “dead-water” vocabulary, two wave-making resistance phenomena have been historically reported. The first, the Nansen wave-making drag, generates a stationary internal wake which produces a kinematic drag with a noticeable hysteresis. The second, the Ekman wave-making drag, is characterized by velocity oscillations caused by a dynamical resistance whose origin is still unclear. The latter has been justified previously by a periodic emission of nonlinear internal waves. Here we show that these speed variations are due to the generation of an internal dispersive undulating depression produced during the initial acceleration of the ship within a linear regime. The dispersive undulating depression front and its subsequent whelps act as a bumpy treadmill on which the ship would move back and forth. We provide an analytical description of the coupled dynamics of the ship and the wave, which demonstrates the unsteady motion of the ship. Thanks to dynamic calculations substantiated by laboratory experiments, we prove that this oscillating regime is only temporary: the ship will escape the transient Ekman regime while maintaining its propulsion force, reaching the asymptotic Nansen limit. In addition, we show that the lateral confinement, often imposed by experimental setups or in harbors and locks, exacerbates oscillations and modifies the asymptotic speed.

The dead-water effect is a physical phenomenon developing in fluids stratified in density, typically in fjords (1, 2) or harbors (3). After recording the testimony of sailors and explorers like Nansen (1), Ekman (4) was the first to study it scientifically in 1904. By reproducing this phenomenon in the laboratory, he observed a higher ship resistance in a stratified fluid than in a homogeneous one as reported in the field. The internal waves’ formation converts the kinetic energy of the ship into the wake potential energy, the so-called wave-making drag due to the generation of an interval waves wake (SI Appendix, Fig. S1 and Movie S1). For a step-like density profile, the maximum interface waves’ velocity is set as (5) $c_{\varphi }=\sqrt{g\frac{{\rho }_2-{\rho }_1}{{\rho }_2}\frac{h_2{h}_1}{h_2+h_1}}$, depending on the pycnocline parameters: the height and the density of the two superposed layers in the gravity field $g$, ($h_1$, ${\rho }_1$), respectively, for the upper layer and ($h_2$, ${\rho }_2$), respectively, for the lower layer. Analytical studies (6) show that the critical velocity is slower than this theoretical prediction, as experimentally confirmed (4, 7, 8); $c_{\mathrm{c}\mathrm{r}\mathrm{i}\mathrm{t}}\approx 0.8c_{\varphi }$, where the physical origin of c_crit is still an open question in the literature. Our own results are consistent with this value in the following. Based on a definition of a renormalized internal Froude number $\mathrm{F}\mathrm{r}=V_s/c_{\mathrm{c}\mathrm{r}\mathrm{i}\mathrm{t}}$, a dimensionless measure of the ship speed, the drag due to the internal wake is all the more important as the ship speed is close to $c_{\mathrm{c}\mathrm{r}\mathrm{i}\mathrm{t}}$ ($\mathrm{F}\mathrm{r}\approx 1$). For larger speeds ($\mathrm{F}\mathrm{r}>1$), the internal wave-making resistance decreases until it becomes negligible compared to the viscous drag. In seeking to impose a constant speed, Ekman (4) showed the existence of a hysteresis cycle: by exceeding a critical pulling force, the speed of the ship jumps to a much higher velocity with a behavior akin to a first-order phase transition in thermodynamics. Thus, a speed range cannot be reached by a constant towing force: this branch of the drag-speed curve is unstable.

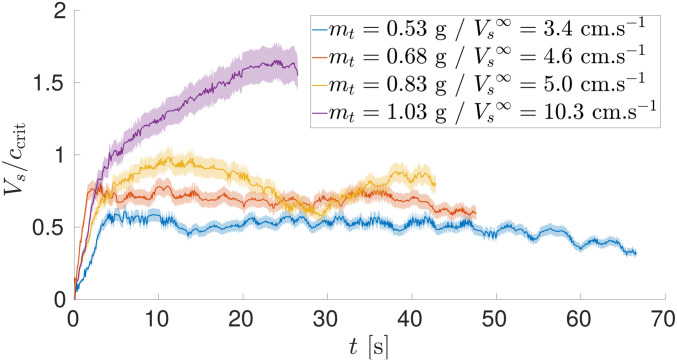
Ekman (4) classified different regimes according to the interface Froude number. If $\mathrm{F}\mathrm{r}<1$, the ship accelerates to an asymptotic speed $V_s<c_{\mathrm{c}\mathrm{r}\mathrm{i}\mathrm{t}}$ (blue and red curves in Fig. 1). With a bigger towing force, it is possible to exceed the local maximum and reach a higher asymptotic speed $V_s>c_{\mathrm{c}\mathrm{r}\mathrm{i}\mathrm{t}}$ (purple curve in Fig. 1). These regimes and their descriptions are taken up by modern studies (7–9) which distinguish a subcritical and a supercritical regime for the wake since the ship reaches an asymptotic speed in both cases.

Fig. 1.

Time evolutions of the ship speed for different constant towing forces. In yellow (purple), the ship reaches an oscillating (ballistic) regime. Speed error $\mathrm{\Delta }{V}_S=7.2\times 10^{-2}{V}_S+1.8\times 10^{-4}\hspace{0.17em}\left[\mathrm{m}\cdot {\mathrm{s}}^{-1}\right]$. Configuration data are given in SI Appendix, Table S1.

In addition to these ballistic regimes, Ekman displayed a periodic behavior for $\mathrm{F}\mathrm{r}<1$. The ship accelerates then oscillates around an average speed $⟨V_s⟩<c_{\mathrm{c}\mathrm{r}\mathrm{i}\mathrm{t}}$. These fluctuations in speed are all the more marked, as $⟨V_s⟩$ is close to $c_{\mathrm{c}\mathrm{r}\mathrm{i}\mathrm{t}}$ (yellow curve in Fig. 1), giving the impression of a false ship stop. These speed oscillations should not be confused with the previously described hysteretic phenomenon, where it is necessary to change the towing force to jump from one speed to another. Mercier et al. (7) suggested that the to and fro motion is due to the interaction of nonlinear internal waves with the ship and that linear models introduced by Ekman (4) or Miloh et al. (6) are not sufficient to explain it. Therefore, under the vocabulary dead water, we must distinguish two wave-making resistance phenomena: the kinematic drag and the dynamic resistance. We choose to name the first “Nansen wave-making drag” and the second the “Ekman wave-making drag,” which is more extensively probed in this paper. Some studies (8, 10–13) make the choice to pull at constant speed, to probe the stationary Nansen wave-making drag, without the dynamic Ekman wave-making drag which is explored by towing at constant force.

Results

Ekman-Like Experiment: Observation of the Ship Dynamics and the Pycnocline.

In order to understand the physical roots of the Ekman wave-making drag, we reproduce the seminal 1904 Ekman’s experiments with a constant towing mass (Experimental Methods and SI Appendix, Fig. S2 and Table S1). The ship model is $0.10\hspace{0.17em}\mathrm{m}$ wide ($B_b$) and $0.20\hspace{0.17em}\mathrm{m}$ long ($L_b$); the canal is $0.37\hspace{0.17em}\mathrm{m}$ wide ($W$) and $3\hspace{0.17em}\mathrm{m}$ long ($L$). The waves observed have a two-dimensional (2D) behavior, and the lateral confinement has an impact on the dynamics of the boat as we will see later. Unlike recent studies, we choose a weaker lateral confinement [$\frac{B_b}{W}=0.27$ compared to 0.95 in Mercier et al.’s experiments (7) or 0.48 in Medjoub et al.’s experiments (8)]. We set an initial double-layer step-like stratification, depositing a layer of freshwater on a layer of colored saline water using a sponge system. The ship is towed using a pulley system that guarantees constant mass and free speed, compensating the towing and drop-down rope weight. The ship model generates only internal waves at the pycnocline but does not reach a speed sufficiently large to generate a surface wake (Theoretical Methods). Thanks to two cameras, we detect the interface by a subpixel method, which allows us to plot space–time diagrams. Diminishing lateral confinement induces a decrease in wave amplitudes and therefore requires a subpixel method in accuracy which allows a gain of a factor of 10 compared to a pixel method. It is then possible to study waves of the order of 100 $\mathrm{\mu }$m in amplitude.

Two kinds of internal waves are observed when a ship is put into motion from rest. First, a subcritical depression forms under the ship and moves at the same speed, as if it were fastened to the ship. In the space–time diagram (Fig. 2A), this depression follows the position of the ship indicated by the dotted curve. This is the classical kinematic internal wake, responsible for the Nansen wave-making drag. When $\mathrm{F}\mathrm{r}>1$, the wake converts to a supercritical hump with negative polarity, and the associated drag decreases. The subcritical wake is isolated and represented by the green dotted curve in Fig. 3. Second, another internal wave is observed at the bow, when $\mathrm{F}\mathrm{r}<1$. In the space–time diagram (Fig. 2A), this front wave with negative polarity and its whelps (secondary waves with oscillating polarities) escape from underneath the vessel and are then reflected on the canal wall. In Fig. 3, red dashed curve, this previous wave is disentangled from the Nansen wake. Since Ekman, this wave has been described as a “solitary wave” (4), which “evolves freely” and whose “shape remains almost unchanged” (7). We will show that this wave is actually not a nonlinear solution of a solitary type as believed by previous authors but a linear internal dispersive undulating depression (14).

Fig. 2.

Space–time and spectral diagrams of (A and B) an Ekman-like experiment and (C and D) a Scott Russell-like experiment. In A, black dash-dotted curves symbolize the ship position. In B and D, red dotted curve represents the dispersion relation discussed by Fructus and Grue (15) (multiplied by a corrective factor 0.8 in the Ekman-like experiment). In B, the purple dashed line represents the advective branch $\omega =V_{s}k$. The vertical white bar in C, at $x\approx 1\hspace{0.17em}\mathrm{m}$, is due to a measuring beam hiding a small part of the measurement zone. Configuration data are given in SI Appendix, Tables S1 and S2.

Fig. 3.

Decomposition of the interface deformation (solid blue curve) into its two components: the dispersive undulating depression (red dashed curve) and the classical internal wake (green dotted curve). The decomposition is done from the spectral space, filtering around the branches corresponding to each wave (SI Appendix, Movie S2). Configuration data are given in SI Appendix, Table S1.

Spectral Domain and Dispersion Relation.

For this purpose, we disentangle these two wave systems in the spectral domain ($k$, $\omega$) obtained by Fourier transform of the space–time diagram. An advective branch $\omega =V_{s}k$ (purple dashed curve in Fig. 2B), with a slope equal to the ship speed, corresponds to the classical kinematic internal wake (Nansen wave-making drag). A S-shaped branch (red dotted curve in Fig. 2B), with a zero-point tangent slope equal to $c_{\mathrm{c}\mathrm{r}\mathrm{i}\mathrm{t}}=0.8\times c_{\varphi }$, coincides with the dispersive undulating depression. This latter curve fits the dispersion relation proposed by Fructus and Grue (15) (Theoretical Methods and Fig. S3). In an Ekman-like experiment featuring the ship, an artificial fitting factor 0.8 must multiply the Grue’s dispersion relation in order to comply with the maximum dispersive undulating depression velocity $c_{\mathrm{c}\mathrm{r}\mathrm{i}\mathrm{t}}$ observed experimentally.

Scott Russell-Like Experiment: Proof of a Linear Dispersive Undulating Depression.

To better study this dispersive undulating depression, we seek to isolate it from the classical kinematic internal wake by removing the ship and replacing it by a withdrawing object. Indeed, we reproduce an 1844 experiment by Scott Russell (16), in shallow layer of an homogeneous fluid by a double-layer one: we create a hollow space in the stratified column at one canal extremity by removing a parallelepiped object plunged initially in the fluid (Experimental Methods and SI Appendix, Fig. S2 and Table S2). A dispersive undulating depression (namely, a linear undulatory structure with a front of negative polarity followed by a tail made of secondary whelps) is created in order to fill the void created at the pycnocline by the withdrawal of the object. It propagates and it is reflected several times on the aquarium walls. Reflections allow a longer acquisition $t_{\mathrm{a}\mathrm{c}}$ of the phenomenon (Fig. 2C), therefore a better frequency resolution ($\mathrm{\Delta }\omega =\frac{2\pi }{t_{\mathrm{a}\mathrm{c}}}$), and an observation of the wave’s evolution. We observe the S-shaped branch describing the dispersive undulating depression in the first and third quadrants (Fig. 2D), as well as its reflection in the second and fourth quadrants. Two advective branches with low speeds can also be observed, resulting from a breaking wave created by the initial perturbation (17) (observable on the corresponding space–time diagram; Fig. 2C). The study of these modes is not the subject of this paper and will be explored in a future work. The maximum dispersive undulating depression velocity equals $c_{\mathrm{c}\mathrm{r}\mathrm{i}\mathrm{t}}=c_{\varphi }$ and not $c_{\mathrm{c}\mathrm{r}\mathrm{i}\mathrm{t}}=0.8c_{\varphi }$ as in an Ekman-like experiment. The subsequent whelps are slower and slower. Thus, unlike a solitonic-type wave, the front wave is asymmetrical, and the front wave and the whelps spread out (their amplitudes decrease, and their wavelengths increase). From the front wave skewness or the ratio between its amplitude and wavelength, Xu et al. (18) give several criteria to decide if an internal wave has a solitonic behavior or a dispersive undulating depression one. According to them, if after 100 s of propagation the wave has an amplitude greater than $3\%$ of its half-length, then the structure is not linear. In the previous Ekman-like experiment (Figs. 2A and 3), we measure after 30 s $\frac{A_w}{L_w}\approx 0.3\%$, which continues to decrease over time (SI Appendix, Fig. S4): the Ekman transient effect does correspond to a linear dispersive undulating depression (14).

The Coupled Dynamics of the Ship and the Wave.

To disentangle the dispersive undulating depression from the wake, we filter separately the different branches in the spectral domain, before reverting to the space–time domain with an inverse Fourier transform (Fig. 3). Each whelp passage under the ship corresponds to a speed variation. Thus, the interactions between the ship and the dispersive undulating depression result in velocity oscillations as if the ship was moving on a bumpy treadmill. Moreover, the amplitudes of the subsequent whelps decrease in time. Therefore, we can assume that by keeping the same towing force for a sufficient duration, the velocity oscillations will decrease in amplitude until their disappearance.

Dynamic Numerical Computation and Effect of Lateral Confinement.

In order to test our analytical description of the coupled dynamics of the ship with the waves, we perform a dynamic numerical calculation. In these simulations the pulling force $F_t$ is constant, and the ship speed $V$ evolves according to Newton’s principle: $m_b\stackrel{\cdot }{V}=F_t+F_d\left(V\right)$, where $F_d\left(V\right)$ is the fluid drag on the moving ship. The drag has two components here: the frictional drag and the internal wave drag. The frictional drag is proportional to the square of the velocity, through a coefficient that can be measured by performing measurements in a fluid with no stratification (Numerical Methods and SI Appendix, Fig. S5). The internal wave drag is computed using the same linearized irrotational two-fluids model from which the dispersion relation was established previously (Experimental Methods). The effect of the ship on the fluid appears through a forcing term in the equation describing the internal wave, which is justified in the dimensionless draft $T_b/h_t\to 0$ limit, with $h_t=h_1+h_2$ the total depth. Hence, the dependence of the internal-wave drag with $V$ is highly nontrivial and involves its history. Simulations allow us to reproduce experiments in an infinitely long canal. Even in cases where we observe an oscillating regime, the ship ends up reaching the asymptotic Nansen limit (Fig. 4). Thus, the Ekman wave-making drag is only a transient quasi-oscillatory regime.

Fig. 4.

Comparison between dynamic calculations and experimental measurements. The simulation allows a longer canal. The ship leaves the quasi-oscillating regime and reaches a ballistic regime. Configuration data are given in SI Appendix, Table S1.

The lateral confinement, defined by the beam-to-width ratio $B_b/W$, strongly impacts the dynamics of the ship. In a highly confined water, amplitudes of the classical wake and of the linear dispersive undulating depression are amplified. Indeed, the linear undulating depression is produced by a displacement of water which cannot propagate laterally because of the channel’s walls. In open sea, the water is laterally unlimited, and the waves created are more divergent (Fig. 5) and with lower amplitude (which justifies requirement of the subpixel accuracy). In the presence of close walls, there are no more 3D effects, and waves are parallel. In an intermediate case, like our configuration, we can observe reflections on the walls which generate minima and maxima in the middle of the channel (SI Appendix, Fig. S6 and Movie S5). Thus, the closer beam-to-width ratio $B_b/W$ is to 1, the greater the amplitudes of the waves, and the stronger the wave-making resistance (SI Appendix, Fig. S7 and Movie S3). This then exacerbates the speed quasi-oscillations and the Ekman wave-making drag. The Nansen wave-making drag is also impacted by the lateral confinement $B_b/W$, as it is well known in a monolayer either in infinite depth (19) or finite depth (20). In subcritical regime $V_b<c_{\mathrm{c}\mathrm{r}\mathrm{i}\mathrm{t}}$, the wake-making resistance is greater in the confined configuration than in the unconfined. On the contrary, in supercritical regime $V_b>c_{\mathrm{c}\mathrm{r}\mathrm{i}\mathrm{t}}$, the wake-making resistance is lower in the confined configuration than in the nonconfined (SI Appendix, Fig. S8). However, this is not just a laboratory’s observation: ships can move in confined and stratified environments and endure this marked phenomenon such as in harbors or locks or in geographical complexities such as the strait of the Ambracian Gulf (21).

Fig. 5.

Numerical calculations of the 2D interface’s deformation (Left) for different lateral confinements ($B_b/W=0.952$ corresponds to ref. 7, $B_b/W=0.670$ corresponds to ref. 8, and $B_b/W=0.270$ corresponds to ref. 4) and our configuration, with $B_b$ the beam and $W$ the channel’s width. A narrow channel prevents 3D effects and amplifies the classical internal wake (Nansen wave-making drag) and the dispersive undulating depression (Ekman wave-making drag). So the dynamics of the boat are impacted (Right). Red circles indicate when deformations are represented; black dotted curve is the limitation of 3 m corresponding to our channel length.

Discussion

A ship moving in a stratified fluid generates an internal wake responsible for a kinematic drag, which we name the Nansen wave-making drag. In addition to this wake, the ship produces during its initial acceleration a linear dispersive undulating depression. The interactions between the vessel and the latter create the ship speed oscillations. Contrary to previous studies, a linear analytical model reproduces numerically for the first time these interactions and the ship behavior (SI Appendix, Movie S4). Due to the linear nature of the dispersive undulating depression, this interaction decreases in amplitude over time. The quasi-oscillating regime, which we name the Ekman wave-making drag, is only a transient regime. Thus, there are two types of waves superimposed with a weak interaction among both but more a superposition. The Ekman wave-making drag modulates the Nansen wave-making drag until it becomes negligible compared to the latter.

A linear analytical calculation makes it possible to model experiments in wider and longer channels than the laboratory’s channels. This made it possible to highlight the impact of lateral confinement on the ship’s dynamics. By amplifying the amplitudes of the waves, the confinement intensifies the Ekman wave-making drag and has facilitated for more than a century the observation of this particular ship’s dynamics. However, such confinement hides the 3D waves’ behavior and does not represent classical ship dynamics in open sea. Future experiments must take this result into consideration. A wide channel allows us to limit the number of speed oscillations and therefore makes it possible to reach the steady state more quickly with a subsequent shorter laboratory channel. On the contrary, a narrow channel amplifies the speed oscillations, so requires a longer channel to study the steady state. Moreover, large amplitudes can cause nonlinear effects. We believe that we have solved a more than 1-century mystery with respect to the true nature of the dead-water effect. Unfortunately, no laboratory experiments have really studied the original Nansen wave-making drag per se.

Materials and Methods

Experimental Methods.

We chose a wide water tank ($L=3\hspace{0.17em}\mathrm{m}$; $W=0.37\hspace{0.17em}\mathrm{m}$; $H=0.40\hspace{0.17em}\mathrm{m}$), which reduces the effects of lateral confinement in comparison to previous studies (7–9) ($B_{b}W=0.27$). A silicon gasket was used to seal the glasses. To better visualize the internal waves, a white board is placed behind the tank to get a uniform background thanks to the use of a light-emitting diode lighting system. Two side cameras, placed $3\hspace{0.17em}\mathrm{m}$ from the tank, record a lateral region of interest $2.25\hspace{0.17em}\mathrm{m}$ long, with a spatial resolution of $\mathrm{\Delta }x=5.6\times 10^{-4}\hspace{0.17em}\mathrm{m}$. These are grayscale Point Grey cameras with complementary metal-oxide-semiconductor technology, triggered and controlled by a user interface. We record at $f_{\mathrm{a}\mathrm{c}}=45\hspace{0.17em}\mathrm{f}\mathrm{p}\mathrm{s}$ during the Ekman-like experiments and at $f_{\mathrm{a}\mathrm{c}}=25\hspace{0.17em}\mathrm{f}\mathrm{p}\mathrm{s}$ during the Scott Russell-like experiments keeping the same maximum number of images (4,096). We set a step-like stratification in density, with the goal of having a two-layer fluid. On the first layer, previously saline and colored in red, we deposit a layer of transparent freshwater. In order to avoid mixing, we need to reduce as much as possible the turbulence. The fresh water is transferred to the experimental tank by gravity and poured on top of three floating sponges ($Q\approx 20\hspace{0.17em}\mathrm{L}/\mathrm{h}$ for each sponge). This process is very slow (about 10 min per centimeter) and allows a good separation between both layers. The density profile is measured with an Anton Paar DMA 35 digital density meter just after the stratification is built. The mass diffusivity of salt in water is measured as $1.8\times 10^{-8}\hspace{0.17em}\mathrm{m}\cdot {\mathrm{s}}^{-\mathrm{1}}$. The water is at room temperature (around 293 K).

In an Ekman-like experiment (SI Appendix, Fig. S2, Top), we tow a ship with a constant force. A small-sized Playmobil ship was used for the experiments ($L_b=20\times 10^{-2}\hspace{0.17em}\mathrm{m}$; $B_b=10\times 10^{-2}\hspace{0.17em}\mathrm{m}$; $T_b=2.4\times 10^{-2}\hspace{0.17em}\mathrm{m}$) (7). We add lead weights to adjust the draft. Its total mass is $M_b=0.354\hspace{0.17em}\mathrm{k}\mathrm{g}$. To remove its holes and irregularities, the ship hull was filled with resin and sanded. The towing system is composed of three pulleys. The first two form a horizontal loop, which is connected to a third one placed above and linked to a vertical wire featuring a towing mass attached by a hook. A wire extension is also hung on the hook, with a sufficient length to keep contact with the ground, compensating for the wire lengthening with the purpose of getting a constant towing mass. An initial mass can be added near the ground to facilitate the start to overcome both the static friction forces and the dynamic ones due to the pulleys. The ship is hooked to the horizontal loop by two independent free vertical T-shape rods connected to the horizontal towing wire, one to the bow and the other to the stern. This setup allows pitches, heaves, and surges, while preventing sways, rolls, and yaws. The ship start is controlled by an electromagnet with a trigger as well as the cameras recording. However, when the ship stops while reaching the aquarium end, perturbations are generated due to the ship final motions.

In a Scott Russell-like experiment (SI Appendix, Fig. S2, Bottom), a negative polarity perturbation is created at the pycnocline, and its evolution is recorded. A parallelepiped object $0.37\hspace{0.17em}\mathrm{m}$ wide, $0.119\hspace{0.17em}\mathrm{m}$ long, and $4.0\times 10^{-2}\hspace{0.17em}\mathrm{m}$ high is placed at the end of the canal, immersed by a draft $T_{\mathrm{S}\mathrm{R}}=2.4\times 10^{-2}\hspace{0.17em}\mathrm{m}$ within the lower layer $h_2$. A counterweight system raises this block with a manual procedure, on a distance equal to the draft. So the block is lifted up to the water level limit, without being fully emerged. In addition to cameras, a Microsonic Mic+340 acoustic sensor measures the deformation of the free surface in one position. Since there is no disturbance created by the ship stop, we can study the dispersive undulating depression and its reflections in the long run. The measurement time is therefore longer, which induces a better frequency resolution in the spectral domain.

The pycnocline is detected by the brightness gradient between the red saline water (appearing black on black and white cameras) and the transparent freshwater (appearing white on cameras). A MATLAB script automates this detection. At first, the script looks for the maximum brightness gradient. This step allows a fast detection of the interface with a precision of the order of the pixel. The brightness profile is fitted with a tanh curve, which increases the precision by a factor 10. This method, called subpixel, is necessary for the study of low-amplitude waves of the order of $10\hspace{0.17em}\mathrm{\mu }\mathrm{m}$ in height. Between two frames, the ship displacement is small. Using a cross-correlation method we can go back to this displacement vector with a subpixel precision. This vector is converted to a velocity using the time and spatial resolutions. The ship speed measurement uncertainty is $\mathrm{\Delta }{V}_S=\pm \left(\frac{0.1\mathrm{\Delta }x}{2\sqrt{3}dt}+\frac{V_s}{2\sqrt{3}{f}_{\mathrm{a}\mathrm{c}}dt}\right)$ with dt the time between the two frames of the cross-correlation. The measurement of the ship displacement is done on four images, so $dt=4/f_{\mathrm{a}\mathrm{c}}$ and $\mathrm{\Delta }{V}_S=7.2\times 10^{-2}{V}_S+1.8\times 10^{-4}\hspace{0.17em}\left[\mathrm{m}\cdot {\mathrm{s}}^{-1}\right]$.

The ship model is subject to separate resistance components:

$$R_t=R_{\nu }+R_s+R_h+R_f+R_W$$

where $R_{\nu }$ is the viscous friction, $R_s$ is the free surface wave-making resistance, $R_h$ is the hydraulic resistance due to confinement, $R_f$ is the solid friction due to pulleys, and $R_W$ is the internal wave-making resistance (with both the Nansen and Ekman contributions). We can have access to the four firsts by tests in homogeneous water. The model speed is less than the Landau threshold ($0.23\hspace{0.17em}\mathrm{m}\cdot {\mathrm{s}}^{-\mathrm{1}}$), so there is no surface wake (22), and $R_s=0$ because of surface tension effects. According to correlation proposed by the International Towing Tank Conference (if $T_b/h\ll 1$ and $B_b/W\ll 1$), the viscous drag is given by $R_{\nu }=K{V}_s^2$ and $R_h\approx 0$. We find empirically in homogeneous configuration (SI Appendix, Fig. S5) a total resistance (with $R_W=0$) $R_t=3.44\times 10^{-1}{V}_s^2+5.2\times 10^{-3}\hspace{0.17em}\left[\mathrm{N}\right]$, including a static resistance, due to the towing system, which must be exceeded to launch the ship. This empirical relation is valid only for our ship model and for $T_b/h\ll 1$. If $T_b/h\approx 1$, greater resistance effects must be taken into account. We add to the homogeneous resistance the internal wave-making resistance calculated below (Numerical Methods).

Theoretical Methods.

The dispersion relation proposed by Fructus and Grue (15) is given by

$$\begin{array}{ll}\hfill & {K_{\delta }}^2-k\left[\coth \left(k{h}_1\right)+\coth \left(k{h}_2\right)\right]K_{\delta }\coth \left(K_{\delta }\delta \right)-k^2\coth \left(k{h}_1\right)\hfill \\ \hfill & \times \coth \left(k{h}_2\right)=0\hfill \end{array}$$

with $K_{\delta }=k\sqrt{{N_0}^2/{\omega }^2-1}$, the thickness of the pycnocline $\delta$, and the constant buoyancy frequency $N_0=\sqrt{-\frac{g}{{\rho }_2}\frac{\partial \rho }{\partial z}}\approx \sqrt{\frac{g}{{\rho }_2}\frac{{\rho }_2-{\rho }_1}{\delta }}$. The limit $\delta \to 0$ matches with the dispersion relation proposed by Stokes (23):

$$\omega =\sqrt{g\frac{\left({\rho }_2-{\rho }_1\right)\left|k\right|}{{\rho }_1\cot \left|k{h}_1\right|+{\rho }_2\cot \left|k{h}_2\right|}}.$$

The latter does not take into account the thickness of the pycnocline. Since the salt diffuses trough the water, the thickness tends to increase. Thus, the relation proposed by Stokes is valid momentarily, when the density profile is close to a step. Moreover, when the wavenumber $k\to 0$, Grue’s and Stokes’s expressions are identical, and $\omega \to c_{\varphi }k$.

Numerical Methods.

Let us describe the calculation of the internal wave resistance. Let us suppose that the hull of the ship can be described by a function $f\left(x,y\right)$ and that its position is $X\left(t\right)$. The shape function $f$ is defined such that it is zero outside of the rectangle $]-L/2,L/2\left[\times \right]-B/2,B/2[$ and defined inside by a fourth-order polynomial:

$$f\left(x,y\right)=T\hspace{0.17em}\frac{\left(x^4-{\left(L/2\right)}^4\right)\left(y^4-{\left(B/2\right)}^4\right)}{{\left(LB/4\right)}^4}.$$

This choice defines a smooth yet bulky hull shape with a length $L$, beam $B$, and depth $T$.

First, using Newton’s second law, the motion of the boat is described by the following differential equation:

$$m_b\stackrel{\cdot \cdot }{X}\left(t\right)=-R_t\left(X\left(t\right),\stackrel{\cdot }{X}\left(t\right)\right),$$ [1]

where $m_b$ is the mass of the boat and $R_t$ is the total resistance experienced by the boat. Let us now describe how the wave component of this resistance is determined (the expression of the other components is detailed in the main article).

Using the equation of Bernoulli, and integrating the pressure on the surface of the hull (24), we obtain

$$R_W={\rho }_1{\int }_0^L{\int }_{-W/2}^{W/2}\frac{\partial \varphi }{\partial t}\left(x,y,t\right)\frac{\partial f}{\partial x}\left(x-X\left(t\right),y\right)dxdy,$$ [2]

where $\varphi$ is the velocity potential at the free surface that is supposed to behave like a wall. Using the linearized theory of internal waves, the 2D Fourier transform of the surface potential evolves according to

$$\frac{{\partial }^2\hat{\varphi }}{\partial t^2}={\omega }^2\hat{\varphi }+\hat{g},$$

where $\omega$ is given by the Stokes dispersion relation (23) and $\hat{g}$ is the forcing term that takes into account the motion of the hull:

$$\hat{g}=\left(\alpha \frac{{\partial }^2}{\partial t^2}+\beta {\omega }^2\right)\lambda \left(t,k\right)$$ [3]

with

$$\alpha =\frac{{\rho }_2\coth \left|k{h}_1\right|\coth \left|k{h}_2\right|+{\rho }_1}{{\rho }_1\coth \left|k{h}_1\right|+{\rho }_2\coth \left|k{h}_2\right|}$$

$$\beta =\frac{\left({\rho }_2\coth \left|k{h}_1\right|\coth \left|k{h}_2\right|+{\rho }_1\right){\sinh }^2\left|k{h}_2\right|+{\rho }_1}{\left({\rho }_1\coth \left|k{h}_1\right|+{\rho }_2\coth \left|k{h}_2\right|\right){\sinh }^2\left|k{h}_2\right|}$$

and

$$\lambda \left(t,k\right)=-i\stackrel{\cdot }{X}\left(t\right)\frac{k_x}{\left|k\right|}{e}^{-ikX\left(t\right)}\hat{f}\left(k\right).$$

From a numerical point of view, we rely on an explicit scheme for the motion of the boat and an exact exponential scheme based on the use of the fast Fourier transform (FFT) for the evolution of the interface. On one hand, since the boat is centered in the $y$ axis, the periodicity induced by FFT is equivalent to wall conditions on the sides; on the other hand, we obtain the wall conditions on both ends of the canal by extending the wave deformation in an even fashion for negative values of $x$. Let us describe one iteration of the numerical code, assuming the ship’s position $X$ and velocity $\stackrel{\cdot }{X}$ and the interface potential $\mathrm{\Phi }$ and its impulsion ${\partial }_t\mathrm{\Phi }$ to be known at a given discrete time $t_n$. First, we compute the wave resistance $R_W$ using Eq. 2 from ${\partial }_t\mathrm{\Phi }$ and $X$ known at time $t_n$. Once the resistance is obtained, we update the ship’s position and velocity by solving Eq. 1 with an explicit Euler’s scheme. Finally, we can update $\mathrm{\Phi }$ and ${\partial }_t\mathrm{\Phi }$ by solving Eq. 3 exactly for the dispersive part using the FFT of $\mathrm{\Phi }$ and ${\partial }_t\mathrm{\Phi }$ from the previous step and using an explicit Euler’s scheme for the source term $ĝ$ (which depends on the ship’s position and velocity that were just updated). Finally, the inverse FFT provides us with $\mathrm{\Phi }$ and ${\partial }_t\mathrm{\Phi }$ at time $t_{n+1}$.

A mesh study has been carried out. If a coarse mesh implies errors on the dynamics of the boat, i.e., the acceleration or speed oscillations (Ekman wave-making drag), it has only a moderate impact on the asymptotic behavior (Nansen wave-making drag).

Data Availability Statement.

The authors will share their data, materials, and code upon reasonable request since they cannot be shared on an accessibility repository due to the fact that the Institut Pprime is a zone with restricted regimes according to the French laws on the protection of the scientific and technical potential (https://www.ssi.gouv.fr/guide/protection-du-potentiel-scientifique-et-technique-de-la-nation/).