Noninvasive acoustic manipulation of objects in a living body

Significance

The significance of this work is the development of a technique and technology to use a steerable beam from one source to safely lift and reposition a stone in a living body. The work has direct application to expelling kidney stones or manipulating an ingestible camera. Our work provides a framework for other medical applications, as well as nonmedical uses that require noninvasively moving sizable, dense objects in a free field or within a container.

Abstract

In certain medical applications, transmitting an ultrasound beam through the skin to manipulate a solid object within the human body would be beneficial. Such applications include, for example, controlling an ingestible camera or expelling a kidney stone. In this paper, ultrasound beams of specific shapes were designed by numerical modeling and produced using a phased array. These beams were shown to levitate and electronically steer solid objects (3-mm-diameter glass spheres), along preprogrammed paths, in a water bath, and in the urinary bladders of live pigs. Deviation from the intended path was on average <10%. No injury was found on the bladder wall or intervening tissue.

Over 50 million inpatient surgeries are performed each year in the United States alone (1). Such procedures carry inherent risks of bleeding, infection, postoperative pain, scarring, and complications of anesthesia (2). Surgical complications occur in approximately one out of every six patients (3). Noninvasive surgery is an emerging area of medicine that is rapidly replacing open procedures and can minimize the risks associated with incisions, punctures, or insertion of instruments into the body. Examples of noninvasive procedures include radiosurgery and focused ultrasound surgery, which are currently in use or under development for over 100 different diseases and conditions (4, 5). These methods use different image-guided technologies to ablate tissue or modify its properties, such as increasing drug susceptibility (6). However, controlled manipulation of structures within the body is a significant component of surgery that has not been achieved noninvasively. In this paper, we demonstrate transcutaneous controlled manipulation of a solid object in vivo using specified ultrasound beams. Such a technology could be useful in various instances, e.g., to control an ingestible pill camera, aid steering of catheters, remove an inaccessible foreign body, or reposition an obstructing urinary stone.

Such a demonstration and technology could lead to a method to noninvasively promote clearance of urinary stones and fragments. Urinary stones affect ∼10% of the population during their lifetime, and the prevalence is increasing (7). Urinary stone disease is the costliest nonmalignant urologic disease and widely regarded as one of the most painful in all of medicine (8). Stones 5 mm or smaller in their largest dimension are likely to spontaneously pass through the urinary tract, but larger stones must be fragmented first by endoscopic techniques or shockwave lithotripsy (9). However, fragments often remain and serve as nidi for future stones to grow, and symptoms recur within 5 y in 50% of residual stone cases (9). Ultrasonic propulsion has been shown to noninvasively reposition stones in human clinical trials and is currently being investigated to expel small stones or residual fragments from the kidney so that they pass naturally and possibly asymptomatically (10, 11). A major limitation of the current technology is that the force can only be directed away from the transducer. Methods to move the stone transverse to the acoustic beam or to steer the stone through the complex three-dimensional (3D) path in the urinary tract have not been realized (11). For example, moving small stones from the ureter into the bladder requires transverse motion because the ureter lies parallel to the skin surface (11).

Acoustic trapping is an emerging technology that enables noninvasive manipulation. It follows on the foundational development of optical manipulation for which the 2018 Nobel Prize in Physics was awarded (12). Trapping occurs when the radiation force of a wavefield acts to prevent an object from moving out of a stable position in the beam. Acoustic waves can penetrate through many materials that light cannot, and the radiation forces generated by an acoustic beam can be much stronger than those associated with an electromagnetic wave. The radiation force is a result of the momentum transfer caused by wave scattering from an object placed in the wavefield. The scattering from an object depends on the wavelength and spatial distribution of the wavefield, fluid properties, and object size and composition. In the case of an object smaller than the wavelength, the scattering is a small perturbation of the incident beam consisting of the two highest-order terms, which simplifies the problem mathematically, and physically (13). For larger objects, the radiation forces are more difficult to predict, but can be calculated by integrating the full scattered field over the object’s surface (14–16). In the case of a standing wave, small objects can be trapped at pressure minima or maxima depending on the object density and compressibility relative to the surrounding fluid (17–19). The object can then be manipulated by moving the source or changing the frequency to adjust the location of the pressure extremum where the object is held.

Although the radiation force depends on many factors, a region of low intensity surrounded by a region of high intensity defines an intensity well that can provide a method to trap and steer an object. Vortex beams are commonly used to create such an intensity well (20–23). The vortex is created by varying the phase of the wave emitted across a transducer surface so that it is generating a helical wavefront (24). In this case, the phase must increase linearly with the circumferential angle and helicity must have a pitch so that it is continuous around the circumference. The outcome is destructive interference of the wave on-axis, but constructive interference off-axis, resulting in an intensity ring in the plane transverse to the beam axis. If the ring is placed around an object and shifted transversely, force from the higher-intensity ring on one side of the object will generally “push” it back toward the center of the ring. An object can then be repositioned by manually moving the acoustic transducer, or by using a transducer array and electronically steering the beam by altering the phase of the wave emitted from each element. Movie S1 illustrates steering of a spherically focused beam and a focused vortex beam. Using this concept, an object can be steered controllably in two dimensions transverse to the beam axis.

For our application, it is desirable to use a single source to trap and move an object in 3D. The vortex beam approach can be extended to control the object along the axis as well. In most cases, the axial force of the beam is directed away from the source because backward scattering and absorption of the vortex by the object dominate forward scattering, especially if the object is large or dense (25, 26). However, the object can be axially stabilized when the force pushing the object away from the transducer is counterbalanced by gravity as the force pulling the object toward it. The beam can then be electronically steered to move the object. The state of the art has demonstrated the ability to move small or lightweight objects, including cells under a microscope (27, 28), 100-µm droplets (29) and polystyrene particles (30) in water, or foam balls in air (23, 31).

The goal of the work presented herein was to transcutaneously manipulate an object within a living animal body using the beam from a single transducer. We developed a system (22, 32) and methods to produce 3D manipulation of a millimeter-sized object chosen to mimic a kidney stone. We successfully demonstrate both in a water bath and in live pigs, the ability to execute complex motion to remotely move an object along a path entirely controlled by the acoustic field under ultrasound image guidance. Analysis of intervening tissue exposed during manipulation confirmed the safety of such a procedure.

Results

Beam Synthesis.

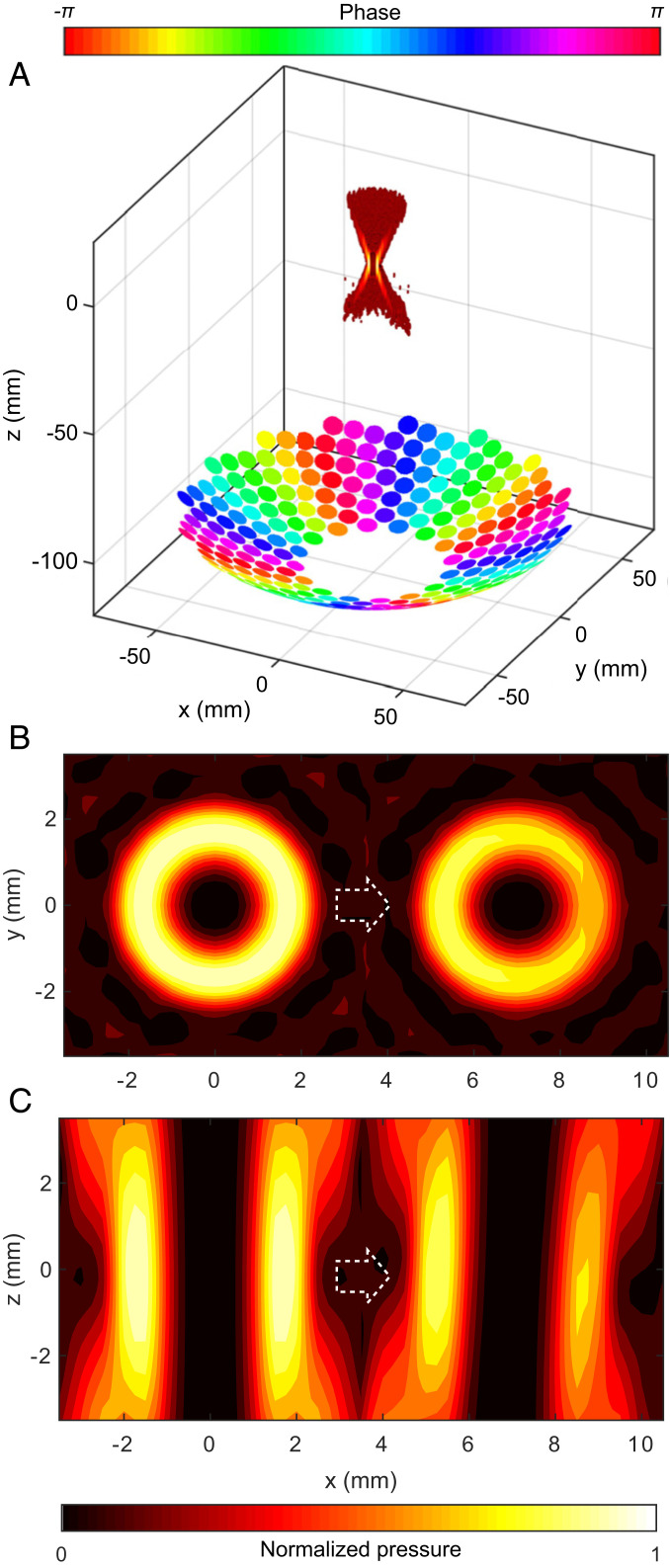
A 256-element, focused array with a 15-cm aperture and a 12-cm focal distance was operated at 1.5 MHz to synthesize vortex beams. Fig. 1 shows the array and the hollow hourglass structure of a vortex beam used for acoustic trapping. The beam is created by altering the phase among elements while their amplitude remains constant. Fig. 1A shows the imposed element-to-element phase delay increases in proportion with the circumferential angle around the array from zero to 2πM, where M is an integer known as the topological charge. M = 0 implies that the entire transducer surface is oscillating in-phase, which produces a spherically focused beam, resulting in a peak rather than a null on-axis at the focus. Otherwise, the magnitude of M controls the diameter of the vortex ring of acoustic intensity or pressure (Fig. 1B), while the sign of M changes the helicity of the wavefront to either clockwise or counterclockwise direction. In this paper, to label the applied beams, we use a nomenclature of M followed by the topological charge with the beam diameter in parentheses. For example, M4 (3.4 mm) denotes a topological charge of alternating pulses of M = 4 and −4 to prevent the object from rotating with the phase of the wavefront (22, 33) as rotation can cause the object to escape the trap and a beam diameter of 3.4 mm measured from peak to peak across the diameter of the ring intensity distribution.

Fig. 1.

A diagram of the element phasing and simulated focal-pressure field of a vortex beam with topological charge M = 4 (A), and transverse (B) and axial (C) slices of the simulated pressure field without focus steering and electronically steered 7 mm horizontally off the axis. The steering to the right is indicated by the white arrows. The pressure amplitude distribution is symmetric when the beam is focused on the array axis but is asymmetric when focused off the axis.

Steering Strategies.

Pressure amplitude distributions of the vortex beams were calculated using the Rayleigh integral (34) and are depicted in Fig. 1 B and C for the vortex M4 (3.4 mm). The Rayleigh integral is a general model for the pressure field produced by a vibrating source, which integrates the acceleration of vibrating point sources over the surface of the source (34). Because of the directivity of the elements which is exacerbated by the curvature of the array, the vortex weakens and distorts as its focus is electronically steered off the axis. Throughout this paper, axis refers to the axis of the array (z axis) and not the acoustic beam axis, which can be steered at different angles. As the array is mounted facing against gravity, steering of the acoustic beam along the z axis is defined as vertical steering, while horizontal steering refers to steering in the transverse xy plane away from the origin, and the zx- and yz planes are referred to as axial planes. The peak intensity across the ring varied by 20% when the ring was moved 5 mm horizontally for M1 (1.4 mm) and 2 mm horizontally for M4 (3.4 mm). Likewise, a 50% decrease in intensity was measured for a spherically focused (M0) beam when the focus was electronically steered 9.1 mm horizontally.

The radiation force was calculated by a theoretical model that was developed for arbitrary beams and elastic spheres of arbitrary size (14). This experimentally validated model (22, 30) represents the beam as a series of plane waves according to the angular spectrum method, and the scattering for each plane wave from the sphere is calculated and summed. The acoustic forces from the scattered field are calculated by integrating over a surface enclosing the sphere. The intensity ring creates horizontal acoustic radiation force F_Ax surrounding the sphere to trap the sphere in the horizontal plane. Vertical levitation is produced from vertical acoustic radiation force F_Az from an intensity ring similar to the sphere’s diameter, which pushes the sphere to a height where it is balanced by the sphere’s weight. Generally, radiation force is not a potential force, although it has been shown as one for spheres that are small compared to a wavelength (13). Here, analogous to the concept of conservative forces derived from potential energy, an effective potential energy is defined as $U_x=-{\displaystyle \int }{F}_{Ax}dx$.

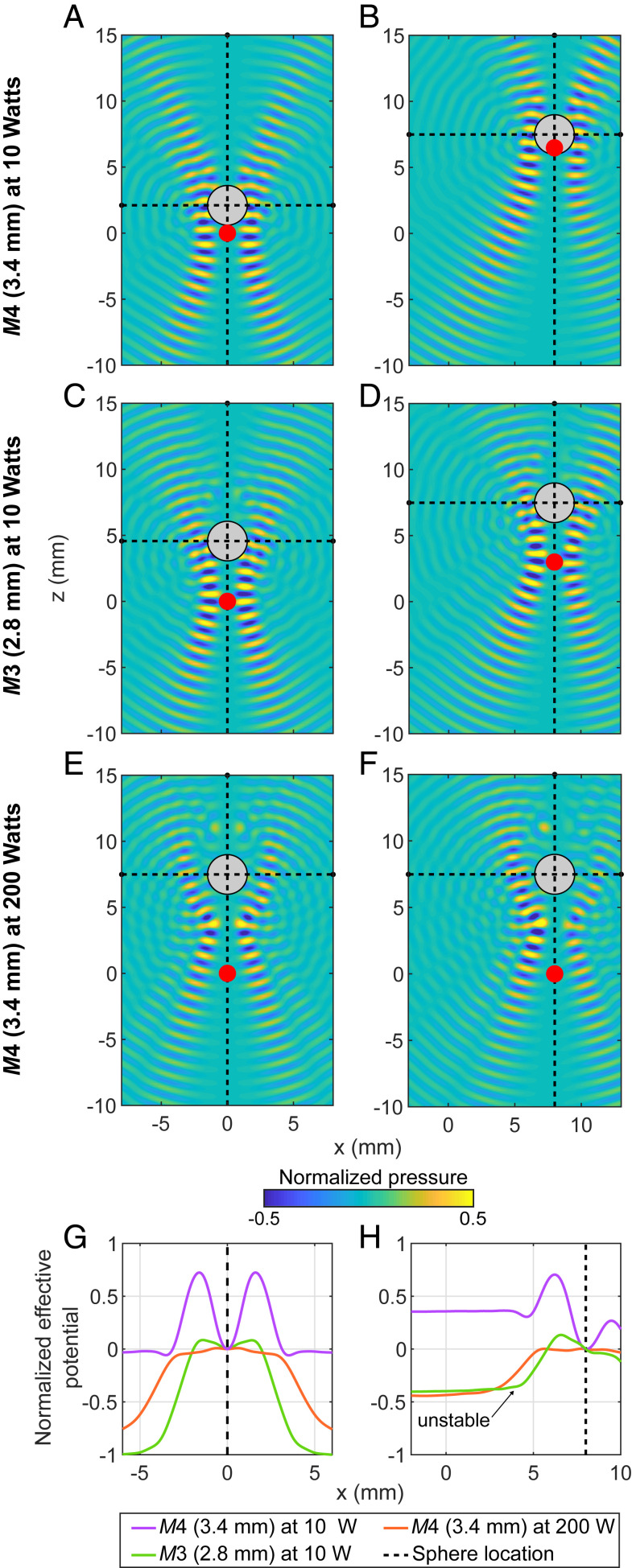
Fig. 2 shows how varying the beam width and acoustic power affects the stability and efficiency of trapping a sphere on-axis and off-axis. A beam slightly narrower than the sphere (Fig. 2C) versus a beam slightly wider (Fig. 2A) at the same power produces greater F_Az so that the sphere is trapped higher in the field and more distal to the acoustic focus. Similarly, comparison of Fig. 2E and Fig. 2A shows that increasing the acoustic power lifts the sphere out of the focus of the trap made with the same beam. Fig. 2G shows that the sphere that sits in the focus rests in the deepest potential well. The right column shows that when the trapped sphere is moved to a new location in the field by steering the beam, the effective energy well (Fig. 2H) becomes asymmetric, and the sphere can fall out. The sphere falls at a shorter steering distance for the shallower well and for the narrower beam. In summary, the beam should be slightly wider than the sphere and the power sufficient to levitate the sphere near the beam focus for the most stable trapping and steering.

Fig. 2.

The simulated position of a 3-mm glass sphere in the vortex beam for beams focused to different locations in the field (Left and Right Columns), for two different beam widths (A–D), and two different acoustic powers W (A, B, E, and F), and the corresponding effective potential energy well U_x of each trap normalized to the extremum value (G and H). In A–F, ultrasound propagates upward and is focused to the red dot. Instantaneous pressure amplitude is plotted. The Left column shows where the sphere sits when the beam is focused at (0, 0), and the Right column shows the beam to position the sphere at the location (8, 7.5). The potential well is deepest for the M4 (3.4-mm) beam at 10 W (G), and the well is lost when the M3 (2.8 mm) beam is moved off-axis to location (8, 7.5) because of the asymmetry of the off-axis beam (H).

In Vitro Manipulation.

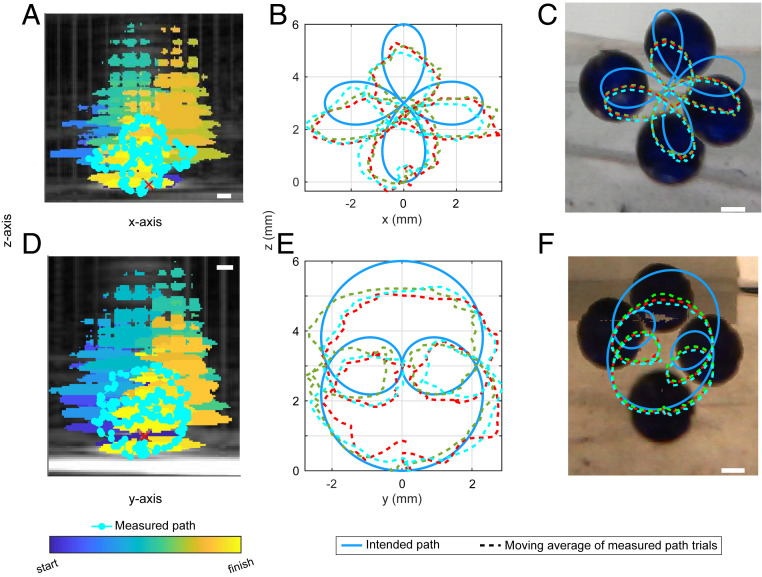
The vortex beam M4 (3.4 mm) at 10-W power was used to trap, lift from a Mylar membrane, and steer in a 3D path a 3-mm glass sphere in a water tank (Fig. 3). Maximum lateral and vertical calculated radiation forces were equivalent to the gravitational force on 40 mg or twice the mass of the sphere. The manipulation was executed slowly to minimize drag force caused by the relative motion between the fluid and the sphere. The total distance moved was 6 mm vertically and 6 mm horizontally. Fig. 3 shows the intended path and the path measured by coaligned axial ultrasound imaging and two orthogonal cameras. The mean and SE of the absolute value of the distance between the intended path and ultrasound-measured path was 0.44 ± 0.06 mm (three repetitions), with a maximum distance of 1.17 ± 0.18 mm, and between the intended path and camera-measured path was 0.47 ± 0.51 mm, with a maximum of 1.3 ± 0.11. The distance between the measured point and the closest point on the intended path was calculated, and on average, the sphere followed the intended path to within 10% of the distance from the focus.

Fig. 3.

Acoustic manipulation of a 3-mm glass sphere in vitro along a 3D path seen from two angles. An ultrasound imaging transducer was placed in the center opening of the array, and its 2D image was aligned to correspond with one camera (A) and then with an orthogonal camera (D). The red “×” marks the acoustic focus of the array which was used as a reference in ultrasound to target the sphere. Images displayed are superimposed from Movies S2, S3, and S4. The ultrasound images of the sphere were identified by different colors at different times in postprocessing (A and D). The measured paths (displayed as a moving average) are shown in each image and the intended paths are also shown in B, E and C, F. The maximum discrepancy occurred farthest from the focus where the effective potential well was the shallowest. (Scale bar, 1 mm.)

A specific technique was developed to trap the sphere and then manipulate the sphere in vitro, which was then used in vivo also. The sphere was targeted on-axis about 2–3 mm distal to the acoustic focus of the array as indicated in the ultrasound image. In order to nudge the object into the exact final axial alignment, a wide-vortex M40 (7.8 mm) was initially transmitted followed by descending topological charges until reaching M4 (3.4 mm). This was done at low power as starting with a narrower beam or a higher power level could result in expelling the sphere. Once trapped, the sphere was levitated by increasing the power to the expected level, and the exact vertical location was known by the ultrasound image. If no levitation was observed, the array was mechanically raised using fine movement achieved by a stepper motor. If unsuccessful, the array was mechanically lowered, and the process repeated at slightly higher power. When instead the procedure was started with the sphere located prefocally, the sphere was accelerated through the focus, where vertical radiation force is largest, and ejected from the trap. Once trapped, the sphere was moved in any direction electronically or by moving the array.

In Vivo Manipulation.

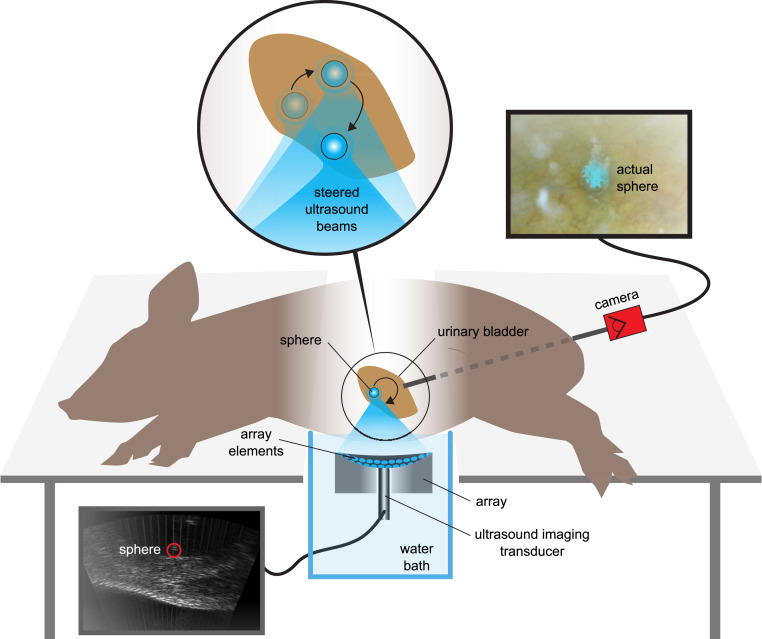
A 3-mm glass sphere was manipulated along three preprogrammed paths in the urinary bladders of three live pigs that were under general anesthesia. The vortex beam M4 (3.4 mm) at about 10-W power was used. The acoustic window was through the abdomen with the pig in a lateral recumbent position, as shown in Fig. 4.

Fig. 4.

Transcutaneous acoustic manipulation of a 3-mm glass sphere inserted through the ureter into the bladder of a pig. The array and center-mounted ultrasound imaging probe were submerged in a water tank with the side of the pig midsection under the water level for acoustic coupling. The glass sphere was painted blue for ease of observation by the camera in the bladder. The ultrasound scanner was synchronized with the manipulation pulses for real-time imaging at 15 Hz.

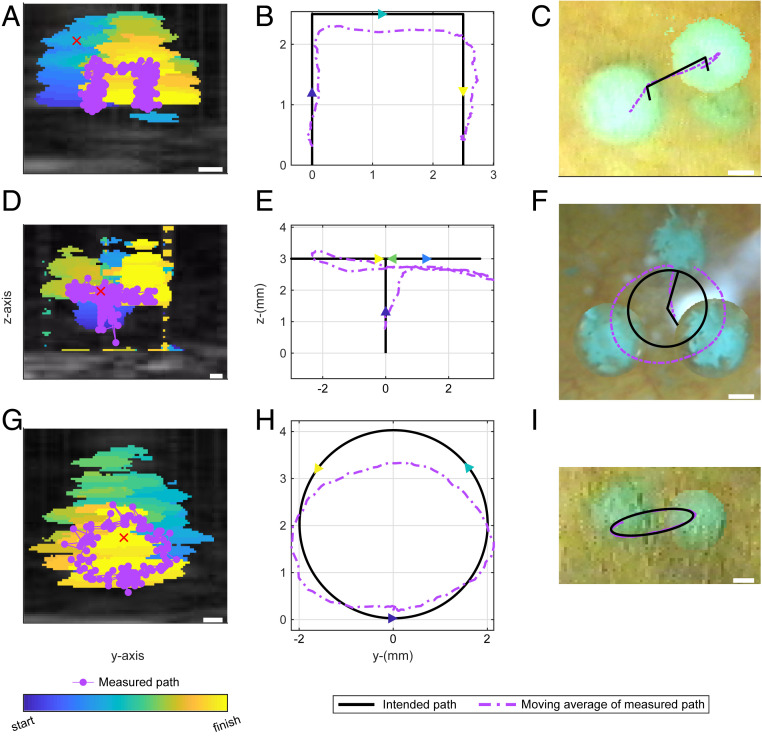
Spheres were successfully moved in three separate paths in vivo. The maximum intended vertical and horizontal excursions of the three paths were 3, 3, and 4 mm and 3, 6, and 4 mm, respectively. The body wall thickness traversed by the beam was measured from ultrasound images to be between 18 and 31 mm. Fig. 5 shows superimposed ultrasound and camera images of the three paths. Movies S5–S7 correspond to the images in Fig. 5 D, F, and G. In addition, Movie S8 shows the result of electronically trapping the sphere and then moving the sphere by mechanically moving the array.

Fig. 5.

Acoustic manipulation of a 3-mm glass sphere in a pig bladder along three different paths. The sphere was levitated along the acoustic axis, moved laterally, and lowered in path 1 (A-C). In path 2 (D–F), the sphere was levitated, then moved in a circular path in a transverse plane where it moved in and out of the ultrasound imaging plane as detected by change in image intensity (Movies S5 and S6). Path 3 (G–I) was a vertical circle in yz focal plane (Movie S7). As in Fig. 3, the superimposed ultrasound images are color-coded to show the sphere’s motion; the position maps for the ultrasound are in the center; and the superimposed camera images are on the right. Each image shows the 2D projection of intended path. (Scale bar, 1 mm.)

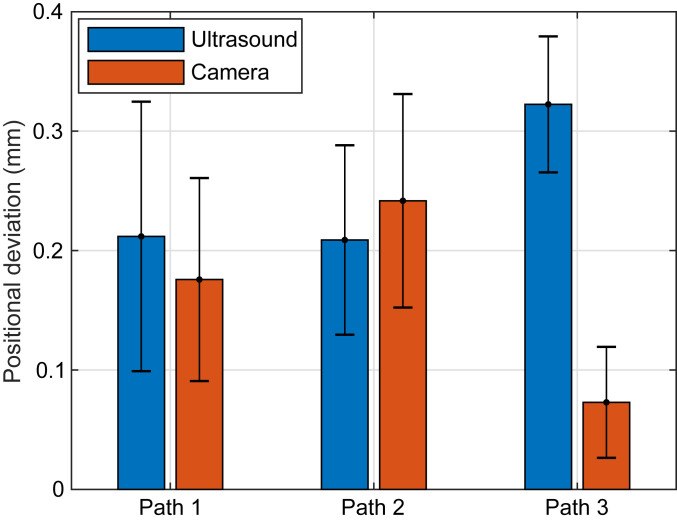
Fig. 6 shows the mean positional deviation between intended and measured paths for the ultrasound and camera measurements for each of the three paths. The best-fit projected two-dimensional (2D) plane of the intended 3D path was used for comparison to the camera measurements. The mean ultrasound-measured positional deviations as a percentage of the maximum axial excursions were 7.5 ± 3.9, 9.5 ± 3.6, and 8.0 ± 1.5% for the three paths. The mean camera-measured positional deviations as a percentage of the maximum lateral excursions were 6.4 ± 3.2, 10.8 ± 2.2, and 1.0 ± 1.3% for the three paths. The mean camera-measured deviations for paths 1 and 3 were low because the angle of recording was from above the sphere, so the difference in height was not captured.

Fig. 6.

Absolute value of the distance between measured and intended paths of a 3-mm glass sphere in vivo. Paths 1 and 2 were performed in all 3 pigs for a total of 13 and 10 trials, respectively, while path 3 was performed in a single pig 6 times. The mean and SD for all of the trials of each path are shown for ultrasound (blue bars) and camera (orange bars) measurements. The average deviation from the intended path is within 10% of the farthest steered distance from the geometric focus of the array.

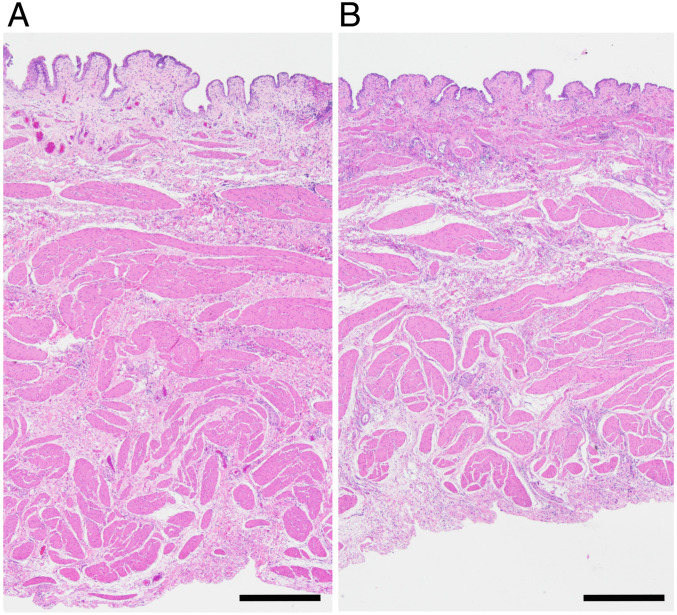
After ultrasound exposure, each pig was evaluated for tissue injury to assess the safety of acoustic manipulation in vivo. No gross injury was observed to the bladder wall in any of the camera-recorded movies. Upon necropsy, no gross injury was observed in the targeted regions as a result of the ultrasound exposure, although some minor injury (i.e., puncture from the guidewire) was observed related to the insertion of the sphere. Gross evaluation of the intervening tissue showed no signs of damage. No histological evidence of injury was observed in Hematoxylin and Eosin (H&E) stained cross-sections of the targeted region of the bladder walls of the three pigs. Histological evaluation showed no signs of damage to the bladder mucosa, submucosa, or underlying tissue from any of the ultrasound exposures (Fig. 7).

Fig. 7.

Representative images of H&E stained cross-sections of the bladder wall taken from a region unexposed (A) and exposed (B) to the trapping ultrasound. No signs of damage were observed. (Scale bar, 500 μm.)

Discussion

The physical foundation to manipulate objects has been known, and others have previously manipulated small or lightweight objects, even pulled specific objects toward the source (26, 30). Here, specific beams were synthesized with a multielement ultrasound phased array and demonstrated to manipulate a 3-mm glass sphere inside a living body, without harmful effects to the intervening tissue. The objects were moved by lifting and electronic steering in the 3D fluid space and by moving the array and dragging the object along the bladder surface. Simply increasing the output power did not improve the trapping, and subtler techniques were developed and described.

The limitations of the present work include theoretical consideration of only spherical shapes and the small range of motion. However, the paint on the glass spheres used in vivo tended to slough and biological material could agglomerate, making them not perfectly spherical when moved. In addition, targets such as urinary stones may be of mixed and heterogeneous composition and contain fluid-filled voids, which affect acoustic scattering. When a vortex beam is used to move an irregularly shaped or heterogeneous object, the object is more likely to spin and slip from the trap, although we have been able with iterative selection of pulsing parameters to trap and move irregular natural stones in 2D (against a surface) and 3D.The design of our array limited the distance the objects could be moved off-axis, and our future work will extend to designing arrays with larger range capability. In particular, lowering the frequency so the wavelength is larger than the object would minimize the effects of geometric heterogeneities and flattening the array would allow a larger manipulation region.

The in vivo tissue barrier possessed particular challenges in that the heterogeneous tissue moving with respiration weakens and disrupts the beam through attenuation and aberration. Existing techniques to compensate for tissue aberration, for example, time-reversal acoustics (35–37), were not employed but would arguably improve the trapping stability and efficiency. Most importantly, our application appeared safe. The highest acoustic exposure, used in the first pig, reached a spatial-peak, temporal-average intensity I_SPTA of 67 W/cm², a spatial-peak, pulse-average intensity I_SPPA of 134 W/cm², and a nonderated mechanical index (MI) of 1.14, where this nonderated MI is the peak pressure measured in water of 1.4 MPa divided by the square root of frequency of 1.5 MHz. For reference, the regulatory limits placed on diagnostic ultrasound instruments are I_SPTA = 0.720 W/cm², I_SPPA = 190 W/cm², and MI = 1.9, where MI uses a peak negative pressure measured in water derated to a lower pressure in situ to account for attenuation of the ultrasound by the tissue (38). The parameters applied during experiments are within the diagnostic limits for I_SPPA and MI, which define safety related to the cavitational mechanism of injury. I_SPTA, which defines the potential for thermal tissue injury, exceeded the diagnostic limit by a factor of 100, but the diagnostic level is conservatively set based on thermal risks to developing embryos. Although gross inspection and histological analysis indicated no apparent thermal effects to the tissue, we did not measure temperature changes in these experiments, and further efforts will be necessary to define the thermal safety margin for these exposures in all targeted tissue such as kidney parenchyma.

The most unique result of acoustic manipulation presented in this paper is toward its medical application. The experiment simulated expelling kidney stones from the urinary collection system. Our team is currently investigating pushing but not trapping stones with acoustic radiation force in human clinical trials. Similar to a stone in the bladder, a movable kidney stone rests in the urine-filled space of the kidney; however, the major differences in application are ribs and intestines that restrict the acoustic window to the kidney more so than to the bladder, and the space for maneuvering a stone within the kidney is smaller than within the bladder. In some ways, it may be easier to move the stone in the confined space of the kidney, because the stone may be pushed against the tissue lining the urine space and then the stone may be moved in 2D rather than 3D. Overall, working within an enclosed fluid space mitigates acoustic streaming, where fluid is accelerated by the acoustic waves over the propagation path and flows away from the transducer. A 2D or 3D path might be preprogrammed from available medical imaging to expel a stone from the kidney. Movie S8 shows that the sphere can be moved at least 10 cm horizontally. Moreover, it can be moved while in contact with and overcoming the friction of the tissue surface. With mechanical steering, a deep potential well can be maintained for the full distance because the trap is always on-axis at the focus (Fig. 2). However, mechanical steering requires a larger acoustic window and can fall apart when motion of the array requires the beam to transverse an area of low acoustic transmission such as rib or bowel gas. The work also opens the door to other possible medical applications such as steering an ingestible camera, guiding a catheter tip, or removing a foreign object from the body. Not described here but described in previous studies and seen in some supplemental movies, the vortex beam can create spinning of the spheres. There may be an application to turning an ingestible camera for a 360° view.

Conclusion

This work demonstrated noninvasive controlled manipulation of solid millimeter-sized objects within a living organism at ultrasound power levels that produced no apparent injury to surrounding tissue. With the aid of numerical modeling, specific beams were produced with a focused ultrasound phased array to synthesize acoustic traps. Such traps were found to capture and move spherical objects w and in vivo. The spheres were both levitated and electronically steered along preprogrammed paths with good accuracy.

Methods

Beam Synthesis.

A multielement phased array was driven using a Verasonics Data Acquisition System (VDAS) (V1, Verasonics LTD.) attached to a 1,200-W power source (QPX600DP, Aim-TTI). All array elements project into a region where their harmonic waves or multicycle bursts interfere and are positioned on a concave spherical surface to concentrate the wave energy within a region around the center of curvature, the focus. The elements were tuned to transmit acoustic waves equal in amplitude and with no relative phase delay between elements when focused to the center of curvature of the array (32). A specific field structure or beam is created by judicious phase delays among the waves transmitted by the elements. The phase delay on element i to produce a vortex beam was determined by the element’s location circumferentially on the aperture of the array with one circumferential loop adding a delay equal to an integer multiple of the acoustic period (2πM). Electronic steering of the vortex beam was achieved by superimposing the phase delay on each element appropriate to refocus the beam at the new location (Movie S1). The phase delay required for steering is defined as the distance from the geometrical focus of the array to the desired location. Thus, the total phase delay of element i to steer the vortex to location p is defined as follows:

$${\varphi }_i=M\times \arctan \left(x_{i2}/x_{i1}\right)+k\times \left[R-{\displaystyle \sum }_{j=1}^3\sqrt{{\left(x_{ij}-p_j\right)}^2}\right],$$ [1]

where ϕ_i is the phase delay on the element i, R is the radius of curvature of the array, x_ij is the x_j coordinate of element i, p_j is the j coordinate of point p along the desired steering path, and k is the wavenumber (22).

The phase delays used to synthesize vortex beams result in a helical wavefront in space (24, 39, 40) that carries an angular momentum component (41–44). This angular momentum can cause rotational instabilities and ejection of objects from the acoustic traps. Therefore, for all experiments, vortex beam traps were synthesized by sending two consecutive vortex pulses of equal duration with opposite topological charge signs and same magnitude (i.e., ± M) to negate the effects of angular momentum and eliminate the net radiation torque (22, 33, 45, 46). The acoustic pulse transmitted initially was M₊ for 661 μs, directly followed by M_- for 661 μs, for a total on-time duration of 1.32 ms repeated every 2.64 ms (i.e., at 50% duty cycle). The pulse duration time of 661 μs for a specific vortex helicity was calculated to be shorter than the minimum acceleration time, $\tau =I/\left(8\pi a^3\rho \nu \right)$ = 374 ms (43) needed for a fully absorbing sphere to reach a terminal angular velocity due to drag torque, where I and a are, respectively, the moment of inertia and radius of the sphere and ν is the kinematic viscosity of the medium.

Ultrasound Imaging.

An ultrasound imaging probe P6-3 (Philips) consisting of 128 linear elements and operating at a center frequency of 4.5 MHz was mounted in the center opening of the array to image the acoustic manipulation near the focal region of the array. The P6-3 had its acoustic axis aligned with that of the 256-element array and programmed to image to a maximum distance of 14 cm along the z direction, being the axis of the array, in either xz- or yz axial plane. The ultrasound imager was driven by a separate VDAS and was synchronized with the 256-element array to send five imaging rays to the specified depth during the off-time of the acoustic manipulation transmits resulting in a full ultrasound image approximately every 26 acoustic manipulation pulses.

In addition to imaging and tracking the motion, the P6-3 probe was used to target the sphere to be manipulated in vitro or in vivo by hard-coding a red cross-hair in the ultrasound image marking the natural acoustic focus of the array. The cross-hair location was marked on the ultrasound image as the location of the maximum acoustic focal pressure recorded by a hydrophone. A parallel screen-capturing script was coded into the VDAS to record the ultrasound motion as movie data.

In Vitro Acoustic Manipulation.

A 3-mm glass sphere was colored using a black marker and was placed over a thin membrane parallel to the aperture of the array in the transverse xy plane. Two underwater cameras were placed orthogonal to each other and were recording the motion in the xz- and yz planes at 30 frames per second. Images were backlit with a camera-mounted light-emitting diode, so the spheres appeared black. The P6-3 imaging probe recorded the ultrasound motion in orthogonal xz- and xy planes, at different runs. The motion path was defined by the following equations along the xy- and xz planes:

$$r_{xy}=r_0\sin 2\theta \hspace{0.17em}\mathrm{and}\hspace{0.17em}{r}_{xz}=-r_0\cos 2\theta ,$$ [2]

where r₀ = 3 mm, and θ varies from 0 to 2π radians.

In Vivo Acoustic Manipulation.

All procedures were approved by the University of Washington’s Institutional Animal Care and Use Committee. Three female pigs (40–42 kg) were used to demonstrate the reproducibility of the procedure. On the day of study, animals were sedated with 4 mg/kg tiletamine/zolazepam and maintained under a surgical plane of anesthesia with isoflurane. All animals were instrumented to monitor heart rate, electrocardiogram, blood oxygen saturation, and temperature during the study. The lower abdomen was depilated, imaged with ultrasound to determine the bladder orientation (left- or right leaning) and washed. A single 3-mm glass sphere was implanted in the bladder of each animal using a cystoscope and surgical stone retrieval basket via the urethra. The camera was kept inserted throughout the study to visualize and record sphere movement and evaluate changes to the bladder wall after each manipulation of the sphere. After the last manipulation, the camera was removed, and the animal was euthanized. The bladder was removed while preserving its orientation with respect to the acoustic axis, and the tissue in the ultrasound path was grossly evaluated. The excised bladder was opened, and the treatment region was inspected for any gross changes. Two samples from the treatment region were fixed in 10% neutral buffered formalin for histological evaluation. The bladder wall was embedded in cross-section and sections were stained with H&E for injury assessment.

Data Availability.

The authors confirm that the data supporting the findings of this study are available within the article and its supporting information. Additional data related to the work may be obtained from the ResearchWorks Archive at https://digital.lib.washington.edu/researchworks/handle/1773/45574.