Significance
Global climate simulations are typically unable to resolve wind and solar data at a resolution sufficient for renewable energy resource assessment in different climate scenarios. We introduce an adversarial deep learning approach to super resolve wind and solar outputs from global climate models by up to 50×. The inferred high-resolution fields are robust, physically consistent with the properties of atmospheric turbulence and solar irradiation, and can be adapted to domains from regional to global scales. This resolution enhancement enables critical localized assessments of the potential long-term economic viability of renewable energy resources.
Keywords: climate downscaling, deep learning, adversarial training
Abstract
Accurate and high-resolution data reflecting different climate scenarios are vital for policy makers when deciding on the development of future energy resources, electrical infrastructure, transportation networks, agriculture, and many other societally important systems. However, state-of-the-art long-term global climate simulations are unable to resolve the spatiotemporal characteristics necessary for resource assessment or operational planning. We introduce an adversarial deep learning approach to super resolve wind velocity and solar irradiance outputs from global climate models to scales sufficient for renewable energy resource assessment. Using adversarial training to improve the physical and perceptual performance of our networks, we demonstrate up to a resolution enhancement of wind and solar data. In validation studies, the inferred fields are robust to input noise, possess the correct small-scale properties of atmospheric turbulent flow and solar irradiance, and retain consistency at large scales with coarse data. An additional advantage of our fully convolutional architecture is that it allows for training on small domains and evaluation on arbitrarily-sized inputs, including global scale. We conclude with a super-resolution study of renewable energy resources based on climate scenario data from the Intergovernmental Panel on Climate Change’s Fifth Assessment Report.
Many aspects of human life, such as energy, transportation, and agriculture, rely on forecasting atmospheric and environmental conditions over a wide range of spatial and temporal scales. Short-term forecasts drive operational decision making, medium-term weather forecasts guide scheduling and resource allocations, and long-term climate forecasts inform infrastructure planning and policy making. Numerical models are tailored for the relevant scale-specific physics, computational resources, and time frames associated with each application; however, simulating all relevant scales is generally intractable.
One particularly difficult scale mismatch arises in the context of assessing energy resources in future climate scenarios. The sensitivity of energy markets (1), renewable energy resources (2, 3), and power systems operation (4) and planning (5) to changes in climate have been the subject of many recent studies. These studies generally rely on a global climate model (GCM) to produce wind and solar data. The typical GCM configuration used in production runs has a resolution of around 1°, or about 100 km close to the equator. Such a resolution is insufficient to accurately assess renewable energy resources, which typically require resolution finer than 10 km, preferably 2 km (6). Consequently, there is a great need for efficient and physically accurate methods to enhance the resolution of GCM output for studying the energy impact of different climate scenarios.
In order to decrease the cost of generating high-resolution (HR) data, various machine learning (ML) techniques have been implemented as part of the GCMs. Since ML takes a statistical approach to making predictions, it is not limited to humans’ understanding of the problem nor does it require solving complex systems of equations. Random forests have been used to solve GCM subgrid convection parameterizations (7), and nearest-neighbor tree hybrid algorithms have approximated long-wave radiation in the National Center of Atmospheric Research (NCAR) Community Atmospheric Model (8). Deep feed-forward neural networks have successfully learned how to model subgrid processes in cloud-resolving models (9). These models, among others (10–12), have demonstrated the advantages of incorporating ML algorithms into weather forecasting by dramatically decreasing the computational cost or improving resolution, leading to calls for hybrid data-driven and physics-based approaches to earth system modeling (13).
In this paper, we present an alternative method of generating HR climate data by enhancing wind and solar GCM outputs using a deep learning technique for a classical image processing problem known as super-resolution (SR). The proposed method produces high-quality output fields using adversarial training that learns and preserves physically relevant characteristics. We demonstrate that this technique can efficiently perform SR on different datasets with variable resolution enhancements and for fields on regional to global scales. The code for the network and its trained weights have been made available (14).
Background
Single-image SR is the process of taking a low-resolution (LR) image and producing an enhanced image that approximates the true HR version of it (15). This framework is in contrast to video SR or multiple-image SR where information overlap within moving pixels helps inform the image enhancement process. For convenience, we refer to single-image SR simply as SR for the remainder of this manuscript. Typical naïve approaches to image SR include bilinear or bicubic interpolation of the LR pixels. This has the advantage of not requiring any training data; however, interpolation tends to significantly smooth out the image and miss small-scale textures and sharp edges. Classic SR algorithms attempt to reconstruct these features by learning priors for edge properties (16, 17), modeling distributions for large gradients (18, 19), and using higher-order statistics to inject textures (20, 21). Other approaches leverage emerging ML tools to learn complex mappings between example pairs of LR/HR images (22, 23).
Similar challenges arise in scientific research, where inadequately resolved data commonly result from insufficient computational resources, physical limitations, or incomplete information. The ability to enhance the resolution of these spatially dependent data fields—often referred to as downscaling—has long been an area of interest (24, 25). Downscaling can be performed by refining coarse data from sparse measurements using data assimilation techniques (26). For GCMs, dynamic downscaling is the preferred method for enhancing data resolution where coarse climate data are used as boundary/initial conditions for solving a refined model on a subregion of the original domain (27). However, these techniques still struggle from issues of smoothing out critical small-scale features or requiring high computational costs.
Recently, deep convolutional neural networks (CNNs) have emerged as a promising technique to performing image SR (28–31)—naturally leading to interest in exploring how to apply these techniques to scientific data. Deep learning-based SR has been performed on various remote sensing datasets such as satellite imagery (32) and sea surface temperature measurements (33). Additionally, these techniques have been used to enhance simulation outputs such as data from models for heat prediction in urban areas (34) and simulated turbulence data (35, 36). For climatological data fields, deep CNNs have successfully increased the resolution of short-term regional precipitation forecasts by 5× (37) and (38). Both studies provide a solid foundation for weather-based SR; however, the scales of the downscaled data are still too coarse to capture features that are critical in informing localized grid resiliency and resource assessment studies.
Data and Methodology
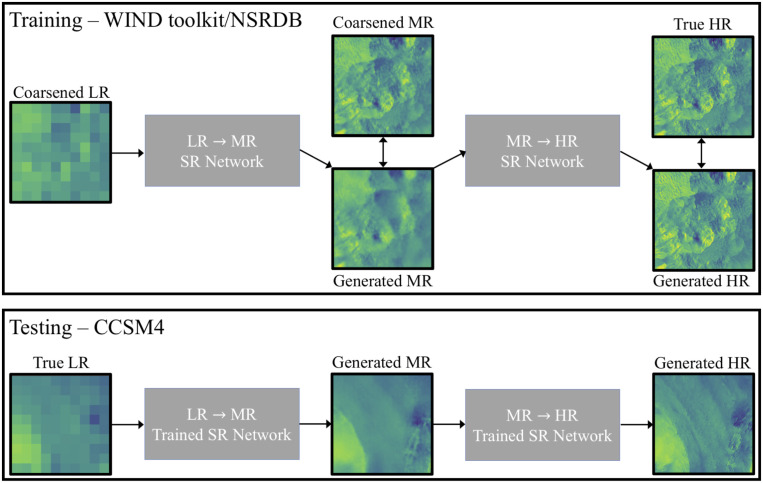
In this paper, we perform SR on GCM data produced by NCAR Community Climate System Model (CCSM) (39, 40) as part of a future climate scenario used in the Intergovernmental Panel on Climate Change’s Fifth Assessment Report. We train a deep fully-convolutional neural network to super-resolve wind velocity and solar irradiance fields. Our SR network is first trained and validated on coarsened HR data obtained from the National Renewable Energy Laboratory (NREL) Wind Integration National Database (WIND) Toolkit (41–44) and the National Solar Radiation Database (NSRDB) (45) before being evaluated on CCSM data. The proposed methodology considers three levels of data resolution—LR, medium resolution (MR), and HR—and implements a two-step procedure that trains two distinct SR networks to perform the LR MR and MR HR mappings. We explore the various data sources and resolutions, network architectures, and the purpose behind the two-step methodology in the remainder of this section. Ultimately, the SR process is capable of downscaling coarse CCSM data to the resolution of the WIND Toolkit and NSRDB data— and jumps in resolution, respectively.
Testing and Training Data.
The testing datasets for the two scenarios are constructed from the Coupled Model Intercomparison Project (CMIP) 5 multimodel ensemble r2i1p1 experiment “1% per year ,” version 20130218, generated by NCAR CCSM. The CCSM data contain daily averages of the various meteorological quantities projected out to years 2020 to 2039 with a spatial resolution of 0.9° latitude × 1.25° longitude. To minimize distortions near the poles, we only use data from latitude and assume an approximate grid spacing of km. The wind velocity data contain easterly and northerly wind components, denoted by and , respectively. We use the lowest vertical slice of the CCSM dataset, which uses a hybrid sigma-pressure vertical coordinate system. This slice most closely matches the nature of the training data, discussed later in this section. Solar data are composed of the direct normal irradiance (DNI) and diffuse horizontal irradiance (DHI) as these values are the most useful for solar power prediction. DNI and DHI are computed from the CCSM’s surface downwelling shortwave radiation, which predicts global horizontal irradiance (GHI). DNI is approximated from GHI using the Direction Insolation Simulation Code model (46), and DHI is computed using the standard formula
| [1] |
where is the solar zenith angle and , , and are DHI, GHI, and DNI, respectively. To obtain average hourly GHI values for this decomposition, we apply the time-dependent autoregressive Gaussian model (47) to the average daily GHI values obtained from the CCSM.
Training data in the WIND Toolkit contain HR wind velocity fields used for wind farm power modeling over the continental United States. We use 100-m height wind speed and direction, which are converted to easterly and northerly wind velocities to match the CCSM data. The data are sampled at a 4-hourly temporal resolution for the years 2007 to 2013. The WIND Toolkit has a spatial resolution of approximately 2 2 km. The NSRDB offers HR (0.04° latitude × 0.04° longitude) data for solar irradiance over the continental United States. This roughly corresponds to a 4-km spatial resolution. Solar training data are composed of DNI and DHI sampled hourly during daylight hours (approximately 6 AM to 6 PM) for 2007 to 2013.
To downscale the coarse CCSM data, we first need to train the network with corresponding pairs of lower- and higher-resolution data. Recall that the proposed methodology uses a two-step SR process of LR MR and MR HR transformations. The HR data in each case correspond to the full-resolution data from the WIND Toolkit and the NSRDB. To generate the training dataset for the wind velocity problem, WIND Toolkit data are partitioned into 1,000 1,000-km patches (i.e., pixels of size 2 km). Each patch is coarsened down to its corresponding MR ( 10-km pixels) and LR ( 100-km pixels) via an average pooling of each or patch of HR data, respectively. The NSRDB data are processed in a similar manner with 2,000 2,000-km HR data patches consisting of pixels of size 4 km. The corresponding MR and LR patches consist of 100 100 20-km pixels and 20 20 100-km pixels, respectively. This results in 42,355 training examples in the WIND Toolkit dataset and 50,075 training examples in the NSRDB dataset. Approximately of the training examples are held out for validation in each case. These characteristics are summarized in Table 1.
Table 1.
Data summary
| Model | CCSM4 | WIND Toolkit | NSRDB |
| Institute | NCAR | NREL | NREL |
| Data | Wind and solar | Wind | Solar |
| Spatial resolution | 0.9° lat × 1.25° lon | 2 km | 0.04° |
| Years | 2020–2039 | 2007–2013 | 2007–2013 |
| Training size | NA | 37,972 | 45,109 |
| Testing size | 7,300 | 4,383 | 4,966 |
NA, not applicable; lat, latitude; lon, longitude.
Network Architecture and Training.
For this work, we require two SR networks for the LR MR and MR HR steps. Each network has a similar architecture that is based off of the state-of-the-art Super Resolution Generative Adversarial Network (SRGAN) (48) with several modifications. Each network is a deep fully convolutional (49) neural net with 16 residual blocks (50) with skip connections (30, 51). All convolutional kernels are and are followed by rectified linear unit activation functions. Experimentation on subsets of the training data uncovered the need to remove batch normalization layers from the Ledig et al. (48) architecture, which were found to hinder the network’s ability to transfer to data coming from different models. Other differences in the proposed network include adapting the SR layers to accommodate the larger-resolution jumps being performed and adjusting the network input layers to consist of two data channels corresponding to either wind velocity components or solar irradiance components. This is in contrast to the three RGB channels typically used for image processing. Finally, we note that since the networks are fully convolutional, they are agnostic to the size of the input data—a property that enables training on smaller patches of the data while running on larger fields in deployment.
The two-step SR process is shown in Fig. 1. For the first SR step, the network is trained on LR/MR data pairs to perform and SR for the wind and solar data, respectively. In the second step, full-resolution data from the WIND Toolkit and NSRDB are matched with the corresponding patches of generated MR data. The second network is trained to learn the mapping from generated MR to HR data, resulting in total resolution enhancements of and for the wind and solar data, respectively.
Fig. 1.
The two-step SR process.
The proposed two-step process manages the complexity of performing such large jumps in resolution better than a single network. A increase in spatial resolution for two-dimensional data means that each pixel is replaced by 2,500 pixels containing all of the small-scale information lost in the coarse data. We experimented with a single-network approach but found that the network did not have the expressive capacity to learn the complex relationships in the data sufficiently well enough to perform the large SR jumps accurately. Network capacity is typically increased by using deeper networks; however, building and training such a complex network come with several difficulties. Networks are trained using stochastic gradient descent with gradients computed using backpropagation. Backpropagation is known to suffer from vanishing gradients in deep networks, where gradient values for each layer tend toward zero and result in slow training. Additionally, deeper layers in the network depend on the output from earlier layers, but all layers are updated simultaneously in the training process. In deep networks, this can require more iterations for the network to converge since deeper layers cannot be appropriately tuned until the shallow layers are essentially fixed. Experiments with a much deeper single-network approach exhibited this prohibitively slow training, leading to the proposed two-step process. Furthermore, the two-step approach enables verification of intermediate results to ensure the network is generating physically consistent fields.
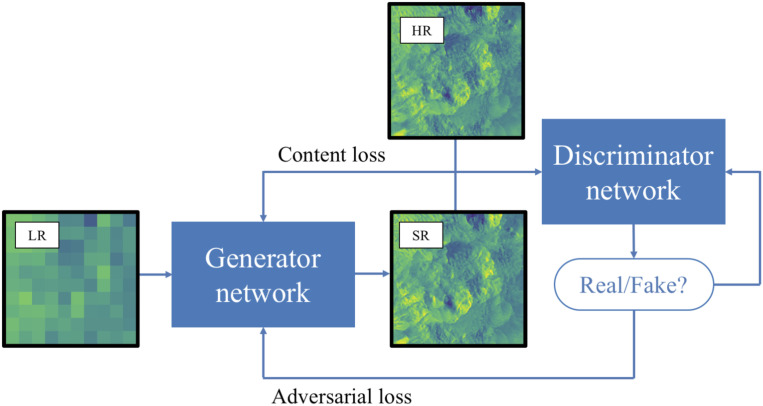
The networks are trained using the generative adversarial network (GAN) approach (52). GANs employ two networks for each resolution enhancement step: 1) a generator and 2) a discriminator . GANs have been able to produce realistic super-resolved images from lower-resolution input images (48, 53). Since the SR process is an inherently ill-posed problem (i.e., a given lower-resolution input could plausibly be mapped to many super-resolved outputs), GANs provide a method for inserting physically realistic, small-scale details that could not have been inferred directly from the coarse input images. The generator network performs SR by mapping input patches of coarse data to the space of the associated higher-resolution patches, , where and denote the spaces of the lower- and higher-resolution data fields, respectively. The discriminator attempts to classify proposed patches as real (i.e., coming from the training set) or fake (i.e., coming from the generator network). That is, where the output is the probability that a given field came from the training data. The two networks are trained against each other iteratively, and over time, the generator produces more realistic fields, while the discriminator becomes better at distinguishing between real and fake data. This training procedure is typically expressed as a minmax optimization problem,
| [2] |
where is the true higher-resolution field and is the input lower-resolution field.
Eq. 2 defines the loss functions we wish to train the networks against. The loss function for the discriminator network is given by
| [3] |
adopting the convention in neural network training that we seek to minimize the loss function. Based on Eq. 2, the loss network for the generator should be defined by
| [4] |
However, in practice this loss function suffers from shallow gradients early in the training procedure. We can reformulate this loss function as
| [5] |
which has the same optimum as Eq. 4 and has better gradients for faster training. The loss function in Eq. 5 is subscripted with “adversarial” because it only makes up one component of the generator loss function. The full-generator loss function is composed of content and adversarial terms,
| [6] |
where . The adversarial loss is from Eq. 5 and captures the ability of the generator network to fool the discriminator in accordance with the minmax problem defined in Eq. 2. The content loss compares the difference between the generated and true higher-resolution data, effectively conditioning the output of the generator network on the coarse input data. For this work, the content loss is defined by a mean-squared error (MSE) over the data field (i.e., pixelwise),
| [7] |
Fig. 2 contains an overview schematic of this GANs training procedure for SR. The networks are trained using the Adam optimizer (54) with gradients of the various loss functions computed by backpropagation.
Fig. 2.
Schematic of GANs.
The SRGAN model (48), which the proposed networks are based on, has set the standard for natural image perceptual quality in SR. SRGAN’s success comes from its deep CNN generator trained using a combination of adversarial losses and the use of perceptual losses. Perceptual losses are a type of content loss that compares output and target images through the lens of key intermediate layers of an auxiliary network, rather than comparing actual pixels themselves. Perceptual losses have been shown to produce more realistic images than traditional MSE losses (53, 55). In ref. 48, the VGG image classification network (56) is used for computing perceptual losses. Simple MSE losses are used here since the information captured by the VGG network is not appropriate for characterizing the key features in the climate data.
The generator network goes through two rounds of training. First, the network is “pretrained” with from Eq. 6 (i.e., the discriminator is removed from the training loop). This allows the generator to roughly learn the mapping from the coarse data to an enhanced resolution output. As we show in Results, the learned mapping tends to smooth out the field in a manner that minimizes the MSE content loss across the training data but produces fields that are not realistic. The discriminator is not trained during the pretraining process to give the generator an appropriate head start. After pretraining, the discriminator is brought into the loop with .
Theoretically, the GANs training procedure works best when the discriminator loss remains around 0.5 (i.e., it effectively cannot distinguish between the real and generated data). If the discriminator performs significantly below (or above) this range, then the generator does not gain any meaningful information from the adversarial training process. To maintain balance between the generator and discriminator, we employ an adaptive training scheme. If the discriminator loss exceeds 0.6 (i.e., the generator starts fooling the discriminator too well), then the discriminator is allowed to train for multiple iterations without updating the generator. Alternatively, the generator is given additional training if the discriminator loss drops below 0.45. Alternative approaches to maintaining this balance between the performance of the two networks (e.g., employing a fixed update ratio or relative learning rate for each network) would likely work as well.
The networks were trained using GPU-accelerated nodes on NREL Eagle computing system. For LR MR wind velocity data, we pretrained the generator network for 2,000 epochs through the 37,972 training examples, which took approximately 10 h. After pretraining was completed, we performed 200 epochs of GANs training over 55.5 h. The GANs training takes significantly longer than the pretraining because each iteration requires an update step for both the generator and discriminator networks. The MR HR step included 200 epochs of pretraining and 20 epochs of GANs training, taking approximately 32 and 240 h, respectively. The MR HR training process is much slower than the LR MR simply because of the difference in the size of the data fields. Training requires us to compute gradients with respect to the size of the enhance fields, which is significantly larger in the second step. The solar data enhancement networks were trained for a similar amount of time on the 45,109 training examples. Despite the long training times, the forward evaluation of the networks is very fast. The full LR MR HR process executes in minutes after the networks are trained, even for large data fields (e.g., continental or global scale).
Validation Methods.
During the training process, the discriminator learns to identify physically relevant characteristics of the training data, such as sharper gradients and specific small-scale structures. The adversarial training pushes the generator to produce outputs that reflect these characteristics. This can lead to increases in the content loss since insufficient information is present in the LR data to know the precise shape or location of these smaller features. This highlights the fact that the GANs are drawing from the conditional distributions of the HR data given an LR input. We examine the MSE of the test data in order to observe this fact. However, we can better validate that the network has learned the appropriate distribution for the climate wind data SR problem by using well-studied turbulent statistics.
When examining the results of the wind SR data, we can exploit known physical characteristics of turbulent flow to validate the data. First, the turbulent kinetic energy spectrum is used in turbulence theory to measure the distribution of energy across the various wave numbers, . For fully developed turbulent flows, energy is conserved in the inertial-range energy and cascades from larger scales to smaller scales leading to an energy spectrum that is proportional to (57–59). Additionally, we examine the probability density function (PDF) of the longitudinal velocity gradients. These distributions are characteristically non-Gaussian in turbulent flows and are indicative of small-scale intermittency. Further, the longitudinal velocity gradient is expected to have a skewness of approximately as is common for atmospheric flows (60).
Validating the enhanced solar data is a more difficult endeavor since these fields depend on cloud cover, pollution, and other particulates in the air for which we do not have a theoretical framework to lean on. In this work, we examine the MSE of the test data as well as a statistical analysis of the spatial autocorrelation. We characterize this autocorrelation using semivariograms, which are a popular tool for characterizing the spatial dependence in geospatial data (61). Semivariograms plot the lag function
| [8] |
for some spatially dependent field where is the total area of the field. This is essentially the mean variance of at some radius .
Results
SR of Wind Data.
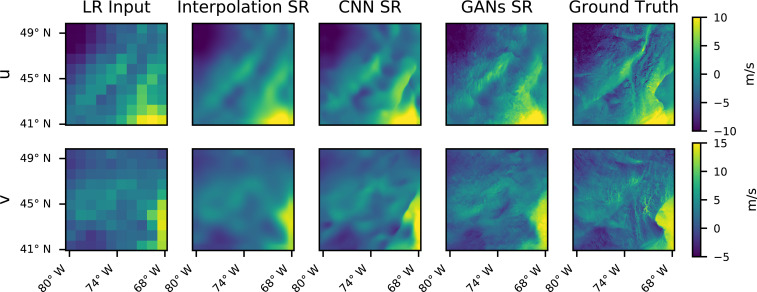
In this section, we explore the SR of wind velocity data from approximately 100- to 2-km resolution. The training data from this problem are composed of data from the WIND Toolkit coarsened to match the CCSM resolution. Fig. 3 contains results from the SR applied to unseen WIND Toolkit data held out as a separate test case. The figure depicts LR and HR wind velocities as well as three SR examples. The first SR field is generated using the naïve bicubic interpolation, which significantly smooths out the data. Next, the CNN SR example is the result of the pretraining process described in Data and Methodology. This SR data field is more physically realistic than the bicubic interpolation field, exhibiting sharper gradients and introducing some small structures similar to the corresponding HR data. Lastly, the GANs SR result produces data with very sharp gradients and significantly more refined small-scale features. This SR qualitatively appears to be the most comparable with the true HR data. Further, the small structures inserted by the GANs exhibit similar patterns and flow directionality as those found in the true data.
Fig. 3.
Comparison of various SR methods on WIND Toolkit data fields.
Table 2 compares the relative MSE of the easterly () and northerly () wind velocities across the WIND Toolkit test set for each of the SR methods. We note that both deep learning methods significantly outperform the bicubic interpolation with respect to this metric. However, the pretrained CNN actually results in a lower pixelwise error than the GANs-based method. The CNN is trained specifically to optimize this content-based loss, resulting in SR fields that are safer—that is, overly smoothed—predictions of the ground truth. The GANs approach changes the landscape of the loss function by adding in the adversarial term, which favors SR fields that are more physically consistent with the training data. The generator learns to make more aggressive predictions, inserting significantly more small-scale features that better represent the nature of the true wind velocity fields. However, these features also cause the SR field to deviate from the ground truth in an MSE sense since they cannot be inferred from the LR input.
Table 2.
Relative MSE of SR techniques on WIND Toolkit test data
| Quantity | Bicubic interpolation | Pretraining | Adversarial |
| 0.205 | 0.135 | 0.157 | |
| 0.265 | 0.168 | 0.193 |
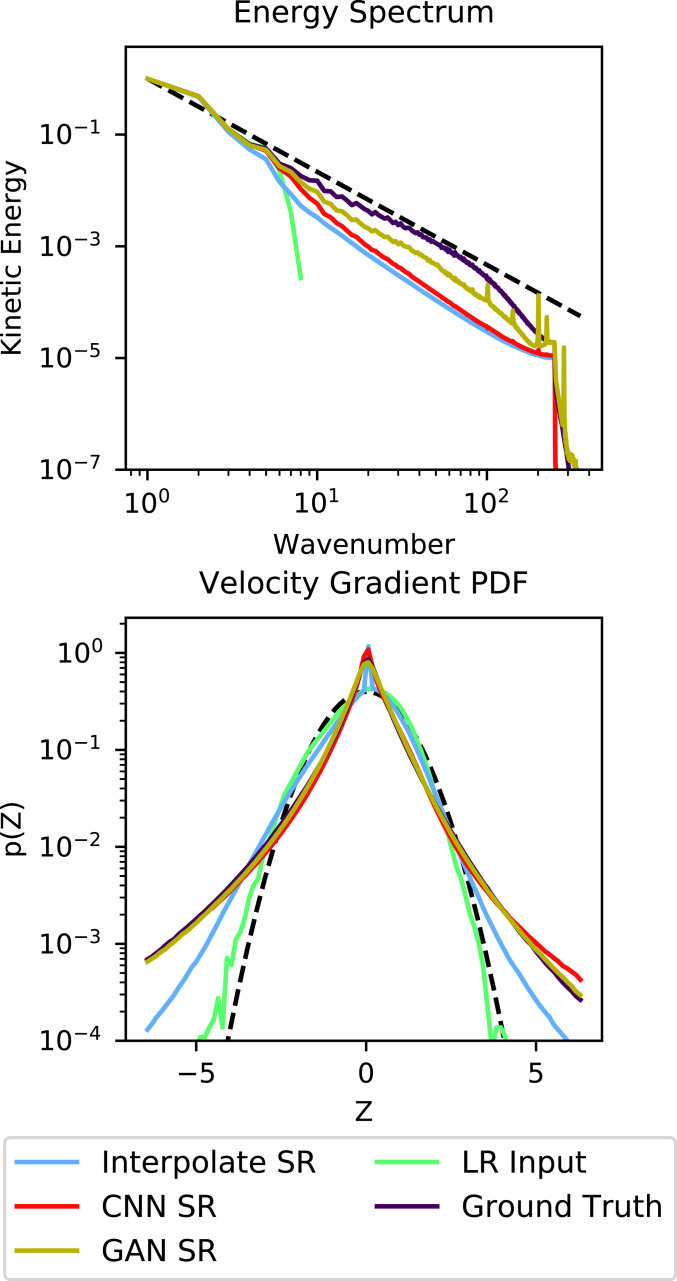
Given the degree of SR being performed and the significant amount of information being injected into the LR data, it is important to verify that the generated field contains physically realistic turbulence. The kinetic energy spectra and PDFs of normalized longitudinal velocity gradient for the various data fields are given in Fig. 4. The coarse input data only contain energy in the smallest wave numbers or largest scales, while the bicubic interpolated SR deviates substantially from the desired inertial-range behavior. The deep learning-based SR techniques improve the agreement with the ground truth in the inertial range, with the adversarial training step in the GANs providing a visible benefit at the highest wave numbers.
Fig. 4.
The kinetic energy spectra (Upper) and velocity gradient (Lower) PDFs for the various data fields. The Kolmogorov scaling (Upper) and a Gaussian PDF (Lower) are show with black dashed lines for reference.
The velocity gradient PDFs for turbulent flow fields theoretically should exhibit a heavy-tailed behavior with negative skewness (60). Our results show that the bicubic interpolation incorrectly preserves the Gaussian distribution of the coarse data, while the deep learning approaches produce the desired heavy-tailed shape and are in much better agreement with the ground truth. Again, we see benefit from the final adversarial training step in the GANs results, particularly in achieving the negative skewness.
Robustness of the SR Process.
Having validated that the GANs approach is generating physically realistic turbulent flow, we next turn to the question of robustness. The GANs methodology produces realizations of SR data conditioned on the given LR input.
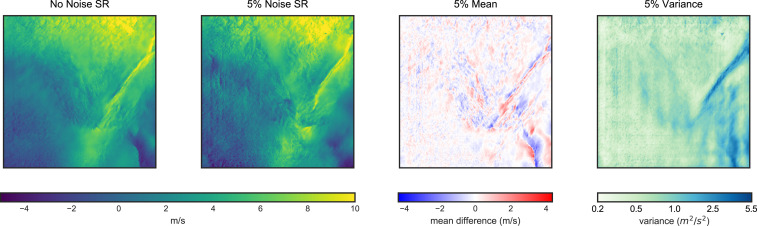
To ensure the results are robust to input noise, we perform SR on an ensemble of noise-corrupted LR fields from the WIND Toolkit. The results from the robustness study are given in Fig. 5. We generate 1,000 fields corrupted by Gaussian noise with 5% of the original data’s variance. Fig. 5 shows the SR output from the GANs trained network for the noiseless LR data and one with 5% noise corruption. We also show the mean and variance of the deviation of the SR noisy data fields from the noiseless case. These plots show that our method is stable in the presence of input noise and that most of the variation is in regions where sharp gradients are inserted. Since these gradients are not reflected in the LR data, it is reasonable that noise corruption could influence the nature of these features.
Fig. 5.
Corrupting the LR inputs with noise produces stable changes in the HR outputs at small scales in regions of high gradients.
Application to Climate Data.
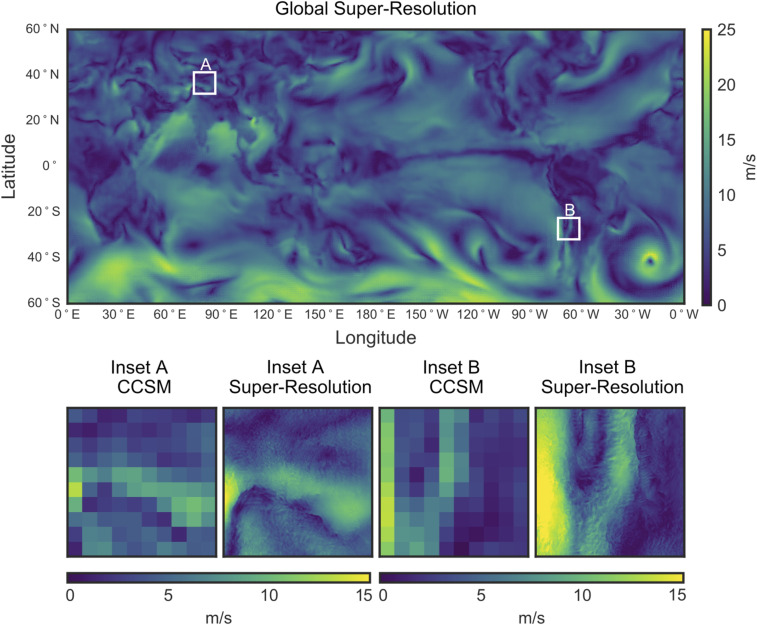
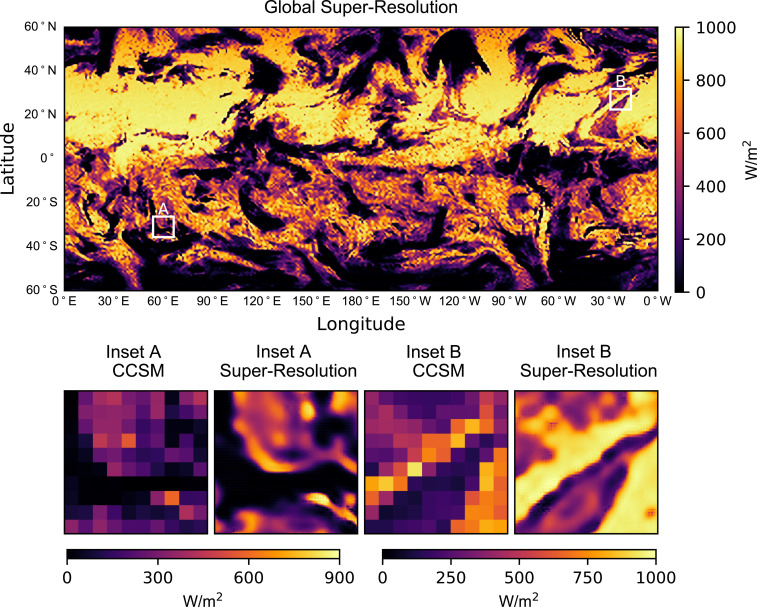
The final step in the SR process is to apply the trained network to the CCSM test data for which no ground truth HR data are available. Recall that the fully convolutional architecture of the generator network means that it can be trained on relatively small regions, such as those in Fig. 3, but the generator can be evaluated on data fields of any size. Fig. 6 shows SR field generated from CCSM data for the entire globe in a single-network evaluation. The original pixel size of the LR field is with a 100-km pixel resolution. The pixel size of the generated SR field is with a 2-km pixel resolution. The figure contains two callouts to highlight the quality of the features generated by the network. Although not shown here, the energy spectra and velocity gradient PDFs for the global SR field also show the correct turbulent flow characteristics. The full LR MR HR process takes about 4 min to evaluate for a global dataset such as this. Note that the network is applied to each time step of data individually so that the time resolution of the enhanced CCSM data remains the same.
Fig. 6.
The global super-resolved velocity magnitudes field for the CCSM data.
In the southern region of the SR global data, we observe a repeated gridded pattern occurring. This pattern is caused by a compression of the longitude/latitude-based mesh near the poles. This causes features in this region to appear stretched out compared with those near the equator. During the SR process, the network views these regions as especially smooth and repetitive, causing the network to inject similar small-scale features multiple times. This issue also appears slightly in the northern region; however, the depicted field has sufficient small-scale features to avoid the expansive flat regions that occur in the southern region. Thus, the gridded behavior is expected given the current formulation of the network, and exploring sensitivities to different projections is a future research direction.
SR of Solar Data.
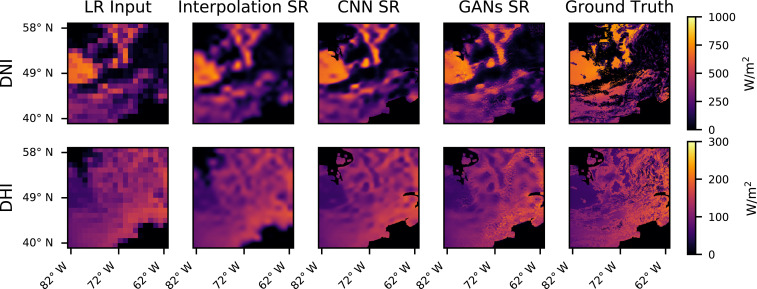
In this section, we examine the performance of this methodology in performing SR on solar irradiance data. Recall that the training data are constructed from coarsened NSRDB data fields for DNI and DHI. Since the spatial resolution of the NSRDB is approximately 4 km, the SR performed in this case is a enhancement. Fig. 7 shows LR, HR, and several examples of SR DNI and DHI data fields for a test sample from the NSRDB. In general, the results and interpretations are similar to those for the WIND Toolkit data. The deep learning approaches produce sharper gradients, more realistic structures, and a lower relative MSE than bicubic interpolation as reported in Table 3. The adversarially trained GANs SR network produces the most perceptually realistic data fields but incurs a slight penalty in the MSE relative to the pretraining CNN. This explanation for this behavior is the same as in Table 2.
Fig. 7.
Comparison of various SR methods on an NSRDB test field. The data field contains DNI and DHI data from 3 August 2012 at 12 PM.
Table 3.
Relative MSE of SR techniques on NSRDB test data
| Quantity | Bicubic interpolation | Pretraining | Adversarial |
| DNI | 0.155 | 0.078 | 0.086 |
| DHI | 0.135 | 0.073 | 0.085 |
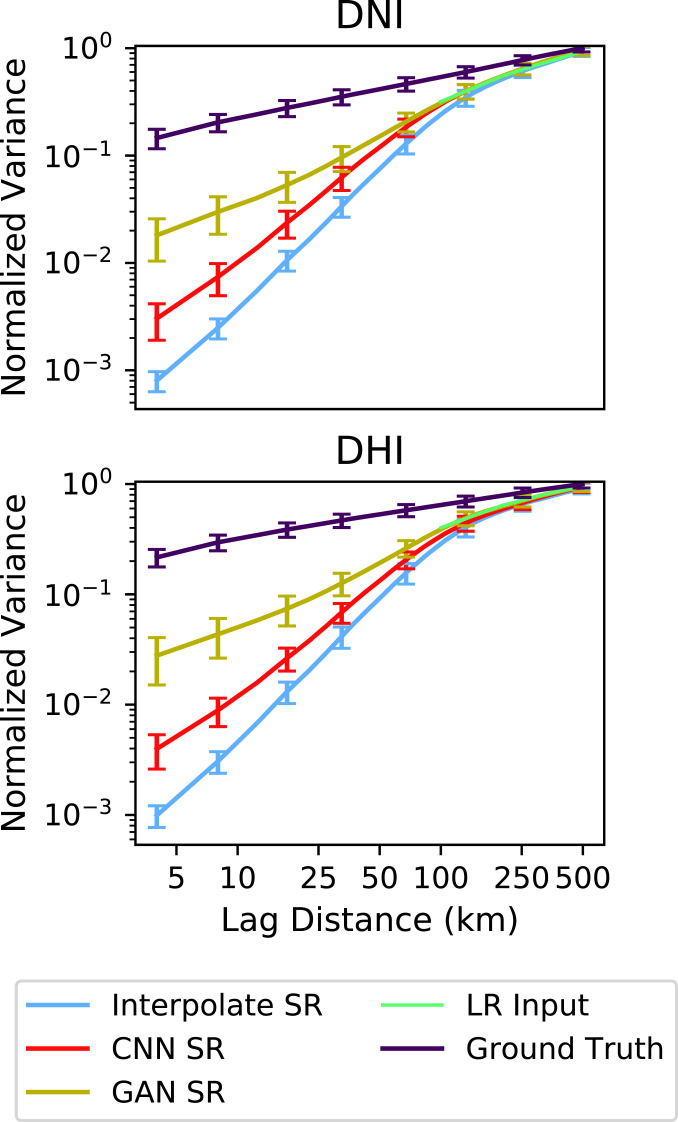
We next examine the spatial autocorrelation of the solar irradiance data using semivariograms. Recall that a semivariogram depicts the lag function from Eq. 8. Fig. 8 contains the mean semivariograms for the LR, HR, and various SR fields over the test NSRDB data normalized by the total variance in the data. Note that we plot the semivariograms using a log–log plot for the lag distance to emphasize the -km region. Recall that the coarse data have a resolution of 100 km per pixel, and note that the semivariogram for the LR input data begins with a lag distance of 100 km. Therefore, the -km region is of primary interest as this is where the SR process is generating new data. The smallest lag distance for the HR and SR data is km, corresponding to the resolution of these data fields.
Fig. 8.
Semivariogram for the enhanced NSRDB DNI (Upper) and DHI (Lower) data.
The semivariograms for the ground truth data show an initial jump in variance (referred to as the “nugget”) caused by the discontinuities in the data due to cloud cover. The interpolated SR and CCN SR are unable to capture the nugget. The adversarially trained SR does better at reproducing this initial jump by learning to replicate the types of small-scale textures and discontinuities in the solar irradiance data. However, it still undershoots the magnitude of the nugget as these structures are very difficult to infer based on the coarse inputs. The error bars on the plot show the SD across the test data. The small range in the sub–100-km regime suggests that the GANs method consistently outperforms the interpolated and the CNN SR at injecting small-scale details. Beyond 100 km, all of the SR methods perform approximately equally well as the long-range details from the input LR data dominate.
Lastly, we apply the full two-step SR process to the coarse CCSM solar data. The results of this for DNI are shown in Fig. 9. The shown field is for 15 March 2030 at 2 PM, and the LR field size is with a 100-km-pixel resolution. The resulting enhanced field is with a 4-km-pixel resolution. We include two callouts to zoom in on specific areas of interest. In these callouts, we see sharper boundaries forming that mimic the impact of cloud cover. We also see smaller textures that are more typical of the HR data from the NSRDB. The two-step resolution enhancement process takes less than 1 min to run for a given input field.
Fig. 9.
The global super-resolved DNI from the CCSM data for 15 March 2030 at 2 PM.
Discussion
These results demonstrate the power of GANs to perform impressive levels of spatial SR of climatological wind ( enhancement) and solar ( enhancement) data. The adversarial training approach learns the physically relevant features from the training data and ensures that the small-scale data injected during the SR process preserve these features for both wind and solar data. Because many HR fields can be consistent with a given LR field, the appropriate mindset when evaluating the SR output fields is not whether they match the underlying true HR data exactly but rather, that they are one of the possible valid HR fields corresponding to the given the LR input. This idea is shown in Figs. 3 and 4. The former shows that the GANs generate a wind velocity fields perceptually similar to, but not necessarily identical to, the corresponding true HR data. The latter demonstrates that the GANs-generated data match the expected turbulent fluid flow statistics in the newly generated scales, satisfying the criteria for a successful SR.
The HR data fields generated by this methodology immediately offer several key uses. GCMs are typically run for a variety of meteorological and policy scenarios. Enhancing the data using GANs is an inexpensive process after the network has been sufficiently trained. This enables the consideration of various climate scenarios in long-term grid planning and renewable energy resource assessments. Additionally, this technique can allow for decreased storage and computation requirements around climate modeling and can potentially be used to spin up simulations with nested computational grids.
Finally, these results demonstrate that GANs are useful for scientific data rather than just natural images and provide a pathway for physically consistent deep learning. The adversarial loss generates overall more realistic and physically relevant predictions than an approach that only focused on minimizing content loss. The idea of whether a generated field is physically consistent addresses a concept from image processing known as the perception–distortion trade-off (62). This trade-off argues that, while no distortion metric (e.g., MSE loss) is perfect, some are better than others at preserving the perceptual quality of image. This is the driving factor behind the use of the VGG16 network for perceptual losses to improve SR of photographic images (48, 53). However, the VGG16 network is not intended to capture features in turbulent flows or solar irradiance. The development of scientifically motivated perceptual loss networks could significantly enhance the performance of these deep learning techniques.
Future Research Directions.
This work offers a variety of research questions to be explored. Recall that the proposed GANs approach generates one plausible realization from the conditional distribution of HR data fields given the coarse input data. This naturally leads to questions related to the field of uncertainty quantification, which seeks to characterize the range of possible outcomes (63, 64). A thorough investigation of this conditional distribution could enhance the use of these data in localized resource assessment or in the generation of extreme events. This technique has been applied to generating specific handwritten digits (65), new images of objects and animals (66), and artwork drawn in a given style (67). The extension of this approach to data SR is nontrivial since the conditional values in this case (i.e., the lower-resolution input images) are high dimensional and continuous.
Another important research direction involves the question of enhancing the temporal resolution of the data. Recent work has made first steps toward addressing this issue by performing spatial SR in a temporally coherent manner (36); however, this work performed significantly smaller spatial SR than we presented here (4× vs. spatial SR). Additionally, the timescales for the turbulence simulations from ref. 36 are so that consecutive frames are highly correlated. The climate data under consideration here contain hourly/daily timescales, leading to significantly different data fields at each time step. Temporal SR goes beyond simple coherence by inserting entirely new snapshots of data (at the also-enhanced spatial resolution) in between given time steps of data. Such enhancements are important open questions in the field of data enhancement and would be beneficial for resource analysis.
Finally, we recall from Data and Methodology that the state-of-the-art SR for photographic images leverages the power perceptual loss functions. These are content-based losses constructed from a previously trained auxiliary network that identifies critical features in image data to improve the perceptual quality of the enhanced output. Currently, the VGG image classification network (56) serves as the primary tool for constructing these loss functions. This network was architected and trained specifically for photographic data and is therefore incompatible with the climate data studied here. However, the development of analogous domain-specific perceptual loss functions could improve the SR results presented here and enhance the performance of other data-driven methods.
Conclusion
In this work, we adapt adversarial deep learning techniques developed for SR in image processing to enhance climatological data. We present a deep fully convolutional neural network that increases the resolution of coarse 100-km climate data by for wind velocity and for solar irradiance data. The fully convolutional architecture of the network enables this technique to be applied to coarse data of any size. We train the wind and solar SR networks on coarsened WIND Toolkit and NSRDB data, respectively. We test the performance of these networks with respect to unseen test data and show that the adversarial training procedure ensures that the small-scale structures introduced by the generator network are physically consistent with those seen in the training data. In this way, the network is able to enhance coarse climate data, when no higher-resolution data exists, in a physically meaningful manner. Code for the networks as well as trained weights have been made available for use (14).
Data Availability.
Software for the trained networks as well as some example data are available on GitHub at https://github.com/NREL/PhIRE. Training data for this work were obtained through the NREL WIND Toolkit, which is available for download from https://www.nrel.gov/grid/wind-toolkit.html, and the NSRDB, which is available for download from https://nsrdb.nrel.gov. Test data come from the NCAR CCSM, which is available through https://esgf-node.llnl.gov/projects/esgf-llnl.
Acknowledgments
We acknowledge the World Climate Research Program’s Working Group which is responsible for the Coupled Model Intercomparison Project (CMIP), and we thank the climate modeling groups (listed in Table 1 of this paper) for producing and making available their model output. For CMIP, the US Department of Energy (DOE) Program for Climate Model Diagnosis and Intercomparison provides coordinating support and led development of software infrastructure in partnership with the Global Organization for Earth System Science Portals. This work was authored by the National Renewable Energy Laboratory (NREL), operated by Alliance for Sustainable Energy, LLC, for the US DOE under Contract DE-AC36-08GO28308. This work was supported by the Laboratory Directed Research and Development (LDRD) program at the NREL. The research was performed using computational resources sponsored by the DOE Office of Energy Efficiency and Renewable Energy and located at the NREL. The views expressed in the article do not necessarily represent the views of the DOE or the US Government. The US Government retains, and the publisher, by accepting the article for publication, acknowledges that the US Government retains a nonexclusive, paid-up, irrevocable, worldwide license to publish or reproduce the published form of this work, or allow others to do so, for US Government purposes.
Footnotes
The authors declare no competing interest.
This article is a PNAS Direct Submission. J.P. is a guest editor invited by the Editorial Board.
Data deposition: Software for the trained networks as well as some example data are available on GitHub at https://github.com/NREL/PhIRE.
References
- 1.Mideksa T. K., Kallbekken S., The impact of climate change on the electricity market: A review. Energy Pol. 38, 3579–3585 (2010). [Google Scholar]
- 2.Karnauskas K. B., Lundquist J. K., Zhang L., Southward shift of the global wind energy resource under high carbon dioxide emissions. Nat. Geosci. 11, 38–43 (2018). [Google Scholar]
- 3.Huber I., et al. , Do climate models project changes in solar resources?. Sol. Energy 129, 65–84 (2016). [Google Scholar]
- 4.Craig M. T., Carreño I. L., Rossol M., Hodge B. M., Brancucci C., Effects on power system operations of potential changes in wind and solar generation potential under climate change. Environ. Res. Lett. 14, 034014 (2019). [Google Scholar]
- 5.Craig M. T., et al. , A review of the potential impacts of climate change on bulk power system planning and operations in the United States. Renew. Sustain. Energy Rev. 98, 255–267 (2018). [Google Scholar]
- 6.Cox S. L., Lopez A. J., Watson A. C., Grue N. W., Leisch J. E., Renewable Energy Data, Analysis, and Decisions: A Guide for Practitioners (National Renewable Energy Lab., Golden, CO, 2018). [Google Scholar]
- 7.O’Gorman P. A., Dwyer J. G., Using machine learning to parameterize moist convection: Potential for modeling of climate, climate change, and extreme events. J. Adv. Model. Earth Syst. 10, 2548–2563 (2018). [Google Scholar]
- 8.Belochitski A., et al. , Tree approximation of the long wave radiation parameterization in the NCAR CAM global climate model. J. Comput. Appl. Math. 236, 447–460 (2011). [Google Scholar]
- 9.Rasp S., Pritchard M. S., Gentine P., Deep learning to represent subgrid processes in climate models. Proc. Natl. Acad. Sci. U.S.A. 115, 9684–9689 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Krasnopolsky V. M., Fox-Rabinovitz M. S., Belochitski A. A., “Development of neural network convection parameterizations for numerical climate and weather prediction models using cloud resolving model simulations” in The 2010 International Joint Conference on Neural Networks (IJCNN) (IEEE, 2010), pp. 1–8. [Google Scholar]
- 11.Brenowitz N. D., Bretherton C. S., Prognostic validation of a neural network unified physics parameterization. Geophys. Res. Lett. 45, 6289–6298 (2018). [Google Scholar]
- 12.Chevallier F., Chéruy F., Scott N., Chédin A., A neural network approach for a fast and accurate computation of a longwave radiative budget. J. Appl. Meteorol. 37, 1385–1397 (1998). [Google Scholar]
- 13.Reichstein M., et al. , Deep learning and process understanding for data-driven earth system science. Nature 566, 195–204 (2019). [DOI] [PubMed] [Google Scholar]
- 14.Stengel K., Glaws A., Hettinger D., King R., Code for “Adversarial super-resolution of climatological wind and solar data.” GitHub. https://github.com/NREL/PhIRE. Deposited 3 April 2020. [DOI] [PMC free article] [PubMed]
- 15.Yang C. Y., Ma C., Yang M. H., “Single-image super-resolution: A benchmark” in European Conference on Computer Vision (Springer, 2014), pp. 372–386. [Google Scholar]
- 16.Fattal R., Image upsampling via imposed edge statistics. ACM Trans. Graph. 26, 95 (2007). [Google Scholar]
- 17.Dai S., Han M., Xu W., Wu Y., Gong Y., “Soft edge smoothness prior for alpha channel super resolution” in Conference on Computer Vision and Pattern Recognition (Citeseer, 2007), vol. 7, pp. 1–8. [Google Scholar]
- 18.Sun J., Xu Z., Shum H. Y., “Image super-resolution using gradient profile prior” in 2008 IEEE Conference on Computer Vision and Pattern Recognition (IEEE, 2008), pp. 1–8. [Google Scholar]
- 19.Kim K. I., Kwon Y., Single-image super-resolution using sparse regression and natural image prior. IEEE Trans. Pattern Anal. Mach. Intell. 32, 1127–1133 (2010). [DOI] [PubMed] [Google Scholar]
- 20.Huang J., Mumford D., “Statistics of natural images and models” in Proceedings of the 1999 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (Cat. No PR00149) (IEEE, 1999), vol. 1, pp. 541–547. [Google Scholar]
- 21.Aly H. A., Dubois E., Image up-sampling using total-variation regularization with a new observation model. IEEE Trans. Image Process. 14, 1647–1659 (2005). [DOI] [PubMed] [Google Scholar]
- 22.Ni K. S., Nguyen T. Q., Image superresolution using support vector regression. IEEE Trans. Image Process. 16, 1596–1610 (2007). [DOI] [PubMed] [Google Scholar]
- 23.He H., Siu W. C., “Single image super-resolution using Gaussian process regression” in CVPR 2011 (IEEE, 2011), pp. 449–456. [Google Scholar]
- 24.Xu Cy., From GCMs to river flow: A review of downscaling methods and hydrologic modelling approaches. Prog. Phys. Geogr. 23, 229–249 (1999). [Google Scholar]
- 25.Wilby R. L., et al. , “Guidelines for use of climate scenarios developed from statistical downscaling methods” in Supporting Material of the Intergovernmental Panel on Climate Change (2004). http://www.ipcc-data.org/guidelines/dgm_no2_v1_09_2004.pdf. Accessed 22 June 2020. [Google Scholar]
- 26.Kaheil Y. H., Gill M. K., McKee M., Bastidas L. A., Rosero E., Downscaling and assimilation of surface soil moisture using ground truth measurements. IEEE Trans. Geosci. Rem. Sens. 46, 1375–1384 (2008). [Google Scholar]
- 27.Rockel B., Castro C. L., Pielke R. A. Sr, von Storch H., Leoncini G., Dynamical downscaling: Assessment of model system dependent retained and added variability for two different regional climate models. J. Geophys. Res. Atmos. 113, D21107 (2008). [Google Scholar]
- 28.Dong C., Loy C. C., He K., Tang X., “Learning a deep convolutional network for image super-resolution” in European Conference on Computer Vision (Springer, 2014), pp. 184–199. [Google Scholar]
- 29.Dong C., Loy C. C., He K., Tang X., Image super-resolution using deep convolutional networks. IEEE Trans. Pattern Anal. Mach. Intell. 38, 295–307 (2015). [DOI] [PubMed] [Google Scholar]
- 30.Kim J., Kwon Lee J., Mu Lee K., “Deeply-recursive convolutional network for image super-resolution” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (IEEE, 2016), pp. 1637–1645. [Google Scholar]
- 31.Kim J., Lee J. K., Lee K. M., “Accurate image super-resolution using very deep convolutional networks” in 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR) (IEEE, 2016), pp. 1646–1654. [Google Scholar]
- 32.Pouliot D., Latifovic R., Pasher J., Duffe J., Landsat super-resolution enhancement using convolution neural networks and Sentinel-2 for training. Rem. Sens. 10, 394 (2018). [Google Scholar]
- 33.Ducournau A., Fablet R., “Deep learning for ocean remote sensing: An application of convolutional neural networks for super-resolution on satellite-derived SST data” in 2016 9th IAPR Workshop on Pattern Recogniton in Remote Sensing (PRRS) (IEEE, 2016), pp. 1–6. [Google Scholar]
- 34.Onishi R., Sugiyama D., Matsuda K., Super-resolution simulation for real-time prediction of urban micrometeorology. arXiv:1902.05631 (14 February 2019).
- 35.Fukami K., Fukagata K., Taira K., Super-resolution reconstruction of turbulent flows with machine learning. J. Fluid Mech. 870, 106–120 (2019). [Google Scholar]
- 36.Xie Y., Franz E., Chu M., Thuerey N., tempoGAN: A temporally coherent, volumetric GAN for super-resolution fluid flow. ACM Trans. Graph. 37, 95 (2018). [Google Scholar]
- 37.Rodrigues E. R., Oliveira I., Cunha R., Netto M., “DeepDownscale: A deep learning strategy for high-resolution weather forecast” in 2018 IEEE 14th International Conference on E-Science (E-Science) (IEEE, 2018), pp. 415–422. [Google Scholar]
- 38.Vandal T., Ganguly A. R., “DeepSD: Generating high resolution climate change projections through single image super-resolution” in Proceedings of the 23rd ACM KDD’17 International Conference on Knowledge Discovery and Data Mining (ACM, 2017), pp. 1663–1672. [Google Scholar]
- 39.Meehl G. A., CCSM4 model run for CMIP5 with 1% increasing CO2 (served by ESGF [Data set]) (Version 2, World Data Center for Climate at DKRZ, 2014).
- 40.Taylor K. E., Stouffer R. J., Meehl G. A., An overview of CMIP5 and the experiment design. Bull. Am. Meteorol. Soc. 93, 485–498 (2012). [Google Scholar]
- 41.Draxl C., Hodge B., Clifton A., McCaa J., Overview and Meteorological Validation of the Wind Integration National Dataset Toolkit (National Renewable Energy Lab., Golden, CO, 2015). [Google Scholar]
- 42.Draxl C., Clifton A., Hodge B. M., McCaa J., The wind integration national dataset (WIND Toolkit). Appl. Energy 151, 355–366 (2015). [Google Scholar]
- 43.Lieberman-Cribbin W., Draxl C., Clifton A., Guide to Using the WIND Toolkit Validation Code (National Renewable Energy Lab., Golden, CO, 2014). [Google Scholar]
- 44.King J., Clifton A., Hodge B. M., Validation of Power Output for the WIND Toolkit (National Renewable Energy Lab., Golden, CO, 2014). [Google Scholar]
- 45.Sengupta M., Shelby J., The national solar radiation data base (NSRDB). Renew. Sustain. Energy Rev. 89, 51–60 (2018). [Google Scholar]
- 46.Maxwell E. L., “A quasi-physical model for converting hourly global horizontal to direct normal insolation” (Rep. SERI/TR-215-3087, Solar Energy Research Institute, Golden, CO, 1987).
- 47.Aguiar R., Collares-Pereira M., TAG: A time-dependent, autoregressive, Gaussian model for generating synthetic hourly radiation. Sol. Energy 49, 167–174 (1992). [Google Scholar]
- 48.Ledig C., et al. , “Photo-realistic single image super-resolution using a generative adversarial network” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (IEEE, 2017), pp. 4681–4690. [Google Scholar]
- 49.Springenberg J. T., Dosovitskiy A., Brox T., Riedmiller M., Striving for simplicity: The all convolutional net. arXiv:1412.6806 (13 April 2015).
- 50.He K., Zhang X., Ren S., Sun J., “Deep residual learning for image recognition” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (IEEE, 2016), pp. 770–778. [Google Scholar]
- 51.He K., Zhang X., Ren S., Sun J., “Identity mappings in deep residual networks” in European Conference on Computer Vision (Springer, 2016), pp. 630–645. [Google Scholar]
- 52.Goodfellow I., Bengio Y., Generative adversarial nets. Adv. Neural. Inf. Process. Syst. 2014, pp. 2672–2680 (2014). [Google Scholar]
- 53.Johnson J., Alahi A., Fei-Fei L., “Perceptual losses for real-time style transfer and super-resolution” in European Conference on Computer Vision (Springer, 2016), pp. 694–711. [Google Scholar]
- 54.Kingma D. P., Ba J., Adam: A method for stochastic optimization. arXiv:1412.6980 (30 January 2017).
- 55.Wang C., Xu C., Wang C., Tao D., Perceptual adversarial networks for image-to-image transformation. IEEE Trans. Image Process. 27, 4066–4079 (2018). [DOI] [PubMed] [Google Scholar]
- 56.Simonyan K., Zisserman A., Very deep convolutional networks for large-scale image recognition. arXiv:1409.1556 (10 April 2015).
- 57.Kolmogorov A. N., The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers. Proc. Roy. Soc. Lond. Math. Phys. Sci. 434, 9–13 (1991). [Google Scholar]
- 58.Kolmogorov A. N., On degeneration (decay) of isotropic turbulence in an incompressible viscous liquid in Dokl. Akad. Nauk SSSR. 31, 538–540 (1941). [Google Scholar]
- 59.Kolmogorov A. N., Dissipation of energy in locally isotropic turbulence. Dokl. Akad. Nauk SSSR. 32, 16 (1941). [Google Scholar]
- 60.Sreenivasan K. R., Antonia R., The phenomenology of small-scale turbulence. Annu. Rev. Fluid Mech. 29, 435–472 (1997). [Google Scholar]
- 61.Matheron G., Principles of geostatistics. Econ. Geol. 58, 1246–1266 (1963). [Google Scholar]
- 62.Blau Y., Tomer M., “The perception-distortion tradeoff” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (IEEE, 2018). [Google Scholar]
- 63.Sullivan T. J., Introduction to Uncertainty Quantification (Springer, 2015), vol. 63. [Google Scholar]
- 64.Smith R. C., Uncertainty Quantification: Theory, Implementation, and Applications (Siam, 2013), vol. 12. [Google Scholar]
- 65.Mirza M., Osindero S., Conditional generative adversarial nets. arXiv:1411.1784 (6 November 2014).
- 66.Denton E., Chintala S., Szlam A., Fergus R., Deep generative image models using a Laplacian pyramid of adversarial networks. Adv. Neural. Inf. Process. Syst. 2015, pp. 1486–1494 (2015). [Google Scholar]
- 67.Tan W. R., Chan C. S., Aguirre H. E., Tanaka K., “ArtGAN: Artwork synthesis with conditional categorical GANs” in 2017 IEEE International Conference on Image Processing (ICIP) (IEEE, 2017), pp. 3760–3764. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Software for the trained networks as well as some example data are available on GitHub at https://github.com/NREL/PhIRE. Training data for this work were obtained through the NREL WIND Toolkit, which is available for download from https://www.nrel.gov/grid/wind-toolkit.html, and the NSRDB, which is available for download from https://nsrdb.nrel.gov. Test data come from the NCAR CCSM, which is available through https://esgf-node.llnl.gov/projects/esgf-llnl.